结构动力学哈工大版课后习题集解答
结构力学课后答案第10章结构动力学

解:
若 为静力荷载,弹簧中反力为 。
已知图示体系为静定结构,具有一个自由度。设为B点处顺时针方向转角 为坐标。建立动力方程:
则弹簧支座的最大动反力为 。
10-21设图a所示排架在横梁处受图b所示水平脉冲荷载作用,试求各柱所受的最大动剪力。已知EI=6×106Nm2,t1=,FP0=8×104N。
(a)
则同样有: 。
10-9图示结构AD和DF杆具有无限刚性和均布质量 ,A处转动弹簧铰的刚度系数为kθ,C、E处弹簧的刚度系数为k,B处阻尼器的阻尼系数为c,试建立体系自由振动时的运动方程。
*
解:
取DF隔离体, :
取AE隔离体:
将R代入,整理得:
/
10-10试建立图示各体系的运动方程。
(a)
解:(1)以支座B处转角作为坐标,绘出梁的位移和受力图如下所示。图中惯性力为三角形分布,方向与运动方向相反。
图 图
(1)求结构运动方程
如所示弯矩图,图乘后,
其中 ,稳态解:
所示结构的运动方程为 ,C点最大动位移幅值为
(2)求B点的动位移反应
,
!
B点的动位移幅值为
(3)绘制最大动力弯矩图
图 图
最大动力弯矩图
10-20试求图示集中质量体系在均布简谐荷载作用下弹簧支座的最大动反力。设杆件为无限刚性,弹簧的刚度系数为k。
(2)画出 和 图(在B点处作用一附加约束)
…
(3)列出刚度法方程
, ,
代入 、 的值,整理得:
(b)
解:
图 图
】
试用柔度法解题
此体系自由度为1 。设质量集中处的竖向位移y为坐标。
y是由动力荷载 和惯性力矩 共同引起的。
哈尔滨工业大学结构力学答案四

哈尔滨工业大学结构力学答案(开卷,时间:120分钟)(所有答案必须写在答题纸上)一、是非题(每题4分共20分,正确的标〇,错误的标 )1.瞬变体系一定具有多余约束( 〇 )2.影响线的横坐标表示移动荷载移动的位置( 〇 )3.用图乘法可以求抛物线拱的顶点竖向位移( )4.力矩分配法的分配系数与荷载有关( )5.杆系结构的单元刚度矩阵具有对称性(〇)二、选择题(每题4分共20分,将正确的答案的字母填在空内)1.静定结构由于安装误差将(B)A. 无内力无位移;B. 无内力有位移;C. 有内力有位移;D. 有内力无位移。
2.水压力作用下,三铰拱的合理拱轴线为(A)A. 圆弧线;B. 抛物线;C. 正弦曲线;D. 三角形。
3.位移法基本结构的物理意义是(D)A. 几何条件;B. 物理条件;C. 外力条件;D. 平衡条件。
4.单自由度体系固有周期表示(B)A. 反应约束的参数;B. 振动一次所用时间;C. 反应结构尺寸的参数;D. 单位时间内振动次数。
5.在温度作用下超静定结构内力与哪些参数无关( D )A. 各杆的绝对刚度;B. 各杆的使用材料;C. 各杆的截面高度;D. 各杆的截面宽度。
三、填空题(每题2分共10分,将正确的叙述填在空内)1.三铰拱结构的受力特点是(在竖向荷载作用下能产生水平方向约束力)2.单元刚度矩阵表示(杆端力)与(杆端位移)之间的变换矩阵3.力矩分配法适用于求解(无结点线位移的)结构。
4.超静定梁在竖向荷载作用下内力包括(弯矩和剪力)5.单自由度体系频率的平方与刚度成(正比例)关系。
四、 计算题(共50分)1. (本题9分)计算并绘制图示刚架的弯矩图、剪力图和轴力图。
2. (本题9分)求图示桁架BC 杆的转角位移(各杆刚度EA = 常数)。
P2(1DH F EA∆=+题1图 M 弯矩图 2M 剪力图 M/l Ө 轴力图 M/lӨ3. (本题8分)用力法计算并绘制图示刚架的弯矩图(EI =常数)。
机械结构有限元分析第二章课后答案 哈工大

σ = 140 MPa
τ=
20 − (−40) sin(−2 × 45 � ) + 20 cos 2(−2 × 45 � ) = −30MPa 2
⎡6 4 0⎤ ⎥ 2.6 相对于 xyz 坐标系,一点的应力如下 σ = ⎢ ⎢4 − 3 0⎥ ,某表面的外法线方向余弦 ⎢ ⎣ 0 0 3⎥ ⎦
n x = n y = 6 / 11 , n z = 7 / 11 ,求该表面的法向和切向应力。
解: u = y × 10
2 2
∂u =0 ∂x
∂u = 2 y × 10 2 ∂y ∂u =0 ∂z
点 P (1,0,2 ) 处,线应变为
εx =
∂u =0 ∂x
点 P (1,0,2 ) 处,剪应变为
ww 课 w. 后 ha 答 ck 案 sh 网 p. cn
[
( )]
v = 3 yz × 10 2
x3 y q ⎛ 6 ⎞ σ x = q 3 + 3 ⎜ − 2 xy 3 + c 2 xy ⎟ 5 4c 4c ⎝ ⎠ σ y = −q
⎛ y3 3y ⎞ x + qx⎜ ⎜ 4c 3 − 4c ⎟ ⎟ 2 ⎝ ⎠
τ xy =
3qx 2 2 q q 3 c − y2 − 3 c4 − y4 + 3 c2 c2 − y2 3 8c 8c 4c 5
常量。为了使应力场满足平衡方程和相容方程,这些常量的约束条件是什么?
解:
∂σ x = 2byx − c ∂x
∂σ x = 3ay 2 + bx 2 ∂y
得 2by + 6ay + 0 + 6dy = 0 即 b + 3a + 3d = 0
结构动力学-习题解答
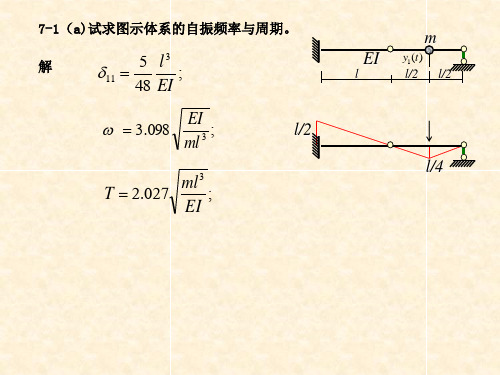
7-1(a)试求图示体系的自振频率与周期。
解
11
5 48
l3 EI
;
3.098
EI ml 3
;
l/2
T 2.027
ml 3 ;
7-6 某结构在自振10个周期后,振幅降为原来初始位移的10% (初位移为零),试求其阻尼比。
解: 1 ln10 0.0366 2 10
8-1试求图示梁的自振频率和振型。 m
y1(t)
解
EI 2m
a
a
y2
(t
)
a
12
21
1 4
a3 EI
a
I 2 m 0
11m1 1/ 2
m212
0
m1 21
22m2 1/ 2
1 1.153
a/2
2 0.181
令
1
11m1
2
1 1/ 2
0
1/ 4 1/3 2 4 / 3 5 / 24 0
x11 / x21 3.277; x12 / x22 0.61
;
9l / 64 (a)
5l / 32
11.817
EI ml 3 ;
l/2
T 0.531
ml3 ;
(b)
EI
7-1(c)试求图示体系的自振频率与周期。
m 刚性杆
解 由右面竖杆的平衡可求出铰处约束力。
EI
由水平杆的平衡:
《结构力学习题集》(下)-结构的动力计算习题及答案

第九章 结构的动力计算一、判断题:1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
4、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
5、图示刚架不计分布质量和直杆轴向变形,图a 刚架的振动自由度为2,图b 刚架的振动自由度也为2。
6、图示组合结构,不计杆件的质量,其动力自由度为5个。
7、忽略直杆的轴向变形,图示结构的动力自由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率,ω与ωD 的关系为ωω=D 。
二、计算题:10、图示梁自重不计,求自振频率ω。
l l /411、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k ,求自振频率ω。
l /2l /212、求图示体系的自振频率ω。
l l0.5l 0.513、求图示体系的自振频率ω。
EI = 常数。
ll 0.514、求图示结构的自振频率ω。
l l15、求图示体系的自振频率ω。
EI =常数,杆长均为l 。
16、求图示体系的自振频率ω。
杆长均为l 。
17、求图示结构的自振频率和振型。
l /2l /2l /18、图示梁自重不计,W EI ==⨯⋅2002104kN kN m 2,,求自振圆频率ω。
B2m2m19、图示排架重量W 集中于横梁上,横梁EA =∞,求自振周期ω。
EIEIW20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
EIEIWEI 221、求图示体系的自振频率ω。
各杆EI = 常数。
a aa22、图示两种支承情况的梁,不计梁的自重。
求图a 与图b 的自振频率之比。
l /2l/2(a)l /2l /2(b)23、图示桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求水平自振周期T 。
结构动力学1~15

《结构动力学》习题答案1~151. 1简述求多自由度体系时程反应的振型叠加法的主要步骤 答1)建立多自由度体系的运动方程)()()()(t p t kv t v c t vm =++ 2)进行振型和频率分析对无阻尼自由振动,这个矩阵方程能归结为特征问题)(ˆ2t p vm k =-ω 由此确定振型矩阵φ和频率向量ω 3)求广义质量和荷载依次取每一个振型向量n φ,计算每一个振型的广义质量和广义荷载n T n nm Mφφ= )()(t p t p Tn n φ=4)求非耦合运动方程用每个振型的广义质量、广义力、振型频率n ω和给定的振型阻尼比n ξ就能写出每一个振型的运动方程2)(2)(ωωξ++t Y t Y n n n n nn nMt P t Y )()(=5)求对荷载的振型反应根据荷载类型,用适当的方法解这些单自由度方程,每一个振型的一般动力反应表达式用Duhamel 积分给出ττωτωξτωd t t P M t Y Dn n n tn nn n )(sin )](exp[)(1)(0---=⎰写出标准积分形式τττd t h P t Y n tn n )()()(0-=⎰式中)](exp[)(sin 1)(τωξτωωτ---=-t t M t h n n Dn nn n 10<<n ξ6)振型自由振动每一个振型有阻尼自由振动反应的通式为)exp[]sin )0()0(cos )0([)(t t Y Y t Y t Y n n Dn Dnnn n n Dn n n ωξωωωξω-++=7)求在几何坐标中的位移反应通过正规坐标变换求几何坐标表示的位移式)()()()(2211t Y t Y t Y t V n n φφφ+++=显然,它反映了各个振型贡献的叠加。
因此命名为振型叠加法。
8)弹性力反应抵抗结构变形的弹性力)()()(t Y k t kv t f s φ==当频率、振型从柔度形式的特征方程中求出时,可以采用另一种弹性力的表达式。
哈工大_结构力学_第一章习题答案解密版
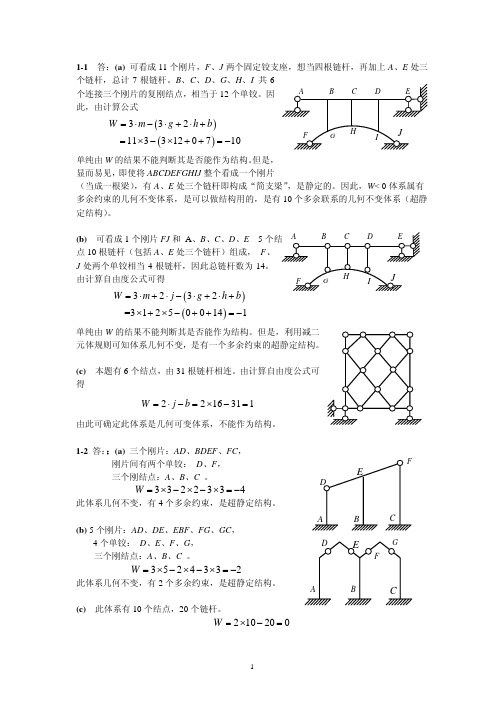
1-1 答:(a) 可看成11个刚片,F 、J 两个固定铰支座,想当四根链杆,再加上A 、E 处三个链杆,总计7根链杆。
B 、C 、D 、G 、H 、I 共6个连接三个刚片的复刚结点,相当于12个单铰。
因此,由计算公式()()20710h b +⋅+++=−33 113312W m g =⋅−⋅=×−×(单纯由W 的结果不能判断其是否能作为结构。
但是,显而易见,即使将ABCDEFGHIJ 整个看成一个刚片(当成一根梁),有A 、E 处三个链杆即构成“简支梁”,是静定的。
因此,W < 0体系属有多余约束的几何不变体系,是可以做结构用的,是有10个多余联系的几何不变体系(超静定结构)。
(b) 可看成1个刚片FJ 和 A 、B 、C 、D 、E 5点10根链杆(包括A 、E 处三个链杆)组成, F 、J 处两个单铰相当4根链杆,因此总链杆数为14。
由计算自由度公式可得 )()3232 =312500141W m j g h b =⋅+⋅−⋅+⋅+×+×−++=−W j单纯由W 的结果不能判断其是否能作为结构。
但是,利用减二元体规则可知体系几何不变,是有一个多余约束的超静定结构。
(c) 本题有6个结点,由31根链杆相连。
由计算自由度公式可得2216311b =⋅−332W =×−×3524332W =×−×−×=−210200W =×−=由此可确定此体系是几何可变体系,不能作为结构。
1-2 答::(a) 三个刚片:AD 、BDEF 、FC ,刚片间有两个单铰: D 、F , 三个刚结点:A 、B 、C 。
2334−×=−此体系几何不变,有4个多余约束,是超静定结构。
(b) 5个刚片:AD 、DE 、EBF 、FG 、GC ,4个单铰: D 、E 、F 、G ,三个刚结点:A 、B 、C 。
【推荐】理论力学(哈工大版)课后的习题答案.doc

理论力学作业答案第一章静力学公理和物体的受力分析1-11-2第二章平面汇交力系与平面力偶系第三章平面任意力系第四章空间力系第五章摩擦第六章点的运动学第七章刚体的简单运动第八章点的合成运动第九章刚体的平面运动第十章质点动力学的基本方程第十一章动量定理第十二章动量矩定理第十三章动能定理赠送以下资料考试知识点技巧大全一、考试中途应饮葡萄糖水大脑是记忆的场所,脑中有数亿个神经细胞在不停地进行着繁重的活动,大脑细胞活动需要大量能量。
科学研究证实,虽然大脑的重量只占人体重量的2%-3%,但大脑消耗的能量却占食物所产生的总能量的20%,它的能量来源靠葡萄糖氧化过程产生。
据医学文献记载,一个健康的青少年学生30分钟用脑,血糖浓度在120毫克/100毫升,大脑反应快,记忆力强;90分钟用脑,血糖浓度降至80毫克/100毫升,大脑功能尚正常;连续120分钟用脑,血糖浓度降至60毫克/100毫升,大脑反应迟钝,思维能力较差。
我们中考、高考每一科考试时间都在2小时或2小时以上且用脑强度大,这样可引起低血糖并造成大脑疲劳,从而影响大脑的正常发挥,对考试成绩产生重大影响。
因此建议考生,在用脑60分钟时,开始补饮25%浓度的葡萄糖水100毫升左右,为一个高效果的考试加油。
二、考场记忆“短路”怎么办呢?对于考生来说,掌握有效的应试技巧比再做题突击更为有效。
1.草稿纸也要逐题顺序写草稿要整洁,草稿纸使用要便于检查。
不要在一大张纸上乱写乱画,东写一些,西写一些。
打草稿也要像解题一样,一题一题顺着序号往下写。
最好在草稿纸题号前注上符号,以确定检查侧重点。
为了便于做完试卷后的复查,草稿纸一般可以折成4-8块的小方格,标注题号以便核查,保留清晰的分析和计算过程。
结构动力学哈工大版课后习题解答

第一章 单自由度系统1.1 总结求单自由度系统固有频率的方法和步骤。
单自由度系统固有频率求法有: 牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守恒定理法。
1. 牛顿第二定律法适用范围: 所有的单自由度系统的振动。
解题步骤: (1) 对系统进行受力分析,得到系统所受的合力;(2) 利用牛顿第二定律∑=F x m,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根, 得到该系统的固有频率。
2. 动量距定理法适用范围: 绕定轴转动的单自由度系统的振动。
解题步骤: (1) 对系统进行受力分析和动量距分析;(2) 利用动量距定理J ∑=M θ,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根, 得到该系统的固有频率。
3. 拉格朗日方程法:适用范围: 所有的单自由度系统的振动。
解题步骤: (1)设系统的广义坐标为 , 写出系统对于坐标 的动能T 和势能U 的表达式;进一步写求出拉格朗日函数的表达式: L=T-U ;(2)由格朗日方程 =0, 得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根, 得到该系统的固有频率。
4. 能量守恒定理法适用范围: 所有无阻尼的单自由度保守系统的振动。
解题步骤: (1)对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能T 和势能U 的表达式;进一步写出机械能守恒定理的表达式 T+U=Const (2)将能量守恒定理T+U=Const 对时间求导得零,即 , 进一步得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根, 得到该系统的固有频率。
1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。
用衰减法求单自由度系统阻尼比的方法有两个: 衰减曲线法和共振法。
方法一: 衰减曲线法。
求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线, 并测得周期和相邻波峰和波谷的幅值 、 。
(2)由对数衰减率定义 , 进一步推导有,因为 较小, 所以有πδζ2=。
结构动力学习题解答(三四章)
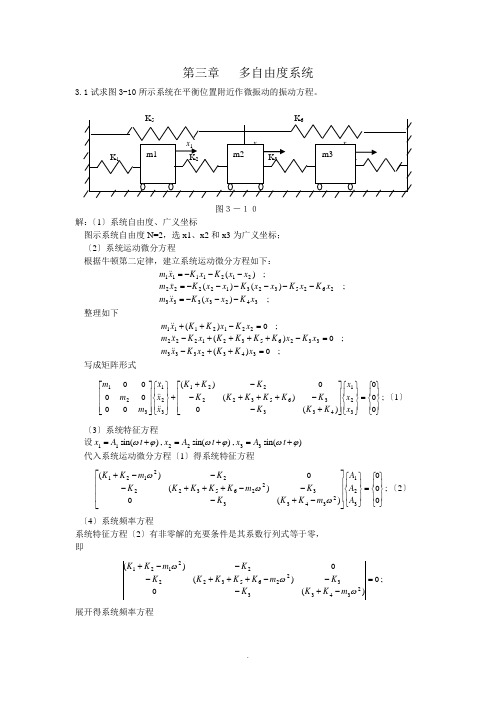
第三章 多自由度系统3.1试求图3-10所示系统在平衡位置附近作微振动的振动方程。
图3-10解:〔1〕系统自由度、广义坐标图示系统自由度N=2,选x1、x2和x3为广义坐标; 〔2〕系统运动微分方程根据牛顿第二定律,建立系统运动微分方程如下:;)(;)()(;)(34233332625323122222121111x K x x K x m x K x K x x K x x K xm x x K x K xm ---=------=---= 整理如下;0)(;0)(;0)(3432333332653212222212111=++-=-++++-=-++x K K x K xm x K x K K K K x K xm x K x K K xm 写成矩阵形式;000)(0)(0)(00000321433365322221321321⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+++--++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡x x x K K K K K K K K K K K K x x x m m m 〔1〕 〔3〕系统特征方程设)sin(,)sin(,)sin(332211ϕωϕωϕω+=+=+=t A x t A x t A x 代入系统运动微分方程〔1〕得系统特征方程;000)(0)(0)(321234333226532222121⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+---+++---+A A A m K K K K m K K K K K K m K K ωωω〔2〕 〔4〕系统频率方程系统特征方程〔2〕有非零解的充要条件是其系数行列式等于零, 即;0)(0)(0)(234333226532222121=-+---+++---+ωωωm K K K K m K K K K K K m K K展开得系统频率方程;0))(())(()))(())(()((21212323432223432265322121=-+--+--+-+++-+ωωωωωm K K K m K K K m K K m K K K K m K K进一步计算得;0;0)()())()(()))(())((())()()(()()()()())(()())(())(())()(())(())(()))(()()())((())(())(()))(())(()((02244662123432265324321236532214321231233224316532214332216321231232123232243226321421434322124321243165322165324323653221653243212121232343222343421221265322165322121212323432223432265322121==++++-+-+++++++++++-++-+++++++++++-=++-++--++++++-++++++++-++++-+++++=-+--+--+++-+++-++++=-+--+--+-+++-+a a a a K K K K K K K K K K K K K K m K K K K K K K K K K m m m K m K m m K K K K m m K K m m K K m m m m m K K K K m K K K K m m m m m K K m m K K K K K K m m m K K K K m K K K K K K m K K K K K K K K K K K K K K m K K K m K K K m K K m m K K m K K K K m K K K K K K m K K K m K K K m K K m K K K K m K K ωωωωωωωωωωωωωωωωωωωωωωωωωω (3)其中;3216m m m a -= ;)()()(316532214332214m m K K K K m m K K m m K K a +++++++=;))(())((36532214321231233222m K K K K K K K K K K m m m K m K a ++++-++-+=);()())()((21234322653243210K K K K K K K K K K K K K K a +-+-+++++=求解方程〔3〕得系统固有频率;)3,2,1(),,,,,,,,,(654321321==i K K K K K K m m m f i i ω 〔4〕 〔5〕系统固有振型 将系统固有频率代入系统特征方程〔2〕得系统固有振型, 即各阶振型之比:)3(3)3(1)3(3)3(2)3(1)3(2)2(3)2(1)2(3)2(2)2(1)2(2)1(3)1(1)1(3)1(2)1(1)1(21,1;1,1,1,1A A A A A A A A A A A A ======γγγγγγ 〔5〕 〔6〕系统振动方程)sin()sin()sin()sin()sin()sin(33)3(1)3(3)3(1)3(2)3(122)2(1)2(3)2(1)2(2)2(111)1(1)1(3)1(1)1(2)1(133)3(3)3(2)3(122)2(3)2(2)2(111)1(3)1(2)1(1321ϕωγγϕωγγϕωγγϕωϕωϕω+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧t A A A tA A A tA A A t A A A t A A A t A A A x x x 〔6〕在方程〔6〕中含有6个待定常数:)1(1A 、)2(1A 、)3(1A 、1ϕ、2ϕ和3ϕ。
哈工大王焕定版结构力学参考答案

王焕定版结构力学第6章习题答案6-1 试确定图示结构位移法的基本未知量。
解(a) n=2(b) n=1(c) n=2 (e) n=5(f) n=2(d) n=36-2 试用位移法作图示刚架的M基本结构解 1111P 0k F Δ+=111P 1245kN m k i F ==−, 1154kN m iΔ=⋅11P M M M =Δ+习题5-2图90M P 图(kNm)1M 图M 图(kNm)6-3试用位移法作图示刚架的M图。
习题5-3图1M图及系数k11、k21的求解i3i/l2M图及系数k12、k22的求解M P 图及自由项F 1P 、F 2P 的求解解111221P 1112222P 111221222221P 2P 231239752124813197254F F k k F k k F i i k i k k k l lql ql ql ql i iΔΔΔΔ===−===Δ=−Δ=−1++=0++=0,,,, 图(ql ×E 25113928ql6-4试用位移法作图示刚架的M 图。
解1111P 111P P P101010k F k i F F lF l iΔ+===Δ=−,习题5-4图基本结构1M 图M p 图ECB0.3图(F6-5 作图示刚架的M 图。
基本结构习题5-5图DA30 9012i /l 2 6i /l6i /l 6i /l6-6习题5-6图 基本结构1M 图及系数k 11、k 21的求解 4i 2i k 12、k 22的求解2i 4i M P 图(kNm)及自由项F 1P 、F 2P 的求解 60535530 712570575F N6-7 试用位移法计算图示结构,并作内力图。
基本体系习题5-7图1M 图及系数k 11、k 21的求解k 11k 212M 图及系数k 12、k 22的求解k 22M P 图(kNm)及自由项F 1P 、F 2P 的求解F 2PM 图(kNm)解111221P 1212222P 1112212221P 2P 2123361m 1m 120kNm 20kN20kNm 40kNm 3k k F k k F ii k i k k k F F iiΔΔΔΔ===−===Δ=−Δ=−1++=0++=0,,, N 图(kN)F Q 206-8基本体系习题5-8图2M 图及系数k 12、k 22的求解3i解111221P 1212222P 111221221P 2P 1252250275505151k k F k k F k i k k i k iF F i i11ΔΔΔΔ======Δ=−Δ=1++=0++=0,,,,6-12 设支座 B 下沉0.5cm B Δ=,5310kN m EI 2=×⋅。
(完整版)哈工大结构力学题库五章.docx

第五章位移法一判断题1.图a为对称结构,用位移法求解时可取半边结构如图 b 所示。
答:(×)题 1 图2.图示结构,用位移法求解,有三个结点角位移和二个结点线位移未知数。
(×)。
题2图题3图3.以下两个单跨梁左端产生 1 所施加的弯矩相同。
(×)4.用位移法计算刚架,常引入轴向刚度条件,即“受弯直杆在变形后两端距离保持不变”。
此结论是由下述假定导出的:( D)A忽略受弯直杆的轴向变形和剪切变形;B弯曲变形是微小的;C变形后杆件截面仍与变形曲线相垂直;D假定 A 与 B 同时成立。
5.用位移法计算图示结构时,独立的基本未知数数目是 4 。
(×)题 5 图题 6 图6.图示结构用位移法计算时,其基本未知量的数目为 3 个(√)。
7.在位移法典型方程的系数和自由项中,数值范围可为正、负实数的有:( D)A主系数;B主系数和副系数;C主系数和自由项D负系数和自由项。
8.用位移法计算超静定结构时考虑了到的条件是:(A)A物理条件、几何条件、和平衡条件;B平衡条件C平衡条件与物理条件D平衡条件与几何条件9.规定位移法的杆端弯矩正负时,对杆端而言,以顺时针为正,对结点则以逆时针为正,这一规定也适合于杆端剪力的符号规定。
(×)10.图 a 对称结构可简化为图( b)来计算。
(×)题10图题11图11.图示结构用位移法求解时,基本未知量个数是相同的(√)12.图示结构用位移法求解时,只有一个未知数(√)题12图题13 图题14图13. 图示结构横梁无弯曲变形,故其上无弯矩。
(×)14.图a对称结构可简化为图b来计算,EI 均为常数。
(×)15.图示结构用位移法求解的基本未知量数目最少为3。
(√)题15图题16图16.图示结构EI=常数,用位移法求解时有一个基本未知量。
(√)。
17.位移法中固端弯矩是当其基本未知量为零时由外界因数所产生的杆端弯矩(√)18.位移法的典型方程与力法的典型方程一样,都是变形协调方程。
结构动力学-2(哈工大结构动力学)

m y(t)
cy(t)
my(t) k11 y(t )
运动方程 my cy k11y 0
令 c / 2m y 2y 2 y 0
设 y(t) Aet
2 2 2 0 特征方程
根为 i 1 2 由初始条件
小阻尼情况
y(0) y0 , y(0) v0
1 (c 2m)
c1 (v0 y0 ) / D , c2 y0
k
k
k
PROBLEMS:
3.A mass m is at rest,partially supported by a spring and partially by stops.In the position shown,the spring force is mg/2. At time t=0 the stops are rotated,suddenly releasing the mass.Determine the motion of the mass.
第二章单自由度体系的振动分析
§2.1 自由振动
一. 无阻尼体系 运动方程
y(t) 11[my(t)] k11y(t) my(t) 令 2 k11 1
m m11
y(t) 2 y(t) 0
二阶线性齐次常微分方程
m
my(t)
y(t)
l EI
km
运动方程的通解 y(t) c1 cost c2 sin t
令 D 1 2
方程的通解为
y(t) Aet sin( Dt D )
A
y02
( v0
y0 D
)2
y(t) et (c1 sin Dt c2 cosDt) tan D y0D /(v0 y0 )
结构动力学参考答案

m u + c u + ku = Pu (t ) 2.13 一根均匀杆,图 P2.13 其单位体积质量密度 ρ ,并具有顶部质量 M,应 用假定法ψ ( x) = x L 来推导该系统轴向自由振动的运动方程。假定 AE = 常数。 解:
.. 1 EA ( ρAL + M ) u + u = P(t ) 3 L
结构动力学习题 参考答案
1
2.3 一根刚梁 AB,用力在弹簧 BC 上去激励它,其 C 点的运动规定为 Z(t),如 图 P2.3. 按 B 点的垂直运动 u 来确定系统的运动方程,假定运动是微小的。 解: 4M u + 3c u + (3k1 + 12k 2 )u = 12k 2 Z (t )
.. .
4
4.17 在振动的结构上一个点,已知其运动为 Ζ = Ζ1 cos(Ω1t ) + Ζ 2 cos(Ω 2 t ) =
0.05 cos ( 60π t ) + 0.02 cos(120π t ) 。
(a)用一加速度计其阻尼因数 ξ = 0.70 和 20 KHz 共振频率来确定振动记录 w p (t ) 。 (b) 加速度计是否会引起有效幅值或相位畸变? 解: (a) w p (t ) = w p1 (t ) + w p 2 (t ) = 6.339 × 10 −11 A1 cos 60π (t − 1.1145 × 10 −5 ) + 6.339 × 10 −11 A2 • cos 120π (t − 1.1146 × 10 −5 ) (b) w p (t ) = C[ A1 cos Ω1 (t − τ ) + A2 cos Ω 2 (t − τ )] A1 , A2 分别表示 Z1 , Z 2 的加速度幅值,所以输出 w p (t ) 与加速度输 入成正比,所以不会发生幅值畸变或相位畸变。 5.2 运送一件仪器设备重 40 1b,是用泡沫包装在一容器内。该容器的有效刚度 k=100 1b/in,有效阻尼因数 ξ = 0.05 ,若整个容器和它的包装以垂直速度 V=150 in/s 碰撞在地面上,求泡沫包装在仪器设备的最大总应力。 (如图 P5.2 所示) 解: f max = 451.739 (1b) 6.5 例 题 4.3 中的 车辆 , 已知 k = 400 × 10 3 , m = 1200kg , ξ = 0.4。 当满 载时以
哈工大结构力学题库三章 2
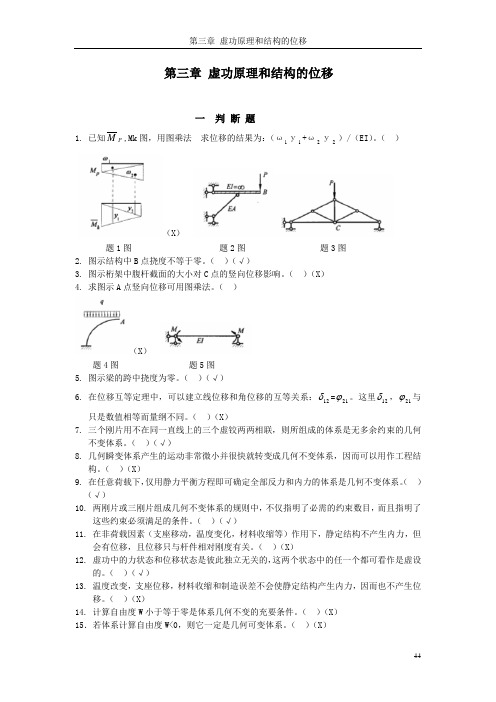
第三章 虚功原理和结构的位移一 判 断 题1. 已知P M ,Mk 图,用图乘法 求位移的结果为:(ω1у1+ω2у2)/(EI )。
( )(X ) 题1图 题2图 题3图2. 图示结构中B 点挠度不等于零。
( )(√)3. 图示桁架中腹杆截面的大小对C 点的竖向位移影响。
( )(X )4. 求图示A 点竖向位移可用图乘法。
( )(X )题4图 题5图5. 图示梁的跨中挠度为零。
( )(√)6. 在位移互等定理中,可以建立线位移和角位移的互等关系:12δ=21ϕ。
这里12δ,21ϕ与只是数值相等而量纲不同。
( )(X )7. 三个刚片用不在同一直线上的三个虚铰两两相联,则所组成的体系是无多余约束的几何不变体系。
( )(√)8. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
( )(X )9. 在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
( )(√)10. 两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必须满足的条件。
( )(√)11. 在非荷载因素(支座移动,温度变化,材料收缩等)作用下,静定结构不产生内力,但会有位移,且位移只与杆件相对刚度有关。
( )(X )12. 虚功中的力状态和位移状态是彼此独立无关的,这两个状态中的任一个都可看作是虚设的。
( )(√)13. 温度改变,支座位移,材料收缩和制造误差不会使静定结构产生内力,因而也不产生位移。
( )(X )14. 计算自由度W 小于等于零是体系几何不变的充要条件。
( )(X )15.若体系计算自由度W<0,则它一定是几何可变体系。
( )(X )16.平面几何不变体系的三个基本组成规则是可以相互沟通的。
( )(√)17.三刚片由三个单铰或任意六根链杆两两相联,体系必为几何不变。
( )(X )18.图示三铰刚架,EI 为常数,A 铰无竖向位移。
(完整版)哈工大结构风工程课后习题答案

结构风工程课后思考题参考答案二、大气边界层风特性1 对地表粗糙度的两种描述方式:指数律和对数律(将公式写上)。
2 非标准地貌下的风速换算原则(P14)和方法(P15公式)。
3 脉动风的生成:近地风在流动过程中由于受到地表因素的干扰,产生大小不同的涡旋,这些涡旋的迭加作用在宏观上表现为速度的随机脉动。
在接近地面时,由于受到地表阻力的影响,导致风速减慢并逐步发展为混乱无规则的湍流。
脉动风的能量及耗散机制:而湍流运动可以看做是能量由低频脉动向高频脉动过渡,并最终被流体粘性所耗散的过程。
在低频区漩涡尺度较大,向中频区(惯性子区)、高频区(耗散区)漩涡尺度逐渐减小,小尺度涡吸收由惯性子区传递过来的能量,能量最终被流体粘性所耗散。
4 Davenport谱的特点:先写出公式通过不同水平脉动风速谱的比较:(1)D谱不随高度变化,而其他谱(如Kaimal谱、Solari谱、Karman谱)则考虑了近地湍流随高度变化的特点;(D谱不随高度变化,在高频区符合-5/3律,没有考虑近地湍流随高度变化的特点;)(2)D谱的谱值比其它谱值偏大,会高估结构的动力反应,计算结果偏于保守。
(3)S u(0)=0,意味着L u=0,与实际不符。
5 湍流度随高度及地面粗糙程度的变化规律:随地面粗糙度的增大而增大,随高度的增加而减小。
积分尺度随高度及地面粗糙程度的变化规律:大量观测结果表明,大气边界层中的湍流积分尺度是地面粗糙度的减函数,而且随着高度的增加而增加。
功率谱随高度及地面粗糙程度的变化规律:随着高度增大和粗糙度的减小,能量在频率上的分布趋于集中,谱形显得高瘦;随着高度减小和粗糙度的增大,能量在频率上的分布趋于分散,谱形显得扁平。
相干函数随高度及地面粗糙程度的变化规律:随地面粗糙度的增大而减小,随高度的增加而增大。
6 阵风因子与峰值因子的区别:阵风因子G=U’/U,是最大风速与平均风速的比值;峰值因子g=u max/σu是最大脉动风速与脉动风速均方根的比值。
结构动力学习题解析
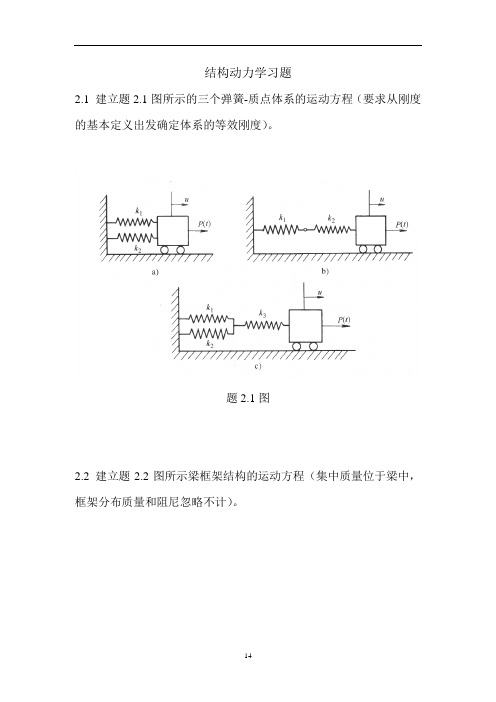
结构动力学习题2.1 建立题2.1图所示的三个弹簧-质点体系的运动方程(要求从刚度的基本定义出发确定体系的等效刚度)。
题2.1图2.2 建立题2.2图所示梁框架结构的运动方程(集中质量位于梁中,框架分布质量和阻尼忽略不计)。
题2.2图2.3 试建立题2.3图所示体系的运动方程,给出体系的广义质量M、广义刚度K、广义阻尼C和广义荷载P(t),其中位移坐标u(t)定义为无重刚杆左端点的竖向位移。
题2.3图2.4 一总质量为m1、长为L的均匀刚性直杆在重力作用下摆动。
一集中质量m2沿杆轴滑动并由一刚度为K2的无质量弹簧与摆轴相连,见题 2.4图。
设体系无摩擦,并考虑大摆角,用图中的广义坐标q1和q2建立体系的运动方程。
弹簧k2的自由长度为b。
题2.4图2.5 如题2.5图所示一质量为m1的质量块可水平运动,其右端与刚度为k的弹簧相连,左端与阻尼系数为c的阻尼器相连。
摆锤m2以长为L的无重刚杆与滑块以铰相连,摆锤只能在图示铅垂面内摆动。
建立以广义坐标u和θ表示的体系运动方程(坐标原点取静平衡位置)。
题2.5图2.6如题2.6图所示一质量为m1的质量块可水平运动,其上部与一无重刚杆相连,无重刚杆与刚度为k2的弹簧及阻尼系数为c2的阻尼器相连,m1右端与刚度为k1的弹簧相连,左端与阻尼系数为c1的阻尼器相连。
摆锤m2以长为L的无重刚杆与滑块以铰相连,摆锤只能在图示铅垂面内摆动。
建立以广义坐标u和θ表示的体系运动方程(坐标原点取静平衡位置,假定系统作微幅振动,sinθ=tanθ=θ)。
计算结果要求以刚度矩阵,质量矩阵,阻尼矩阵的形式给出。
3.1单自由度建筑物的重量为900kN,在位移为3.1cm时(t=0)突然释放,使建筑产生自由振动。
如果往复振动的最大位移为2.2cm(t =0.64s),试求:(1)建筑物的刚度k;(2)阻尼比ξ;(3)阻尼系数c。
3.2 单自由度体系的质量、刚度为m=875t,k=3500kN/m,且不考虑阻尼。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、 拉格朗日方程法:
适用围:所有的单自由度系统的振动。
解题步骤:(1)设系统的广义坐标为 ,写出系统对于坐标 的动能 T 和势能 U 的表达式;
进一步写求出拉格朗日函数的表达式:L=T-U ;
(2)由格朗日方程
dt
(
L
)
L
=0,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
则固有频率为: k
48EIl3
;
m
48EI k1l 3 m
(b)此系统相当于两个弹簧并联, 等效刚度为:
k
k1
48EI l3
;
k1 则固有频率为:
k k1l 3 48EI
m
ml 3
l
l
2
2
m
k1
图 1-33(b)
(c)系统的等效刚度
k
k1
3EI l3
k1
3EI l3
则系统的固有频率为
解:以 为广义坐标,则
系统的动能为
T
T重物
T轮子
1(m)x 2
2
1 2
I 0 2
1( P )x2 1 ( 1 P R 2 ) x 2 P x 2 P x 2
2 2g
2 2 g R 4g 4g
P x 2 2g
系统的势能为: 拉格朗日函数为
U
U重物
U弹簧
-Px
1 2
kx2
;
A
图 1-34
则
Amax xst 2 ,
得
max 1 2 , 2 max 。
1.4 求图 1-35 中标出参数的系统的固有频率。 m
(a)此系统相当于两个弹簧串联,弹簧刚度为 k1、
简支梁刚度为
k2
48EI l3
;
等效刚度为 k;
l 2
k1 l 2
则有
1 1 1 ; k k1 k2
图 1-33(a)
B
0
x
L=T-U ;
由拉格朗日方程
dt
(Lx )
L x
0
得
P x kx P g
则,
0 =
kg P
所以:系统的固有频率为 kg P
1.6 求图 1-35 所示系统的固有频率。图中磙子半径为 R,质量为 M,作纯滚动。弹簧刚
度为 K 。 解:磙子作平面运动, 其动能 T=T 平动 +T 转动 。
k
R
x
M
图 2 ;
T转动
1 2
I
x R
2
1 2
MR2 2
x R
2
;
T 1 Mx 2 1 Mx 2 3 Mx 2 ;
2
4
4
而势能
U 1 Kx 2 ; 2
系统机械能
T U 3 Mx 2 1 Kx 2 C ;
4
2
由 d T U 0 得系统运动微分方程
4、 能量守恒定理法
适用围:所有无阻尼的单自由度保守系统的振动。
解题步骤:(1)对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能 T 和势能 U 的表达式;进一步写出机械能守恒定理的表达式 T+U=Const
(2)将能量守恒定理 T+U=Const 对时间求导得零,即 d(T U) 0 ,进一步得到
谷的幅值 Ai 、 Ai1 。
(2)由对数衰减率定义 ln( Ai ) , Ai 1
进一步推导有
2 , 1 2
因为 较小, 所以有 。 2
方法二:共振法求单自由度系统的阻尼比。
(1)通过实验,绘出系统的幅频曲线, 如下图:
单自由度系统的幅频曲线
(2)分析以上幅频曲线图,得到:
于是 进一步 最后
1,2 max / 2 2 / 4 ;
12
(1
2
)
2 n
;
2 2
(1
2
)
2 n
;
2 1 / 2n / 2n ;
1.3 叙述用正选弦激励求单自由度系统阻尼比的方法和步骤。 用正选弦激励求单自由度系统阻尼比的方法有两个:幅频(相频)曲线法和功率法。
方法一:幅频(相频)曲线法
当单自由度系统在正弦激励 F0 sin t 作用下其稳态响应为:
dt
3 Mx Kx 0 ; 2
得系统的固有频率
n
2K 3M
;
1.7 求图 1-36 所示齿轮系统的固有频率。已知齿轮 A 的质量为 mA,半径为 rA,齿轮 B 的
质量为 mB,半径为 rB,杆 AC 的扭转刚度为 KA, ,杆 BD 的扭转刚度为 KB,
第一章 单自由度系统
1.1 总结求单自由度系统固有频率的方法和步骤。
单自由度系统固有频率求法有:牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守
恒定理法。
1、 牛顿第二定律法
适用围:所有的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析,得到系统所受的合力;
(2) 利用牛顿第二定律 m x F ,得到系统的运动微分方程;
弹性力作功为
Wc 0 、
阻尼力做功为
Wd c A2 、
激振力做作功为
W f F0 sin ;
(2) 由机械能守恒定理得,弹性力、阻尼力和激振力在一个周期所作功为零,
即:
Wc +Wd +W f 0 ;
于是
F0 sin - c A2 0
进一步得:
A F0 sin c ;
(3) 当n 时, sin 1,
dt 系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。
用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。
方法一:衰减曲线法。
求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波
k k1l3 3EI
m
ml 3
m
k1
k1
图 1-3(3 c)
(d)由动量距定理 m0 F I0得:
(
1 2
l
k1
1 2
l
1 2
l
k1
1 2
l
)=
1 2
ml
2
得:
k1 0 , 2m
则
k1 。
2m
m
k1
l 2
k1
l 2
图 1-33
(d)
1.5 求下图所示系统的固有频率。图中匀质轮 A 半径 R,重物 B 的重量为 P/2,弹簧刚度为 k.
x Asin( t ) ,
其中:
A
F0
x st
;
m
2 n
2 0
4n 2 2
1 2 4 2 2
(1)
arctan2 /1 2
(2)
从实验所得的幅频曲线和相频曲线图上查的相关差数,由上述(1),(2)式求得阻尼比 。
方法二:功率法:
(1) 单自由度系统在 F0 sin t 作用下的振动过程中,在一个周期,
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
2、 动量距定理法
适用围:绕定轴转动的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析和动量距分析;
(2) 利用动量距定理 J M ,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
