哈工大结构动力学第一章课后作业解答
(完整版)结构化学课后答案第一章

(完整版)结构化学课后答案第⼀章01.量⼦⼒学基础知识【1.1】将锂在⽕焰上燃烧,放出红光,波长λ=670.8nm ,这是Li 原⼦由电⼦组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产⽣的,试计算该红光的频率、波数以及以k J ·mol -1为单位的能量。
解:811412.99810m s 4.46910s 670.8m cνλ--??===? 41711 1.49110cm 670.810cm νλ--===??%3414123-1 -16.62610J s 4.46910 6.602310mol 178.4kJ mol A E h N sν--===?【1.2】实验测定⾦属钠的光电效应数据如下:波长λ/nm 312.5365.0404.7546.1光电⼦最⼤动能E k /10-19J 3.41 2.56 1.95 0.75 作“动能-频率”,从图的斜率和截距计算出Plank 常数(h)值、钠的脱出功(W)和临阈频率(ν0)。
解:将各照射光波长换算成频率v ,并将各频率与对应的光电⼦的最⼤动能E k 列于下表:λ/nm 312.5 365.0 404.7 546.1v /1014s -19.59 8.21 7.41 5.49 E k /10-19J 3.412.561.950.75由表中数据作图,⽰于图1.2中E k /10-19Jν/1014g-1图1.2 ⾦属的k E ν-图由式 0k hv hv E =+ 推知0k kE E h v v v ?==-?即Planck 常数等于k E v -图的斜率。
选取两合适点,将k E 和v 值带⼊上式,即可求出h 。
例如: ()()19341412.70 1.0510 6.60108.5060010J h J s s ---?==?-?g图中直线与横坐标的交点所代表的v 即⾦属的临界频率0v ,由图可知,1410 4.3610v s -=?。
【哈工大 结构动力学】SD 第1章 运动方程 2020

实际动荷载产生的位移相等!
29
已经知道柔度
和刚度 k
之间的关系为:k 1
表达式成为:
比较:
简支梁: 刚架:
my cy ky FE (t) my cy ky FP (t)
基本质量弹簧体系: my cy ky F(t)
(2-3)
结论:任何一个单自由度体系的运动方程都可以抽象成为一
质量、弹簧、阻尼器体系的运动方程,一般形式为:
FIGURE 2-3 (a) Motion of system
(b) Equilibrium forces
46
体系的力的平衡条件为 : 惯性力为 :
因为地面加速度可以表示为结构的特定动力输入,运 动方程可表示为:
等效支座 激励荷载
47
另一种推导方法:
将 v(t t及)其导数代入方程
地震运动一般测量的是加速度,此时的等效荷载 需要由地震记录积分一次和二次而获得地面位移和速 度来计算,因此很难获得这种形式方程的解答。
q ( t)
q ( t)
EI
m
y(t )
l
[解]
FD FI
1) 确定自由度数: 集中质量,仅竖向位移: 1个自由度。
2) 确定自由度的位移参数:质量 m 的位移: y(t )
3) 体系受力分析:取梁整体为隔离体,确定所受的所有外力!
4) 列位移方程:
y P (FI FD )
改写成:
FI
FD
1
思考题:
• 地震动输入 (ground motions inputs) • 大跨度结构非一致激励 (Spatial Variability) • 地震动如何传递到结构
58
FP (t ) FI FD FS1 FS2 0
【推荐】理论力学(哈工大版)课后习题答案

理论力学作业答案
第一章静力学公理和物体的受力分析1-1
1-2
第二章平面汇交力系与平面力偶系
第三章平面任意力系
第四章空间力系
第五章摩擦
第六章点的运动学
第七章刚体的简单运动
第八章点的合成运动
第九章刚体的平面运动
第十章质点动力学的基本方程
第十一章动量定理
第十二章动量矩定理
第十三章动能定理
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求。
第1章 习题解答 哈工大习题册

第一章 电路元件与电路基本定律1.1 图示电路,设元件A 消耗功率为10W ,求A u ;设元件B 消耗功率为-10W ,求B i ;设元件C 发出功率为-10W ,求C u 。
Au +-10V +-Cu +-(a)(b)(c)图 1.1解:(a)元件A 电压和电流为关联参考方向。
元件A 消耗的功率为A A A p u i =,则A A A 10W 5V 2Ap u i ===,真实方向与参考方向相同。
(b) 元件B 电压和电流为关联参考方向。
元件B 消耗的功率为B B B p u i =,则B B B 10W 1A 10Vp i u -===-,真实方向与参考方向相反。
(c) 元件C 电压和电流为非关联参考方向。
元件C 发出的功率为C C C p u i =,则C C C 10W 10V 1Ap u i -===-,真实方向与参考方向相反。
1.2 图示电路中,电容C = 2F ,电容电压()C u t 的波形如图所示。
(1)求电容电流()C i t ,并绘出波形图; (2)求电容功率表达式,并绘出功率波形图;(3)当t = 1.5s 时,电容是吸收功率还是放出功率?其值是多少?电容储能为多少?u +-图 1-2解:(1)有题可知电容电压的表达式为0201421202c t t t U t t t <⎧⎪<<⎪=⎨-<<⎪⎪>⎩又由电容的性质可知故当t<0时 i =0A0<t<1时1<t<2时 综上所述,可得到电容电流为:故电容电流波形如图1-2-1所示。
(2)电容上所消耗的功率为c c P U I = 当t<0时 0P = 当 0<t<1时 248P t t =⨯=当1<t<2时 4(42)816P t t =-⨯-=- 当t>2时 0P =故功率波形图如图1-2-2所示。
C i(3)t=1.5s 时电容两端电压为421V U t =-=,电容所消耗功率为21121122W CU J ==⨯⨯=由图中电压电流的参考方向可知电容是发出功率且发出功率为4W 。
结构动力学习题答案
3.4
m2 g k
( m1 + m2 ) u (0) = m2 2 gh
即 u (0) =
i
i
m2 2 gh m1 + m2
动力方程: ( m1 + m2 )( u − ust )′′ + K ( u − ust ) = 0
5 .0 1 = u st 2ξ
(1)
当 w wn = 1 时,发生共振有: Rd 1 =
当 w wn = 1 10 时, Rd 1 =
0 .5 = u st
(1 − 0.1 ) + (2ξ × 0.1)
2 2
1
(2)
2
由式(1),(2)可以解得 ξ = 4.95%
3.6 解:
TR =
[1 − (w w ) ] + [2ξ w w ]
ii
ii
ii
ii
ii
δ Wp = −m2 g sin θ i Lδθ
虚 功原理: δ Ws
+ δ WI + δ W D +δ W p = 0 得:
⎡ m1 + m2 ⎢ mL ⎣ 2
2.6 解:
ii ⎫ ⎧i⎫ m2 L ⎤ ⎧ 0 ⎫ ⎪ u ⎪ ⎡C 0 ⎤ ⎪ u ⎪ ⎡ k 0 ⎤ ⎧ u ⎫ ⎧ +⎢ ⎨ i ⎬+ ⎢ ⎨ ⎬=⎨ ⎬ ⎥ ⎥ 2 ⎥ ⎨ ii ⎬ m2 L ⎦ ⎪ ⎪ ⎣ 0 0 ⎦ ⎪ ⎪ ⎣ 0 0 ⎦ ⎩θ ⎭ ⎩−m2 g sin θ i L ⎭ ⎩θ ⎭ ⎩θ ⎭
结构动力学1~15

《结构动力学》习题答案1~151. 1简述求多自由度体系时程反应的振型叠加法的主要步骤 答1)建立多自由度体系的运动方程)()()()(t p t kv t v c t vm =++ 2)进行振型和频率分析对无阻尼自由振动,这个矩阵方程能归结为特征问题)(ˆ2t p vm k =-ω 由此确定振型矩阵φ和频率向量ω 3)求广义质量和荷载依次取每一个振型向量n φ,计算每一个振型的广义质量和广义荷载n T n nm Mφφ= )()(t p t p Tn n φ=4)求非耦合运动方程用每个振型的广义质量、广义力、振型频率n ω和给定的振型阻尼比n ξ就能写出每一个振型的运动方程2)(2)(ωωξ++t Y t Y n n n n nn nMt P t Y )()(=5)求对荷载的振型反应根据荷载类型,用适当的方法解这些单自由度方程,每一个振型的一般动力反应表达式用Duhamel 积分给出ττωτωξτωd t t P M t Y Dn n n tn nn n )(sin )](exp[)(1)(0---=⎰写出标准积分形式τττd t h P t Y n tn n )()()(0-=⎰式中)](exp[)(sin 1)(τωξτωωτ---=-t t M t h n n Dn nn n 10<<n ξ6)振型自由振动每一个振型有阻尼自由振动反应的通式为)exp[]sin )0()0(cos )0([)(t t Y Y t Y t Y n n Dn Dnnn n n Dn n n ωξωωωξω-++=7)求在几何坐标中的位移反应通过正规坐标变换求几何坐标表示的位移式)()()()(2211t Y t Y t Y t V n n φφφ+++=显然,它反映了各个振型贡献的叠加。
因此命名为振型叠加法。
8)弹性力反应抵抗结构变形的弹性力)()()(t Y k t kv t f s φ==当频率、振型从柔度形式的特征方程中求出时,可以采用另一种弹性力的表达式。
哈工大_结构力学_第一章习题答案解密版
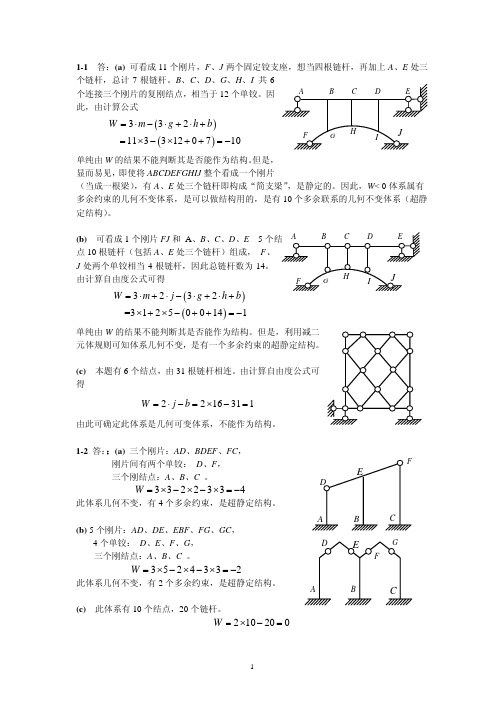
1-1 答:(a) 可看成11个刚片,F 、J 两个固定铰支座,想当四根链杆,再加上A 、E 处三个链杆,总计7根链杆。
B 、C 、D 、G 、H 、I 共6个连接三个刚片的复刚结点,相当于12个单铰。
因此,由计算公式()()20710h b +⋅+++=−33 113312W m g =⋅−⋅=×−×(单纯由W 的结果不能判断其是否能作为结构。
但是,显而易见,即使将ABCDEFGHIJ 整个看成一个刚片(当成一根梁),有A 、E 处三个链杆即构成“简支梁”,是静定的。
因此,W < 0体系属有多余约束的几何不变体系,是可以做结构用的,是有10个多余联系的几何不变体系(超静定结构)。
(b) 可看成1个刚片FJ 和 A 、B 、C 、D 、E 5点10根链杆(包括A 、E 处三个链杆)组成, F 、J 处两个单铰相当4根链杆,因此总链杆数为14。
由计算自由度公式可得 )()3232 =312500141W m j g h b =⋅+⋅−⋅+⋅+×+×−++=−W j单纯由W 的结果不能判断其是否能作为结构。
但是,利用减二元体规则可知体系几何不变,是有一个多余约束的超静定结构。
(c) 本题有6个结点,由31根链杆相连。
由计算自由度公式可得2216311b =⋅−332W =×−×3524332W =×−×−×=−210200W =×−=由此可确定此体系是几何可变体系,不能作为结构。
1-2 答::(a) 三个刚片:AD 、BDEF 、FC ,刚片间有两个单铰: D 、F , 三个刚结点:A 、B 、C 。
2334−×=−此体系几何不变,有4个多余约束,是超静定结构。
(b) 5个刚片:AD 、DE 、EBF 、FG 、GC ,4个单铰: D 、E 、F 、G ,三个刚结点:A 、B 、C 。
【推荐】理论力学(哈工大版)课后的习题答案.doc

理论力学作业答案第一章静力学公理和物体的受力分析1-11-2第二章平面汇交力系与平面力偶系第三章平面任意力系第四章空间力系第五章摩擦第六章点的运动学第七章刚体的简单运动第八章点的合成运动第九章刚体的平面运动第十章质点动力学的基本方程第十一章动量定理第十二章动量矩定理第十三章动能定理赠送以下资料考试知识点技巧大全一、考试中途应饮葡萄糖水大脑是记忆的场所,脑中有数亿个神经细胞在不停地进行着繁重的活动,大脑细胞活动需要大量能量。
科学研究证实,虽然大脑的重量只占人体重量的2%-3%,但大脑消耗的能量却占食物所产生的总能量的20%,它的能量来源靠葡萄糖氧化过程产生。
据医学文献记载,一个健康的青少年学生30分钟用脑,血糖浓度在120毫克/100毫升,大脑反应快,记忆力强;90分钟用脑,血糖浓度降至80毫克/100毫升,大脑功能尚正常;连续120分钟用脑,血糖浓度降至60毫克/100毫升,大脑反应迟钝,思维能力较差。
我们中考、高考每一科考试时间都在2小时或2小时以上且用脑强度大,这样可引起低血糖并造成大脑疲劳,从而影响大脑的正常发挥,对考试成绩产生重大影响。
因此建议考生,在用脑60分钟时,开始补饮25%浓度的葡萄糖水100毫升左右,为一个高效果的考试加油。
二、考场记忆“短路”怎么办呢?对于考生来说,掌握有效的应试技巧比再做题突击更为有效。
1.草稿纸也要逐题顺序写草稿要整洁,草稿纸使用要便于检查。
不要在一大张纸上乱写乱画,东写一些,西写一些。
打草稿也要像解题一样,一题一题顺着序号往下写。
最好在草稿纸题号前注上符号,以确定检查侧重点。
为了便于做完试卷后的复查,草稿纸一般可以折成4-8块的小方格,标注题号以便核查,保留清晰的分析和计算过程。
结构动力学哈工大版课后习题解答

第一章 单自由度系统1.1 总结求单自由度系统固有频率的方法和步骤。
单自由度系统固有频率求法有: 牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守恒定理法。
1. 牛顿第二定律法适用范围: 所有的单自由度系统的振动。
解题步骤: (1) 对系统进行受力分析,得到系统所受的合力;(2) 利用牛顿第二定律∑=F x m,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根, 得到该系统的固有频率。
2. 动量距定理法适用范围: 绕定轴转动的单自由度系统的振动。
解题步骤: (1) 对系统进行受力分析和动量距分析;(2) 利用动量距定理J ∑=M θ,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根, 得到该系统的固有频率。
3. 拉格朗日方程法:适用范围: 所有的单自由度系统的振动。
解题步骤: (1)设系统的广义坐标为 , 写出系统对于坐标 的动能T 和势能U 的表达式;进一步写求出拉格朗日函数的表达式: L=T-U ;(2)由格朗日方程 =0, 得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根, 得到该系统的固有频率。
4. 能量守恒定理法适用范围: 所有无阻尼的单自由度保守系统的振动。
解题步骤: (1)对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能T 和势能U 的表达式;进一步写出机械能守恒定理的表达式 T+U=Const (2)将能量守恒定理T+U=Const 对时间求导得零,即 , 进一步得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根, 得到该系统的固有频率。
1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。
用衰减法求单自由度系统阻尼比的方法有两个: 衰减曲线法和共振法。
方法一: 衰减曲线法。
求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线, 并测得周期和相邻波峰和波谷的幅值 、 。
(2)由对数衰减率定义 , 进一步推导有,因为 较小, 所以有πδζ2=。
哈工大张金生结构动力学-1

三、例题 例1. m
y (t )
P(t )
=1
δ 11
P(t )
l
y (t )
− m&&(t ) y
l
EI EI
2l 3 δ 11 = 3EI 3EI m&&(t) + 3 y(t) = P(t) y 2l
∆1P
P(t)
l 例2. l
EI
m y (t )
P(t )
l/2
EI
y (t ) − m&&(t ) y
EI = ∞
W=1
三. 自由度的确定 8) 平面上的一个刚体
11) W=1
y2
ϕ
y1 W=3
12)
9)弹性地面上的平面刚体 9)弹性地面上的平面刚体 W=3 10)
W=13 自由度为1的体系称作单自由度体系; 自由度为1的体系称作单自由度体系; 自由度大于1的体系称作多(有限)自由度体系; 自由度大于1的体系称作多(有限)自由度体系; 自由度无限多的体系为无限自由度体系。 自由度无限多的体系为无限自由度体系。
二.动荷载的分类
简谐荷载 周期 确定 非周期 动荷载 风荷载 不确定 地震荷载 其他无法确定变化规律的荷载 非简谐荷载 冲击荷载 突加荷载 其他确定规律的动荷载
§1.3 振动系统的力学模型及其分类
振动系统的基本参数:质量、阻尼、弹性。 振动系统的基本参数:质量、阻尼、弹性。
铝质与有机玻璃试件的 自由振动试验
二. 自由度的简化 常用简化方法有:集中质量法,广义坐标法,有限元法。 常用简化方法有:集中质量法,广义坐标法,有限元法。 1) 集中质量法 将实际结构的质量看成(按一定规则) 将实际结构的质量看成(按一定规则)集中在某些几 何点上,除这些点之外物体是无质量的。 何点上,除这些点之外物体是无质量的。这样就将无限自由 度系统变成一有限自由度系统。 度系统变成一有限自由度系统。
(完整版)哈工大结构力学题库一章

第一章平面体系的几何组成分析一判断题1. 图示体系是几何不变体系。
(×)题1图题2图题3图题4图2. 图示体系为几何可变体系。
(×)3. 图示体系是几何不变体系。
(×)4. 图示体系是几何不变体系。
(√)5. 图示体系是几何不变体系。
(×)题5图题6图题19图题20图6. 图示体系为几何不变有多余约束。
(×)7. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
(×)8. 两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必需满足的条件。
(√)9. 在任意荷载下,仅用静力平衡方程即可确定全不反力和内力的体系是几何不变体系。
(√)10. 计算自由度W小于等于零是体系几何不变的充要条件。
(×)11. 几何可变体系在任何荷载作用下都不能平衡。
(×)12. 三个刚片由三个铰相联的体系一定是静定结构。
(×)13. 有多余约束的体系一定是超静定结构。
(×)14. 有些体系为几何可变体系但却有多余约束存在。
(√)15. 平面几何不变体系的三个基本组成规则是可以相互沟通的。
(√)16. 三刚片由三个单铰或任意六根链杆两两相联,体系必为几何不变。
(×)17. 两刚片用汇交于一点的三根链杆相联,可组成几何不变体系。
(×)18. 若体系计算自由度W<0,则它一定是几何可变体系。
(×)19. 在图示体系中,去掉其中任意两根支座链杆后,所余下都是几何不变的。
(×)20. 图示体系按三刚片法则分析,三铰共线,故为几何瞬变体系。
(×)21. 有多余约束的体系一定是几何不变体系。
(×)22. 几何不变体系的计算自由度一定等于零。
(×)23. 几何瞬变体系的计算自由度一定等于零。
(×)24. 图中链杆1和2的交点O可视为虚铰。
结构动力学参考答案

m u + c u + ku = Pu (t ) 2.13 一根均匀杆,图 P2.13 其单位体积质量密度 ρ ,并具有顶部质量 M,应 用假定法ψ ( x) = x L 来推导该系统轴向自由振动的运动方程。假定 AE = 常数。 解:
.. 1 EA ( ρAL + M ) u + u = P(t ) 3 L
结构动力学习题 参考答案
1
2.3 一根刚梁 AB,用力在弹簧 BC 上去激励它,其 C 点的运动规定为 Z(t),如 图 P2.3. 按 B 点的垂直运动 u 来确定系统的运动方程,假定运动是微小的。 解: 4M u + 3c u + (3k1 + 12k 2 )u = 12k 2 Z (t )
.. .
4
4.17 在振动的结构上一个点,已知其运动为 Ζ = Ζ1 cos(Ω1t ) + Ζ 2 cos(Ω 2 t ) =
0.05 cos ( 60π t ) + 0.02 cos(120π t ) 。
(a)用一加速度计其阻尼因数 ξ = 0.70 和 20 KHz 共振频率来确定振动记录 w p (t ) 。 (b) 加速度计是否会引起有效幅值或相位畸变? 解: (a) w p (t ) = w p1 (t ) + w p 2 (t ) = 6.339 × 10 −11 A1 cos 60π (t − 1.1145 × 10 −5 ) + 6.339 × 10 −11 A2 • cos 120π (t − 1.1146 × 10 −5 ) (b) w p (t ) = C[ A1 cos Ω1 (t − τ ) + A2 cos Ω 2 (t − τ )] A1 , A2 分别表示 Z1 , Z 2 的加速度幅值,所以输出 w p (t ) 与加速度输 入成正比,所以不会发生幅值畸变或相位畸变。 5.2 运送一件仪器设备重 40 1b,是用泡沫包装在一容器内。该容器的有效刚度 k=100 1b/in,有效阻尼因数 ξ = 0.05 ,若整个容器和它的包装以垂直速度 V=150 in/s 碰撞在地面上,求泡沫包装在仪器设备的最大总应力。 (如图 P5.2 所示) 解: f max = 451.739 (1b) 6.5 例 题 4.3 中的 车辆 , 已知 k = 400 × 10 3 , m = 1200kg , ξ = 0.4。 当满 载时以
结构动力学习题+讲解

结构动力学*本章讨论结构在动力荷载作用下的反应。
**学习本章注重动力学的特征------惯性力。
*结构动力计算的目的在于确定结构在动力荷载作用下的位移、内力等量值随时间变化的规律,从而找出其最大值作为设计的依据。
*动力学研究的问题:动态作用下结构或构件的强度、刚度及稳定性分析。
一、本章重点1.振动方程的建立2.振动频率和振型的计算3.振型分解法求解多自由度体系4.最大动位移及最大动应力二、基础知识1.高等数学2.线性代数3.结构力学三、动力荷载的特征1.大小和方向是时间t的函数例如:地震作用,波浪对船体的作用,风荷载,机械振动等2.具有加速度,因而产生惯性力四、动力荷载的分类1.周期性动力荷载例如:①机械运转产生的动力荷载,②打桩时的锤击荷载。
P(t) Pt t(机械运转荷载)(打桩荷载)2.冲击荷载例如:①爆炸力产生的动力荷载,②车轮对轨道连接处的冲击。
P(t)P(t)P(t)t t t(爆炸力动力荷载)(吊车起吊钢索的受力)(随机动力荷载)3.突加常量荷载例如:吊车起吊重物时钢索的受力。
4.随机动力荷载前3类荷在是时间t的确定函数,称为确定性动力荷载;而地震作用,波浪对船体的作用,风荷载等其作用大小只能用统计的方法获得。
五、动力荷载的计算方法1.原理:达朗贝尔原理,动静法建立方程2.计算工具:微分方程,线性代数,结构力学六、体系振动的自由度---------动力自由度结构具有质量,有质量在运动时就有惯性力。
在进行动力计算时,一般把结构的质量简化为若干质点的质量,整个结构的惯性力就成为各质点的惯性力问题。
1.质点简化的一般要求①简单,②能反映主要的振动特性例如:楼房;质量集中在各层楼板平面内水塔:质量集中在水箱部分梁:无限自由度集中质量(楼房质量集中)(水塔质量集中)(梁的质量集中)2.位移y(t)即指质点的位移y(t),其加速度为y&&)(t3.动力自由度的确定即质点位移数量的确定。
结构动力学习题解答

ω2 =
1 192 EI EI = = 13.86 , ρ2 = 1 3 mδ 11 ml ml
l/4 P=1 3l/16
δ11 =
1 1 3l l 2 l 1 5l l 1 l ( × × × × − × × × × ) EI 2 16 2 3 2 2 32 2 3 2 7l 3 = 768 EI
结构力学Ⅱ
习题解答
14-14 试求图示刚架的 自振频率和主振型
m 正对称
l/2 m l/2 l/2 l/2 反对称
14-14 试求图示刚架的自振频率和主振型
l/8 P=1 l/8
l/8 P=1
2 1 l l 2 l 1 l l 1 l ( × × × × − × × × × ) δ 11 = EI 2 8 2 3 4 2 8 2 3 4 Mp l3 = 192 EI
FI0 = 1
ql 12
反对称
y2 = δ11 (− m&&2 ) + δ12 y
4l 4 δ12 = 768EI
q sin θt 2
ql 2 32
7l 3 δ11 = 768EI
l/2
P=1
7 ml 3 2ql 4 0 ( 2− ) FI 1 = θ 768EI 768EI 1
FI02 =
2ql 9
kθ1 − Py1 = 0
代入几何关系
k k 2 y1 − y2 − Py1 = 0 a a k k − y1 + 2 y2 − Py2 = 0 a a
k k 2 P − 4 P + 3( ) = 0 a a k 3 a k P= , 故PCR = k a a
2
2
5ql 2 96
(完整版)结构动力学-习题解答

解
11
5 48
l3 EI
;
3.098
EI ml 3
;
l/2
ml 3 T 2.027 ;
EI
m
EI y1(t)
l
l/2 l/2
l/4
7-1(b)试求图示体系的自振频率与周期。
解: 求柔度系数: 用位移法或力矩分配法 求单位力作用引起的弯矩图(图a); 将其与图b图乘,得
48EI 2k
T 2 ( 1 l3 1 )m
48 EI 2k
m
k EI
k
l/2
l/2
7-3 试求图示体系质点的位移幅值和最大弯矩值。
已知 0.6
l
解:
yst
FPl 3 EI
m
y1(t)
1
1
2
/
2
1.5625
位移幅值
A
yst
1.5625
FPl 3 EI
2l
yst
11
5 3
l3 EI
1 11
l
X11 0.4612 ; X12 4.336
X 21
X 22
12 7.965 EI / ml 3
2 2
65.53EI
/
ml 3
1 2.822 EI / ml3
8-6.试求图示刚架的自振频率和振型。设楼面质量分别为m1=120t和m2=100t,
柱的质量已集中于楼面, 柱的线刚度分别为i1=20MN.m和i2=14MN.m,横梁
m 2 A 0.3375 FP
l/2
EI=常数
FP sin t
2l
FP
FPl
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Q 35kN , P 10kN , n 500转 / 分. l3 0.722107 m/N 解. 11 l/2 48EI 1 M Ql 35 kN 重力引起的弯矩 Q 4
3 Q 2 . 53 10 m 重力引起的位移 Q 11
P sin t
yst
(t ) m y
稳态解
P* y (t ) sin t 2 m
11
y (t ) P* sin t
仍是位移动力系数 是内力动A sin t
(t ) A 2 sin t y I (t ) mA sin t
三.动位移、动内力幅值计算
计算步骤: 1.计算荷载幅值作为静荷载所引起的 位移、内力; 2.计算动力系数; 3.将得到的位移、内力乘以动力系数 即得动位移幅值、动内力幅值。
y (t ) A sin t
A yst 1 1 2 / 2
例2.5 解.
求图示体系振幅和动弯矩幅值图,已知
A
1 1 Pl l 5 5 Pl 3 l 解: yst EI 2 2 2 6 48 EI 1 4 1 2 / 2 3 5 Pl 3 A yst 36 EI
l
=1
11
1 2 A I m A m A 4 4 11 5 P 48
l
=1
11
1 2 A I m A m A 4 4 11 5 P 48
2
29 Pl 48
P
5 P 48
5 Pl 96 动弯矩幅值图
0.5 例2.7:求图示体系振幅、动弯矩幅值图.已知
P sin t
l/2
EI
l/2
m y(t )
P
m 2 A
Pl / 2
P
yst
2
同频同步变化
P(t ) P sin t
0.5 例2.7:求图示体系振幅、动弯矩幅值图.已知
P sin t
l/2
EI
l/2
m y(t )
P
m 2 A
Pl / 2
P
yst
A
1 1 Pl l 5 5 Pl 3 l 解: yst EI 2 2 2 6 48 EI 1 4 1 2 / 2 3 5 Pl 3 A yst 36 EI
11 l/4
2n / 60 52.3 1 / S
1 1 /
2 2
M max M Q M D 69kN.m
3.4
f max Q A 4.98103 m
[动荷载不作用于质点时的计算]
m
P sin t
y(t ) P sin t
(t ) m y
Q l/2
1
振幅 yst P11 0.722103 m A yst 2.45103 m 1 动弯矩幅值 M st Pl 10 kN.m 4 M D M st 34kN.m 1 / m 11 g / Q 62.3 1 / S 跨中最大弯矩 跨中最大位移
12
=1
11
P
yst
=1
运动方程
) y(t ) 12 P sin t 11 (m y 1 12 my (t ) y(t ) P sin t
令
振幅
P* * A P 11 2 m
11 12 * P P 11
1
11
12 P 11 12 P 11
2
29 Pl 48
P
5 P 48
5 Pl 96 动弯矩幅值图
例2.8:求图示体系右端的质点振幅
P sin t
P m o
1 mA 2 3
m A 2
m
l 解: l
o
EI
k l
A
2 Ak 3
M
A
0
3P
10 m 2 4k
作业: 165页7-3 166页7-4(a)
m
EI1 EI EI
0.5
P
24 EI P sin t k11 l3 l P Pl3 yst k11 24EI 1 4 1 2 / 2 3
Pl/4
1 Pl A yst 18 EI
3
Pl/3
动弯矩幅值图
例2.6
求图示梁中最大弯矩和跨中点最大位移 已知: l 4m, I 8.8 105 m 4 , E 210 GPa,
