数值分析最小二乘法ppt课件
合集下载
最小二乘法示例(共7张PPT)

最小二乘法示例
用Excel求解a、b、r
例如:用Excel求解a、b、r
设铜丝电阻随温度变化的实验数据如下,用Excel 求解a、b、r求解步骤
t(℃) 25.1 32.0 40.1 47.0 54.0 60.8 67.1 73.7 Rt(Ω) 21.34 21.91 22.58 23.15 23.73 24.27 24.80 25.32
4. 同样可在C3、D3空白格内分别输入说明'r= , 函数=correl(B1:B8,A1:A8),回车后,显示
r=0.99998
5. 用Excel作图得:
1. 把t、Rt 数据按列对应输入Excel表格内,如 把t输在第一列〔A1:A8), Rt输在第二列 〔B1:B8)
2. 在相邻两个空白格〔如C1、D1格〕内,分别输入说明和函
数。如在C1中输入说明‘a= ,回车;在D1中输入函数
=intercept(B1:B8,A1:A8),其中A1:A8、B1:B8分别给出自
变量、因变量的对应位置,回车,即显示a= 19.28848
同样可在C3、D3空白格内分别输入说明'r= , 函数=correl(B1:B8,A1:A8),回车后,显示r=0. 把t、Rt 数据按列对应输入Excel表格内,如把t输在第一列〔A1:A8), Rt输在第二列〔B1:B8) 设铜丝电阻随温度变化的实验数据如下,用Excel求解a、b、r求解步骤 把t、Rt 数据按列对应输入Excel表格内,如把t输在第一列〔A1:A8), Rt输在第二列〔B1:B8) 同样可在C2、D2空白格内分别输入说明'b=, 函数=slope(B1:B8,A1:A8),回车后,显示b=0. 设铜丝电阻随温度变化的实验数据如下,用Excel求解a、b、r求解步骤 如在C1中输入说明‘a= ,回车; 例如:用Excel求解a、b、r 设铜丝电阻随温度变化的实验数据如下,用Excel求解a、b、r求解步骤 把t、Rt 数据按列对应输入Excel表格内,如把t输在第一列〔A1:A8), Rt输在第二列〔B1:B8) 在相邻两个空白格〔如C1、D1格〕内,分别输入说明和函数。 如在C1中输入说明‘a= ,回车; 在相邻两个空白格〔如C1、D1格〕内,分别输入说明和函数。 同样可在C2、D2空白格内分别输入说明'b=, 函数=slope(B1:B8,A1:A8),回车后,显示b=0. 在D1中输入函数=intercept(B1:B8,A1:A8),其中A1:A8、B1:B8分别给出自变量、因变量的对应位置,回车,即显示a= 19.
用Excel求解a、b、r
例如:用Excel求解a、b、r
设铜丝电阻随温度变化的实验数据如下,用Excel 求解a、b、r求解步骤
t(℃) 25.1 32.0 40.1 47.0 54.0 60.8 67.1 73.7 Rt(Ω) 21.34 21.91 22.58 23.15 23.73 24.27 24.80 25.32
4. 同样可在C3、D3空白格内分别输入说明'r= , 函数=correl(B1:B8,A1:A8),回车后,显示
r=0.99998
5. 用Excel作图得:
1. 把t、Rt 数据按列对应输入Excel表格内,如 把t输在第一列〔A1:A8), Rt输在第二列 〔B1:B8)
2. 在相邻两个空白格〔如C1、D1格〕内,分别输入说明和函
数。如在C1中输入说明‘a= ,回车;在D1中输入函数
=intercept(B1:B8,A1:A8),其中A1:A8、B1:B8分别给出自
变量、因变量的对应位置,回车,即显示a= 19.28848
同样可在C3、D3空白格内分别输入说明'r= , 函数=correl(B1:B8,A1:A8),回车后,显示r=0. 把t、Rt 数据按列对应输入Excel表格内,如把t输在第一列〔A1:A8), Rt输在第二列〔B1:B8) 设铜丝电阻随温度变化的实验数据如下,用Excel求解a、b、r求解步骤 把t、Rt 数据按列对应输入Excel表格内,如把t输在第一列〔A1:A8), Rt输在第二列〔B1:B8) 同样可在C2、D2空白格内分别输入说明'b=, 函数=slope(B1:B8,A1:A8),回车后,显示b=0. 设铜丝电阻随温度变化的实验数据如下,用Excel求解a、b、r求解步骤 如在C1中输入说明‘a= ,回车; 例如:用Excel求解a、b、r 设铜丝电阻随温度变化的实验数据如下,用Excel求解a、b、r求解步骤 把t、Rt 数据按列对应输入Excel表格内,如把t输在第一列〔A1:A8), Rt输在第二列〔B1:B8) 在相邻两个空白格〔如C1、D1格〕内,分别输入说明和函数。 如在C1中输入说明‘a= ,回车; 在相邻两个空白格〔如C1、D1格〕内,分别输入说明和函数。 同样可在C2、D2空白格内分别输入说明'b=, 函数=slope(B1:B8,A1:A8),回车后,显示b=0. 在D1中输入函数=intercept(B1:B8,A1:A8),其中A1:A8、B1:B8分别给出自变量、因变量的对应位置,回车,即显示a= 19.
数值分析5.2 最小二乘法
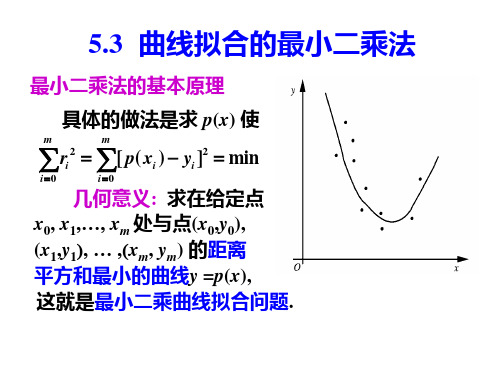
0 1 1 n
可以证明这样得到的S*(x) ,对任何形如(2)式的S(x) ,
都有
m m
( x )[S ( x ) f ( x )] ( x )[S ( x ) f ( x )] ,
* 2 2 i 0 i i i i 0 i i i
即S*(x)必为所求的最小二乘解.
0 1 2 3 4
1.00 1.25 1.50 1.75 2.00 5.10 5.79 6.53 7.45 8.46
1.629 1.756 1.876 2.008 2.135
yi
zi
解 根据给定数据(xi, yi)(i=0,1,2,3,4)描图可确定拟
合曲线方程为y=aebx,它不是线性形式.
对方程y=aebx 两边取对数得lny=lna+bx,如果令
( 0 , 0 ) ( 0 , 1 ) ( 1 , 0 ) ( 1 , 1 ) G ( , ) ( , ) n 1 n 0 ( 0 , n ) ( 1 , n ) . ( n , n )
i 0 i 0 i 0 m i 0 m i 0
m
m
m
其法方程为
n
jk k ( x ) a x i j i yi (k 0,1,, n) j 0 i 0 i 0
m
m
此时矩阵为
( 0 , 0 ) ( 0 , 1 ) ( 0 , n ) ( 1 , 0 ) ( 1 , 1 ) ( 1 , n ) G ( , ) ( , ) ( , ) n 1 n n n 0 m m n m 1 xi xi i 0 i 0 m m m 2 n1 x x x . i i i i 0 i 0 i 0 m m m xn n1 2n x x i i i i 0 i 0 i 0
可以证明这样得到的S*(x) ,对任何形如(2)式的S(x) ,
都有
m m
( x )[S ( x ) f ( x )] ( x )[S ( x ) f ( x )] ,
* 2 2 i 0 i i i i 0 i i i
即S*(x)必为所求的最小二乘解.
0 1 2 3 4
1.00 1.25 1.50 1.75 2.00 5.10 5.79 6.53 7.45 8.46
1.629 1.756 1.876 2.008 2.135
yi
zi
解 根据给定数据(xi, yi)(i=0,1,2,3,4)描图可确定拟
合曲线方程为y=aebx,它不是线性形式.
对方程y=aebx 两边取对数得lny=lna+bx,如果令
( 0 , 0 ) ( 0 , 1 ) ( 1 , 0 ) ( 1 , 1 ) G ( , ) ( , ) n 1 n 0 ( 0 , n ) ( 1 , n ) . ( n , n )
i 0 i 0 i 0 m i 0 m i 0
m
m
m
其法方程为
n
jk k ( x ) a x i j i yi (k 0,1,, n) j 0 i 0 i 0
m
m
此时矩阵为
( 0 , 0 ) ( 0 , 1 ) ( 0 , n ) ( 1 , 0 ) ( 1 , 1 ) ( 1 , n ) G ( , ) ( , ) ( , ) n 1 n n n 0 m m n m 1 xi xi i 0 i 0 m m m 2 n1 x x x . i i i i 0 i 0 i 0 m m m xn n1 2n x x i i i i 0 i 0 i 0
最小二乘法简介PPT课件

为消除异方差的影响,使各项的地位相 同,观测值的权数取观测值误差项方差 的倒数,即 ωi=1/σi2
在实际问题中,σi2通常是未知的,当自 变量水平以系统的形式变化时,取 ωi=1/xi2
-
15
5.3 WLS模型
加权后的最小二乘估计模型为:
n
s (i yi a bxi)2 i 1
令 s 0, s 0 a b
n
n
n
xi
y
-
i
xi
yi
i1
i1
i1
n
n
i1
x
2 i
-
n
i1
xi
2
-
a
=
1 n
n
y
-
i
i1
b n
n
xi
i1
8
2、多元性拟合
设变量y与n个变量x1,x2,…,xn(n≥1)内在联系是
线性的,即有y=a0+∑ajxj(j=1,...,n)。
m
n
s (yi a0 a j xij)2
i 1
j 1
令 s 0, s 0 a0 a j
s
a
0
m
2
yi
i1
a0
n
a
j xij
j 1
0
s a1
2
m
i1
yi
a0
n
j 1
a
j
x ij
x
i1
0
s
a
n
m
2
yi
a0
n
a
j xij
x
i
n
i1
j 1
0
- a0,a1,,am的值9
在实际问题中,σi2通常是未知的,当自 变量水平以系统的形式变化时,取 ωi=1/xi2
-
15
5.3 WLS模型
加权后的最小二乘估计模型为:
n
s (i yi a bxi)2 i 1
令 s 0, s 0 a b
n
n
n
xi
y
-
i
xi
yi
i1
i1
i1
n
n
i1
x
2 i
-
n
i1
xi
2
-
a
=
1 n
n
y
-
i
i1
b n
n
xi
i1
8
2、多元性拟合
设变量y与n个变量x1,x2,…,xn(n≥1)内在联系是
线性的,即有y=a0+∑ajxj(j=1,...,n)。
m
n
s (yi a0 a j xij)2
i 1
j 1
令 s 0, s 0 a0 a j
s
a
0
m
2
yi
i1
a0
n
a
j xij
j 1
0
s a1
2
m
i1
yi
a0
n
j 1
a
j
x ij
x
i1
0
s
a
n
m
2
yi
a0
n
a
j xij
x
i
n
i1
j 1
0
- a0,a1,,am的值9
最小二乘估计课件(43张)

栏目导航
30
2.已知变量 x,y 有如下对应数据:
x
1
2
3
4
y
1
3
4
5
(1)作出散点图;
(2)用最小二乘法求关于 x,y 的回归直线方程.
栏目导航
[解] (1)散点图如下图所示.
31
栏目导航
(2) x =1+2+4 3+4=52, y =1+3+4 4+5=143,
4
i∑=1xiyi=1+6+12+20=39, i∑=41x2i =1+4+9+16=30, b=393-0-4×4×52×521243=1130,
(1)判断它们是否有相关关系,若有相关关系,请作一条拟合直 线;
(2)用最小二乘法求出年龄关于脂肪的线性回归方程.
栏目导航
25
[思路探究] (1)作出散点图,通过散点图判断它们是否具有相关 关系,并作出拟合直线;
(2)利用公式求出线性回归方程的系数 a,b 即可.
栏目导航
26
[解] (1)以 x 轴表示年龄,y 轴表示脂肪含量(百分比),画出散 点图,如下图.
32
栏目导航
a=143-1130×52=0, 故所求回归直线方程为 y=1130x.
33
栏目导航
34
1.求回归直线的方程时应注意的问题 (1)知道 x 与 y 呈线性相关关系,无需进行相关性检验,否则应首先进 行相关性检验.如果两个变量之间本身不具有相关关系,或者说,它们之
间的相关关系不显著,即使求出回归方程也是毫无意义的,而且用其估计
栏目导航
8
2.下表是 x 与 y 之间的一组数据,则 y 关于 x 的线性回归方程 y
=bx+a 必过( )
x
30
2.已知变量 x,y 有如下对应数据:
x
1
2
3
4
y
1
3
4
5
(1)作出散点图;
(2)用最小二乘法求关于 x,y 的回归直线方程.
栏目导航
[解] (1)散点图如下图所示.
31
栏目导航
(2) x =1+2+4 3+4=52, y =1+3+4 4+5=143,
4
i∑=1xiyi=1+6+12+20=39, i∑=41x2i =1+4+9+16=30, b=393-0-4×4×52×521243=1130,
(1)判断它们是否有相关关系,若有相关关系,请作一条拟合直 线;
(2)用最小二乘法求出年龄关于脂肪的线性回归方程.
栏目导航
25
[思路探究] (1)作出散点图,通过散点图判断它们是否具有相关 关系,并作出拟合直线;
(2)利用公式求出线性回归方程的系数 a,b 即可.
栏目导航
26
[解] (1)以 x 轴表示年龄,y 轴表示脂肪含量(百分比),画出散 点图,如下图.
32
栏目导航
a=143-1130×52=0, 故所求回归直线方程为 y=1130x.
33
栏目导航
34
1.求回归直线的方程时应注意的问题 (1)知道 x 与 y 呈线性相关关系,无需进行相关性检验,否则应首先进 行相关性检验.如果两个变量之间本身不具有相关关系,或者说,它们之
间的相关关系不显著,即使求出回归方程也是毫无意义的,而且用其估计
栏目导航
8
2.下表是 x 与 y 之间的一组数据,则 y 关于 x 的线性回归方程 y
=bx+a 必过( )
x
高等数学课件第八章最小二乘法

第八验数据
求它们的近似函数关系 y=f (x) .
需要解决两个问题:
1. 确定近似函数的类型
根据数据点的分布规律
根据问题的实际背景
2. 确定近似函数的标准
实验数据有误差,
不能要求
最小二乘法
偏差
有正有负,
值都较小且便于计算,
可由偏差平方和最小
为使所有偏差的绝对
物的量.
试根据上述数据定出经验公式
(P70例2)
解:
由化学反应速度的理论知, 经验公式应取
其中k , m 为待定常数.
对其取对数得
(线性函数)
(书中取的是常用对数)
因此 a , b 应满足法方程组:
经计算得
解得:
所求经验公式为
其均方误差为
观测数据:
用最小二乘法确定a, b
通过计算确定某些经验公式类型的方法:
-0.125 -0.018 0.189 -0.003
-0.021 0.086 0.093 -0.200
例2. 在研究某单分子化学反应速度时, 得到下列数据:
57.6 41.9 31.0 22.7 16.6 12.2 8.9 6.5
作业 (习题8 -10 ) P72 1 , 2
来确定近似函数 f (x) .
最小二乘法原理:
设有一列实验数据
分布在某条曲线上,
通过偏差平方和最小求该曲线的方
法称为最小二乘法,
找出的函数关系称为经验公式 .
, 它们大体
特别, 当数据点分布近似一条直线时,
问题为确定 a, b
令
满足:
使
得
解此线性方程组 即得 a, b
称为法方程组
数值分析34(最小二乘法)

但遗憾的是,在实际中噪声的形式往往是 未知的。在上个世纪60年代,Tukey说明了在 现实情况中,噪声的形式与高斯或拉普拉斯规 律都相去甚远。
回到起点!
作业: 习题 16,17,18 (数据有删减)
S1(x)Abx
得法方程
1A 63.380 b77 3.5 26394 3.380A 71.3 584 b31 5.6 82229
解得
A 4 .48,0 b 7 1 .0 2567
从而得到 a e A 1.3 12 15 3 03
y 1 . 3 1 2 1 3 e 5 0 1 . 0t5 3 F 6 ( 2 ) ( t 7 )
根据这些条件,可设想两种形式的函数关系:
y = F(t) 是双曲线型
1ab,即 y t
yt
(a t b)
y = F(t) 是指数形式 yaeb/t
b<0
y = F(t) 是双曲线型
1ab,即 y t
yt
(a t b)
为了确定a、b,令
y 1, x1
y
t
于是可用 x 的线性函数 S1(x)abx拟合 数据 (x i,y i) (i 1 ,.1 .)。.6 (,xi, yi) 可由原始 数据 (ti , yi ) 计算出来。
例2. 在某化学反应里,根据实验所得生成物的 浓度与时间关系如下表,求浓度y与时间t的拟 合曲线y=F(t).
t 12345678 Y 4.00 6.40 8.00 8.80 9.22 9.50 9.70 9.86 t 9 10 11 12 13 14 15 16 y 10.00 10.20 10.32 10.42 10.50 10.55 10.58 10.60
高斯提出了最小二乘法,而拉普拉斯提出了 最小模方法。从那时起就有了下面的问题:
最小二乘估计PPT课件

第21页/共29页
1.已知x,y之间的一组数据如下表,则y与x的线性 回归方程y=a+bx必经过点 ( D )
x
0
1
2
3
y
1Leabharlann 357A.(2,2) C.(1,2)
B.(1.5,0) D.(1.5,4)
第22页/共29页
2.(2014·湖北高考)根据如下样本数据 x3 4 5 6 7 8 y 4.0 2.5 -0.5 0.5 -2.0 -3.0
yi
1 4 9 16 25 36 49 64 204
x2 i 1 4 9 16 25 36 49 64
204
xi yi
1 8 27 64 125 216 343 512 1 296
第19页/共29页
y=-15+9x.
思考:哪一个对呢?
第20页/共29页
所以,利用最小二乘法估计时,要先作出数据的散 点图.如果散点图呈现一定的规律性,我们再根据这 个规律性进行拟合.如果散点图呈现出线性关系,我 们可以用最小二乘法估计出线性回归方程;如果散 点图呈现出其他的曲线关系,我们就要利用其他的 工具进行拟合.
1.了解最小二乘法的思想. 2. 能根据给出的线性回归方程系数公式建立线性 回归方程.(重点) 3.会用线性回归方程对总体进行估计.(难点)
第2页/共29页
思考1.用什么样的方法刻画点与直线的距离会更方
便有效?设直线方程为y=a+bx,样本点A(xi,yi)
方法一:点到直线的距离公式
y
A xi , yi
第25页/共29页
(1)散点图如图 所示:
y /百万元
解:(1)
0
(2)数据如下表: 可以求得 b=0.5,a=0.4 线性回归方程为:
1.已知x,y之间的一组数据如下表,则y与x的线性 回归方程y=a+bx必经过点 ( D )
x
0
1
2
3
y
1Leabharlann 357A.(2,2) C.(1,2)
B.(1.5,0) D.(1.5,4)
第22页/共29页
2.(2014·湖北高考)根据如下样本数据 x3 4 5 6 7 8 y 4.0 2.5 -0.5 0.5 -2.0 -3.0
yi
1 4 9 16 25 36 49 64 204
x2 i 1 4 9 16 25 36 49 64
204
xi yi
1 8 27 64 125 216 343 512 1 296
第19页/共29页
y=-15+9x.
思考:哪一个对呢?
第20页/共29页
所以,利用最小二乘法估计时,要先作出数据的散 点图.如果散点图呈现一定的规律性,我们再根据这 个规律性进行拟合.如果散点图呈现出线性关系,我 们可以用最小二乘法估计出线性回归方程;如果散 点图呈现出其他的曲线关系,我们就要利用其他的 工具进行拟合.
1.了解最小二乘法的思想. 2. 能根据给出的线性回归方程系数公式建立线性 回归方程.(重点) 3.会用线性回归方程对总体进行估计.(难点)
第2页/共29页
思考1.用什么样的方法刻画点与直线的距离会更方
便有效?设直线方程为y=a+bx,样本点A(xi,yi)
方法一:点到直线的距离公式
y
A xi , yi
第25页/共29页
(1)散点图如图 所示:
y /百万元
解:(1)
0
(2)数据如下表: 可以求得 b=0.5,a=0.4 线性回归方程为:
最小二乘法-PPT课件

请用最小二乘法求出这两个变量之间的线性回归方程.
解 根据上表数据,可以计算出:x 4.5, y 25.5 其他数据如下表
-
19
i 1 2 3 4 5 6 7 8 合计
,
xi
yi
1
1
2
4
3
9
4
16
5
25
6
36
7
49
8
64
36
204
x2 i
xi yi
1
1
4
8
9
27
16
64
25
125
36
216
49
343
d bxi yi a b2 1
方法二:
xi,abix
yi a bxi 2 0 -
yabx
x
4
显然方法二能有效地表示点A与直线y=a+bx的距离, 而且比方法一计算更方便,所以我们用它来表示二者 之间的接近程度.
-
5
思考2.怎样刻画多个点与直线的接近程度? 提示:
例如有5个样本点,其坐标分别为(x1,y1),(x2, y2),(x3,y3),(x4,y4),(x5,y5),与直 线y=a+bx的接近程度:
使上式达到最小值的直线y=a+bx就是所要求的直线, 这种方法称为最小二乘法.
-
7
思考3:怎样使 [y1 (a bx1)]2 [yn (a bxn )]2 达到最小值?
先来讨论3个样本点的情况
…………………①
-
8
3 a 2 - 2 ( a y - b x ) ( y 1 - b x 1 ) 2 ( y 2 - b x 2 ) 2 ( y 3 - b x 3 ) 2
解 根据上表数据,可以计算出:x 4.5, y 25.5 其他数据如下表
-
19
i 1 2 3 4 5 6 7 8 合计
,
xi
yi
1
1
2
4
3
9
4
16
5
25
6
36
7
49
8
64
36
204
x2 i
xi yi
1
1
4
8
9
27
16
64
25
125
36
216
49
343
d bxi yi a b2 1
方法二:
xi,abix
yi a bxi 2 0 -
yabx
x
4
显然方法二能有效地表示点A与直线y=a+bx的距离, 而且比方法一计算更方便,所以我们用它来表示二者 之间的接近程度.
-
5
思考2.怎样刻画多个点与直线的接近程度? 提示:
例如有5个样本点,其坐标分别为(x1,y1),(x2, y2),(x3,y3),(x4,y4),(x5,y5),与直 线y=a+bx的接近程度:
使上式达到最小值的直线y=a+bx就是所要求的直线, 这种方法称为最小二乘法.
-
7
思考3:怎样使 [y1 (a bx1)]2 [yn (a bxn )]2 达到最小值?
先来讨论3个样本点的情况
…………………①
-
8
3 a 2 - 2 ( a y - b x ) ( y 1 - b x 1 ) 2 ( y 2 - b x 2 ) 2 ( y 3 - b x 3 ) 2
最小二乘法PPT课件

教学内容 最小二乘法
教学目的:1.通过实例使学生体会变量间的相关 性 2.根据散点图对线性相关关系进行直 线拟合,从而对整体进行估计 教学重点:1、相关关系的判断
2、画散点图
3、用最小二乘法求回归直线方程
教学器材:多媒体电脑
复习:
1ቤተ መጻሕፍቲ ባይዱ相关关系的判断
2、线性相关:寻找一条直线。
y
O
X
求最小值----最小二乘法
(1)列表
2 3 4
5
2.2 3.8 5.5
6.5
4 9
4.4
11.4 22
32.5
16
25
6
合计
20
7.0
25
36
90
42
112.3
(2)x = 10
, y = 12.38
自学: P65
探究: P67
例1
例2
作业:P79
复习题一
4、 7
步骤:1、列表求出 2、代入公式求 a 、b 3、写出线性回归方程
例1、假设关于某设备的使用年限x和所支出
的维修费用y(万元)有如下统计资料:
x y 2 2.2 3 3.8 4 5.5 5 6.5 6 7.0
(1) 求回归直线方程;(2)估计使用10年 时,维修费用约是多少? 解:根据散点图知 x 与 y 成线性相关关系
教学目的:1.通过实例使学生体会变量间的相关 性 2.根据散点图对线性相关关系进行直 线拟合,从而对整体进行估计 教学重点:1、相关关系的判断
2、画散点图
3、用最小二乘法求回归直线方程
教学器材:多媒体电脑
复习:
1ቤተ መጻሕፍቲ ባይዱ相关关系的判断
2、线性相关:寻找一条直线。
y
O
X
求最小值----最小二乘法
(1)列表
2 3 4
5
2.2 3.8 5.5
6.5
4 9
4.4
11.4 22
32.5
16
25
6
合计
20
7.0
25
36
90
42
112.3
(2)x = 10
, y = 12.38
自学: P65
探究: P67
例1
例2
作业:P79
复习题一
4、 7
步骤:1、列表求出 2、代入公式求 a 、b 3、写出线性回归方程
例1、假设关于某设备的使用年限x和所支出
的维修费用y(万元)有如下统计资料:
x y 2 2.2 3 3.8 4 5.5 5 6.5 6 7.0
(1) 求回归直线方程;(2)估计使用10年 时,维修费用约是多少? 解:根据散点图知 x 与 y 成线性相关关系
数值分析 第七章最小二乘法

对于有些不能化为多项式形式的函数,照此矩阵形式,计算较 简单.
9
例:给出数据
xi yi
0.1
0.2
0.3
0.4
0. 5
0.6
0.172 0.323 0.484 0.690 1.000 1.579
现在用最小二乘法求拟合曲线 作变换 z =
y=
cx 1 + ax + bx2
1 1 a b 1 1 = + + x = a0 + a1 + a2 x , Φ = span{ ,1, x} y cx c c x x 1 10 5 5 = 5.814 2 10 5 a0 3 2 3 r 0.172 ur T 1 1 1 1 1 z = 3.096 A = 1 C = a1 M a 0.1 0.2 0.3 0.4 0.5 0.6 2 0.633 ur r T T 则最小二乘法的法方程组就可以写为: A AC = A z 求得: a0 = 0.503, a1 = 0.976, a2 = −1.967
i=1 i=1
⇒a0 ∑ ϕ j ( xi )ϕ0 ( xi ) ρ ( xi ) +L+ an ∑ ϕ j ( xi )ϕn ( xi ) = ∑ f ( xi )ρ ( xi ) ϕ j ( xi )
i=1 i=1 i=1
m
m
m
j = 0,1,L, n
这就得到了一个线性方程组,这个方程组称为最小二乘法的 法方程组(又称正规方程组). 由这个法方程组的解就可得到所要求的函数 ϕ ( x ) = a 0 ϕ 0 ( x ) + a1ϕ 1 ( x ) + L + a n ϕ n ( x )
数值分析课件Chapter7曲线拟合与线性最小二乘问题.ppt

法方程组可写成:GT F T FGx GT F T b
可以验证 x GT (GGT )1(F T F )1 F T b
是法方程组的一个解,故是原方程组的一个最小二乘解
推论7.1.2 若 rankA ,r则方n程组
有无穷多个最小二乘解。
Ax b
Def 2 方程组 Ax b 的所有最小二乘解中2-范数最小
8.9
8.5
10
4
3.5
22
9
8
11
4.5
4.2
23
9.5
8.1
12
4.6
3.5
24
10
8.1
可以看出,纤维强度随 拉伸倍数增加而增加
并且24个点大致分 布在一条直线附近
因此可认为强度与 拉伸倍数之间的主 要关系是线性关系
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
y ( x ) a bx
该直线称为这一问题的数学模型。
线性无关,下面讨论正交分解的具体实现方法。
记 A [a1, a2 , , an ],Q [q1, q2 , , qr ] 其中 a1, a2 , , ar线性无关,q1, q2 , , qr两两正交。
Gram-Schmidt正交化方法: 由 A QU 得
a1 u11q1 a2 u12q1 u22q2
y a bx c 1 x
1( x) 1;
2(x)
x;
3(x)
1 x
三、最小二乘问题解的存在性、唯一性
Def 1 设 A R,m若n 存在 x 精R确n地满足
可以验证 x GT (GGT )1(F T F )1 F T b
是法方程组的一个解,故是原方程组的一个最小二乘解
推论7.1.2 若 rankA ,r则方n程组
有无穷多个最小二乘解。
Ax b
Def 2 方程组 Ax b 的所有最小二乘解中2-范数最小
8.9
8.5
10
4
3.5
22
9
8
11
4.5
4.2
23
9.5
8.1
12
4.6
3.5
24
10
8.1
可以看出,纤维强度随 拉伸倍数增加而增加
并且24个点大致分 布在一条直线附近
因此可认为强度与 拉伸倍数之间的主 要关系是线性关系
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
y ( x ) a bx
该直线称为这一问题的数学模型。
线性无关,下面讨论正交分解的具体实现方法。
记 A [a1, a2 , , an ],Q [q1, q2 , , qr ] 其中 a1, a2 , , ar线性无关,q1, q2 , , qr两两正交。
Gram-Schmidt正交化方法: 由 A QU 得
a1 u11q1 a2 u12q1 u22q2
y a bx c 1 x
1( x) 1;
2(x)
x;
3(x)
1 x
三、最小二乘问题解的存在性、唯一性
Def 1 设 A R,m若n 存在 x 精R确n地满足
数值分析3-4(最小二乘法)

i F ( xi ) yi (i 0,1,..., m)
按某种标准最小。
度量标准不同,将导致不同的拟合结果,常用的准则有如下三种:
(1)使残差的最大绝对值为最小
max i
ei
max i
yi
F(xi )
min
(2)使残差的绝对值之和为最小
ei min i
(3)使残差的平方和为最小
ei2 min i
A 4.48072, b 1.0567 a e A 11.3253103
y 11.3253 103 e1.0567t F (2) (t )
请回答: 怎样比较这两个数学模型的好坏呢? 答:只要分别计算这两个数学模型的误差,从中挑选误差较小的模型即可。
本例经过计算可得
max i
|
(1) i
三、求解步骤
确定拟合曲线的形式 确定变量对应的数据
确定法方程 求解法方程
最困难!
四、举例
例1. 已知一组实验数据如下,求它的拟合曲线.
xi
1
2
3
4
5
fi
4 4.5 6
8 8.5
ωi
21311
解
根据所给数据,在坐标纸上标出,从图中看到各点在一条直线附近,故
可选择线性函数作拟合曲线,即令
S1( x) a0 a1 x
|
0.568
103
, max i
可由原始数据
计算出来。
拟合S数1(据x) a bx
。
( xi , yi ) (i 1,...,16) ( xi , yi )
(ti , yi )
这里0( x) 1,1( x) x 可求得 (k , j ),( y,代j入),法j方, 程k 得 0,1
按某种标准最小。
度量标准不同,将导致不同的拟合结果,常用的准则有如下三种:
(1)使残差的最大绝对值为最小
max i
ei
max i
yi
F(xi )
min
(2)使残差的绝对值之和为最小
ei min i
(3)使残差的平方和为最小
ei2 min i
A 4.48072, b 1.0567 a e A 11.3253103
y 11.3253 103 e1.0567t F (2) (t )
请回答: 怎样比较这两个数学模型的好坏呢? 答:只要分别计算这两个数学模型的误差,从中挑选误差较小的模型即可。
本例经过计算可得
max i
|
(1) i
三、求解步骤
确定拟合曲线的形式 确定变量对应的数据
确定法方程 求解法方程
最困难!
四、举例
例1. 已知一组实验数据如下,求它的拟合曲线.
xi
1
2
3
4
5
fi
4 4.5 6
8 8.5
ωi
21311
解
根据所给数据,在坐标纸上标出,从图中看到各点在一条直线附近,故
可选择线性函数作拟合曲线,即令
S1( x) a0 a1 x
|
0.568
103
, max i
可由原始数据
计算出来。
拟合S数1(据x) a bx
。
( xi , yi ) (i 1,...,16) ( xi , yi )
(ti , yi )
这里0( x) 1,1( x) x 可求得 (k , j ),( y,代j入),法j方, 程k 得 0,1
最小二乘法线性详细说明.ppt

19
3. 回归方程的精度和相关系数
用最小二乘法确定a, b存在误差。 总结经验公式时,我们初步分析判断所假定
的函数关系是正确,为了解决这些问题,就 需要讨论回归方程的精度和相关性。 为了估计回归方程的精度,进一步计算数据
点 xi,yi 偏离最佳直线y=a+bx的大小,我们 引入概念——剩余标准差 s ,它反映着回
一种可能是各数据点与该线偏差较小,一种可能是各数据 点与该线偏差较大。
当R 1时,s 减小,一般的数据点越靠近最佳值两旁。两
变量间的关系线性相关,可以认为是线性关系,最佳直线 所反应的函数关系也越接近两变量间的客观关系。同时还 说明了测量的精密度高。
当条“R 最佳1时”,直线s 增。大然,而根,据数数据据点点与的“分最布佳,”也直许线能的得偏到差一过
14
根据二元函数求极值法,把③式对a和b分 别求出偏导数。得:
n
v2 i
i1
a n
2yi a bxi
4
v2 i
i1 2
b
yi a bxi xi
15
令④等于零,得:
n
n
yi na b xi 0
i1 n
i1
n
n
5
yixi
i1
a xi i1
b
x2 i
i1
0
解方程,得:
而且: b 1.993 0.006
31
第二节 二元线性回归
已知函数形式(或判断经验公式的函数形式)为 y a b1x1 b2x2
式中,均为独立变量,故是二元线性回归。 若有实验数据:
x1 x11, x12,......... .x1n x2 x21, x22,......... .x2n
3. 回归方程的精度和相关系数
用最小二乘法确定a, b存在误差。 总结经验公式时,我们初步分析判断所假定
的函数关系是正确,为了解决这些问题,就 需要讨论回归方程的精度和相关性。 为了估计回归方程的精度,进一步计算数据
点 xi,yi 偏离最佳直线y=a+bx的大小,我们 引入概念——剩余标准差 s ,它反映着回
一种可能是各数据点与该线偏差较小,一种可能是各数据 点与该线偏差较大。
当R 1时,s 减小,一般的数据点越靠近最佳值两旁。两
变量间的关系线性相关,可以认为是线性关系,最佳直线 所反应的函数关系也越接近两变量间的客观关系。同时还 说明了测量的精密度高。
当条“R 最佳1时”,直线s 增。大然,而根,据数数据据点点与的“分最布佳,”也直许线能的得偏到差一过
14
根据二元函数求极值法,把③式对a和b分 别求出偏导数。得:
n
v2 i
i1
a n
2yi a bxi
4
v2 i
i1 2
b
yi a bxi xi
15
令④等于零,得:
n
n
yi na b xi 0
i1 n
i1
n
n
5
yixi
i1
a xi i1
b
x2 i
i1
0
解方程,得:
而且: b 1.993 0.006
31
第二节 二元线性回归
已知函数形式(或判断经验公式的函数形式)为 y a b1x1 b2x2
式中,均为独立变量,故是二元线性回归。 若有实验数据:
x1 x11, x12,......... .x1n x2 x21, x22,......... .x2n
最小二乘法PPT课件

第2页/共74页
一、问题背景
• 在多数估计和曲线拟合的问题中,不论是 参数估计还是曲线拟合,都要求确定某些(或 一个)未知量,使得所确定的未知量能最好地 适应所测得的一组观测值,即对观测值提供 一个好的拟合。
• 解决这类问题最常用的方法就是最小二乘 法。
• 在一些情况下,即使函数值不是随机变量, 最小二乘法也可使用。
数
,aˆ1
,…,
aˆ2
。这样aˆk求出的参数叫参数的最小二乘估计。
第6页/共74页
正规方程
=最小
• 根据数学分析中求函数极值的条件:
共得k个方程,称正规方程,求此联立方程的解可得出诸参数估计值
(j=1,2,…,k)。 aˆ 等精度观测的情况,若诸观测值yi是不等精度的观测,即它们服从不 同的方差σi2的正态分布N(0,1),那么也不难证明,在这种情况下,最小二乘 法可改为:
正规方程(5—19)组,还可表示成如下形式
表示成矩阵形式为
第23页/共74页
线性参数正规方程的矩阵形式
又因
(5-21)
有 即 若令 则正规方程又可写成 若矩阵C是满秩的,则有
(5-22)
(5-22) (5-23)
第24页/共74页
的数学期望Xˆ
因 可见 Xˆ 是X的无偏估计。
式中Y、X为列向量(n ×1阶矩阵和t×l阶矩阵)
例5.3
• 试求例5.1中铜棒长度的测量精度。
已知残余误差方程为 将ti,li,值代人上式,可得残余误差为
第43页/共74页
(二)不等精度测量数据的精度估计
不等精度测量数据的精度估计与等精度测量数据的精度估计相似,只是公 式中的残余误差平方和变为加权的残余误差平方和,测量数据的单位权方差 的无偏估计为
一、问题背景
• 在多数估计和曲线拟合的问题中,不论是 参数估计还是曲线拟合,都要求确定某些(或 一个)未知量,使得所确定的未知量能最好地 适应所测得的一组观测值,即对观测值提供 一个好的拟合。
• 解决这类问题最常用的方法就是最小二乘 法。
• 在一些情况下,即使函数值不是随机变量, 最小二乘法也可使用。
数
,aˆ1
,…,
aˆ2
。这样aˆk求出的参数叫参数的最小二乘估计。
第6页/共74页
正规方程
=最小
• 根据数学分析中求函数极值的条件:
共得k个方程,称正规方程,求此联立方程的解可得出诸参数估计值
(j=1,2,…,k)。 aˆ 等精度观测的情况,若诸观测值yi是不等精度的观测,即它们服从不 同的方差σi2的正态分布N(0,1),那么也不难证明,在这种情况下,最小二乘 法可改为:
正规方程(5—19)组,还可表示成如下形式
表示成矩阵形式为
第23页/共74页
线性参数正规方程的矩阵形式
又因
(5-21)
有 即 若令 则正规方程又可写成 若矩阵C是满秩的,则有
(5-22)
(5-22) (5-23)
第24页/共74页
的数学期望Xˆ
因 可见 Xˆ 是X的无偏估计。
式中Y、X为列向量(n ×1阶矩阵和t×l阶矩阵)
例5.3
• 试求例5.1中铜棒长度的测量精度。
已知残余误差方程为 将ti,li,值代人上式,可得残余误差为
第43页/共74页
(二)不等精度测量数据的精度估计
不等精度测量数据的精度估计与等精度测量数据的精度估计相似,只是公 式中的残余误差平方和变为加权的残余误差平方和,测量数据的单位权方差 的无偏估计为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i F ( x i) y i ( i 0 , 1 ,. m ) ..,
按某种标准最小。
度量标准不同,将导致不同的拟合结果,常用 的准则有如下三种:
(1)使残差的最大绝对值为最小
m i a ei x m i ayix F(xi)min
(2)使残差的绝对值之和为最小
ei min i
4. 广义定义
通常把最小二乘法
2 都考虑为加权平方和
2
即
m
2 2 (x i)S [ (x i)y i]2 (x ) 0
i 0
其中
S ( x ) a 0 0 ( x ) a 1 1 ( x ) . a . n n ( x . ) ( n m )
个函数 yS(x),使误差平方和最小,
即
m
m
2 2
i2
[S(xi ) yi ]2
i0
i0
m
Sm(x)in i0[S(xi ) yi ]2
这里
S ( x ) a 0 0 ( x ) a 1 1 ( x ) . a . n n ( x . ) ( n m )
n
2 (xi)[ ajj(xi)f(xi)]k(xi)
i0
j0
展开
n m
m
a j (x i)j(x i)k (x i) (x i)f(x i)k (x i)
j 0 i 0
i 0
法方程
解方程组
有唯 ak 一 ak (k 解 0,1,.n .).,
根据这些条件,可设想两种形式的函数关系:
y = F(t) 是双曲线型
1ab,即 y t
yt
(a t b)
y = F(t) 是指数形式 yaeb/t
b<0
y = F(t) 是双曲线型
1ab,即 y t
yt
(a t b)
为了确定a、b,令
y 1, x1
y
t
于是可用 x 的线性函数 S1(x)abx拟合 数据 (x i,y i) (i 1 ,.1 .)。.6 (,xi, yi) 可由原始 数据 (ti , yi ) 计算出来。
第3章 函数逼近与曲线拟合 §4 曲线拟合的最小二乘法
一、最小二乘法的定义 二、求解方法 三、求解步骤 四、举例
一、最小二乘法的定义
1. “曲线拟合”问题 已知:一组实验数据(xi,yi)(i=0,1,…,m), 且观测数据有误差
求:自变量x与因变量y之间的函数关系 y=F(x) ,不要求y=F(x)经过所有点,而只要 求在给定点上误差
i0
i0
这里
m
Sm(x)in i0[S(xi ) yi ]2
S (x ) a 0 a 1 x . .a .n x n ( n m )
3. 一般定义
已知: 一组数据(xi,yi)(i=0,1,…,m),
求: 在函数类 sp {0 ,a 1 ,n .n .} 中.找,一
从而得到
y
t
F (1 )(t)
8.6 06 t 1 2.6 11 822
y = F(t) 是指数形式 yabe /t (b0)
为了确定a 与b,对上式两边取对数得
lnylnab
令
yˆlny,Aln ta,x1
t
于是由 (ti , yi ) 计算出 (xi, yˆi) ,拟合数 据 (xi, yˆi) 的曲线仍设为
t 从图中可以看出开始时浓度增加较快,后来 逐渐减弱,到一定时间就基本稳定在一个数 值上,即当t→∞时,y趋于某个常数,故有一 水平渐近线。另外 t = 0 时,反应未开始,浓 度为0。概括起来为
(1)y是t的增函数 ; (2)当t 0时,y 0; (3)t 时,y趋于一个定值
注:权函数在实际问题中有重要作用!
二、求解方法
求S*(x)
求如下多元函数的最小值
m
n
I(a 0,a 1,.a .n.) , (xi)[aj j(xi)f(xi)2]
i 0
j 0
由多元函数 求极值的必 要条件
I 0, (k0,1,,n) 即 ak
I
ak
m
S1(x)Abx
得法方程
1A 63.380 b77 3.5 26394 3.380A 71.3 584 b31 5.6 82229
S 1(x )a 0 a 1x
得法方程为
82a2a00272a41a14174.5
解得
a 02 .7,a 7 1 1 .13
于是所求拟合曲线为
S 1 (x )2 .7 7 1 .1x 3
例2. 在某化学反应里,根据实验所得生成物的 浓度与时间关系如下表,求浓度y与时间t的拟 合曲线y=F(t).
则 S(x)a0 0(x)a1 1(x).. .an n(x)
三、求解步骤
确定拟合曲线的形式
最困难!
确定变量对应的数据
确定法方程
求解法方程
四、举例
例1. 已知一组实验数据如下,求它的拟合曲线.
xi 1 2 3 4 5
fi 4 4.5 6 8 8.5
ωi
21311
解 根据所给数据,在坐标纸上标出,从图 中看到各点在一条直线附近,故可选择 线性函数作拟合曲线,即令
(3)使残差的平方和为最小
ei2 min i
最小二乘法
2. 多项式拟合的一般定义
已知: 一组数据(xi,yi)(i=0,1,…,m),
求: 在函数类 sp{ a 1,x n,..x.n} , 中找一
个函数 yS(x),使误差平方和最小,
即
m
m
2 2
i2
[S(xi ) yi ]2
t 12345678 Y 4.00 6.40 8.00 8.80 9.22 9.50 9.70 9.86 t 9 10 11 12 13 14 15 16 y 10.00 10.20 10.32 10.42 10.50 10.55 10.58 10.60
解 根据所给数据,在坐标纸上标出,得下图 y
这 0 ( x ) 里 1 ,1 ( x ) x
可求得 (k , j)(y ,,j)j,,k 0 ,1 代入法方程得
1a63.38b 01 7.8337 132 0 3.38a 01 7.538b 43 0.552 818 306
解得
a8.6 06 , 2 b 1 1.6 61 822
按某种标准最小。
度量标准不同,将导致不同的拟合结果,常用 的准则有如下三种:
(1)使残差的最大绝对值为最小
m i a ei x m i ayix F(xi)min
(2)使残差的绝对值之和为最小
ei min i
4. 广义定义
通常把最小二乘法
2 都考虑为加权平方和
2
即
m
2 2 (x i)S [ (x i)y i]2 (x ) 0
i 0
其中
S ( x ) a 0 0 ( x ) a 1 1 ( x ) . a . n n ( x . ) ( n m )
个函数 yS(x),使误差平方和最小,
即
m
m
2 2
i2
[S(xi ) yi ]2
i0
i0
m
Sm(x)in i0[S(xi ) yi ]2
这里
S ( x ) a 0 0 ( x ) a 1 1 ( x ) . a . n n ( x . ) ( n m )
n
2 (xi)[ ajj(xi)f(xi)]k(xi)
i0
j0
展开
n m
m
a j (x i)j(x i)k (x i) (x i)f(x i)k (x i)
j 0 i 0
i 0
法方程
解方程组
有唯 ak 一 ak (k 解 0,1,.n .).,
根据这些条件,可设想两种形式的函数关系:
y = F(t) 是双曲线型
1ab,即 y t
yt
(a t b)
y = F(t) 是指数形式 yaeb/t
b<0
y = F(t) 是双曲线型
1ab,即 y t
yt
(a t b)
为了确定a、b,令
y 1, x1
y
t
于是可用 x 的线性函数 S1(x)abx拟合 数据 (x i,y i) (i 1 ,.1 .)。.6 (,xi, yi) 可由原始 数据 (ti , yi ) 计算出来。
第3章 函数逼近与曲线拟合 §4 曲线拟合的最小二乘法
一、最小二乘法的定义 二、求解方法 三、求解步骤 四、举例
一、最小二乘法的定义
1. “曲线拟合”问题 已知:一组实验数据(xi,yi)(i=0,1,…,m), 且观测数据有误差
求:自变量x与因变量y之间的函数关系 y=F(x) ,不要求y=F(x)经过所有点,而只要 求在给定点上误差
i0
i0
这里
m
Sm(x)in i0[S(xi ) yi ]2
S (x ) a 0 a 1 x . .a .n x n ( n m )
3. 一般定义
已知: 一组数据(xi,yi)(i=0,1,…,m),
求: 在函数类 sp {0 ,a 1 ,n .n .} 中.找,一
从而得到
y
t
F (1 )(t)
8.6 06 t 1 2.6 11 822
y = F(t) 是指数形式 yabe /t (b0)
为了确定a 与b,对上式两边取对数得
lnylnab
令
yˆlny,Aln ta,x1
t
于是由 (ti , yi ) 计算出 (xi, yˆi) ,拟合数 据 (xi, yˆi) 的曲线仍设为
t 从图中可以看出开始时浓度增加较快,后来 逐渐减弱,到一定时间就基本稳定在一个数 值上,即当t→∞时,y趋于某个常数,故有一 水平渐近线。另外 t = 0 时,反应未开始,浓 度为0。概括起来为
(1)y是t的增函数 ; (2)当t 0时,y 0; (3)t 时,y趋于一个定值
注:权函数在实际问题中有重要作用!
二、求解方法
求S*(x)
求如下多元函数的最小值
m
n
I(a 0,a 1,.a .n.) , (xi)[aj j(xi)f(xi)2]
i 0
j 0
由多元函数 求极值的必 要条件
I 0, (k0,1,,n) 即 ak
I
ak
m
S1(x)Abx
得法方程
1A 63.380 b77 3.5 26394 3.380A 71.3 584 b31 5.6 82229
S 1(x )a 0 a 1x
得法方程为
82a2a00272a41a14174.5
解得
a 02 .7,a 7 1 1 .13
于是所求拟合曲线为
S 1 (x )2 .7 7 1 .1x 3
例2. 在某化学反应里,根据实验所得生成物的 浓度与时间关系如下表,求浓度y与时间t的拟 合曲线y=F(t).
则 S(x)a0 0(x)a1 1(x).. .an n(x)
三、求解步骤
确定拟合曲线的形式
最困难!
确定变量对应的数据
确定法方程
求解法方程
四、举例
例1. 已知一组实验数据如下,求它的拟合曲线.
xi 1 2 3 4 5
fi 4 4.5 6 8 8.5
ωi
21311
解 根据所给数据,在坐标纸上标出,从图 中看到各点在一条直线附近,故可选择 线性函数作拟合曲线,即令
(3)使残差的平方和为最小
ei2 min i
最小二乘法
2. 多项式拟合的一般定义
已知: 一组数据(xi,yi)(i=0,1,…,m),
求: 在函数类 sp{ a 1,x n,..x.n} , 中找一
个函数 yS(x),使误差平方和最小,
即
m
m
2 2
i2
[S(xi ) yi ]2
t 12345678 Y 4.00 6.40 8.00 8.80 9.22 9.50 9.70 9.86 t 9 10 11 12 13 14 15 16 y 10.00 10.20 10.32 10.42 10.50 10.55 10.58 10.60
解 根据所给数据,在坐标纸上标出,得下图 y
这 0 ( x ) 里 1 ,1 ( x ) x
可求得 (k , j)(y ,,j)j,,k 0 ,1 代入法方程得
1a63.38b 01 7.8337 132 0 3.38a 01 7.538b 43 0.552 818 306
解得
a8.6 06 , 2 b 1 1.6 61 822
