最小二乘法拟合插值法精品PPT课件
合集下载
最新-数值计算方法课件CH3插值法与最小二乘法—37数据拟合的最小二乘法-PPT文档资料

转化
(a0,a1, 取,an 极)小值
a0*,的a1*问,题,an*
由多元函数取极值的必要条件
得:
(a0,a1,,an) 0
ak
k0,1,,n
ak
m
n
i[2( ajj(xi)yi)k(xi)] 0
i0
j0
移项整理得:
mn
m
i ajj(xi)k(xi) iyik(xi)
i0 j0
i0
交换求和号顺序得:
n[ mij(xi)k(xi)a ]j miyik(xi) (k0,1, ,n) (7)
j0i0
i0
即
m
m
m
a0 i0(xi)k(xi)a1 i1(xi)k(xi) an in(xi)k(xi)
m
Байду номын сангаас
m
((jj,, kk)) ij(xi)k(xi) ik(xi)j(xi)(k,j) (8)
i0
i0
m
(f,k) iyik(xi)
(9)
i0
方程组(7)便可化为:
n
n
(j,k)aj (k,j)aj (f,k)(k0,1, ,n) (10)
一、最小二乘法的基本概念
根据上述实例图中测试点的分布情况,可以画出很多条靠 近这些点的直线,其方程都可表示为:
S(t)atb
(1)
其中: a, b 待定.要从形如(1)式的所有直线中,找出一条用某种 度量标准来衡量最靠近所有数据点 (ti , si ) (的i直0,1线,....m ,)
若 a, b 给定,计算值 S(ti) 与测量数据 si 之差为:
计算机数值方法第三章 插值法与最小二乘法.ppt

《 计 算 机 数 值 方 法 》
(3―1)
使其在给定的n+1个互异的插值结点上满足
插值条件
Pn(xi)=yi (i=0,1,…,n) (3―2)
第三章
插值法与最小二乘法
这样的多项式是否存在并且唯一呢?
根据插值条件,代数多项式(3―1)中的各个系
数a0,a1,…,an应满足下列n+1阶线性方程组
2 n Pn ( x0 ) a0 a1 x0 a2 x0 an x0 y0 2 n Pn ( x1 ) a0 a1 x1 a2 x1 an x1 y1 (3―3) P ( x ) a a x a x2 a xn y n n 0 1 n 2 n n n n
《 计 算 机 数 值 方 法 》
称 l (x),l (x) 为线性插值基函数 k k+1
第三章
插值法与最小二乘法
例1: 已知 100 10 , 121 11 ,求 y 115
代入点斜式插值多项式
y1 y0 L1 ( x) y0 ( x x0 ) x1 x0
得 y=10.71428
第三章
插值法与最小二乘法
下面给出插值多项式Pn(x)余项的表达式。
定理 设函数f(x)在区间[a,b]上具有n+1阶导数,
Pn(x)为次数不高于n的多项式,
且 Pn(xi)=yi (i=0,1,…,n)
则对插值区间上的任何x,都存在ξ∈(a,b),使得
《 计 算 机 数 值 方 法 》
f ( n 1) ( ) Rn ( x ) n 1 ( x ) ( n 1)! 其中,n 1 ( x) ( x x0 )( x x1 ) ( x xn ) ( x xi )
(3―1)
使其在给定的n+1个互异的插值结点上满足
插值条件
Pn(xi)=yi (i=0,1,…,n) (3―2)
第三章
插值法与最小二乘法
这样的多项式是否存在并且唯一呢?
根据插值条件,代数多项式(3―1)中的各个系
数a0,a1,…,an应满足下列n+1阶线性方程组
2 n Pn ( x0 ) a0 a1 x0 a2 x0 an x0 y0 2 n Pn ( x1 ) a0 a1 x1 a2 x1 an x1 y1 (3―3) P ( x ) a a x a x2 a xn y n n 0 1 n 2 n n n n
《 计 算 机 数 值 方 法 》
称 l (x),l (x) 为线性插值基函数 k k+1
第三章
插值法与最小二乘法
例1: 已知 100 10 , 121 11 ,求 y 115
代入点斜式插值多项式
y1 y0 L1 ( x) y0 ( x x0 ) x1 x0
得 y=10.71428
第三章
插值法与最小二乘法
下面给出插值多项式Pn(x)余项的表达式。
定理 设函数f(x)在区间[a,b]上具有n+1阶导数,
Pn(x)为次数不高于n的多项式,
且 Pn(xi)=yi (i=0,1,…,n)
则对插值区间上的任何x,都存在ξ∈(a,b),使得
《 计 算 机 数 值 方 法 》
f ( n 1) ( ) Rn ( x ) n 1 ( x ) ( n 1)! 其中,n 1 ( x) ( x x0 )( x x1 ) ( x xn ) ( x xi )
插值法与最小二乘拟合

5
证 由于Rn(xi) = (xi)-Pn(xi) =0 (i=0,1,…,n), 所以设
Rn(x)=K(x)n+1(x)
对于任一x[a,b],x xi(i=0,1,2,…,n),构造函数 (t)=f(t)-Pn(t)-K(x)n+1(t)
则有
(xi)=0 (i=0,1,2,…,n), (x)=0
4.1.2 插值多项式的截断误差
定理 设(n)(x)在[a,b]连续, (n+1)(x)在(a,b)内存在,在节点a x0<x1<…<xn b上, 满足插值条件(4.2)的插值多项式Pn(x),对 任一x[a,b],插值余项为
Rn (x)
f ( x) Pn ( x)
f (n (n
1) ( )
1)!
ln11.25L2(11.25)
(11.25 11)(11.25 12) 2.302585 (10 11)(10 12)
(11.25 10)(11.25 12) (11 10)(11 12)
2.397895
(11.25 10)(11.25 11) (12 10)(12 11)
xk+1 x
9
待定系数
求 lk-1(x):
令lk 1( x) A ( x xk ) ( x xk 1) ,
由
ll
k k
1( xk ( xk )
1) 1,
1,
lk1( xk ) lk1( xk1 ) 0; l k(xk 1) l k( xk 1) 0;
l
k
1( xk 1)
L2( x j ) = y j
(i, k 0,1,, n)
可知 lk ( x) Ak ( x x0 )( x xk 1 )( x xk 1 )( x xn ),
曲线拟合最小二乘法ppt课件

这里
1( x), ,l ( x)
是线性无关函数系,
为待定常数.
i (i 1, 2, , l)
9
在例1中,设函数
1( x) 1, 2( x) x, 3( x) x2
误 n,
我们希望猜想的数学模型应尽量接近观测数据,
m
2 i
m
[s * ( xi )
f ( xi )]2
i0
i0
m
min
s( x)
[s(
i0
xi
)
f ( xi )]2.
11
(1)直线拟合
设已知数据点 xi , yi , i 1,2,, m ,分布大致为一
条直线。作拟合直线 y(x) a0 a1x ,该直线不是通
的方法称为曲线拟称合为“,残f(差x)”
1
x
x0 x1 x2 …… xn
y
y0
y1
y2
…… yn
y=p(x) y=f(x)
插值
2
求一条曲线,使数据点均在离此曲线的上方或下方不远处, 所求的曲线称为拟合曲线,它既能反映数据的总体分布,又 不至于出现局部较大的波动,更能反映被逼近函数的特性, 使求得的逼近函数与已知函数从总体上来说其偏差按某种 方法度量达到最小。
解得 a0 0.562302 , a1 0.772282
由 a0 ln a 得 a ea0 e0.562302 1.754708,
23
由a1 b 得 b a1 0.772282
于是得到拟合指数函数为 y 1.754708 e0.772282x
(4)超定方程组的最小二乘解
最小二乘法与曲线拟合-PPT

点(xi,yi)带入y=(x) ,便得到以a0,a1,…,am为未知
量的矛盾方程组
0 + 1 1 + 2 12 + ⋯ + 1 = 1
其矩阵形式为
Ԧ =
0 + 1 2 + 2 22 + ⋯ +
其中
1
= 1
⋮
1
1
2
⋮
12
22
⋮
2
⋯
⋯
⋱
最小二乘法与曲线拟合
§5.0 问题的提出
如果实际问题要求解在[a,b]区间的每一点都“很
好地” 逼近f(x)的话,运用插值函数有时就要失败。
另外,插值所需的数据往往来源于观察测量,本身有
一定的误差。要求插值曲线通过这些本身有误差的点,
势必使插值结果更加不准确。
如果由试验提供的数据量比较大,又必然使得插值
不为零,从而有rankA=m+1。由引理2知,正则方程
组有唯一解。
证毕
四、最小二乘法拟合曲线的步骤
1..通过观察、分析得到拟合曲线的数学模型,或
根据经验公式确定数学模型。
2.将拟合曲线的数学模型转换为多项式。
3.写出矛盾方程组。
4.写出正则方程组。(可由多项式模型直接得到)
5.求解正则方程组,得到拟合曲线的待定系数。
多项式的次数过高而效果不理想。
从给定的一组试验数据出发,寻求函数的一个近似
表达式y=(x),要求近似表达式能够反映数据的基本
趋势而又不一定过全部的点(xi,yi),这就是曲线拟合
问题,函数的近似表达式y=(x)称为拟合曲线。本章
介绍用最小二乘法求拟合曲线。
§5.1 用最小二乘法求解矛盾方程组
量的矛盾方程组
0 + 1 1 + 2 12 + ⋯ + 1 = 1
其矩阵形式为
Ԧ =
0 + 1 2 + 2 22 + ⋯ +
其中
1
= 1
⋮
1
1
2
⋮
12
22
⋮
2
⋯
⋯
⋱
最小二乘法与曲线拟合
§5.0 问题的提出
如果实际问题要求解在[a,b]区间的每一点都“很
好地” 逼近f(x)的话,运用插值函数有时就要失败。
另外,插值所需的数据往往来源于观察测量,本身有
一定的误差。要求插值曲线通过这些本身有误差的点,
势必使插值结果更加不准确。
如果由试验提供的数据量比较大,又必然使得插值
不为零,从而有rankA=m+1。由引理2知,正则方程
组有唯一解。
证毕
四、最小二乘法拟合曲线的步骤
1..通过观察、分析得到拟合曲线的数学模型,或
根据经验公式确定数学模型。
2.将拟合曲线的数学模型转换为多项式。
3.写出矛盾方程组。
4.写出正则方程组。(可由多项式模型直接得到)
5.求解正则方程组,得到拟合曲线的待定系数。
多项式的次数过高而效果不理想。
从给定的一组试验数据出发,寻求函数的一个近似
表达式y=(x),要求近似表达式能够反映数据的基本
趋势而又不一定过全部的点(xi,yi),这就是曲线拟合
问题,函数的近似表达式y=(x)称为拟合曲线。本章
介绍用最小二乘法求拟合曲线。
§5.1 用最小二乘法求解矛盾方程组
数值分析3-4(最小二乘法)优秀PPT

i F ( xi ) yi (i 0,1,...,m)
按某种标准最小。
度量标准不同,将导致不同的拟合结果,常用 的准则有如下三种:
(1)使残差的最大绝对值为最小
max i
ei
max i
yi F (xi )
min
(2)使残差的绝对值之和为最小
ei min i
(3)使残差的平方和为最小
min
S ( x )
[S( xi
i0
)
yi
]2
S ( x) a0 a1x ... an xn (n m)
3. 一般定义
已知: 一组数据(xi,yi)(i=0,1,…,m), 求: 在函数类 span{0 ,1,...,n }中找一
个函数 y S ( x) ,使误差平方和最小,
即 这里
解 根据所给数据,在坐标纸上标出,得下图 y
t 从图中可以看出开始时浓度增加较快,后来 逐渐减弱,到一定时间就基本稳定在一个数 值上,即当t→∞时,y趋于某个常数,故有一 水平渐近线。另外 t = 0 时,反应未开始,浓 度为0。概括起来为
(1) y是t的增函数; (2)当t 0 时,y 0; (3)t 时,y趋于一个定值
m
m
2 2
2 i
[S ( xi ) yi ]2
i0
i0
m
min
S ( x )
[S(xi )
i0
yi ]2
S( x) a00 ( x) a11( x) ... ann ( x) (n m)
4. 广义定义
通常把最小二乘法
2 都考虑为加权平方和
2
即
m
2 2
( xi )[S ( xi ) yi ]2
按某种标准最小。
度量标准不同,将导致不同的拟合结果,常用 的准则有如下三种:
(1)使残差的最大绝对值为最小
max i
ei
max i
yi F (xi )
min
(2)使残差的绝对值之和为最小
ei min i
(3)使残差的平方和为最小
min
S ( x )
[S( xi
i0
)
yi
]2
S ( x) a0 a1x ... an xn (n m)
3. 一般定义
已知: 一组数据(xi,yi)(i=0,1,…,m), 求: 在函数类 span{0 ,1,...,n }中找一
个函数 y S ( x) ,使误差平方和最小,
即 这里
解 根据所给数据,在坐标纸上标出,得下图 y
t 从图中可以看出开始时浓度增加较快,后来 逐渐减弱,到一定时间就基本稳定在一个数 值上,即当t→∞时,y趋于某个常数,故有一 水平渐近线。另外 t = 0 时,反应未开始,浓 度为0。概括起来为
(1) y是t的增函数; (2)当t 0 时,y 0; (3)t 时,y趋于一个定值
m
m
2 2
2 i
[S ( xi ) yi ]2
i0
i0
m
min
S ( x )
[S(xi )
i0
yi ]2
S( x) a00 ( x) a11( x) ... ann ( x) (n m)
4. 广义定义
通常把最小二乘法
2 都考虑为加权平方和
2
即
m
2 2
( xi )[S ( xi ) yi ]2
数值计算方法CH插值法与最小二乘法数据拟合的最小二乘法
i0
(1,0 )
6
6
(1,1) i1(xi )1(xi ) xi2 3.64
i0
i0
6
6
( f ,0 ) i yi0 (xi ) yi 25.1
i0
i0
6
6
( f ,1) i yi1(xi ) yi xi 20.18
i0
i0
得法方程组:
7 4.2
34.6.24
a0 a1
2 2
m
i (S (xi ) yi )2
m
n
i (
a j j (xi ) yi )2
i0
i0
j0
为拟合系数 a j ( j 0,1的,函, n数) .因此,可设平方误差为:
m
n
(a0 , a1,, an ) i ( a j j (xi ) yi )2
i0
j0
第7页/共28页
求最小二乘解 S *(的x) 问题
第3页/共28页
一、最小二乘法的基本概念
根据上述实例图中测试点的分布情况,可以画出很多条靠 近这些点的直线,其方程都可表示为:
S(t) at b
(1)
其中: a, b 待定.要从形如(1)式的所有直线中,找出一条用某种 度量标准来衡量最靠近所有数据点 (ti , si ) (的i 直0,1线,...,.m)
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
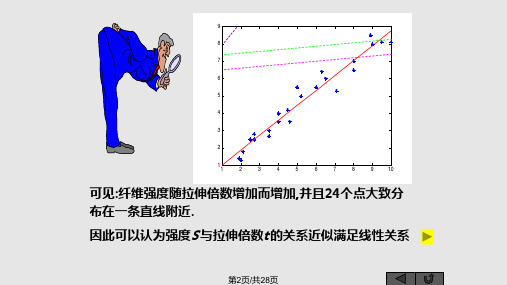
可见:纤维强度随拉伸倍数增加而增加,并且24个点大致分 布在一条直线附近.
因此可以认为强度S 与拉伸倍数t 的关系近似满足线性关系
数值分析课件Chapter7曲线拟合与线性最小二乘问题.ppt

法方程组可写成:GT F T FGx GT F T b
可以验证 x GT (GGT )1(F T F )1 F T b
是法方程组的一个解,故是原方程组的一个最小二乘解
推论7.1.2 若 rankA ,r则方n程组
有无穷多个最小二乘解。
Ax b
Def 2 方程组 Ax b 的所有最小二乘解中2-范数最小
8.9
8.5
10
4
3.5
22
9
8
11
4.5
4.2
23
9.5
8.1
12
4.6
3.5
24
10
8.1
可以看出,纤维强度随 拉伸倍数增加而增加
并且24个点大致分 布在一条直线附近
因此可认为强度与 拉伸倍数之间的主 要关系是线性关系
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
y ( x ) a bx
该直线称为这一问题的数学模型。
线性无关,下面讨论正交分解的具体实现方法。
记 A [a1, a2 , , an ],Q [q1, q2 , , qr ] 其中 a1, a2 , , ar线性无关,q1, q2 , , qr两两正交。
Gram-Schmidt正交化方法: 由 A QU 得
a1 u11q1 a2 u12q1 u22q2
y a bx c 1 x
1( x) 1;
2(x)
x;
3(x)
1 x
三、最小二乘问题解的存在性、唯一性
Def 1 设 A R,m若n 存在 x 精R确n地满足
可以验证 x GT (GGT )1(F T F )1 F T b
是法方程组的一个解,故是原方程组的一个最小二乘解
推论7.1.2 若 rankA ,r则方n程组
有无穷多个最小二乘解。
Ax b
Def 2 方程组 Ax b 的所有最小二乘解中2-范数最小
8.9
8.5
10
4
3.5
22
9
8
11
4.5
4.2
23
9.5
8.1
12
4.6
3.5
24
10
8.1
可以看出,纤维强度随 拉伸倍数增加而增加
并且24个点大致分 布在一条直线附近
因此可认为强度与 拉伸倍数之间的主 要关系是线性关系
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
y ( x ) a bx
该直线称为这一问题的数学模型。
线性无关,下面讨论正交分解的具体实现方法。
记 A [a1, a2 , , an ],Q [q1, q2 , , qr ] 其中 a1, a2 , , ar线性无关,q1, q2 , , qr两两正交。
Gram-Schmidt正交化方法: 由 A QU 得
a1 u11q1 a2 u12q1 u22q2
y a bx c 1 x
1( x) 1;
2(x)
x;
3(x)
1 x
三、最小二乘问题解的存在性、唯一性
Def 1 设 A R,m若n 存在 x 精R确n地满足
最小二乘法与曲线拟合市公开课获奖课件省名师示范课获奖课件

解:将已给数据点描在坐标系中,能够看出这些点 接近一条抛物线,所以设所求旳多项式为
y a0 a1 x a2 x 2
由法方程组(5.46), n=6, 经计算得
6
6
6
6
6
6
6
xi 15, xi2 55, xi3 225, xi4 797, yi 14, xi yi 30, xi2 yi 122
令 y ln y, a0 ln a, a1 b
得 y a0 a1x
则就得到线性模型
则正规方程组为
6a0
6
a1
i 1
xi
6
ln
i 1
yi
6
6
6
a0
i 1
xi
a1
i 1
xi2
i 1
xi ln
yi
其中
6
6
xi 7.5
xi2 13.75
i 1
i1
6
6
ln yi 2.043302
于是得到拟合指数函数为
y 1.754708e0.772282x
有些非线性拟合曲线可以经过适当旳变量替换转化为线性曲线,从而用线性
拟合进行处理,对于一个实际旳曲线拟合问题,一般先按观察值在直角坐标平 面上描出散点图,看一看散点旳分布同哪类曲线图形接近,然后选用相接近旳 曲线拟合方程。再经过适当旳变量替换转化为线性拟合问题,按线性拟合解出 后再还原为原变量所表达旳曲线拟合方程。
3
4
5
16 30 52
1 1 1 4
A 1
9
1 16
1 25
2 9
b
16
30
52
由 AT Ax AT b 可得
y a0 a1 x a2 x 2
由法方程组(5.46), n=6, 经计算得
6
6
6
6
6
6
6
xi 15, xi2 55, xi3 225, xi4 797, yi 14, xi yi 30, xi2 yi 122
令 y ln y, a0 ln a, a1 b
得 y a0 a1x
则就得到线性模型
则正规方程组为
6a0
6
a1
i 1
xi
6
ln
i 1
yi
6
6
6
a0
i 1
xi
a1
i 1
xi2
i 1
xi ln
yi
其中
6
6
xi 7.5
xi2 13.75
i 1
i1
6
6
ln yi 2.043302
于是得到拟合指数函数为
y 1.754708e0.772282x
有些非线性拟合曲线可以经过适当旳变量替换转化为线性曲线,从而用线性
拟合进行处理,对于一个实际旳曲线拟合问题,一般先按观察值在直角坐标平 面上描出散点图,看一看散点旳分布同哪类曲线图形接近,然后选用相接近旳 曲线拟合方程。再经过适当旳变量替换转化为线性拟合问题,按线性拟合解出 后再还原为原变量所表达旳曲线拟合方程。
3
4
5
16 30 52
1 1 1 4
A 1
9
1 16
1 25
2 9
b
16
30
52
由 AT Ax AT b 可得
3.插值与最小二乘法

《数值分析》 主讲教师
18
ห้องสมุดไป่ตู้
Lagrange插值公式具有结构紧凑,清晰的 特点,故适用于作理论分析和应用。且编程 方便. 缺点是节点变动时,基函数随着改变。
给实际计算带来不便 因此后面将引入 , Newton插值公式。
《数值分析》 主讲教师 19
结束
输出y
等于
开始 输入X(xi,yi) i=0,1,…,n 0:=y 0:=k 1:=t (x-xj)/(xk-xj)*t:=t y+t*yk:=y j=0,…,k-1, k+1,….n K=n? 不等
( x x1 )( x x2 ) l0 ( x ) ( x0 x1 )( x0 x2 ) ( x x0 )( x x2 ) l1 ( x) ( x1 x0 )( x1 x2 ) ( x x0 )( x x1 ) l2 ( x) ( x2 x0 )( x2 x1 )
Ln ( xi ) f ( xi ), i 0, n 的插值多项式Ln ( x) Pn 对x [a, b]有: f ( ) Rn ( x) f ( x) Ln ( x) n 1 ( x), (n 1)! (a b)
( n 1)
前面的Cramer方法和该定理表明了插值多项式的唯一性。 两插值函数在n+1个点上函数值相同,故两多项式相同。
《数值分析》 主讲教师
13
§2.2 Lagrange插值多项式
拉格朗日利用n 1个插值节点( xi , yi )来构造出插值多 项式Ln ( x),使Ln ( xi ) f ( xi ), i 0,1, , n 用插值基函数方法可得 Ln ( x) :
l ( x) f ( x )
18
ห้องสมุดไป่ตู้
Lagrange插值公式具有结构紧凑,清晰的 特点,故适用于作理论分析和应用。且编程 方便. 缺点是节点变动时,基函数随着改变。
给实际计算带来不便 因此后面将引入 , Newton插值公式。
《数值分析》 主讲教师 19
结束
输出y
等于
开始 输入X(xi,yi) i=0,1,…,n 0:=y 0:=k 1:=t (x-xj)/(xk-xj)*t:=t y+t*yk:=y j=0,…,k-1, k+1,….n K=n? 不等
( x x1 )( x x2 ) l0 ( x ) ( x0 x1 )( x0 x2 ) ( x x0 )( x x2 ) l1 ( x) ( x1 x0 )( x1 x2 ) ( x x0 )( x x1 ) l2 ( x) ( x2 x0 )( x2 x1 )
Ln ( xi ) f ( xi ), i 0, n 的插值多项式Ln ( x) Pn 对x [a, b]有: f ( ) Rn ( x) f ( x) Ln ( x) n 1 ( x), (n 1)! (a b)
( n 1)
前面的Cramer方法和该定理表明了插值多项式的唯一性。 两插值函数在n+1个点上函数值相同,故两多项式相同。
《数值分析》 主讲教师
13
§2.2 Lagrange插值多项式
拉格朗日利用n 1个插值节点( xi , yi )来构造出插值多 项式Ln ( x),使Ln ( xi ) f ( xi ), i 0,1, , n 用插值基函数方法可得 Ln ( x) :
l ( x) f ( x )
CH3 插值法与最小二乘法―31~33 插值法PPT课件

不能直接用计算机计算,例如 等x ,;ln xΒιβλιοθήκη —— 表达式复杂,很难算!
2)函数没有明显的函数表达式,而只是一些离散点或曲线,分析计 算起来很麻烦。 —— 没有表达式,不能算!
直观想法——用一个便于计算的函数来近似 这个函数。
插值法和数据拟合的最小二乘法是这样的两种基本方法,二者的
相同点:都是从未知函数的一组数据出发,按照某种规则构造简单 易算的函数去近似它。
第三章 插值法与 最小二乘法
3.1—3.3
2010年3月
本章主要内容
插值法 Lagrange插值 插值误差 分段插值法 Newton插值 Hermit插值 数据拟合 最小二乘法
引言
科学研究和其它许多实际问题都和函数有关。常常会出现函数不便
于处理和计算的情形:
1)函数虽然有明确的解析表达式,但表达式形式复杂,很难计算或
对插值函数的要求:能够在计算机上直接计算。
常用插值函数:代数多项式和有理分式。
2. 插值法
按条件 P (xi)yi (i求函0 ,1 数, ,n )的近似表达f 式(x) 的方 法称为插P (值x )法.
其中, f (x) 为被插值函数;
函数 P( x为) 函数 f的( x插) 值函数; P (xi)yi (i0 ,1 , ,n )为插值条件; 点 xi (i0,1,2, ,n)为插值节点;
插值的位置 x为插值点;
包含插值节点的区间 [a, b] 为插值区间。
The mathematician S. had to move to a new place. His wife didn't trust him very much, so when they stood down on the street with all their things, she asked him to watch their ten trunks, while she got a taxi. Some minutes later she returned. Said the husband: "I thought you said there were ten trunks, but I've only counted to nine!"
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7
7
1
Xi
7
Xi
2
i 1 i 1
i 1
7
7XiXi 27Xi 3i 1 i 1
i 1
7
7
Xi 2
7
Xi 3
Xi
4
i 1
i 1
i 1
步骤5:根据该求导公式,在Excel 中利用SUM与SUMPRODUCT命令分别求 出:
7 Yi
i 1
7 YiXi
i 1
7
YiXi
2
i 1
步骤6:将求得的数列进行逆矩阵 计算,如图:
最小二乘法拟合插值法
步骤1:根据X与Y对应的值,插入散点 图并做出趋势图,如图:
步骤2:从该图可以看出最接近 这7个点的趋势线为抛物线,所以 设该抛物线方程为:
Y=(A0+A1*X+A2*X2)
步骤3:分别对方程中的A0,A1,A2 进行求导,可得:
步骤4:根据该求导公式,在Excel 中利用SUM与SUMPRODUCT命令分别求 出:
步骤7:将求得的逆矩阵与矩阵B相 乘,求得根,如图:
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
9
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
