哈工程模式识别实验
哈工大模式识别课件

1. Richard Duda, Peter Hart, David Stork, Pattern Classification, 2nd edition, John Wiley, 2001 2. 《模式分类》,机械工业出版社,Richard O. Duda 3. 《模式识别》清华大学出版社,边肇祺,张学工
应用领域
小结
本章小结
【小结】
(1)模式识别是每时每刻都发生的,重点强调分类。 (2)具有广泛的应用。 (3)对控制科学与工程学科的意义 (4)发展历程 (5)重要研究期刊 (6)参考书目
【4.发展历程】
1. 模式识别诞生于20世纪20年代; 2. 随着40年代计算机的出现,50年代人工智能的兴起, 模式识别在60年代迅速发展成一门学科; 3. 经过几十年的发展目前取得了大量的成果,在很多地 方得到应用。目前一直是热门的学科。
【5.重要期刊】
1. IEEE Transaction on Pattern Analysis and Machine Intelligence,PAMI 2. Pattern Recognition 3. Pattern Recognition Letter 4. 模式识别与人工智能
【6.参考书目】
它利用了训练样本的信息就可以认为学习,学习的目的是指 利用某种算法来降低由于训练样本的差异导致的分类误差。
学习的分类:
监督学习:存在一个教师信号,对训练样本集的每个输入样本能提供 无监督学习:没有显示的教师指导整个训练过程。(图像检索) 类别标记和分类代价并寻找能够降低总体代价的方向。(人脸识别) 半监督学习:半监督学习是利用少部分标记数据集及未标记样本进 行学习的主流技术。(如医学图像)
【性能评价】
最新哈工大 模式识别第2章ppt教学课件

▪ 因而,按最大后验概率作出的决策,其平均错误 率为最小。
▪
C类别情况
如 果 : P (i|X ) m j 1 a ,...x ,cP (j|X )
则: X i
也可写成先验概率与条件概率密度形式:
如 果 :p ( X |i) P (i) m j 1 a ,... x ,c p ( X | j) P (j)
则: X i
多类别决策过程中的错误率计算:
1、把特征空间分割成R1,R2,…,Rc,C个区域 2、在每个区域Ri统计将所有其它类错误划为该区 域对应的类的概率,则每个区域共有c-1项错误率, 总共有c(c-1) 项 。(计算复杂)
正确率:
所以:P(e)=1-P(c)
(可见:每次决策,正确率最大,即:P(C)最大,
P(e)R1p(X|2)P(2)dxR2p(X|1)P(1)dx
P(2)R1p(X|2)dxP(1)R2p(X|1)dx
P(2)P2(e)P(1)P1(e)
ห้องสมุดไป่ตู้
如 果 l(x)p p((X X|| 2 1))P P(( 2 1)),
X 1
▪ 在R1区内任一个x值都有P(w2|x)<P(w1|x), ▪ 在R2区内任一个x值都有P(w1|x)<P(w2|x) ▪ 错误率在每个x值处都取小者,因而平均错误率
– 在作出决策时,要考虑所承担的风险。
– 基于最小风险的贝叶斯决策规则正是为了体现这 一点而产生的。
基于最小风险的贝叶斯决策
▪ 最小错误率贝叶斯决策规则
如 果 :P (i|X ) jm 1 ,2 a ,. x ..,c P (j|X ) X i
▪ 实际上,C类中的每一类都有一定的样本的特征向 量取值X,只不过可能性大小不同而已。
哈工大模式识别课件.pptx

Duda
《模式识别》(第二版),清华大学出版社,边
肇祺,张学工;
模式识别 – 绪论
期刊
IEEE Transaction on Pattern Analysis and Machine Intelligence,PAMI;
Pattern Recognition; Pattern Recognition Letter; 模式识别与人工智能;
x
2
1
2
n
exp
1 2
n n
2
d
f , n
2 n
exp
1 2
x
n 2
2
2 n
f ,n
exp
1 2
2
2 n
2 2 n
2 n
x
2
n
2
2 n
2
du
模式识别 – 绪论
3.3期望最大化算法(EM算法)
EM算法的应用可以分为两个方面:
1. 训练样本中某些特征丢失情况下,分布参数的最大 似然估计;
特征提取与选 择
识别结果 模式分类
分类 训练
分类器设计
模式识别 – 绪论
六、模式识别问题的描述
给定一个训练样本的特征矢量集合:
D x1, x2, , xn, xi Rd
分别属于c个类别:
1,2, ,c
设计出一个分类器,能够对未知类别样本x进行分类
y g x, Rd 1, ,c
模式识别 – 绪论
率满足正态分布,即:
px N , 2
p
N
0
,
2 0
模式识别 – 绪论
哈工大 模式识别第四章第五章

c
J d ( x) tr( Sb Sw )
2016/1/23 哈尔滨工业大学电信院 宿富林
tr:迹
15
考虑类内类间欧氏距离的其它判据
判据Jd(X)是计算特征 向量的总平均距离,以 下一些判据则基于使类 间离散度尽量大,类内 离散度尽量小的考虑而 提出。
J 2 ( x ) tr ( S S ) | Sb | J( ) ln[ ] 3 x | Sw | trSb J( ) 4 x trS w | S w Sb | J( ) 5 x | Sw |
2016/1/23 哈尔滨工业大学电信院 宿富林 12
两类之间的距离:ω1任一点与ω2中任一点的距离 和的平均。 多类:各类之间的平均距离
1 1 J d ( x ) Pi Pj 2 i 1 j 1 ni n j
(i ) k ( j) l
c
c
(i ) ( j) ( x , x k l ) k 1 l 1
2016/1/23
哈尔滨工业大学电信院 宿富林
6
特征提取
找到一个映射关系: A:Y→X 使新样本特征描述维数比原维数降低。其中每个 分量xi是原特征向量各分量的函数,即 Xi=fi(y1,y2,…,yD)
这两种降维的基本方法是不同的。在实际应用中可 将两者结合起来使用,比如先进特征提取,然后再 进一步选择其中一部分,或反过来。
2016/1/23
哈尔滨工业大学电信院 宿富林
3
例 用RGB颜色空间和HSI颜色空间
右边是原始图像,左边是用HSI空间描述的同一图 像(但是为了显示出来,用H对应R,S对应G,I对应 B,然后再以RGB的方式显示出来
2016/1/23
哈工大系统辨识实验一教材

实验1 白噪声和M序列的产生实验报告哈尔滨工业大学航天学院控制科学与工程系专业:自动化班级:110410420姓名:日期:2014 年10 月12 日1.实验题目:白噪声和M序列的产生3、M 序列生成原理用移位寄存器产生M 序列的简化框图如下图所示。
该图表示一个由4个双稳态触发器顺序连接而成的4级移位寄存器,它带有一个反馈通道。
当移位脉冲来到时,每级触发器的状态移到下一级触发器中,而反馈通道按模2加法规则反馈到第一级的输入端。
1、生成均匀分布随机序列(1)利用混合同余法生成[0, 1]区间上符合均匀分布的随机序列,并计算该序列的均值和方差,与理论值进行对比分析。
要求序列长度为1200,推荐参数为a=65539,M=2147483647,0<x 0<M 。
(2)将[0, 1]区间分为不重叠的等长的10个子区间,绘制该随机序列落在每个子区间的频率曲线图,辅助验证该序列的均匀性。
(3)对上述随机序列进行独立性检验。
(该部分为选作内容)2、生成高斯白噪声利用上一步产生的均匀分布随机序列,令n=12,生成服从N(0,1)的白噪声,序列长度为100,并绘制曲线。
3、生成M 序列M 序列的循环周期取为63126=-=P N ,时钟节拍Sec 1=∆t ,幅度1=a ,逻辑“0”为a ,逻辑“1”为-a ,特征多项式65()F s s s =⊕。
生成M 序列的结构图如下所示。
x(j+1)=x(j);endx(1)=temp;endfor i=1:Npif(y(i)==0)y(i)=a;elsey(i)=-a;endendfigure(5)stairs(y);ylim([-1.5,1.5]);7.实验结果及分析实验1.1程序运行计算出序列的均值:mean_r =0.4897,与理论值0.5很接近;序列的方差var_r =0.0824,与理论值1/12很接近使用混合同余法得到生成的0-1均布随机序列如下所示:得到的该随机序列落在10个子区间的频率曲线图如下:从上图可以发现用混合同余法得到的随机序列平均分布性较好。
哈工程自动化学院各实验室详细介绍

欢迎报考自动化学院,很荣幸为大家介绍四系,希望对大家有所帮助!四系共有双控、导航、模式、检测、精密仪器、系统工程、电力电子、电力系统、生物医学、电机、探测制导等学科其中导航国家重点学科排名前三,双控排名20左右模式识别排名20左右双控、导航两专业师资最强其次是模式识别、精密仪器四系共有大小教研室11个401~412,其中研究所10个其中所有教研室都招双控专业,其他专业主要分布402、407、411导航、精密仪器、检测,408模式识别,401 系统工程、模式识别,406 模式识别,检测,等等401系统工程402测控技术与惯性导航研究所招收导航制导、精密、探测制导、双控等主要方向有惯性技术(光纤陀螺)、精密仪器、惯性技术(光纤惯导系统)应用(海陆空天),探测制导、导弹控制(张晓宇老师),小型水下机器人。
导师高延斌李绪友,李光春,张晓宇,何坤鹏等。
学生待遇比较好。
403 本科教学404自动控制系统所做减摇旗,主要收双控、检测、模式三个专业,主要导师博导金鸿章(双控学科带头人)、梁利华硕导吉明405电气工程研究所主要收电气方面和双控导师姚续梁等,主要方向电力系统、船舶电气系统、船舶控制406机器人与智能控制研究所招双控模式检测导师:朱齐丹孟浩夏桂华等,主要方向全景视觉、机器臂控制、双目视觉等407组合导航招导航、精密等导师郝艳玲(导航学科带头人)孙枫(精密带头人)徐定杰袁赣南赵琳等,主要有惯性技术(孙枫、高伟、王伟)、电子海图(赵玉新)、组合导航综显台(袁赣南),卫星导航与惯性技术(赵琳部分),雷达无线电、卫星(徐定杰)。
学生待遇比较好,实验室项目基本是由老师们做的。
很少有硕士参与,参与也是体力活。
408模式识别及智能系统招模式、双控导师王科俊(模式带头人、副院长)叶秀芬(水下机器人、图像处理、声纳图像、虚拟现实)郭书祥(长江学者、与叶秀芬同是仿生微机器人实验室,基本不在学校)王宗义(机器视觉)莫宏伟汝长海(不在学校)等,推荐叶秀芬教授长江学者实验室网址/409北飒所招双控模式检测等导师边信黔(学科带头人、牛人)、严浙平(水下机器人方向)、林教工、付明玉、王宏建、夏国清等410 自动化工程所411探测制导与控制所导师史震(导弹控制)412生物医学模式生物医学等导师李金以上导师均可以在百度搜索到简介其中规模大小407规模最大其次是409、402 再次是406、408、405三个教研室差不多大404等每年所有专业招生共300人左右含保送。
哈工大模式识别第3章

▪ 对线性判别函数的研究就是从R.A.Fisher在 1936年发表的论文开始的。
▪ Fisher线性判别函数基本原理
– 设计线性分类器首先要确定准则函数,然后再利 用训练样本集确定该分类器的参数,以求使所确 定的准则达到最佳。
最佳法线向量W*
▪ 使Fisher准则函数JF达极大值的解,也就是按 Fisher准则将d维X空间投影到一维Y空间的最 佳投影方向。
▪
是在两类正态分布但具有相同的
协方差矩阵Σ时,按最小错误率的贝叶斯决策
得到的结果。
如果P(ωi)=P(ωj),则最佳分界线就是两类概率 密度函数值相等的点的集合。
▪ 按Fisher准则,Sw=Σ1+ Σ2=2 Σ,
向量W的意义
▪ 设在该决策平面上有两个特征向量X1与X2,则
▪ W与该平面上任两点组成的向量(X1-X2)正交 ▪ W是该超平面的法线向量
X g(X) / ||W||
R0=w0 / ||W||
r Xp
正侧 R1: g>0
负侧
R2: g<0
H: g=0
g(X)、 w0的意义
▪ g(X)是d维空间任一点X到决策面H的距离的代数度量 ▪ w0体现该决策面在特征空间中的位置
3.2.2 广义线性判别函数
▪ 欲设计这样一个一维样本 的分类器,使其性能为:
▪ 线性判别函数:无能为力 ▪ 若设计判别函数(非线性)
g(x)=(x-a)(x-b) 决策规则
若:g(x)>0, 决策:X∈w1 g(x)<0, 决策:X∈w2
则可正确分类
广义线性判别函数
▪ 选择一种映射X→Y,将原样本特征向量X映射成另 一向量Y,从而可以采用线性判别函数的方法。
哈工大模式识别实验报告
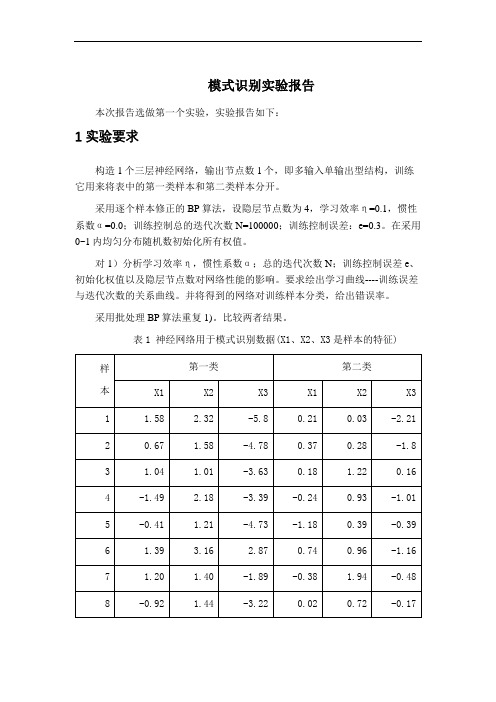
模式识别实验报告本次报告选做第一个实验,实验报告如下:1 实验要求构造1个三层神经网络,输出节点数1个,即多输入单输出型结构,训练它用来将表中的第一类样本和第二类样本分开。
采用逐个样本修正的BP算法,设隐层节点数为4,学习效率η=0.1,惯性系数α=0.0;训练控制总的迭代次数N=100000;训练控制误差:e=0.3。
在采用0~1内均匀分布随机数初始化所有权值。
对1)分析学习效率η,惯性系数α;总的迭代次数N;训练控制误差e、初始化权值以及隐层节点数对网络性能的影响。
要求绘出学习曲线----训练误差与迭代次数的关系曲线。
并将得到的网络对训练样本分类,给出错误率。
采用批处理BP算法重复1)。
比较两者结果。
表1 神经网络用于模式识别数据(X1、X2、X3是样本的特征)2 BP 网络的构建三层前馈神经网络示意图,见图1.图1三层前馈神经网络①网络初始化,用一组随机数对网络赋初始权值,设置学习步长η、允许误差ε、网络结构(即网络层数L 和每层节点数n l );②为网络提供一组学习样本; ③对每个学习样本p 循环a .逐层正向计算网络各节点的输入和输出;b .计算第p 个样本的输出的误差Ep 和网络的总误差E ;c .当E 小于允许误差ε或者达到指定的迭代次数时,学习过程结束,否则,进行误差反向传播。
d .反向逐层计算网络各节点误差)(l jp δ如果l f 取为S 型函数,即xl e x f -+=11)(,则 对于输出层))(1()()()()(l jp jdp l jp l jp l jp O y O O --=δ 对于隐含层∑+-=)1()()()()()1(l kj l jp l jp l jp l jp w O O δδe .修正网络连接权值)1()()()1(-+=+l ip l jp ij ij O k W k W ηδ式中,k 为学习次数,η为学习因子。
η取值越大,每次权值的改变越剧烈,可能导致学习过程振荡,因此,为了使学习因子的取值足够大,又不至产生振荡,通常在权值修正公式中加入一个附加动量法。
哈工大模式识别课程7近邻法

,则
不可能是 不可能是 中的样本到
的最近邻。 的最近邻。 的
17
:当前已经涉及到的样本集 最 近距离。 近距离。
【搜索算法的基本思想 】
搜索算法的大体过程是这样的: 搜索算法的大体过程是这样的: 当搜索树形样本 集结构由高层次向低层次深入时, 由高层次向低层次深入时 集结构由高层次向低层次深入时,对同一层次的 所有结点,可以利用规则 规则1排除掉一些不可能包含 所有结点,可以利用规则 排除掉一些不可能包含 待识别样本的近邻的结点(样本子集 样本子集)。 待识别样本的近邻的结点 样本子集 。但是这往往 不能做到只留下唯一的待搜索结点,因此必须选 不能做到只留下唯一的待搜索结点,因此必须选 择其中某一结点先深入搜索, 择其中某一结点先深入搜索,以类似于深度优先 的方法确定搜索路径直至叶结点。 的方法确定搜索路径直至叶结点。然而在该叶结 点中找到的近邻并不能保证 不能保证确实是全样本集中的 点中找到的近邻并不能保证确实是全样本集中的 最近邻者, 最近邻者,所找到的该近邻样本需要在那些有可 能包含最近邻的样本子集中核对与修正,直至找 能包含最近邻的样本子集中核对与修正, 核对与修正 到真正的最近邻样本为止。 到真正的最近邻样本为止。
23
【基本步骤】
两分剪辑近邻法 假定样本集被分为两个独立的样本集-考试集和参考集,分别对 假定样本集被分为两个独立的样本集-考试集和参考集, 应于错误率估计中的考试集和设计集。 应于错误率估计中的考试集和设计集。 剪辑: 剪辑:利用参考集的中样本对考试集的每个样本利用最近邻法 进行分类决策,剪辑掉那些被参考集中样本错分类的样本, 进行分类决策,剪辑掉那些被参考集中样本错分类的样本, 然后将参考集中剩余样本构成剪辑样本集。 然后将参考集中剩余样本构成剪辑样本集。
哈工大模式识别课程11.模糊模式识别

16
• 模糊集合
– 模糊集通常可以用来表示某种人为的概念(比如上 面提到的“开水”),即用数学形式来表达人们的 语言变量,因此隶属度函数需要人为定义。 – 一些常见的单变量隶属度函数的形式包括斜台阶型 、三角型、梯型、高斯函数型等。
MATLAB Fuzzy Logic Toolbox: dsigmf gauss2mf gaussmf gbellmf pimf psigmf sigmf smf trapmf trimf zmf
25
几个概念: A ∈ F ( X ) 支集 sup p( A) = {x | A( x) > 0} 高度 hgt ( A) = sup A( x)
x∈X
1
核 ker( A) = {x | A( x) = 1} 正规模糊集:ker(A) ≠ φ 例如:
A = 0.3 / 1 + 0.7 / 2 + 1 / 3 + 1 / 4 + 0.3 / 5
a
E
f
b
e
d
c
19
S-型隶属度函数 (Zadeh,1975) 型隶属度函数
b=(a+c)/2;
20
∏-型隶属度函数 型隶属度函数
c=(a+a’)/2, b=(a+c)/2, b’=(c+a’)/2
21
2. 模糊集的集运算
它们的并A ∪ B、交A ∩ B分别定义为: 设A, B ∈ F ( X ), ( A ∪ B )( x) = max( A( x), B ( x)) = A( x) ∨ B ( x)
17
【模糊集基础知识 】
模糊集的例子。 例 论域E={1,2,3,4,5},用模糊集表示“大”和“ 小”。 解:设A、B分别表示“大”与“小”的模糊集, µA ,µB分别为相应的隶属函数。 A={0, 0, 0.1, 0.6, 1} B={1, 0.5, 0.01, 0,0} 其中:µA(1)=0,µA(2)=0 ,µA(3)=0.1 ,µA(4)=0.6 ,µA(5)=1 µB(1)=1,µB(2)=0.5 ,µB(3)=0.01 ,µB(4)=0,µB(5)=0
哈工大模式识别课程6特征的提取与选择

散度
【基于概率分布的可分性判据】
正态分布情况下: 正态分布情况下:
【基于概率分布的可分性判据】
几种常见的概率距离准则( 和概率相关性准则( 几种常见的概率距离准则(J ) 和概率相关性准则(I )
【熵可分性判据】
熵:事件不确定性的度量 A事件的不确定性大(熵大),则对 事件的观察所提供的信 事件的不确定性大( ),则对 事件的不确定性大 熵大),则对A 息量大。 息量大。 思路: 思路:
【用于可分性判据的类内类间距离】
几种常见的距离度量
(1)Minkovski Metric (of order s) )
(2)城市块(City Block) )城市块( )
(3)欧氏距离(Euclidean) )欧氏距离( )
பைடு நூலகம்
【用于可分性判据的类内类间距离】
Chobychev 距离
平方距离
非线性距离度量
第7章 特征的选择与提取
主讲人: 主讲人:邱剑彬 李君宝
哈尔滨工业大学
1.引言 1.引言 2 类别可分离性判据 3 特征选择 4.特征提取 4.特征提取
1.引言 1.引言
【问题的提出】
对特征空间的改造、优化、主要的目的是降维, 对特征空间的改造、优化、主要的目的是降维,即把维数 高的特征空间改成维数低的特征空间。 高的特征空间改成维数低的特征空间。
【最优搜索方法】
穷举法存在的问题: 穷举法存在的问题:
特征总数D以及选择特征数d增加时,穷举法计算量迅速上升。 特征总数D以及选择特征数d增加时,穷举法计算量迅速上升。
【非最优搜索方法】
非最优,但某些情况下最优, 非最优,但某些情况下最优,实现简单
(1)单独最优组合选前d 个单独最佳的特征 Selection:顺序前进): ):从 (2)SFS 法(Sequential Forward Selection:顺序前进):从 底向上每加入一个特征寻优一次, 底向上每加入一个特征寻优一次,使加入该特征后所得组合最大 特点:考虑了特征间的相关性,但某特下一经入选, 特点:考虑了特征间的相关性,但某特下一经入选,即无法淘汰 GSFS)从底向上, 个特征。 (3)广义SFS 法(GSFS)从底向上,每次增加l 个特征。 广义SFS 考虑了新增特征中的相关性计算量比SFS ,(一步 考虑了新增特征中的相关性计算量比SFS 大,若l = d ,(一步 加满), ),则就是穷举法 加满),则就是穷举法 顺序后退,后向贯序)从顶向下, (4)SBS 法(顺序后退,后向贯序)从顶向下,每次减一个特征 相对,一旦失去,无法换回。 与SFS 相对,一旦失去,无法换回。 GSBS)从顶向下,每次减r (5)广义SBS 法(GSBS)从顶向下,每次减r 个特征 广义SBS
模式识别实验报告一二.doc

信息与通信工程学院模式识别实验报告班级:姓名:学号:日期:2011年12月实验一、Bayes 分类器设计一、实验目的:1.对模式识别有一个初步的理解2.能够根据自己的设计对贝叶斯决策理论算法有一个深刻地认识3.理解二类分类器的设计原理二、实验条件:matlab 软件三、实验原理:最小风险贝叶斯决策可按下列步骤进行: 1)在已知)(i P ω,)(i X P ω,i=1,…,c 及给出待识别的X 的情况下,根据贝叶斯公式计算出后验概率:∑==cj iii i i P X P P X P X P 1)()()()()(ωωωωω j=1,…,x2)利用计算出的后验概率及决策表,按下面的公式计算出采取ia ,i=1,…,a 的条件风险∑==cj j jii X P a X a R 1)(),()(ωωλ,i=1,2,…,a3)对(2)中得到的a 个条件风险值)(X a R i ,i=1,…,a 进行比较,找出使其条件风险最小的决策ka ,即()()1,min k i i aR a x R a x ==则ka 就是最小风险贝叶斯决策。
四、实验内容假定某个局部区域细胞识别中正常(1ω)和非正常(2ω)两类先验概率分别为 正常状态:P (1ω)=0.9; 异常状态:P (2ω)=0.1。
现有一系列待观察的细胞,其观察值为x :-3.9847 -3.5549 -1.2401 -0.9780 -0.7932 -2.8531 -2.7605 -3.7287 -3.5414 -2.2692 -3.4549 -3.0752 -3.9934 2.8792 -0.9780 0.7932 1.1882 3.0682 -1.5799 -1.4885 -0.7431 -0.4221 -1.1186 4.2532 已知先验概率是的曲线如下图:)|(1ωx p )|(2ωx p 类条件概率分布正态分布分别为(-2,0.25)(2,4)试对观察的结果进行分类。
哈工程自动化学院各实验室详细介绍教学文案

欢迎报考自动化学院,很荣幸为大家介绍四系,希望对大家有所帮助!四系共有双控、导航、模式、检测、精密仪器、系统工程、电力电子、电力系统、生物医学、电机、探测制导等学科其中导航国家重点学科排名前三,双控排名20左右模式识别排名20左右双控、导航两专业师资最强其次是模式识别、精密仪器四系共有大小教研室11个401~412,其中研究所10个其中所有教研室都招双控专业,其他专业主要分布402、407、411导航、精密仪器、检测,408模式识别,401 系统工程、模式识别,406 模式识别,检测,等等401系统工程402测控技术与惯性导航研究所招收导航制导、精密、探测制导、双控等主要方向有惯性技术(光纤陀螺)、精密仪器、惯性技术(光纤惯导系统)应用(海陆空天),探测制导、导弹控制(张晓宇老师),小型水下机器人。
导师高延斌李绪友,李光春,张晓宇,何坤鹏等。
学生待遇比较好。
403 本科教学404自动控制系统所做减摇旗,主要收双控、检测、模式三个专业,主要导师博导金鸿章(双控学科带头人)、梁利华硕导吉明405电气工程研究所主要收电气方面和双控导师姚续梁等,主要方向电力系统、船舶电气系统、船舶控制406机器人与智能控制研究所招双控模式检测导师:朱齐丹孟浩夏桂华等,主要方向全景视觉、机器臂控制、双目视觉等407组合导航招导航、精密等导师郝艳玲(导航学科带头人)孙枫(精密带头人)徐定杰袁赣南赵琳等,主要有惯性技术(孙枫、高伟、王伟)、电子海图(赵玉新)、组合导航综显台(袁赣南),卫星导航与惯性技术(赵琳部分),雷达无线电、卫星(徐定杰)。
学生待遇比较好,实验室项目基本是由老师们做的。
很少有硕士参与,参与也是体力活。
408模式识别及智能系统招模式、双控导师王科俊(模式带头人、副院长)叶秀芬(水下机器人、图像处理、声纳图像、虚拟现实)郭书祥(长江学者、与叶秀芬同是仿生微机器人实验室,基本不在学校)王宗义(机器视觉)莫宏伟汝长海(不在学校)等,推荐叶秀芬教授长江学者实验室网址/409北飒所招双控模式检测等导师边信黔(学科带头人、牛人)、严浙平(水下机器人方向)、林教工、付明玉、王宏建、夏国清等410 自动化工程所411探测制导与控制所导师史震(导弹控制)412生物医学模式生物医学等导师李金以上导师均可以在百度搜索到简介其中规模大小407规模最大其次是409、402 再次是406、408、405三个教研室差不多大404等每年所有专业招生共300人左右含保送。
模式识别实验报告哈工程

一、实验背景随着计算机科学和信息技术的飞速发展,模式识别技术在各个领域得到了广泛应用。
模式识别是指通过对数据的分析、处理和分类,从大量数据中提取有用信息,从而实现对未知模式的识别。
本实验旨在通过实践操作,加深对模式识别基本概念、算法和方法的理解,并掌握其应用。
二、实验目的1. 理解模式识别的基本概念、算法和方法;2. 掌握常用的模式识别算法,如K-均值聚类、决策树、支持向量机等;3. 熟悉模式识别在实际问题中的应用,提高解决实际问题的能力。
三、实验内容本次实验共分为三个部分:K-均值聚类算法、决策树和神经网络。
1. K-均值聚类算法(1)实验目的通过实验加深对K-均值聚类算法的理解,掌握其基本原理和实现方法。
(2)实验步骤① 准备实验数据:选取一组二维数据,包括100个样本,每个样本包含两个特征值;② 初始化聚类中心:随机选择K个样本作为初始聚类中心;③ 计算每个样本到聚类中心的距离,并将其分配到最近的聚类中心;④ 更新聚类中心:计算每个聚类中所有样本的均值,作为新的聚类中心;⑤ 重复步骤③和④,直到聚类中心不再变化。
(3)实验结果通过实验,可以得到K个聚类中心,每个样本被分配到最近的聚类中心。
通过可视化聚类结果,可以直观地看到数据被分成了K个类别。
2. 决策树(1)实验目的通过实验加深对决策树的理解,掌握其基本原理和实现方法。
(2)实验步骤① 准备实验数据:选取一组具有分类标签的二维数据,包括100个样本,每个样本包含两个特征值;② 选择最优分割特征:根据信息增益或基尼指数等指标,选择最优分割特征;③ 划分数据集:根据最优分割特征,将数据集划分为两个子集;④ 递归地执行步骤②和③,直到满足停止条件(如达到最大深度、叶节点中样本数小于阈值等);⑤ 构建决策树:根据递归分割的结果,构建决策树。
(3)实验结果通过实验,可以得到一棵决策树,可以用于对新样本进行分类。
3. 神经网络(1)实验目的通过实验加深对神经网络的理解,掌握其基本原理和实现方法。
哈工大模式识别——核方法概要

在
的概率下泛化误差的界:
硬间隔:必须用在可分离情况,对噪声敏感——不健壮 软间隔:容忍部分分错,对噪声不敏感——健壮
软间隔分类器
软间隔分类器
软间隔分类器
与最大间隔的结果相同,仅约束条件不同:
软间隔分类器
最大化:
约束: 凸二次规划:
In 是一个 n 阶单位阵, 时总可逆
9.1核方法概述——对偶岭回归
训练点的线性组合 :对偶变量
称
为Gram 矩阵
G:训练点对间的内积
k:训练点和测试点之间的内积
9.1核方法概述——核函数
考虑一个嵌入映射
将
上的非线性关系转化为
高维空间上的线性关系
直接法:N 很大时,
解N × N 的方程组代价过大
凸优化与SVM
• 超球体
– 在嵌入空间中,寻找包含训练数据集的最小超 球体。并构建检测新颖(反常)数据的算法。
• 最大间隔超平面
– 在嵌入空间中,寻找能将两类样本分开的最大 间隔超平面,构建分类算法
凸二次规划问题
包含点集合的最小超球体
训练集
嵌入到特征空间 F 中
寻找一个包含所有特征点的最小超球体
PA算法
模式函数
• 核方法的4个关键:
– 数据嵌入特征空间
从基于线性函数类的模式 中抽取出来的模式函数
– 在特征空间中寻找线性模式
– 在嵌入空间中,不需要计算点的坐标,只用两两内积
– 利用核函数,可以直接从初始数据高效地计算内积。
9.1核方法概述——线性回归
• 给定n维空间中训练集合
,寻
找齐次线性函数
在
的概率下,来自训练分布D的点落在
以c为中心,
哈尔滨工程大学模式识别实验报告

实验报告实验课程名称:模式识别:班级: 20120811 学号:注:1、每个实验中各项成绩按照5分制评定,实验成绩为各项总和2、平均成绩取各项实验平均成绩3、折合成绩按照教学大纲要求的百分比进行折合2015年 4月实验1 图像的贝叶斯分类1.1 实验目的将模式识别方法与图像处理技术相结合,掌握利用最小错分概率贝叶斯分类器进行图像分类的基本方法,通过实验加深对基本概念的理解。
1.2 实验仪器设备及软件HP D538、MATLAB1.3 实验原理1.3.1基本原理阈值化分割算法是计算机视觉中的常用算法,对灰度图象的阈值分割就是先确定一个处于图像灰度取值围的灰度阈值,然后将图像中每个像素的灰度值与这个阈值相比较。
并根据比较的结果将对应的像素划分为两类,灰度值大于阈值的像素划分为一类,小于阈值的划分为另一类,等于阈值的可任意划分到两类中的任何一类。
此过程中,确定阈值是分割的关键。
对一般的图像进行分割处理通常对图像的灰度分布有一定的假设,或者说是基于一定的图像模型。
最常用的模型可描述如下:假设图像由具有单峰灰度分布的目标和背景组成,处于目标和背景部相邻像素间的灰度值是高度相关的,但处于目标和背景交界处两边的像素灰度值有较大差别,此时,图像的灰度直方图基本上可看作是由分别对应于目标和背景的两个单峰直方图混合构成。
而且这两个分布应大小接近,且均值足够远,方差足够小,这种情况下直方图呈现较明显的双峰。
类似地,如果图像中包含多个单峰灰度目标,则直方图可能呈现较明显的多峰。
上述图像模型只是理想情况,有时图像中目标和背景的灰度值有部分交错。
这时如用全局阈值进行分割必然会产生一定的误差。
分割误差包括将目标分为背景和将背景分为目标两大类。
实际应用中应尽量减小错误分割的概率,常用的一种方法为选取最优阈值。
这里所谓的最优阈值,就是指能使误分割概率最小的分割阈值。
图像的直方图可以看成是对灰度值概率分布密度函数的一种近似。
如一幅图像中只包含目标和背景两类灰度区域,那么直方图所代表的灰度值概率密度函数可以表示为目标和背景两类灰度值概率密度函数的加权和。
哈工大模式识别-绪论

例:两类训练样本圆形分布
分类函数类型的确定:圆形的分布与线性方程。一般来说,决定使用什么类型的分类函数往往是人为决定的。
数学式子中参数的确定
是一种学习过程。如果当前采用的分类函数会造成分类错误,利用错误提供应如何纠错的信息,纠正分类函数。
分类器设计:求解优化问题的过程
模式识别中的学习与训练是从训练样本提供的数据中找出某种数学式子的最优解,这个最优解使分类器得到一组参数,按这种参数设计的分类器使人们设计的某种准则达到极值。 分类器参数的选择或者学习过程得到的结果取决于设计者选择什么样的准则函数。不同准则函数的最优解对应不同的学习结果,得到性能不同的分类器。
模式的描述方法
一种是对事物的属性进行度量,属于定量的表示方法。 另一种则是对事务所包含的成分进行分析,称为定性的描述或结构性描述
定量的表示方法
特征:模式就是用它们所具有的特征(Feature) (反映事物的本质属性)描述的。 特征向量:对一种模式与它们的样本来说,将描述它们的所有特征用一特征集表示 : 例如对水果进行分类 :用水果的重量,近似球体直径表示水果: 一只苹果重0.3斤,直径10厘米, 则可表示成(0.3,1.0)
特征空间
特征空间中的一个样本点
时域信号的向量表示法
语音信号这种随时间变化的信号,属于时域信号。此时,元素之间的时间先后顺序很重要,因此可用向量的形式将它们排列起来。说的严格一些,对语音信号进行采样,然后将在不同时刻采样值排列起来,组成向量。
图像的表示方法
数字图像:它由排列整齐的二维网格组成,分为若干行与若干列,相当于一个二维数组,或称矩阵。 每个元素称为像素。 图像的运算是向量运算。
模式类与模式
模式类与模式 :所见到的具体事物称为模式,而将他们的归属类别称为模式类。 样本与模式(模式类) :所见到的具体事物称为样本,而他们所属的事物类别,代表着这些事物的“概念”是模式。 模式与样本在集合论中是子集与元素之间的关系 模式识别:将某一具体事物(样本)正确地归入某一(模式)类别。
哈工大 模式识别

模式识别模式识别及其应用摘要:模式还可分成抽象的和具体的两种形式。
前者如意识、思想、议论等,属于概念识别研究的范畴,是人工智能的另一研究分支。
我们所指的模式识别主要是对语音波形、地震波、心电图、脑电图、图片、照片、文字、符号、生物的传感器等对象进行测量的具体模式进行分类和辨识。
关键词:模式识别应用模式识别(Pattern Recognition)是人类的一项基本智能,在日常生活中,人们经常在进行“模式识别”。
随着20世纪40年代计算机的出现以及50年代人工智能的兴起,人们当然也希望能用计算机来代替或扩展人类的部分脑力劳动。
(计算机)模式识别在20世纪60年代初迅速发展并成为一门新学科。
一,模式识别基本概念模式识别(Pattern Recognition)是指对表征事物或现象的各种形式的(数值的、文字的和逻辑关系的)信息进行处理和分析,以对事物或现象进行描述、辨认、分类和解释的过程,是信息科学和人工智能的重要组成部分。
什么是模式呢?广义地说,存在于时间和空间中可观察的事物,如果我们可以区别它们是否相同或是否相似,都可以称之为模式。
但模式所指的不是事物本身,而是我们从事物获得的信息。
因此,模式往往表现为具有时间或空间分布的信息。
模式还可分成抽象的和具体的两种形式。
前者如意识、思想、议论等,属于概念识别研究的范畴,是人工智能的另一研究分支。
我们所指的模式识别主要是对语音波形、地震波、心电图、脑电图、图片、照片、文字、符号、生物的传感器等对象进行测量的具体模式进行分类和辨识。
模式识别研究主要集中在两方面,一是研究生物体(包括人)是如何感知对象的,属于认识科学的范畴,二是在给定的任务下,如何用计算机实现模式识别的理论和方法。
前者是生理学家、心理学家、生物学家和神经生理学家的研究内容,后者通过数学家、信息学专家和计算机科学工作者近几十年来的努力,已经取得了系统的研究成果。
应用计算机对一组事件或过程进行鉴别和分类。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一、 图像的贝叶斯分类一、实验目的将模式识别方法与图像处理技术相结合,掌握利用最小错分概率贝叶斯分类器进行图像分类的基本方法,通过实验加深对基本概念的理解。
二、实验仪器设备及软件HP D538、MA TLAB 三、实验原理阈值化分割算法是计算机视觉中的常用算法,对灰度图象的阈值分割就是先确定一个处于图像灰度取值范围内的灰度阈值,然后将图像中每个像素的灰度值与这个阈值相比较。
并根据比较的结果将对应的像素划分为两类,灰度值大于阈值的像素划分为一类,小于阈值的划分为另一类,等于阈值的可任意划分到两类中的任何一类。
此过程中,确定阈值是分割的关键。
对一般的图像进行分割处理通常对图像的灰度分布有一定的假设,或者说是基于一定的图像模型。
最常用的模型可描述如下:假设图像由具有单峰灰度分布的目标和背景组成,处于目标和背景内部相邻像素间的灰度值是高度相关的,但处于目标和背景交界处两边的像素灰度值有较大差别,此时,图像的灰度直方图基本上可看作是由分别对应于目标和背景的两个单峰直方图混合构成。
而且这两个分布应大小接近,且均值足够远,方差足够小,这种情况下直方图呈现较明显的双峰。
类似地,如果图像中包含多个单峰灰度目标,则直方图可能呈现较明显的多峰。
上述图像模型只是理想情况,有时图像中目标和背景的灰度值有部分交错。
这时如用全局阈值进行分割必然会产生一定的误差。
分割误差包括将目标分为背景和将背景分为目标两大类。
实际应用中应尽量减小错误分割的概率,常用的一种方法为选取最优阈值。
这里所谓的最优阈值,就是指能使误分割概率最小的分割阈值。
图像的直方图可以看成是对灰度值概率分布密度函数的一种近似。
如一幅图像中只包含目标和背景两类灰度区域,那么直方图所代表的灰度值概率密度函数可以表示为目标和背景两类灰度值概率密度函数的加权和。
如果概率密度函数形式已知,就有可能计算出使目标和背景两类误分割概率最小的最优阈值。
假设目标与背景两类像素值均服从正态分布且混有加性高斯噪声,上述分类问题可以使用模式识别中的最小错分概率贝叶斯分类器来解决。
以1p 与2p 分别表示目标与背景的灰度分布概率密度函数,1P 与2P 分别表示两类的先验概率,则图像的混合概率密度函数可用下式表示1122()()()p x P p x P p x =+式中1p 和2p 分别为2121()21()x p x μσ--=2222()22()x p x μσ--=121P P +=1σ、2σ是针对背景和目标两类区域灰度均值1μ与2μ的标准差。
若假定目标的灰度较亮,其灰度均值为2μ,背景的灰度较暗,其灰度均值为1μ,因此有12μμ<现若规定一门限值T 对图像进行分割,势必会产生将目标划分为背景和将背景划分为目标这两类错误。
通过适当选择阈值T ,可令这两类错误概率为最小,则该阈值T 即为最佳阈值。
把目标错分为背景的概率可表示为12()()TE T p x dx -∞=⎰把背景错分为目标的概率可表示为21()()TE T p x dx +∞=⎰总的误差概率为2112()()()E T P E T PE T =+为求得使误差概率最小的阈值T ,可将()E T 对T 求导并令导数为零,可得1122()()P p T P p T =代换后,可得221212222111()()ln 22P T T P σμμσσσ---=-此时,若设12σσσ==,则有2122121ln 2P T P μμσμμ⎛⎫+=+ ⎪-⎝⎭若还有12P P =的条件,则122T μμ+=这时的最优阈值就是两类区域灰度均值1μ与2μ的平均值。
上面的推导是针对图像灰度值服从正态分布时的情况,如果灰度值服从其它分布,依理也可求出最优阈值来。
一般情况下,在不清楚灰度值分布时,通常可假定灰度值服从正态分布。
因此,本课题中亦可使用此方法来求得最优阈值,来对实验图像进行分割。
1.3.2 最优阈值的迭代算法在实际使用最优阈值进行分割的过程中,需要利用迭代算法来求得最优阈值。
设有一幅数字图像(,)f x y ,混有加性高斯噪声,可表示为(,)(,)(,)g x y f x y n x y =+此处假设图像上各点的噪声相互独立,且具有零均值,如果通过阈值分割将图像分为目标与背景两部分,则每一部分仍然有噪声点随机作用于其上,于是,目标1(,)g x y 和2(,)g x y 可表示为11(,)(,)(,)g x y f x y n x y =+ 22(,)(,)(,)g x y f x y n x y =+迭代过程中,会多次地对1(,)g x y 和2(,)g x y 求均值,则111{(,)}{(,)(,)}{(,)}E g x y E f x y n x y E f x y =+= 222{(,)}{(,)(,)}{(,)}E g x y E f x y n x y E f x y =+=可见,随着迭代次数的增加,目标和背景的平均灰度都趋向于真实值。
因此,用迭代算法求得的最佳阈值不受噪声干扰的影响。
利用最优阈值对实验图像进行分割的迭代步骤为: (1)确定一个初始阈值0T ,0T 可取为min max02S S T +=式中,min S 和max S 为图像灰度的最小值和最大值。
(2)利用第k 次迭代得到的阈值将图像分为目标1R 和背景2R 两大区域,其中1{(,)|(,)}k R f x y f x y T =≥ 2{(,)|0(,)}k R f x y f x y T =<<(3)计算区域1R 和2R 的灰度均值1S 和2S 。
(4)计算新的阈值1k T +,其中1212k S S T ++=(5)如果1||k k T T +-小于允许的误差,则结束,否则1k k =+,转步骤(2)。
利用迭代法求得最优阈值后,仍需进行一些人工调整才能将此阈值用于实验图像的分割,这是因为,这种最优阈值仍然属于全局阈值,它利用了图像中所有像素点的信息,但当光照不均匀时,图像中部分区域的灰度值可能差距较大,造成计算出的最优阈值分割效果不理想,此时,可设一人工经验因子进行校正。
四 实验步骤及程序实验程序:I=imread('peppers.bmp'); ZMax=max(max(I)); ZMin=min(min(I)); TK=(ZMax+ZMin)/2; bCal=1; iSize=size(I); while (bCal) iForeground=0; iBackground=0; ForegroundSum=0; BackgroundSum=0; for i=1:iSize(1) for j=1:iSize(2) tmp=I(i,j); if (tmp>=TK)iForeground=iForeground+1;ForegroundSum=ForegroundSum+double(tmp); elseiBackground=iBackground+1;BackgroundSum=BackgroundSum+double(tmp);endendendZO=ForegroundSum/iForeground;ZB=BackgroundSum/iBackground;TKTmp=double((ZO+ZB)/2);if(TKTmp==TK)bCal=0;elseTK=TKTmp;endenddisp(strcat('µü´úºóµÄãÐÖµ£º',num2str(TK)));newI=im2bw(I,double(TK)/255);subplot(121),imshow(I)title('Ô-ͼÏñ')subplot(122),imshow(newI)title('·Ö¸îºóµÄͼÏñ')五实验结果与分析原图像分割后的图像图1-1迭代后的阈值:102.3649遥感:%% Àý12.2 ¶àÆ×Êý¾ÝµÄ±´Ò¶Ë¹·ÖÀà(ÏÔʾÁË´íÎóµã)clcclearf1 = imread('Fig1125(a)(WashingtonDC_Band1_512).tif');f2 = imread('Fig1125(b)(WashingtonDC_Band2_512).tif');f3 = imread('Fig1125(c)(WashingtonDC_Band3_512).tif');f4 = imread('Fig1125(d)(WashingtonDC_Band4_512).tif');B1 = roipoly(f1);B2 = roipoly(f1);B3 = roipoly(f1);B = B1|B2|B3;imshow(B)stack = cat(3,f1,f2,f3,f4);[X1,R1] = imstack2vectors(stack, B1);[X2,R2] = imstack2vectors(stack, B2);[X3,R3] = imstack2vectors(stack, B3);Y1 = X1(1:2:end,:);Y2 = X2(1:2:end,:);Y3 = X3(1:2:end,:);[C1,m1] = covmatrix(Y1);[C2,m2] = covmatrix(Y2);[C3,m3] = covmatrix(Y3);CA = cat(3,C1,C2,C3);MA = cat(2,m1,m2,m3);dY{1} = bayesgauss(Y1,CA,MA);dY{2} = bayesgauss(Y2,CA,MA);dY{3} = bayesgauss(Y3,CA,MA);IY{1} = find(dY{1} ~=1 );IY{2} = find(dY{2} ~=2 );IY{3} = find(dY{3} ~=3 );%------------------------------------ ѵÁ·Ä£Ê½QQ_training = zeros(3,5);for i = 1:3QQ_training(i,4) = length(dY{i});for j = 1:3QQ_training(i,j) = length(find(dY{i} == j ));endQQ_training(i,5) = 100*(1 - length(IY{i})/length(dY{i})); end% %------------------------------------ ¶ÀÁ¢Ä£Ê½% Y1 = X1(2:2:end,:);% Y2 = X2(2:2:end,:);% Y3 = X3(2:2:end,:);%% dY{1} = bayesgauss(Y1,CA,MA);% dY{2} = bayesgauss(Y2,CA,MA);% dY{3} = bayesgauss(Y3,CA,MA);%% IY{1} = find(dY{1} ~=1 );% IY{2} = find(dY{2} ~=2 );% IY{3} = find(dY{3} ~=3 );%% QQ_test = zeros(3,5);%% for i = 1:3% QQ_test(i,4) = length(dY{i});% for j = 1:3% QQ_test(i,j) = length(find(dY{i} == j ));% end% QQ_test(i,5) = 100*(1 - length(IY{i})/length(dY{i})); % endwww1 = R1(IY{1},:);for i=1:length(www1)B(www1(i,1),www1(i,2)) = 0;endwww2 = R2(IY{2},:);for i=1:length(www2)B(www2(i,1),www2(i,2)) = 0;endwww3 = R3(IY{3},:);for i=1:length(www3)B(www3(i,1),www3(i,2)) = 0;endimshow(B)图1-2 QQ_training =68 0 0 68 1000 150 0 150 1000 0 128 128 100实验2 K均值聚类算法一、实验目的将模式识别方法与图像处理技术相结合,掌握利用K均值聚类算法进行图像分类的基本方法,通过实验加深对基本概念的理解。
