统计软件选讲
1第一讲++SPSS统计软件概述.[1]
![1第一讲++SPSS统计软件概述.[1]](https://img.taocdn.com/s3/m/ab55630a4a7302768e9939af.png)
数据编辑窗口的构成
标题栏:显示当前工作文件名称 主菜单栏:排列spss的所有菜单命令 工具栏:排列系统默认的标准工具图标按钮 状态栏:显示当前工作状态 数据编辑栏:显示用户录入的数据信息 数据显示区域:显示用户编辑确认的数据
工具栏:排列系统默认的标准工具图标按钮 •标题栏:显示当前工作文件名称 数据编辑栏:显示用户录入的数据信息 •主菜单栏:排列spss的所有菜单命令 数据显示区域:显示用户编辑确认的数据 状态栏:显示当前工作状态
(四) Data 菜单
子菜单
Define Date Insert Variable Insert Case Goto Case Sort Case Transpose
用途说明
定义日期 插入变量 插入观测量 定位到观测量 观测量排序分类 转置
子菜单
Restructure…** Merge Files Add Cases Add Variables Aggregate Split File
参数选择框
选择参数的数值。该项为一个矩形框,填入 所需的参数数值。默认情况下,系统会自动 填入默认值。
结果输出窗口
(1)结果输出窗口的右侧是一个文本窗口, 可对其中的内容进行编辑; (2)结果输出窗口的左侧是一个导航窗口, 也可以对其中的内容进行编辑。
四、SPSS的主菜单及其功能
(一) (二) (三) (四) (五) (六) (七) File 菜单 Edit 菜单 View 菜单 Data 菜单 Transform菜单 Analyze 菜单 Graph 菜单
三、SPSS的基本特点
使用windows的窗口方式展示各种管理和分 析数据的方法, 使用对话框展示出各种功能选择项 只要掌握了一定的windows操作技能,并了 解统计分析原理,就可以使用该软件为特 定的工作服务
数学软件选讲mathematica

2. 截取矩阵块 M[[i]] Map[#[[i]]&, M] M[[i, j ]] 取矩阵M的第 i 行 取矩阵M的第 i 列 取矩阵M的i, j 位置的元素
M[[{i1,…,ir}, {j1,…,js}]] 矩阵M的r×s子 矩阵,元素行标为ik,列标为jk M[[Range{i0,i1}, Range{j0,j1}]] 矩阵M的从 i0到i1行, j0到j1列元素组成的子矩阵
ymax}],用于绘制形如z =f (x, y)的函数 的密度图。 例:绘制函数 f=sinx· siny的等高线图和密度图
3. 三维图形 ① Plot3D[ f,{x,xmin,xmax},{y,ymin,ymax}] 绘制形如Z = f (x, y)的三维图形。
例:绘制以下的函数图形: Z = 10sin(x+siny)
Plot[Evaluate[Table[y[i,x],{i,Pi/12,5Pi/12,
Pi/12}]],{x,0,4000}]
② ListPlot [List],用于绘制散点图。 注意,List的形式应为:
{{ x0 , y0 },{x1 , y1},,{xn , yn }}
例:在同一坐标系下绘制下列两组散点图
例:有如下的抛物线簇:
gx 2 sec 2 y (tan ) x 2 2v0 ( g 9.8,v0 200)
当从15 变化到75,以15 为间隔时,绘出这组图形
程序: Clear[a,y,x] v=200;g=9.8; y[a_,x_]:=Tan[a]*x-g*x^2*Sec[a]^2/(2v^2)
Integrate[ f ,{x,xmin,xmax}, {y,ymin,ymax}]
求 f 的多重积分
(完整版)EXCEL统计学应用教程

数学与统计学院本科教学实验讲义(实验)课程名称统计学贵州财经学院教务处制表统计学实验教学讲义Excel 工作界面简介附图1 Excel 工作界面按附图1 从上到下的顺序,Excel 工作界面包含如下几项内容:“标题”栏、“菜单”栏、“工具”栏、“编辑”栏、工作表、工作表标签、滚动条、和“状态”栏。
下面分别介绍它们的作用。
(一)“标题”’栏“标题”栏告诉用户正在运行的程序名称和正在打开的文件的名称。
如图附-1 所示,标题栏显示“Microsoft Excel-Book1”表示此窗口的应用程序为Microsoft Excel ,在Excel 中打开的当前文件的文件名为Book1.xls。
(二)“菜单”栏“菜单”栏按功能把Excel 命令分成不同的菜单组,它们分别是“文件”、“编辑”、“视图”、“插入”、“格式”、“工具”、“表格”、“帮助”。
当菜单项被选中时,引出一个下拉式菜单,可以从中选取相应的子菜单。
另外,在屏幕的不同地方单击鼠标右键时,“快捷菜单”将出现在鼠标指针处。
选取“快捷菜单”中的命令同从菜单栏的菜单上选取相应命令的效果是一样的,但选取速度明显增快。
(三)“工具”栏Excel 可显示几种工具栏,这些工具可控制简化用户的操作。
“工具”栏中的按钮都是菜单中常用命令的副本,当鼠标指向某一按钮后,稍等片刻在按钮右下方会显示该按扭命令的含意。
用户可以配置“工具”栏的内容,通过“视图”菜单中的“工具”栏子菜单来选择显示不同类型的“工具”或全部显示出来。
下面介绍出现在Excel 开始屏幕中的两种“工具”栏。
1.“常用”工具栏“常用”工具栏中为用户准备了访问Excel 最常用命令的快捷按钮,如“新建文件”按扭,“打开文件”按扭,“保存文件”按钮等。
2.“格式”工具栏“格式”工具栏专门放那些和文本外观有关的命令,如字体、字号、对齐方式及其他选项。
(四)“编辑”栏“编辑”栏给用户提供活动单元格的信息。
在“编辑”栏中用户可以输入和编辑公式,“编辑”栏位于图1 中第5 行。
第一讲SPSS统计分析软件概述

第一讲SPSS统计分析软件概述教学目标1.明确SPSS软件是一种专业的统计分析软件,了解SPSS的主要应用领域;2.熟练掌握SPSS进入和退出等基本操作,了解SPSS的基本窗口和菜单安排;3.掌握SPSS的三种使用方式以及它们的特点和应用场合;4.掌握利用SPSS进行数据分析的基本步骤。
教学内容1.SPSS使用基础;2.SPSS基本运行方式;3.SPSS进行数据分析的基本步骤。
第一节SPSS使用基础一、SPSS的含义SPSS是软件英文名称的首字母缩写,全称为Statistical Package For The Social Sciences,即社会科学统计软件包。
SPSS软件由美国斯坦福大学三位研究生所研发,并于1975年在芝加哥成立了专门研发和经营SPSS软件的SPSS公司。
于2000正式将公司全称改为“Statistical Product and Service Solutions”即统计产品与服务解决方案。
SPSS软件是世界三大软件之一,应用领域十分广泛,应用于经济学、金融学、市场研究、社会民族学、人类学、社会工作、医学、农学、工学等多个领域。
被称为“真正的统计,确实简单”。
二、SPSS for windows的特点1.操作界面极为友好,易于学习,易于使用,是非专业统计人员的首选统计软件。
2.无需花费大量时间记忆大量命令、过程、选择项等。
3.只要粗通统计分析原理,就能得到统计分析的结果。
4.可以根据计算机的设备来选择安装,灵活方便。
5.能非常方便地与其他软件的数据进行转换。
6.分析方法丰富,图表功能强大,输出结果美观漂亮。
三、SPSS的启动与退出1.SPSS的启动使用开始菜单启动SPSS双击SPSS图标启动SPSS2.SPSS的退出使用“文件”菜单中的“退出”菜单项退出SPSS单击数据编辑窗右上角“x”的退出SPSS在退出SPSS之前,一般会提示用户以下两个问题:第一,是否将数据编辑器窗口中的数据保存到磁盘上,文件扩展名为.sav。
(完整版)Excel教案全集

具栏” → “格式工具栏” → “编辑栏” → “工作区” → “工作表课题: 认识 Excel教学目标: 了解 Excel 的启动、退出熟悉电子表格的功能、特点及应 用, 掌握 Excel 窗口各个组成部分,学会区分工作表和工作簿,了解 工具菜单自定义与选项命令教学重点:工作表和工作簿的关系,制定义 Excel 窗口界面教学难点:灵活使用各种工具制定义 Excel 窗口界面教学方法: 教授 、演示教学过程:一、 组织教学二、 复习导入在前面学习了排版、 编辑文件考试试卷等文件操作, 我们使用的是 word 软件。
如果我们要想对考试成绩进行数据处理和数据分析, 那我们要使用的就是 Excel 软件了。
Excel 的界面友好,操作简单; 兼容性好; 使用方便; 也具有网络功能。
这节课我们来认识 Excel [板 书]三、 讲授新课1. Excel 的启动提问: Word 软件是怎样启动的?引出 excel 的启动。
三种方法: 1) “开始” → “程序” →“Micro soft Excel ”2)双击“桌面”上的 Excel 快捷方式3)右击“桌面”空白处 →“新建”→Excel 工作表2. Excel 的窗口1) . 比较 Execl 窗口与 Word 窗口的异同按由上到下的顺序为: “标题栏” → “菜单栏” → “常用工... ... 标.签. ” → “水平滚动栏” → “状态栏” → “垂直滚动栏”2)工作区:全选按钮;行号;列标;单元格;水平分割框(右上角) ;垂直分割框(右下角) 。
(介绍 Excel 的工作表)3. Excel 工具栏的显示与隐藏(可略)方法: 1)右击键菜单栏或工具栏,选快捷菜单显示或隐藏的工具栏名称。
2) “视图”→ “工具栏” → 常用、格式、绘图。
适宜: Word/Excel 等大部分编辑软件。
说明:本命令属于开关命令(单击就打开、再单击就隐藏) 4.菜单栏与工具栏的移动(可略)方法:鼠标指向菜单栏的双线处,拖动菜单栏到指定位置。
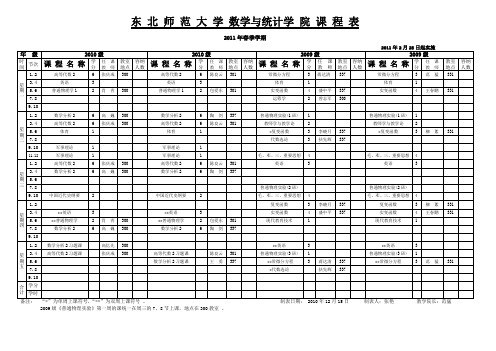
东北师范大学数学与统计学院课程表
秦德生
韩继伟
307
233
中学数学课程标准及教材研究
2
郭 民
300
7.8
微格教学
1
韩继伟
233
星期三
1.2
现代分析学基础
3
张凯军
307
现代分析学基础
3
张凯军
307
3.4
初等数论
微格教学
2
1
程传平
李 清
307
233
5.6
星期四
1.2
微分流形
3
王 勇
307
微分流形
3
王 勇
307
凸分析
2
刁怀安
307
3.4
学分
任 课
教 师
教室地点
容纳人数
星期一
1.2
高数(城环)
4
宋海燕
孙雪楠
逸10
逸11
5.6
7.8
高数(计算机)
高数(软 件)
4
李亚军
孙佳宁
传西402
软322
11.12
数学建模
2
曾志军
331
线性代数
3
李亚军
政6
星期二
1.2
3.4
5.6
高数(物理)
4
王 静王 勇
物3
物4
7.8
11.12
实用数值分析
2
孙佳宁
军事理论
1
军事理论
1
毛、邓、三、重要思想
4
毛、邓、三、重要思想
4
星期三
1.2
高等代数2
6
张庆成
300
高等代数2
SPSS_入门讲义

③自从1995年SPSS公司与微软公司合作开发 SPSS界面后,SPSS界面变得越来越友好,操 作也越来越简单。熟悉微软公司产品的用户学 起SPSS操作很容易上手。与其它统计软件相比, spss不用记忆繁琐、枯燥的语句和命令,只要 用户具有一般的计算机和统计学知识,就能运 用鼠标进行操作,得到所需要的统计分析结果。 SPSS for Windows界面完全是菜单式,一般稍 有统计基础的人经过三天培训即可用SPSS做简 单的数据分析,包括绘制图表、简单回归、相 关分析等等,关键在于如何进行结果分析及解 释,这一方面需要学习一些数理统计的基本知 识,另一方面也要多进行实践,在实践中了解 各种统计结果的实际意义
SPSS的界面
2.1创建SPSS数据文件
File: 文件操作
完成文件的调入、存储、
显示和打印等操作。
2.1创建SPSS数据文件
1.在Variables View 视区定义变量及其变量的 属性 2.在Date View视区录入数据文件的内容
浏览数据文件变量名的三种方法 在Variable View视区中浏览 在SPSS菜单中选择Utilities →Varibles 在SPSS主界面选择File → Display Date File information
建立数据集
Name: 变量名
在该栏输入变量名(只能用 字母) 本例定义5个变量: Number Sex Age Height weight
1.2变量的类型(Type)
数值型:根据其功能和形式又可细分为(标准 型、逗号型、句点型、科学计数型、美元 型和自定义货币型) 字符型 日期型 系统默认为标准数值型
1.单样本T检验
检验单个变量的均值是否与给定的常 数之间存在差异。样本均数与总体均数 之间的差异显著性检验属于单一样本T 检验。
SAS介绍(第一讲)

命 令 框
新 建
保 存
打 印 预 览
复 制
撤 消
浏 览
清 除
帮 助
SAS基本概念
• SAS数据集: • 临时数据集 • 永久数据集 • SAS数据库: • 临时数据库 • 永久数据库 • 注: 理解它们之间的联系和区别
SAS数据集
• SAS数据集是SAS系统的基本操作对象,是 数据在SAS系统中的存储形式. • SAS数据集可以看成是由若干行和列组成 的一个 表格(矩阵),每个列可以取不同类型 的值(整数型,浮点值,时间值,字符等). • SAS数据集以.sas7bdat为扩展名. • 命名方式:由英文字母,数字,下划线组成,且 第一个字母必须是字母或下划线,最多8个字 符. • 不区分大小写.
Байду номын сангаас
为什么选择SAS?
• 运行稳定,功能强大 • 结果可靠,人们认可 • 在财富500强企业中,有90%以上都使用 SAS软件,并且只承认SAS计算的结果.在财 富100强的企业中,甚至有95%以上都在使 用SAS. • 在以苛刻严格著称于世的美国FDA新药审 批程序中,新药试验结果的统计分析规定 只能用SAS进行,其他软件的计算结果一 律无效
(4)利用SAS/Import菜单进行数据导入
可以导入 excel 和 txt 等其它格式的文件
SAS数据库
• SAS数据库的概念与通常所讲的数据库的 概念不同,它是SAS系统特有的一个概念. • SAS数据库是比数据集高一级的目录,比如 刚才的work,sasuser都是数据库. • 在SAS系统中自定义的三个数据库分别是 WORK, SASUSER, SASHELP.
☆ SAS集“问卷设计、数据汇总和精辟分析”于 一身,是国际上最知名的软件之一。在国际学术 界有条不成文的规定,凡是用SAS和SPSS统计 分析的结果,在国际学术交流可以不必说明算法, 由此可见其权威性和信誉度。
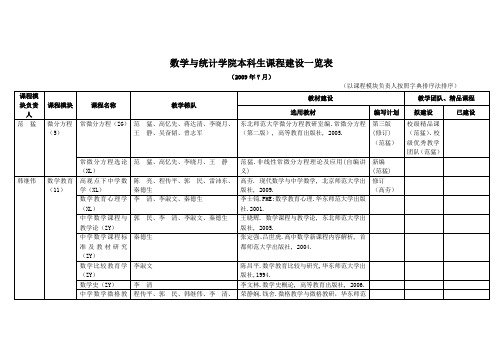
数学与统计学院本科生课程建设一览表-东北师范大学数学与统计学院
索伯列夫空间
蔡守峰、刁怀安、孙佳宁、盛中平
邵勇译.数学软件入门,高等教育出版社, 2003.
编写中
(盛中平)
陶剑
概率统计
(8)
概率论基础(ZG)
高巍、郭建华、刘红、宋海燕、陶剑、杨青山
Mood A. M., Gray F. A., and Boes D. C. Introduction to the Theory of Statistics, McGraw-Hill Book Company, 1974.
张同君.竞赛数学,高等教育出版社, 2007.
教育实习(ZY)
陈亮、刁怀安、韩继伟、李淑文、秦德生、孙佳宁、曾志军
教育见习(ZY)
郭民、韩继伟、李淑文、秦德生、沈广艳、孙佳宁、孙雪楠
裴东河
几何拓扑
(5)
解析几何
陈亮、李宾、裴东河、王勇、沈广艳
1.丘维生.解析几何(第二版),北京大学出版社,1996
2.吕林根.解析几何(第四版),高教出版社,2006
胡果荣、宋海燕、朱文圣
孙山泽.抽样调查,北京大学出版社, 2004.
袁岗华
运筹与控制
偏微分方程(XL)
雷沛东、柳絮、袁岗华、赵宏亮
陈祖墀.偏微分方程(第三版),中国科学技术出版社, 2008.
运筹学(XL)
刁怀安、曾志军
何坚勇.《运筹学基础》,清华大学出版社, 2000年7月.
控制论基础(XL)
高忆先、雷沛东、李亚军、林萍、柳絮、赵宏亮、曾志军
陈维桓.微分流形初步,高等教育出版社, 1998.
数学思想方法(XL)
新编(史宁中)
代数拓扑学
沈广艳、裴东河、王勇
统计软件论文 王铁

《统计软件选讲》课程论文基于统计软件SPSS、EXCEL、EVIEWS的回归分析数学与统计学院统计08-2王铁08071601018基于统计软件SPSS、EXCEL、EVIEWS的回归分析摘要:回归分析是数量统计中一种常用的方法。
本文首先简要介绍SPSS、EXCEL、EVIEWS这三种统计软件,然后通过实例,分别用这三种软件进行回归并进行分析比较。
关键词:统计软件回归分析1.SPSS、EXCEL、EVIEWS的简介1.1 SPSS的简介SPSS(Statistical Package for the Social Science)的中文译名为社会科学统计软件包,它是世界著名的、优秀的统计分析软件之一。
该软件包理论严谨,各种统计分析功能齐全,其内容覆盖了从描述统计、探索性数据分析到多元分析的几乎所有统计分析功能,目前已经在国内逐渐流行起来。
SPSS的基本功能包括数据管理、统计分析、图表分析、输出管理等等。
SPSS统计分析过程包括描述性统计、均值比较、一般线性模型、相关分析、回归分析、对数线性模型、聚类分析、数据简化、生存分析、时间序列分析、多重响应等几大类,每类中又分好几个统计过程,比如回归分析中又分线性回归分析、曲线估计、两阶段最小二乘法、非线性回归等多个统计过程,而每个过程中又允许用户选择不同的方法及参数。
SPSS又有专门的绘图系统,可以根据数据绘制各种图形。
SPSS for Windows的分析结果清晰、直观、易学易用,而且可以直接读取EXCEL数据文件,它使用Windows的窗口方式展示各种管理和分析数据方法的功能,使用对话框展示出各种功能选择项,只要掌握一定的Windows操作技能,粗通统计分析原理,就可以使用该软件为特定的科研工作服务。
由于其操作简单,已经在我国的社会科学、自然科学的各个领域发挥了巨大作用。
该软件还可以应用于经济学、生物学、心理学、医疗卫生、体育、农业、林业、商业、金融等各个领域。
STATA入门PPT课件

一、数据录入、打开与保存
1.数据录入与读取
直接录入数据 input命令 读入ASCII格式原始数据——使用insheet、 infile、infix等命令 使用Stat/Transfer软件
一、数据录入、打开与保存
2. STATA数据打开 双击直接打开
Do文件中使用use命令
一、数据录入、打开与保存
[STATA演示]
三、变量类型与简单描述统计方法
7. 离散与连续变量
通常,离散变量包括了定类变量和定序变量,统计 描述可参照之;而连续变量包括了定距变量和定比 变量,统计描述同样可参照之。 值得注意的是,在社会科学研究中,定距变量和定 比变量很少单独区分。
四、练习与作业
【1】请在2014年卫计委流动人口动态监测调查数据 之“社会融合与心理健康问卷”部分识别各变量 设置的层次。
二、基本的STATA数据处理命令
6.生成虚拟(哑)变量的命令 –tab region, generate(region) 7.帮助命令
–help command
三、变量类型与简单描述统计方法
1. 变量类型
区分标准之一:离散变量与连续变量
区分标准之二:定比变量、定距变量、 定序变量与定类变量
三、变量类型与简单描述统计方法
第二讲:STATA入门
1.统计软件:STATA14.0
2.数据准备:① 2014年卫计委流动人口动态监测调 查数据之“社会融合与心理健康问卷”部分;②农 民工随迁子女城市融入课题组的“外出务工调查数 据”。
1. 数据录入、打开与保存 2. 基本的STATA数据处理命令 3. 变量类型与简单描述统计方法 4. 练习与作业
4.删除变量或观察值命令 – drop命令 – drop in 1/10 or (-10/-1) – keep命令 – keep var1 var2… – keep if
Stata操作讲义

Stata操作讲义第一讲Stata操作入门第一节概况Stata最初由美国计算机资源中心(Computer Resource Center)研制,现在为Stata公司的产品,其最新版本为7.0版。
它操作灵活、简单、易学易用,是一个非常有特色的统计分析软件,现在已越来越受到人们的重视与欢迎,并且与SAS、SPSS一起,被称为新的三大权威统计软件。
Stata最为突出的特点是短小精悍、功能强大,其最新的7.0版整个系统只有10M左右,但已经包含了全部的统计分析、数据管理与绘图等功能,尤其是他的统计分析功能极为全面,比起1G以上大小的SAS系统也毫不逊色。
另外,由于Stata在分析时是将数据全部读入内存,在计算全部完成后才与磁盘交换数据,因此运算速度极快。
由于Stata的用户群始终定位于专业统计分析人员,因此他的操作方式也别具一格,在Windows席卷天下的时代,他一直坚持使用命令行/程序操作方式,拒不推出菜单操作系统。
但是,Stata的命令语句极为简洁明快,而且在统计分析命令的设置上又非常有条理,它将相同类型的统计模型均归在同一个命令族下,而不同命令族又可以使用相同功能的选项,这使得用户学习时极易上手。
更为令人叹服的是,Stata语句在简洁的同时又拥有着极高的灵活性,用户可以充分发挥自己的聪明才智,熟练应用各种技巧,真正做到随心所欲。
除了操作方式简洁外,Stata的用户接口在其他方面也做得非常简洁,数据格式简单,分析结果输出简洁明快,易于阅读,这一切都使得Stata成为非常适合于进行统计教学的统计软件。
Stata的另一个特点是他的许多高级统计模块均是编程人员用其宏语言写成的程序文件(ADO文件),这些文件可以自行修改、添加与下载。
用户可随时到Stata网站寻找并下载最新的升级文件。
事实上,Stata的这一特点使得他始终处于统计分析方法发展的最前沿,用户几乎总是能很快找到最新统计算法的Stata程序版本,而这也使得Stata自身成了几大统计软件中升级最多、最频繁的一个。
sas课件第讲基本知识

SAS课件第讲基本知识1. 引言SAS(Statistical Analysis System)是一种通用的统计分析软件,被广泛应用于数据处理、数据管理和数据分析领域。
本课件将介绍SAS的基本知识,包括SAS 的起源和发展、SAS的应用领域、SAS的主要特点以及SAS的安装和配置。
2. SAS的起源和发展2.1 起源SAS起源于上世纪60年代,最初是由北卡罗来纳州立大学开发的一个统计分析系统。
起初,SAS主要用于大规模的数据处理和统计分析,随着时间的推移,SAS逐渐发展成为一个全面的数据处理和分析平台。
2.2 发展在过去的几十年里,SAS经历了快速的发展,成为全球最受欢迎的数据分析软件之一。
SAS的发展主要得益于其强大的功能和灵活性,同时也得益于SAS公司对产品研发和技术支持的不断投入。
3. SAS的应用领域SAS在各个行业和领域都有广泛的应用,包括金融、医疗、营销、制造业等。
下面将介绍SAS在几个典型领域的应用。
3.1 金融在金融领域,SAS被广泛用于风险管理、信用评级、欺诈检测等方面。
SAS提供了一系列的数据处理和分析功能,可以帮助金融机构更好地理解和管理风险,提高运营效率。
3.2 医疗在医疗领域,SAS被用于疾病预测、临床试验分析、医疗资源管理等方面。
SAS可以帮助医疗机构从大量的医疗数据中发现规律和趋势,为医疗决策提供科学依据。
3.3 营销在营销领域,SAS的应用主要集中在市场调研、客户细分和推荐系统等方面。
SAS可以帮助企业分析大量的市场数据,了解消费者需求和行为,从而制定更有效的营销策略。
3.4 制造业在制造业领域,SAS被用于供应链管理、质量控制和生产优化等方面。
SAS可以帮助制造企业优化供应链流程,提高产品质量和生产效率,降低成本。
4. SAS的主要特点4.1 数据处理能力强SAS具有强大的数据处理能力,可以处理大规模的数据集。
SAS提供了丰富的数据处理函数和过程,可以对数据进行清洗、转换、合并等操作。
第一讲 stata基础----山大stata实验课讲义

不同版本对样本容量、变量个数、矩阵阶数、 宏的字符长度等有着不同的限制。 以stata 12的SE版为例,其最大变量个数为 32767,最大字符长度为244字节,最大矩 阵阶数为11000(即1100011000)。 Stata默认值为:变量个数为5000,最大矩 阵阶数为400,内存容量为10兆。如果用户 需要更多的内存或者更多的变量,可以在命 令栏输入如下命令进行扩展。 set maxvar 8000 <最大变量个数8000个。 > set memory 50m <占内存50兆。>
Stata的文件
最重要的有三类文件 1。文件名.dta 数据文件 2。文件名.do 命令文件 3。文件名.ado 程序文件
Stata自带的示例数据表
为了方便大家学习,stata中有很多自带示例 数据,绝大部分数据都是美国的一些真实统 计数据,较新的数据和统计资料可以到stata 网站中下载。 注意:所有系统自带的数据需要用sysuse命 令打开。
Stata的窗口介绍
命令窗口 结果窗口 命令回顾窗口 变量窗口 变量和数据属性窗口
Stata的菜单介绍
最重要的菜单项: Data菜单 Graphic菜单 Statistics菜单 每执行一个菜单性会自动产生相应的命令。(我们 以summarize为例加以阐述)。 我们的讲述尽量兼顾到命令操作和菜单操作两种方 法,以命令方式为主。
命令格式简介
stata命令格式 [by varlist:] command [varlist] [=exp] [if exp] [in range] [weight] [, options] 1。Command 命令动词,经常用缩写。 2。varlist 表示一个变量或者多个变量,多 个变量之间用空格隔开。如 sum price weight 3。 by varlist 分类信息 按照某一变量的 不同特性分类
江苏省建筑业统计信息系统软件操作讲解

上级管理代码一般为“001+本地行政区划代码”,不清楚 的可电话询问主管部门。
填写组织机构代码证时,注意“-”为半角,不能在全角输 入法的状态下填写“-”。
江苏省建筑业统计信息系统软件操作讲解
附库一中人数是指公司的总人数,而工程库中 “计算劳动生产率平均人数”是指工程项目部的 直接从事生产的工人与管理人员。
公司“本部计算劳动生产率平均人数”是指公司 后方机关的行政、经济、技术管理人员。不能为 “0”,也不可能有上百人。
工程库与附库一填写完毕后,必须进行报表计算。 如果报表计算后发现工程库或附库一数据有错误, 修改保存后需重新进行报表计算。
江苏省建筑业统计信息系统软件操作讲解
年报中的财务报表注意事项:
所有者权益=资产总额-负债总额=实收资本 +资本公积+盈余公积+未分配利润
工程结算收入涉及到企业资质核查以及资 质升级,一定要掌握标准。
江苏省建筑业统计信息系统软件操作讲解
工程结算税金及附加包括营业税+城建税+ 教育费附加+相关规费,不含企业所得税及 个人所得税。
江苏省建筑业统计信息系统软件操作讲解
1
江苏省建筑业统计信息系统软件操作讲解
新企业初始使用软件讲解
已注册用户使用软件讲解
异地、重装系统或更换电脑后申报报表流 程讲解
江苏省建筑业统计信息系统软件操作讲解
直接登录江苏建筑业统计信息网jstjbb
或者从江苏建筑业网首页左 侧点“江苏建筑业统计信息网”
进行“报表查询”,查询一下所要报的报表是 否有数据,季报中的财务报表(不是自动生成, 需手工填写)是否填写。
SPSS应用讲义

SPSS应用讲义一、SPSS是软件英文名称的首字母缩写,原意为Statistical Package for the Social Sciences,即“社会科学统计软件包”。
随着SPSS产品服务领域的扩大和服务深度的增加,SPSS公司已于2000年正式将英文全称更改为Statistical Product and Service Solutions,意为“统计产品与服务解决方案”。
SPSS现在的最新版本为11.03,大小约为200M。
它是世界上最早的、应用最广泛的统计分析软件,应用于通讯、医疗、银行、证券、保险、制造、商业、市场研究、科研教育等多个领域和行业。
也是目前权威统计软件中界面最为友好,使用最为方便的。
在国际学术界有条不成文的规定,即在国际学术交流中,凡是用SPSS软件完成的计算和统计分析,可以不必说明算法,由此可见其影响之大和信誉之高。
二、优点S PSS最突出的特点就是操作界面极为友好,输出结果美观漂亮(从国外的角度看),它使用Windows的窗口方式展示各种管理和分析数据方法的功能,使用对话框展示出各种功能选择项,只要掌握一定的Windows操作技能,粗通统计分析原理,就可以使用该软件为特定的科研工作服务。
SPSS采用类似EXCEL表格的方式输入与管理数据,数据接口较为通用,能方便的从其他数据库中读入数据。
其统计过程包括了常用的、较为成熟的统计过程,完全可以满足非统计专业人士的工作需要。
是非专业统计人员的首选统计软件。
三、缺点:该软件只吸收较为成熟的统计方法,而最新的统计方法,在SPSS中均难觅芳踪。
另外,其输出结果虽然漂亮,但不能为WORD等常用文字处理软件直接打开,只能采用拷贝、粘贴的方式加以交互。
知道吗?在计算机领域中有个著名的80/20规则,也就是在奔腾及更早的CPU所采用的CISC指令集中,有80%的任务是被20%的最常用指令所完成的;换言之,另外80%的复杂指令只完成20%的不常用任务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录Chapter 1-2Recipe1.Vector向量定义、性质、选取子集、判断Recipe2.Factor因子Recipe3.Matrix矩阵定义、转化、基本运算Recipe4.List清单Recipe5.Data Frame数据框Chapter 3Recipe1.Sample随机数Recipe2.Central Limit Theorem中心极限定理Chapter 4Recipe1.Functions函数Recipe2.Loops循环Forloops、ifelse、while、stretch、powRecipe3.防错&除错Max.power、max.power_bookRecipe4.Examples例子Basic_funs、is.symChapter 5Recipe1.读取和整理Chapter 6Recipe1.Linear Regression Model线性回归模型散点图、回归分析、作图、分析图,多元线性回归、lmcurve Recipe2.Analysis of Variance Model方差分析模型盒子图、方差分析Recipe3.Generalized Linear Models广义线性模型Binomial Model(Logistic Regression)Chapter 7Recipe1.Linear Discriminant Analysis线性判别分析Recipe2.Cluster Analysis聚类分析分层聚类分析、非分层聚类分析Recipe3.Library程序馆Chapter 8Recipe1.Multiframe Graphic多重图框Recipe2.增加直线一、R软件教程Chapter 1-2Recipe1.Vector向量rm(list = ls())x <- c(1, 2, 3, 4) ##c(向量内容,若是字符需要加"")y <- 1:100 ##连续型z <- seq(1, 100, by = 8) ##等差数列seq(首项, 最大值, by = 公差)w <- rep(1:4, each = 2, times = 2)##重复性rep(内容, c(各项重复次数) or each = n全部都重复n次, times = m整体重复m次)#####3倍向量#####r <- NULLfor (i in 1:50){r <- c(r,3*i)}#################性质length(x) ##求长度mean(y) ##求均值var(z) ##求方差#选取子集x[1] ##选取第一个分量y[2:4] ##选取第2到4个分量z[c(1, 5, 1)] ##选取第1,5,1个分量w[-1] ##去除第1个分量r[r < 25] ##选取小于25的分量#判断Is.vector(x) ##是否为向量Is.numeric(x) ##是否为数字构成的向量Recipe2.Factor因子rm(list = ls())medicine <- c(rep("Jack", 3), rep("A", 4), rep("B", 3))is.factor(medicine) ##检验is.**()medicine <- as.factor(medicine) ##转化as.**() 因子levels(medicine) ##水平Recipe3.Matrix矩阵rm(list = ls())x1 <- matrix(1:9, 3, ) ##(向量,行数,列数),向量数=行数*列数,默认按列排列x2 <- matrix(2:10, , 3, byrow=TRUE) ##byrow=TRUE按行排列diag(5) ##5*5单位阵dim(x1) ##维数colnames(x1) <- c("c1", "c2", "c3") ##列名rownames(x1) <- c("r1", "r2", "r3") ##行名x2[c(1, 3), c(2, 3)] ##调动子矩阵#转化t1 <- as.vector(x1) ##将x1转变为向量t2 <- as.matrix(t1) ##将t1转变为矩阵,默认列向量t(x1) ##转置t(t1) ##将t1转为矩阵,默认行向量q <- solve( matrix( c(1, 5, 6, 3), 2, ) ) ##求逆矩阵dim(q) ##求行数列数#基本运算x1 + x2 ##矩阵加法x1 * x2 ##对应元素相乘(错误做法,注意)x1 %*% x2 ##矩阵乘法v1 <- 1:3x1 * v1 ##第n行*第n元素(错误做法,注意)x1 %*% as.matrix(v1) ##向量乘矩阵要先转化A <- matrix(c(1, 2, 3, 4, 5, 6, 7, 8, 10), 3, , byrow = TRUE)e <- eigen(A) ##求特征值及特征向量e$values ##调用特征值svd(A) ##奇异值分解B <- matrix(1:6, 2, )C <- matrix(5:10, , 2)rbind(A, B) ##按行合并cbind(A, C) ##按列合并apply(A, 1, sum) ##按行加和apply(A, 2, sum) ##按列加和sd(标准差)medina####定义3维矩阵####a <- 1:24dim(a) <- c(2, 3, 4)#################Recipe4.List清单rm(list = ls())a <- 1b <- 5:8c <- matrix(1:10, 2, )d <- c("Jack", "Lucy", "Mark", "L.C.")x <- list(sex = a, age = b, birth = c, name = d) ##定义清单各名字x[[1]] ##调用第1对象x$age ##调用此名称对象x[["birth"]] ##调用此名称对象Recipe5.Data Frame数据框rm(list = ls())grade <- read.csv("Book1.csv") ##读取数据part <- names(grade) ##名字grade <- as.matrix(grade)grade <- as.factor(grade)gradepart <- rep(part, each=16)parttemp <- matrix(c(grade, part), nc=2) ##结合grade与part,nc列数temptemp <- temp[!is.na(temp[,1])] ##除去NA项temptemp <- matrix(c(grade, part), nc=2)tempbeauties <- data.frame(temp) ##数据框beautiescolnames(beauties) <- c("Grade", "Name") ##改名字attach(beauties) ##通过名字寻访数据###########################################rm(list=ls())grade <- read.csv("Book1.csv") ##读取数据gradegrade1 <- read.csv("Book1.csv", header=FALSE) ##将名字默认为数据grade1attributes(grade) ##总结数据grade[,1]min(grade[,1])grade[2,]max(grade[2,])attach(grade) ##方便调用g_matrix <- as.matrix(grade) ##数据框转矩阵g_matrixis.matrix(g_matrix)g_frame <- data.frame(g_matrix) ##矩阵转数据框g_frameis.matrix(g_frame)Recipe1.Sample随机数rm(list = ls())set.seed(20140919) ##设置随机种子,下次再启用数据不变v1 <- sample(1:100, 9, replace = TRUE) ##随机向量,有放回v2 <- sample(1:100, 9, replace = FALSE)Recipe2.Central Limit Theorem中心极限定理rm(list = ls())set.seed(12345)u = runif(10000) ##均匀分布summary(u) ##总结var(u) ##方差hist(u, main = "U(0, 1)") ##直方图u = matrix(u, nc = 10)m = apply(u, 1, mean) ##计算u内每一行的平均数summary(m)var(m)hist(m, main = "样本平均(n=10)的抽样分布")Recipe1.Functions函数rm(list = ls())fix(ifelse) ##找出函数,修改后源文件不变,但再次fix版改变edit(max.power) ##找出函数,修改后皆不变Recipe2.Loops循环######forloops######求和rm(list = ls())VC_loops <- function(a){##a must be a vector!n <- length (a)s <- 0for(i in 1:n){ s <- s + a[i] }s ##or return (s)}————RUN————rm(list = ls())source("forloops.r")x <- c(1, 2, 3, rep(3, 10), sample(10))VC_loops(x)######ifelse######求数值为0和21的数的总数rm(list = ls())VC_ifelse1 <- function(vec){n <- length(vec)s <- 0for(i in 1:n){if(vec[i]==0){ s <- s + 1 }else if(vec[i]==21){ s <- s + 1 }}s}VC_ifelse2 <- function(vec){n <- length(vec)s <- 0for(i in 1:n){if(vec[i]==0 || vec[i]==21)##||or &&and ==is !=not{ s <- s + 1 }else{ s <- s }}return (s)}————RUN————source("ifelse.r")VCvec <- c(0, 56, 21, 21, 21, 0, 59, 98, 356, 847, 21, 0)VC_ifelse1(VCvec)VC_ifelse2(VCvec)######while######rm(list = ls())VC_while <- function(x, y){n <- 0while (x < y){n <- n + 1x <- x^n}n}————RUN————source("while.r")x <- 10y <- 1001VC_while(x, y)######stretch######rm(list = ls())VC_stretch <- function(vec, num){output <- NULLnn <- length(vec)for(i in 1:nn){ output <-c(output, rep(vec[i], num)) } output}————RUN————source("stretch.r")VCvec2 <- c("VC", "JC", "Cara", "Cuckoo")VC_stretch(VCvec2, 10)######pow######rm(list = ls())VC_pow <- function(x, y){if(x > y){ return ("Error! x is bigger than y!") } else{n <- 0for(i in 1:100){if(x^(n+1) < y){ n <- n + 1 }}x^n}}————RUN————source("pow.r")x <- 10y <- 1001z <- 101VC_pow(x, y)VC_pow(y, z)Recipe3.防错&除错rm(list = ls())######max.power#######max.power <- function(x, y){if(x < y & x > 0){n <- 1midx <- xwhile(x < y){n <- n + 1x <- midx ^ n}return(n - 1)}Else{ stop("x is bigger than y or something else!") ##防错} }debug(max.power) ##除错max.power(2,9) ##运行后,按步骤运行undebug(max.power) ##退出除错######max.power_book######max.power_book <- function(x, y){if(x < y & x > 0)if(x > 1){i <- 1total <- xwhile(total*x < y){i <- i+1total <- total*x}i}else"Infinity"else NULL}Recipe4.Examples例子######Basic_funs######rm(list = ls()) ##Definition of functions in R! VC_sum <- function(a, b){ a+b } ##定义VC_sumVC_odds <- function(a, b) ##定义VC_odds {if(a-b !=0){ return((a+b)/(a-b)) }else{ return("Error!") }}————RUN————rm(list = ls())source("Basic_funs.r") ##读取文件a <- 2b <- 2VC_sum(a, b)VC_odds(a, b)######is.sym######rm(list = ls())is.sym <- function(x){if(!is.matrix(x)){ stop("The input must be a matrix!") }n <- dim(x)[1]m <- dim(x)[2]if(n != m){ stop("Matrix is not squared!") }for(i in 1:n){for(j in 1:n){if(x[i, j] != x[j, i]){ stop("Matrix is not synetric!") } }}return("The input is a symetric matrix!")}————RUN————rm(list = ls())source("is.sym.r")x <- 1:9is.sym(x)x <- matrix(1:9, 3, )is.sym(x)x <- matrix(1:12, 3, )is.sym(x)x <- matrix(rep(1, 9), 3, )is.sym(x)Recipe1.读取和整理rm(list = ls())x <- read.csv("replace.csv") ##读取数据y <- replace(x, is.na(x), 0) ##替换数据z <- replace(y, y < 6, NA)Recipe1.Linear Regression Model线性回归模型rm(list = ls())data(faithful) ##调动R中原有数据attach(faithful) ##分量数据化plot(eruptions, waiting) ##散点图faithful.lm <- lm(waiting ~ eruptions) ##回归分析summary(faithful.lm) ##总结curve(33.47 + x * 10.73, 1.5, 5.0, add = TRUE, lwd = 3, col = 4)##作图(方程,左区间,右区间,add:if TRUE 加入已有的散点图,,线粗,颜色)par.lm <- par(mfrow = c(2,2))plot(faithful.lm) ##分析图par(par.lm)######多元线性回归######rm(list = ls())data(stackloss)attach(stackloss)y <- stackloss&stack.lossx1 <- Air.Flowx2 <- Water.Tempx3 <- Acid.Conc.a <- lm(y ~ x1 + x2 + x3)summary(a)b <- lm(y ~ x1 + x2 + x3, subset = -21)summary(b)######lmcurve######rm(list = ls())x <- rnorm(100)y <- rnorm(100)a <- lm(y ~ x)res <- a$coefficientsplot(x, y)curve(res[1] + res[2]*x,-3, 3)rm(list = ls())for(i in 1:3){x <- rnorm(10)y <- rnorm(10)a <- lm(y ~ x)res <- a$coefficientsplot(x, y)curve(res[1] + res[2]*x,-3, 3, lwd = 2, col = 3, add = T) savePlot(paste(i), type = "jpg")}Recipe2.Analysis of Variance Model方差分析模型rm(list = ls())data(PlantGrowth)attach(PlantGrowth)plot(weight~group, main = "Plant weight", xlab = "Fri")##盒子图黑线为中位数,框上下线分别为75%、25%分位数,上下线分别为最大小值————————————————x_weight <- weightx_group <- groupx_group <- as.vector(x_group)x_group[which(x_group == "ctrl")] <- 0x_group[which(x_group == "trt1")] <- 1x_group[which(x_group == "trt2")] <- 2windows()plot(x_group, x_weight, main = "Plant weight", xlab = "Fri")##与上图作对比,如果x轴为数字,一定要把它变为因子————————————————windows()x-group <- as.factor(x_group)plot(x_group, x_weight, main = "Plant weight", xlab = "Fri")a <- aov(weight ~ group) ##方差分析summary(a)Recipe3.Generalized Linear Models广义线性模型####Binomial Model(Logistic Regression)####rm(list = ls())neuro <- read.csv("neuro.csv")attach(neuro)y <- cbind(Cured, NotCured)a <- glm(y ~ Sex + Treat, family = binomial) ##广义线性模型anova(a)Recipe1.Linear Discriminant Analysis线性判别分析rm(list = ls())library(MASS) ##程序馆data(iris)attach(iris)a <- lda(Species ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width)##线性判别分析aRecipe2.Cluster Analysis聚类分析rm(list = ls())set.seed(20141112)x <- rnorm(100)a <- hclust(dist(x)) ##分层聚类分析plot(a)kmeans(x, 3) ##非分层聚类分析Recipe3.Library程序馆rm(list = ls())##以lasso2为例##download lasso2 from Beijing2 first!install.packages("lasso2")library(lasso2)data(Iowa)l1c.I <- l1ce(Yiels ~ ., Iowa, bound = 10, absolute.t = TRUE)l1c.IRecipe1.Multiframe Graphic多重图框rm(list = ls())data(faithful)attach(faithful)op <- par(mfrow = c(2, 2)) ##2行2列hist(waiting) ##直方图hist(eruptions)qqnorm(waiting)qqline(waiting) ##qqnorm与qqline在一个图里qqnorm(eruptions)qqline(eruptions)par(op) ##停止作图savePlot("hist_qq", type = "jpeg")Recipe2.增加直线rm(list = ls())data(faithful)attach(faithful)plot(eruptions, waiting, main = "Springs")abline(lsfit(eruptions, waiting), lwd=3, col=5) ##拟合直线abline(h=70, v=3, lwd=2, col=4) ##随便画的,h平行于x轴,v平行于y轴。
