小波去噪阈值的确定和分解层数的确定-PPT课件
合集下载
小波去噪PPT课件

t
具^ 0有 波动td性t 0。为了使信号重构的实现上是稳定的,除了满足重构
条件外,还要求 t 的傅立叶变换满足如下稳定性条件:
^
2
A 2 j w B
式中,0 A B 。
小波的选择并不是任意的,也不是唯一的。它的选择应满足定义域是紧 支撑的(Compact Support),即在一个很小的区间之外,函数值为零,函数 应有速降特性,以便获得空间局域化。另外,它还要满足平均值为零。也就 是说,小波应具有振荡性,而且是一个迅速衰减的函数。
先沿方向分别用做分析把分解成平滑和细节两部分然后对这两部分再沿方向用处理所得的一路是第一级平滑逼近其它三路输设想成理想的半带低通滤波器和高通滤波器两个方向的低频分量反映的是水平方向的低频分量和垂直方向的高频分量反映的是水平方向的高频分量和垂直方向的低频分量反映的是两个方向的高频分量
基于小波去噪的图像处理
模式识别与智能系统
刘新菊
研1206
1
主讲内容
• 噪声特性 • 传统去噪方法 • 小波阈值去噪原理 • 常用几种阈值去噪比较
2
噪声特性
经常影响图像质量的噪声源可分为三类。人们对其生成原因及相应的模 型作了大量研究:
1、电子噪声。在阻性器件中由于电子随机热运动而造成的电子噪声是三 种模型中最简单的,一般常用零均值高斯白噪声作为其模型,它可用 其标准差来完全表征。
4
传统去噪方法
经典去噪方法要么完全在频率域,要么完全 在空间域展开。这两类消噪方法造成了顾此失彼 的局面,虽然抑制了噪声,却损失了图像边缘细 节信息,造成图像模糊。因此,提出了基于小波 变换的去噪方法研究。小波分析由于在时域频域 同时具有良好的局部化性质和多分辨率分析的特 点,能有效地把信号和噪声区别开来,因此不仅 能满足各种去噪要求如低通、高通、陷波、随机 噪音的去除等,而且与传统的去噪方法相比较, 有着无可比拟的优点,成为信号分析的一个强有 力的工具,被誉为分析信号的数学显微镜。
矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
信号去噪PPT课件_19-36

标志one:上述求出的四个阀值和 u , j 无关 标志sln:上述求出的四个阈值和 u , j相乘,其中 u , j 取尺度一 下的估计值 标志mln:上述求出的四个阀值和各个尺度下算出得 u , j 相乘
16 .
小波去噪—其他阈值
基于3准则的阈值确定法
Ⅰ 计算初始均方值
^
1 N
N
di2
i 1
小波去噪—分解层数
说明 理论上可选取的最大尺度为J= log2 N, L 表示向下取整运算,N
为信号长度。但实际上没有必要取太大。尺度越大,则噪声和信号 表现的不同特性越明显,越有利于信噪分离;但另一方面,对于重构 来讲,分解的次数越多,则失真越大,即重构误差越大。所以必须选 择合适的尺度参数,兼顾二者。
^
Ⅱ
每个 cd
的绝对值与3
i
的大小进行比较,大于认为是
粗差,予以去除;
Ⅲ 重新计算均方值
^
Ⅳ 重复Ⅰ、Ⅱ、Ⅲ,直至没有大于3 的cd i
^
Ⅴ 以3 作为每个分解尺度上处理小波系数cd i的阈值。
17 .
总结 ▪ 通过上面对小波去噪方法的分析可知,基于噪
声相关系数的小波分解层数确定法和基于3σ准 则的阈值确定法具有很好的自适应能力.
固定阈值(sqtwolog)
2logN()
启发式阈值(rigrsure)
crit
1
ln
N
3
N ln2
N 2
eta Sj N/N
j1
如果eta<crit,则选用sqtwolog阈值;否则选取sqtwolog阈值和 rigrsure阈值中的较小者作为本准则选定的阈值。
14 .
小波去噪—阈值
16 .
小波去噪—其他阈值
基于3准则的阈值确定法
Ⅰ 计算初始均方值
^
1 N
N
di2
i 1
小波去噪—分解层数
说明 理论上可选取的最大尺度为J= log2 N, L 表示向下取整运算,N
为信号长度。但实际上没有必要取太大。尺度越大,则噪声和信号 表现的不同特性越明显,越有利于信噪分离;但另一方面,对于重构 来讲,分解的次数越多,则失真越大,即重构误差越大。所以必须选 择合适的尺度参数,兼顾二者。
^
Ⅱ
每个 cd
的绝对值与3
i
的大小进行比较,大于认为是
粗差,予以去除;
Ⅲ 重新计算均方值
^
Ⅳ 重复Ⅰ、Ⅱ、Ⅲ,直至没有大于3 的cd i
^
Ⅴ 以3 作为每个分解尺度上处理小波系数cd i的阈值。
17 .
总结 ▪ 通过上面对小波去噪方法的分析可知,基于噪
声相关系数的小波分解层数确定法和基于3σ准 则的阈值确定法具有很好的自适应能力.
固定阈值(sqtwolog)
2logN()
启发式阈值(rigrsure)
crit
1
ln
N
3
N ln2
N 2
eta Sj N/N
j1
如果eta<crit,则选用sqtwolog阈值;否则选取sqtwolog阈值和 rigrsure阈值中的较小者作为本准则选定的阈值。
14 .
小波去噪—阈值
小波阈值去噪研究 PPT

39.8826
22.5237
19.0702
16.1042
39.9330
23.3555
17.3288
通过5组数据的比较,可以得出结论, 使用最佳软阈值算法得到的性噪比明显比 硬、软阈值得到的高,而均方差又明显比 较小。虽然硬阈值的数据比最佳软阈值差 不多,但是最佳软阈值对图像细节的保护 明显比硬阈值的好。
(3)二维小波的重构,根据小波分解的第 N 层的 低频系数和经过修改的从第一层到第 N 层的高频 系数,来计算二维信号的小波重构。
4.小波阈值去噪的仿真结果
5 5
5.去噪结果分析
(1)均方误差(MSE):
1 M N
2
MSE = M N
i 1
j 1
ui, j -u0i, j
2.2 常用的小波阈值函数
阈值函数法(又称小波阈值去噪法)是目前研究和 应用比较广泛的去噪方法之一。
阈值函数法主要是基于在小波高频子空间中,比较大 的小波系数一般都是以实际信号为主,而比较小的小波系 数则很大程度上都是由噪声产生,因此可通过设定合适的 阈值去除噪声。
首先将小于阈值的系数置为零,而保留大于阈值的小 波系数,再通过一个阈值函数映射,得到估计系数,最后 对估计系数进行逆小波变换,就可以得到去噪后的信号重 建。但噪声水平比较高时,容易将原信号的高频部分模糊 掉。在这里如何对小波系数进行筛选是阈值函数法的关键 步骤,小波系数的筛选又主要依赖于阈值函数和阈值的选 择。
注:MSE越小说明去噪效果越好。
Tianjin University
(2)峰值信噪比(PSNR):PSNR值越大, 就代表失真越少。
其中,MSE是原图像与处理图像之间均方误 差。
去噪方法
小波去噪阈值的确定和分解层数的确定
小波包阈值去噪的过程
4 Reconstruction Compute wavelet packet reconstruction based on the original approximation coefficients at level N and the modified coefficients.(根据计算后的小 波包系数重构原信号。)
1
0.5
0
-0.5
获得单个阈值,对所有的高频小波系数进行处理。
-1
-1.5
0
50
100
150
200
250
300
350
400
450
软阈值去噪 1.5
1
0.5
0
-0.5
-1
-1.5
0
50
100
150
200
250
300
350
400
450
小波去噪阈值的几种方法
1.5 1
小波包分解和重构去噪
[c,l]=wavedec(x,level,wname); ca3=appcoef(c,l,wname,3); cd3=detcoef(c,l,3); cd2=detcoef(c,l,2); cd1=detcoef(c,l,1); xd4=wrcoef('a',c,l,wname,level);
小波包阈值去噪的过程
1 Decomposition For a given wavelet, compute the wavelet packet decomposition of signal x at level N.(计算信号x在N层小波包分解的系数) 2 Computation of the best tree For a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.(以熵为准则,计算最佳树,当然 这一步是可选择的。) 3 Thresholding of wavelet packet coefficients For each packet (except for the approximation), select a threshold and apply thresholding to coefficients.(对于每一个小波包分解系数,选择阈值 并应用于去噪) The graphical tools automatically provide an initial threshold based on balancing the amount of compression and retained energy. This threshold is.(工具箱会根据压缩量和剩余能量提供一个初始化的阈值,不过仍需要不 断测试来选择阈值优化去噪效果) a reasonable first approximation for most cases. However, in general you will have to refine your threshold by trial and error so as to optimize the results to fit your particular analysis and design criteria.
信号去噪PPT课件

10 .
小波去噪
基本原理
含噪信号f(k)=s(k)+n(k)
s
小波分解
cA1 cD1 cA2 cD2
cA3 cD3
细节分量 (高频信号)
低频系数
11 .
基本原理
小波去噪
细节分量 (高频信号)
阈值处理
低频系数
小波反变换
重构信号
12 .
小波分解图
小波去噪
s cA1 cD1 cA2 cD2 cA3 cD3
R(ik)s h N 2 k k f(j) (N k)f(N k) /N
缺陷:实测信号无法获取SNR值
20 .
小波去噪—分解层数
方案二
由随机过程的认识可知,离散 白噪声的自相关序列为
(k)
1 0
k 0 k 0
假设离散数据序列dk(k=1,2,….,N)
的自相关序列为 i(i=0,1,…,M)
若 i
满足式: i
1.95, N
i 1
则可认为dk为白噪声序列,M通
常取5~10即可。
(1)把信号s(i)中的每一个元素取绝对值,再由小到大排序,然后 将各个元素取平方,从而得到新的信号序列
f(k ) (so (s)r 2 ,)t(k 0 ,1 ,.N . .1 ),
(2)若取阈值为f(k)的第k个元素的平方根,即
kf(k), (k 0 ,1 ,..N . 1 .),
则该阈值产生的风险为
缺点 当|w|≥λ时, w与 总w存在恒定的偏差,直接影响着重构 信号与真实信号的逼近程度
28 .
阈值的选取
小波去噪—阈值
常见软阈值
无偏风险估计阈值(rigrsure) 固定阈值(sqtwolog) 启发式阈值(heursure)
小波去噪
基本原理
含噪信号f(k)=s(k)+n(k)
s
小波分解
cA1 cD1 cA2 cD2
cA3 cD3
细节分量 (高频信号)
低频系数
11 .
基本原理
小波去噪
细节分量 (高频信号)
阈值处理
低频系数
小波反变换
重构信号
12 .
小波分解图
小波去噪
s cA1 cD1 cA2 cD2 cA3 cD3
R(ik)s h N 2 k k f(j) (N k)f(N k) /N
缺陷:实测信号无法获取SNR值
20 .
小波去噪—分解层数
方案二
由随机过程的认识可知,离散 白噪声的自相关序列为
(k)
1 0
k 0 k 0
假设离散数据序列dk(k=1,2,….,N)
的自相关序列为 i(i=0,1,…,M)
若 i
满足式: i
1.95, N
i 1
则可认为dk为白噪声序列,M通
常取5~10即可。
(1)把信号s(i)中的每一个元素取绝对值,再由小到大排序,然后 将各个元素取平方,从而得到新的信号序列
f(k ) (so (s)r 2 ,)t(k 0 ,1 ,.N . .1 ),
(2)若取阈值为f(k)的第k个元素的平方根,即
kf(k), (k 0 ,1 ,..N . 1 .),
则该阈值产生的风险为
缺点 当|w|≥λ时, w与 总w存在恒定的偏差,直接影响着重构 信号与真实信号的逼近程度
28 .
阈值的选取
小波去噪—阈值
常见软阈值
无偏风险估计阈值(rigrsure) 固定阈值(sqtwolog) 启发式阈值(heursure)
小波去噪剖析课件

随着小波去噪技术的不断发展和完善,其应用领域将更加广泛 ,包括但不限于信号处理、图像处理、音频处理等。
将小波去噪技术与其它技术进行交叉融合,如与机器学习、统 计学习等技术的结合,有望产生一些创新性的研究成果和应用
。
THANKS
感谢观看
实验结果展示
展示一
小波去噪在音频信号处理中的应用。我们使用小波去噪方法对受到噪声干扰的音 频信号进行了处理。处理后的音频信号明显去除了噪声,音质得到了显著改善。
展示二
小波去噪在图像信号处理中的应用。我们使用小波去噪方法对受到噪声干扰的图 像信号进行了处理。处理后的图像信号明显去除了噪声,图像质量得到了显著提 升。
基于小波变换的去噪算法具有较好的去噪效果,能够保留信号中的重要特征。
小波去噪算法的步骤
对原始ห้องสมุดไป่ตู้号进行小波变换,将信号分 解成多个频带。
通过逆小波变换,将去噪后的信号重 新合成。
对每个频带进行阈值处理,将噪声与 信号分离。
经过小波去噪处理后,原始信号中的 噪声得到有效抑制,保留了信号中的 重要特征。
多尺度分析
利用多尺度分析技术,对信号进行多尺度分解和重构,以更好地提取 信号特征和抑制噪声。
对小波去噪的未来展望
更优的性能 更高的鲁棒性 更广泛的应用 更多的交叉融合
通过不断的研究和探索,有望进一步提高小波去噪算法的性能 ,以实现对复杂噪声环境下的信号去噪处理。
针对不同类型和级别的噪声,设计具有更强鲁棒性的去噪算法 ,以适应各种实际应用场景。
结果分析
分析一
小波去噪算法能够有效地去除信号中的 噪声,同时保留信号的重要特征。在音 频信号处理中,小波去噪能够有效地去 除环境噪声和设备噪声,提高了音频的 质量和可听性。在图像信号处理中,小 波去噪能够有效地去除椒盐噪声和随机 噪声,提高了图像的质量和可用性。
将小波去噪技术与其它技术进行交叉融合,如与机器学习、统 计学习等技术的结合,有望产生一些创新性的研究成果和应用
。
THANKS
感谢观看
实验结果展示
展示一
小波去噪在音频信号处理中的应用。我们使用小波去噪方法对受到噪声干扰的音 频信号进行了处理。处理后的音频信号明显去除了噪声,音质得到了显著改善。
展示二
小波去噪在图像信号处理中的应用。我们使用小波去噪方法对受到噪声干扰的图 像信号进行了处理。处理后的图像信号明显去除了噪声,图像质量得到了显著提 升。
基于小波变换的去噪算法具有较好的去噪效果,能够保留信号中的重要特征。
小波去噪算法的步骤
对原始ห้องสมุดไป่ตู้号进行小波变换,将信号分 解成多个频带。
通过逆小波变换,将去噪后的信号重 新合成。
对每个频带进行阈值处理,将噪声与 信号分离。
经过小波去噪处理后,原始信号中的 噪声得到有效抑制,保留了信号中的 重要特征。
多尺度分析
利用多尺度分析技术,对信号进行多尺度分解和重构,以更好地提取 信号特征和抑制噪声。
对小波去噪的未来展望
更优的性能 更高的鲁棒性 更广泛的应用 更多的交叉融合
通过不断的研究和探索,有望进一步提高小波去噪算法的性能 ,以实现对复杂噪声环境下的信号去噪处理。
针对不同类型和级别的噪声,设计具有更强鲁棒性的去噪算法 ,以适应各种实际应用场景。
结果分析
分析一
小波去噪算法能够有效地去除信号中的 噪声,同时保留信号的重要特征。在音 频信号处理中,小波去噪能够有效地去 除环境噪声和设备噪声,提高了音频的 质量和可听性。在图像信号处理中,小 波去噪能够有效地去除椒盐噪声和随机 噪声,提高了图像的质量和可用性。
《小波阈值图像去噪》课件

《小波阈值图像去噪》 PPT课件
本PPT课件将深入介绍小波阈值图像去噪的原理、方法和应用。通过本课件, 你将了解到噪声对图像的影响,掌握常见的图像去噪方法,并学习小波变换 及其原理。欢迎加入这个有趣而充满挑战的领域!
什么是噪声?
噪声指的是图像中的非期望信号,常见的有高斯噪声、椒盐噪声等。噪声会降低图像质量,影响图像分 析和识别的准确性。
计算小波系数的方法
常见的计算小波系数的方法有级联算法、快速小波变换等。这些方法能够高效地计算小波系数,提高处 理速度。
去噪中的阈值选择问题
阈值的选择对去噪效果有重要影响。常用的阈值选择方法有固定阈值、自适 应阈值和统计阈值等,根据具体场景来选择合适的阈值方法。
经典的软、硬阈值算法
软阈值算法通过保留能量大于阈值的小波系数,将能量较小的小波系数置零;硬阈值算法则直接将能量 小于阈值的小波系数置零。
为了进一步提高去噪效果,可以结合其他图像处理技术,如边缘保留滤波器、 稀疏表示等,实现更精确的图像恢复。
基于小波能量和熵的去噪算法
基于小波能量的去噪算法通过设定能量阈值来去除能量较小的高频噪声;基 于小波熵的去噪算法通过最大化小波系数的熵,实现图像的复杂度和纹理保 留。
基于小波去噪的边缘保留滤波器算法
如均值滤波、中值滤波等。
非线性滤波器
如双边滤波、非局部均值滤波等。
小波阈值去噪
这种方法更适用于处理复杂、有噪声结构的图像。
小波变换及其原理
小波变换是一种基于频域的信号分析方法,通过将信号分解成不同频率的小 波基函数,实现信号的时频分析。
小波阈值去噪方法
小波阈值去噪是一种基于小波变换的图像去噪方法,它利用小波分解系数的 能量分布来判断和抑制噪声。
动态阈值去噪和多阈值去噪
本PPT课件将深入介绍小波阈值图像去噪的原理、方法和应用。通过本课件, 你将了解到噪声对图像的影响,掌握常见的图像去噪方法,并学习小波变换 及其原理。欢迎加入这个有趣而充满挑战的领域!
什么是噪声?
噪声指的是图像中的非期望信号,常见的有高斯噪声、椒盐噪声等。噪声会降低图像质量,影响图像分 析和识别的准确性。
计算小波系数的方法
常见的计算小波系数的方法有级联算法、快速小波变换等。这些方法能够高效地计算小波系数,提高处 理速度。
去噪中的阈值选择问题
阈值的选择对去噪效果有重要影响。常用的阈值选择方法有固定阈值、自适 应阈值和统计阈值等,根据具体场景来选择合适的阈值方法。
经典的软、硬阈值算法
软阈值算法通过保留能量大于阈值的小波系数,将能量较小的小波系数置零;硬阈值算法则直接将能量 小于阈值的小波系数置零。
为了进一步提高去噪效果,可以结合其他图像处理技术,如边缘保留滤波器、 稀疏表示等,实现更精确的图像恢复。
基于小波能量和熵的去噪算法
基于小波能量的去噪算法通过设定能量阈值来去除能量较小的高频噪声;基 于小波熵的去噪算法通过最大化小波系数的熵,实现图像的复杂度和纹理保 留。
基于小波去噪的边缘保留滤波器算法
如均值滤波、中值滤波等。
非线性滤波器
如双边滤波、非局部均值滤波等。
小波阈值去噪
这种方法更适用于处理复杂、有噪声结构的图像。
小波变换及其原理
小波变换是一种基于频域的信号分析方法,通过将信号分解成不同频率的小 波基函数,实现信号的时频分析。
小波阈值去噪方法
小波阈值去噪是一种基于小波变换的图像去噪方法,它利用小波分解系数的 能量分布来判断和抑制噪声。
动态阈值去噪和多阈值去噪
小波理论及小波滤波去噪方法课件

第九章 小波理论及小波滤波去噪方法
9.2.2连续小波变换
§ 9.2.小波变换
第21页,共28页。
*
(2) 缩放。就是压缩或伸展基本小波, 缩放系数越小, 则小波越窄
第九章 小波理论及小波滤波去噪方法
9.2.2连续小波变换
§ 9.2.小波变换
第22页,共28页。
*
第九章 小波理论及小波滤波去噪方法
§ 9.1 从傅里叶变换到小波分析
第11页,共28页。
第九章 小波理论及小波滤波去噪方法
由此可见,STFT虽然在一定程度上克服了标准傅里叶变换不具有时域局部分析能力的缺陷,但他也存在着自身不可克服的缺陷——其时间频率窗口是固定不变的,一旦窗口函数选定其时频分辨率也就确定了。而时间和频率的最高分辨率受制约,任一方分辨率的提高都意味着另一方分辨率的降低。 可以说STFT实质上是具有单一分辨率的信号分析方法,若要改变分辨率,则必须重新选择窗口函数g(t)。 因此STFT用来分析平稳信号犹可,但对非平稳信号,在信号波形变化剧烈的时刻,主频是高频,要求有较高的时间分辨率,即δ要小,而波形变化比较平缓的时刻,主频是低频,则要求有较高的频率分辨率,ε要小,而STFT不能兼顾二者。
(3) 平移。小波的延迟或超前。在数学上,函数f(t)延迟k的表达式为f(t-k),
(a) 小波函数ψ(t); (b) 位移后的小波函数ψ(t-k)
9.2.2连续小波变换
§ 9.2.小波变换
第23页,共28页。
*
(4)小波变换的步骤: 第一步: 取一个小波与信号的最前面部分比较; 第二步: 计算相关因子C,C代表小波和这段数据的相关性 即:C越大,两者越相似;
(1)继承和发展了STFT的局部化思想。 (2)克服了窗口大小不随频率变化、缺乏离散正交基的缺点。
小波变换及消噪PPT文档19页

名的阈 值形式:
(式3-4)
门限阈值处理可以表示为 ,可以证明当n 趋于无穷大时使用阈
值公式(3-4)对小波系数作软阈值处理可以几乎完全去除观测数据中的
噪声。
3) 对处理过的小波系数作逆变换
重构信号
(式3-5) 即可得到受污染采样信号去噪后的信号。
小波消噪
软、硬阈值处理方法
硬阈值处理只保留较大的小波系数并将较小的小波系数置零: 软阈值处理将较小的小波系数置零但对较大的小波系数向零作了收缩:
(式3-8)
(3) rigrsure:采用史坦的无偏似然估计原理进行阈值选择,首先得到一个给 定阈值的风险估计,选择风险最小的阈值 作为最终选择。 (4) heursure:选择启发式阈值它是sqtwolog和rigrsure 的综合,当信噪比 很小时,估计有很大的噪声,这时heursure, 采用固定阈值sqtwolog。
小波消的噪。
➢ 消噪步骤: 1) 对观测数据作小波分解变化:
(式3-,…y,f是真实信号向量f1,f2,…fn, z是高斯随机向量z1,z2,…zn ,其中用到了小波分解变换是线性变 换的性质。
2) 对小波系数W0作门限阈值处理,(根据具体情况可以使用软阈值 处 理或硬阈值处理,而且可以选择不同的阈值形式)比如选取最著
小波消噪
阈值的选取形式
选取规则都是基于含噪信号模型 (式3-1)中信号水平为1 的情况,对于 噪声水平未知或非白噪声的情况可以在去噪时重新调整得到的阈值。
在MATLAB中有4种阈值函数形式可以选用: (1) sqtwolog:采用固定的阈值形式,如(式3-4),因为这种阈值形式在软门 限阈值处理中能够得到直观意义上很好的去噪效果。 (2) minimaxi采用极大极小原理选择的阈值,和sqtwolog一样也是一种固 定的阈值,它产生一个最小均方误差的极值,计算公式为:
小波去噪阈值的确定和分解层数的确定课件

主观评估指标
01
02
03
可视度
对于图像和视频等视觉媒 体,去噪后的可视度是评 估去噪效果的重要指标。
清晰度
对于图像和视频等视觉媒 体,去噪后的清晰度是评 估去噪效果的重要指标。
自然度
对于图像和视频等视觉媒 体,去噪后的自然度是评 估去噪效果的重要指标。
05
小波去噪算法实现流程
算法流程概述
信号预处理ຫໍສະໝຸດ 04小波去噪效果评估
客观评估指标
信噪比(SNR)
信噪比用于衡量去噪后信号的信噪比,通常使用原始信号的信噪 比与去噪后信号的信噪比之差来表示。
均方误差(MSE)
均方误差是衡量去噪后信号与原始信号之间的误差的标准,通常使 用原始信号与去噪后信号之间的均方误差来表示。
峰值信噪比(PSNR)
峰值信噪比用于衡量去噪后信号的峰值信噪比,通常使用原始信号 的峰值信噪比与去噪后信号的峰值信噪比之差来表示。
电子测量
在电子测量中,小波去噪技术可以 有效地去除噪声干扰,提取有用的 电信号特征,常用于电力系统的监 测和故障诊断。
02
小波去噪阈值的确定
基于信号本身特征的方法
固定阈值法
根据信号本身特征,设定一个固 定阈值进行去噪。
自适应阈值法
根据信号的局部特征,自适应地 确定每个像素的阈值。
基于统计的方法
法和思路。
压缩感知
03
压缩感知与小波去噪的结合将为信号处理领域带来新的突破。
THANK YOU
03
小波分解层数的确定
基于信号本身特征的方法
该方法根据信号自身的特征,如频率、幅值等来确定小波分解的 层数。这种方法通常需要对信号进行详细分析,以了解其特征和 性质。
小波去噪阈值确定和分解层数确定35页PPT

小波去噪阈值确定和分解层数确定
16、人民应该为法律而战斗,就像为 了城墙 而战斗 一样。 ——赫 拉克利 特 17、人类对于不公正的行为加以指责 ,并非 因为他 们愿意 做出这 种行为 ,而是 惟恐自 己会成 为这种 行为的 牺牲者 。—— 柏拉图 18、制定法律法令,就是为了不让强 者做什 么事都 横行霸 道。— —奥维 德 19、法律是社会的习惯和思想的结晶 。—— 托·伍·威尔逊 20、人们嘴上挂着的法律,其真实含 义是财 富。— —爱献 生
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没—笛 卡儿
16、人民应该为法律而战斗,就像为 了城墙 而战斗 一样。 ——赫 拉克利 特 17、人类对于不公正的行为加以指责 ,并非 因为他 们愿意 做出这 种行为 ,而是 惟恐自 己会成 为这种 行为的 牺牲者 。—— 柏拉图 18、制定法律法令,就是为了不让强 者做什 么事都 横行霸 道。— —奥维 德 19、法律是社会的习惯和思想的结晶 。—— 托·伍·威尔逊 20、人们嘴上挂着的法律,其真实含 义是财 富。— —爱献 生
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没—笛 卡儿
小波去噪阈值确定和分解层数确定

“最优树”的搜索方法:
二元树搜索方法: M1
M2
M3
选择准则: 若M1 M 2 M 3,则选M 2+M 3
否则,选M1
小波去噪阈值确定和分解层数确定
选择步骤:
➢(1)将代表信息代价的数字写在树的结点里。 ➢(2)从最下层开始,为在每个代表结点的框中的代价函数 值都标上*号。
小波去噪阈值确定和分解层数确定
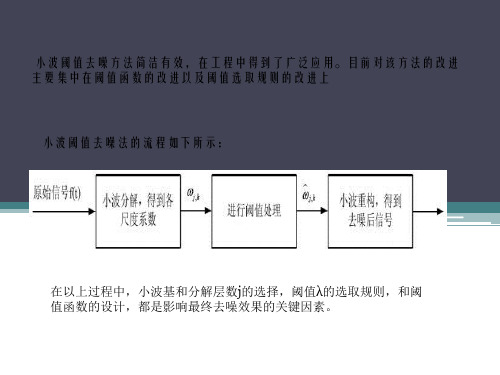
小波阈值去噪方法简洁有效,在工程中得到了广泛应用。目前对该方 法的改进主要集中在阈值函数的改进以及阈值选取规则的改进上
小波阈值去噪法的流程如下所示:
小波去噪阈值确定和分 解层数确定
在以上过程中,小波基和分解层数j的选择,阈值λ的选取规则,和阈 值函数的设计,都是影响最终去噪效果的关键因素。
小波基的选择
Scal=‘one’,不随噪声水平变化。
Scal=‘sln’,根据第一层小波分解的系数估计各层阈值。
Scal=‘mln’,根据每一层小波分解的系数估计阈值。
rigrsure
0
50 100 150 200 250 300 350 400 450
-2
-1.5
-1
-0.5
0
0.5
1
1.5 自适应小波去噪
小波去噪阈值确定和分解 层数确定
小波去噪阈值的几种方法 小波包分解和重构去噪 1.5
1
[c,l]=wavedec(x,level,wname); ca3=appcoef(c,l,wname,3); cd3=detcoef(c,l,3); cd2=detcoef(c,l,2); cd1=detcoef(c,l,1); xd4=wrcoef('a',c,l,wname,level);
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分解尺度的选择
不同信号,不同信噪比下都存在一个去噪效果最好或接近最好 的分解层数。分解层数对于消噪效果的影响很大, 通常分解 层数过多, 而且对所有的各层小波空间的系数都进行阈值处 理会造成信号的信息丢失严重, 消噪后的信噪比反而下降, 同 时导致运算量增大, 使处理变慢。分解层数过少则消噪效果 不理想, 信噪比提高不多, 但不会出现信噪比下降的情况。
k
(与均方意义下恢复原始 信号所需的系数个数成 正比。)
常用代价函数:
4、能量对数
M ({xk }) log | xk |2
k
(表征信号的系数间的相 关性。)
“最优树”的搜索方法:
二元树搜索方法:
M1
M2
M3
选择准则: 若M 1 M 2 M 3 , 则选M 2+M 3 否则,选M 1
(4)检查所有结点,取最上层所标记的结点,一经选定,其下方各 层的值就不考虑。选出带有*号框的全体组成VN的一组正交基。
例:
50 20 11 1 2 3 12 4 5 13 6 7 22 14 8
例:
50 10(20) 3(11) 1* 2* 7(12) 3* 4* 22 11(13) 5* 6* 7
常用代价函数:
1、数列中大于给定门限的系数的个数。即预先给 定一门限值 0 ,并计数数列中绝对值大于 的 元素的个数。
2、范数。
M ({xk }) {xk } 通常选, {xk } =( x kp )
k 1 p
p0
(范数愈小,能量愈集 中。)
常用代价函数:
3、熵
M ({xk }) | xk |2 log | xk |2
选择步骤:
(1)将代表信息代价的数字写在树的结点里。 (2)从最下层开始,为在每个代表结点的框中的代价函数 值都标上*号。
(3)将最低层的信息代价作为一个初始值,称上层结点为父结点, 下层结点为子结点,若父结点的信息代价比子结点低,那么就标记父 结点,否则不标记,将该值加上括号且把两个子结点的和值写在括号 外,如此上推,直到顶层。
小波包阈值去噪的过程
4 Reconstruction Compute wavelet packet reconstruction based on the original approximation coefficients at level N and the modified coefficients.(根据计算后的小 波包系数重构原信号。)
最优小波包分解树的选择
在对函数或信号进行小波包分解时,由于Wj有不同的分解方式, 我们面临“最优分解树”的选择问题。
代价函数M:
定义一个序列的代价函数,、寻找使代价函数最 小的分解树 ,对一个给定向量来说,代价最小 就是最有效的表示,此基便为“最优树”。 代价函数的基本要求: 1.单调性。 2.可加性(次可加性)
小波阈值去噪方法简洁有效,在工程中得到了广泛应用。目前对该方法的改进 主要集中在阈值函数的改进以及阈值选取规则的改进上
小波阈值去噪法的流程如下所示:
在以上过程中,小波基和分解层数j的选择,阈值λ的选取规则,和阈 值函数的设计,都是影响最终去噪效果的关键因素。
小波基的选择Leabharlann • 小波基的选择 • 对于连续性较差的信号,Haar小波的去噪效果要好于 Sym8小波。 • 对于连续性和光滑性较好的信号,Sym8小波的去噪 效果更好。sym8小波函数具有紧支集,且具有良好 的连续性和对称性,因此其更适合于对连续性较好的 信号进行去噪。 • 由于小波基函数在处理信号时各有特点,且没有任何 一种小波基函数可以对所有类型信号都取得最优的去 噪效果。一般来讲,db小波系和sym小波系在语音去 噪中是经常会被用到的两族小波基。
小波包阈值去噪的过程
1 Decomposition For a given wavelet, compute the wavelet packet decomposition of signal x at level N.(计算信号x在N层小波包分解的系数) 2 Computation of the best tree For a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.(以熵为准则,计算最佳树,当然 这一步是可选择的。) 3 Thresholding of wavelet packet coefficients For each packet (except for the approximation), select a threshold and apply thresholding to coefficients.(对于每一个小波包分解系数,选择阈值 并应用于去噪) The graphical tools automatically provide an initial threshold based on balancing the amount of compression and retained energy. This threshold is.(工具箱会根据压缩量和剩余能量提供一个初始化的阈值,不过仍需要不 断测试来选择阈值优化去噪效果) a reasonable first approximation for most cases. However, in general you will have to refine your threshold by trial and error so as to optimize the results to fit your particular analysis and design criteria.
*
14* 8
例:
50 10(20) 3(11) 1* 2* 7(12) 3* 4* 22 11(13) 5* 6* 7
