数字信号处理课后习题答案(吴镇扬)
数字信号处理课后习题答案(全)1-7章

(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
所以 T[ax1(n)+bx2(n)]=aT[x1(n)]+bT[x2(n)]
第 1 章 时域离散信号和时域离散系统
(2) 令输入为
输出为
x(n-n0)
y′(n)=2x(n-n0)+3 y(n-n0)=2x(n-n0)+3=y′(n) 故该系统是非时变的。 由于
T[ax1(n)+bx2(n)]=2ax1(n)+2bx2(n)+3 T[ax1(n)]=2ax1(n)+3 T[bx2(n)]=2bx2(n)+3 T[ax1(n)+bx2(n)]≠aT[x1(n)]+bT[x2(n)] 故该系统是非线性系统。
=2x(n)+x(n-1)+ x(n-2)
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
第 1 章 时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况,
(3) 如果|x(n)|≤M, 则|y(n)|≤ nn0|x(k)|≤|2n0+1|M, 因 k nn0
东南大学 数字信号处理 吴镇扬 3_2

由图中看到,在零频率附近,Ω~ω接近于线性关系,Ω进 一步增加时,ω增长变得缓慢, 时, (ω终止于折叠 频率处),所以双线性变换不会出现由于高频部 分超过折叠频率
2)双线性变换缺点: Ω与ω成非线性关系,导致: a. 数字滤波器的幅频响应相对于模拟滤波器的幅频响应有畸 变,(使数字滤波器与模拟滤波器在响应与频率的对应关系上 发生畸变)。 例如,一个模拟微分器,它的幅度与频率是直线关系, 但通过双线性变换后,就不可能得到数字微分器
令 c 1 ,得归一化的三阶BF:
H a (s)
如果要还原的话,则有
1 S 3 2S 2 2S 1
1 H a ( s) ( s / c )3 2( s / c ) 2 2( s / c ) 1
MATLAB设计模拟Butterworth filter
•[z,p,k]=buttap(N)
N为滤波器阶数, 如图1
图1 巴特沃兹滤波器 振幅平方函数
通带: 使信号通过的频带 阻带:抑制噪声通过的频带 过渡带:通带到阻带间过渡的频率范围 Ωc :通带边界频率。 过渡带为零, 阻带|H(jΩ)|=0 通带内幅度|H(jΩ)|=const., H(jΩ)的相位是线性的。
理想滤波器
图1中,N增加,通带和阻带的近似性越好,过渡带越陡。 在过渡带内,阶次为N的巴特沃兹滤波器的幅度响应趋于 斜率为-6NdB/倍频程的渐近线。
§3.2
常用模拟低通滤波器特性
为了方便学习数字滤波器,先讨论几种常用的模拟低通滤波 器设计方法,高通、带通 、带阻等模拟滤波器可利用变量变换 方法,由低通滤波器变换得到。 模拟滤波器的设计就是根据一组设计规范设计模拟系统函数 Ha(s),使其逼近某个理想滤波器特性。 因果系统中
数字信号处理(吴镇扬)课后习题答案(比较详细的解答过程)chap6

至今, 至今,我们讨论的信号处理的各种理论与算法 视为恒定值, 都是把抽样频率 f s 视为恒定值,即在一个数字系 统中只有一个采样率。 统中只有一个采样率。 在实际数字信号处理系统中, 在实际数字信号处理系统中,经常会遇到采样 率转换问题。 率转换问题 。 或者要求一个数字系统能工作在 多采样率”状态, “多采样率”状态,或者要求其将采样信号转换 为新的采样率下工作。 为新的采样率下工作。
6.2 信号的插值
如果将 x(n) 的抽样频率 f s 增加 L 倍, w(n), w(n) 即 得 的插值,用符号↑ 表示。插值的方法很多, 是对 x(n) 的插值,用符号↑L 表示。插值的方法很多, 一个简单的方法就是信号抽取的逆处理过程。 一个简单的方法就是信号抽取的逆处理过程。 回想信号抽取前后的傅立叶变换关系
而 X 1 (e ) =
jω n = −∞
∞
∑ x ( n ) p ( n)e
− jωn
1 M −1 j 2πnk / M − jωn = ∑ [ x ( n) ]e ∑e n = −∞ M k =0 1 M −1 = X (e j (ω − 2πk / M ) ) (6.3b (6.3b) ∑ M k =0
信号抽取示意图,M=3, 图6.1.1 信号抽取示意图,M=3,横坐标为抽样点数 原信号; 中间信号; (a)原信号;(b)中间信号;(c)抽取后的信号
显然
X ′(e ) = ∑ x′(n)e
jω n = −∞ ∞ n = −∞ ∞
∞
− j ωn
= ∑ x( Mn)e
n = −∞
∞
− j ωn
= ∑ x1 ( Mn)e − jωn = X 1 (e jω / M ) (6.3a) (6.3a
数字信号处理(吴镇扬)第一章习题解答
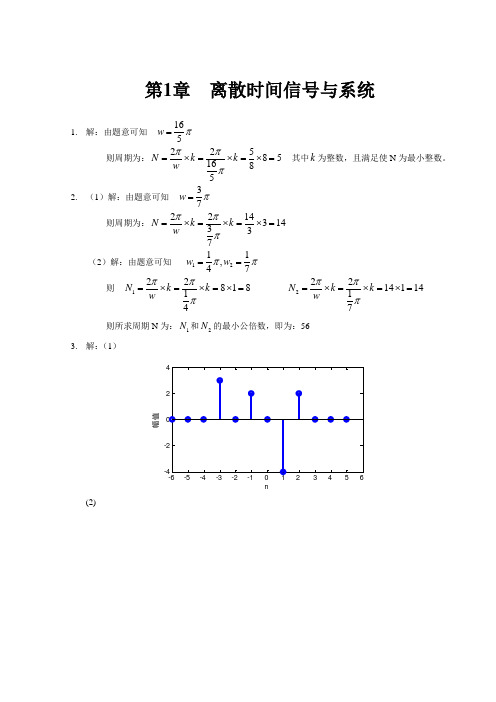
提示:与理想采样信号的频谱进行比较。上述过程是物理采样后的频谱。
1.6解:
(1) (性质1)
(2) (性质4)
(3)
(4)1.7(1)Fra bibliotek:(2)解:
(3)解:
(4)解:
(5)解:
1.8 (1)解:令
由题意可知,所求序列等效为 。
而
故:
(2)解:
因为:
所以,
1.10 (1)解:
,为双边序列
本小题采用部分分式法求逆Z变换,可以使用“留数法”…..
所以
(3)解:
1.18y(n)=1,n=0
y(n)=3*2-n,n≥1
解:
1.19
(1)解:
无论 还是 ,右边序列的围线C内包含 两个极点。
当 时
当 时
因此
思考:1、为何讨论当 时的情况;2、为何不用讨论 的情况
解答过程如下:
(2)解:
右边序列的围线C内包含 一个极点。故
当 时
因此,
思考:1、为何只讨论当 时的情况
(3) 当n0>0时,该系统是因果系统;当n0<0时,该系统是非因果系统;系统稳定。
(4)因果、稳定。
(5)因果、稳定。
(6)因果、稳定。
(7)因果,但由于 。
(8) 在 时刻有值,故非因果。由于 的值都在 的时刻内,那么 ,故系统稳定。
1.17解:由图可知:
所以
(1)解:
(2)解:
通解
特解
带入方程得:
(3)解:
当 时,右边序列的围线C内包含 两个极点。故
因此
第1章
1.解:由题意可知
则周期为: 其中 为整数,且满足使N为最小整数。
数字信号处理课后习题答案(全)1-7章

2. 给定信号:
2n+5
-4≤n≤-1
(x(n)=
6
0
0≤n≤4 其它
(1) 画出x(n)序列的波形, 标上各序列值;
(2) 试用延迟的单位脉冲序列及其加权和表示x(n)序列;
第 1 章 时域离散信号和时域离散系统
(3) 令x1(n)=2x(n-2), 试画出x1(n)波形; (4) 令x2(n)=2x(n+2), 试画出x2(n)波形; (5) 令x3(n)=x(2-n), 试画出x3(n)波形。 解: (1) x(n)序列的波形如题2解图(一)所示。 (2) x(n)=-3δ(n+4)-δ(n+3)+δ(n+2)+3δ(n+1)+6δ(n)
第 1 章 时域离散信号和时域离散系统
题8解图(一)
第 1 章 时域离散信号和时域离散系统
x(n)=-δ(n+2)+δ(n-1)+2δ(n-3)
h(n)=2δ(n)+δ(n-1)+ δ(n-2)
由于
x(n)*δ(n)=x(n)
1
x(n)*Aδ(n-k)=Ax(n-k)
2
故
第 1 章 时域离散信号和时域离散系统
y(n)=x(n)*h(n)
=x(n)*[2δ(n)+δ(n-1)+ δ(n-2) 1 2
, 这是2π有理1数4, 因此是周期序
3
(2) 因为ω=
,
所以
1
8
=16π, 这是无理数, 因此是非周期序列。
2π
第 1 章 时域离散信号和时域离散系统
4. 对题1图给出的x(n)要求:
(1) 画出x(-n)的波形;
数字信号处理实验(吴镇扬)答案-2
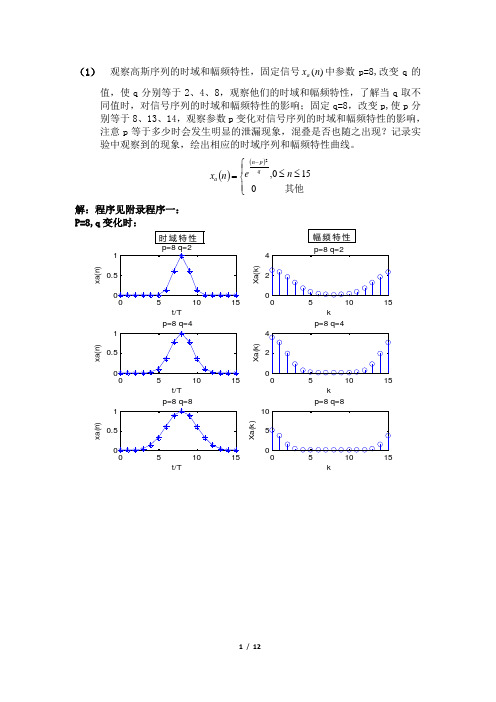
(1) 观察高斯序列的时域和幅频特性,固定信号)(n x a 中参数p=8,改变q 的值,使q 分别等于2、4、8,观察他们的时域和幅频特性,了解当q 取不同值时,对信号序列的时域和幅频特性的影响;固定q=8,改变p,使p 分别等于8、13、14,观察参数p 变化对信号序列的时域和幅频特性的影响,注意p 等于多少时会发生明显的泄漏现象,混叠是否也随之出现?记录实验中观察到的现象,绘出相应的时域序列和幅频特性曲线。
()()⎪⎩⎪⎨⎧≤≤=-其他0150,2n e n x q p n a解:程序见附录程序一:P=8,q 变化时:t/T x a (n )k X a (k )t/T x a (n )p=8 q=4k X a (k )p=8 q=4t/Tx a (n )p=8 q=8kX a (k )p=8 q=8幅频特性时域特性t/T x a (n )p=8 q=8k X a (k )p=8 q=8t/T x a (n )51015k X a (k )p=13 q=8t/Tx a (n )p=14 q=851015kX a (k )p=14 q=8时域特性幅频特性分析:由高斯序列表达式知n=p 为期对称轴; 当p 取固定值时,时域图都关于n=8对称截取长度为周期的整数倍,没有发生明显的泄漏现象;但存在混叠,当q 由2增加至8过程中,时域图形变化越来越平缓,中间包络越来越大,可能函数周期开始增加,频率降低,渐渐小于fs/2,混叠减弱;当q 值固定不变,p 变化时,时域对称中轴右移,截取的时域长度渐渐地不再是周期的整数倍,开始无法代表一个周期,泄漏现象也来越明显,因而图形越来越偏离真实值,p=14时的泄漏现象最为明显,混叠可能也随之出现;(2) 观察衰减正弦序列 的时域和幅频特性,a=0.1,f=0.0625,检查谱峰出现的位置是否正确,注意频谱的形状,绘出幅频特性曲线,改变f ,使f 分别等于0.4375和0.5625,观察这两种情况下,频谱的形状和谱峰出现的位置,有无混叠和泄漏现象?说明产生现象的原因。
数字信号处理课后习题答案(吴镇扬)

习题一 (离散信号与系统)1.1周期序列,最小周期长度为5。
1.2 (1) 周期序列,最小周期长度为14。
(2) 周期序列,最小周期长度为56。
1.5()()()()()()()11s a s s s a n s s a s n X j x t p t X j ΩP j Ω2n τn τj sin j Ωjn e X 2n π2n n τj Sa X j jn e 2T 2πττ∞=-∞∞=-∞Ω==*⎡⎤⎣⎦ΩΩ⎛⎫-=-Ω ⎪⎝⎭ΩΩ⎛⎫-=Ω-Ω ⎪⎝⎭∑∑F 1.6 (1) )(ωj e kX (2) )(0ωωj n j e X e (3) )(21)(2122ωωj j e X e X -+ (4) )(2ωj e X1.7 (1)0n z -(2)5.0||,5.0111>--z z(3)5.0||,5.0111<--z z(4)0||,5.01)5.0(11101>----z zz1.8 (1) 0,)11()(211>--=---z z z z z X N (2) a z az az z X >-=--,)1()(211(3)a z az z a az z X >-+=---,)1()(311211.9 1.10(1))1(2)(1----+n u n u n (2))1(24)()5.0(6--⋅--n u n u n n (3))()sin sin cos 1(cos 000n u n n ωωωω++(4) )()()(1n u a a a n a n ---+-δ1.11 (1) )(1z c X - (2) )(2z X (3) )()1(21z X z -+ (4) -+<<x x R z R z X /1/1),/1(1.12 (1)1,11<-ab ab(2) 1 (3) 00n a n1.13 (1) 该系统不是线性系统;该系统是时不变系统。
数字信号处理_吴镇扬_第二版_第五章习题答案

5.7 (1)由于h2(n)是h1(n)圆周移位的序列,根据DFT的 2π 性质有: −j 4k − jπ k
H 2 (k ) = e
8
H 1 (k ) = e
H 1 (k )
~ ~ H1 ( k ) = H 2 ( k ) 成立 所以
(2)由于h1 (n ) 和h2 (n ) 均为偶对称序列,以其构成的低通滤波器
(3)若采用海明窗设计,则
⎡ ⎛ 2πn ⎞⎤ wHam ( n) = ⎢0.54 − 0.46 cos ⎜ ⎟ ⎥ RN ( n ) ⎝ N − 1 ⎠⎦ ⎣ 2 h( n) = sin[(n − α )ωc ]cos[(n − α )ω0 ]wHam (n) N 为奇数时, (n − α )π
h( n N 为偶数时, ) =
0 −ωc
e − jωα e jω nd ω
可见h(n)关于(N-1)/2偶对称,即 h( n) = h( N − 1 − n)
(1)当 N 为奇数时,为第一类滤波器。 (2)当N为偶数时,为第二类滤波器
⎧hd ( n) h( n) = hd ( n) ⋅ R(n ) = ⎨ ⎩0 0 ≤ n ≤ N −1
解:由经验公式可知若 不小于 At 40dB , 则
β = 0.5842 At - 21)0.4 + 0.07886(At - 21) ≈ 3.3953 ( At − 8 40 − 8 N= = ≈ 22.28 2.286∆ω 2.286× 0.2π ωc + ωr ωc′ = = 0.2π 2 ′ ⎧ωc ′ ⎪ π Sa[ωc (n − α )] n ≠ α ′ 1 ωc − jωα jωn ⎪ hd (n) = ∫ ′ e e dω = ⎨ ′ 2π −ωc ωc ⎪ n =α ⎪ ⎩ π
南邮 数字信号处理 吴镇扬 课后习题详细答案 DSP 期末复习

•pp 35: 1.11 (3)
判断系统
yn
n
xm
是否为线性系统?时不变系统
m
解:线性性判断 令x(n)=ax1(n)+bx2(n)
n
n
yn xm ax1 m bx2 m
m
m
n
n
n
n
ax1m bx2 m a x1m b x2 m
y(n) 4 (n 1) 4 (n 1) (n 3) 2 (n 5) (n 7)
•pp 35: 1.12 (3)
利用卷积性质
y(n) x1(n) x2 (n)
(n) 2 (n 2) (n 4)2 (n 1) (n 3)
(n) 2 (n 2) (n 4) 2 (n 1) 2(n()n21) (n42()n1)(n24)(n 5(n) 3)
• 解:
a nu n
1
1 aZ
1
,
Z a
n
a nu n
Z
d 1
1 aZ
1
,
dZ
Z
1 1 aZ 1
2
d
1 aZ dZ
1
,
Z
1 1 aZ 1
2
a
d
Z 1 dZ
,
Z
1 1 aZ 1
2
a
Z
2
,
数字信号处理(吴镇扬)课后习题答案(比较详细的解答过程)第二章测试训练题解

数字信号处理(吴镇扬)课后习题答案(比较详细的解答过程)第二章测试训练题解1.DFT和DTFT之间的关系是2.DFT和DFS之间的关系是3.对于一个128点的DFT,最先4个DFT相应于数字频率4.某滤波器的频响为H(ω) = 0.3cos2ω- 0.2cosω+ 0.05,相应于6点的DFT的H[k]为5.采样频率为22.05kHz的1024点DFT所对应的频率分辨率为6.采样率为8kHz的信号的256点DFT的第一个周期覆盖的频率范围是从0Hz至7.信号[ 1 0 2 ]的DFT每隔3个样点值重复,为8.以1600Hz对一220Hz的信号采样,进行64点DFT,最接近的DFT频率为9.以12kHz的信号对一4.25kHz的信号抽样,其256点DFT幅谱图的基带最大峰值点所对应的下标为10.采样频率为6kHz,1kHz信号的频率分辨率要达到50Hz,需11.采样频率为16kHz,1024点DFT的窗口长度为12.关于谱泄漏与窗口长度的关系是13.频谱图是展现信号的什么14.周期性方波的频谱图15.在FFT中的乘数因子是16.与512点的DFT相比,512点的FFT只需约几分之一的计算量17、一个长度为N的有限长序列可否用N个频域的采样值唯一地确定?18、计算两个N点序列的线性卷积,至少要做多少点的DFT?19、x(2n)与x(n)的关系20、对于高斯序列x(n)=exp[-(n-p)2/q],取16点作FFT,其幅度谱中低频分量最多的是21、一般地说按时间抽取基二FFT的_______序列是按位反转重新排列的。
22、信号x(n)=sin(nπ/4) - cos(nπ/7)的数字周期为23、N=2L点基二FFT,共有______列蝶形,每列有____个蝶形。
24、信号s(t)=sin(4000πt)+sin(600πt),则采样频率至少应为25、用按时间抽取法计算256点的FFT时,n=233的二进制位反转值是26、FFT之所以能减少DFT的运算量,是因为:,FFT减少DFT 运算量的基本处理思想是。
数字信号处理课后习题答案(吴镇扬)(精编文档).doc

【最新整理,下载后即可编辑】习题一 (离散信号与系统)1.1周期序列,最小周期长度为5。
1.2 (1) 周期序列,最小周期长度为14。
(2) 周期序列,最小周期长度为56。
1.5()()()()()()()11s a s s s a n s s a s n X j x t p t X j ΩP j Ω2n τn τj sin j Ωjn e X 2n π2n n τj Sa X j jn e 2T 2πττ∞=-∞∞=-∞Ω==*⎡⎤⎣⎦ΩΩ⎛⎫-=-Ω ⎪⎝⎭ΩΩ⎛⎫-=Ω-Ω ⎪⎝⎭∑∑ 1.6 (1) )(ωj e kX (2) )(0ωωj n j e X e (3) )(21)(2122ωωj j e X e X -+ (4) )(2ωj e X1.7 (1) 0n z -(2) 5.0||,5.0111>--z z (3) 5.0||,5.0111<--z z (4)0||,5.01)5.0(11101>----z z z1.8 (1) 0,)11()(211>--=---z zz z z X N(2) a z az az z X >-=--,)1()(211 (3) a z az z a az z X >-+=---,)1()(311211.91.10 (1))1(2)(1----+n u n u n (2))1(24)()5.0(6--⋅--n u n u n n (3))()sin sin cos 1(cos 000n u n n ωωωω++(4) )()()(1n u a a a n a n ---+-δ 1.11(1))(1z c X - (2) )(2z X (3))()1(21z X z -+ (4)-+<<x x R z R z X /1/1),/1(1.12 (1) 1,11<-ab ab(2) 1 (3)00n a n1.13 (1) 该系统不是线性系统;该系统是时不变系统。
数字信号处理Matlab课后实验(吴镇扬)

J I A N G S U U N I V E R S I T Y数字信号处理实验报告实验一熟悉MATLAB环境实验二快速变换及其应用实验三 IIR数字滤波器的设计实验四 FIR数字滤波器的设计实验八信号的谱分析及分段卷实验一熟悉MATLAB环境一、实验目的(1)熟悉MATLAB的主要操作命令。
(2)学会简单的矩阵输入和数据读写。
(3)掌握简单的绘图命令。
(4)用MATLAB编程并学会创建函数。
(5)观察离散系统的频率响应。
二、实验内容认真阅读本章附录,在MATLAB环境下重新做一遍附录中的例子,体会各条命令的含义。
在熟悉了MATLAB基本命令的基础上,完成以下实验。
上机实验内容:(1)数组的加、减、乘、除和乘方运算。
输入A=[1 2 3 4],B=[3 4 5 6],求C=A+B,D=A-B,E=A.*B,F=A./B,G=A.^B并用stem语句画出A、B、C、D、E、F、G。
实验程序:A=[1 2 3 4];B=[3 4 5 6];n=1:4;C=A+B;D=A-B;E=A.*B;F=A./B;G=A.^B;subplot(4,2,1);stem(n,A,'fill');xlabel ('时间序列n');ylabel('A');subplot(4,2,2);stem(n,B,'fill');xlabel ('时间序列n ');ylabel('B');subplot(4,2,3);stem(n,C,'fill');xlabel ('时间序列n ');ylabel('A+B');subplot(4,2,4);stem(n,D,'fill');xlabel ('时间序列n ');ylabel('A-B');subplot(4,2,5);stem(n,E,'fill');xlabel ('时间序列n ');ylabel('A.*B');subplot(4,2,6);stem(n,F,'fill');xlabel ('时间序列n ');ylabel('A./B');subplot(4,2,7);stem(n,G,'fill');xlabel ('时间序列n ');ylabel('A.^B');运行结果:(2)用MATLAB实现以下序列。
数字信号处理(吴镇扬)课后习题答案(比较详细的解答过程)chap5_6

在数字信号处理的滤波器、FFT、卷积及各种矢量 运算中,由于要执行Σb(n)*x(n - k)一类的运算,这类运 算的乘法和加法总是同时出现,因此DSP中就希望将乘法
器和加法器相结合,在一个时钟周期完成一次乘、加运算,
并且累加乘法运算的结果。这样的运算单元称为乘法累加 器(MAC)。
对于乘法累加器,除了要求能在一个时钟周期完成一
5.6-1。
输入设备
运算器
输出设备
控制器
存储器
数据线 控制线
图5.6-1 冯.诺曼结构
冯.诺曼结构处理器具有以下几个特点:
(1) 必须有一个存储器;
(2) 必须有一个控制器;
(3) 必须有一个运算器,用于完成算术
运算和逻辑 运算;
(4) 必须有输入和输出设备,用于进行
人机通信。
冯.诺曼的主要贡献就是提出并实现了“ 存储程序”的概念。由于指令和数据都是二
若干位 。右移使得符号位扩展,也就是在左边填
入符号位,这样可以保留原有的正号或负号。左 移操作用0填入最低位,如果数的最高位不是符号 位,则左移的结果就造成了溢出,这时溢出标志 被置1。逻辑移位用来做某些逻辑操作,如用于位
屏蔽等。逻辑移位把无符号数左移或右移,腾空
位填0。
通用微处理器的移位操作是一位一位移的
生。
5.6.2 DSP硬件构成 典型的DSP处理器中的运算/处理功能单元 主要包括以下几个部分: ● 乘法器/乘加器(MAC) ● 算术逻辑运算单元(ALU) ● 移位器 ● 数据地址发生器(DAG) ● 程序定序器,又称指令定序器 ● 存储器
5.6.2.1 DSP的乘法器/乘加器(MAC) DSP乘法器应具有以下基本功能: 1. 要求在一个时钟周期里对两个字长为 b位的输入由硬件作快速并行乘法; 2. 应能通过格式控制来执行无符号或带 符号或混合的乘法操作、小数或整数乘法操 作以及扩展精度或双精度运算,并有合适的 舍位方法; 3.应有输入和输出寄存器,这样可以锁 存数据,配合流水线操作。也可不用寄存器 ,使乘法器在透明方式下工作,这样可以有 最小的等待时间。
数字信号处理实验(吴镇扬)答案-2
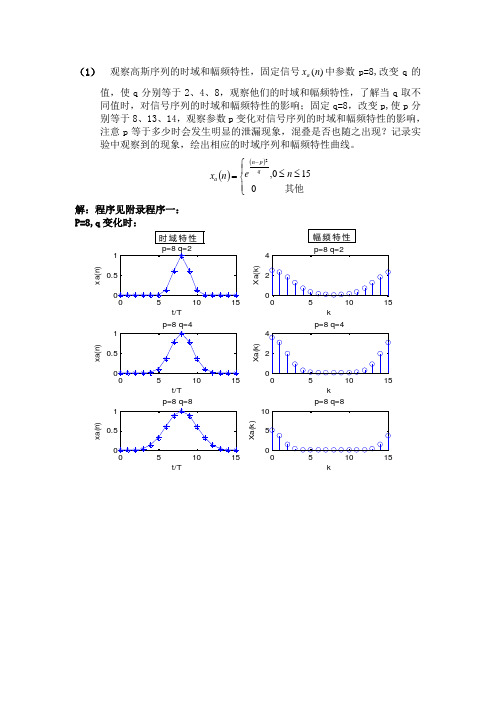
(1) 观察高斯序列的时域和幅频特性,固定信号)(n x a 中参数p=8,改变q 的值,使q 分别等于2、4、8,观察他们的时域和幅频特性,了解当q 取不同值时,对信号序列的时域和幅频特性的影响;固定q=8,改变p,使p 分别等于8、13、14,观察参数p 变化对信号序列的时域和幅频特性的影响,注意p 等于多少时会发生明显的泄漏现象,混叠是否也随之出现?记录实验中观察到的现象,绘出相应的时域序列和幅频特性曲线。
()()⎪⎩⎪⎨⎧≤≤=-其他0150,2n e n x q p n a解:程序见附录程序一:P=8,q 变化时:t/T x a (n )p=8 q=2k X a (k )t/T x a (n )p=8 q=4k X a (k )p=8 q=4t/Tx a (n )p=8 q=8kX a (k )p=8 q=8幅频特性时域特性t/T x a (n )p=8 q=8k X a (k )p=8 q=8t/T x a (n )p=13 q=851015k X a (k )p=13 q=8t/Tx a (n )p=14 q=851015kX a (k )p=14 q=8时域特性幅频特性分析:由高斯序列表达式知n=p 为期对称轴; 当p 取固定值时,时域图都关于n=8对称截取长度为周期的整数倍,没有发生明显的泄漏现象;但存在混叠,当q 由2增加至8过程中,时域图形变化越来越平缓,中间包络越来越大,可能函数周期开始增加,频率降低,渐渐小于fs/2,混叠减弱;当q 值固定不变,p 变化时,时域对称中轴右移,截取的时域长度渐渐地不再是周期的整数倍,开始无法代表一个周期,泄漏现象也来越明显,因而图形越来越偏离真实值,p=14时的泄漏现象最为明显,混叠可能也随之出现;(2) 观察衰减正弦序列 的时域和幅频特性,a=0.1,f=0.0625,检查谱峰出现的位置是否正确,注意频谱的形状,绘出幅频特性曲线,改变f ,使f 分别等于0.4375和0.5625,观察这两种情况下,频谱的形状和谱峰出现的位置,有无混叠和泄漏现象?说明产生现象的原因。
数字信号处理_吴镇扬_习题解答

(k
)
+
F*
(
N
−
k
)⎤⎦
=
1− aN 1 − aWNk
Y
(k)
=
DFT
⎡⎣Im{
f
( n )}⎤⎦
=
DFT
⎡1 ⎢⎣ 2 j
{
f
(n)
−
f
* (n)}⎤⎥ ⎦
=
1 2j
⎡⎣ F
(k)
−
F*(N
−
k )⎤⎦
=
1− bN 1 − bWNk
对 X (k ) 、Y (k ) 作 IDFT 得到:
⎧⎪x (n) = anRN (n)
(3) 通过 z 平面上作图,可以发现,极点 a 在单位圆内的实轴上,零点 1/a 在单位圆外的实轴上, 它们各自到单位圆上任一点的矢量长度可由余弦定理求取,分别为
极点矢量长度= a 2 + 1 − 2acos(ω)
零点矢量长度= a -2 + 1 − 2a -1cos(ω) = 1 a 2 + 1 − 2acos(ω) a
⎨ ⎪⎩
y
(
n
)
=
b
n
RN
(
n
)
注意:
根据 DFT 的线性性质可以得到,当 f (n) = x(n) + jy (n) 时, F (k ) = X (k ) + jY (k ) ,其中
X (k ) 、 Y (k ) 均为复序列。但并不是对于形如 F (k ) = X (k ) + jY (k ) 进行 IDFT 就一定形成
= e 2N
-j2π k n
=e N 2
kn
数字信号处理Matlab课后实验(吴镇扬)

J I A N G S U U N I V E R S I T Y数字信号处理实验报告实验一熟悉MATLAB环境实验二快速变换及其应用实验三 IIR数字滤波器的设计实验四 FIR数字滤波器的设计实验八信号的谱分析及分段卷实验一熟悉MATLAB环境一、实验目的(1)熟悉MATLAB的主要操作命令。
(2)学会简单的矩阵输入和数据读写。
(3)掌握简单的绘图命令。
(4)用MATLAB编程并学会创建函数。
(5)观察离散系统的频率响应。
二、实验内容认真阅读本章附录,在MATLAB环境下重新做一遍附录中的例子,体会各条命令的含义。
在熟悉了MATLAB基本命令的基础上,完成以下实验。
上机实验内容:(1)数组的加、减、乘、除和乘方运算。
输入A=[1 2 3 4],B=[3 4 5 6],求C=A+B,D=A-B,E=A.*B,F=A./B,G=A.^B并用stem语句画出A、B、C、D、E、F、G。
实验程序:A=[1 2 3 4];B=[3 4 5 6];n=1:4;C=A+B;D=A-B;E=A.*B;F=A./B;G=A.^B;subplot(4,2,1);stem(n,A,'fill');xlabel ('时间序列n');ylabel('A');subplot(4,2,2);stem(n,B,'fill');xlabel ('时间序列n ');ylabel('B');subplot(4,2,3);stem(n,C,'fill');xlabel ('时间序列n ');ylabel('A+B');subplot(4,2,4);stem(n,D,'fill');xlabel ('时间序列n ');ylabel('A-B');subplot(4,2,5);stem(n,E,'fill');xlabel ('时间序列n ');ylabel('A.*B');subplot(4,2,6);stem(n,F,'fill');xlabel ('时间序列n ');ylabel('A./B');subplot(4,2,7);stem(n,G,'fill');xlabel ('时间序列n ');ylabel('A.^B');运行结果:(2)用MATLAB实现以下序列。
南邮数字信号处理吴镇扬-课后习题详细答案-DSP期末复习PPT课件

• 解:
DTxF n T n0 xnn0ejwn
n
令 n ' n n 0 xn ' e jw n ' n 0xn ' e jw ' jn w 0
n '
n '
e jw 0 nxn 'e jw ' n e jw 0 D n T xn ' F e jT w 0X n e jw
•pp 34: 1.5 (3)
1
X Z x n Z n 0 . 5 n u n 1 Z n 0 . 5 n Z n
n
n
n
变 量 n ' n 替 换 0 .5 n 'Z n ' 0 .5 1 Z n '
n ' 1
n ' 1
0
Re[z]
• pp 34: 1.5 (2n Z n0 .5 n u n Z n0 .5 n Z n
n
n
n 0
n 00 .5 Z 1 n 1 0 1 .5 Z 1 ,0 .5 Z 1 1 1 0 1 .5 Z 1 ,0 .5 Z
n ' 1
n ' 1
•变量替换易出问题
1 0 . 0 5 . 5 1 Z 1 Z 1 0 1 . 5 Z 1 ,0 . 5 1 Z 1 1 0 1 . 5 Z 1 ,Z 0 . 5
零点:z
2z 1 2z
0
z
z
1 2
j Im[z]
极点: z 1
收敛域:
2 z
1
2
1/2
DSP考试题型
• 填空题20分(每空1分) • 判断题10分(每题2分) • 简答题10分 • 画图题15分 • 计算题45分
数字信号处理Matlab课后实验(吴镇扬)

数字信号处理实验报告实验一熟悉MATLAB环境实验二信号的采样与重建实验三快速变换及其应用实验四 IIR数字滤波器的设计实验五 FIR数字滤波器的设计实验一熟悉MATLAB环境一、实验目的(1)熟悉MATLAB的主要操作命令。
(2)学会简单的矩阵输入和数据读写。
(3)掌握简单的绘图命令。
(4)用MATLAB编程并学会创建函数。
(5)观察离散系统的频率响应。
二、实验内容认真阅读本章附录,在MATLAB环境下重新做一遍附录中的例子,体会各条命令的含义。
在熟悉了MATLAB基本命令的基础上,完成以下实验。
上机实验内容:(1)数组的加、减、乘、除和乘方运算。
输入A=[1 2 3 4],B=[3 4 5 6],求C=A+B,D=A-B,E=A.*B,F=A./B,G=A.^B并用stem语句画出A、B、C、D、E、F、G。
实验程序:A=[1 2 3 4];B=[3 4 5 6];n=1:4;C=A+B;D=A-B;E=A.*B;F=A./B;G=A.^B;subplot(4,2,1);stem(n,A,'fill');xlabel ('时间序列n');ylabel('A');subplot(4,2,2);stem(n,B,'fill');xlabel ('时间序列n ');ylabel('B');subplot(4,2,3);stem(n,C,'fill');xlabel ('时间序列n ');ylabel('A+B');subplot(4,2,4);stem(n,D,'fill');xlabel ('时间序列n ');ylabel('A-B');subplot(4,2,5);stem(n,E,'fill');xlabel ('时间序列n ');ylabel('A.*B');subplot(4,2,6);stem(n,F,'fill');xlabel ('时间序列n ');ylabel('A./B');subplot(4,2,7);stem(n,G,'fill');xlabel ('时间序列n ');ylabel('A.^B');运行结果:(2)用MATLAB实现以下序列。
数字信号处理_吴镇扬_习题解答 第二版

1. 解丗由题意可知 N=5
则周期为丗其中为整数丆且满足使N为最小整数。
2. •i1•j解丗由题意可知 N=14
则周期为丗
•i2•j解丗由题意可知 N= 8
则
则所求周期 N=14
最小公倍数丆即为丗56
3.19 (1)周期卷积的主值序列为丗f(n)R(n) ={6,3, 6,10,14,12,9};
(2)循环卷积f (n) ={6,3, 6,10,14,12,9};
•i3•j线性卷积为f(n) ={1,3, 6,10,14,12,9,5, 0, 0, 0, 0}
2.21 •i 第二种方法乯按频率抽取算法丗输入顺
序丆
输出倒序(0,8,4,12,2,10,6,14,1,9,5,13,3,11,7, 15);
4
共有4(16=2*2*2*2 )节
第一节丗数据点间距、蝶形类型均是8•C
0 1 2 3 4 5 6 7
所乘因子丗W ,W ,W ,W ,W ,W ,
W ,W ;
N N N N N N N N N
第二节丗数据点间距、蝶形类型均是4 •C
0 2 4 6
所乘因子丗W ,W ,W ,W ;
N N N N
0 4
第三节丗数据点间距、蝶形类型均是2 •C所乘因
子丗W ,W ;
N N
第四节丗数据点间距、蝶形类型均是1 •C所乘因
子丗W ;
N。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题一 (离散信号与系统)1.1周期序列,最小周期长度为5。
1.2 (1) 周期序列,最小周期长度为14。
(2) 周期序列,最小周期长度为56。
1.5()()()()()()()11s a s s s a n s s a s n X j x t p t X j ΩP j Ω2n τn τj sin j Ωjn e X 2n π2n n τj Sa X j jn e 2T 2πττ∞=-∞∞=-∞Ω==*⎡⎤⎣⎦ΩΩ⎛⎫-=-Ω ⎪⎝⎭ΩΩ⎛⎫-=Ω-Ω ⎪⎝⎭∑∑F 1.6 (1) )(ωj e kX (2) )(0ωωj n j e X e (3) )(21)(2122ωωj j e X e X -+ (4) )(2ωj e X1.7 (1)0n z -(2)5.0||,5.0111>--z z(3)5.0||,5.0111<--z z(4)0||,5.01)5.0(11101>----z zz1.8 (1) 0,)11()(211>--=---z z z z z X N (2) a z az az z X >-=--,)1()(211(3)a z az z a az z X >-+=---,)1()(311211.9 1.10(1))1(2)(1----+n u n u n (2))1(24)()5.0(6--⋅--n u n u n n (3))()sin sin cos 1(cos 000n u n n ωωωω++(4) )()()(1n u a a a n a n ---+-δ1.11 (1) )(1z c X - (2) )(2z X (3) )()1(21z X z -+ (4) -+<<x x R z R z X /1/1),/1(1.12 (1)1,11<-ab ab(2) 1 (3) 00n a n1.13 (1) 该系统不是线性系统;该系统是时不变系统。
(2) 该系统不是线性系统;该系统是时不变系统。
(3) 线性系统时不变系统。
(4) 线性系统时不变系统。
(5) 线性系统时变系统。
1.14 (1))7()5(2)3()1(4)1(4)(-----+-++=n n n n n n y δδδδδ(2) ⎩⎨⎧≥-≤≤-=-5)5.02(5.0405.02)(44n n n y n n (3) )5(8)4(4)3(6)2(3)1(2)()(-----+-+-+=n n n n n n n y δδδδδδ 1.16 (1) 因果、稳定。
(2) n 0<0时系统非因果,不稳定。
(3) 当n 0>0时,该系统是因果系统,当n 0<0时,该系统是非因果系统;系统稳定。
(4)因果、稳定。
(5)因果、稳定。
(6)因果、稳定。
(7)因果、不稳定。
(8)非因果、稳定。
1.17 (1) y(n)=1, n =0 y(n)=4*3-n , n ≥1(2) )(])31(2123[)(n u n y n⋅-= (3) )5(])31(1[23)(])31(2123[)(5--+⋅-=-n u n u n y n n1.18 y(n)=1,n =0y(n)=3*2-n , n ≥11.19 (1) )(])([1)(11n u b a ba n f n n ++--=(2) )2()(2-=-n u a n f n (3)1.22 (3) ae H j 1)(=ω习题二 (离散傅里叶变换及其快速算法)2.11,1,00)12()()2(212-==+=N k k X k X k X2.6 (1) 1 (2) kn N W 0 (3) kNN aW a --11 (4) ⎪⎪⎩⎪⎪⎨⎧=-≠-=02)1(01)(k N N k W N k X k N2.10 (1) )()2cos(2n R n NN N π (2) )()2cos(2n R n N N N π- (3) )()2sin(2n R n N N N π2.12 (1)[][])()(21)())(())((21)2cos()(DFT *m k X m k X k R m k N X m k X m n N n x N N N ++-=+-+-=⎥⎦⎤⎢⎣⎡π(2)[][])()(21)())(())((21)2sin()(DFT *m k X m k X jk R m k N X m k X j m n N n x N N N +--=+---=⎥⎦⎤⎢⎣⎡π 2.131,,2,1,0)()(-==N k k X rk Y2.141,,1,0)())(()(-==rN k k R k X k Y rN N2.15 (1) )()(n R a n x N n = )()(n R b n y N n =(2) )()(n n x δ= )()(n N n y δ=2.16)(11N R a aN n N- 2.17 (1) )2/(N k X + (2) )(k X W kN --2.18 7≤n ≤19 2.19(1)}9,12,14,10,6,3,6{)()(~7=n R n f (2)的主值序列是)(~)(n f n f(3){1,3,6,10,14,12,9,5,0,0,0,0} 2.20 125.8ms, 0.712ms 2.252.27 (1) N=49 (2) M=51 (3) 49-99 2.28 (1)854Hz (2) 815Hz习题三(IIR 滤波器设计)3.1 1312231122223()2()1()z e e H z ee z e z ---------=-++3.2 (1) ()()111122()11a bj T a bj TH z eze z -+----=+--=221)()(1][1)cos(1---+-----++--ze z e e z bT e aT T bj a T bj a aT(2)01()[](1)!m ms TAT d zH z z m dz z e -=---3.4 12212()3z z H Z z---++=+3.6 1s f K H Z = 100c f HZ =5s f K H Z = 500c f HZ = 200s f HZ = 20c f HZ =3.7 1112110.665()10.36810.7860.368z H z z z z -----+=+--+3.81231231231231231235.196(133)()15.6615.129.12 1.661333.014 2.91 1.7550.31950.331800.99540.99540.331810.96550.58060.106z z z H z z z z z z z z z zz z z z z z ------------------+++=++++++=+++-+-=-+-3.9123123221330.16670.50.50.1667()6210.3333z z z z z z H z z z---------+--+-==++3.106426425.196(331)()15.6615.129.12 1.66z z z H z z z z -+-=-+-2462462462461333.014 2.91 1.7550.31950.33180.99540.99540.331810.96580.58270.1060z z z z z z z z z z z z -------------+-=-+--+-=-+-3.1212120.0674553(12)()1 1.142980.412802z z H z z z -----+=++3.14 55.747.192.7577.3611.828.036.036.028.0)(1234134+-+--+-=-------z z z z z z z z H习题四(FIR 滤波器)4.1 (1))]([sin[)()1()(αωαπ---=n n n h c nd其中,21-=N α (2)因为h(n)偶对称,所以若N 为奇数,则属于第一种线性相滤波器,若N 为偶数,则属于第二种线性相位滤波器(3) )()]12cos(1[21)(n R N nn w N --=π ∴)()()(n h n w n h d =4.2 (1) )()](sin[)](cos[2)(0απαωαω---=n n n n h c d 其中21-=N α,4.3 (1) ])s i n [(])s i n [()(2)(0ωαωαπα---=n n n n h c d4.4 (2) ())()(n h n n h BP BR --=αδ N N 21-=α必须为奇数4.6 用k N k H H -=,又 N 为奇数∴k N N k πθ2)21()(--==)11(N k --π=1514πk - )21(1]2/)/2sin[()2/sin()(1)(Nk N j N k j e N k N k H Ne H πωωπωω+---=∑-=将kj k eH k H θ=)( 带入上式,则∑=+---=140)157(1514]2/)15/2sin[()2/15sin(151)(k k j k j k j eek H e H πωπωπωω=ωπωωπωωωω7])15/2/sin()2/15sin(5.0)15/2/sin()2/15sin(5.0)2/sin()2/15sin([151j e-+--- 140)]1514152cos(1[151)(≤≤-+=n n n h ππ4.7 (1))()()(224821k H e k H ek H k j k jππ--==故 )(~)(~21k H k H =(2) 线性相位, (N-1)/2, h 1(n )好于h 2(n )4.8 ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-==-==----k k ek e k e k ek H k j k j k j k j 其它02439.0839.031,...26,257,...1,0)(3231323132313231ππππ 4.9 (1) ⎪⎪⎪⎩⎪⎪⎪⎨⎧====--32,...22;11,..0020,...14,1321,1239.0)(33323332k k ek ek H k j k j ππ(2) ⎪⎪⎪⎩⎪⎪⎪⎨⎧====+-33,...23;11,..0021,...,14,1322,1239.0)(3432)23432(k k e k ek H k j k j πππ4.10 (1)⎪⎪⎩⎪⎪⎨⎧-=-====+--+--2,...3,21,14.000)()21()21(N k eN k k ek k H N N k j N N k j ππππ(2)⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=--===其他11,214.023,14.000N N k N k k H k⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=+----===+--+--其他)21()21(1,21)21(4.023,14.000)(ππππππN N k j N N k j e N N k N N k j e N k e k k H习题五(数字信号处理系统的实现)5.1 (1) 2113.025.0125.02)(---+-+=z z z z H(2) 5432143213221212108.062.098.026.05.112.739.156.3616.076.016.36.065.05.1125.01)(--------------------+-++++=++++⋅--++=z z z z z zz z z z z z z z z z z z H5.7 +--=--11611)[1(161)(z z z H ]414.1141.1185.1198.12211211------+--++--zz z z z z 5.8222222022222()(2())111[2]2/12111nn nn n f een n b e e e ac aac c a ac c ∞∞==-=+=++=++=---∑∑σσσσ5.9 (1)21)(cos 21022=+=⎰-θθωπσππd n xbex q q 222222661221⋅===∴σσ(2) b=(80-1.249)/6.02=13.08 (取整)=145.10 (1) 284.2e σ (3) 293.7e σ。
