数字信号处理(第三版)课后习题答案全.

《数字信号处理》第三版课后习题答案

数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n =-，试画出1()x n 波形；（4）令2()2(2)x n x n =+，试画出2()x n 波形；（5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14；（2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

《数字信号处理》第三版课后答案

数字信号处理(西电科大第三版)课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n =-，试画出1()x n 波形；（4）令2()2(2)x n x n =+，试画出2()x n 波形；（5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14；（2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

《数字信号处理》第三版课后习题答案

因为
x(n) (n 2) (n 1) 2 ( n 3)
h(n) 2 (n)
1 (n 1) (n 2)
2
x( n) * (n ) x (n ) x( n) * A (n k ) A x( n )k
所以
1
y( n) x(n)*[2 ( n) (n 1)
(n 2)]
2
2 x(n) x( n 1) 1 x( n 2) 2
6
y( n)
1 y(n 1) x(n)
1 x(n
1) ；
2
2
设系统是因果的，利用递推法求系统的单位取样响应。
解：
令： x(n) (n)
1
1
h(n) h(n 1) (n)
(n 1)
2
2
1
1
n 0,h(0) h( 1) (0) ( 1) 1
2
2
1
1
n 1,h(1) h(0) (1) (0) 1
2
2
n 2,h(2) 1 h(1) 1
n n0
（ 3）如果 x( n) M ， y(n)
x( k) 2n0 1 M ，因此系统是稳定的。
k n n0
系统是非因果的，因为输出还和 x(n)的将来值有关 .
（5）系统是因果系统，因为系统的输出不取决于 x(n)的未来值。如果 x(n) M ，则 y(n) ex(n) ex(n) eM ，因此系统是稳定的。
（ 1） y( n) x(n) 2x(n 1) 3x( n 2) ；
（ 3） y( n) x(n n0) ， n0 为整常数；
（ 5） y(n) x2 (n) ；
n
（ 7） y( n) x(m) 。
m0

数字信号处理(第三版)-课后习题答案全-(原题+答案+图)

=2x(n)+x(n－1)+ x(n－2)
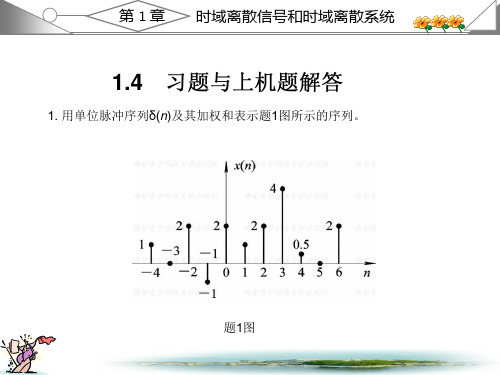
将x(n)的表示式代入上式，得到 1 y(n)=－2δ(n+2)－δ(n+1)－0.5δ(2n)+2δ(n－1)+δ(n－2)
+4.5δ(n－3)+2δ(n－4)+δ(n－5)
第 1 章时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况，
第 1 章时域离散信号和时域离散系统
(3) 这是一个延时器，延时器是线性非时变系统，下面证明。令输入为
输出为
x(n－n1)
y′(n)=x(n－n1－n0) y(n－n1)=x(n－n1－n0)=y′(n) 故延时器是非时变系统。由于
T［ax1(n)+bx2(n)］=ax1(n－n0)+bx2(n－n0) =aT［x1(n)］+bT［x2(n)］
（5）y(n)=x2(n)
（6）y(n)=x(n2)
（7）y(n)=
n
（8）y(n)=x(n)sin(ωxn(m) )
m0
解：（1）令输入为
输出为
x(n－n0)
y′(n)=x(n－n0)+2x(n－n0－1)+3x(n－n0－2) y(n－n0)=x(n－n0)+2x(n—n0—1)+3(n－n0－2)
x(m)h(n－m)
m
第 1 章时域离散信号和时域离散系统
题7图
第 1 章时域离散信号和时域离散系统
y(n)={－2,－1,－0.5, 2, 1, 4.5, 2, 1; n=－2, －1, 0, 1, 2, 3, 4, 5}

《数字信号处理》第三版课后答案

《数字信号处理》第三版课后答案1 数字信号处理(西电科大第三版)课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+- 2. 给定信号：25,41()6,040,n n x n n +-≤≤-??=≤≤其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n =-，试画出1()x n 波形；（4）令2()2(2)x n x n =+，试画出2()x n 波形；（5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+- （3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n eπ-=。

解：。

《数字信号处理》第三版答案(非常详细完整)

答案很详细，考试前或者平时作业的时候可以好好研究，祝各位考试成功！！电子科技大学微电子与固体电子学陈钢教授著数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n =-，试画出1()x n 波形；（4）令2()2(2)x n x n =+，试画出2()x n 波形；（5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如 5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

（1）()()2(1)3(2)y n x n x n x n =+-+-；（3）0()()y n x n n =-，0n 为整常数；（5）2()()y n x n =；（7）0()()nm y n x m ==∑。

《数字信号处理》第三版答案(非常详细完整)

答案很详细，考试前或者平时作业的时候可以好好研究，祝各位考试成功！！电子科技大学微电子与固体电子学陈钢教授著数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n =-，试画出1()x n 波形；（4）令2()2(2)x n x n =+，试画出2()x n 波形；（5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如 5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

（1）()()2(1)3(2)y n x n x n x n =+-+-；（3）0()()y n x n n =-，0n 为整常数；（5）2()()y n x n =；（7）0()()nm y n x m ==∑。

数字信号处理》第三版课后习题答案

数字信号处理课后答案教材第一章习题解答1.用单位脉冲序列()nδ及其加权和表示题1图所示的序列。

解：2.给定信号：25,41 ()6,040,n nx n n+-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n序列；（3）令1()2(2)x n x n=-，试画出1()x n波形；（4）令2()2(2)x n x n=+，试画出2()x n波形；（5）令3()2(2)x n x n=-，试画出3()x n波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）（3）1()x n的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n时，先画x(-n)的波形，然后再右移2位，3()x n波形如题2解图（四）所示。

3.判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14；（2）12,168w wππ==，这是无理数，因此是非周期序列。

5.设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

（1）()()2(1)3(2)y n x n x n x n =+-+-；（3）0()()y n x n n =-，0n 为整常数；（5）2()()y n x n =；（7）0()()nm y n x m ==∑。

解：（1）令：输入为0()x n n -，输出为'000'0000()()2(1)3(2)()()2(1)3(2)()y n x n n x n n x n n y n n x n n x n n x n n y n =-+--+---=-+--+--=故该系统是时不变系统。

《数字信号处理》第三版答案(非常详细完整)

答案很详细，考试前或者平时作业的时候可以好好研究，祝各位考试成功！！电子科技大学微电子与固体电子学陈钢教授著数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n =-，试画出1()x n 波形；（4）令2()2(2)x n x n =+，试画出2()x n 波形；（5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如 5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

（1）()()2(1)3(2)y n x n x n x n =+-+-；（3）0()()y n x n n =-，0n 为整常数；（5）2()()y n x n =；（7）0()()nm y n x m ==∑。

《数字信号处理》第三版高西全版课后习题答案详解

数字信号处理课后答案高西全、丁美玉版1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n =-，试画出1()x n 波形；（4）令2()2(2)x n x n =+，试画出2()x n 波形；（5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14；（2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

《数字信号处理》第三版课后答案

《数字信号处理》第三版课后答案D解：（1）令：输入为0()x n n -，输出为'000'0000()()2(1)3(2)()()2(1)3(2)()y n x n n x n n x n n y n n x n n x n n x n n y n =-+--+---=-+--+--=故该系统是时不变系统。

12121212()[()()]()()2((1)(1))3((2)(2))y n T ax n bx n ax n bx n ax n bx n ax n bx n =+=++-+-+-+- 1111[()]()2(1)3(2)T ax n ax n ax n ax n =+-+- 2222[()]()2(1)3(2)T bx n bx n bx n bx n =+-+-1212[()()][()][()]T ax n bx n aT x n bT x n +=+故该系统是线性系统。

（3）这是一个延时器，延时器是一个线性时不变系统，下面予以证明。

令输入为1()x n n -，输出为'10()()y n x n n n =--，因为'110()()()y n n x n n n y n -=--=故延时器是一个时不变系统。

又因为12102012[()()]()()[()][()]T ax n bx n ax n n bx n n aT x n bT x n +=-+-=+ 故延时器是线性系统。

（5）2()()y n x n =令：输入为0()x n n -，输出为'2()()y n x n n =-，因为2'()()()y n n x n n y n -=-=故系统是时不变系统。

又因为21212122212[()()](()()) [()][()]()()T ax n bx n ax n bx n aT x n bT x n ax n bx n +=+≠+=+因此系统是非线性系统。