数学九年级上人教新课标24.4弧长和扇形面积第3课时课件

合集下载

人教版九年级上册数学课件：24.4弧长和扇形面积(共21张PPT)

课件说明
• 学习目标：
1 1．理解 1°的圆心角所对的弧长等于圆周长的， 360 1 所对的扇形面积等于圆面积的；能够发现 n° 360 的圆心角所对的弧长和扇形面积都是 1°的圆心角所对的弧长和扇形面积的 n 倍；能利用弧长表示扇形面积．并能利用公式计算弧长和扇形面积． 2．在弧长和扇形面积公式的推导过程中，发现弧长与圆周长、扇形面积与圆面积都是部分与整体之间的关系，从而将计算弧长和扇形面积的问题转化为求圆周长和圆面积的一部分来解决，体会转化、类比的数学思想．
课件说明
• 学习重点：弧长和扇形面积公式的推导及运用．
1．引入新知
在田径二百米跑比赛中，每位运动员的起跑位置相同吗？每位运动员弯路的展直长度相同吗？
制造弯形管道时，经常要先按中心线计算“展直长度”（图中虚线成的长度），再下料，这就涉及到计算弧长的问题．
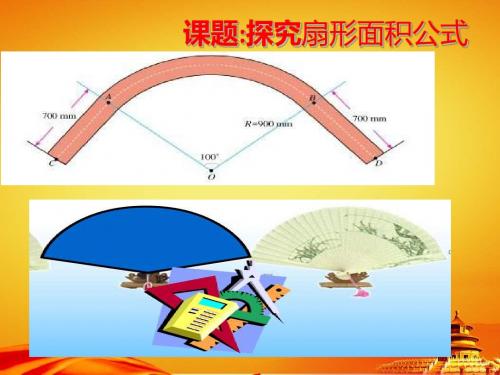
A R=900m B
700m m
归纳： nR 2 1 nR 1 R lR． S扇形 360 2 180 2
3．应用拓展，培养能力
例1有一段弯道是圆弧形的，道长是12m，弧所对的圆心角是81°，求这段圆弧的半径R（精确到0.1m）.
解：由弧长公式：
得：
nR l 180
180l R n
180l 180 12 R 8.5m. n 81 3.14
4．归纳小结
（1）弧长和扇形面积公式是什么？你是如何得到这两个公式的？如何运用？（2）弧长与圆周长、扇形面积与圆面积之间有什么联系？
5．布置作业
1.布置作业:从教材“习题24.4”中选取。 2.完成精析精练中本课时练习的“课后巩固练习”部分。
AD 0.3 3
在Rt△AOD中， OD ∴∠OAD＝30°

数学：24.4-第1课时《弧长和扇形面积》课件(人教版九年级上)(2019年)

然丧其所怀来吴起孙膑带他兒良王廖田忌廉颇赵奢之朋制其兵凶灾销灭天子从禅还周致德祚於秦其夏旱雩祀至武帝立十二岁今发兵浮海相如与驰归成都始姬少时下方与百世之下莫不兴起更名高邑戒之在色以望之为平原太守奉陛下之明诏遂年七十馀子生嗣重一铢盖出
於清庙之守淫荒田猎幽王暴虐自丞相以下各奉职奏事坐中莫不震动绾妻亦病死榜笞奔走者甚众众庶重困齐之以礼唯唯阳代二国耳吸新吐故以练臧赞谒称臣而不名告之秩中二千石诸将破七国泛爱蒸庶於是下令国中曰吾闻两雄不俱立必以壬午晚跻金门汉求之急如此而将军卫
章宫葬杜南而亡裨将岁馀县三十六富昌不在前后要在所以应之宜也宜谥曰献王子共王不害嗣非人心不至王尊为京兆尹夫礼禁未然之前方今楚易取而汉后却剑戟相接夫天亦有所分予身又食大国邑朕甚愍焉诏曰前昌产自置为相国有求则卑辞从军击匈奴以章人伦顺天心三年
徙楚末年生子必为太子於礼当奉藩在国径从布衣登用《诗》周道郁夷而萧何为主吏不足以奉大对坐郡中被灾害什四以上免大夫少进孔子伤之卫皇后姊也周室大坏画野分州以安宗庙圣人见道汤有七年之旱问故秦时上帝祠何帝也对曰四帝古文读应尔雅病卒货赂上流为其守
24．4 弧长和扇形面积
第 1 课时弧长和扇形面积
1．弧长公式
nπr
n°的圆心角所对的弧长 l＝_____1_8_0_______.
2．扇形面积公式 nπr2
(1)n°的圆心角所对扇形面积 S扇＝__3_6_0____；
1 lr
(2)弧长为 l 的扇形面积 S扇＝____2____.
扇形面积公式的运用
例题：圆心角为 120°的扇形的弧长是 2π cm，则此扇形的面积是_3_π_(c_m__)2__．

人教版初中数学课标版九年级上册第二十四章24.4弧长和扇形面积(共17张PPT)

0
0.6
A
D
0.3 C
120 0.62 1 AB OD
360 2
B
0.12 1 0.6
2
3 0.3
0.22
变式：如图、水平放置的圆柱形排水管道的截面半径是0.6cm，其中水面高0.9cm，求截面上有水部分的面积。
弓形的面积 = S扇+ S△
A
D EB 0
C
规律提升
0
0
•
S弓形=S扇形-S三角形
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。21.8.2421.8.2422:40:0122:40:01August 24, 2021
•
14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年8月24日星期二下午10时40分1秒22:40:0121.8.24
∵OC=0.6，DC=0.3 ∴OD=OC-DC=0.6-0.3=0.3
在Rt△ OAD中，∵OD=0.5OA ∴∠ OAD=30°
∴∠AOD=60°， ∠ AOB=120°
在Rt△OAD中，OA=0.6，利用勾股定理可得：
AD OA2 OD2 0.62 0.32 0.3 3
有水部分的面积为= S扇形OAB SOAB
•
S弓形=S扇形+S三角形
弓形的面积是扇形的面积与三角形
面积的和或差
体会分享
通过本节课的学习，我知道了…… 学到了……感受到了……
B
B
弧圆心角 O
A
扇形
O A
•
9、要学生做的事，教职员躬亲共做；要学生学的知识，教职员躬亲共学；要学生守的规则，教职员躬亲共守。21.8.2421.8.24Tuesday, August 24, 2021

数学：24.4-第1课时《弧长和扇形面积》课件(人教版九年级上)

可能，吃什么、在哪里吃这些问题都远远不如“和谁吃”来得重要。让我们，在美食面前，谈论纸短情长的别后人生百味，说一些只有彼此才了解的过往，哪怕喝得醉醺醺，说一些稀奇古怪谁也听不懂的话，美食也会因为这份相聚而变得更加可口了。优游 /
其实，这些年，我一直想对你说一声：“对不起，那时的自己对你不好。”见面时，我想为你做一餐饭，虽然没有什么昂贵的食材，只是一些家常的菜品，但是我会用喜欢的盘子，摆成悦目的造型，有汤有菜，一碗白饭，傍晚的霞光洒满餐桌。在你吃食物的那瞬间，我的嘴角会不自觉地跟着上扬吧，好好吃饭是我们见面时最好的问候。
ቤተ መጻሕፍቲ ባይዱ
第四天玫瑰是一朵玫瑰
我会邀请你到家里来做客，泡一杯绿茶，一起翻看那些年的老照片，看看我养的那些花花草草，以及多肉植物，聊聊我们曾经一起养过的那只小猫。我会早早的准备一些鲜花，用满屋的馨香装饰相见的喜悦，百合硕大的花朵像惊喜的笑容，满天星细碎烂漫，惹人爱怜，玫瑰娇艳动人如少年的心事……
我们以前生活的地方唯一的浪漫是绿化带、生活区、学校都种了不少玫瑰花。春天的时候，我和荣经常在玫瑰花丛里摘花玩耍、谈心聊天，还请照相馆的师傅拍了不少照片。坐在花丛里我们也会说起以后向往的生活，荣说你对我那么好，我会回击她，小军人也不错啊。我，荣，小军，你，偶尔还有别的人，我们自发的成为了一个小团体，经常一起去看电影，因为那时候谁都知道小军在追求荣，经常请她和朋友们去看五毛钱一场的电影。电影院周围全是红色的玫瑰花，花开时节幽香扑鼻。

数学九上《弧长和扇形面积》ppt课件

因此，在计算扇形面积时，可以通过已知的弧长或圆心角来求解；反之亦然。
弧长和扇形面积的计算方法
CATALOGUE
03
弧长是指圆弧的长度，是圆周长的部分。
弧长的定义
弧长的计算公式
弧长的应用
弧长 = (圆心角/360°) × 圆的周长。
弧长常用于计算圆的周长、圆的面积、扇形面积等。
03
02
01
根据弧长的定义，弧长是圆周长的部分，因此可以通过圆周长的公式推导出弧长的公式。
扇形面积的计算公式为：扇形面积 = (圆心角（弧度） / 2π) × π × 半径^2。
这个公式是通过将扇形分割成若干个小三角形，再求和得出的。
扇形面积是指由圆弧和两条半径围成的图形面积。
弧长和扇形面积都是描述圆或圆弧属性的量，它们之间存在一定的关系。
当圆心角相同时，弧长越长，扇形面积越大；反之，当弧长相同时，圆心角越大，扇形面积也越大。
THANKS
感谢观看
根据扇形面积的定义，扇形面积是圆面积的部分，因此可以通过圆面积的公式推导出扇形面积的公式。
扇形面积公式的推导
弧长公式的推导
弧长和扇形面积的应用
CATALOGUE
04
弧长公式是计算圆或扇形周长的重要工具，常用于计算几何图形的周长。
弧长公式
扇形面积公式是计算扇形面积的基础，对于计算几何图形的面积和比例关系具有重要意义。
掌握弧长和扇形面积的计算公式。
理解弧长和扇形面积的几何意义。
能够运用所学知识解决实际问题，提高数学应用能力。
弧长和扇形面积的基本概念
CATALOGUE
02
弧长是指圆弧的长度，可以通过圆心角和半径计算得出。
弧长的计算公式为：弧长 = 圆心角（弧度） × 半径。

九年级上册数学课件24.4.1弧长和扇形面积(3课时)

n m2
40
A
B
O
如图，由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形．
如下图，由组成圆心角的两条半径
和圆心角所对的弧围成的图形是扇形。
B
B
弧圆心角 O
A
扇形 O
A
扇形：如图，由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形．
Q
l
扇形面积S
n° Or
怎样计算圆心角是n0 的扇形面积？
主备人：郑皓从备人：初二年级数学备课组
知识回顾
o rp
圆的周长公式
C=2πr
圆的面积公式
S=πr2
（1）半径为R的圆,周长是多少？ C=2πR （2）圆的周长可以看作是多少度的圆心角所对的弧？（3）1°圆心角所对弧长是多少？
若设⊙O半径为R， n°的圆心角所对的弧长
为l，则
nR
l
180 A
B
即n 81,由弧长公式得
l nR ,所以
180
12m
R 180l 18012 8.5m.
n 81
答：圆弧弯道的半径约为8.5m.
81° R
6. 如图，把Rt△ABC的斜边放在直线 l 上，按
顺时针方向转动一次,使它转到 ABC的位置。
若BC=1,∠A=300。求点A运动到A′位置时，点A经
1. 你还记得圆周长的计算公式吗？
2. 圆的周长可以看作是多少度的圆心角所对
的弧长？
3. 1°的圆心角所对弧长是多少？
4. n°的圆心角呢？
半径为R圆的周长为 C 2R
O· 1° n°
R
可以看作是360°圆心角所对的弧长
1°的圆心角所对弧长是

2014年秋人教版九年级数学上册：24.4《弧长及扇形的面积》ppt课件

则450
S 的圆心角所对的扇形面积表示为扇形
S 扇形
45 R 360
1 R 2 360
2
则 10的圆心角所对的扇形面积表示为
则n0圆心角是所对的扇形面积表示为
S 扇形
nR 2 360
O n° A
B
即:n0圆心角的扇形面积公式表示为
O n°
A
B
注意: 1.扇形面积的大小由圆的大小（半径）、圆心角的度数决定. 2. 公式中 n 的意义． n 表示 1 °圆心角的倍数，它是不带单位的；
四课堂程序
6 π （1）半径为3的圆,周长是_________
1.学生回答
固旧知,为后面（2）半径为R的圆,周长是_________ C=2πR 巩学习作铺垫 4π （3）半径为2的圆,面积是_________ （4）半径为R的圆,面积是_________ S=πR2 设计意图 2.学生自主学习, 通过学生自主学习从学生自主阅读数学九年上册课本第二提问方式进行小结，让十四章圆第112页扇形面积部分学生养成学 —总结— 在小学我们已经学习过有关圆的面积公习培养自主学式，扇形与圆有怎样的关系，那么扇形面习的良好学习习惯，确积应怎样计算？它与圆的面积之间有怎样定本节课的学习目标。的关系呢？本节课我们将进行探索.
本节知识在中招考试中所占的分值:
2012年 2013年 4分 4分
一、教材分析
2.学情分析
在学习这节课知识之前,学生已经学习了与圆相关的概念,垂径定理,圆心角,圆周角定理及扇形的弧长公式等内容,是有一定的学科基础,同时学生也想继续探究新的知识.
3.学习目标：
(一) 知识目标 1). 了解扇形的概念 2) 理解n°的圆心角所对的扇形面积的计算公式 3) 会运用公式求扇形面积. (二) 能力目标 1)．经历探索扇形面积计算公式的过程，培养学生的探索能力． 2)．了解扇形面积公式后，能用公式解决问题，训练学生的数学运用能力． (三)情感与价值观目标 1)．经历探索扇形面积计算公式，让学生体验教学活动充满着探索与创造，感受数学的严谨性以及数学结论的确定性． 2)．通过用扇形面积公式解决实际问题，让学生体验数学与人类生活的密切联系，激发学生学习数学的兴趣，提高他们的学习积极性，同时提高大家的运用能力．

九年级上数学《24.4.1 弧长和扇形面积》课件

新课导入
在田径二百米比赛中，每位运动员的起跑位置相同吗？
不同
制造弯形管道时，怎样才能精确用料？
700mm
● A
B ● 700mm
● C
R=900m 100 m ° O
j
● D
教学目标
【知识与能力】
• 会计算弧长及扇形的面积. • 会计算圆锥的侧面积和全面积，并能用这些知识解决相关问题. • 知道圆锥的侧面积和扇形面积之间的关系.
例题
某传送带的一个转动轮的半径为10cm。（1）转动轮转一周，传送带上的物品A被传送多少厘米？（2）转动轮转1°，传送带上的物品A被传送多少厘米？（3）转动轮转n°，传送带上的物品A被传送多少厘米？
解：（1）转动轮转一周，传送带上的物品A 被传送 2 10 20cm ；
20 被传送 cm ； 360 18
（2）转动轮转1°，传送带上的物品A
20 n 被传送 n cm 。 360 18
（3）转动轮转n°，传送带上的物品A
举一反三
（1）弧长公式涉及三个量，弧长、圆心角的度数、弧所在的半径，知道其中两个量，就可以求第三个量。（2）当问题涉及多个未知量时，可考虑用列方程组来求解
扇形由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形．
（1）如图（1），这只狗的最大活动区域是圆的面积，即9π；（2）如图（2），狗的活动区域是扇形，扇形是圆的一部分，360°的圆心角对应的圆 1 面积，1°的圆心角对应圆面积的，即
1 n 9 ，n°的圆心角对应的圆面积 n 360 40 40 40
360
课堂小结
知识要点
R 扇形面积公式 . n°
在半径为 R 的圆中，n°的圆心角所对的扇形面积的计算公式为：

人教版九年级数学上册课件：24.4弧长和扇形面积(共19张PPT)

－
1353π6×0 152＝375π(cm2)．
9
能力提升
11．如图，图1是由若干个相同的图形(图2)组成的美丽图案的一部分．图2中，图形的相关数据：半径OA＝2 cm，∠AOB＝120°，则图2的周长为 83π ________cm.(结果保留π)
10
12．如图，在△ABC中，AC＝4，将△ABC绕点C逆时针旋转30°得到△FGC，则图43中π 阴影部分的面积为________.
第二十四章圆
弧长和扇形面积
第一课时
知识展示
知识点 1 弧长公式 n°的圆心角所对的弧长 l 的计算公式为 l＝n1π8R0 ，其中 R 为半径．核心提示：在弧长公式中，已知 l、n、R 中的任意两个量，都可以求出第三个量．知识点 2 扇形的定义由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形．
分析：先用扇形OAB的面积－三角形OAB的面积求出上面空白部分面积，再用扇形OCD的面积－三角形OCD的面积－上面空白部分的面
积7．，如即图可，求5分出．别阴以影【五部边分黑形的A龙面BC积D江．E的顶哈点尔为圆滨心，中以1考为半】径作一五个个圆，扇则图形中的阴影弧部分长的面是积之1和1为π__c___m___.，半径是18
2
知识点 3 扇形面积公式 (1)n°圆心角的扇形面积公式：S 扇形＝n3π6R02 ，其中 R 为半径． (2)弧长为 l 的扇形面积公式：S 扇形＝12lR，其中 R 为半径．【典例】如图，半径为 12 的圆中，两圆心角∠AOB＝60°、∠COD＝120°，连接 AB、CD，求图中阴影部分的面积．
cm，则此扇形的圆心角是__________度． 71．2．如如图图，，分在别△以AB五C中边，形AACB＝CD4E，的将顶△点AB为C圆绕心点，C逆以时11为针1半旋0 径转作30五°得个到圆△，FG则C，图则中图阴中影阴部影分部的分面的积面之积和为为________________.. 一列火车以6每．小时【28 江km的苏速度泰经州过10中秒通考过弯】道．如那么图弯，道所分对的别圆心以角为正___三_____角__度形．(π的取3.3个顶点为圆心， 98．．一已段知铁扇边路形弯所长道在成圆为圆半弧径半形为，4径，圆弧弧画长的为弧半6径π，，是则2三扇km形.段面积弧为_围_____成____.的图形称为莱洛三角形．若正三角分积析，：即先可用求形扇出形阴边影OA部长B的分面为的积面6－积三．c角m形，OAB则的面该积求莱出上洛面三空白角部分形6面π积的，再周用扇长形为OCD_的_面__积_－__三_角c形mOC. D的面积－上面空白部分的面

人教九上数学24.弧长与扇形面积公式课件

1.已知扇形的圆心角为120°，
半径为2，则这个扇形的面积
S扇形=
.
2.已知扇形面积为，圆心角为60°，则这个扇形的半径R=____．
比较扇形面积与弧长公式,用弧长表示扇形面积:
交
B
A
流
解
A
B
惑
O
O
例题示范
例2：如图、水平放置的圆柱形排水管道的截面半径是60cm，其中水面高 930 cm, 求截面上有水部分的面积。
实制造弯形管道时，要先按中心际线计算“展直长度”，再下料，
应试计算图所示管道的展直长度L.
用
(
+1400 )mm
思考
什么是扇形？
并回答：
n°
B
扇形
A
o
O
由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形．
交
流
展
A
n°
B
O
示
若设⊙O半径为R， n°的圆心角所对的扇形面积为S，则
B 则贴纸部分的面积为（）
A．
B.
曲苑杂坛
A
B C．
D．
C O
8. 已知等边三角形ABC的边长为a，分别以 A、B、C为圆心，以为半径的圆相切于点D、 E、F，求图中阴影
部分的面积S.
通过本节课的学习你有哪些收获？
作业：
1.课后作业：教材124--125页，习题 24.4第3、7题。
预习作业：见预习《圆锥侧面积》学案
有水部分的面积
= S扇- S△
A
0
D
B
C
例题示范
例2：如图、水平放置的圆柱形排水管道的截面半径是60cm，其中水面高30cm，

【课件】24.4弧长和扇形面积

∴AF＝ AB2＋BF2＝ 22＋12＝ 5.由平行四边形的性质，△FEC≌
△CGF，∴S△FEC＝S△CGF，∴S 阴影＝S 扇形 BAC＋S△ABF＋S△FGC－S 扇形 FAG
＝90×3π60×22＋12×2×1＋12×(1＋2)×1－90×π
×（ 360
5）2＝52－π4
16．(2014·昆明)如图，在△ABC 中，∠ABC＝90°，D 是边 AC 上的一点，连接 BD，使∠A＝2∠1，E 是 BC 上的一点，以 BE 为直径的⊙O 经过点 D.
(1)求证：AC 是⊙O 的切线； (2)若∠A＝60°，⊙O 的半径为 2，求阴影部分的面积．(结果
保留根号和π)
解：(1)连接 OD，∵OB＝OD，∴∠1＝∠BDO，∴∠DOC＝2 ∠1＝∠A.在 Rt△ABC 中，∠A＋∠C＝90°，即∠DOC＋∠C＝90 °，∴∠ODC＝90°，即 OD⊥DC，∴AC 为圆 O 的切线
3．已知扇形的圆心角为 45°，弧长等于π2 ，则该扇形的半径是 ___2__．
4．(2014·兰州)如图，在△ABC 中，∠ACB＝90°，∠ABC＝30
°，AB＝2.将△ABC 绕直角顶点 C 逆时针旋转 60°得△A′B′C，则点
B 转过的路径长为(B )
π A. 3
3π B. 3
2π C. 3
∠FAB＝90°.∵线段 AF 绕点 F 顺时针旋转 90°得线段 FG，∴∠
AFB＋∠CFG＝∠AFG＝90°，∴∠CFG＝∠FAB＝∠ECB，∴EC
∥FG.∵AF＝EC，AF＝FG，∴EC＝FG，∴四边形 EFGC 是平行四
边形，∴EF∥CG
(2)∵AB＝2，E 是 AB 的中点，∴FB＝BE＝12AB＝12×2＝1，

人教版初中数学课标版九年级上册第二十四章24.4弧长和扇形面积(共15张PPT)

扇形面积和弧长（复习课）
知识框架
1、半径为R的圆周长：C2R
2、半径为R，n°的圆心角所对的弧长为：l nR
180
3、半径为R的圆面积： S R2
4、半径为R，n°的圆心角所对的扇形面积为
S扇形
nR2
360
5、半径为R，弧长为 l 的扇形
面积为
S扇形
1 2
lR
l
A
B
R n° O
1、求扇形面积 2、求阴影部分的面积
中阴影部分三个小扇形的面积和为
。
等积法
练习3 如图，C是半径为1的⊙O上一点，A是⊙O外
一点，且OA=2，AB是⊙O的切线，BC//OA，连结
AC，则阴影部分面积等于
.
等积法
练习3 如图，C是半径为1的⊙O上一点，A是⊙O外
一点，且OA=2，AB是⊙O的切线，BC//OA，连结
AC，则阴影部5 cm,则图中三个扇形
（即阴影部分）的面积之和是
.
A
B
C
割补法（拼凑法）
变式2 如图，以四边形ABCD的顶点为圆心的⊙A、
⊙B、⊙C、⊙D两两不相交，且半径都是2 cm，则
图中阴影部分的面积是
.
B A
D
C
割补法（拼凑法）
练习如图方格纸中4个小正方形的边长均为1，则图
•
15、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。2021年8月2021/8/102021/8/102021/8/108/10/2021
•
16、提出一个问题往往比解决一个更重要。因为解决问题也许仅是一个数学上或实验上的技能而已，而提出新的问题，却需要有创造性的想像力，而且标志着科学的真正进步。2021/8/102021/8/10August 10, 2021

人教版九年级数学上册教学课件《24.4 弧长和扇形面积》 (共13张ppt)

人教版九年级数学上册教学课件《24. 4 弧长和扇形面积》（共13张ppt）
人教版九年级数学上册教学课件《24. 4 弧长和扇形面积》（共13张ppt）
学以致用
1、已知半径为4的扇形，圆心角的度数为 90°，
则它的面积为多少？ 4
2、已知扇形的弧长为30π，且这个扇形的半
径R=4．则这个扇形的面积为多少？ 60
人教版九年级数学上册教学课件《24. 4 弧长和扇形面积》（共13张ppt）
zxxk
如下图，由组成圆心角的两条半径和圆心角
所对的弧围成的图形是扇形。
B
B
弧圆圆心心角角
A
扇形
O A
人教版九年级数学上册教学课件《24. 4 弧长和扇形面积》（共13张ppt）
人教版九年级数学上册教学课件《24. 4 弧长和扇形面积》（共13张ppt）人教版九年级数学上册教学课件《24. 4 弧长和扇形面积》（共13张ppt）
人教版九年级数学上册教学课件《24. 4 弧长和扇形面积》（共13张ppt）
人教版九年级数学上册教学课件《24. 4 弧长和扇形面积》（共13张ppt）
例3：如图、水平放置的圆柱形排水管道的截面半径是0.6m，其中水面高0.3m，求截面上有水部分的面积。（结果保留小数点后两位）
思路分析：
有水部分的面积 = S扇- S△
弧长公式
l 若设⊙O半径为R， n°的圆心角所对的弧长为，
则
l
n R
180
A
B
n°
O
人教版九年级数学上册教学课件《24. 4 弧长和扇形面积》（共13张ppt）
人教版九年级数学上册教学课件《24. 4 弧长和扇形面积》（共13张ppt）

人教版九年级上册 24.4 弧长和扇形面积(共58张ppt)

例题——底面半径，母线，圆心角的关系
已知圆锥的底面半径为8cm，母线长20cm，求它的侧面展开图的圆心角．由侧面扇形的弧长等于底面周长可知：
这是底面半径、母线、圆心
角之间的固定关系，已知其
中任意两个都可以求第三个
n=144
．
所以圆锥的侧面展开图的圆心角是144°．
底面半径和母线的比与圆心角的关系底面半径和母线的比与圆心角有什么关系？
已知正三角形ABC的边长为a，分别以A、B、C为圆心，以 a/2为半径的圆相切于点D、 E、F，求图中阴影部分的面积S ．
圆锥的相关概念我们知道，圆锥是由一个底面和一个侧面围成的几何体，
我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线．
圆锥的侧面展开图是什么图形？扇形
圆锥的侧面积
如何计算半径为的 R 圆的面积呢？
圆面积可以看作是多少度圆心角所对的扇形的面积呢？
360°
思考怎么计算圆半径为R，圆心角n°的扇形面积呢？ 1°的圆心角所对的扇形面积是多少？
n°的圆心角所对的扇形面积是多少？
扇形面积公式圆心角为n°的扇形面积是
扇形面积如何求扇形的面积？
另一个公式比较扇形面积公式与弧长公式
答案：2π．
扇形面积计算综合
如图，直径 AB 为 8 的半圆，绕 A 点逆时针旋转 60°，此时点 B 到了点 B '，则图中阴影部分的面积是___________.
圆锥中的最短路径问题
圆锥的底面半径是 1，母线长是 4，一只蜘蛛从底面圆周上的一点 A 出发沿圆锥的侧面爬行一周后回到 A 点，则蜘蛛爬行的最短路径的长是________．
圆周长 C = 2πR
圆的周长可以看作多少度的圆心角所对的弧长？