2014年新版苏科版九年级上3.4方差课件

合集下载

苏教科版初中数学九年上册3.4 方差 PPT课件

3.4 方差
小结
谈谈你的收获.
课后作业课本P116-117页习题第1、2、3题.
B厂：40.0，40.2，39.8，40.1，39.9， 40.1，39.9，40.2，39.8，40.0．
由
，可知A厂生产的乒乓球直径的离散程度
较小，说明A厂生产的乒乓球质量比较稳定．
3.4 方差
例题在一次芭蕾舞比赛中，甲、乙两个芭蕾舞团都表演了
舞剧《天鹅湖》，参加表演的女演员身高（单位：cm）如下表所示：
甲 163 164 164 165 165 166 166 167 乙 163 165 165 166 166 167 168 168
哪个芭蕾舞团女演员的身高更整齐？
3.4 方差
归纳
在有些情况下，需要用方差的算术平方根，即
来描述一组数据的离散程度，并把它叫做这组数据的标准差．
3.4 方差
练习Байду номын сангаас
初中数学九年级(上册)
3.4 方差
3.4 方差
生活数学乒乓球的标准直径为40mm．质检部门对A、B两厂
生产的乒乓球的直径进行检测，从A、B两厂生产的乒乓球中各抽取了10只，测量结果如下（单位：mm）：
A厂：40.0，39.9，40.0，40.1，40.2， 39.8，40.0，39.9，40.0，40.1；
15
19
14
1（0 2）（为1方）便哪游段客台行阶走路，走需起要来重更新舒整服修？
14 16
17 18
上山的为小什路么．？对于这两段台阶路，在台
16 15
15 11
阶数不变的情况下，请你提出合理的整修建议．
甲路段乙路段
3.4 方差

3.4 方差-2020秋苏科版九年级数学上册课件(共21张PPT)

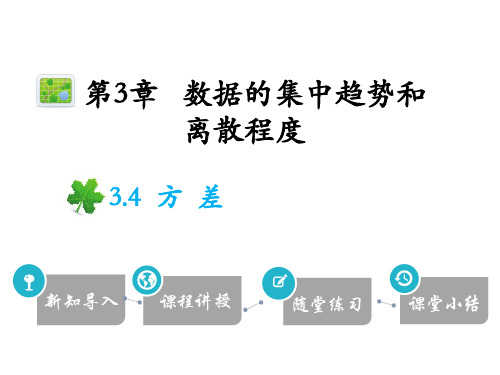
xA=
40.0
39.9
10
40.0
40.1
40(mm)
xB =
40.0
40.2
10
39.8
40.0
40(mm)
课程讲授
2 方差
问题1：两组数据的方差分别是：
sA2 =（40.0-40）2+（39.9-40）2+
+（40.010
40）2 +（40.1-
40）2
=0.012（mm2）
sB2 =（40.0-40）2+（40.2-40）2+
课程讲授
2 方差
练一练：
（中考·岳阳）现有甲、乙两个合唱队，队员的平
均身高为170 cm，方差分别是s2甲，s2乙，且s2甲>s2乙，则两个队的队员的身高较整齐的是( B )
A．甲队
B．乙队
C．两队一样整齐
D．不能确定
随堂练习
1.（中考·通辽）若数据10，9，a，12，9的平
均数是10，则这组数据的方差是( B )
+（39.8- 40）2 （40.0-40）2 10
=0.02（mm2）
由sA2＜ sB2，可以推断A厂生产的乒乓球直径的离散程度
较小，A厂生产的乒乓球质量比较稳定．
课程讲授
2 方差
例1 在一次芭蕾舞比赛中，甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位： cm)如表所示.
课程讲授
2 方差
练一练：
（中考·自贡）对于一组统计数据3，3，6，5，3.
下列说法错误的是( D )
A．众数是3
B．平均数是4
C．方差是1.6
D．中位数是6

江苏省盐城市大丰区城东实验初中苏科版九年级上册数学课件：34方差(共18张PPT)

哪个芭蕾舞团女演员的身高更整齐？
1．某地某日最高气温为12℃，最低气温为－7℃，该日气
温的极差是
．
2.一组数据1，2，3，4，5的平均数是3，则方差是．
一组数据3，6，9，12，15的方差是．
一组数据4，7，10，13，16的方差是，标准差是．
3.数据-1,3,0，x的极差是5，则x=
.
4.同班的两名同学在一年的各次数学考试成绩的平均分相
方差用来衡量一组数据的波动大小(即这组数据偏离平均数的大小),方差越大，说明数据离散程度越大，越不稳定.
例题
乒乓球的标准直径为40mm.质检部门各抽取了A、B两厂生产的10只乒乓球，对其直径进行检测，结果如下(单位：mm)： A： 40.0,39.9,40.0,40.1,40.2,39.8,40.0,39.9,40.0, 40.1 B： 40.0,40.2,39.8,40.1,39.9,40.1,39.9,40.2,39.8, 40.0.
, 85成绩2, , 85 1,
90成绩, , 90成绩2, , 90
系列 3, 类别 3,成绩
3
成系绩列2
系成列绩22,,类, 8别5 3, 1.8
系列
2, 类系别列43, 2.8系列 2
1, 类系别列41,
4
4.3
系列 1, 类别 3,
4.5
82
系列 1, 类别 2,
3.5
2 80
2.5
0
(3)通类过别 1统计图类，别 2你认为类挑别 3选哪一类位别 4比较合
差
计算出A、B两厂的方差.
解：
在有些情况下，需要用方差的算术平方根，即
来描述一组数据的离散程度，并把它叫做这组数据的标准差．

苏科版数学九年级上册3.4 方差教案

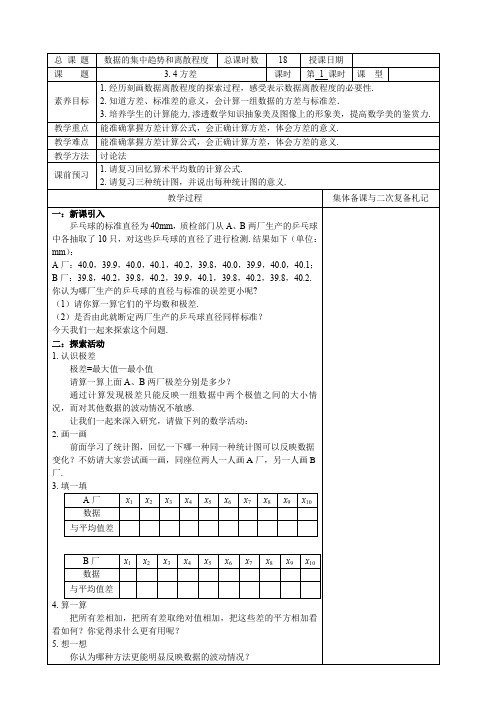
A厂：40.0，39.9，40.0，40.1，40.2，39.8，40.0，39.9，40.0，40.1；
B厂：39.8，40.2，39.8，40.2，39.9，40.1，39.8，40.2，39.8，40.2.
你认为哪厂生产的乒乓球的直径与标准的误差更小呢?
（1）请你算一算它们的平均数和极差.
（2）是否由此就断定两厂生产的乒乓球直径同样标准？
三：例题教学
例1．（1）在统计中，样本的方差可以近似的反映总体的（）．
A.平均状态B.离散程度C.分布规律D.最大值和最小值
（2）如果样本方差，那么这个样本的平均数为，样本容量为.
例2．对于数据3、2、1、0、-1,求它的极差和方差.
四：课堂小结
1.什么是方差？
2.说说你的疑问：
（1）为什么要这样定义方差？
能准确掌握方差计算公式，会正确计算方差，体会方差的意义.
教学难点
能准确掌握方差计算公式，会正确计算方差，体会方差的意义.
教学方法
讨论法
课前预习
1.请复习回忆算术平均数的计算公式.
2.请复习三种统计图，并说出每种统计图的意义.
教学过程
集体备课与二次复备札记
一：新课引入
乒乓球的标准直径为40mm，质检部门从A、B两厂生产的乒乓球中各抽取了10只，对这些乒乓球的直径了进行检测.结果如下（单位：mm）：
3.填一填
A厂
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10
数据
与平均
x5
x6
x7
x8
x9
x10
数据
与平均值差
4.算一算
把所有差相加，把所有差取绝对值相加，把这些差的平方相加看看如何？你觉得求什么更有用呢？

新苏科版九年级上册初中数学 3-4 方差教学课件

当堂小练
1.某地某日最高气温为12℃，最低气温为－7 ℃，该日
气温的极差是 19℃． 2.一组数据1，2，3，4，5的平均数是3，则方差是．2 一组数据3，6，9，12，15的方差是 1．8 一组数据4，7，10，13，16的方差是 1. 8
第十五页，共十八页。
当堂小练
3.设数据x1，x2，…，xn的平均数为则( ) D
第十七页，共十八页。
布置作业
请完成《少年班》P2-P3对应习题
第十八页，共十八页。
A厂
直径/mm
40.3
40.2 40.1
40.0
39.9
39.8 39.7
B厂
怎样用数量来描述这两组数据的离散程度呢？
第九页，共十八页。
新课讲解
数据
与平均数的差
x1 x2
40.0 39.9
0 －0.1
x3 x4 x5 x6 x7 x8 x9 x10
40.0 40.1 40.2 39.8 40.0 39.9 40.0 40.1 A厂
A．x ＝0 B．x1＋x2＋…＋xn＝0 C．x1＝x2＝…＝xn＝0 D．x1＝x2＝…＝xn
，x方差为s2，若s2＝0，
第十六页，共十八页。
拓展与延伸
现有甲、乙两个合唱队队员的平均身高为170 cm，
方差分别是s甲2，s乙2，且s甲2>s乙2，则两个队的队
员的身高较整齐的是( )B A．甲队 B．乙队 C．两队一样整齐 D．不能确定
第五页，共十八页。
新课讲解
知识点1 极差
乒乓球的标准直径为40mm。质检部门抽取了A厂生产的10只乒乓球，对其直径进行检测，结果如下（单位：mm）： 40.0 ， 39.9 ， 40.0 ， 40.1 ， 40.2 ， 39.8 ， 40.0 ， 39.9 ， 40.0 ， 40.1

苏科版九年级数学上册方差同步课件

思考与探索
A厂
数据
与平均数的差
x1 x2 x3
40.0 39.9 40.0
0 －0.1 0
x4 x5 x6 x7 x8 x9 x10
40.1 40.2 39.8 40.0 39.9 40.0 40.1
0.1 0.2 －0.2 0 －0.1 0 0.1
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
4.（202X•滨州）某芭蕾舞团新进一批女演员，她们的身高及其对应人数情况如表所示：
身高（cm） 163
164
165
166
168
人数
1
2
3
1
1
那么，这批女演员身高的方差为 2 cm2 ．
课堂小结极差
一组数据的最大值与最小值的差叫做极差.
方差
方差
公式：s2
1 n
(x1
x )2
( x2
x )2
166)2
(165
166)2 8
(168 166)2 2.5.
由s甲2 ＜ s乙2 可知，甲芭蕾舞团女演员的身高更整齐.
随堂演练
1.某地某日最高气温为12℃，最低气温为－7 ℃，该日气温的极差是 19 ℃ ．
2.一组数据4，7，10，13，16的方差是 18 ，标准差是 3 2 ．
3.（202X•锦州）甲、乙两名射击运动员参加预选赛，他们每人10次射击成绩的平均数都是9环，方差分别是s2甲＝1.2 ，s2乙＝2.4．如果从这两名运动员中选取成绩稳定的一人参赛，那么应选甲（填“甲”或“乙”）．
39.8，40.0，39.9，40.0，40.1；
40.1，39.9，40.2，39.8，40.0．

方差-苏科版九年级数学上册课件

2. 段巍和金志强两人参加体育项目训练，近期的5次测试成绩如下表所示，谁的成绩比较稳定？为什么？
测试次数 1
2
3
4
5
段巍
13 14
13
12
13
金志强 10 13
16
14
12
若 x1, x2,xn 的平均数为3，方差为6 求：3x1+2,3x2 +2,3xn +2 的平均数为：_____ 则：3x1+2,3x2 +2,3xn +2 的方差_____
1、样本方差的作用是（ D ） A、估计总体的平均水平 B、表示样本的平均水平 C、表示总体的波动大小 D、表示样本的波动大小，从而估计总体的波动大小
2.若1、2、3、x的平均数是2； 5、1、2、3、y 的众数是2，则1、2、3、x、y的极差是 2 。
3、计算下列各组数据的方差：（1） 6 6 6 6 6 6 6；（2） 5 5 6 6 6 7 7；
A 8.3 7.4 8.0 8.5 8.3 7.9 8.3 7.8 7.5 8.0
B 7.0 7.2 6.0 9.0 9.9 9.8 8.4 7.0 7.3 6.4
若让你选派最后的参赛选手，应选哪位？
1. 从甲、乙两种农作物中各抽取1株苗，分别测得它的苗高如下：（单位：cm）甲：9、10、11、12、7、13、10、8、12、8；乙：8、13、12、11、10、12、7、7、9、11；问：（1）哪种农作物的苗长的比较高？（2）哪种农作物的苗长得比较整齐？
请你用发现的结论来解决以下的问题：
已知数据a1，a2，a3，…，an的平均数为X，方差为Y标准差为Z。则
①数据a1+3，a2 + 3，a3 +3 ，…，an +3的平均数为-X---+--3--，方差为--Y-----，

方差课件苏科版数学九年级上册

根据以上信息，整理分析数据如下：
平均成绩/环中位数/环众数/环
甲
a
7
7
乙
7
b
8
方差 1.2
c
（1）写出表格中a，b，c的值；
平均成绩/环中位数/环众数/环
方差
甲
7
7
7
1.2
乙
7
7.5
8
4.2
根据以上信息：（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？
趋
位置的数或中间两数的平均数;
势 3.众数:出现次数最多的数;
离散
4.极
差:反映数据变化范围的大小,易受极端值影响;
程 5.方差:反映数据波动的大小;
度 6.标准差:反映数据波动的大小,且与数据
单位一致.
甲
85 90 90 95 95 85
乙
95 85 95 85 90
上述各偏差的平方和的大小还与什么有关？与考试的次数有关
甲
85
90
90
95
95
85
乙
95
85
95
85
90
所以要进一步用“各偏差的平均数”来衡量数据的稳定性.
3.4方差
方差用来衡量一组数据的波动大小(即这组数据偏离平均数的大小),方差越大，说明数据离散程度越大，越不稳定.
在有些情况下，需要用方差的算术平方根，即
来描述一组数据的离散程度，并把它叫做这组数据的标准差．
例1 计算下列两组数据的方差与标准差： (1) 1， 2， 3， 4， 5； (2)104，101，96，102，97。

苏科版九年级上册数学教学课件第3章数据的集中趋势和离散程度用计算器求方差

课程讲授
1 用计算器求方差
• (1)按开机键ON/C后，首先将计算器功能模式设定为为统计模式；
• (2)依次按键：MODE 1 ALPHA M+ 10 ▼ ▼ 7 ▼ ▼ 8 ▼ 6 ▼ 9 ▼ ▼ 6 ▼ ALPHA M+；(可以8 ▼ 6 的方式输入)
• (3) ALPHA 4 =8(平均数)； (4) ALPHA × =1(方差)；即小明射击的平均数 x =8，方差s2=1； (5)依次按键：MODE 1 ALPHA M+ 8 ▼ 4 ▼ 5 ▼ ▼ 8 ▼ 2
第3章数据的集中趋势和离散程度
3.5 用计算器求方差
新知导入课程讲授
随堂练习课堂小结
知识要点
用计算器求方差
新知导入
想一想： • 1.什么是方差？
方差是各个数据与平均数之差的平方的平均数
2.方差反映了一组数据的_离__散___程度.
课程讲授
1 用计算器求方差
问题1：甲、乙两人在相同条件下10次射击的成绩如下（单位：环）：甲：10，7，8，8，8，8，8，8，9，6；乙： 8，8，8，8，5，8，8，9，9，9 用计算器计算小这两组数据的平均数、方差，比较甲、乙两人射击成绩的稳定性.
甲、乙的方差分别是s2甲=2，s2乙=1.2
（2）根据计算结果比较两人的射击水平。 ∵s2甲＞s2乙，∴乙的射击水平高
课堂小结
用计算器求方差
一般具有统计功能的计算器都可以直接求出一组数据的平均数，而不能直接求出方差，要求方差，需要再做一次平方运算.
▼ 9 ▼ 3▼ ALPHA M+； (6) ALPHA 4 =8(平均数)； (7) ALPHA × =1.2(方差)

苏科版九年级上册数学方差课件

2
1
0
（2）5 5 6 6 6 7 7
s2 (5 6)2 (5 6)2 (6 6)2 (6 6)2 (6 6)2 (6 7)2 (6 7)2 4
7
7
x 256372 6 7
8
7
6
5
4
3
2
1
0
（3）3 3 4 6 8 9 9
s2 (3 6)2 (3 6)2 (4 6)2 (6 6)2 (8 6)2 (9 6)2 (9 6)2 48
根据这些数据估计，农科院应该选择哪种甜玉米种子呢？
甲、乙两种甜玉米的平均产量相差不大，由此可以
估计出这个地区种植这两种甜玉米，它们的平均产量相差不大.
比较上面两幅图可以看出，甲种甜玉米在各实验田的产量波动较大，乙种甜玉米在各实验田的产量较集中地散布在平均产量附近.从图中看出的结果能否用一个量来刻画呢？
+ 13.2
=
12.3（t）
说明甲、乙两个新品种平均每公顷的产量一样高.
下面我们来考察甲、乙两个新品种的稳定性.
说明甲、乙两个新品种平均每公顷的产量一样高.
下面我们来考察甲、乙两个新品种的稳定性.
s
2 甲
=
1 5
12.6
-
12.3
2

+
12.3
-
12.3
2
+
11.7
-
12.3
2
+
12.9
方差越大，数据的波动越大；方差越小，数据的波动就越小
分析甲、乙两种甜玉米的波动程度:
s2 甲= 1 [（7.65-7.54）2+（7.50-7.54）2+ …+（7.41-7.54）2）] ≈ 0.01， 10

3.4 方差 3.5 用计算器求方差课件(共26张PPT)苏科版数学九年级上册

感悟新知
2. 公式若n个数据x1，x2，…，xn的平均数为x，则方差s2＝n1［(x1－x)2＋(x2－x)2＋…＋(xn－x)2］.
感悟新知
3. 求方差的步骤第一步：先求原始数据的平均数；第二步：求原始数据中各数据与平均数的差；第三步：求所得各个差的平方；第四步：求所得各平方数的平均数.
2. 只有在数据的平均数相等或比较接近时，才能用方差比较数据的波动大小新知
例2 [三模·南通] 一组数据4，5，a，6，8 的平均数x＝6，则方差s2＝____2___．解题秘方：紧扣方差公式求方差.
视野拓展一般地，设n个数据x1，x2，…，xn的平均数为x，则方差
第3章数据的集中趋势和离散程度 3.4 方差 3.5 用计算器求方差
学习目标
利用极差分析数据方差用计算器计算方差
课时导入
在实际生产、生活中，我们不仅需要描述一组数据的集中趋势，而且还需要描述一组数据的离散程度.
知识点 1 利用极差分析数据
感悟新知
特别提醒 1. 极差能够反映数据的变化范围，在一定程度上描述
感悟新知
特别解读
利用计算器可以计算一组数据的平均数、方差. 使用计算器时要注意参考说明书，型号不同，按键顺序也可能不同.
感悟新知
例4 计算数据501，502，503，504，505，506，507， 508，509 的方差. 解题秘方：可以先算出平均数，再根据方差公式计算方差；也可以用计算器直接计算. 方法提醒用计算器可快速、准确计算. 根据数据的特征选择合适的计算方法，可使计算过程简化.
解法提醒
感悟新知
此题也可直接观察折线统计图，发现乙同学投篮成绩的波动比甲同学投篮成绩的波动小，所以乙同学投篮成绩比较稳定.

九年级数学上册第3章数据的集中趋势和离散程度3.4方差课件(新版)苏科版

问题2 在这次篮球联赛中,最后是九班和三班争夺这次篮球赛冠军, 赛前两个班的拉拉队都表演了啦啦操,参加表演的女同学的身高(单位:cm)分别是：九班 163 163 165 165 165 166 166 167 三班 163 164 164 164 165 166 167 167
哪班啦啦操队女同学的身高更整齐?
s九班 2
7 4
s三班2 2
求一组较大数据的方差，有如下简便计算方法：
1 任取一个基准数a
方法拓展
2 将原数据减去a，得到一组新数据
3 求新数据的方差
使用计算器说明：
1.不同品牌的计算器的操作步骤有所不同，操作时需要参阅计算器的使用说明书.
2.通常需要先按动有关键，使计算器进入统计状态；
生成绩平均水平相同；②乙班优秀的人数多于甲班
优秀的人数(每分钟输入汉字≥150个为优秀)；③甲班成绩的波动比乙班大.上述结论正确的有 ①②③ .
知识拓展若数据x1、x2、…、xn平均数为 x ,方差为s2，则
①对于数据x1-3，x2-3，x3-3，…，xn-3 平均数为 x-3 ，方差为 s2 .
4. SHIFT + S-Var + xσn + = ； 5. 将求出的结果平方，就得到方差 .
做一做
甲、乙两班举行电脑汉字输入比赛，参赛学生每分钟输入汉字的个数统计结果如下表：
班级参加人数中位数方差平均数
甲
55
乙
55
149
191
135
151
110
135
某同学分析上表后得出如下结论：①甲、乙两班学
②请利用方差公式分析甲、乙两种甜玉米产量的波动程度．两组数据的方差分别是：

苏科版初中九年级上册数学：方差_课件1(1)

39.9
39.9
39.8
39.8
39.7怎么描述这些数据相对39于.7 它们的平均数的
离散程度呢？
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
数据 40.0 39.9 40.0 40.1 40.2 39.8 40.0 39.9 40.0 40.1 A厂
与平
均数 0
的差
-0.1 0
0.1 0.2 -0.2 0 -0.1 0 0.1
7
8
8
8
9
10 6 10 6
8
哪个射击手稳定？为什么？甲稳定，甲的方差为0.4，乙的方差为3.2，故甲稳定
已知三组数据1、2、3、5；11、12、13、14、15
和3、6、9、12、15。 1、求这二组数据的平均数、方差。
平均数
方差
1、2、3、4、5
3
2
11、12、13、14、15 13
2
3、6、9、12、15
9
18
2、对照以上结果，你能从中发现哪些有趣的结论？想看一看下面的问题吗？
请你用发现的结论来解决以下的问题：已知数据a1，a2，a3，…，an的平均数为X，方差为Y。则 ①数据a1+3，a2 + 3，a3 +3 ，…，an +3的平均数为_X_+_3_ ，方差为 __Y__。 ②数据a1-3，a2 -3，a3 -3 ，…，an -3的平均数为 _X_-_3_ ，方差为_Y___ 。 ③数据3a1，3a2 ，3a3 ，…，3an的平均数为__3_X_，方差为__9_Y_ 。
方差是___6____
(3)人数相同的九年级甲、乙两班学生在同一次数学单元测试，班级平均分和方差如下x甲= x乙=80，S2甲 =240,S2乙=180,则成绩较为稳定的班级是__乙__班__

苏科版-数学-九年级上册-怎样理解方差的意义

初中-数学-打印版
怎样理解方差的意义
方差这个概念是刻画波动大小的一个重要的数字。

与平均数一样，仍然采用样本的波动大小去估计总体的波动大小的方法，方差越小则波动越小，稳定性也越好。

应当注意：
①方差公式s2＝中有差、方、和、均四步运算。

差是减法，方是平方，和是加法，均则为除法，就是求差、方的平均值，这也是“方差”的由来。

②方差的单位是已知数据的平方单位。

在有些情况下，需要用到方差的算术平方根，即为标准差。

它也是用来衡量一组数据的波动大小的重要的量，其单位和已知数据的单位是一致的。

初中-数学-打印版。