我国城市居民消费价格指数时间序列分析
我国全体居民消费水平的动态分析基于 1953-2011 年时间序列数 据

种, 外 文学 位论 文 1 7种 , 外 文会 议 论 文 3 7 4种 。我
国 研究 人 员也 有 大量 的 科研 成果 , 郭新 华 ( 2 0 1 2 1 、 刘
秋红 ( 2 0 0 7 ) 、 张 文爱 ( 2 0 0 7 ) 等 结 合相 关 模 型对 居 民
消 费结 构 的数量特 征进 行实 证分析 。[ 8 1 3 6 - 4 0 , [ 9 ] 4 9 - 5 3
在 对 消 费 水 平 的研 究 中 ,有 人 从 人 均 消 费 支 ( 一) 数 据收集 样本 数 据 主 要 来源 于 1 9 9 3年 一 2 0 1 2年 中 国统
出、 人 均收 入 、 人 均 储蓄 、 住 房价 格 以及 贷 款 利 率等
方 面建 立 变量 之 间 的关 系 , 『 l 】 ㈣ 通过 模 型分 析 提 出 政 府 应该 从提 高 居 民收 入水 平 、 降 低房 价 以及 推动 利 率 的市 场化 等 方面 提 高 居民 消费 水 平 ; 还 有 在 分
收 藕 日期 : 2 0 1 3 — 0 3 — 3 0
计年 鉴 。样 本 选 择 为 1 9 5 3年 到 2 0 1 1 年共 5 9期 数 据 。数据 包括 : 全 体居 民消 费水平 ( 元) 、 就业 人 员平
均 工资 ( 元) 、居民 人 民 币储 蓄存 款 年 底余 额 ( 亿
关 键词 : 时间序 列 ; 消费水 平 ; 人均 G D P 中 图分 类 号 : F 7 1 3 文献标 识码 : A 文章编 号 : 1 6 7 2 — 4 4 7 X( 2 0 1 3 ) 0 6 — 0 0 3 8 — 0 4
析 方法 上结 合 了主 成 分 分 析 方 法和 岭 回 归分 析 方
我国居民的消费水平时间序列分析及预测

我国居民的消费水平时间序列分析及预测作者:刘敏来源:《商场现代化》2014年第21期摘要:本文采用时间序列分析及预测的方法对我国居民的消费水平的发展趋势进行分析预测。
通过EViews7.0建立时间序列模型,选择合适模型进行拟合,并作出预测。
利用二次型模型和指数型模型,用最小二乘法进行参数估计。
利用拟合优度大小和拟合图相结合,选出最优模型及预测值。
关键词:消费水平;时间序列;二次型模型;指数型模型一、引言居民消费水平是指居民在物质产品和劳务的消费过程中,对满足人们生存、发展和享受需要方面所达到的程度。
通过消费的物质产品和劳务的数量和质量反映出来。
现在物价上涨,我国的消费水平和消费能力提高,对我国的经济发展有一定的推动作用。
所谓时间序列是按照时间的顺序排列的统计数据。
对时间序列进行观察,研究,找出一定的规律,预测将来的趋势。
在日常生活,生产中,时间序列随处可见,时间序列分析的应用领域很广泛。
本文将运用于经济领域。
二、样本与数据处理本文选用1993年-2012年的居民的消费水平年度数据作为样本。
(数据来源:中国统计年鉴2012)根据EViews7.0得到时序图,知样本总体呈现出不断上升的趋势。
进一步做单位根检验可得:P值为1,P值大于0.05,故不能拒绝原假设,即存在单位根,该序列不平稳。
由于序列不平稳,所以对样本数据进行差分处理。
经过一阶差分后的单位根检验结果中,P值为0.4349,P值大于0.05,故接受原假设,即存在单位根,该序列不平稳。
经过二阶差分后的单位根检验结果中,P值为0.01,P值小于0.05,故拒绝原假设,即不存在单位根,该序列平稳。
三、模型的选择1. 二次型模型的建立由于原序列经过二阶差分得到平稳序列可知,此序列可能为二次型序列,所以对其进行二次型模型处理。
(1)确定二次型模型由EViews7.0图对原序列的二次型拟合图由图1可得到二次型模型,但也需要对其残差自相关等分析,而后对残差进行模型拟合。
我国居民消费价格指数时间序列模型与预测

我国居民消费价格指数时间序列模型与预测摘要: 居民消费价格指数CPI 是具有重要经济意义的指标,它的增长具有一定的内在规律性,而大多数经济时间序列存在惯性或者说是迟缓性,通过对这种惯性的分析可以由时间序列的当前值和过去值对未来值进行预测。
本文利用了ARMA 模型对我国1993年8月—2014年10月的月度CPI 的时间序列数据进行建模分析,并利用所建立的模型对我国的居民消费价格指数进行了短期预测。
关键词: CPI ARMA 模型 时间序列 预测时间序列预测是通过对预测目标自身时间序列的处理来研究其变化趋势的。
即通过时间序列的历史数据揭示现象随时间变化的规律,将这种规律延伸到未来从而对该现象的未来作出预测。
文中所用的ARMA 模型是目前最常用的随机时间序列拟合模型。
其基本思想是:某些时间序列是依赖于时间t 的一组随机变量,构成该时序的单个序列值虽然具有不确定性。
但整个序列的变化却有一定的规律性,可以用相应的数学模型近似描述。
通过对该数学模型的分析研究,能够更本质地认识时间序列的结构与特征达到最小方差意义下的最优预测。
研究我国的居民消费价格指数CPI 的统计规律性和变动趋势,对于我国相关的经济发展政策有特别重要的意义。
本文利用我国1993年8月—2014年10月的月度CPI 历史数据为样本,利用在研究一个国家或地区经济和商业预测中比较先进适用的时间序列模型之一的ARMA 模型对样本进行统计分析,以揭示我国居民消费价格指数CPI 变化的内在规律性,并进行后期预测。
一、数据预处理1.平稳性检验 (1)时序图96100104108112116120124128255075100125150175200225250居民消费价格指数(上年同月=100)从上图可知,该数据有截距项,无明显变动趋势。
(2)ADF 单位根检验Null Hypothesis: CPI has a unit rootExogenous: ConstantLag Length: 12 (Automatic - based on SIC, maxlag=15)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -4.798075 0.0001 Test critical values: 1% level -3.4572865% level -2.87328910% level -2.573106*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(CPI)Method: Least SquaresDate: 11/26/14 Time: 22:25Sample (adjusted): 14 255Included observations: 242 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.CPI(-1) -0.032085 0.006687 -4.798075 0.0000 D(CPI(-1)) 0.168383 0.053134 3.169021 0.0017 D(CPI(-2)) 0.075710 0.053347 1.419191 0.1572 D(CPI(-3)) 0.043381 0.053218 0.815167 0.4158 D(CPI(-4)) 0.106993 0.053157 2.012767 0.0453 D(CPI(-5)) 0.059208 0.052698 1.123534 0.2624 D(CPI(-6)) 0.022702 0.052143 0.435374 0.6637 D(CPI(-7)) 0.077984 0.051391 1.517469 0.1305 D(CPI(-8)) 0.112575 0.051273 2.195607 0.0291 D(CPI(-9)) 0.028500 0.051586 0.552476 0.5812 D(CPI(-10)) -0.039258 0.051568 -0.761295 0.4473 D(CPI(-11)) 0.210599 0.051451 4.093188 0.0001 D(CPI(-12)) -0.481773 0.049770 -9.680053 0.0000C 3.261175 0.693266 4.704072 0.0000R-squared 0.474112 Mean dependent var -0.100000 Adjusted R-squared 0.444127 S.D. dependent var 0.690841 S.E. of regression 0.515070 Akaike info criterion 1.567081Sum squared resid 60.48765 Schwarz criterion 1.768920Log likelihood -175.6168 Hannan-Quinn criter. 1.648389F-statistic 15.81172 Durbin-Watson stat 2.004497Prob(F-statistic) 0.000000由检验结果可知,在5%的置信度水平下,p=0.0001<0.05, 通过单位根检验,数据平稳。
我国居民消费价格指数时间序列研究

t St ts i P o . — a itc r b
A u m e t d Dik y Fu l r t s t ts i 一 9 3 9 6 0 0 0 g ne ce - l e t s a itc e . 5 7 1 . 00 Te tc ii a a u s 1 1 v l s r t 1v l e : c e e 5 lv l e e 1 lv l 0 e e 一 2 5 5 8 .857 一 1 9 3 8 .468 一 1 6 4 5 . 1 80
摘 要 :0 1 以来, 国的居 民消 费价格 指数 不断创新 高 , 内通 胀压 力很 大 , 21 年 我 国 这主要 是 因 为 2 0 0 8年底 以来执 行 的
投 资拉 动 经 济 的 方 针 , 得 信 贷 投 放 大 量 增 加 , 动 性 过 剩 导 致 。 对 居 民 消 费 价 格 月 环 比 指 数 ( 月 一 i 0 时 间 序 列 进 行 使 流 上 0) 研 究 , 用 AR( ) 型进 行 实证 分 析 。结 果 说 明 了本 期 居 民 消 费 价 格 月环 比指 数 受 前 4期 居 民 消 费 价 格 月 环 比 指 数 的 影 使 P模 响 , 且 受 上 一 期 的 影 响 最 大 。这 反 映 出 通 胀 预 期 对 居 民 消 费 价 格 的 推 动 作 用 , 控 制 居 民 消 费 价 格 , 定 要 改 变居 民 的 并 要 一
2 消 费价格 指 数 时 间序 列 的特 征 分析
本 文 研 究 居 民 消 费 价 格 指 数 的 时 间 序 列 特 征 , 实 证 从 的 角 度 研 究 居 民 消 费 价 格 指 数 , 期 得 到 居 民 消 费 价 格 指 以 数 序 列 的 内在 关 系 。 本 文 采 用 自 2 0 0 1年 1月 至 2 1 0 1年 5 月 的居 民 消 费 价 格 月 环 比指 数 进 行 实 证 研 究 。 本 文 采 用 居 民 消 费 价 格 月 环 比 指 数 。 之 所 以采 用 居 民 消 费 价 格 月 环 比 指 数 , 为 这 更 具 有 实 际 意 义 。 如 果 使 用 因 同 比增 长 数 据 , 么 两 个 数 据 之 间 相 差 1 那 2个 月 , 样 的 比 这 较 不 具 有 实 时 意 义 。 目前 居 民 消 费 价 格 变 化 很 快 , 民 也 居 更 看 重 价 格 的 近 期 涨 幅 , 不 会 关 注 现 在 的 消 费 价 格 与 上 而
时间序列分析论文

关于居民消费价格指数的时间序列分析摘要本文以我国1997年4月至2014年4月间每月的烟酒及用品类居民消费价格指数为原始数据,利用EVIEWS软件判断该序列为平稳序列且为非白噪声序列,通过对数据一系列的处理,建立AR(1)模型拟合时间序列,由于时间序列之间的相关关系和历史数据对未来的发展有一定的影响,对我国的烟酒及用品类居民消费价格指数进行了短期预测,阐述该价格指数所表现的变化规律。
关键字:烟酒及用品类居民消费价格指数,时间序列,AR模型,预测引言一、理论准备时间序列分析是按照时间顺序的一组数字序列。
时间序列分析就是利用这组数列,应用数理统计方法加以处理,以预测未来事物的发展。
时间序列分析是定量预测方法之一。
基本原理:1.承认事物发展的延续性。
应用过去数据,就能推测事物的发展趋势。
2.考虑到事物发展的随机性。
任何事物发展都可能受偶然因素影响,为此要利用统计分析中加权平均法对历史数据进行处理。
该方法简单易行,便于掌握,但准确性差,一般只适用于短期预测。
时间序列分析是根据系统观测得到的时间序列数据,通过曲线拟合和参数估计来建立数学模型的理论和方法。
二、基本思想1. 拿到一个观测值序列之后,首先判断它的平稳性,通过平稳性检验,判断序列是平稳序列还是非平稳序列。
2.若为非平稳序列,则利用差分变换成平稳序列。
3.对平稳序列,计算相关系数和偏相关系数,确定模型。
4.估计模型参数,并检验其显著性及模型本身的合理性。
5.检验模型拟合的准确性。
6.根据过去行为对将来的发展做出预测。
三、背景知识CPI(居民消费价格指数),是反映与居民生活有关的商品及劳务价格统计出来的物价变动指标,通常作为观察通货膨胀水平的重要指标。
居民消费价格指数,是对一个固定的消费品篮子价格的衡量,主要反映消费者支付商品和劳务的价格变化情况,也是一种通货膨胀水平的工具。
一般来说,当CPI>3%的增幅时我们称为通货膨胀。
国外许多发达国家非常重视消费价格统计,美国、加拿大等国家都计算和公布每月经过季节调整的消费价格指数,以满足不同信息使用者的要求。
1994—2012年江苏省居民消费价格指数的时间序列分析

1994-2012年江苏省居民消费价格指数的时间序列分析班级:统计1班姓名:陈晶晶学号:09704122摘要居民消费价格指数(CPI)是宏观经济分析和决策,价格总水平监测和调控以及国民经济核算的重要指标。
本文利用1994-2012年江苏省居民消费价格指数的月度数据,运用Eviews 软件建立一个乘积季节模型,并用这个模型对江苏省未来的居民消费价格指数进行合理的预测。
关键词居民消费价格指数时间序列分析乘积季节模型预测分析一.引言居民消费价格指数(CPI)是用来测定一定时期内居民支付所消费商品和服务价格变化程度的相对数指标。
它既是反映通货膨胀程度的重要指标,也是国民经济核算中的缩减指标。
一般说来,当CPI>3% 的增幅时,我们称为通货膨胀;而当CPI>5% 的增幅时,我们把它称为严重的通货膨胀。
这一指标影响着政府制定货币、财政、消费、价格、工资、社会保障等政策,同时,也直接影响居民的生活水平及评价。
居民消费价格指数反映的市场价格信号真实.带动价格舆论导向正确,有利于改善价格总水平调控。
首先,它有利于维护正常的经济生活和市场价格信息秩序。
其次,有利于引导消费形成合理的消费价格,促进有效需求。
再次,它有利于综合运用价格和其他经济手段,实现价格总水平调控目标。
【1】所以,对该指标的分析与预测是非常有意义的工作。
本人在阅读与之有关的参考文献时,发现很多学者采用全国的CPI数据进行时间序列分析,就某个省份或某个城市的CPI数据研究很少,而且采用的模型也各不相同,所以本人就用江苏省1994-2012年的居民消费价格指数进行了时间序列分析。
二.数据描述和模型说明1.数据描述1994年1月——2012年3月江苏省居民消费价格指数如下表:(数据来源:/data/mac/jmxf_dq.php?symbol=320000)1月2月3月4月5月6月7月8月9月10月11月12月1994年123.9 125.9 122.6 121.4 119.8 120.6 122.3 123.4 125.5 125.6 124.9 121.61995年120.8 119.6 119.1 118.1 118.4 117.4 115.4 113.1 112.5 112.1 111.6 1121996年112.6 111.9 111.8 111.5 109.9 108.9 109.3 109.2 107.6 106.9 106.6 105.51997年104.2 104.3 103.1 103 102.4 101.8 101 100.8 100.9 100.1 99.7 99.41998年99.5 99.5 100.4 99.5 99.4 99 99 99.6 99.2 99.4 99.5 99.21999年98.9 98.8 98.1 97.6 97.9 98.7 99.3 98.9 98.9 99.3 99.2 99.32000年100.4 101.4 100.4 100.1 99.7 99.6 99.7 99.4 99.5 99.4 100.3 100.72001年101.6 100.4 101 101.9 102 101.4 101.4 101.2 100.3 100 99.4 99.32002年99.2 99.9 99.3 98.6 99 99.5 99.3 99.4 99.1 99 99.1 99.42003年100 100.2 100.6 100.7 100.1 99.6 100.3 101 101.2 102.2 103.2 103.22004年103.2 102.4 103.6 104.3 105.1 105.6 105.3 105.5 105.1 104.1 102.5 102.12005年102.2 104.4 103 102 101.5 101.4 101.8 101.3 101.4 102.1 102 102.32006年102.5 101.2 100.9 101.4 101.5 101.4 101.3 101.5 101.3 101 102 103.12007年102 102 102.5 102.7 103.1 104 105.2 106 105.9 106.2 106.5 105.62008年106.1 107.7 107.7 107.6 107.1 106.9 106 104.6 104.3 103.5 101.9 101.42009年101.4 99.5 99.6 98.9 98.8 98.3 98 98.8 99.3 99.6 100.6 102.12010年101.7 102.4 102.4 103.2 103.7 103.5 104.1 103.9 104.6 105.2 106.1 1052011年105.1 105.7 105.6 105.3 105.7 106.9 106.4 106 105.4 104.8 103.5 103.62012年103.9 102.9 103.5首先,做出序列时序图和自相关图,如下:X13012512011511010510095949698000204060810可以看出该序列是不平稳的序列,做1阶12步差分dx=d(x,1,12)得到如下时序图:DX4321-1-2-3-4949698000204060810可以看出差分后的序列是平稳序列。
我国居民消费价格指数ARCH模型实证分析

我国居民消费价格指数的ARCH模型实证分析【摘要】本文基于1999年1月---2012年6月的月度居民消费价格指数,建立自回归模型,对cpi的波动性进行检验,发现存在明显的arch效应。
在此基础上建立了arch(3)和garch(1,1)模型,解释了月度cpi的波动性,并且样本区间预测结果良好。
【关键词】中国居民消费者价格指数;自回归模型;arch模型;预测自1982年engle提出条件异方差模型之后,arch模型及其扩展模型被广泛运用于股票市场、货币市场、外汇市场等的研究,揭示股票价格、收益率、汇率等时间序列的波动性并加以预测。
居民消费价格指数cpi反映居民家庭购买代表性的消费品及服务水平价格变动情况,是衡量通货膨胀的主要指标。
已有学者运用arch模型对通货膨胀进行研究,本文在此基础上检验我国居民消费价格指数是否存在arch效应,并建立相应的模型实证分析。
一、arch模型理论简述1. arch(p)模型首先定义时间序列:;其中,是独立同分布的随机变量;且。
arch模型的基本思想是在以前信息集下,某一时刻一个干扰项的发生是服从正态分布。
随时间变化的方差是过去有限项干扰项平方的线性组合(即为自回归部分)。
这样就构成了自回归条件异方差模型。
2. garch(p,q)模型garch模型是arch模型的扩展形式,即在arch模型中加入了的自回归部分。
garch模型更适合描述高阶的条件异方差模型,因而应用更广泛。
二、数据选取及arch模型实证分析本文选取中国居民消费价格指数的月度数据,时间跨度为1999年1月——2012年6月,数据来自中国统计年鉴。
本文模型均在stata12.0中实现,预测部分使用eviews7.0。
首先,定义时间序列和,分别对居民消费价格指数序列和其一阶差分序列进行单位根检验。
由于的df统计量为-1.576,均大于1%、5%、10%显著性水平下的临界值,因此序列是非平稳的时间序列。
的df统计量-7.293小于1%的显著性水平下的临界值,可知序列是平稳序列。
时间序列分析在中国城镇居民消费水平中的应用

D。 一 一 0 2 7 t 】 0 1 5 Z 2+ . 3 D。 y + . 9 D。y
其 进行 二阶 差分使 其平 稳 . AD 其 F检验 如表 1 . 都 小 于 1 , , O 的 临 界 值 , 以 该 二 阶 差 分 % 5 1 所
1 2 时 间序 列模 型 的 建 立 .
水平 的值 进行 建 模 , 其 作 为 时 间序 列 , 立 预 测 将 建 模 型. 为了验 证模 型 的正确 性 , 1 5 —2 0 把 9 2 0 7年 的 数据 参与 建 模 , 0 8年 的值 用 于检 验 模 型 的拟 合 20 效果 , 后 进 行 2 0 —2 1 最 0 9 0 1年 的预 测 ( 据来 源 : 数 中国经济信 息 网综合 年 度库 ) .
型 , 用 该模 型 对 当前 值 和 未 来 值 作 出预 测 , 到 误 差 较 小 、 期 预 测 较 为 满 意 的结 果 . 并 得 短
关 键 词 :时 间 序 列 分 析 ; 镇 居 民 消 费 水 平 ; MA 模 型 ; 测 城 AR 预
中 图 分 类 号 : 1. 1T 1 4 02 1 6 ; B 1 文献标志码 : A 文 章 编 号 :1 7 —9 7 ( 0 1 0 — 0 7 2 6 1 4 6 2 1 ) 2 0 3 —0
3 8
周 口师范学 院学 报
21 0 1年 3月
从 图 3可 以看 出残 差 对 应 的பைடு நூலகம்自相 关 和偏 自相
A O a I
I I 暖 l 图 I I l I
p a c r lt n l or ao e i
I l 匿 I I 霹 I l I l E I I I 匿 1 f I I 圈
基于时间序列的居民消费价格指数分析(全文)

基于时间序列的居民消费价格指数分析一、居民消费价格指数居民消费价格指数,即CPI(Consumer Price Index),是一个反映居民家庭一般所购买的消费商品和服务价格水平变动情况的宏观经济指标。
其衡量的是一定数量具代表性的商品或服务项目的价格随时间变动而变动的程度,通常这一指数也被用于反映居民家庭购买消费商品及服务的价格水平的变动情况。
因此,在考察一国或某一地区宏观经济运行进展状况时,其居民消费价格指数是必不可少的重要数据从指标。
这一指标不仅反映一定时期内居民购买的商品和服务价格变动,还体现了在不同时期居民生活费用的变动状况。
同时,居民消费价格指数还被广泛应用于判定经济体是否存在通货膨胀,故此,CPI也是市场经济状态的晴雨表。
所以,从宏观治理层面讲,居民消费价格指数是各级政府部门了解居民消费价格状况,研究制定价格政策、工资政策、货币政策,以及为国民经济核算的重要依据和关键指标。
从投资层面讲,居民消费价格指数是企业增加或减少投资的重要决策依据。
从就业层面看,CPI是政府和企业调整雇员工资和津贴的重要指标。
本文用过Eviews软件建立RIM模型,对我国近年来居民消费价格指数的统计数据进行分析和估量。
二、时间序列模型对居民消费价格指数的分析(一)应用模型概述1.时间序列模型。
RM模型是目前应用较为广泛的平稳时间序列分析模型,模型具体可分为:R模型、M模型、RM模型。
RM模型表达式如下:Xt=φ0+φ1Xt-1+φ2Xt-2+...+φpXt-p+εt-θ1εt-1-...-θqεt-qφp≠0,θq≠0E(εt)=0,Vr(εt)=σ2ε,E(εtεs)=0,s=tExsεt=0,?坌s引进延迟算子,RM(p,q)模型简记为:φ(B)xt=θ(B)εt,其中:φ(B)=1-?渍1B-…-?渍pBp。
为p阶自回归系数多项式;θ(B)=1-θ1B-…-θqBq为q阶移动平均系数多项式。
令q=0,我们就从RM(p,q)模型得到了R(p)模型。
我国居民消费价格指数(CPI)影响因素的分析

一、研究背景及意义1.研究背景CPI 是度量通货膨胀的一个重要指标。
通货膨胀是物价水平普遍而持续的上升。
CPI 的高低可以在一定水平上说明通货膨胀的严重程度。
近年来,我国的通货膨胀问题非常值得重视。
一方面,多年来我国强烈的固定资产投资需求冲动,使经济实际增长率高于潜在增长率。
过高的增长需求必然伴随信贷货币的超量发行从而构成通胀压力;另一方面,有数据表明中国1990年的货币总量为1.53万亿元,2011达到89.56万亿元,是1990年的58.5倍。
近年来我国央行为缓解人民币升值过快压力给经济带来的问题不得不大量投放人民币进行对冲,现阶段我国面临的通胀压力仍不容小觑。
2.研究意义CPI 是一个滞后性的数据,但它往往是市场经济活动与宏观经济政策的一个重要参考指标,长期以来,随着人们对通胀成因以及市场形势认识的深入与发展,CPI 稳定成为了最重要的宏观经济目标之一。
因此,为了让我国消费者价格指数在合理预期内稳定变动,了解分析其影响因素并通过相关政策与手段加以控制是至关重要的。
本文意在通过相关数据处理与分析,对变量因素之间的相关关系进行一定的论证,为我国CPI 影响因素的分析提供一定的理论基础。
二、我国CPI 现状整理数据我们可以发现,近20年来,物价飞涨问题一直困扰着我国政府,也是国内外关注和研究的焦点。
1998年-2003年我国CPI 变动相对平稳,至2007年-2018年全球金融危机爆发之前我国使用了“从紧的货币政策”,金融危机爆发后我国的通货膨胀问题逐渐开始严重,当年居民消费价格指数达到了493.6(1978=100)。
2008年,为了应对全球性的金融危机,我国采取宽松的货币政策更是让通货膨胀进一步加剧,当年达到522.7。
金融危机过后,随着国家总体经济状况的发展,中国近几年CPI 指数增长率相对稳定,如2015年12月CPI 为101.6,同比增长1.6%;2014年12月CPI 为101.5,同比增长1.5%;2013年12月CPI 为102.5,同比增长2.5%;2012年12月CPI 为102.5,同比增长2.5%,CPI 变动处于一个相对平稳的状态。
我国城镇居民消费价格指数、人均可支配收入与消费水平关系的实证分析

我国城镇居民消费价格指数、人均可支配收入与消费水平关系的实证分析作者:林红菊来源:《现代经济信息》 2018年第23期要:本文在计量经济学的基础上,基于1978-2015 共35 年的相关数据,运用eviews 统计软件,分析我国城镇居民消费水平与城镇居民消费价格指数、城镇居民家庭人均可支配收入的关系。
结果表明:我国城镇居民消费价格指数、人均可支配收入与消费水平之间存在长期协整关系。
我国城镇居民消费价格指数增加1%,城镇居民消费水平长期上将增长0.412%,短期上增长0.488%;城镇居民人均可支配收入增加1%,城镇居民消费水平长期上将增长0.781%,短期上增长0.716%。
关键词:消费水平;平稳及协整;误差修正中图分类号:F062.5 文献识别码:A 文章编号:1001-828X(2018)034-0010-02消费作为拉动经济增长的三驾马车之一,对国民经济的影响有着不可替代的作用。
影响我国城镇居民消费结构的因素很多,如城镇居民可支配收入、消费物价指数、GDP 增长速率、利率水平等。
通过利用时间序列、计量经济等方法建立经济模型,实证分析我国城镇居民消费水平的现状及预测其发展趋势,以保持我国经济的持续发展。
本文基于1978 年-2012 年35 年间的相关数据,建立相应的计量经济学模型,研究我国城镇居民消费物价指数(1978=100)、城镇居民家庭人均可支配收入与城镇居民消费水平之间的关系,包括平稳性、协整、误差修正等方面的研究。
一、变量定义与模型设定( 一) 被解释变量定义过程由统计年鉴数据显示,1978 年改革开放之初我国的城镇居民消费水平为405 元,2016 年已经上升为29295 元。
居民的消费水平很大程度上受整体经济状况的影响。
经济扩张时期,居民收入稳定,GDP 增加,居民的消费支出增加,消费水平较高。
为了更好地探究我国城镇居民的消费水平,对我国城镇居民消费水平的影响因素建立模型研究。
中国CPI指数的时间序列分析
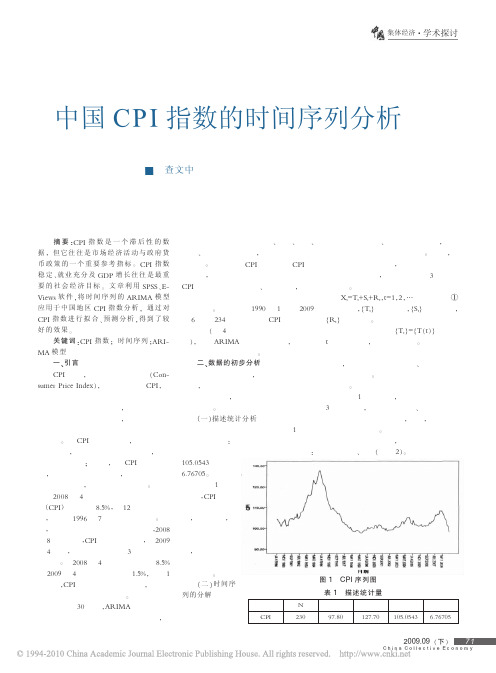
Xt=Tt+St+Rt,t=1 ,2 ,… ① 其 中 , {Tt} 是 趋 势 项 , {St} 是 季 节 项 , {Rt} 是随机项 。
通 常 认 为 趋 势 项 {Tt}={T (t )} 是 时 间
CPI 指 数 进 行 拟 合 、 预 测 分 析 , 得 到 了 较
好的效果。 关 键 词 :CPI 指 数 ; 时 间 序 列 ;ARI-
自相关 。 自 相关程 度 由 自 相 关 系 数 γk 度 量 , 表示时间序列中相隔 k 期 的观测值 之
xt, 在给 定 xt-1,xt-2, …,xt-k+1 的 条 件 下 ,xt 与 xt-k 之间的条件相关关系 。 其相关程度 用偏自相关系数 覬kk 度量 , 有 -1≤覬kk≤1 。
内外的学者将其运用于经济 、 旅游 、 能源 、 医 学 、环 境 等 许 多 领 域 ,出 现 了 一 批 较 好 的 成 果 。 以 每 月 的 CPI 指 数 构 成 CPI 指 数序列, 运用时间序列的建模方法对该
都 表 现 出 趋 势 性 、季 节 性 和 随 机 性 ,或 者 只表现出三者中的其二或 其一 。 这样 , 可 以认为每个时间序列 , 或经过适当 的函数 变换的时间序列 , 都可以分解 成 3 个部分 的叠加 。
CPI N 230
2008 年 4 月 份 中 国 居 民 消 费 价 格 指 数 (CPI)同比上涨 8.5% , 为 12 年以来的新 高 ,超过了 1996 年 7 月份创下的高点 。 然 而 ,由于受全球性的金融危机的影响 ,2008 年 8 月份开始 ,CPI 指数一路下滑 ,到 2009 年 4 月份 , 更是出现了连续 3 个月的同比 负增长 。 从 2008 年 4 月份的同比上涨 8.5% 到 2009 年 4 月份的同比下降 1.5%, 短短 1 年时间 ,CPI 指数如此大幅的波动 , 引发了
关于居民消费价格指数的时间序列分析论文

关于居民消费价格指数的时间序列分析摘要本文以我国1997年4月至2014年4月间每月的烟酒及用品类居民消费价格指数为原始数据,利用EVIEWS软件判断该序列为平稳序列且为非白噪声序列,通过对数据一系列的处理,建立AR(1)模型拟合时间序列,由于时间序列之间的相关关系和历史数据对未来的发展有一定的影响,对我国的烟酒及用品类居民消费价格指数进行了短期预测,阐述该价格指数所表现的变化规律。
关键字:烟酒及用品类居民消费价格指数,时间序列,AR模型,预测引言一、理论准备时间序列分析是按照时间顺序的一组数字序列。
时间序列分析就是利用这组数列,应用数理统计方法加以处理,以预测未来事物的发展。
时间序列分析是定量预测方法之一。
基本原理:1.承认事物发展的延续性。
应用过去数据,就能推测事物的发展趋势。
2.考虑到事物发展的随机性。
任何事物发展都可能受偶然因素影响,为此要利用统计分析中加权平均法对历史数据进行处理。
该方法简单易行,便于掌握,但准确性差,一般只适用于短期预测。
时间序列分析是根据系统观测得到的时间序列数据,通过曲线拟合和参数估计来建立数学模型的理论和方法。
二、基本思想1. 拿到一个观测值序列之后,首先判断它的平稳性,通过平稳性检验,判断序列是平稳序列还是非平稳序列。
2.若为非平稳序列,则利用差分变换成平稳序列。
3.对平稳序列,计算相关系数和偏相关系数,确定模型。
4.估计模型参数,并检验其显著性及模型本身的合理性。
5.检验模型拟合的准确性。
6.根据过去行为对将来的发展做出预测。
三、背景知识CPI(居民消费价格指数),是反映与居民生活有关的商品及劳务价格统计出来的物价变动指标,通常作为观察通货膨胀水平的重要指标。
居民消费价格指数,是对一个固定的消费品篮子价格的衡量,主要反映消费者支付商品和劳务的价格变化情况,也是一种通货膨胀水平的工具。
一般来说,当CPI>3%的增幅时我们称为通货膨胀。
国外许多发达国家非常重视消费价格统计,美国、加拿大等国家都计算和公布每月经过季节调整的消费价格指数,以满足不同信息使用者的要求。
居民消费价格指数的时间序列模型分析

居民消费价格指数的时间序列模型分析标题一:研究背景与目的居民消费价格指数(CPI)是一个衡量消费者购买一定量的商品和服务时所支付的价格变动的指标。
它是一个经济学中很重要的数据,因为CPI的变化会对通货膨胀率和货币政策产生影响。
本论文旨在分析CPI的时间序列模型,以了解CPI的变化趋势及其对经济的影响。
标题二:时间序列概述时间序列是指按顺序排列的时间间隔内的数据。
在经济学中,时间序列模型是一种分析时间序列数据的方法,用于预测未来的趋势和变化。
时间序列中的变量通常具有时间相关性,因此时间序列模型可以捕捉到数据中的趋势和周期性变化。
我们将运用时间序列模型来分析CPI指数。
标题三:时间序列模型本论文采用的时间序列模型是ARIMA模型。
ARIMA是一种常用的时间序列预测模型,它可以分析数据的趋势、季节性、周期性等,以预测未来的趋势和变化。
ARIMA模型可以表示成ARIMA(p, d, q),其中p是自回归项,d是差分阶数,q 是移动平均项。
标题四:CPI的时间序列分析通过对CPI数据的时间序列分析,可以得出以下结论:1. CPI指数存在明显的季节性和周期性变化。
在经济好转时期,CPI指数通常会上升,而在经济衰退时期则会下降。
2. CPI的趋势通常是上升的,不断增长的经济条件下,CPI指数也会随之增长。
3. CPI指数受到供求关系的影响,当供给不足或需求增加时,价格也会上升。
随着供给增加或需求下降,价格也会下降。
4. CPI指数与通货膨胀率之间存在相关性。
当CPI指数上升时,通货膨胀率也会上升。
5. CPI指数可能受政府干预的影响。
政府对通货膨胀率的控制以及货币政策的实施都会影响CPI指数的变化。
标题五:CPI的影响因素分析CPI的影响因素有很多,我们从以下几个方面来分析:1.货币供应量:当货币供应量增加时,消费者购买力会增强,需求上升,价格也会上升,从而导致CPI指数上升。
2.生产成本:生产成本上升会导致生产者的价格上升,然后从生产者的价格上升反过来作用到消费者价格上升,CPI指数上升。
时间序列组合预测模型在我国居民消费价格指数中的应用

时间序列组合预测模型在我国居民消费价格指数中的应用时间序列组合预测模型在我国居民消费价格指数中的应用摘要:时间序列分析是经济学中常用的一种预测方法,其在经济领域中的应用已经得到广泛认可。
本文将探讨时间序列组合预测模型在我国居民消费价格指数中的应用,以期提供一种有效的预测方法,为我国的宏观调控提供参考依据。
一、引言居民消费价格指数是衡量居民消费水平和通货膨胀程度的重要指标,对于评估经济发展和制定宏观经济政策具有重要作用。
然而,受到多种因素的影响,我国居民消费价格指数具有复杂性和不确定性,使得准确预测成为一项具有挑战性的任务。
二、时间序列分析时间序列分析是一种基于时间数据的预测分析方法,其核心思想是将过去的观测数据应用于预测未来的数据。
时间序列分析有几个基本假设:1. 时间序列数据存在一定的模式和规律;2. 这些模式和规律在未来一段时间内仍然有效;3. 这些模式和规律与其他因素的影响相对较小。
因此,时间序列分析可以通过对已有数据的拟合,推断出未来的数据。
三、时间序列组合预测模型时间序列组合预测模型是一种将多个时间序列预测模型进行组合的方法,以提高预测的准确性和可信度。
常用的时间序列组合预测模型有加权平均法、回归组合法和模型选择法等。
1. 加权平均法加权平均法是一种简单而常用的时间序列组合预测模型,其基本思想是对多个预测模型的预测结果进行加权平均。
不同的预测模型可以根据其预测准确性和可靠性进行加权。
加权平均法的优点是简单易行,但在加权分配上存在一定的主观性。
2. 回归组合法回归组合法是一种基于回归分析的时间序列组合预测模型,其通过建立多个时间序列变量之间的回归关系,对未来的数据进行预测。
回归组合法的优点是能够考虑到不同变量之间的相互关系,具有较好的预测效果。
3. 模型选择法模型选择法是根据预测模型的准确性和稳定性来选择最优的预测模型。
通过对比不同的预测模型,选择最适合当前数据的模型进行预测。
模型选择法的优点是能够避免人为主观性的干扰,选择最具准确性的预测模型。
居民消费价格指数的时间序列分析

居民消费价格指数的时间序列分析摘要:时间序列分析是一种根据动态数据揭示系统动态结构和规律的统计方法。
本文以我国2007年1月至2011年4月居民消费价格指数为研究对象,基于居民消费价格指数存在明显的非平稳性和季节性特征,运用自回归移动平均季节模型进行建模分析,并利用SPSS建立了居民消费价格指数时间序列的相关关系模型,并对其进行预测,取得较好的效果。
关键词:居民消费价格指数SPSS软件时间序列分析预测、引言(一)问题的基本情况及背景居民消费价格指数的调查范围和内容是居民用于日常生活消费品的全部商品和服务项目价格。
包括食品、烟酒及用品、衣着、家庭设备用品及维修服务、和个人用品、交通和通讯、娱乐教育文化用品及服务、居住等八大类商品及服务项目价格。
既包括居民从商店、工厂、集市所购买的价格,也包括从购买的价格。
该指数以实际调查的综合平均单价和根据住户调查有关资料确定的权数,按加权算术平均公式计算。
全国居民消费价格指数是反映居民家庭购买生活消费品和支出服务项目费用价格变动趋势和程度的相对数。
其目的在于观察居民生活消费品及服务项目价格的变动对城乡居民生活的影响,为各级党政领导掌握居民消费状况,研究和制定居民消费价格政策、工资政策以及为新国民经济核算体系中有消除价格变动因素的不变价格核算提供科学依据。
居民消费价格指数还是反映通货膨胀的重要指标。
当居民消费价格指数上升时,表明通货膨胀率上升,消费者的生活成本提高,货币的购买能力减弱;相反,当居民消费价格指数下降时,表明通货膨胀率下降,亦即消费者的生活成本降低,货币的购买能力增强。
居民消费价格指数的高低直接影响居民的生活水平,因此,准确的分析并及时的对居民消费价格指数做出合理的预测,对国家制定相应的经济政策,实行宏观调控,稳定物价,保证经济的增长平稳发展具有重要意义。
(二)问题的提出时间序列是指同一种现象在不同时间上的相继观察值排列而成的一组数字序列。
时间序列预测方法的基本思想是:预测一个现象的未来变化时, 用该现象的过去行为来预测未来。
居民消费价格指数的时间序列模型分析

居民消费价格指数时间序列模型分析内容摘要由于去年来我国居民消费价格指数(CPI)出现了持续较快上涨,而CPI对经济生活各个方面都有重要影响,因此本文选用时间序列模型来分析其变化规律,以期能够根据其规律对经济生活中某些决策起到某些借鉴作用。
本文首先描述性分析了我国CPI数据变动情况,然后用乘积季节模型来拟合该数据变动规律,并根据拟合模型作了短期预测。
从模型拟合效果和预测结果看,乘积季节模型能够较好地说明CPI数据变动规律。
关键词:居民消费价格指数(CPI)乘积季节模型预测相关图ABSTRACTBecause the CPI (Consumer Price Index) has been going up increasingly and sharply since last year and it' s very important for the people in all the aspects of the economy life, this text selects the time series model in order to draw up the regulations in the data of the CPI and make use of them in the decision-makings・ First of all, this text described fluctuations of the CPI in China, fitted the regulations with the multiplicative seasonal model and forecasted the short-term CPI with the mode1・ Compared with the estimation and the forecast in the model, the multiplicative seasonal model made a good descriptionof the regulations and trends about the data・KEY WORDS: Consumer Price Index Multiplicative Seasonal ModelsForecastCorrelation Function Charts---------------------------------------------- 1页一、居民消费价格指数概念和经济意义 ------------------------------------ 1页二、数据结构检验及初步分析 -------------------------------------------- 2页三、季节调整模型历史和建模思想 ---------------------------------------- 3页四、我国CPI数据建模和预测-------------------------------------------- 4页(一)、数据平稳化检验(二)---------------------------------------------------------------- 、数据平稳化过程--------------------------------------------------------------- 5页(三)------------------------------------------------------------------- 、建立乘积季节模型------------------------------------------------------------ 7页(四)------------------------------------------------------------------- 、预测和分析------------------------------------------------------------------ 8页结语--------------------------------------------------------------------------------------------------- 9页(一)-------------------------------------------------- 预测合理性和可行性9页(二)-------------------------------------------------------- CPI预测意义9页(三)------------------------------------------------------ 预测中存在问题9页参考文献10页居民消费价格指数时间序列模型分析居民消费价格指数不仅是反映通货膨胀首要指标,也是及居民生活水平密切相关重要指数,该指数被用来监控和预警宏观经济运行状态,并作为重要依据来调整我国财政政策和货币政策。
居民消费价格指数的时间序列模型分析

居民消费价格指数的时间序列模型分析一、居民消费价格指数居民消费价格指数(CPI),作为一种常用的总体价格水平指标,是反映居民购买并用于消费商品和服务项目价格水平的变化趋势和变动幅度的统计指标,用来度量消费者在购买商品和劳务时的花费。
价格稳定对于一个国家来说至关重要,一个稳健运行的市场系统要求价格能够准确、迅速地传递稀缺资源的信息,并且通过价格机制来调节资源配置。
居民消费价格指数还是衡量通货膨胀的重要指标。
研究居民消费价格指数的发展特征及其未来发展趋势,使价格水平稳定在有利于经济发展的合理水平是十分必要的。
时间序列分析就是一种根据动态数据揭示系统动态结构和规律的统计方法,其基本思想是根据系统的观测数据,建立能够比较精确地反应时间序列中所包含的动态依存关系的数学模型,并借此对系统的未来行为进行预测。
因此,由时间序列模型分析居民消费价格指数的发展变化趋势,并对短期内的居民消费价格进行预测具有重要的意义。
二、居民消费价格指数的时间序列模型分析时间序列分析是一种应用广泛的数量分析方法,它主要用于描述和探索事物随时间变化的数量规律性。
时间序列分析模型主要有ARMA 模型和ARIMA模型。
ARMA模型只能用于平稳时间序列的分析。
然而,在实际的经济和生活中绝大部分的时间序列是非平稳的,但对这些非平稳的时间序列经过差分后就会显示出平稳时间序列的性质,这时称非平稳时间序列为差分平稳时间序列。
对差分平稳时间序列可以用ARIMA模型拟合。
1.数据的收集及平稳性检验选取1996年1月~2013年11月我国居民消费价格指数为样本数据(数据来源于《中国统计年鉴》及东方财富网),运用EViews软件对数据进行处理。
研究时间序列之前,首先要对其平稳性和随机性进行检验,目的是对平稳且非随机序列进行研究。
由图1时序图可以看出:1996~1998年居民消费价格指数大幅下降;在1998~2003年间,居民消费价格指数小幅度上下震荡;2004年至今,大幅度波动震荡。
居民消费价格指数的时间序列分析及预测

关 键 词 :时 间 序 列 ;CPI;趋 势 ;预 测
中 图 分 类 号 :F126;C913
文 献 标 识 码 :A
文 章 编 号 :1002-6487(2009)04-0117-02
1 我国居民消费价格指数的现状
居 民 消 费 价 格 指 数 (Consumer Price Index,CPI)是 一 个 反映居民家庭一般所购买的消费商品和服务价格水平变动 情况的指标。 一般说来当 CPI>3%的增幅时,我们称为通货膨 胀;而当 CPI>5%的增幅时,我们把他称为严重的通货膨胀。 如 果消费价格指数升幅过大,表明通胀已经成为经济不稳定因 素,央行会有紧缩货币政策和财政政策的风险,从而造成经济 前景不明朗。
2 趋势模型的选择(统计学时间数列分解模型)
为 了 对 我 国 CPI 的 变 化 有 更 加 全 面 和 深 入 的 把 握 和 认 识, 现观测从 1990~2007 年居民消费价格指数的全部数据, 见表 1。
由以上数据可以看出,因为居民消费价格指数受到如经 济增长、特别是国家宏观货币政策等因素的影响,分析我国 居民消费价格指数的变动不能简单地用一个线性模型来解 释。 但是可以看出在一定的时期内,宏观经济波动不大的情 况下,居民消费价格指数基本还是呈线性的。 因此,笔者将这 时间数列分段, 用线性模型分别分析居民消费价格指数在 1990~1994 年 、1994~1999 年 以 及 1999~2007 年 这 三 个 不 同 的经济状况下的变动情况。 下面,就详细的分析这几个阶段 CPI 的变动规律。 2.1 分析方法的选择
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辽宁工业大学时间序列分析课程设计题目:中国城市居民消费价格指数的分析与预测院(系):经济学院专业班级:统计学 091学号: 090707016学生姓名:胡迪指导教师:姜健教师职称:教授起止时间: 2011.12.19—12.23课程设计任务院(系):经济学院教研室:统计教研室学号090707016 学生姓名胡迪专业班级统计学091班课程设计(论文)题目中国城市居民消费价格指数的分析与预测课程设计(论文)任务1、画出时间序列的时序图,根据所画的时序图粗略判别序列是否平稳;2、根据序列的自相关图判别序列是否平稳;3、利用单位根检验方法,判别序列的平稳性;4、模型识别。
根据自相关系数和偏自相关系数的性质和特点,判别模型属于哪种类型;5、参数估计。
根据选定的模型类别进行模型的参数估计;6、进行相应的检验。
包括模型的稳定性、可逆性的判定;参数的显著性检验;残差的白噪声检验等;7、模型优化。
对所建立的多个模型,根据AIC准则等进行优化选择;9、预测。
应用所建立的模型,进行未来5期的预测;10、模型的评价。
应用相关的评价准则,对所选择的模型进行评价。
11、撰写设计报告。
报告一律要求用Word文档纂写,3000字左右,内容及要求见指导书。
摘要时间序列就是按照时间的顺序记录的一列有序数据。
对时间序列进行观察、研究,找寻它变化发展的规律,预测它将来的走势。
时间序列分析在日常生活中随处可见,有着非常广泛的应用领域。
本文用时间序列分析方法,对城市居民消费价格指数序列进行了拟合。
通过对1960年至2005年期间中国城市居民消费价格指数进行观察分析,建立合适的ARMA模型,对未来五年的城市居民消费价格指数进行预测。
然后对预测值和真实值进行比较,得出结论,所建立的模型有较好的拟合效果,从而提供了一个经济预测和结构分析的有效方法。
关键词:时间序列城市居民消费价格指数平稳性白噪声单位根目录1引言 (1)2模型的判别 (2)2.1原始序列分析 (2)2.2模型判别 (4)3中国城市居民消费价格指数模型的建立 (5)3.1有常数项的AR(1)模型 (5)3.2有常数项的ARMA(1,2)模型 (7)3.3没有常数项的ARMA(1,2)模型 (9)4模型优化 (11)4.1模型选择 (11)5中国城市居民消费价格指数模型的预测 (12)6模型评价与分析 (14)6.1中国城市居民消费价格指数模型评价 (14)6.2中国城市居民消费价格指数分析 (15)参考文献 (15)1引言城市居民消费价格指数(Urban Consumer Price Index),是反映城市居民家庭所购买的生活消费品价格和服务项目价格变动趋势和程度的相对数。
城市居民消费价格指数可以观察和分析消费品的零售价格和服务项目价格变动对职工货币工资的影响,作为研究职工生活和确定工资政策的依据,是用来反映通货膨胀(紧缩)程度的指标。
城市居民消费价格指数的调查范围和内容是居民用于日常生活消费品的全部商品和服务项目价格。
包括食品、烟酒及用品、衣着、家庭设备用品及维修服务、医疗保健和个人用品、交通和通讯、娱乐教育文化用品及服务、居住等八大类商品及服务项目价格。
既包括居民从商店、工厂、集市所购买商品的价格,也包括从餐饮行业购买商品的价格。
本文应用时间序列方法对城市居民消费价格指数进行建模分析和经济预测,结果可以反映一定时期居民生活消费品及服务项目价格变动趋势和程度,可以观察居民生活消费品及服务项目价格变动对居民生活的影响,为各级政府掌握居民消费状况,研究和制定居民消费价格政策、工资政策以及为新国民经济核算体系中消除价格变动因素的核算提供科学依据。
2模型的判别2.1原始序列分析对1951-2005年中国城市居民消费价格指数(上年=100)序列建模(单位:%)。
数据见表2-1。
表2-1年份指数(%)年份指数(%)年份指数(%)年份指数(%)年份指数(%)1951 112.5 1962 103.8 1973 100.1 1984 102.7 1995 116.8 1952 102.7 1963 94.1 1974 100.7 1985 111.9 1996 108.8 1953 105.1 1964 96.3 1975 100.4 1986 107 1997 103.1 1954 101.4 1965 98.8 1976 100.3 1987 108.8 1998 99.4 1955 100.3 1966 98.8 1977 102.7 1988 120.7 1999 98.7 1956 99.9 1967 99.4 1978 100.7 1989 116.3 2000 100.8 1957 102.6 1968 100.1 1979 101.9 1990 101.3 2001 100.7 1958 98.9 1969 101 1980 107.5 1991 105.1 2002 991959 100.3 1970 100 1981 102.5 1992 108.6 2003 100.9 1960 102.5 1971 99.9 1982 102 1993 116.1 2004 103.3 1961 116.1 1972 100.2 1983 102 1994 125 2005 101.6数据来源:中国统计年鉴数据库①做原始序列时序图与自相关图(x表示1951-2005年中国城市居民消费价格指数序列)JUMIN13012512011511010510095905560657075808590950005图2-1 中国城市居民消费价格指数时序图由图2-1可以看出,时间序列没有明显的趋势效应,也没有季节变动效应,可以认为原时间序列为平稳时间序列。
图2-2 中国城市居民消费价格指数相关图由图2-2可知,自相关系数只有前两阶在2倍标准差之外,其余均在2倍标准差之内;偏自相关系数只有一阶在2倍标准差之外,其余均在2倍标准差之内。
Q 统计量的相伴概率p 值均小于0.05,可以认为该时间序列平稳,可以根据此表选择模型进行建立。
②对原始时间序列做单位根检验,判别该时间序列是否平稳。
图2-3 原始序列单位根检验由图2-3可以看出,检验t 统计量的值为-3.539492,显著性水平5%、10%的临界值分别为-2.916566、-2.596116,可见t 统计量的值小于各显著性水平的临界值,显著性水平1%的临界值为-3.557472,虽然小于t 统计量值,但是很接近,故拒绝原假设,认为序列平稳,可以对原始序列考虑建模。
2.2模型判别根据原始时间序列自相关图,偏自相关图考虑建模。
初步拟定建立有常数项的AR(1)模型,有常数项的ARMA(1,2)模型,有常数项的MA(2)模型,有常数项的MA(1)模型,无常数项的AR(1)模型,无常数项的ARMA(1,2)模型,无常数项的MA(2)模型,无常数项的MA(1)模型,一阶差分后的有常数项的AR(1)模型,一阶差分后的有常数项的ARMA(1,2)模型,一阶差分后的有常数项的MA(2)模型,一阶差分后的有常数项的MA(1)模型,一阶差分后的无常数项的AR(1)模型,一阶差分后的无常数项的ARMA(1,2)模型,一阶差分后的无常数项的MA(2)模型,一阶差分后的无常数项的MA(1)模型。
t-Statistic Prob.*Augmented Dickey-Fuller test statistic -3.539492 0.0105 Test critical values: 1% level -3.557472 5% level -2.916566 10% level -2.5961163中国城市居民消费价格指数模型的建立3.1有常数项的AR(1)模型Variable Coefficient Std. Error t-Statistic Prob.C 103.3539 1.783128 57.96215 0.0000AR(1) 0.629088 0.104792 6.003189 0.0000R-squared 0.409348 Mean dependent var 103.6963Adjusted R-squared 0.397989 S.D. dependent var 6.240614S.E. of regression 4.842053 Akaike info criterion 6.028888Sum squared resid 1219.165 Schwarz criterion 6.102554Log likelihood -160.7800 Hannan-Quinn criter. 6.057298F-statistic 36.03828 Durbin-Watson stat 1.661689Prob(F-statistic) 0.000000Inverted AR Roots .63图3-1 模型的参数估计模型为:x t=103.3539+0.629088x t1-+εt,参数的显著性检验均通过了,特征根也在单位圆内,模型平稳,AIC为6.6028888。
图3-2 残差相关图图3-2的P值均大于0.05,说明残差序列为纯随机序列,互不相关。
F-statistic 7.249813 Prob. F(2,51) 0.0017Obs*R-squared 11.95396 Prob. Chi-Square(2) 0.0025Scaled explained SS 23.43989 Prob. Chi-Square(2) 0.0000 图3-3 残差方差齐性检验图3-3上面的的Proc.Chi-Square(2)值小于0.05,认为残差序列没通过方差齐性检验,存在异方差。
Sample Mean = 0.166292Sample Std. Dev. = 4.908975Method Value Probabilityt-statistic 0.251224 0.8026图3-4 残差零均值检验图3-4的Probability值大于0.05,认为残差序列通过了零均值检验。
-15-10-5051015901001101201305560657075808590950005ResidualActual Fitted图3-5 模型拟合图形3.2有常数项的ARMA(1,2)模型VariableCoefficient Std. Error t-StatisticProb.C 103.3703 1.124717 91.90784 0.0000 AR(1) -0.884055 0.028473 -31.04900 0.0000 MA(1) 1.900897 0.039167 48.53254 0.0000 MA(2) 0.905352 0.037142 24.37568 0.0000R-squared0.584059 Mean dependent var 103.6963 Adjusted R-squared 0.559103 S.D. dependent var 6.240614 S.E. of regression 4.143773 Akaike info criterion 5.752278 Sum squared resid 858.5428 Schwarz criterion 5.899610 Log likelihood -151.3115 Hannan-Quinn criter. 5.809098 F-statistic23.40315 Durbin-Watson stat 1.640252 Prob(F-statistic)0.000000Inverted AR Roots -.88 Inverted MA Roots-.95+.04i -.95-.04i图3-6 模型的参数估计模型为:x t =103.3703-0.884055x t 1-+εt +1.900897ε1-t +0.905352ε2-t ,参数的显著性检验均通过了,特征根也在单位圆内,模型平稳可逆,AIC 为5.752278。
