白噪声讲义 - 360文档中心

白噪声

白噪声
物理学概念
01 定义
03 参数 05 应用
目录
02 起源 04 通信中的
白噪声（white noise）是指功率谱密度在整个频域内是常数的噪声。所有频率具有相同能量密度的随机噪声称为白噪声。
定义
白噪声是指在较宽的频率范围内，各等带宽的频带所含的噪声功率谱密度相等的噪声。
一般在物理上把它翻译成白噪声（white noise）。
人生充满声音和噪声干扰,如轿车鸣喇叭、汪汪狗叫、吵邻打鼾、警报器、大喊大叫.白噪声并不增加烦躁，而是包含所有同等频率的声音.研究表明,一个稳定、平和的声音流,如白噪声、可过滤和分散噪音，可以帮助减轻噪音分心，这也正是为什么它用来帮助人们放松、睡眠。
上市销售的白噪声机器产品有睡眠辅助器、私密性增强器以及掩饰耳鸣。
白噪声可以用于放大器或者电子滤波器的频率响应测试，有时它与响应平坦的话筒或和自动均衡器一起使用。这个设计的思路是系统会产生白噪声，话筒接收到扬声器产生的白噪声，然后在每个频率段进行自动均衡从而得到一个平坦的响应。这种系统用在专业级的设备、高端的家庭立体声系统或者一些高端的汽车收音机上。
白噪声也作为一些随机数字生成器的基础使用，常用于计算机科学领域。
白噪声的应用领域之一是建筑声学，为了减弱内部空间中分散人注意力并且不希望出现的噪声（如人的交谈)，使用持续的低强度噪声作为背景声音。
在电子通信中也有白噪声的应用，它被直接或者作为滤波器的输入信号以产生其它类型的噪声信号，尤其是在信号合成中，经常用来重现有很高噪声成分信号。
白噪声也用来产生冲击响应。为了在一个演出地点保证音乐会或者其它演出的均衡效果，从P A系统发出一个瞬间的白噪声或者粉红噪声，并且在不同的地方监测噪声信号，这样工程师就能够建筑物的声学效应能够自动地放大或者削减某些频率，从而就可以调整总体的均衡效果以得到一个平衡的和声。

通信原理之白噪声

§3.7通信原理之白噪声
通信原理之白噪声综述
1.1 白噪声
定义：凡功率谱密度在整个频域内都是均匀分布的噪声，称为白噪声。

即：
双边谱密度：
单边谱密度：
其中：n0为常数，W/Hz。

一般默认白噪声为平稳的。

1.2 白噪声的功率
由于白噪声的带宽无限，其平均功率为无穷大。

即或。

因此，真正“白”的噪声是不存在的，它只是构造的一种理想化的噪声形式。

实际中，只要噪声的功率谱均匀分布的频率范围远远大于通信系统的工作频带，我们就可以把它视为白噪声。

如果白噪声取值的概率分布服从高斯分布，则称之为高斯白噪声。

高斯白噪声在任意两个不同时刻上的随机变量之间，不仅是互不相关的，而且还是统计独立的。

1.3 自相关函数
据：功率信号的功率谱密度与其自相关函数互为傅氏变换对。

图3-6 白噪声的功率谱密度与自相关函数
图3-6 白噪声的功率谱密度与自相关函数
2.1 带限白噪声
1.低通白噪声白噪声经理想低通滤波器| f |≤后而形成的噪声，被称为低通白噪声，即其功率谱密度为：
由上式可见，白噪声的功率谱密度被限制在| f |≤内，通常把这样的噪声也称为带限白噪声。

2.2带通白噪声
白噪声经理想带通滤波器后而形成的噪声，被称为低通白噪声，即其功率谱密度为：
式中：f c －中心频率，B－通带宽度则其输出噪声的功率谱密度为：
2.3窄带高斯白噪声
通常，带通滤波器的 B << fc ，因此称窄带滤波器，相应地把带通白高斯噪声称为窄带高斯白噪声。

其统计特性与一般窄带随机过程相同：
平均功率N=n0B。

白噪声的产生

σ 2 , ω ≤ ω0 （ ω0 为给定的远大于过程的截止频率）谱密度： SW (ω ) = 0, ω > ω0 σ 2ω0 sin ω0τ 相关函数： RW (τ ) = ⋅
π
ω0τ
讨论白噪声时，还要涉及到白噪声的概率分布，服从正态分布的白噪声称为高斯白噪声。 n 维白噪声：一个 n 维随机过程 W (t ) 满足： E{W (t )} = 0 Cov{W (t ),W (t + τ )} = E{W (t )W (t + τ )} = Qδ (τ ) 其中 Q 为正定常数矩阵，则称 W (t ) 为 n 维白噪声过程。 ● 白噪声序列白噪声序列是白噪声过程的离散形式。如果序列 {W (k )} 满足：相关函数： RW (l ) = σ 2δ l , l = 0,±1,±2,L 则称为白噪声序列。谱密度： SW (ω ) =
N 2 = i =1 N / 12
∑ξ
N
i
−
N 12 2 由此可得正态分布η ~ N ( µη ,σ η ) 的随机数。
取 N = 12 时，有
η = µη + σ η
∑ξ
i =1
N
i
−
N 2
η = µη + σ η ∑ ξi − 6
i =1
● 变换抽样法理论依据：设 ξ1 和 ξ 2 是相互独立的（0，1）均匀分布随机变量，则
● M 序列的生成结构图 ● M 序列的波形 1.2.3 特征多项式解决如何选取反馈通道的问题，以保证生成 M 序列。 ● 定义多项式： G ( s ) = ∑ x i s i （无限阶）
i =0 P 1 , F ( s ) = 1 ⊕ ∑ a j s j （有限阶） F ( s) j =1 称 F ( s ) 为 M 序列的特征多项式。注意 1：此时选取 M 序列初始状态为： x1 = 1, x 2 = 0, L , x P = 0 。注意 2：生成 M 序列的结构图完全由特征多项式 F ( s ) 确定。 ∞

通信原理之白噪声

谱密度为：
H
(
f
)

1
0
fc

B 2

f

fc

B 2
其他f
n0 / 2 Pn f
B
o
fc
fc
f
式中： fc －中心频率，B －通带宽度则其输出噪声的功率谱密度为
n0
Pn(f )
2

0
fc

B
2
f

fc

B
2
其它f
2.3窄带高斯白噪声
通常，带通滤波器的 B << fc ，因此称窄带滤波器，相
低通白噪声，即其功率谱密度为：
Pn() Nhomakorabean0 2
,
0,
( fH , fH ) 其它
Pn ()
n0 / 2
fH 0 fH
f
H 0 H
由上式可见，白噪声的功率谱密度被限制在| f | fH 内，通常把这样的噪声也称为带限白噪声。
2.2带通白噪声
白噪声经理想带通滤波器后而形成的噪声，被称为低通白噪声，即其功率
实际中，只要噪声的功率谱均匀分布的频率范围远远大于通信系统的工作频带，我们就可以把它视为白噪声。
如果白噪声取值的概率分布服从高斯分布，则称之为高斯白噪声。
高斯白噪声在任意两个不同时刻上的随机变量之间，不仅是互不相关的，而且还是统计独立的。
1.3 自相关函数
据：功率信号的功率谱密度与其自相关函数互为傅氏变换对。
应地把带通白高斯噪声称为窄带高斯白噪声。其统计特性与一般窄带随机过程相同：
平均功率N=n0B

白噪声的定义式

白噪声的定义式白噪声是一个经典的信号处理问题，它在工程、物理、生物等领域都有广泛的应用。

在本文中，我们将介绍白噪声的定义式，并探讨其在实际应用中的意义和应用。

1. 白噪声的定义白噪声是一种特殊的随机信号，其功率谱密度在所有频率范围内均匀分布，即具有平坦的功率谱密度。

这意味着在所有频率上，白噪声的功率都是相等的。

白噪声的名称源于其类似于白光的性质，即白光是由所有频率的光波组成的，而白噪声是由所有频率的信号组成的。

白噪声的数学定义式为：$$P(f)=K$$其中，$P(f)$ 是白噪声在频率 $f$ 处的功率谱密度，$K$ 是一个常数。

这个定义式表示白噪声在所有频率上具有相同的功率，即功率谱密度是常数 $K$。

在实际应用中，我们通常使用功率谱密度的对数形式来描述白噪声的特性。

因为在对数坐标下，平坦的功率谱密度将呈现为一条水平的直线。

因此，我们可以将白噪声的定义式改写为：$$log P(f)=log K$$这个等式表示在对数坐标下，白噪声的功率谱密度是一个常数。

2. 白噪声的特性白噪声具有以下特性：(1) 平稳性：白噪声是一种平稳随机过程，即其统计特性在时间上不变。

这意味着在任何时间点，白噪声的统计特性都是相同的。

(2) 独立性：白噪声的各个样本之间是相互独立的。

这意味着在任何时间点，白噪声的各个样本之间是不相关的。

(3) 均匀性：白噪声的功率谱密度在所有频率上均匀分布。

这意味着在所有频率上，白噪声的功率都是相等的。

(4) 白噪声是高斯分布的：白噪声的各个样本是服从高斯分布的。

3. 白噪声的应用白噪声在实际应用中有广泛的应用。

以下是一些常见的应用领域：(1) 信号处理：白噪声在信号处理中有广泛的应用，例如在滤波、降噪、信号分析等方面。

(2) 通信系统：白噪声在通信系统中也有广泛的应用，例如在信道建模、信道估计、信号检测等方面。

(3) 物理学：白噪声在物理学中也有重要的应用，例如在热力学、量子力学、天文学等方面。

白噪声

白噪声白噪声是指功率谱密度在整个频域内均匀分布的噪声。

所有频率具有相同能量密度的随机噪声称为白噪声。

从我们耳朵的频率响应听起来它是非常明亮的“咝”声（每高一个八度，频率就升高一倍。

因此高频率区的能量也显著增强）。

1概述白噪声是指在较宽的频率范围内，各等带宽的频带所含的噪声能量相等的噪声。

一般在物理上把它翻译成白噪声（white noise）。

白噪声或白杂讯，是一种功率频谱密度为常数的随机信号或随机过程。

换句话说，此信号在各个频段上的功率是一样的，由于白光是由各种频率（颜色）的单色光混合而成，因而此信号的这种具有平坦功率谱的性质被称作是“白色的”，此信号也因此被称作白噪声。

相对的，其他不具有这一性质的噪声信号被称为有色噪声。

理想的白噪声具有无限带宽，因而其能量是无限大，这在现实世界是不可能存在的。

实际上，我们常常将有限带宽的平整讯号视为白噪音，因为这让我们在数学分析上更加方便。

然而，白噪声在数学处理上比较方便，因此它是系统分析的有力工具。

一般，只要一个噪声过程所具有的频谱宽度远远大于它所作用系统的带宽，并且在该带宽中其频谱密度基本上可以作为常数来考虑，就可以把它作为白噪声来处理。

例如，热噪声和散弹噪声在很宽的频率范围内具有均匀的功率谱密度，通常可以认为它们是白噪声。

当你需要专心工作，而周遭总是有繁杂的声音时，就可以选用这两种声音来加以遮蔽。

一般来说，通常的情况下你可以选用白色噪音，而粉红色噪音则是特别针对说话声的遮蔽材料。

粉红色噪音又被称做频率反比(1/f) 噪音，因为它的能量分布与频率成反比，或者说是每一个八度音程(Octave) 能量就衰退3 dB。

高斯白噪声高斯白噪声：如果一个噪声，它的幅度分布服从高斯分布，而它的功率谱密度又是均匀分布的，则称它为高斯白噪声。

热噪声和散粒噪声是高斯白噪声。

所谓高斯白噪声中的高斯是指概率分布是正态函数，而白噪声是指它的二阶矩不相关，一阶矩为常数，是指先后信号在时间上的相关性。

白噪声的科学原理

白噪声的科学原理在平静的夜晚，你是否曾经听到过窗外传来的嘈杂声？或者是邻居打扫卫生的吵闹声？这些声音会干扰你的休息，使你难以入眠。

对于这种情况，很多人会选择使用白噪声来解决问题。

那么白噪声到底是什么？它是如何产生的？本篇文章将介绍白噪声的科学原理。

一、什么是白噪声？白噪声是一种特殊的声音信号，它是由一系列的等能量频率组成。

相比其他类型的信号，白噪声没有频率成分上的偏差，因此得名为“白噪声”。

人类的听觉可以感知的声音范围大约在20Hz到20kHz之间，而白噪声包含了所有这个范围内的频率。

如果我们将这些频率的能量相等地混合在一起，就可以得到一种类似于“ssssss……”的连续声音信号，这就是白噪声。

二、白噪声的产生方式产生白噪声的方式有多种，其中最常见的是通过使用白噪声发生器。

这种发生器使用随机信号的方法来产生等能量频率的声波信号，从而形成白噪声。

在这个过程中，发生器会不断地产生随机信号，而随机信号的音高和音量都是根据一定的规律变化的。

正是由于这种变化方式的不确定性，所以才能保证白噪声中每个频率分量的能量相等。

另外，白噪声还可以通过数字信号处理的方式产生。

这种方法通常使用电脑进行模拟计算，通过将不同频率的信号按照一定比例叠加在一起，达到产生白噪声的目的。

三、白噪声的应用场景白噪声在很多场合都有着非常广泛的应用。

最常见的就是在睡眠环境中使用，以遮盖其他噪声的干扰，帮助人们更快地入睡。

除此之外，白噪声在音频工程中也经常被应用。

由于其等能量分布的特性，白噪声可以用来测试音响系统的频率响应，帮助音频工程师更好地调试音响设备。

此外，白噪声还可以用来测试传感器或其他电子设备的性能。

通过测量设备对白噪声的响应，来判断其对不同频率的信号的灵敏度和准确度，以便在实际应用中更好地使用。

四、总结综上所述，白噪声是一种由等能量频率组成的连续信号。

它的产生方式有多种，最常见的是通过使用发生器或数字处理等方式。

白噪声在睡眠环境中应用尤为广泛，同时也是音频工程和电子设备测试中不可或缺的一部分。

《高斯噪声和白噪声》课件

《高斯噪声和白噪声》 PPT课件
# 高斯噪声和白噪声
概述
定义和性质
了解噪声的概念、特性以及对信号处理的影响。
种类
研究不同类型的噪声，如高斯噪声、白噪声等。
应用领域
了解噪声在通信、图像处理等领域中的应用。
高斯噪声
高斯分布的概念
介绍高斯分布及其在噪声中的应用。
性质
探讨高斯噪声的特性，如均值、方差等。
应用场景
了解在不同的应用领域中，高斯噪声和白噪声的应用。
噪声的处理和降噪
1
噪声的去除方法
介绍降低噪声对信号质量的影响的方法。
2
噪声的抑制方法
探讨噪声抑制技术，如滤波器设计和信号增强。
3
噪声的评估方法了解如何Fra bibliotek估噪声的强度和对信号的影响。
应用案例
语音信号中的噪声抑制
讨论在语音信号处理中抑制噪声的方法和技术。
统计特性
分析高斯噪声的概率密度函数和累积分布函数。
白噪声
定义和特性
了解白噪声的定义及其在信号处理中的重要性。
白噪声模型及产生机理
介绍白噪声的模型以及产生机理，如随机过程等。
功率谱密度函数
探讨白噪声的频谱特性和谱密度函数。
高斯噪声和白噪声的区别和联系
统计特性上的差异
对比高斯噪声和白噪声在统计特性上的差异。
图像信号中的噪声去除
介绍图像信号处理中的噪声去除技术。
视频信号中的噪声降噪
了解如何降低视频信号中的噪声。
结论
1 噪声对信号处理的影响
2 实际应用中的噪声处理策略
总结噪声对信号处理的重要性和影响。
探讨在实际应用中噪声处理的实用策略。
3 未来噪声处理技术的发展方向

白噪声

白噪声滚降噪声源能够驱动耳机或小型扬声器的音频噪声发生器这是一个产生白噪声的电路，会滚降以驱动耳机或小型扬声器。

白噪声产生的是一种“ rush”的声音，听起来像是您的耳朵在吹着空气。

白噪声会随频率变化而平坦，并且由于该电路会在音频范围内滚降，因此我将其称为“滚降”噪声。

据说白噪声（或滚降噪声）可用于帮助人们提高注意力，制造“噪音墙”以改善隐私，用声音填充空白空间，使他们不会感到那么空虚（较大的声音做了很多办公大楼），并被吹捧为耳鸣疗法（耳鸣）。

如果您决定建立并使用此电路来驱动EPHPHONES或扬声器，则您将自行承担风险。

请务必谨慎使用，否则可能会永久损坏您的听力。

怎么运行的？Q2是接地的发射极（反相）放大器，其反馈路径中带有Q1。

请注意，Q1以“上下颠倒”的方式连接，因为发射极相对于其基极为正，因此结雪崩，结两端下降约5至6伏。

Q2的目的是提供足够的偏置电流，以使Q1的发射极-基极击穿，并且在这种情况下，Q2两端也将出现一毫伏或两伏的宽带噪声。

请注意，Q1的集电极没有连接任何东西。

在2003年7月的版本中，Q1的集电极连接到Q2的基极，但是自那以后，我了解到有些晶体管在以这种方式连接时表现出负阻抗特性，因此对电路进行了修改，以从基极获取电流信号。

而不是收藏家。

A1是一个电压跟随器，用于缓冲由连接到其同相输入的两个470k电阻所产生的50％的电池电压。

50％的电压用作芯片上其他三个放大器的DC偏置电源。

A2和A3分别提供50倍的增益，总增益为2500倍。

LM324的开环增益与频率的关系图显示，带宽在大约5 kHz时截取了50X增益点，因此该滤波可以使噪声“变色”。

您选择的耳机或扬声器也会使信号变色。

您可以通过在一个或两个20k电阻器之间放置一个小电容器来获得一些带宽。

在我使用的耳机中，将一个.001 uF电容器跨接在一个20k电阻器中几乎是正确的。

通过在1兆欧的反馈电阻上放一些小电阻（例如5至100 pF），可以降低噪声。

计量经济学中白噪声的定义

计量经济学中白噪声的定义1. 引言嘿，朋友们，今天我们要聊聊一个看似复杂却其实挺有趣的话题，那就是“白噪声”。

你可能会想，“白噪声”是什么？是不是跟我耳朵里的嗡嗡声有关？哈哈，其实这个词在计量经济学中可是大有讲究的哦！就像生活中的小插曲一样，白噪声在数据分析中扮演着重要的角色。

那么，我们就来深入了解一下吧！2. 什么是白噪声？2.1 定义简单来说，白噪声是一种随机信号，具有恒定的功率谱密度。

听起来复杂对吧？其实可以理解为，它是没有规律可循的，像是你在街上听到的各种声音：汽车的喇叭声、路人的聊天声，这些声响一起混杂，听上去就像是一种背景噪音。

这个“背景噪音”在计量经济学中，通常被视为误差项，帮助我们理解数据中的不确定性。

2.2 特性白噪声有几个关键特性，首先，它是“零均值”的，意味着在长时间内，它的平均值为零。

想象一下，你每天的心情波动，有时开心得像个孩子，有时又低落得像个西红柿，但总体上，你的心情是有波动的，对吧？这就是白噪声的一个特点！其次，它的自相关性为零，也就是说，今天的噪声和明天的噪声没有关系，就像你今天吃了什么和明天的天气没啥关联一样。

3. 白噪声的应用3.1 在经济学中的作用那么，白噪声在经济学上有什么用处呢？哎呀，它可不是闲着没事做的！在建立经济模型时，经济学家常常会把白噪声用作随机干扰，帮助他们更好地解释观测数据。

比如说，某种商品的价格波动可能受多种因素影响，白噪声就能帮助我们捕捉那些无法预测的因素。

简单来说，就是给数据加点调味料，让分析更真实、更全面。

3.2 检测与识别当然，要识别白噪声并不是一件容易的事。

经济学家们通常会运用一些统计检验方法，比如自相关函数和单位根检验，来判断数据是否为白噪声。

说白了，就是看这些数据的“性格”，是不是像个无忧无虑的孩子，还是有些小心眼和阴暗面。

4. 结论说了这么多，白噪声其实并不神秘，它像是生活中的小插曲，虽然没有规律，但却在我们的分析中扮演着不可或缺的角色。

加性高斯白噪声知识点

AWGN（加性高斯白噪声）加性高斯白噪声（AWGN）从统计上而言是随机无线噪声，其特点是其通信信道上的信号分布在很宽的频带范围内。

高斯白噪声的概念."白"指功率谱恒定;高斯指幅度取各种值时的概率p (x)是高斯函数.加性高斯白噪声在通信领域中指的是一种各频谱分量服从均匀分布（即白噪声），且幅度服从高斯分布的噪声信号。

因其可加性、幅度服从高斯分布且为白噪声的一种而得名。

该噪声信号为一种便于分析的理想噪声信号，实际的噪声信号往往只在某一频段内可以用高斯白噪声的特性来进行近似处理。

由于AWGN信号易于分析、近似，因此在信号处理领域，对信号处理系统（如滤波器、低噪音高频放大器、无线信号传输等）的噪声性能的简单分析(如：信噪比分析)中，一般可假设系统所产生的噪音或受到的噪音信号干扰在某频段或限制条件之下是高斯白噪声。

加性高斯白噪声只是白噪声的一种，另有泊松白噪声等1. 高斯型白噪声可用具体数学表达式表述，便于推导分析和运算；2. 高斯型白噪声确实反映了实际信道中的加性噪声情况，比较真实地代表。

了信道噪声的特性。

高斯白噪声：如果一个噪声，它的幅度分布服从高斯分布，而它的功率谱密度又是均匀分布的，则称它为高斯白噪声。

热噪声和散粒噪声是高斯白噪声。

所谓高斯白噪声中的高斯是指概率分布是正态函数，而白噪声是指它的二阶矩不相关，一阶矩为常数，是指先后信号在时间上的相关性。

这是考查一个信号的两个不同方面的问题。

高斯白噪声是指信号中包含从负无穷到正无穷之间的所有频率分量，且各频率分量在信号中的权值相同。

白光包含各个频率成分的光，白噪声这个名称是由此由此而来的。

它在任意时刻的幅度是随机的，但在整体上满足高斯分布函数。

时变信号的知识参考《信号与系统》，高斯白噪声参考《通信原理》类书籍。

白噪声放大器PPT课件

Vin
Vout
输入缓冲
可控增益放大输出功率放大
第15页/共33页
白噪声放大器设计
• 输入缓冲
要满足输入电阻大于1kΩ的要求，必须加入输入缓冲以提高输入阻抗；输入缓冲对降低系统噪声起了至关重要的作用，所以需要采用低噪声放大器。
Vin
Vout
输入缓冲
可控增益放大输出功率放大
第16页/共33页
白噪声放大器设计
• 可控增益放大
+15V -15V
V1 3
8
+
6
AD603
4
5
1
2
Vc1 Vc2
+15V -15V
C 3
8
+
6
V2
AD603
4
5
1
2
第21页/共33页
白噪声放大器设计
• 可控增益放大
◆级联增益为：
+15V -15V
+15V -15V
Gain(dB) 40Vc1
V1 3 + 8 6
Vin
Vout
输入缓冲
可控增益放大输出功率放大
第18页/共33页
白噪声放大器设计
• 可控增益放大
+15V -15V
◆AD603通频带为90MHz，增益为10～+30dB
V1 3 + 8 6
V2
AD603
4
5
1
2
Vc
◆AD603增益和控制电压的关系：
Gain(dB) 10lg(V 2 / V1)
第30页/共33页
白噪声放大器测试
• 频率特性测试表格（继续）

白噪声(WhiteNoise)

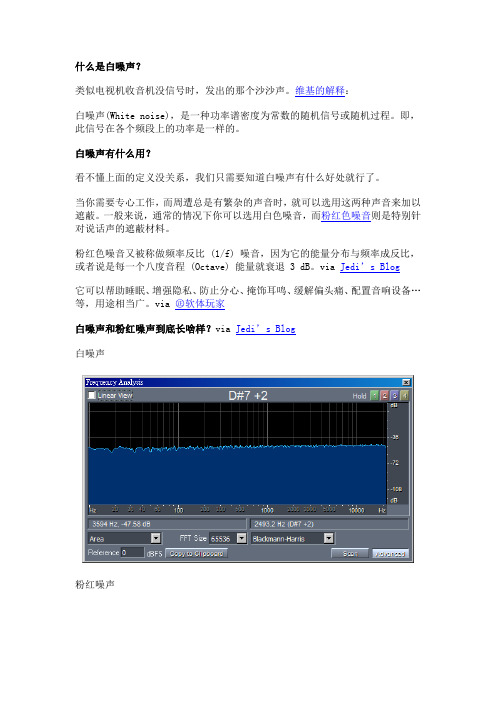
什么是白噪声？类似电视机收音机没信号时，发出的那个沙沙声。

维基的解释：白噪声(White noise)，是一种功率谱密度为常数的随机信号或随机过程。

即，此信号在各个频段上的功率是一样的。

白噪声有什么用？看不懂上面的定义没关系，我们只需要知道白噪声有什么好处就行了。

当你需要专心工作，而周遭总是有繁杂的声音时，就可以选用这两种声音来加以遮蔽。

一般来说，通常的情况下你可以选用白色噪音，而粉红色噪音则是特别针对说话声的遮蔽材料。

粉红色噪音又被称做频率反比 (1/f) 噪音，因为它的能量分布与频率成反比，或者说是每一个八度音程 (Octave) 能量就衰退 3 dB。

via Jedi’s Blog它可以帮助睡眠、增强隐私、防止分心、掩饰耳鸣、缓解偏头痛、配置音响设备…等，用途相当广。

via ㊣软体玩家白噪声和粉红噪声到底长啥样？via Jedi’s Blog白噪声粉红噪声说了那么多，改请主角上场了：Mac OS X上有一款软件叫Noise，它可以随机产生白色噪音 (White Noise) 或粉红色噪音 (Pink Noise)。

该软件发出的“噪声”比 windows 上的SoundMasker专业。

详细测试与比较结果请看Jedi’s Blog。

还有一款soundtrack，感谢Paveo在 mac 下，把这两个软件截图。

前面的是Noise。

所以 windows 我就不推荐什么“噪声”软件了，如果你有什么好推荐可以留言。

下面介绍一个通杀所有系统平台的，专门制造白噪声的网站：simplynoise。

进入网站之后拖动左边的进度条，调到你合适的音量就可以了。

via ㊣软体玩家另外，我还挖到一个专门卖“白噪声”的网站：whitenoisemp3s，它提供了一些免费的白噪声下载。

10 白噪声过程通过线性系统讲解

f

df
FY f0
H jf 2 df
0 H jf0 2

2、噪声等效通频带－低通
对低通滤波器来说：
fe
0
FY

f
df
FY 0

0
H jf 2 H 0 2
df
3、噪声等效通频带－结论：
噪声通频带如信号通频带那样，仅由线性电路本身决定。
0
cos cos0 sin sin 0 d

N0
K
2 0
2
0 0
e2 / 2
cos
cos0 d

N0
K
2 0

cos 0
0 e2 / 2 cos d
0

N0
K
2 0

cos 0
e2 / 2 cos d
2
H j 2d
0
或
2 Y

N0

H

jf

2
df
这里

2
f
0
4、冲击响应法
RX ( )

N0 2
( ),因此
RY ( ) RX ( ) h( ) h( )
N0 ( ) h( ) h( )
2
N0 h( ) h( ) N0
(0)

sin
相关时间0
sin d 1
0
2 4f
3、噪声通频带
由于输出噪声的功率谱为矩形，系统的噪声通频带等于信号的通频带，即：
fe

3.7理想白噪声及特性

随机信号分析目录CONTENTS白噪声的定义白噪声的时频域特性物理可实现的白噪声小结随机过程的分类⚫按分布函数或概率密度函数特性：正态过程、马尔可夫过程、独立增量过程等；⚫按功率谱特性：宽带过程、窄带过程；白噪声、色噪声等。

定义：若N(t)为一个具有零均值的平稳随机过程，其功率谱密度均匀的分布在整个频率区间，即其中，N0为一个正实常数，则称N(t)为白噪声过程或简称白噪声。

“白”字借用光学中的“白光”术语。

N 120S N ω()白噪声的功率谱ω0=ωS N N 2()10∈−∞+∞ω(,)结论：功率谱在整个频率轴上满足均匀分布。

有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）根据维纳-辛钦定理，白噪声的自相关函数为00111()()222j N R N e d N ωττωδτπ+∞−∞==⎰0)(τN R 021N 结论：白噪声的自相关函数是一个δ函数，其面积等于功率谱密度。

白噪声的时频域特征白噪声的自相关系数为⎩≠⎨===⎧=τττττK R r K R N N N N N (0)(0)0 0()()() 1 0 结论：白噪声在任何两个相邻时刻的取值都是不相关的，白噪声过程随时间的起伏极快，过程的功率谱密度极宽。

有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）物理可实现的白噪声实际上，白噪声是不存在的，因为在实际应用中，当研究随机过程通过某一系统时，只要过程的功率谱密度在一个比系统带宽大得多的频率范围内近似均匀分布，就可以把它作为白噪声来处理。

2(0)(0)N N R σδ==→∞白噪声的功率谱在整个频率轴上满足均匀分布。

白噪声的自相关函数是一个δ函数，其面积等于功率谱密度，在任何两个相邻时刻的取值都是不相关的。

理想白噪声不存在，但某些情况下随机过程可近似看作白噪声。

对于一个具有零均值的平稳随机过程，其功率谱密度均匀的分布在整个频率区间，则称其为白噪声。

白噪声深度分析

1.什么是白噪声？答：白噪声是指功率谱密度在整个频域内均匀分布的噪声。

白噪声或白杂讯，是一种功率频谱密度为常数的随机信号或随机过程。

换句话说，此信号在各个频段上的功率是一样的，由于白光是由各种频率（颜色）的单色光混合而成，因而此信号的这种具有平坦功率谱的性质被称作是“白色的”，此信号也因此被称作白噪声。

相对的，其他不具有这一性质的噪声信号被称为有色噪声。

理想的白噪声具有无限带宽，因而其能量是无限大，这在现实世界是不可能存在的。

实际上，我们常常将有限带宽的平整讯号视为白噪音，因为这让我们在数学分析上更加方便。

然而，白噪声在数学处理上比较方便，因此它是系统分析的有力工具。

一般，只要一个噪声过程所具有的频谱宽度远远大于它所作用系统的带宽，并且在该带宽中其频谱密度基本上可以作为常数来考虑，就可以把它作为白噪声来处理。

例如，热噪声和散弹噪声在很宽的频率范围内具有均匀的功率谱密度，通常可以认为它们是白噪声。

高斯白噪声的概念——."白"指功率谱恒定;高斯指幅度取各种值时的概率p (x)是高斯函数高斯噪声——n维分布都服从高斯分布的噪声高斯分布——也称正态分布，又称常态分布。

对于随机变量X，记为N（μ，σ2），分别为高斯分布的期望和方差。

当有确定值时，p(x)也就确定了，特别当μ=0，σ2=1时，X的分布为标准正态分布。

2.matlab中白噪声和有色噪声怎么表示？答：假设V和W是2个n维噪声序列，其中V表示白噪声，W表示有色噪声，在MATLAB中表示方法为：V=randn(m,n)W = filter(b,1,V);b为滤波器系数。

3. 什么叫单边功率谱和双边功率谱？他们如何计算?答：单边功率谱密度(N0)主要用在复数信号中，双边功率谱密度(N0/2)主要用在实信号中。

单边功率谱适于基带分析，在基带中是0中频。

如果信号通过了调制，将原中频搬移到了高频段，原来的负频部分就成了正频，利用双边功率谱进行分析。