2020新人教A版高中数学必修一2.1.2指数函数及其性质一课时作业

合集下载

2.1.2__指数函数及其性质(第一课时)

2.1.2 指数函数及其性质（第一课时）1、若函数f(x)＝3x ＋3－x 与g(x)＝3x －3－x 的定义域为R ，则( )A ．f(x)与g(x)均为偶函数B ．f(x)为偶函数，g(x)为奇函数C ．f(x)与g(x)均为奇函数D ．f(x)为奇函数，g(x)为偶函数2、已知函数f(x)＝⎩⎨⎧ 2x＋1，x ＜1x 2＋ax ，x≥1，若f[f(0)]＝4a ，则实数a 等于( )A.12B.45 C ．2 D ．9 3．不论a 取何正实数，函数f(x)＝a x ＋1－2恒过点( )A ．(－1，－1)B ．(－1,0)C ．(0，－1)D ．(－1，－3)4、使不等式23x －1＞2成立的x 的取值为( )A ．(23，＋∞)B ．(1，＋∞)C ．(13，＋∞)D ．(－13，＋∞)5、为了得到函数y ＝3×(13)x 的图象，可以把函数y ＝(13)x 的图象( )A ．向左平移3个单位长度B ．向右平移3个单位长度C ．向左平移1个单位长度D ．向右平移1个单位长度6、在同一平面直角坐标系中，函数f(x)＝ax 与g(x)＝a x (a ＞0且a≠1)的图象可能是()7、当x>0时，指数函数f(x)＝(a －1)x <1恒成立，则实数a 的取值范围是( )A ．a>2B ．1<a<2C ．a>1D ．a ∈R8、函数y ＝a x (a>0且a≠1)在[0,1]上的最大值与最小值的和为3，则a 的值为( )A.12 B ．2 C ．4 D.149、函数y ＝a x －1的定义域是(－∞，0]，则a 的取值范围为( )A ．a ＞0B ．A ＜1C ．0＜a ＜1D ．a≠110、函数y ＝－2－x 的图象一定过第________象限．11、方程4x ＋1－4＝0的解是x ＝________.12、函数y ＝a 2x ＋b ＋1(a ＞0，且a≠1)的图象恒过定点(1,2)，则b ＝________.13、方程|2x －1|＝a 有唯一实数解，则a 的取值范围是________．14、函数y ＝(12)|x|的图象有什么特征？你能根据图象指出其值域和单调区间吗？15、若关于x 的方程a x ＝3m －2(a ＞0且a≠1)有负根，求实数m 的取值范围．16、已知－1≤x≤2，求函数f(x)＝3＋2·3x ＋1－9x的值域．17、用计算机作出的图像，并在同一坐标系下作出下列函数的图象，并指出它们与指数函数y=x 2的图象的关系，⑴y =12+x 与y=22+x . ⑵y =12-x 与y=22-x .18、求下列函数的定义域、值域（1）110.3x y -=（2）y =19、求下列函数的定义域与值域（1）412-=x y ；（2）||2()3x y =；（3）1241++=+x x y ；20、用函数单调性定义证明a ＞1时，y = a x 是增函数.。

高中数学必修一第二章2.1.2指数函数及其性质习题(含答案)

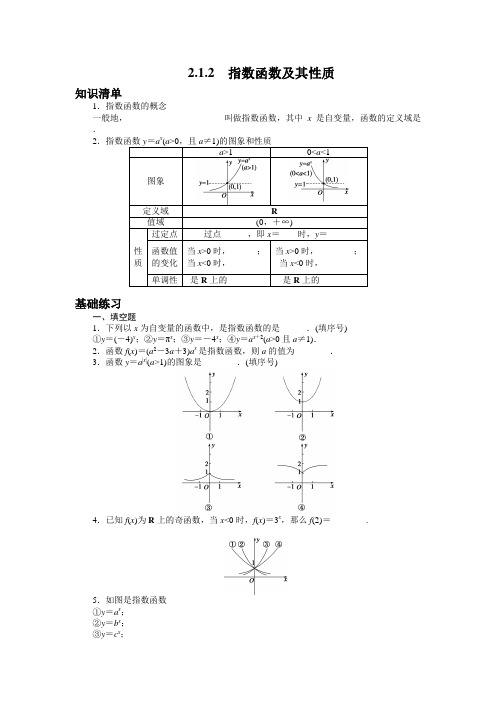
2.1.2 指数函数及其性质知识清单1．指数函数的概念一般地，______________________叫做指数函数，其中x 是自变量，函数的定义域是____．2．指数函数y ＝a x (a >0，且a ≠1)的图象和性质a >1 0<a<1图象定义域 R 值域 (0，＋∞)性质过定点过点______，即x ＝____时，y ＝____函数值的变化当x >0时，______；当x <0时，________ 当x >0时，________；当x <0时，________单调性是R 上的________是R 上的________基础练习一、填空题1．下列以x 为自变量的函数中，是指数函数的是______．(填序号)①y ＝(－4)x ；②y ＝πx ；③y ＝－4x ；④y ＝a x ＋2(a >0且a ≠1)． 2．函数f (x )＝(a 2－3a ＋3)a x 是指数函数，则a 的值为________． 3．函数y ＝a |x |(a >1)的图象是________．(填序号)4．已知f (x )为R 上的奇函数，当x <0时，f (x )＝3x，那么f (2)＝________.5．如图是指数函数 ①y ＝a x ； ②y ＝b x ； ③y ＝c x ；④y ＝d x 的图象，则a 、b 、c 、d 与1的大小关系是________．6．函数y ＝(12)x －2的图象必过第________象限．7．函数f (x )＝a x 的图象经过点(2,4)，则f (－3)的值为____．8．若函数y ＝a x －(b －1)(a >0，a ≠1)的图象不经过第二象限，则a ，b 需满足的条件为________．9．函数y ＝8－23－x (x ≥0)的值域是________．二、解答题10．比较下列各组数中两个值的大小：(1)0.2－1.5和0.2－1.7； (2)1314⎛⎫⎪⎝⎭和2314⎛⎫⎪⎝⎭； (3)2－1.5和30.2.11．2000年10月18日，美国某城市的日报以醒目标题刊登了一条消息：“市政委员会今天宣布：本市垃圾的体积达到50 000 m 3”，副标题是：“垃圾的体积每三年增加一倍”．如果把3年作为垃圾体积加倍的周期，请你完成下面关于垃圾的体积V (m 3)与垃圾体积的加倍的周期.(1) (2)根据报纸所述的信息，你估计3年前垃圾的体积是多少？ (3)如果n ＝－2，这时的n ，V 表示什么信息？(4)写出n 与V 的函数关系式，并画出函数图象(横轴取n 轴)． (5)曲线可能与横轴相交吗？为什么？12．定义运算a ⊕b ＝⎩⎪⎨⎪⎧a (a ≤b )b (a >b )，则函数f (x )＝1⊕2x 的图象是________．(填序号)13．定义在区间(0，＋∞)上的函数f (x )满足对任意的实数x ，y 都有f (x y )＝yf (x )． (1)求f (1)的值；(2)若f (12)>0，解不等式f (ax )>0.(其中字母a 为常数)．能力提升一、填空题1．设P ＝{y |y ＝x 2，x ∈R }，Q ＝{y |y ＝2x ，x ∈R }，则P 、Q 的关系为________． 2．函数y ＝16－4x 的值域是________．3．函数y ＝a 在[0,1]上的最大值与最小值的和为3，则函数y ＝2ax －1在[0,1]上的最大值是________．4．若函数f (x )＝3x ＋3－x 与g (x )＝3x －3－x 的定义域均为R ，则下列命题正确的是________．(填序号)①f (x )与g (x )均为偶函数；②f (x )为偶函数，g (x )为奇函数； ③f (x )与g (x )均为奇函数；④f (x )为奇函数，g (x )为偶函数．5．函数y ＝f (x )的图象与函数g (x )＝e x ＋2的图象关于原点对称，则f (x )的解析式为________． 6．已知a ＝1335-⎛⎫ ⎪⎝⎭，b ＝1235-⎛⎫⎪⎝⎭，c ＝1243-⎛⎫ ⎪⎝⎭，则a ，b ，c 三个数的大小关系是________．7．春天来了，某池塘中的荷花枝繁叶茂，已知每一天新长出荷叶覆盖水面面积是前一天的2倍，若荷叶20天可以完全长满池塘水面，当荷叶刚好覆盖水面面积一半时，荷叶已生长了________天．8．已知函数f (x )是定义在R 上的奇函数，当x >0时，f (x )＝1－2－x ，则不等式f (x )<－12的解集是________．9．函数y ＝2212x x-+⎛⎫ ⎪⎝⎭的单调递增区间是________．二、解答题10．(1)设f (x )＝2u ，u ＝g (x )，g (x )是R 上的单调增函数，试判断f (x )的单调性； (2)求函数y ＝2212x x --的单调区间．11．函数f (x )＝4x －2x ＋1＋3的定义域为[－12，12]．(1)设t ＝2x ，求t 的取值范围； (2)求函数f (x )的值域．12．函数y ＝2x －x 2的图象大致是________．(填序号)13．已知函数f (x )＝2x－12x ＋1.(1)求f [f (0)＋4]的值；(2)求证：f (x )在R 上是增函数；(3)解不等式：0<f (x －2)<1517.知识清单1．函数y ＝a x (a >0，且a ≠1) R 2.(0,1) 0 1 y >1 0<y <1 0<y <1 y >1 增函数减函数基础练习 1．②解析 ①中－4<0，不满足指数函数底数的要求，③中因有负号，也不是指数函数，④中的函数可化为y ＝a 2·a x ，a x 的系数不是1，故也不是指数函数． 2．2解析由题意得⎩⎪⎨⎪⎧a 2－3a ＋3＝1，a >0且a ≠1，解得a ＝2. 3．②解析该函数是偶函数．可先画出x ≥0时，y ＝a x 的图象，然后沿y 轴翻折过去，便得到x <0时的函数图象．4．－19解析当x >0时，－x <0，∴f (－x )＝3－x ，即－f (x )＝(13)x ，∴f (x )＝－(13)x .因此有f (2)＝－(13)2＝－19.5．b <a <1<d <c解析作直线x ＝1与四个指数函数图象交点的坐标分别为(1，a )、(1，b )、(1，c )、(1，d )，由图象可知纵坐标的大小关系． 6．二、三、四解析函数y ＝(12)x 的图象上所有的点向下平移2个单位，就得到函数y ＝(12)x －2的图象，所以观察y ＝(12)x －2的图象可知．7.18解析由题意a 2＝4，∴a ＝2.f (－3)＝2－3＝18.8．a >1，b ≥2解析函数y ＝a x －(b －1)的图象可以看作由函数y ＝a x 的图象沿y 轴平移|b －1|个单位得到．若0<a <1，不管y ＝a x 的图象沿y 轴怎样平移，得到的图象始终经过第二象限；当a >1时，由于y ＝a x 的图象必过定点(0,1)，当y ＝a x 的图象沿y 轴向下平移1个单位后，得到的图象不经过第二象限．由b －1≥1，得b ≥2.因此，a ，b 必满足条件a >1，b ≥2. 9．[0,8)解析 y ＝8－23－x ＝8－23·2－x ＝8－8·(12)x＝8[1－(12)x ]．∵x ≥0，∴0<(12)x ≤1，∴－1≤－(12)x <0，从而有0≤1－(12)x <1，因此0≤y <8.10．解 (1)考察函数y ＝0.2x . 因为0<0.2<1，所以函数y ＝0.2x 在实数集R 上是单调减函数．又因为－1.5>－1.7，所以0.2－1.5<0.2－1.7.(2)考察函数y ＝(14)x .因为0<14<1，所以函数y ＝(14)x 在实数集R 上是单调减函数．又因为13<23，所以1314⎛⎫ ⎪⎝⎭>2314⎛⎫ ⎪⎝⎭1.(3)2－1.5<20，即2－1.5<1；30<30.2，即1<30.2，所以2－1.5<30.2.11．解 (1)由于垃圾的体积每3年增加1倍，24年后即8个周期后，该市垃圾的体积是50 000×28＝12 800 000(m 3)．(2)根据报纸所述的信息，估计3年前垃圾的体积是50 000×2－1＝25 000(m 3)．(3)如果n ＝－2，这时的n 表示6年前，V 表示6年前垃圾的体积． (4)n 与V 的函数关系式是V ＝50 000×2n ，图象如图所示．(5)因为对任意的整数n,2n >0，所以V ＝50 000×2n >0，因此曲线不可能与横轴相交． 12．①解析由题意f (x )＝1⊕2x＝⎩⎪⎨⎪⎧1， x ≥0；2x ， x <0.13．解 (1)令x ＝1，y ＝2，可知f (1)＝2f (1)，故f (1)＝0.(2)设0<x 1<x 2，∴存在s ，t 使得x 1＝(12)s ，x 2＝(12)t ，且s >t ，又f (12)>0，∴f (x 1)－f (x 2)＝f [(12)s ]－f [(12)t ]＝sf (12)－tf (12)＝(s －t )f (12)>0，∴f (x 1)>f (x 2)．故f (x )在(0，＋∞)上是减函数．又∵f (ax )>0，x >0，f (1)＝0， ∴0<ax <1，当a ＝0时，x ∈∅，当a >0时，0<x <1a ，当a <0时，1a<x <0，不合题意．故x ∈∅.综上：a ≤0时，x ∈∅；a >0时，不等式解集为{x |0<x <1a}．能力提升 1．Q P解析因为P ＝{y |y ≥0}，Q ＝{y |y >0}，所以Q P . 2．[0,4)解析 ∵4x >0，∴0≤16－4x <16， ∴16－4x ∈[0,4)． 3．3解析函数y ＝a x 在[0,1]上是单调的，最大值与最小值都在端点处取到，故有a 0＋a 1＝3，解得a ＝2，因此函数y ＝2ax －1＝4x －1在[0,1]上是单调递增函数，当x ＝1时，y max ＝3. 4．②解析 f (－x )＝3－x ＋3x ＝f (x )，g (－x )＝3－x －3x ＝－g (x )．5．f (x )＝－e －x －2解析 ∵y ＝f (x )的图象与g (x )＝e x ＋2的图象关于原点对称，∴f (x )＝－g (－x )＝－(e －x ＋2)＝－e －x －2. 6．c <a <b解析 ∵y ＝(35)x 是减函数，－13>－12，∴b >a >1.又0<c <1，∴c <a 0时，由1－2－x <－12，(12)x >32，得x ∈∅；当x ＝0时，f (0)＝0<－12不成立；当x <0时，由2x －1<－12，2x <2－1，得x <－1.综上可知x ∈(－∞，－1)． 9．[1，＋∞)解析利用复合函数同增异减的判断方法去判断．令u ＝－x 2＋2x ，则y ＝(12)u 在u ∈R 上为减函数，问题转化为求u ＝－x 2＋2x 的单调递减区间，即为x ∈[1，＋∞)．10．解 (1)设x 1<x 2，则g (x 1)<g (x 2)．又由y ＝2u 的增减性得()12g x<()22g x ，即f (x 1)<f (x 2)，所以f (x )为R 上的增函数．(2)令u ＝x 2－2x －1＝(x －1)2－2，则u 在区间[1，＋∞)上为增函数．根据(1)可知y ＝2212x x --在[1，＋∞)上为增函数．同理可得函数y 在(－∞，1]上为单调减函数．即函数y 的增区间为[1，＋∞)，减区间为(－∞，1]．11．解 (1)∵t ＝2x 在x ∈[－12，12]上单调递增，∴t ∈[22，2]．(2)函数可化为：f (x )＝g (t )＝t 2－2t ＋3，g (t )在[22，1]上递减，在[1，2]上递增，比较得g (22)<g (2)． ∴f (x )min ＝g (1)＝2， f (x )max ＝g (2)＝5－2 2.∴函数的值域为[2,5－22]． 12．①解析当x →－∞时，2x →0，所以y ＝2x －x 2→－∞，所以排除③、④.当x ＝3时，y ＝－1，所以排除②.13．(1)解 ∵f (0)＝20－120＋1＝0，∴f [f (0)＋4]＝f (0＋4)＝f (4)＝24－124＋1＝1517.(2)证明设x 1，x 2∈R 且x 1<x 2，则22x>12x>0,22x－12x>0，∴f (x 2)－f (x 1)＝212121212121x x x x ---++ ＝()()()21212222121x x x x -++>0，即f (x 1)<f (x 2)，所以f (x )在R 上是增函数．(3)解由0<f (x －2)<1517得f (0)<f (x －2)<f (4)，又f (x )在R 上是增函数，∴0<x －2<4，即2<x <6，所以不等式的解集是{x |2<x <6}．。

(人教a版)数学必修一课时训练：2.1.2(第1课时)指数函数的图象及性质(含答案)

关闭Word文档返回原板块。

课时提升卷(十六)指数函数的图象及性质（45分钟 100分）一、选择题(每小题6分,共30分)1.若函数y=(2a-3)x是指数函数,则a的取值范围是( )A.a>B.a>,且a≠2C.a<D.a≠22.指数函数y=f(x)的图象经过点(-2,),那么f(4)·f(2)等于( )A.8B.16C.32D.643.(2013·黄冈高一检测)已知集合M={y|y=-x2+2,x∈R},集合M)∩N=( )N={y|y=2x,0≤x≤2},则(RA.[1,2]B.(2,4]C.[1,2)D.[2,4)4.当x>0时,指数函数f(x)=(a-1)x<1恒成立,则实数a的取值范围是( )A.a>2B.1<a<2C.a>1D.a∈R5.(2012·四川高考)函数y=a x-(a>0,a≠1)的图象可能是( )二、填空题(每小题8分,共24分)6.已知函数f(x)=则f(2)+f(-2)= .7.(2012·山东高考改编)若函数f(x)=a x(a>0,a≠1)在[-1,2]上的最大值为4,最小值为m,且函数g(x)=(1-4m)x2在[0,+∞)上是增函数,则a= .8.(2013·长沙高一检测)关于下列说法:(1)若函数y=2x的定义域是{x|x≤0},则它的值域是{y|y≤1}.(2)若函数y=的定义域是{x|x≥2},则它的值域是{y|y≤}.(3)若函数y=2x的值域是{y|0<y≤4},则它的定义域一定是{x|0<x≤2}.其中不正确的说法的序号是.三、解答题(9题,10题14分,11题18分)9.已知函数f(x)=a x+b(a>0,且a≠1).若f(x)的图象如图所示,求a,b 的值.10.(2013·长春高一检测)已知函数f(x)=a x-1(x≥0)的图象经过点(2,),其中a>0且a≠1.(1)求a的值.(2)求函数y=f(x)(x≥0)的值域.11.(能力挑战题)已知函数y=a x(a>0且a≠1)在[1,2]上的最大值与最小值之和为20,记f(x)=.(1)求a的值.(2)证明f(x)+f(1-x)=1.(3)求f()+f()+f()+…+f()的值.答案解析1.【解析】选B.由题意得2a-3>0,且2a-3≠1,所以a>,且a≠2.2.【解析】选D.设f(x)=a x(a>0且a≠1),由已知得=a-2,a2=4,所以a=2,于是f(x)=2x,所以f(4)·f(2)=24·22=26=64.3.【解析】选B.由题可知M=(-∞,2],N=[1,4],∴R M=(2,+∞),(RM)∩N=(2,4].【变式备选】若集合M={y|y=2-x},P={y|y=},则M∩P等于( ) A.{y|y>1} B.{y|y≥1}C.{y|y>0}D.{y|y≥0}【解析】选C.y=2-x的值域为{y|y>0},y=的值域为{y|y≥0},因此,其交集为{y|y>0}.故选C.4.【解题指南】结合指数函数的图象,若x>0时,(a-1)x<1恒成立,则必有0<a-1<1,进而求解.【解析】选B.∵x>0时,(a-1)x<1恒成立,∴0<a-1<1,∴1<a<2.5.【解析】选D.当a>1时,y=a x-在R上为增函数,且与y轴的交点为(0,1-),又0<1-<1,故排除A,B.当0<a<1时,y=a x-在R上为减函数,且与y轴的交点为(0,1-),又1-<0,故选D.6.【解析】f(2)+f(-2)=22+3-2=.答案:【举一反三】若对于本题中的函数f(x),有f(a)=16,试求a的值.【解析】当a≤1时,f(a)=3a≤3<16,故a>1,此时有f(a)=2a=16,所以a=4.7.【解析】当a>1时,有a2=4,a-1=m,此时a=2,m=,此时g(x)=-x2在[0,+∞)上是减函数,不合题意.若0<a<1,则a-1=4,a2=m,故a=,m=,检验知符合题意.答案:8.【解题指南】解答本题一方面要注意利用函数的单调性由定义域求值域,由值域求定义域;另一方面要注意结合函数的图象,弄清楚函数值与自变量的关系.【解析】(1)不正确.由x≤0得0<2x≤20=1,值域是{y|0<y≤1}.(2)不正确.由x≥2得0<≤,值域是{y|0<y≤}.(3)不正确.由2x≤4=22得x≤2,所以若函数y=2x的值域是{y|0<y≤4},则它的定义域一定是{x|x≤2}.答案:(1)(2)(3)9.【解析】由图象得,点(2,0),(0,-2)在函数f(x)的图象上,所以解得10.【解析】(1)∵函数f(x)=a x-1(x≥0)的图象经过点(2,),∴=a2-1,∴a=.(2)由(1)知f(x)=()x-1=2·()x,∵x≥0,∴0<()x≤()0=1,∴0<2·()x≤2,∴函数y=f(x)(x≥0)的值域为(0,2].11.【解析】(1)函数y=a x(a>0且a≠1)在[1,2]上的最大值与最小值之和为20,∴a+a2=20,得a=4或a=-5(舍去).(2)由(1)知f(x)=,∴f(x)+f(1-x)=+=+=+=+=1.(3)由(2)知f()+f()=1,f()+f()=1,…,f()+f()=1,∴f()+f()+f()+…+f()=++…+=1+1+…+1=1 006.关闭Word文档返回原板块。

人教A版高中数学必修一：第2章指,对,幂函数2.1.2指数函数及其性质

年份 1999 2000 2001 2002 „ 1999+x 经过年数 0 1 2 3 „ x
• x y=13(1+1%)
人口数（亿）
练习
1设y1=a3x+1，y2=a-2x，其中a>0且a1, 确定x为何值时,有（1）y1=y2（2）y1>y2
1 2 求函数y 2
x2 2x 1
的单调递增区间。
•
1、指数函数的定义。 2、指数函数简图的作法以及应注意的地方。 3、指数函数的图像和性质。

•
2.1.2指数函数及其性质
•
材料1:某种细胞分裂时,由1个分
裂成2个,2个分裂成4个……一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x的函数关系是什么?
材料2:当生物死后,它机体内原有
的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为‘‘半衰期”.根据此规律,人们获得了生物体内碳14含量P与死亡年数t之间的关系,这个关系式应该怎样表示呢?
•
•
•
•
•
•
•
•
4 2 练习：将 பைடு நூலகம்2 , 3 3
1 2
1 3
2 3
3
3 , 用“”号连接起来。 4
1 3
1 2
2 3 4 2 3 4 3
•
3
2 3
例8、截止到1999年底，我国人口约13亿。如果今后能将人口年平均增长率控制在1%，那么经过20年后，我国人口数最多为多少（精确到亿）？

2.1.2指数函数及其性质(1)

1.图像向左、向右是无限延伸的。 (0,1)
2.图像都在x轴的上方。 3.都过定点（0，1）。
0
x
y a x (a 0且a 1) 的图象和特征：
a>1
图
6
5
象 4
3
2
11
-4
-2
0
2
4
6
-1
1.图象在x轴上方
特 2.从左到右上升征 3.过定点 (0，1)
4、a越大，向上越靠近y轴
0<a<1
2.1.2指数函数及其性质
第一课时
问题引入
问题1、某种细胞分裂时，由1个分裂成 2个，2个分裂成4个，1个这样的细胞分裂x次后，得到的细胞个数y与x的函数关系式是什么？
研究
分裂
次数 1次 2次 3次 4次
x次
……
y 2x
细胞 2个 4个 8个 16个
总数
21
22
23
24
2x
问题引入
质
4.单调性：
在R上是增函数
单调性: 在R上是减函数
对称性: y=ax和y=a-x关于y轴对称
例3、如图为指数函数：
(1) y ax (2) y bx (3) y cx (4) y d x的图象,
y
(2) (3)
(1)
(4)
比较 a, b, c, d 与1的大小关系.
O
x
c d 1 a b
例5、已知指数函数 f (x) ax (a 0且a 1）的图像经过点（3，π）求 f(0), f(1), f(-3)的值。
解：因为 f (x) a x 的图像过点(3, ),所以

高中数学课时作业二十二指数函数的概念图象及性质新人教A版必修第一册

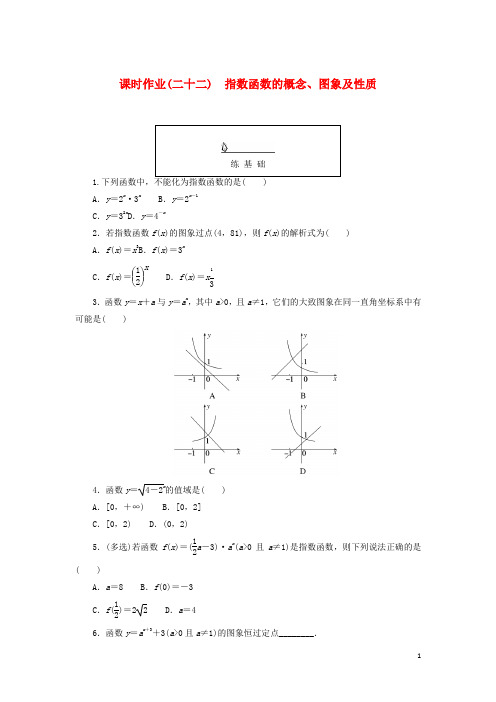
课时作业(二十二) 指数函数的概念、图象及性质练基础1.下列函数中，不能化为指数函数的是( ) A ．y ＝2x ·3x B ．y ＝2x －1C ．y ＝32xD ．y ＝4－x2．若指数函数f (x )的图象过点(4，81)，则f (x )的解析式为( ) A ．f (x )＝x 3B ．f (x )＝3xC ．f (x )＝⎝ ⎛⎭⎪⎫12xD ．f (x )＝x 133．函数y ＝x ＋a 与y ＝a x，其中a >0，且a ≠1，它们的大致图象在同一直角坐标系中有可能是( )4．函数y ＝4－2x的值域是( ) A ．[0，＋∞) B ．[0，2] C ．[0，2) D ．(0，2)5．(多选)若函数f (x )＝(12a －3)·a x(a >0且a ≠1)是指数函数，则下列说法正确的是( )A ．a ＝8B ．f (0)＝－3C ．f (12)＝2 2 D ．a ＝46．函数y ＝ax ＋3＋3(a >0且a ≠1)的图象恒过定点________．7．[2022·山东烟台高一期末]函数f (x )＝2x－1＋1x －1的定义域为________． 8．已知函数f (x )＝a x －1(x ≥0)的图象经过点⎝ ⎛⎭⎪⎫2，12，其中a ＞0且a ≠1. (1)求a 的值；(2)求函数y ＝f (x )(x ≥0)的值域提能力9.已知函数f (x )＝a x ＋b (a >0，a ≠1)的定义域和值域都是[－1，0]，则a ＋b ＝( ) A ．－32 B ．－1C ．1D ．3210．(多选)已知实数a ，b 满足等式2 021a ＝2 022b，下列式子可以成立的是( ) A ．a ＝b ＝0 B ．a <b <0 C ．0<a <b D ．0<b <a11．函数y ＝2x的图象与函数y ＝2－x的图象关于________对称，它们的交点坐标是________．12．求函数y ＝4x－2x＋1的定义域、值域．13.已知函数f (x )＝⎩⎪⎨⎪3x －1，x ≥0的值域为R ，则实数a 的取值范围为________．课时作业(二十二) 指数函数的概念、图象及性质1．解析：对于A ，y ＝2x·3x＝6x是指数函数；对于B ，y ＝2x －1＝2x2不是指数函数；对于C ，y ＝32x＝9x是指数函数；对于D ，y ＝4－x＝(14)x 是指数函数．答案：B2．解析：设f (x )＝a x (a >0且a ≠1)，则81＝a 4，∴a ＝3， ∴f (x )＝3x. 答案：B3．解析：∵a >0，则y ＝x ＋a 单调递增，故排除AC ；对于BD ，y ＝a x单调递减，则0<a <1， ∴y ＝x ＋a 与y 轴交于0和1之间，故排除B. 答案：D4．解析：∵2x >0，故0≤4－2x<4，∴函数值域为[0，2). 答案：C5．解析：因为函数f (x )是指数函数，所以12a －3＝1，所以a ＝8，所以f (x )＝8x，所以f (0)＝1，f (12)＝812＝22，故B 、D 错误，A 、C 正确．答案：AC6．解析：当x ＝－3时，y ＝a 0＋3＝4，所以函数y ＝ax ＋3＋3(a >0且a ≠1)的图象恒过定点(－3，4).答案：(－3，4)7．解析：根据题意，由⎩⎪⎨⎪⎧2x－1≥0x ≠1，解得x ≥0且x ≠1，因此定义域为[0，1)∪(1，＋∞).答案：[0，1)∪(1，＋∞)8．解析：(1)∵f (x )的图象过点(2，12)，∴a2－1＝12，则a ＝12. (2)由(1)知，f (x )＝⎝ ⎛⎭⎪⎫12x －1，x ≥0.由x ≥0，得x －1≥－1，于是0＜⎝ ⎛⎭⎪⎫12x －1≤⎝ ⎛⎭⎪⎫12－1＝2，所以函数y ＝f (x )(x ≥0)的值域为(0，2].9．解析：当a >1时，⎩⎪⎨⎪⎧f （－1）＝a －1＋b ＝－1f （0）＝a 0＋b ＝0，方程组无解；当0<a <1时，⎩⎪⎨⎪⎧f （－1）＝a －1＋b ＝0f （0）＝a 0＋b ＝－1，解得⎩⎪⎨⎪⎧a ＝12b ＝－2∴a ＋b ＝12－2＝－32.答案：A 10.解析：分别画出y ＝2 021x ，y ＝2 022x的图象，如示意图：实数a ，b 满足等式2 021a ＝2 022b，可得：a >b >0，或a 0，∴当2x＝12，即x ＝－1时，y 取最小值34，同时y 可以取一切大于等于34的实数，∴值域为[34，＋∞).13．解析：∵函数f (x )＝⎩⎪⎨⎪⎧（1－a ）x ＋2a ，x <03x －1，x ≥0的值域为R ，又当x ≥0时，3x －1≥13，∴⎩⎪⎨⎪⎧1－a >02a ≥13，解得16≤a <1.答案：16≤a <1。

数学新课标人教A版必修1教学课件：2.1.2.1 第1课时指数函数的图象及性质

数由小变大．(2)指数函数的底数与图象间的关系可概括记忆为：在第一象限内，底数自下而上依次增大．
必修1 第二章基本初等函数（I）
栏目导引第二十二页，编辑于星期日：十一点三十五分。
3.如图所示是指数函数的图象，已
知 a 的值取 2，43，130，15，则相应曲线 C1，C2，
C3，C4 的 a 依次为( )
必修1 第二章基本初等函数（I）
栏目导引第四页，编辑于星期日：十一点三十五分。
1．指数函数的概念函数y＝ax(a＞0，且a≠1，x∈R)叫做指数函数，其中 x为自变量． 2．指数函数的图象和性质
a>1
0<a<1
图象
必修1 第二章基本初等函数（I）
栏目导引第五页，编辑于星期日：十一点三十五分。
栏目导引第三页，编辑于星期日：十一点三十五分。
(4)当a＝0时，n取__零__或__负__数__没有意义．如果y＝f(x)在D上是增函数，则对任意x1， x2∈D且x1<x2，有f(x1)<(填“>”、“<”或 “＝”)f(x2)，y＝f(x)的图象从左至右逐渐__上__升 (填“上升”或“下降”)．
(4)∵－233<0，4313>430＝1，3412<340＝1， ∴－233<3412<4313.12 分
必修1 第二章基本初等函数（I）
栏目导引第二十八页，编辑于星期日：十一点三十五分。
[题后感悟] 比较幂的大小的常用方法： (1)对于底数相同，指数不同的两个幂的大小比较，可以利用指数函数的单调性来判断．(2)对于底数不同，指数相同的两个幂的大小比较，可以利用指数函数图象的变化规律来判断．(3)

人教版高中数学必修一第2章课件+课时作业+章末总结(29份)(2.1.2.1)

4．观察同一直角坐标系中函数y＝2x，y＝3x，y＝4x，y ＝(12)x，y＝(13)x，y＝(14)x的图象如图所示，能得到什么规律？
提示：(1)当a>1时，a的值越大，图象越靠近y轴，递增速度越快．
(2)当0<a<1时，a的值越小，图象越靠近y轴，递减的速度越快．
(3)底互为倒数时，图象关于y轴对称，即y＝ax与y＝ (1a)x图象关于y轴对称．
预习篇01
新知导学
指数函数的概念
一般地，函数 y＝ax (a>0，且a≠1)叫做指数函数，其中x是自变量，函数的定义域是 R .
1．下列函数是指数函数吗？ ①y＝3x＋1；②y＝3x＋1；③y＝3×2x；④y＝5x＋2－2. 提示：它们都不满足指数函数的定义，所以都不是指数函数．
2．指数函数定义中为什么规定a>0且a≠1? 提示：①如果a＝0，当x>0时，ax恒等于0；当x≤0 时，ax无意义． ②如果a<0，例如y＝(－4)x，这时对于x＝12，14，…，在实数范围内的函数值不存在． ③如果a＝1，则y＝1x是一个常量，无研究的必要．为了避免上述各种情况，所以规定a>0且a≠1.
答案：(1)C (2)(1,2)
指数函数的定义域与值域【例3】 (1)函数y＝ 1－3x的定义域是________；
(2)求函数y＝
的定义域和值域．
【解】 (1)由1－3x≥0，得3x≤1＝30. 因为函数y＝3x在实数集上是增函数，所以x≤0，故函数y＝ 1－3x的定义域为(－∞，0]． (2)由x－2≥0，得x≥2，所以此函数的定义域为[2，＋∞)．当x∈[2，＋∞)时， x－2≥0，又0<13<1.
由指数函数的性质知，y＝ y>0，故此函数的值域为(0,1]．

新人教A版必修1高中数学2.1.2-1指数函数及其性质导学案

高中数学 2.1.2-1指数函数及其性质导学案新人教A 版必修1学习目标：1、理解指数函数的定义 2、掌握指数函数的图象和性质学习重点：指数函数性质的应用学习过程：一、情景体验、获得新知1、一张纸对折1次，厚度变为原来的2倍；对折2次，厚度变为原来的倍；对折3次，厚度变为原来的2倍；对折4次，厚度变为原来的____ 倍；对折次，厚度变为原来的______倍。

2、指数函数的概念____________________ 练习：1、下列函数中是指数函数的是________ ① ② ③ ④ ⑤ ⑥2、函数是指数函数，则a=_________二、指数函数的图象与性质1、图象：在直角坐标系中作出下列函数的图象(1)(2)2、指数函数的图象和性质练习：1、若a>1，-1<b<0，则函数的图象一定在第_____象限 2、比较大小（1），（2），(3) ,一、选择题(每小题5分，共20分)1．设y 1＝40.9，y 2＝80.48，y 3＝(12)－1.5，则( )A ．y 3>y 1>y 2B ．y 2>y 1>y 3C ．y 1>y 2>y 3D ．y 1>y 3>y 22．若⎝ ⎛⎭⎪⎫142a ＋1<⎝ ⎛⎭⎪⎫143－2a，则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫12，＋∞ B.()1，＋∞C ．(－∞，1) D.⎝⎛⎭⎪⎫－∞，123．设函数f(x)定义在实数集上，它的图象关于直线x ＝1对称，且当x≥1时，f(x)＝3x －1，则有( )A ．f(13)<f(32)<f(23)B ．f(23)<f(32)<f(13)C ．f(23)<f(13)<f(32)D ．f(32)<f(23)<f(13)4．如果函数f(x)＝(1－2a)x 在实数集R 上是减函数，那么实数a 的取值范围是( )A ．(0，12)B ．(12，＋∞)C ．(－∞，12)D ．(－12，12)5．已知集合M ＝{－1,1}，N ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12<2x ＋1<4，x∈Z，则M∩N 等于( )A ．{－1,1}B ．{－1}C ．{0}D ．{－1,0} 6．设14<⎝ ⎛⎭⎪⎫14b <⎝ ⎛⎭⎪⎫14a<1，那么( )A ．a a <a b 0，f(x)＝e x a ＋ae x (e>1)，是R 上的偶函数，则a ＝________.10．下列空格中填“>、<或＝”．(1)1.52.5________1.53.2，(2)0.5－1.2________0.5－1.5.三、解答题(每小题10分，共20分)11．根据下列条件确定实数x 的取值范围：a<⎝ ⎛⎭⎪⎫1a 1－2x(a >0且a ≠1)．12．已知a>0且a≠1，讨论f(x)＝a－x2＋3x＋2的单调性．．．13．(10分)已知函数f(x)＝3x＋3－x.(1)判断函数的奇偶性；(2)求函数的单调增区间，并证明．。

2.1.2指数函数及其性质-2020-2021学年高一数学尖子生同步培优题典(人教A版必修1)

专题2.1.2 指数函数及其性质姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分100分，考试时间45分钟，试题共20题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共12小题，每小题4分，共48分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．函数()f x = ） A ．(2,)-+∞ B ．[1,)-+∞C ．(,1)-∞-D ．(,2)-∞-【答案】B【解析】要使函数有意义，需满足2113027x --≥，即：21333x --≥，因为3xy =为增函数，所以213x -≥-，解得：1x ≥-.2．（2020·浙江高一课时练习）函数2212x xy -⎛⎫=⎪⎝⎭的值域为（）A ．1,2⎡⎫+∞⎪⎢⎣⎭B ．1,2⎛⎤-∞ ⎥⎝⎦C ．(,2]-∞D ．(0,2]【答案】D【解析】由二次函数的性质可知222(1)1[1,)x x x -=--∈-+∞，因此221(0,2]2x xy -⎛⎫=∈⎪⎝⎭，即函数2212x xy -⎛⎫= ⎪⎝⎭的值域为(0,2].3．（2020·安徽高一月考）若函数xy a b =-，（0a >，且1a ≠）的图像经过第一，第三和第四象限，则一定有（） A ．01a <<且1b > B ．1a >且1b > C ．01a <<且1b < D ．1a >且1b <【答案】B【解析】根据指数函数的图象和性质可知，要使函数y ＝a x ﹣（b +1）（a ＞0且a ≠1）的图象经过第一、三、四象限，则函数为增函数，∴a ＞1，且f （0）＜0，即f （0）＝1﹣b ＜0，解得b ＞1．4．（2020·上海华师大二附中高一期末）若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( ) A ．9,34⎛⎫⎪⎝⎭B ．9,34⎡⎫⎪⎢⎣⎭C ．()1,3D ．()2,3【答案】B【解析】函数6(3)3,7(),7x a x x f x a x ---⎧=⎨>⎩单调递增，()301373a a a a⎧->⎪∴>⎨⎪-⨯-≤⎩解得934a ≤<所以实数a 的取值范围是9,34⎡⎫⎪⎢⎣⎭．5．如果1111222b a⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭，那么（）A ．a b a a a b <>>，所以a ab a b a <<，故选C .6．若函数f(x)＝a |2x －4|(a>0，a≠1)满足f(1)＝19，则f(x)的单调递减区间是( ) A ．(－∞，2] B ．[2，＋∞) C ．[－2，＋∞) D ．(－∞，－2]【答案】B【解析】由f(1)=得a 2=,∴a=或a=-(舍),即f(x)=(.由于y=|2x -4|在(-∞,2]上单调递减,在[2,+∞)上单调递增,所以f(x)在(-∞,2]上单调递增,在[2,+∞)上单调递减,故选B.7．函数f (x )＝x 2－bx ＋c 满足f (x ＋1)＝f (1－x )，且f (0)＝3，则f (b x )与f (c x )的大小关系是 A ．f (b x )≤f (c x ) B ．f (b x )≥f (c x ) C ．f (b x )>f (c x ) D ．与x 有关，不确定【答案】A【解析】∵f （1+x ）＝f （1﹣x ），∴f （x ）图象的对称轴为直线x ＝1，由此得b ＝2．又f （0）＝3，∴c ＝3． ∴f （x ）在（﹣∞，1）上递减，在（1，+∞）上递增．若x ≥0，则3x ≥2x ≥1，∴f （3x ）≥f （2x ）．若x ＜0，则3x ＜2x ＜1，∴f （3x ）＞f （2x ）．∴f （3x ）≥f （2x ）． 8．函数2x y a a a =-+（0a >且1a ≠）的图象不可能是（）A ．B ．C ．D ．【答案】D【解析】当01a <<时，2x y a a a =-+为减函数，取0x =时，函数值202155244y a a a a ⎛⎫=-+=--+= ⎪⎝⎭，又01a <<，所以2021551244a a a a ⎛⎫<-+=--+≤ ⎪⎝⎭故C 选项符合题意，D 选项不符合题意；当1a >时，函数2xy a a a =-+为增函数，取0x =时，函数值2021524y a a a a ⎛⎫=-+=--+ ⎪⎝⎭，又1a >，所以20215124a a a a ⎛⎫-+=--+< ⎪⎝⎭，故A 选项符合题意，B 选项也符合题意.故选：D.9．（2020·河南高一月考）已知()g x 为偶函数，()h x 为奇函数，且满足()()2xg x h x -=.若存在[]1,1x ∈-，使得不等式()()0m g x h x ⋅+≤有解，则实数m 的最大值为（） A ．35B ．35C ．1D ．-1【答案】A 【解析】()g x 为偶函数，()h x 为奇函数，且()()2x g x h x -=①，()()()()2x g x h x g x h x -∴---=+=②①②两式联立可得()222x x g x -+=，()222x x h x --=.由()()0m g x h x ⋅+≤得224121224141x x x x x x x m ----≤==-+++，∵2141xy =-+在[]1,1x ∈-为增函数，∴max231415x ⎛⎫-= ⎪+⎝⎭，故选：A. 10．已知实数a ，b 满足等式1123ab⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，给出下列五个关系式：①0<b<a ；②a ＜b ＜0；③0＜a ＜b ；④b ＜a ＜0；⑤a ＝b.其中，不可能成立的有( ) A ．1个 B ．2个C ．3个D ．4个【答案】B【解析】作y ＝12x ⎛⎫ ⎪⎝⎭与y ＝13x⎛⎫ ⎪⎝⎭的图象．当a ＝b ＝0时， 1123a b ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭；当a<b<0时，可以使1123a b ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭；当a>b>0时，也可以1123a b⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭故①②⑤都可能成立，不可能成立的关系式是③④.故选B.11．（2020·四川西昌高一期末）已知函数()228f x x x =+-，则不等式()13516x f --≤的解集是（）A ．[]1,3B ．[]1,9C ．[)1,∞D ．(],3-∞【答案】A【解析】函数()228f x x x =+-的定义域为R ，关于原点对称，且()()()222828f x x x x x f x -=-+--=+-=，该函数为偶函数，当0x ≥时，()()222819f x x x x =+-=+-，该函数在区间[)0,+∞上为增函数，由()13516x f --≤，得()()1354x f f --≤，1354x -∴-≤，即14354x --≤-≤，得1139x -≤≤，可得012x ≤-≤，解得13x ≤≤.因此，不等式()13516x f --≤的解集是[]1,3.12．（2020·广东濠江金山中学高一期末）已知函数2()33x xf x -=+，则（）A ．()f x 在(0,2)单调递增B ．()f x 在(0,2)单调递减C ．()y f x =的图像关于直线1x =对称D ．()y f x =的图像关于y 轴对称【答案】C【解析】930,xt y t t =>=+，根据对勾函数的图像特征，9y t t=+在(0,3)单调递减，在(3,)+∞单调递增，3x t =在R 上单调递增，根据复合函数的单调性可得，当(0,3)t ∈，即(,1)x ∈-∞，函数2()33x x f x -=+单调递减，当(3,)t ∈+∞，即(1,)x ∈+∞，函数2()33x x f x -=+单调递增，所以选项A,B 错误；由22(2)2(2)3333()xx x x f x f x -----=+=+=，()y f x =的图像关于直线1x =对称，选项C 正确；由82(1)6,(1)3f f =-=，()y f x =的图像不关于y 轴对称，选项D ，错误.故选C. 二、填空题（本大题共4小题，每小题4分，共16分．不需写出解答过程，请把答案直接填写在横线上）13．已知函数2221()2x x f x ++⎛⎫= ⎪⎝⎭，则该函数的单调递增区间是__________.【答案】(,1]-∞-【解析】由题得函数的定义域为R .设2122,()2uu x x v =++=，函数222,u x x =++在∞(-,-1]单调递减，在[1,)-+∞单调递增，函数1()2u v =在其定义域内单调递减，所以2221()2x x f x ++⎛⎫= ⎪⎝⎭在∞(-,-1]单调递增，在[1,)-+∞单调递减.14．已知02x ≤≤，则函数124325x x y -=-⨯+的最大值为__________. 【答案】52【解析】设2x t =，02x ≤≤，则14t ≤≤，()12221114325353222x x y t t t -=-⨯+=-+=-+，故当1t =，即0x =时，函数有最大值为52. 15．已知函数|2|()21x f x -=-在区间[0,]m 上的值域为[0,3]，则实数m 的取值范围为__________．【答案】[2,4] 【解析】函数()221x f x -=-的对称轴为2x =，且在(],2-∞上单调递减，在()0,∞+上单调递增，由函数()221x f x -=-在区间[]0,m 上的值域为[]0,3，知022,m ≤-≤ 即[]2,4m ∈。

高中数学人教版A版必修一课时作业及解析：第二章2-1指数函数

∴原式＝－－24x1－≤2x<3 －3<x<1 .
12．解
1
1
1
原式＝
a3
2
a 8b
1
2
a3
2b3
1
1
×a3
4b3 2a3 a 3
a3
13．解 ∵x－ xy－2y＝0，x>0，y>0， ∴( x)2－ xy－2( y)2＝0， ∴( x＋ y)( x－2 y)＝0，由 x>0，y>0 得 x＋ y>0， ∴ x－2 y＝0，∴x＝4y， ∴y2＋x－2 xxyy＝8yy＋－42yy＝65.
6
1
－32>0， 33
<0，C
选项错．故选
D.]
6．B [①中，当 a<0 时，
a2
3 2
a2
1 2
3
＝(－a)3＝－a3，
∴①不正确；
②中，若 a＝－2，n＝3，
则3 －23＝－2≠|－2|，∴②不正确；
x－2≥0， ③中，有3x－7≠0，
即 x≥2 且 x≠73，
故定义域为[2，73)∪(73，＋∞)，∴③不正确； ④中，∵100a＝5,10b＝2， ∴102a＝5,10b＝2,102a×10b＝10，即 102a＋b＝10.
1 2
3
xy
1 2
·(xy)－1
12
＝ x3 ·y 3
1
x6
y
1 6
x
1 2
y
1 2
＝x1 3·x1 31，＝－1，x<0
x>0
.
(2)原式＝ 1 ＋ 1 ＋ 2＋1－22 22
＝2 2－3.

2.1.2指数函数及其性质(第一课时)

2.1.2指数函数及其性质
莘县一中袁迪
学习目标:
1、了解指数函数模型的实际背景 2、理解指数函数的概念，掌握指数函数的性质
3、会利用指数函数的单调性比较大小
一、情景引入
情景1、把一张厚度为1毫米的纸对折1次，2次，3次的厚度分别是多少？对折30次呢？
2
2
223ຫໍສະໝຸດ 230那么，假设厚度为1，对折x次后，厚度y如何表示？
q x = ( ) 3
1x
6
h x =
x 3
5
4
g x =
(2 )
-2
1x
3
fx = 2 x
2
1
-4
2
4
y
y
y
1 y 2
x
1 y 3
x
x
y 3
x
y 2
x
ya
( a 1)
ya
x
( 0 a 1)
1 1
1 1
0
x
0
16
0
1
14
1
3
2
9
3
27 1/27
…
… …
y3
…
x
1/27 1/9 27 9
1/3 3
12 10
1 y 3
…
1
1/3 1/9
g x =
(3 )
1x
8
6
fx =
x 3
4
2
-10
-5
5
10
q x = ( ) 3
1x
6
h x =
x 3
5
4
g x =

必修1教案2.1.2指数函数及其性质(一)

2.1.2 指数函数及其性质（一）（一）教学目标1．知识与技能了解指数函数模型的实际背景，理解指数函数的概念，掌握指数函数的图象．2．过程与方法能借助计算器或计算机画出具体指数函数的图象，探索指数函数图象特征．3．情感、态度与价值观在解决简单实际问题的过程中，体会指数函数是一类重要的函数模型，激发学生学习数学的兴趣，努力培养学生的创新意识．（二）教学重点、难点1．教学重点：指数函数的概念和图象．2．教学难点：指数函数的概念和图象．（三）教学方法采用观察、分析、归纳、抽象、概括，自主探究，合作交流的教学方法，通过各种教学媒体（如计算机或计算器），调动学生参与课堂教学的主动性和积极性．（四）教学过程教学环节教学内容师生互动设计意图复习引入1. 在本章的开头，问题（1）中时间x与GDP值中的 1.073(20)xy x x=∈≤与问题(2)中时间t和C-14含量P的对应关系]t51301P=[()2，请问这两个函数有什么共同特征.2. 这两个函数有什么共同特征157301][()]2tP=t57301把P=[()变成2，从而得出这学生思考回答函数的特征．由实际问题引入，不仅能激发学生的学习兴趣，而且可以培养学生解决实际问题的能力．两个关系式中的底数是一个正数，自变量为指数，即都可以用xy a =（a ＞0且a ≠1来表示）.形成概念理解概念指数函数的定义一般地，函数xy a =（a ＞0且a ≠1）叫做指数函数，其中x 是自变量，函数的定义域为R .回答：在下列的关系式中，哪些不是指数函数，为什么？（1）22x y +=（2）(2)xy =- （3）2xy =-（4）xy π=（5）2y x = （6）24y x=（7）xy x =（8）(1)xy a =- （a ＞1，且2a ≠）小结：根据指数函数的定义来判断说明：因为a ＞0，x 是任意一个实数时，xa 是一个确定的实数，所以函数的定义域为实数集R .000,0xx a a x a ⎧>⎪=⎨≤⎪⎩x当时,等于若当时,无意义若a ＜0，如1(2),,8x y x x =-=1先时,对于=等等,6在实数范围内的函数值不存在.若a =1, 11,xy == 是一个常量，没有研究的意义，只有满足学生独立思考，交流讨论，教师巡视，并注意个别指导，学生探讨分析，教师点拨指导．由特殊到一般，培养学生的观察、归纳、概括的能力．使学生进一步理解指数函数的概念.(0,1)x y a a a =>≠且的形式才能称为指数函数，a 为常数,如：,,xy x =1xxy=2-3,y=253,31x x y y +==+等等,不符合(01)x y a a a =>≠且的形式,所以不是指数函数 .深化概念我们在学习函数的单调性的时候，主要是根据函数的图象，即用数形结合的方法来研究. 下面我们通过先来研究xy a =（a ＞1）的图象，用计算机完成以下表格，并且用计算机画出函数2xy =的图象x3.00- 2.50- 2.00- 1.50-2x y =18-141.00- 0.00 0.50 1.00 1.502.00 121 2 4再研究先来研究xy a =（0＜a ＜1）的图象，用计算机完成以下表格并绘出函数1()2xy =的图象.x2.50- 2.00- 1.50- 1.00- 0.001()2x y =141211.00 1.502.00 2.50学生列表计算，描点、作图．教师动画演示．学生观察、归纳、总结，教师诱导、点评．通过列表、计算使学生体会、感受指数函数图象的化趋势，通过描点，作图培养学生的动手实践能力．不同情况进行对照，使学生再次经历从特殊到一般，由具体到抽象的思维过程．培养学生的归纳概括能力．从图中我们看出12()2x x y y ==与的图象有什么关系?通过图象看出12()2x x y y y ==与的图象关于轴对称,实质是2xy =上的x,y 点(-)x y x,y y 1与=()上点(-)关于轴对称.2讨论：12()2xx y y ==与的图象关于y 轴对称，所以这两个函数是偶函数，对吗？②利用电脑软件画出115,3,(),()35x x x x y y y y ====的函数图象.2 4所以0(0)1f π==，133(0)f ππ==，11(3)f ππ--==.归纳总结1、理解指数函数(0),xy a a =>101a a ><<注意与两种情况2、解题利用指数函数的图象，可有利于清晰地分析题目，培养数型结合与分类讨论的数学思想 .学生先自回顾反思，教师点评完善．通过师生的合作总结，使学生对本节课所学知识的结构有一个明晰的认识，形成知识体系.课后作业作业：2.1 第四课时习案学生独立完成巩固新知提升能力备选例题例1 指出下列函数哪些是指数函数：（1）x y 4=；（2）4x y =；（3）x y 4-=；（4）xy )4(-=；（5）xy π=；（6）24x y =；（7）x x y =；（8）,21()12(>-=a a y x且)1≠a . 【分析】根据指数函数定义进行判断. 【解析】（1）、（5）、（8）为指数函数；（2）是幂函数（后面2.3节中将会学习）；（3）是1-与指数函数x 4的乘积；（4）底数04<-，∴不是指数函数；（6）指数不是自变量x ，而底数是x 的函数；（7）底数x 不是常数. 它们都不符合指数函数的定义.【小结】准确理解指数函数的定义是解好本问题的关键.例 2 用计算机作出的图像，并在同一坐标系下作出下列函数的图象，并指出它们与指数函数y =x 2的图象的关系，⑴y =12+x 与y =22+x . ⑵y =12-x 与y =22-x .解：⑴作出图像，显示出函数数据表比较函数y =12+x 、y =22+x 与y =x2的关系：将指数函数y =x2的图象向左平行移动1个单位长度，就得到函数y =12+x 的图象，将指数函数y =x2的图象向左平行移动2个单位长度，就得到函数y =22+x 的图象⑵作出图像，显示出函数数据表比较函数y =12-x 、y =22-x 与y =x 2的关系：将指数函数y =x 2的图象向右平行移动1个单位长度，就得到函数y =12-x 的图象，将指数函数y =x 2的图象向右平行移动2个单位长度，就得到函数y =22-x 的图象小结：⑴当m >0时，将指数函数y =x 2的图象向右平行移动m 个单位长度，就得到函数y =m x -2的图象；当m >0时，将指数函数y =x 2的图象向左平行移动m 个单位长度，就得到函数y =2x m +的图象。

人教版高中数学必修一2.1.2.1课时练习习题(含答案解析)

2.1.2.1一、选择题1．下列函数中，值域是(0，＋∞)的函数是( )A ．y ＝21xB ．y ＝2x －1C ．y ＝2x ＋1D ．y ＝(12)2－x [答案] D [解析] 在A 中，∵1x≠0，∴21x ≠1，所以函数y ＝21x 的值域是{y |y >0，且y ≠1}．在B 中，∵2x －1≥0，∴2x －1≥0，所以函数y ＝2x －1的值域是[0，＋∞)．在C 中，∵2x ＋1>1，∴2x ＋1>1，所以函数y ＝2x ＋1的值域是(1，＋∞)．在D 中，由于函数y ＝(12)2－x 的定义域是R ，也就是自变量x 可以取一切实数，所以2－x 也就可以取一切实数，所以(12)2－x 取一切正实数，即函数y ＝(12)2－x 的值域为(0，＋∞)，故选D. 2．某种细菌在培养过程中，每20分钟分裂一次(一个分裂为两个)．经过3个小时，这种细菌由1个可繁殖成( )A ．511个B ．512个C ．1 023个D ．1 024个 [答案] B[解析] ∵每20分钟分裂一次，故3个小时共分裂了9次，∴29＝512，故选B.3．如果函数y ＝(a x －1)－12的定义域为(0，＋∞)那么a 的取值范围是( )A ．a >0B ．0<a <1C ．a >1D ．a ≥1 [答案] C[解析] y ＝(a x －1)－12＝1a x －1，因此a x －1>0 ∴a x >1，又∵x >0，∴a >1，故选C.4．函数y ＝a |x |(0<a <1)的图象是( )[答案] C[解析] y ＝⎩⎪⎨⎪⎧ a x (x ≥0)⎝⎛⎭⎫1a x (x <0)，∵0<a <1，∴在[0，＋∞)上单减，在(－∞，0)上单增，且y ≤1，故选C.[点评] 可取a ＝12画图判断．A ．a >b >cB ．b >a >cC ．b >c >aD ．c >b >a[答案] B即a >c ，∴b >a >c .[点评] 指数函数的图象第一象限内底大图高，6．函数y ＝a x 在[0,1]上的最大值与最小值的和为3，则a 等于( )A.12 B ．2C ．4 D.14[答案] B[解析] 当a >1时，y min ＝a 0＝1；y max ＝a 1＝a ，由1＋a ＝3，所以a ＝2.当0<a <1时，y max ＝a 0＝1，y min ＝a 1＝a .由1＋a ＝3，所以a ＝2矛盾，综上所述，有a ＝2.7．在同一平面直角坐标系中，函数f (x )＝ax 与指数函数g (x )＝a x 的图象可能是()[答案] B[解析] 由指数函数的定义知a >0，故f (x )＝ax 的图象经过一、三象限，∴A 、D 不正确．若g (x )＝a x 为增函数，则a >1，与y ＝ax 的斜率小于1矛盾，故C 不正确．B 中0<a <1，故B 正确．8．函数y ＝(12)x 2＋2x 的值域是( ) A ．(0，＋∞)B ．(0,2]C ．(12，2] D ．(－∞，2][答案] B[解析] ∵u ＝x 2＋2x ＝(x ＋1)2－1≥－1，y ＝(12)u 在[－1，＋∞)上是减函数， ∴y ≤⎝⎛⎭⎫12－1＝2.∴y ∈(0,2]．二、填空题9．指数函数y ＝f (x )的图象过点(－1，12)，则f [f (2)]＝________. [答案] 16[解析] 设f (x )＝a x (a >0且a ≠1)，∵f (x )图象过点(－1，12)，∴a ＝2，∴f (x )＝2x ， ∴f [f (2)]＝f (22)＝f (4)＝24＝16.10．当x ∈[－1,1]时，函数f (x )＝3x －2的值域为__________．[答案] {y |－53≤y ≤1} [解析] 当－1≤x ≤1时，13≤3x ≤3，∴y ∈[－53，1]，值域为{y |－53≤y ≤1}． 11．已知x >0时，函数y ＝(a 2－8)x 的值恒大于1，则实数a 的取值范围是________．[答案] a >3或a <－3[解析] 当x >0时(a 2－8)x >1，∴a 2－8>1，∴a >3或a <－3.12．(09·江苏文)已知a ＝5－12，函数f (x )＝a x ，若实数m ，n 满足f (m )>f (n )，则m ，n 的大小关系为________．[答案] m <n[解析] ∵a ＝5－12，∴0<a <1， ∴函数f (x )＝a x 在R 上单调递减，∵f (m )>f (n )，∴m <n .三、解答题13．已知f (x )＝12(a x －a －x )，g (x )＝12(a x ＋a －x )，求证：[f (x )]2＋[g (x )]2＝g (2x )．[解析] f 2(x )＋g 2(x )＝14(a x －a －x )2＋14(a x ＋a －x )2 ＝14(2a 2x ＋2a －2x )＝12(a 2x ＋a －2x )＝g (2x )成立． 14．分别把下列各题中的三个数按从小到大的顺序用不等号连接起来．15．已知f (x )＝73x ＋1，g (x )＝2x ，在同一坐标系中画出这两个函数的图象．试问在哪个区间上，f (x )的值小于g (x )？哪个区间上，f (x )的值大于g (x )?[解析] 在同一坐标系中，画出函数f (x )＝2x 与g (x )＝7x 3＋1的图象如图所示，两函数图象的交点为(0,1)和(3,8)，显然当x ∈(－∞，0)或x ∈(3，＋∞)时，f (x )>g (x )，当x ∈(0,3)时，f (x )<g (x )．16．判断函数f (x )＝x 2x －1＋x 2的奇偶性．[解析] ∵2x －1≠0，∴x ≠0，定义域{x ∈R |x ≠0}∵f (x )＝x 2x －1＋x 2＝x (2x ＋1)2(2x －1)，∴f (－x )＝－x (2－x ＋1)2(2－x －1)＝－x (1＋2x )2(1－2x )＝x (2x ＋1)2(2x －1)＝f (x )，∴f (x )为偶函数．17．求下列函数的定义域和值域[解析] (1)函数的定义域为R ，值域为(0，＋∞)(2)要使函数有意义，必须且只须3x －2≥0，即x ≥23，∴函数的定义域为[23，＋∞)设t ＝3x －2，则t ≥0，y ＝5t ∴y ≥1∴函数的值域为[1，＋∞)．(3)要使函数有意义，必须且只须x ＋1≠0，即x ≠－1.∴函数的定义域为{x ∈R |，x ≠－1}设t ＝x ＋2x ＋1，则t ∈R 且t ≠1，y ＝(13)t ，∴y >0且y ≠13∴函数的值域为(0，13)∪(13，＋∞)。

新教材高中数学指数函数的图象和性质第2课时指数函数的图象和性质的综合应用课时作业新人教A版必修第一册

第2课时指数函数的图象和性质的综合应用必备知识基础练1．函数f (x )＝(a －1)x是R 上的单调减函数,则a 的取值范围是( ) A ．a >2 B ．1<a <2 C ．0<a <1 D ．a >12．已知指数函数f (x )＝(2a 2－5a ＋3)a x在(0,＋∞)上单调递增,则实数a 的值为( ) A ．12 B ．1 C ．32D ．2 3．下列不等式中成立的是( ) A ．1.12.1<1.11.9B ．0.82.1<0.81.9C ．0.82.1>1.11.9D ．1.12.1<0.82.14．[2022·广东汕尾高一期末]若a ＝(12)13,b ＝(14)13,c ＝(12)14,则( )A ．c >a >bB ．c >b >aC ．b >c >aD ．a >b >c5．[2022·江苏宿迁高一期末]函数f (x )＝x 22x＋2－x的图象大致是( )6．(多选)已知函数f (x )＝e x－e －x,则下列说法正确的是( ) A ．函数f (x )是奇函数 B ．函数f (x )是偶函数 C ．函数f (x )在R 上是减函数 D ．函数f (x )在R 上是增函数7．函数f (x )＝2|x |的递增区间是________． 8．已知a ＝5＋12,函数f (x )＝a x,若实数m 、n 满足f (m )>f (n ),则m 、n 的大小关系为________．关键能力综合练1．已知函数y ＝(a －2)x,且当x <0时,y >1,则实数a 的取值范围是( ) A ．a >3 B ．2<a <3 C ．a >4 D ．3<a <42．若(13)2a ＋1>(13)4－a,则实数a 的取值范围是( )A ．(－∞,1)B ．(1,＋∞)C ．(3,＋∞)D ．(－∞,3)3．已知实数x ,y 满足(12)x <(12)y,则下列关系式中恒成立的是( )A.x 2>y 2B ．πx >πyC ．1x <1yD ．x >y4．已知函数f (x )＝⎩⎪⎨⎪⎧（2－a ）x ＋1，x ≥1a x ，x <1是R 上的单调递增函数,则实数a 的取值范围是( )A ．a >1B ．1<a <32C ．1<a <2D ．1<a ≤325．设14<(14)b <(14)a<1,那么( )A ．a a<a b<b aB ．a a<b a<a bC ．a b<a a<b aD ．a b<b a<a a6．[2022·重庆九龙坡高一期末](多选)已知函数f (x )＝2x－12x ＋1,则下列结论正确的是( )A ．函数f (x )的定义域为R B.函数f (x )的值域为(－1,1)C ．函数f (x )的图象关于y 轴对称D ．函数f (x )在R 上为增函数7．若f (x )＝a 2x －1＋12是奇函数．则实数a 的值是________.8．函数f (x )＝(12)x2－2x －3的单调减区间是________．9．[2022·湖南邵阳高一期末]已知函数f (x )＝a 3－x,(a 为常数,a >0且a ≠1),若f (2)＝3.(1)求a 的值； (2)解不等式f (x )>9.10．[2022·广东广州高一期末]已知f (x )＝a ·2x ＋a －22x＋1是定义在R 上的奇函数．(1)求实数a 和f (1)的值；(2)根据单调性的定义证明：f (x )在定义域上为增函数．核心素养升级练1．(多选)设函数f (x )＝2x,对于任意的x 1,x 2(x 1≠x 2),下列命题中正确的是( ) A ．f (x 1＋x 2)＝f (x 1)·f (x 2) B ．f (x 1·x 2)＝f (x 1)＋f (x 2) C ．f （x 1）－f （x 2）x 1－x 2<0D ．f (x 1＋x 22)<f （x 1）＋f （x 2）22．写出一个同时具有下列性质①②③的函数f (x )＝________． ①定义域为R ； ②值域为(－∞,1)；③对任意x 1,x 2∈(0,＋∞)且x 1≠x 2,均有f （x 1）－f （x 2）x 1－x 2>0.3．[2022·湖北十堰高一期末]已知函数f (x )＝2a ＋2x ＋11＋2x .(1)当a ＝6时,求方程f (x )＝2x的解；(2)若对任意x ∈(0,＋∞),不等式f (x )≥a 恒成立,求a 的取值范围．第2课时指数函数的图象和性质的综合应用必备知识基础练1．答案：B解析：函数f (x )＝(a －1)x是R 上的单调减函数, 所以0<a －1<1,解得1<a <2. 2．答案：D解析：由题得2a 2－5a ＋3＝1,∴2a 2－5a ＋2＝0,∴a ＝2或a ＝12.当a ＝2时,f (x )＝2x在(0,＋∞)上单调递增,符合题意；当a ＝12时,f (x )＝(12)x在(0,＋∞)上单调递减,不符合题意．所以a ＝2. 3．答案：B解析：A.因为y ＝1.1x 在R 上是增函数,所以1.12.1>1.11.9,故错误； B ．因为y ＝0.8x 在R 上是减函数,所以0.82.1<0.81.9,故正确； C ．因为0.82.1<1,1.11.9>1,所以0.82.1<1.11.9,故错误； D ．因为1.12.1>1,0.82.1<1,所以1.12.1>0.82.1,故错误． 4．答案：A解析：b ＝(14)13＝(12)23,因为y ＝(12)x 在R 上为减函数,且14<13<23,所以(12)14>(12)13>(12)23,所以c >a >b .5．答案：C 解析：x ∈R ,f (－x )＝x 22－x＋2x＝f (x ),所以f (x )为偶函数,图象关于y 轴对称,排除选项AB ；当x >0时,f (x )＝x 22－x ＋2x >0,故D 错误．6．答案：AD解析：f (－x )＝e －x－e x ＝－f (x ),函数f (x )＝e x －e －x的定义域为R , 函数f (x )是奇函数,A 正确,B 错误；y ＝e x 为R 上的增函数,y ＝e －x 为R 上的减函数,则函数f (x )＝e x－e －x为R 上的增函数,C 错误,D 正确． 7．答案：(0,＋∞)解析：因为f (x )＝2|x |＝⎩⎪⎨⎪⎧2x，x >0（12）x ，x ≤0,故函数f (x )的单调递增区间为(0,＋∞).8．答案：m >n 解析：∵a ＝5＋12>1,所以,函数f (x )＝a x为R 上的增函数, ∵f (m )>f (n ),∴m >n .关键能力综合练1．答案：B解析：∵当x <0时,y >1,∴0<a －2<1,解得2<a <3. 2．答案：A解析：因为函数y ＝(13)x在R 上为减函数,∴(13)2a ＋1>(13)4－a,等价于2a ＋1<4－a ,解得a <1, 所以实数a 的取值范围是(－∞,1). 3．答案：B解析：由(12)x <(12)y 以及指数函数y ＝(12)x为减函数,可得x >y ,对于A,当x ＝1>y ＝－1时,x 2>y 2不成立,故A 不正确；对于B,根据指数函数y ＝πx为R 上的增函数可知,πx>πy恒成立,故B 正确；对于C,当x >0,y <0时,1x <1y不成立,故C 不正确；对于D,当x 或y 为负数时,x 或y 无意义,所以D 不正确． 4．答案：D解析：根据题意可列不等式如下,⎩⎪⎨⎪⎧2－a >0a >1（2－a ）＋1≥a 解得 1<a ≤32,选项D 正确． 5．答案：C解析：∵14<(14)b <(14)a<1,∴0<a a b, 因为y ＝x a在(0,1)单调递增,所以a a0,所以函数f (x )的定义域为R ,因此本选项结论正确；B ：f (x )＝2x－12x ＋1＝1－22x ＋1,由2x >0⇒2x＋1>1⇒0<12x ＋1<1⇒－2<－22x ＋1<0⇒－1<1－22x＋1<1,所以函数f (x )的值域为(－1,1),因此本选项结论正确； C ：因为f (－x )＝2－x －12－x ＋1＝1－2x1＋2x ＝－f (x ),所以函数f (x )是奇函数,其图象关于原点对称,不关于y 轴对称,因此本选项说法不正确；D ：因为函数y ＝2x ＋1是增函数,因为y ＝2x＋1>1,所以函数y ＝22x ＋1是减函数,因此函数f (x )＝1－22x ＋1是增函数,所以本选项结论正确．7．答案：1解析：由题意f (－x )＋f (x )＝0即a2－x－1＋12＋a 2x －1＋12＝0,－a ＋1＝0,a ＝1. 8．答案：(1,＋∞)解析：由题知函数f (x )的定义域为R ,∵y ＝(12)x 单调递减,故只需求出y ＝x 2－2x －3的单调递增区间即可,∵y ＝x 2－2x －3开口向上,对称轴为x ＝1,故在(1,＋∞)单调递增,∴f (x )＝(12)x 2－2x －3的单调递减区间是(1,＋∞).9．解析：(1)∵函数f (x )＝a 3－x,f (2)＝3,∴f (2)＝a3－2＝a ＝3,∴a ＝3.(2)由(1)知f (x )＝33－x,由f (x )>9,得33－x>32,∴3－x >2,即x <1,∴f (x )>9的解集为(－∞,1).10．解析：(1)因为f (x )是定义在R 上的奇函数,所以f (0)＝0,a ＝1, f (x )＝2x－12x ＋1＝1－22x ＋1, f (1)＝13.(2)设任意x 1<x 2,则f (x 1)－f (x 2)＝－22x 1＋1＋22x 2＋1＝2（2x 1－2x 2）（2x 1＋1）（2x 2＋1）, ∵x 1<x 2,∴2x 1<2x 2,2x 1－2x 2<0, 所以f (x 1)－f (x 2)<0,f (x 1)<f (x 2), 故f (x )在定义域上为增函数．核心素养升级练1．答案：AD 解析：2x 1·2x 2＝2x 1＋x 2,所以A 项成立；2x 1＋2x 2≠2x 1x 2,所以B 项不成立；函数f (x )＝2x在R 上是单调递增函数,若x 1>x 2,则f (x 1)>f (x 2),则f （x 1）－f （x 2）x 1－x 2>0,若x 1<x 2,则f (x 1)<f (x 2),则f （x 1）－f （x 2）x 1－x 2>0,故C 项不正确；函数f (x )＝2x任意两点之间的连线在其图象的上方,所以f (x )＝2x的图象满足f (x 1＋x 22)<f （x 1）＋f （x 2）2,故D 项正确．2．答案：f (x )＝1－12x (答案不唯一)解析：f (x )＝1－12x ,定义域为R ；12x >0,f (x )＝1－12x <1,值域为(－∞,1)；是增函数,满足对任意x 1,x 2∈(0,＋∞)且x 1≠x 2,均有f （x 1）－f （x 2）x 1－x 2>0.3．解析：(1)当a ＝6时,由f (x )＝2x,可得12＋2x ＋11＋2x ＝2x,则(2x )2－2x －12＝0,所以2x ＝4或2x＝－3(舍去),解得x ＝2. 故方程f (x )＝2x的解为2.(2)由题意知2a ＋2x ＋11＋2x ≥a 在(0,＋∞)上恒成立,即2×2x ≥a (2x－1)在(0,＋∞)上恒成立．又因为x ∈(0,＋∞),所以2x－1>0,则a ≤2×2x2x －1＝2＋22x －1.因为22x －1>0,所以2＋22x －1>2,所以a ≤2,即a 的取值范围是(－∞,2].。