15准静态电磁场1
合集下载
准静态电磁场
低频时，时变电磁场可以简化为准静态场(仍时变）。
电准静态场（Electroquasistatic） 简写 EQS
感应电场远小于库仑电场，可忽略 Β t
磁准静态场（Magnetoquasistatic ）简写 MQS
位移电流远小于传导电流，可忽略 D t
解题方法：
利用静态场的方法求解出电(磁)准静态场的电(磁)
5.3.1 电荷在均匀导体中的驰豫过程
（Charge Relaxation Process in Uniform Conductive Medium)
在导体中，自由电荷体密度随时间衰减的过
程称为电荷驰豫。
设导电媒质 均,匀，且各向同性，在EQS场
中
J
t
J D/ D
0 t
返回 上页 下页
第五章
其解为
0 t
t
oe e
准静态电磁场
式中 o 为 t 0 时的电荷分布 ，τe / ━驰
豫时间，说明在导体中，若存在体分布的电荷，因
而EQS场的磁场按
H
J
D
计算。
t
返回 上页 下页
第五章
准静态电磁场
MQS场的磁场与恒定磁场满足相同的基本方程，
在任一时刻 t ，两种磁场分布一致，解题方法相同。
而MQS场的电场按 E B 计算。 t
以下两种情况可看作磁准静态场来计算： 1，对于导体中的时变电磁场，满足： = 1 则位移电流可以忽略，可按磁准静态场来处理。把 满足上述条件的导体称为良导体。
返回 上页 下页
第五章
准静态电磁场
2. 对于理想介质中的时变电磁场满足：
R
即当场点到源点的距离远小于场的波长时，略去位移 电流才是合理的。
第四章准静态电磁场
第四章 准静态电磁场4．1 准静态电磁场1．电准静态场由麦克斯韦方程组知，时变电场由时变电荷和时变磁场产生的感应电压产生。
时变电荷产生库仑电场，时变磁场产生感应电场。
在低频情况下，一般时变磁场产生的感应电场远小于时变电荷产生的库仑电场，可以忽略。
此时，时变电场满足ρ=∙∇≈⨯∇D 0E 称为电准静态场。
可见，电准静态场与静电场类似，可以定义时变电位函数ϕ ，即ϕ-∇=E且满足泊松方程ερϕ-=∇2 与电准静态场对应的时变磁场满足 0t =∙∇∂∂+=⨯∇B DE H γ 2．磁准静态场由麦克斯韦方程组知，时变磁场由时变传导电流和时变电场产生的位移电流产生。
在低频情况下，一般位移电流密度远小于时变传导电流密度，可以忽略。
此时，时变磁场满足0=∙∇≈⨯∇B J H c称为磁准静态场。
可见，磁准静态场与恒定磁场类似，可以定义时变矢量位函数A ，即A B ⨯∇=且满足矢量泊松方程c J A μ-=∇2与磁准静态场对应的时变电场满足ρ=∙∇∂∂-=⨯∇D B E t例1：图示圆形平板电容器，极板间距d = 0.5 cm ，电容器填充εr =5.4的云母介质。
忽略边缘效应，极板间外施电压t t u 314cos 2110)(=V ，求极板间的电场与磁场。
[解]：极板间的电场由极板上的电荷和时变磁场产生。
在工频情况下，忽略时变磁场的影响，即极板间的电场为电准静态场。
在如示坐标系下，得()()()V/m t 31410113t 31410501102d u z 4z 2z e e e E -⨯=-⨯⨯=-=-cos .cos . 由全电流定律得出，即由()z z 20r 4Sl t 31431410113d t H 2d e e S D l H ∙-π⨯⨯-=∙∂∂=π=∙⎰⎰ρεερφsin . 极板间磁场为φφφρe e H t 314103352H 4sin .-⨯== A/m也可以由麦克斯韦方程直接求解磁场强度，如下tt 0r ∂∂=∂∂=⨯∇E D H εε 展开，得t 314106694H 14sin .)(-⨯=∂∂φρρρ 解得φφφρe e H t 314103352H 4sin .-⨯== A/m 讨论：若考虑时变磁场产生的感应电场，则有tt ∂∂-=∂∂-=⨯∇H B E 0μ 展开，得t E z 314cos 103.231440ρμρ-⨯⨯-=∂∂- 解得 t E z 314cos 10537.428ρ-⨯= V/m可见，在工频情况下，由时变磁场产生的感应电场远小于库仑电场。
第六章 准静态场1 电磁场 华科电气
第6章准静态场
叶齐政，2009，4
一根直导线，当频率很高时，它是发射电磁波的天线；降低频率，它具有电感—电容的特性；再降低频率，它具有电感的特性；通以直流电时，它就相当于一个电阻。
一对平行板，当外加高频电源时，它是一个传播电磁波的导波装置；当频率降低时，它将只具有电容的特性。
电磁装置本身的特性除了依赖结构、材料以外，也依赖电磁场的频率变化。
高压传输线，晶体管，静电除尘器以及静电传感器等都可按电准静态场处理；
继电器，电动机和磁记录媒质等都可按磁准静态场处理。
()()
20/t ωsin I t i π+=。
第2章静态电磁场Ⅰ静电场精品PPT课件
(3) = 0
dl drdrer
a. r > a
P 2(r) P E 2• d l P E 2 d r3 0 a 0 3 rr 1 2d r 3 0 0 a r P 3
P2
(r) Q
40rP
0a3 30rP
b. r < a
P(r) E•dl
P
a
rP
0rdr0a3
30
a 30
0
P r E • dl P
工程上，以大地表面为电位参考面
大地 0
2.2.2 场分布：基于场量 E 的( r )分析
E (r) (r) V 4 r r rdV
r
V
4
1 rr
dV
1
4
V
Rr2eRdV
• dq = dV= dS= dl
(r )
(r )
E(r) 1
4
SRr2eRdS
1
4
V
r
r r
dV
Ar41V r ErrdV0
E(r) (r)
(r) E(r)
z
dV (x, y, z)
(r )
R r r eR
r
V
r
o
P(x, y, z) •
y
x
求任意场点 P 处的 E ( r ) 示意图
• 规定电位的参考点 Q 后，任一场点 P 处的电位为
Q
P r E • dl P
(4)画出球内外 E、 随 r 变化的分布图。
E
球状电荷分布 [解] (1) a. r<a
dS
a
(r) const 0 or
rP dl
0 P
S (高斯面) 0
静态电磁场I恒定电流的电场和磁场.pptx
5. 矢量磁位的泊松方程和拉普拉斯方程
1. 恒定磁场的矢量磁位 矢量磁位的定义
矢量磁位或称磁矢位
由 B 0
B A
即恒定磁场可以用一个矢量函数的旋度来表示。
3.利用矢量磁位A计算磁场
体电流分布:
A(r) 0 Jc (r' )dV '
4 V ' r r'
面电流分布:
A(r) 0 K (r' )dS '
4 S' r r'
线电流分布:
A(r) 0 I dl'
4 l' r r'
由于元电流矢量产生相同方向的元矢量磁位,故与基于B的分析计算相比，相 对较为简单，尤其在二维磁场(平行平面或轴对称磁场)。
dV
'
毕奥-萨伐尔定律（矢量积分关系式）
第21页/共59页
3.3.4 毕奥-萨法尔定律（矢量磁位）
根据导体中电流分布的不同形态：
体电流密度矢量 Jc v 面电流密度矢量 K v 线电流密度矢量 I v
元电流密度矢量 dqv
JcdV KdS Idl dq
因此，面、线电流分布情况下的磁感应强度为：
Jc dS 0
S
J1n J2n
E dl 0
l
E1t E2t
对线性各向同性媒质， J1 1E1 J2 2E2 (2) 良导体与不良导体分界面上的边界条件
tg1 1 tg2 2
1 2 1 90 o
2 0o
J2
n
例如，钢的电导率 1 = 5106 S/m，周围
2
土壤的电导率2 = 10-2 S/m，1 = 89， 可知，2 8。
sin2
e
工程电磁场倪光正第2章静态电磁场Ⅰ：静电场
电位
电位是描述电场中某点电荷所具有的能量的物理量，单位是焦耳/库仑 （J/C）。
在静电场中，电位与电场强度之间存在一定的关系，即电位等于电场强度 与距离的乘积。
电位具有相对性，其大小与参考点的选择有关，参考点不同，电位值也会 发生变化。
02
静电场的物理量
电场力
库仑定律
描述点电荷之间的相互作用力，公式为F=k*q1*q2/r^2，其中q1 和q2是点电荷的电量，r是两点电荷之间的距离，k是库仑常数。
03
静电场的数学模型
静电场的微分方程
01
静电场的基本方程是高斯定理和泊松方程。
02
高斯定理表明，在静电场中，穿过任意闭合曲面的 电场线数等于该闭合曲面所包围的电荷量。
03
泊松方程则描述了电场强度与电荷分布之间的关系。
静电场的边界条件
边界条件是指静电场在物体表面或不同媒质的分 界面上的行为。
电场线在物体表面上必须垂直于物体表面，即电 场切向分量连续。
的疏密程度表示电场强度的大小。
电场是一种物质，具有能量和动量，可以与重力场、磁场等相
03
互转化。
电场强度
01
电场强度是描述电场中电场力作 用强弱的物理量，单位是牛顿/ 库仑（N/C）。
02
电场强度的大小与电场中某点 的电荷量成正比，与该点放置 的试探电荷所受的电场力成正 比。
03
电场强度具有方向，其方向与 正电荷在该点所受的电场力方 向相同。
电容器的应用
在电子电路中广泛应用，如滤波、耦合、去 耦、储能等。
电场能量
01
电场能量的定义
02
电场能量的特点
03
电场能量的应用
电场能量是指静电场中储存的能 量，公式为W=1/2*ε0*E^2，其 中ε0是真空电容率，E是电场强 度。
第3章 静态电磁场分析01
dϕ = −El dl = − E ⋅ dl
◇ 空间A、B 两点的电位差
B
◇ 若选取
P( xP , yP , zP )为电位参考 （令ϕ P = 0 ），
的电位为
( xP , yP ,zP )
则任意点 A( x, y , z )
ϕB − ϕ A = ∫ −El ⋅ dl
A
ϕ = ϕ A − ϕP =
dWe = (αϕ ) d (αρ ) dV
◇ 整个充电过程外界对整个系统提供的总能量
1
We = ∫ dWe = ∫∫ αρϕdαdV =
0V
1 ρϕdV ∫ 2V
说明： 1）此公式只适用于静电场能量求解；
2) 3）
1 ρϕ 2
不表示能量密度； 为空间中自由电荷分布；
ρ
4）积分范围为整个空间，但可退化到电荷分布区域。
坐标增加的方向。 二者关系： 广义力×广义坐标=功 广义坐标 广义力 （单位） 距 离 面 积 体 积 角 度
机械力 （N ）
表面张力 （N/m）
压强 （N/m2）
转矩 N•m
设 N 个导体组成的系统,只有i号导体发 生位移 dg ，此时系统中带电体的电压或电荷将 发生变化，其功能关系为
N
dW = dWe + fdg = ∑ ϕ i dqi
N
, Cii = ∑ βij ，方程 qi = ∑ βijϕ j 可写为
j =1 j =1
N
N
qi = Cii (ϕi − 0) + ∑Cij (ϕi − ϕ j )
j =1 j ≠i
其比值
Cii =
qii ϕi − 0 qij
C11
C12 = C21
准静态电磁场
4.3 电磁场能量守恒定理 坡印廷矢量
1.电磁场能量守恒定理
S
(E
H
)
dS
d dt
V
(1 2
E
D
1 2
H
B)
dV
V
E
J
dV
物理意义：单位时间内，通过曲面S 进入体积V的电磁能量等于 体积V 中所增加的电磁场能量与损耗的能量之和。
2. 坡印廷矢量（电磁能流密度矢量）
D
D
H J t
H dl (J ) dS
l
S
t
全电流定律
E B t
E dl B dS 电磁感应定律
l
S t
B 0 D
SB dS 0
s D dS q
磁通连续性原理 高斯定律
J
2
2
t 2
Leabharlann 准静态电磁场知识结构 时变电磁场
动态场（高频）
准静态电磁场
似稳场 电磁波 （忽略推迟效应）
磁准静态场
( D 0) t
电准静态场
( B 0) t
具有静态电磁场的特点
返回 上页 下页
描述时变电磁场中电磁能量传输的一个重要物理量
定义：S
Ε
H
( W/m2 )
E
物理意义：
O
S
S 的方向 —— 电磁能量传输的方向
H
S
的大小
——
通过垂直于能量传输方
准静态静电场
图5.5.1 涡流
工程应用：叠片铁芯（电机、变压器、电抗器等）、电磁屏蔽、电磁炉等。 5 .5 .2 涡流场分布
以变压器铁芯叠片为例，研究涡流场分布。
图5.5.2 变压器铁芯叠片
图5.5.3 薄导电平板
假设：· l , h a ，场量仅是 x的函数； · B Bz ez ,故 E, J 分布在 xoy 平面，且仅有 y分量；
a 讨论当频率较低的特殊情况时，即当 较小时，则 d
P
1 2 2 a 2 BzavV 12
可以看出，为了减小涡流损耗，薄板应尽量薄，电导率应尽量小。因此， 交流电器的铁心都是由彼此绝缘的硅钢片叠装而成的。
5.1
电 准 静 态 场
电准静态场和磁准静态场
的作用，即 Ei 0, 电磁场基本方程为 D H J , B 0 , t E 0 , D
B ( 0) 低频时，忽略二次源 t
特点： 电场的有源无旋性与静电场相同，称为电准静态场（EQS）。 用洛仑兹规范 A t ，得到动态位满足的微分方程
· 磁场呈 y 轴对称,且 x 0 时， Bz B0。
在MQS场中，磁场满足涡流场方程（扩散方程）
图5.5.4 薄导电平板的磁场
. 2 H k H 2
d 2H z jH z k 2 H z 2 dx
解方程，代入假设条件，可以得到
H Z B0 ch( kx ) /
A J , 2 /
5.2
磁准静态场与集总电路
在MQS场中， J 0 即 J dS 0 ，故有 s J1 dS J 2dS J3dS i1 i2 i3 0 J dS S S S
工程应用：叠片铁芯（电机、变压器、电抗器等）、电磁屏蔽、电磁炉等。 5 .5 .2 涡流场分布
以变压器铁芯叠片为例，研究涡流场分布。
图5.5.2 变压器铁芯叠片
图5.5.3 薄导电平板
假设：· l , h a ，场量仅是 x的函数； · B Bz ez ,故 E, J 分布在 xoy 平面，且仅有 y分量；
a 讨论当频率较低的特殊情况时，即当 较小时，则 d
P
1 2 2 a 2 BzavV 12
可以看出，为了减小涡流损耗，薄板应尽量薄，电导率应尽量小。因此， 交流电器的铁心都是由彼此绝缘的硅钢片叠装而成的。
5.1
电 准 静 态 场
电准静态场和磁准静态场
的作用，即 Ei 0, 电磁场基本方程为 D H J , B 0 , t E 0 , D
B ( 0) 低频时，忽略二次源 t
特点： 电场的有源无旋性与静电场相同，称为电准静态场（EQS）。 用洛仑兹规范 A t ，得到动态位满足的微分方程
· 磁场呈 y 轴对称,且 x 0 时， Bz B0。
在MQS场中，磁场满足涡流场方程（扩散方程）
图5.5.4 薄导电平板的磁场
. 2 H k H 2
d 2H z jH z k 2 H z 2 dx
解方程，代入假设条件，可以得到
H Z B0 ch( kx ) /
A J , 2 /
5.2
磁准静态场与集总电路
在MQS场中， J 0 即 J dS 0 ，故有 s J1 dS J 2dS J3dS i1 i2 i3 0 J dS S S S
准静态电磁场-PPT课件
H J B E t B 0 D
H J
2 H H E
• 同理
H 2 H t E 2 E t J 2 J t
E J J E C D t R R j ( t ) v 2）理想介质中 E Re E e 1 R 0 v
1）导体内
§5-2 磁准静态场与电路
磁准静态场是交流电路的场理论基础。 恒定电流场： S J d s 0
§5-4 集肤效应
导体内通过交变电流时，周围、内部产生交变的磁场， 而交变的磁场产生感应电场，使导体内部的电流分布不均， 在靠近导体表面处电流密度增加，而内部电密减小，高频时 更趋于只有表面有电流通过，这种现象称为集肤效应。
Ei Ec Jc
一、E、H和J的微分方程
磁 准 静 态 场
一、涡流
1.定义：位于交变磁场中的导体，在其内部产生与磁场交 链的感应电流，由于感应电流自成闭合回路，呈旋涡状流 动，故称为涡流。
程。
3.了解导体中电流流动、涡流和磁扩散过程。
4.定性说明集肤效应、邻近效应、电磁屏蔽。
5.了解交流内阻抗的概念。
§5-1 电准静态场和磁准静态场
• 时变场中，一些场量（B、D）随时间变化，但变化的速 度很慢（可以忽略），可以按照静态场来处理。这样的场 称为准静态场。
D r , t H r , t J r , t t B r , t E r , t t B r , t 0 D r , t r , t
D t B t
静态电磁场I恒定电流的电场和磁场课件
磁场中的电流
恒定电流
磁场强度
电流的大小和方向保持不变的电流。
描述磁场强弱的物理量，与电流成正 比。
磁感应线
描述磁场分布的假想曲线，类似于电 场线。
磁场中的力
安培力
通电导线在磁场中受到的力，与电流和磁感应线的夹角有关 。
洛伦兹力
带电粒子在磁场中受到的力，与粒子的速度和磁感应线的夹 角有关。
霍尔效应
04
磁场基础
磁场的概念
磁场
是存在于磁体或电流周围的一种 特殊物质，能够传递磁力作用的
场。
磁力线
描述磁场分布的一种方式，磁力线 是闭合的曲线，表示磁场的方向和 强弱。
磁感应
当导体或电流在磁场中受到力的作 用时，会在导体或电流中产生电动 势或电流的现象。
磁感应线和磁感应强度
磁感应线
描述磁场分布的一种方式，磁感 应线是闭合的曲线，表示磁场的 方向和强弱。
磁感应强度
描述磁场强弱的物理量，表示单 位面积内的磁力线数量。
安培环路定律
安培环路定律
表示磁场与电流之间的关系，即磁场 对电流的作用力与电流成正比，与环 绕电流的导线的长度成正比，与导线 之间的距离成反比。
应用
安培环路定律是电磁学中的基本定律 之一，广泛应用于电磁场理论和电路 分析中。
05
恒定电流的磁场
欧姆定律和焦耳定律
总结词
欧姆定律是描述电路中电压、电流和电阻之间关系的定律，焦耳定律则是描述电路中热量产生与电流、电阻和时 间之间关系的定律。
详细描述
欧姆定律是电路分析中的基本定律之一，它指出在恒定温度下，电路中的电压（V）与电流（I）成正比，与电阻 （R）成反比，即 V=IR。焦耳定律则指出在电路中，电流通过导体时会产生热量，产生的热量（Q）与电流（I ）、电阻（R）和时间（t）的乘积成正比，即 Q=I²Rt。
090525第五章准静态电磁场
s
教材P335 教材
∫ J ⋅ dS = 0
流出任意闭合曲面的总传导电流是0。 流出任意闭合曲面的总传导电流是 。
５. ２磁准静态场和电路
∫ J ⋅ dS = 0
s
i1 i1 +i2 +i3 =0 i3 基尔霍夫电压定律（自学） 二、基尔霍夫电压定律（自学）
i2
５. 4 集肤效应
交流电流流过线圈， 交流电流流过线圈，导线周围变化的磁场在导线中感应电 流，从而使导线截面的电流分布步均匀。尤其频率较高时 从而使导线截面的电流分布步均匀。 电流几乎在导线表面附近的一薄层中流动， 集肤效应。 电流几乎在导线表面附近的一薄层中流动，即集肤效应。 （讨论导线自身有电流，其内部电流流动及电磁场分布） 讨论导线自身有电流，其内部电流流动及电磁场分布） 导线自身有电流 磁准静态场（ＭＱＳ）：位移电流密度忽略不计。 磁准静态场（ＭＱＳ）：位移电流密度忽略不计。 （ＭＱＳ）：位移电流密度忽略不计
二、磁准静态场Ｅ、Ｂ与动态位Ａ和φ关系 磁准静态场Ｅ、Ｂ与动态位Ａ Ｅ、Ｂ 关系
同恒定磁场
（1）矢量动态位
： A
B = ∇× A
∂A ∴∇ × E + =0 ∂t
（2）标量动态位 ϕ ：Φ标量函数 标量函数
∂B ∂ ∵ ∇× E = − = − (∇ × A) ∂t ∂t
令
∂A E+ = −∇ϕ ∂t
∇ × (∇ × H ) = ∇(∇ ⋅ H ) − ∇ H
2
得
∇ × J = ∇(∇ ⋅ H ) − ∇ H
2
∇ × (∇ × H ) = ∇(∇ ⋅ H ) − ∇ 2 H ∇ × J = ∇(∇ ⋅ H ) − ∇ 2 H
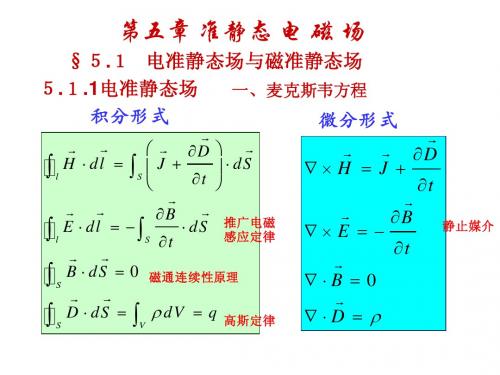
教材P335 教材
∫ J ⋅ dS = 0
流出任意闭合曲面的总传导电流是0。 流出任意闭合曲面的总传导电流是 。
５. ２磁准静态场和电路
∫ J ⋅ dS = 0
s
i1 i1 +i2 +i3 =0 i3 基尔霍夫电压定律（自学） 二、基尔霍夫电压定律（自学）
i2
５. 4 集肤效应
交流电流流过线圈， 交流电流流过线圈，导线周围变化的磁场在导线中感应电 流，从而使导线截面的电流分布步均匀。尤其频率较高时 从而使导线截面的电流分布步均匀。 电流几乎在导线表面附近的一薄层中流动， 集肤效应。 电流几乎在导线表面附近的一薄层中流动，即集肤效应。 （讨论导线自身有电流，其内部电流流动及电磁场分布） 讨论导线自身有电流，其内部电流流动及电磁场分布） 导线自身有电流 磁准静态场（ＭＱＳ）：位移电流密度忽略不计。 磁准静态场（ＭＱＳ）：位移电流密度忽略不计。 （ＭＱＳ）：位移电流密度忽略不计
二、磁准静态场Ｅ、Ｂ与动态位Ａ和φ关系 磁准静态场Ｅ、Ｂ与动态位Ａ Ｅ、Ｂ 关系
同恒定磁场
（1）矢量动态位
： A
B = ∇× A
∂A ∴∇ × E + =0 ∂t
（2）标量动态位 ϕ ：Φ标量函数 标量函数
∂B ∂ ∵ ∇× E = − = − (∇ × A) ∂t ∂t
令
∂A E+ = −∇ϕ ∂t
∇ × (∇ × H ) = ∇(∇ ⋅ H ) − ∇ H
2
得
∇ × J = ∇(∇ ⋅ H ) − ∇ H
2
∇ × (∇ × H ) = ∇(∇ ⋅ H ) − ∇ 2 H ∇ × J = ∇(∇ ⋅ H ) − ∇ 2 H
第五章准静态电磁场.教程文件
即集总电路的基尔霍夫电压定律 u0
表明电路理论是特殊情况下得麦克斯韦电磁理论的近似。 当满足MQS的似稳条件时，研究场的问题时可以采用路 的方法。
返回 上页 下页
第五章
准静态电磁场
5.3 电准静态场与电荷驰豫
EQS Field and Charge Relaxation
5.3.1 电荷在均匀导体中的驰豫过程
第五章
准静态电磁场
第五章准静态电磁场.
第五章
准静态电磁场
本章要求
了解EQS和MQS的共性和个性， 掌握工程计算中简化为准静态场的条件； 掌握准静态场的计算方法。
返回 上页 下页
第五章
准静态电磁场知识结构 时变电磁场
准静态电磁场
动态场（高频）
准静态电磁场
似稳场 电磁波 （忽略推迟效应）
R 1
磁准静态场
B 0 B A
E B t
(EA)0 t
EA
t
特点：磁场的有旋无源性与恒定磁场相同，称为磁准
静态场（MQS）。 用库仑规范 A0，得到泊松方程
2 A J, 2 / 返 回 上 页 下 页电磁场
, A 满足静态泊松方程，说明 EQS 和 MQS 没有波动性(忽
注意：电准静态场中的电场方程与静电场中方程相同， 但电准静态场中的电场是时变的，这区别于静电场。
在低频交流情况下，平板电容器中的电磁场属于电 准静态场
P187例
第五章
磁准静态场（MQS）。
准静态电磁场
若传导电流远大于位移电流，忽略二次源 D 的
作用，即 J d 0
t
HJ, B0,
EB/t, D0
当 l0时，有
J2n
J1n
t
表明电路理论是特殊情况下得麦克斯韦电磁理论的近似。 当满足MQS的似稳条件时，研究场的问题时可以采用路 的方法。
返回 上页 下页
第五章
准静态电磁场
5.3 电准静态场与电荷驰豫
EQS Field and Charge Relaxation
5.3.1 电荷在均匀导体中的驰豫过程
第五章
准静态电磁场
第五章准静态电磁场.
第五章
准静态电磁场
本章要求
了解EQS和MQS的共性和个性， 掌握工程计算中简化为准静态场的条件； 掌握准静态场的计算方法。
返回 上页 下页
第五章
准静态电磁场知识结构 时变电磁场
准静态电磁场
动态场（高频）
准静态电磁场
似稳场 电磁波 （忽略推迟效应）
R 1
磁准静态场
B 0 B A
E B t
(EA)0 t
EA
t
特点：磁场的有旋无源性与恒定磁场相同，称为磁准
静态场（MQS）。 用库仑规范 A0，得到泊松方程
2 A J, 2 / 返 回 上 页 下 页电磁场
, A 满足静态泊松方程，说明 EQS 和 MQS 没有波动性(忽
注意：电准静态场中的电场方程与静电场中方程相同， 但电准静态场中的电场是时变的，这区别于静电场。
在低频交流情况下，平板电容器中的电磁场属于电 准静态场
P187例
第五章
磁准静态场（MQS）。
准静态电磁场
若传导电流远大于位移电流，忽略二次源 D 的
作用，即 J d 0
t
HJ, B0,
EB/t, D0
当 l0时，有
J2n
J1n
t
准静态电磁场
② 电场分布同静电场，利用静电场的方法求解出电 场后，再用Maxwell方程求解与之共存的磁场。
③ 工程中如两线间的电磁场和电容器中的电磁场可 以看作EQS。
上页 下页
第五章
准静态电磁场
磁准静态场（MQS）
时变电磁场中各处位移电流密度远小于传导电流密 度时（忽略电场变化对磁场分布的影响）称为磁准静 态场。
当f2=15千兆赫
2π1 5 190 2 50 0 8.8 5 1 1 022.085
蒸馏水为有损耗的介质，计算这一频率时的电磁波 要考虑位移电流。
注意 导电媒质的似稳条件说明时变场中良导体是一
个相对的概念。
上页 下页
第五章
准静态电磁场
理想介质中的磁准静态场（MQS）
理想介质中 0 C J0只有位移电流
R 2R 2R 1U sU s(C 2C 1C 1R 2R 2R 1)eτ t
U 1R 2R 1R 1U s U s(C 2 C 2C 1R 2R 1R 1)eτ t
R1
R2
C1
C2
上页 上页
取洛仑兹规范 A
t
2AJ
t
上页 下页
第五章
准静态电磁场
磁准静态场 D 0 t
B 0 B A E B
t
(EA)0 t
H J
D
EA
A ( Α ) 2Α J
t
取库仑规范 A0
2AJ
D
(A)
t
2 A
t
2
上页 下页
第五章
准静态电磁场
问题
满足怎样的条件可以不考虑场的滞后效应，把电磁场 可作准静态场？
例 已知蒸馏水的物理参数为 μ r 1 ,εr 5,0 γ 2s0/m
《电磁场与电磁波》准静态电磁场
导电媒质的典型特征是电导率 ≠ 0
电磁波在导电媒质中传播时，有传导电流J=E
存在，同时伴随着电磁能量的损耗
1 导电媒质的复介电常数
D
H E
t
H = E +j E j ( j ) E
c j
H j c E
复介电常数
电磁波的相位速度仅与媒质相关
z 增大，相位滞后变
大，故k 称相位常数
dz
1
vp
dt k
真空中电磁波的相位速度： v0
1
0 0
5）电磁场关系—波阻抗
Ex Ex0 cos t kz
Hy
k
Ex 0 cos t kz
Z
Hy
理想介质
Z
（实数，纯电阻性质）
Ɛ替换为Ɛc
导电媒质 Z c
c
Zc
Z c e j
j
1
1
tan
2
π
0~
4
（呈电阻电感性）
6）相位速度（波速）
1
理想媒质中：v k
损耗媒质中：
媒质损耗使波的传播速度变慢，波长变短
波长 λ：相位差2π的两个相邻空间点的间隔
k 2π
k
2π
=
波数 k：2π距离内的波长数
k ：相移常数
单位距离内相位的变化量
相位变化的快慢: 随时间--频率
随空间--波数
电磁波在导电媒质中传播时，有传导电流J=E
存在，同时伴随着电磁能量的损耗
1 导电媒质的复介电常数
D
H E
t
H = E +j E j ( j ) E
c j
H j c E
复介电常数
电磁波的相位速度仅与媒质相关
z 增大，相位滞后变
大，故k 称相位常数
dz
1
vp
dt k
真空中电磁波的相位速度： v0
1
0 0
5）电磁场关系—波阻抗
Ex Ex0 cos t kz
Hy
k
Ex 0 cos t kz
Z
Hy
理想介质
Z
（实数，纯电阻性质）
Ɛ替换为Ɛc
导电媒质 Z c
c
Zc
Z c e j
j
1
1
tan
2
π
0~
4
（呈电阻电感性）
6）相位速度（波速）
1
理想媒质中：v k
损耗媒质中：
媒质损耗使波的传播速度变慢，波长变短
波长 λ：相位差2π的两个相邻空间点的间隔
k 2π
k
2π
=
波数 k：2π距离内的波长数
k ：相移常数
单位距离内相位的变化量
相位变化的快慢: 随时间--频率
随空间--波数
电磁场导论之准静态电磁场
y hx l
B
2020/1/31
第六章准静态电磁场
20
设硅钢片外磁场B沿z向，
宽度h≫厚度a，可忽略边缘效
y EJ
x EJ
a
应，认为E和J仅有y分量Ey和Jy。
h≫a
由于磁路长度l和宽度h远远大
一片薄板的横截面
于其厚度a，可近似认为E和H
与y和z无关，仅是x的函数
磁场扩散方程简化为
d2 H z dx 2
6-5 半径为a的长直圆柱型导
线为理想导体（1=）。设导 线中通有缓变电流
l1 H(t) i (t)
i(t)= Imsintez
l2
求：导线外的磁场强度H(t)和 感应电场E(t)。
E(t) 6-5题图
2020/1/31
第六章准静态电磁场
14
6-3 集肤效应与邻近效应
6-3-1 集肤效应
假设 x0的半无限大空间导体，
H ( H ) 2 H J
由于H= 0 ，J = E，因而 2 H E
将E = H/t 代入，得
t
H 2
H
由于导体中 = 0，同理 2 E E
t
2020/1/31
第六章准静态电磁场
12
而且相位x也随之改变。
频率很高时，电流密度几乎只在导体表面附近一薄层中。
场量主要集中在导体表面附近的这种现象，称为 集肤效应。
2020/1/31
第六章准静态电磁场
16
工程上常用透入深度d表示场量的集肤程度
定义：透入深度d为场量振幅衰减到其表面值的 1/e时所经过的距离。
d 1/ 2 /
第六章 准静态电磁场
第二章_静态电磁场I静电场
•电场强度的求解思路
思路一：先求电位，再利用
E r r
，求电场强度。
思路二：利用直接表达式求电场强度
E r
1 4 0
V
r
R
2
e R dV
n
思路三：利用高斯定理求电场强度
E dS q
S 0 i 1
1
i
2、电偶极子
• 相距很小距离l 的一对等值异号的 电荷，称为电偶极子. • 定义偶极子的电矩为电偶极矩以表 征其特性 :
自由空间中的E和
电位函数的引入 •亥姆霍兹定理（回顾） 当静电场电场强度E的散度及旋度给定后，该矢量场 E(r) 可以表示为
E (r ) (r ) A(r )
、
z
dV
式中
(r )
1 E(r) V r r dV 4π
0
(r )
r r
E [
ex ey ez ] x y z
根据 E 与 的微分关系，试问静电场中的某一点
0 E 0
E 0 0
？ ？
( (
) )
3. E与 的积分关系
E dl dl
[ x dx y
q 4 0
1 1 q r r 4 0 1 2
r2 r1 rr 12
当r很大时，r1、r2和r三者将近乎平行，此 时r2 r1 dcos，r1r2 r2代入上式，得
qd cos 1 p er 2 4 0 r 4 0 r 2
图 点电荷与不接地导体的电场
图
均匀场中放进了介质球的电场
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.求解步骤
电流 静磁场公式 分布
H、B
E B ,
精品课件
t
D
E、D 9
忽略位移电流的条件（似稳条件）
a.导体内的时变电磁场
ωε<<γ
D | J | E | J |
t
t
J | J | t
涡流场：导体中的磁准静态场。
良导体：满足ωε<<γ的导体。
b. 理想介质中的时变电磁场
R <<λ
S场的电场按
E 精品课件Bt
计算。
12/48
10 21 10 -12
10 18 10 -9
10 15 10 -6
10 12 10 -3
10 9 10 0
10 6 10 3
10 3 10 6
精品课件
13
10 0
§5-2 磁准静态场与电路
磁准静态方程是交流电路的场理论基础。
精品课件
14
（一）基尔霍夫电流定律
场
EHJB Dt
0 J
t
•B 0
•D
对(1)左 右取散度：
•J
• ( H )
0
SJ • dS 0
意义：
路
i1
(1)
S1 S
i2
i3
S2
S3
J • dS J • dS J • dS J • dS
器的轴线重合。由全电流定律有
Hdl l
Jdπ2
2πH
π2
πa2
ic
ic H
H 2π a2id(e)2.25sin314t(e) A/ m u
Jd
精品课件
图5.8.1 两圆电极的平板电6容器
例2、同轴圆柱形电容器，尺寸如图，长l，(l>>a,b)，填充有电介质(、 )， 内外导体之间的电压为U0sint， (不大)可认为电容器内的电场磁场分布
低频交流情况下，平板电容器中的电磁场属于电准静态场； 低频交流电感线圈导线中的电场可看作恒定电场。
精品课件
4
二、基本方程：
l l
H E
• dl
• dl
S (J
S
B t
D ) t0 • dS
• dS
=0
EH JB
t
D t0
=0
SB
•
dS
0
•B 0
SD • dS q
•D
B 0 B A
HJD t
AJ()
t
2AJ(A)
t
EB t
(EE At ) A0
D(A) t
t
2 A
t
取洛仑兹规范 A
t
取 A0, 得 2
2A J
精品课件
11
思考 EQS 与 MQS 的共性与个性
1. , A 满足泊松方程，说明 EQS 和 MQS 忽略了滞后效
0 • dS
SJ
•
dS
EHJB Dt
0 J
t
SB
•
dS
0
•B 0
SD • dS q
•D
1.磁准静态场与静态情况相比：只是电场的方程有变化。
(考虑了电磁感应)
2.磁场的方程与恒定磁场的方程完全一样；虽然此刻的磁场
强度H和磁感应强度B都是时间的函数，但它们的瞬时对应
关系，即每一时刻的关系类似于恒定磁场。
U0 cost ln( b / a)
ab
U0sint
则通过半径为 的圆柱面的位移电流总值为：
id
S
Jd
• dS
U 0 cost 2l
ln( b / a)
2lU0 cost
ln( b / a)
CU0 cost
则通过半径为 的圆柱面的位移电精流品课总件值等于电容器引线中的传导电流7 。
应，属于似稳场。 2. 在 EQS 和 MQS 场中，同时存在着电场与磁场，两者相
互 3. EQ依S存场。的电场与静电场满足相同的微分方程，在任一时
刻 t ，两种电场分布一致，解题方法相同。
EQS场的磁场按 H J D 4. 计M算QS。场的磁场与恒定磁场满足t相同的基本方程，在任一时
刻 t ，两种磁场分布一致，解题方法相同。
t
Ｈ、Ｂ 5
例1：有一圆形平行板空气电容器，极板半径 a =10cm。边缘
效应可以忽略。现设有频率为50Hz、有效值为0.1A的正弦电流 通过该电容器。求电容器中的磁场强度。
解：电容器中位移电流密度为
ic 0, id i
Jd
i πa2
(
ez
)
式中电流 i0.1 2sin31t4A。设圆柱坐标系的z轴与电容
• 任意两种场之间的空间尺度和时间尺度没有绝对的分界线。
• 工程应用（电气设备及其运行、精生品物课电件磁场等）
2
§5-1 电准静态场与磁准静态场
精品课件
3
（一）电准静态场
一、定义(EQS)：
时变场中各处感应电场Ei<<库仑电场Ec(电场呈现无 旋性)；即忽略电磁感应项 B ，则：
t
E (Ec Ei ) Ec 0
第五章 准静态电磁场
准静态电磁场: 感应电场远小于库仑电场或 位移电流密度远小于传导电
精品课件
1
时变电磁场
准静态电磁场（低频）
电准静态场
( B /t 0)
磁准静态场
( D /t 0)
动态场（高频）
似稳场 （忽略推迟效应）
电磁波
具有静态电 磁场的特点
• 电准静态场——Electroquasitatic 简写 EQS 磁准静态场—— Magnetoquasistatic 简写 MQS
- jR
e v 1
R 2R 1
v
近区或似稳区
R
精品课件
10
试证明在EQS场中，A, 满足 2AJ 和 2
证明： 在EQS场中
E0 E
试证明在MQS场中，A, 满足
2AJ 和 2
证明： 在MQS场中
B0
BA
D
()
2
HJ AJ
2 A J ( A )
2A J
库仑规范 A0
（二）磁准静态场
一、定义(MQS)：
时变场中各处位移电流密度<<传导电流密度，即忽
略位移电流项 D ，则磁场可看作恒定磁场：
t
H
J
D
J
t
低频交流电感线圈导线中的磁场属于磁准静态场；
精品课件
8
二、基本方程：
l l
H E
• dl
• dlS ( S来自J B tD ) t • dS
与恒定情况相同。求：(1)电容器中电场； (2)证明：通过半径为 (b>
>a)的圆柱面的位移电流总值等于电容器引线中的传导电流。
解: (1)在频率较低的情况下，电容内的电场为电准静态场
电场可用静电场的方法求解。
E
e
U 0 sin t ln( b / a)
(2)介质Jd中的位Dt移电流密Et度为e：
1.电准静态场与静态情况相比：只是磁场的方程有变化。
(考虑了位移电流引起的磁场)
2.电场强度E和电位移D的方程与静电场的方程完全一样；虽然
此刻的E和D都是时间的函数，但它们与源的瞬时对应关系， 即每一时刻场与源的关系类似于静电场。
3.求解步骤
电荷 分布
静电场公式
H J D , B 0
Ｅ、Ｄ 精品课件