深圳市平冈中学08-09必修一测试题

合集下载

深圳平冈中学必修一第四单元《函数应用》测试卷(答案解析)

一、选择题1．若函数2()f x x x a =--有四个零点，则关于x 的方程210ax x ++=的实根个数为（） A ．0B ．1C ．2D ．不确定2．已知函数()22020,0,,0,x x f x x x x <⎧=⎨-≥⎩若关于x 的方程()()21610f x kf x ++=有四个不同的实数根，则k 的取值范围为（） A ．(4,)+∞B ．(8,)+∞C ．(,4)-∞-D ．(,8)-∞-3．已知关于x 的方程2(3)10ax a x +-+=在区间1(,)2+∞上存在两个实数根，则实数a 的取值范围是（） A ．2332a << B ．213a < C ．9aD ．293a < 4．已知函数24,?0()7,?0x f x x x x x ⎧<⎪=⎨⎪-≥⎩，()()g x f x x a =+-，若()g x 存在两个零点，则a的取值范围是（） A ．(﹣4，0] B ．(-∞，﹣9) C ．(-∞，﹣9)(﹣4，0]D ．(﹣9，0]5．已知函数21,1()1,1x x x f x x x⎧-+<⎪=⎨⎪⎩，若函数()y f x a =-有三个零点，则实数a 的取值范围为（）A ．3[4，1]B ．3(4，1)C ．(0,1)D ．3(4，)+∞6．已知关于x 的方程|2|1x m -=有两个不等实根，则实数m 的取值范围是( ) A ．(-∞，1]-B ．(,1)-∞-C ．[1，)+∞D ．(1,)+∞7．新冠肺炎疫情防控中，核酸检测是新冠肺炎确诊的有效快捷手段．某医院在成为新冠肺炎核酸检测定点医院并开展检测工作的第n 天，每个检测对象从接受检测到检测报告生成平均耗时()t n （单位：小时）大致服从的关系为()0n N t n n N <=≥（0t 、0N 为常数）.已知第16天检测过程平均耗时为16小时，第64天和第67天检测过程平均耗时均为8小时，那么可得到第49天检测过程平均耗时大致为（） A ．16小时 B ．11小时 C ．9小时D ．8小时8．对任意实数a ，b 定义运算“”：,1,1b a b ab a a b -≥⎧=⎨-<⎩，设()()()214f x x x k =-++，若函数()f x 的图象与x 轴恰有三个交点，则k 的取值范围是（） A ．[)2,1-B ．[]0,1C ．(]0,1D ．()2,1-9．下列函数中，既是偶函数又存在零点的是（） A ．y =lnxB ．21y x =+C ．y =sinxD ．y =cosx10．统计学家克利夫兰对人体的眼睛详细研究后发现；我们的眼睛看到图形面积的大小与此图形实际面积的0.7次方成正比.例如：大图形是小图形的3倍，眼睛感觉到的只有0.73（约2.16）倍.观察某个国家地图，感觉全国面积约为某县面积的10倍，那么这国家的实际面积大约是该县面积的（lg 20.3010≈，lg30.4771=，lg70.8451≈）（） A ．l 8倍B ．21倍C ．24倍D ．27倍11．某工厂生产某产品2019年每月生产量基本保持稳定，2020年由于防疫需要2、3、4、5月份停产，6月份恢复生产时月产量仅为去年同期的一半，随着疫情缓解月产量逐步提高．该工厂如果想8月份产量恢复到去年同期水平，那么该工厂从6月开始月产量平均增长率至少需到达多少个百分点？（） A ．25B ．35C ．42D ．5012．已知函数,0()ln ,0x e x f x x x ⎧≤=⎨>⎩，若函数g （x ）＝f （x ）+2x +ln a （a ＞0）有2个零点，则数a 的最小值是（）A ．1eB ．12C ．1D ．e二、填空题13．已知函数22122,0()2log ,0x x x f x x x ⎧++≤⎪=⎨⎪>⎩，若关于x 的方程()f x a =有四个不同的解1x ，2x ，3x ，4x ，且1234x x x x <<<，则212344x x x x x ++的取值范围是____________. 14．已知函数2log ,02()25(),239x x x f x x <<⎧⎪=⎨+≥⎪⎩，若函数g (x )=f (x )-k 有两个不同的零点，则实数k的取值范围是________.15．已知函数()2log ,02 sin ,2104x x f x x x π⎧<<⎪=⎨⎛⎫≤≤ ⎪⎪⎝⎭⎩，若1234x x x x <<<且()()()()1234f x f x f x f x ===，则()()341222x x x x --的取值范围为____________.16．若y a x =的图象与直线y x a =+（0a >）有两个不同交点，则a 的取值范围是__________.17．函数()()23xf x x e =-，关于x 的方程()()210fx mf x -+=恰有四个不同的实数解，则正数m 的取值范围为______.18．关于x 的方程()2310xx x e b -+-=恰好有3个实数根，则实数b 的取值范围是__________.19．设函数31()(2)()2xf x x =+-的零点在区间(,1)n n +(n Z ∈)上，则n =______.20．已知()14f x x=-，若存在区间[]()0a b ⊆+∞，，，使得()[]{}[]|y y f x x a b ma mb =∈=，，，．则实数m 的取值范围是__________．三、解答题21．已知函数()f x 为偶函数，当0x ≥时，()11x x e f x e -=+.（1）求当0x <时，函数()f x 的解析式；（2）判断函数()f x 在(),0-∞上的单调性并证明；（3）设函数()()()2g x f ax f x a =--+，使函数()g x 有唯一零点的所有a 构成的集合记为M ，求集合M .22．有A 、B 两城相距120km ，某天然气公司计划修建一条管道为两城供气，并在两城之间设立供气站点D （如图），为保证城市安全，规定站点D 距两城市的距离均不得少于15km ．又已知A 城一边有段10km 长的旧管道AC ，准备改造利用，改造费用为5万元//km ，其余地段都要新建，新建的费用（含站点D ）与站点D 到A 、B 两城方向上新修建的长度的平方和成正比．．．．．．．．．，并且当站点D 距A 城距离为40km 时，新建的费用为1825万元．设站点D 距A 城的距离为km x ，A ，B 两城之间天然气管道的建设总费用为y 万元．（1）求y 与x 之间的函数关系式，并写出其定义域；（2）天然气站点D 距A 城多远时，建设总费用最小？最小总费用多少？23．某种商品的市场需求量1y （万件）、市场供应量2y （万件）与市场价格x （元/件）分别近似地满足下列关系：180y x =-+，2210y x =-，其中580x ≤≤，当12y y =时的市场价格称为市场平衡价格，此时的需求量称为平衡需求量．（1）求平衡价格和平衡需求量．（2）若该商品的市场销售量P （万件）是市场需求量1y 和市场供应量2y 两者中的较小者，该商品的市场销售额W （万元）等于市场销售量P 与市场价格x 的乘积．当市场价格x 取何值时，市场销售额W 取得最大值，并求出最大值．24．某工厂生产某产品x 件所需成本费用为P 元，且2110005,10P x x =++而每件售出的价格为Q 元，其中(),xQ a a b R b=+∈. （1）问:该工厂生产多少件产品，使得每件产品所需成本费用最少?（2）若生产出的产品能全部售出，且当产量为150件时利润最大，此时每件价格为30，求a b 、的值.25．宜城市流水镇是全国闻名的西瓜基地，流水西瓜含糖量高，口感好，多次入选全国农博会并获金奖，畅销全国12省百余个大中城市.实践证明西瓜的产量和品质与施肥关系极大，现研究发现该镇礼品瓜“金皇后”的每亩产量L （单位：百斤）与施用肥料x （单位：百斤）满足如下关系：238(2),02()603,312x x L x x x x ⎧+<≤⎪⎪=⎨⎪<≤⎪+⎩，肥料成本投入为5x （单位：百元），其它成本投入为10x （单位：百元）.已知“金皇后”的市场批发价为2元/斤，且销路畅通供不应求，记每亩“金皇后”的利润为()f x （单位：百元）. （1）求()f x 的函数关系式；（2）当施用肥料为多少斤时，每亩“金皇后”的利润最大，最大利润是多少元？1.414≈）.26．已知()y f x =（x D ∈，D 为此函数的定义域）同时满足下列两个条件：①函数()f x 在D 内单调递增或单调递减；②如果存在区间[,]a b D ⊆，使函数()f x 在区间[,]a b 上的值域为[,]a b ，那么称()y f x =，x D ∈为闭函数（1）判断函数2()1((0,))f x x x x =+-∈+∞是否为闭函数？并说明理由；（2）求证：函数3y x =-（[1,1]x ∈-）为闭函数；（3）若0)y k k =+<是闭函数，求实数k 的取值范围【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】由()0f x =可得出2x x a =-，将问题转化为曲线2yx 与曲线y x a =-有4个交点，数形结合可求得实数a 的取值范围，进而结合判别式可判断出方程210ax x ++=的实数根个数. 【详解】由()0f x =可得出2x x a =-，作出函数2yx 与函数y x a =-的图象如下图所示：,,x a x a y x a x a x a-≥⎧=-=⎨-+<⎩，若使得函数()2f x x x a =--有4个零点，则直线y x a =-与y x a =-+均与函数2y x 的图象有两个交点，联立2y x a y x =-⎧⎨=⎩可得20x x a -+=，1140a ∆=->，解得14a <，联立2y x a y x =-+⎧⎨=⎩可得20x x a +-=，2140a ∆=+>，解得14a >-，当0a =时，则()()21f x x x xx =-=-，令()0f x =，可得0x =或1x =±，此时，函数()y f x =只有3个零点，不合乎题意. 综上所述，实数a 的取值范围是11,00,44⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭. 对于二次方程210ax x ++=，140a ∆=->，因此，关于x 的二次方程210ax x ++=有两个实根. 故选：C. 【点睛】方法点睛：本题考查根据方程实数根的个数求参数的取值范围，一般可采用1.直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围；（2）分离参数法：先将参数分离，转化成求函数值域问题加以解决；（3）数形结合：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后观察求解，此时需要根据零点个数合理寻找“临界”情况，特别注意边界值的取舍.2．B解析：B 【分析】设()f x t =，可得方程21610t kt ++=有两个不同的实数根214t <- ，1104t -<<，再利用一元二次方程根的分布列不等式求解即可. 【详解】作出()f x 的图象如图所示，设()f x t =，要使方程()()21610fx kf x ++=有四个不同的实数根，则方程()21610g t t kt =++=有两个不同的实数根1t ，2t . 且()1f x t =有三个根，方程()2f x t =有一个根，由图可知，214t <-1104t -<<. 设2()161g t t kt =++，则()10,400,g g ⎧⎛⎫-<⎪ ⎪⎝⎭⎨⎪>⎩，解得8k >. 故选：B.【点睛】函数零点的几种等价形式：函数()()y f x g x =-的零点⇔函数()()y f x g x =-在x 轴的交点⇔方程()()0f x g x -=的根⇔函数()y f x =与()y g x =的交点.3．B解析：B可设2()(3)1f x ax a x =+-+，0a ≠，讨论0a >，0a <，结合对称轴与区间的关系和1()2f 的符号、判别式的符号，解不等式可得所求范围．【详解】解：方程有两个实数根，显然0a ≠，可设2()(3)1f x ax a x =+-+，对称轴是32ax a-=，当0a >时，要使二次方程在区间1(,)2+∞上有两个实数根，如图所示，则需3122a a ->，且113()10242a f a -=++>，且2(3)40a a ∆=--，即为302a <<且23a >，且9a 或1a ，则213a <；当0a <时，要使二次方程在区间1(,)2+∞上有两个实数根，如图所示，则需3122a a ->，且113()10242a f a -=++<，且2(3)40a a ∆=--，即为302a <<且23<a ，且9a 或1a ，则a ∈∅．综上可得，a 的取值范围是213a <．故选：B ．【点睛】本题解题关键是结合二次函数的图象特征研究二次方程根的分布，分类讨论借助图象准确列出不等关系，突破难点.4．C【分析】令()()0g x f x x a =+-=，将()g x 存在两个零点，转化为两函数24,?0,6,?0x x y a y x x x x ⎧+<⎪==⎨⎪-≥⎩有两个交点，在同一坐标系中，作出两个函数的图象，利用数形结合法求解. 【详解】令()()0g x f x x a =+-=，得24,?06,?0x x a x x x x ⎧+<⎪=⎨⎪-≥⎩，令24,?0,6,?0x x y a y x x x x ⎧+<⎪==⎨⎪-≥⎩，在同一坐标系中，作出两个函数的图象，如图所示：因为()g x 存在两个零点，由图象可得：a <﹣9或﹣4<a ≤0，故选：C 【点睛】方法点睛：函数零点问题：若方程可解，通过解方程即可得出参数的范围，若方程不易解或不可解，则将问题转化为构造两个函数，利用两个函数图象的关系求解，这样会使得问题变得直观、简单，这也体现了数形结合思想的应用．5．B解析：B 【分析】画出函数21,1()1,1x x x f x x x⎧-+<⎪=⎨⎪⎩的图象，函数()y f x a =-有三个零点等价于()y f x =与y a=的图象有3个不同交点，数形结合得答案.【详解】作出函数21,1 ()1,1x x xf xxx⎧-+<⎪=⎨⎪⎩的图象如图，函数()y f x a=-有三个零点，即()y f x=与y a=的图象有3个不同交点，由图可知，实数a的取值范围为3(4，1).故选：B.【点睛】方法点睛：由零点求参数范围：若方程可解，通过解方程即可得出参数的范围，若方程不易解或不可解，则将问题转化为构造两个函数，利用两个函数图象的关系求解，这样会使得问题变得直观、简单，这也体现了数形结合思想的应用．6．D解析：D【分析】分离参数，再根据指数函数性质求出．【详解】解：21x m-=或21x m-=-，即21xm=-，或者21xm=+，当211xm=->-时，有一个解，当211xm=+>时，有一个解，所以1m时，方程|2|1x m-=有两个不等实根，故选：D．【点睛】考查方程根的个数问题，利用了分类讨论法，分离参数法，属于中档题．7．C解析：C【分析】根据题意求得0t和0N的值，然后计算出()49t的值即可得解.【详解】由第64天和第67天检测过程平均耗时均为8小时知，016N <，所以1616=，得064t =．又由8N =知，064N =，所以当49n =时，()64499749t ==≈，故选：C ．【点睛】本题考查分段函数模型的应用，求出0t 和0N 的值是解题的关键，考查计算能力，属于中等题.8．A解析：A 【分析】利用新定义化简()f x 解析式，做出()g x 的函数图象，根据图象即可得出k 的范围. 【详解】解：有题意：21(4)1x x --+，解得：2x -或3x ，所以()24,(,2][3,)1,(2,3)x k x f x x k x ++∈-∞-⋃+∞⎧=⎨-+∈-⎩，令()24,(,2][3,)1,(2,3)x x g x x x +∈-∞-⋃+∞⎧=⎨-∈-⎩画出()g x 的函数图象，如图：因为函数()f x 的图象与x 轴恰有三个交点，所以()y g x k =+有三个零点，由图可得：21k -<．故选：A ．【点睛】本题考查根据零点个数求参数的范围，求解一元二次不等式，是中档题．9．D解析：D【详解】选项A ：ln y x =的定义域为（0,+∞），故ln y x =不具备奇偶性，故A 错误；选项B ：21y x =+是偶函数，但210y x =+=无解，即不存在零点，故B 错误；选项C ：sin y x =是奇函数，故C 错；选项D ：cos y x =是偶函数，且cos 02y x x k ππ==⇒=+，k z ∈，故D 项正确.考点：本题主要考查函数的奇偶性和零点的概念.10．D解析：D 【分析】根据已知条件可构造出函数关系式，进而得到0.710x =，根据对数运算法则可解方程求得近似值. 【详解】由题意可知，看到图形面积大小y 与图形实际面积x 之间满足0.7y x=∴若看到全国面积约为某县面积的10倍，则0.710x =，解得：10lg 1.437x =≈ lg 273lg3 1.43=≈ 27x ∴≈故选：D 【点睛】本题考查利用函数模型求解实际问题，关键是能够根据已知条件构造出合适的函数模型，结合对数运算性质求得结果.11．C解析：C 【分析】设该工厂从6月开始月产量平均增长率至少需到达x ，8月份产量去年同期水平为a ，则21(1)2a x a +=．由此能求出该工厂从6月开始月产量平均增长率至少需到达多少个百分点．【详解】设该工厂从6月开始月产量平均增长率至少需到达x ，8月份产量去年同期水平为a ，则21(1)2a x a +=．解得10.41442%x =≈≈．∴该工厂从6月开始月产量平均增长率至少需到达42个百分点．故选：C ．【点睛】本题考查百分点的求法，考查等比数列的性质等基础知识，考查运算求解能力，是基础题．12．A解析：A 【分析】令()0g x =，将问题转化为函数()f x 与函数()2ln 0y x a a =-->的图象有两个不同的交点来求解. 【详解】令()0g x =得()2ln f x x a =--，若()g x 有两个零点，则函数()f x 与函数()2ln 0y x a a =-->的图象有两个不同的交点.画出函数()f x 与函数()2ln 0y x a a =-->的图象如下图所示，当直线过点()0,1时，两个函数图象有两个交点，此时1120ln a a e=-⨯-⇒=.由图可知，当直线向下平移时，可使两个函数图象有两个交点，所以1ln 1a a e -≤⇒≥，所以a 的最小值为1e. 故选：A【点睛】本小题主要考查函数零点问题的求解，考查数形结合的数学思想方法，属于中档题.二、填空题13．【分析】作出函数的图象及直线它们的交点的横坐标即为由图象可得出它们的性质：范围关系然后现求的范围【详解】解：作出函数的图象如图所示（1）由解得或（2）关于直线对称则综上由函数在上单调递增可得故答案为解析：(3,3]-【分析】作出函数()f x 的图象及直线y a =，它们的交点的横坐标即为1234,,,x x x x ，由图象可得出它们的性质：范围，关系．然后现求212344x x x x x ++的范围．【详解】解：作出函数22122,0()2log ,0x x x f x x x ⎧++≤⎪=⎨⎪>⎩的图象如图所示（1）由2|log |2x =解得14x =或4x =，123410144x x x x ∴<≤<≤<<≤，3422|log ||log |x x =，2324log log x x ∴-=，341x x ∴=，（2）12,x x 关于直线2x =-对称，则124x x +=-，综上，2123444444(14)x x x x x x x x ++=-<≤.由函数4y x x-=+在(1,4]上单调递增，可得212344(3,3]x x x x x ++∈-. 故答案为：(3,3]-．【点睛】方法点睛：本题考查方程根的分布问题，解题关键是作出函数图象与直线，把方程的根转化为函数图象与直线交点横坐标，从图象易得它们的性质．从而求得结论．14．【分析】作出函数f(x)的图象将函数g(x)=f(x)-k 有两个不同的零点转化为y=f(x)y=k 的图象又两个不同的交点求解【详解】函数的图象如图所示：若函数g(x)=f(x)-k 有两个不同的零点等解析：5,19⎛⎫⎪⎝⎭【分析】作出函数f (x )，的图象，将函数g (x )=f (x )-k 有两个不同的零点，转化为y =f (x )，y =k 的图象又两个不同的交点求解. 【详解】函数2log,02 ()25(),239xx xf xx<<⎧⎪=⎨+≥⎪⎩的图象如图所示：若函数g(x)=f(x)-k有两个不同的零点，等价于y=f(x)，y=k的图象又两个不同的交点，由图知：519k<<故答案为：5,19⎛⎫⎪⎝⎭【点睛】方法点睛：由函数零点或个数求参数范围问题：若方程可解，通过解方程即可得出参数的范围；若方程不易解或不可解，则将问题转化为构造两个函数，利用两个函数图象的关系求解，这样会使得问题变得直观、简单，这也体现了数形结合思想的应用．15．【分析】根据解析式画出函数图象去绝对值并结合对数的运算性质求得根据正弦函数的对称性求得将化为结合二次函数的性质即可得出结果【详解】函数画出函数图象如下图所示:由函数图象可知若则因为与关于对称则且去绝解析：()0,12【分析】根据解析式,画出函数图象.去绝对值并结合对数的运算性质求得12x x⋅，根据正弦函数的对称性求得34x x+，将()()341222x xx x--化为2441220x x-+-，结合二次函数的性质，即可得出结果.【详解】函数()2log,02sin,2104x xf xx xπ⎧<<⎪=⎨⎛⎫≤≤⎪⎪⎝⎭⎩，画出函数图象如下图所示:由函数图象可知，若()()()()1234f x f x f x f x k ====，则()0,1k ∈，因为1234x x x x <<<，3x 与4x 关于6x =对称，则2122log log x x =，3412x x +=，且4810x <<，去绝对值化简可得2122log log x x -=，即2122log log 0x x +=，由对数运算可得()212log 0x x ⋅= 所以121x x ⋅=，则()()()3434343412222420x x x xx x x x x x --=-=++-()23444442012201220x x x x x x =-=--=-+-，令21220y x x =-+-，()8,10x ∈，因为21220y x x =-+-是开口向下，对称轴为6x =的二次函数，所以21220y x x =-+-在()8,10x ∈上单调递减，所以10012020649620y -+-<<-+-，即012y <<；即()()()34244122212200,12x x x xx x --=-+-∈故答案为: ()0,12.【点睛】本题考查了分段函数的性质及应用，涉及求二次函数的最值，根据数形结合的方法求解即可，属于中档题.16．【分析】首先根据已知题意画出图形然后根据数形结合分析的取值范围需要注意为的斜率【详解】根据题意的图象如图：结合图象知要想有两个不同交点的斜率要大于的斜率的取值范围是故答案为：【点睛】本题考查函数图象解析：()1,+∞【分析】首先根据已知题意画出图形，然后根据数形结合分析a 的取值范围，需要注意a 为y ax =的斜率. 【详解】根据题意y a x =的图象如图：()0a >，结合图象知，要想有两个不同交点y ax ∴=的斜率要大于y x a =+的斜率a ∴的取值范围是1a >.故答案为：()1,+∞ 【点睛】本题考查函数图象的交点问题，考查数形结合能力，属于中等题型.17．【分析】先利用导数求出函数的单调区间和极值令由题意可知方程有两个不同的实数根根据数形结合和韦达定理可知一个根在内一个根在内再令因为所以只需由此即可求出的取值范围【详解】解：令得或1当时函数在上单调递解析：3366e m e >+【分析】先利用导数求出函数()f x 的单调区间和极值，令()f x t =，由题意可知，方程210t mt -+=有两个不同的实数根1t ，2t ，根据数形结合和韦达定理可知，一个根在36,e ⎛⎫∞ ⎪⎝⎭内，一个根在36,e ⎛⎫∞ ⎪⎝⎭内，再令()21g t t mt =-+，因为()010g =>，所以只需360g e ⎛⎫< ⎪⎝⎭，由此即可求出m 的取值范围．【详解】解：()()()()22331x xx x e x f e x x =+-=+-'，令()0f x '=得，3x =-或1，当3x <-时，()0f x '>，函数()f x 在(),3-∞-上单调递增，且()0f x >，当31x -<<时，()0f x '<，函数()f x 在()3,1-上单调递减，当1x >时，()0f x '>，函数()f x 在()1,+∞上单调递增，所以()()363f x f e=-=极大值，()()12f x f e ==-极小值，令()f x t =，因为关于x 的方程()()210fx mf x -+=恰有四个不同的实数解，所以方程210t mt -+=有两个不同的实数根1t ，2t ，且一个根在360,e ⎛⎫⎪⎝⎭内，一个根在36,e ⎛⎫+∞ ⎪⎝⎭内，或者两个根都在()2,0e -内，或者一根为36e ，另一根在()2,0e -内；因为m 为正数，所以121t t =，120t t m +=>，所以1t ，2t 都为正根，所以两个根不可能在()2,0e -内，也不可能一根为36e ，另一根在()2,0e -内；所以实数根1t ，2t ，且一个根在360,e ⎛⎫ ⎪⎝⎭内，一个根在36,e ⎛⎫+∞ ⎪⎝⎭内，令()21g t t mt =-+，因为()010g =>，所以只需360g e ⎛⎫< ⎪⎝⎭，即6336610m e e -+<，得3366e m e>+，即m 的取值范围为：336,6e e ⎛⎫++∞ ⎪⎝⎭.故答案为：336,6e e ⎛⎫++∞ ⎪⎝⎭. 【点睛】本题主要考查了利用导数研究函数的单调性和极值，考查了函数的零点与方程根的关系，是中档题．18．【分析】将方程转化为两个函数与的交点问题通过求导分析函数的单调性和极值画出的图形则问题即可迎刃而解【详解】由题意有：设∴问题转化为与有三个交点∴对进行分析可知：∴令有：或者当有：当有：或者∴在单调递解析：50,e ⎛⎫⎪⎝⎭【分析】将方程转化为两个函数2()(31)x f x x x e =-+与()g x b =的交点问题，通过求导分析函数()f x 的单调性和极值，画出()f x 的图形，则问题即可迎刃而解.【详解】由题意有：设2()(31)x f x x x e =-+，()g x b =， ∴问题转化为()f x 与()g x 有三个交点 ∴对()f x 进行分析可知： 2()(3123)x f x x x x e '=-++- 2(2)x x x e =-- (2)(1)x x x e =-+∴令()0f x '=有：1x =-或者2x =，当()0f x '<有：12x -<<，当()0f x '>有：1x <-或者2x >∴()f x 在(,1)-∞-单调递增，在(1,2)-单调递减，在(2,)+∞单调递增； ∴()f x 有极大值5(1)f e'-=，极小值2(2)f e '=-，又∵当x →-∞时，()0f x →， ∴()f x 的图像如下图，故答案为：50,e ⎛⎫ ⎪⎝⎭【点睛】本题通过求方程中参数的范围，考查了学生运用导数工具处理函数中交点个数问题，也考验了学生用导数作复合函数图像的能力，以及用数形结合思想处理函数交点个数引起的参量的范围问题，对学生要求较高，为中等难度题目.19．【分析】由函数单调性质判断函数是增函数运用零点存在性定理得解【详解】是上增函数是上减函数在上增函数又在上存在零点函数的零点在区间上故答案为：【点睛】本题考查函数零点分布区间判断函数零点分布区间的方法解析：1-【分析】由函数单调性质判断函数31()(2)()2xf x x =+-是增函数，(1)0f -< ，(0)0f >运用零点存在性定理得解. 【详解】3(2)y x =+是R 上增函数，1()2x y = 是R 上减函数，31()(2)()2x f x x ∴=+-在R 上增函数，又(1)0f -< ，(0)0f >，31()(2)()2x f x x ∴=+-在(1,0)-上存在零点函数31()(2)()2xf x x =+-的零点在区间(,1)n n +上1n ∴=-故答案为：1- 【点睛】本题考查函数零点分布区间. 判断函数零点分布区间的方法：（1）解方程法：当对应方程易解时，可通过解方程确定方程是否有根落在给定区间上；（2）定理法：利用零点存在性定理进行判断；（3）数形结合法：画出相应的函数图象，通过观察图象与x 轴在给定区间上是否有交点来判断，或者转化为两个函数图象在给定区间上是否有交点来判断.20．【分析】依题意在上单调增则（a ）（b ）从而可得必须有两个不相等的正根利用该方程有二异正根的条件即可求得实数的取值范围【详解】在是增函数在上值域为（a ）（b ）所以（a ）且（b ）即且所以且所以必须有两个解析：(0,4)【分析】依题意，1()4f x x=-在[a ，]b 上单调增，则f （a ）ma =，f （b ）mb =，从而可得210mx x -+=必须有两个不相等的正根，利用该方程有二异正根的条件即可求得实数m 的取值范围．【详解】 1()4f x x=-在(0,)+∞是增函数， ()f x ∴在[x a ∈，]b 上值域为[f （a ），f （b ）]所以f （a ）ma =且f （b ）mb =，即14ma a-=且14mb b -=，所以2410ma a -+=且2410mb b -+=，所以2410mx x -+=必须有两个不相等的正根，故0m ≠，∴40101640m mm ⎧>⎪⎪⎪>⎨⎪=->⎪⎪⎩，解得04m <<． ∴实数m 的取值范围是(0,4)．故答案为：(0,4)．【点睛】本题主要考查函数单调性的性质，着重考查二次函数根的分布问题，将所求的问题转化为210mx x -+=必须有两个不相等的正根是关键，属于中档题．三、解答题21．（1）()11xxe f x e-=+；（2）函数()f x 在(),0-∞上单调递减，证明见详解；（3）{}1,0,1,2M =-.【分析】（1）当0x <时，0x ->，()1111x xx xe ef x e e -----==++，利用函数的奇偶性求解即可；（2）函数()f x 在(),0-∞上单调递减，利用定义证明函数的单调性即可；（3）把函数()g x 有唯一零点的问题转化为方程()()20f ax f x a --+=有唯一的解的问题，利用函数的奇偶性和单调性得到2ax x a =-+，两边平方，利用方程有唯一的解即可得出结果. 【详解】（1）当0x <时，0x ->，又函数()f x 为偶函数，则()()1111x xx x e e f x f x e e-----===++，所以函数()f x 的解析式为()11xx e f x e-=+；（2）函数()f x 在(),0-∞上单调递减，设任意120x x <<，则()()()()()12212112212111111x x x x x x x x e e e e f x f x e e e e ----=-=++++，因为x y e =在R 上单调递增，所以12x x e e <，即120x x e e -<，所以()()21f x f x <，所以函数()f x 在(),0-∞上单调递减；（3）因为函数()f x 为偶函数，所以函数()f x 在()0,∞+上单调递减，函数()()()2g x f ax f x a =--+的零点就是方程()()20f ax f x a --+=的解，因为函数()g x 有唯一零点，所以方程()()20f ax f x a --+=有唯一的解，因为函数()f x 为偶函数，所以方程变形为：()()2f ax f x a =-+，因为函数()f x 在()0,∞+上单调递减，所以2ax x a =-+，平方得：()()()22212220a x a x a -+-+-=，当210a -=时，即1a =±，经检验方程有唯一解；当210a -≠时，()()()222424120a aa ∆=----=，得()22200a a a -=⇒=或2a =，综上可得：集合{}1,0,1,2M =-.【点睛】关键点睛：把函数()g x 有唯一零点的问题转化为方程()()20f ax f x a --+=有唯一的解的问题是解决本题的关键.22．（1）y 21(1307350)2x x =-+，定义域为[15,105]（2）天然气站点D 距A 城65km 时，建设总费用最小,最小总费用为1562.5万元.【分析】（1）根据站点D 距两城市的距离均不得少于15km ．可求得15105x ≤≤，设22[(10)(120)]510y k x x =-+-+⨯，根据当40x =时，1825501875y =+=，求出k ，从而可得y 与x 之间的函数关系式；（2）根据二次函数知识可求得最值.【详解】（1）因为站点D 距两城市的距离均不得少于15km ．所以1512015x x ≥⎧⎨-≥⎩，解得15105x ≤≤，设22[(10)(120)]510y k x x =-+-+⨯，15105x ≤≤，当40x =时，1825501875y =+=，所以22(3080)501875k ++=，解得14k =，所以221[(10)(120)]5104y x x =-+-+⨯21(1307350)2x x =-+，15105x ≤≤. （2）y 21(1307350)2x x =-+21(65)1562.52x =-+，所以当65x =时，min 1562.5y =万元.所以当天然气站点D 距A 城65km 时，建设总费用最小,最小总费用为1562.5万元.【点睛】关键点点睛：理解题意，建立正确的数学模型是解决函数应用题的关键.23．（1）平衡价格是30元，平衡需求量是50万件；（2）市场价格是40元时，市场总销售额W 取得最大值，最大值为1600万元．【分析】（1）令12y y =可解得结果；（2）根据题意求出W （万元）关于x （元/件）的函数关系式，再分段求出最大值，取更大的函数值即可得解.【详解】（1）令12y y =，得80210x x -+=-，解得30x =，此时1250y y ==，所以平衡价格是30元，平衡需求量是50万件．（2）由题意可知：210,53080,3080x x P x x -≤≤⎧=⎨-+<≤⎩，故22210,53080,3080x x x W x x x ⎧-≤≤=⎨-+<≤⎩，当530x ≤≤时，22525210222W x x x ⎛⎫=-=-- ⎪⎝⎭，即30x =时，max 1500W =；当3080x <≤时，2280(40)1600W x x x =-+=--+，即40x =时，max 16001500W =>，综述：当580x ≤≤时，40x =时，max 1600W =．答：市场价格是40元时，市场总销售额W 取得最大值，最大值为1600万元．【点睛】关键点点睛：正确理解题意，建立W （万元）关于x （元/件）的函数关系式是解题关键. 24．（1）该工厂生产100件产品时,使得每件产品所需成本费用最少；（2）25,30.a b ==【分析】（1）建立函数的解析式，再利用基本不等式求函数的最值；（2）根据利润=销售收入-成本，求出利润函数，再利用当产量为150套时利润最大，此时每套价格为30元，结合二次函数的性质建立条件关系，即可求a ，b 的值【详解】解：（1）由题意，每套玩具所需成本费用为211000510001000105255251010x x P x x x x x x++==+++==，当且仅当100010x x=，即100x =时，每套玩具所需成本费用最少为25元．（2）利润22111()()(10005)()(5)10001010x y xQ x P x a x x x a x b b =-=+-++=-+--，若生产出的玩具能全部售出，且当产量为150套时利润最大，此时每套价格为30元，∴满足5150112()1015030a b a b -⎧=⎪-⎪⎨⎪+=⎪⎩，解得25a =，30b =．【点睛】本题考查函数模型的构建，考查利用基本不等式求函数的最值，考查二次函数的最值，确立函数模型是关键，属于中档题．25．（1）()f x 23161532,02120315,312x x x x x x x ⎧-+<≤⎪⎪=⎨⎪-<≤⎪+⎩；（2）182.8斤，最大利润为5016元. 【分析】（1）由()()215f x L x x =-以及()L x 的解析式可得结果；（2）分段求出最大值，再取更大的函数值即可得解.【详解】（1）()()215f x L x x =-23161532,02120315,312x x x x x x x⎧-+<≤⎪⎪=⎨⎪-<≤⎪+⎩，（2）①当302x <≤时，对称轴3015323224x +=<=， ∴当32x =时，()max 45.5f x =百元， ②当332x <≤时，()()12013515113513550.161f x x x ⎡⎤=-++≤-=-≈⎢⎥+⎣⎦百元，当且仅当()1201511x x =++即1 1.828x =≈百斤，由①②可知： 1.828x =时，()max 50.16f x ≈百元.∴当施用肥料为182.8斤时，每亩“金皇后”的利润最大，最大利润为5016元.【点睛】本题考查了分段函数的最值，考查了基本不等式求最值，考查了二次函数求最值，属于中档题.26．（1）见解析；(2)见解析；（3）1(,0)4-【分析】（1）可判断函数f （x ）在定义域内不单调，由闭函数的定义可作出判断；（2）按照闭函数的定义只需证明两条：①在定义域内单调；②该函数值域也为[﹣1，1]；（3）由y k =0，+∞）上的增函数，知其符合条件①；设函数符合条件②的区间为[a ，b ]，从而有a k b k ⎧=+⎪⎨=+⎪⎩x k =+用二次方程根的分布知识可得k 的限制条件；【详解】（1）函数f （x ）在区间1,2⎛⎤-∞ ⎥⎝⎦上单调递减，在1,2⎛⎫+∞ ⎪⎝⎭上单调递增；所以，函数在定义域上不是单调递增或单调递减函数，从而该函数不是闭函数．。

广东省深圳市平冈中学高一生物上册必修一月考选择题专项试卷

广东省深圳市平冈中学高一生物上册必修一月考选择题专项试卷一、单选题1．图为某动物细胞合成的分泌蛋白运输到细胞外的过程图。

下列叙述错误的是（）A．研究分泌蛋白的形成过程可用同位素标记法B．结构③在分泌蛋白运输中起交通枢纽的作用C．分泌蛋白的合成和分泌与④有密切关系D．此图所示结构①能进行细胞间的信息交流2．下列关于糖类和脂质的叙述，错误的是（）A．糖原、淀粉、纤维素的单体都是葡萄糖B．糖类都是细胞内的能源物质C．糖原、淀粉、脂肪都能作为细胞内的储能物质D．原核细胞和真核细胞都含有磷脂3．下列关于无机盐的叙述，错误的是（）A．缺铁性贫血是因为体内缺乏铁，导致血红蛋白合成不足B．镁是叶绿素的成分之一，缺镁影响光合作用C．细胞中的无机盐大多数以化合物形式存在，如CaCO3是人体的骨中的重要成分. D．碘是合成甲状腺激素的原料，所以有些地区在食盐中加碘以预防地方性甲状腺肿4．糖类和脂质是细胞中两种重要的有机物，相关的叙述错误的是（）A．胆固醇可参与构成动物细胞膜B．糖类中的淀粉、纤维素和糖原都完全由葡萄糖缩合而成C．淀粉和脂肪水解的终产物是二氧化碳和水D．质量相同的糖类和脂肪被彻底氧化分解时，糖类耗氧少5．美国科考团在南极湖泊深水无光区发现了生活在此的不明细菌，并获得了该细菌的DNA，以下叙述正确的是（）A．该细菌无高尔基体，无法形成细胞壁B．该细菌中没有染色体，所以繁殖方式为无丝分裂C．该细菌细胞主要在细胞质中进行有氧呼吸D．该细菌环状DNA中也存在游离的磷酸基团，且其遗传特征主要由DNA决定6．下列关于生物膜结构、功能的叙述，不正确的是（）A．细胞膜、内质网膜与小肠黏膜都属于细胞内的生物膜系统B．细胞膜均以磷脂双分子层为基本结构支架C．细胞内的囊泡可来自于内质网和高尔基体膜D．细胞膜上的受体是参与细胞间信息交流的结构7．以下二倍体生物的细胞中含有两个染色体组的是（）①有丝分裂中期细胞②有丝分裂后期细胞③减数第一次分裂中期细胞④减数第二次分裂中期⑤减数第一次分裂后期细胞⑥减数第二次分裂后期细胞A．①②③B．①③⑤C．①③⑤⑥D．①④⑤⑥8．某一不可逆化学反应在无酶和有酶催化时均可以进行，当该反应在无酶条件下进行到时间t时，向反应液中加入催化该反应的酶。

深圳平冈中学必修第一册第一单元《集合与常用逻辑用语》测试卷(答案解析)

一、选择题1．已知ABC 中，A ，B ，C 所对的边分别为a ，b ，c ，则“0,3B π⎛⎤∈ ⎥⎝⎦”是“2b ac =”的（） A ．充分不必要条件 B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件2．以下四个命题中，真命题的是（）A ．()0π,sin tan x x x ∃∈=，B ．ABC 中，sin sin cos cos A B A B +=+是2C π=的充要条件C ．在一次跳伞训练中，甲，乙两位同学各跳一次，设命题p 是“甲降落在指定范围”，q 是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示p q ∧ D ．∀∈θR ，函数()()sin 2f x x θ=+都不是偶函数 3．已知命题2:11xp x <-，命题:()(3)0q x a x -->，若p 是q 的充分不必要条件，则实数a 的取值范围是（） A ．(,1]-∞B ．[1,3]C ．[1,)+∞D ．[3,)+∞4．已知:250p x ->，2:20q x x -->，则p 是q 的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分又不必要条件5．下列命题中，不正确．．．的是（） A ．0x R ∃∈，200220x x -+≥B ．设1a >，则“b a <”是“log 1a b <”的充要条件C ．若0a b <<，则11a b> D ．命题“[]1,3x ∀∈，2430x x -+≤”的否定为“[]01,3x ∃∈，200430x x -+>”6．若实数a ，b 满足0a >，0b >，则“a b >”是“ln ln a b b a ->+-”的( )（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件 7．命题“ax 2－2ax + 3 > 0恒成立”是假命题, 则实数a 的取值范围是( ) A ．a < 0或a ≥3B ．a ≤0或a ≥3C ．a < 0或a >3D ．0<a <38．已知等比数列{}n a 的前n 项和为n S ，则“10a >”是“20210S >”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件9．“3k >”是“方程22133x y k k -=-+表示双曲线”的（）A ．充分不必要条件B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件10．设等比数列{}n a 中，10a >，公比为q ，则“1q >”是“{}n a 是递增数列”的（）. A ．充分非必要条件 B ．必要非充分条件 C ．充分必要条件D ．既非充分又非必要条件11．下列命题中，不正确的是（）A ．0x R ∃∈，20010x x -+≥B ．若0a b <<则11a b> C ．设0a >，1a ≠，则“log 1a b >”是“b a >”的必要不充分条件D ．命题“2[1,2],320x x x ∀∈-+≤”的否定为“2000[1,2],320x x x -∃∈+>”12．设{}n a 是等差数列，且公差不为零，其前n 项和为n S ．则“*n N ∀∈，1n n S S +>”是“{}n a 为递增数列”的（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件二、填空题13．集合{}22221,2,3,,A n =中所有3个元素的子集的元素和为__________．14．已知：条件p ：120x-≥和q ：()()22110x a x a a -+++<，若p ⌝是q ⌝的必要不充分条件，则实数a 的取值范围是______.15．已知互异复数120z z ≠，集合{}{}221212,,z z z z =，则12z z +=__________．16．已知集合{}{}21,,A m B m ==，若B A ⊆，则实数m 的值是__________．17．若命题：“2000,10x R ax ax ∃∈-->”为假命题，则实数a 的取值范围是__________．18．已知集合{}12A =，，{}12B =-，，则A B =______．19．已知命题：①将一组数据中的每个数都变为原来的2倍，则方差也变为原来的2倍； ②命题“2,10x R x x ∃∈++<”的否定是“2,10x R x x ∀∈++<”； ③在ABC ∆中，若sin sin A B A B ><，则； ④在正三棱锥S ABC -内任取一点P ，使得12P ABC S ABC V V --<的概率是78； ⑤若对于任意的()2,430n N n a n a *∈+-++≥恒成立，则实数a 的取值范围是1,3⎡⎫+∞⎪⎢⎣⎭. 以上命题中正确的是__________（填写所有正确命题的序号）.20．某学校举办运动会时，高一（1）班共有26名学生参加比赛，有15人参加游泳比赛，有8人参加田径比赛，有14人参加球类比赛，同时参加游泳比赛和田径比赛的有3人，同时游泳比赛和球类比赛的有3人，没有人同时参加三项比赛，则同时参加球类比赛和田径比赛的学生有__人．参考答案三、解答题21．在①()RB A ⊆，②()A B R =R ，③A B B =这三个条件中任选一个，补充在下面问题中.若问题中的实数a 存在，求a 的取值范围；若问题中的实数a 不存在，请说明理由.已知集合{}2540A x x x =-+≤，{}121B x a x a =+<<-，是否存在实数a ，使得________？22．已知命题p ：01x ≤≤；q ：()120a x a a -≤≤>. （1）若1a =，写出命题“若p 则q ”的逆否命题，并判断真假；（2）若p 是q 的充分不必要条件，求实数a 的取值范围. 23．已知22:|27|3,:430p x q x mx m -<-+<，其中m ＞0. （1）若m ＝4且p ∧q 为真，求x 的取值范围；（2）若p 是q 的充分不必要条件，求实数m 的取值范围.24．设集合{}22240A x x x =+-≥，集合1,11B y y x x x ⎧⎫==+>-⎨⎬+⎩⎭，集合1C x ax a ⎧⎛⎫=-⎨ ⎪⎝⎭⎩()}60x +≤．（1）求AB ；（2）若C A ⊆，求实数a 的取值范围．25．若集合A={x|x 2+5x ﹣6=0}，B={x|x 2+2（m+1）x+m 2﹣3=0}．（1）若m=0，写出A ∪B 的子集；（2）若A∩B=B ，求实数m 的取值范围．26．已知0a >，设p ：实数x 满足22430x ax a -+<，q ：实数x 满足()231x -<．（1）若1a =，且p q ∧为真，求实数x 的取值范围；（2）若p ⌝是q ⌝的充分不必要条件，求实数a 的取值范围．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】分别从充分性和必要性入手进行分析即可得解. 【详解】充分性：若0,3B π⎛⎤∈ ⎥⎝⎦，则2221cos 122a c b B ac+-≤=<，即2222ac a c b ac ≤+-<，即222222a c ac b a c ac +-<≤+-，并不能得出2b ac =一定成立，故充分性不成立；必要性：若2b ac =，由余弦定理得：2221cos 222a c ac ac ac B ac ac +--=≥=，因为()0,B π∈，所以0,3B π⎛⎤∈ ⎥⎝⎦，故必要性成立，综上，“0,3B π⎛⎤∈ ⎥⎝⎦”是“2b ac =”的必要不充分条件，故选：C . 【点睛】方法点睛：判断充要条件的四种常用方法：定义法、传递性法、集合法、等价命题法.2．B解析：B 【分析】分析()0π,sin tan x x x ∀∈≠，即得A 错误；利用充要条件的定义判断B 正确；利用复合命题的定义判断C 错误；通过特殊值验证D 错误即可. 【详解】选项A 中，,2x ππ⎛⎫∈⎪⎝⎭时，sin 0,tan 0x x ><，即sin tan x x ≠；2x π=时，sin 1x =，tan x 无意义；0,2x π⎛⎫∈ ⎪⎝⎭时，设()sin tan sin sin cos x h x x x x x =-=-，则()32211cos cos 0cos cos xh x x x x-'=-=>，故()tan sin h x x x =-在0,2π⎛⎫ ⎪⎝⎭上单调递增，故()()tan sin 00h x x x h =->=，即sin tan x x <；综上可知，()0π,sin tan x x x ∀∈≠，，故A 错误；选项B 中，ABC 中，若sin sin cos cos A B A B +=+，则sin cos cos sin A A B B -=-，44A B ππ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭，即sin sin 44A B ππ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭，又33,,,444444A B ππππππ⎛⎫⎛⎫-∈--∈-⎪ ⎪⎝⎭⎝⎭，故44A B ππ-=-或44A B πππ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭，所以2A B π+=或A B π-=，ABC 中A B π-≠，故2A B π+=，即2C π=；反过来，若2C π=，则2A B π+=，结合诱导公式可知，sin sin cos 2A B B π⎛⎫=-=⎪⎝⎭， sin sin cos 2B A A π⎛⎫=-= ⎪⎝⎭，所以sin sin cos cos A B A B +=+；综上，sin sin cos cos A B A B +=+是2C π=的充要条件，故B 正确；选项C 中，依题意，命题p ⌝是“甲没有降落在指定范围”， q ⌝是“乙没有降落在指定范围”，故复合命题()()p q ⌝∨⌝ 是“至少有一位学员没有降落在指定范围”，故C 错误；选项D 中，存在2πθ=时，函数()sin 2cos 22f x x x π⎛⎫=+= ⎪⎝⎭，满足()()f x f x -=，即()f x 是偶函数，故D 错误. 故选：B. 【点睛】方法点睛：（1）证明或判断全称命题为真命题时，要证明对于,()x I p x ∀∈成立；证明或判断它是假命题时，只需要找到一个反例，说明其不成立即可.（2）证明或判断特称命题为真命题时，只需要找到一个情况，说明其成立即可；证明或判断它是假命题时，要证明对于,()x I p x ∀∈⌝成立.3．C解析：C 【分析】化简命题q ，分类讨论a 解不等式()(3)0x a x -->，根据p 是q 的充分不必要条件列式可解得结果. 【详解】因为211xx <-，所以2101x x x -+<-，所以(1)(1)0x x -+<，所以11x -<<，当3a <时，由()(3)0x a x -->得x a <或3x >，因为p 是q 的充分不必要条件，所以1a ≥，所以13a ≤<，当3a =时，由()(3)0x a x -->得3x ≠，满足题意，当3a >时，由()(3)0x a x -->得3x <或x a >，满足题意，综上所述：1a ≥. 故选：C 【点睛】关键点点睛：本题考查由充分不必要条件求参数的取值范围，一般可根据如下规则求解：（1）若p 是q 的必要不充分条件，则q 对应集合是p 对应集合的真子集；（2）p 是q 的充分不必要条件，则p 对应集合是q 对应集合的真子集；（3）p 是q 的充分必要条件，则p 对应集合与q 对应集合相等；（4）p 是q 的既不充分又不必要条件， q 对的集合与p 对应集合互不包含．4．A解析：A 【分析】先求出,p q 对应的不等式的解，再利用集合包含关系，进而可选出答案. 【详解】由题意，5:2502p x x ->⇒>，设5|2A x x ⎧⎫=>⎨⎬⎩⎭2:20q x x -->，解得：2x >或1x <-，设{|2B x x =>或}1x <-显然A 是B 的真子集，所以p 是q 的充分不必要条件. 故选：A. 【点睛】结论点睛：本题考查充分不必要条件的判断，一般可根据如下规则判断：（1）若p 是q 的必要不充分条件，则q 对应集合是p 对应集合的真子集；（2）p 是q 的充分不必要条件，则p 对应集合是q 对应集合的真子集；（3）p 是q 的充分必要条件，则p 对应集合与q 对应集合相等；（4）p 是q 的既不充分又不必要条件， q 对的集合与p 对应集合互不包含．5．B解析：B 【分析】由()2200022110x x x -+=-+≥，可判断A ；由对数函数的定义域和对数函数的单调性得充分性不一定成立，必要性成立，可判断B ；运用作差法，判断其差的符号可判断C ；根据全称命题的否定是特称命题可判断D. 【详解】由()2200022110x x x -+=-+≥，得A 为真命题；由“b a <”不能推出“log 1a b <”，所以充分性不一定成立，由“log 1a b <”得“b a <”，所以必要性成立，故B 不正确；由0a b <<，则110b aa b ab --=>，∴11a b>，故C 正确；根据全称命题的否定是特称命题知D 正确. 故选：B. 【点睛】本题考查判断命题的真假，对数函数的定义域，单调性，全称命题与特称命题的关系，属于中档题．6．C解析：C 【分析】构造函数()ln f x x x =+，据a ，b 的范围结合函数的单调性确定充分条件，还是必要条件即可．【详解】设()ln f x x x =+，显然()f x 在(0,)+∞上单调递增，a b >，所以()()f a f b >ln ln a a b b ∴+>+，即ln ln a b b a ->+-，故充分性成立，因为ln ln a b b a ->+-ln ln a a b b ∴+>+，所以()()f a f b >，a b ∴>，故必要性成立，故“a b >”是“ln ln a b b a ->+-”的充要条件，故选：C ．【点睛】本题考查了函数的单调性，必要条件、充分条件与充要条件的判断，考查了构造函数法的应用，是基础题．7．A解析：A 【分析】根据题意得出命题“x R ∃∈，2230ax ax -+≤”是真命题，然后对a 分情况讨论，根据题意得出关于a 的不等式，即可得出实数a 的取值范围. 【详解】命题“2230ax ax -+>恒成立”是假命题，即命题“x R ∃∈，2230ax ax -+≤”是真命题. 当0a =时，2230ax ax -+≤不成立；当0a <时，合乎题意；当0a >时，则24120a a ∆=-≥，解得3a ≥. 综上所述，实数a 的取值范围是0a <或3a ≥.故选：A. 【点睛】本题考查由全称命题的真假求参数，考查计算能力，属于中等题.8．C解析：C 【分析】结合等比数列的前n 项和公式，以及充分、必要条件的判断方法，判断出正确选项. 【详解】由于数列{}n a 是等比数列，所以2021111n q S a q -=⋅-，由于101nq q ->-，所以 2021111001nq S a a q-=⋅>⇔>-，所以“10a >”是“20210S >”的充要条件. 故选：C 【点睛】本小题主要考查等比数列前n 项和公式，考查充分、必要条件的判断，属于中档题.9．A解析：A 【分析】根据充分条件、必要条件的定义，结合双曲线的方程即可判定. 【详解】因为当3k >时，30k ->，30k +>，方程22133x y k k -=-+表示双曲线；当方程22133x y k k -=-+表示双曲线时，(3)(3)0k k -+>，即3k >或3k <-，不能推出3k >，所以“3k >”是“方程22133x y k k -=-+表示双曲线”的充分不必要条件，故选：A 【点睛】本题主要考查了充分条件、必要条件，双曲线的标准方程，属于中档题.10．C解析：C 【分析】根据等比数列的通项公式和单调性的判定方法，结合充分条件、必要条件的判定，即可求解. 【详解】在等比数列{}n a 中，可得11n n a a q -=，若10,1a q >>，可得11111()(1)0n n n n n a a a q q a q q --+-=-=->，即1n n a a +>，所以数列{}n a 为递增数列，故充分性是成立的；反之：若等比数列{}n a 为递增数列，即111(1)0n n n a a a qq -+-=->，若10a >，则1(1)0n q q -->，可得1q >，故必要性是成立的，所以“1q >”是“{}n a 是递增数列”的充分必要条件. 故选：C. 【点睛】本题主要考查了充分条件、必要条件的判定，以及数列的单调性的判定方法及应用，其中解答中熟记数列的单调性的判定方法是解答的关键，着重考查推理与论证能力.11．C解析：C 【分析】根据存在性命题的判定方法，可判定A 正确；根据不等式的性质，可判定B 正确；根据对数的运算性，可判定C 不正确；根据含有一个量词的否定，可判定D 正确. 【详解】对于A 中，由2000131()024x x x -+=-+≥，所以A 为真命题；对于B 中，由0a b <<，则110b aa b ab --=>，所以11a b>，所以B 是正确的；对于C 中，设0a >，1a ≠，例如11,24a b ==，则121log log 24a b ==，所以充分性不成立，又如1,22a b ==，此时12log log 21a b ==-，所以必要性不成立，所以“log 1a b >”是“b a >”的既不充分也不必要条件，所以C 是错误的；对于D 中，根据全称命题和存在性命题的关系，可得命题“2[1,2],320x x x ∀∈-+≤”的否定为“2000[1,2],320x x x -∃∈+>”，所以是正确的.故选：C. 【点睛】本题主要考查了命题的真假判定及应用，其中解答中涉及到含有一个量词的真假判定及否定，对数的运算性质，不等式的性质等知识的综合应用，属于中档试题.12．A解析：A 【分析】根据等差数列的前n 项和公式以及充分条件和必要条件的定义进行判断即可．【详解】{}n a 是等差数列，且公差d 不为零，其前n 项和为n S ，充分性：1n n S S +>，则10n a +>对任意的n *∈N 恒成立，则20a >，0d ≠，若0d <，则数列{}n a 为单调递减数列，则必存在k *∈N ，使得当n k >时，10n a +<，则1n n S S +<，不合乎题意；若0d >，由20a >且数列{}n a 为单调递增数列，则对任意的n *∈N ，10n a +>，合乎题意.所以，“*n N ∀∈，1n n S S +>”⇒“{}n a 为递增数列”；必要性：设10n a n =-，当8n ≤时，190n a n +=-<，此时，1n n S S +<，但数列{}n a 是递增数列.所以，“*n N ∀∈，1n n S S +>”⇐/“{}n a 为递增数列”.因此，“*n N ∀∈，1n n S S +>”是“{}n a 为递增数列”的充分而不必要条件. 故选：A. 【点睛】本题主要考查充分条件和必要条件的判断，结合等差数列的前n 项和公式是解决本题的关键，属于中等题．二、填空题13．【分析】集合A 中所有元素被选取了次可得集合中所有3个元素的子集的元素和为即可得结果【详解】集合中所有元素被选取了次∴集合中所有3个元素的子集的元素和为故答案为【点睛】本题考查了集合的子集正整数平方和解析：(2)(1)(1)(21)12n n n n n --++【分析】集合A 中所有元素被选取了21n C -次，可得集合{}22221,2,3,,A n =中所有3个元素的子集的元素和为()222122123n n C -+++⋯+即可得结果.【详解】集合{}22221,2,3,,A n =中所有元素被选取了21n C -次，∴集合{}22221,2,3,,A n =中所有3个元素的子集的元素和为()()()()()22222112121 12326n n n n n n C n ---+++++⋯+=⨯()()()()2112112n n n n n --++=，故答案为(2)(1)(1)(21)12n n n n n --++．【点睛】本题考查了集合的子集、正整数平方和计算公式，属于中档题．14．【分析】根据是的必要不充分条件得到计算得到答案【详解】即；即是的必要不充分条件故得到解得故答案为：【点睛】本题考查了根据必要不充分条件求参数意在考查学生的推断能力解析：102-<≤a【分析】根据p ⌝是q ⌝的必要不充分条件，得到{}1012x x x a x a ≠⎧⎫<≤⊂<<+⎨⎬⎩⎭，计算得到答案. 【详解】120x-≥，即102x <≤；()()22110x a x a a -+++<，即1a x a <<+.p ⌝是q ⌝的必要不充分条件，故{}1012x x x a x a ≠⎧⎫<≤⊂<<+⎨⎬⎩⎭，得到0112a a ≤⎧⎪⎨+>⎪⎩，解得102-<≤a .故答案为：102-<≤a .【点睛】本题考查了根据必要不充分条件求参数，意在考查学生的推断能力.15．【分析】根据集合相等可得或可解出【详解】①或②由①得（舍）由②两边相减得故答案为【点睛】本题主要考查了集合相等集合中元素的互异性复数的运算属于中档题解析：1-【分析】根据集合相等可得211222z z z z ⎧=⎨=⎩或212221z z z z ⎧=⎨=⎩，可解出12z z +. 【详解】{}{}221212,,z z z z =，211222z z z z ⎧=∴⎨=⎩①或212221z z z z ⎧=⎨=⎩②. 120z z ≠，∴由①得121z z ==（舍），由②两边相减得，221212z z z z -=-121z z ⇒+=-，故答案为121z z +=-. 【点睛】本题主要考查了集合相等，集合中元素的互异性，复数的运算，属于中档题.16．【解析】分析：根据集合包含关系得元素与集合属于关系再结合元素互异性得结果详解：因为所以点睛：注意元素的互异性在解决含参数的集合问题时要注意检验集合中元素的互异性否则很可能会因为不满足互异性而导致解题解析：0【解析】分析：根据集合包含关系得元素与集合属于关系，再结合元素互异性得结果.详解：因为B A ⊆，所以22110.m m m m m m m =≠⎧⎧∴=⎨⎨≠=⎩⎩或点睛：注意元素的互异性.在解决含参数的集合问题时，要注意检验集合中元素的互异性，否则很可能会因为不满足“互异性”而导致解题错误.17．【解析】由题意得解析：[]4,0-【解析】由题意得2004040a a a a a <⎧=∴-≤≤⎨∆=+≤⎩或 18．{-112}；【解析】=={-112}解析：{-1,1,2}；【解析】A B ⋃={}{}1212，，⋃-={-1,1,2} 19．③④⑤【解析】所以将一组数据中的每个数都变为原来的2倍则方差也变为原来的4倍；故①错误；命题的否定是故②错误；在中若则由正弦定理得故③正确；在正三棱锥内任取一点P 使得则在与底面平行的中截面上则中截面解析：③④⑤ 【解析】,所以将一组数据中的每个数都变为原来的2倍，则方差也变为原来的4倍；故①错误；命题“2,10x R x x ∃∈++<”的否定是“”，故②错误；在ABC ∆中，若，则，由正弦定理,得,故③正确；在正三棱锥S ABC -内任取一点P ，使得12P ABC S ABC V V --<，则,在与底面平行的中截面上，则中截面将正三棱锥的体积分成的两部分，所以所求概率是78，即④正确；⑤若对于任意的()2,430n N n a n a *∈+-++≥恒成立，则，即，令，显然在上为减函数，且，即，即实数a 的取值范围是1,3⎡⎫+∞⎪⎢⎣⎭，故⑤正确；所以选③④⑤.考点：命题的判定.20．5【解析】【分析】根据15人参加游泳比赛有8人参加田径比赛同时参加游泳和田径的有3人同时参加游泳和球类比赛的有3人可以求得只参加游泳比赛的人数；再结合总人数即可求得同时参加田径和球类比赛的人数【详解解析：5 【解析】【分析】根据15人参加游泳比赛，有8人参加田径比赛，同时参加游泳和田径的有3人，同时参加游泳和球类比赛的有3人，可以求得只参加游泳比赛的人数；再结合总人数即可求得同时参加田径和球类比赛的人数．【详解】解：有15人参加游泳比赛，有8人参加田径比赛，有14人参加球类比赛，这三项累加时，比全班人数多算了三部分，即同时参加游泳比赛和田径比赛的、同时参加游泳比赛和球类比赛的和同时参加田径比赛和球类比赛的重复算了两次所以15+8+14﹣3﹣3﹣26＝5，就是同时参加田径比赛和球类比赛的人数，所以同时参加田径比赛和球类比赛的有5人．故答案为5．【点睛】本题主要考查集合之间的元素关系，注意每两种比赛的公共部分，属于中档题．三、解答题21．答案见解析. 【分析】若选①：求出A R，分B =∅和B ≠∅两种情况，列出不等式组可得答案；若选②：由()A B R =R，得B ≠∅，列出不等式组可得答案；若选③：由A B B =可知B A ⊆，分B =∅和B ≠∅列出不等式组可得答案.【详解】集合{}{}254014A x x x x x =-+≤=≤≤. 若选①：{1RA x x =<或4}x >，由()RB A ⊆得，当B =∅时，121a a +≥-，解得2a ≤；当B ≠∅时，121211a a a +<-⎧⎨-≤⎩或12114a a a +<-⎧⎨+≥⎩，解得a ∈∅或3a ≥，所以实数a 的取值范围是[)3,+∞. 综上，存在实数a ，使得()RB A ⊆，且a 的取值范围为(][),23,-∞⋃+∞. 若选②：{1RA x x =<或4}x >，由()A B R =R，得B ≠∅，所以21411a a ->⎧⎨+<⎩，解得a ∈∅，所以不存在实数a ，使得()A B R =R.若选③：由AB B =可知B A ⊆，当B =∅时，121a a +≥-，解得2a ≤；当B ≠∅时，12111214a a a a +<-⎧⎪+≥⎨⎪-≤⎩，解得522a <≤.综上，存在实数a ，使得A B B =，且a 的取值范围为5,2⎛⎤-∞ ⎥⎝⎦.【点睛】本题考查了集合的运算，解题关键点是对于()RB A ⊆和()A B R =R 中含有参数的集合要分情况进行讨论，要熟练掌握集合间的基本运算.22．（1）逆否命题为“若0x <或2x >，则0x <或1x >”，真命题；（2）112a ≤≤.【分析】（1）直接写出命题“若p 则q ”逆否命题并判断真假即可；（2）由题意得{}|01x x ≤≤(){}|120x a x a a -≤≤>，即1021a a -≤⎧⎨≥⎩解不等式组可得答案. 【详解】（1）若1a =，则q ：02x ≤≤，命题“若p 则q ”为“若01x ≤≤，则02x ≤≤”，命题“若p 则q ”的逆否命题为“若0x <或2x >，则0x <或1x >”，是真命题；（2）若p 是q 的充分不必要条件，{}|01x x ≤≤(){}|120x a x a a -≤≤>则1021a a -≤⎧⎨≥⎩，解得112a ≤≤，实数a 的取值范围为112a ≤≤. 【点睛】结论点睛：充分不必要条件的判断，一般可根据如下规则判断：（1）若p 是q 的必要不充分条件，则q 对应集合是p 对应集合的真子集；（2）p 是q 的充分不必要条件，则p 对应集合是q 对应集合的真子集；（3）p 是q 的充分必要条件，则p 对应集合与q 对应集合相等；（4）p 是q 的既不充分又不必要条件， q 对的集合与p 对应集合互不包含. 23．（1）45x <<（2）523m ≤≤ 【分析】（1）分别求解绝对值不等式和一元二次不等式，化简p 与q ，结合p q ∧为真，解不等式组，即可得出x 的取值范围；（2）由p 是q 的充分不必要条件，建立关于m 的不等式组，求解即可得出答案. 【详解】（1）由|27|3x -<，解得25x <<由22430x mx m -+<以及0m >，解得3m x m << 当4m =时，q :412x <<p q ∧为真，25412x x <<⎧∴⎨<<⎩，解得45x <<（2）:25,:3p x q m x m <<<<p 是q 的充分不必要条件2350m m m ≤⎧⎪∴≥⎨⎪>⎩，解得523m ≤≤当53m =时，5:53q x <<成立当2m =时，:26q x <<成立523m ∴≤≤ 【点睛】本题主要考查了根据复合命题的真假求参数的范围以及由充分不必要条件求参数的范围，属于中档题.24．（1）[)4,+∞；（2）1,02⎡⎫-⎪⎢⎣⎭. 【分析】（1）解二次不等式求出集合A ，利用基本不等式求出集合B ，进而可得AB ；（2）由()2160a x x a ⎛⎫-+≤ ⎪⎝⎭，知0a ≠，分0a >和0a <两类讨论，利用C A ⊆，即可求得a 的取值范围．【详解】解：（1）集合{}22240A x x x =+-≥, 即满足()()640x x +-≥,解一元二次不等式可得{6A x x =≤-或}4x ≥, 而集合1,11B y y x x x ⎧⎫==+>-⎨⎬+⎩⎭,则111111y x x x x =+=++-++11≥=,当且仅当111x x +=+时,即0x =时取等号所以{}1B y y =≥；由集合交集运算可得{6A B x x ⋂=≤-或}4x ≥{}1y y ⋂≥{}4x x =≥ 即[)4,AB =+∞；（2）集合()160C x ax x a ⎧⎫⎛⎫=-+≤⎨⎬ ⎪⎝⎭⎩⎭．则0a ≠．化简可得()2160a x x a ⎛⎫-+≤ ⎪⎝⎭当0a >时,可得216C x x a ⎧⎫=-≤≤⎨⎬⎩⎭,{6A x x =≤-或}4x ≥ 则C A ⊆不成立．当0a <时,可得{6C x x =≤-或21x a ⎫≥⎬⎭若C A ⊆,则214a≤,解得102a -≤<或102a <≤．又由于0a <,所以102a -≤<. 综上可知,当C A ⊆时实数a 的取值范围为1,02a ⎡⎫∈-⎪⎢⎣⎭. 【点睛】本题主要考查交集及其运算，考查集合的包含关系，考查学生计算能力和分类讨论的思想，是中档题.25．（1）A ∪B 的子集：Φ，{﹣6}，{﹣3}，{1}，{﹣6，﹣3}，{﹣6，1}，{﹣3，1}，{﹣6，﹣3，1}（2）m 的取值范围是（﹣∞，﹣2]．【分析】（1）由x 2+5x ﹣6=0得6,1x x =-=或,所以{1-6}A =，，当0m =时，化简{}1,3B =-,求出A ∪B {}6,3,1=--，写出子集即可（2）由A B B ⋂=知B A ⊆,对判别式进行分类讨论即可. 【详解】（1）根据题意，m=0时，B={1，﹣3}，A ∪B={﹣6，﹣3，1}；∴A ∪B 的子集：Φ，{﹣6}，{﹣3}，{1}，{﹣6，﹣3}，{﹣6，1}，{﹣3，1}，{﹣6，﹣3，1}，（2）由已知B ⊆A ， •①m ＜﹣2时，B=Φ，成立 ‚②m=﹣2时，B={1}⊆A ，成立ƒ③m ＞﹣2时，若B ⊆A ，则B={﹣6，1}； ∴⇒m 无解，综上所述：m 的取值范围是（﹣∞，﹣2]．【点睛】本题主要考查了集合的并集运算，子集的概念，分类讨论的思想，属于中档题. 26．(1) 23x <<;(2) 4,23⎡⎤⎢⎥⎣⎦.【解析】试题分析：（1）p 为真时实数x 的取值范围是13x <<，q 为真时实数x 的取值范围是，然后求交集即可；（2）p ⌝是q ⌝的充分不必要条件即即q 是p 的充分不必要条件，易得：2a ≤且43a ≤.试题（1）由22430x ax a -+<得()()30x a x a --<当1a =时，13x <<，即p 为真时实数x 的取值范围是13x <<. 由()231x -<，得24x <<，即q 为真时实数x 的取值范围是24x <<因为p q ∧为真，所以p 真且q 真，所以实数x 的取值范围是23x <<. （2）由22430x ax a -+<得()()30x a x a --<，所以，p 为真时实数x 的取值范围是3a x a <<.因为 p ⌝是q ⌝的充分不必要条件，即q 是p 的充分不必要条件所以2a ≤且43a ≤ 所以实数a 的取值范围为：4,23⎡⎤⎢⎥⎣⎦.。

深圳语文试卷高中必修一(含答案)

深圳语文试卷高中必修一（含答案）下载温馨提示:该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪个字在古代汉语中的本义是“种植”？A. 种B. 植C. 種D. 栽2. 《诗经》按内容分为哪三类？A. 风、雅、颂B. 赋、比、兴C. 诗、词、曲D. 散文、辞赋、骈文3. 下列哪个诗人不属于唐代？A. 杜甫B. 白居易C. 苏轼D. 李白4. 《红楼梦》的作者是谁？A. 曹雪芹B. 吴承恩C. 罗贯中D. 施耐庵5. 下列哪个成语出自《论语》？A. 温故知新B. 诲人不倦C. 有教无类D. 不耻下问二、判断题（每题1分，共5分）1. 《离骚》是屈原的作品。

深圳平冈中学必修第一册第五单元《三角函数》测试卷(答案解析)

解析：
【分析】
根据角的范围和同角三角函数的关系求得，从而求得答案.
【详解】
因为，，所以，，
所以，
故答案为： .
19．【分析】由图象求得再根据求得从而求得函数解析式再根据由函数图象的对称轴为直线x=t求解【详解】由图象知：即则由五点法得所以即因为所以所以又因为所以函数图象的对称轴为直线x=t则所以解得当k=0时t取
【分析】
（1）先利用二倍角公式和辅助角公式化简，然后根据周期计算公式求解出，再采用整体替换法求解出单调递增区间；
（2）采用整体替换的方法先分析出的取值范围，然后再结合正弦函数的单调性，求解出的最值.
【详解】
（1）因为，
所以，所以最小正周期，
令，所以，
所以单调递增区间为：；
（2）因为，所以，
解析：或
【分析】
根据两角差的余弦公式和余弦的二倍角展开，再进行平方，再根据正弦的二倍角公式可答案得．
【详解】
由，得，即，
所以或，
当时，两边同时平方得，所以 .解得；
当时，，所以所以所以，
故答案为：或 .
三、解答题
21．（1）；（2）最小值为1，最大值为4．
【分析】
（1）由二倍角降幂，由两角差的正弦公式化函数为一个角的一个三角函数形式，然后结合正弦函数性质可求得最小正周期；
25．已知函数
（1）求函数的最小正周期及单调递增区间.
（2）当时，求函数的最大值和最小值.
26．已知，且， .
（1）求的值；
（2）求 .
【参考答案】***试卷处理标记，请不要删除
一、选择题
1．B
解析：B

深圳平冈中学高中物理必修一第一章《运动的描述》测试卷(答案解析)

一、选择题1．第 18届亚运会于 2018年 8月 18日至 9月 02日在印度尼西亚雅加达举行，中国体育健儿们奋力拼搏，最终以 132金 92银 65铜的成绩排在奖牌榜第一位。

下列说法正确的是（）A．远方看台的观众观看排球运动员的发球动作时，可将运动员视为质点B．在跳水比赛中，如果以运动员为参考系，该运动员下方的水面一定是上升的C．本次亚运会的新增项目男女 4×100米混合泳接力决赛中，中国队以 3分 40秒 45的成绩夺得金牌，并且打破了亚洲纪录。

这里提到的“3分 40秒45”指的是时间D．本次亚运会男子200米自由泳决赛中，中国选手孙杨以1分45秒43的成绩夺冠，200米指的是位移大小2．下列速度表示平均速度的是（）A．子弹射出枪口时的速度是800 m/sB．汽车速度计某时刻的读数是90 km/hC．运动员冲过终点时的速度是10 m/sD．“和谐号”动车从厦门到福州的速度是l60 km/h3．下列说法中正确的是（）A．研究花样滑冰运动员的技术动作时，可将运动员看作质点B．研究绕地球运转的人造卫星的位置及其变化时，可将卫星看作质点C．“两岸青山相对出”中的运动所选取的参考系是“青山”D．“宁停三分，不抢一秒”中的“一秒”是时刻4．2008年8月16日，在国家体育场“鸟巢”进行的北京奥运会男子100米决赛中，尤塞恩·博尔特以9秒69的成绩夺取金牌，冲过终点线时的速度为9.5m/s，打破了这个项目的奥运会纪录和世界纪录。

下列说法正确的是（）A．博尔特冲过终点线的瞬时速度大小不是9.5m/sB．博尔特冲过终点线的瞬时速度大小为10.3m/sC．博尔特在百米赛跑中的平均速度大小为9.5m/sD．博尔特在百米赛跑中的平均速度大小为10.3m/s5．下列关于质点的说法中，正确的是（）A．只有体积很小的物体才能看作质点B．学生会人员检查某班级课间操人数时，可以把该班级的每一位同学看做质点C．政教处老师检查某班级课间操质量时，可以把该班级的每一位同学看做质点D．某体育老师研究某同学的起跑动作时，可以把该同学看做一个质点6．某校举行2020年度游泳运动会中，高一小明同学在50m自由泳比赛中游出了26.98s的成绩；高二小陈同学在100m蛙泳比赛中游出了70.84s的成绩，都获得了第一名，（学校泳池长度为25m），下列说法正确的是（）A．小明的平均速度等于小陈的平均速度B．小明的速度一定比小陈的速度快C．在研究小陈和小明泳姿的时候，可以将他们俩当质点D．比赛过程中，以小明为参考系，他的对手一定向后运动7．下列说法不可能的是（）A．物体运动的加速度等于0，而速度却不等于0B．物体做直线运动，后一阶段的加速度比前一阶段大，但速度却比前一阶段小C．物体做直线运动，前一阶段的加速度比后一阶段大，但速度却比后一阶段小D．两物体相比，在相同的时间内一个物体的速度变化量比较大，而加速度却比较小8．下列所描述的运动中，可能的是（）①速度变化很大，加速度很小②速度变化方向为正，加速度方向为负③速度变化越来越快，加速度越来越小④速度越来越大，加速度越来越小A．①②B．②③C．①③D．①④9．以下各种运动的速度和加速度的关系可能存在的是（）A．速度向东，正在增大；加速度向东，正在增大B．速度向东，正在增大；加速度向西，正在减小C．速度向东，正在增大；加速度向西，正在增大D．速度向东，正在减小；加速度向东，正在减小10．一辆小车沿某一方向做变速直线运动，全程的平均速度为6m/s。

深圳平冈中学高中物理必修一第四章《运动和力的关系》测试卷(答案解析)

一、选择题1．如图所示为“摘灯笼”游戏示意图，要求游戏者在规定的时间内将尽可能多的灯笼摘下即可获胜，已知灯笼上下用两根相同的细绳L 1、L 2连接后悬挂于天花板上，人只能拉下面的细绳L 1，若两根细线绳能承受的最大拉力相同，则为了顺利摘下灯笼（）A ．在细绳L 1下端缓慢增加拉力B ．在细绳L 1下端突然猛一拉C ．由于细绳L 2中的拉力大于细绳L 1中的拉力，故细绳L 2一定先断D ．细绳L 1与细绳L 2一定同时断2．如图所示，水平面的物体质量m =1.0kg ，与水平面间的动摩擦因数μ=0.50，现受到一斜向上拉力F 的作用向右运动，F =10N ，与水平面夹角θ=37°，g 取10m/s 2，下列说法正确的是（已知sin37°=0.6，cos37°=0.8）（）A ．物体一共受到5个力B ．物体匀速运动C ．物体受到的支持力大小为6ND ．物体受到各个力的合力大小为6N3．从地面上以初速度v 0竖直上抛一质量为m 的小球，若运动过程中受到的空气阻力与其速率成正比，球运动的速率随时间变化的规律如图所示，t 1时刻到达最高点，再落回地面，落地速率为v 1，且落地前小球已经做匀速运动，则下列说法中正确的是（）A ．小球加速度在上升过程中逐渐减小，在下降过程中也逐渐减小B ．小球抛出瞬间的加速度大小为011g v v ⎛⎫+ ⎪⎝⎭C ．小球被抛出时的加速度值最大，最高点的加速度值最小D ．小球上升过程的平均速度等于02v4．如图，箱子内，一物体静止在倾斜固定的木板上。

现将箱子轻放到弹性安全气垫上并由静止释放，在箱子从A 向下压缩气垫至最低点B 的过程中，物体始终相对木板静止。

设木板对物体的支持力和摩擦力分别为N 和f ，则从A 到B 的过程中（）A ．N 先增大后减小，f 先减小后增大B ．N 先减小后增大，f 先增大后减小C ．N 和f 都是一直减小D ．N 和f 都是一直增大5．磁性车载支架（图甲）使用方便，它的原理是将一个引磁片贴在手机背面，再将引磁片对准支架的磁盘放置，手机就会被牢牢地吸附住（图乙）。

深圳平冈中学高中化学必修一第一章《物质及其变化》经典练习题(培优提高)

一、选择题1．室温下，下列各组离子在指定溶液中一定能大量共存的是 A ．0.1mol·L −1FeCl 3溶液中：Na +、I −、NO -3、K + B ．透明溶液中：Cu 2+、NH 4+、NO -3、SO 2-4C ．使紫色石蕊变红的溶液中：Ba 2+、K +、CH 3COO −、Cl –D ．0.1mol·L −1NaOH 溶液中：Mg 2+、Na +、SO 2-4、HCO -3 答案：B 【详解】A ．0.1mol·L −1FeCl 3溶液中：Fe 3+能将I −氧化为I 2，故A 不选；B ．透明溶液中：Cu 2+、NH 4+、NO -3、SO 2-4之间不反应，故B 选；C ．使紫色石蕊变红的溶液呈酸性：H +、CH 3COO −反应生成CH 3COOH 分子，故C 不选；D ． 0.1mol·L −1NaOH 溶液中：Mg 2+、HCO -3与OH -均可发生反应生成Mg(OH)2和CO 2-3，故D 不选；故选B 。

2．关于物质的类别，下列说法正确的是 A ．冰水属于混合物 B ．烧碱属于碱C ．H 2O 属于酸D ．溶液、胶体、浊液都属于纯净物答案：B 【详解】A ．冰和水是一种物质，属于纯净物，A 项错误；B ．烧碱是氢氧化钠的俗称，氢氧化钠属于碱，B 项正确；C ．H 2O 是中性物质，不属于酸，C 项错误；D ．浊液不稳定，放置产生沉淀，不属于纯净物，D 项错误；答案选B 。

3．已知常温下可用：Co 2O 3制备Cl 2，反应前后存在六种微粒：Co 2O 3、H 2O 、Cl 2、H +、Cl -和Co 2+。

下列叙述不正确的是( ) A ．氧化产物为Cl 2B ．氧化剂与还原剂的物质的量之比为1∶2C ．若有1molCl 2生成，则反应前HCl 的物质的量为6molD ．当该反应生成4.48LCl 2时，反应中有0.2mol 电子转移答案：D 【分析】用Co 2O 3制备Cl 2的反应中，Co 2O 3中的Co 由+3价变为+2，Co 2O 3做氧化剂，浓盐酸做还原剂，反应的方程式为Co 2O 3+6H ++2Cl -═2Co 2++3H 2O+Cl 2↑，据此分析解答。

深圳平冈中学高中化学必修1第一章《物质及其变化》测试卷(答案解析)(1)

一、选择题1．(0分)[ID ：135798]下列指定反应的离子方程式不正确的是A ．向氯化钙溶液中通入2CO 气体：2223CaCO H O=CaCO 2H ++++↓+B ．醋酸除水垢离子方程式：2333222CH COOH CaCO 2CH COO Ca H O CO -++++=+↑C ．石灰水与过量碳酸氢钠溶液反应：223323=2HCO Ca 2OH CaCO H O CO -+--++↓++D ．制备3Fe(OH)胶体：3++23ΔFe +3H O Fe(OH)(胶体)+3H 2．(0分)[ID ：135795]下列说法中，正确的是( )A ．液态HCl 、固态NaCl 均不导电，所以HCl 、NaCl 均是非电解质B ．NH 3、CO 2的水溶液均能导电，所以NH 3、CO 2均是电解质C ．蔗糖、酒精在水溶液里或熔融状态时均不导电，所以它们是非电解质D ．铜、石墨均导电，所以它们是电解质3．(0分)[ID ：135782]下列离子方程式书写正确的是A ．三氯化铁溶液与氢氧化钠溶液反应：FeCl 3+3OH -=Fe(OH)3↓+3Cl -B ．向Ca(HCO 3)2溶液中滴加盐酸：2H ++Ca(HCO 3)2=Ca 2++2H 2O+2CO 2↑C ．向Na 2CO 3溶液中加入过量CH 3COOH 溶液：2-3CO +2CH 3COOH=2CH 3COOH+CO 2↑+H 2OD ．向Ba(OH)2溶液中加少量NaHSO 3溶液：2-3HSO +Ba 2++2OH -=BaSO 3↓+2-3SO +2H 2O4．(0分)[ID ：135774]下列离子反应方程式正确的是A ．将NaOH 溶液和3NaHCO 溶液充分混合：OH -+-3HCO =2-3CO +H 2OB ．过量的2SO 通入NaOH 溶液这中：SO 2+2OH -=2-3SO +H 2OC ．2Cl 通入水中：Cl 2+H 2O ⇌2H ++Cl -+ClO -D ．向23Na CO 溶液中滴加少量稀盐酸：2H ++2-3CO =CO 2↑+H 2O5．(0分)[ID ：135773]已知：①2KMnO 4+16HCl=2KCl+2MnCl 2+5Cl 2↑+8H 2O②6FeCl 2+3Br 2=4FeCl 3+2FeBr 3③Cl 2+2KBr=Br 2+2KCl 。

广东省深圳市平冈中学高一生物上册必修一月考试卷

广东省深圳市平冈中学高一生物上册必修一月考试卷一、单选题1．伞藻是一种能进行光合作用的单细胞绿藻，由伞帽、伞柄和假根三部分构成，细胞核在假根内。

科学家用伞形帽和菊花形帽两种伞藻做嫁接和核移植实验（如图）。

下列相关叙述错误的是（）A．图1中②的帽形因嫁接伞柄而发生改变B．图2中③与图1中①的伞帽都是菊花形C．图2中去核的甲伞藻的生命活动将逐渐减缓直至停止D．上述实验说明生物体形态结构的建成与细胞核有关2．肠腺细胞能够分泌脂肪酶等多种消化酶，下列叙述正确的是（）A．脂肪酶的分泌与高尔基体有关B．合成和分泌脂肪酶的过程不消耗能量C．肠腺细胞中含量最多的化合物是脂肪D．脂肪酶能被苏丹Ⅲ染液染成橘黄色3．下图是在不同光照强度下测得的桑树与大豆间作（两种隔行种植）和大豆单作（单独种植）时大豆的光合速率。

下列叙述错误的是（）A．大豆植株的呼吸强度单作大于间作B．大豆植株的光合速率单作大于间作C．大豆植株开始积累有机物的最低光照强度单作大于间作D．为减小误差，间作与单作植株间的株距、行距均需相同4．下列对实验的相关叙述，正确的是（）A．双缩脲试剂可以与所有酶发生紫色反应B．观察植物有丝分裂实验可以用洋葱鳞片叶表皮细胞作实验材料C．若探究温度对酶活性的影响，用斐林试剂检测还原糖的生成D．在纸层析法分离叶绿体色素的结果中，第一个条带为橙黄色5．为了证明酶的作用具有专一性，某同学设计了如下5组实验，分别选择一定的试剂进行检测，下列有关实验方案和检测结果的叙述，正确的是（）组别①②③④⑤酶蛋白酶蛋白酶淀粉酶淀粉酶淀粉酶反应物蛋白质淀粉蛋白质淀粉麦芽糖A．①和③对比，用双缩脲试剂检测；①中不变紫色，③中呈现紫色B．③和④对比，用斐林试剂检测；水浴加热下③中不出现砖红色沉淀，④中出现砖红色沉淀C．②和④对比，用斐林试剂检测；水浴加热下②中不出现砖红色沉淀，④中出现砖红色沉淀D．④和⑤对比，用斐林试剂检测；水浴加热下④和⑤中均出现砖红色沉淀6．下列关于组成细胞的化合物的叙述，正确的是（）A．在任何活细胞中数量最多的化学元素都是氧B．在活细胞中各种化合物含量最多的化合物是蛋白质C．在活细胞中的各种化合物与食物中的各种成分相同D．在不同的细胞中各种化合物的种类基本相同，含量有所差别7．下列关于生物膜结构、功能的叙述，不正确的是（）A．细胞膜、内质网膜与小肠黏膜都属于细胞内的生物膜系统B．细胞膜均以磷脂双分子层为基本结构支架C．细胞内的囊泡可来自于内质网和高尔基体膜D．细胞膜上的受体是参与细胞间信息交流的结构8．图是研究物质A和物质B对某种酶活性影响的曲线，下列叙述错误的是（）A．底物浓度不能改变酶催化活性B．物质B能通过破坏酶的空间结构，使酶变性而降低反应速度C．减小底物浓度不能消除物质A对该种酶的影响D．增大底物浓度可以消除物质B对该种酶的影响9．下列关于酶和ATP的叙述，错误的是（）A．不是所有的酶都在核糖体上合成B．同一种酶可存在于不同的组织细胞中C．酶的合成需要ATP供能D．细胞质中有ATP的分布，细胞核中没有10．下列模式图表示真核细胞的细胞器，有关细胞器的说法不正确的是（）A．④的膜可以转化为②的膜B．在细胞中联系最广泛的细胞器是④C．③中可发生CO2→C3→C6H12O6，①中则会发生C6H12O6→丙酮酸→CO2D．⑤是植物、细菌、酵母菌唯一共有的细胞器11．下列有关细胞凋亡的例子，叙述不正确的是（）A．细胞的凋亡对于维持生物体内部环境的稳定是不利的B．人的胚胎发育早期有尾部，最后尾部消失属于细胞凋亡C．细胞的自然更新、被病原体感染的细胞的清除也是通过细胞凋亡完成的D．子宫内膜的周期性脱落属于细胞凋亡12．如图1～6为动物细胞的主要细胞器，相关叙述正确的是（）A．1能合成多种水解酶来分解细胞内衰老、损伤的细胞器B．2在有丝分裂的间期能发出星射线形成纺锤体C．3和6都能加工蛋白质，都能形成包裹蛋白质的囊泡D．有氧呼吸时O2与［H］在5的基质中结合产生ATP，这些ATP可用于4中的脱水缩合反应13．如图是在有氧条件下某高等植物体内有关的生理过程的示意图，①～⑤表示有关过程，X、Y、Z和W表示相关物质。

广东省深圳市平冈中学高一生物上册必修一月考多选题不定项选择题专项试卷

广东省深圳市平冈中学高一生物上册必修一月考多选题不定项选择题专项试卷一、多选题1．{下列有关图中的结构和功能叙述正确的是A．并非所有大分子物质都可通过④进出细胞核，④可参与信息交流B．所有真核细胞分裂过程中都会出现①②③周期性的出现和消失C．该结构的功能是遗传信息库，细胞代谢和遗传的中心D．②的结构是流动镶嵌模型，RNA 经过④需要穿过 0 层膜结构且需消耗能量2．{下图为真核细胞蛋白质合成和转运的示意图。

下列叙述正确的是A．图中由双层膜包被的结构有①⑤⑥B．图中与胰岛素合成有关的结构有①②③④⑤C．若②合成的是丙酮酸脱氢酶，则该酶在⑥中发挥作用D．若②合成的是染色体蛋白，则该蛋白会运送到①⑤⑥中3．{下面关于蛋白质分子结构与功能的叙述，正确的是（）A．不同蛋白质含有的氨基酸数量不尽相同B．组成蛋白质的氨基酸可按不同的排列顺序脱水缩合C．组成蛋白质的氨基酸之间可按不同的方式脱水缩合D．有些结构不同的蛋白质具有相似的功能4．{阿胶原产于山东，已有两千多年的应用历史，与人参、鹿茸一起被誉为中药三宝。

阿胶的滋补作用主要体现为：加快机体的新陈代谢，促进组织细胞再生和增强免疫力，下列说法正确的是（）A．中药三宝具有滋补作用的原因可能是含有对人体有益的微量元素B．驴皮细胞的脂肪含量较低，其主要储能物质是葡萄糖C．食用阿胶能减少人体对糖类的摄入，因为阿胶中含有的多糖主要是纤维素D．用驴皮熬成的阿胶为人体提供的主要营养物质可能是必需氨基酸5．{脂质普遍存在于生物体内，在细胞中具有独特的生物学功能，下列叙述与脂质不相符的是（）A．构成脂质的主要化学元素为C、H、O、N四种B．磷脂是构成生物膜的重要物质，但并不是所有的细胞膜中都含磷脂C．脂肪是细胞内的主要能源物质D．固醇类物质在动物体内可以起到促进肠道内某些营养物质的吸收、促进生殖器官的发育等作用6．{下列是几种常见的单细胞生物的结构示意图。

有关这些生物的叙述，错误的是（）A．图中生物都有细胞膜和核糖体B．具有核膜、核仁的生物是①②③④C．生物②③④一定是异养生物D．⑤含有叶绿素和藻蓝素，能进行光合作用7．{蛋白质与核酸是细胞中重要的两类有机物，下列叙述错误的是（）A．蛋白质的多样性与氨基酸的种类、数目、排列顺序有关B．低温、高温与重金属盐都能破坏蛋白质的空间结构C．绝大多数生物的遗传信息都储存在RNA中D．核酸在蛋白质的生物合成中具有重要作用8．{媒体报道的地沟油的主要成分是脂质，还有一些致病、致癌的毒性物质。

深圳平冈中学高中物理必修一第一章《运动的描述》测试卷(答案解析)

一、选择题1．质点是一个理想化模型，下列说法中正确的是（）A．研究运动员110m栏比赛的跨栏技术时，其身体可看作质点B．研究地球的公转轨迹时，地球可看作质点C．研究火车通过隧道所需的时间时，火车可看作质点D．研究“嫦娥一号”在轨道上的飞行姿态时，“嫦娥一号”可看作质点2．一质点以初速度v0沿x轴正方向运动，已知加速度方向沿x轴正方向，在加速度a的值由零逐渐增大到某一值后再逐渐减小到零的过程中，该质点（）A．速度先增大后减小，直到加速度等于零为止B．速度一直在先减小后增大，直到加速度等于零为止C．位移先增大，后减小，直到加速度等于零为止D．位移一直在增大，到加速度等于零之后仍继续增大3．物体做方向不变的直线运动，若以该运动方向为正方向，且在任意连续相等位移内速度∆相等，关于物体的运动情况，下列说法正确的是（）变化量vA．若v∆=0，做匀速运动B．若v∆﹤0，做匀减速运动C．若v∆﹤0，做加速度逐渐变大的减速运动D．若v∆﹥0，做加速度逐渐变小的加速运动4．关于瞬时速度和平均速度，下列说法正确的是（）A．瞬时速度是质点在某一段时间的运动快慢B．平均速度是变速运动各部分速度的平均值C．说到平均速度必须指明是哪一位移或哪一时刻的D．无限逼近某一位置附近的足够小位移内的平均速度，可看作质点在这位置的瞬时速度5．在“练习打点计时器”的实验中，下列说法正确的是（）A．电磁打点计时器使用的是6V以下的直流电源B．在测量物体速度时，先让物体运动，后接通打点计时器的电源C．纸带上的点迹记录了物体运动的时间及位移信息D．纸带上相邻计数点间的时间间隔一定是0.02s6．关于加速度与速度，下列说法正确的是（）A．物体的加速度增大，速度可能减小B．物体的加速度减小，速度一定减小C．物体的速度为零时，加速度一定为零a≠）始终不变，速度也始终不变D．物体的加速度（07．如图是一辆汽车做直线运动的s﹣t图像，对线段OA、AB、BC、CD所表示的运动，下列说法正确的是（）A．OA段运动速度最大B．AB段物体做匀速运动C．CD段的运动方向与初始运动方向相反D．运动4h汽车的位移大小为60km8．智能手机上装载的众多app软件改变着我们的生活，如图所示为百度地图的一张截图，表示了张同学从金陵中学步行到南京一中的导航具体路径，其推荐路线中有两个数据，39分钟，2.5公里，关于这两个数据，下列说法正确的是（）A．2.5公里表示了此次行程的位移的大小B．39分钟表示到达目的地的时刻C．39分钟表示通过这段路程可能所需要的时间D．根据这两个数据，我们可以算出此次行程的平均速度9．如图所示，汽车向右沿直线运动，原来的速度是v1，经过一小段时间之后，速度变为v2，Δv表示速度的变化量。

深圳平冈中学必修一第一单元《集合》测试卷(答案解析)

一、选择题1．由实数x ，﹣x ，|x |，2x ，33x -组成的集合中，元素最多有（） A ．2个B ．3个C ．4个D ．5个2．下图中的阴影部分，可用集合符号表示为（）A ．()()U U A B ⋂ B ．()()U UA BC ．()UA BD ．()UA B ⋂3．已知集合P 的元素个数为()*3n n N∈个且元素为正整数，将集合P 分成元素个数相同且两两没有公共元素的三个集合,,A B C ，即P A B C =⋃⋃，AB =∅，A C ⋂=∅，BC =∅，其中{}12,,,n A a a a =，{}12,,,n B b b b =，{}12,,,n C c c c =，若集合,,A B C 中的元素满足12n c c c <<<，k k k a b c +=，1,2,,k n =,则称集合P 为“完美集合”例如:“完美集合”{}11,2,3P =,此时{}{}{}1,2,3A B C ===．若集合{}21,,3,4,5,6P x =，为“完美集合”,则x 的所有可能取值之和为（） A ．9 B ．16 C ．18 D ．27 4．已知集合{,}P a b =,{|}Q M M P =⊆，则P 与Q 的关系为（）A ．P Q ⊆B ．Q P ⊆C ．P Q ∈D ．P Q ∉5．已知{}22(,)1,,A x y x y x Z y Z =+≤∈∈，{}(,)3,3,,B x y x y x Z y Z =≤≤∈∈.定义集合{}12121122(,)(,),(,),A B x x y y x y A x y B ⊕=++∈∈，则A B ⊕的元素个数n 满足（） A ．77n =B ．49n ≤C ．64n =D ．81n ≥6．在整数Z 集中，规定被5除所得余数为k 的所有整数组成“一类”，记为[]k ，即[]{}|5,k x x n n Z k ==+∈，0,1,2,3,4k =，给出如下四个结论：①[]20183∈；②[]20183-∈；③[][][][][]01234Z =；④“整数a ，b 属于同‘一类’”的充要条件是“[]0a b -∈”；其中正确结论的个数是（）A ．1B ．2C ．3D ．47．定义一个集合A 的所有子集组成的集合叫做A 的幂集，记为()P a ，用()n A 表示有限集A 的元素个数，给出下列命题：（1）对于任意集合A ，都有()A P A ∈；（2）存在集合A ，使得()3nP A =；（3）若AB =Φ，则()()P A P B ⋂=Φ；（4）若A B ⊆，则()()P A P B ⊆；（5）若()()1n A n B -=，则[][]()2()n P A n P B =.其中正确命题的序号为（）A ．（1）（2）（5）B ．（1）（3）（5）C ．（1）（4）（5）D ．（2）（3）（4）8．设全集为R ，集合{}2log 1A x x =<，{}21B x y x ==-，则()RAB =（）A ．{}02x x <<B ．{}01x x <<C ．{}11x x -<<D ．{}12x x -<<9．若集合2{||31|2},{|0},1x A x x B x x -=-≥=≤-则()R C A B =（）A ．1[,2]3-B ．∅C ．1(,)(1,2]3-∞-⋃D ．1,1(1,2]3⎛⎫-⋃ ⎪⎝⎭10．已知集合{}2230A x x x =--≤，{}22B x m x m =-≤≤+．若R A C B A =，则实数m 的取值范围为（） A ．5m >B ．3m <-C ．5m >或3m <-D ．35m -<<11．已知全集U =R ，集合(){}{}20,1A x x x B x x =+<=≤，则图中阴影部分表示的集合是（）A ．()2,1-B ．[][)1,01,2-C ．()[]2,10,1--D ．0,112．设{}2|8150A x x x =-+=，{}|10B x ax =-=，若AB B =，求实数a 组成的集合的子集个数有 A ．2B ．3C ．4D ．8二、填空题13．已知集合2|230A x x x ，{}|0B x x a =-=，若B A ≠⊂，则实数a 的值为______.14．设不等式20x ax b ++≤的解集为[]A m n =，，不等式()()2101x x x ++>-的解集为B ，若()(]213A B A B =-+∞=，，，∪∩，则m n +=__________.15．若集合{}2210,A x ax x a R =++=∈至多有一个元素，则a 的取值范围是___________．16．已知集合{}10,A x ax x R =+=∈，集合{}2280B x x x =--=，若A B ⊆,则a 所有可能取值构成的集合为______________ 17．设集合A 、B 是实数集R 的子集，[2,0]AB =-R，[1,2]BA =R，()()[3,5]A B =R R ，则A =________18．若集合{}2|20N x x x a =-+=，{}1M =，且N M ⊆，则实数a 的取值范围是_________19．已知集合{}{}2|21,|20xA y yB x x x ==+=--<，则()R C A B =__________．20．若集合2{320}A x ax x =++=中至多有一个元素，则a 的取值范围是__________．三、解答题21．设集合A ={x ∣2x −3x +2=0}，B ={x ∣2x +2(a +1)x +2a −5=0} （1）若A ∩B ={2}，求实数a 的值；（2）若U =R ，A ∩(UB )=A .求实数a 的取值范围.22．已知集合{|37},{|210},{|}A x x B x x C x x a =≤≤=<<=<，全集为实数集R . （1）求AB ，()R A B ⋂；（2）若A C ⋂≠∅，求a 的取值范围.23．设集合{}240A x x =-=，(){}222150B x x a x a =+++-=.（1）若{}2AB =-，求实数a 的值；（2）若A B A ⋃=，求实数a 的取值范围. 24．已知函数()()2log 4f x x =-的定义域为集合A ，集合{}211B x m x m =-≤<+.（1）当0m =时，求A B ；（2）若B A ⊆，求实数m 的取值范围；（3）若AB =∅，求实数m 的取值范围.25．已知不等式()210x a x a -++≤的解集为A . （1）若2a =，求集合A ；（2）若集合A 是集合{}4|2x x -≤≤的真子集，求实数a 的取值范围. 26．已知集合{}|2,12xA y y x ==≤≤，()(){}|20B x x a x a =---≤.（1）若3a =，求A B ；（2）若()R B C A ⊆.求实数a 的取值范围.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】根据绝对值的定义和开平方、立方的方法,应对x 分0,0,0x x x >=<三种情况分类讨论,根据讨论结果可得答案. 【详解】当0x >时，0x x x ===-<，此时集合共有2个元素，当0x =时，0x x x ====-=，此时集合共有1个元素，当0x <时，0x x -===>，此时集合共有2个元素，综上所述，此集合最多有2个元素. 故选：A . 【点睛】本题考查了元素与集合关系的判断及根式的化简求值,其中解答本题的关键是利用分类讨论思想,对x 分三种情况进行讨论,是基础题.2．C解析：C 【分析】图中阴影部分是集合A 与集合B 的补集的交集. 【详解】图中阴影部分是集合A 与集合B 的补集的交集，所以图中阴影部分，可以用()UA B 表示. 【点睛】本题考查了用韦恩图表示集合间的关系，考查了学生概念理解，数形结合的能力，属于基础题.3．D解析：D 【分析】讨论集合A 与集合B ，根据完美集合的概念知集合C ，根据k k k a b c +=建立等式求x 的值．【详解】首先当2x =时，{}21,2,3,4,5,6P =不可能是完美集合，证明：假设{}21,2,3,4,5,6P =是完美集合，若C 中元素最小为3，则11123a b +=+=，222456a b c +=+==不可能成立；若C 中元素最小为4，则11134a b +=+=，222256a b c +=+==不可能成立；若C 中元素最小为5，则11145a b +=+=，222236a b c +=+==不可能成立；故假设{}21,2,3,4,5,6P =是完美集合不成立，则{}21,2,3,4,5,6P =不可能是完美集合．所以2x ≠；若集合{1,5},{3,6}A B ==，根据完美集合的概念知集合{}4,,5611C x x =∴=+=；若集合{1,3},{4,6}A B ==，根据完美集合的概念知集合{}5,,369C x x =∴=+=；若集合{1,4},{3,5}A B ==，根据完美集合的概念知集合{}6,,347C x x =∴=+=；则x 的所有可能取值之和为791127++=，故选：D ．【点睛】本题是新概念题，考查学生分析问题，理解问题的能力，是中档题．4．C解析：C 【分析】用列举法表示集合Q ,这样就可以选出正确答案. 【详解】{}M P M a ⊆⇒=或{}b 或{},a b 或∅.因此{}{}{}{}{|},,,,Q M M P a b a b =⊆=∅,所以P Q ∈.故选：C 【点睛】本题考查了集合与集合之间的关系,理解本题中集合Q 元素的属性特征是解题的关键.5．A解析：A 【分析】先理解题意，然后分①当11x =±,10y =时,②当10x =,11y =±时, ③当10x =,10y =时,三种情况讨论即可. 【详解】解:由{}22(,)1,,A x y x y x Z y Z =+≤∈∈，{}(,)3,3,,B x y x y x Z y Z =≤≤∈∈, ①当11x =±,10y =时, 124,3,2,1,0,1,2,3,4x x +=----,123,2,1,0,1,2,3y y +=---,此时A B ⊕的元素个数为9763⨯=个,②当10x =,11y =±时, 123,2,1,0,1,2,3x x +=---,124,3,2,1,0,1,2,3,4y y +=----,这种情况和第①种情况除124,4y y +=-外均相同,故新增7214⨯=个, ③当10x =,10y =时, 123,2,1,0,1,2,3x x +=---,123,2,1,0,1,2,3y y +=---,这种情况与前面重复,新增0个,综合①②③可得:A B ⊕的元素个数为6314077++=个, 故选:A. 【点睛】本题考查了元素与集合关系的判断，重点考查了计数原理的应用，属中档题.6．C解析：C 【分析】根据“一类”的定义分别进行判断即可．【详解】①201854033÷=⋯，2018[3]∴∈，故①正确； ②20185(404)2-=⨯-+，2018[3]-∉，故②错误；③因为整数集中的数被5除的数可以且只可以分成五类，故[0][1][2][3][4]Z =⋃⋃⋃⋃，故③正确；④整数a ，b 属于同 “一类”， ∴整数a ，b 被5除的余数相同，从而-a b 被5除的余数为0，反之也成立，故“整数a ，b 属于同一“类”的充要条件是“[0]a b -∈”．故④正确．正确的结论为①③④3个．故选：C ．【点睛】本题主要考查新定义的应用，利用定义正确理解“一类”的定义是解决本题的关键，是中档题．7．C解析：C 【分析】直接利用新定义判断五个命题的真假即可．【详解】由P （A ）的定义可知①正确，④正确，设n （A ）＝n ，则n （P （A ））＝2n ，∴②错误，若A ∩B ＝∅，则P （A ）∩P （B ）＝{∅}，③不正确； n （A ）﹣n （B ）＝1，即A 中元素比B 中元素多1个，则n [P （A ）]＝2×n [P （B ）]．⑤正确，故选：C ．【点睛】本题考查集合的子集关系，集合的基本运算，新定义的理解与应用．8．B解析：B 【解析】【分析】解出集合A 、B ，再利用补集和交集的定义可得出集合()RA B .【详解】由2log 1x <，02x <<，{}02A x x ∴=<<.由210x -≥，得1x ≤-或1x ≥，则{}11B x x x =≤-≥或，{}11R B x x ∴=-<<，因此，(){}01A B x x ⋂=<<R ，故选：B. 【点睛】本题考查交集和补集的混合运算，同时也考查了对数不等式以及函数定义域的求解，考查计算能力，属于中等题.9．D解析：D 【分析】解绝对值不等式求得集合A ，解分式不等式求得集合B ，求得集合A 的补集，然后求此补集和集合B 的并集，由此得出正确选项. 【详解】由|31|2x -≥得312x -≤-或312x -≥，解得13x ≤-或1x ≥，故1,13R C A ⎛⎫=- ⎪⎝⎭.由201x x -≤-得()()12010x x x ⎧--≤⎨-≠⎩，解得12x <≤，所以()R C A B =1,1(1,2]3⎛⎫-⋃ ⎪⎝⎭.故选：D. 【点睛】本小题主要考查绝对值不等式的解法，考查分式不等式的解法，考查集合补集、并集的计算，属于基础题.10．C解析：C 【分析】首先根据题意，求得{|2R C B x x m =>+或}2x m <-，由R AC B A =可以得到R A C B ⊆，根据子集的定义求得参数所满足的条件，得到结果.【详解】{}{}2230=|13A x x x x x =--≤-≤≤，∵{}22B x m x m =-≤≤+． ∴{2R C B x x m =>+或2}x m <-， ∵R AC B A =即R A C B ⊆，∴23m ->或21m +<-．即5m >或3m <-，即实数m 的取值范围是5m >或3m <-．故选：C. 【点睛】该题考查的是有关集合的问题，涉及到的知识点有集合的补集，根据子集求参数的取值范围，属于简单题目.11．C解析：C 【分析】由集合描述求集合,A B ，结合韦恩图知阴影部分为()()U C A B A B ⋂⋂⋃，分别求出()U C A B 、()A B ⋃，然后求交集即可.【详解】(){}20{|20}A x x x x x =+<=-<<，{}1{|11}B x x x x =≤=-≤≤，由图知：阴影部分为()()U C A B A B ⋂⋂⋃，而{|10}A B x x ⋂=-≤<，{|21}A B x x ⋃=-<≤，∴(){|1U C A B x x ⋂=<-或0}x ≥，即()(){|21U C A B A B x x ⋂⋂⋃=-<<-或01}x ≤≤，故选：C 【点睛】本题考查了集合的基本运算，结合韦恩图得到阴影部分的表达式，应用集合的交并补混合运算求集合.12．D解析：D 【分析】先解方程得集合A ，再根据A B B =得B A ⊂，最后根据包含关系求实数a ，即得结果.【详解】{}2|8150{3,5}A x x x =-+==,因为AB B =，所以B A ⊂，因此,{3},{5}B =∅，对应实数a 的值为110,,35，其组成的集合的子集个数有328=，选D. 【点睛】本题考查集合包含关系以及集合子集，考查基本分析求解能力，属中档题.二、填空题13．-1或3【分析】解方程用列举法表示集合AB 由即得解【详解】集合若故a=-1或3故答案为：-1或3【点睛】本题考查了集合的包含关系考查了学生概念理解数学运算能力属于基础题解析：-1或3 【分析】解方程，用列举法表示集合A ，B ，由B A ≠⊂，即得解. 【详解】集合2|230{1,3}Ax x x ，{}|0{}B x x a a =-==若B A ≠⊂，故a =-1或3 故答案为：-1或3 【点睛】本题考查了集合的包含关系，考查了学生概念理解，数学运算能力，属于基础题.14．【分析】计算得到根据得到得到答案【详解】则或即故故故答案为：【点睛】本题考查了不等式的解集根据集合的运算结果求参数意在考查学生的综合应用能力解析：2【分析】计算得到()()2,11,B =--+∞，根据()(]213A B A B =-+∞=，，，∪∩得到[]1,3A =-，得到答案.【详解】()()2101x x x ++>-，则1x >或21x -<<-，即()()2,11,B =--+∞.()(]213A B A B =-+∞=，，，∪∩，故[]1,3A =-，故2m n +=. 故答案为：2. 【点睛】本题考查了不等式的解集，根据集合的运算结果求参数，意在考查学生的综合应用能力.15．或【分析】根据讨论方程解的情况即得结果【详解】时满足题意；时要满足题意需综上的取值范围是或故答案为：或【点睛】本题考查根据集合元素个数求参数考查基本分析求解能力属中档题解析：{0a a =或}1a ≥ 【分析】根据a 讨论2210ax x ++=方程解的情况，即得结果【详解】0a =时，21212102ax x x x ++=+=∴=-，12A ⎧⎫=-⎨⎬⎩⎭满足题意；0a ≠时，要满足题意，需4401a a ∆=-≤∴≥综上a 的取值范围是{0a a =或}1a ≥ 故答案为：{0a a =或}1a ≥ 【点睛】本题考查根据集合元素个数求参数，考查基本分析求解能力，属中档题.16．【分析】先化简集合利用分类讨论和即可求出构成的集合【详解】由可得:即:解得或故:由可得:当时方程无实数解此时满足当时方程的实数解为故:由可得:或解得或的所有取值构成的集合为:故答案为:【点睛】本题主解析：11{0,,}24-【分析】先化简集合B ,利用A B ⊆,分类讨论=0a 和0a ≠,即可求出构成a 的集合. 【详解】由{}2280B x x x =--=可得:2280x x --= 即:()()240x x +-= 解得2x =-或4x = 故:{}2,4B =- {}10,A x ax x R =+=∈由10ax += 可得:1ax =-当0a =时,方程1ax =-无实数解,此时A =∅,满足A B ⊆ 当0a ≠时,方程1ax =-的实数解为1x a =-,故:1{}A a=- 由A B ⊆可得:12a -=-或14a -= 解得12a =或14a =-a 的所有取值构成的集合为:11{0,,}24-.故答案为:11{0,,}24-. 【点睛】本题主要考查了集合间的基本关系以及一元二次方程的解法,要注意集合A 是集合B 的子集时,集合A 有可能是空集.17．【分析】根据条件可得结合的意义可得集合【详解】因为集合是实数集的子集若则但不满足所以因为所以所以有又因为表示集合的元素去掉集合中的元素表示A 集合和B 集合中的所有元素所以把中的元素去掉中元素即为所求的解析：(,1)(2,3)(5,)-∞+∞【分析】根据条件()()[3,5]A B =R R 可得()(),35,A B =-∞+∞，结合[1,2]B A =R 的意义，可得集合A .【详解】因为集合A 、B 是实数集R 的子集，若A B =∅,则[2,0]A B A =-=R ，[1,2]BA B ==R ，但不满足()()[3,5]A B =R R ，所以A B ⋂≠∅. 因为()()[3,5]A B =R R ,所以()()()[3,5]AB A B ==R R R ，所以有()(),35,A B =-∞+∞.又因为[1,2]B A =R 表示集合B 的元素去掉集合A 中的元素，()(),35,A B =-∞+∞表示A 集合和B 集合中的所有元素，所以把()(),35,A B =-∞+∞中的元素去掉[1,2]B A =R 中元素，即为所求的集合A ，所以(,1)(2,3)(5,)A =-∞+∞.故答案为(,1)(2,3)(5,)-∞+∞.【点睛】本题主要考查集合的运算，根据集合的运算性质可求也可借助数轴或者韦恩图求解，侧重考查逻辑推理的核心素养.18．【分析】根据条件得到或分别计算得到答案【详解】则或当时解得；当时满足综上所述：故答案为：【点睛】本题考查了根据集合的包含关系求参数忽略掉空集的情况是容易发生的错误解析：[1,)+∝【分析】根据条件得到{}1N =或N =∅，分别计算得到答案.【详解】N M ⊆，则{}1N =或N =∅当{}1N =时，{}{}2|201N x x x a =-+==，解得1a =；当N =∅时，{}2|20N x xx a =-+=，满足4401a a ∆=-<∴>.综上所述：1a ≥故答案为：[1,)+∝【点睛】本题考查了根据集合的包含关系求参数，忽略掉空集的情况是容易发生的错误. 19．【分析】求函数的值域求得集合解一元二次不等式求得集合由此求得【详解】根据指数函数的性质可知所以有解得即所以故答案为【点睛】本小题主要考查集合交集补集的运算考查指数型函数值域的求法考查一元二次不等式的解析：(]1,1-【分析】求函数的值域求得集合A ，解一元二次不等式求得集合B ，由此求得()R C A B ⋂.【详解】根据指数函数的性质可知，211x y =+>，所以()1,A =+∞，有()()22210x x x x --=-+<解得12x -<<，即()1,2B =-，所以()R C A B =(]1,1-. 故答案为(]1,1-.【点睛】本小题主要考查集合交集、补集的运算，考查指数型函数值域的求法，考查一元二次不等式的解法，属于基础题.20．或【分析】分情况讨论:当时和当时两种情况;当时由即可求出答案分类讨论最后把的范围合并即可【详解】若则集合符合题意；若则解得故答案为：或【点睛】本题考查集合中元素个数问题;分类讨论和两种情况是求解本题解析：98a ≥或0a = 【分析】分情况讨论:当0a =时和当0a ≠时两种情况;当0a ≠时由0∆≤即可求出答案.分类讨论最后把a 的范围合并即可.【详解】若0a =，则集合2{|320}3A x x ⎧⎫=+==-⎨⎬⎩⎭，符合题意；若0a ≠，则980a ∆=-≤，解得98a ≥．故答案为：98a ≥或0a =．【点睛】本题考查集合中元素个数问题;分类讨论0a =和0a ≠两种情况是求解本题关键; 0a =时易忽略;属于中档题，易错题. 三、解答题21．（1）1-或3-；（2）1a ≠-且3a ≠-且1≠-±a 【分析】（1）由条件可知集合B 中包含元素2，所以代入求a ，并验证是否满足条件；（2）由条件得A B =∅，分∆<0和0,0∆>∆=三种情况讨论，得到a 的取值范围.【详解】（1）{}1,2A =，由{}2A B ⋂=可知，()2224150a a +++-=，即2430a a ++=，解得：1a =-或3a =-，当1a =-时，2402x x -=⇒=±，此时2,2B ，满足{}2A B ⋂=，当3a =-时，24402x x x -+=⇒=，此时{}2B =，满足{}2A B ⋂=.所以实数a 的值是1-或3-；（2）U =R ，A ∩(U B )=A ，U A B ∴⊆，则A B =∅ ①当()()2241458240a a a ∆=+--=+<，即3a <-时，此时B =∅，满足条件； ②当0∆=时，3a =-，即{}2B =，{}2A B ⋂=，不满足条件；③当0∆>时，即3a >-时，此时只需1B ∉，2∉B ，将2代入方程得1a =-或3a =-，将1代入方程得2220a a +-=，得13=-±a ，综上可知，a 的取值范围是1a ≠-且3a ≠-且13≠-±a【点睛】易错点睛：1.当集合的元素是方程的实数根时，根据集合的运算结果求参数时，注意回代检验，否则会造成增根情况，当集合是区间形式表示时，注意端点值的开闭； 2.当集合的运算结果转化为集合的包含关系时，注意讨论空集情况，容易忽略这一点. 22．（1）{}210A B x x ⋃=<<，()R A B ={}23710x x x <<<<或；（2）3a >．【分析】（1）利用集合交并补的定义进行计算即可；（2）利用A C ⋂≠∅结合数轴，可求得a 的取值范围．【详解】（1）∵{}37A x x =≤≤，{}210B x x =<<， ∴{}210A B x x ⋃=<<.∵{}37A x x =≤≤，∴{|3R C A x x =<或}7x >，∴()RA B ={|3x x <或}7x >{}210x x ⋂<<{}23710x x x =<<<<或. （2）如图所示，当3a >时，A C ⋂≠∅（或用补集思想）3a ∴>．【点睛】本题考查集合的交并补运算，考查利用集合间的关系求参数范围，属于基础题．23．（1）5；（2）{3a a ≤-或}1a =-.【分析】（1）求得集合A ，由题意可得2B ∈，可求得a 的值，再验证{}2AB =-是否满足，由此可求得实数a 的值；（2）由题意可得B A ⊆，分B =∅、{}2B =-、{}2B =、2,2B四种情况讨论，求得实数a 的值，并检验A B ⊆是否成立，由此可求得实数a 的取值范围. 【详解】（1）{}{}2402,2A x x =-==-，因为{}2A B =-，所以2B -∈，所以()244150a a -++-=，整理得2450a a --=，解得1a =-或5a =.当1a =-时，{}{}2402,2B x x =-==-，不满足{}2A B =-；当5a =时，{}{}2122002,10B x xx =++==--，满足{}2A B =-；故5a =；（2）由题意，知{}2,2A =-，由A B A ⋃=，得B A ⊆.①当集合B =∅时，关于x 的方程()222150x a x a +++-=没有实数根，所以()()2241458240a a a ∆=+--=+<，即30a +<，解得3a <-； ②当集合{}2B =-时，()242145a a ⎧-=-+⎨=-⎩，无解； ③当集合{}2B =时，()242145a a ⎧=-+⎨=-⎩，解得3a =-， ④当2,2B 时，21054a a +=⎧⎨-=-⎩，解得1a =- 综上，可知实数a 的取值范围为{3a a ≤-或}1a =-.【点睛】本题考查交集的计算，同时也考查了利用集合的包含关系求参数，考查分类讨论思想的应用与运算求解能力，属于中等题. 24．（1）[)1,4A B =-（2）3,4⎛⎫+∞ ⎪⎝⎭（3）[)1,2,2⎛⎤-∞-+∞ ⎥⎝⎦ 【分析】（1）计算得到142A x x ⎧⎫=<<⎨⎬⎩⎭，[)1,1B =-，求并集得到答案. （2）讨论B =∅和B ≠∅两种情况，分别计算到答案.（3）讨论B =∅和B ≠∅两种情况，分别计算到答案.【详解】（1）由40210x x ->⎧⎨->⎩，解得142A x x ⎧⎫=<<⎨⎬⎩⎭，当0m =时，[)1,1B =-，所以[)1,4A B =-.（2）当B =∅时，211m m -≥+，2m ≥，符合B A ⊆.当B ≠∅时，根据B A ⊆得211121214m m m m -<+⎧⎪⎪->⎨⎪+≤⎪⎩，解得324m <<. 综上所述，m 的取值范围是3,4⎛⎫+∞ ⎪⎝⎭. （3）当B =∅时，211m m -≥+，2m ≥，符合A B =∅.当B ≠∅时，211112m m m -<+⎧⎪⎨+≤⎪⎩或211214m m m -<+⎧⎨->⎩，解得12m ≤-. 综上所述，m 的取值范围是[)1,2,2⎛⎤-∞-+∞ ⎥⎝⎦.【点睛】本题考查了集合的并集，根据集合包含关系求参数，根据交集结果求参数，意在考查学生对于集合运算的综合应用.25．（1）{}|12x x ≤≤；（2）[]4,2.【分析】（1）当2a =时，不等式化为2320x x -+≤，结合一元二次不等式的解法，即可求解；（2）把不等式化为()()10x x a --≤，分类讨论，结合集合的包含关系，即可求解.【详解】（1）由题意，当2a =时，不等式()210x a x a -++≤，即2320x x -+≤，即()()120x x --≤，解得12x ≤≤，所以集合{}|12A x x =≤≤.（2）由()210x a x a -++≤，可得()()10x x a --≤，当1a <时，不等式()()10x x a --≤的解集为{}|1x a x ≤≤.由集合A 是集合{}4|2x x -≤≤的真子集可得4a ≥-，所以41a -≤<，当1a =时，不等式()()10x x a --≤的解集为{}|1x x =满足题意；当1a >时，不等式()()10x x a --≤的解集为{}|1x x a ≤≤，由集合A 是集合{}4|2x x -≤≤的真子集，可得2a ≤，所以11a <≤，综上可得：42x -≤≤，即实数a 的取值范围为[]4,2-.【点睛】本题主要考查了一元二次不等式的求解及其应用，其中解答中熟记一元二次不等式的解法，结合集合的关系求解是解答的关键，着重考查了推理与运算能力，属于中档试题. 26．（1）=[3,4]A B ；（2）4a >或0a < 【分析】（1）写出集合A ，B 的区间形式，代入数值计算即可；（2）写出集合R C A ，根据边界判断a 的取值范围即可.【详解】集合{}|2,12=[2,4]x A y y x ==≤≤，()(){}|20[,2]B x x a x a a a =---≤=+ （1）若3a =，[3,5]B =，则=[3,4]A B ；（2）(,2)(4,)R C A =-∞+∞，()R B C A ⊆，因此：4a >或22a +<故：4a >或0a <【点睛】本题考查了集合的交并补运算，考查了学生的数学运算能力，属于基础题.。

深圳平冈中学高中物理必修一第二章《匀变速直线运动的研究》测试卷(答案解析)

一、选择题1．无风秋日，晚霞满天，一片梧桐叶从高为5m 的枝头自静止飘落至地面，所用时间可能是（g 取10m/s 2）（） A ．0.1sB ．0.5sC ．1sD ．3s2．一物体做匀加速直线运动，相继经过两段距离均为20m 的位移，第一段用时4s ，第二段用时2s ，则物体的加速度大小为（） A ．24m/s 9B ．216m/s 9 C ．24m/s 3D ．25m/s 33．2016年里约奥运会女子3米跳板比赛中，我国跳水运动员施廷懋获得金牌。

经过对跳水过程录像的理想化处理，将施廷懋（可视为质点）离开跳板时作为计时起点，其运动过程的v -t 图像简化为如图所示，忽略空气阻力，则运动员（）A ．0-t 1运动员自由下落B ．在t 2时刻开始进入水面C ．在t 2时刻在空中最高点D ．在t 3时刻浮出水面4．如图所示是物体在某段运动过程中的v －t 图像，在t 1和t 2时刻的瞬时速度分别为v 1和v 2，则从t 1到t 2的过程中（）A ．加速度的方向和速度方向相同B ．加速度逐渐减小C ．平均速度v ＝122v v + D ．平均速度v >122v v + 5．甲乙两物体从同一点开始沿一直线运动，甲的x -t 和乙的v -t 图象如图所示，下列说法中正确的是（）A．甲为匀速直线运动，乙为匀加速直线运动B．甲、乙均在3s末回到出发点，距出发点的最大距离均为4mC．0~2s内与4s~6s内，甲的速度等大反向，乙的加速度等大反向D．6s内甲的路程为16m，乙的路程为12m6．对于如图所示的情境，交通法规定“车让人”，否则驾驶员将受到处罚，若以8m/s匀速行驶的汽车即将通过路口，有行人正在过人行横道，此时汽车的前端距停车线8m，该车5m/s，下列说法中正确的是（）减速时的加速度大小为2A．驾驶员立即刹车制动，则至少需2s汽车才能停止B．在距停车线6m处才开始刹车制动，汽车前端恰能止于停车线处C．若经0.2s后才开始刹车制动，汽车前端恰能止于停车线处D．若经0.4s后才开始刹车制动，汽车前端恰能止于停车线处7．龟兔赛跑的故事家喻户晓。

深圳平冈中学必修一第二单元《函数》测试卷(答案解析)

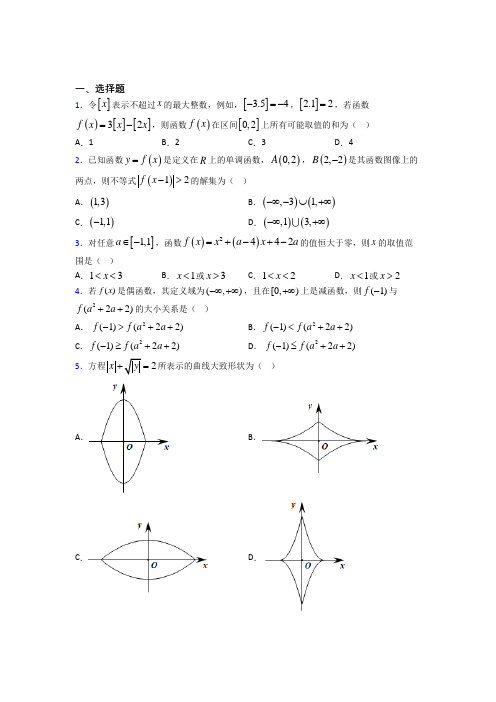
一、选择题1．令[]x 表示不超过x 的最大整数，例如，[]3.54-=-，[]2.12=，若函数()[][]32f x x x =-，则函数()f x 在区间[]0,2上所有可能取值的和为（）A ．1B ．2C ．3D ．42．已知函数()y f x =是定义在R 上的单调函数，()0,2A ，()2,2B -是其函数图像上的两点，则不等式()12f x ->的解集为（） A ．()1,3 B ．()(),31,-∞-⋃+∞ C ．()1,1-D ．()(),13,-∞+∞3．对任意[]1,1a ∈-，函数()()2442f x x a x a =+-+-的值恒大于零，则x 的取值范围是（） A ．13x <<B ．1x <或3x >C ．12x <<D ．1x <或2x >4．若()f x 是偶函数，其定义域为(,)-∞+∞，且在[0,)+∞上是减函数，则(1)f -与2(22)f a a ++的大小关系是（）A ． 2(1)(22)f f a a ->++B ．2(1)(22)f f a a -<++C ．2(1)(22)f f a a -≥++D ． 2(1)(22)f f a a -≤++5．方程2x y +=所表示的曲线大致形状为（）A ．B ．C ．D ．6．若函数()()21225,012,1bb x f x x x b x x -⎧-+<<⎪=⎨⎪+-≥⎩对于任意的实数12x x ≠，都有()()()12120x x f x f x -->⎡⎤⎣⎦成立，则实数b 的取值范围为（）A ．1,42⎛⎤ ⎥⎝⎦B ．[)4,+∞C ．[]1,4D ．1,2⎛⎫+∞⎪⎝⎭7．对x R ∀∈，用()M x 表示()f x ，()g x 中较大者，记为()()()max{,}M x f x g x =，若()()2{3,1}M x x x =-+-，则()M x 的最小值为（）A ．-1B ．0C ．1D ．48．设()f x 是奇函数，且在(0,)+∞内是增函数，又(2)0f -=，则()0f x x<的解集是（）A ．{2002}xx x -<<<<∣或 B ．{22}xx x <->∣或 C ．{202}xx x <-<<∣或 D ．{202}xx x -<<>∣或 9．已知函数()f x 的定义域为R ，()0f x >且满足()()()f x y f x f y +=⋅，且()112f =，如果对任意的x 、y ，都有()()()0x y f x f y ⎡⎤--<⎣⎦，那么不等式()()234f x f x -⋅≥的解集为（）A ．(][),12,-∞+∞ B ．[]1,2 C ．()1,2 D ．(],1-∞10．已知函数()y f x =的定义域为[]0,4，则函数0(2)y x =-的定义域是（） A ．[1,5]B ．((1,2)(2,5) C ．(1,2)(2,3]⋃D ．[1,2)(2,3]⋃11．已知定义在R 上的函数()f x 的图像关于y 轴对称，且当0x >时()f x 单调递减，若()()()1.360.5log 3,0.5,0.7,a f b f c f -===则,,a b c 的大小关系（）A ．c a b >>B ．b a c >>C ．a c b >>D ．c b a >>12．设函数()y f x =在(),-∞+∞上有定义，对于给定的正数K ，定义函数(),()()()k f x f x K f x K f x K≤⎧=⎨>⎩，，取函数()||()1x f x a a -=>，当1K a =时，函数()k f x 在下列区间上单调递减的是（）A ．(),0-∞B ．(),a -+∞C ．(),1-∞-D ．()1,+∞二、填空题13．已知函数(3)5,1()2,1a x x f x a x x--≤⎧⎪=⎨->⎪⎩是R 上的增函数，则a 的取值范围是________.14．函数()()2325f x kx k x =+--在[)1+∞，上单调递增，则k 的取值范围是________. 15．若函数()y f x =的定义域是[0,2]，则函数()g x =______． 16．函数1,1()32,12x a x f x a x x ⎧+>⎪=⎨⎛⎫-+≤ ⎪⎪⎝⎭⎩是R 上的单调递增函数，则实数a 取值范围为________.17．设函数2222,0(),0x x x f x x x ⎧++=⎨->⎩，若(())2f f a =，则a =___________.18．定义域为R 的函数()f x 满足(2)2()f x f x +=，当[0,2)x ∈时，2 1.5,[0,1)()0.5,[1,2)x x x x f x x -⎧-∈⎪=⎨-∈⎪⎩，若[4,2)x ∈--时，1()42t f x t ≥-恒成立，则实数t 的取值范围是______．19．若函数()f x 满足()()1f x f x =-，()()13f x f x +=--当且仅当(]1,3x ∈时，()f x x =，则()57f =______．20．已知函数2262()2x ax x f x a x x⎧-+⎪=⎨>⎪⎩，≤，，是R 上的减函数，则a 的取值范围为______．三、解答题21．已知函数()()(),f x x x a a R g x x =-∈= （1）若0a =，试写出函数()f x 的单调区间；（2）记()()()F x g x f x =⋅，若()F x 为偶函数，求实数a 的值；（3）当1a >时，记()()()Gx f x g x =+，试求函数()G x 在区间[]1,2上的最大值．22．已知函数1()(1)1x x a f x a a -=>+，求：（1）判断函数的奇偶性；（2）证明()f x 是R 上的增函数；（3）求该函数的值域. 23．已知函数()21axf x x =-（0a ≠）．（1）判断函数()f x 的奇偶性并给予证明；（2）若函数()f x 满足()1242f f ⎛⎫-= ⎪⎝⎭，判断函数()f x 在区间()1,+∞的单调性，并用单调性的定义证明．24．已知函数()222f x x ax =++，[]5,5x ∈-．（1）当1a =-时，求函数()f x 的最大值和最小值；（2）求实数a 的取值范围，使()y f x =在区间[]5,5-上是单调函数．（3）求函数()f x 的最小值()g a 的表达式，并求()g a 的最大值． 25．已知定义在R 上的函数()f x 的单调递增函数，且对∀x ，y ∈R ，都有()()()1f x y f x f y +=++，f (2)=5.（1）求f (0)，f (1)的值；（2）若对11,32x ⎡⎤∈⎢⎥⎣⎦∀，都有2()(21)1f kx f x +-<成立，求实数k 的取值范围.26．已知函数()f x 对一切实数,x y 都有()()f x y f y +-=(21)x x y ++成立，且(1)0f =.（1）求(0)f 的值，及()f x 的解析式；（2）当21x -≤≤时，不等式()(1)5f x a a x -≥-- 恒成立，求a 的取值范围.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】根据[]x 表示不超过x 的最大整数，分5种情况讨论，分别求出[]x 和[2]x 的值，即可以计算()3[][2]f x x x =-的函数值，相加即可得答案．【详解】因为[]x 表示不超过x 的最大整数，所以：当102x <时，有021x <，则[]0x =，则3[]0x =，[2]0x =，此时()0f x =，当112x <时，有122x <，则[]0x =，则3[]0x =，[2]1x =，此时()1f x =-，当312x <时，有223x <，则[]1x =，则3[]3x =，[2]2x =，此时()1f x =，当322x <时，有324x <，则[]1x =，则3[]3x =，[2]3x =，此时()0f x =，当2x =时，24=x ，则[]2x =，则3[]6x =，[2]4x =，此时()2f x =，函数()f x 在区间[0，2]上所有可能取值的和为011022-+++=；故选：B ．【点睛】结论点睛：分类讨论思想的常见类型（1）问题中的变量或含有需讨论的参数的，要进行分类讨论的；（2）问题中的条件是分类给出的；（3）解题过程不能统一叙述，必须分类讨论的；（4）涉及几何问题时，由几何元素的形状、位置的变化需要分类讨论的.2．D解析：D 【分析】根据题意可得出(0)2,(2)2f f ==-，从而得出()f x 在R 上为减函数，从而根据不等式()12f x ->得，(1)(2)f x f -<或(1)(0)f x f ->，从而得出12x ->或10x -<，解出x 的范围【详解】解：由题意得(0)2,(2)2f f ==-，因为函数()y f x =是定义在R 上的单调函数，所以()f x 在R 上为减函数，由()12f x ->，得(1)2f x ->或(1)2f x -<-，所以(1)(0)f x f ->或(1)(2)f x f -<，所以10x -<或12x ->，解得1x <或3x >，所以不等式()12f x ->的解集为()(),13,-∞+∞，故选：D 【点睛】关键点点睛：此题考查函数单调性的应用，考查绝对值不等式的解法，解题的关键是把()12f x ->转化为(1)(0)f x f ->或(1)(2)f x f -<，再利用()f x 在R 上为减函数，得10x -<或12x ->，考查数学转化思想，属于中档题 3．B解析：B 【分析】将函数()f x 的解析式变形为()2()244f x x a x x =-+-+，并构造函数()2()244g a x a x x =-+-+，由题意得出()()1010g g ⎧->⎪⎨>⎪⎩，解此不等式组可得出实数x 的取值范围【详解】对任意[]1,1a ∈-，函数()()2442f x x a x a =+-+-的值恒大于零设()()2244g a x a x x =-+-+，即()0g a >在[]1,1a ∈-上恒成立.()g a 在[]1,1a ∈-上是关于a 的一次函数或常数函数，其图象为一条线段.则只需线段的两个端点在x 轴上方，即()()2215601320g x x g x x ⎧-=-+>⎪⎨=-+>⎪⎩ ，解得3x >或1x < 故选：B 【点睛】关键点睛：本题考查不等式在区间上恒成立问题，解答本题的关键是构造函数()()2244g a x a x x =-+-+，将问题转化为()0g a >在[]1,1a ∈-上恒成立，从而得到()()1010g g ⎧->⎪⎨>⎪⎩，属于中档题.4．C解析：C 【分析】由()f x 是偶函数，可知(1)(1)f f -=，故只需比较(1)f 与2(22)f a a ++的大小即可，而2222(1)11a a a ++=++≥，再结合函数()f x 的单调性，即可得(1)f 与2(22)f a a ++大小关系.【详解】因为()f x 是偶函数，所以(1)(1)f f -=，又2222(1)11a a a ++=++≥，()f x 在[0,)+∞上是减函数，所以2(22)(1)f a a f ++≤，即2(22)(1)f a a f ++≤-. 故选：C 【点睛】关键点点睛：本题主要考查利用函数的单调性比较大小，关键是借助函数的奇偶性，将要比较的函数值对应的自变量转化到同单调区间上，并且比较它们的大小，再利用单调性作出判断．5．D解析：D 【分析】先利用方程得到图像的对称性，再作0y ≥，0x ≥时的图像，利用对称性即得结果.由方程2x y +=可知图像关于原点中心对称，也关于坐标轴对称.20,44x y y =-≥-≤≤，20,22y x x =-≥-≤≤.当0y ≥，0x ≥时，方程2x y +=转化成()22y x =-，作图如下：再利用对称性即得图像为 D. 故选：D. 【点睛】本题解题关键是利用绝对值的性质得到图像的对称性，就只需要画0y ≥，0x ≥部分图像，即突破问题.6．C解析：C 【分析】根据函数单调性的定义判断出函数()f x 为()0,∞+上的增函数，进而可得出关于实数b 的不等式组，由此可解得实数b 的取值范围. 【详解】对任意的正实数1x 、2x ，当12x x ≠时，()()()12120x x f x f x -->⎡⎤⎣⎦，不妨设12x x >，则()()120f x f x ->，即()()12f x f x >，所以，函数()f x 为()0,∞+上的增函数，则()()120212122512b b b b b -<⎧⎪-⎪≤⎨⎪--+≤+-⎪⎩，解得14b ≤≤. 因此，实数b 的取值范围是[]1,4. 故选：C. 【点睛】思路点睛：利用分段函数的单调性求参数范围，应该各支函数在各自的区间内利用单调性以及函数在间断点处端点值的大小关系得出参数的不等式组，从而解得参数的取值范围.7．C【分析】根据定义求出()M x 的表达式，然后根据单调性确定最小值．【详解】由23(1)x x -+=-解得：1x =-或2x =，2(1)3x x -≥-+的解集为1x ≤-或2x ≥，2(1)3x x -<-+的解为12x -<<，∴2(1),12()3,12x x x M x x x ⎧-≤-≥=⎨-+-<<⎩或，∴2x ≤时，()M x 是减函数，2x >时，()M x 是增函数，∴min ()(2)1M x M ==．故选：C ．【点睛】关键点点睛：本题考查新定义函数，解题关键是确定新定义函数的解析式，根据新定义通过求最大值得出新函数的解析式，然后根据分段函数研究新函数的性质．8．A解析：A 【分析】由()0f x x <对0x >或0x <进行讨论，把不等式()0f x x<转化为()0f x >或()0f x <的问题解决，根据()f x 是奇函数，且在(0,)+∞内是增函数，又(2)0f -=，把函数值不等式转化为自变量不等式，求得结果．【详解】解：()f x 是R 上的奇函数，且在(0,)+∞内是增函数，∴在(,0)-∞内()f x 也是增函数，又(2)0f -=，()20f ∴=，∴当(x ∈-∞，2)(0-⋃，2)时，()0f x <；当(2x ∈-，0)(2⋃，)+∞时，()0f x >；∴()0f x x <的解集是{|20x x -<<或02}x <<．故选：A ．【点睛】本题考查函数的奇偶性的应用，解决此类问题的关键是理解奇偶函数在关于原点对称的区间的单调性，奇函数在关于原点对称的区间上单调性相同，偶函数在关于原点对称的区间上单调性相反；9．B【分析】计算出()24f -=，并由()()()0x y f x f y ⎡⎤--<⎣⎦可得出函数()y f x =在R 上为减函数，再由()()234f x f x-⋅≥，可得出()()232f xx f -≥-，再由函数()y f x =在R 上的单调性可得出232x x -≤-，解出该不等式即可. 【详解】由于对任意的实数x 、y ，()()()f x y f x f y +=⋅且()0f x >. 令0x y ==，可得()()()000f f f =⋅，且()00f >，解得()01f =. 令y x =-，则()()()01f x f x f ⋅-==，()()1f x f x -=，()()1121f f -==. ()()()211224f f f ∴-=-⋅-=⨯=.设x y <，则0x y -<，由()()()0x y f x f y ⎡⎤--<⎣⎦，得()()f x f y >. 所以，函数()y f x =在R 上为减函数，由()()234f x f x-⋅≥，可得()()232f x x f -≥-.所以232x x -≤-，即2320x x -+≤，解得12x ≤≤. 因此，不等式()()234f x f x -⋅≥的解集为[]1,2.故选B. 【点睛】本题考查抽象函数的单调性解不等式，解题的关键就是将不等式左右两边转化为函数的两个函数值，并利用函数的单调性进行求解，考查分析问题和解决问题的能力，属于中等题.10．C解析：C 【分析】由函数定义域的定义，结合函数0(2)y x =-有意义，列出相应的不等式组，即可求解. 【详解】由题意，函数()y f x =的定义域为[]0,4，即[]0,4x ∈，则函数0(2)y x =-满足0141020x x x ≤+≤⎧⎪->⎨⎪-≠⎩，解得13x <≤且2x ≠，所以函数0(2)y x =+-的定义域是(1,2)(2,3]⋃. 故选：C.本题主要考查了抽象函数的定义域的求解，其中解答中熟记函数的定义域的定义，根据题设条件和函数的解析式有意义，列出不等式组是解答的关键，着重考查推理与运算能力.11．A解析：A 【分析】函数()f x 是偶函数，判断出自变量的大小，利用函数的单调性比较大小得出答案．【详解】函数()f x 的图像关于y 轴对称， ∴函数()f x 为偶函数， ∵0.50.5log 3log 10<=，∴()()120.52log 3log 3log 3f f f ⎛⎫== ⎪⎝⎭，∴2221log 2log 3log 42=<<=， 1.3 1.30.522-=>，600.71<<． ∵当0x >时，()f x 单调递减，∴c a b >>，故选：A 【点睛】本题考查函数性质的综合应用，考查函数的单调性和奇偶性，考查指数和对数的单调性，属于中档题．12．D解析：D 【分析】作出函数()y f x =与1y a=的图象，数形结合可得()k f x ，即可得解. 【详解】令||1()x f x aa-==，解得1x =±，在同一直角坐标系中作出()y f x =与1y a=的图象，如图，所以,11()11,1x k x a x f x x a a x --⎧≤-⎪⎪=-<<⎨⎪⎪≥⎩，，所以函数()k f x 的单调减区间为()1,+∞. 故选：D. 【点睛】本题考查了函数图象的应用及函数单调性的求解，考查了运算求解能力与数形结合思想，属于中档题.二、填空题13．【分析】函数是增函数可得且即可求解【详解】因为函数为上的增函数所以当时递增即当时递增即且解得∴综上可知实数的取值范围是故答案为：【点睛】易错点睛：本题考查根据分段函数的单调性求参数范围需满足分段函数解析：(]0,2【分析】函数是增函数可得30a ->，0a >且2(3)151aa -⨯-≤-，即可求解. 【详解】因为函数()f x 为R 上的增函数，所以当1x ≤时，()f x 递增，即30a ->，当1x >时，()f x 递增，即0a >，且2(3)151aa -⨯-≤-，解得2a ≤，∴02a <≤，综上可知实数a 的取值范围是(]0,2. 故答案为：(]0,2. 【点睛】易错点睛：本题考查根据分段函数的单调性求参数范围，需满足分段函数每部分分别单调，还应注意在分段处的函数值大小问题，这是容易漏掉的地方.14．【分析】根据函数的解析式分和两种情况讨论利用一次二次函数的性质即可求解【详解】由已知函数在上单调递增可得当时函数在上单调递减不满足题意；当时则满足解得综上所述实数的取值范围是故答案为：【点睛】本题主解析：25⎡⎫+∞⎪⎢⎣⎭，【分析】根据函数的解析式，分0k =和0k ≠两种情况讨论，利用一次、二次函数的性质，即可求解. 【详解】由已知函数()()2325f x kx k x =+--在[)1+∞，上单调递增可得，当0k =时，函数()25f x x =--在[)1+∞，上单调递减，不满足题意；当0k ≠时，则满足03212k k k>⎧⎪-⎨-≤⎪⎩，解得25k ≥，综上所述，实数k 的取值范围是25⎡⎫+∞⎪⎢⎣⎭，. 故答案为：25⎡⎫+∞⎪⎢⎣⎭，. 【点睛】本题主要考查了函数单调性的应用，其中解答中熟记一次函数、二次函数的图象与性质是解答的关键，着重考查了分类讨论思想，以及推理与计算能力，属于基础题.15．【分析】根据抽象函数的定义域的求法结合函数列出不等式组即可求解【详解】由题意函数的定义域是即则函数满足解得即函数的定义域是故答案为：【点睛】求抽象函数定义域的方法：已知函数的定义域为求复合函数的定义解析：31,2⎛⎤⎥⎝⎦【分析】根据抽象函数的定义域的求法，结合函数()g x =. 【详解】由题意，函数()y f x =的定义域是[0,2]，即02x ≤≤，则函数()g x =021210x x ≤-≤⎧⎨->⎩，解得312x <≤，即函数()g x =31,2⎛⎤⎥⎝⎦. 故答案为：31,2⎛⎤⎥⎝⎦.【点睛】求抽象函数定义域的方法：已知函数()f x 的定义域为[],a b ，求复合函数()[]f g x 的定义域时：可根据不等式()a g x b ≤≤解得x ，则x 的取值范围即为所求定义域；已知复合函数()[]f g x 的定义域为[],a b ，求函数()f x 的定义域，求出函数()y g x =([,])x a b ∈的值域，即为()y f x =的定义域.16．【分析】根据指数函数和一次函数的性质得出关于的不等式组即可求解【详解】由题意函数是上的单调递增函数可得解得即实数取值范围故答案为：【点睛】利用函数的单调性求解参数的取值范围：根据函数的单调性将题设条解析：8[,6)3【分析】根据指数函数和一次函数的性质，得出关于a 的不等式组，即可求解. 【详解】由题意，函数1,1()32,12x a x f x a x x ⎧+>⎪=⎨⎛⎫-+≤ ⎪⎪⎝⎭⎩是R 上的单调递增函数，可得13021322a a a a ⎧⎪>⎪⎪->⎨⎪⎪+≥-+⎪⎩，解得863a ≤<，即实数a 取值范围8[,6)3.故答案为：8[,6)3. 【点睛】利用函数的单调性求解参数的取值范围：根据函数的单调性，将题设条件转化为函数的不等式（组），即可求出参数的值或范围；若分段函数是单调函数，则不仅要保证在各区间上单调性一致，还要确保在整个定义域内是单调的.17．【分析】先令则求解的值然后再分类讨论求解的值【详解】令则当时有无解当时有解得或所以或当时故无解；当时若则得若则即无解综上所述：故答案为：【点睛】本题考查分段函数的应用考查根据函数值求参难度一般解答时【分析】先令()f a t =，则()2f t =，求解t 的值，然后再分类讨论，求解a 的值. 【详解】令()f a t =，则()2f t =，当0t >时，有22t -=，无解，当0t ≤时，有2222t t ++=，解得0t =，或2t =-，所以()0f a =或()2f a =-，当()0f a =时，()2222110a a a ++=++>，20a -<，故 ()0f a =无解；当()2f a =-时，若0a >，则22a -=-，得a =若0a ≤，则2222a a ++=-，即2240a a ++=，无解，综上所述：a =【点睛】本题考查分段函数的应用，考查根据函数值求参，难度一般，解答时注意分类讨论思想的运用.18．【分析】由分段函数根据单调性求得在的最小值根据求出的最小值将问题转化为解不等式即可得出结果【详解】根据已知当时则当时在处取到最小值当时在处取到最小值所以在时在处取到最小值又因为可知当时在时取到最小值解析：(,2](0,1]-∞-⋃【分析】由分段函数根据单调性求得()f x 在[0,2)x ∈的最小值，根据(2)2()f x f x +=求出[4,2)x ∈--，()f x 的最小值，将问题转化为min 1()42t f x t≥-解不等式即可得出结果．【详解】根据已知，当[0,2)x ∈时，2 1.5,[0,1)()0.5,[1,2)x x x x f x x -⎧-∈⎪=⎨-∈⎪⎩，则当[0,1)x ∈时，()f x 在0.5x =处取到最小值(0.5)0.25f =-，当[1,2)x ∈时，()f x 在 1.5x =处取到最小值(1.5)1f =-，所以()f x 在[0,2)x ∈时在 1.5x =处取到最小值(1.5)1f =-，又因为(2)2()f x f x +=，可知当[4,2)x ∈--时， ()f x 在 2.5x =-时取到最小值，且(1.5)2(0.5)4( 2.5)f f f =-=-，则1( 2.5)(1.5)0.254f f -=⨯=-．为使[4,2)x ∈--，1()42t f x t≥-恒成立，需11424t t -≤-，当0t >时，可整理为220t t +-≤，解得(0,1)t ∈；当0t <时，可整理为220t t +-≥，解得(,2]t ∈-∞-．故答案为(,2](0,1]-∞-⋃. 【点睛】本题考查分段函数的应用，考查函数的单调性，将恒成立问题转化为函数的最值问题是解题的关键，属于中档题．19．2【分析】根据函数满足的关系可得是以6最小正周期的周期函数根据代入解析式即可【详解】根据已知条件进而有于是显然则是以6最小正周期的周期函数∵当时则故答案为：2【点睛】本题以抽象函数为载体研究抽象函数解析：2 【分析】根据函数满足的关系可得()f x 是以6最小正周期的周期函数，根据()()573f f =代入解析式即可. 【详解】根据已知条件()()()()113f x f x f x f x ⎧=-⎪⎨+=--⎪⎩，进而有()()()()()1133f x f x f x f x f x =-=+-=⎡⎤⎡⎤⎣⎦⎣⎦---=-+，于是()()3+=-f x f x ，显然()()()()()6333f x f x f x f x f x +=++=-⎡⎤⎡⎤+=--⎦⎦=⎣⎣，则()f x 是以6最小正周期的周期函数， ∵当(]1,3x ∈时()f x x =，则()()()57693332f f f =⨯+===．故答案为：2. 【点睛】本题以抽象函数为载体，研究抽象函数的结构特征，且挖掘暗含条件，巧妙地对复合函数的连续变形，体现了数学抽象，数学化归等关键能力与学科素，属于中档题.20．2【分析】由已知利用分段函数的性质及二次函数与反比例函数的单调性可求【详解】解；是上的减函数解可得故答案为：【点睛】本题主要考查了分段函数的单调性的应用二次函数及反比例函数性质的应用是求解问题的关键解析：[2，209] 【分析】由已知利用分段函数的性质及二次函数与反比例函数的单调性可求．【详解】解；226,2(),2x ax x f x a x x⎧-+⎪=⎨>⎪⎩是R 上的减函数，∴204462a a a a ⎧⎪⎪>⎨⎪⎪-+⎩，解可得，2029a．故答案为：202,9⎡⎤⎢⎥⎣⎦【点睛】本题主要考查了分段函数的单调性的应用，二次函数及反比例函数性质的应用是求解问题的关键，属于中档题．三、解答题21．（1）()f x 的单调增区间为(),-∞+∞，无单调递减区间；（2）0a =；（3）()()2max1,13422,3a a G x a a ⎧+⎪<≤=⎨⎪->⎩．【分析】（1）0a =时，求出()f x 的解析式，可得函数的单调区间；（2）由函数是偶函数，利用特值列出方程解出实数a 的值；（3）化简函数()G x ，按1a >，12a <≤，23a <≤和3a >四种情况，分别判断对称轴和区间端点的关系，判断出单调性得出最值．【详解】（1）0a =时，()22,0,0x x f x x x x x ⎧≥==⎨-<⎩，则()f x 在R 上单调递增，即函数()f x 的单调增区间为(),-∞+∞，无单调递减区间；（2）()()()2F x g x f x x x a =⋅=-，()F x 为偶函数，()()11F F ∴-=，即11a a --=-，平方解得0a =检验0a =时，()f x x x =，符合题意，故0a =；（3）()()()()()221,1,x a x x aG x f x g x x x a x x a x x a ⎧--≥⎪=+=-+=⎨-++<⎪⎩若1a >，当x a ≥时，对称轴为102a x -=<恒成立；当x a <时，对称轴为12a x a +=<恒成立；若12a <≤，当x a ≥时，1012a -<≤；当x a <时，13122a +≤≤；又[]1,2x ∈，此时()()()2max 111,224a G x G G a a G a +⎧+⎫+⎛⎫⎛⎫===⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎩⎭ 若23a <≤，当x a ≥时，11122a -<≤；当x a <时，31222a +<≤；又[]1,2x ∈，此时()()2max 1124a a G x G ++⎛⎫==⎪⎝⎭若3a >，当x a ≥时，112a ->；当x a <时，122a +>；又[]1,2x ∈，此时()()max 222G x G a ==- 综上，()()2max 1,13422,3a a G x a a ⎧+⎪<≤=⎨⎪->⎩【点睛】关键点点睛：本题考查分段函数的单调性，奇偶性和最值，考查二次函数的性质，解决本题的关键点是分情况讨论二次函数的对称轴与区间端点的关系，从而确定出函数的单调性和最值，考查学生分类讨论思想和计算能力，属于中档题． 22．（1）奇函数；（2）证明见解析；（3）()1,1-. 【分析】（1）根据函数奇偶性的定义即可判断函数的奇偶性；（2）结合单调性的定义可证明()f x 是R 上的增函数；（3）根据指数函数的性质即可求该函数的值域.【详解】解：（1）函数的定义域为R ，则111()()111x x x x xx a a a f x f x a a a ------===-=-+++，则函数()f x 是奇函数；（2）1122()1111x x x x xa a f x a a a -+-===-+++，1a >，x y a ∴=是增函数，设12x x <，则()()()()()12122121122222211111111x x x x x x x x a a f x f x a a a a a a -⎛⎫⎛⎫-=---=-= ⎪ ⎪++++++⎝⎭⎝⎭，因为120x x a a <<，所以()()120f x f x -<，即()()12f x f x <，即2()11xf x a =-+为增函数，即()f x 是R 上的增函数；（3）1122()1111x x x x xa a f x a a a -+-===-+++，1a >， 11x a ∴+>，则1011x a <<+，所以2021x a <<+，即2201x a -<-<+，所以21111xa -<-<+，即11y -<<，故函数的值域为(1,1)-. 【点睛】方法点睛：高一阶段求函数的单调性常用的思路有：一、紧扣单调性的定义；二、画出函数的图象，结合图象进行求解；三、结合函数单调性的性质，如增函数+增函数=增函数，减函数+减函数=减函数，增函数-减函数=增函数，减函数-增函数=减函数.23．（1）奇函数，证明见解析；（2）在区间()1,+∞单调递减，证明见解析．【分析】（1）求出函数的定义域，直接得到()f x 和()f x -的关系即可得结果；（2）由题意解出a 的值，由单调性的定义即可得结果. 【详解】（1）函数()y f x =是奇函数，证明如下：()y f x =的定义域为{}1x x ≠±，又()()()()2211a x axf x f x x x --==-=--+-+ ∴()y f x =是定义在{}1x x ≠±的奇函数．（2）∵()1242f f ⎛⎫-= ⎪⎝⎭，即21242433112aa a -==⎛⎫- ⎪⎝⎭，解得：3a = ∴()231xf x x =-，1x ，()21,x ∈+∞且12x x < ()()()()()()()()()()1212221222122112212222121231313111331111x x x x x x x x x x x x f x f x x x x x -=----+-=---=--- ∵1x ，()21,x ∈+∞且12x x <，∴2110x ->，2210x ->，1210x x ->，210x x ->∴()()12f x f x >，∴()y f x =在区间()1,+∞单调递减．【点睛】利用定义证明函数单调性的步骤：（1）取值；（2）作差；（3）化简；（4）下结论. 24．（1）最大值为37，最小值为1；（2）(][),55,-∞-+∞；（3）()22710,52,552710,5a a g a a a a a +≤-⎧⎪=--<<⎨⎪-≥⎩，()max 2g a =.【分析】（1）利用二次函数的基本性质可求得函数()f x 在区间[]5,5-上的最大值和最小值；（2）分析二次函数()y f x =图象的开口方向和对称轴，然后对函数()y f x =在区间上为增函数或减函数两种情况分类讨论，结合题意可得出关于实数a 的不等式，进而可求得实数a 的取值范围；（3）对实数a 的取值进行分类讨论，分析二次函数()f x 在区间[]5,5-上的单调性，进而可求得()g a 关于a 的表达式，并求出a 在不同取值下()g a 的取值范围，由此可得出()g a 的最大值.【详解】（1）当1a =-时，()()222211f x x x x =-+=-+.所以，函数()f x 在区间[]5,1-上为减函数，在区间[]1,5上为减函数，当[]5,5x ∈-时，()()min 11f x f ==，()517f =，()537f -=，所以，()()max 537f x f =-=；（2）二次函数()222f x x ax =++的图象开口向上，对称轴为直线x a =-.①若函数()y f x =在区间[]5,5-上是增函数，则5a -≤-，解得5a ≥；②若函数()y f x =在区间[]5,5-上是减函数，则5a -≥，解得5a ≤-. 综上所述，实数a 的取值范围是(][),55,-∞-+∞；（3）二次函数()222f x x ax =++的图象开口向上，对称轴为直线x a =-. ①当5a -≤-时，即当5a ≥时，函数()y f x =在区间[]5,5-上为增函数，则()()52710g a f a =-=-，此时()23g a ≤-； ②当55a -<-<时，即当55a -<<时，函数()y f x =在区间[)5,a --上为减函数，在区间(],5a -上为增函数，则()()22g a f a a =-=-，此时()(]2223,2g a a =-∈-；③当5a -≥时，即当5a ≤-时，函数()y f x =在区间[]5,5-上为减函数，则()()52710g a f a ==+，此时()271023g a a =+≤-.综上所述，()22710,52,552710,5a a g a a a a a +≤-⎧⎪=--<<⎨⎪-≥⎩，()max 2g a =.【点睛】方法点睛：“动轴定区间”型二次函数最值的方法：（1）根据对称轴与区间的位置关系进行分类讨论；（2）根据二次函数的单调性，分别讨论参数在不同取值下的最值，必要时需要结合区间端点对应的函数值进行分析；（3）将分类讨论的结果整合得到最终结果. 25．（1）(0)1f =-；()12f =；（2）4k <. 【分析】（1）令0x y ==可得(0)f ，令1x y ==可得()1f ；（2）转化条件为222k x x <-对11,32x ⎡⎤∈⎢⎥⎣⎦∀恒成立，换元后求得222x x -的最小值即可得解. 【详解】（1）令0x y ==，则(0)(0)(0)1f f f =++，所以(0)1f =-；令1x y ==，则(2)(1)(1)15f f f =++=，所以()12f =；（2）由题意，不等式2()(21)1f kx f x +-<可转化为2()(21)12f kx f x +-+<，所以()()2211f kx x f +-<，因为函数()f x 单调递增，所以2211kx x +-<，所以222k x x <-对11,32x ⎡⎤∈⎢⎥⎣⎦∀恒成立，令[]12,3t x =∈，则221122222t t t ⎛⎫-=-- ⎪⎝⎭，所以当2t =即12x =时，222t t -取最小值4，所以4k <.【点睛】关键点点睛：解决本题的关键是利用函数的单调性转化不等式为222k x x<-对11,32x ⎡⎤∈⎢⎥⎣⎦∀恒成立，再转化为求222x x -的最小值即可得解. 26．（1）()02f =-；()22f x x x =+-；（2）2a ≤. 【分析】（1）通过对抽象函数赋值，令1,1x y =-=进行求解，即得(0)f ；令0y =可消去y ，再结合()0f 的值，即求得解析式；（2）先讨论1x =时不等式恒成立，21x 时，再通过分离参数法求得a 的取值范围即可.【详解】解：（1）令1,1x y =-=，可得()()()01121f f -=--++，又由()10f =，解得()02f =-；令0y =，得()()()01f x f x x -=+，又因()02f =-，解得()22f x x x =+-；（2）当21x -≤≤时，不等式()(1)5f x a a x -≥-- 恒成立，即()213x a x -≤+，若1x =时不等式即04≤，显然成立；若21x 时，10x ->，故231x a x +≤-恒成立，只需2min31x a x ⎛⎫+≤ ⎪-⎝⎭，设()()()22121434()12111x x x g x x x x x---++===-+----，设(]1,0,3t x t =-∈ 则4()2g t t t=+-是对勾函数，在()0,2递减，在()2,3递增，故2t =时，即1x =-时min ()2g x =，故2a ≤，综上， a 的取值范围为2a ≤.【点睛】方法点睛：抽象函数通常利用赋值法求函数值或者求解析式；二次函数含参恒成立的问题，一般是通过分离参数进行求解，当然也可以根据判别式法进行求解，视具体情况而定.。

深圳平冈中学高中物理必修一第三章《相互作用》测试卷(答案解析)

一、选择题1．如图所示，在水平传送带上有三个质量分别为m 1、m 2、m 3的木块1、2、3，1和2及2和3间分别用原长为L ，劲度系数为k 的轻弹簧连接起来，木块与传送带间的动摩擦因数均为μ，现用水平细绳将木块1固定在左边的墙上，传送带按图示方向匀速运动，当三个木块达到平衡后，1、3两木块之间的距离是（）A ．23()2m m g L k μ++B ．123()2m m m g L k μ+++C ．23(2)2m m gL k μ++ D ．32m gL k μ+2．静止在水平地面上的物体ABC 由两部分构成，AOB 为斜面体，BOC 为14光滑圆柱体，截面图如图所示。

跨过B 点处定滑轮的光滑轻绳两端分别连接a 、b 两个小滑块，用平行于AB 的外力F 缓慢拉动a ，a 与接触面间的动摩擦因数不为零。

在b 沿BC 间曲面缓慢上升的过程中（初始时b 已离开地面），轻绳始终平行于接触面，物体ABC 始终静止，以下说法正确的是( )A ．绳的拉力大小不变B ．拉力F 逐渐增大C ．物体ABC 对地面的压力逐渐减小D ．物体ABC 对地面的摩擦力水平向右 3．如图所示的一根轻弹簧，其自由端B 在未悬挂重物时指针正对刻度5，在弹性限度内，当挂上80N 重物时指针正对刻度45，若要指针正对刻度20应挂重物的重力是（）A ．40NB ．30NC ．20ND ．因k 值未知，无法计算4．如图所示是剪式千斤顶，当摇动把手时，螺纹轴就能迫使千顶的两臂靠拢，从而将汽车顶起。

当车轮刚被顶起时，汽车对千斤顶的压力为51.010N ⨯，此时千斤顶两臂间的夹角为120︒，则下列判断正确的是（）A ．此时两臂受到的压力大小均为45.010N ⨯B ．此时千斤顶对汽车的支持力大小为52.010N ⨯C ．若继续摇动把手，将汽车顶起，两臂受到的压力将增大D ．若继续摇动把手，将汽车顶起，两臂受到的压力将减小5．如图a 所示，质量为m 的半球体静止在倾角为θ的平板上，当θ从0缓慢增大到90︒的过程中，半球体所受摩擦力f F 与θ的关系如图b 所示，已知半球体始终没有脱离平板，半球体与平板间的动摩擦因数为33，最大静摩擦力与滑动摩擦力相等，重力加速度为g ，则（）A ．~O q 段图像可能是直线B ．π~2q 段图像可能是直线 C ．π4q = D ．2mg p = 6．如图是同一型号灯笼的四种悬挂方式，其中绳子O A 所受拉力最大的是（） A ． B ．C ．D ．7．如图所示为两个共点力的合力F 随两分力的夹角变化的图象，则这两个分力的大小可能为（）A ．1N 和4NB ．2N 和3NC ．1N 和5ND ．2N 和4N 8．下列有关力的说法正确的是（）A ．力可以脱离物体而单独存在B ．摩擦力的方向总是与物体的运动方向相反C ．质量均匀分布，形状规则的物体的重心可能在物体外D ．木块放在水平桌面上受到一个向上的弹力，这是由于木块发生微小形变而产生的 9．如图所示，斜面上有一与斜面垂直的固定挡板，挡板与14圆柱体A 之间夹有圆柱体B ，A 、B 在沿斜面向上的力F 作用下处于静止，现力F 缓慢沿斜面向上推A ，使A 沿斜面向上移动一小段距离，则在此过程中圆柱体B 对A 的压力1N 和对挡板的压力2N 大小怎样变化（所有接触面均光滑）（）A ．1N 变小、2N 变小B ．1N 变大、2N 变大C ．1N 变大、2N 变小D ．1N 变小、2N 变大 10．如图，一只可视为质点的蚂蚁在半球形碗内缓慢从底部爬到a 处，则下列说法正确的是（）A．在a点蚂蚁受到的合力大于在b点受到的合力B．在a点碗对蚂蚁的作用力大于在b点的作用力C．在a点蚂蚁能静止，在b点也一定能静止D．以上说法均不对11．关于摩擦力下列叙述中正确的是（）A．两物体之间有摩擦力，但不一定存在相互作用的弹力B．静止的物体受到的摩擦力一定为静摩擦力C．滑动摩擦力的大小与物体间的正压力大小成正比D．滑动摩擦力的方向，总是与物体的运动方向相反12．如图所示，小球a的质量为小球b的质量的一半，分别与轻弹簧A、B和轻绳相连接并处于平衡状态。

【单元练】深圳平冈中学高中物理必修1第二章【匀变速直线运动的研究】经典练习题(培优提高)

一、选择题1．无风秋日，晚霞满天，一片梧桐叶从高为5m 的枝头自静止飘落至地面，所用时间可能是（g 取10m/s 2）（） A ．0.1s B ．0.5sC ．1sD ．3s D解析：D 根据212h gt =解得1s t =从高为5m 的枝头落下的树叶由于受到空气阻力作用，其运动不是自由落体运动，时间大于自由落体运动的时间；故梧桐叶落地时间一定大于1s 。

故选D 。

2．汽车从制动到停止共用了5s ，这段时间内汽车每1s 前进的距离分别为9m 、7m 、5m 、3m 、1m 。

可知（） A ．初速度为9m/s B ．末速度为1m/s C ．加速度方向一定向后 D ．加速度一定减小C 解析：CAB ．汽车在整个过程的平均速度为97531m/s 5m/s 5x v t ++++=== 因为汽车在连续相等时间内的位移之差是相等的，都是2m ，所以汽车做的是匀减速运动，由题可知汽车的末速度v 为零，根据2v v v +=可得汽车的初速度为0225m/s 10m/s v v ⨯＝＝＝故AB 错误；C ．因为汽车是从制动到停止，汽车做的是减速运动，所以汽车的加速度方向和速度方向相反，即加速度方向向后，故C 正确；D ．汽车在连续相等时间内的位移之差△x 是一个定值，所以汽车做的是匀减速运动，即加速度大小不变，故D 错误。

故选C 。

3．从离地面高为 1.25m h =的高空自由落下一个小球，不计空气阻力，取210m/s g =。

小球落地的速度大小和最后0.1s 内下落的位移大小分别为（）A ．5m/s ，0.45mB ．5m/s ，0.25mC ．10m/s ，0.45mD ．10m/s ，0.25m A解析：A 根据212h gt =，解得小球自由下落所需要的时间为 22 1.25s 0.5s 10h t g ⨯=== 则小球落地的速度100.5m/s 5m/s v gt ==⨯=小球落地前最后0.1s 内下落的位移大小()2110.45m 2h h g t t ∆=--=故选A 。

广东省深圳中学08-09年高三第一学段考试英语(附答案)

广东省深圳中学2008—2009学年度高三第一学段考试英语试题本试卷分第Ⅰ部分（选择题、填空题）和第Ⅱ部分（作文）两部分。

第Ⅰ部分（选择题共80分）注意事项：1．答第一部分前，考生务必将姓名、班级、考号、考试科目、试卷类型用2B铅笔填涂在答题卡．．．上。

2．每小题选出答案后，用2B铅笔把答题卡．．．上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上。

一、听力（共两节，每小题1分，满分20分）做题时，先将答案划在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节听力理解（共15小题；每小题1分，满分15分）每段播放2遍。

各段后有几个小题，各段播放前每小题有5秒钟的阅题时间。

请根据各段播放内容及其相关小题，在5秒钟内从题中所给的A、B、C项中，选出最佳选项。

听下面一段对话，回答第1—3三个小题。

1．What is the manA．A doctor. B．A nurse. C．A worker.2．How many people work in the hospitalA．50. B．60. C．110.3．Which department does the man work inA．In the X-ray department.B．In the skin department.C．In the hospital office.听下面一段对话，回答第4—6三个小题。

4．Why does the man want to drive thereA．It’s too far away. B．It’s too crowded on a bus. C．It’s cheaper to drive.5．Where will the man spend his weekendA．In the countryside.B．In the center of the city.C．In another city.6．How much will the man pay for the car this weekendA．20 dollars. B．40 dollars. C．60 dollars.听下面一段对话，回答第7—9三个小题。

深圳市平冈中学08-09必修一测试题

深圳平冈中学必修一第四单元《函数应用》测试卷(答案解析)

广东省深圳市平冈中学高一生物上册必修一月考选择题专项试卷

深圳平冈中学必修第一册第一单元《集合与常用逻辑用语》测试卷(答案解析)

深圳语文试卷高中必修一(含答案)

深圳平冈中学必修第一册第五单元《三角函数》测试卷(答案解析)

深圳平冈中学高中物理必修一第一章《运动的描述》测试卷(答案解析)

深圳平冈中学高中物理必修一第四章《运动和力的关系》测试卷(答案解析)

深圳平冈中学高中化学必修一第一章《物质及其变化》经典练习题(培优提高)

深圳平冈中学高中化学必修1第一章《物质及其变化》测试卷(答案解析)(1)

广东省深圳市平冈中学高一生物上册必修一月考试卷

广东省深圳市平冈中学高一生物上册必修一月考多选题 不定项选择题专项试卷

深圳平冈中学高中物理必修一第一章《运动的描述》测试卷(答案解析)

深圳平冈中学必修一第一单元《集合》测试卷(答案解析)

深圳平冈中学高中物理必修一第二章《匀变速直线运动的研究》测试卷(答案解析)

深圳平冈中学必修一第二单元《函数》测试卷(答案解析)

深圳平冈中学高中物理必修一第三章《相互作用》测试卷(答案解析)

【单元练】深圳平冈中学高中物理必修1第二章【匀变速直线运动的研究】经典练习题(培优提高)

广东省深圳中学08-09年高三第一学段考试英语(附答案)

广东省深圳市平冈中学高一生物上册必修一月考多选题不定项选择题专项试卷