《二次根式加减》课件1
合集下载
《二次根式的加减》_完美课件

第三步的依据是:合并同类项.
【获奖课件ppt】《二次根式的加减》 _完美 课件1- 课件分 析下载
例2 计算:
讲授新课
(1)( 2+3)( 2-5) ;(2)( 5+ 3)( 5- 3).
解:(2)( 5+ 3)( 5- 3)=( 5)2 -( 3)2
= 5-3= 2 .
思考1:(2)中,每一步的依据是什么?
(2)先算除,再化简,若有相同的二次根 式进行合并,把所有的二次根式化成最简二次根式.
【获奖课件ppt】《二次根式的加减》 _完美 课件1- 课件分 析下载
【获奖课件ppt】《二次根式的加减》 _完美 课件1- 课件分 析下载
讲授新课
例2 计算: (1)( 2+3)( 2-5) ;(2)( 5+ 3)( 5- 3).
8+ 18=2 2+3 2 =(2+3) 2=5 2
化为最简 二次根式
用分配 律合并
整式 加减
【获奖课件ppt】《二次根式的加减》 _完美 课件1- 课件分 析下载 【获奖课件ppt】《二次根式的加减》 _完美 课件1- 课件分 析下载
讲授新课
二次根 式性质
分配律
整式加 减法则
8+ 18=2 2+3 2 =(2+3) 2=5 2
【获奖课件ppt】《二次根式的加减》 _完美 课件1- 课件分 析下载
【获奖课件ppt】《二次根式的加减》 _完美 课件1- 课件分 析下载
讲授新课
算式 8+ 18与算式 3 2- 2 有什么相同点与不同
点? 请化简算式
8+
18 ,并说出每一步化简的理由.
【获奖课件ppt】《二次根式的加减》 _完美 课件1- 课件分 析下载
人教版初三数学上册第二十一章《二次根式的加减》优秀课件

练习
1.判断:下列计算是否正确?为什么?
1
2 3
5 ; 22 2 2 2 ;
3
8 18 2
4 9 2 3 5
2.在下列各组根式中,是同类二次根式的 是( B )
A. C. 3. 与 A.
2 , 12
B.
2
2,
4ab , ab
D.
a 1, a 1
(1)两列火车分别运煤2x吨和3x吨,问这两 +3x=5x吨 列火车共运多少?2x _______________ (2)两列火车分别运煤2x吨和3y吨,问这两 (2x +3y)吨 列火车共运多少?_______________
以下问题你能用同样的方法计算吗?
13
2 4 2
2
5 2
3
75 2 3 5 3 (2 5) 3 7 3 45 4 5 3 5 (4 3) 5 5
3.
9a 25a 3 a 5 a (3 5) a 8 a
先化简,后合并
计算:
8 18 4 2
如何合并 同类二次 根式?
2 23 24 2 2 3 4 2 9 2
8 18 4 2
运用以前所学知识进行总结
例1计算: (1) 12 75 (2) 80 45 (3) 9a 25a
解:
比较二次根式的加减 与整式的加减,你能 得出什么结论? 二次根式的加减实质是 合并同类二次根式. 整式的加减的实质是合 并同类项.
1. 12 2. 80
2 3
2 10 3 9 4 b 2 ab 3
8ab 2b 2ab
a 2b
6b
《二次根式的加减》课件1

这几个二次根式就叫做同类二次根式。 2可、直下接面根哪据些分根配式律是进最行简加二减次运根算式。,哪些不是?不是最简二次根式的,把它化简成最简二次根式。
几观个察二 下次列根式式子化各成是什__么__运__算___?__以后,如果_______相同,这几个二次根式就叫做同类二次根式 。
(4)
()
若二式次子 根式加减和运算的步是骤同: 类二次根式,求x的值。
1、判断下列各组二次根式是否为同类二次根式?
(1) 50与 0.5 1、判断下列各组二次根式是否为同类二次根式?
(只能合并被开方数相同的二次根式)
(是 )
如果所给的二次根式不是最简二次根式,
判断:下列计算是否正确?为什么?
判断几个二次根式是
(2) 12与 18 (不是 ) 同类二次根式的方法
几个二次根式化成___________以后,如果_______相同,这几个二次根式就叫做同类二次根式 。 同类二次根式的定义:几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式。
二同次类根 二式次加根减式运的算定的义基:本几方个法二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式。
同二类次二 根次式根加式减的运定算义的:基几本个方二法次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式。
12、判 下断面下哪列些各根组式二是次最根简式二是次否根为式同,类哪二些次不根是式?不? 是最简二次根式的,把它化简成最简二次根式。
练习
152871820 2
2 8 4 12 =1
2
3 80 20 5 3 5
练习
4 18( 98 27) 1023 3
人教版八年级下册数学《二次根式的加减》说课教学课件

第十六章 二次根式
二次根式的加减
目录
学习目标
01
LEARNING OBJEC
1、了解同类二次根式的意义。
2、能熟练进行二次根式的加减运算。
3、在探索中培养学生分析、转化、归纳、总结的能力。
02
03
重点
A KEY
二次根式加减法的运算。
难点
DIFFICUL
熟练进行二次根式加减法的运算。
学习目标
01
= (2 + 1) 3 + (2 − 1) 5
=3 3+ 5
02
练一练
1.下列各式中,与 是同类二次根式的是(
A.
B.
C.
D.
) 2.下列计算中正确的是( )
A. + =
C. ÷ =
B.
−
【答案】D
【详解】
【详解】
A、 9=3,与 3不是同类二次根式;
= 14 3
1
3
4)( 12+ 20)+( 3- 5)
+ 3 48
+ 3 48
6× 1
+ 3 16
3
6× 1× 3
+3
3× 3
×3
16 × 3
4)( 12+ 20)+( 3- 5)
= 12+ 20+ 3- 5
= 4 × 3+ 4 × 5 + 3- 5
= 2 3+2 5 + 3- 5
= 2 3 + 3 +2 5 - 5
3.14 −
42 =4
52 =5
2
二次根式的加减
目录
学习目标
01
LEARNING OBJEC
1、了解同类二次根式的意义。
2、能熟练进行二次根式的加减运算。
3、在探索中培养学生分析、转化、归纳、总结的能力。
02
03
重点
A KEY
二次根式加减法的运算。
难点
DIFFICUL
熟练进行二次根式加减法的运算。
学习目标
01
= (2 + 1) 3 + (2 − 1) 5
=3 3+ 5
02
练一练
1.下列各式中,与 是同类二次根式的是(
A.
B.
C.
D.
) 2.下列计算中正确的是( )
A. + =
C. ÷ =
B.
−
【答案】D
【详解】
【详解】
A、 9=3,与 3不是同类二次根式;
= 14 3
1
3
4)( 12+ 20)+( 3- 5)
+ 3 48
+ 3 48
6× 1
+ 3 16
3
6× 1× 3
+3
3× 3
×3
16 × 3
4)( 12+ 20)+( 3- 5)
= 12+ 20+ 3- 5
= 4 × 3+ 4 × 5 + 3- 5
= 2 3+2 5 + 3- 5
= 2 3 + 3 +2 5 - 5
3.14 −
42 =4
52 =5
2
人教版八年级数学课件《二次根式的加减》

达标检测
人教版数学八年级下册
12.计算:
(1)2 20 + 45 − 8 + 32;
(2)2 12 − 27 − 6
1
;
3
(3) − 2 −
3− 2 −
3−2 .
(1)解:原式= 4 5 + 3 5 − 2 2 + 4 2 = 7 5 + 2 2.
(2)解:原式= 2 × 2 3 − 3 3 − 6 ×
人教版数学八年级下册
复习回顾
人教版数学八年级下册
一、满足什么条件的根式是最简二次根式?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
简记为:一根号无分母,分母无根号;二不能再开方.
在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中
2
2
2 6
+ 6
2
4
10 2 3 3;
3 6
2
.
4
典例解析
人教版数学八年级下册
例4.如图,用四张一样大小的长方形纸片拼成一个面积是125的正方形ABCD,
= 3 5,图中空白部分是一个小正方形,求这个小正方形的周长.
解:∵正方形ABCD的面积是125,
∴ = 125 = 5 5,
mn
的值.
2n 1 2,
解:由题意得
3m 2n 3,
解得
4
m
,
3
n 1,
2
即 mn 4 1 6 .
3
2
3
16.3 二次根式的加减(第1课时)(课件)八年级数学下册(人教版)

知识点一 同类二次根式
活动1 观察下列二次根式的被开数有什么共同特征:
(1) 2,3 2,-
2
5
1
2,
3
2 ···
2
(2) 3,17 3,- 5 3, ·
3··
13
每组的二次根式的被开方数相同
活动2 思考下列二次根式具有的被开数以上特征吗?你怎样发现的?:
9
(3) 2, 8, 18, 32, 0.5,2
2 10
8
2
3
5
3
2
ab
2
b
(1) 75 =____;(2) 8a b =_______;(3) =_____.
5
5
问题 现有一块长 7.5 dm、宽 5 dm 的木板,能否采用如图的方式,在这
块木板上截出两个分别是 8 dm2 和 18 dm2 的正方形木板?
5 dm
5 dm
8 18
8
18
2
2
2
5
2
1 4.
课堂总结
一般地,二次根式的
法
则
加减时,可以先将二次根
式化成最简二次根式,再
将被开方数相同的二次根
二次根
式加减
式进行合并.
注
运算原理
运算律仍然适用
运算顺序
与实数的运
算顺序一样
意
(乘法分配律逆用)
5 2
(有理数的加减)
归纳知识
2.二次根式的加减法法则
将二次根式化成最简二次根式,再将同类二次根式进行合并.
简记:一化、二找、三合并
典例精析
【例3】计算:
(1) 80 45;
1
二次根式的加法与减法课件

(3)3 3-2 2+ 3- 2 4 3-3 2
作业
❖ 习题9.2的1(3)(4)、2题
拓展提升
❖把二次根式 23-a与 8 分别化成最简二次根式后, 被开方式相同.
❖(1)如果a是正整数,那么符合条件的a有哪些? ❖(2)如果a是整数,那么符合条件的a有多少个?最大
值是什么?有没有最小值?
(3) 2 3
先化为最简二次根式, 把同类二次根式的系数相加减,做为结果的系数, 根号及根号内部都不变。
你有什么发现?
归纳总结
二次根式加减法法则:
目标2.通过具体题目的运算,得到二次根式 的加法与减法的运算步骤及注意问题.
m a n a =(m n) a
二次根式相加减,应先把各个二次根式化为最简二次根式, 然后把其中的同类二次根式分别合并(. 不是同类二次根式的不能合并).
2、4 2- 2=43 2 3、2+ 3= 5
× ( )为结果的系数; × 2、指数和被开方式都不变;
( )3、不是同类二次根式的不能合并;
× 4、3 2- 1 2=2 51 22 ( )4、系数是带分数的要化为假分数,若
× 2
22
是一个二次根式与一个多项式的积,则
5、a 5+b 5=(aa++bb)5 5 ( )多项式加括号.
2.字母和字母的指数有何变化? 不改变
3.不是同类项的能否合并?
不能合并
温故知新
目标1. 类比“合并同类项”的知识, 推导二次根式的加法与减法运算法则。
2、化简下列二次根式
化成最简二次根式后,
8 __2__2__; 12 _2__3__; 被开方式相同的二次根
18 ___3 _2___; 27 _3_3___; 式
二次根式的加减(讲学练全套资料)精选教学PPT课件

聚焦中考
1. ( 2006. 衡 阳 ) 下 列 计 算 正 确 的 是 (
)
A 2 3= 5 B 2 3=2 3
C 8 2 2=0 D 5 1=2
2. ( 2006. 枣 庄 ) 下 列 计 算 正 确 的 是 (
)
A 8 2= 2
B 27 12 = 9 4=1 3
C 2 52 5=1
清晨,当欢快的小鸟把我从睡中唤醒,我推开窗户,放眼蓝蓝的天,绿绿的草,晶莹的露珠,清清爽爽的早晨,我感恩上天又给予我一个美好的一天。 入夜,夜幕中的天空繁星点点,我打开日记,用笨拙的笔描画着一天的生活感受,月光展露着温柔的笑容,四周笼罩着夜的温馨,我充满了感恩,感谢大地赋予的安宁。
朋友相聚,酒甜歌美,情浓意深,我感恩上苍,给了我这么多的好朋友,我享受着朋友的温暖,生活的香醇,如歌的友情。 走出家门,我走向自然。放眼花红草绿,我感恩大自然的无尽美好,感恩上天的无私给予,感恩大地的宽容浩博。生活的每一天,我都充满着感恩情怀,我学会了宽容,学会了承接,学会了付出,学会了感动,懂得了回报。用微笑去对待每一天,用微笑去对待世界,对待人生,对待朋友,对待困难。所以,每天,我都有一个好心情,我幸福的生活着每一天。
3
=12 3 -3 3 +6 3 =(12-3+6) 3 =15 3 (2)( 48 + 20 )+( 12 - 5 ) = 48 + 20 + 12 - 5 =4 3 +2 5 +2 3 - 5 =6 3 + 5
反馈练习
课本 P19 练习第 1,2 题
补充练习
计练习算2:计算:
(1) 80 20 5
生活给予我挫折的同时,也赐予了我坚强,我也就有了另一种阅历。对于热爱生活的人,它从来不吝啬。 要看你有没有一颗包容的心,来接纳生活的恩赐。酸甜苦辣不是生活的追求,但一定是生活的全部。试着用一颗感恩的心来体会,你会发现不一样的人生。不要因为冬天的寒冷而失去对春天的希望。我们感谢上苍,是因为有了四季的轮回。拥有了一颗感恩的心,你就没有了埋怨,没有了嫉妒,没有了愤愤不平,你也就有了一颗从容淡然的心! 我常常带着一颗虔诚的心感谢上苍的赋予,我感谢天,感谢地,感谢生命的存在,感谢阳光的照耀,感谢丰富多彩的生活。
16.3二次根式的加减(第1课时)

计算下列各式:
问题:1.什么是同类项? 2.同类项怎样合并?
a b ab ab a b(a≥0,b≥0)
a b
a b
a b
a (a≥0,b>0) b
1.被开方数中不 含分母; 下列根式中,哪些是最简二次根式? 2.被开方数中 不含开得尽方 的因数或因式
15a , 18, x 1, 5 x y , 24abc,
2 3
√
×
√
×
×
ab 3xy 2 2 2 x y, , , 6(a b ) 3 3
2
√
×
√
√
二次根式在什么条件下可以合并?
探究
如何计算 8
2 4 2 呢?
分析: 类似8a+4a=12a,我们可以 根据乘法分配律的逆用来进行运算。 解: 8 2 4 2
(8 4) 2
12 2
下列计算哪些正确,哪些不正确? (不正确) 3 2 5
a b a b
a b a b
(不正确) (不正确)
⑷
a a b a (a b) a
1 3a 2 2a a
(正确)
a 0 (不正确)
1 ⑸ 3
下列解答是否正确?为什么?
(1)2 75 3 27 3 2 75 9 3 3 10 3 10 3 0
注意:被开方数不相同的二次根式 (如 2 与 3 )不能合并
例题讲解
(2) 80 45 计算: (1) 9a 25a
解: (1) 9a 25a
(2) 80 45
3 a 5 a
4 5 3 5
(3 5) a
(4 3) 5
问题:1.什么是同类项? 2.同类项怎样合并?
a b ab ab a b(a≥0,b≥0)
a b
a b
a b
a (a≥0,b>0) b
1.被开方数中不 含分母; 下列根式中,哪些是最简二次根式? 2.被开方数中 不含开得尽方 的因数或因式
15a , 18, x 1, 5 x y , 24abc,
2 3
√
×
√
×
×
ab 3xy 2 2 2 x y, , , 6(a b ) 3 3
2
√
×
√
√
二次根式在什么条件下可以合并?
探究
如何计算 8
2 4 2 呢?
分析: 类似8a+4a=12a,我们可以 根据乘法分配律的逆用来进行运算。 解: 8 2 4 2
(8 4) 2
12 2
下列计算哪些正确,哪些不正确? (不正确) 3 2 5
a b a b
a b a b
(不正确) (不正确)
⑷
a a b a (a b) a
1 3a 2 2a a
(正确)
a 0 (不正确)
1 ⑸ 3
下列解答是否正确?为什么?
(1)2 75 3 27 3 2 75 9 3 3 10 3 10 3 0
注意:被开方数不相同的二次根式 (如 2 与 3 )不能合并
例题讲解
(2) 80 45 计算: (1) 9a 25a
解: (1) 9a 25a
(2) 80 45
3 a 5 a
4 5 3 5
(3 5) a
(4 3) 5
九年级上数学《21.3 二次根式的加减》课件
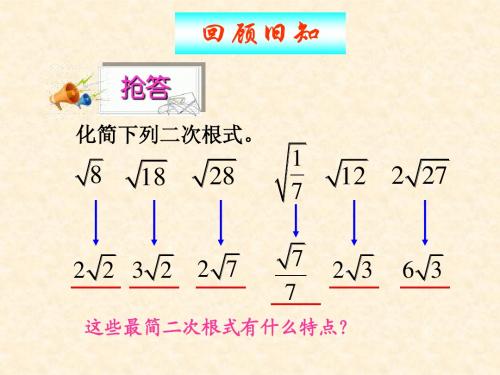
回顾旧知
抢答
化简下列二次根式。
8
18
28
1 7
12 2 27
2 2 3 2
2 7
7 7
2 3
6 3
这些最简二次根式有什么特点?
新课导入
有一个三角形,它的两边长分别为 20 和 5 , 如果该三角形的周长为 9 5 ,你能求出第三边吗?
提示 根据三角形的周长公式 C = a+ b+ c 求解。
?
a 20
答:35 秒后△PBQ 的面积为 35 cm2 , PQ的距离为 5 7 cm 。
例题
计算
8 3 6 8 6 3 6
8 6 3 6
注意
4 3 3 2
(1)加减与乘除的混合运算,先乘除, 后加减,使难点分散。 (2)在运算中,对于各根式不一定要先 化简,而是先乘除,进行约分,达到化简的 目的,但最后结果一定要化简。
【情感态度与价值观】
利用规定准确计算和化简的严谨的科 学精神。 经过探索二次根式的重要结论,发展 学生观察、分析、发现问题的能力。
教学重难点
二次根式化简为最简二次根式以及二 次根式的判定。
二次根式的加减、乘除、乘方等运算 规律。 由整式运算知识迁移到含二次根式的 运算。
我们可以这样来计算
一化
二找
三合并
例题
解答
如图所示的 Rt△ABC中,∠B=90°,点 P 从点 B 开始沿 BA 边以 1 cm/s 的速度向点 A 移动。同时, 点 Q 也从点 B 开始沿 BC 边以 2 cm/s 的速度向点 C 移动。问:几秒后△PBQ 的面积为 35 cm2 ?PQ 的 距离是多少厘米?(结果用最简二次根式)
抢答
化简下列二次根式。
8
18
28
1 7
12 2 27
2 2 3 2
2 7
7 7
2 3
6 3
这些最简二次根式有什么特点?
新课导入
有一个三角形,它的两边长分别为 20 和 5 , 如果该三角形的周长为 9 5 ,你能求出第三边吗?
提示 根据三角形的周长公式 C = a+ b+ c 求解。
?
a 20
答:35 秒后△PBQ 的面积为 35 cm2 , PQ的距离为 5 7 cm 。
例题
计算
8 3 6 8 6 3 6
8 6 3 6
注意
4 3 3 2
(1)加减与乘除的混合运算,先乘除, 后加减,使难点分散。 (2)在运算中,对于各根式不一定要先 化简,而是先乘除,进行约分,达到化简的 目的,但最后结果一定要化简。
【情感态度与价值观】
利用规定准确计算和化简的严谨的科 学精神。 经过探索二次根式的重要结论,发展 学生观察、分析、发现问题的能力。
教学重难点
二次根式化简为最简二次根式以及二 次根式的判定。
二次根式的加减、乘除、乘方等运算 规律。 由整式运算知识迁移到含二次根式的 运算。
我们可以这样来计算
一化
二找
三合并
例题
解答
如图所示的 Rt△ABC中,∠B=90°,点 P 从点 B 开始沿 BA 边以 1 cm/s 的速度向点 A 移动。同时, 点 Q 也从点 B 开始沿 BC 边以 2 cm/s 的速度向点 C 移动。问:几秒后△PBQ 的面积为 35 cm2 ?PQ 的 距离是多少厘米?(结果用最简二次根式)
16.3.1 二次根式的加减 大赛获奖精美课件 公开课一等奖课件

高考总分:711分 毕业学校:北京八中 语文139分 数学140分 英语141分 理综291分 报考高校:
北京大学光华管理学院
北京市理科状元杨蕙心
三、巩固练习 教材第 13 页练习第 1,2 题. 【答案】第 1 题:(1)不正确,两边不相等;(2)不正确,两边不相 等;(3)正确. 1 第 2 题:(1)-4 7;(2)3 5;(3)10 2-3 3;(4)3 6+4 2.
四、课堂小结
本节课应掌握进行二次根式加减运算时,先把不是最简二次根式的化 成最简二次根式,再把相同被开方数的最简二次根式进行合并.
16.3
二次根式的加减
第1课时 二次根式的加减
理解并掌握二次根式加减的方法,并能用二次根式加减法法则 进行二次根式的加减运算.
重点 理解并掌握二次根式加减计算的方法. 难点 二次根式的化简、合并被开方数相同的最简二次根式.
一、复习导入
(学生活动) 1.计算:
(1)x+2x;(2)3a-2a+4a;(3)2x2-3x2+5x2;(4)2a2-4a2+3a.
2.教师点评:上面的运算实际上就是以前所学习的合并同类项 ,合并同类项就是字母连同指数不变,系数相加减.
二、新课教授 (学生活动) 1.类比计算,说明理由. (1) 2+2 2;(2)3 8-2 8+4 8; (3)3 2+ 8;(4)2 3-3 3+ 12. 2.教师点评: (1) 2+2 2=(1+2) 2=3 2; (2)3 8-2 8+4 8=(3-2+4) 8=5 8=10 2; (3)虽然表面上 2与 8的被开方数不同, 不能当作被开方数相同, 但 8 可化为 2 2,3 2+ 8=3 2+2 2=(3+2) 2=5 2;
16 (2) =________, 4 81 (3) =________, 49 (4) 36 =________, 64
冀教版八年级数学上册15.3《二次根式的加减运算》课件

第十五章 二次根式
15.3 二次根式的加减运算
学习目标
1.了解同类二次根式的概念,掌握判断同类二次根式的方法,能正 确合并同类二次根式,进行二次根式的加减运算. 2.通过整式的加减运算与二次根式的加减运算比较,体会类比思想. 3.通过对二次根式加减法的探究,激发学生的探索热情,让学生充 分参与到数学学习的过程中来,使他们体会到成功的乐趣。
回顾复习
口答:
探究新知
学生活动一 【一起探究】
计算:Biblioteka 探究新知二次根式加减运算的方法: 1.先将每个二次根式化成最简二次根式. 2.再将被开方数相同的最简二次根式的项进行合并.
巩固练习
巩固练习
回顾反思
1. 同类二次根式 2. 二次根式加减法的步骤
15.3 二次根式的加减运算
学习目标
1.了解同类二次根式的概念,掌握判断同类二次根式的方法,能正 确合并同类二次根式,进行二次根式的加减运算. 2.通过整式的加减运算与二次根式的加减运算比较,体会类比思想. 3.通过对二次根式加减法的探究,激发学生的探索热情,让学生充 分参与到数学学习的过程中来,使他们体会到成功的乐趣。
回顾复习
口答:
探究新知
学生活动一 【一起探究】
计算:Biblioteka 探究新知二次根式加减运算的方法: 1.先将每个二次根式化成最简二次根式. 2.再将被开方数相同的最简二次根式的项进行合并.
巩固练习
巩固练习
回顾反思
1. 同类二次根式 2. 二次根式加减法的步骤
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解: R r S
s
18
8
2
3 2
2 2
R-r
答:圆环的宽度 d为
2
cm.
反馈练习
(1) 18 8
2
(4)下列计算正确的是( D ) A. 5 2 3 B.8 3 2 11 2 C.4 5 5 4
3 1 D. a a a 2 2
3.几个二次根式相加减先把各个二次根式化成最简二 次根式,再把同类二次根式分别合并.
同类二次根式合并: 把根号外系数或字母相加减,根指 数和被开方数不变 注意:不是同类二次根式的二次根式 (如
2与 3 )不能合并
例2计算: 1 (1)2 12 6 3 48 3 (2)( 12 20) ( 3 5) 2 x 1 (3) 9x 6 2x 3 4 x
80 45 4 5 3 5 (4 3) 5 5
9a 25a 3 a 5 a (3 5) a 8 a
先化简,后合并
计算:
8 18 4 2
如何合并 同类二次 根式?
2 23 24 2 2 3 4 2 9 2
与合并同类项类似,把同类二次根式的系 数相加减,做为结果的系数,根号及根号内部 都不变, 总结二次根式加减运算的步骤
20 2 5
BC BD 2 CD2 22 12 5
所需钢材的长度为: AB BC AC BD 2 5 5 5 2 答:大约需要13.7m的钢材.
3 5 7 13.7
练习3: 如图,两个圆的圆心相同,它们的面 积分别是8cm2和18cm2,求圆环的宽度 d(两圆半径之差).
是同类二次根式,求m、n 的值.
(1)两列火车分别运煤2x吨和3x吨,问这两 列火车共运多少?2x +3x=5x吨 _______________ (2)两列火车分别运煤2x吨和3y吨,问这两 (2x +3y)吨 列火车共运多少?_______________
以下问题你能用同样的方法计算吗?
1 3
2 2
2 3 3
1.在下列各组根式中,是同类二次根 式的是( B )
A.
2 , 12
2
B.
2,
1 2
C. 4ab , ab D. a 1 , a 1 2. 与 12 是同类二次根式的是(
D )
1 A. 32 B. 24 C. 125 D. 6 27 3.如果最简二次根式m n 2 2 与 m n
(2) 75 27 8 3 1 6 3 (3) 48 6 3
计算:
15
2
2
8 7 18
4 8 2
1
2
1 32 12 4 3 48, 27
1 1 5 0.5 2 75 3 8
(3)10 2 3 3
1 (4)3 6 2 4
注意:不是同类二次根式的二次根式
(如 2 与 3 )不能合并
练习 1.判断:下列计算是否正确?为什么?
1
8 3 8 3;
F F
2
33
4 9 4 9;
2 2 2 2
T
练习 判断:下列计算是否正确?为什么?
8 18 5 2 7.5
5dm
18dm
8dm
8 18 dm
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
例3 要焊接一个如图所示的钢架,大约 需要多少米钢材(精确到0.1米)? B
2m 解: 根据勾股定理得:
2 2 2
A
2
D 4m 1m C
AB AD BD 4 2
2 4 3
x 1 9x 6 2x 4 x
2 计算: 5
(1) 75 2 8 200 (2)2 20 3 45 80 (3)2 48 ( 27 243) (4)(5 75 4 12) (5 108 3 27)
3.细心算一算 1 2 (1)( 8 2 0.25) ( 1 50 72) 8 3 4 1 4 (2)( 80 1 ) ( 3 45) 5 5 5
解:
3 3 5
问题:
现有一块长7.5dm、宽5dm的木板,能否采用 如图的方式,在这块木板上截出两个分别是 8dm2和18dm2的正方形木板? 7.5dm
8 18
2 2 3 2(化成最简二次根式)
(2 3) 2 (分配律) 5 2 18 3 2 5
21.3
二次根式的加减(一)
复习回顾
二次根式计算、化简的结果符合什么要求? (1)被开方数不含分母; 分母不含根号; (2)被开方数中不含能开得尽方的因数 或因式.
把下列各根式化简
(1) 12
(2) 48
(3) 18
(4) 50
2 3
1 (5) 2
4 3
(6) 32
3 2
5 2
1 (7) 45 (8) 1 3
1
2 3 5;
F
22
3
2 2 2;
F
8 18 4 9 2 3 5 2
F
练习:计算
(1)3 2 3 2 2 3 3
解:原式 3 2 2 2) 3 3 3) ( (
2 2 3
强调: 先化简,
(2) 8 18 12
解:原式 4 2 9 2 4 3 2 2 3 2 2 3 5 2 2 3
再合并
例2计算: 1 (1)2 12 6 3 48 3 (2)( 12 20) ( 3 5) 2 x 1 (3) 9x 6 2x 3 4 x
1 2 12 6 20x 3 3 4 32 2 3 12 33 145 3 1 3 5 1..2 12x 6 2 x 48 52 x 3 x2 2 x x 2. 9 3 3 3 3 4 x
b 3 3 (3)2a 3ab ( 27a 2ab a) 6 4
2
课堂小结
1.同类二次根式的定义?
2.二次根式加减运算的步骤?
3.如何合并同类二次根式?
合并同类二次根式与合并同类项类似.
1.同类二次根式是相对于一组二次根式而言的.判 断几个二次根式是否为同类二次根式,首先要把这几 个二次根式化为最简二次根式,然后再看它们的被开 方数,如果被开方数相同,那么原来的几个二次根式 就是同类二次根式. 2.同类二次根式不一定是最简二次根式.如: 2 8 50 等.
判断同类二次根式的关键是什么? (1)化成最简二次根式, (2)被开方数相同,根指数相同(都等于2)
例1: 下列各式中,哪些是同类二次根式?
12
2 3
1 2
48
4 3
32
4 2
18 3 2
45
3 5
50 5 2
1 1 3
注意:判断一组式子是否为同类二次根式,只需看化 为最简二次根式后的被开方数是否相同,与最简二次 根式前面的因式及符号无关.
2 2
4 2
3 5
2 3 3
下列3组根式各有什么特征?
2 (1) 2, 2, 2 2, 2, 2 3 15 3 2 (2) 3,5 3,6 3,17 3, 3 13
(3) 2 , 8 ,5 18 , 32 ,
1 2
几个二次根式化成最简二次根式以后, 如果被开方数相同,这几个二次根式就 叫做同类二次根式.
二次根式; (2)找出其中的同类二次根式;
(3)合并同类二次根式。
一化
二找
三合并
2.计算:
先化简,后合并
(1) 4 7
(2)2 5 5
(1)2 7 6 7
(2) 80 20 5
(3) 18 ( 98 27 )
1 ( 4)( 24 0.5 ) ( 6) 8
2 4 2
2
5
2
3
8 18 4 2
例1计算: (1)12 75 (2) 80 45 (3) 9a 25a
解:
比较二次根式的加减 与整式的加减,你能 得出什么结论?
二次根式的加减实质是 合并同类二次根式.
整式的加减的实质是合 并同类项.
2
3
1
12 75 2 3 5 3 (2 5) 3 7 3
s
18
8
2
3 2
2 2
R-r
答:圆环的宽度 d为
2
cm.
反馈练习
(1) 18 8
2
(4)下列计算正确的是( D ) A. 5 2 3 B.8 3 2 11 2 C.4 5 5 4
3 1 D. a a a 2 2
3.几个二次根式相加减先把各个二次根式化成最简二 次根式,再把同类二次根式分别合并.
同类二次根式合并: 把根号外系数或字母相加减,根指 数和被开方数不变 注意:不是同类二次根式的二次根式 (如
2与 3 )不能合并
例2计算: 1 (1)2 12 6 3 48 3 (2)( 12 20) ( 3 5) 2 x 1 (3) 9x 6 2x 3 4 x
80 45 4 5 3 5 (4 3) 5 5
9a 25a 3 a 5 a (3 5) a 8 a
先化简,后合并
计算:
8 18 4 2
如何合并 同类二次 根式?
2 23 24 2 2 3 4 2 9 2
与合并同类项类似,把同类二次根式的系 数相加减,做为结果的系数,根号及根号内部 都不变, 总结二次根式加减运算的步骤
20 2 5
BC BD 2 CD2 22 12 5
所需钢材的长度为: AB BC AC BD 2 5 5 5 2 答:大约需要13.7m的钢材.
3 5 7 13.7
练习3: 如图,两个圆的圆心相同,它们的面 积分别是8cm2和18cm2,求圆环的宽度 d(两圆半径之差).
是同类二次根式,求m、n 的值.
(1)两列火车分别运煤2x吨和3x吨,问这两 列火车共运多少?2x +3x=5x吨 _______________ (2)两列火车分别运煤2x吨和3y吨,问这两 (2x +3y)吨 列火车共运多少?_______________
以下问题你能用同样的方法计算吗?
1 3
2 2
2 3 3
1.在下列各组根式中,是同类二次根 式的是( B )
A.
2 , 12
2
B.
2,
1 2
C. 4ab , ab D. a 1 , a 1 2. 与 12 是同类二次根式的是(
D )
1 A. 32 B. 24 C. 125 D. 6 27 3.如果最简二次根式m n 2 2 与 m n
(2) 75 27 8 3 1 6 3 (3) 48 6 3
计算:
15
2
2
8 7 18
4 8 2
1
2
1 32 12 4 3 48, 27
1 1 5 0.5 2 75 3 8
(3)10 2 3 3
1 (4)3 6 2 4
注意:不是同类二次根式的二次根式
(如 2 与 3 )不能合并
练习 1.判断:下列计算是否正确?为什么?
1
8 3 8 3;
F F
2
33
4 9 4 9;
2 2 2 2
T
练习 判断:下列计算是否正确?为什么?
8 18 5 2 7.5
5dm
18dm
8dm
8 18 dm
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
例3 要焊接一个如图所示的钢架,大约 需要多少米钢材(精确到0.1米)? B
2m 解: 根据勾股定理得:
2 2 2
A
2
D 4m 1m C
AB AD BD 4 2
2 4 3
x 1 9x 6 2x 4 x
2 计算: 5
(1) 75 2 8 200 (2)2 20 3 45 80 (3)2 48 ( 27 243) (4)(5 75 4 12) (5 108 3 27)
3.细心算一算 1 2 (1)( 8 2 0.25) ( 1 50 72) 8 3 4 1 4 (2)( 80 1 ) ( 3 45) 5 5 5
解:
3 3 5
问题:
现有一块长7.5dm、宽5dm的木板,能否采用 如图的方式,在这块木板上截出两个分别是 8dm2和18dm2的正方形木板? 7.5dm
8 18
2 2 3 2(化成最简二次根式)
(2 3) 2 (分配律) 5 2 18 3 2 5
21.3
二次根式的加减(一)
复习回顾
二次根式计算、化简的结果符合什么要求? (1)被开方数不含分母; 分母不含根号; (2)被开方数中不含能开得尽方的因数 或因式.
把下列各根式化简
(1) 12
(2) 48
(3) 18
(4) 50
2 3
1 (5) 2
4 3
(6) 32
3 2
5 2
1 (7) 45 (8) 1 3
1
2 3 5;
F
22
3
2 2 2;
F
8 18 4 9 2 3 5 2
F
练习:计算
(1)3 2 3 2 2 3 3
解:原式 3 2 2 2) 3 3 3) ( (
2 2 3
强调: 先化简,
(2) 8 18 12
解:原式 4 2 9 2 4 3 2 2 3 2 2 3 5 2 2 3
再合并
例2计算: 1 (1)2 12 6 3 48 3 (2)( 12 20) ( 3 5) 2 x 1 (3) 9x 6 2x 3 4 x
1 2 12 6 20x 3 3 4 32 2 3 12 33 145 3 1 3 5 1..2 12x 6 2 x 48 52 x 3 x2 2 x x 2. 9 3 3 3 3 4 x
b 3 3 (3)2a 3ab ( 27a 2ab a) 6 4
2
课堂小结
1.同类二次根式的定义?
2.二次根式加减运算的步骤?
3.如何合并同类二次根式?
合并同类二次根式与合并同类项类似.
1.同类二次根式是相对于一组二次根式而言的.判 断几个二次根式是否为同类二次根式,首先要把这几 个二次根式化为最简二次根式,然后再看它们的被开 方数,如果被开方数相同,那么原来的几个二次根式 就是同类二次根式. 2.同类二次根式不一定是最简二次根式.如: 2 8 50 等.
判断同类二次根式的关键是什么? (1)化成最简二次根式, (2)被开方数相同,根指数相同(都等于2)
例1: 下列各式中,哪些是同类二次根式?
12
2 3
1 2
48
4 3
32
4 2
18 3 2
45
3 5
50 5 2
1 1 3
注意:判断一组式子是否为同类二次根式,只需看化 为最简二次根式后的被开方数是否相同,与最简二次 根式前面的因式及符号无关.
2 2
4 2
3 5
2 3 3
下列3组根式各有什么特征?
2 (1) 2, 2, 2 2, 2, 2 3 15 3 2 (2) 3,5 3,6 3,17 3, 3 13
(3) 2 , 8 ,5 18 , 32 ,
1 2
几个二次根式化成最简二次根式以后, 如果被开方数相同,这几个二次根式就 叫做同类二次根式.
二次根式; (2)找出其中的同类二次根式;
(3)合并同类二次根式。
一化
二找
三合并
2.计算:
先化简,后合并
(1) 4 7
(2)2 5 5
(1)2 7 6 7
(2) 80 20 5
(3) 18 ( 98 27 )
1 ( 4)( 24 0.5 ) ( 6) 8
2 4 2
2
5
2
3
8 18 4 2
例1计算: (1)12 75 (2) 80 45 (3) 9a 25a
解:
比较二次根式的加减 与整式的加减,你能 得出什么结论?
二次根式的加减实质是 合并同类二次根式.
整式的加减的实质是合 并同类项.
2
3
1
12 75 2 3 5 3 (2 5) 3 7 3
