浙江省初中数学竞赛试题 (3)

合集下载

初中中数学竞赛试题及答案

初中中数学竞赛试题及答案初中数学竞赛试题一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 3.14159B. πC. 0.33333D. √22. 一个数的立方等于它本身，这个数是：A. 0B. 1C. -1D. 0或13. 若a，b，c是三角形的三边，且满足a^2 + b^2 = c^2，则这个三角形是：A. 直角三角形B. 等边三角形C. 等腰三角形D. 钝角三角形4. 一个多项式f(x) = x^3 - 6x^2 + 11x - 6，它的根是：A. 1, 2, 3B. 2, 3, 4C. 1, 3, 4D. 2, 2, 35. 一个圆的半径为5，圆心到直线的距离为4，那么直线与圆的位置关系是：A. 相离B. 相切C. 相交D. 内切6. 以下哪个是二次函数的图像？A. 直线B. 抛物线C. 双曲线D. 椭圆7. 一个数列1, 3, 5, ..., 19，这个数列共有多少项？A. 10B. 11C. 12D. 138. 一个等差数列的首项是2，公差是3，那么第10项是：A. 29B. 32C. 35D. 389. 一个长方形的长是宽的两倍，如果长增加2米，宽增加1米，面积增加8平方米，求原长方形的宽是多少？A. 2米B. 3米C. 4米D. 5米10. 一个分数的分子与分母的和是21，如果分子增加5，分母增加1，新的分数等于1，求原分数是多少？A. 3/18B. 4/17C. 5/16D. 6/15二、填空题（每题4分，共20分）11. 如果一个数的平方根等于它本身，那么这个数是________。

12. 一个数的绝对值是它本身，这个数是非负数，即这个数是________。

13. 一个多项式f(x) = x^2 - 5x + 6可以分解为________。

14. 一个数的立方根等于它本身，这个数是________。

15. 如果一个数列的前三项是1, 2, 3，且每一项都是前一项的两倍，这个数列的第5项是________。

初中数学全国竞赛各省市试题汇编附答案

初中数学全国竞赛各省市试题汇编（附答案）2012全国初中数学竞赛各省市试题汇编重排版目录一2012广东初中数学竞赛预赛1二2012年全国初中数学竞赛预赛试题及参考答案（河南赛区）4三2012年北京市初二数学竞赛试题9四2012年全国初中数学竞赛（海南赛区）10五2012年全国初中数学竞赛（海南赛区）初赛试卷参考答案13六2012年全国初中数学竞赛试卷答案（福建赛区）14七2012年全国初中数学竞赛试题19八2012年全国初中数学竞赛天津赛区初赛试卷20九2012年全国初中数学联赛（浙江赛区）试题及参考答案26十2012年四川初中数学联赛(初二组)初赛试卷28十一2012年全国初中数学竞赛试题【安徽赛区】29十二2012届湖北省黄冈地区九年级四科联赛数学试题34 十三2012年全国初中数学竞赛试题（副题）38十四2012年全国初中数学竞赛试题（副题）参考答案40十五2012年全国初中数学竞赛试题（正题）49十六2012年全国初中数学竞赛试题（正题）参考答案54 小贴士：word目录发生下列问题ctrl+左键显示“由于本机的限制，该操作已被取消，请与系统管理员联系”请按下列步骤自行解决1.开始，运行里输入regedit,回车2.在注册表中，找到HKEY_CURRENT_USERSoftwareClasses.html项3.在默认项上点右键选择修改4.将Max2.Association.HTML改为Htmlfile，确认，然后退出注册表5.重启正在使用的Office程序，然后再次点Office里面超链接，ok了一2012广东初中数学竞赛预赛二2012年全国初中数学竞赛预赛试题及参考答案（河南赛区）一、选择题（共6小题，每小题6分，共36分.1．在1,3,6,9四个数中，完全平方数、奇数、质数的个数分别是【】（A）2,3,1（B）2,2,1（C）1,2,1（D）2,3,2【答】A．解：完全平方数有1,9；奇数有1,3,9；质数有3．2．已知一次函数的图象经过一、二、三象限，则下列判断正确的是【】（A）（B）（C）（D）【答】C．解：一次函数的图象经过一、二、三象限，说明其图象与y轴的交点位于y轴的正半轴，且y随x的增大而增大，所以解得．3．如图，在⊙O中，，给出下列三个结论：（1）DC=AB；（2）AO⊥BD；（3）当∠BDC=30°时，∠DAB=80°．其中正确的个数是【】（A）0（B）1（C）2（D）3【答】D．解：因为，所以DC=AB；因为，AO是半径,所以AO⊥BD；设∠DAB=x度，则由△DAB的内角和为180°得：，解得．4.有4张全新的扑克牌，其中黑桃、红桃各2张，它们的背面都一样，将它们洗匀后，背面朝上放到桌面上，从中任意摸出2张牌，摸出的花色不一样的概率是【】（A）（B）（C）（D）【答】B．解：从4张牌中任意摸出2张牌有6种可能，摸出的2张牌花色不一样的有4种可能，所以摸出花色不一样的概率是.5．在平面直角坐标系中，点A的坐标是，点B的坐标是，点C是y轴上一动点，要使△ABC为等腰三角形，则符合要求的点C的位置共有【】（A）2个（B）3个（C）4个（D）5个【答】D．解：由题意可求出AB=5，如图，以点A为圆心AB的长为半径画弧，交y轴于C1和C2，利用勾股定理可求出OC1=OC2=，可得，以点B为圆心BA的长为半径画弧，交y轴于点C3和C4，可得，AB的中垂线交y轴于点C5，利用三角形相似或一次函数的知识可求出．6．已知二次函数（为常数），当取不同的值时，其图象构成一个“抛物线系”，图中的实线型抛物线分别是b 取三个不同的值时二次函数的图象，它们的顶点在一条抛物线上（图中虚线型抛物线），这条抛物线的解析式是【】（A）（B）（C）（D）【答】A．解：的顶点坐标是，设，，由得，所以．二、填空题（共6小题，每小题6分，共36分）7．若，则的值为．【答】7．解：．8．方程的解是．【答】．解：.∴，解得.9．如图，在平面直角坐标系中，点B的坐标是（1,0），若点A的坐标为（a，b），将线段BA绕点B顺时针旋转90°得到线段，则点的坐标是．【答】．解：分别过点A、作x轴的垂线，垂足分别为C、D．显然Rt△ABC≌Rt△BD．由于点A的坐标是，所以，，所以点的坐标是．10．如图，矩形ABCD中，AD=2，AB=3，AM=1，是以点A为圆心2为半径的圆弧，是以点M为圆心2为半径的圆弧，则图中两段弧之间的阴影部分的面积为．【答】2．解：连接MN，显然将扇形AED向右平移可与扇形MBN重合，图中阴影部分的面积等于矩形AMND的面积，等于．11．已知α、β是方程的两根，则的值为．【答】．解：∵α是方程的根，∴．∴，又∵∴=．12．现有145颗棒棒糖，分给若干小朋友，不管怎样分，都至少有1个小朋友分到5颗或5颗以上，这些小朋友的人数最多有个．【答】36．解：利用抽屉原理分析，设最多有x个小朋友，这相当于x个抽屉，问题变为把145颗糖放进x个抽屉，至少有1个抽屉放了5颗或5颗以上,则≤145，解得≤36，所以小朋友的人数最多有36个．三、解答题（第13题15分，第14题15分，第15题18分，共48分）13．王亮的爷爷今年（2012年）80周岁了，今年王亮的年龄恰好是他出生年份的各位数字之和，问王亮今年可能是多少周岁？解：设王亮出生年份的十位数字为，个位数字为（x、y均为0~9的整数）．∵王亮的爷爷今年80周岁了，∴王亮出生年份可能在2000年后，也可能是2000年前．故应分两种情况：…………………2分（1）若王亮出生年份为2000年后，则王亮的出生年份为，依题意，得，整理，得x、y均为0~9的整数，∴此时∴王亮的出生年份是2005年，今年7周岁．…………………8分（2）若王亮出生年份在2000年前，则王亮的出生年份为，依题意，得，整理，得，故x为偶数，又∴∴此时∴王亮的出生年份是1987年，今年25周岁．…………………14分综上，王亮今年可能是7周岁，也可能是25周岁．……………15分14．如图，在平面直角坐标系中，直角梯形OABC的顶点A、B的坐标分别是、，点D在线段OA上，BD=BA，点Q 是线段BD上一个动点，点P的坐标是，设直线PQ的解析式为．（1）求k的取值范围；（2）当k为取值范围内的最大整数时，若抛物线的顶点在直线PQ、OA、AB、BC围成的四边形内部，求a的取值范围．解：（1）直线经过P，∴．∵B，A，BD=BA，∴点D的坐标是，∴BD的解析式是,依题意，得，∴∴解得……………………………………………7分（2）且k为最大整数，∴.则直线PQ的解析式为.……………………………………………9分又因为抛物线的顶点坐标是，对称轴为．解方程组得即直线PQ与对称轴为的交点坐标为，∴．解得．……………………………………15分15.如图，扇形OMN的半径为1，圆心角是90°．点B是上一动点，BA⊥OM于点A，BC⊥ON于点C，点D、E、F、G分别是线段OA、AB、BC、CO的中点，GF与CE相交于点P，DE与AG相交于点Q．（1）求证：四边形EPGQ是平行四边形；（2）探索当OA的长为何值时，四边形EPGQ是矩形；（3）连结PQ，试说明是定值．解：（1）证明：如图①，∵∠AOC=90°，BA⊥OM，BC⊥ON，∴四边形OABC是矩形．∴．∵E、G分别是AB、CO的中点，∴∴四边形AECG为平行四边形. ∴……………………………4分连接OB，∵点D、E、F、G分别是线段OA、AB、BC、CO的中点，∴GF∥OB，DE∥OB，∴PG∥EQ，∴四边形EPGQ是平行四边形．………………………………………………6分（2）如图②，当∠CED=90°时，□EPGQ是矩形．此时∠AED+∠CEB=90°．又∵∠DAE=∠EBC=90°，∴∠AED=∠BCE．∴△AED∽△BCE．………………………………8分∴．设OA=x，AB=y，则∶=∶，得．…10分又，即．∴，解得．∴当OA的长为时，四边形EPGQ是矩形．………………………………12分（3）如图③，连结GE交PQ于，则．过点P作OC的平行线分别交BC、GE于点、．由△PCF∽△PEG得，∴==AB，=GE=OA，∴．在Rt△中，，即，又，∴，∴．……………………………………18分三2012年北京市初二数学竞赛试题．选择题(每小题5分，共25分)．方程|2x－4|＝5的所有根的和等于()．A．－0.5B．4.5C．5D．4．在直角坐标系xOy中，直线y＝ax＋24与两个坐标轴的正半轴形成的三角形的面积等于72，则不在直线y＝ax＋24上的点的坐标是()．A．(3，12)B．(1，20)C．(－0.5，26)D．(－2.5，32) ．两个正数的算术平均数等于，它们乘积的算术平方根等于，则期中的大数比小数大()．A．4B．C．6D．3．在△ABC中，M是AB的中点，N是BC边上一点，且CN ＝2BN，连接AN与MC交于点O，四边形BMON的面积为14cm2，则△ABC的面积为()．A．56cm2B．60cm2C．64cm2D．68cm2．当a＝1.67，b＝1.71，c＝0.46时，等于()．A．20B．15C．10D．5.55．填空题(每小题7分，共35分)．计算：1×2－3×4＋5×6－7×8＋…＋2009×2010－2011×2012＝＿＿＿．．由1到10这十个正整数按某个次序写成一行，记为a1，a2，…，a10，S1＝a1，S2＝a1＋a2，…，S10＝a1＋a2＋…＋a10，则在S1，S2，…，S10中，最多能有＿＿个质数．．△ABC中，AB＝12cm，AC＝9cm，BC＝13cm，自A分别作∠C平分线的垂线，垂足为M，作∠B的平分线的垂线，垂足为N，连接MN，则＿＿＿＿．．实数x和y满足x2＋12xy＋52y2－8y＋1＝0，则x2－y2＝＿＿＿．．P为等边△ABC内一点，AP＝3cm，BP＝4cm，CP＝5cm，则四边形ABCP的面积等于＿＿cm2．(满分10分)．求证：对任意两两不等的三个数a，b，c，是常数．(满分15分)．已知正整数n可以表示为2011个数字和相同的自然数之和，同时也能表示为2012个数字和相同的自然数之和，试确定n的最小值．(满分15分)．如图，在△ABC中，∠ABC＝∠BAC＝70°，P为形内一点，∠PAB＝40°，∠PBA＝20°，求证：PA＋PB＝PC．四2012年全国初中数学竞赛（海南赛区）初赛试卷（本试卷共4页，满分120分，考试时间：3月11日8:30——10:30）一、选择题（本大题满分50分，每小题5分）1、下列运算正确的是（）A．x2‧x3=x6B．2x3x=5x2C．(x2)3=x6D ．x6x2=x32、有大小两种游艇，2艘大游艇与3艘小游艇一次可载游客57人，3艘大游艇与2艘小游艇一次可载游客68人，则3艘大游艇与6艘小游艇一次可载游客的人数为（）A．129B．120C．108D．963、实数a＝20123－2012，下列各数中不能整除a的是（）A．2013B．2012C．2011D．20104、如图1所示的两个圆盘中，指针落在每一个数所在的区域上的机会均等，则两个指针同时落在数“1”所在的区域上的概率是（）A．B．C．D．5、一辆公共汽车从车站开出，加速行驶一段时间后匀速行驶，过了一段时间，汽车到达下一个车站．乘客上下车后汽车开始加速，一段时间后又开始匀速行驶，下面可以近似地刻画出汽车在这段时间内的速度变化情况的图象是（）6、要使有意义，则的取值范围为A．B．C．D．7、菱形的两条对角线之和为L、面积为S，则它的边长为（）A．B．C．D．8、如图2，将三角形纸片ABC沿DE折叠，使点A落在BC 边上的点F处，且DE∥BC，下列结论中，一定正确的个数是（）①△CEF是等腰三角形②四边形ADFE是菱形③四边形BFED是平行四边形④∠BDF+∠CEF＝2∠AA．1B．2C．3D．49、如图3，直线x＝1是二次函数y＝ax2＋bx＋c的图象的对称轴，则有()A．a＋b＋c＝0B．b＞a＋cC．b＝2aD．abc＞010、铁板甲形状为直角梯形，两底边长分别为4cm，10cm，且有一内角为60°；铁板乙形状为等腰三角形，其顶角为45°，腰长12cm．在不改变形状的前提下，试图分别把它们从一个直径为8.5cm的圆洞中穿过，结果是（）A．甲板能穿过，乙板不能穿过B．甲板不能穿过，乙板能穿过C．甲、乙两板都能穿过D．甲、乙两板都不能穿过二、填空题（本大题满分40分，每小题5分）11、x与y互为相反数，且，那么的值为__________.12、一次函数y=ax+b的图象如图4所示，则化简得________.13、若x=－1是关于x的方程a2x2+2011ax－2012=0的一个根，则a的值为__________.14、一只船从A码头顺水航行到B码头用6小时，由B码头逆水航行到A码头需8小时，则一块塑料泡沫从A码头顺水漂流到B码头要用______小时（设水流速度和船在静水中的速度不变）．15、如图5，边长为1的正方形ABCD的对角线相交于点O，过点O的直线分别交AD、BC于E、F，则阴影部分的面积是．16、如图6，直线l平行于射线AM，要在直线l与射线AM上各找一点B和C，使得以A、B、C为顶点的三角形是等腰直角三角形，这样的三角形最多能画_______个．17、如图7，△ABC与△CDE均是等边三角形，若∠AEB=145°，则∠DBE的度数是________.18、如图8所示，矩形纸片ABCD中，AB＝4cm，BC＝3cm，把∠B、∠D分别沿CE、AG翻折，点B、D分别落在对角线AC的点B＇和D＇上，则线段EG的长度是________.三、解答题(本大题满分30分，每小题15分)19、某市道路改造工程，如果让甲工程队单独工作，需要30天完成，如果让乙工程队单独工作，则需要60天方可完成；甲工程队施工每天需付施工费2.5万元，乙工程队施工每天需付施工费1万元.请解答下列问题：（1）甲、乙两个工程队一起合作几天就可以完成此项工程？（2）甲、乙两个工程队一起合作10天后，甲工程队因另有任务调离，剩下的部分由乙工程队单独做，请问共需多少天才能完成此项工程？（3）如果要使整个工程施工费不超过65万元，甲、乙两个工程队最多能合作几天？（4）如果工程必须在24天内（含24天）完成，你如何安排两个工程队施工，才能使施工费最少？请说出你的安排方法，并求出所需要的施工费.20、如图9，四边形ABCD是矩形，点P是直线AD与BC外的任意一点，连接PA、PB、PC、PD．请解答下列问题：（1）如图9（1），当点P在线段BC的垂直平分线MN上（对角线AC与BD的交点Q除外）时，证明△PAC≌△PDB；（2）如图9（2），当点P在矩形ABCD内部时，求证：PA2+PC2=PB2+PD2；（3）若矩形ABCD在平面直角坐标系xoy中，点B的坐标为（1，1），点D的坐标为（5，3），如图9（3）所示，设△PBC的面积为y，△PAD的面积为x，求y与x之间的函数关系式．五2012年全国初中数学竞赛（海南赛区）初赛试卷参考答案一、选择题（本大题满分50分，每小题5分）题号12345678910答案CDDACBABDB7、提示：可设菱形的两条对角线长分别为a、b，利用对角线互相垂直进行解答.9、分析:由函数的图象可知:当x=1时有a＋b＋c＜0,当x=-1时有a-b＋c＞0,即a＋c＞b,即b＜a＋c，函数的对称轴为，则b＝－2a，因为抛物线的开口向上，所以a＞0，抛物线与y轴的交点在负半轴，所以c＜0，由b＝－2a可得b＜0．所以abc＞0，因而正确答案为D10、分析：分别计算铁板的最窄处便可知，如图Ａ，直角梯形，AD=4cm，BC=10cm，∠C=60°，过点A过AE//CD，交BC于点E，过点B作BE⊥CD于点F，可求得AB=cm＞8.5cm，BE=cm＞8.5cm铁板甲不能穿过，如图Ｂ，等腰三角形ABC中，顶角∠A=45°，作腰上的高线BD，可求得BD=cm＜8.5cm，所以铁板乙可以穿过；所以选择Ｂ二、填空题（本大题满分40分，每小题5分）11、12、a+113、a1=2012,a2=－114、4815、单位面积16、3个17、85°18、17、分析：易证△CEA与△CDB全等，从而有∠DBC=∠EAC，因为，∠ABE+∠BAE=180°-145°=35°所以有∠EAC+∠EBC=120°-35°=85°，所以∠EBD=∠EBC+∠DBC=85°18、分析：AB＝4cm，BC＝3cm，可求得AC=5cm，由题意可知CB＇=BC=3cm，AB＇=2cm设BE=x，则AE=4-x，则有(4-x)2-x2=22,x=1.5cm，即BE=DG=1.5cm，过点G作GF⊥AB于点F，则可求出EF=1cm，所以EG=三、解答题(本大题满分30分，每小题15分)19、本题满分15分，第（1）、（2）、（3）小题，每小题4分，第（4）小题3分.解：（1）设甲、乙两个工程队一起合作x天就可以完成此项工程，依题意得：，解得：x=20答：甲、乙两个工程队一起合作20天就可以完成此项工程.（2）设完成这项道路改造工程共需y天，依题意得：，解得y=40。

初中数学竞赛专题训练试题及解析(共10套)

初中数学竞赛专项训练（1）（实数）一、选择题1、如果自然数a 是一个完全平方数，那么与a 之差最小且比a 大的一个完全平方数是（） A. a ＋1B. a 2+1C. a 2+2a+1D. a+2a +12、在全体实数中引进一种新运算*，其规定如下：①对任意实数a 、b 有a *b=（a ＋b ）(b －1)②对任意实数a 有a *2＝a *a 。

当x ＝2时，［3*（x *2）］－2*x ＋1的值为（） A. 34B. 16C. 12D. 63、已知n 是奇数，m 是偶数，方程⎩⎨⎧=+=+m y x n y 28112004有整数解x 0、y 0。

则（）A. x 0、y 0均为偶数B. x 0、y 0均为奇数C. x 0是偶数y 0是奇数D. x 0是奇数y 0是偶数4、设a 、b 、c 、d 都是非零实数，则四个数-ab 、ac 、bd 、cd （） A. 都是正数B. 都是负数C. 两正两负D. 一正三负或一负三正5、满足等式2003200320032003=+--+xy x y x y y x 的正整数对的个数是（） A. 1B. 2C. 3D. 46、已知p 、q 均为质数，且满足5p 2+3q=59，由以p ＋3、1－p ＋q 、2p ＋q －4为边长的三角形是 A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形7、一个六位数，如果它的前三位数码与后三位数码完全相同，顺序也相同，由此六位数可以被（）整除。

A. 111B. 1000C. 1001D. 11118、在1、2、3……100个自然数中，能被2、3、4整除的数的个数共（）个 A. 4 B. 6C. 8D. 16二、填空题 1、若20011198********⋯⋯++=S ，则S 的整数部分是____________________2、M 是个位数字不为零的两位数，将M 的个位数字与十位数字互换后，得另一个两位数N ，若M －N 恰是某正整数的立方，则这样的数共＿＿＿个。

浙教版八年级数学竞赛试卷与答案

浙教版八年级数学竞赛试题卷（一、精心选一选（本题有10个小题，每小题4分，共40分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母填在相应的括号内。

1．不论x 、y 为何实数，346422+-+-y y xy x 的值总是（）A.正数B.负数 C . 0 D. 非负数2．一次函数y=ax-3a+1的图象必通过一定点,此定点坐标是（） A. （1，3） B. （0，1） C. （3，1） D.（0，3）3．若关于x 的方程x 2-2k x-1=0有两个不相等的实数根，则直线y=kx +3必不经过（）A. 第三象限B. 第四象限C. 第一、二象限D. 第三、四象限 4．某商品的进价是100元，标价为150元，商店要求以利润率不低于5%的售价打折出售，售货员最低可打（）A.8折B. 7折C.6折D. 9折 5．梯形的两底角之和为900，上底长为5，下底长为11，则连结两底中点的线段长是（）A. 3B.4C.5D.6 6．已知M （3，2）、N （1，-1），点P 在y 轴上，使PM+PN 最短，则点P 的坐标是（）A ．（0，21-） B. （0，0） C. （0，611） D.（0，41-）7．如果等腰三角形一腰上的高线等于腰长的一半,那么它的底角等于（）A ．750 B. 150 C. 300 D 750或1508．如图,D 、E 分别是△ABC 的边BC 、AC 上的点，若AB=AC ，AD=AE ，∠α=300时，则∠CDE （） A ．150 B.300 C.450 D.2009．某商店有5袋面粉，各袋重量在25～30公斤之间，店里有一磅秤，但只有能称50～70公斤重量的秤砣，现要确定各袋面粉的重量，至少要称（）A ．4次B ．5次C ．6次 D. 7次10．如图，正方形ABCD 的边长为2，点E 在AB 边上．四边形EFGB 也为正方形，设△AFC 的面积为S ，则（） A ．S=2 B ．S=2.4 C ．S=4 D ．S 与BE 长度有关二．细心填一填（本题有10个小题，每小题4分，共40分）11．如果不等式组⎩⎨⎧<->-01a x x 无解，则a 的取值范围是____________12．如图的号码是由14位数字组成的，每一位数字写在下面的方格中，若任何相邻的三个数字之和都等于14，则x 的值等于13. 若一个数的平方根等于这个数的立方根，则这个数是14．.如图是2002年北京第24届国际数学家大会会标，它由4个全等的直角三角形拼合而成，若图中大、小正方形的面积分别为13和1，则直角三角形的较长直角边长为 .15．如图△ABC 中，AC ＞AB ，AB=4，AC=x ，AD 平分∠BAC ，BD ⊥AD 于D ，点E 是BC 的中点，DE=y ，则y 关于x 的函数关系式为 16．已知1=-b a ，122-=-b a ，则=-20082008b a_________17.已知方程0119992001)2000(2=-⨯-x x 较大的根为α，方程0199919982=-+x x 较小的根为βαβ-则,的值是。

初中数学竞赛试题及答案解析

初中数学竞赛试题二、填空题1、 41-的负倒数与4-的倒数之和等于 . 2、甲、乙、丙、丁四个数之和等于90-.甲数减4-,乙数加4-,丙数乘4-,丁数除以4-彼此相等.则四个数中的最大的一个数比最小的一个数大 .3、已知a 1999=,则=-+---+-200133314232323a a a a a a .4、填数计算:〇中填入的最小的自然数.△中填入最小的非负数.□中填入不小于5-且小于3的整数的个数.将下式的计算结果写在等号右边的横线上.(〇+□)⨯△= .5、从集合}5,4,1,2,3{---中取出三个不同的数,可能得到的最大乘积填在□中,可能得到的最小乘积填在〇中,并将下式计算的结果写在等号右边的横线上.-(-□)÷〇= .6、计算:=------------)4151()3141()2131(1)4151()3141()2131(1 . 7、 x 是有理数,则22195221100++-x x 的最小值是 . 8、如图,C 是线段AB 的中点,D 是线段AC 的中点.已知图中所有线段的长度之和为23,则线段AC 的长度为.9、在1000到5000之间同时被24,36,30整除的最小整数是_________,最大整数是__________.10、一个有理数的倒数的相反数的3倍是31,那么这个有理数是 . 11、一个有理数的二次幂大于这个有理数,那么这样的有理数的取值范围是 .12、若8919+=+=+c b a ,则=-+-+-222)()()(a c c b b a .13、 a 1的倒数是51-,那么=a _____. 14、小丽写出三个有理数,其中每两个有理数的平均值分别是326,217,7,那么这三个有理数的平均值是 .15、计算:=--+-)36173)(72.0()722(125.11.16、 m ，y 互为相反数,n 和y 互为倒数,则5)(y my n -的值是_____.17、已知1171=x ,则3)114(3)711)(1(2++--x x x 的值是 . 18、已知52,32<-<-b a a b .则化简98272-+++-----b a a b a b 所得的结果是 .19、 m ,n 是正整数,mn =120,则m +n 可能取到的最小值是_____.20、若a=1997,则7122----+a a a a 的值是 .21、若x = -0.239,则199********-------++-+-x x x x x x 的值等于_____.参考答案二、填空题1、 417- 解：41-的负倒数为411--,4-的倒数为41-, 二者之和为:411--+41-417414-=--=.2、 204解：设等数为a ,则 90)4()4()]4([)]4([-=-⨯+-+--+-+a a a a 即90412-=-a ,∴ a =40, 因此,甲数为36,乙数为44,丙数为-10,丁数为-160,其中,最大数-最小数=44-(-160)=204.3、 4000000 解：当a 1999=时,142314232323-+-=-+-a a a a a a=-+-200133323a a a 200133323-+-a a a ,所以,原式=142323-+-a a a )2001333(23-+--a a a2000200019992000)1(20002+⨯=++=++=a a a a400000020002000=⨯=.4、 0解：〇中填1,△中0,□填8. []⎣⎦⎡⎤00)81(=⨯+.5、 ⎣⎦⎡⎤2160)30(-=÷-- 解：由-3,-2,-1,4,5中任取三个相乘可得10种不同的乘积,它们是:124)1)(3(,205)2)(3(,244)2)(3(,6)1)(2)(3(=⋅--=⋅--=⋅--=---,105)1)(2(,84)1)(2(,6054)3(,155)1)(3(=⋅--=⋅---=⋅⋅-=⋅--,2054)1(,4054)2(-=⋅⋅--=⋅⋅-,最大乘积是30,最小的乘积是-60.∴ ⎣⎦⎡⎤2160)30(-=÷--.6、 137 解：)4151()3141()2131(1)4151()3141()2131(1------------ )4151()3141()2131(1)]4151([)]3141([)]2131([1---------------= )4151()3141()2131(1)4151()3141()2131(1-------+-+-+= 41513141213114151314121311+-+-+--+-+-+= 13710131075121151211==-++-=.7、 1715 解：一般解法是分三种情况讨论:（1）当22195-<x 时 ,,（2）当22110022195≤≤-x 时 ,,（3）当221100>x 时 ,.综合（1）,（2）,（3）可得,最小值是1715.最简单的解法是:根据绝对值的几何意义,22195221100++-x x 表示数轴上x 对应的点P 到22195-对应的点A 和221100对应的点B 的距离之和,易知当P 在线段AB 上时,P A +PB 最小值为2211001715)22195(=--.8、 1373 解：设线段AC 的长度为x ,则AD =2x ,则AB =2x ,DC =2x ,DB =x 23,CB =x ,所以 232321221=+++++x x x x x x ,即23213=x .∴13731346==x .即AB 长度为1373.9、 4680解：24,30,36三个数的最小公倍数是360,10803360=⨯,∴大于10000且能被24,30,36整除的最小整数是1080,又36010805000⋅+>n ,其中n 为自然数,解得9810<n .∴取10=n ,得4680360101080=⋅+.∴具有这种性质的最大整数是4680.10、 -9解：利用还原算法:某数a 的3倍是31,显然91=a ,而91应是一个有理数倒数的相反数,所以这个有理数的倒数为91-,故这个有理数是-9.11、大于1的有理数和负有理数解：画出数轴如图.大于1的有理数的二次幂大于它自身；1的二次幂等于1;大于0且小于1的有理数的二次幂小于它本身;0的二次幂是0；负有理数的二次幂是正数,大于它自身.综上可知,二次幂大于其自身的有理数的范围,是大于1的有理数和负有理数.12、 222解：由8919+=+=+c b a 得:11,1,10=--=--=-a c c b b a .∴+-+-22)()(c b b a =-2)(a c 222121110011)1()10(222=++=+-+-.13、 51- 解：a 1的倒数是51-,那么a 1=-5,51-=a .14、 1817 解：设小丽写出的三个有理数为x ,y ,z ,则3262,2172,72=+=+=+z y z x y x , 所以15,340,14=+=+=+x z z y y x ,三式相加,3127)(2=++z y x , 则1817181273==++z y x .15、 -14 解：因为2179167212518511.125(2)(0.72)(3)73687100367214-+--=-+=-+=-. 所以原分式的值为-14.16、 0解：由m 和y 互为相反数,知m = -y ,由n 和y 互为倒数,知道0,0≠≠y n 且yn 1= ∴0=-=-y y y y y m y n ,故5)(ym y n -=0. ∴17、 38 解：由1171=x ，可知2114,1171=+=-x x ，所以原式= 37772(1117)322113838111111-+=+=.18、 -6解：由32<-a b ,得03272<--<--a b a b .由52<-b a ,得052>+-a b ,得 05282>+->+-a b a b .而853)2()2(=+<-+-=+b a a b a b . 089<-+<-+∴a b b a98272-+++-----b a a b a b9)()82()72(-+-+----=b a a b a b987+--=6-=.19、 22解：由222)(1204)(4)(n m n m mn n m -+⋅=-+=+当2)(n m -愈小时,2)(n m +越小,从而m +n 也愈小,m 、n 为120的约数,且n m -要最小,由53222120⋅⋅⋅⋅==mn所以,当m =12,n =10时,m +n =22为最小值.20、 4000解：当a =1997时,0719971997,011997199722>-->-+7122----+a a a a)7()1(22----+=a a a a7122++--+=a a a a62+=a4000619972=+⋅=.21、 999解：由b a x <≤,可得a b a x b x -=---,则原式)19961997()23()1(---++---+--=x x x x x x)19961997()23()01(-++-+-=个99921998111=÷+++= 999=.。

2023年浙江省第四届初中生学科素养测评(竞赛选拔)数学试卷

2023年浙江省第四届初中生学科素养测评（竞赛选拔）
一、选择题
数学试卷
1.如果m+n+p=0，且|m|＞|n|＞|p|．则下列说法中可能成立的是( C
)
A.m,n为正数，p为负数
B.m,p为正数，n为负数
C.n,p为正数，m为负数
D.m,p为负数，n为正数
【解析】解：∵m+n+p=0，
∴m、n、p至少有一个为正数，至少有一个为负数，
=(49-1)÷2
=48÷2
=24，
故答案为：(7×7-1)÷2(答案不唯一)．
12.2 ，3 ，5 ，6 这四个数中最小的数是
55
44
33
55
．
22
5 11
11
44
4 11
11
33
3 11
11
【解析】解：2 =(2 ) =32 ，3 =(3 ) =81 ，5 =(5 ) =125 ，
22
2 11
故选：D．
7.已知m1，m2，m3，……m100均为整数，则|m1+m2|，|m2+m3|，
|m3+m4|，……|m99+m100|，|m100+m1|D中必有(
)
A.奇数个奇数，奇数个偶数
B.偶数个奇数，奇数个偶数
C.奇数个奇数，偶数个偶数
D.偶数个奇数，偶数个偶数
【解析】解：由
m1+m2+m2+m3+m3+m4+……+m99+m100+m100+m1=2(m1+m2+m3+……+m99
如图1叠放，将三角板绕顶点O以2度1秒

浙江七年级数学竞赛试题

浙江七年级数学竞赛试题浙江七年级数学竞赛试题通常包括选择题、填空题和解答题。

以下是一份模拟试题的示例内容：一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. 0B. 1C. -1D. 22. 如果一个数的平方等于16，那么这个数是：A. 4B. ±4C. 16D. ±163. 一个直角三角形的两条直角边分别为3和4，那么斜边的长度是：A. 5B. 6C. 7D. 84. 一个数的绝对值是5，这个数可能是：A. 5B. -5C. 5或-5D. 都不是5. 以下哪个选项是方程 \( x^2 - 5x + 6 = 0 \) 的解？A. 2B. 3C. 1和2D. 1和36. 一个数列的前三项是1, 1, 2，如果每一项都是前两项的和，那么第四项是：A. 3B. 4C. 5D. 67. 一个圆的半径是5，那么它的面积是：A. 25πB. 50πC. 100πD. 125π8. 一个长方体的长、宽、高分别是2、3和4，那么它的体积是：A. 24B. 36C. 48D. 609. 如果一个角的补角是它的3倍，那么这个角的度数是：A. 45°B. 60°C. 90°D. 120°10. 以下哪个是等差数列 2, 5, 8, 11, ... 的第10项？A. 32B. 33C. 34D. 35二、填空题（每题4分，共20分）11. 如果一个数的立方等于-27，那么这个数是______。

12. 一个数的平方根是4，那么这个数是______。

13. 如果一个等差数列的第5项是20，第1项是10，那么这个数列的公差是______。

14. 一个正五边形的内角是______度。

15. 如果一个分数的分子和分母都增加1，那么这个分数的值会______。

（增加/减少）三、解答题（每题10分，共50分）16. 解方程 \( x^2 - 4x + 4 = 0 \)。

浙江省初中数学竞赛试题及答案

BC（第2题）全国初中数学竞赛（浙江赛区）初赛试题一、选择题（共8小题，每小题5分，满分40分．以下每小题均给出了代号为A ，B ，C ，D 的四个选项，其中有且只有一个选项是正确的．请将正确选项的代号填入题后的括号里．不填、多填或错填均得零分）1．要使方程组⎩⎨⎧=+=+232,23y x a y x 的解是一对异号的数，则a 的取值范围是（(A)34＜a ＜3 (B) a ＜34 (C) a ＞3 (D) a ＜34，或a ＞3 2．一块含30°角的直角三角板（如图），它的斜边AB =8cm ，里面空心△DEF 的各边与△ABC 的对应边平行，且各对应边的距离都是1 cm ，那么△DEF 的周长是（）(A) 5 cm (B) 6 cm (C)（36-）cm (D)（33+）cm 3．将长为15 dm 的木棒截成长度为整数的三段，使它们构成一个三角形的三边，则不同的截法有（）(A) 5种 (B) 6种 (C) 7种 (D) 8种 4．作抛物线A 关于x 轴对称的抛物线B ，再将抛物线B 向左平移2个单位，向上平移1个单位，得到的抛物线C 的函数解析式是1)1(22-+=x y ，则抛物线A 所对应的函数表达式是（）(A) 2)3(22-+-=x y (B) 2)3(22++-=x y (C) 2)1(22---=x y (D) 2)1(22+--=x y5．书架上有两套同样的教材，每套分上、下两册，在这四册教材中随机抽取两册，恰好组成一套教材的概率是（）(A)32 (B) 31 (C) 21 (D) 616．如图，一枚棋子放在七边形ABCDEFG 的顶点A 处，现顺时针方向移动这枚棋子10次，移动规则是：第k 次依次移动k 个顶点．如第一次移动1个顶点，棋子停在顶点B 处，第二次移动2个顶点，棋子停在顶点D 处．在这10次移动的过程中，棋子不可能停到的顶点是（ (A) C ，E ，F (B) C ，E ，G (C) C ，E (D) E ，F(第8题)7．一元二次方程)0(02≠=++a c bx ax 中，若a ，b 都是偶数，c 是奇数，则这个方程（）(A) 有整数根 (B) 没有整数根 (C) 没有有理数根 (D) 没有实数根 8．如图所示的阴影部分由方格纸上3个小方格组成，我们称这样的图案为L 形，那么在由4×5个小方格组成的方格纸上可以画出不同位置的L 形图案个数是（）(A) 16 (B) 32 (C) 48 (D) 64二、填空题（共6小题，每小题5分，满分30分）9．已知直角三角形的两直角边长分别为3 cm 和4 cm ，那么以两直角边为直径的两圆公共弦的长为 cm ．10．将一组数据按由小到大（或由大到小）的顺序排列，处于最中间位置的数（当数据的个数是奇数时），或最中间两个数据的平均数（当数据的个数是偶数时）叫做这组数据的中位数．现有一组数据共有100个数，其中有15个数在中位数和平均数之间，如果这组数据的中位数和平均数都不在这100个数中，那么这组数据中小于平均数的数据占这100个数据的百分比是．11．△ABC 中，a ，b ，c 分别是∠A 、∠B 、∠C 的对边．已知a =10，b =23+，c =23-，则b sin B +c sin C 的值等于．12．设直线1-+=k kx y 和直线k x k y ++=)1(（k 是正整数）及x 轴围成的三角形面积为k S ，则1232006S S S S ++++的值是．13．如图，正方形ABCD 和正方形CGEF 的边长分别是2和3，且点B ，C ，G 在同一直线上，M 是线段AE 的中点，连结MF ，则MF 的长为． 14．边长为整数的等腰三角形一腰上的中线将其周长分为1∶2的两部分，那么所有这些等腰三角形中，面积最小的三角形的面积是．EC（第13题）三、解答题（共4题，分值依次为12分、12分、12分和14分，满分50分）15．已知a ，b ，c 都是整数，且24a b -=，210ab c +-=，求a b c ++的值．16．做服装生意的王老板经营甲、乙两个店铺，每个店铺在同一段时间内都能售出A ，B 两种款式的服装合计30件，并且每售出一件A 款式和B 款式服装，甲店铺获毛利润分别为30元和40元，乙店铺获毛利润分别为27元和36元．某日王老板进货A 款式服装35件，B 款式服装25件．怎样分配给每个店铺各30件服装，使得在保证乙店铺获毛利润不小于950元的前提下，王老板获取的总毛利润最大？最大的总毛利润是多少？17．如图所示，⊙O 沿着凸n 边形A 1 A 2 A 3…A n -1A n 的外侧(圆和边相切)作无滑动的滚动一周回到原来的位置． (1) 当⊙O 和凸n 边形的周长相等时，证明⊙O 自身转动了两圈．(2) 当⊙O 的周长是a ，凸n 边形的周长是b 时，请写出此时⊙O 自身转动的圈数．18．已知二次函数1)1(22+-++=m x m x y ．(1) 随着m 的变化，该二次函数图象的顶点P 是否都在某条抛物线上？如果是，请求出该抛物线的函数表达式；如果不是，请说明理由．(2) 如果直线1+=x y 经过二次函数1)1(22+-++=m x m x y 图象的顶点P ，求此时m的值．A 3n -1（第17题）B C （第2题）2006年全国初中数学竞赛（浙江赛区）初赛试题参考答案一、选择题（共8小题，每小题5分，满分40分） 1．答案：D解：解方程组，得⎪⎩⎪⎨⎧-=-=.526,543a y a x 只需⎩⎨⎧>-<-;026,043a a 或⎩⎨⎧<->-.026,043a a 即a ＜34或a ＞3．2．答案：B解：连结BE ，分别过E ，F 作A C 的平行线交BC 于点M 和N ，则EM =1，BM =3，MN =33134-=--．∴ 小三角形的周长是632=++MN MN MN cm ． 3．答案：C解：能组成三角形的只有（1，7，7）、（2，6，7）、（3，5，7）、（3，6，6）、（4，4，7）、（4，5，6）、（5，5，5）七种．4．答案：D解：将抛物线C 再变回到抛物线A ：即将抛物线1)1(22-+=x y 向下平移1个单位，再向右平移2个单位，得到抛物线2)1(22--=x y ，而抛物线2)1(22--=x y 关于x 轴对称的抛物线是2)1(22+--=x y ．5．答案：A解：四册教材任取两册共有6种不同的取法，取出的两册是一套教材的共有4种不同的取法，故所求概率是3264=．6．答案：A解：经实验或按下述方法可求得顶点C ，E 和F 棋子不可能停到．设顶点A ，B ，C ，D ，E ，F ，G 分别是第0，1，2，3，4，5，6格，因棋子移动了k 次后走过的总格数是()121321+=++++k k k ，应停在第()p k k 7121-+格，这里p 是整数，且使0≤()p k k 7121-+≤6，分别取k =1，2，3，4，5，6，7，时，()p k k 7121-+=1，3，6，3，1，0，0，发现第2，4，5格没有停棋．若7＜k ≤10，设t k +=7（t =1，2，3）代入可得，()p k k 7121-+=()1217++t t m ，由此可知，停棋的情形与tk =时相同．故第2，4，5格没有停棋，即顶点C ，E 和F 棋子不可能停到．7．答案：B解：假设有整数根，不妨设它的根是2k 或2k +1（k 为整数），分别代入原方程得方程两边的奇偶性不同的矛盾结果，所以排除A ；若a ，b ，c 分别取4，8，3则排除C ，D ．8．答案：C解：每个2×2小方格图形有4种不同的画法，而位置不同的2×2 小方格图形共有12个，故画出不同位置的L 形图案个数是12×4=48．二、填空题（共6小题，每小题5分，满分30分）9．答案：512解：不难证明其公共弦就是直角三角形斜边上的高(设为h )，则5h =3×4，h =512．10．答案：35％或65％（答对一个给3分）解：如果平均数小于中位数，那么小于平均数的数据有35个；如果平均数大于中位数，那么小于平均数的数据有65个，所以这组数据中小于平均数的数据占这100个数据的百分比是35％或65％． 11．答案：10解：不难验证，a 2=b 2+c 2．所以△ABC 是直角三角形，其中a 是斜边．b sin B +c sin C =a b b ⋅+ac c ⋅=a b c 22+=a a 2=a =10．12．答案：00720031解：方程组()⎩⎨⎧++=-+=k x k y k kx y 1,1的解为⎩⎨⎧-=-=.1,1y x 直线的交点是()1,1--．直线1y kx k =+-，1y k x k =++（）与x 轴的交点分别是（kk-1，0）、（1+-k k，0）．11121+---⨯-⨯=k k k k S k =11121+-k k ．所以1232006S S S S ++++=⎪⎪⎭⎫⎝⎛-++-+-+-00721006214131312121121 =0072003100721121=⎪⎭⎫ ⎝⎛-⨯． 13．答案：22解：连结DM 并延长交EF 于N ，则△ADM ≌△ENM ，∴FN =1，则FM 是等腰直角△DFN 的底边上的高，所以FM =22．EC（第13题）(第8题)14．答案：463 解：设这个等腰三角形的腰为x ，底为y ，分为的两部分边长分别为n 和2n ，得⎪⎩⎪⎨⎧=+=+;22,2n y x n x x 或⎪⎩⎪⎨⎧=+=+.2,22n y x n x x 解得⎪⎩⎪⎨⎧==;35,32n y n x 或⎪⎩⎪⎨⎧==.3,34n y n x ∵ 35322n n <⨯(此时不能构成三角形，舍去)，∴ 取⎪⎩⎪⎨⎧==,3,34n y n x 其中n 是3的倍数．三角形的面积2223663)6()34(321n n n n S =-⨯⨯=∆．对于23663n S =∆，当n ≥0时，∆S 随着n 的增大而增大，故当n =3时，463=∆S 取最小．三、解答题（共4题，分值依次为12分、12分、12分和14分，满分50分） 15．(12分)解：将b a 24+=代入210ab c +-=，得2b 2+4b +c 21-=0， ……………2分∴ 22622c b -±-=． …………………………………2分∵ b ，c 都是整数，∴ 只能取⎩⎨⎧==;1,011c b ⎩⎨⎧-==;1,022c b ⎩⎨⎧=-=;1,233c b ⎩⎨⎧-=-=1,244c b ，…4分相对应a 1=4，a 2=4，a 3=０，a 4=0．故所求a b c ++的值有4个：5，3，1-，3-． ……………………………4分16．(12分)解：设分配给甲店铺A 款式服装x 件(x 取整数，且5≤x ≤30)，则分配给甲店铺B 款式服装(30x -)件，分配给乙店铺A 款式服装(35－x )件，分配给乙店铺B 款式服装[25－(30x -)]= (x 5-)件，总毛利润(设为y 总)为：y 总=30x +40(30x -)+27(35x -)+36(x 5-)= x -+1 965．………………………4分乙店铺的毛利润(设为y 乙)应满足：y 乙=27(35x -)+36(x 5-)≥950，得x ≥9520．…………………………………3分对于y 总=x -+1 965，y 总随着x 的增大而减小，要使y 总最大，x 必须取最小值，又x ≥9520，故取x =21．即分配给甲店铺A ，B 两种款式服装分别为21件和9件，分配给乙店铺A ，B 两种款式服装分别为14件和16件，此时既保证了乙店铺获毛利润不小于950元，又保证了在此前提下王老板获取的总毛利润最大， ………………………………………3分其最大的总毛利润为：y 总最大=21-+1 965=1 944(元)．…………………………2分17．(12分)解：(1) 一个圆沿着线段的一个端点无滑动地滚动到另一个端点，圆自身转动的圈数n -1（第17题）=(线段的长度÷圆的周长)圈．因此若不考虑⊙O 滚动经过n 个顶点的情况，则⊙O 自身恰好转动了一圈． ……………………………………………3分现证明，当⊙O 在某边的一端，滚动经过该端点(即顶点)时，⊙O 自身转动的角度恰好等于n 边形在这个顶点的一个外角．如图所示，设∠A 2 A 1 A n 为钝角，已知A n A 1是⊙O 的切线，⊙O 滚动经过端点A 1后到⊙O '的位置，此时A 1A 2是⊙O '的切线，因此OA 1⊥A n A 1，O 'A 1⊥A 1 A 2．当⊙O 转动至⊙O '时，则∠γ 就是⊙O 自身转动的角度．∵∠γ +∠β =90º，∠α+∠β =90º，∴∠γ =∠α ．即⊙O 滚动经过顶点A 1自身转动的角度恰好等于顶点A 1的一个外角． ………………………3分对于顶点是锐角或直角的情况，类似可证．（注：只证明直角的情况，只给2分） ∵ 凸n 边形的外角和为360º，∴ ⊙O 滚动经过n 个顶点自身又转动了一圈．………………………………3分∴ ⊙O 自身转动了两圈．(2) ⊙O 自身转动的圈数是)1(+ab圈． …………………………………………3分18．(14分)解：(1) 该二次函数图象的顶点P 是在某条抛物线上． ……………………2分求该抛物线的函数表达式如下：利用配方，得y =(x +m +1)2m m 32--，顶点坐标是P (1--m ，m m 32--)．……………………2分方法一：分别取m =0，1-，1，得到三个顶点坐标是P 1(1-，0)、P 2(0，2)、 P 3(2-，4-)，过这三个顶点的二次函数的表达式是y =2x -+x +2． …………3分将顶点坐标P (1--m ，m m 32--)代入y =－x 2+x +2的左右两边，左边=m m 32--，右边=(-1--m )2+(1--m )+2=m m 32--，∴ 左边=右边．即无论m 取何值，顶点P 都在抛物线y =2x -+x +2上．即所求抛物线的函数表达式是y =2x -+x +2．…3分（注：如果没有“左边=右边”的证明，那么解法一最多只能得4分）方法二：令1--m =x ，将m =1--x 代入m m 32--，得(-1--x )2－3(1--x )=2x -+x +2．………………………………………………3分即所求抛物线的函数表达式是y =2x -+x +2上． ………………………………3分 (2) 如果顶点P (1--m ，m m 32--)在直线y =x +1上，则m m 32--=1--m +1， …………………………………2分即m m 22-=． ∴ m =0或 m =2-．∴当直线y =x +1经过二次函数y =x 2+2(m +1)x m -+1图象的顶点P 时，m 的值是2-或0． ………………2分2006年全国初中数学竞赛（浙江赛区）复赛试题（2006年4月2日下午1：00—3：00）一、选择题（共6小题，每小题5分，满分30分．以下每小题均给出了代号为A ，B ，C ，D 的四个选项，其中有且只有一个选项是正确的．请将正确选项的代号填入题后的括号里．不填、多填或错填均得零分）1． 5个相异自然数的平均数为12，中位数为17，这5个自然数中最大一个的可能值的最大值是（）（A ）21 （B ）22 （C ）23 （D ）24 2．如图，长方形ABCD 恰好可分成7个形状大小相同的小长方形，如果小长方形的面积是3，则长方形ABCD 的周长是（）（A ）17 （B ）18 （C ）19 （D ）317 3．设0＜k ＜1，关于x 的一次函数)1(1x kkx y -+=，当1≤x ≤2时的最大值是（）（A ）k （B ）k k 12- （C ）k 1 （D ）kk 1+4．钟面上的1~12这12个数字把圆周12等分，以其中任意4个等分点为顶点作四边形，其中矩形的个数是（）（A ）10个（B ）14个（C ）15个（D ）30个5．平面直角坐标系中，如果把横坐标、纵坐标都是整数的点叫做整点，那么函数1212-+=x x y 的图象上整点的个数是（）（A ）2个（B ）4个（C ）6个（D ）8个6．用标有1克，2克，6克，26克的法码各一个，在一架无刻度的天平上称量重物，如果天平两端均可放置法码，那么可以称出的不同克数（正整数的重物）的种数共有（）（A ）15种（B ）23种（C ）28种（D ）33种二、填空题（共6小题，每小题6分，满分36分）7．三个实数按从小到大排列为1x ，2x ，3x ，把其中每两个数作和得到三个数分别是14，PADBC（第2题）17，33，则2x = ．8．如图，AB 为半⊙O 的直径，C 为半圆弧的三等分点，过B ，C 两点的半⊙O 的切线交于点P ，若AB 的长是2a ，则P A 的长是．9．函数1422-+=x x y 的最小值是．10．在正方形ABCD 中，点E 是BC 上的一定点，且BE =10，EC =14，点P 是BD 上的一动点，则PE +PC 的最小值是．11．某商店出售A 、B 、C 三种生日贺卡，已知A 种贺卡每张0.5元，B 种贺卡每张1元，C 种贺卡每张2.5元．营业员统计3月份的经营情况如下：三种贺卡共售出150张，营业收入合计180元．则该商店3月份售出的C 种贺卡至少有张．12．有一个英文单词由5个字母组成，如果将26个英文字母a ，b ，c ，…，y ，z 按顺序依次对应0到25这26个整数，那么这个单词中的5个字母对应的整数按从左到右的顺序分别为x 1，x 2，x 3，x 4，x 5．已知x 1+3x 2，4x 2，x 3+2x 4,，5x 4，6x 4+x 5 除以26所得的余数分别为15，6，20，9，9．则该英文单词是．DE（第10题）三、解答题（共4小题，满分54分）13．（本题满分12分）某列从上海到温州的火车，包括起始和终点在内共有6个停靠站，将这6个站按火车到达的先后次序，依次记为A ，B ，C ，D ，E ，F ．小张乘坐这趟列车从上海出发去温州，火车驶离上海时，小张发现他乘坐的车厢里连他自己在内共19名旅客，这些旅客小张都认识，其中有些是浙江人，其他的都是上海人．一路上小张观测到下列情况：①除了终点站，在每一站，当火车到达时这节车厢里浙江人的人数与下车旅客的人数相同，且这次行程中没有新的旅客进入这节车厢；②当火车离开车站B 时，车厢里有12名旅客；当火车离开车站D 时，还有7名旅客在这一车厢里；在F 站下车的旅客包括小张在内共5人．（1）火车驶离上海时，小张乘坐的这节车厢里共有多少浙江人？多少上海人？（2）在B 到C 、C 到D 、D 到E 的旅途中，分别有多少浙江人？多少上海人？14．（本题满分12分）如图，M 、N 、P 分别为△ABC 三边AB 、BC 、CA 的中点，BP 与MN 、AN 分别交于E 、F ，（1）求证：BF =2FP ；（2）设△ABC 的面积为S ，求△NEF 的面积．15．（本题满分15分）设,,,321x x x ...2006,x 是整数，且满足下列条件： ① -1≤n x ≤2，n =1，2，3，...，2006； ②+++321x x x ...2002006=+x ； ③+++232221x x x (20062)2006=+x ．求 +++333231x x x (3)2006x + 的最小值和最大值． 16．（本题满分15分）BACMPEF一只青蛙在平面直角坐标系上从点（1，1）开始，可以按照如下两种方式跳跃： ①能从任意一点（a ，b ），跳到点（2a ，b ）或（a ，2b ）；②对于点（a ，b ），如果a ＞b ，则能从（a ，b ）跳到（a －b ，b ）；如果a ＜b ，则能从（a ，b ）跳到（a ，b －a ）．例如，按照上述跳跃方式，这只青蛙能够到达点（3，1），跳跃的一种路径为：（1，1）→（2，1）→（4，1）→（3，1）．请你思考：这只青蛙按照规定的两种方式跳跃，能到达下列各点吗？如果能，请分别给出从点（1，1）出发到指定点的路径；如果不能，请说明理由．（１）（3, 5）；（２）（12，60）；（3）（200，5）；（4）（200，6）．2006年全国初中数学竞赛（浙江赛区）复赛试题参考答案一、选择题（共6小题，每小题5分，满分30分） 1．答案：D解：设这5个自然数从小到大排列依次为x 1，x 2，x 3，x 4，x 5，则x 3=17．当这5个自然数中最大一个x 5的可能值最大时，其他3个自然数必取最小的可能值，x 1=0，x 2=1，x 4=18，此时x 5=24． 2．答案：C解：设小长方形的长、宽分别为x ，y ，则3 x = 4 y ，y x 34=． ∴334=⋅y y ．23=y ，x =2．∴ 长方形ABCD 的周长为19． 3．答案：A 解：k x k k y 1)1(+-=，∵ 0＜k ＜1，∴ kk k k k )1)(1(1-+=-＜0，该一次函数的值随x 的增大而减小，当1≤x ≤2时，最大值为k kk k =+-11．4．答案：C解：连结圆周上12个等分点，得6条直径，以其中任意两条为对角线的四边形即为矩形，共15个矩形． 5．答案：C解：将函数表达式变形，得122+=-x y xy ，24224=--x y xy ，25)12)(12(=--x y ．∵ x ，y 都是整数，∴ )12(),12(--x y 也是整数．∴ ⎩⎨⎧=-=-2512,112x y 或⎩⎨⎧-=--=-2512,112x y 或 ⎩⎨⎧=-=-112,2512x y 或 ⎩⎨⎧-=--=-112,2512x y 或 ⎩⎨⎧=-=-512,512x y 或⎩⎨⎧-=--=-.512,512x y 解得整点为（13，1），（-12，0），（1，13），（0，-12），（3，3），（-2，-2）． 6．答案：C解：（1）当天平的一端放1个砝码，另一端不放砝码时，可以称量重物的克数有1克，2克，6克，26克；（2）当天平的一端放2个砝码，另一端不放砝码时，可以称量重物的克数有3克，7克，8克，27克， 28克，32克；（3）当天平的一端放3个砝码，另一端不放砝码时，可以称量重物的克数有9克，29克，33克，34克；（4）当天平的一端放4个砝码时，可以称量重物的克数有35克．（5）当天平的一端放1个砝码，另一端也放1个砝码时，可以称量重物的克数有1克，4克，5克，20克，24克，25克；（6）当天平的一端放1个砝码，另一端放2个砝码时，可以称量重物的克数有3克，5克，7克，18克，19克，21克，22克，23克，25克，27克，30克，31克；（7）当天平的一端放1个砝码，另一端放3个砝码时，可以称量重物的克数有17 克，23克，31克，33克；（8）当天平的一端放2个砝码，另一端也放2个砝码时，可以称量重物的克数有19克，21克，29克．去掉重复的克数后，共有28种．二、填空题（共6小题，每小题6分，满分36分） 7．答案：15解： 1421=+x x ，1731=+x x ，3332=+x x ， ∴ 32321=++x x x ，152=x ．8．答案：a 7解：连结OC ，OP ，则∠OCP =90°，∠COP =60°，OC = a∴ PC =a 3，PB =PC =a 3，P A =a 7． 9．答案：1-解：y =3)1(22-+x =⎪⎩⎪⎨⎧≤--≥-+.0,3)1(2,0,3)1(222x x x x 其图象如图，由图象可知，当x = 0时，y 最小为 -1．10．答案：26（第9题）解：连结AP ，则PE +PC =PE +P A ，当点P 在AE 上时，其值最小，最小值为26102422=+．11．答案：20解：设A 、B 、C 三种贺卡售出的张数分别为x ，y ，z ，则 ⎩⎨⎧=++=++.1805.25.0,150z y x z y x消去y 得，305.15.0-=z x ．由0305.1≥-z ，得20≥z ．12．答案：right ，evght解：由题意得，⎪⎪⎪⎩⎪⎪⎪⎨⎧+=++=+=++=+=+.9266,9265,20262,6264,152635544434322121k x x k x k x x k x k x x （54321,,,,k k k k k 为非负整数）．由0≤54321,,,,x x x x x ≤25，可分析得出，123454,17,8,216,7,19.x x x x x =⎧⎪=⎪⎪=⎨⎪=⎪⎪=⎩或或，三、解答题（共4题，满分54分） 13．(12分)解：（1）由条件得，在B 站有7人下车，∴ 19名旅客中有7位浙江人，即火车驶离上海时，车厢里有7个浙江人，12个上海人． ……………2分（2）在E 站有2人下车，即在D —E 途中有2个浙江人，5个上海人， ……………2分从而C —D 途中至少有2位浙江人，在D 站至少有2人下车， ……………2分 ∴ C 站后车厢里至少有9个人． ∵ 火车离开B 站时车厢里有12人，离开D 站时有7人， ∴ 在C 站至少有3人下车，即经过C 站后车厢里至多9人，故经过C 站后车厢里有9人，即在C 站有3人下车． ……………2分 ∴ B —C 途中车厢里还有3个浙江人，9个上海人． ……………2分在D 站有2人下车，C —D 途中车厢里还有2个浙江人，7个上海人．……………2分14．(12分)解：（1）如图1，连结PN ，则PN ∥AB ，且 AB PN 21=． ……………………2分∴ △ABF ∽△NPF ，2===PNABFN AF FP BF ． ∴ BF =2FP ． ……………………2分（2）如图2，取AF 的中点G ，连结MG ，则 MG ∥EF ，AG =GF =FN ． ……………………2分∴ S △NEF =41S △MNG ……………………2分 =41×32S △AMN ……………………2分 =41×32×41S △ABC =241S ． ……………2分15．(15分)解：设,,,321x x x …2006,x 中有r 个－1、s 个1、t 个2，则⎩⎨⎧=++=++-.20064,2002t s r t s r ………………5分两式相加，得s ＋3t ＝1103，故0367t ≤≤． ………………2分∵ +++333231x x x …t s r x 832006++-=+ ………………2分=2006+t ． ………………2分∴ 200≤+++333231x x x (32006)x +≤6×367+200=2402．当0,1103,903t s r ===时，+++333231x x x ...32006x +取最小值200，.........2分当367,2,536t s r ===时，+++333231x x x (32006)x +取最大值2402．………2分16．(15分)解：（1）能到达点（3，5）和点（200，6）． ………………2分从（1，1）出发到（3，5）的路径为：（1，1）→（2，1）→（4，1）→（3，1）→（3，2）→（3，4）→（3，8）→（3，5）． ………………3分从（1，1）出发到（200，6）的路径为：（1，1）→（1，2）→（1，4）→（1，3）→（1，6）→（2，6）→（4，6） →（8，6）→（16，6）→（10，6）→（20，6）→（40，6）→（80，6） →（160，6）→（320，6）→（前面的数反复减20次6）→（200，6）．……3分BACM N PE F（图1） BA CM N PE F（图2）G（2）不能到达点（12，60）和（200，5）．………………2分理由如下：∵a和b的公共奇约数=a和2b的公共奇约数=2a和b的公共奇约数，∴由规则①知，跳跃不改变前后两数的公共奇约数．∵如果a＞b，a和b的最大公约数=（a－b）和b的最大公约数，如果a＜b，a和b的最大公约数=（b－a）和b的最大公约数，∴由规则②知，跳跃不改变前后两数的最大公约数．从而按规则①和规则②跳跃，均不改变坐标前后两数的公共奇约数．…………3分∵1和1的公共奇约数为1，12和60的公共奇约数为3，200和5的公共奇约数为5．………………2分∴从（1,1）出发不可能到达给定点（12，60）和（200，5）．。

浙江省初中数学竞赛试卷

浙江省初中数学竞赛试卷姓名:________ 班级:________ 成绩:________一、单选题 (共40题；共80分)1. （2分）下列运动中：①荡秋千；②钟摆的摆动；③拉抽屉时的抽屉；④工厂里的输送带上的物品，不属于平移的有（）A . 4个B . 3个C . 2个D . 1个2. （2分） (2017七下·如皋期中) 如图，棋子“车”的坐标为（﹣2，3），棋子“马”的坐标为（1，3），则棋子“炮”的坐标为（）A . （2，3）B . （3，2）C . （﹣2，﹣3）D . （﹣3，2）3. （2分）(2016·黄陂模拟) 在平面直角坐标系中，把△ABC经过平移得到△A′B′C′，若A（1，m），B （4，2），点A的对应点A′（3，m+2），则点B对应点B′的标为（）A . （6，5）B . （6，4）C . （5，m）D . （6，m）4. （2分）如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是（）A . △ABC绕点C顺时针旋转90°，再向下平移3B . △ABC绕点C顺时针旋转90°，再向下平移1C . △ABC绕点C逆时针旋转90°，再向下平移1D . △ABC绕点C逆时针旋转90°，再向下平移35. （2分）点A（﹣3，﹣4）到原点的距离为（）A . 3B . 4C . 5D . 76. （2分） (2017七下·长安期中) 如图，将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为（）A . 11B . 10C . 9D . 87. （2分） (2020七下·北京期末) 若点在第三象限，且点P到x轴的距离为3，到y轴的距离为2，则点P的坐标是（）A .B .C .D .8. （2分）如图在平面直角坐标系中，□ MNEF的两条对角线ME，NF交于原点O，点F的坐标是（3，2），则点N的坐标为（）。

浙江初三初中数学竞赛测试带答案解析

浙江初三初中数学竞赛测试班级:___________ 姓名：___________ 分数：___________一、选择题1.下列等式一定成立的是（）A．B．C．D．2.下列式子成立的是（）A．a a=a B．（a b）= a bC．0.0081=8.1×10D．3.以下列各组数为边长，能构成直角三角形的是 ( )A．，，B．，，C．32，42，52D．1，2，34.使式子有意义的x的取值范围是（）A．x≤1B．x≤1且x≠－2C．x≠－2D．x＜1且x≠－25.解关于x的方程时产生增根，则m的值等于（）A．－2B．－1C．1D．26.二次函数的图象可能是（）7.如图几何体的俯视图是（）8.已知：如图，正方形ABCD的边长为8，M在DC上，且DM＝2，N是AC上一动点，则DN＋MN的最小值为（）A．8B．10C．11D．129.如图，已知矩形ABCD，R、P分别是DC、BC上的点，E、F分别是AP，RP的中点，当P在BC上从B向C 移动而R不动时，那么下列结论成立的是（）A．线段EF的长逐渐增大 B．线段EF的长逐渐减小C．线段EF的长不改变 D．线段EF的长不能确定二、填空题1.⊙O的半径是13，弦AB∥CD，AB=24，CD=10，则AB与CD的距离是 .2.规定"*"为一种运算，它满足a*b=，那么1992*(1992*1992)=____。

3.已知直角三角形的两条边x、y的长满足，则第三边长为4.有五根木条，分别为12cm，10cm，8cm，6cm，4cm，则从中任取三根能组成三角形的概率为5.如图所示，二次函数的图象经过点，且与x轴交点的横坐标为、，其中、下列结论：①；②；③；④；正确的结论是 .三、解答题1.解方程：2.某商场将进价40元一个的某种商品按50元一个售出时，能卖出500个，已知这种商品每个涨价一元，销量减少10个，为赚得最大利润，售价定为多少？最大利润是多少？3.如图，在△ABC中，点O是AC边上的一动点，过点O作直线MN//BC，MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F。

j初中九年级数学竞赛试题下载

j初中九年级数学竞赛试题下载一、选择题（每题3分，共15分）1. 下列哪个数是无理数？A. πB. 0.33333（无限循环）C. √2D. 1/32. 如果一个圆的半径是5，那么它的周长是多少？A. 10πB. 20πC. 30πD. 40π3. 以下哪个方程的解集是空集？A. x^2 + 4x + 4 = 0B. x^2 - 1 = 0C. x^2 + 2x + 1 = 0D. x^2 + 3x + 2 = 04. 一个数列的前三项为1, 1, 2，从第四项开始，每一项都是前三项的和。

这个数列的第10项是多少？A. 143B. 144C. 145D. 1465. 一个长方体的长、宽、高分别是2, 3, 4，那么它的对角线长度是多少？A. 5B. √29C. √35D. √41二、填空题（每题4分，共20分）6. 如果一个三角形的三边长分别为a, b, c，且满足a^2 + b^2 =c^2，那么这个三角形是_________三角形。

7. 一个数的立方根等于它本身，这个数可能是_________。

8. 将一个圆分成四个扇形，每个扇形的圆心角为90°，那么这四个扇形的面积之和等于_________。

9. 如果一个多项式f(x) = ax^3 + bx^2 + cx + d，且f(1) = 2，f(-1) = -2，那么a + c的值是_________。

10. 一个数列的前n项和为S(n)，如果S(3) = 9，S(5) = 25，那么S(4)的值是_________。

三、解答题（每题10分，共30分）11. 证明：对于任意实数x，等式e^x ≥ x + 1成立。

12. 给定一个等差数列，首项为a1，公差为d。

如果这个数列的前n 项和为S(n)，证明S(n) = na1 + n(n-1)d/2。

13. 一个直角三角形的两条直角边分别为6和8，求斜边的长度，并证明勾股定理。

四、综合题（每题15分，共20分）14. 有一个长方体，其长、宽、高分别是a, b, c。

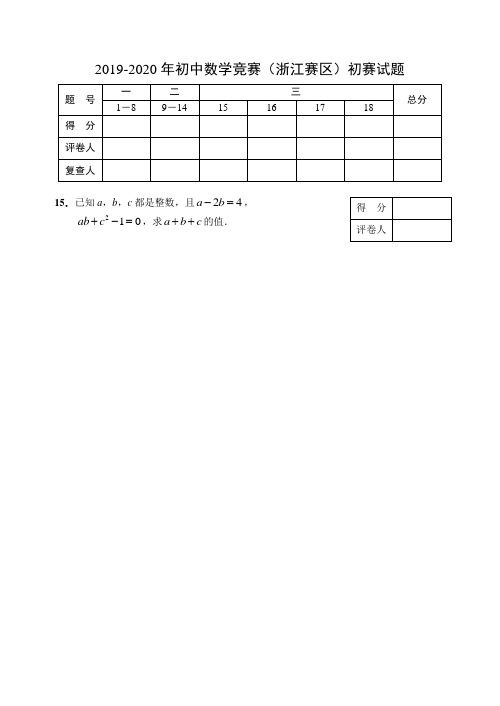
2019-2020年初中数学竞赛(浙江赛区)初赛试题

2019-2020年初中数学竞赛（浙江赛区）初赛试题15．已知a ，b ，c 都是整数，且24a b -=，210ab c +-=，求a b c ++的值．16．做服装生意的王老板经营甲、乙两个店铺，每个店铺在同一Array段时间内都能售出A，B两种款式的服装合计30件，并且每售出一件A款式和B款式服装，甲店铺获毛利润分别为30元和40元，乙店铺获毛利润分别为27元和36元．某日王老板进货A款式服装35件，B款式服装25件．怎样分配给每个店铺各30件服装，使得在保证乙店铺获毛利润不小于950元的前提下，王老板获取的总毛利润最大？最大的总毛利润是多少？17．如图所示，⊙O沿着凸n边形A1 A2 A3…A n-1A n的外侧Array (圆和边相切)作无滑动的滚动一周回到原来的位置．(1) 当⊙O和凸n边形的周长相等时，证明⊙O自身转动了两圈．(2) 当⊙O的周长是a，凸n边形的周长是b时，请写出此时⊙O自身转动的圈数．A3n-1（第17题）18．已知二次函数1)1(22+-++=m x m x y ．(1) 随着m 的变化，该二次函数图象的顶点P 是否都在某条抛物线上？如果是，请求出该抛物线的函数表达式；如果不是，请说明理由．(2) 如果直线1+=x y 经过二次函数1)1(22+-++=m x m x y 图象的顶点P ，求此时m的值．BC（第2题）2006年全国初中数学竞赛（浙江赛区）初赛试题参考答案一、选择题（共8小题，每小题5分，满分40分） 1．答案：D解：解方程组，得⎪⎩⎪⎨⎧-=-=.526,543a y a x 只需⎩⎨⎧>-<-;026,043a a 或⎩⎨⎧<->-.026,043a a 即a ＜34或a ＞3．2．答案：B解：连结BE ，分别过E ，F 作A C 的平行线交BC 于点M 和N ，则EM =1，BM =3，MN =33134-=--．∴ 小三角形的周长是632=++MN MN MN cm ． 3．答案：C解：能组成三角形的只有（1，7，7）、（2，6，7）、（3，5，7）、（3，6，6）、（4，4，7）、（4，5，6）、（5，5，5）七种．4．答案：D解：将抛物线C 再变回到抛物线A ：即将抛物线1)1(22-+=x y 向下平移1个单位，再向右平移2个单位，得到抛物线2)1(22--=x y ，而抛物线2)1(22--=x y 关于x 轴对称的抛物线是2)1(22+--=x y ．5．答案：A解：四册教材任取两册共有6种不同的取法，取出的两册是一套教材的共有4种不同的取法，故所求概率是3264=．6．答案：A解：经实验或按下述方法可求得顶点C ，E 和F 棋子不可能停到．设顶点A ，B ，C ，D ，E ，F ，G 分别是第0，1，2，3，4，5，6格，因棋子移动了k 次后走过的总格数是()121321+=++++k k k ，应停在第()p k k 7121-+格，这里p 是整数，且使0≤()p k k 7121-+≤6，分别取k =1，2，3，4，5，6，7，时，()p k k 7121-+=1，3，6，3，1，0，0，发现第2，4，5格没有停棋．若7＜k ≤10，设t k +=7（t =1，2，3）代入可得，()p k k 7121-+=()1217++t t m ，由此可知，停棋的情形与t k =时相同．故第2，4，5格没有停棋，即顶点C ，E 和F 棋子不可能停到．7．答案：B解：假设有整数根，不妨设它的根是2k 或2k +1（k 为整数），分别代入原方程得方程两边的奇偶性不同的矛盾结果，所以排除A ；若a ，b ，c 分别取4，8，3则排除C ，D ．8．答案：C解：每个2×2小方格图形有4种不同的画法，而位置不同的2×2 小方格图形共有12个，故画出不同位置的L 形图案个数是12×4=48．二、填空题（共6小题，每小题5分，满分30分）9．答案：512解：不难证明其公共弦就是直角三角形斜边上的高(设为h )，则5h =3×4，h =512．10．答案：35％或65％（答对一个给3分）解：如果平均数小于中位数，那么小于平均数的数据有35个；如果平均数大于中位数，那么小于平均数的数据有65个，所以这组数据中小于平均数的数据占这100个数据的百分比是35％或65％．11．答案：10解：不难验证，a 2=b 2+c 2．所以△ABC 是直角三角形，其中a 是斜边．b sin B +c sin C =a b b ⋅+ac c ⋅=a b c 22+=a a 2=a =10．12．答案：00720031解：方程组()⎩⎨⎧++=-+=k x k y k kx y 1,1的解为⎩⎨⎧-=-=.1,1y x 直线的交点是()1,1--．直线1y kx k =+-，1y k x k =++（）与x 轴的交点分别是（kk-1，0）、（1+-k k，0）．11121+---⨯-⨯=k k k k S k =11121+-k k ．所以 1232006S S S S ++++=⎪⎪⎭⎫⎝⎛-++-+-+-00721006214131312121121 =0072003100721121=⎪⎭⎫ ⎝⎛-⨯． 13．答案：22解：连结DM 并延长交EF 于N ，则△ADM ≌△ENM ，EC（第13题）(第8题)∴FN =1，则FM 是等腰直角△DFN 的底边上的高，所以FM =22． 14．答案：463 解：设这个等腰三角形的腰为x ，底为y ，分为的两部分边长分别为n 和2n ，得⎪⎩⎪⎨⎧=+=+;22,2n y x n x x 或⎪⎩⎪⎨⎧=+=+.2,22n y x n x x 解得⎪⎩⎪⎨⎧==;35,32n y n x 或⎪⎩⎪⎨⎧==.3,34n y n x ∵ 35322n n <⨯(此时不能构成三角形，舍去)，∴ 取⎪⎩⎪⎨⎧==,3,34n y n x 其中n 是3的倍数．三角形的面积2223663)6()34(321n n n n S =-⨯⨯=∆．对于23663n S =∆，当n ≥0时，∆S 随着n 的增大而增大，故当n =3时，463=∆S 取最小．三、解答题（共4题，分值依次为12分、12分、12分和14分，满分50分） 15．(12分)解：将b a 24+=代入210ab c +-=，得2b 2+4b +c 21-=0， ……………2分∴ 22622c b -±-=． …………………………………2分∵ b ，c 都是整数，∴ 只能取⎩⎨⎧==;1,011c b⎩⎨⎧-==;1,022c b ⎩⎨⎧=-=;1,233c b ⎩⎨⎧-=-=1,244c b ，…4分相对应a 1=4，a 2=4，a 3=０，a 4=0．故所求a b c ++的值有4个：5，3，1-，3-． ……………………………4分16．(12分)解：设分配给甲店铺A 款式服装x 件(x 取整数，且5≤x ≤30)，则分配给甲店铺B 款式服装(30x -)件，分配给乙店铺A 款式服装(35－x )件，分配给乙店铺B 款式服装[25－(30x -)]= (x 5-)件，总毛利润(设为y 总)为：y 总=30x +40(30x -)+27(35x -)+36(x 5-)= x -+1 965．………………………4分乙店铺的毛利润(设为y 乙)应满足：y 乙=27(35x -)+36(x 5-)≥950，得x ≥9520．…………………………………3分对于y 总=x -+1 965，y 总随着x 的增大而减小，要使y 总最大，x 必须取最小值，又x ≥9520，故取x =21．即分配给甲店铺A ，B 两种款式服装分别为21件和9件，分配给乙店铺A ，B 两种款式服装分别为14件和16件，此时既保证了乙店铺获毛利润不小于950元，又保证了在此前提下王老板获取的总毛利润最大， ………………………………………3分n -1（第17题）其最大的总毛利润为：y 总最大=21-+1 965=1 944(元)．…………………………2分17．(12分)解：(1) 一个圆沿着线段的一个端点无滑动地滚动到另一个端点，圆自身转动的圈数=(线段的长度÷圆的周长)圈．因此若不考虑⊙O 滚动经过n 个顶点的情况，则⊙O 自身恰好转动了一圈． ……………………………………………3分现证明，当⊙O 在某边的一端，滚动经过该端点(即顶点)时，⊙O 自身转动的角度恰好等于n 边形在这个顶点的一个外角．如图所示，设∠A 2 A 1 A n 为钝角，已知A n A 1是⊙O 的切线，⊙O 滚动经过端点A 1后到⊙O '的位置，此时A 1A 2是⊙O '的切线，因此OA 1⊥A n A 1，O 'A 1⊥A 1 A 2．当⊙O 转动至⊙O '时，则∠γ 就是⊙O 自身转动的角度．∵∠γ +∠β =90º，∠α+∠β =90º，∴∠γ =∠α ．即⊙O 滚动经过顶点A 1自身转动的角度恰好等于顶点A 1的一个外角． ………………………3分对于顶点是锐角或直角的情况，类似可证．（注：只证明直角的情况，只给2分） ∵ 凸n 边形的外角和为360º，∴ ⊙O 滚动经过n 个顶点自身又转动了一圈．………………………………3分∴ ⊙O 自身转动了两圈．(2) ⊙O 自身转动的圈数是)1(+ab圈． …………………………………………3分18．(14分)解：(1) 该二次函数图象的顶点P 是在某条抛物线上． ……………………2分求该抛物线的函数表达式如下：利用配方，得y =(x +m +1)2m m 32--，顶点坐标是P (1--m ，m m 32--)．……………………2分方法一：分别取m =0，1-，1，得到三个顶点坐标是P 1(1-，0)、P 2(0，2)、 P 3(2-，4-)，过这三个顶点的二次函数的表达式是y =2x -+x +2． …………3分将顶点坐标P (1--m ，m m 32--)代入y =－x 2+x +2的左右两边，左边=m m 32--，右边=(-1--m )2+(1--m )+2=m m 32--，∴ 左边=右边．即无论m 取何值，顶点P 都在抛物线y =2x -+x +2上．即所求抛物线的函数表达式是y =2x -+x +2．…3分（注：如果没有“左边=右边”的证明，那么解法一最多只能得4分）方法二：令1--m =x ，将m =1--x 代入m m 32--，得(-1--x )2－3(1--x )=2x -+x +2．………………………………………………3分即所求抛物线的函数表达式是y =2x -+x +2上． ………………………………3分 (2) 如果顶点P (1--m ，m m 32--)在直线y =x +1上，则m m 32--=1--m +1， …………………………………2分即m m 22-=． ∴ m =0或 m =2-．∴当直线y =x +1经过二次函数y =x 2+2(m +1)x m -+1图象的顶点P 时，m 的值是2-或0． ………………2分。

初中数学奥林匹克竞赛全真试题

初中数学奥林匹克竞赛全真试题第一题：简单的数列已知一个数列的前五项分别是：1，3，5，7，9问：这个数列的第六项是多少？解析：根据已知条件，我们可以看出这个数列是一个等差数列，且公差为2。

我们可以用递推公式来求解这个数列的第六项。

设数列的第一个项为a，公差为d，则数列的第n项可以表示为：a + (n-1)d。

将已知条件代入可得：a = 1， d = 2。

所以，第六项的值为：1 + (6-1)*2 = 11。

答案：第六项为11。

第二题：寻找规律观察以下数字序列：1，3，6，10，15，21，28...问：这个序列中的第十项是多少？解析：我们可以看出，这个数字序列是一个递增的等差数列，且首项为1，公差为1。

我们可以使用递推公式来寻找这个序列中的第十项。

设数列的第一个项为a，公差为d，则数列的第n项可以表示为：a + (n-1)d。

将已知条件代入可得：a = 1， d = 1。

所以，第十项的值为：1 + (10-1)*1 = 46。

答案：第十项为46。

第三题：求三角形面积已知一个三角形的底边长为6 cm，高为8 cm。

问：这个三角形的面积是多少？解析：三角形的面积可以通过底边长和高来计算，公式为：面积 = 底边长* 高 / 2。

将已知条件代入可得：面积= 6 * 8 / 2 = 24 cm²。

答案：这个三角形的面积为24 cm²。

第四题：求方程的解解方程：2x + 3 = 7解析：为了求解方程，我们需要将x的系数移到等式的右边，并将常数项移到等式的左边。

将方程化简可得：2x = 7 - 3继续化简可得：2x = 4最后，将方程两边同除以2可得：x = 2。

答案：方程的解为x = 2。

第五题：追赶问题A、B两个人同时从同一起点出发，A的速度为6 m/s，B的速度为8 m/s。

问：如果A比B慢12秒钟到达终点，终点离起点多远？解析：设终点距离起点的距离为d，根据题意可以列出等式：d / 6 = d / 8 + 12。

全国初中数学联赛浙江省复赛试卷

全国初中数学联赛浙江省复赛试卷一、解答题（共5小题，满分100分）1．（20分）已知a2+b2＝1，对于满足条件0≤x≤1的一切实数x，不等式a（1﹣x）（1﹣x ﹣ax）﹣b x（b﹣x﹣b x）≥0（1）恒成立．当乘积ab取最小值时，求a，b的值．2．（20分）如图，圆O与圆D相交于A，B两点，BC为圆D的切线，点C在圆O上，且AB＝BC．（1）证明：点O在圆D的圆周上．（△2）设ABC的面积为S，求圆D的半径R的最小值．3．（20分）设a为质数，b为正整数，且9（2a+b）2＝509（4a+511b）（1）求a，b的值．4．（20分）已知a2+b2＝1，对于满足条件x+y＝1，xy≥0的一切实数对（x．y），不等式ay2﹣xy+b x2≥0（1）恒成立．当乘积ab取最小值时，求a，b的值．5．（20分）设a为质数，b，c为正整数，且满足求a（b+c）的值．全国初中数学联赛浙江省复赛试卷参考答案与试题解析一、解答题（共5小题，满分100分）1．（20分）已知a2+b2＝1，对于满足条件0≤x≤1的一切实数x，不等式a（1﹣x）（1﹣x ﹣ax）﹣b x（b﹣x﹣b x）≥0（1）恒成立．当乘积ab取最小值时，求a，b的值．【分析】由已知条件a2+b2＝1，代入已知不等式重新整理，利用特殊值法确定关于a，b 的不等式，利用二次函数的增减性，确定判别式的取值范围，进而可以解决．【解答】解：整理不等式（1）并将a2+b2＝1代入，得（1+a+b）x2﹣（2a+1）x+a≥0（2）在不等式（2）中，令x＝0，得a≥0；令x＝1，得b≥0．易知1+a+b＞0，0＜＜1，故二次函数y＝（1+a+b）x2﹣（2a+1）x+a的图象（抛物线）的开口向上，且顶点的横坐标在0和1之间．由题设知，不等式（2）对于满足条件0≤x≤1的一切实数x恒成立，所以它的判别式＝（△2a+1）2﹣4（1+a+b）a≤0，即ab≥．由方程组（3）消去b，得16a4﹣16a2+1＝0，所以a2＝又因为a≥0，所以a＝或a＝或a2＝，．于是方程组（3）的解为或，所以ab的最小值为，此时a，b的值有两组，分别为a＝，b＝和a＝，b＝．（【点评】此题主要考查了二次函数与不等式以及二元二次方程的解法，综合性较强，需耐心思考．2．（20 分）如图，圆 O 与圆 D 相交于 A ，B 两点，BC 为圆 D 的切线，点 C 在圆 O 上，且AB ＝BC ．（1）证明：点 O 在圆 D 的圆周上．（△2）设 ABC 的面积为 S ，求圆 D 的半径 R 的最小值．【分析】 1）连 OA ，OB ，OC ，△AC ，可证 OBA ∽△OBC ，即可证明∠OBA ＝∠OBC ，所以 DB ＝DO ，即可证点 O 在圆 D 的圆周上；（2）设圆 O 的半径为 a ，BO 的延长线交 AC 于点 E ，设 AC ＝2y （0＜y ≤△a ）即可求证BDO ∽△ABC ，进而可以 r ，即可求 r 的最小值，即可解题．【解答】解：（1）连 OA ，OB ，OC ，AC ，因为 O 为圆心，AB ＝BC ，所以△OBA ∽△OBC ，从而∠OBA ＝∠OBC ．因为 OD ⊥AB ，DB ⊥BC ，所以∠DOB ＝90°﹣∠OBA ＝90°﹣∠OBC ＝∠DBO ，所以 DB ＝DO ，因此点 O 在圆 D 的圆周上．（2）设圆 O 的半径为 a ，BO 的延长线交 AC 于点 E ，易知 BE ⊥AC ．设 AC ＝2y （0＜y ≤a ），OE ＝x ，AB ＝l ，则 a 2＝x 2+y 2，S ＝y （a +x ），l 2＝y 2+（a +x ）2＝y 2+a 2+2ax +x 2＝2a 2+2ax ＝2a （a +x ）＝因为∠ABC ＝2∠OBA ＝2∠OAB ＝∠BDO ，AB ＝BC ，DB ＝DO ，所以△BDO∽△ABC，所以＝，即，故r＝．所以r2＝＝×＝×≥，即r≥，其中等号当a＝y时成立，这时AC是圆O的直径．所以圆D的半径r的最小值为．【点评】本题考查了相似三角形对应角相等、对应边比值相等的性质，考查了不等式的极值问题，考查了勾股定理在直角三角形中的运用，本题中求点O在圆D的圆周上是解题的关键．3．（20分）设a为质数，b为正整数，且9（2a+b）2＝509（4a+511b）（1）求a，b的值．【分析】首先将9（2a+b）2＝509（4a+511b）变形为＝，此时假设m＝，n＝，则可得到b＝＝与n＝m2．因而可转化为关于m的一元二次方程3m2﹣511m+6a＝0．利用根与系数的关系，求得m的取值进而讨论a、b的取值．【解答】解：①式即＝，故设m＝，n＝，则b＝＝②∴3n﹣511m+6a＝0，又n＝m2，所以3m2﹣511m+6a＝0③由①式可知，（2a+b）2能被509整除，而509是质数，于是2a+b能被509整除，故m 为整数，即关于m的一元二次方程③有整数根，所以它的判别式△＝5112﹣72a为完全平方数．不妨设△＝5112﹣72a＝t2（t为自然数），则72a＝5112﹣t2＝（511+t）（511﹣t）．由于511+t和511﹣t的奇偶性相同，且511+t≥511，所以只可能有以下几种情况：①②③④两式相加，得36a+2＝1022，没有整数解．两式相加，得18a+4＝1022，没有整数解．两式相加，得12a+6＝1022，没有整数解．两式相加，得6a+12＝1022，没有整数解．⑤⑥两式相加，得4a+18＝1022，解得a＝251．两式相加，得2a+36＝1022，解得a＝493，而493＝17×29不是质数，故舍去．综合可知a＝251．此时方程③的解为m＝3或m＝（舍去）．把a＝251，m＝3代入②式，得b＝＝7．答：a＝251，b＝7．【点评】本题考查一元二次方程整数根与有理根、数的整除性问题．解决本题的关键是将问题转化为一元二次方程来解决．4．（20分）已知a2+b2＝1，对于满足条件x+y＝1，xy≥0的一切实数对（x．y），不等式ay2﹣xy+b x2≥0（1）恒成立．当乘积ab取最小值时，求a，b的值．【分析】利用特殊值法可得出a、b的范围，把y＝1﹣x代入不等式，可整理成（1+a+b）x2﹣（2a+1）x+a≥0，再利用二次函数的性质可得到关于a、b的不等式，可求得ab的最小值，结合条件a2+b2＝1，可得到关于a、b的方程组，则可求得a、b的值．【解答】解：∵x+y＝1，xy≥0，∴0≤x≤1，0≤y≤1．在（1）式中，令x＝0，y＝1，得a≥0；令x＝1，y＝0，得b≥0．将y＝1﹣x代入（1）式，得a（1﹣x）2﹣x（1+x）+b x2≥0，即（1+a+b）x2﹣（2a+1）x+a≥0（2），∵a2+b2＝1，∴1+a+b＞0，0＜＜1，∴二次函数y＝（1+a+b）x2﹣（2a+1）x+a的图象（抛物线）的开口向上，且顶点的横坐标在0和1之间．∵不等式（2）对于满足条件0≤x≤1的一切实数x恒成立，∴＝（△2a+1）2﹣4（1+a+b）﹣a≤0，即ab．由方程组（3），消去b，得16a4﹣16a2+1＝0，解得∵a≥0，∴a＝或a＝．∴方程组（3）的解为或或a2＝，∴满足条件的a，b的值有两组，分别为a＝，b＝和a＝，b＝．【点评】本题为二次函数的综合应用，构造二次函数，根据二次函数的性质得到ab≥，从而求得ab的最小值是解题的关键．本题综合性较强，涉及构造的思想，难度较大．5．（20分）设a为质数，b，c为正整数，且满足求a（b+c）的值．【分析】先把（1）式化为完全平方的形式，再把原方程化为关于m、n、a的三元二次方程，再根据n＝m2，此方程化为二元二次方程，由（1）可判断出m为整数，再由一元二次方程的判别式可得5112﹣72a为完全平方数，设5112﹣72a＝t（t为自然数），再把关于t的方程进行因式分解，求出符合条件的a的值代入（2）即可求解．【解答】解：把（1）式化为＝，设m＝2b﹣c＝，n＝＝（3），则故3n﹣511m+6a＝0，又n＝m2，所以3m2﹣511m+6a＝0（4）（5分）由（1）式可知，（2a+2b﹣c）2能被509整除，而509是质数，于是2a+2b﹣c能被509整除，故m为整数，即关于m的一元二次方程（4）有整数根，所以它的判别式＝511△2﹣72a为完全平方数．（10分）不妨设△＝5112﹣72a＝t2（t为自然数），则72a＝5112﹣t2＝（511+t）（511﹣t）．由于511+t和511﹣t的奇偶性相同，且511+t≥511，所以只可能有以下几种情况：①②③④⑤⑥舍去．两式相加，得36a+2＝1022，没有整数解；两式相加，得18a+4＝1022，没有整数解；两式相加，得12a+6＝1022，没有整数解；两式相加，得6a+12＝1022，没有整数解；两式相加，得4a+18＝1022，解得a＝251；两式相加，得2a+36＝1022，解得a＝493，而493＝17×29不是质数，故综合可知a＝251，此时方程（4）的解为m＝3或m＝把a＝251，m＝3代入（3）式，得2b﹣c＝（舍去）．（20分）＝7，即c＝2b﹣7．代入（2）式得b＝（2b﹣7）＝2，所以b＝5，c＝3，因此a（b+c）＝251×（5+3）＝2008．（25分）故答案为：2008．【点评】本题考查的是质数与合数的定义、奇数与偶数、一元二次方程根的判别式，涉及面较广，难度较大．。