2003北美数学建模试题(MCM试题)
北美精算师 exam P 2003 真题

Which of the following represents g?
(A)
15 y for 0 < y < 1 g ( y) = otherwise 0 15 y 2 for x 2 < y < x g ( y) = 2 0 otherwise 15 y 2 for 0 < y < 1 g ( y) = 2 0 otherwise
(A) (B) (C) (D) (E)
0.07 0.29 0.38 0.42 0.57
May 2003
9
Course 1
5.
An insurance company examines its pool of auto insurance customers and gathers the following information:
Course 1
10
Form 03A
6.
Let X and Y be continuous random variables with joint density function
8 xy f ( x, y ) = 3 0
for 0 ≤ x ≤ 1, x ≤ y ≤ 2 x otherwise.
Let X be a continuous random variable with density function
x for − 2 ≤ x ≤ 4 f ( x ) = 10 0 otherwise.
Calculate the expected value of X.
(A)
1 5 3 5
Calculate g′(3).
(A)
−34e −3 −29e −3 −5e −3 −4e −3 63e −3
美赛历年赛题

美赛历年赛题
美国数学建模竞赛(MCM/ICM)自1985年创办以来已有35年的历史,每年都会发布三个模型问题供参赛选手在限定时间内进行研究和解答。
经过不断发展和完善,MCM/ICM成为了世界范围内最具影响力的数学建模竞赛之一。
以下是MCM/ICM历年来的一些典型赛题:
1985年 MCM A题:研究在给定经济情况下,如何规划BMW公司未来的生产计划及车型。
1987年 MCM A题:在地球上一个非常均匀的平面,建立一个小型城市,考虑各种环境因素如何影响城市的设施和功能。
1991年 MCM D题:分析社会上性别和种族歧视。
1997年 MCM C题:分析为什么珊瑚礁的污染问题比林区污染问题显得更为严重。
2002年 MCM A题:研究货轮舱位的装载问题,最大化收益同时保证船上货物负荷均衡。
2006年 MCM A题:建立模型研究地球大气环境中的水循环,探究人类活动对水循环的影响。
2010年 MCM A题:分析美国电力网络的可靠性,研究如何在自然灾害和人为故障的情况下使电力网络正常运作。
2014年 MCM A题:分析对于Fermi问题和经济增长的数学建模,探究经济增长的限制因素和未来发展趋势。
2018年 MCM A题:研究美国国家公园的野生动植物种类和数量变化,确定如何平衡保护野生动植物和国家公园的多个目的。
从这些题目中可以看出,MCM/ICM的竞赛内容涵盖了众多领域,如管理学、环保、气象、物流、生物学等等。
这不仅考验了参赛选手的数学建模水平,更需要他们具备良好的跨学科素养。
正是这种多学科交叉融合的特性,使得MCM/ICM成为了培养未来数学、理工科人才的重要平台之一。
MCM美国大学生数学建模比赛2000-2011年题目

2000 Mathemat ical Contest in ModelingThe ProblemsProblem A: Air traffic ControlProblem B: Radio Channel AssignmentsProblem A Air traffic ControlDedicated to the memory of Dr. Robert Machol, former chief scientist of the Federal Aviation AgencyTo improve safety and reduce air traffic controller workload, the Federal Aviation Agency (FAA) is considering adding software to the air traffic control system that would automatically detect potential aircraft flight path conflicts and alert the controller. To that end, an analyst at the FAA has posed the following problems.Requirement A: Given two airplanes flying in space, when should the air traffic controller consider the objects to be too close and to require intervention?Requirement B: An airspace sector is the section of three-dimensional airspace that one air traffic controller controls. Given any airspace sector, how do we measure how complex it is from an air traffic workload perspective? To what extent is complexity determined by the number of aircraft simultaneously passing through that sector (1) at any one instant? (2) during any given interval of time?(3) during a particular time of day? How does the number of potential conflicts arising during those periods affect complexity?Does the presence of additional software tools to automatically predict conflicts and alert the controller reduce or add to this complexity?In addition to the guidelines for your report, write a summary (no more than two pages) that the FAA analyst can present to Jane Garvey, the FAA Administrator, to defend your conclusions.Problem BRadio Channel AssignmentsWe seek to model the assignment of radio channels to a symmetric network of transmitter locations over a large planar area, so as to avoid interference. One basic approach is to partition the region into regular hexagons in a grid (honeycomb-style), as shown in Figure 1, where a transmitter is located at the center of each hexagon.Figure 1An interval of the frequency spectrum is to be allotted for transmitter frequencies. The interval will be divided into regularly spaced channels, which we represent by integers 1, 2, 3, ... . Each transmitter will be assigned one positive integer channel. The same channel can be used at many locations, provided that interference from nearby transmitters is avoided. Our goal is to minimize the width of the interval in the frequency spectrum that is needed to assign channels subject to some constraints. This is achieved with the concept of a span. The span is the minimum, over all assignments satisfying the constraints, of the largest channel used at any location. It is not required that every channel smaller than the span be used in an assignment that attains the span.Let s be the length of a side of one of the hexagons. We concentrate on the case that there are two levels of interference.Requirement A: There are several constraints on frequency assignments. First, no two transmitters within distance 4s of each other can be given the same channel. Second, due to spectral spreading, transmitters within distance 2s of each other must not be given the same or adjacent channels: Their channels must differ by at least 2. Under these constraints, what can we say about the span in,Requirement B: Repeat Requirement A, assuming the grid in the example spreads arbitrarily far in all directions.Requirement C: Repeat Requirements A and B, except assume now more generally that channels for transmitters within distance 2s differ by at least some given integer k, while those at distance at most 4s must still differ by at least one. What can we say about the span and about efficient strategies for designing assignments, as a function of k?Requirement D: Consider generalizations of the problem, such as several levels of interference or irregular transmitter placements. What other factors may be important to consider?Requirement E: Write an article (no more than 2 pages) for the local newspaper explaining your findings.2001Problem A: Choosing a Bicycle WheelCyclists have different types of wheels they can use on their bicycles. The two basic types of wheels are those constructed using wire spokes and those constructed of a solid dis k (see Figure 1) The spoked wheels are lighter, but the solid wheels are more aerodynamic. A solid wheel is never used on the front for a road race but can be used on the rear of the bike.Professional cyclists look at a racecourse and make an educated guess as to what kind of wheels should be used. The decision is based on the number and steepness of the hills, the weather, wind speed, the competition, and other considerations. The director sportif of your favorite team would like to have a better system in place and has asked your team for information to help determine what kind of wheel should be used for a given course.Figure 1: A solid wheel is shown on the left and a spoked wheel is shown on theright.The director sportif needs specific information to help make a decision and has asked your team to accomplish the tasks listed below. For each of the tasks assume that the same s poked wheel will always be used on the front but there is a choice of wheels for the rear.Task 1. Provide a table giving the wind speed at which the power required for a solid rear wheel is less than for a spoked rear wheel. The table should include the windspeeds for different road grades starting from zero percent to ten percent in onepercent increments. (Road grade is defined to be the ratio of the total rise of a hilldivided by the length of the road. If the hill is viewed as a triangle, the grade is the sine of the angle at the bottom of the hill.) A rider starts at the bottom of the hill at a speed of 45 kph, and the deceleration of the rider is proportional to the road grade. A riderwill lose about 8 kph for a five percent grade over 100 meters.∙Task 2. Provide an example of how the table could be used for a specific time trial course.∙Task 3. Determine if the table is an adequate means for deciding on the wheel configuration and offer other suggestions as to how to make this decision.Problem B: Escaping a Hurricane's Wrath (An Ill Wind...)Evacuating the coast of South Carolina ahead of the predicted landfall of Hurricane Floyd in 1999 led to a monumental traffic jam. Traffic slowed to a standstill on Interstate I-26, which is the principal route going inland from Charleston to the relatively safe haven of Columbia in the center of the state. What is normally an easy two-hour drive took up to 18 hours to complete. Many cars simply ran out of gas along the way. Fortunately, Floyd turned north a nd spared the state this time, but the public outcry is forcing state officials to find ways to avoid a repeat of this traffic nightmare.The principal proposal put forth to deal with this problem is the reversal of traffic on I-26, so that both sides, including the coastal-bound lanes, have traffic headed inland from Charleston to Columbia. Plans to carry this out have been prepared (and posted on the Web) by the South Carolina Emergency Preparedness Division. Traffic reversal on principal roads leading i nland from Myrtle Beach and Hilton Head is also planned.A simplified map of South Carolina is shown. Charleston has approximately 500,000 people, Myrtle Beach has about 200,000 people, and another 250,000 people are spread out along the rest of the coastal strip. (More accurate data, if sought, are widely available.)The interstates have two lanes of traffic in each direction except in the metropolitan areas where they have three. Columbia, another metro area of around 500,000 people, does not have sufficient hotel space to accommodate the evacuees (including some coming from farther north by other routes), so some traffic continues outbound on I-26 towards Spartanburg; on I-77 north to Charlotte; and on I-20 east to Atlanta. In 1999, traffic leaving Columbia going northwest was moving only very slowly. Construct a model for the problem to investigate what strategies may reduce the congestion observed in 1999. Here are the questions that need to be addressed:1.Under what conditions does the plan for turning the two coastal-bound lanes of I-26into two lanes of Columbia-bound traffic, essentially turning the entire I-26 intoone-way traffic, significantly improve evacuation traffic flow?2.In 1999, the simultaneous evacuation of the state's entire coastal region was ordered.Would the evacuation traffic flow improve under an alternative strategy that staggers the evacuation, perhaps county-by-county over some time period consistent with thepattern of how hurricanes affect the coast?3.Several smaller highways besides I-26 extend inland from the coast. Under whatconditions would it improve evacuation flow to turn around traffic on these?4.What effect would it have on evacuation flow to establish more temporary shelters inColumbia, to reduce the traffic leaving Columbia?5.In 1999, many families leaving the coast brought along their boats, campers, andmotor homes. Many drove all of their cars. Under what conditions should there berestrictions on vehicle types or numbers of vehicles brought in order to guaranteetimely evacuation?6.It has been suggested that in 1999 some of the coastal residents of Georgia and Florida,who were fleeing the earlier predicted landfalls of Hurricane Floyd to the south, came up I-95 and compounded the traffic problems. How big an impact can they have on the evacuation traffic flow? Clearly identify what measures of performance are used tocompare strategies. Required: Prepare a short newspaper article, not to exceed twopages, explaining the results and conclusions of your study to the public.Clearly identify what measures of performance are used to compare strategies.Required: Prepare a short newspaper article, not to exceed two pages, explaining the results and conclusions of your study to the public.2002 Mathemat ical Contest in ModelingThe ProblemsProblem AAuthors: Tjalling YpmaTit le: Wind and WatersprayAn ornamental fountain in a large open plaza surrounded by buildings squirts water high into the air. On gusty days, the wind blows spray from the fountain onto passersby. The water-flow from the fountain is controlled by a mechanism linked to an anemometer (which measures wind speed and direction) located on top of an adjacent building. The objective of this control is to provide passersby with an acceptable balance between an attractive spectacle and a soaking: The harder the wind blows, the lower the water volume and height to which the water is squirted, hence the less spray falls outside the pool area.Your task is to devise an algorithm which uses data provided by the anemometer to adjust the water-flow from the fountain as the wind conditions change.Problem BAuthors: Bill Fox and Rich WestTit le: Airline OverbookingYou're all packed and ready to go on a trip to visit your best friend in New York City. After you check in at the ticket counter, the airline clerk announces that your flight has been overbooked. Passengers need to check in immediately to determine if they still have a seat.Historically, airlines know that only a certain percentage of passengers who have made reservations on a particular flight will actually take that flight. Consequently, most airlines overbook-that is, they take more reservations than the capacity of the aircraft. Occasionally, more passengers will want to take a flight than the capacity of the plane leading to one or more passengers being bumped and thus unable to take the flight for which they had reservations.Airlines deal with bumped passengers in various ways. Some are given nothing, some are booked on later flights on other airlines, and some are given some kind of cash or airline ticket incentive.Consider the overbooking issue in light of the current situa tion:Less flights by airlines from point A to point BHeightened security at and around airportsPassengers' fearLoss of billions of dollars in revenue by airlines to dateBuild a mathematical model that examines the effects that different overbooking schemes have on the revenue received by an airline company in order to find an optimal overbooking strategy,i.e., the number of people by which an airline should overbook a particular flight so that the company's revenue is maximized. Insure that your model reflects the issues above, and consider alternatives for handling "bumped" passengers. Additionally, write a short memorandum to the airline's CEO summarizing your findings and analysis.2003 MCM ProblemsPROBLEM A: The Stunt PersonAn exciting action scene in a m ovie is going to be filmed, and you are the stunt coordinator! A stunt person on a m otorcycle will jump over an elephant and land in a pile of cardboard boxes to cushion their fall. You need to protect the stunt person, and also use relatively few cardboard boxes (lower cost, not seen by cam era, etc.).Your job is to:∙determine what size boxes to use∙determine how many boxes to use∙determine how the boxes will be stacked∙determine if any modifications to the boxes would help∙generalize to different combined weights (stunt person & motorcycle) and different jump heightsNote that, in "Tomorrow Never Dies", the Jam es Bond character on a m otorcycle jumps over a helicopter.PROBLEM B: G amma Knife Treat ment PlanningStereotactic radiosurgery delivers a single high dose of ionizing radiation to a radiographically well-defined, sm all intracranial 3D brain tum or without delivering any significant fraction of the prescribed dose to the surrounding brain tissue. Three modalities are commonly used in this area; they are the gamma knife unit, heavy charged particle beam s, and external high-energy photon beams from linear accelerators.The gamma knife unit delivers a single high dose of ionizing radiation emanating from201 cobalt-60 unit sources through a heavy helmet. All 201 beams simultaneously intersect at the isocenter, resulting in a spherical (approximately) dose distribution at the effective dose levels. Irradiating the isocenter to deliver dose is termed a “shot.” Shots can be represented as diff erent spheres. Four interchangeable outer collimator helmets with beam channel diameters of 4, 8, 14,and 18 mm are available for irradiating different size volumes. For a target volum e larger than one shot, m ultiple shots can be used to cover the entire t arget. In practice, m ost target volum es are treated with 1 to 15 shots. The target volum e is a bounded, three-dimensional digital image that usually consists of m illions of points.The goal of radiosurgery is to deplete tum or cells while preserving norma l structures. Since there are physical limitations and biological uncertainties involved in this therapy process, a treatm ent plan needs to account for all those limitations and uncertainties. In general, an optimal treat m ent plan is designed to m eet the following requirements.1.Minimize the dose gradient across the target volume.2.Match specified isodose contours to the target volumes.3.Match specified dose-volume constraints of the target and critical organ.4.Minimize the integral dose to the entire volume of normal tissues or organs.5.Constrain dose to specified normal tissue points below tolerance doses.6.Minimize the maximum dose to critical volumes.In gamma unit treatm ent planning, we have the following constraints:1.Prohibit shots from protruding outside the target.2.Prohibit shots from overlapping (to avoid hot spots).3.Cover the target volume with effective dosage as much as possible. But at least 90% ofthe target volume must be covered by shots.e as few shots as possible.Your tasks are to formulate the optim al treat m ent planning for a gamma knife unit as a sphere-packing problem, and propose an algorithm to find a solution. While designing your algorithm, you must keep in mind that your algorithm must be reasonably efficient.2003 ICM ProblemPROBLEM C:To view and print problem C, you will need to have the Adobe Acrobat Reader installed in your Web browser. Downloading and installing acrobat is simple, safe, and only takes a few minutes. Download Acrobat Here.2004 MCM ProblemsPROBLEM A: Are Fingerprints Unique?It is a commonplace belief that the thumbprint of every human who has ever lived is different. Develop and analyze a model that will allow you to assess the probability that this is true. Compare the odds (that you found in this problem) of misidentification by fingerprint evidence against the odds of misidentification by DNA evidence.PROBLEM B: A Faster QuickPass System"QuickPass" systems are increasingly appearing to reduce people's time waiting in line, whether it is at tollbooths, amusement parks, or elsewhere. Consider the design of a QuickPass system for an amusement park. The amusement park has experimented by offering QuickPasses for several popular rides as a test. The idea is that for certain popular rides you can go to a kiosk near that ride and insert your daily park entrance ticket, and out will come a slip that states that you can return to that ride at a specific time later. For example, you insert your daily park entrance ticket at 1:15 pm, and the QuickPass states that you can come back between 3:30 and 4:30 pm when you can use your slip to enter a second, and presumably much shorter, line that will get you to the ride faster. To prevent people from obtaining QuickPasses for several rides at once, the QuickPass machines allow you to have only one active QuickPass at a time.You have been hired as one of several competing consultants to improve the operation of QuickPass. Customers have been complaining about some anomalies in the test system. For example, customers observed that in one instance QuickPasses were being offered for a return time as long as 4 hours later. A short time later on the same ride, the QuickPasses were given for times only an hour or so later. In some instances, the lines for people with Quickpasses are nearly as long and slow as the regular lines.The problem then is to propose and test schemes for issuing QuickPasses in order to increase people's enjoyment of the amusement park. Part of the problem is to determine what criteria to use in evaluating alternative schemes. Include in your report a non-technical summary for amusement park executives who must choose between alternatives from competing consultants.2005 MCM ProblemsPROBLEM A: Flood PlanningLake Murray in central South Carolina is formed by a large earthen dam, which was completed in1930 for power production. Model the flooding downstream in the event there is a catastrophic earthquake that breaches the dam.Two particular questions:Rawls Creek is a year-round stream that flows into the Saluda River a short distance downriver from the dam. How much flooding will occur in Rawls Creek from a dam failure, and how far back will it extend?Could the flood be so massive downstream that water would reach up to the S.C. State Capitol Building, which is on a hill overlooking the Congaree River?PROBLEM B: TollboothsHeavily-traveled toll roads such as the Garden State Parkway , Interstate 95, and so forth, are multi-lane divided highways that are interrupted at intervals by toll plazas. Because collecting tolls is usually unpopular, it is desirable to minimize motorist annoyance by limiting the amount of traffic disruption caused by the toll plazas. Commonly, a much larger number of tollbooths is provided than the number of travel lanes entering the toll plaza. Upon entering the toll plaza, the flow of vehicles fans out to the larger number of tollbooths, and when leaving the toll plaza, the flow of vehicles is required to squeeze back down to a number of travel lanes equal to the number of travel lanes before the toll plaza. Consequently, when traffic is heavy, congestion increases upon departure from the toll plaza. When traffic is very heavy, congestion also builds at the entry to the toll plaza because of the time required for each vehicle to pay the toll.Make a model to help you determine the optimal number of tollbooths to deploy in a barrier-toll plaza. Explicitly consider the scenario where there is exactly one tollbooth per incoming travel lane. Under what conditions is this more or less effective than the current practice? Note that the definition of "optimal" is up to you to determine.2006 MCM ProblemsPROBLEM A: Posit ioning and Moving Sprinkler Systems for Irrigat ionThere are a wide variety of techniques available for irrigating a field. The technologies range from advanced drip systems to periodic flooding. One of the systems that is used on smaller ranches is the use of "hand move" irrigation systems. Lightweight aluminum pipes with sprinkler heads are put in place across fields, and they are moved by hand at periodic intervals to insure that the whole field receives an adequate amount of water. This type of irrigation sys tem is cheaper and easier to maintain than other systems. It is also flexible, allowing for use on a wide variety of fields and crops. The disadvantage is that it requires a great deal of time and effort to move and set up the equipment at regular intervals.Given that this type of irrigation system is to be used, how can it be configured to minimize the amount of time required to irrigate a field that is 80 meters by 30 meters? For this task you are asked to find an algorithm to determine how to irrigate the rectangular field that minimizes the amount of time required by a rancher to maintain the irrigation system. One pipe set is used in the field. Y ou should determine the number of sprinklers and the spacing between sprinklers, and you should find a sch edule to move the pipes, including where to move them.A pipe set consists of a number of pipes that can be connected together in a straight line. Each pipe has a 10 cm inner diameter with rotating spray nozzles that have a 0.6 cm inner diameter. When pu t together the resulting pipe is 20 meters long. At the water source, the pressure is 420 Kilo- Pascal’s and has a flow rate of 150 liters per minute. No part of the field should receive more than 0.75 cm per hour of water, and each part of the field should receive at least 2 centimeters of water every 4 days. The total amount of water should be applied as uniformly as possiblePROBLEM B: Wheel Chair Access at AirportsOne of the frustrations with air travel is the need to fly through multiple airports, and each stop generally requires each traveler to change to a different airplane. This can be especially difficult for people who are not able to easily walk to a different flight's waiting area. One of the ways that an airline can make the transition easier is to provide a wheel chair and an escort to those people who ask for help. It is generally known well in advance which passengers require help, but it is not uncommon to receive notice when a passenger first registers at the airport. In rare instances an airline may not receive notice from a passenger until just prior to landing.Airlines are under constant pressure to keep their costs down. Wheel chairs wear out and are expensive and require maintenance. There is also a cost for making the escorts available. Moreover, wheel chairs and their escorts must be constantly moved around the airport so that they are available to people when their flight lands. In some large airports the time required to move across the airport is nontrivial. The wheel chairs must be stored somewhere, but space is expensive and severely limited in an airport terminal. Also, wheel chairs left in high traffic areas represent a liability risk as people try to move around them. Finally, one of the biggest costs is the cost of holding a plane if someone must wait for an escort and becomes late for their flight. The latter cost is especially troubling because it can affect the airline's average flight delay which can lead to fewer ticket sales as potential customers may choose to avoid an airline.Epsilon Airlines has decided to ask a third party to help them obtain a detailed analysis of the issues and costs of keeping and maintaining wheel chairs and escorts available for passengers. The airline needs to find a way to schedule the movement of wheel chairs throughout each day in a cost effective way. They also need to find and define the costs for budget planning in both the short and long term.Epsilon Airlines has asked your consultant group to put together a bid to help them solve their problem. Your bid should include an overview and analysis of the situation to help them decide if you fully understand their problem. They require a detailed description of an algorithm that you would like to implement which can determine where the escorts and wheel chairs should be and how they should move throughout each day. The goal is to keep the total costs as low as possible. Your bid is one of many that the airline will consider. You must make a strong case as to why your solution is the best and show that it will be able to handle a wide range of airports under a variety of circumstances.Your bid should also include examples of how the algorithm would work for a large (at least 4 concourses), a medium (at least two concourses), and a small airport (one concourse) under high and low traffic loads. You should determine all potential costs and balance their respective weights. Finally, as populations begin to include a higher percentage of older people who have more time to travel but may require more aid, your report should include projections of potential costs and needs in the future with recommendations to meet future needs.2007 MCM ProblemsPROBLEM A: G errymanderingThe United States Constitution provides that the House of Representatives shall be composed of some number (currently 435) of individuals who are elected from each state in proportion to the state’s population relative to that of the country as a whole. While this provides a way of determining how many representatives each state will have, it says nothing about how the district represented by a particular representative shall be determined geographically. This oversight has led to egregious (at least some people think so, usually not the incumbent) district shapes that look “un natural” by some standards.Hence the following question: Suppose you were given the opportunity to draw congressional districts for a state. How would you do so as a purely “baseline” exercise to create the “simplest” shapes for all the districts in a state? The rules include only that each district in the state must contain the same population. The definition of “simple” is up to you; but you need to make a convincing argument to voters in the state that your solution is fair. As an application of your method, draw geographically simple congressional districts for the state of New Y ork.PROBLEM B: The Airplane Seat ing ProblemAirlines are free to seat passengers waiting to board an aircraft in any order whatsoever. It has become customary to seat passengers with special needs first, followed by first-class passengers (who sit at the front of the plane). Then coach and business-class passengers are seated by groups of rows, beginning with the row at the back of the plane and proceeding forward.Apart from consideration of the passengers’ wait time, from the airline’s point of view, time is money, and boarding time is best minimized. The plane makes money for the airline only when it is in motion, and long boarding times limit the number of trips that a plane can make in a day.The development of larger planes, such as the Airbus A380 (800 passengers), accentuate the problem of minimizing boarding (and deboarding) time.Devise and compare procedures for boarding and deboarding planes with varying numbers of passengers: small (85–210), midsize (210–330), and large (450–800).Prepare an executive summary, not to exceed two single-spaced pages, in which you set out your conclusions to an audience of airline executives, gate agents, and flight crews.Note: The 2 page executive summary is to be included IN ADDITION to the reports required by the contest guidelines.An article appeared in the NY Times Nov 14, 2006 addressing procedures currently being followed and the importance to the airline of finding better solutions. The article can be seen at: http://travel2.nyt /2006/11/14/business/14boarding.ht ml2008 MCM ProblemsPROBLEM A: Take a Bat hConsider the effects on land from the melting of the north polar ice cap due to the predicted increase in global temperatures. Specifically, model the effects on the coast of Florida every ten years for the next 50 years due to the melting, with particular attention given to large metropolitan areas. Propose appropriate responses to deal with this. A careful discussion of the data used is an important part of the answer.PROBLEM B: Creat ing Sudoku PuzzlesDevelop an algorithm to construct Sudoku puzzles of varying difficulty. Develop metrics to define a difficulty level. The algorithm and metrics should be extensible to a varying number of difficulty levels. You should illustrate the algorithm with at least 4 difficulty levels. Your algorithm should guarantee a unique solution. Analyze the complexity of your algorithm. Your objective should be to minimize the complexity of the algorithm and meet the above requirements.2009 MCM Problems。
AMC 美国数学竞赛 2003 AMC 10A 试题及答案解析培训资料

2003 AMC 10A1、What is the difference between the sum of the first even counting numbers and the sum of the first odd counting numbers?SolutionThe first even counting numbers are .The first odd counting numbers are .Thus, the problem is asking for the value of..Alternatively, using the sum of an arithmetic progression formula, we can write .2、Members of the Rockham Soccer League buy socks and T-shirts. Socks cost per pair and each T-shirt costs more than a pair of socks. Each member needs one pair of socks and a shirt for home games and another pair of socks and a shirt for away games. If the total cost is , how many members are in the League?SolutionSince T-shirts cost dollars more than a pair of socks, T-shirts cost dollars.Since each member needs pairs of socks and T-shirts, the total cost for member is dollars.Since dollars was the cost for the club, and was the cost per member, the number of members in the League is .3、A solid box is cm by cm by cm. A new solid is formed by removing a cube cm on a side from each corner of this box. What percent of the original volume is removed?SolutionThe volume of the original box isThe volume of each cube that is removed isSince there are corners on the box, cubes are removed.So the total volume removed is .Therefore, the desired percentage is .4、It takes Mary minutes to walk uphill km from her home to school, but it takes her only minutes to walk from school to home along the same route. What is her average speed, in km/hr, for the round trip?SolutionSince she walked km to school and km back home, her total distance is km.Since she spent minutes walking to school and minutes walking back home, her total time is minutes = hours.Therefore her average speed in km/hr is5、Let and denote the solutions of . What is the value of ?SolutionUsing factoring:orSo and are and .Therefore the answer isOR we can use sum and product.6、Define to be for all real numbers and . Which of the following statements is not true?SolutionExamining statement C:when , but statement C says that it does for all . Therefore the statement that is not true is "for all " Alternatively, consider that the given "heart function" is actually the definition of the distance between two points. Examining all of the statements, only C is not necessarily true; if c is negative, the distance between and is the absolute value of , not itself, because distance is always nonnegative.7、How many non-congruent triangles with perimeter have integer side lengths?SolutionBy the triangle inequality, no one side may have a length greater than half the perimeter, which isSince all sides must be integers, the largest possible length of a side isTherefore, all such triangles must have all sides of length , , or . Since , at least one side must have a length of Thus, the remaining two sides have a combined length of . So, the remaining sides must be either and or and . Therefore, the number of triangles is .8、What is the probability that a randomly drawn positive factor ofis lessthan ?SolutionFor a positive number which is not a perfect square, exactly half of the positive factors will be less than .Since is not a perfect square, half of the positive factors of will be less than .Clearly, there are no positive factors of between and . Therefore half of the positive factors will be less than .So the answer is .9、SimplifySolution.Therefore:10、The polygon enclosed by the solid lines in the figure consists of congruent squares joined edge-to-edge. One more congruent square is attached to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing?SolutionLet the squares be labeled , , , and .When the polygon is folded, the "right" edge of square becomes adjacent to the "bottom edge" of square , and the "bottom" edge of square becomes adjacent to the "bottom" edge of square .So, any "new" square that is attached to those edges will prevent the polygon from becoming a cube with one face missing.Therefore, squares , , and will prevent the polygon from becoming a cube with one face missing.Squares , , , , , and will allow the polygon to become a cube with one face missing when folded.Thus the answer is .Another way to think of it is that a cube missing one face has of it's faces. Since the shape has faces already, we need another face. The only way to add anopther face is if the added square does not overlap any of the others. ,, and overlap, while 9 do not. The answer is11、The sum of the two -digit numbers and is . What is ?SolutionSince , , and are digits, , , .Therefore, .12、A point is randomly picked from inside the rectangle withvertices , , , and . What is the probability that ?SolutionThe rectangle has a width of and a height of .The area of this rectangle is .The line intersects the rectangle at and .The area which is the right isosceles triangle with side length that has vertices at , , and .The area of this triangle isTherefore, the probability that is13、The sum of three numbers is . The first is times the sum of the other two. The second is seven times the third. What is the product of all three?SolutionSolution 1Let the numbers be , , and in that order. The given tells us thatTherefore, the product of all three numbers is.Solution 2Alternatively, we can set up the system in matrix form:Or, in matrix formTo solve this matrix equation, we can rearrange it thus:Solving this matrix equation by using inverse matrices and matrix multiplication yieldsWhich means that , , and . Therefore,14、Let be the largest integer that is the product of exactly distinct prime numbers, , , and , where and are single digits. What is the sum of the digits of ?SolutionSince is a single digit prime number, the set of possible values of is .Since is a single digit prime number and is the units digit of the prime number , the set of possible values of is .Using these values for and , the set of possible values of isOut of this set, the prime values areTherefore the possible values of are:The largest possible value of is .So, the sum of the digits of is15、What is the probability that an integer in the set is divisible by and not divisible by ?SolutionThere are integers in the set.Since every 2nd integer is divisible by , there are integers divisible by in the set.To be divisible by both and , a number must be divisible by .Since every 6th integer is divisible by , there are integers divisible by both and in the set.So there are integers in this set that are divisible by and not divisible by .Therefore, the desired probability is16、What is the units digit of ?SolutionSince :Therefore, the units digit is17、The number of inches in the perimeter of an equilateral triangle equals the number of square inches in the area of its circumscribed circle. What is the radius, in inches, of the circle?SolutionLet be the length of a side of the equilateral triangle and let be the radius of the circle.In a circle with a radius the side of an inscribed equilateral triangle is .So .The perimeter of the triangle isThe area of the circle isSo:18、What is the sum of the reciprocals of the roots of the equationSolutionMultiplying both sides by :Let the roots be and .The problem is asking forBy Vieta's formulas:So the answer is .19、A semicircle of diameter sits at the top of a semicircle of diameter , as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.SolutionThe shaded area is equal to the area of the smaller semicircle minus the area of a sector of the larger circle plus the area of a triangle formed by two radii of the larger semicircle and the diameter of the smaller semicircle.The area of the smaller semicircle is .Since the radius of the larger semicircle is equal to the diameter of the smaller semicircle, the triangle is an equilateral triangle and the sector measures .The area of the sector of the larger semicircle is . The area of the triangle isSo the shaded area is20、A base-three-digit number is selected at random. Which of the following is closest to the probability that the base-representation and the base-representation of are both three-digit numerals?SolutionTo be a three digit number in base-10:Thus there are three-digit numbers in base-10To be a three-digit number in base-9:To be a three-digit number in base-11:So,Thus, there are base-10 three-digit numbers that are three digit numbers in base-9 and base-11.Therefore the desired probability is .21、Pat is to select six cookies from a tray containing only chocolate chip, oatmeal, and peanut butter cookies. There are at least six of each of these three kinds of cookies on the tray. How many different assortments of six cookies can be selected?SolutionSolution 1Let the ordered triplet represent the assortment of chocolate chip cookies, oatmeal cookies, and peanut butter cookies.Using casework:Pat selects chocolate chip cookies:Pat needs to select more cookies that are either oatmeal or peanut butter.The assortments are:assortments.Pat selects chocolate chip cookie:Pat needs to select more cookies that are either oatmeal or peanut butter.The assortments are:assortments.Pat selects chocolate chip cookies:Pat needs to select more cookies that are either oatmeal or peanut butter.The assortments are:assortments.Pat selects chocolate chip cookies:Pat needs to select more cookies that are either oatmeal or peanut butter.The assortments are:assortments.Pat selects chocolate chip cookies:Pat needs to select more cookies that are either oatmeal or peanut butter.The assortments are: assortments.Pat selects chocolate chip cookies:Pat needs to select more cookies that are either oatmeal or peanut butter.The assortments are: assortments.Pat selects chocolate chip cookies:Pat needs to select more cookies that are either oatmeal or peanut butter.The only assortment is: assortment.The total number of assortments of cookies that can be collected isSolution 2It is given that it is possible to select at least 6 of each. Therefore, we can make a bijection to the number of ways to divide the six choices into three categories, since it is assumed that their order is unimportant. Using the ball and urns formula, the number of ways to do this is22、In rectangle , we have , , is on with, is on with , line intersects line at , and is on line with . Find the length .SolutionS olution 1(Opposite angles are equal).(Both are 90 degrees).(Alt. Interior Angles are congruent).Therefore and are similar. and are also similar.is 9, therefore must equal 5. Similarly, must equal 3. Because and are similar, the ratio of and , must also hold true for and . , so is of . By Pythagorean theorem, ..So ..Therefore .Solution 2Since is a rectangle, .Since is a rectangle and ,.Since is a rectangle, .So, is a transversal, and .This is sufficient to prove that and .Using ratios:Since can't have 2 different lengths, both expressions for must be equal.Solution 3Since is a rectangle, , , and . From the Pythagorean Theorem, .LemmaStatement:Proof: , obviously.Since two angles of the triangles are equal, the third angles must equal each other. Therefore, the triangles are similar.Let .Also, , thereforeWe can multiply both sides by to get that is twice of 10, orSolution 4We extend BC such that it intersects GF at X. Since ABCD is a rectangle, it follows that CD=8, therefore, XF=8. Let GX=y. From the similarity of triangles GCH and GEA, we have the ratio 3:5 (as CH=9-6=3, and EA=9-4=5). GX and GF are the altitudes of GCH andGEA, respectively. Thus, y:y+8 = 3:5, from which we have y=12, thus GF=y+8=12+8=20. B.23、A large equilateral triangle is constructed by using toothpicks to create rows of small equilateral tr iangles. For example, in the figure we have rows of small congruent equilateral triangles, with small triangles in the base row. How many toothpicks would be needed to construct a large equilateral triangle if the base row of the triangle consists of small equilateral triangles?SolutionSolution 1There are small equilateral triangles.Each small equilateral triangle needs toothpicks to make it.But, each toothpick that isn't one of the toothpicks on the outside of the large equilateral triangle is a side for small equilateral triangles.So, the number of toothpicks on the inside of the large equilateral triangle isTherefore the total number of toothpicks isSolution 2We see that the bottom row of small triangles is formed from downward-facing triangles and upward-facing triangles. Since each downward-facing triangle uses three distinct toothpicks, andsince the total number of downward-facing triangles is, we have that the total number of toothpicks is24、Sally has five red cards numbered through and four blue cards numbered through . She stacks the cards so that the colors alternate and so that the number on each red card divides evenly into the number on each neighboring blue card. What is the sum of the numbers on the middle three cards?SolutionLet and designate the red card numbered and the blue card numbered , respectively.is the only blue card that evenly divides, so must be at one end of the stack and must be the card next to it.is the only other red card that evenly divides , so must be the other card next to .is the only blue card that evenly divides, so must be at the other end of the stack and must be the card next to it.is the only other red card that evenly divides , so must be the other card next to .doesn't evenly divide , so must be next to , must be next to , and must be in the middle.This yields the following arrangement from top to bottom:Therefore, the sum of the numbers on the middle three cards is.25、Let be a -digit number, and let and be the quotient and remainder, respectively, when is divided by . For how many values of is divisible by ?SolutionSolution 1When a -digit number is divided by , the first digits become the quotient, , and the last digits become the remainder, .Therefore, can be any integer from to inclusive, and can be any integer from to inclusive.For each of the possible values of , there are at least possible values of such that .Since there is "extra" possible value of that is congruent to , each of the values of that are congruent tohave more possible value of such that .Therefore, the number of possible values of such that is .Solution 2Let equal , where through are digits. Therefore,We now take :The divisor trick for 11 is as follows:"Let be an digit integer. Ifis divisible by , then is also divisible by ."Therefore, the five digit number is divisible by 11. The 5-digit multiples of 11 range from to . There aredivisors of 11 between those inclusive.学习资料Solution 3Since q is a quotient and r is a remainder when n is divided by 100. So we have . Since we are counting choices where q+r is divisible by 11, we have for some k. This means that n is the sum of two multiples of 11 and would thus itself be a divisor of 11. Then we can count all the four digit divisors of 11 as in Solution 2. (This solution is essentially the same as solution 2, but it does not necessarily involve mods and so could potentially be faster.)NotesThe part labeled "divisor trick" actually follows from the same observation we made in the previous step: , therefore and for all . For a digit numberwe get, as claimed.Also note that in the "divisor trick" we actually want to assign the signs backwards - if we make sure that the last sign is a , the result will have the same remainder modulo as the original number.精品文档。
AMC 美国数学竞赛 2003 AMC 10B 试题及答案解析

2003 AMC 10B1、Which of the following is the same asSolution2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pills cost a total of for the two weeks. How much does one green pill cost?Solution3、The sum of 5 consecutive even integers is less than the sum of the first consecutive odd counting numbers. What is the smallest of the even integers?Solution4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the figure. She plants one flower per square foot in each region. Asters cost 1 each, begonias 1.50 each, cannas 2 each, dahlias 2.50 each, and Easter lilies 3 each. What is the least possible cost, in dollars, for her garden? Solution5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches to make sure that no grass is missed. He walks at the rate offeet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?Solution.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen is closest, in inches, to which of the following?Solution7、The symbolism denotes the largest integer not exceeding . For example. , and . ComputeSolution.8、The second and fourth terms of a geometric sequence are and . Which of the following is a possible first term?Solution9、Find the value of that satisfies the equationSolution10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased? Solution11、A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two lines?Solution12、Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al’s original portion?Solution.13、Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of is ?Solution14、Given that , where both and are positive integers, find the smallest possible value for .Solution15、There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played isSolution16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year ?Solution.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly fill the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radius?Solution18、What is the largest integer that is a divisor offor all positive even integers ?Solution19、Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?Solution20、In rectangle , and . Points and are onso that and . Lines and intersect at . Find the area of .Solution21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?Solution22、A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , , on what date will the chime occur?Solution23、A regular octagon has an area of one square unit. What is the area of the rectangle ?Solution24、The first four terms in an arithmetic sequence are , , , and , in that order. What is the fifth term?Solution25、How many distinct four-digit numbers are divisible by and have as their last two digits?Solution。
美赛历年题目_pdf

马剑整理历年美国大学生数学建模赛题目录MCM85问题-A 动物群体的管理 (3)MCM85问题-B 战购物资储备的管理 (3)MCM86问题-A 水道测量数据 (4)MCM86问题-B 应急设施的位置 (4)MCM87问题-A 盐的存贮 (5)MCM87问题-B 停车场 (5)MCM88问题-A 确定毒品走私船的位置 (5)MCM88问题-B 两辆铁路平板车的装货问题 (6)MCM89问题-A 蠓的分类 (6)MCM89问题-B 飞机排队 (6)MCM90-A 药物在脑内的分布 (6)MCM90问题-B 扫雪问题 (7)MCM91问题-B 通讯网络的极小生成树 (7)MCM 91问题-A 估计水塔的水流量 (7)MCM92问题-A 空中交通控制雷达的功率问题 (7)MCM 92问题-B 应急电力修复系统的修复计划 (7)MCM93问题-A 加速餐厅剩菜堆肥的生成 (8)MCM93问题-B 倒煤台的操作方案 (8)MCM94问题-A 住宅的保温 (9)MCM 94问题-B 计算机网络的最短传输时间 (9)MCM-95问题-A 单一螺旋线 (10)MCM95题-B A1uacha Balaclava学院 (10)MCM96问题-A 噪音场中潜艇的探测 (11)MCM96问题-B 竞赛评判问题 (11)MCM97问题-A Velociraptor(疾走龙属)问题 (11)MCM97问题-B为取得富有成果的讨论怎样搭配与会成员 (12)MCM98问题-A 磁共振成像扫描仪 (12)MCM98问题-B 成绩给分的通胀 (13)MCM99问题-A 大碰撞 (13)MCM99问题-B “非法”聚会 (14)MCM2000问题-A空间交通管制 (14)MCM2000问题-B: 无线电信道分配 (14)MCM2001问题- A: 选择自行车车轮 (15)MCM2001问题-B 逃避飓风怒吼(一场恶风...) .. (15)MCM2001问题-C我们的水系-不确定的前景 (16)MCM2002问题-A风和喷水池 (16)MCM2002问题-B航空公司超员订票 (16)MCM2002问题-C (16)MCM2003问题-A: 特技演员 (18)MCM2003问题-B: Gamma刀治疗方案 (18)MCM2003问题-C航空行李的扫描对策 (19)MCM2004问题-A:指纹是独一无二的吗? (19)MCM2004问题-B:更快的快通系统 (19)MCM2004问题-C安全与否? (19)MCM2005问题A.水灾计划 (19)MCM2005B.Tollbooths (19)MCM2005问题C:不可再生的资源 (20)MCM2006问题A: 用于灌溉的自动洒水器的安置和移动调度 (20)MCM2006问题B: 通过机场的轮椅 (20)MCM2006问题C : 抗击艾滋病的协调 (21)MCM2007问题B :飞机就座问题 (24)MCM2007问题C:器官移植:肾交换问题 (24)MCM2008问题A:给大陆洗个澡 (28)MCM2008问题B:建立数独拼图游戏 (28)MCM85问题-A 动物群体的管理在一个资源有限,即有限的食物、空间、水等等的环境里发现天然存在的动物群体。
历年美国大学生数学建模竞赛试题MCM.(翻译版)doc

1985 年美国大学生数学建模竞赛MCM 试题1985年MCM:动物种群选择合适的鱼类和哺乳动物数据准确模型。
模型动物的自然表达人口水平与环境相互作用的不同群体的环境的重要参数,然后调整账户获取表单模型符合实际的动物提取的方法。
包括任何食物或限制以外的空间限制,得到数据的支持。
考虑所涉及的各种数量的价值,收获数量和人口规模本身,为了设计一个数字量代表的整体价值收获。
找到一个收集政策的人口规模和时间优化的价值收获在很长一段时间。
检查政策优化价值在现实的环境条件。
1985年MCM B:战略储备管理钴、不产生在美国,许多行业至关重要。
(国防占17%的钴生产。
1979年)钴大部分来自非洲中部,一个政治上不稳定的地区。
1946年的战略和关键材料储备法案需要钴储备,将美国政府通过一项为期三年的战争。
建立了库存在1950年代,出售大部分在1970年代初,然后决定在1970年代末建立起来,与8540万磅。
大约一半的库存目标的储备已经在1982年收购了。
建立一个数学模型来管理储备的战略金属钴。
你需要考虑这样的问题:库存应该有多大?以什么速度应该被收购?一个合理的代价是什么金属?你也要考虑这样的问题:什么时候库存应该画下来吗?以什么速度应该是画下来吗?在金属价格是合理出售什么?它应该如何分配?有用的信息在钴政府计划在2500万年需要2500万磅的钴。
美国大约有1亿磅的钴矿床。
生产变得经济可行当价格达到22美元/磅(如发生在1981年)。
要花四年滚动操作,和thsn六百万英镑每年可以生产。
1980年,120万磅的钴回收,总消费的7%。
1986 年美国大学生数学建模竞赛MCM 试题1986年MCM A:水文数据下表给出了Z的水深度尺表面点的直角坐标X,Y在码(14数据点表省略)。
深度测量在退潮。
你的船有一个五英尺的草案。
你应该避免什么地区内的矩形(75200)X(-50、150)?1986年MCM B:Emergency-Facilities位置迄今为止,力拓的乡牧场没有自己的应急设施。
历届美国数学建模竞赛赛题

? 对正常组织或器官的整个体积照射要剂量总和最小
对指定的正常组织点的剂量要限制在忍耐剂量以下?
使关键体积所需的最大剂量达到最小?
在Gamma单元治疗方案中,有以下限制:
禁止“shot”伸展到目标以外?
禁止“shot”交迭(避免热点)?
? 用有效的剂量覆盖尽可能多的目标体积,但至少90%目标体积要被“shot”覆盖
你的任务是设计一个算法,随着风力条件的变化,运用风速计给出的数据来调整由喷泉射出的水流。
AMCM2002问题-B航空公司超员订票
你备好行装准备去旅行,访问New York城的一位挚友。在检票处登记之后,航空公司职员告诉说,你的航班已经超员订票。乘客们应当马上登记以便确定他们是否还有一个座位。
任务1. 提供一个给出风速的表格,在这种速度下实体后轮所需要的体能少于辐条后轮。这个表格应当包括相应于从百分之零到百分之十增量为百分之一的不同公路陡度的风速。(公路陡度定义为一座山丘的总升高除以公路长度。如果把山丘看作一个三角形,它的陡度是指山脚处倾角的正弦。)一位骑手以初始速度45kph从山脚出发,他的减速度与公路陡度成正比。对于百分之五的陡度,骑上100米车速要下降8kph左右。
2005A.水灾计划
南卡罗来纳州中部的磨累河是由北部的一个巨大水坝形成的,这是在1930年为了发电而修建的,模拟一起洪水淹没下游的事件,这起事件是由于一次灾难性的地震损毁了水坝造成的。
两个问题:
Rawls Creek是水坝下游流入Saluda河的一条终年流动的河流,则当水坝损毁后在Rawls Creek将会出现多大的洪流,洪水的波及面将有多大?
AMCM2002问题-A风和喷水池
在一个楼群环绕的宽阔的露天广场上,装饰喷泉把水喷向高空。刮风的日子,风把水花从喷泉吹向过路行人。喷泉射出的水流受到一个与风速计(用于测量风的速度和方向)相连的机械装置控制,前者安装在一幢邻近楼房的顶上。这个控制的实际目标,是要为行人在赏心悦目的景象和淋水浸湿之间提供可以接受的平衡:风刮得越猛,水量和喷射高度就越低,从而较少的水花落在水池范围以外。
2003年5月北美精算第四门考试试题

Course 4Fall 2003 Society of Actuaries**BEGINNING OF EXAMINATION** 1. You are given the following information about a stationary AR(2) model:=.(i) ρ105(ii) ρ201=.Determine φ2.(A) –0.2(B) 0.1(C) 0.4(D) 0.7(E) 1.0(i) Losses follow a loglogistic distribution with cumulative distribution function:F x x x b g b g b g =+//θθγγ1(ii)The sample of losses is:10 35 80 86 90 120 158 180 200 210 1500Calculate the estimate of θ by percentile matching, using the 40th and 80th empirically smoothed percentile estimates.(A) Less than 77(B) At least 77, but less than 87(C) At least 87, but less than 97(D) At least 97, but less than 107(E) At least 107(i) The number of claims has a Poisson distribution.(ii) Claim sizes have a Pareto distribution with parameters θ=0.5 and α=6.(iii) The number of claims and claim sizes are independent.(iv) The observed pure premium should be within 2% of the expected pure premium 90% of the time.Determine the expected number of claims needed for full credibility.(A) Less than 7,000(B) At least 7,000, but less than 10,000(C) At least 10,000, but less than 13,000(D) At least 13,000, but less than 16,000(E) At least 16,0004. You study five lives to estimate the time from the onset of a disease to death. The times todeath are:2 3 3 3 7Using a triangular kernel with bandwidth 2, estimate the density function at 2.5.(A) 8/40(B) 12/40(C) 14/40(D) 16/40(E) 17/405. For the model i i i Y X αβε=++, where 1,2,...,10i =, you are given:(i) X i i =R S T1, if the th individual belongs to a specified group 0, otherwise(ii) 40 percent of the individuals belong to the specified group.(iii) The least squares estimate of β is β=4.(iv) ()2ˆˆ92i i Y X αβ−−=∑Calculate the t statistic for testing H 00:β=.(A) 0.9(B) 1.2(C) 1.5(D) 1.8(E) 2.1(i) Losses follow a Single-parameter Pareto distribution with density function:()()1,1f x x xαα+=>, 0 < α < ∞ (ii) A random sample of size five produced three losses with values 3, 6 and 14, and twolosses exceeding 25.Determine the maximum likelihood estimate of α.(A) 0.25(B) 0.30(C) 0.34(D) 0.38(E) 0.42(i) The annual number of claims for a policyholder has a binomial distribution withprobability function:()()221x x p x q q q x −⎛⎞=−⎜⎟⎝⎠, x = 0, 1, 2(ii) The prior distribution is:()34,01q q q π=<<This policyholder had one claim in each of Years 1 and 2.Determine the Bayesian estimate of the number of claims in Year 3.(A) Less than 1.1(B) At least 1.1, but less than 1.3(C) At least 1.3, but less than 1.5(D) At least 1.5, but less than 1.7(E) At least 1.78. For a sample of dental claims 1210,,...,x x x , you are given:(i) 23860 and 4,574,802i i x x ==∑∑(ii) Claims are assumed to follow a lognormal distribution with parameters µ and σ.(iii)µ and σ are estimated using the method of moments.Calculate ∧ for the fitted distribution.(A) Less than 125(B) At least 125, but less than 175(C) At least 175, but less than 225(D) At least 225, but less than 275(E) At least 2759. You are given:(i)Y tij is the loss for the j th insured in the i th group in Year t . (ii)ti Y is the mean loss in the i th group in Year t . (iii)X j i j i ij =R S T0, if the th insured is in the first group (=1)1, if the th insured is in the second group (=2) (iv)21ij ij ij ij Y Y X δφθε=+++, where 1,2i = and 1,2,...,j n = (v)Y Y Y Y 2122111230374041====,,, (vi) ˆ0.75φ=Determine the least-squares estimate of θ.(A) 5.25(B) 5.50(C) 5.75(D) 6.00(E) 6.2510. Two independent samples are combined yielding the following ranks:Sample I: 1, 2, 3, 4, 7, 9, 13, 19, 20Sample II: 5, 6, 8, 10, 11, 12, 14, 15, 16, 17, 18You test the null hypothesis that the two samples are from the same continuous distribution.The variance of the rank sum statistic is:()112n m n m ++Using the classical approximation for the two-tailed rank sum test, determine the p -value.(A) 0.015(B) 0.021(C) 0.105(D) 0.210(E) 0.420(i) Claim counts follow a Poisson distribution with mean θ. (ii) Claim sizes follow an exponential distribution with mean 10θ. (iii) Claim counts and claim sizes are independent, given θ. (iv) The prior distribution has probability density function:b g=5, θ>1πθθCalculate Bühlmann’s k for aggregate losses.(A) Less than 1(B) At least 1, but less than 2(C) At least 2, but less than 3(D) At least 3, but less than 4(E) At least 4(i) A survival study uses a Cox proportional hazards model with covariates Z 1 and Z 2,each taking the value 0 or 1.(ii) The maximum partial likelihood estimate of the coefficient vector is:, .,.ββ12071020e j b g=(iii) The baseline survival function at time t 0 is estimated as .S t 0065b g =.Estimate S t 0b gfor a subject with covariate values 121Z Z ==.(A) 0.34(B) 0.49(C) 0.65(D) 0.74(E) 0.84(i) Z 1 and Z 2 are independent N(0,1) random variables.(ii) a , b , c , d , e , f are constants.(iii) Y a bZ cZ X d eZ f Z =++=++1212 andDetermine ()E Y X .(A) a(B) ()()a b c X d ++−(C) a be cf X d ++−b gb g(D) a be cf e f +++g d /22(E) a be cf e f X d +++−g d g/22(i) Losses on a company’s insurance policies follow a Pareto distribution with probabilitydensity function:()(),0f x x x θθθ=<<∞+(ii) For half of the company’s policies θ=1, while for the other half θ=3.For a randomly selected policy, losses in Year 1 were 5.Determine the posterior probability that losses for this policy in Year 2 will exceed 8.(A) 0.11(B) 0.15(C) 0.19(D) 0.21(E) 0.2715. You are given total claims for two policyholders:Year1 2 3 4PolicyholderX 730 800 650 700Y 655 650 625 750Using the nonparametric empirical Bayes method, determine the Bühlmann credibilitypremium for Policyholder Y.(A) 655(B) 670(C) 687(D) 703(E) 71916. A particular line of business has three types of claims. The historical probability and thenumber of claims for each type in the current year are:Type HistoricalProbabilityNumber of Claimsin Current YearA 0.2744 112B 0.3512 180C 0.3744 138You test the null hypothesis that the probability of each type of claim in the current year is the same as the historical probability.Calculate the chi-square goodness-of-fit test statistic.(A) Less than 9(B) At least 9, but less than 10(C) At least 10, but less than 11(D) At least 11, but less than 12(E) At least 1217. Which of the following is false?(A) If the characteristics of a stochastic process change over time, then the process isnonstationary.(B) Representing a nonstationary time series by a simple algebraic model is often difficult.(C) Differences of a homogeneous nonstationary time series will always be nonstationary.(D) If a time series is stationary, then its mean, variance and, for any lag k, covariancemust also be stationary.(E) If the autocorrelation function for a time series is zero (or close to zero) for all lagsk>0, then no model can provide useful minimum mean-square-error forecasts offuture values other than the mean.18. The information associated with the maximum likelihood estimator of a parameter θ is 4n,where n is the number of observations.Calculate the asymptotic variance of the maximum likelihood estimator of 2θ.(A) 12n(B) 1n(C) 4n(D) 8n(E) 16n19. You are given:(i) The probability that an insured will have at least one loss during any year is p.(ii) The prior distribution for p is uniform on []0,0.5.(iii) An insured is observed for 8 years and has at least one loss every year.Determine the posterior probability that the insured will have at least one loss during Year 9.(A) 0.450(B) 0.475(C) 0.500(D) 0.550(E) 0.62520. At the beginning of each of the past 5 years, an actuary has forecast the annual claims for agroup of insureds. The table below shows the forecasts (X) and the actual claims (Y). Atwo-variable linear regression model is used to analyze the data.t X t Y t1 475 2542 254 4633 463 5154 515 5675 567 605You are given:(i) The null hypothesis is0:0,1Hαβ==.(ii) The unrestricted model fit yields ESS = 69,843.Which of the following is true regarding the F test of the null hypothesis?(A) The null hypothesis is not rejected at the 0.05 significance level.(B) The null hypothesis is rejected at the 0.05 significance level, but not at the 0.01 level.(C) The numerator has 3 degrees of freedom.(D) The denominator has 2 degrees of freedom.(E) TheF statistic cannot be determined from the information given.21-22. Use the following information for questions 21 and 22.For a survival study with censored and truncated data, you are given:Time (t) Number at Riskat Time t Failures at Time t1 30 52 27 93 32 64 25 55 20 4 21. The probability of failing at or before Time 4, given survival past Time 1, is31q.Calculate Greenwood’s approximation of the variance of 31 q.(A) 0.0067(B) 0.0073(C) 0.0080(D) 0.0091(E) 0.010521-22. (Repeated for convenience) Use the following information for questions 21 and 22.For a survival study with censored and truncated data, you are given:Time (t) Number at Riskat Time t Failures at Time t1 30 52 27 93 32 64 25 55 20 4 22. Calculate the 95% log-transformed confidence interval for H3b g, based on the Nelson-Aalenestimate.(A) (0.30,0.89)(B) (0.31,1.54)(C) (0.39,0.99)(D) (0.44,1.07)(E) (0.56,0.79)(i) Two risks have the following severity distributions:Amount of Claim Probability of ClaimAmount for Risk 1Probability of ClaimAmount for Risk 2250 0.5 0.72,500 0.3 0.260,000 0.2 0.1(ii) Risk 1 is twice as likely to be observed as Risk 2.A claim of 250 is observed.Determine the Bühlmann credibility estimate of the second claim amount from the same risk.(A) Less than 10,200(B) At least 10,200, but less than 10,400(C) At least 10,400, but less than 10,600(D) At least 10,600, but less than 10,800(E) At least 10,800(i) A sample x x x 1210,,,… is drawn from a distribution with probability density function:1211exp()exp(), 0[]x x x θθσσ−+−<<∞(ii)θσ>(iii) x x i i ==∑∑15050002 andEstimate θ by matching the first two sample moments to the corresponding population quantities.(A) 9(B) 10(C) 15(D) 20(E) 2125. You are given the following time-series model:115.028.0−−−++=t t t t y y εεWhich of the following statements about this model is false?(A) 10.4ρ=(B) 1,2,3,4,....k k ρρ<=(C) The model is ARMA(1,1).(D) The model is stationary.(E) The mean, µ, is 2.26. You are given a sample of two values, 5 and 9.You estimate Var(X ) using the estimator g (X 1, X 2) = 21().2i X X −∑Determine the bootstrap approximation to the mean square error of g .(A) 1(B) 2(C) 4(D) 8(E) 1627. You are given:(i) The number of claims incurred in a month by any insured has a Poisson distributionwith mean λ.(ii) The claim frequencies of different insureds are independent.(iii) The prior distribution is gamma with probability density function:()()6100100120efλλλλ−=(iv) Month Number of Insureds NumberofClaims1 100 62 150 83 200 114 300 ?Determine the Bühlmann-Straub credibility estimate of the number of claims in Month 4.(A) 16.7(B) 16.9(C) 17.3(D) 17.6(E) 18.028. You fit a Pareto distribution to a sample of 200 claim amounts and use the likelihood ratio testto test the hypothesis that 1.5α= and 7.8θ=.You are given:(i) The maximum likelihood estimates are α= 1.4 and θ = 7.6.(ii) The natural logarithm of the likelihood function evaluated at the maximum likelihoodestimates is −817.92.(iii) ()ln 7.8607.64i x +=∑Determine the result of the test.(A) Reject at the 0.005 significance level.(B) Reject at the 0.010 significance level, but not at the 0.005 level.(C) Reject at the 0.025 significance level, but not at the 0.010 level.(D) Reject at the 0.050 significance level, but not at the 0.025 level.(E) Do not reject at the 0.050 significance level.29. You are given:(i) The model is Y X i i i =+βε, i = 1, 2, 3.(ii)i X i Var εi b g11 12 2 93 316 (iii)The ordinary least squares residuals are εβi i i Y X =−, i = 1, 2, 3.Determine E X X X ,,ε12123d i.(A) 1.0(B) 1.8(C) 2.7(D) 3.7(E) 7.630. For a sample of 15 losses, you are given:(i)Interval Observed Number ofLosses(0, 2] 5(2, 5] 5(5, ∞) 5 (ii) Losses follow the uniform distribution on 0,θb g.Estimate θ by minimizing the function()231j jjjE OO=−∑, where j E is the expected number oflosses in the j th interval andjO is the observed number of losses in the j th interval.(A) 6.0(B) 6.4(C) 6.8(D) 7.2(E) 7.631. You are given:(i) The probability that an insured will have exactly one claim is θ.(ii) The prior distribution of θ has probability density function:πθθθb g=<<3201,A randomly chosen insured is observed to have exactly one claim.Determine the posterior probability that θ is greater than 0.60.(A) 0.54(B) 0.58(C) 0.63(D) 0.67(E) 0.7232. The distribution of accidents for 84 randomly selected policies is as follows:Number of Accidents Number of Policies0 321 262 123 74 45 26 1Total 84 Which of the following models best represents these data?binomial(A) Negativeuniform(B) Discrete(C) Poisson(D) Binomial(E) Either Poisson or Binomial33. A time series yt follows an ARIMA(1,1,1) model with φ107=., θ103=−. and σε210=..Determine the variance of the forecast error two steps ahead.(A) 1(B)5(C) 8(D)10(E) 12(i) Low-hazard risks have an exponential claim size distribution with mean θ. (ii) Medium-hazard risks have an exponential claim size distribution with mean 2θ. (iii) High-hazard risks have an exponential claim size distribution with mean 3θ. (iv) No claims from low-hazard risks are observed.(v) Three claims from medium-hazard risks are observed, of sizes 1, 2 and 3. (vi) One claim from a high-hazard risk is observed, of size 15.Determine the maximum likelihood estimate of θ.(A) 1(B) 2(C) 3(D) 4(E) 5(i)partial X =pure premium calculated from partially credible data(ii)partial E X µ⎡⎤=⎣⎦ (iii) Fluctuations are limited to ±k µ of the mean with probability P(iv) Z = credibility factorWhich of the following is equal to P ?(A) partial Pr k X k µµµµ⎡⎤−≤≤+⎣⎦(B) partial Pr +Z k Z X Z k µµ⎡⎤−≤≤⎣⎦(C) partial Pr +Z Z X Z µµµµ⎡⎤−≤≤⎣⎦(D) ()partial Pr 111k Z X Z k µ⎡⎤−≤+−≤+⎣⎦(E) ()partial Pr 1k Z X Z k µµµµµ⎡⎤−≤+−≤+⎣⎦36. For the model 1223344i i i i i Y X X X ββββε=++++, you are given:(i) N = 15(ii)(iii) ESS =28282.Calculate the standard error of 32ˆˆββ−.(A) 6.4(B) 6.8(C) 7.1(D) 7.5(E) 7.837. You are given:Assume a uniform distribution of claim sizes within each interval.Estimate E X X 2150c h g −∧.(A)Less than 200(B)At least 200, but less than 300(C)At least 300, but less than 400(D)At least 400, but less than 500(E)At least 50038. Which of the following statements about moving average models is false?(A) Both unweighted and exponentially weighted moving average (EWMA) models canbe used to forecast future values of a time series.(B) Forecasts using unweighted moving average models are determined by applying equalweights to a specified number of past observations of the time series.(C) Forecasts using EWMA models may not be true averages because the weights appliedto the past observations do not necessarily sum to one.(D) Forecasts using both unweighted and EWMA models are adaptive because theyautomatically adjust themselves to the most recently available data.(E) Using an EWMA model, the two-period forecast is the same as the one-periodforecast.39. You are given:(i) Each risk has at most one claim each year.(ii)Type of Risk Prior Probability Annual Claim ProbabilityI 0.7 0.1II 0.2 0.2III 0.1 0.4 One randomly chosen risk has three claims during Years 1-6.Determine the posterior probability of a claim for this risk in Year 7.(A) 0.22(B) 0.28(C) 0.33(D) 0.40(E) 0.4640. You are given the following about 100 insurance policies in a study of time to policysurrender:(i) The study was designed in such a way that for every policy that was surrendered, ar, is always equal to 100.new policy was added, meaning that the risk set,j(ii) Policies are surrendered only at the end of a policy year.(iii) The number of policies surrendered at the end of each policy year was observed to be:1 at the end of the 1st policy year2 at the end of the 2nd policy year3 at the end of the 3rd policy yearn at the end of the n th policy year(iv) The Nelson-Aalen empirical estimate of the cumulative distribution function at time n, F, is 0.542.)(ˆnWhat is the value of n?(A) 8(B) 9(C) 10(D) 11(E) 12**END OF EXAMINATION**Course 4, Fall 2003PRELIMINARY ANSWER KEYQuestion # Answer Question # Answer 1 A21 A 2 E22 D 3 E23 D 4 B24 D 5 D25 E 6 A26 D 7 C27 B 8 D28 C 9 E29 B 10 D30 E 11 C31 E 12 A32 A 13 E33 B 14 D34 B 15 C35 E 16 B36 C 17 C37 C 18 B38 C 19 A39 B 20 A40 E。
全美数学建模往年试题2003

2003 MCM ProblemsPROBLEM A: The Stunt PersonAn exciting action scene in a movie is going to be filmed, and you are the stunt coordinator! A stunt person on a motorcycle will jump over an elephant and land in a pile of cardboard boxes to cushion their fall. Y ou need to protect the stunt person, and also use relatively few cardboard boxes (lower cost, not seen by camera, etc.).Your job is to:∙determine what size boxes to use∙determine how many boxes to use∙determine how the boxes will be stacked∙determine if any modifications to the boxes would help∙generalize to different combined weights (stunt person & motorcycle) and different jump heightsNote that, in "Tomorrow Never Dies", the James Bond character on a motorcycle jumps over a helicopter.PROBLEM B: Gamma Knife Treatment PlanningStereotactic radiosurgery delivers a single high dose of ionizing radiation to a radiographically well-defined, small intracranial 3D brain tumor without delivering any significant fraction of the prescribed dose to the surrounding brain tissue. Three modalities are commonly used in this area; they are the gamma knife unit, heavy charged particle beams, and external high-energy photon beams from linear accelerators.The gamma knife unit delivers a single high dose of ionizing radiation emanating from 201 cobalt-60 unit sources through a heavy helmet. All 201 beams simultaneously intersect at the isocenter, resulting in a spherical (approximately) dose distribution at the effective dose levels. Irradiating the isocenter to deliver dose is termed a “shot.” Shots can be represented as different spheres. Four interchangeable outer collimator helmets with beam channel diameters of 4, 8, 14, and 18 mm are available for irradiating different size volumes. For a target volume larger than one shot, multiple shots can be used to cover the entire target. In practice, most target volumes are treated with 1 to 15 shots. The target volume is a bounded, three-dimensional digital image that usually consists of millions of points.The goal of radiosurgery is to deplete tumor cells while preserving normal structures. Since there are physical limitations and biological uncertainties involved in this therapy process, a treatment plan needs to account for all those limitations and uncertainties. In general, an optimal treatment plan is designed to meet the following requirements.1Minimize the dose gradient across the target volume.2Match specified isodose contours to the target volumes.3Match specified dose-volume constraints of the target and critical organ.4Minimize the integral dose to the entire volume of normal tissues or organs.5Constrain dose to specified normal tissue points below tolerance doses.6Minimize the maximum dose to critical volumes.In gamma unit treatment planning, we have the following constraints:7Prohibit shots from protruding outside the target.8Prohibit shots from overlapping (to avoid hot spots).9Cover the target volume with effective dosage as much as possible. But at least 90% of the target volume must be covered by shots.10Use as few shots as possible.Y our tasks are to formulate the optimal treatment planning for a gamma knife unit as a sphere-packing problem, and propose an algorithm to find a solution. While designing your algorithm, you must keep in mind that your algorithm must be reasonably efficient.。
AMC10美国数学竞赛真题2003B卷

Problem 1Which of the following is the same asSolutionProblem 2Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al's pills cost a total of for the two weeks. How much does one green pill cost?SolutionProblem 3The sum of consecutive even integers is less than the sum of the first consecutive odd counting numbers. What is the smallest of the even integers?SolutionProblem 4Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the figure. She plants one flower per square foot in each region. Asters cost each, begonias each, cannas each, dahlias each, and Easter lilies each. What is the least possible cost, in dollars, for her garden?SolutionProblem 5Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches to make sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow the lawn?SolutionProblem 6Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a "-inch" television screen is closest, in inches, to which of the following?SolutionProblem 7The symbolism denotes the largest integer not exceeding . For example, and . ComputeSolutionProblem 8The second and fourth terms of a geometric sequence are and . Which of the following is a possible first term?SolutionProblem 9Find the value of that satisfies the equationSolutionProblem 10Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of the three letters followed by three digits. By how many times is the number of possible license plates increased?SolutionProblem 11A line with slope intersects a line with slope at point . What is the distance between the -intercepts of these two lines?SolutionProblem 12Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year, they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al's original portion?SolutionProblem 13Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of is ?SolutionProblem 14Given that where both and are positive integers, find the smallest possible value for .SolutionProblem 15There are players in a single tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The tournament continues until only one player remains unbeaten. The total number of matches played isSolutionProblem 16A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that a restaurant should offer so that a customer could have a different dinner each night in the year ?SolutionProblem 17An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it willexactly fill the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone's height to its radius?(Note: a cone with radius and height has volume and a sphere with radius has volume .)SolutionProblem 18What is the largest integer that is a divisor offor all positive even integers ?SolutionProblem 19Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?SolutionProblem 20In rectangle and . Points and are on so that and . Lines and intersect at . Find the area of .SolutionProblem 21A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?SolutionProblem 22A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at there is one chime and at noon and midnight there are twelve chimes. Starting at onon what date will the chime occur?SolutionProblem 23A regular octagon has an area of one square unit. What is the area of the rectangle ?SolutionProblem 24The first four terms in an arithmetic sequence are and in that order. What is the fifth term?SolutionProblem 25How many distinct four-digit numbers are divisible by and have as their last two digits?Solution。
数学建模(2003)1

位置报上来,然后,铺开一张大白纸,画出飞机的轮廓,再把那
些小窟窿一个一个地添上去。
We are located in CHENGDU
School of Electrical Engineering and Information SEEI
Sichuan University
画完后,大家一看,飞机浑身上下都是窟窿,只有飞行员座
数学建模的一般步骤
模型准备 模型检验 模型应用 模型假设 模型分析 模型构成 模型求解
School of Electrical Engineering and Information SEEI
We are located in CHENGDU
Sichuan University
模型准备: 首先要了解问题的实际背景,明确题目的要求,收集各种
储油罐的变位识别与罐容表标定
通常加油站都有若干个储存燃油的地下储油罐,并且一般 都有与之配套的“油位计量管理系统”,采用流量计和油位计来 测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表
(即罐内油位高度与储油量的对应关系)进行实时计算,以得到
罐内油位高度和储油量的变化情况。 许多储油罐在使用一段时间后,由于地基变形等原因,使罐 体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位), 从而导致罐容表发生改变。按照有关规定,需要定期对罐容表进
V = r 2 h
由于上底强度比其他部位高,厚度是其它部位三倍,因
此,材料总体积:
A=3 r b r b 2 rhb (4 r 2 rh)b
2 2 2
We are located in CHENGDU
School of Electrical Engineering and Information SEEI
历年MCM赛题

历年mcm数学建模赛题目录MCM85问题-A 动物群体的管理 (3)MCM85问题-B 战购物资储备的管理 (3)MCM86问题-A 水道测量数据 (4)MCM86问题-B 应急设施的位置 (4)MCM87问题-A 盐的存贮 (4)MCM87问题-B 停车场 (5)MCM88问题-A 确定毒品走私船的位置 (5)MCM88问题-B 两辆铁路平板车的装货问题 (5)MCM89问题-A 蠓的分类 (5)MCM89问题-B 飞机排队 (6)MCM90-A 药物在脑内的分布 (6)MCM90问题-B 扫雪问题 (6)MCM91问题-B 通讯网络的极小生成树 (6)MCM 91问题-A 估计水塔的水流量 (7)MCM92问题-A 空中交通控制雷达的功率问题 (7)MCM 92问题-B 应急电力修复系统的修复计划 (7)MCM93问题-A 加速餐厅剩菜堆肥的生成 (7)MCM93问题-B 倒煤台的操作方案 (8)MCM94问题-A 住宅的保温 (8)MCM 94问题-B 计算机网络的最短传输时间 (9)MCM-95问题-A 单一螺旋线 (9)MCM95题-B A1uacha Balaclava学院 (10)MCM96问题-A 噪音场中潜艇的探测 (10)MCM96问题-B 竞赛评判问题 (10)MCM97问题-A Velociraptor(疾走龙属)问题 (11)MCM97问题-B为取得富有成果的讨论怎样搭配与会成员 (11)MCM98问题-A 磁共振成像扫描仪 (12)MCM98问题-B 成绩给分的通胀 (13)MCM99问题-A 大碰撞 (13)MCM99问题-B “非法”聚会 (13)MCM2000问题-A空间交通管制 (13)MCM2000问题-B: 无线电信道分配 (14)MCM2001问题- A: 选择自行车车轮 (14)MCM2001问题-B 逃避飓风怒吼(一场恶风...) .. (15)MCM2001问题-C我们的水系-不确定的前景 (15)MCM2002问题-A风和喷水池 (15)MCM2002问题-B航空公司超员订票 (16)MCM2002问题-C (16)MCM2003问题-A: 特技演员 (17)MCM2003问题-B: Gamma刀治疗方案 (18)MCM2003问题-C航空行李的扫描对策 (18)MCM2004问题-A:指纹是独一无二的吗? (18)MCM2004问题-B:更快的快通系统 (18)MCM2004问题-C安全与否? (19)MCM2005问题A.水灾计划 (19)MCM2005B.Tollbooths (19)MCM2005问题C:不可再生的资源 (20)MCM2006问题A: 用于灌溉的自动洒水器的安置和移动调度 (20)MCM2006问题B: 通过机场的轮椅 (20)MCM2006问题C : 抗击艾滋病的协调 (21)MCM2008问题A:给大陆洗个澡 (23)MCM2008问题B:建立数独拼图游戏 (23)MCM85问题-A 动物群体的管理在一个资源有限,即有限的食物、空间、水等等的环境里发现天然存在的动物群体。
2000-2013美国数学建模竞赛(MCM、ICM)历年试题汇总

目录2000 年美国大学生数学建模竞赛MCM、ICM 试题 (3)2000 MCM A: Air Traffic Control (3)2000 MCM B: Radio Channel Assignments (3)2000 ICM: Elephants: When is Enough, Enough? (5)2001 年美国大学生数学建模竞赛MCM、ICM 试题 (7)2001 MCM A: Choosing a Bicycle Wheel (7)2001 MCM B: Escaping a Hurricane's Wrath (An Ill Wind...). (8)2001 ICM: Our Waterways - An Uncertain Future (10)2002 年美国大学生数学建模竞赛MCM、ICM 试题 (14)2002 MCM A: Wind and Waterspray (14)2002 MCM B: Airline Overbooking (14)2002 ICM: Scrub Lizards (15)2003 年美国大学生数学建模竞赛MCM、ICM 试题 (19)2003 MCM A: The Stunt Person (19)2003 MCM B: Gamma Knife Treatment Planning (19)2003 ICM: Aviation Baggage Screening Strategies: To Screen or Not to Screen, that is the Question (20)2004 年美国大学生数学建模竞赛MCM、ICM 试题 (24)2004 MCM A: Are Fingerprints Unique? (24)2004 MCM B: A Faster QuickPass System (24)2004 ICM: To Be Secure or Not to Be? (24)2005 年美国大学生数学建模竞赛MCM、ICM 试题 (25)2005 MCM A: Flood Planning (25)2005 MCM B: Tollbooths (25)2005 ICM: Nonrenewable Resources (25)2006 年美国大学生数学建模竞赛MCM、ICM 试题 (27)2006 MCM A: Positioning and Moving Sprinkler Systems for Irrigation (27)2006 MCM B: Wheel Chair Access at Airports (27)2006 ICM: Trade-offs in the fight against HIV/AIDS (28)2007 年美国大学生数学建模竞赛MCM、ICM 试题 (32)2007 MCM A: Gerrymandering (32)2007 MCM B: The Airplane Seating Problem (32)2007 ICM: Organ Transplant: The Kidney Exchange Problem (33)2008 年美国大学生数学建模竞赛MCM、ICM 试题 (38)2008 MCM A: Take a Bath (38)2008 MCM B: Creating Sudoku Puzzles (38)2008 ICM: Finding the Good in Health Care Systems (38)2009 年美国大学生数学建模竞赛MCM、ICM 试题 (40)2009 MCM A: Designing a Traffic Circle (40)2009 MCM B: Energy and the Cell Phone (40)2009 ICM: Creating Food Systems: Re-Balancing Human-Influenced Ecosystems41 2010年美国大学生数学建模竞赛 MCM、ICM 试题 (42)2010 MCM A: The Sweet Spot (42)2010 MCM B: Criminology (43)2010 ICM: The Great Pacific Ocean Garbage Patch (44)2011年美国大学生数学建模竞赛 MCM、ICM 试题 (45)2011 MCM A: Snowboard Course (45)2011 MCM B: Repeater Coordination (45)2011 ICM: Environmentally and Economically Sound (46)2012年美国大学生数学建模竞赛 MCM、ICM 试题 (48)2012 MCM A: The Leaves of a Tree (48)2012 MCM B: Camping along the Big Long River (50)2012 ICM: Modeling for Crime Busting (51)2013年美国大学生数学建模竞赛 MCM、ICM 试题 (59)2013 MCM A: The Ultimate Brownie Pan (59)2013 MCM B: Water, Water, Everywhere (61)2013 ICM: NetworkModeling of Earth's Health (62)2000 年美国大学生数学建模竞赛MCM、ICM 试题2000 MCM A: Air Traffic ControlTo improve safety and reduce air traffic controller workload, the Federal Aviation Agency (FAA) is considering adding software to the air traffic control system that would automatically detect potential aircraft flight path conflicts and alert the controller. To that end, an analysit at the FAA has posed the following problems.Requirement A: Given two airplanes flying in space, when should the air traffic controller consider the objects to be too close and to require intervention? Requirement B: And airspace sector is the section of three-dimensional airspace that one air traffic controller controls. Given any airspace sector, how do we measure how complex it is from an air traffic workload perspective? To what extent is complexity determined by the number of aircraft simultaneously passing through that sector1.at any one instant?2.during any given interval of time?3.during a particular time of day?How does the number of potential conflicts arising during those periods affect complexity? Does the presence of additional software tools to automatically predict conflicts and alert the controller reduce or add to this complexity? In addition to the guidelines for your report, write a summary (no more than two pages) that the FAA analyst can present to Jane Garvey, the FAA Administrator, to defend your conclusions.2000 MCM B: Radio Channel AssignmentsWe seek to model the assignment of radio channels to a symmetric network of transmitter locations over a large planar area, so as to avoid interference. One basic approach is to partition the region into regular hexagons in a grix (honeycomb-style), as shown in Figure 1, where a transmitter is located at the center of each hexagon.An interval of the frequency spectrum is to be alloted for transmitter frequencies. The interval will be divided into regularly spaced channels, which we represent by integers 1,2,3, … . Each transmitter wil be assigned one positive integer channel. The same channel can be used at many locations, provided that interference from nearby transmitters is avoided.Our goal is to minimize the width of the interval in the frequency spectrum that is needed to assugn channels subject to some constraints. This is achieved with the concept of a span. The span is the minimum, over all assignments satisfying the constraints, of the largest channel used at any location. It is not required that every channel smaller than the span be used in an assignment that attains the span.Let s be the length of a side of one of the hexagons. We concentrate on the case that there are two levels of interference.Requirement A: There are several contrainsts on the frequency assignments. First, no two transmitters within distance 4s of each other can be given the same channel. Second, due to spectral spreading, transmitters within distance 2s of each other must not be given the same or adjacent channels: Their channels must differ by at least 2. Under these contraints, what can we say about the span in Figure 1?Requirement B: Repeat Requirement A, assuming the grid in the example spreads arbitrarily far in all directions.Requirement C: Repeat Requirements A and B, except assume now more generally that channels for transmitters within distance 2s differ by at least some given integer k, while those at distance at most 4s must still differ by at least one. What cna we say about the span and about efficient strategies for designing assignments, as a function of k?Requirement D: Consider generalizations of the problem, such as several levels of interference or irregular transmitter placements. What other factors may be important to consider?Requirement E: Write an article (no more than 2 pages) for the local newspaper explaining your findings.2000 ICM: Elephants: When is Enough, Enough?“Ultimately, if a habitat is undesirably changed by elephants, then their removal should be considered -even by culling.”National Geographic (Earth Almanac) –December 1999 A large National Park in South Africa contains approximately 11,000 elephants. Management policy requires a healthy environment that can maintain a stable herf of 11,000 elephants. Each year park rangers count the elephant population. During the past 20 years whole herds have been removed to keep the population as close to 11,000 as possible. The process involved shooting (for the most part) and occasionally relocating approximately 600 to 800 elephants per year.Recently, there has been a public outcry against the shooting of these elephants. In addition, it is no longer feasible to relocate even a small population of elephants each year. A contraceptive dart, however, has been developed that can prevent a mature elephant cow from conceiving for a period of two years.Here is some information about eh elephants in the Park:∙There is very little emigration of immigration of elephants.∙The gender ratio is very close to 1:1 and control measures have endeavored to maintain parity.∙The gender ratio of newborn calves is also about 1:1. Twins are born about 1.35% of the time.∙Cows first conceive between the ages of 10 and 12 and produce, on average, a calf every 3.5 years until they reach an age of about 60.Gestation is approximately 22 months.∙The contraceptive dart causes an elephant cow to come into oestrus every month (but not conceiving). Elephants usually have courtship only once in 3.5 years, so the monthly cycle can cause additional stress.∙ A cow can be darted every year without additional detrimental effects. A mature elephant cow will not be able to conceive for 2 years after thelast darting.∙Between 70% and 80% of newborn calves survive to age 1 year.Thereafter, the survival rate is uniform across all ages and is very high(over 95%), until about age 60; it is a good assumption that elephantsdie before reading age 70.There is no hunting and negligible poaching in the Park.The park management has a rough data file of the approximate ages and gender of the elephants they have transported out of the region during the past 2 years. This data is available on website: icm2000data.xls. Unfortunately no data is available for the elephants that have been shot or remain in the Park.Your overall task is to develop and use models to investigate how the contraceptive dart might be used for population control. Specifically:Task 1: Develop and use a model to speculate about the likely survival rate for elephants aged 2 to 60. Also speculate about the current age structure of the elephant population.Task 2: Estimate how many cows would need to be darted each year to keep the population fixed at approximately 11,000 elephants. Show how the uncertainty in the data at your disposal affects your estimate. Comment on any changes in the age structure of the population and how this might affect tourists. (You may want to look ahead about 30-60 years.)Task 3: If it were feasible to relocate between 50 and 300 elephants per year, how would this reduce the number of elephants to be darted? Comment on the trade-off between darting and relocation.Task 4: Some opponents of darting argue that if there were a sudden loss of a large number of elephants (due to disease or uncontrolled poaching), even if darting stopped immediately, the ability of the population to grow again would be seriously impeded. Investigate and respond to this concer.Task 5: The management in the Park is skeptical about modeling. In particular, they argue that a lack of complete data makes a mockery of any attempt to use models to guide their decision. In addition to your technical report, include a carefully crafted report (3-page maximum) written explicitly for the park management that responds to their concerns and provides advice. Also suggest ways to increase the park managers confidence in your model and your conclusions.Task 6: If your model works, other elephant parks in Africa would be interested in using it. Prepare a darting plan for parks of various sizes (300-25,000 elephants), with slightly different survival rates and transportation possibilities.2001 年美国大学生数学建模竞赛MCM、ICM 试题2001 MCM A: Choosing a Bicycle WheelCyclists have different types of wheels they can use on their bicycles. The two basic types of wheels are those constructed using wire spokes and those constructed of a solid disk (see Figure 1) The spoked wheels are lighter, but the solid wheels are more aerodynamic. A solid wheel is never used on the front for a road race but can be used on the rear of the bike.Professional cyclists look at a racecourse and make an educated guess as to what kind of wheels should be used. The decision is based on the number and steepness of the hills, the weather, wind speed, the competition, and other considerations. The director sportif of your favorite team would like to have a better system in place and has asked your team for information to help determine what kind of wheel should be used for a given course.Figure 1: A solid wheel is shown on the left and a spoked wheel is shown on the right.The director sportif needs specific information to help make a decision and has asked your team to accomplish the tasks listed below. For each of the tasks assume that the same spoked wheel will always be used on the front but there is a choice of wheels for the rear.Task 1. Provide a table giving the wind speed at which the power required for a solid rear wheel is less than for a spoked rear wheel. The table should include the wind speeds for different road grades startingfrom zero percent to ten percent in one percent increments. (Roadgrade is defined to be the ratio of the total rise of a hill divided by thelength of the road. If the hill is viewed as a triangle, the grade is the sine of the angle at the bottom of the hill.) A rider starts at the bottom of the hill at a speed of 45 kph, and the deceleration of the rider is proportionalto the road grade. A rider will lose about 8 kph for a five percent grade over 100 meters.∙Task 2. Provide an example of how the table could be used for a specific time trial course.∙Task 3. Determine if the table is an adequate means for deciding on the wheel configuration and offer other suggestions as to how to make this decision.2001 MCM B: Escaping a Hurricane's Wrath (An Ill Wind...)Evacuating the coast of South Carolina ahead of the predicted landfall of Hurricane Floyd in 1999 led to a monumental traffic jam. Traffic slowed to a standstill on Interstate I-26, which is the principal route going inland from Charleston to the relatively safe haven of Columbia in the center of the state. What is normally an easy two-hour drive took up to 18 hours to complete. Many cars simply ran out of gas along the way. Fortunately, Floyd turned north and spared the state this time, but the public outcry is forcing state officials to find ways to avoid a repeat of this traffic nightmare.The principal proposal put forth to deal with this problem is the reversal of traffic on I-26, so that both sides, including the coastal-bound lanes, have traffic headed inland from Charleston to Columbia. Plans to carry this out have been prepared (and posted on the Web) by the South Carolina Emergency Preparedness Division. Traffic reversal on principal roads leading inland from Myrtle Beach and Hilton Head is also planned.A simplified map of South Carolina is shown. Charleston has approximately 500,000 people, Myrtle Beach has about 200,000 people, and another 250,000 people are spread out along the rest of the coastal strip. (More accurate data, if sought, are widely available.)The interstates have two lanes of traffic in each direction except in the metropolitan areas where they have three. Columbia, another metro area of around 500,000 people, does not have sufficient hotel space to accommodate the evacuees (including some coming from farther north by other routes), so some traffic continues outbound on I-26 towards Spartanburg; on I-77 north to Charlotte; and on I-20 east to Atlanta. In 1999, traffic leaving Columbia going northwest was moving only very slowly. Construct a model for the problem to investigate what strategies may reduce the congestion observed in 1999. Here are the questions that need to be addressed:1.Under what conditions does the plan for turning the two coastal-boundlanes of I-26 into two lanes of Columbia-bound traffic, essentiallyturning the entire I-26 into one-way traffic, significantly improveevacuation traffic flow?2.In 1999, the simultaneous evacuation of the state's entire coastal regionwas ordered. Would the evacuation traffic flow improve under analternative strategy that staggers the evacuation, perhapscounty-by-county over some time period consistent with the pattern of how hurricanes affect the coast?3.Several smaller highways besides I-26 extend inland from the coast.Under what conditions would it improve evacuation flow to turn around traffic on these?4.What effect would it have on evacuation flow to establish moretemporary shelters in Columbia, to reduce the traffic leaving Columbia?5.In 1999, many families leaving the coast brought along their boats,campers, and motor homes. Many drove all of their cars. Under whatconditions should there be restrictions on vehicle types or numbers ofvehicles brought in order to guarantee timely evacuation?6.It has been suggested that in 1999 some of the coastal residents ofGeorgia and Florida, who were fleeing the earlier predicted landfalls ofHurricane Floyd to the south, came up I-95 and compounded the traffic problems. How big an impact can they have on the evacuation trafficflow? Clearly identify what measures of performance are used tocompare strategies. Required: Prepare a short newspaper article, not to exceed two pages, explaining the results and conclusions of your study to the public.Clearly identify what measures of performance are used to compare strategies. Required: Prepare a short newspaper article, not to exceed two pages, explaining the results and conclusions of your study to the public.2001 ICM: Our Waterways - An Uncertain FutureZebra mussels, Dreissena polymorpha, are small, fingernail-sized, freshwater mollusks unintentionally introduced to North America via ballast water from a transoceanic vessel. Since their introduction in the mid 1980s, they have spread through all of the Great Lakes and to an increasing number of inland waterways in the United States and Canada. Zebra mussels colonize on various surfaces,such as docks, boat hulls, commercial fishing nets, water intake pipes and valves, native mollusks and other zebra mussels. Their only known predators, some diving ducks, freshwater drum, carp, and sturgeon, are not numerous enough to have a significant effect on them. Zebra mussels have significantly impacted the Great Lakes ecosystem and economy. Many communities are trying to control or eliminate these aquatic pests. SOURCE: Great Lakes Sea Grant Network /.Researchers are attempting to identify the environmental variables related to the zebra mussel infestation in North American waterways. The relevant factors that may limit or prevent the spread of the zebra mussel are uncertain. You will have access to some reference data to include listings of several chemicals and substances in the water system that may affect the spread of the zebra mussel throughout waterways. Additionally, you can assume individual zebra mussels grow at a rate of 15 millimeters per year with a life span between 4 - 6 years. The typical mussel can filter 1 liter of water each day.Requirement A: Discuss environmental factors that could influence the spread of zebra mussels.Requirement B: Utilizing the chemical data provided at:ap/undergraduate/contests/icm/imagesdata/LakeAChem1.xls, and the mussel population data provided at:ap/undergraduate/contests/icm/imagesdata/LakeAPopulation 1.xls model the population growth of zebra mussels in Lake A. Be sure to review the Information about the collection of the zebra mussel data. Requirement C: Utilizing additional data on Lake A from another scientist provided at :ap/undergraduate/contests/icm/imagesdata/LakeAChem2.xls and additional mussel population data provided at:ap/undergraduate/contests/icm/imagesdata/LakeAPopulation 2.xls corroborate the reasonableness of your model from Requirement B. As a result of this additional data, adjust your earlier model. Analyze the performance of your model. Discuss the sensitivity of your model. Requirement D: Utilizing the Chemical data from two lakes (Lake B and Lake C) in the United States provided atap/undergraduate/contests/icm/imagesdata/LakeB.xls and ap/undergraduate/contests/icm/imagesdata/LakeC.xls determine if these lakes are vulnerable to the spread of zebra mussels. Discuss your prediction.Requirement E: The community in the vicinity of Lake B (in requirement D) is considering specific policies for the de-icing of roadways near the lake duringthe winter season. Provide guidance to the local government officials regarding a policy on “de-icing agents.”In your guidance include predictions on the long-term impact of de-icing on the zebra mussel population. Requirement F: It has been recommended by a local community in the United States to introduce round goby fish. Zebra mussels are not often eaten by native fish species so they represent a dead end ecologically. However, round gobies greater than 100 mm feed almost exclusively on zebra mussels. Ironically, because of habitat destruction, the goby is endangered in its native habitat of the Black and Caspian Seas in Russia. In addition to your technical report, include a carefully crafted report (3-page maximum) written explicitly for the local community leaders that responds to their recommendation to introduce the round goby. Also suggest ways to help reduce the growth of the mussel within and among waterways.Information about the collection of the zebra mussel dataThe developmental state of the Zebra mussel is categorized by three stages: veligers (larvae), settling juveniles, and adults. Veligers (microscopic zebra mussel larvae) are free-swimming, suspended in the water for one to three weeks, after which they begin searching for a hard surface to attach to and begin their adult life. Looking for zebra mussel veligers is difficult because they are not easily visible by the naked eye. Settled juvenile zebra mussels can be felt on smooth surfaces like boats and motors. An advanced zebra mussel infestation can cover a surface, even forming thick mats sometimes reaching very high densities. The density of juveniles was determined along the lake using three 15×15 cm settling plates. The top plate remained in the water for the entire sampling season (S - seasonal) to estimate seasonal accumulation. The middle and bottom plates are collected after specific periods (A –alternating ) of time denoted by “Lake Days”in the data files.The settling plates are placed under the microscope and all juveniles on the undersides of the plate are counted and densities are reported as juveniles/m^2.2002 年美国大学生数学建模竞赛MCM、ICM 试题2002 MCM A: Wind and WatersprayAn ornamental fountain in a large open plaza surrounded by buildings squirts water high into the air. On gusty days, the wind blows spray from the fountain onto passersby. The water-flow from the fountain is controlled by a mechanism linked to an anemometer (which measures wind speed and direction) located on top of an adjacent building. The objective of this control is to provide passersby with an acceptable balance between an attractive spectacle and a soaking: The harder the wind blows, the lower the water volume and height to which the water is squirted, hence the less spray falls outside the pool area. Your task is to devise an algorithm which uses data provided by the anemometer to adjust the water-flow from the fountain as the wind conditions change.2002 MCM B: Airline OverbookingYou're all packed and ready to go on a trip to visit your best friend in New York City. After you check in at the ticket counter, the airline clerk announces that your flight has been overbooked. Passengers need to check in immediately to determine if they still have a seat.Historically, airlines know that only a certain percentage of passengers who have made reservations on a particular flight will actually take that flight. Consequently, most airlines overbook-that is, they take more reservations than the capacity of the aircraft. Occasionally, more passengers will want to take a flight than the capacity of the plane leading to one or more passengers being bumped and thus unable to take the flight for which they had reservations. Airlines deal with bumped passengers in various ways. Some are given nothing, some are booked on later flights on other airlines, and some are given some kind of cash or airline ticket incentive.Consider the overbooking issue in light of the current situation: Less flights by airlines from point A to point B Heightened security at and around airports Passengers' fear Loss of billions of dollars in revenue by airlines to dateBuild a mathematical model that examines the effects that different overbooking schemes have on the revenue received by an airline company in order to find an optimal overbooking strategy, i.e., the number of people by which an airline should overbook a particular flight so that the company's revenue is maximized. Insure that your model reflects the issues above, andconsider alternatives for handling “bumped”passengers. Additionally, write a short memorandum to the airline's CEO summarizing your findings and analysis.2002 ICM: Scrub LizardsThe Florida scrub lizard is a small, gray or gray-brown lizard that lives throughout upland sandy areas in the Central and Atlantic coast regions of Florida. The Florida Committee on Rare and Endangered Plants classified the scrub lizard as endangered.You will find a fact sheet on the Florida Scrub Lizard at/undergraduate/contests/mcm/contests/2002/problem s/icm2002data/scrublizard.pdfThe long-term survival of the Florida scrub lizard is dependent upon preservation of the proper spatial configuration and size of scrub habitat patches.Task 1: Discuss factors that may contribute to the loss of appropriate habitat for scrub lizards in Florida. What recommendations would you make to the state of Florida to preserve these habitats and discuss obstacles to the implementation of your recommendations?Task 2: Utilize the data provided in Table 1 to estimate the value for Fa (the average fecundity of adult lizards); Sj (the survivorship of juvenile lizards- between birth and the first reproductive season); and Sa (the average adult survivorship).Table 1Summary data for a cohort of scrub lizards captured and followed for 4 consecutive years. Hatchling lizards (age 0) do not produce eggs during the summer they are born. Average clutch size for all other females is proportional to body size according to the function y = 0.21*(SVL)-7.5, where y is the clutch size and SVL is the snout-to-vent length in mm.Year Age Total NumberLivingNumber of LivingFemalesAvg. Female Size(mm)1 0 972 495 30.32 1 180 92 45.83 2 20 11 55.84 3 2 2 56.0Task 3: It has been conjectured that the parameters Fa , Sj , and Sa , are related to the size and amount of open sandy area of a scrub patch. Utilize the data provided in Table 2 to develop functions that estimate Fa, Sj , and Sa for different patches. In addition, develop a function that estimates C, the carrying capacity of scrub lizards for a given patch.Table 2Summary data for 8 scrub patches including vital rate data for scrub lizards. Annual female fecundity (Fa), juvenile survivorship (Sj), and adult survivorship (Sa) are presented for each patch along with patch size and the amount of open sandy habitat.Patch Patch Size (ha) Sandy Habitat (ha) Fa Sj Sa Density (lizards/ha)a 11.31 4.80 5.6 0.12 0.06 58b 35.54 11.31 6.6 0.16 0.10 60c 141.76 51.55 9.5 0.17 0.13 75d 14.65 7.55 4.8 0.15 0.09 55e 63.24 20.12 9.7 0.17 0.11 80f 132.35 54.14 9.9 0.18 0.14 82g 8.46 1.67 5.5 0.11 0.05 40h 278.26 84.32 11.0 0.19 0.15 115Task 4: There are many animal studies that indicate that food, space, shelter, or even reproductive partners may be limited within a habitat patch causing individuals to migrate between patches. There is no conclusive evidence on why scrub lizards migrate. However, about 10 percent of juvenile lizards do migrate between patches and this immigration can influence the size of the population within a patch. Adult lizards apparently do not migrate. Utilizing the data provided in the histogram below estimate the probability of lizards surviving the migration between any two patches i and patch j.Table 3HistogramMigration data for juvenile lizards marked, released, and recaptured up to 6 months later. Surveys for recapture were conducted up to 750m from release sites.Task 5: Develop a model to estimate the overall population size of scrub lizards for the landscape given in Table 3. Also, determine which patches are suitable for occupation by scrub lizards and which patches would not support a viable population.Patch size and amount of open sandy habitat for a landscape of 29 patches located on the Avon Park Air Force Range. See:/undergraduate/contests/icm/2002problem/map.jpg for a map of the landscape.Patch Identification Patch Size (ha) Sandy Habitat (ha)1 13.66 5.382 32.74 11.913 1.39 0.234 2.28 0.765 7.03 3.626 14.47 4.387 2.52 1.998 5.87 2.499 22.27 8.44。
[小学]数学建模大赛历年试题
![[小学]数学建模大赛历年试题](https://img.taocdn.com/s3/m/7ac40fd6d4bbfd0a79563c1ec5da50e2524dd149.png)
数学建模大赛历年试题1.MCM(美国大学生数学建模竞赛)1985 A题动物群体管理1985 B题战略物资存储管理1986 A题水道测量数据1986 B题应急设施的位置1987 A题盐的贮存1987 B题停车场1988 A题确定走私船的位置1988 B题两辆铁路平板车的装货问题1989 A题蠓的分类1989 B题飞机排队1990 A题药物在大脑中的分布1990 B题扫雪问题1991 A题估计水箱的流水量1991 B题最小费用极小生成树1992 A题航空控制雷达的功率1992 B题应急电力修复系统1993 A题加速餐厅剩菜堆肥的生成1993 B题倒煤台的操作方案1994 A题建筑费用1994 B题计算机传输1995 A题单螺旋线1995 B题教师薪金分配1996 A题海底探测1996 B题竞赛论文的评定1997 A题疾走龙属问题1997 B题开会决策1998 A题MRI扫描仪1998 B题学生等级划分1999 A题小型星撞击1999 B题非法集会1999 C题大地污染2000 A题空中交通控制2000 C题大象的数量2002 A题风和喷水池2002 B题航空公司超员订票2003 A题特技人员2003 B题GAMMA刀治疗计划2004 A题指纹是独一无二的吗?2004 B题更快的快通系统2.CUMCM(全国大学生数学建模竞赛)1993年A题非线性交调的频率设计1993年B题球队排名问题1994年A题逢山开路1994年B题锁具装箱1995年A题一个飞行管理模型1995年B题天车与冶炼炉的作业调度1996年A题最优捕鱼策略1996年B题节水洗衣机1997年A题零件的参数设计1997年B题截断切割1998年A题投资的收益和风险1998年B题灾情巡视路线1999年A题自动化车床管理1999年B题钻井布局2000年A题DNA序列分类2000年B题钢管定购和运输2001年A题血管的三维重建2001年B题公交车调度2002年A题车灯线光源的优化设计2002年B题彩票中的数学2003年A题SARS的传播2003年B题露天矿生产的车辆安排2004年A题奥运会临时超市网点设计2004年B题电力市场的输电阻塞管理。
2003年美国大学生数学建模竞赛题目

2003年美国大学生数学建模竞赛题目问题A: 特技演员影片在拍摄中影片在拍摄中, , , 一个激动人心的动作场景将要摄入镜头一个激动人心的动作场景将要摄入镜头一个激动人心的动作场景将要摄入镜头, , , 而你是特技协而你是特技协调员调员! ! ! 一位特技演员驾驶着摩托车跨越一头大象,一位特技演员驾驶着摩托车跨越一头大象,随后跌落在借以缓冲的一堆纸箱上一堆纸箱上. . . 你需要保护特技演员你需要保护特技演员你需要保护特技演员,,而且而且, , , 也要使用相对而言较少的纸箱也要使用相对而言较少的纸箱(较低的花费(较低的花费, , , 不能进入镜头不能进入镜头不能进入镜头, , , 等等)。
等等)。
你的工作如下:? 确定所用纸箱的大小确定所用纸箱的大小确定所用纸箱的数目确定所用纸箱的数目? 确定纸箱的堆放办法确定纸箱的堆放办法? 还请确定还请确定还请确定, , , 通过对纸箱的各种调整通过对纸箱的各种调整通过对纸箱的各种调整, , , 是否会有所帮助是否会有所帮助? 请把你的研究推广到不同组合重量(特技演员请把你的研究推广到不同组合重量(特技演员请把你的研究推广到不同组合重量(特技演员 & & & 摩托车)和不同跨越摩托车)和不同跨越高度的情形留心一下留心一下, , , 在影片“明日帝国”中,角色在影片“明日帝国”中,角色James Bond Bond 驾驶着摩托车飞过驾驶着摩托车飞过一架直升机一架直升机. .问题B: Gamma 刀治疗方案立体定位放射外科立体定位放射外科, , , 用单一高剂量离子化射束在用单一高剂量离子化射束在X 光机精确界定下照射颅内的一个小的3D 脑瘤脑瘤, , , 与此同时与此同时与此同时, , , 并没有处方剂量的任何显著份额伤并没有处方剂量的任何显著份额伤及周边的脑组织及周边的脑组织. . . 在这个领域中在这个领域中在这个领域中,,一般有三种形式的射束可以采用,分别是Gamma 刀单元刀单元, , , 带电重粒子射束带电重粒子射束带电重粒子射束, , , 以及来自直线加速器的外用高能光以及来自直线加速器的外用高能光子束子束. .Gamma 刀单元具备的单一高剂量离子化射束刀单元具备的单一高剂量离子化射束, , , 是是201个钴个钴-60-60单位源通过厚重的盔状物发射出来的。
2003年5月北美精算第四门考试试题

Course 4Fall 2003 Society of Actuaries**BEGINNING OF EXAMINATION** 1. You are given the following information about a stationary AR(2) model:=.(i) ρ105(ii) ρ201=.Determine φ2.(A) –0.2(B) 0.1(C) 0.4(D) 0.7(E) 1.0(i) Losses follow a loglogistic distribution with cumulative distribution function:F x x x b g b g b g =+//θθγγ1(ii)The sample of losses is:10 35 80 86 90 120 158 180 200 210 1500Calculate the estimate of θ by percentile matching, using the 40th and 80th empirically smoothed percentile estimates.(A) Less than 77(B) At least 77, but less than 87(C) At least 87, but less than 97(D) At least 97, but less than 107(E) At least 107(i) The number of claims has a Poisson distribution.(ii) Claim sizes have a Pareto distribution with parameters θ=0.5 and α=6.(iii) The number of claims and claim sizes are independent.(iv) The observed pure premium should be within 2% of the expected pure premium 90% of the time.Determine the expected number of claims needed for full credibility.(A) Less than 7,000(B) At least 7,000, but less than 10,000(C) At least 10,000, but less than 13,000(D) At least 13,000, but less than 16,000(E) At least 16,0004. You study five lives to estimate the time from the onset of a disease to death. The times todeath are:2 3 3 3 7Using a triangular kernel with bandwidth 2, estimate the density function at 2.5.(A) 8/40(B) 12/40(C) 14/40(D) 16/40(E) 17/405. For the model i i i Y X αβε=++, where 1,2,...,10i =, you are given:(i) X i i =R S T1, if the th individual belongs to a specified group 0, otherwise(ii) 40 percent of the individuals belong to the specified group.(iii) The least squares estimate of β is β=4.(iv) ()2ˆˆ92i i Y X αβ−−=∑Calculate the t statistic for testing H 00:β=.(A) 0.9(B) 1.2(C) 1.5(D) 1.8(E) 2.1(i) Losses follow a Single-parameter Pareto distribution with density function:()()1,1f x x xαα+=>, 0 < α < ∞ (ii) A random sample of size five produced three losses with values 3, 6 and 14, and twolosses exceeding 25.Determine the maximum likelihood estimate of α.(A) 0.25(B) 0.30(C) 0.34(D) 0.38(E) 0.42(i) The annual number of claims for a policyholder has a binomial distribution withprobability function:()()221x x p x q q q x −⎛⎞=−⎜⎟⎝⎠, x = 0, 1, 2(ii) The prior distribution is:()34,01q q q π=<<This policyholder had one claim in each of Years 1 and 2.Determine the Bayesian estimate of the number of claims in Year 3.(A) Less than 1.1(B) At least 1.1, but less than 1.3(C) At least 1.3, but less than 1.5(D) At least 1.5, but less than 1.7(E) At least 1.78. For a sample of dental claims 1210,,...,x x x , you are given:(i) 23860 and 4,574,802i i x x ==∑∑(ii) Claims are assumed to follow a lognormal distribution with parameters µ and σ.(iii)µ and σ are estimated using the method of moments.Calculate ∧ for the fitted distribution.(A) Less than 125(B) At least 125, but less than 175(C) At least 175, but less than 225(D) At least 225, but less than 275(E) At least 2759. You are given:(i)Y tij is the loss for the j th insured in the i th group in Year t . (ii)ti Y is the mean loss in the i th group in Year t . (iii)X j i j i ij =R S T0, if the th insured is in the first group (=1)1, if the th insured is in the second group (=2) (iv)21ij ij ij ij Y Y X δφθε=+++, where 1,2i = and 1,2,...,j n = (v)Y Y Y Y 2122111230374041====,,, (vi) ˆ0.75φ=Determine the least-squares estimate of θ.(A) 5.25(B) 5.50(C) 5.75(D) 6.00(E) 6.2510. Two independent samples are combined yielding the following ranks:Sample I: 1, 2, 3, 4, 7, 9, 13, 19, 20Sample II: 5, 6, 8, 10, 11, 12, 14, 15, 16, 17, 18You test the null hypothesis that the two samples are from the same continuous distribution.The variance of the rank sum statistic is:()112n m n m ++Using the classical approximation for the two-tailed rank sum test, determine the p -value.(A) 0.015(B) 0.021(C) 0.105(D) 0.210(E) 0.420(i) Claim counts follow a Poisson distribution with mean θ. (ii) Claim sizes follow an exponential distribution with mean 10θ. (iii) Claim counts and claim sizes are independent, given θ. (iv) The prior distribution has probability density function:b g=5, θ>1πθθCalculate Bühlmann’s k for aggregate losses.(A) Less than 1(B) At least 1, but less than 2(C) At least 2, but less than 3(D) At least 3, but less than 4(E) At least 4(i) A survival study uses a Cox proportional hazards model with covariates Z 1 and Z 2,each taking the value 0 or 1.(ii) The maximum partial likelihood estimate of the coefficient vector is:, .,.ββ12071020e j b g=(iii) The baseline survival function at time t 0 is estimated as .S t 0065b g =.Estimate S t 0b gfor a subject with covariate values 121Z Z ==.(A) 0.34(B) 0.49(C) 0.65(D) 0.74(E) 0.84(i) Z 1 and Z 2 are independent N(0,1) random variables.(ii) a , b , c , d , e , f are constants.(iii) Y a bZ cZ X d eZ f Z =++=++1212 andDetermine ()E Y X .(A) a(B) ()()a b c X d ++−(C) a be cf X d ++−b gb g(D) a be cf e f +++g d /22(E) a be cf e f X d +++−g d g/22(i) Losses on a company’s insurance policies follow a Pareto distribution with probabilitydensity function:()(),0f x x x θθθ=<<∞+(ii) For half of the company’s policies θ=1, while for the other half θ=3.For a randomly selected policy, losses in Year 1 were 5.Determine the posterior probability that losses for this policy in Year 2 will exceed 8.(A) 0.11(B) 0.15(C) 0.19(D) 0.21(E) 0.2715. You are given total claims for two policyholders:Year1 2 3 4PolicyholderX 730 800 650 700Y 655 650 625 750Using the nonparametric empirical Bayes method, determine the Bühlmann credibilitypremium for Policyholder Y.(A) 655(B) 670(C) 687(D) 703(E) 71916. A particular line of business has three types of claims. The historical probability and thenumber of claims for each type in the current year are:Type HistoricalProbabilityNumber of Claimsin Current YearA 0.2744 112B 0.3512 180C 0.3744 138You test the null hypothesis that the probability of each type of claim in the current year is the same as the historical probability.Calculate the chi-square goodness-of-fit test statistic.(A) Less than 9(B) At least 9, but less than 10(C) At least 10, but less than 11(D) At least 11, but less than 12(E) At least 1217. Which of the following is false?(A) If the characteristics of a stochastic process change over time, then the process isnonstationary.(B) Representing a nonstationary time series by a simple algebraic model is often difficult.(C) Differences of a homogeneous nonstationary time series will always be nonstationary.(D) If a time series is stationary, then its mean, variance and, for any lag k, covariancemust also be stationary.(E) If the autocorrelation function for a time series is zero (or close to zero) for all lagsk>0, then no model can provide useful minimum mean-square-error forecasts offuture values other than the mean.18. The information associated with the maximum likelihood estimator of a parameter θ is 4n,where n is the number of observations.Calculate the asymptotic variance of the maximum likelihood estimator of 2θ.(A) 12n(B) 1n(C) 4n(D) 8n(E) 16n19. You are given:(i) The probability that an insured will have at least one loss during any year is p.(ii) The prior distribution for p is uniform on []0,0.5.(iii) An insured is observed for 8 years and has at least one loss every year.Determine the posterior probability that the insured will have at least one loss during Year 9.(A) 0.450(B) 0.475(C) 0.500(D) 0.550(E) 0.62520. At the beginning of each of the past 5 years, an actuary has forecast the annual claims for agroup of insureds. The table below shows the forecasts (X) and the actual claims (Y). Atwo-variable linear regression model is used to analyze the data.t X t Y t1 475 2542 254 4633 463 5154 515 5675 567 605You are given:(i) The null hypothesis is0:0,1Hαβ==.(ii) The unrestricted model fit yields ESS = 69,843.Which of the following is true regarding the F test of the null hypothesis?(A) The null hypothesis is not rejected at the 0.05 significance level.(B) The null hypothesis is rejected at the 0.05 significance level, but not at the 0.01 level.(C) The numerator has 3 degrees of freedom.(D) The denominator has 2 degrees of freedom.(E) TheF statistic cannot be determined from the information given.21-22. Use the following information for questions 21 and 22.For a survival study with censored and truncated data, you are given:Time (t) Number at Riskat Time t Failures at Time t1 30 52 27 93 32 64 25 55 20 4 21. The probability of failing at or before Time 4, given survival past Time 1, is31q.Calculate Greenwood’s approximation of the variance of 31 q.(A) 0.0067(B) 0.0073(C) 0.0080(D) 0.0091(E) 0.010521-22. (Repeated for convenience) Use the following information for questions 21 and 22.For a survival study with censored and truncated data, you are given:Time (t) Number at Riskat Time t Failures at Time t1 30 52 27 93 32 64 25 55 20 4 22. Calculate the 95% log-transformed confidence interval for H3b g, based on the Nelson-Aalenestimate.(A) (0.30,0.89)(B) (0.31,1.54)(C) (0.39,0.99)(D) (0.44,1.07)(E) (0.56,0.79)(i) Two risks have the following severity distributions:Amount of Claim Probability of ClaimAmount for Risk 1Probability of ClaimAmount for Risk 2250 0.5 0.72,500 0.3 0.260,000 0.2 0.1(ii) Risk 1 is twice as likely to be observed as Risk 2.A claim of 250 is observed.Determine the Bühlmann credibility estimate of the second claim amount from the same risk.(A) Less than 10,200(B) At least 10,200, but less than 10,400(C) At least 10,400, but less than 10,600(D) At least 10,600, but less than 10,800(E) At least 10,800(i) A sample x x x 1210,,,… is drawn from a distribution with probability density function:1211exp()exp(), 0[]x x x θθσσ−+−<<∞(ii)θσ>(iii) x x i i ==∑∑15050002 andEstimate θ by matching the first two sample moments to the corresponding population quantities.(A) 9(B) 10(C) 15(D) 20(E) 2125. You are given the following time-series model:115.028.0−−−++=t t t t y y εεWhich of the following statements about this model is false?(A) 10.4ρ=(B) 1,2,3,4,....k k ρρ<=(C) The model is ARMA(1,1).(D) The model is stationary.(E) The mean, µ, is 2.26. You are given a sample of two values, 5 and 9.You estimate Var(X ) using the estimator g (X 1, X 2) = 21().2i X X −∑Determine the bootstrap approximation to the mean square error of g .(A) 1(B) 2(C) 4(D) 8(E) 1627. You are given:(i) The number of claims incurred in a month by any insured has a Poisson distributionwith mean λ.(ii) The claim frequencies of different insureds are independent.(iii) The prior distribution is gamma with probability density function:()()6100100120efλλλλ−=(iv) Month Number of Insureds NumberofClaims1 100 62 150 83 200 114 300 ?Determine the Bühlmann-Straub credibility estimate of the number of claims in Month 4.(A) 16.7(B) 16.9(C) 17.3(D) 17.6(E) 18.028. You fit a Pareto distribution to a sample of 200 claim amounts and use the likelihood ratio testto test the hypothesis that 1.5α= and 7.8θ=.You are given:(i) The maximum likelihood estimates are α= 1.4 and θ = 7.6.(ii) The natural logarithm of the likelihood function evaluated at the maximum likelihoodestimates is −817.92.(iii) ()ln 7.8607.64i x +=∑Determine the result of the test.(A) Reject at the 0.005 significance level.(B) Reject at the 0.010 significance level, but not at the 0.005 level.(C) Reject at the 0.025 significance level, but not at the 0.010 level.(D) Reject at the 0.050 significance level, but not at the 0.025 level.(E) Do not reject at the 0.050 significance level.29. You are given:(i) The model is Y X i i i =+βε, i = 1, 2, 3.(ii)i X i Var εi b g11 12 2 93 316 (iii)The ordinary least squares residuals are εβi i i Y X =−, i = 1, 2, 3.Determine E X X X ,,ε12123d i.(A) 1.0(B) 1.8(C) 2.7(D) 3.7(E) 7.630. For a sample of 15 losses, you are given:(i)Interval Observed Number ofLosses(0, 2] 5(2, 5] 5(5, ∞) 5 (ii) Losses follow the uniform distribution on 0,θb g.Estimate θ by minimizing the function()231j jjjE OO=−∑, where j E is the expected number oflosses in the j th interval andjO is the observed number of losses in the j th interval.(A) 6.0(B) 6.4(C) 6.8(D) 7.2(E) 7.631. You are given:(i) The probability that an insured will have exactly one claim is θ.(ii) The prior distribution of θ has probability density function:πθθθb g=<<3201,A randomly chosen insured is observed to have exactly one claim.Determine the posterior probability that θ is greater than 0.60.(A) 0.54(B) 0.58(C) 0.63(D) 0.67(E) 0.7232. The distribution of accidents for 84 randomly selected policies is as follows:Number of Accidents Number of Policies0 321 262 123 74 45 26 1Total 84 Which of the following models best represents these data?binomial(A) Negativeuniform(B) Discrete(C) Poisson(D) Binomial(E) Either Poisson or Binomial33. A time series yt follows an ARIMA(1,1,1) model with φ107=., θ103=−. and σε210=..Determine the variance of the forecast error two steps ahead.(A) 1(B)5(C) 8(D)10(E) 12(i) Low-hazard risks have an exponential claim size distribution with mean θ. (ii) Medium-hazard risks have an exponential claim size distribution with mean 2θ. (iii) High-hazard risks have an exponential claim size distribution with mean 3θ. (iv) No claims from low-hazard risks are observed.(v) Three claims from medium-hazard risks are observed, of sizes 1, 2 and 3. (vi) One claim from a high-hazard risk is observed, of size 15.Determine the maximum likelihood estimate of θ.(A) 1(B) 2(C) 3(D) 4(E) 5(i)partial X =pure premium calculated from partially credible data(ii)partial E X µ⎡⎤=⎣⎦ (iii) Fluctuations are limited to ±k µ of the mean with probability P(iv) Z = credibility factorWhich of the following is equal to P ?(A) partial Pr k X k µµµµ⎡⎤−≤≤+⎣⎦(B) partial Pr +Z k Z X Z k µµ⎡⎤−≤≤⎣⎦(C) partial Pr +Z Z X Z µµµµ⎡⎤−≤≤⎣⎦(D) ()partial Pr 111k Z X Z k µ⎡⎤−≤+−≤+⎣⎦(E) ()partial Pr 1k Z X Z k µµµµµ⎡⎤−≤+−≤+⎣⎦36. For the model 1223344i i i i i Y X X X ββββε=++++, you are given:(i) N = 15(ii)(iii) ESS =28282.Calculate the standard error of 32ˆˆββ−.(A) 6.4(B) 6.8(C) 7.1(D) 7.5(E) 7.837. You are given:Assume a uniform distribution of claim sizes within each interval.Estimate E X X 2150c h g −∧.(A)Less than 200(B)At least 200, but less than 300(C)At least 300, but less than 400(D)At least 400, but less than 500(E)At least 50038. Which of the following statements about moving average models is false?(A) Both unweighted and exponentially weighted moving average (EWMA) models canbe used to forecast future values of a time series.(B) Forecasts using unweighted moving average models are determined by applying equalweights to a specified number of past observations of the time series.(C) Forecasts using EWMA models may not be true averages because the weights appliedto the past observations do not necessarily sum to one.(D) Forecasts using both unweighted and EWMA models are adaptive because theyautomatically adjust themselves to the most recently available data.(E) Using an EWMA model, the two-period forecast is the same as the one-periodforecast.39. You are given:(i) Each risk has at most one claim each year.(ii)Type of Risk Prior Probability Annual Claim ProbabilityI 0.7 0.1II 0.2 0.2III 0.1 0.4 One randomly chosen risk has three claims during Years 1-6.Determine the posterior probability of a claim for this risk in Year 7.(A) 0.22(B) 0.28(C) 0.33(D) 0.40(E) 0.4640. You are given the following about 100 insurance policies in a study of time to policysurrender:(i) The study was designed in such a way that for every policy that was surrendered, ar, is always equal to 100.new policy was added, meaning that the risk set,j(ii) Policies are surrendered only at the end of a policy year.(iii) The number of policies surrendered at the end of each policy year was observed to be:1 at the end of the 1st policy year2 at the end of the 2nd policy year3 at the end of the 3rd policy yearn at the end of the n th policy year(iv) The Nelson-Aalen empirical estimate of the cumulative distribution function at time n, F, is 0.542.)(ˆnWhat is the value of n?(A) 8(B) 9(C) 10(D) 11(E) 12**END OF EXAMINATION**Course 4, Fall 2003PRELIMINARY ANSWER KEYQuestion # Answer Question # Answer 1 A21 A 2 E22 D 3 E23 D 4 B24 D 5 D25 E 6 A26 D 7 C27 B 8 D28 C 9 E29 B 10 D30 E 11 C31 E 12 A32 A 13 E33 B 14 D34 B 15 C35 E 16 B36 C 17 C37 C 18 B38 C 19 A39 B 20 A40 E。
数学建模竞赛试题(2003年)
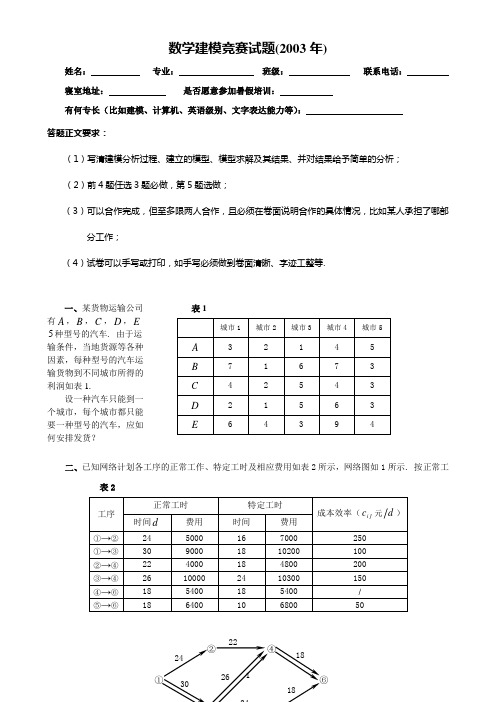
数学建模竞赛试题(2003年)姓名:专业:班级:联系电话:寝室地址:是否愿意参加暑假培训:有何专长(比如建模、计算机、英语级别、文字表达能力等):答题正文要求:(1)写清建模分析过程、建立的模型、模型求解及其结果、并对结果给予简单的分析;(2)前4题任选3题必做,第5题选做;(3)可以合作完成,但至多限两人合作,且必须在卷面说明合作的具体情况,比如某人承担了哪部分工作;(4)试卷可以手写或打印,如手写必须做到卷面清晰、字迹工整等.一、某货物运输公司表1有A,B,C,D,E5种型号的汽车.由于运输条件,当地货源等各种因素,每种型号的汽车运输货物到不同城市所得的利润如表1.设一种汽车只能到一个城市,每个城市都只能要一种型号的汽车,应如何安排发货?二、已知网络计划各工序的正常工作、特定工时及相应费用如表2所示,网络图如1所示. 按正常工表226 ①②③④⑤⑥2430222418 18图-1作则从图1中计算出总工期为74天. 关键路线为①→③→④→⑥ . 由表2可得正常工作条件下,总费用为47800元.设正常工作条件下,任务总间接费用8000元. 工期每缩短一天则间接费用减少330元,求最低成本日程.三、SARS是一种传染性极强且难以治愈的流行性传染病. 据研究SARS病毒具有七种形体,因此,它属于非获得性免疫流行病. 试以一个人数为n的区域为例,建立一个数学模型,并且给出在何种条件下,能够有效抑制疾病传播,你们需要考虑的因素包括疫区内人口流动量、治愈率、传染率等诸方面因素. 给出合理的假设及其参数,建立出自己的模型,并以我国的北京、广东两地的疫情为例. 验证自己模型的合理性(数据自己收集),并且给出一套有效控制疫情传播的方案.四、中国足球甲级队比赛,分成甲A和甲B两组进行主客场双循环制,1997年足协决定:12支甲B 球队的前四名将升入甲A,球队排序的原则如下:(1)胜一场积3分,平一场积1分,负一场积0分;(2)球队的名次按积分多少排序,积分高的队排名在前;(3)积分相同的球队,按净胜球的多少排序,净胜球(踢进球数减被踢入球数)多的队排名在前;(4)若积分相同、净胜球数也相同,则按进球数排序,踢进球总数多的队排名在前.以下是甲B联赛(共赛22轮)第19轮后的形势:队名胜平负得失球积分队名胜平负得失球积分武汉雅琪 10 6 3 29/18 36 佛山佛斯弟 8 2 9 26/28 26 深圳平安 9 5 5 34/27 32 辽宁双星 7 4 8 20/19 25 深圳金鹏 8 5 6 32/38 29 上海浦东 7 4 8 28/23 25 河南建业 8 5 6 20/18 29 上海豫园 6 5 8 23/29 23 广州松日 7 7 5 27/19 28 天津万科 5 7 7 22/23 22 沈阳海狮 7 7 5 28/23 28 火车头杉杉 2 3 14 14/48 9 还剩三轮,对阵表如下:上海浦东——深圳平安广州松日——河南建业杉杉——广州松日深圳平安——辽宁双星河南建业——上海浦东广州松日——天津万科深圳平安——沈阳海狮上海豫园——河南建业辽宁双星——天津万科深圳金鹏——上海豫园武汉雅琪——佛斯第沈阳海狮——杉杉沈阳海狮——深圳金鹏天津万科——佛斯第上海豫园——武汉雅琪辽宁双星——深圳金鹏佛斯第——杉杉武汉雅琪——上海浦东试问:武汉雅琪队是否一定可以提前三轮晋升甲A?说明理由.五、附加题:有12个苹果,其中有一个与其它的11个不同,或者比它们轻,或者比它们重,试用没有砝码的天平称量三次,找出这个苹果,并说明它的轻重情况.注:交卷时间:6月9日(周一),具体时间与地点如下:西区:9.50~10.30,地点:3号楼(物理楼)510室(陈老师)南区:9.50~10.30,地点:3—212 (李老师)东区:9.50~10.30,地点:1号楼(主楼)427室(王老师)。
1021-数学建模-AMCM2003A

AMCM2003问题-A: 特技演员
影片在拍摄中, 一个激动人心的动作场景将要摄入镜头, 而你是特技协调员! 一位特技演员驾驶着摩托车跨越一头大象,随后跌落在借以缓冲的一堆纸箱上. 你需要保护特技演员,而且, 也要使用相对而言较少的纸箱(较低的花费, 不能进入镜头, 等等)。
你的工作如下:
●确定所用纸箱的大小
●确定所用纸箱的数目
●确定纸箱的堆放办法
●还请确定, 通过对纸箱的各种调整, 是否会有所帮助
请把你的研究推广到不同组合重量(特技演员 & 摩托车)和不同跨越高度的情形
留心一下, 在影片“明日帝国”中,角色James Bond 驾驶着摩托车飞过一架直升机。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2003 年美国大学生数学建模竞赛 MCM 试题
2003 MCM A: The Stunt Person
An exciting action scene in a movie is going to be filmed, and you are the stunt coordinator! A stunt person on a motorcycle will jump over an elephant and land in a pile of cardboard boxes to cushion their fall. You need to protect the stunt person, and also use relatively few cardboard boxes (lower cost, not seen by camera, etc.).
Your job is to:
∙determine what size boxes to use
∙determine how many boxes to use
∙determine how the boxes will be stacked
∙determine if any modifications to the boxes would help
∙generalize to different combined weights (stunt person & motorcycle) and different jump heights
Note that, in “Tomorrow Never Dies”, the James Bond character on a motorcycle jumps over a helicopter.
2003 MCM B: Gamma Knife Treatment Planning
Stereotactic radiosurgery delivers a single high dose of ionizing radiation to a radiographically well-defined, small intracranial 3D brain tumor without delivering any significant fraction of the prescribed dose to the surrounding brain tissue. Three modalities are commonly used in this area; they are the gamma knife unit, heavy charged particle beams, and external high-energy photon beams from linear accelerators.
The gamma knife unit delivers a single high dose of ionizing radiation emanating from 201 cobalt-60 unit sources through a heavy helmet. All 201 beams simultaneously intersect at the isocenter, resulting in a spherical (approximately) dose distribution at the effective dose levels. Irradiating the isocenter to deliver dose is termed a “shot.” Shots can be represented as different spheres. Four interchangeable outer collimator helmets with beam channel diameters of 4, 8, 14, and 18 mm are available for irradiating different size volumes. For a target volume larger than one shot, multiple shots can be used to cover the entire target. In practice, most target volumes are treated with 1 to 15 shots. The target volume is a bounded, three-dimensional digital image that usually consists of millions of points.
The goal of radiosurgery is to deplete tumor cells while preserving normal structures. Since there are physical limitations and biological
uncertainties involved in this therapy process, a treatment plan needs to account for all those limitations and uncertainties. In general, an optimal treatment plan is designed to meet the following requirements.
1.Minimize the dose gradient across the target volume.
2.Match specified isodose contours to the target volumes.
3.Match specified dose-volume constraints of the target and critical
organ.
4.Minimize the integral dose to the entire volume of normal tissues
or organs.
5.Constrain dose to specified normal tissue points below tolerance
doses.
6.Minimize the maximum dose to critical volumes.
In gamma unit treatment planning, we have the following constraints:
1.Prohibit shots from protruding outside the target.
2.Prohibit shots from overlapping (to avoid hot spots).
3.Cover the target volume with effective dosage as much as possible.
But at least 90% of the target volume must be covered by shots.
e as few shots as possible.
Your tasks are to formulate the optimal treatment planning for a gamma knife unit as a sphere-packing problem, and propose an algorithm to find a solution. While designing your algorithm, you must keep in mind that your algorithm must be reasonably efficient.。
