4,5,6,7年级奥数培优经典试题16(配详解)

合集下载

四年级下册数学奥数试题-培优拓展训练：第16讲：体育比赛中的数学(学生版)

第十六讲体育比赛中的数学一．体育比赛中的数学对于体育比赛形式的逻辑推理题，注意“”必然对应着“另一队的负、胜、平”。

有时综合性的逻辑推理题需要将比赛情况用点以及来表示，从整体考虑，通过数量比较、等方式寻找解题的突破口。

一．学会分析题，比赛的中的切入点是比赛规则二．胜，负，平，单循环赛，复赛，冠军赛的公式掌握1.一场比赛中一共有六个队参赛，如果每两个队之间都进行一场比赛，一共要比赛多少场？解析：每队赛的场数×参赛队数÷2=单循环总场数．要比赛6×5÷2=15场．2.市里举行足球联赛，有5个区参加比赛，每个区出2个代表队．每个队都要与其他队赛一场，这些比赛分别在5个区的体育场进行，那么平均每个体育场都要举行多少场比赛？解析：2×5×（10-1）除以2=45场45除以5=9场3.学校进行乒乓球选拔赛，每个参赛选手都要和其他所有选手各赛一场，一共进行了78场比赛，有人参加了选拔赛．解析：根据“每个参赛选手都要和其他所有选手赛一场，一共进行了78场比赛，”知道有几个人参加比赛，就需要赛几乘几减一场，但每两个人只赛一场，所以这里有一半是重复的，所以实际除以2才是78场，由此列式解答即可．解：设x个人参加比赛，每个参赛选手都要和其他选手赛一场，则每个选手赛（x-1）场，x个人赛（x-1）×x场，但每两个人只赛一场，所以这里有一半是重复的，所以实际应赛：x×（x-1）÷2=78，即 x ×（x-1）=156；因为，13×12=156，所以x=13；4.学校六年级8个班举行篮球单循环比赛，即每个班都要与其他班比赛一场，那么一共要进行多少场比赛？解析：举行篮球单循环比赛，是每个班级都要和其它7个班进行比赛，要进行7场比赛，所以8个班一共进行：7×8=56（场），又因为每两个班重复计算了一次，所以实际全年级一共要进行了56÷2=28（场）．解：要进行的比赛场数为：7×8÷2=28（场）．5.有8个选手进行乒乓球单循环赛，结果每人获胜局数各不相同，那么冠军胜了几局？解析：冠军胜了7局，其他人分别胜6，5，4，3，2，1，0局。

4,5,6,7年级奥数培优经典试题17(配详解)

成功＝勤奋＋正确的方法＋少说空话四年级第 1 关：在 1 至 13 中，都有谁能够整除689686868个？第 2 关：我国古代的“河图”是由 3×3 的方格构成，每个方格内均有数目不同的点图，每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.图中给出了“河图”的部分点图，请你推算出 P 处所对应的点图是（）A. B. C. D.第 3 关：一个数列，从第 3 项开始，每一项等于前面两项之和，这个数列的第 2 项为 39，第 100 项为 2017，那么前 98 项的和是多少？第 4 关：甲、乙两人在长 30 米的泳池内游泳，甲每分钟游 35 米，乙每分钟游 50 米。

两人同时分别从泳池的两端出发，触壁后原路返回。

如果不计转向的时间，则从出发开始计算的 6 分钟内两人共相遇多少次？（迎面相遇和背后追及都算相遇）第 5 关：如图，有 36 个方格，在方格中放入 12 个棋子，每个方格中只能放入一个棋子，使得每一行、每一列和两条对角线上都恰好有两个棋子，给出一种放法。

五年级第 1 关： 201710201720172017个除以45的余数是 _________第 2 关：从 11，12，13，…，91 这 81 个数中，任选两个数，使得它们的乘积被 5 除后余 2，那么一共有多少种选法？第 3 关：已知1+52+3n n 不是最简分数，且 n 为三位数，那么所有 n 之和为多少？第 4 关：纯循环小数 b a . 0化为最简分数后，分子与分母之差为 5，则这个最简分数的分子和分母之和最小为多少？第 5 关：如下图所示，由 18 个同样大小的小正方形组成一个图形，则图中共有多少个正方形和长方形？六年级第 1 关：化简繁分数＝____________________第 2 关：已知 a 与 l ﹣2b 互为相反数，则代数式 2a ﹣4b ﹣3 的值是_______________．第 3 关：下列判断：①若 ab ＝0，则 a ＝0 或 b ＝0；②若 a 2＝b 2，则 a ＝b ；③若 ac 2＝bc 2，则a ＝b ；④若|a |＞|b |，则（a ＋b ）•（a －b ）是正数．其中正确的有_________（填序号）第 4 关：已知在纸面上有一数轴（如图），折叠纸面．（1）若折叠后，数 1 表示的点与数﹣1 表示的点重合，则此时数﹣2 表示的点与数___________表示的点重合；（2）若折叠后，数 3 表示的点与数－1 表示的点重合，则此时数 5 表示的点与数_____________表示的点重合；若这样折叠后，数轴上有 A 、B 两点也重合，且 A 、B 两点之间的距离为 9 （A 在 B 的左侧），则 A 点表示的数为______________，B 点表示的数为_______________．第 5 关：将 2017 表示成两个整数的平方差的形式，可以有几种不同的表示方法．．．．．．．．．．．．？（注：平方差公式22b a －= (a + b)(a －b) ，例如 2017 = (1009 +1008) ×(1009－1008) = 10092－10082 ）成功＝勤奋＋正确的方法＋少说空话修建一所房子有一系列工作要做，其中某些工作要在其他一些工作完成之后才能进行，如图表列出修建一所房子的每项工作的前面的工作和完成该工作所需的时间．问修建该房子最快的时间是_______________天．编号工作前面的工作延续的时间（天）1 地基无 4.02 挖沟无 1.73 管线 2 2.04 砌砖1，2，3 15.05 喷漆 4 4.86 木工 4 8.47 屋顶 6 10.0成功＝勤奋＋正确的方法＋少说空话七年级第1关：如图所示，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠J＋∠K＋∠L 的度数。

小学数学奥数题及答案

小学数学奥数题及答案题目一：数字变换小明有一串数字：1, 2, 3, 4, 5, 6, 7, 8, 9。

他想通过变换这些数字，使得每个数字都变成它后面第二个数字的两倍。

例如，如果2后面是4，那么2应该变成8。

请问小明需要如何变换这些数字？答案：小明可以将数字变换为：2, 4, 6, 8, 10, 12, 14, 16, 18。

这样每个数字都是它后面第二个数字的两倍。

题目二：年龄问题小华和小亮是好朋友，小华比小亮大3岁。

5年后，小华的年龄将是小亮年龄的两倍。

问现在小华和小亮各多少岁？答案：设小亮现在的年龄为x岁，那么小华现在的年龄为x+3岁。

根据题意，5年后小华的年龄是x+3+5=x+8岁，小亮的年龄是x+5岁。

根据题意，我们有方程x+8=2*(x+5)，解得x=7。

所以小亮现在7岁，小华现在10岁。

题目三：图形面积一个长方形的长是宽的两倍，如果将这个长方形的长增加10厘米，宽增加5厘米，那么新的长方形面积比原来的长方形面积大135平方厘米。

求原来长方形的长和宽。

答案：设原来长方形的宽为x厘米，那么长为2x厘米。

根据题意，新的长方形长为2x+10厘米，宽为x+5厘米。

根据题意，我们有方程(2x+10)*(x+5) - 2x*x = 135，解得x=6。

所以原来长方形的宽为6厘米，长为12厘米。

题目四：速度问题一辆汽车从A地到B地，如果速度提高20%，可以提前1小时到达。

如果速度降低20%，将晚到1小时。

求A地到B地的原始行驶时间。

答案：设原始速度为v，原始行驶时间为t小时。

根据题意，速度提高20%后，速度变为1.2v，行驶时间为t-1小时；速度降低20%后，速度变为0.8v，行驶时间为t+1小时。

根据距离相等，我们有方程vt = 1.2v*(t-1) = 0.8v*(t+1)，解得t=6小时。

题目五：分数问题一个分数的分子与分母之和为23，如果将分子增加3，得到的新分数等于原分数的两倍。

求原分数。

7年级奥数题及答案数学奥数题七年级

7年级奥数题及答案数学奥数题七年级7年级奥数题及答案7年级奥数题及答案刚步入7年级的学生对于自己的基础知识要求扎实之外，也要多做奥数题为自己铺一个垫脚石，下面是WTT为你们准备的7年级的相关奥数题目以及相关的奥数答案，希望能帮助你们。

7年级奥数题1：把1至205这205个自然数依次写下来得到一个多位数 123456789..205,这个多位数除以9余数是多少解：首先研究能被9整除的数的特点：如果各个数位上的数字之和能被9 整除，那么这个数也能被9整除;如果各个位数字之和不能被9整除，那么得的余数就是这个数除以9得的余数。

解题：1+2+3+4+5+6+7+8+9=45;45能被9整除依次类推：1~1999这些数的个位上的数字之和可以被9整除 10~19，20~29……90~99这些数中十位上的数字都出现了10次，那么十位上的数字之和就是10+20+30+……+90=450 它有能被9整除同样的道理，100~900 百位上的数字之和为4500 同样被9整除也就是说1~999这些连续的自然数的各个位上的数字之和可以被9整除;同样的道理：1000~1999这些连续的自然数中百位、十位、个位上的数字之和可以被9整除(这里千位上的“1”还没考虑，同时这里我们少2021__022******** 从1000~1999千位上一共999个“1”的和是999，也能整除;2021__022********的各位数字之和是27，也刚好整除。

最后答案为余数为0。

7年级奥数题2：A和B是小于100的两个非零的不同自然数。

求A+B分之A-B的最小值解：(A-B)/(A+B) = (A+B - 2B)/(A+B) = 1 - 2B/(A+B) 前面的 1 不会变了，只需求后面的最小值，此时 (A-B)/(A+B) 最大。

对于 B / (A+B) 取最小时，(A+B)/B 取最大，问题转化为求 (A+B)/B 的最大值。

(A+B)/B = 1 + A/B ，最大的可能性是 A/B = 99/1 (A+B)/B = 100 (A-B)/(A+B) 的最大值是：98 / 100 7年级奥数题3：已知A.B.C都是非0自然数,A/2 + B/4 + C/16的近似值市6.4,那么它的准确值是多少答案为6.375或6.4375 因为A/2 + B/4 + C/16=8A+4B+C/16≈6.4，所以8A+4B+C≈102.4，由于A、B、C为非0自然数，因此8A+4B+C为一个整数，可能是102，也有可能是103。

4,5,6,7年级奥数培优经典试题1(配详解)

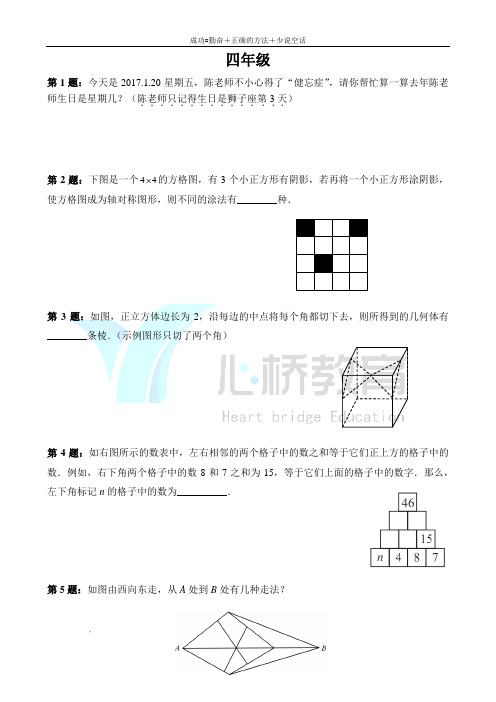
第1题：今天是2017.1.20星期五，陈老师不小心得了“健忘症”，请你帮忙算一算去年陈老师生日是星期几？（陈老师．．是狮子座第．．．．．3．天．）．．．生日．．．只记得第2题：下图是一个44的方格图，有3个小正方形有阴影，若再将一个小正方形涂阴影，使方格图成为轴对称图形，则不同的涂法有________种．第3题：如图，正立方体边长为2，沿每边的中点将每个角都切下去，则所得到的几何体有________条棱．（示例图形只切了两个角）第4题：如右图所示的数表中，左右相邻的两个格子中的数之和等于它们正上方的格子中的数．例如，右下角两个格子中的数8和7之和为15，等于它们上面的格子中的数字．那么，左下角标记n的格子中的数为__________．第5题：如图由西向东走，从A处到B处有几种走法？第1题：用1、2、2、3、3、3、0、0、0、0组成十位数，一个0都不读的有_______个，只读一个0的有__________个。

第2题：在下面的正方形区域中再涂一个色块，使之与原有的三个色块形成轴对称图形，共有________种涂法．第3题：如图，在圆心为O的半圆上，三个长方形的对角线长分别为a、b、c，请比较a、b、c的大小关系。

第4题：有7只小猴A、B、C、D、E、F、G，每只小猴有若干粒花生。

它们互相赠送：第一次由A给其它小猴，所给的花生数等于其它小猴手中原有的花生粒数；第二次由B给其它小猴，所给的花生数等于其它小猴手中现有的花生粒数，……最后由G给其它小猴，所给的花生数等于其它小猴手中现有的花生粒数。

结果每只小猴都有花生640粒。

那么D原有的花生粒数为___________。

第5题：将正方形纸片由下往上对折，再由左向右对折，称为完成一次操作(见下图).按上边规则完成五次操作以后，剪去所得小正方形的左下角.问:当展开这张正方形纸片后，一共有________个小孔第1题：同种型号的两辆车，每辆车里最多能载20桶油（包括油箱内的油），每桶油能使汽车前进54千米，每辆车都可向另一辆车借油。

小学至中学奥数题及答案

小学至中学奥数题及答案奥数，即奥林匹克数学竞赛，是一种旨在培养学生数学思维和解决问题能力的竞赛。

下面是一些适合小学至中学学生的奥数题目及答案：1. 题目：一个数列，前三个数为 1，2，3，从第四个数开始，每个数都是前三个数的和。

求第 10 个数是多少？答案：这个数列是一个斐波那契数列，第 10 个数是 144。

2. 题目：一个长方体的长、宽、高分别是 10 厘米、8 厘米和 6 厘米。

如果把这个长方体的表面涂上油漆，然后切成 1 立方厘米的小正方体，那么至少有多少个小正方体没有被涂上油漆？答案：首先，计算长方体的体积：10×8×6=480 立方厘米。

切成1 立方厘米的小正方体后，共有 480 个。

由于长方体的内部小正方体不会被涂上油漆，所以需要计算内部的层数。

内部的长、宽、高分别是 8 厘米、6 厘米和 4 厘米，因此内部的小正方体数量是8×6×4=192 个。

所以至少有 192 个小正方体没有被涂上油漆。

3. 题目：一个圆的半径是 5 厘米，求这个圆的面积。

答案：圆的面积公式是 \( A = \pi r^2 \)，其中 \( r \) 是圆的半径。

将半径 5 厘米代入公式，得到 \( A = \pi \times 5^2 = 25\pi \) 厘米²。

取 \( \pi \) 为 3.14，计算得到面积约为\( 78.5 \) 厘米²。

4. 题目：一个班级有 40 名学生，其中 2/3 的学生喜欢数学，1/4 的学生喜欢英语。

如果喜欢数学的学生中有 1/5 也喜欢英语，那么喜欢数学但不喜欢英语的学生有多少人？答案：首先计算喜欢数学的学生数：40 × 2/3 = 26.67，向下取整为 26 人。

喜欢英语的学生数为40 × 1/4 = 10 人。

喜欢数学且英语的学生数为26 × 1/5 = 5.2，向下取整为 5 人。

初一奥数竞赛试题及答案

初一奥数竞赛试题及答案一、选择题（每题5分，共20分）1. 下列哪个数是最小的正整数？A. 0B. 1C. -1D. 2答案：B2. 一个数的平方是16，这个数可能是：A. 4B. -4C. 4或-4D. 以上都不是答案：C3. 一个数的立方是27，这个数是：A. 3B. -3C. 3或-3D. 以上都不是答案：A4. 以下哪个分数是最接近0.5的？A. 1/2B. 2/3C. 3/5D. 4/7答案：B二、填空题（每题5分，共20分）1. 一个数的相反数是-5，那么这个数是______。

答案：52. 如果一个数的绝对值是8，那么这个数可能是______或______。

答案：8，-83. 一个数的平方是25，那么这个数是______或______。

答案：5，-54. 一个数的立方是-8，那么这个数是______。

答案：-2三、解答题（每题10分，共60分）1. 计算下列表达式的值：\((3x - 2) + (2x + 5)\)。

答案：\(5x + 3\)2. 一个数加上它的相反数等于多少？答案：03. 一个数乘以它的倒数等于多少？答案：14. 一个数的立方等于它本身，这个数可能是多少？答案：1，-1，05. 一个数的平方加上它的两倍等于8，求这个数。

答案：2或-46. 一个数的立方加上它的平方加上它本身等于64，求这个数。

答案：4四、证明题（每题10分，共20分）1. 证明：如果一个数的平方等于它的相反数，那么这个数只能是1或-1。

答案：设这个数为x，则有\(x^2 = -x\)。

移项得\(x^2 + x = 0\)，因式分解得\(x(x + 1) = 0\)，所以\(x = 0\)或\(x = -1\)。

但题目要求是正数，所以只能是1或-1。

2. 证明：如果一个数的立方等于它本身，那么这个数只能是1，-1或0。

答案：设这个数为x，则有\(x^3 = x\)。

移项得\(x^3 - x = 0\)，因式分解得\(x(x^2 - 1) = 0\)，即\(x(x - 1)(x + 1) = 0\)，所以\(x = 0\)或\(x = 1\)或\(x = -1\)。

4,5,6,7,8年级奥数培优经典试题23(配详解)

第1关：计算：20172016201620172016201720172017-⨯-⨯第2关：一座99层摩天大楼的电梯上，有如图所示显示楼层的液晶屏，由于屏幕受到损坏，显示左边数字的7根线段中有1根不能亮，显示右边数字的7根线段中有3根不能亮，那么在电梯运行的过程中，最多还有多少个楼层的数字显示是正确的？第3关：甲、乙、丙、丁、戊五位同学的座位如图所示，现要求每个人都换到与原来座位不相邻的位置上，总共有多少种换座位的方法？第4关：甲、乙、丙、丁、戊、己六位同学的座位如图，现要求每个人都换到与原来不相邻（没有公共边）的位置上，那么有多少种换座位的方法？第5关：给四（1）班同学分苹果，第一组每人3个，第二组每人4个，第三组每人5个，第四组每人6个。

已知第二组和第三组共有19个小朋友，第一组人数是第二组的2倍，第三组和第四组人数相等，总共分出去201个苹果，那么该班共有多少位同学？甲乙丙丁戊第1关：从1~11这11个数中去掉1个数，将剩下的10个数分别填入图中，使得每条直线上的各数之和都相等。

第2关：如左图是一个四位数除以一个一位数的除法竖式，右图是这个四位数除以另一个一位数的除法竖式，求这个四位数是多少？第3关：排成一行的学生，从左到右1至3报数，最后一人报2.从右到左1至m报数，最后一人报1，这里m与3互质。

现凡报过1的学生出列，其余原地不动，共留下62名学生，其中有21对学生原来是相邻的，请问原来共有多少名同学？m的值是多少？第4关：甲、乙、丙、丁四车在一条路上行驶。

甲车8点追上乙车，10点与丁车相遇，12点与乙相遇；乙车13点与丙车相遇，14点追上乙车。

请问：丙车和丁车几点几分相遇？第5关：现有甲、乙、丙、丁、戊5个人，每个人都来自不同的城市，开不同品牌的车，喝不同种类的茶，穿不同颜色的衬衫，一次聚会上他们遇到了一起，把车从左到右排成了一行，已知：（1）甲开奔驰；（2）乙穿绿衬衫；（3）丙喝碧螺春；（4）宝马车紧挨在奥迪车的左边；（5）宝马车的主人喝铁观音；（6）北京人穿蓝衬衫；（7）丰田主人来自天津；（8）中间那辆车的主人喝龙井茶；（9）丁的车在最左边；（10）上海人的车在穿红衬衫人的车旁边；（11）穿白衬衫人的车在天津人的车旁；（12）广州人喝菊花茶；（13）戊是重庆人；（14）丁的车在别克车的旁边；（15）上海人的车挨着喝乌龙茶的人的车。

初一培优数学试题及答案

初一培优数学试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. 0B. -1C. 1D. 2答案：C2. 一个数的相反数是-5，那么这个数是：A. 5B. -5C. 0D. 10答案：A3. 如果一个角的补角是120°，那么这个角的度数是：A. 60°B. 120°C. 180°D. 240°答案：A4. 一个数的绝对值是5，那么这个数可能是：A. 5B. -5C. 0D. 以上都是答案：D5. 一个三角形的两个内角分别是30°和60°，那么第三个内角的度数是：A. 90°B. 60°C. 30°D. 120°答案：A6. 计算下列表达式的值：(3x - 2) + (2x + 1) =A. 5x - 1B. 5x + 1C. 3x - 1D. 3x + 1答案：B7. 一个数的平方是36，那么这个数是：A. 6B. -6C. 6或-6D. 36答案：C8. 一个数的立方是-8，那么这个数是：A. 2B. -2C. 8D. -8答案：B9. 一个数的倒数是1/2，那么这个数是：A. 2B. -2C. 1/2D. 1答案：A10. 一个数的平方根是4，那么这个数是：A. 4B. -4C. 16D. -16答案：C二、填空题（每题4分，共20分）1. 一个数的立方等于它本身，这个数是_______。

答案：0或1或-12. 如果一个数的绝对值是它本身，那么这个数是_______。

答案：非负数3. 一个数的相反数是它本身，这个数是_______。

答案：04. 一个数的平方等于它本身，这个数是_______。

答案：0或15. 一个数的立方等于它本身，这个数是_______。

答案：0或1或-1三、解答题（每题10分，共50分）1. 计算：(2x + 3)(x - 4) = _______。

小学数学6年级培优奥数讲义第16讲比较数的大小(含解析)

第16讲比较数的大小①小数的大小比较常用方法；②分数的大小比较常用方法；③数的估算时常用方法。

一、小数的大小比较常用方法为方便比较，往往把这些小数排成一个竖列，并在它们的末尾添上适当的“0”，使它们都变成小数位数相同的小数.(如果是循环小数，就把它改写成一般写法的形式)二、分数的大小比较常用方法⑴通分母：分子小的分数小.⑵通分子：分母小的分数大.⑶比倒数：倒数大的分数小.⑷与1相减比较法：分别与1相减，差大的分数小．(适用于真分数)⑸重要结论：①对于两个真分数，如果分子和分母相差相同的数，则分子和分母都大的分数比较大；②对于两个假分数，如果分子和分母相差相同的数，则分子和分母都小的分数比较大．⑹放缩法在实际解题的过程中，我们还会用到其它一些思路！同学们要根据具体情况展开思维！三、数的估算时常用方法(1)放缩法：为求出某数的整数部分，设法放大或缩小．使结果介于某两个接近数之间，从而估算结果．(2)变换结构：将原来算式或问题变形为便于估算的形式．考点一：两个数的大小比较例1、如果a=20052006，b=20062007，那么a，b中较大的数是学习目标典例分析知识梳理例2、如果A =111111110222222221，B =444444443888888887,A 与B 中哪个数较大？例3、在 a=20032003×2002和 b=20022003×2003中，较大的数是______ ，比较小的数大______ 。

例4、试比较: 29622222⨯⨯⨯⨯个与18533333⨯⨯⨯⨯个哪一个大?例5、已知：258998369999A =⨯⨯⨯⨯，那么A 与0.1中比较大，说明原因；考点二：多个数的比较例1、(1)把下列各数按照从小到大的顺序排列：37　，513，916，1528(2)(幼苗杯数学邀请赛)把下列分数用“<”号连接起来：1017 ，1219，1523，2033，6091例2、在下面9个算式中:① 35520+，② 36620+,③ 37720+,④ 38820+,⑤ 39920+，⑥ 3101020+，⑦ 3111120+，⑧ 3121220+,⑨ 3131320+,第几个算式的答数最小，这个答数是多少?考点三：数的估算例1、求数10100a =+ 10101+ 10102++ 10110的整数部分．例2、求数1111110111219+++的整数部分是几？例3、已知()111111115111929411110099N k k =++++++++++-，求N 的整数部分．➢课堂狙击1、如果222221333331,222223333334A B==，那么A和B中较大的数是.2、有8个数，0.51，23,59, 0.51,2413,4725是其中6个，如果按从小到大的顺序排列时，第4个数是0.51，那么按从大到小排列时，第4个数是哪一个数?3、将131250、2140、0.523、0.523、0.52从小到大排列，第三个数是________.4、甲、乙两个天平上都放着一定重量的物体，问：哪—个是平衡的?5、a=10.8+10.98+10.998+10.9998+10.99998，a的整数部分是。

小学数学奥数题及答案110道(完整版)

小学数学奥数题及答案110道(完整版)题目1：在一个减法算式里，被减数、减数与差的和等于120，而减数是差的3 倍，那么差等于多少？答案：因为被减数= 减数+ 差，被减数+ 减数+ 差= 120，所以被减数= 60。

又因为减数是差的3 倍，设差为x，则减数为3x，可得4x = 60，x = 15，所以差等于15。

题目2：两个数的和是682，其中一个加数的个位是0，若把0 去掉则与另一个加数相同，这两个数分别是多少？答案：一个加数个位是0，去掉0 与另一个加数相同，说明一个加数是另一个加数的10 倍。

较小的加数为682÷(10 + 1) = 62，较大的加数为62×10 = 620。

题目3：鸡兔同笼，共有30 个头，88 只脚。

求笼中鸡兔各有多少只？答案：假设全是鸡，共有脚30×2 = 60 只，比实际少88 - 60 = 28 只。

因为每只兔比鸡多4 - 2 = 2 只脚，所以兔有28÷2 = 14 只，鸡有30 - 14 = 16 只。

题目4：小明在计算除法时，把除数72 写成27，结果得到的商是26 还余18，正确的商应该是多少？答案：先求出被除数：27×26 + 18 = 702 + 18 = 720，正确的商为720÷72 = 10。

题目5：一条公路长1800 米，在公路的两侧从头到尾每隔9 米栽一棵杨树，一共栽多少棵杨树？答案：一侧栽树：(1800÷9 + 1) = 201 棵，两侧共栽树201×2 = 402 棵。

题目6：甲、乙两数的平均数是40，乙、丙两数的平均数是45，甲、丙两数的平均数是53，求甲、乙、丙三个数的平均数。

答案：甲+ 乙= 80，乙+ 丙= 90，甲+ 丙= 106，三式相加得2×(甲+ 乙+ 丙) = 276，甲+ 乙+ 丙= 138，平均数为138÷3 = 46。

4,5,6,7,8年级奥数培优经典试题24(配详解)

第1关：下列质数中不能写成三个合数之和的是（）A．13 B．17 C．19 D．23第2关：用三个小正方形仅能拼出和两种不同的图形（拼图时要求两个相连接的单位正方形有一条边完全重合，并且各正方形不重叠），如果旋转之后能够重合的图形算一种，那么用四个单位正方形能拼出的四个不同图形的种数是（）.A.4种B.5 种C.6种D.大于6种第3关：甲、乙、丙、丁四人，每三个人的平均年龄加上余下一人年龄分别为29，23，21和17，这四人中最大年龄与最小年龄的差是（）A．6 B.9 C.12 D.18第4关：1到100的一百个自然数中，每次取出两个数，使和大于100，这样的取法共有（）A.2500种B.2000种C.1250种D.500种第5关：甲、乙、丙、丁4位老师各教2门不同的课，已知：①甲在星期二没课；②乙在星期一不给一班上课；③丙星期二前两节都有课；④物理老师星期一前两节没课。

请问甲、乙、丙、丁4位老师各教哪两门课？第1关：x 表示不超过x 的质数的个数，如5＝3，即不超过5的质数有2、3、5共有3个，试求1+9×19的值。

第2关：从甲地到乙地的公路，只有上坡路和下坡路，没有平路。

一辆汽车上坡时每小时行驶20千米，下坡时每小时行驶35千米，车从甲地开往乙地需9个小时，从乙地到甲地需217小时，那么从甲地到乙地需行驶的上坡路和下坡路分别为（）A.140千米，70千米B.70千米和140千米C.210千米，140千米D.140千米和210千米第3关：“早”“上”“好”表示三个由小到大的不超过5的整数，并且早＋上＋好＝早×上×好，符合条件的数组“早”“上”“好”共有多少组？分别是？第4关：如图，在9×9格子纸上，三角形ABC 的三个顶点都是格点。

若存在格点P 使得三角形P AB 与三角形P AC 的面积相等，就称P 点为“好点”。

那么在这张格子纸上共有_________个“好点”。

4,5,6,7年级奥数培优经典试题8(配详解)

四年级第1题：计算：__1.1=3.37.79.9+5.5+++++11+++17.19.__________1917151311.13.15.第2题：某年五月份所有周日的日期数之和等于85（例如：5月3日是周日，日期数为3），问：这一年的儿童节是星期几？第3题：电影院有30排座位，每排40个座位，如果有1000人看电影，那么至少有多少排坐的人数相同？第4题：在餐厅里小明的爸妈和小红的爸妈四人在聚会，分别是A、B、C、D，他们分别穿着红、蓝、黑、白色的衣服，坐在同一张桌子两边，桌子每边坐两人，并且他们正好和另一边的某人面对面。

已知：①小明的妈妈坐在穿黑色衣服人C的左侧；②A穿着白色的衣服；③穿红色衣服和穿蓝色衣服的人坐在同一边；④穿白色衣服的对面是穿蓝色衣服的人；⑤面对面的两人性别相同；⑥C的对面是B；⑦小红的爸爸穿红衣服。

请问A、B、C、D分别是谁？穿着什么颜色的衣服？第5题：认真观察图一中的4个图中阴影部分构成的图案，回答下列问题.图一（1）请写出这四个图案都具有的两个特征。

特征1：________________________；特征2：________________________.（2）请在图二中设计出你心中最美丽的图案，使它也具备你所写出的上述特征.图二第1题：三个质数的倒数之和为2431551，那么这三个质数之和是多少？第2题：将一个棱长为整厘米数的长方体六个面都涂上红色，然后将它切割成边长为1厘米的正方体。

在这些正方体中，6个面都没有涂红色的有165块，求长方体的体积是多少？第3题：（1）满足万位>百位>个位，千位<十位的五位数有____________个（2）满足万位<百位<个位，千位>十位的五位数有____________个第4题：有一种足球是由32块黑白相间的牛皮缝制而成的，黑皮可看做正五边形；白皮可看做正六边形，请你求出白皮、黑皮的块数.第5题：上周我们出了一道题，说有1000个一模一样的瓶子，其中有999瓶是普通的水，有1瓶是毒药，任何喝下毒药的生物都会在一星期之后死亡，现在已经知道如果有10个小白鼠和一星期的时间的答案是将瓶子从0至999依次编号，然后全部转换为10位二进制数，让第一只老鼠喝掉所有二进制数右起第一位是1的瓶子，让第二只老鼠喝掉所有二进制数右起第二位是1的瓶子，依次类推，第十只老鼠喝掉所有二进制数右起第十位是1的瓶子。

六年级奥数强化训练16(含答案)

六年级奥数强化训练161．计算：1002－992＋982－972＋…＋22－12 =（5050 ）。

2．两个自然数和是72，最大公约数与最小公倍数的和是216，这两个数分别是（3042 ）。

3．下图中,有( 17 )个三角形。

4．一小长方体的各棱长之和是48cm，并且它的长是宽的2倍，高和宽相等，那么，这个长方体的体积是（54 ）cm3。

5．一次测验共出5道，做对一道题得1分，已知26人平均分不少于4.8分，最低得3分，至少有3人得4分，则得5分的有（22 ）人。

6．从一张19厘米长、14厘米宽的长方形纸上最多能剪下（17 ）张5厘米长、3厘米宽的长方形小纸片。

7．从小到大排列着十个自然数4，5，6，7，8，9这六个数，从中取出若干个相邻的数相加，使其和是11的倍数为一组，那么不同的取法共有（10 ）组。

8．在正方形ABCD中，E，F是所在边中点，如果正方形面积是20，四边形ABCP的面积是（15 ）。

9．用甲乙两种糖配成什锦糖，如果用3份甲种糖和2份乙种糖配成什锦糖，比用2份甲种糖和3份乙种糖配成的什锦糖每千克贵1.32元，那么，每千克甲种糖比每千克乙种糖贵（ 6.6 ）元。

10．有四位小朋友的体重都是整千克数，他们两两合称体重，共称了5次，称得的千克数是99、113、125、130、144，其中有两人没有一起称过，那么，这两人中体重较重的是（66 ）千克。

11．六年二班部分学生学工劳动，由张师傅领队到工厂学习加工零件，张师傅和学生加工的零件一样多，半天加工零件共374个，学生分成三组，每组不少于10人，每组学生有（11 ）人，每人加工（11 ）个零件。

12．某人乘船由A地顺流而下到达B地，然后又逆流而上到达C地，共用3时。

船在静水中的速度每时8千米，水速每时2千米，如果A、C两地距离为2千米，求A、B两地距离。

10或12.5。

初一奥数竞赛考试题及答案

初一奥数竞赛考试题及答案一、选择题1. 一个数列的前三项为 2, 3, 5，每一项都是前两项的和，那么第10项是多少？A. 144B. 145C. 146D. 147答案：D2. 一个正整数，如果加上100后是一个完全平方数，那么这个数最小是多少？A. 49B. 50C. 51D. 52答案：B3. 一个长方体的长、宽、高分别为 a, b, c，且 a < b < c，如果长方体的体积是 216 立方厘米，那么 a 的可能值是？A. 3B. 4C. 6D. 8答案：C二、填空题1. 一个数的平方比它本身大 40，这个数是 _______。

答案：7 或 -72. 一个数列的前三项为 1, 2, 3，每一项都是前一项的两倍加上 1，那么第 5 项是多少？答案：11三、解答题1. 一个水池有一个进水管和一个出水管，单独开进水管 5 小时可以注满水池，单独开出水管 3 小时可以放空水池。

现在同时打开进水管和出水管，需要多少时间才能注满水池？解答：设水池的容量为 V 升。

进水管的流量为 V/5 升/小时，出水管的流量为 V/3 升/小时。

设同时打开两个水管需要 t 小时注满水池，则有：(V/5 - V/3) * t = V解得 t = 15/2 = 7.5 小时。

2. 一个班级有 40 名学生，其中 1/4 喜欢数学，1/3 喜欢英语，1/6 喜欢历史，剩下的学生喜欢科学。

问喜欢科学的有几人？解答：喜欢数学的学生有 40 * 1/4 = 10 人，喜欢英语的学生有40 * 1/3 ≈ 13.33，取整数为 13 人，喜欢历史的学生有 40 * 1/6 ≈ 6.67，取整数为 7 人。

喜欢科学的人数为：40 - 10 - 13 - 7 = 10 人。

结束语：以上是初一奥数竞赛考试题及答案，希望同学们能够通过这些题目，锻炼自己的逻辑思维能力和数学解题技巧，为未来的学习打下坚实的基础。

人教版2021-2022学年小升初奥数培优竞赛精选题(附答案)

人教版2021-2022学年小升初奥数培优竞赛精选题姓名：___________班级：___________考号：___________一、选择题1．某大学某班学生总数为32人，在第一次考试中有26人及格，在第二次考试中有24人及格，若两次考试中，都没有及格的有4人，那么两次考试都及格的人数是（）。

A．22 B．18 C．28 D．262．林辉在自助餐店就餐，他准备挑选三种肉类中的一种肉类，四种蔬菜中的二种不同蔬菜，以及四种点心中的一种点心。

若不考虑食物的挑选次序，则他可以有多少不同选择方法？（）。

A．4 B．24 C．72 D．1443．欲建一道长100尺，高7尺的单层砖墙，能够使用的砖块有两种：长2尺高1尺或长1尺高1尺（砖块不能切割）。

垂直连接砖块必须如右图所示交错间隔，且墙的两端必须砌平整。

试问至少需要多少砖块才能建成此道墙？（）。

A．347 B．350 C．353 D．3664．在一幅比例尺为1∶200的地图上标注有一个长方形的鱼塘，该鱼塘的长与宽之比为3∶2，在地图上量得的周长为30厘米。

则该鱼塘的实际面积是（）平方米。

A．216 B．432 C．864 D．9005．某集团三个分公司共同举行技能大赛，其中成绩靠前的X人获奖。

如获奖人数最多的分公司获奖的人数为Y，问以下哪个图形能反映Y的上、下限分别与X的关系（）。

A．B．C．D．6．一个圆形的草地中央有一个与之同心的圆形花坛，在花坛圆周和草地圆周上各有3个不同的点，安放了洒水的喷头，现用直管将这些喷头连上，要求任意两个喷头都能被一根水管连通，问至少需要几根直管？（一根水管上可以连接多个喷头）（）。

7．有一个水池，池底不断有泉水涌出，且每小时涌出的水量相同。

现要把水池里的水抽干，若用5台抽水机40小时可以抽完，若用10台抽水机15小时可以抽完。

现在用14台抽水机，多少小时可以把水抽完（）。

A．10小时B．9小时C．8小时D．7小时8．甲乙两个班的士兵同时从起点出发，向10公里外的目的地匀速急行军，甲乙两班的速度分别为每分钟250米和200米。

奥数培优超常思维竞赛初一年级数学试卷及答案

超常思维竞赛数学初一年级考试时间：100 分钟满分 150 分1. 一个正三角形全涂上黑色，每次做一个变换，即把正黑三角形分成四个全等的小三角形，中间的小正三角形涂上白色(如图). 经过五次变换后，仍是黑色的部分占整个三角形的（）.A.(12)5B.(23)5C.(34)5D.(45)5E.132.在某种计算机语言(例如 APL)中，当一个代数式中没有圆括号时，式中的运算规定为从右到左逐一进行.例如，在这种语言中的a ×b −c ，就相当于在通常代数记号中的a(b −c) . 现在用这种语言书写了一个式子：a ÷b −c +d ，那么用通常代数记号表示时，它应是（）.A.ab −c +dB.ab −c −dC.d+c−b aD.ab−c+dE.ab−c−d3.冥王星有三颗卫星，卫星1绕冥王星一周为6天，卫星2绕冥王星一周为10天，卫星3绕冥王星一周为15天. 从图中所示的位置开始，三颗卫星最少需要（）天才能同时回到原来的位置.A.20B.30C.60D.100E.3604.如图所示，等腰△ABC 中，AB =AC ，△DEF 为内接正三角形，∠BFD =α，∠ADE =β，∠FEC =γ，则（）.A.β=α+γ2B.β=α−γ2C.α=β−γ2D.α=β+γ2E.以上都不对5.若(r +1r )2=3,则r 3+1r 3=( ). A.−1B.0C.1D.2E.36.一个裁缝在一棵树下遇见一只乌龟. 当乌龟是裁缝现在年龄时，裁缝只有其现在年龄的14. 当树是乌龟现在年龄时，乌龟只有其现在年龄的17. 若三者现在年龄之和为264岁，则乌龟的现在年龄为（）岁.A.55B.66C.77D.88E.997.循环小数0.328181818181⋯可以被等同表示为m n，m 与n 为互素正整数，则m +n 的值为( ) A.1000B.1461C.2021D.19181E.无法确定8.一个正方形的地面用同样大小的正方形瓷砖铺满，两条对角线上铺黑色的，其他地方铺白色的，如图所示. 如果铺满地面共用101块黑色的瓷砖，那么，铺满地面所用瓷砖的总块数是（）.A.121B.625C.676D.2500E.26019.在锐角△ABC 中，三个内角的度数都是质数，以下说法错误的有( ).A.只有一个，且为等腰三角形 B.至少有两个，且都为等腰三角形C.只有一个，但不是等腰三角形D.至少有一个，其中有非等腰三角形E.这样的三角形根本不存在10.有四个数，每次从中挑选三个数，求其平均数，再把第四个数加上.因为每次可留下一个不同的数不选，因此这样的操作有四种不同的方式. 已知得出的四个结果为7，21，23与29，则原来的四个数中最大的数是（）.A.18B.19C.20D.21E.以上都不对11.如图所示，在一个4×6的球台上，有两个小球P和Q. 若小球P依次经过球台边AB，BC，CD和DA反弹后，恰好击中小球Q. 则小球P击出时，瞄准应是AB边上的(图中A k(k=1，2，…，5)为AB边的六等分点)（）.A.A2B.A3C.A4D.A5E.其他点12. 音乐家勃拉姆斯曾经给一位名为Agade(阿加特)的歌唱家写过一首六重奏.如果字母I不为零，当如下加法算式成立时，S+I+N+G=（）.(相同的字母代表相同的数字，不同的字母代表不同的数字.)A.20B.21C.22D.24E.2613.如图所示，在各边都相等的五边形ABCDE中，∠ABC=2∠DBE，那么∠ABC=（）.A.45°B.60°C.75°D.90°E.以上都不对14.在英国的康沃尔语(Cornish)中，对于200以下的数字读法都是采取二十进制的. 如果十进制中的147在二十进制中的读音是“seyth ha seyth ugens”，而十进制中的49在二十进制中的读音是“naw ha dew ugens”，那么二十进制中读音是“dew ha naw ugens”的数指的是十进制中的（）.A.168B.180C.182D.186E.以上都不对15.△ABC的三个内角∠BAC，∠ABC，∠ACB的外角依次记为α，β，γ，若β=2∠ABC，α−γ=40°，则∠BAC=（）.A.30°B.40°C.45°D.60°E.以上都不对16.某次数学竞赛共有12道试题，答对者每题得8分；未作答者每题得3分；答错者每题得0分. 小威在此次竞赛中的得分是35分，则他在此次竞赛中最多答错（）道题.A.4B.5C.6D.7E.以上都不对17.A，B，C 在距离为dm的跑道上等速赛跑，到终点时，A超过B为20m，B超过C为10m，A超过C为28m，则d=（）m.A.100B.150C.200D.400E.以上都不对18.如图所示，一个线快用完了的绕线筒，由绕在它上面的细线沿着很平的表面拉动.它的内筒的直径是5cm，外轮的直径是10cm. 假设只有滚动而没有滑动，当细线的端点移动12cm时，绕线筒将移动（）cm.A.8B.10C.8πD.10πE.以上都不对19.1898年6月9日英国强迫清政府签约，将香港975.1平方公里土地租借给英国99年. 1997年7月1日香港回归祖国，中国人民终于洗刷了百年耻辱. 已知1997年7月1日是星期二，那么，1898年6月9日是星期（）.A.一B.二C.六D.日E.以上都不对20.分数3713可以写成形式2+1x+1y+1 z其中(x，y，z)=（）.A.（1，5，3）B.（1，5，4）C.（1，4，3）D.（2，2，3）E.以上都不对21. 已知一数列有58项，每项都具有p+n型，其中p代表小于或等于61的所有质数2， 3，5，…，61之积，而n依次取2，3，4，…，59之值，设N为此数列中出现质数的数目，则N=（）.A.0B.1C.2D.3E.422. 如图所示，在大房间的一面墙壁上，边长为15cm的正六边形A横排20片和以其一部分所形成的梯形B，三角形C，D，E，菱形F等六种瓷砖毫无空隙地排列在一起. 已知墙壁高3.3m，仔细观察各层瓷砖的排列特点，其中菱形F瓷砖需使用（）片.A.180B.190C.200D.210E.以上都不对23.如图所示，3条直线p，q，r中的每条直线把此图分成2个具有相同面积的区域，则X，Y的大小关系是（）.A.X>YB.X≥YC.X<YD.X≤YE.以上都不对24.矩形PQRS按下图的方式分成9个大小都不相同的正方形(注意这是示意图，未按比例画出).所有正方形的边长都等于单位长的整数倍，其中最小的是一个2×2的正方形. 次小的正方形的边长等于（）个单位长.A.1B.2C.3D.4E.以上都不对25.小明有2cm×1cm×1cm的砖块若干块，打算用它们来构造一个大的积木. 当小明拼到如图所示的形状时，已用尽了所有的砖块，则小明原来有（）块砖块.A.50B.52C.54D.56E.以上都不对26.如图所示，点M是△ABC两个内角平分线的交点，点N是△ABC两个外角平分线的交点，已知∠CMB∶∠CNB=3∶2，则∠CAB的度数是（）.A.30°B.35°C.40°D.45°E.以上都不对27.一只狗追一只兔子，狗跳6次的时间兔子只跳了5次，狗跳4次的距离和兔子跳7次的距离相等. 兔子跑出5.5千米后狗开始在后面追，则兔子再跑出（）千米的路程时被狗追上.A.4B.4.5C.5D.5.5E.以上都不对28.有九个分数的和为1，它们的分子都是1，其中的五个分数是13，17，19，111，133，又其余四个分数的分母个位数字均为5，则这些分数的分母分别是( )A.5，15，35，105B.5，25，35，135C.5，15，45，385D.5，25，105，385E.5，15，25，45，13529.凸四边形ABCD中，∠ADB=∠ABC=105°，∠DAB=∠DCB=45°，若A点到直线BD的距离为101，则线段CD的长度是（）.A.101B.151.5C.202D.303E.以上都不对30.平行四边形内的一点到四条边的距离分别是1，2，3，4，则这样的平行四边形面积的最小值为（）.A.21B.24C.25D.20E.以上都不对超常思维竞赛数学初一年级答案考试时间：100分钟满分150分。