一个简单的频率谱瀑布图
瀑布图分析注意事项

瀑布图分析经常用于评估旋转机械噪声和/或振动的表现。
这个处理过程要对随转速变化的每个固定长度的子段数据块使用FFT变换计算频谱,转速的变化可能是升速也可能是降速。
需要花时间去采集足够的数据以便得到一个时域数据块用于瞬时(单次)FFT计算(实际时域数据块是很短的),而在采集这个数据块的同时,机械设备的转速将从时域数据块采集开始时到结束一直在发生变化。
跟踪转速的瀑布图分析仍然采用“跳跃的FFT变换”方式,与跳跃时间(跟踪时间方式)的区别在于,当执行FFT变换时,跳跃的步长为等转速步长,而非等时间步长。
以等转速步长计算瞬时FFT频谱,如转速步长为25rpm,则表示转速每变化25rpm,计算一次瞬时频谱,每次FFT变换对应的时域数据长度为频率分辨率的倒数。
每个数据块对应一个转速(实际上各个数据块对应的转速一直在变化,软件会按某种算法得到这个数据块对应的转速,如平均转速),然后按照转速的先后顺序将各瞬时频谱排列得到三维瀑布图。
而彩图则是用二维图来显示,只不过用颜色深浅来表示幅值大小。
在瀑布图或彩图中,频谱并不连续,各频谱之间有间距,间距为等转速步长。
在瀑布图中可以看出各频谱有间距,但在彩图中看不出来这种间距。
在这以发动机噪声数据为例说明以跟踪转速方式进行瀑布图分析的全过程。
图11中左上角为测试的全程时域数据,按等转速步长(跟踪时间则为等时间步长)计算每个固定长度的时域数据块(时间长度为频率分辨率的倒数)得到各数据块对应的瞬时频谱图。
然后按照等转速步长的时域数据块先后顺序将所有对应的瞬时FFT进行排列,得到三维瀑布图。
从测试的全程时域数据中取3个数据块进行说明,左上角三个阴影区域对应这3个时域数据块。
时域数据块长度为1s(频率分辨率为1Hz),计算其相应的瞬时频谱,由于采样频率不变,所以瞬时频谱对应的带宽都相同,这三个数据块对应的瞬时频谱如图8中间所示,对应的转速分别为1400.28,2799.91和4225.15rpm。
如何绘制频率分布图

频率 1 2 4 14 24 15 12 9 11 6 2 100 0.01 0.02 0.04 0.14 0.24 0.15 0.12 0.09 0.11 0.06 0.02 1
频数/组距 0.002 0.004 0.008 0.028 0.048 0.03 0.024 0.018 0.022 0.012 0.004 0.2
7 6 5 4 3 2 1 0 一
一 6 6
二 2 8
三 3 11
四 5 16
五 1
频数条 形图
17
系列1
二
三
四
五
作频率分布直方图的方法:
• 1、把横轴分成若干段,每一线段对应一个组的组 距; • 2、然后以此线段为底作一矩形,它的高等于该组 的频率/组距; • 这样得出一系列的矩形,每个矩形的面积恰好是 该组上的频率,这些矩形就构成了频率分布直方 图。
频率/组距
频率折 线图
0.08 0.06 0.04 0.02
频率直方 图
150.5 153.5
180.5
身高/cm
越光滑 思考: 若组距取得越小,则频率折线光滑程度会怎样?
例4、为了了解一大片经济林的生长情况,随机测量其中的100株的 底部周长,得到如下数据表(长度单位:cm):
135 125 98 97 102 117 110 113 99 110 121 92 110 102 96 109 100 104 103 112
解: (1)从表中可以看出,这组数据的最大值为135, 最小值为80,故全距为55,可将其分为11组,组距为5。 从第1组[80,85)开始,将各组的频数、频率和频率/组 距 填入表中
分组 频数 [80,85) [85,90) [90,95) [95,100) [100,105) [105,110) [110,115) [115,120) [120,125) [125,130) [130,135) 合计
按频率由低到高排列的电磁波谱

电磁波谱是按照电磁波的频率或波长来分类的。
以下是按频率从低到高排列的电磁波谱:1. 极低频 (ELF,Extremely Low Frequency):3 Hz - 30 Hz2. 超低频 (ULF,Ultra Low Frequency):30 Hz - 300 Hz3. 声 (Voice Frequency,VF) 或对讲 (Telecommunication Frequency):300 Hz - 3 kHz4. 甚低频 (VLF, Very Low Frequency):3 kHz - 30 kHz5. 低频 (LF, Low Frequency):30 kHz - 300 kHz6. 中频 (MF, Medium Frequency):300 kHz - 3 MHz7. 高频 (HF, High Frequency):3 MHz - 30 MHz8. 甚高频 (VHF, Very High Frequency):30 MHz - 300 MHz9. 超高频 (UHF, Ultra High Frequency):300 MHz - 3 GHz10. 卫星通信频率(SHF, Super High Frequency):3 GHz - 30 GHz11. 极高频 (EHF, Extremely High Frequency):30 GHz - 300 GHz在频谱范围的 300 GHz 之后,开始出现其他类型的电磁波,例如:12. 太赫兹波 (Terahertz waves):0.3 THz - 3 THz13. 红外线 (Infrared):3 THz - 430 THz14. 可见光 (Visible light):430 THz - 770 THz15. 紫外线 (Ultraviolet):770 THz - 30 PHz16. X射线 (X-rays):30 PHz - 3 EHz17. 伽马射线 (Gamma rays):3 EHz 及以上。
什么是瀑布图分析

什么是瀑布图分析分析旋转机械的振动噪声,离不开瀑布图分析,瀑布图分析是旋转机械振动噪声分析最常用的方法。
它采用“跳跃式的FFT变换”方式计算瞬时频谱,用三维图(瀑布图或colormap图)来显示分析结果,是所有瞬时FFT频谱的集总显示,如图1所示,各瞬时频谱按时间或转速先后顺序排列。
瀑布图分析不平均任何瞬时频谱,这对于待测旋转机械时刻变化的转速来说,非常有利于突出显示随转速变化的特征,如阶次特征;同时也能反映出共振特征。
图1 瀑布图显示分析结果1为什么要做瀑布图分析通常情况下,非旋转结构的频谱分析,我们使用二维频谱图来显示相应的结果,且二维频谱是平均之后的频谱,这时,频谱主要反映的是结构的共振特征。
对于旋转机械而言,结果显示谱图除了反映共振特性之外,还需要反映出与转速变化相关的信息。
这个信息就是所谓的阶次信息,我们知道旋转机械任一时刻的响应大多数都是以阶次的形式体现出来的,因此,在谱图中应能反映出结构相应的响应阶次。
如图2所示是某旋转机械的一个瞬时二维频谱,这个频谱图反映不出阶次随转速的变化关系。
另外,如果使用二维频谱图来分析旋转机械的共振特征,那么,将分不清楚共振频率与阶次对应的频率,特别是二者一致的情况下。
图2 二维频谱图另一方面,由于转速时刻变化,每一帧数据与下一帧数据对应的转频也是不相同的,如图3所示,对于这样的数据是不能使用平均处理的。
由于转速时刻变化,二维频谱图反映不出这种时刻变化的特性。
图3 重叠相邻两帧频域数据另一方面,对于某些特定的结构,如混合动力汽车,除了内燃机产生的阶次之外,还存在电机脉冲宽度调制产生的开关频率和伞状阶次,因此,阶次相当混乱,如图4所示。
对于这样凌乱的阶次,二维频谱图不足以显示其相应的特性。
图4 混合动力汽车的colormap图因此,对于旋转机械而言,需要这样一种分析方式:分析结果既能反映出与随转速变化的阶次信息,又能反映出结构的共振特性。
瀑布图分析刚好就是这样一种分析方式。
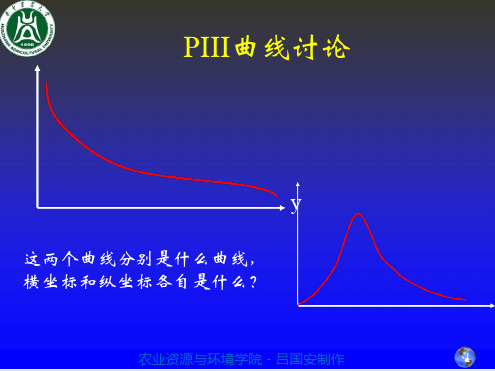
水文频率曲线的绘制

(2) 1500.0 959.8 1112.3 1005.6 780.6 901.4 1019.4 847.9 897.2 1158.9 1165.3 835.8 641.9 1112.3 527.5 1133.5 898.3 957.6
17454.7
(3)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
配线图
Q
Cs=2Cv
Cs=3Cv
1289.7
10%
频率p(%)
本节小结
一、经验频率计算公式 二、经验频率曲线的绘制及应用 三、重现期的概念 四、频率与重现期的关系 五、百年一遇洪水的含义 六、配线法步骤
(4)
1500.0 1165.3 1158.9 1133.5 1112.3 1112.3 1019.4 1005.6 959.8 957.6 901.4 898.3 897.2 847.9 835.8 780.0 641.9 527.5 17454.7
(5)
1.5469 1.2017 1.1951 1.1689 1.1470 1.1470 1.0512 1.0370 0.9898 0.9875 0.9296 0.9264 0.9252 0.8744 0.8619 0.8044 0.6621 0.5440 18
p
取标准化变量:
xx (称为离均系数) x Cv P( p ) f ( , Cs )d
p
x p ( p Cv 1) x
令模比系数
kp
xp x
xp k p x
实例 根据某地年雨量资料,已求得统计参数:
x =1000mm, CV=0.50,CS=2CV=1.0,若该地年
如何绘制伯德图课件PPT

,
其误20差lg均2为正3d分B贝数,误差范围与惯性环节类似。
相频特性是
当 时, G(j);arctg
(5-78)
0 G(j0)00
2021/3/10
12
当 1 时,G( j 1) 450 ;
当时,G(j)900 。
dbL()
20
一阶微分环节的相频特
20dB/dec
性如图 5-16 所示,相
角变化范是 00 至 900, 转折频率 1 处的相角
T
为450。比较 图 5-16和
5-14,可知,一阶微分
10
0
11 度 100
900 ()
450
精确特性
11
1
10 1
10
渐近特性
45o / dec
100 1
环节与惯性环节的对数 幅频特性和相频特性是
00
11
11
100
10
1
10 1
100 1
以横轴(ω轴)为对称的。 图5-16 一阶微分环节的Bode图
2021/3/10
6
设 ' 10 ,则有
2l0 g ' 2l1 0 g 0 2 2 0 l0 g (5-68)
可见,其对数幅频特性是一条在
d B L()
60
ω=1(弧度/秒)处穿过零分贝线
40
(ω轴),且以每增加十倍频降
20
20dB/dec
低20分贝的速度(-20dB/dec ) 变化的直线。
特性如图 5-20 所示。
00
0.05
2021/3/10
900
1.0
1800
1 10
自动控制理论5-2频域:伯德图共43页文档

比例因子 一阶因子
K
1jT1
微分和积分因子 二阶因子 滞后因子
j1
1 2T nj jT n2 1
j
4
1 比例因子
GjωK
L ( )
20 10 0 ( ) 10o
0o
2 0 lg K 10
10
100
100
比例因子的对数幅频特性是一条幅值为20lgK分贝,且 平行于横轴的直线,相频特性是一条和横轴重合的直线,相 角为00。K>1时,20lgK>0dB;K<1时,20lgK<0dB。
当出现揩振峰值时,Gjω 有最大值,即 gω 有最小值。
得到
d d ω ω g d d ω 1 T n 2 ω 22 2 ζT n ω 2 0
谐振频率 式中,
ωrT1n 12ζ2ωn 12ζ2
ωn
1 Tn
0 ζ 1
2
说明积分环节的对数幅频曲线是一条经过横轴 上ω=1这一点,且斜率为-20的直线。
6
相频与ω无关,值为-90°且平行于横轴的直线。
L ( ) 20
0 0 .1
( )
0o 0 .1
90o
20 1
1
10
10
7
3 微分因子
Gjωjω
微分环节是积分环节的倒数,它们的 曲线斜率和相位移也正好相差一个负号。
5-2 对数坐标图
表示系统频率特性的图形有三种: 对数坐标图 极坐标图 对数幅相图
1
一、对数坐标图
1. 对数幅频特性图: 横坐标:用频率ω的对数lgω分度。
纵坐标:L(ω)= 20lg|G(jω)| (dB), 采用线性分
度;
2.相频特性图
计算机绘制理论频率曲线
农业资源与环境学院-吕国安制作
29
农业资源与环境学院-吕国安制作
31
X 值 的 选 定
农业资源与环境学院-吕国安制作
34
农业资源与环境学院-吕国安制作
93 94 95 96 97
99 99.1 99.2 99.3 99.4
99.9 99.91 99.92 99.93 99.94
99.95 99.96 99.97 99.98 99.99
农业资源与环境学院-吕国安制作
16
利用XY散点图的输出结果
1000
900
800
700
600
横坐标和纵坐标都是等分
为什么要有实线与虚线?
农业资源与环境学院-吕国安制作
24
农业资源与环境学院-吕国安制作
25
选 择第 数一 据步 源
选
择 图 表 类
第 二 步
型
第三步:调整图表 线型 纵横坐标的最大值 纵横坐标的标题和单位 不显示横坐标的数据 标题
农业资源与环境学院-吕国安制作
28
第四步 横坐标频率数据的显示
3.28
20
经过海森转换
1000
900
800
700
600
500
400
300
200
100
0
0.00
1.00
2.00
3.00
4.00
5.00
6.00
7.00
农业资源与环境学院-吕国安制作
21
2 横坐标数据点位(实线)
水文频率曲线线型

第四节 水文频率曲线线型
内容提要:
正态分布,对数正态分布,皮尔逊Ⅲ型分布, 经验频率曲线
1.38 -1.35 -1.32
-2.33 -2.25 -2.18 -2.10 -2.03 -1.96 -1.88 -1.81 -1.74 -1.66 -1.59
99.9 -3.09 -2.95 -2.81 -2.67 -2.54 -2.40 -2.27 -2.14 -2.02 -1.90 -1.79
3、皮尔逊Ⅲ型频率曲线的应用
★ 在频率计算时,由已知的Cs值,查 值表得出不 同的P的 值,然后利用已知的 、Cv,通过式 即可求出与各种P相应的xp 值,从 而可绘制出皮尔逊Ⅲ型频率曲线。
★ 当Cs等于Cv的一定倍数时,P-Ⅲ型频率曲线的模比 系数KP = , 也已制成表格,见附表2"皮尔逊Ⅲ
型频率曲线的模比系数KP值表“。频率计算时,由 已知的Cs和Cv可以从附表2中查出与各种频率P相对 应的KP值,然后即可算出与各种频率对应的 =KP 。有了P和 的一些对应值,即可绘制出皮尔 逊Ⅲ型频率曲线。
20 50
80 95 99
2.33 1.67 2.47 2.54 2.62 2.68 2.75 2.82 2.89 2.96 3.02
1.64 2.0 1.70 1.73 1.75 1.77 1.80 1.82 1.84 1.86 1.88
0.84 0.84 0.83 0.82 0.82 0.81 0.80 0.79 0.78 0.77 0.76
03频率特性法——奈氏图和伯德图画法

1)
30
20db
[-20]
[-40]
0db
0.1
0.5 1
2
[-20]
10
30
100
ω
-20db --40db
[-40]
转折频率:0.5 2 30
例:已知单位反馈系统的开环传递函数 G(s) 100(s 2) s(s 1)(s 20)
试绘制开环对数频率特性曲线。 解:典型环节传递函数表示的标准形式
G(s) 10(0.5s 1) s(s 1)(0.05s 1)
其对应的频率特性表达式为
G( j )
10(0.5 j 1)
j( j 1)(0.05 j 1)
k 10, v 1
直接绘制系统开环
G( j )
10(0.5 j 1)
对数幅频特性的步骤
j( j 1)(0.05 j 1)
(1) 转折频率为: 1 1, 2 1 / 0.5 2, 3 20
(2) 在 1时: L() 20lg K 20lg10 20(dB)
(3) 过 =1、L() 20dB 的点,画一条斜率为-20dB/dec的斜
线,以此作为低频渐近线。
(4) 因第一个转折频率ω1=1,故低频渐近线画至ω1 =1为止, ➢经过ω1=1后曲线的斜率应为-40dB/dec; ➢当曲线延伸至第二个转折频率ω2 =2时,斜率又恢复 为-20dB/dec ; ➢直至ω3 =20时,曲线斜率再增加-20dB/dec,变为 -40dB/dec的斜线。至此已绘出系统的开环对数幅频特性 渐近线。
(3) 过ω=1 rad/s,20lgK这个点,作斜率等于 -20v dB/dec 的低频段的渐近线。
(4) 向右延长最低频段渐近线,每遇到一个转折频率改变一 次渐近线斜率:
求频率的流程图如下

接左边流程
接右下得出的数组Wn
上述流程图有如下说明:
1)全零点数字滤波器的转换函数为:
12212123()()()()(1)(1)(1)H Z H Z H Z H Z Z Z Z Z -----=⨯⨯=-+++
该全零点数字滤波器由三个简单滤波器1()H Z 、2()H Z 、3()H Z 级联而成,相应于各简单
12113222()()(1)(2)()()(2)
()()(1)(2)
y n x n x n x n y n y n y n y n y n n y n =--+-=+-=-+-
即前一个简单滤波器的输出作为后一个简单滤波器的输入,x(n)为输入,即为公式中的n x ,来自于数据文件1中的数据。
所以全零滤波器的最后输出3()()y n y n =,即流程图中的n w 。
2)在打开数据文件进行滤波之前,应先初始化使:
(1)0,(2)0x x -=-=;11(1)0,(2)0y y -=-=;22(1)0,(2)0y y -=-=,但
由于在C 中没有负下标的概念,所以在流程图中用变量,a b x x 分别代替(1),(2)x x --。
3)数据文件为1min 的采样数据,即共60×50×128个数据,循环次数即为该值。
4)公式中的f0=50Hz 。
频数分布图的做法(宏法)
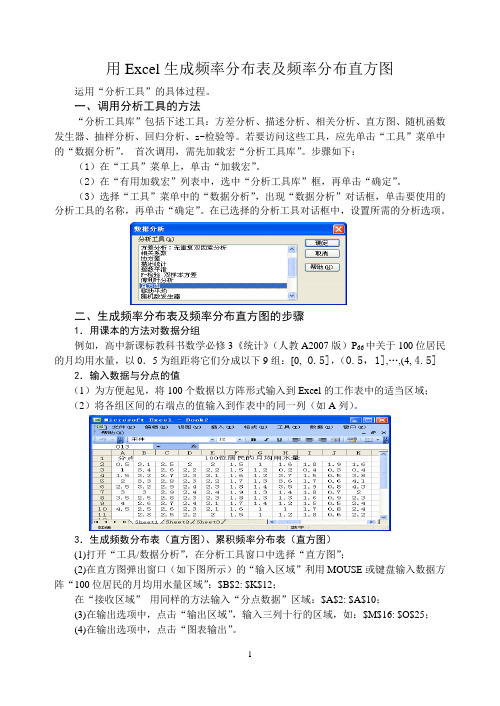
用Excel生成频率分布表及频率分布直方图运用“分析工具”的具体过程。
一、调用分析工具的方法“分析工具库”包括下述工具:方差分析、描述分析、相关分析、直方图、随机函数发生器、抽样分析、回归分析、z-检验等。
若要访问这些工具,应先单击“工具”菜单中的“数据分析”。
首次调用,需先加载宏“分析工具库”。
步骤如下:(1)在“工具”菜单上,单击“加载宏”。
(2)在“有用加载宏”列表中,选中“分析工具库”框,再单击“确定”。
(3)选择“工具”菜单中的“数据分析”,出现“数据分析”对话框,单击要使用的分析工具的名称,再单击“确定”。
在已选择的分析工具对话框中,设置所需的分析选项。
二、生成频率分布表及频率分布直方图的步骤1.用课本的方法对数据分组例如,高中新课标教科书数学必修3《统计》(人教A2007版)P66中关于100位居民的月均用水量,以0.5为组距将它们分成以下9组:[0, 0.5],(0.5,1],…,(4, 4.5] 2.输入数据与分点的值(1)为方便起见,将100个数据以方阵形式输入到Excel的工作表中的适当区域;(2)将各组区间的右端点的值输入到作表中的同一列(如A列)。
3.生成频数分布表(直方图)、累积频率分布表(直方图)(1)打开“工具/数据分析”,在分析工具窗口中选择“直方图”;(2)在直方图弹出窗口(如下图所示)的“输入区域”利用MOUSE或键盘输入数据方阵“100位居民的月均用水量区域”:$B$2: $K$12;在“接收区域”用同样的方法输入“分点数据”区域:$A$2: $A$10;(3)在输出选项中,点击“输出区域”,输入三列十行的区域,如:$M$16: $O$25;(4)在输出选项中,点击“图表输出”。
完成以上四步,点击“确定”按钮,立即出现如下所示的频数分布表(直方图)、累积频率分布表(直方图或折线图)运用中,应特别关注以下三点:(1)勿将频数当频率。
将容易验证,上述图表中的“频率”其实表示频数,这极可能是汉化Excel 时翻译的错误,所以应将表中“频率”改为“频数”,接收区的数据表示各组区间的右端值;(2) Excel 是按照左开右闭的方式对落在各区间的数据进行频数统计的;(3)Excel 对输入区域中的样本数据按区段分别统计频数时,遇到空单元格,系统会自动跳过。
振幅频谱图

1振幅频谱图:设想用一些不同线段的长度分别代表直流分量,一次谐波、二次谐波、n次谐波的振幅,然后将这些线段按频率的高低依次排序起来,用横坐标表示w=nw0的值,纵坐标表示n次谐波的振幅值,所画成的坐标图叫做振幅频谱图,表示2谱线:n次谐波振幅大小的线段叫做谱线。
3频带宽度:对于一个信号,从零频开始到需要考虑的最高分量的频率区间,称为频带宽度,简称频宽。
4过冲:由测量装置的惯性引起的波形幅度第一个达到最大值与稳定值之差。
5前沿上升时间:波形幅度从稳态的10%到90%所需的时间。
6固有频率:物体作自由振动时,与初始条件无关,而与系统的固有特性有关的振动频率。
7频率保持特性:若线性系统的输入为某一频率的简谐信号,则其稳态响应必是同一频率的简谐信号。
8线性度:线性度是指测量系统的输入、输出关系保持常值线性比例关系的程度。
即在系统的全量程A内,标定曲线与参考直线的最大偏差B与A的百分比。
9灵敏度:灵敏度为测量装置的输出与输入量变化之比。
10分辨力与分辨率:对于实际标定过程的第i个测点xi,当有Δxi,min变化时,输出就有可观测到的变化,那么Δxi,min就是该测点处的分辨力,分辨力与测量范围之比称为分辨率。
11截止频率:当保持电路输入信号的幅度不变,改变频率使输出信号降至最大值得0.707倍或某一特殊额定值时,该频率称为截止频率。
12传递函数:将输出与输入两者的拉普拉斯变换之比定义为传递函数。
13频率响应函数:定义为输出的傅里叶变化和输入的傅里叶变化之比。
是输出信号达到稳态后,输入信号与输出信号幅值之比,以及输入、输出信号的相位差随角频率变化的规律。
14幅频特性:输出、输入正弦信号振幅之比随频率的变化叫测量装置的幅频特性。
15相频特性:输出、输入正弦信号的相位差随频率的变化叫作测量装置的相频特性。
16集肤效应:随着电流频率的增高,越接近导线的表面,电流密度越大。
当频率很高时,电流绝大部分都集中在导线表皮的某一薄层内,而导线内部的电流密度几乎等于零,这种现象称为集肤效应。
探究频率分布表以及频率分布图的绘制

探究频率分布表以及频率分布图的绘制频率分布表以及频率分布图的绘制方法是这一节的基础知识,也是掌握本节知识的关键。
如果理解并掌握了这两种图表的绘制方法,我们相信,无论高考题怎样在本知识点出题,我们都不会束手无策。
频率分布表尤其是频率分布图的绘制过程要深刻理解。
初中我们曾经学过频率分布图和频数分布表,这使我们清楚的知道数据分布在各个小组的个数;频率分布表和频率分布图则是从各个小组数据在样本中所占的比例大小的角度,来表示数据分布的规律,具体的做法如下:1、求极差(即每一组中最大值与最小值的差)2、决定组距与组数组距与组数的确定没有固定的标准常常需要一个尝试和选择的过程。
将数据分组时,组数应力求合适,以使数据的分布规律能较清楚的呈现出来,组数太多或太少,都会影响我们了解数据的分布情况。
数据分组的组数与样本容量有关,一般样本容量越大,所分组数越多。
级差组数=组距3、将数据分组4、列频率分布表频率分布表中频数总合计为样本容量,频率合计为1;5、画频率分布直方图在频率分布直方图中,各小长方形与横轴平行的边长为组距,与横轴平行的边长为频率/组距,所以各长方形的面积表示相应各组的频率;这样频率分布直方图就以面积的形式反映了数据落在各个小组的频率的大小,各小长方形的面积的合等于1.例1 、在一小时内统计一传呼台接收到用户的呼唤次数,按每分钟统计如下:0 0 1 2 1 2 2 3 4 10 1 2 3 5 1 2 2 2 42 43 1 1 3 2 34 61 2 0 2 3 1 3 1 4 11 2 0 2 3 4 2 5 0 21 123 2 1 3 1 2 0写出每分钟内传呼呼唤次数的频率分布表,并画出频率分布图。
解:一分钟传呼呼唤次数的频率分布表及频率分布入图下:用样本频率分布估计总体频率分布,在生产生活中应用广泛,为考查学生的应用能力和应用意识,往往在该考点上设计考题,在考查该点时,也涉及到转化意识的渗透,会考查基本概念、基本方法、和计算。
