Robust Control Based on Feedback Linearization for Roll Stabilizing of Autonomous Underwater Ve

合集下载

Design and Implementation of a Bionic Robotic Hand

Design and Implementation of a Bionic Robotic Hand with Multimodal Perception Based on ModelPredictive Controlline 1:line 2:Abstract—This paper presents a modular bionic robotic hand system based on Model Predictive Control (MPC). The system's main controller is a six-degree-of-freedom STM32 servo control board, which employs the Newton-Euler method for a detailed analysis of the kinematic equations of the bionic robotic hand, facilitating the calculations of both forward and inverse kinematics. Additionally, MPC strategies are implemented to achieve precise control of the robotic hand and efficient execution of complex tasks.To enhance the environmental perception capabilities of the robotic hand, the system integrates various sensors, including a sound sensor, infrared sensor, ultrasonic distance sensor, OLED display module, digital tilt sensor, Bluetooth module, and PS2 wireless remote control module. These sensors enable the robotic hand to perceive and respond to environmental changes in real time, thereby improving operational flexibility and precision. Experimental results indicate that the bionic robotic hand system possesses flexible control capabilities, good synchronization performance, and broad application prospects.Keywords-Bionic robotic hand; Model Predictive Control (MPC); kinematic analysis; modular designI. INTRODUCTIONWith the rapid development of robotics technology, the importance of bionic systems in industrial and research fields has grown significantly. This study presents a bionic robotic hand, which mimics the structure of the human hand and integrates an STM32 microcontroller along with various sensors to achieve precise and flexible control. Traditional control methods for robotic hands often face issues such as slow response times, insufficient control accuracy, and poor adaptability to complex environments. To address these challenges, this paper employs the Newton-Euler method to establish a dynamic model and introduces Model Predictive Control (MPC) strategies, significantly enhancing the control precision and task execution efficiency of the robotic hand.The robotic hand is capable of simulating basic human arm movements and achieves precise control over each joint through a motion-sensing glove, enabling it to perform complex and delicate operations. The integration of sensors provides the robotic hand with biological-like "tactile," "auditory," and "visual" capabilities, significantly enhancing its interactivity and level of automation.In terms of applications, the bionic robotic hand not only excels in industrial automation but also extends its use to scientific exploration and daily life. For instance, it demonstrates high reliability and precision in extreme environments, such as simulating extraterrestrial terrain and studying the possibility of life.II.SYSTEM DESIGNThe structure of the bionic robotic hand consists primarily of fingers with multiple joint degrees of freedom, where each joint can be controlled independently. The STM32 servo acts as the main controller, receiving data from sensors positioned at appropriate locations on the robotic hand, and controlling its movements by adjusting the joint angles. To enhance the control of the robotic hand's motion, this paper employs the Newton-Euler method to establish a dynamic model, conducts kinematic analysis, and integrates Model Predictive Control (MPC) strategies to improve operational performance in complex environments.In terms of control methods, the system not only utilizes a motion-sensing glove for controlling the bionic robotic hand but also integrates a PS2 controller and a Bluetooth module, achieving a fusion of multiple control modalities.整整整整如图需要预留一个图片的位置III.HARDWARE SELECTION AND DESIGN Choosing a hardware module that meets the functional requirements of the system while effectively controlling costs and ensuring appropriate performance is a critical consideration prior to system design.The hardware components of the system mainly consist of the bionic robotic hand, a servo controller system, a sound module, an infrared module, an ultrasonic distance measurement module, and a Bluetooth module. The main sections are described below.A.Bionic Mechanical StructureThe robotic hand consists of a rotating base and five articulated fingers, forming a six-degree-of-freedom motion structure. The six degrees of freedom enable the system to meet complex motion requirements while maintaining high efficiency and response speed. The workflow primarily involves outputting different PWM signals from a microcontroller to ensure that the six degrees of freedom of the robotic hand can independently control the movements of each joint.B.Controller and Servo SystemThe control system requires a variety of serial interfaces. To achieve efficient control, a combination of the STM32 microcontroller and Arduino control board is utilized, leveraging the advantages of both. The STM32 microcontroller serves as the servo controller, while the Arduino control board provides extensive interfaces and sensor support, facilitating simplified programming and application processes. This integration ensures rapid and precise control of the robotic hand and promotes efficient development.C.Bluetooth ModuleThe HC-05 Bluetooth module supports full-duplex serial communication at distances of up to 10 meters and offers various operational modes. In the automatic connection mode, the module transmits data according to a preset program. Additionally, it can receive AT commands in command-response mode, allowing users to configure control parameters or issue control commands. The level control of external pins enables dynamic state transitions, making the module suitable for a variety of control scenarios.D.Ultrasonic Distance Measurement ModuleThe US-016 ultrasonic distance measurement module provides non-contact distance measurement capabilities of up to 3 meters and supports various operating modes. In continuous measurement mode, the module continuously emits ultrasonic waves and receives reflected signals to calculate the distance to an object in real-time. Additionally, the module can adjust the measurement range or sensitivity through configuration response mode, allowing users to set distance measurement parameters or modify the measurement frequency as needed. The output signal can dynamically reflect the measurement results via level control of external pins, making it suitable for a variety of distance sensing and automatic control applications.IV. DESIGN AND IMPLEMENTATION OF SYSTEMSOFTWAREA.Kinematic Analysis and MPC StrategiesThe control research of the robotic hand is primarily based on a mathematical model, and a reliable mathematical model is essential for studying the controllability of the system. The Denavit-Hartenberg (D-H) method is employed to model the kinematics of the bionic robotic hand, assigning a local coordinate system to each joint. The Z-axis is aligned with the joint's rotation axis, while the X-axis is defined as the shortest distance between adjacent Z-axes, thereby establishing the coordinate system for the robotic hand.By determining the Denavit-Hartenberg (D-H) parameters for each joint, including joint angles, link offsets, link lengths, and twist angles, the transformation matrix for each joint is derived, and the overall transformation matrix from the base to the fingertip is computed. This matrix encapsulates the positional and orientational information of the fingers in space, enabling precise forward and inverse kinematic analyses. The accuracy of the model is validated through simulations, confirming the correct positioning of the fingertip actuator. Additionally, Model Predictive Control (MPC) strategies are introduced to efficiently control the robotic hand and achieve trajectory tracking by predicting system states and optimizing control inputs.Taking the index finger as an example, the Denavit-Hartenberg (D-H) parameter table is established.The data table is shown in Table ITABLE I. DATA SHEETjoints, both the forward kinematic solution and the inverse kinematic solution are derived, resulting in the kinematic model of the ing the same approach, the kinematic models for all other fingers can be obtained.The movement space of the index finger tip is shownin Figure 1.Fig. 1.Fig. 1.The movement space at the end of the index finger Mathematical Model of the Bionic Robotic Hand Based on the Newton-Euler Method. According to the design, each joint of the bionic robotic hand has a specified degree of freedom.For each joint i, the angle is defined as θi, the angular velocity asθi, and the angular acceleration as θi.The dynamics equation for each joint can be expressed as:τi=I iθi+w i(I i w i)whereτi is the joint torque, I i is the joint inertia matrix, and w i and θi represent the joint angular velocity and acceleration, respectively.The control input is generated by the motor driver (servo), with the output being torque. Assuming the motor input for each joint is u i, the joint torque τi can be mapped through the motor's torque constant as:τi=kτ∙u iThe system dynamics equation can be described as:I iθi+b iθi+c iθi=τi−τext,iwhere b i is the damping coefficient, c i is the spring constant (accounting for joint elasticity), and τext,i represents external torques acting on the joint i, such as gravity and friction.The primary control objective is to ensure that the end-effector of the robotic hand (e.g., fingertip) can accurately track a predefined trajectory. Let the desired trajectory be denoted as y d(t)and the actual trajectory as y(t)The tracking error can be expressed as:e(t)=y d(t)−y(t)The goal of MPC is to minimize the cumulative tracking error, which is typically achieved through the following objective function:J=∑[e(k)T Q e e(k)]N−1k=0where Q e is the error weight matrix, N is the prediction horizon length.Mechanical constraints require that the joint angles and velocities must remain within the physically permissible range. Assuming the angle range of the i-th joint is[θi min,θi max]and the velocity range is [θi min,θi max]。

最近鲁棒优化进展Recent Advances in Robust Optimization and Robustness An Overview

Recent Advances in Robust Optimization and Robustness:An OverviewVirginie Gabrel∗and C´e cile Murat†and Aur´e lie Thiele‡July2012AbstractThis paper provides an overview of developments in robust optimization and robustness published in the aca-demic literature over the pastﬁve years.1IntroductionThis review focuses on papers identiﬁed by Web of Science as having been published since2007(included),be-longing to the area of Operations Research and Management Science,and having‘robust’and‘optimization’in their title.There were exactly100such papers as of June20,2012.We have completed this list by considering 726works indexed by Web of Science that had either robustness(for80of them)or robust(for646)in their title and belonged to the Operations Research and Management Science topic area.We also identiﬁed34PhD disserta-tions dated from the lastﬁve years with‘robust’in their title and belonging to the areas of operations research or management.Among those we have chosen to focus on the works with a primary focus on management science rather than system design or optimal control,which are broadﬁelds that would deserve a review paper of their own, and papers that could be of interest to a large segment of the robust optimization research community.We feel it is important to include PhD dissertations to identify these recent graduates as the new generation trained in robust optimization and robustness analysis,whether they have remained in academia or joined industry.We have also added a few not-yet-published preprints to capture ongoing research efforts.While many additional works would have deserved inclusion,we feel that the works selected give an informative and comprehensive view of the state of robustness and robust optimization to date in the context of operations research and management science.∗Universit´e Paris-Dauphine,LAMSADE,Place du Mar´e chal de Lattre de Tassigny,F-75775Paris Cedex16,France gabrel@lamsade.dauphine.fr Corresponding author†Universit´e Paris-Dauphine,LAMSADE,Place du Mar´e chal de Lattre de Tassigny,F-75775Paris Cedex16,France mu-rat@lamsade.dauphine.fr‡Lehigh University,Industrial and Systems Engineering Department,200W Packer Ave Bethlehem PA18015,USA aure-lie.thiele@2Theory of Robust Optimization and Robustness2.1Deﬁnitions and BasicsThe term“robust optimization”has come to encompass several approaches to protecting the decision-maker against parameter ambiguity and stochastic uncertainty.At a high level,the manager must determine what it means for him to have a robust solution:is it a solution whose feasibility must be guaranteed for any realization of the uncertain parameters?or whose objective value must be guaranteed?or whose distance to optimality must be guaranteed? The main paradigm relies on worst-case analysis:a solution is evaluated using the realization of the uncertainty that is most unfavorable.The way to compute the worst case is also open to debate:should it use aﬁnite number of scenarios,such as historical data,or continuous,convex uncertainty sets,such as polyhedra or ellipsoids?The answers to these questions will determine the formulation and the type of the robust counterpart.Issues of over-conservatism are paramount in robust optimization,where the uncertain parameter set over which the worst case is computed should be chosen to achieve a trade-off between system performance and protection against uncertainty,i.e.,neither too small nor too large.2.2Static Robust OptimizationIn this framework,the manager must take a decision in the presence of uncertainty and no recourse action will be possible once uncertainty has been realized.It is then necessary to distinguish between two types of uncertainty: uncertainty on the feasibility of the solution and uncertainty on its objective value.Indeed,the decision maker generally has different attitudes with respect to infeasibility and sub-optimality,which justiﬁes analyzing these two settings separately.2.2.1Uncertainty on feasibilityWhen uncertainty affects the feasibility of a solution,robust optimization seeks to obtain a solution that will be feasible for any realization taken by the unknown coefﬁcients;however,complete protection from adverse realiza-tions often comes at the expense of a severe deterioration in the objective.This extreme approach can be justiﬁed in some engineering applications of robustness,such as robust control theory,but is less advisable in operations research,where adverse events such as low customer demand do not produce the high-proﬁle repercussions that engineering failures–such as a doomed satellite launch or a destroyed unmanned robot–can have.To make the robust methodology appealing to business practitioners,robust optimization thus focuses on obtaining a solution that will be feasible for any realization taken by the unknown coefﬁcients within a smaller,“realistic”set,called the uncertainty set,which is centered around the nominal values of the uncertain parameters.The goal becomes to optimize the objective,over the set of solutions that are feasible for all coefﬁcient values in the uncertainty set.The speciﬁc choice of the set plays an important role in ensuring computational tractability of the robust problem and limiting deterioration of the objective at optimality,and must be thought through carefully by the decision maker.A large branch of robust optimization focuses on worst-case optimization over a convex uncertainty set.The reader is referred to Bertsimas et al.(2011a)and Ben-Tal and Nemirovski(2008)for comprehensive surveys of robust optimization and to Ben-Tal et al.(2009)for a book treatment of the topic.2.2.2Uncertainty on objective valueWhen uncertainty affects the optimality of a solution,robust optimization seeks to obtain a solution that performs well for any realization taken by the unknown coefﬁcients.While a common criterion is to optimize the worst-case objective,some studies have investigated other robustness measures.Roy(2010)proposes a new robustness criterion that holds great appeal for the manager due to its simplicity of use and practical relevance.This framework,called bw-robustness,allows the decision-maker to identify a solution which guarantees an objective value,in a maximization problem,of at least w in all scenarios,and maximizes the probability of reaching a target value of b(b>w).Gabrel et al.(2011)extend this criterion from aﬁnite set of scenarios to the case of an uncertainty set modeled using intervals.Kalai et al.(2012)suggest another criterion called lexicographicα-robustness,also deﬁned over aﬁnite set of scenarios for the uncertain parameters,which mitigates the primary role of the worst-case scenario in deﬁning the solution.Thiele(2010)discusses over-conservatism in robust linear optimization with cost uncertainty.Gancarova and Todd(2012)studies the loss in objective value when an inaccurate objective is optimized instead of the true one, and shows that on average this loss is very small,for an arbitrary compact feasible region.In combinatorial optimization,Morrison(2010)develops a framework of robustness based on persistence(of decisions)using the Dempster-Shafer theory as an evidence of robustness and applies it to portfolio tracking and sensor placement.2.2.3DualitySince duality has been shown to play a key role in the tractability of robust optimization(see for instance Bertsimas et al.(2011a)),it is natural to ask how duality and robust optimization are connected.Beck and Ben-Tal(2009) shows that primal worst is equal to dual best.The relationship between robustness and duality is also explored in Gabrel and Murat(2010)when the right-hand sides of the constraints are uncertain and the uncertainty sets are represented using intervals,with a focus on establishing the relationships between linear programs with uncertain right hand sides and linear programs with uncertain objective coefﬁcients using duality theory.This avenue of research is further explored in Gabrel et al.(2010)and Remli(2011).2.3Multi-Stage Decision-MakingMost early work on robust optimization focused on static decision-making:the manager decided at once of the values taken by all decision variables and,if the problem allowed for multiple decision stages as uncertainty was realized,the stages were incorporated by re-solving the multi-stage problem as time went by and implementing only the decisions related to the current stage.As theﬁeld of static robust optimization matured,incorporating–ina tractable manner–the information revealed over time directly into the modeling framework became a major area of research.2.3.1Optimal and Approximate PoliciesA work going in that direction is Bertsimas et al.(2010a),which establishes the optimality of policies afﬁne in the uncertainty for one-dimensional robust optimization problems with convex state costs and linear control costs.Chen et al.(2007)also suggests a tractable approximation for a class of multistage chance-constrained linear program-ming problems,which converts the original formulation into a second-order cone programming problem.Chen and Zhang(2009)propose an extension of the Afﬁnely Adjustable Robust Counterpart framework described in Ben-Tal et al.(2009)and argue that its potential is well beyond what has been in the literature so far.2.3.2Two stagesBecause of the difﬁculty in incorporating multiple stages in robust optimization,many theoretical works have focused on two stages.Regarding two-stage problems,Thiele et al.(2009)presents a cutting-plane method based on Kelley’s algorithm for solving convex adjustable robust optimization problems,while Terry(2009)provides in addition preliminary results on the conditioning of a robust linear program and of an equivalent second-order cone program.Assavapokee et al.(2008a)and Assavapokee et al.(2008b)develop tractable algorithms in the case of robust two-stage problems where the worst-case regret is minimized,in the case of interval-based uncertainty and scenario-based uncertainty,respectively,while Minoux(2011)provides complexity results for the two-stage robust linear problem with right-hand-side uncertainty.2.4Connection with Stochastic OptimizationAn early stream in robust optimization modeled stochastic variables as uncertain parameters belonging to a known uncertainty set,to which robust optimization techniques were then applied.An advantage of this method was to yield approaches to decision-making under uncertainty that were of a level of complexity similar to that of their deterministic counterparts,and did not suffer from the curse of dimensionality that afﬂicts stochastic and dynamic programming.Researchers are now making renewed efforts to connect the robust optimization and stochastic opti-mization paradigms,for instance quantifying the performance of the robust optimization solution in the stochastic world.The topic of robust optimization in the context of uncertain probability distributions,i.e.,in the stochastic framework itself,is also being revisited.2.4.1Bridging the Robust and Stochastic WorldsBertsimas and Goyal(2010)investigates the performance of static robust solutions in two-stage stochastic and adaptive optimization problems.The authors show that static robust solutions are good-quality solutions to the adaptive problem under a broad set of assumptions.They provide bounds on the ratio of the cost of the optimal static robust solution to the optimal expected cost in the stochastic problem,called the stochasticity gap,and onthe ratio of the cost of the optimal static robust solution to the optimal cost in the two-stage adaptable problem, called the adaptability gap.Chen et al.(2007),mentioned earlier,also provides a robust optimization perspective to stochastic programming.Bertsimas et al.(2011a)investigates the role of geometric properties of uncertainty sets, such as symmetry,in the power ofﬁnite adaptability in multistage stochastic and adaptive optimization.Duzgun(2012)bridges descriptions of uncertainty based on stochastic and robust optimization by considering multiple ranges for each uncertain parameter and setting the maximum number of parameters that can fall within each range.The corresponding optimization problem can be reformulated in a tractable manner using the total unimodularity of the feasible set and allows for aﬁner description of uncertainty while preserving tractability.It also studies the formulations that arise in robust binary optimization with uncertain objective coefﬁcients using the Bernstein approximation to chance constraints described in Ben-Tal et al.(2009),and shows that the robust optimization problems are deterministic problems for modiﬁed values of the coefﬁcients.While many results bridging the robust and stochastic worlds focus on giving probabilistic guarantees for the solutions generated by the robust optimization models,Manuja(2008)proposes a formulation for robust linear programming problems that allows the decision-maker to control both the probability and the expected value of constraint violation.Bandi and Bertsimas(2012)propose a new approach to analyze stochastic systems based on robust optimiza-tion.The key idea is to replace the Kolmogorov axioms and the concept of random variables as primitives of probability theory,with uncertainty sets that are derived from some of the asymptotic implications of probability theory like the central limit theorem.The authors show that the performance analysis questions become highly structured optimization problems for which there exist efﬁcient algorithms that are capable of solving problems in high dimensions.They also demonstrate that the proposed approach achieves computationally tractable methods for(a)analyzing queueing networks,(b)designing multi-item,multi-bidder auctions with budget constraints,and (c)pricing multi-dimensional options.2.4.2Distributionally Robust OptimizationBen-Tal et al.(2010)considers the optimization of a worst-case expected-value criterion,where the worst case is computed over all probability distributions within a set.The contribution of the work is to deﬁne a notion of robustness that allows for different guarantees for different subsets of probability measures.The concept of distributional robustness is also explored in Goh and Sim(2010),with an emphasis on linear and piecewise-linear decision rules to reformulate the original problem in aﬂexible manner using expected-value terms.Xu et al.(2012) also investigates probabilistic interpretations of robust optimization.A related area of study is worst-case optimization with partial information on the moments of distributions.In particular,Popescu(2007)analyzes robust solutions to a certain class of stochastic optimization problems,using mean-covariance information about the distributions underlying the uncertain parameters.The author connects the problem for a broad class of objective functions to a univariate mean-variance robust objective and,subsequently, to a(deterministic)parametric quadratic programming problem.The reader is referred to Doan(2010)for a moment-based uncertainty model for stochastic optimization prob-lems,which addresses the ambiguity of probability distributions of random parameters with a minimax decision rule,and a comparison with data-driven approaches.Distributionally robust optimization in the context of data-driven problems is the focus of Delage(2009),which uses observed data to deﬁne a”well structured”set of dis-tributions that is guaranteed with high probability to contain the distribution from which the samples were drawn. Zymler et al.(2012a)develop tractable semideﬁnite programming(SDP)based approximations for distributionally robust individual and joint chance constraints,assuming that only theﬁrst-and second-order moments as well as the support of the uncertain parameters are given.Becker(2011)studies the distributionally robust optimization problem with known mean,covariance and support and develops a decomposition method for this family of prob-lems which recursively derives sub-policies along projected dimensions of uncertainty while providing a sequence of bounds on the value of the derived policy.Robust linear optimization using distributional information is further studied in Kang(2008).Further,Delage and Ye(2010)investigates distributional robustness with moment uncertainty.Speciﬁcally,uncertainty affects the problem both in terms of the distribution and of its moments.The authors show that the resulting problems can be solved efﬁciently and prove that the solutions exhibit,with high probability,best worst-case performance over a set of distributions.Bertsimas et al.(2010)proposes a semideﬁnite optimization model to address minimax two-stage stochastic linear problems with risk aversion,when the distribution of the second-stage random variables belongs to a set of multivariate distributions with knownﬁrst and second moments.The minimax solutions provide a natural distribu-tion to stress-test stochastic optimization problems under distributional ambiguity.Cromvik and Patriksson(2010a) show that,under certain assumptions,global optima and stationary solutions of stochastic mathematical programs with equilibrium constraints are robust with respect to changes in the underlying probability distribution.Works such as Zhu and Fukushima(2009)and Zymler(2010)also study distributional robustness in the context of speciﬁc applications,such as portfolio management.2.5Connection with Risk TheoryBertsimas and Brown(2009)describe how to connect uncertainty sets in robust linear optimization to coherent risk measures,an example of which is Conditional Value-at-Risk.In particular,the authors show the link between polyhedral uncertainty sets of a special structure and a subclass of coherent risk measures called distortion risk measures.Independently,Chen et al.(2007)present an approach for constructing uncertainty sets for robust opti-mization using new deviation measures that capture the asymmetry of the distributions.These deviation measures lead to improved approximations of chance constraints.Dentcheva and Ruszczynski(2010)proposes the concept of robust stochastic dominance and shows its applica-tion to risk-averse optimization.They consider stochastic optimization problems where risk-aversion is expressed by a robust stochastic dominance constraint and develop necessary and sufﬁcient conditions of optimality for such optimization problems in the convex case.In the nonconvex case,they derive necessary conditions of optimality under additional smoothness assumptions of some mappings involved in the problem.2.6Nonlinear OptimizationRobust nonlinear optimization remains much less widely studied to date than its linear counterpart.Bertsimas et al.(2010c)presents a robust optimization approach for unconstrained non-convex problems and problems based on simulations.Such problems arise for instance in the partial differential equations literature and in engineering applications such as nanophotonic design.An appealing feature of the approach is that it does not assume any speciﬁc structure for the problem.The case of robust nonlinear optimization with constraints is investigated in Bertsimas et al.(2010b)with an application to radiation therapy for cancer treatment.Bertsimas and Nohadani (2010)further explore robust nonconvex optimization in contexts where solutions are not known explicitly,e.g., have to be found using simulation.They present a robust simulated annealing algorithm that improves performance and robustness of the solution.Further,Boni et al.(2008)analyzes problems with uncertain conic quadratic constraints,formulating an approx-imate robust counterpart,and Zhang(2007)provide formulations to nonlinear programming problems that are valid in the neighborhood of the nominal parameters and robust to theﬁrst order.Hsiung et al.(2008)present tractable approximations to robust geometric programming,by using piecewise-linear convex approximations of each non-linear constraint.Geometric programming is also investigated in Shen et al.(2008),where the robustness is injected at the level of the algorithm and seeks to avoid obtaining infeasible solutions because of the approximations used in the traditional approach.Interval uncertainty-based robust optimization for convex and non-convex quadratic programs are considered in Li et al.(2011).Takeda et al.(2010)studies robustness for uncertain convex quadratic programming problems with ellipsoidal uncertainties and proposes a relaxation technique based on random sampling for robust deviation optimization sserre(2011)considers minimax and robust models of polynomial optimization.A special case of nonlinear problems that are linear in the decision variables but convex in the uncertainty when the worst-case objective is to be maximized is investigated in Kawas and Thiele(2011a).In that setting,exact and tractable robust counterparts can be derived.A special class of nonconvex robust optimization is examined in Kawas and Thiele(2011b).Robust nonconvex optimization is examined in detail in Teo(2007),which presents a method that is applicable to arbitrary objective functions by iteratively moving along descent directions and terminates at a robust local minimum.3Applications of Robust OptimizationWe describe below examples to which robust optimization has been applied.While an appealing feature of robust optimization is that it leads to models that can be solved using off-the-shelf software,it is worth pointing the existence of algebraic modeling tools that facilitate the formulation and subsequent analysis of robust optimization problems on the computer(Goh and Sim,2011).3.1Production,Inventory and Logistics3.1.1Classical logistics problemsThe capacitated vehicle routing problem with demand uncertainty is studied in Sungur et al.(2008),with a more extensive treatment in Sungur(2007),and the robust traveling salesman problem with interval data in Montemanni et al.(2007).Remli and Rekik(2012)considers the problem of combinatorial auctions in transportation services when shipment volumes are uncertain and proposes a two-stage robust formulation solved using a constraint gener-ation algorithm.Zhang(2011)investigates two-stage minimax regret robust uncapacitated lot-sizing problems with demand uncertainty,in particular showing that it is polynomially solvable under the interval uncertain demand set.3.1.2SchedulingGoren and Sabuncuoglu(2008)analyzes robustness and stability measures for scheduling in a single-machine environment subject to machine breakdowns and embeds them in a tabu-search-based scheduling algorithm.Mittal (2011)investigates efﬁcient algorithms that give optimal or near-optimal solutions for problems with non-linear objective functions,with a focus on robust scheduling and service operations.Examples considered include parallel machine scheduling problems with the makespan objective,appointment scheduling and assortment optimization problems with logit choice models.Hazir et al.(2010)considers robust scheduling and robustness measures for the discrete time/cost trade-off problem.3.1.3Facility locationAn important question in logistics is not only how to operate a system most efﬁciently but also how to design it. Baron et al.(2011)applies robust optimization to the problem of locating facilities in a network facing uncertain demand over multiple periods.They consider a multi-periodﬁxed-charge network location problem for which they ﬁnd the number of facilities,their location and capacities,the production in each period,and allocation of demand to facilities.The authors show that different models of uncertainty lead to very different solution network topologies, with the model with box uncertainty set opening fewer,larger facilities.?investigate a robust version of the location transportation problem with an uncertain demand using a2-stage formulation.The resulting robust formulation is a convex(nonlinear)program,and the authors apply a cutting plane algorithm to solve the problem exactly.Atamt¨u rk and Zhang(2007)study the networkﬂow and design problem under uncertainty from a complexity standpoint,with applications to lot-sizing and location-transportation problems,while Bardossy(2011)presents a dual-based local search approach for deterministic,stochastic,and robust variants of the connected facility location problem.The robust capacity expansion problem of networkﬂows is investigated in Ordonez and Zhao(2007),which provides tractable reformulations under a broad set of assumptions.Mudchanatongsuk et al.(2008)analyze the network design problem under transportation cost and demand uncertainty.They present a tractable approximation when each commodity only has a single origin and destination,and an efﬁcient column generation for networks with path constraints.Atamt¨u rk and Zhang(2007)provides complexity results for the two-stage networkﬂow anddesign plexity results for the robust networkﬂow and network design problem are also provided in Minoux(2009)and Minoux(2010).The problem of designing an uncapacitated network in the presence of link failures and a competing mode is investigated in Laporte et al.(2010)in a railway application using a game theoretic perspective.Torres Soto(2009)also takes a comprehensive view of the facility location problem by determining not only the optimal location but also the optimal time for establishing capacitated facilities when demand and cost parameters are time varying.The models are solved using Benders’decomposition or heuristics such as local search and simulated annealing.In addition,the robust networkﬂow problem is also analyzed in Boyko(2010),which proposes a stochastic formulation of minimum costﬂow problem aimed atﬁnding network design andﬂow assignments subject to uncertain factors,such as network component disruptions/failures when the risk measure is Conditional Value at Risk.Nagurney and Qiang(2009)suggests a relative total cost index for the evaluation of transportation network robustness in the presence of degradable links and alternative travel behavior.Further,the problem of locating a competitive facility in the plane is studied in Blanquero et al.(2011)with a robustness criterion.Supply chain design problems are also studied in Pan and Nagi(2010)and Poojari et al.(2008).3.1.4Inventory managementThe topic of robust multi-stage inventory management has been investigated in detail in Bienstock and Ozbay (2008)through the computation of robust basestock levels and Ben-Tal et al.(2009)through an extension of the Afﬁnely Adjustable Robust Counterpart framework to control inventories under demand uncertainty.See and Sim (2010)studies a multi-period inventory control problem under ambiguous demand for which only mean,support and some measures of deviations are known,using a factor-based model.The parameters of the replenishment policies are obtained using a second-order conic programming problem.Song(2010)considers stochastic inventory control in robust supply chain systems.The work proposes an inte-grated approach that combines in a single step dataﬁtting and inventory optimization–using histograms directly as the inputs for the optimization model–for the single-item multi-period periodic-review stochastic lot-sizing problem.Operation and planning issues for dynamic supply chain and transportation networks in uncertain envi-ronments are considered in Chung(2010),with examples drawn from emergency logistics planning,network design and congestion pricing problems.3.1.5Industry-speciﬁc applicationsAng et al.(2012)proposes a robust storage assignment approach in unit-load warehouses facing variable supply and uncertain demand in a multi-period setting.The authors assume a factor-based demand model and minimize the worst-case expected total travel in the warehouse with distributional ambiguity of demand.A related problem is considered in Werners and Wuelﬁng(2010),which optimizes internal transports at a parcel sorting center.Galli(2011)describes the models and algorithms that arise from implementing recoverable robust optimization to train platforming and rolling stock planning,where the concept of recoverable robustness has been deﬁned in。

《蛋白转移酶AtSEC61-β调节拟南芥Ca依赖性生长的功能研究》范文

《蛋白转移酶AtSEC61-β调节拟南芥Ca依赖性生长的功能研究》篇一摘要本研究着重于探讨蛋白转移酶AtSEC61-β在拟南芥Ca依赖性生长过程中的作用。

通过构建遗传模型、生化分析以及细胞生物学研究，揭示了AtSEC61-β在调节植物生长发育过程中的重要功能。

本研究为理解植物Ca信号通路和其相关蛋白的转运机制提供了新的视角。

一、引言近年来，植物生物学领域对于蛋白转移酶在细胞内蛋白质转运及植物生长发育中的重要性日益关注。

AtSEC61-β作为一种重要的蛋白转移酶，其在拟南芥中的功能尚未完全明确。

本研究旨在探讨AtSEC61-β如何参与调控拟南芥Ca依赖性生长过程，为深入理解植物生长发育的分子机制提供依据。

二、材料与方法（一）实验材料本研究以拟南芥为实验材料，通过遗传学方法构建了AtSEC61-β基因的过表达和敲除模型。

（二）实验方法1. 遗传模型构建：构建AtSEC61-β基因的过表达和敲除的转基因拟南芥模型。

2. 生化分析：利用蛋白质印迹法、免疫共沉淀等技术，分析AtSEC61-β与相关蛋白的相互作用。

3. 细胞生物学研究：利用荧光显微镜、激光共聚焦等技术，观察AtSEC61-β在细胞内的定位及其与Ca信号的关系。

4. 生长表型分析：通过观察转基因拟南芥的生长情况，分析AtSEC61-β对拟南芥生长的影响。

三、结果与分析（一）AtSEC61-β的定位与互作蛋白分析通过蛋白质印迹法和免疫共沉淀技术，我们发现AtSEC61-β主要定位在细胞膜上，并与一些Ca相关蛋白存在相互作用。

这些互作蛋白可能参与了Ca信号的传递和调控过程。

（二）AtSEC61-β对拟南芥生长的影响在过表达AtSEC61-β的转基因拟南芥中，我们观察到植株表现出较强的Ca依赖性生长能力，表现为根长增加、叶片扩张等表型。

相反，在敲除AtSEC61-β的转基因拟南芥中，植株表现出Ca依赖性生长受阻的现象。

（三）AtSEC61-β与Ca信号的关系通过细胞生物学研究，我们发现AtSEC61-β与Ca信号存在密切关系。

基于扩张状态观测器的非线性变结构控制器研究

第29卷　第5期2007年10月电气电子教学学报J OURNAL OF EEEVol.29　No.5Oct.2007基于扩张状态观测器的非线性变结构控制器研究康忠健1,孟繁玉1,魏志远2(1.中国石油大学电气工程系,山东东营,257061;2.中石油华北油田公公司采油五厂,河北辛集052360)收稿日期:2007203212;修回日期:2007207215作者简介康忠健(2),男,四川安岳人,博士,副教授,硕士生导师。

主要研究方向为电力系统稳定分析及非线性控制、电力系统故障检测与诊断孟繁玉(82),女,山东淄博人,硕士研究生。

主要研究方向为电力系统稳定分析及非线性控制、微机自动控制魏志远(2),男,河北辛集人,硕士研究生。

主要研究方向为油田配电网规划与设计摘　要:本文针对极点配置法扩张状态观测器ESO 的不足,充分利用系统已知信息设计出一种新型ESO ,并将其与变结构控制理论相结合,提出一种非线性鲁棒变结构控制器的设计方法,克服了基于反馈线性化理论的非线性控制因数学模型的误差而影响控制器性能的缺点。

仿真结果表明所设计的非线性鲁棒变结构控制器对于对象模型参数摄动和外扰具有良好的适应性和鲁棒性。

关键词:非线性控制;变结构控制;鲁棒控制;扩张状态观测器中图分类号:TP13 文献标识码:A 文章编号:100820686(2007)0520056204R ese ar ch for the N onlinear V ar i able Str uctu re Co ntroller B ased o n Extended State Observ erK ANG Zhong 2j ian 1,MENG Fan 2yu 1,WEI Zhi 2yuan 2(1.Engi neerin g Depart ment ,Uni versi t y o f P et roleum o f C hina ,Don gyi ng ,257061,C hina;2.The 5th Oil F act ory of Hua 2Bei Oi l 2f i el d ,Chi na Pet roleum Comp orati on ,Xi nj i 052360,Chi na)Abstract :In order to overcome t he shortcomi ng of t he pole 2configuration 2met hod extended st ate observer(ESO ),a new model of ESO ,ba se d on usi ng known i nformat ion of detected system ,i s put forward in t his paper.And a new cont roll er of nonlinear robust variable st ruct ure cont roll er (NLRVSC )i s put forward by cooperat ing va ria ble st ruct ure cont rol (VSC )t heory wit h ESO to ove rcome t he short coming of feedback li nea rizat io n excit at ion cont roller ,which perfor ma nce i s affected by t he mat hemati cal model error.The si mula tion re sult s indicat e t he NL RVSC ha s a n excellent adapt abilit y and a st rong robust to t he object ’s model a nd di st ur bance.K eyw or ds :nonlinea r cont rol ;va riabl e st r uct ure cont rol ;robust cont rol ;ext ended stat e observer0　引言反馈线性化是目前非线性系统控制中应用较多的控制方法。

一类非线性系统模糊积分滑模控制及其在电液伺服系统的应用

(1. The Second Ar tiller y Engineering College , Xi’ an Shaanxi 710025 , Chintitute , Taiyuan Univer sity of Technology , Taiyuan Sha nxi 030024 , China)
0 引言
滑模变结构控制因其对系统参数不确定性和外部扰动具良好的不敏感性而获得了广泛应用 [1 ] 。该控制策略可通过控制器结构的不断调整和变化 , 有效控制有参数变化和外部扰动的被控制对象 [2 ] 。这与具不定性的电液伺服系统的控制要求一致 , 因此滑模变结构控制在电液伺服系统设计中受到广泛重 4] 视 [ 3、。但该控制方法需假设被跟踪信号及其一阶
2008 年第 4 期
刘云峰 , 等 :一类非线性系统模糊积分滑模控制及其在电液伺服系统的应用
7
强鲁棒性。为此 , 提出了一种模糊积分滑模控制策略 , 并用于电液伺服系统的跟踪控制。
等于零时 , 系统的输入输出传递函数为
X1 (s) k = n . ( 6) n- 1 2 Yd ( s) s + cn- 1 s + … + c2 s + c1 s + k
振方法是用连续饱和非线性控制替代切换控制 , 光滑不连续切换控制 , 但系统的稳定性仅在临界层外才有保证 , 且跟踪误差与临界层宽度有关 [ 6 ] 。在常规滑模控制中引入积分控制 , 可只要求获知被跟踪信号 , 无需常规滑模变结构控制中被跟踪信号的一阶及高阶导数已知。在此基础上引入模糊控制 , 能有效削弱积分滑模非线性项产生的抖振 , 而不影响滑模控制系统对参数变化和外干扰不确定的
Fuzzy In tegr al Slid in g Mode Contr ol f or Nonlinear System an d Appl icat ion f or Electr o2hydr aulic Ser vo System

殷保群教授个人简历范文

以下是为⼤家整理的关于殷保群教授个⼈简历范⽂的⽂章，希望⼤家能够喜欢！殷保群，男，教授，博⼠⽣导师。

中国科学技术⼤学教授。

1962年2⽉⽣，1985年7⽉毕业于四川⼤学数学系基础数学专业，随后考⼊中国科学技术⼤学基础数学研究⽣班，1987年7⽉毕业，并留校任教。

1993年5⽉在中国科学技术⼤学数学系应⽤数学专业获得理学硕⼠学位，1998年12⽉在中国科学技术⼤学⾃动化系模式识别与智能系统专业获得⼯学博⼠学位，现在中国科学技术⼤学⾃动化系任教。

长期从事随机系统、系统优化以及信息络系统理论及其应⽤等⽅⾯的研究⼯作，⽬前感兴趣的主要⽅向为Markov决策过程、络建模与优化、络流量分析、媒体服务系统的接⼊控制以及云计算等。

在国内外主要学术刊物上发表学术论⽂100余篇，其中SCI收录10余篇，EI收录30余篇，出版学术专著1部。

曾于2004年4⽉⾄12⽉在⾹港科技⼤学做访问学者。

第xx届（2006年）何潘清漪优秀论⽂获奖者。

⽬前感兴趣的主要研究⽅向：1、离散事件动态系统； 2、Markov决策过程； 3、排队系统； 4、信息络论⽂著作主要著作殷保群，奚宏⽣，周亚平，排队系统性能分析与Markov控制过程,合肥：中国科学技术⼤学出版社，2004.期刊论⽂Yin, B. Q., Guo, D., Huang, J., Wu, X. M., Modeling and analysis for the P2P-based media delivery network, Mathematical and Computer Modelling (2011), doi:10.1016/j.mcm.2011.10.043. (SCI 收录, JCR II 区) Yin, B. Q., Lu, S., Guo, D., Analysis of Admission Control in P2P-Based Media Delivery Network Based on POMDP, International Journal of Innovative Computing, Information and Control, 2011, 7(7B): 4411-4422. (SCI收录, JCR II 区) Kang, Yu, Yin, Baoqun, Shang, Weike, Xi, Hongsheng, Performance sensitivity analysis and optimization for a class of countable semi-Markov decision processes, Proceedings of the World Congress on Intelligent Control and Automation (WCICA2011), June 21, 2011 - June 25, 2011, Taipei, Taiwan. (EI收录20113614311870) Li, Y. J., Yin, B. Q., Xi, H. S., Finding Optimal Memoryless Policies of POMDPs under the Expected Average Reward Criterion, European Journal of Operational Research, 2011, 211(2011): 556-567. (SCI 收录, JCR II 区) 江琦，奚宏⽣，殷保群，事件驱动的动态服务组合策略在线⾃适应优化，控制理论与应⽤，2011, 28(8): 1049-1055. (EI收录20114214431454) Jiang, Q., Xi, H. S., Yin, B. Q., Adaptive Optimization of Timeout Policy for Dynamic Power Management Based on Semi-Markov Control Processes, IET Control Theory and Applications, 2010, 4(10): 1945-1958. (SCI收录) Tang, L., Xi, H. S., Zhu, J., Yin, B. Q., Modeling and Optimization of M/G/1-Type Queueing Networks: An Efficient Sensitivity Analysis Approach, Mathematical Problems in Engineering, 2010, 2010: 1-20. (SCI收录) Shan Lu, Baoqun Yin, Dong Guo, Admission Control for P2P-Based Media Delivery Network, Proceedings of the 29th Chinese Control Conference, July 29-31, 2010, Beijing, China, 2010: 1494-1499. ( EI收录20105113504286) ⾦辉宇，康宇，殷保群，局部Lipschitz系统的采样控制，Proceedings of the 29th Chinese Control Conference, July 29-31, 2010, Beijing, China, 2010: 992-997. ( EI收录20105113504436) 江琦，奚宏⽣，殷保群，络新媒体服务系统事件驱动的动态服务组合，Proceedings of the 29th Chinese Control Conference, July 29-31, 2010, Beijing, China, 2010: 1121-1125. ( EI收录20105113504230) Dong Guo, Baoqun Yin, Shan Lu, Jing Huang, Jian Yang, A Novel Dynamic Model for Peer-to-Peer File Sharing Systems, ICCMS, 2010 Second International Conference on Computer Modeling and Simulation, 2010, 1: 418-422. ( EI收录20101812900175) Jing Huang, Baoqun Yin, Dong Guo, Shan Lu, Xumin Wu, An Evolution Model for P2P File-Sharing Networks, ICCMS, 2010 Second International Conference on Computer Modeling and Simulation, 2010, 2: 361-365. ( EI收录20101712882202) 巫旭敏，殷保群，黄静，郭东，流媒体服务系统中⼀种基于数据预取的缓存策略，电⼦与信息学报，2010，32(10): 2440-2445. (EI 收录20104513372577) 马军，郑烇，殷保群，基于CDN和P2P的分布式络存储系统，计算机应⽤与软件，2010，27(2):50-52. Bao, B. K., Xi, H. S., Yin, B. Q., Ling, Q., Two Time-Scale Gradient Approximation Algorithm for Adaptive Markov Reward Processes, International Journal of Innovative Computing, Information and Control, 2010, 6(2): 655-666. (SCI收录, JCR II 区) Jiang, Q., Xi, H. S., Yin, B. Q., Dynamic File Grouping for Load Balancing in Streaming Media Clustered Server Systems, International Journal of Control, Automation, and Systems, 2009, 7(4): 630-637. (SCI收录) 江琦，奚宏⽣，殷保群，动态电源管理超时策略与随机型策略的等效关系，计算机辅助设计与图形学学报，2009, 21(11): 1646-1651. (EI 收录20095012535449) 唐波，李衍杰，殷保群，连续时间部分可观Markov决策过程的策略梯度估计，控制理论与应⽤，2009，26(7)：805-808. (EI 收录20093712302646) 芦珊，黄静，殷保群，基于POMDP的VOD接⼊控制建模与仿真，中国科学技术⼤学学报，2009，39(9)：984-989. 李洪亮，殷保群，郑诠，⼀种基于负载均衡的数据部署算法，计算机仿真，2009，26(4)：177-181. 鲍秉坤，殷保群，奚宏⽣，基于性能势的Markov控制过程双时间尺度仿真算法，系统仿真学报，2009，21(13)：4114-4119. Jin Huiyu; Yin Baoqun; Ling Qiang; Kang Yu; Sampled-data Observer Design for Nonlinear Autonomous Systems, 2009 Chinese Control and Decision Conference, CCDC 2009, 2009: 1516-1520. ( EI收录20094712469527) ⾦辉宇，殷保群，⾮线性采样系统指数稳定的新条件，控制理论与应⽤，2009，26(8)：821-826. (EI 收录20094512429319) Yin, B. Q., Li, Y. J., Zhou, Y. P., Xi, H. S., Performance Optimization of Semi-Markov Decision Processes with Discounted-Cost Criteria. European Journal of Control, 2008, 14(3): 213-222. (SCI收录) Li, Y. J., Yin, B. Q. and Xi, H. S., Partially Observable Markov Decision Processes and Performance Sensitivity Analysis. IEEE Trans. System, Man and cybernetics-Part B., 2008, 38(6): 1645-1651. (SCI收录, JCR II 区) Tang, B., Tan, X. B., Yin, B. Q. , Continuous-time hidden markov models in network simulation, 2008 IEEE International Symposium on Knowledge Acquisition and Modeling Workshop Proceedings, Wuhan, China, DEC 21-22, 2008: 667-670. (EI收录20092812179753) Bao, B. K., Yin, B. Q., Xi, H. S., Infinite-Horizon Policy-Gradient Estimation with Variable Discount Factor for Markov Decision Process. icicic,pp.584,2008 3rd International Conference on Innovative Computing Information and Control, 2008. ( EI收录************) Chenfeng Xu, Jian Yang, Hongsheng Xi, Qi Jiang, Baoqun Yin, Event-related optimization for a class of resource location with admission control, 2008. IJCNN 2008. (IEEE World Congress on Computational Intelligence). IEEE International Joint Conference on Neural Networks, 1-8 June 2008: 1092 – 1097. ( EI收录************)JinHuiyu;KangYu;YinBaoqun; Synchronization of nonlinear systems with stair-step signal, 2008. CCC 2008. 27th Chinese Control Conference,16-18 July 2008: 459 – 463. ( EI收录************)JiangQi;XiHongsheng;YinBaoqun;XuChenfeng;Anevent-drivendynamicload balancing strategy for streaming media clustered server systems, 2008. CCC 2008. 27th Chinese Control Conference, 16-18 July 2008: 678 – 682. ( EI收录************)⾦辉宇，殷保群，唐波，⾮线性采样观测器的误差分析，中国科学技术⼤学学报，2008, 38(10): 1226-1231. 黄静，殷保群，李俊，基于观测的POMDP优化算法及其仿真，信息与控制，2008, 37(3): 346-351. 马军，殷保群，基于POMDP模型的机器⼈⾏动的仿真优化，系统仿真学报，2008, 20(21): 5903-5906. (EI 收录************)江琦，奚宏⽣，殷保群，动态电源管理超时策略⾃适应优化算法，控制与决策，2008, 23(4): 372-377. (EI 收录************)徐陈锋，奚宏⽣，江琦，殷保群，⼀类分层⾮结构化P2P系统的随机切换模型，控制与决策，2008, 23(3): 263-266. (EI 收录************)徐陈锋，奚宏⽣，殷保群，⼀类混合资源定位服务的优化模型，微计算机应⽤，2008，29(9)：6-11. 郭东，郑烇，殷保群，王嵩，基于P2P媒体内容分发络中分布式节点的设计与实现，电信科学，2008，24(8): 45-49. Tang, H., Yin, B. Q., Xi, H. S., Error bounds of optimization algorithms for semi-Markov decision processes. International Journal of Systems Science, 2007, 38(9): 725-736. (SCI收录) 徐陈锋，奚宏⽣，江琦，殷保群，⼀类分层⾮结构化P2P系统的随机优化，系统科学与数学，2007, 27(3): 412-421. 蒋兆春，殷保群，李俊，基于耦合技术计算Markov链性能势的仿真算法，系统仿真学报，2007, 19(15): 3398-3401. (EI收录************)庞训磊，殷保群，奚宏⽣，⼀种使⽤TCP/ IP 协议实现⽆线传感器络互连的新型设计，传感技术学报，2007, 20(6): 1386-1390. Niu, L. M., Tan, X. B., Yin, B. Q. , Estimation of system power consumption on mobile computing devices, 2007. International Conference on Computational Intelligence and Security, Harbin, China, DEC 15-19, 2007: 1058-1061. (EI收录************)Jiang,Q.,Xi, H. S., Yin, B. Q., Dynamic file grouping for load balancing in streaming media clustered server systems. Proceedings of the 2007 International Conference on Information Acquisition, ICIA, Jeju City, South Korea, 2007:498-503. (EI收录************)徐陈锋, 奚宏⽣, 江琦, 殷保群，⼀类分层⾮结构化P2P系统的随机优化，第2xx届中国控制会议论⽂集，2007: 693-696. (EI收录************)Jiang,Q.,Xi,H.S.,Yin,B.Q.,OptimizationofSemi-MarkovSwitchingState-spaceControl Processes for Network Communication Systems. 第2xx届中国控制会议论⽂集，2007: 707-711. (EI收录************) Jiang, Q., Xi, H. S., Yin, B. Q., Adaptive Optimization of Time-out Policy for Dynamic Power Management Based on SMCP. Proc. of the 2007 IEEE Multi-conference on Systems and Control, Singapore, 2007: 319-324. (EI收录************)Jin,H. Y., Yin, B. Q., New Consistency Condition for Exponential Stabilization of Smapled-Data Nonlinear Systems. 第2xx届中国控制会议论⽂集，2007: 84-87. (EI收录************)江琦，奚宏⽣，殷保群，⽆线多媒体通信适应带宽配置在线优化算法，软件学报， 2007, 18(6): 1491-1500. (EI收录************)Ou,Q.,Jin,Y.D.,Zhou,T.,Wang,B.H.,Yin,B.Q.,Power-law strength-degree correlation from resource-allocation dynamics on weighted networks, Physical Review E, 2007, 75(2): 021102 (SCI收录) Yin, B. Q., Dai, G. P., Li, Y. J., Xi, H. S., Sensitivity analysis and estimates of the performance for M/G/1 queueing systems, Performance Evaluation, 2007, 64(4): 347-356. (SCI收录) 江琦，奚宏⽣，殷保群，动态电源管理的随机切换模型与在线优化，⾃动化学报，2007, 33(1): 66-71. (EI收录************)Zhang,D.L.,Yin,B.Q.,Xi,H.S.,Astate aggregation approach to singularly perturbed Markov reward processes. International Journal of Intelligent Technology, 2006, 2(4): 230-239. 欧晴，殷保群，奚宏⽣，基于动态平衡流的络赋权，中国科学技术⼤学学报，2006, 36(11): 1196-1201.殷保群，李衍杰，周亚平，奚宏⽣，可数半Markov控制过程折扣代价性能优化，控制与决策，2006, 21(8): 933-936. (EI收录************)江琦，奚宏⽣，殷保群，动态电源管理的随机切换模型与策略优化，计算机辅助设计与图形学学报，2006, 18(5): 680-686. (EI收录***********)代桂平，殷保群，李衍杰，奚宏⽣，半Markov控制过程基于性能势仿真的并⾏优化算法，中国科学技术⼤学学报，2006, 36(2): 183-186. 殷保群，李衍杰，唐昊，代桂平，奚宏⽣，半Markov决策过程折扣模型与平均模型之间的关系，控制理论与应⽤，2006, 23(1): 65-68. (EI收录***********)江琦，奚宏⽣，殷保群，半Markov控制过程在线⾃适应优化算法，第2xx届中国控制会议论⽂集，2006: 1066-1071. (ISTP收录BFQ63) Dai, G. P., Yin, B. Q., Li, Y. J., Xi, H. S., Performance Optimization Algorithms based on potential for Semi-Markov Control Processes. International Journal of Control, 2005, 78(11): 801-812. (SCI收录) Zhang, D. L., Xi, H. S., Yin, B. Q., Simulation-based optimization of singularly perturbed Markov reward processes with states aggregation. Lecture Notes in Computer Science, 2005, 3645: 129-138. (SCI 收录) Tang, H., Xi, H. S., Yin, B. Q., The optimal robust control policy for uncertain semi-Markov control processes. International Journal of System Science, 2005, 36(13): 791-800. (SCI收录) 张虎，殷保群，代桂平，奚宏⽣，G/M/1排队系统的性能灵敏度分析与仿真，系统仿真学报，2005, 17(5): 1084-1086. (EI收录***********)陈波，周亚平，殷保群，奚宏⽣，隐马⽒模型中的标量估计，系统⼯程与电⼦技术，2005, 27(6): 1083-1086. (EI收录***********)代桂平，殷保群，李衍杰，周亚平，奚宏⽣，半Markov控制过程在平均准则下的优化算法，中国科学技术⼤学学报，2005, 35(2): 202-207. 殷保群，李衍杰，奚宏⽣，周亚平，⼀类可数Markov控制过程的平稳策略，控制理论与应⽤，2005, 22(1): 43-46. (EI收录***********)Li,Y.J.,Yin,B.Q.,Xi,H.S.,Thepolicygradientestimationofcontinuous-timeHiddenMarkovDecision Processes. Proc. of IEEE ICIA, Hong Kong, 2005. (EI收录************)Sensitivity analysis and estimates of the performance for M/G/1 queueing systems, To Appear in Performance Evaluation, 2006.Performance optimization algorithms based on potential for semi-Markov control processes. International Journal of Control, Vol.78, No.11, 2005.The optimal robust control policy for uncertain semi-Markov control processes. International Journal of System Science, Vol.36, No.13, 2005.A state aggregation approach to singularly perturbed Markov reward processes. International Journal of Intelligent Technology, Vol.2, No.4, 2005.Simulation optimization algorithms for CTMDP based on randomized stationary policies, Acta Automatics Sinica, Vol. 30, No. 2, 2004.Performance optimization of continuous-time Markov control processes based on performance potentials, International Journal of System Science, Vol.34, No.1, 2003.Optimal Policies for a Continuous Time MCP with Compact Action set, Acta Automatics Sinica, Vol. 29, No. 2, 2003. Relations between Performance Potential and Infinitesimal Realization Factor in Closed Queueing Networks, Appl. Math. J. Chinese Univ. Ser. B, Vol. 17, No. 4, 2002.Sensitivity Analysis of Performance in Queueing Systems with Phase-Type Service Distribution, OR Transactions, Vol.4, No.4, 2000.Sensitivity Formulas of Performance in Two-Server Cyclic Queueing Networks with Phase-Type Distributed Service Times, International Transaction in Operational Research, Vol.6, No.6, 1999.Simulation-based optimization of singularly perturbed Markov reward processes with states aggregation. Lecture Notes in Computer Science, 2005.Markov decision problems with unbounded transition rates under discounted-cost performance criteria. Proceedings of WCICA, Vol.1, Hangzhou, China, 2004.排队系统性能分析与Markov控制过程,合肥：中国科学技术⼤学出版社，2004.可数半Markov控制过程折扣代价性能优化. 控制与决策，Vol.21, No.8, 2006.动态电源管理的随机切换模型与策略优化. 计算机辅助设计与图形学学报，Vol.18, No.5, 2006.半Markov决策过程折扣模型与平均模型之间的关系.控制理论与应⽤，Vol.23, No.1, 2006.⼀类可数Markov控制过程的平稳策略. 控制理论与应⽤，Vol.22, No.1, 2005.G/M/1排队系统的性能灵敏度分析与仿真.系统仿真学报，Vol.17, No.5, 2005.M/G/1排队系统的性能优化与算法，系统仿真学报，Vol.16, No.8, 2004.半Markov过程基于性能势的灵敏度分析和性能优化. 控制理论与应⽤，Vol.21, No.6, 2004.半Markov控制过程在折扣代价准则下的平稳策略. 控制与决策，Vol.19, No.6, 2004.Markov控制过程在紧致⾏动集上的迭代优化算法. 控制与决策，Vol.18, No.3, 2003.闭Jackson络的优化中减少仿真次数的算法研究，系统仿真学报，Vol.15, No.3, 2003.M/G/1排队系统的性能灵敏度估计与仿真，系统仿真学报，Vol.15, No.7, 2003.Markov控制过程基于性能势仿真的并⾏优化，系统仿真学报，Vol.15, No.11, 2003.Markov控制过程基于性能势的平均代价策略. ⾃动化学报，Vol.28, No.6, 2002.⼀类受控闭排队络基于性能势的性⽅程.控制理论与应⽤，Vol.19, No.4, 2002.Markov控制过程基于单个样本轨道的在线优化算法.控制理论与应⽤，Vol.19, No.6, 2002.闭排队络当性能函数与参数相关时的性能灵敏度分析，控制理论与应⽤，Vol.19, No.2, 2002.M/G/1 排队系统的性能灵敏度分析，⾼校应⽤数学学报，Vol.16, No.3, 2001.连续时间Markov决策过程在呼叫接⼊控制中的应⽤，控制与决策，Vol.19, 2001.具有不确定噪声的连续时间⼴义系统确保估计性能的鲁棒Kalman滤波器，控制理论与应⽤，Vol.18, No.5, 2001.状态相关闭排队络中的性能指标灵敏度公式，控制理论与应⽤，Vol.16, No.2, 1999.科研项⽬半Markov控制过程基于性能势的优化理论和并⾏算法,2003.1-2005.12,国家⾃然科学基⾦,60274012隐Markov过程的性能灵敏度分析与优化,2006.1-2008.12,国家⾃然科学基⾦, 60574065部分可观Markov系统的性能优化,2005.1-2006.12,安徽省⾃然科学基⾦, 050420301宽带信息运营⽀撑环境及接⼊系统的研制――⼦课题: 流媒体服务器研究及实现, 2005.1-2006.12, 国家863计划,2005AA103320离散复杂系统的控制与优化研究,2006.9-2008.8,中国科学院⾃动化研究所中国科学技术⼤学智能科学与技术联合实验室⾃主研究课题基⾦络新媒体服务系统的建模及其动⼒学⾏为分析研究，2012.01-2015.12，国家⾃然科学基⾦；⾯向服务任务的快速机器视觉与智能伺服控制，2010.01-2013.12，国家⾃然科学基⾦重点项⽬；新⼀代业务运⾏管控协同⽀撑环境的开发，2008.07-2011.06，国家863计划；多点协作的流媒体服务器集群系统及其性能优化，2006.12-2008.12，国家863计划；获奖情况第xx届何潘清漪优秀论⽂奖联系信息办公室地址：电⼆楼223 实验室地址：电⼆楼227 办公室电话：************。

Adaptive neural tracking control for stochastic nonlinear strict-feedback systems

Adaptive neural tracking control for stochastic nonlinear strict-feedback systems with unknown inputsaturationHuanqing Wang a ,c ,Bing Chen a ,⇑,Xiaoping Liu b ,Kefu Liu b ,Chong Lin aaInstitute of Complexity Science,Qingdao University,Qingdao,266071Shandong,PR China bFaculty of Engineering,Lakehead University,Orillia,ON P7A 5E1,Canada cSchool of Mathematics and Physics,Bohai University,Jinzhou,121000Liaoning,PR Chinaa r t i c l e i n f o Article history:Received 11January 2013Received in revised form 4June 2013Accepted 22September 2013Available online 2October 2013Keywords:Adaptive neural tracking control Stochastic nonlinear system Input saturationBackstepping techniquea b s t r a c tIn this paper,the problem of adaptive neural tracking control is considered for a class of single-input/single-output (SISO)strict-feedback stochastic nonlinear systems with input saturation.To deal with the non-smooth input saturation nonlinearity,a smooth nonafﬁne function of the control input signal is used to approximate the input saturation function.Classical adaptive technique and backstepping are used for control synthesis.Based on the mean-value theorem,a novel adaptive neural control scheme is systematically derived without requiring the prior knowledge of bound of input saturation.It is shown that under the action of the proposed adaptive controller all the signals of the closed-loop system remain bounded in probability and the tracking error converges to a small neighborhood around the origin in the sense of mean quartic value.Two simulation examples are pro-vided to demonstrate the effectiveness of the presented results.Ó2013Elsevier Inc.All rights reserved.1.IntroductionIt is well known that stochastic disturbance,which is usually a source of instability of control systems,often exists in practical systems.Therefore,the control design of nonlinear stochastic systems has attracted increasing attention in recent years [9,10,16,27,29,30,36–38,49–54].Many control design approaches for deterministic nonlinear systems have been suc-cessfully extended to stochastic nonlinear systems.Especially,backstepping technique [18]has been a popular tool for con-trol design of stochastic nonlinear systems,see, e.g.,[9,10,16,27,29,30,49–52]and the reference therein.In [30],the quadratic Lyapunov function is used to solve the stabilization problem for stochastic nonlinear strict-feedback systems based on a risk-sensitive cost criterion,and the proposed controller guarantees globally asymptotic stability in probability.In [9,10],a quartic Lyapunov function is applied for control design and stability analysis of stochastic nonlinear strict-feedback and output-feedback pared with the quadratic Lyapunov function,the quartic Lyapunov function can be used to easily deal with the high-order Hessian term.Since then,the quartic Lyapunov function has been widely applied for con-trol design of stochastic nonlinear systems [16,29,49–52].However,the aforementioned control schemes maybe invalid to control stochastic systems with unknown nonlinear function,because they require that the nonlinear dynamics models are known precisely or the unknown parameters appear linearly with respect to known nonlinear functions.During the past decades,many approximation-based adaptive neural (or fuzzy)control approaches have been developed to control uncertain lower-triangular nonlinear systems,and lots of signiﬁcant results have been reported,for example,see [2–5,12–14,19,22,23,25,26,28,35,39–42,44,46,55–58]for deterministic nonlinear systems and [8,21,33,43,47]for stochastic 0020-0255/$-see front matter Ó2013Elsevier Inc.All rights reserved./10.1016/j.ins.2013.09.043⇑Corresponding author.Tel.:+86053285953607.E-mail address:chenbing1958@ (B.Chen).nonlinear systems.In these proposed control schemes,radial basis function (RBF)neural networks (or fuzzy logic systems)are used to approximate uncertain smooth nonlinear functions,and then adaptive backstepping technique is applied to de-sign controllers.For the deterministic systems,Ge et al.[12–14]develop several adaptive neural control schemes for SISO nonlinear systems and multi-input and multi-output (MIMO)nonlinear systems.In [57,58],the problem of adaptive neural tracking control is considered for MIMO nonlinear systems with dead-zone.Then,for stochastic systems,Psillakis and Alex-andridis [33]proposes an adaptive neural network control scheme to solve the problem of output tracking control for uncer-tain stochastic nonlinear strict-feedback systems with unknown covariance noise.Alternatively,in [47],a fuzzy-based adaptive control scheme is presented for a class of uncertain strict-feedback stochastic nonlinear systems with unknown vir-tual control gain function.The proposed controller guarantees that all the signals in the closed-loop systems are semi-glob-ally uniformly bounded in probability.Recently,in [8,21,24,43],several approximation-based adaptive control approaches are proposed for some classes of stochastic nonlinear strict-feedback time-delay (or delay-free)systems.In many practical systems,input saturation is one of the most important non-smooth nonlinearities.It often severely lim-its the system performance,gives rise to undesirable inaccuracy or leads to instability [32].Therefore,the phenomenon of input saturation has to be considered when the controller is designed in practical industrial process control ﬁeld.So far,many signiﬁcant results on control design of the systems with input saturation have been obtained,for example,see [6,7,11,48,59].In [59],a globally stable adaptive control approach is presented for minimum phase SISO systems with input saturation.Chen et al.[6]proposes a robust adaptive neural control for a class of MIMO nonlinear systems with input non-linearities.By introducing auxiliary design systems to analyze the effect of input constraints,in [7],an adaptive tracking con-trol is proposed for a class of uncertain nonlinear systems with non-symmetric input constraints,and the derived controller guarantees that the closed-loop system is semi-globally uniformly ultimately bounded stability.Wen et al.[48]considers the problem of adaptive control for a class of uncertain nonlinear systems in the presence of input saturation and external dis-turbance,in which two new schemes are developed to compensate for the effects of the saturation nonlinearity and distur-bances.Though the aforementioned results take input saturation nonlinearity into account,the effect of stochastic disturbance is ignored.Note that stochastic disturbance and input constraint could be existed in many practical systems.Motivated by the above observations,this paper considers the problem of adaptive neural tracking control for the case of nonlinear strict-feedback systems with stochastic disturbance and input saturation simultaneously.The proposed adaptive neural control scheme guarantees that all the signals in the closed-loop system are bounded in probability and the tracking error eventually con-verges to a small neighborhood around the origin in the sense of mean quartic pared with the existing results,the main idea of control design in this paper is that a smooth non-afﬁne function of the control input signal is ﬁrstly used to approximate the saturation function,and furthermore,the mean-value theorem is used to transform the non-afﬁne function into afﬁne form,i.e.,g ðv Þ¼g v l v .Then,the classical adaptive technique and backstepping are used to design controller.The proposed design approach does not require the prior knowledge of the bound of input saturation.In addition,the number of adaptive parameters just depends on the order of the considered systems.So,it is reduced considerably.In this way,the computational burden is signiﬁcantly alleviated.This paper is organized as follows.The preliminaries and problem formulation are given in Section 2.A novel adaptive neural control scheme is presented in Section 3.Section 4gives two simulation examples to illustrate the effectiveness of our results,and Section 5concludes the work.2.Preliminaries and problem formulationThe following notations are used throughout this paper.R denotes the set of all real numbers;R n indicates the real n-dimensional space.For a given vector or matrix X ,X T denotes its transpose;Tr{X }is its trace when X is a square matrix;and k X k denotes the Euclidean norm of a vector X .C i denotes the set of all functions with continuous i th partial derivative.Consider the following strict-feedback stochastic nonlinear system given by:dx i ¼ðg i ðx i Þx i þ1þf i ð x i Þþd i ðt ;x ÞÞdt þw T i ð x i Þdw ;16i 6n À1;dx n ¼ðg n ð x n Þu ðv Þþf n ð x n Þþd n ðt ;x ÞÞdt þw Tn ð x n Þdw ;y ¼x 1;8><>:ð1Þwhere x i ¼½x 1;x 2;...;x i T 2R i ,x =[x 1,x 2,...,x n ]T 2R n and y 2R are the state variables and the system output,respectively;w denotes an r-dimensional standard Brownian motion deﬁned on the complete probability space (X ,F ,P )with X being a sam-ple space,F being a r -ﬁeld,and P being a probability measure;f i (Á),g i (Á):R i ?R ,w i (Á):R i ?R r ,(i =1,2,...,n )stand for the unknown smooth nonlinear functions with f i (0)=0and w i (0)=0(16i 6n ),d i (Á),i =1,2,...,n are the external disturbance uncertainties of the system.v is the control signal to be designed,and u (v )denotes the plant input subject to saturation non-linearity described byu ðv Þ¼sat ðv Þ¼sign ðv Þu max ;j v j P u max ;v ;j v j <u max ;&ð2Þwhere u max is a unknown parameter of input saturation.H.Wang et al./Information Sciences 269(2014)300–315301Remark 1.There exist many practical systems which are described by strict-feedback form,such as One-Link Robot system,Pendulum System With Motor,Single-Link Manipulator system [55],and Brusselator model [45].Meanwhile,stochastic disturbance and input saturation are inevitable in practical process.Therefore,the aforementioned systems can be governed by nonlinear differential equations of the form (1).The control objective is to design an adaptive neural controller for system (1)such that the system output y follows the speciﬁed desired trajectory y d and all the signals in the closed-loop systems remain bounded in probability.From (2),it can be seen that there exists a sharp corner when j v j =u max .So backstepping technique cannot be directly applied to construct control input signal.To solve this problem,the method proposed in [48]will be implemented.By this method,a smooth function is used to approximate the saturation function and deﬁned asg ðv Þ¼u max Ãtanh ðv =u max Þ¼u max Ãe v =u max Àe Àv =u maxv max v max:ð3ÞThen,sat (v )in (2)can be expressed in the following form:sat ðv Þ¼g ðv Þþd ðv Þ;ð4Þwhere d (v )=sat (v )Àg (v )is a bounded function and its bound can be obtained asj d ðv Þj ¼j sat ðv ÞÀg ðv Þj 6u max ð1Àtanh ð1ÞÞ¼D :ð5ÞFig.1shows the saturation nonlinearity in (2)and its approximation function in (3).According to the mean-value theorem [1],there exists a constant l with 0<l <1,such thatg ðv Þ¼g ðv 0Þþg v l ðv Àv 0Þ;ð6Þwhere g v l ¼@g ðv Þv j v ¼v l¼4ðe =u max þe À=u max Þj v ¼v l ,v l =l v +(1Àl )v 0.By choosingv 0=0,(6)can be written asg ðv Þ¼g v l v ;ð7ÞSubstituting (4)into (1)and using (7)givesdx i ¼ðg i ðx i Þx i þ1þf i ð x i Þþd i ðt ;x ÞÞdt þw T i ð x i Þdw ;16i 6n À1;dx n ¼ðg n ð x n Þðg v l v þd ðv ÞÞþf n ð x n Þþd n ðt ;x ÞÞdt þw T n ð x n Þdw ;y ¼x 1:8><>:ð8ÞTo facilitate control system design,the following assumptions and lemmas are presented and will be used in the subsequent developments.Assumption 1([3,14]).For 16i 6n ,the function g i ðx i Þis unknown,but the sign of g i ð x i Þdoes not change,and there exist unknown constants b m and b M ,such that0<b m 6j g i ð x i Þj 6b M <1;8 x i 2R i :ð9ÞApparently,(9)implies that g i ðx i Þis strictly either positive or negative.Without loss of generality,it is further assumed that 0<b m 6g i ð x i Þ6b M ;8x i 2R i :ð10ÞAssumption 2[45].For 16i 6n ,thereexistunknownsmoothpositivefunctionsh i ð x i Þsuchthat8ðt ;x Þ2R þÂX ;j d i ðt ;x Þj 6h i ðx i Þ.302H.Wang et al./Information Sciences 269(2014)300–315Assumption 3[3].The desired trajectory y d (t )and its n th order time derivatives are continuous and bounded.To introduce some useful conceptions and lemmas,consider the following stochastic system:dx ¼f ðx Þdt þh ðx Þdw ;ð11Þwhere x and w are deﬁned in (1),and f (Á)and h (Á)are locally Lipschitz functions in x and satisfy f (0)=0and h (0)=0.Deﬁnition 1.For any given V (x )2C 2,associated with the stochastic differential Eq.(11),deﬁne the differential operator L as follows:LV ¼@V @x f þ12Tr h T@2V @x 2h ();ð12Þwhere Tr (A )is the trace of A .Remark 2.As stated in [29],the term 1Tr h T @2Vh n ois called It ^o correction term or high-order Hessian term,in which the second-order differential @2V2makes the controller design much more difﬁcult than that of the deterministic system.Deﬁnition 2[17].The solution process {x (t ),t P 0}of stochastic system (11)is said to be bounded in probability,if lim c ?1sup 06t <1P{k x (t )k >c }=0,where P{B }denotes the probability of event B .Lemma 1[33].Consider the stochastic system (11).If there exists a positive deﬁnite,radially unbounded,twice continuously dif-ferentiable Lyapunov function V :R n !R ,and constants a 0>0,b 0P 0such thatLV ðx Þ6Àa 0V ðx Þþb 0;then (i)the system has a unique solution almost surely and (ii)the system is bounded in probability.Lemma 2(Young’s inequality [9]).For "(x,y)2R 2,the following inequality holds:xy 6e ppj x j p þ1q eq j y j q ;where e >0,p >1,q >1,and (p À1)(q À1)=1.Lemma 3[31].For any variable g 2R and constant>0,the following inequality holds.06j g j Àg tanhg6d ;d ¼0:2785:ð13ÞIn this note,the following RBF neural networks will be used to approximate any continuous function f (Z ):R n ?R ,f nn ðZ Þ¼W T S ðZ Þ;ð14Þwhere Z 2X Z &R q is the input vector with q being the neural networks input dimension,weight vector W =[w 1,w 2,...,w l ]-T2R l ,l >1is the neural networks node number,and S (Z )=[s 1(Z ),s 2(Z ),...,s l (Z )]T means the basis function vector with s i (Z )being chosen as the commonly used Gaussian function of the forms i ðZ Þ¼exp ÀðZ Àl i ÞT ðZ Àl i Þr 2"#;i ¼1;2;...;l ;ð15Þwhere l i =[l i 1,l i 2,...,l iq ]T is the center of the receptive ﬁeld and r is the width of the Gaussian function.In [34],it has been indicated that with sufﬁciently large node number l ,the RBF neural networks (14)can approximate any continuous function f (Z )over a compact set X Z &R q to arbitrary any accuracy e >0asf ðZ Þ¼W ÃTS ðZ Þþd ðZ Þ;8z 2X z 2R q ;ð16Þwhere W ⁄is the ideal constant weight vector and deﬁned asW Ã:¼arg min W 2lsup Z 2X Zj f ðZ ÞÀW T S ðZ Þj ();and d (Z )denotes the approximation error and satisﬁes j d (Z )j 6e .H.Wang et al./Information Sciences 269(2014)300–315303Lemma 4[20].Consider the Gaussian RBF networks (14)and (15).Let q :¼12min i –j kl i Àl j k ,then an upper bound of k S(Z)k istaken ask S ðZ Þk 6X 1k ¼03q ðk þ2Þq À1e À2q 2k 2=r 2:¼s :ð17ÞIt has been shown in [44]that the constant s in Lemma 3is a limited value and is independent of the variable Z and the dimension of neural weights l .3.Adaptive neural control designIn this section,a backstepping-based design procedure will be proposed to construct the adaptive neural tracking control-ler for the original systems (1)with input saturation nonlinearity (2).The design procedure contains n steps and involves the following coordinate transformation:z 1¼x 1Ày d ;z i ¼x i Àa i À1;i ¼2;...;n ;ð18Þwhere a i is a virtual control signal to be designed for the corresponding i -subsystem based on an appropriate Lyapunov func-tion V i .During the design procedure,the virtual control signal and adaptive law will be constructed in the following form:a i ðZ i Þ¼Àk i z i À^h i k S i ðZ i Þk tanhz 3i k S i ðZ i Þk i;ð19Þ_^h i ¼Àc i ^h i þk i z 3i k S i ðZ i Þk tanh z 3i k S i ðZ i Þk a i;ð20Þwhere 16i 6n ,k i ,a i ,c i and k i are positive design contants,S i (Z i )is the RBF neural network basis function vector with Z 1¼½x 1;y d ;_y d T 2X Z 1&R 3;Z i ¼ x T i ; ^h T i À1; y ði ÞT d h i T 2X Z i &R 2i þ2ði ¼2;...;n Þ; ^h i ¼½^h 1;^h 2;...;^h i T . yði Þd denotes the vector composed of y d and up to its i th order time derivative,^h i is the estimation of an unknown constant h i which will be given at the i th step,Specially,a n denotes the actual control input v .Remark 3.It is easy to prove from (20)that if initial condition ^h i ð0ÞP 0,then ^h i ðt ÞP 0for all t P 0.Note that ^h i is an estimation of h i ,and the initial condition of (20)can be given by designer.So,it is reasonable to choose ^h i ð0ÞP 0.Thisproperty will be used in each step of control design.In the following,for simplicity,the time variable t and the state vector x i will be omitted from the corresponding functions and denote S i (Z i )by S i .Step 1:Since z 1=x 1Ày d ,the ﬁrst subsystem of (1)givesdz 1¼ðg 1x 2þf 1þd 1À_y d Þdt þw T 1dw :ð21ÞConsider Lyapunov function candidate asV 1¼1z 41þb m 1~h 21;ð22Þwhere ~h 1¼h 1À^h 1is the parameter error.It can be veriﬁed easily from (12)along (21)and using the completion of squares thatLV 16z 31g 1x 2þf 1þd 1À_y d þ34l À21z 1k w 1k 4þ34l 21Àb m k 1~h 1_^h 1;ð23Þwhere l 1is a design constant.By means of Assumption 3,the following inequality holds:z 31d 16j z 1j 3h 1ðx 1Þ612g211z 61h 21ðx 1Þþ12g 211:ð24ÞSubstituting (24)into (23)yieldsLV 16z 31ðg 1x 2þ f 1ðZ 1ÞÞÀ3z 41À3g 1z 41þ3l 21þ1g 211Àb m 1~h 1_^h 1;ð25Þwhere f 1ðZ 1Þ¼f 1À_y d þ12g 211z 31h 21ðx 1Þþ34l À21z 1k w 1k 4þ34z 1þ34g 1z 1.Since the smooth functions f 1,g 1,h 1and w 1are unknown, f 1ðZ 1Þcannot be directly used to construct virtual control signal a 1.Thus,an RBF neural network W T 1S 1ðZ 1Þis employed toapproximate the function f 1ðZ 1Þsuch that,for any given e 1>0,f 1ðZ 1Þ¼W T 1S 1ðZ 1Þþd 1ðZ 1Þ;j d 1ðZ 1Þj 6e 1ð26Þ304H.Wang et al./Information Sciences 269(2014)300–315with d 1(Z 1)being the approximation error.Then,according to Lemma 3,one hasz 31 f 1ðZ 1Þ¼z 31W T1S 1þz 31d 16j z 31jk W 1kk S 1kþ34z 41þ14e 416z 31b m h 1k S 1k tanh z 31k S 1k a 1þd b m h 1a 1þ34z 41þ14e 41;ð27Þwhere the unknown constant h 1¼k W 1k m.Substituting (26)into (25)and using (27)givesLV 16z 31g 1z 2þz 31g 1a 1þz 31b m h 1k S 1k tanhz 31k S 1k 1þd b m h 1a 1þ1e 41À3g 1z 41þ3l 21þ1g 211Àb m 1~h 1_^h 1;ð28Þwhere z 2=x 2Àa 1.At the present stage,constructing the virtual control signal a 1asa 1¼Àk 1z 1À^h 1k S 1k tanhz 31k S 1k a 1;ð29Þthen using (10),we havez 31g 1a 16Àk 1b m z 41Àz 31b m ^h 1k S 1k tanhz 31k S 1k a 1:ð30ÞFrom (30),rewrite (28)asLV 16Àk 1b m z 41þz 31g 1z 2À3g 1z 41þd b m h 1a 1þ1e 41þ3l 21þ1g 211þb m 1~h 1k 1z 31k S 1k tanh z 31k S 1k 1 À_^h 1:ð31ÞBy choosing adaptive law _^h 1in (20)with i =1,it followsLV 16Àk 1b m z 41þz 31g 1z 2þd b m h 1a 1þ14e 41þ34l 21þ12g 211þb m c1k 1~h 1^h 1:ð32ÞFurthermore,applying Young’s inequality yieldsz 31g 1z 263g 1z 41þ1g 1z 42;ð33Þb m c 1k 1~h 1^h 1¼Àb m c 1k 1~h 21þb m c 1k 1~h 1h 16Àb m c 12k 1~h 21þb m c 12k 1h 21:ð34ÞUsing (33)and (34),we can further haveLV 16Àk 1b m z 41Àb mc 12k 1~h 21þd b m h 1a 1þ14e 41þ34l 21þ12g 211þb m c 12k 1h 21þ14g 1z 426Àc 1z 41Àb m c 12k 1~h 21þq 1þ14g 1z 42;ð35Þwhere c 1¼k 1b m ;q 1¼d b m h 1a 1þb m c 11h 21þ1e 41þ3l 21þ1g 211.The term 1g 1z 42will be dealt with in the next step.Step 2:From z 2=x 2Àa 1and It ^oformula,we have dz 2¼ðg 2x 3þf 2þd 2À‘a 1Þdt þw 2À@a 1@x 1w 1Tdw ;ð36Þwhere‘a 1¼@a 1@x 1ðg 1x 2þf 1þd 1ÞþN 1ð37ÞwithN 1¼X 1j ¼0@a 1@y ðj Þdy ðj þ1Þdþ@a 1@^h 1_^h 1þ12@2a 1@x 21w T1w 1:ð38ÞChoose the Lyapunov function asV 2¼V 1þ14z 42þb m 2k 2~h 22:ð39ÞFurthermore,by (12)it can be veriﬁed thatLV 2¼LV 1þz 32ðg 2x 3þf 2þd 2À‘a 1Þþ3z 22w 2À@a 11w 1 T w 2À@a 11w 1Àb m 2~h 2_^h 2:ð40ÞBy substituting (31)and (37)into (40)and using the completion squares to the term next to the last one in (40),one hasH.Wang et al./Information Sciences 269(2014)300–315305LV26Àc1z41Àb m c12k1~h21þq1þ14g1z42þz32g2x3þf2þd2À@a1@x1ðg1x2þf1þd1ÞÀN1þ34lÀ22z2k w2À@a1@x1w1k4þ34l22Àb mk2~h2_^h2;ð41Þwhere l2is a positive design ing the similar way to(24)yieldsÀz32@a1@x1d16j z32j@a1@x1h1612g21z62@a1@x12h21þ12g221;ð42Þz3 2d2612g222z62h22þ12g222:ð43ÞWith the help of(42)and(43),(41)can be written asLV26Àc1z41Àb m c11~h21þq1þz32g2x3þ f2ðZ2ÞÀÁÀ3z42À3g2z42þ3l22þ1X2j¼1g22jÀb m2~h2_^h2;ð44Þwheref 2ðZ2Þ¼f2À@a1@x1ðg1x2þf1Þþ14g1z2ÀN1þ3z24l2k w2À@a1@x1w1k4þ12g21z32@a1@x12h21þ12g22z32h22þ34z2þ34g2z2:ð45ÞNote that f2ðZ2Þis an unknown smooth function.Therefore,an RBF neural network W T2S2ðZ2Þis used to model the unknownf2ðZ2Þsuch thatf 2ðZ2Þ¼W T2S2ðZ2Þþd2ðZ2Þ;ð46Þwhere the approximate error d2(Z2)satisﬁes j d2(Z2)j6e2with e2being a given positive constant.Similar to(27),the following inequality holds.z3 2 f2ðZ2Þ6z32b m h2k S2k tanhz32k S2ka2þd b m h2a2þ34z42þ14e42;ð47Þwhere the unknown constant h2¼k W2kb m.Substituting(46)into(44)and using the inequality(47),we haveLV26Àc1z41Àb m c11~h21þq1þd b m h2a2þ1e42þ3l22þ1X2j¼1g22jþz32g2z3þz32g2a2þz32b m h2k S2k tanhz32k S2k2À34g2z42Àb mk2~h2_^h2;ð48Þwhere z3=x3Àa2.Then,take a2in(19)and^h2in(20)into account with i=2,the following inequalities can be obtained.z3 2g2a26Àk2b m z42Àz32b m^h2k S2k tanhz32k S2ka2;ð49Þz3 2g2z3634g2z42þ14g2z43:ð50ÞBy using the above inequalities,we can rewrite(48)asLV26ÀX2j¼1c j z4jÀb m c12k1~h21þq1þd b m h2a2þ14e42þ34l22þ12X2j¼1g22jþb m c2k2~h2^h2þ14g2z436ÀX2j¼1c j z4jÀX2j¼1b mc jj~h2jþX2j¼1qjþ1g2z43;ð51Þwhere c j¼k j b m;q j¼d b m h j a jþb m c jj h2jþ1e4jþ3l2jþ1P jk¼1g2jk;j¼1;2,and the inequality~h2^h26À1~h22þ1h22has been used.Step i(36i6nÀ1):By using(18)and It^o formula,one hasdz i¼ðg i x iþ1þf iþd iÀ‘a iÀ1Þdtþw iÀX iÀ1j¼1@a iÀ1@x jwj!Tdw;ð52Þwhere‘a iÀ1¼X iÀ1j¼1@a iÀ1jðg j x jþ1þf jþd jÞþN iÀ1ð53Þ306H.Wang et al./Information Sciences269(2014)300–315with N iÀ1¼P iÀ1j¼1@a iÀ1@^h j_^hjþP iÀ1j¼0@a iÀ1@yðjÞdyðjþ1Þdþ12P iÀ1p;q¼1@2a iÀ1@x p@x qw Tpwq.Consider Lyapunov function asV i¼V iÀ1þ1z4iþb mi~h2i:ð54ÞIt follows immediately from(12)thatLV i¼LV iÀ1þz3i ðg i x iþ1þf iþd iÀ‘a iÀ1Þþ32z2iwiÀX iÀ1j¼1@a iÀ1@x jwj!TwiÀX iÀ1j¼1@a iÀ1@x jwj!Àb mk i~hi_^hi;ð55Þwhere the term LV iÀ1can be obtained by a straightforward calculation as former steps.LV iÀ16ÀX iÀ1j¼1c j z4jÀX iÀ1j¼1b mc jj~h2jþX iÀ1j¼1qjþ1giÀ1z4i;ð56Þwhere c j¼k j b m;q j¼d b m h j a jþb m c jj h2jþ1e4jþ3l2jþ1P jk¼1g2jk;j¼1;2;...;iÀ1.By using the completion of squares,the following inequality holds:3 2z2iwiÀX iÀ1j¼1@a iÀ1@x jwj2634l2iþ34lÀ2iz4iwiÀX iÀ1j¼1@a iÀ1@x jwj4;ð57Þwhere l i is a positive design parameter.Next,by following a same line used in the procedures from(42)and(43),we haveÀz3iX iÀ1j¼1@a iÀ1@x jd j6X iÀ1j¼1j z i j3j@a iÀ1@x jj h j6X iÀ1j¼112g2ijz6i@a iÀ1@x j2h2jþX iÀ1j¼112g2ij;ð58Þz3 i d i612g2iiz6ih2iþ12g2ii:ð59ÞFurther,substituting(53),(56)and(57)into(55)and using the formulas(58),(59)and(55)can be rewritten asLV i6ÀX iÀ1j¼1c j z4jÀX iÀ1j¼1b mc jj~h2jþX iÀ1j¼1qjþz3iðg i x iþ1þ f iðZ iÞÞÀ3z4iÀ3giz4iþ3l2iþ1X ij¼1g2ijÀb mi~hi_^hi;ð60Þwhere f iðZ iÞis deﬁned asf i ðZ iÞ¼f iÀX iÀ1j¼1@a iÀ1@x jðg j x jþ1þf jÞÀN iÀ1þ34lÀ2iz i k w iÀX iÀ1j¼1@a iÀ1@x jwjk4þX iÀ1j¼112g ijz3i@a iÀ1@x j2h2jþ12g iiz3ih2iþ14giÀ1z i þ34z iþ34giz ið61ÞCurrently,by employing a neural networks W TiS iðZ iÞto approximate the unknown smooth function f iðZ iÞand constructing the virtual control law a i and adaptive law_^h i deﬁned respectively in(19)and(20),and then repeating the similar procedure from(27)–(35)in Step1,the following result is true.LV i6ÀX ij¼1c j z4jÀX ij¼1b mc j2k j~h2jþX ij¼1qjþ14giz4iþ1;ð62Þwhere c j¼k j b m;q j¼d b m h j a jþb m c j2k j h2jþ14e4jþ34l2jþ12P jk¼1g2jk;j¼1;2; (i)Step n:This is theﬁnal step,and the actual control input v will be constructed.By(18)and It^o formula,we havedz n¼ðg nðg vl vþdðvÞÞþf nþd nÀ‘a nÀ1ÞdtþwnÀX nÀ1j¼1@a nÀ1jwj!Tdw;where‘a nÀ1is given in(53)with i=n.Choose the following Lyapunov function candidate:V n¼V nÀ1þ14z4nþg2k n~h2n;H.Wang et al./Information Sciences269(2014)300–315307。

有源滤波器的无源性控制方法研究

Stud y on Pa ssiv ity2Ba sed C on tr o l Stra teg ies of Act ive Power F ilter
SON G Chuan yu
( Shanghai Shenhuo A lum inium Foil Co. , L td. , Shangha i 201319, China. )
D }, R es = Rs I2 , u 12 = [ u1 u2 ] , q �= [ q � � � � e q 3 ] = [ q 1 q 2 q � � ) = [Ls q � � � 3 ] , c(q 2 - Ls q 1 ] , Ce ( q 3 ) = u3 L s J 2 ,
u3 ] = [ u sd u sq uC ], 分别为输出电压的 d、 q分量及
输出电容电压。同步旋转坐标系下可等效变换为
D¨ q + C ( q) �q �+ Rq � = [ u 12 0 ]
T T T T
( 1)
式中 : D = diag { De , C } , D e = Ls I2 , R = diag { R e s,
1 并联型 A PF 的 EL 系统模型
根据 Euler2 Lagrange ( EL ) 系统的控制特性 , 可将并联型三相 APF 看作是由两个电气子系统构成的负反馈连接的 EL 系统。定义系统状态变量 [q � � � 1 q 2 q 3 ] = [ isd isq U d ], 分别为 APF 输入电流的 d、 q 分量及直流侧电压 ; 系统控制变量 [ u1 u2
Abstr ac t: A i m ing a t the time2 va rying unknown condition of non 2 linear load, passivity2 ba sed contr ol ( P BC )

multivariable feedback control analysis and design

Multivariable Feedback Control Analysis and Design1. IntroductionIn modern control systems, it is often necessary to control multiple variables simultaneously in order to meet specific performance requirements. This is known as multivariable control. Multivariable feedback control analysis and design involves the study of techniques for designing control systems that can handle multiple variables simultaneously. In this article, we will explore various aspects of multivariable feedback control analysis and design.2. Multivariable Control SystemsMultivariable control systems are systems that have multiple inputs and multiple outputs. These systems are typically more complex than single-input single-output (SISO) systems because the interactions between different variables can complicate the control design process. Understanding the characteristics and behavior of multivariable control systems is crucial for their effective analysis and design.2.1 System IdentificationBefore designing a multivariable control system, it is important to identify the dynamic behavior of the system. System identification techniques can be used to determine the mathematical models that describe the relationships between inputs and outputs of the system. This involves collecting input-output data and using various modeling techniques such as empirical modeling, transfer function modeling, or state-space modeling.2.2 Control ObjectivesIn multivariable control, there are often multiple conflicting control objectives that need to be satisfied simultaneously. These control objectives can include stability, desired transient response, disturbance rejection, and tracking of setpoints. Balancing theseobjectives and designing controllers that achieve them is a central aspect of multivariable control analysis and design.2.3 Interactions and CouplingOne of the key challenges in multivariable control is the presence of interactions and coupling between the different variables. Interactions occur when changes in one variable affect the behavior of another variable. These interactions can make it difficult to design controllers that do not interfere with each other. Understanding and mitigating interactions is essential for effective multivariable control.2.4 Controller StructureThe selection of an appropriate controller structure is critical to the success of multivariable control design. There are various types of controller structures that can be used, such as decentralized control, centralized control, and decentralized control with optimization. Each structure has its advantages and disadvantages, and the choice depends on the specific requirements of the control problem.3. Multivariable Control AnalysisMultivariable control analysis involves studying the behavior and performance of multivariable control systems. It aims to provideinsights into the system’s dynamics, stability, and robustness.3.1 Stability AnalysisStability is a fundamental requirement for any control system. In multivariable control, stability analysis becomes more complex due to the interactions and couplings between variables. Stability analysis techniques such as eigenvalue analysis, Nyquist stability criterion, and pole placement methods can be used to investigate and ensure thestability of a multivariable control system.3.2 Performance AnalysisPerformance analysis involves evaluating the performance of a multivariable control system in terms of its response to inputs and disturbance rejection. Performance measures such as rise time, settling time, overshoot, and steady-state error can be used to assess the system’s performa nce. Analysis techniques like frequency response analysis, time response analysis, and sensitivity analysis can provide valuable insights into the system’s performance characteristics.3.3 Robustness AnalysisRobustness analysis is concerned with the ability of a multivariable control system to withstand uncertainties and variations in the system’s parameters. Robust control techniques aim to designcontrollers that can provide satisfactory performance over a range of operating conditions and system uncertainties. Sensitivity analysis, robust stability analysis, and the use of optimal control techniques are commonly employed for robustness analysis in multivariable control.3.4 Interaction AnalysisInteraction analysis is crucial for understanding and managing the interactions between variables in a multivariable control system. Interaction measures such as relative gain array (RGA) and condition number matrix (CN) can be used to quantify the strength and direction of interactions. Analysis of interaction patterns can help in choosing appropriate control strategies and gain scheduling techniques to minimize interactions.4. Multivariable Control DesignMultivariable control design involves designing controllers that achieve the desired control objectives while taking into account the system’s dynamics, interactions, and constraints.4.1 Decentralized Control DesignDecentralized control design involves designing individual controllers for each variable in a multivariable control system. Each controller operates based on its local measurements and controls its respective variable. Decentralized control can be advantageous when theinteractions between variables are weak, and the system can be effectively decoupled.4.2 Centralized Control DesignCentralized control design aims to design a single controller that regulates all variables simultaneously. This approach considers the interactions between variables explicitly and can achieve better overall control performance. However, centralized control can be computationally complex and may require accurate modeling of the entire system.4.3 Decentralized Control with OptimizationDecentralized control with optimization is an intermediate approach that combines the advantages of both decentralized and centralized control. It involves designing decentralized controllers for individual variables while optimizing their performance collectively. This approach can provide a good balance between performance and complexity.4.4 Controller Tuning MethodsOnce the controller structure is selected, tuning methods are used to determine the controller parameters. Various tuning methods are available, such as PID tuning, gain scheduling, pole placement, and optimization-based methods. Each method has its advantages and limitations, and the choice depends on the specific control problem and requirements.5. ConclusionMultivariable feedback control analysis and design are essential for the effective control of systems with multiple variables. This article discussed key aspects of multivariable control systems, including systemidentification, control objectives, interactions and coupling, and controller structure selection. It also explored multivariable control analysis techniques, such as stability analysis, performance analysis, robustness analysis, and interaction analysis. Furthermore, the article covered various multivariable control design approaches like decentralized control, centralized control, and decentralized control with optimization. By understanding and applying these concepts and techniques, engineers can design robust and efficient multivariable control systems to meet desired control objectives.。

高精度定位系统的摩擦力自适应前馈补偿

电气传动2021年第51卷第4期ELECTRIC DRIVE 2021Vol.51No.4摘要：为了有效抑制机电系统摩擦力等外部扰动对系统动态性能的影响，针对直驱伺服系统中往复定位存在的摩擦力，提出了一种基于自适应前馈控制器的摩擦力补偿策略，此方法能够有效利用参考模型与被控对象的位置跟踪误差等信息，在线实时确定自适应控制率，在保证系统稳定的条件下，能够有效克服系统摩擦力及模型慢时变等引起的系统动态性能异常。

针对直驱伺服系统建立其数学模型，根据数学模型确定自适应补偿环节的数学形式，并利用Lyapunov 函数证明了自适应控制率的稳定性。

最后通过试验表明，在跟踪正弦位置指令时，基于自适应前馈补偿的方法动态跟踪误差的均方根值为4.8μm ，与PID 无摩擦补偿控制方法相比，提高了47.3%，与传统模型参考自适应控制方法相比，提高了17.9%。

综上所述，所提方法可以有效抑制系统摩擦力干扰，提高系统动态跟踪精度。

关键词：自适应；前馈补偿；定位系统；摩擦力中图分类号：TP273+.5文献标识码：ADOI ：10.19457/j.1001-2095.dqcd20741Friction Adaptive Feedforward Compensation for High Precision Positioning SystemYANG Hong ，LI Shengming（College of Electromechanic and Automotive Engineering ，Qingyuan Polytechnic ，Qingyuan 511510，Guangdong ，China ）Abstract:In order to suppress the influence of external disturbances such as friction on the dynamic performance of electromechanical systems ，considering friction force for reciprocating positioning in direct drive servo system ，a friction compensation strategy based on adaptive feedforward controller was proposed.The method can effectively utilize the information of reference model and position tracking error of controlled object and determine the control rate on line.Under the condition of guaranteeing the stability of the system ，it can effectively overcome the abnormal dynamic performance of the system caused by system friction and slow time-varying model.The mathematical model of direct drive servo system and adaptive compensation component were established.Lyapunov function was adopted to guarantee the stability of the adaptive control rate.Finally ，experiments show that the root mean square value of dynamic tracking error based on adaptive feedforward compensation is 4.8μm when tracking sinusoidal position commands ，which is 47.3%higher than that of PID friction-free compensation control method and 17.9%higher than that of traditional model reference adaptive control method.In conclusion ，the proposed method can effectively suppress the friction interference and improve the dynamic tracking accuracy of the system.Key words:adaptive ；feedforward compensation ；positioning system ；friction高精度定位系统的摩擦力自适应前馈补偿杨红，李生明（清远职业技术学院机电与汽车工程学院，广东清远511510）基金项目：广东省高等职业教育教学改革研究与实践项目（GDJG2019380）作者简介：杨红（1969—），女，硕士，副教授，Email ：高精度定位系统广泛应用于航空航天、军工打印机、医疗器械及IC 装备等领域，定位系统的精度和响应速度等指标直接影响军用设备的加工精度及医疗器械的治疗效果等，因此研究有效提高定位系统的精度对国防军工、医疗卫生和生产生活的各领域有着重要意义。

基于PLC的电解加工机床控制系统的设计与实现

文章编号:1001-2265(2008)07-0077-04收稿日期:2007-12-06作者简介:陈远龙(1964 ),男,安徽来安人,合肥工业大学特种加工研究所副研究员,博士,研究方向为特种加工工艺及设备,(E -m ail)chenyuan l ong @s i na .co m 。

基于PLC 的电解加工机床控制系统的设计与实现陈远龙1,贾志华1,黄振东2,万胜美1(1.合肥工业大学特种加工研究所,合肥 230009;2.安徽省六安恒源机械有限公司,安徽六安 237004)摘要:介绍了基于O MRON 公司CJ1M 可编程逻辑控制器(PLC )设计的D J K3225型电解加工机床控制系统。

详细阐述了该系统的控制要求、硬件组成及相关软件设计要点。

触摸屏作为人机接口,实现了对运动和加工参数的修改、控制加工流程的执行、显示运动参数的变化,使系统控制界面友好,简单直观,便于操作。

关键词:电解加工机床;可编程逻辑控制器;触摸屏中图分类号:TG65 文献标识码:AD evelopm ent and R ealization of ECM M achi n e Tool Contro l System Based on PLCC H EN Yuan long 1,JIA Zh i hua 1,HUANG Zhen dong 2,WAN Sheng m e i1(1.Acade m y o f Non trad itional M achining ,H efe i University o f Techno logy ,H efe i 230009;2.LiuanH eng Yuan M echan is m Li m ited Co m pany of An H u i Prov i n ce ,Liu A n H efei 237004,Ch i n a)Abst ract :Intr oduci n g the D J K3225EC M M ach i n e Too l con tro l syste m w hich B ased on CJ1M PLC ofOMRON Co m pany ,elabo rati n g control request of the syste m ,the hardw are co m position and the a i m po i n t of so ft w are de si g n .As a hum an co mputer interface ,it can realize the para m eter m odificati o n o fm ove m ent and m achining ,contro l the executi o n o fm achi n i n g fl o w ,and d i s play the variety of t h e para m eter .The i n terface of t h e syste m is friend l y ,and itm akes the syste m operated and hand led easily .K ey w ords :EC M m ach i n e too ;l PLC ;touch screen0 引言DJ K3225型电解加工机床是针对航空航天、武器装备等制造领域中广泛应用的高强度、高韧性、高硬度等难加工材料的加工所设计的专用机床,主要适用于长筒形零件的型孔及扩孔加工[1]。

【国家自然科学基金】_捕食策略_基金支持热词逐年推荐_【万方软件创新助手】_20140802

推荐指数 4 3 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年序号 1 2 3 4 5 6 7 8 9
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82
科研热词蝙蝠算法捕食搜索策略函数优化粒子群算法粒子群优化算法仿真测试黑眶蟾蜍黑斑侧褶蛙黑叶猴食物选择颏花金龟族领导者策略逻辑自映射进化方向识别访问蜘蛛表型可塑性行为时间分配蛛网虎纹蛙花金龟亚科胖树型结构组合优化生பைடு நூலகம்史生境利用狼群搜索算法片上网络灭绝混沌搜索混沌水质模型横向扩散系数标准函数极小碰集权衡最优税收策略最优收获最优值映射矩阵旱季无尾类支持向量机捕食风险捕食系统捕食模型捕食搜索捕食性持续生存投资组合模型幽蚊幼虫年龄依赖性差分进化算法
推荐指数 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41

基于响应分组的仲裁器PUF偏置控制方法

现代电子技术Modern Electronics Technique2024年5月1日第47卷第9期May 2024Vol. 47 No. 90 引言基于静态随机存取存储器（SRAM ）的现场可编程门阵列（FPGA ）通常缺少用于存储密钥的片上非易失性存储器，因此难以保证应用的安全性。

而物理不可克隆函数（PUF ）技术具有从芯片制造过程中不可控的工艺偏差中提取硬件指纹的能力，可为FPGA 提供轻量级安全解决方案[1]。

典型的PUF 主要包括基于存储器的SRAM PUF [2]、蝶形PUF [3]和基于延时的环形振荡器PUF [4]、仲裁器PUF [5]等。

其中，仲裁器PUF 能够以较少的硬件开销产生大量响应，是最具应用潜力的轻量级PUF 之一。

仲裁器PUF 根据两个可配置路径之间的延迟差产生一个响应位。

其设计基本原则是对两条延时路径进行对称布局和布线，保证两条路径具有相同的标称延迟，使响应完全依赖于工艺偏差引入的随机延迟变化。

基于响应分组的仲裁器PUF 偏置控制方法刘海龙，严清虎，何佳洛（湖北大学人工智能学院，湖北武汉 430062）摘要：针对在现场可编程门阵列（FPGA ）平台上实现的仲裁器物理不可克隆函数（PUF ）响应唯一性和稳定性较差的问题，提出一种基于响应分组的仲裁器PUF 偏置控制方法。

在基于可编程延时线（PDL ）的仲裁器PUF 电路中插入多路选择器（MUX ）粗调开关单元和PDL 微调开关单元，使路径延时可受调节激励控制。

通过实时改变调节激励，控制每个响应分组中有效响应的汉明重量达到50%可提高响应唯一性；通过偏置控制筛选出延时差异较大的响应可提高响应稳定性。

在Xilinx XC7Z020 FPGA 器件上实现带偏置控制功能的64级仲裁器PUF 电路，仅消耗143个查找表（LUT ）和425个触发器（DFF ）资源。

在温度为-20~80 ℃、供电电压0.9~1.1 V 范围内，该仲裁器PUF 响应唯一性为49.89%，有效响应稳定性可达到100%。

Tactile feedback device providing tactile sensatio

专利名称：Tactile feedback device providing tactile sensations from host commands发明人：Louis B. Rosenberg,Adam C. Braun,Mike D.Levin申请号：US09815872申请日：20010322公开号：US20010030658A1公开日：20011018专利内容由知识产权出版社提供摘要：A method and apparatus for controlling and providing force feedback using an interface device manipulated by a user. A microprocessor is provided local to the interface device and reads sensor data from sensors that describes the position and/or other information about a user object moved by the user, such as a joystick. The microprocessor controls actuators to provide forces on the user object and provides the sensor data to a host computer that is coupled to the interface device. The host computer sends high level host commands to the local microprocessor, and the microprocessor independently implements a local reflex process based on the high level command to provide force values to the actuators using sensor data and other parameters. A provided host command protocol includes a variety of different types of host commands and associated command parameters. By providing a relatively small set of high level host commands and parameters which are translated into a panoply of forces, the protocol further shifts the computational burden from the host computer to the local microprocessor and allows a software developer to easily create force feedback applications.申请人：IMMERSION CORPORATION 更多信息请下载全文后查看。

Control Systems Engineering

Control Systems Engineering Research Report2002Control Systems EngineeringSection CROSS(Control,Risk,Optimization,Stochastics and Systems)Faculty of Information Technology and SystemsDelft University of TechnologyPostal address:Visiting addressP.O.Box5031Mekelweg42600GA Delft2628CD DelftThe Netherlands The NetherlandsPhone:+31-15-2785119Fax:+31-15-2786679Email:control@its.tudelft.nlc 2002Control Systems Engineering,rmation Technology and Systems,Delft University ofTechnologyAll rights reserved.No part of the publication may be reproduced in any form by print,photoprint, microﬁlm or any other means without written permission from the publisher.Contents1Introduction11.1Overview (1)1.2Address and location (3)1.3Staﬀin2002 (4)2Intelligent modeling,control&decision making52.1Aﬀordable digitalﬂy-by-wireﬂight control systems for small commercial aircraft52.2Intelligent adaptive control of bioreactors (6)2.3Fuzzy control of multivariable processes (7)2.4Neuro-fuzzy modeling in model-based fault detection,fault isolation and con-troller reconﬁguration (7)2.5Intelligent molecular diagnostic systems (7)2.6Model based optimization of fed-batch bioprocesses (9)2.7Estimation of respiratory parameters via fuzzy clustering (10)2.8Fuzzy model based control with use of a priori knowledge (10)3Distributed and hybrid systems123.1Modeling and analysis of hybrid systems (12)3.2Model predictive control for discrete-event systems (13)3.3Model predictive control for piece-wise aﬃne systems (13)3.4Model predictive control for hybrid systems (14)3.5Optimal traﬃc control (14)3.6Advanced control techniques for optimal adaptive traﬃc control (15)3.7Optimal transfer coordination for railway systems (16)3.8Real-time control of smart structures (17)4Fault-tolerant control194.1Model-based fault detection and controller reconﬁguration for wind turbines.194.2Model-based fault detection and identiﬁcation of sensor and actuator faults forsmall commercial aircraft (20)5Nonlinear analysis,control and identiﬁcation215.1System identiﬁcation of bio-technological processes (21)5.2Classiﬁcation of buried objects based on ground penetrating radar signals..215.3Control of a jumbo container crane(JCC project) (22)5.4X-by-wire (23)5.5Analysis and design of nonlinear control systems for switching networks (24)5.6Bounding uncertainty in subspace identiﬁcation (25)5.7New passivity properties for nonlinear electro-mechanical systems (26)5.8Relating Lagrangian and Hamiltonian descriptions of electrical circuits (27)5.9Discrete-time sliding mode control (27)5.10Nonlinear control systems analysis (28)5.11Model and controller reduction for nonlinear systems (28)5.12Robust and predictive control using neural networks (29)5.13The standard predictive control problem (30)5.14Predictive control of nonlinear systems in the process industry (30)5.15Identiﬁcation of nonlinear state-space systems (31)5.16Development of computationally eﬃcient and numerically robust system iden-tiﬁcation software (32)1Introduction1.1OverviewThis report presents an overview of the ongoing research projects during2002at the Control Systems Engineering(CSE)group of the Faculty of Information Technology and Systems of Delft University of Technology.As revealed by the new logo of the group,a number of major changes have taken place. Three of these major events will be brieﬂy discussed.First,the stronger emphasis on a systems oriented research approach has motivated a change of the name from Control Laboratory into Control Systems Engineering group.Second,in September2001Prof.dr.ir.M.Verhaegen was appointed as the new chairman of the CSE group.With his arrival an impulse was given to strengthen the development of new methods and techniques for identiﬁcation and fault-tolerant control design.The primary focus of the programme development is to formulate new research initiatives and to initiate research alliances with established Dutch and European research-oriented laboratories and industry.New research proposals will be formulated within the four main themes:intelligent modeling,control and decision making;distributed and hybrid systems;fault-tolerant control; and analysis,control and identiﬁcation of nonlinear systems—as depicted by the vertical columns in Figure1.The overall focus will remain on complex nonlinear systems,new application directions,however,may be included,such as adaptive optics which more and more rely on advanced control techniques.The CSE group is also taking part in new research programme deﬁnitions of the Faculty of Information Technology and Systems,such as the Intelligent Systems Consortium(iSc)chaired by Prof.P.Dewilde.Third,the CSE group strives to strengthen the research and teaching cooperation in the area of control systems engineering with other leading Systems and Control Engineering groups in Delft.To accomplish this goal,the CSE actively supports the creation of a joint Delft Center on Systems and Control Engineering.The research interests of the CSE group are focused on the following areas:•Intelligent modeling,control and decision making:black-box and gray-box modeling of dynamic systems with fuzzy logic and neural net-works,and design of controllers using fuzzy set techniques.•Distributed and hybrid systems:analysis and control methods,multi-agent control,hierarchical control,and model pre-dictive control of hybrid systems.•Fault-tolerant control:fault detection and isolation with system identiﬁcation and extended Kalmanﬁltering, probabilistic robust control.•Nonlinear analysis,control and identiﬁcation:nonlinear predictive control,sliding mode control,iterative learning control,nonlinear dynamic model inversion,Lagrangian and Hamiltonian modeling and control frame-works(energy based),identiﬁcation of a composite of numerical local linear state space models to approximate nonlinear dynamics.The goal of the CSE group is to develop innovative methodologies in theﬁelds indicated above.An important motive in demonstrating their relevance is to cooperate with nationalFigure1:Overview of the research topics of the Control System Engineering group. and international research organizations and industry to validate the real-life potential of the new methodologies.The main applicationﬁelds are:•Smart structures:X-by-wire,road traﬃc sensors,high performance control using smart materials,adaptive optics,laboratory-on-a-chip,micro robotics.•Power engineering:switching networks,power distribution and conversion,condition monitoring in oﬀ-shore wind turbines.•Telecommunication•Motion control:autonomous and intelligent mobile systems,mobile robots,container transport,aircraft and satellite control,traﬃc control.•Bioprocess technology:fermentation processes,waste-water treatment.The CSE group currently consists of27scientiﬁc and support staﬀ:8permanent scientiﬁc staﬀ,10PhD students,2postdoctoral researchers,and7support personnel.The research activities are for a large partﬁnanced from external sources including the Dutch National Science Foundation(STW),Delft University of Technology,the European Union,and indus-try.Additional information can be found at http://lcewww.et.tudelft.nl/.1.2Address and locationControl Systems EngineeringFaculty of Information Technology&SystemsDelft University of TechnologyPostal address:P.O.Box50312600GA DelftThe NetherlandsVisiting address:Mekelweg42628CD DelftThe NetherlandsPhone:+31-15-2785119Fax:+31-15-27866791.3Staﬀin2002Scientiﬁc staﬀProf.dr.ir.M.H.G.VerhaegenProf.dr.ir.J.HellendoornProf.dr.ir.R.Babuˇs kaDr.ir.T.J.J.van den BoomDr.ir.B.De SchutterDr.ir.J.B.KlaassensDr.ir.J.M.A.ScherpenDr.ir.V.VerdultPhD students&postdoctoral researchers Dr.J.Clemente GallardoIr.P.R.FraanjeIr.A.HegyiIr.K.J.G.HinnenIr.D.JeltsemaR.Lopez Lena,MScIr.S.Meˇs i´cIr.M.L.J.OosteromIr.G.PastoreNon-scientiﬁc staﬀC.J.M.DukkerIng.P.M.EmonsP.MakkesIng.W.J.M.van GeestD.NoteboomG.J.M.van der WindtIng.R.M.A.van PuﬀelenAdvisorsProf.ir.G.Honderd,em.Prof.ir.H.R.van Nauta Lemke,em. Prof.ir.H.B.Verbruggen,em.2Intelligent modeling,control&decision makingThis research theme focuses on the use of fuzzy logic,neural networks and evolutionary al-gorithms in the analysis and design of models and controllers for nonlinear dynamic systems. Fuzzy logic systems oﬀer a suitable framework for combining knowledge of human experts with partly known mathematical models and data,while artiﬁcial neural networks are eﬀec-tive black-box function approximators with learning and adaptation capabilities.Evolution-ary algorithms are randomized optimization techniques useful in searching high-dimensional spaces and tuning of parameters in fuzzy and neural systems.These techniques provide tools for solving complex design problems under uncertainty by providing the ability to learn from past experience,perform complex pattern recognition tasks and fuse information from various sources.Application domains include fault-tolerant control,nonlinear system identiﬁcation, autonomous and adaptive control,among others.2.1Aﬀordable digitalﬂy-by-wireﬂight control systems for small commer-cial aircraftProject members:M.L.J.Oosterom,R.Babuˇs ka,H.B.VerbruggenSponsored by:European Community GROWTH project ADFCS–IIThe objective of this project is to apply theﬂy-by-wire(FBW)technology inﬂight control systems of a smaller category of aircraft(see Figure2).In FBW digitalﬂight control systems, there is no direct link between the control stick and pedals,which are operated by the pilot, and the control surfaces.All measured signals,including the pilot inputs,are processed by the ﬂight control computer that computes the desired control surface deﬂections.This scheme enables theﬂight control engineer to alter the dynamic characteristics of the bare aircraft through an appropriate design of theﬂight control laws.Moreover,important safety features can be included in the control system,such asﬂight envelope protection.This increases the safety level compared to aircraft with mechanical control systems.Our task in the project is to assess the beneﬁts and to verify the validity of the soft-computing techniques in the FBW control system design and sensor management.These novel techniques are combined with standard,well-proven methods of the aircraft industry.Figure2:The Galaxy business jet(left)and validation of the control system through pilot-in-the-loop simulations at the Research Flight Simulator of the NLR(right).Figure3:The experimental laboratory setup(left)and the basic model-based adaptive control scheme(right).The research topics are the design of gain-scheduled control laws,fault detection,isolation and reconﬁguration,and an expert system monitoring of the overall operational status of both the pilot and the aircraft.For control design,fault detection and identiﬁcation system,fuzzy logic approaches are adopted in order to extend linear design techniques to nonlinear systems. Moreover,a neuro-fuzzy virtual sensor will be developed in close cooperation with Alenia to replace hardware sensors.For the pilot-aircraft status monitor a fuzzy expert system will be developed that has the functionality of a warning and advisory/decision aiding system.2.2Intelligent adaptive control of bioreactorsProject members:R.Babuˇs ka,M.Damen,S.Meˇs i´cSponsored by:SenterThe goal of this research is the development and implementation of a robust self-tuning con-troller for fermentation processes.To ensure an optimal operating conditions,the pH value, the temperature and the dissolved oxygen concentration in the fermenter must be controlled within tight bounds.Ideally,the same control unit should be able to ensure the required performance for a whole variety of fermentation processes(diﬀerent microorganisms),diﬀer-ent scales(volume of1liter to10000liters)and throughout the entire process run.Figure3 shows an experimental laboratory setup used in this project.The main control challenge is the fact that the dynamics of the system depend on the particular process type and scale and moreover are strongly time-varying,due to gradual changes in the process operating conditions.Controllers withﬁxed parameters cannot fulﬁll these requirements.Self-tuning(adaptive) control is applied to address the time-varying nature of the process.Among the diﬀerent types of adaptive controllers(model-free,model-based,gain-scheduled,etc.),the model-based approach is pursued.The model is obtained through a carefully designed local identiﬁcation experiment.Special attentions is paid to the robustness of the entire system in order to ensure safe and stable operation under all circumstances.The main contribution of this research is the development,implementation and experimental validation of a complete self-tuning control system.The robustness of the system is achieved by combining well-proven identiﬁcation and control design methods with a supervisory fuzzy expert system.This research is being done a cooperation between Applikon Dependable Instruments B.V.,Schiedam,Faculty of Electrical Engineering,Eindhoven University of Technology and Faculty of Information Technology and Systems and Kluyver Laboratory for Biotechnology, both at Delft University of Technology.2.3Fuzzy control of multivariable processesProject members:R.Babuˇs ka,S.Mollov,H.B.VerbruggenFuzzy control provides eﬀective solutions for nonlinear and partially unknown processes, mainly because of its ability to combine information form diﬀerent sources,such as avail-able mathematical models,experience of operators,process measurements,etc.Extensive research has been devoted to single-input single-output fuzzy control systems,including mod-eling and control design aspects,analysis of stability and robustness,adaptive control.Mul-tivariable fuzzy control,however,have received considerably less attention,despite strong practical needs for multivariable control solutions,indicated among otherﬁelds from process industry,(waste)water treatment,or aerospace engineering.Yet,theoretical foundations and methodological aspects of multivariable control are not well developed.This research project focuses on the use of fuzzy logic in model-based control of multiple-input,multiple-output(MIMO)systems.Recent developments include eﬀective optimization techniques and robust stability constraints for nonlinear model predictive control.The devel-oped predictive control methods have been applied to the design of an Engine Management System for the gasoline direct injection engine benchmark,developed as a case study within the European research project FAMIMO(see Figure4).An extension of the Relative Gain Array approach has been proposed that facilitates the analysis of interactions in MIMO fuzzy models.2.4Neuro-fuzzy modeling in model-based fault detection,fault isolationand controller reconﬁgurationProject members:M.H.G.Verhaegen,J.Hellendoorn,R.Babuˇs ka,S.Kanev,A.Ichtev Sponsored by:STWMost fault tolerant control systems rely on two modules:(model-based)fault detection and isolation module and controller reconﬁguration module.The two key elements in designing these two systems are the development of a mathematical model and a suitable decision mechanism to localize the failure and to select a new controller conﬁguration.This project focuses on the development of a design framework in which the mathematical model and the corresponding observer are represented as a composition of local models,each describing the system in a particular operating regime or failure mode.The use of fuzzy Takagi-Sugeno models for residual generation has been investigated.On the basis of residuals soft fault detection and isolation and controller reconﬁguration are performed.2.5Intelligent molecular diagnostic systemsProject members:L.Wessels,P.J.van der Veen,J.HellendoornAir BurngasesFigure4:Fuzzy predictive control of a gasoline directinjection engine. Sponsored by:DIOC-5:Intelligent Molecular Diagnostic SystemsIt is the goal of the DIOC-5(DIOC:Delft Interfaculty Research Center)program to produce an Intelligent Molecular Diagnostic System(IMDS).The IMDS will consist of two basic com-ponents:a measurement device and an information processing unit(IPU).The measurement device is a chemical sensor on a chip,which will be capable of rapidly performing vast num-bers of measurements simultaneously,consuming a minimal amount of chemical reagents and sample(see Figure5).Figure5:A prototype IMDS chip containing a matrix of25pico-liter wells.The IPU transforms the complex,raw measurements obtained from the sensor into output that can be employed as high-level decision support in various application domains.See[41]for a possible realization of the IPU.Members of the Control Systems Engineering group and the Information and Communica-tion Theory group are responsible for the realization of the Information Processing Unit.Un-raveling the metabolic processes and the associated regulatory mechanisms of yeast is a very interesting application area for the DIOC-5technology.We are focusing on problems associ-ated with gene and protein levels,and will integrate this information with existing knowledge about metabolic processes developed at the Kluyver Laboratory(One of the DIOC-5part-ners).More speciﬁcally,gene expression data and protein concentration measurements are employed to model the genetic networks,i.e.,to postulate possible‘genetic wiring diagrams’based on the expression data(See[40]for some preliminary results in this area.) It is envisaged that at the end of this project,genetic network information,protein func-tional knowledge and metabolic models can be integrated into a single hierarchical model, capable of providing metabolic engineers with greater insight into the yeast metabolism.For additional information see the IMDS Web page.12.6Model based optimization of fed-batch bioprocessesProject members:J.A.Roubos,P.Krabben,R.Babuˇs ka,J.J.Heijnen,H.B.Verbruggen Sponsored by:DIOC-6:Mastering the Molecules in Manufacturing,DSM Anti Infectives Many biotechnological production systems are based on batch and fed-batch processes.Op-timization of the product formation currently requires a very expensive and time consuming experimental program to determine the optima by trial and error.The aim of this project is to ﬁnd a more eﬃcient development path for fed-batch bioprocesses by an optimal combination of experiments and process models.The two main research topics of this project are:•Development of a user friendly modeling environment for fed-batch processes.The soft-ware tool must be able to use diﬀerent types of knowledge coming from experts,experi-ments andﬁrst-principles,i.e.,conservation laws.New modeling methods such as fuzzy logic,neural networks and hybrid models will be used.•Iterative optimal experiment design.First some basic experiments can be done to esti-mate some preliminary parameters for the system.The idea is to make a rough model to design the next experiment.First,a stoichiometric model is made and thereafter a structured biochemical model that will be gradually improved according to the fermen-tation data.The main objective is to predict the right trends.The actual values are less important at the initial stages.Once the model is suﬃcient in terms of quantitative prediction of the production process for a variable external environment,it will be used to determine optimal feeding strategies for the reactor in order to improve product quality and/or quantity.These feeding strategies will be applied in an on-line process control environment.Recent developments and publications can be found at the project Web page2.1http://www.ph.tn.tudelft.nl/Projects/DIOC/Progress.html2http://lcewww.et.tudelft.nl/˜roubos/02401020Time [s]p h a s e 1p h a s e 2p h a s e 3phase 4P r e s s u r e [h P a ]Figure 6:Partitioning of the respiratory cycle is obtained automatically by fuzzy clustering.Each segment represents a characteristic phase of the respiratory cycle.2.7Estimation of respiratory parameters via fuzzy clusteringProject members:R.Babuˇs ka,M.S.Lourens,A.F.M.Verbraak and J.Bogaard (University Hospital Rotterdam)The monitoring of respiratory parameters estimated from ﬂow-pressure-volume measurements can be used to assess patients’pulmonary condition,to detect poor patient-ventilator interac-tion and consequently to optimize the ventilator settings.A new method has been investigated to obtain detailed information about respiratory parameters without interfering with the ven-tilation.By means of fuzzy clustering,the available data set is partitioned into fuzzy subsets that can be well approximated by linear regression models locally.Parameters of these models are then estimated by least-squares techniques.By analyzing the dependence of these local parameters on the location of the model in the ﬂow-volume-pressure space,information on the patients’pulmonary condition can be gained.The eﬀectiveness of the proposed approaches has been studied by analyzing the dependence of the expiratory time constant on the volume in patients with chronic obstructive pulmonary disease (COPD)and patients without COPD.2.8Fuzzy model based control with use of a priori knowledgeProject members:R.Babuˇs ka,J.Abonyi (University of Veszpr´e m,Hungary)Eﬀective development of nonlinear dynamic process models is of great importance in the application of model-based control.Typically,one needs to blend information from diﬀerent sources:experience of operators and designers,process data and ﬁrst principle knowledge formulated by mathematical equations.To incorporate a priori knowledge into data-driven identiﬁcation of dynamic fuzzy models of the Takagi-Sugeno type a constrained identiﬁcation algorithm has been developed,where the constrains on the model parameters are based on the knowledge about the process stability,minimal or maximal gain,and the settling time.The algorithm has been successfully applied to oﬀ-line and on-line adaptation of fuzzy models.When no a priori knowledge about the local dynamic behavior of the process is available, information about the steady-state characteristic could be extremely useful.Because of the diﬃcult analysis of the steady-state behavior of dynamic fuzzy models of the Takagi-Sugeno type,block-oriented fuzzy models have been developed.In the Fuzzy Hammerstein(FH) model,a static fuzzy model is connected in series with a linear dynamic model.The obtained FH model is incorporated in a model-based predictive control scheme.Results show that the proposed FH modeling approach is useful for modular parsimonious modeling and model-based control of nonlinear systems.3Distributed and hybrid systemsHybrid systems typically arise when a continuous-time system is coupled with a logic con-troller,or when we have a system in which external inputs or internal events may cause a sudden change in the dynamics of the system.So hybrid systems exhibit both continuous-variable and discrete-event behavior.Due to the intrinsic complexity of hybrid systems control design techniques for hybrid systems we could either focus on special subclasses of hybrid sys-tems,or use a distributed or hierarchical approach to decompose the controller design problem into smaller subproblems that are easier to solve.In our research we use both approaches.3.1Modeling and analysis of hybrid systemsProject members:B.De Schutter,W.M.P.H.Heemels(Eindhoven University of Technology), A.Bemporad(ETH Z¨u rich)Hybrid systems arise from the interaction between continuous-variable systems(i.e.,systems that can be described by a system of diﬀerence or diﬀerential equations)and discrete-event systems(i.e.,asynchronous systems where the state transitions are initiated by events;in general the time instants at which these events occur are not equidistant).In general we could say that a hybrid system can be in one of several modes whereby in each mode the behavior of the system can be described by a system of diﬀerence or diﬀerential equations, and that the system switches from one mode to another due to the occurrence of an event (see Figure7).We have shown that several classes of hybrid systems:piecewise-aﬃne systems,mixed logical dynamical systems,complementarity systems and max-min-plus-scaling systems are equivalent[6,7,24,25].Some of the equivalences are established under(rather mild)addi-tional assumptions.These results are of paramount importance for transferring theoreticalFigure7:Schematic representation of a hybrid system.properties and tools from one class to another,with the consequence that for the study of a particular hybrid system that belongs to any of these classes,one can choose the most convenient hybrid modeling framework.Related research is described under Project3.3.In addition,we have also shown an equivalence between two type of mathematical pro-gramming problems:the linear complementarity problem(LCP)and the extended linear complementarity problem(ELCP)[17].More speciﬁcally,we have shown that an ELCP with a bounded feasible set can be recast as an LCP.This result allows us to apply existing LCP algorithms to solve ELCPs[16].3.2Model predictive control for discrete-event systemsProject members:B.De Schutter,T.J.J.van den BoomModel predictive control(MPC)is a very popular controller design method in the process industry.An important advantage of MPC is that it allows the inclusion of constraints on the inputs and ually MPC uses linear discrete-time models.In this project we extend MPC to a class of discrete-event systems.Typical examples of discrete-event systems are:ﬂexible manufacturing systems,telecommunication networks,traﬃc control systems, multiprocessor operating systems,and logistic systems.In general models that describe the behavior of a discrete-event system are nonlinear in conventional algebra.However,there is a class of discrete-event systems–the max-plus-linear discrete-event systems–that can be described by a model that is“linear”in the max-plus algebra.We have further developed our MPC framework for max-plus-linear discrete-event systems and included the inﬂuences of noise and disturbances[33,34,35,36,37].In addition,we have also extended our results to discrete-event systems that can be described by models in which the operations maximization,minimization,addition and scalar multiplication appear[22], and to discrete-event systems with both hard and soft synchronization constraints[19](see also Project3.7).3.3Model predictive control for piece-wise aﬃne systemsProject members:B.De Schutter,T.J.J.van den BoomWe have extended our results on model predictive control(MPC)for discrete event systems (see Project3.2)to a class of hybrid systems that can be described by a continuous piecewise-aﬃne state space model.More speciﬁcally,we have considered systems of the formx(k)=P x(x(k−1),u(k))y(k)=P y(x(k),u(k)),where x,u and y are respectively,the state,the input and the output vector of the system,and where the components of P x and P y are continuous piecewise-aﬃne(PWA)scalar functions,i.e.,functions that satisfy the following conditions:1.The domain space of f is divided into aﬁnite number of polyhedral regions;2.In each region f can be expressed as an aﬃne function;3.f is continuous on any boundary between two regions.。

Frequency Based Feedback Control

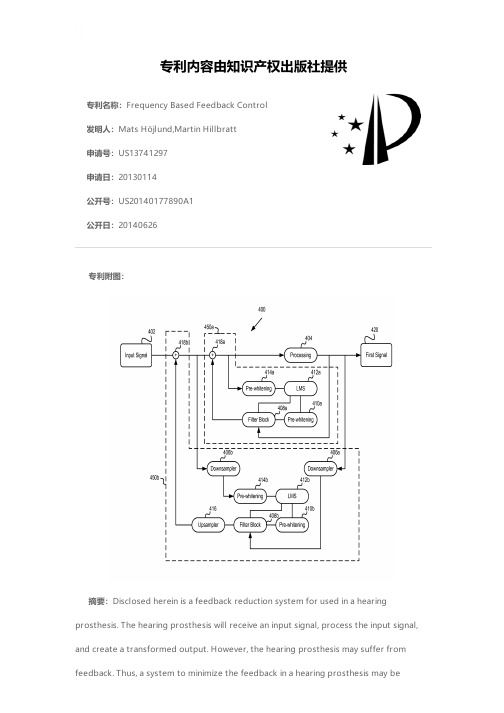
专利名称：Frequency Based Feedback Control发明人：Mats Höjlund,Martin Hillbratt申请号：US13741297申请日：20130114公开号：US20140177890A1公开日：20140626专利内容由知识产权出版社提供专利附图：摘要：Disclosed herein is a feedback reduction system for used in a hearingprosthesis. The hearing prosthesis will receive an input signal, process the input signal,and create a transformed output. However, the hearing prosthesis may suffer from feedback. Thus, a system to minimize the feedback in a hearing prosthesis may bedesirable. One system to minimize the feedback includes down-sample circuitry configured to down-sample a first signal, creating a down-sampled signal. They system also includes a filter circuit. The filter circuit filters both the first signal and the down-sampled signal. The filter will output a filtered signal and a filtered down-sampled signal, respectively. Additionally, the system features up-sample circuitry that up-samples the filtered down-sampled signal. The output of the up-sample circuitry is an up-sampled signal. Further, the system features combining circuitry that creates a feedback-reduced signal based on the up-sampled signal, the filtered signal, and an input signal.申请人：Mats Höjlund,Martin Hillbratt地址：Monlnlycke SE,Lindome SE国籍：SE,SE更多信息请下载全文后查看。

Robust Control

Robust ControlRobust control is a field of engineering that deals with the design and implementation of control systems that are able to perform reliably in the presence of uncertainties and disturbances. It is an essential aspect of modern engineering, as it ensures that control systems can operate effectively even in the face of unpredictable factors. One perspective on robust control is from the standpoint of an engineer designing a control system. From this perspective, the goal is to create a control system that can handle a wide range of uncertainties and disturbances. This requires a deep understanding of the system being controlled, as well as the ability to model and predict the effects of uncertainties and disturbances. To achieve robust control, engineers utilize various techniques and tools. One common approach is to use feedback control, where the output of the system is measured and compared to a desired reference value. Any difference between the measured output and the reference value is used to adjust the control inputs in order to minimize the error. This feedback loop helps to compensate for uncertainties and disturbances, ensuring that the system remains stable and performs as desired. Another important aspect of robustcontrol is the use of robust design methods. These methods involve designing the control system to be inherently robust to uncertainties and disturbances. This can be achieved through techniques such as loop shaping, where the frequency response of the control system is modified to ensure stability and performance in the presence of uncertainties. From the perspective of a system being controlled, robust control can provide numerous benefits. For example, in a manufacturing process, robust control can help to ensure that the process operates consistently and produces high-quality products, even in the presence of variations in raw materials or operating conditions. Similarly, in a flight control system, robust control can help to ensure the stability and safety of the aircraft, even in the face of unpredictable weather conditions or system failures. Robust control also has implications for society as a whole. For example, in the field of autonomous vehicles, robust control is crucial to ensure the safety and reliability of these vehicles. By designing control systems that can handle uncertainties and disturbances, engineers can help to prevent accidents and improve the overallefficiency of transportation systems. In conclusion, robust control is a vital aspect of modern engineering. It allows control systems to operate effectively in the presence of uncertainties and disturbances, ensuring stability, performance, and safety. From the perspective of an engineer, robust control involves designing control systems that can handle a wide range of uncertainties and disturbances. This requires a deep understanding of the system being controlled and the use of techniques such as feedback control and robust design methods. From the perspective of a system being controlled, robust control provides numerous benefits, including consistent operation and high-quality output. In society as a whole, robust control has implications for safety, reliability, and efficiency in various domains, such as manufacturing and transportation.。

烟碱上调大鼠脑纹状体多巴胺D_1受体mRNA表达诱导其行为改变(英文)

烟碱上调大鼠脑纹状体多巴胺D_1受体mRNA表达诱导其行为改变(英文)陈涛;唐北沙;廖小平;文国强;严新翔;江泓;张玉虎;龙志刚;欧阳锋;郭纪锋【期刊名称】《中国临床康复》【年(卷),期】2006(10)38【摘要】背景:研究提示,烟碱对帕金森病小鼠具有神经保护效应,临床试验也观察到,帕金森病患者在吸烟过程中其震颤、僵直、运动减少等症状减轻,但其作用机制目前尚不明了。

目的:观察烟碱对大鼠脑纹状体多巴胺D1,D2受体mRNA表达的影响,分析烟碱对帕金森病神经保护效应的作用机制。

设计:完全随机分组设计,对照试验。

单位:中南大学湘雅医院神经病学研究所。

材料:选用健康雄性清洁级SD大鼠24只,10周龄,体质量180～200g。

主要试剂及仪器:烟碱(美国Sigma公司)、反转录试剂盒(美国MBI公司)、聚合酶链反应热循环仪(美国Beckman)、全自动紫外分光光度计(美国BeckmanDu-70)、图像分析处理系统(美国StratageneEagleEyeⅡ型)。

方法:实验于2001-07/2002-07在中南大学湘雅医院神经病学研究所实验室完成。

①按随机抽签法将大鼠随机分为2组:对照组、烟碱组,每组12只。

分别皮下注射生理盐水、烟碱溶液4mg/(kg·d),2次/d,共14d。

注射药物后0.5h观察大鼠行为活动,包括定型活动、走动活动、攀爬行为、旋转行为、理毛行为、张口行为、呕吐行为等,观察时间为0.5h。

②于末次注射药物后0.5h处死动物,快速分离纹状体,提取总RNA,采用美国MBI反转录试剂盒反转录cDNA,在特定条件下进行聚合酶链反应扩增,将电泳凝胶在EagleEyeⅡ图像处理系统上分析计算出多巴胺D1,D2受体及内对照β-actin吸光度(A值),检测大鼠脑纹状体多巴胺D1,D2受体mRNA的表达。

③两样本均数比较采用t检验。

主要观察指标:①大鼠行为学改变。

②大鼠脑纹状体多巴胺D1,D2受体mRNA的表达。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。