位似图形课件45928
合集下载
《位似图形》PPT课件

位似图形
- .
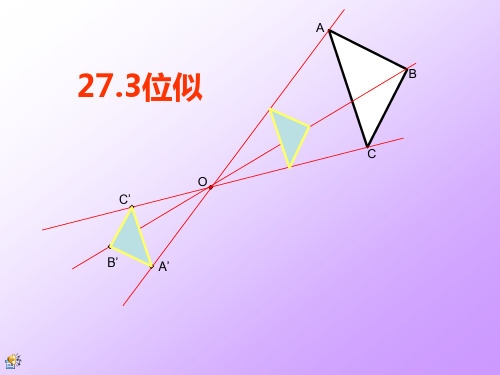
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?
明晰新知
如果两个相似图形的每组对应点所在的直线都交于一点,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心, 这时两个相似图形的相似比又叫做它们的位似比.
观察下图中的五个图,回答下列问题:
(1)在各图中,位似图形的位似中心与这两个图形有什么位置关系?
(2)在各图中,任取一对对应点,度量这两个点到位似中心的距离.它们的比与位似比有什么关系?再换一对对应点试一试.
位置不一样,位似中心就不一样.
相等.
议一议
位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比.
在下列每个图形中,位似图形的对应线段AB与A′B′是否平行?BC与B′C′,CD与C′D′,已知△ABC∽△DEF, 它们对应顶点的连线AD,BE,CF相交于点O,这两个三角形是不是位似三角形?
0
B
E
C
F
A
D
通过这节课的学习,你有哪些收获?
课堂小结
1.如果两个相似图形的每组对应点所在的直线都交于一点,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心, 这时两个相似图形的相似比又叫做它们的位似比.
典例解析
如图,D,E分别AB,AC上的点.
(1)如果DE∥BC,那么∆ADE和 ∆ABC是位似图形吗?为什么?
(2)如果∆ADE和 ∆ABC是位似图形,那么DE∥BC吗?为什么?
解:(2) DE∥BC.理由是:
∆ADE和 ∆ABC是位似图形,
∆ADE∽ ∆ABC
∠ADE=∠B
《位似图形》ppt教材课件

观察与思考☞
下列图形中,每个图中的
四边形ABCD和四边形A′B′C′D′都是相似图形.分
别观察这五个图,你发现每个图中的两个四边形
各对应点的连线有什么特征?
如果两个相似图形的每组对应点所 在的直线都交于一点,那么这样的 两个图形叫做位似图形, 这个交点 叫做位似中心, 这时两个相似图形 的相似比又叫做它们的位似比.
什么位置关系? 位置不一样,位似中心就不一样.
(2)在各图中,任取一对对应点,度量这两个点到位 似中心的距离.它们的比与位似比有什么关系?再换一对 对应点试一试. 相等.
位似图形的对应点和位似中心在 同一条直线上,它们到位似中心的 距离之比等于相似比.如图,D,分别AB,AC上的点.A
(1)如果DE∥BC,那么∆ADE和 D E
在下列每个图形中,位似图形的对
应线段AB与A′B′是否平行?BC与
B′C′,CD与C′D′,AD与A′D′是否平
行?为什么?
不经过位似
中心的对应
线段平行.
为了便于学习和使用,本文 档下载后内容可随意修改调 整及打印,欢迎下载。
A
如图,已知△ABC∽△DEF, 它们对应顶点的连线
AD,BE,CF相交于点O,这 D
两个三角形是不是位似三 角形?
B E
0
F
C
课堂小结
通过这节课的学习,你有哪些收获?
1.如果两个相似图形的每组对应点所在的直 线都交于一点,那么这样的两个图形叫做位似 图形, 这个交点叫做位似中心, 这时两个相 似图形的相似比又叫做它们的位似比.
2.位似图形的对应点和位似中心在同一条直线 上,它们到位似中心的距离之比等于相似比.
∆ABC是位似图形吗?为什么? B
下列图形中,每个图中的
四边形ABCD和四边形A′B′C′D′都是相似图形.分
别观察这五个图,你发现每个图中的两个四边形
各对应点的连线有什么特征?
如果两个相似图形的每组对应点所 在的直线都交于一点,那么这样的 两个图形叫做位似图形, 这个交点 叫做位似中心, 这时两个相似图形 的相似比又叫做它们的位似比.
什么位置关系? 位置不一样,位似中心就不一样.
(2)在各图中,任取一对对应点,度量这两个点到位 似中心的距离.它们的比与位似比有什么关系?再换一对 对应点试一试. 相等.
位似图形的对应点和位似中心在 同一条直线上,它们到位似中心的 距离之比等于相似比.如图,D,分别AB,AC上的点.A
(1)如果DE∥BC,那么∆ADE和 D E
在下列每个图形中,位似图形的对
应线段AB与A′B′是否平行?BC与
B′C′,CD与C′D′,AD与A′D′是否平
行?为什么?
不经过位似
中心的对应
线段平行.
为了便于学习和使用,本文 档下载后内容可随意修改调 整及打印,欢迎下载。
A
如图,已知△ABC∽△DEF, 它们对应顶点的连线
AD,BE,CF相交于点O,这 D
两个三角形是不是位似三 角形?
B E
0
F
C
课堂小结
通过这节课的学习,你有哪些收获?
1.如果两个相似图形的每组对应点所在的直 线都交于一点,那么这样的两个图形叫做位似 图形, 这个交点叫做位似中心, 这时两个相 似图形的相似比又叫做它们的位似比.
2.位似图形的对应点和位似中心在同一条直线 上,它们到位似中心的距离之比等于相似比.
∆ABC是位似图形吗?为什么? B
位似精品PPT课件
y A′(2,1), B′(2,0)
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原 点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0) y
A〞(-2,-1),B(-2,0)
A
A'
B〞
x
o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现?
y
A'
6
4 A
3
2
B'
C
1
B
o
2
4
6
还有其他办法吗?
C'
x
12
在平面直角坐标系中, △ABC三个顶点的坐标分别 为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相 似比为2,将△ABC放大.
放大后对应点的坐标分别是多少?
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
你还有其他办法吗?试试看.
练一练:
1.如图表示△AOB和把它缩小后得到的△COD,求它们的相似比 y
A
C
o
D
B
x
练一练:
2.如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以 原点O为位似中心,将这个三角形放大为原来的2倍.
y
o
x
A
C
B
结束语
当你尽了自己的最大努力时,失败 也是伟大的,所以不要放弃,坚持
以0为中心把△ABC 缩小为原来的一半。
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原 点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0) y
A〞(-2,-1),B(-2,0)
A
A'
B〞
x
o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现?
y
A'
6
4 A
3
2
B'
C
1
B
o
2
4
6
还有其他办法吗?
C'
x
12
在平面直角坐标系中, △ABC三个顶点的坐标分别 为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相 似比为2,将△ABC放大.
放大后对应点的坐标分别是多少?
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
你还有其他办法吗?试试看.
练一练:
1.如图表示△AOB和把它缩小后得到的△COD,求它们的相似比 y
A
C
o
D
B
x
练一练:
2.如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以 原点O为位似中心,将这个三角形放大为原来的2倍.
y
o
x
A
C
B
结束语
当你尽了自己的最大努力时,失败 也是伟大的,所以不要放弃,坚持
以0为中心把△ABC 缩小为原来的一半。
位似图形精品课件

THANKS
感谢观看
相似多边形位似
总结词
多边形位似是指两个多边形在平面上 以相同的方向和比例放大或缩小,从 而得到的两个位似多边形。
详细描述
多边形位似的判断条件与四边形相似, 需要满足对应角相等和对应边成比例。 此外,还需要考虑多边形的边数和顶 点数是否相等。
相似圆位似
总结词
圆位似是指两个圆在平面上以相同的方向和比例放大或缩小,从而得到的两个位似圆。
图形。
利用位似变换作图
要点一
总结词
通过位似变换,可以将一个图形放大或缩小,从而得到另 一个图形。
要点二
详细描述
位似变换是一种常见的几何变换,它可以将一个图形放大 或缩小,同时保持其形状不变。利用这个变换,我们可以 方便地作出各种不同大小的位似图形。
利用位似图形构造复杂图形
总结词
通过组合和拼接位似图形,可以构造出复杂 的几何图形。
强化位似图形的应用能力培养
总结词
提升应用能力
详细描述
位似图形的应用是教学的重点和难点,教师需要结合实 际问题,引导学生运用位似图形的知识解决实际问题。 可以通过设计案例分析、数学建模等方式,提高学生的 应用能力。
提倡探究学习和合作学习相结合的教学方式
总结词
创新教学方式
详细描述
探究学习和合作学习是促进学生主动学习和合作学习 的有效方式。教师可以设置探究性问题,引导学生自 主探究,同时组织学生进行合作学习,通过交流、讨 论、分享等方式,促进学生对位似图形知识的深入理 解和掌握。
详细描述
位似图形是研究图形相似性的基础,它们在几何学中扮演着重要的角色。通过研 究位似图形的性质和特点,可以深入了解图形的相似性,进而解决各种几何问题 。位似图形在几何学中具有广泛的应用,如建筑设计、地图绘制等领域。
《图形的位似》PPT课件 (共16张PPT)

1对称图形,中心对称与中心对 称图形):对称轴,对称中心. 平移:平移的方向,平移的距离. 旋转:旋转中心,旋转方向,旋转角度. 相似:相似比.
注:图形这些不同的变换是我们学习几何必不可少的重要 工具,它不但装点了我们的生活,而且是学习后续知识的基础.
概念与性质 2. 位似图形的性质
从第 (1),(2)图中,我们可以看到,△OAB∽△O A′B′,
则OOAA′ =OOBB′ =A′ABB′ .从第(3)图中同样可以看到
AF AD
=AAPC
=AABE
=EBPC
=FDPC
性质:位似图形上任意一对对应点到位似中心 的距离之比等于位似比.
• 若△ABC与△A’B’C’的相似比为:1:2, 则OA:OA’=( 1:2 )。
译:同心协力的人,他们的力量足以把坚硬的金属弄断;同心同德的人发表一致的意见,说服力强,人们就像嗅到芬芳的兰花香味,容易接受。
11.君子藏器于身,待时而动。 ——《周易》
译:君子就算有卓越的才能超群的技艺,也不会到处炫耀、卖弄。而是在必要的时刻把才能或技艺施展出来。
12.满招损,谦受益。 ——《尚书》
A’
A
B
B’
O
C
C’
利用位似,可以将一个图形放大或缩小.
例如,要把四边形ABCD缩小到原来的1/2, 1.在四边形外任选一点O(如图),
2.分别在线段OA、OB、OC、OD上取点A'、B'、C'、D', 使得 OA' OB' OC' OD' 1
OA OB OC OD 2 3.顺次连接点A'、B'、C'、D',所得四边形A'B'C'D' 就是所要求的图形.
注:图形这些不同的变换是我们学习几何必不可少的重要 工具,它不但装点了我们的生活,而且是学习后续知识的基础.
概念与性质 2. 位似图形的性质
从第 (1),(2)图中,我们可以看到,△OAB∽△O A′B′,
则OOAA′ =OOBB′ =A′ABB′ .从第(3)图中同样可以看到
AF AD
=AAPC
=AABE
=EBPC
=FDPC
性质:位似图形上任意一对对应点到位似中心 的距离之比等于位似比.
• 若△ABC与△A’B’C’的相似比为:1:2, 则OA:OA’=( 1:2 )。
译:同心协力的人,他们的力量足以把坚硬的金属弄断;同心同德的人发表一致的意见,说服力强,人们就像嗅到芬芳的兰花香味,容易接受。
11.君子藏器于身,待时而动。 ——《周易》
译:君子就算有卓越的才能超群的技艺,也不会到处炫耀、卖弄。而是在必要的时刻把才能或技艺施展出来。
12.满招损,谦受益。 ——《尚书》
A’
A
B
B’
O
C
C’
利用位似,可以将一个图形放大或缩小.
例如,要把四边形ABCD缩小到原来的1/2, 1.在四边形外任选一点O(如图),
2.分别在线段OA、OB、OC、OD上取点A'、B'、C'、D', 使得 OA' OB' OC' OD' 1
OA OB OC OD 2 3.顺次连接点A'、B'、C'、D',所得四边形A'B'C'D' 就是所要求的图形.
位似图形的概念及画法公开课PPT课件
课堂小结
自由讨论 本节课你学习了哪些知识?
1 位似图形的概念:
B′
两个相似图形,如果对应点 B
. 的连线都经过同一点,则这样的 O
A
两个图形称为位似图形。
C
A′ C′
2 位似图形的性质:
(1)位似图形一定是相似图形,而相
似图形不一定是位似图形. (2)位似图形的对应点的连线相交于
B′
一点.
. (3)位似图形的对应边互相平行或在 B
之比等于相似比 D.位似图形中每组对应点所在的直线必相互平行
2.用作位似图形的方法,可以将一个图形放 大或缩小,位似中心( D ) A.只能选在原图形的外部 B.只能选在原图形的内部 C.只能选在原图形的边上 D.可以选择任意位置
3.如图, △ABC与△DEF是位似图形, 相似
比为2∶3, 已知AB=4, 则DE的长等于( A )
新课导入
在日常生活中,我们经常见到这样一类相 似的图形,它们有什么特征?
在日常生活中,经常遇到一些把图形放大或 缩小,但不改变图形的形状的情形。经过放大或 缩小的图形,与原图形是相似的.用这样的方法, 我们可以得到真实的图片和满意的照片.
这样的图形有 什么特点呢?
思考
探索新知
知识点1 位似图形的概念
④连线:顺次连接各关键点的对应点,即可得到要求
的新图形.
拓展延伸
如图, △ABC与△A′B′C′是位似图形, 点A, B, A′, B′,O共线, 点O为位似中心. (1)AC与A′C′平行吗? 请说明理由; (2)若AB=2A′B′, OC′=5, 求CC′的长. C
C′
A B A′ B′ O
解:(1)AC∥A′C′.
位似比等于相似比
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精选
(2)位似图形上任意一对对应点到位似中心的 距离之比等于相似比.
(3)位似图形中的对应线段平行(或在一条直线上).
精选
• 若△ABC与△A’B’C’的相似比为:1:2, 则OA:OA’=( 1:2 )。
A’
A
B
B’
O
C
C’
精选
图形与画法
1.如图,已知△ABC和点O.以O为 位似中心,求作△ABC的位似图形,并 把△ABC的边长扩大到原来的两倍.
相似 对应点的连线相交一点 对应边平行
精选
• 作出下列位似图形的位似中心:
O
O
精选
判断下面的正方形是不是位似图形?
A
D
(1) B
不是
E
F
C
G
显然,位似图形是相似图形的特殊情形.相似
图形不一定是位似图形,可位似图形一定是
相似图形
精选
议一议☞
观察下图中的五个图,回答下列问题:
(1)在各图中,位似图形的位似中心与这两个图形有什么位置关 系?
的相似比
y
A
C
o
D
B
x
精选
课堂小结 一、定义及性质: 二、位似图形的画法:
1.画出基本图形 2.选取位似中心 3.根据条件确定对应点,并描出对应点 4.顺次连结各对应点,所成的图形就是
所求的图形 三、位似变换与坐标的关系:
在平面直角坐标系中,如果位似变换 是以原点为位似中心,相似比为k, 那么位似图形对应点的坐标的比等于k或-k
E
B
O
C
F
D
A
D
B
O
C
F
A
E
利用位似可以把一个图形放大或缩小 如果把位似图形放到直角体系中,又如何
去探究位似变换与坐标之精选间的关系呢?
位似变换与坐标 A′(2,1), B′(2,0)
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点 O为位似中心,相y似比为1:3,把线段AB缩小.
A
A'
下面请欣赏如下图形的变换
精选
观察与思考☞
下列图形中,每个图中的四边形ABCD和四边形 A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边 形各对应点的连线有什么特征?对应边有何位置关系?
精选
概念与性质
1.位似图形的概念
如果两个图形不仅相似,而且每组对应点所 在的直线都经过同一点,对应边互相平行,那 么这样的两个图形叫做位似图形,这个点叫 做位似中心.这时两个相似图形的相似比又 叫做它们的位似比.
精选
课堂小结
回味无穷
• 位似图形的概念: 如果两个图形不仅形状相同,而且所在的直线都
经过同一个点,那么这样的两个图形叫做位似图形, 这个点叫做位似中心,这时的相似比又称为位似比. • 位似图形的性质: 1.位似图形是相似图形,具备相似图形的所有性质 2.位似图形上的任意一对对应点到位似中心的距离 之比等于位似比
E
①
F
.C
②
.D
③ ④⑤
P
A
B
精选
回顾与反思
1. 前面我们已经学习了图形的哪些变换? 平移:平移的方向,平移的距离. 轴对称:对称轴, 旋转:(中心对称)旋转中心,旋转方向,旋转角度. 相似:相似比.
注:图形这些不同的变换是我们学习几何必不可少的重要 工具,它不但装点了我们的生活,而且是学习后续知识的基础.
位似中心可以在两个图形的同侧,或两个图形之间,或 图形内还可以在一个图形的边上或顶点.
精选
议一议☞
观察下图中的五个图,回答下列问题:
(2)在各图中,任意一对对应点到位似中心的距离比与位似比有 什么关系?
位似图形上任意一对对应点到位似中心的距离之比等
于位似比.
精选
概念与性质
2. 位似图形的性质 (1)位似图形是相似图形,具备相似图形的所有性质
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现?
精选
在平面直角坐标系中,有两点A(6,3),B(6,0),以原 点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0) y
A〞(-2,-1),B(-2,0)
A
A'
B〞
x
o B'
B
A〞
观察对应点之间 ,yA'=yA×(-k) 即A’(-kx,-
精选
ky)
△ABC三个顶点坐标分别为A(2,3), B(2,1),C(6,2),以点O为位似中心, 相似比为2,将△ABC放大,点A的 对应点A′的坐标为____________
A′( 4,6 )或(-4,-6)
精选
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐
在平面直角坐标系中,如果位似变换是以原点
为位似中心,相似比为k,那么位似图形对应点
的坐标的比等于k或-k精.选
归纳:
在平面直角坐标系中,
如果位似变换是以原点为位似中心, 相似比为k, 那么位似图形对应点的坐标的比等于k或-k
例如:点A(x,y)的对应点为A’,则A’点的 坐标可以这样确定
xA’=xA×k , yA'=yA×k 即A’(kx,ky)
标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以 原点O为位似中心,相似比为1/2的位似图形.
y
A
D
A′
B
D′
B′
C
C′
o
x
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
你还有其他办法吗?试试看.
精选
练一练:
如图表示△AOB和把它缩小后得到的△COD,写出它们
3.位似图形中的对应线段平行(或在一条直线上).
精选
我们学过的图形变换有:平移,轴对称,旋转,位似。
(1)平移: 上下移:横坐标不变,纵坐标随之平移 左右移:纵坐标不变,横坐标随之平移 (2)轴对称 关于x轴对称:横坐标不变,纵坐标互为相反数 关于y轴对称:纵坐标不变,横坐标互为相反数 (3)旋转 绕原点旋转180度(中心对称):横坐标、纵坐标都 互为相反数 (4)位似 以原点为位似中心,相似比为k:位似图形对应点的 坐标的比等于k或-k
(2)位似图形上任意一对对应点到位似中心的 距离之比等于相似比.
(3)位似图形中的对应线段平行(或在一条直线上).
精选
• 若△ABC与△A’B’C’的相似比为:1:2, 则OA:OA’=( 1:2 )。
A’
A
B
B’
O
C
C’
精选
图形与画法
1.如图,已知△ABC和点O.以O为 位似中心,求作△ABC的位似图形,并 把△ABC的边长扩大到原来的两倍.
相似 对应点的连线相交一点 对应边平行
精选
• 作出下列位似图形的位似中心:
O
O
精选
判断下面的正方形是不是位似图形?
A
D
(1) B
不是
E
F
C
G
显然,位似图形是相似图形的特殊情形.相似
图形不一定是位似图形,可位似图形一定是
相似图形
精选
议一议☞
观察下图中的五个图,回答下列问题:
(1)在各图中,位似图形的位似中心与这两个图形有什么位置关 系?
的相似比
y
A
C
o
D
B
x
精选
课堂小结 一、定义及性质: 二、位似图形的画法:
1.画出基本图形 2.选取位似中心 3.根据条件确定对应点,并描出对应点 4.顺次连结各对应点,所成的图形就是
所求的图形 三、位似变换与坐标的关系:
在平面直角坐标系中,如果位似变换 是以原点为位似中心,相似比为k, 那么位似图形对应点的坐标的比等于k或-k
E
B
O
C
F
D
A
D
B
O
C
F
A
E
利用位似可以把一个图形放大或缩小 如果把位似图形放到直角体系中,又如何
去探究位似变换与坐标之精选间的关系呢?
位似变换与坐标 A′(2,1), B′(2,0)
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点 O为位似中心,相y似比为1:3,把线段AB缩小.
A
A'
下面请欣赏如下图形的变换
精选
观察与思考☞
下列图形中,每个图中的四边形ABCD和四边形 A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边 形各对应点的连线有什么特征?对应边有何位置关系?
精选
概念与性质
1.位似图形的概念
如果两个图形不仅相似,而且每组对应点所 在的直线都经过同一点,对应边互相平行,那 么这样的两个图形叫做位似图形,这个点叫 做位似中心.这时两个相似图形的相似比又 叫做它们的位似比.
精选
课堂小结
回味无穷
• 位似图形的概念: 如果两个图形不仅形状相同,而且所在的直线都
经过同一个点,那么这样的两个图形叫做位似图形, 这个点叫做位似中心,这时的相似比又称为位似比. • 位似图形的性质: 1.位似图形是相似图形,具备相似图形的所有性质 2.位似图形上的任意一对对应点到位似中心的距离 之比等于位似比
E
①
F
.C
②
.D
③ ④⑤
P
A
B
精选
回顾与反思
1. 前面我们已经学习了图形的哪些变换? 平移:平移的方向,平移的距离. 轴对称:对称轴, 旋转:(中心对称)旋转中心,旋转方向,旋转角度. 相似:相似比.
注:图形这些不同的变换是我们学习几何必不可少的重要 工具,它不但装点了我们的生活,而且是学习后续知识的基础.
位似中心可以在两个图形的同侧,或两个图形之间,或 图形内还可以在一个图形的边上或顶点.
精选
议一议☞
观察下图中的五个图,回答下列问题:
(2)在各图中,任意一对对应点到位似中心的距离比与位似比有 什么关系?
位似图形上任意一对对应点到位似中心的距离之比等
于位似比.
精选
概念与性质
2. 位似图形的性质 (1)位似图形是相似图形,具备相似图形的所有性质
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现?
精选
在平面直角坐标系中,有两点A(6,3),B(6,0),以原 点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0) y
A〞(-2,-1),B(-2,0)
A
A'
B〞
x
o B'
B
A〞
观察对应点之间 ,yA'=yA×(-k) 即A’(-kx,-
精选
ky)
△ABC三个顶点坐标分别为A(2,3), B(2,1),C(6,2),以点O为位似中心, 相似比为2,将△ABC放大,点A的 对应点A′的坐标为____________
A′( 4,6 )或(-4,-6)
精选
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐
在平面直角坐标系中,如果位似变换是以原点
为位似中心,相似比为k,那么位似图形对应点
的坐标的比等于k或-k精.选
归纳:
在平面直角坐标系中,
如果位似变换是以原点为位似中心, 相似比为k, 那么位似图形对应点的坐标的比等于k或-k
例如:点A(x,y)的对应点为A’,则A’点的 坐标可以这样确定
xA’=xA×k , yA'=yA×k 即A’(kx,ky)
标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以 原点O为位似中心,相似比为1/2的位似图形.
y
A
D
A′
B
D′
B′
C
C′
o
x
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
你还有其他办法吗?试试看.
精选
练一练:
如图表示△AOB和把它缩小后得到的△COD,写出它们
3.位似图形中的对应线段平行(或在一条直线上).
精选
我们学过的图形变换有:平移,轴对称,旋转,位似。
(1)平移: 上下移:横坐标不变,纵坐标随之平移 左右移:纵坐标不变,横坐标随之平移 (2)轴对称 关于x轴对称:横坐标不变,纵坐标互为相反数 关于y轴对称:纵坐标不变,横坐标互为相反数 (3)旋转 绕原点旋转180度(中心对称):横坐标、纵坐标都 互为相反数 (4)位似 以原点为位似中心,相似比为k:位似图形对应点的 坐标的比等于k或-k
