2014年海南省高考理科数学试卷及答案解析【word版】

合集下载

2014年高考真题——理科数学(新课标卷Ⅰ)精校版 Word版含答案

2014全国全国课标1理科数学一．选择题1.已知集合A={x |2230x x --≥}，B={x |－2≤x ＜2＝，则A B ⋂=A .[-2,-1]B .[-1,2）C .[-1,1]D .[1,2）2.32(1)(1)i i +-= A .1i + B .1i - C .1i -+ D .1i --3.设函数()f x ，()g x 的定义域都为R ，且()f x 时奇函数，()g x 是偶函数，则下列结论正确的是A .()f x ()g x 是偶函数B .|()f x |()g x 是奇函数C .()f x |()g x |是奇函数D .|()f x ()g x |是奇函数4.已知F 是双曲线C ：223(0)x my m m -=>的一个焦点，则点F 到C 的一条渐近线的距离为AB .3 CD .3m5.4位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率A .18 B .38 C .58 D .786.如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP的距离表示为x 的函数()f x ，则y =()f x 在[0,π]上的图像大致为7.执行下图的程序框图，若输入的,,a b k 分别为1,2,3，则输出的M=A .203 B .165 C .72 D .1588.设(0,)2πα∈，(0,)2πβ∈，且1sin tan cos βαβ+=，则 A .32παβ-=B .22παβ-=C .32παβ+=D .22παβ+=9.不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .有下面四个命题：1p ：(,),22x y D x y ∀∈+≥-，2p ：(,),22x y D x y ∃∈+≥, 3P ：(,),23x y D x y ∀∈+≤，4p ：(,),21x y D x y ∃∈+≤-.其中真命题是A .2p ，3PB .1p ，4pC .1p ，2pD .1p ，3P10.已知抛物线C ：28y x =的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个焦点，若4FP FQ =，则||QF =A .72 B .52C .3D .2 11.已知函数()f x =3231ax x -+，若()f x 存在唯一的零点0x ，且0x ＞0，则a 的取值范围为A .（2，+∞）B .（-∞，-2）C .（1，+∞）D .（-∞，-1）12.如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的个条棱中，最长的棱的长度为A. B. C .6 D .4二．填空题：本大题共四小题，每小题5分。

2014年高考全国卷1理科数学试题及标准答案-(word版)

2０14年普通高等学校招生全国统一考试全国课标1理科数学注意事项：1．本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题）两部分。

答题前,考生务必将自己的姓名、准考证号填写在答题卡上.2. 回答第Ⅰ卷时，选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑，如需改动,用橡皮搽干净后,再选涂其他答案标号，写在本试卷上无效.３. 回答第Ⅱ卷时,将答案写在答题卡上,答在本试题上无效.4．考试结束,将本试题和答题卡一并交回.第Ⅰ卷一.选择题：共12小题，每小题５分，共６0分。

在每个小题给出的四个选项中,只有一项是符合题目要求的一项。

1．已知集合A ＝｛x |2230x x --≥}，B={x |－2≤x <2=,则A B ⋂= A .[-2,-1] B .[-1,２) C .[-1,1］ D ．[1，２)２. 32(1)(1)i i +-＝ A ．1i + B ．1i - C .1i -+ D .1i --3. 设函数()f x ，()g x 的定义域都为R,且()f x 时奇函数,()g x 是偶函数，则下列结论正确的是 A .()f x ()g x 是偶函数 B .|()f x ｜()g x 是奇函数C .()f x ｜()g x ｜是奇函数D .|()f x ()g x |是奇函数4. 已知F 是双曲线C :223(0)x my m m -=>的一个焦点，则点F 到C 的一条渐近线的距离为 A .3 B ．３ C .3m D .3m5. ４位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率A .18B .38C .58D .78６．如图,圆O 的半径为1，A 是圆上的定点,P 是圆上的动点，角x 的始边为射线OA ,终边为射线OP ,过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示为x 的函数()f x ，则y =()f x 在[0,π]上的图像大致为７. 执行下图的程序框图，若输入的,,a b k 分别为1,2,3，则输出的M =A .203B .165C .72D .1588. 设(0,)2πα∈，(0,)2πβ∈,且1sin tan cos βαβ+=，则 A .32παβ-= B .22παβ-=C .32παβ+=D .22παβ+= 9．不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .有下面四个命题:1p ：(,),22x y D x y ∀∈+≥-，2p ：(,),22x y D x y ∃∈+≥,3P :(,),23x y D x y ∀∈+≤,4p :(,),21x y D x y ∃∈+≤-.其中真命题是A ．2p ,3PB .1p ,4pC .1p ,2pD .1p ，3P10. 已知抛物线C :28y x =的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个焦点,若4FP FQ =,则||QF =A .72B .52C .３D .2 11. 已知函数()f x =3231ax x -+,若()f x 存在唯一的零点0x ，且0x ＞0,则a 的取值范围为A .(２,＋∞)B ．(-∞，-2）C .(1，+∞）D .(-∞，-1)12．如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图，则该多面体的个条棱中,最长的棱的长度为A .62B .42C .6D .4第Ⅱ卷。

全国统一高考数学真题及逐题详细解析理科—海南卷

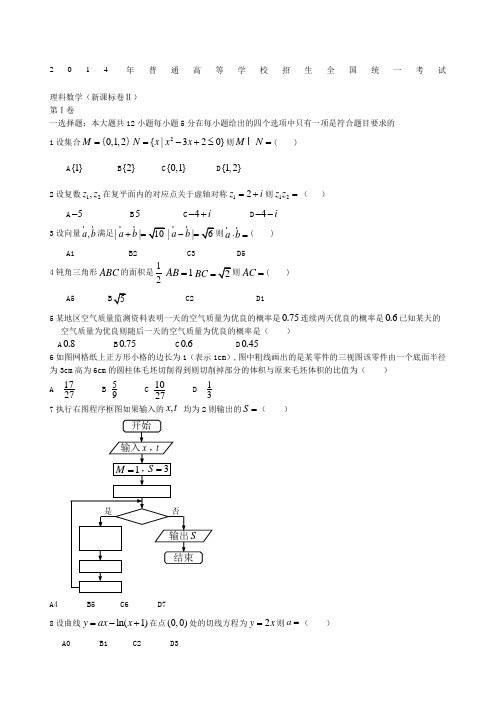
2014年普通高等学校招生全国统一考试理科数学（新课标卷Ⅱ）第Ⅰ卷一选择题：本大题共12小题每小题5分在每小题给出的四个选项中只有一项是符合题目要求的1设集合0,1,2M =｛｝2{|320}N x x x =-+≤则M N =I ( )A {1}B {2}C {0,1}D {1,2} 2设复数12,z z 在复平面内的对应点关于虚轴对称12z i =+则12z z =（）A 5-B 5C 4i -+D 4i --3设向量,a b r r满足||a b +=rr ||a b -=r r a b ⋅=r r ( )A1 B2 C3 D54钝角三角形ABC 的面积是121AB=BC =AC =( )A5 B 5某地区空气质量监测资料表明一天的空气质量为优良的概率是075．连续两天优良的概率是06．已知某天的空气质量为优良则随后一天的空气质量为优良的概率是（）A 08．B 075．C 06．D 045．6如图网格纸上正方形小格的边长为1（表示1cm ）,图中粗线画出的是某零件的三视图该零件由一个底面半径为3cm 高为6cm 的圆柱体毛坯切削得到则切削掉部分的体积与原来毛坯体积的比值为（） A1727 B 59 C 1027 D 13 7执行右图程序框图如果输入的,x t 均为2则输出的S =（）A4 B5 C6 D78设曲线ln(1)y ax x =-+在点(0,0)处的切线方程为2y x =则a =（）A0 B1 C2 D39设,x y 满足约束条件70,310,350.x y x y x y +-≤⎧⎪-+≤⎨⎪--≥⎩则2z x y =-的最大值为（）A10 B8 C3 D210设F 为抛物线2:3C y x =的焦点过F 且倾斜角为30o 的直线交C 于,A B 两点O 为坐标原点则OAB V 的面积为（）C 6332D 94 11直三棱柱111ABC A B C -中90BCA ∠=︒M N ,分别是1111A B AC ,的中点1BC CA CC ==则BM 与AN所成的角的余弦值为（） A 110 B 2512设函数()xf x m π=若存在()f x 的极值点0x 满足22200[()]x f x m +<则m 的取值范围是（）A ()(),66,-∞-⋃∞B ()(),44,-∞-⋃∞C ()(),22,-∞-⋃∞D ()(),14,-∞-⋃∞第Ⅱ卷本卷包括必考题和选考题两部分第13题~第21题为必考题每个试题考生必须做答第22题~第24题为选考题考生根据要求做答二填空题1310()x a +的展开式中7x 的系数为15则a =________(用数字填写答案) 14函数()sin(2)2sin cos()f x x x ϕϕϕ=+-+的最大值为_________15已知偶函数()f x 在[0,)+∞单调递减(2)0f =若(1)0f x ->则x 的取值范围是______16设点0(,1)M x 若在圆22:1O x y +=上存在点N 使得45OMN∠=︒则0x 的取值范围是____三解答题：解答应写出文字说明证明过程或演算步骤 17（本小题满分12分）已知数列{}n a 满足11a =，131n n a a +=+ （Ⅰ）证明1{}2n a +是等比数列并求{}n a 的通项公式；（Ⅱ）证明：1211132n a a a +++<L 18（本小题满分12分）如图四棱锥P-ABCD 中底面ABCD 为矩形PA ABCD ⊥平面 E 为PD 的中点（Ⅰ）证明：PB AEC ∥平面；（Ⅱ）设二面角D AE C --为60°1AP =AD =求三棱锥E ACD - 的体积19 （本小题满分12分）某地区2007年至2013年农村居民家庭纯收入y （单位：千元）的数据如下表：（Ⅰ）求关于的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况并预测该地区2015年农村居民家庭人均纯收入附：回归直线的斜率和截距的最小二乘法估计公式分别为：()()()121ni ii n i i t t y y b t t ∧==--=-∑∑ˆˆay bt =- 20（本小题满分12分）设12,F F 分别是椭圆22221x y a b+= （0a b >> ）的左右焦点M 是C 上一点且2MF 与x 轴垂直直线1MF 与C 的另一个交点为N（Ⅰ）若直线MN 的斜率为34求C 的离心率；（Ⅱ）若直线MN 在y 轴上的截距为2且1||5||MN F N =求,a b21（本小题满分12分）已知函数()2x x f x e ex -=--。

2014年高考理科数学全国卷2(含答案解析)

绝密★启用前2014年普通高等学校招生全国统一考试（全国新课标卷2）理科数学使用地区：海南、宁夏、黑龙江、吉林、新疆、云南、内蒙古、青海、贵州、甘肃、西藏注意事项：1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效.4.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷一、选择题：本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|(1)4,}M x x x =-<∈R ,{1,0,1,2,3}N =-,则MN = ( )A .{0,1,2}B .{1,0,1,2}-C .{1,0,2,3}-D .{0,1,2,3} 2.设复数z 满足(1i)2i z -=,则z =( )A .1i -+B .1i --C .1i +D .1i -3.等比数列{}n a 的前n 项和为n S .已知32110S a a =+,59a =,则1a =( )A .13B .13-C .19D .19-4.已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l m ⊥,l ⊥n ,l α⊄,l β⊄,则( )A .αβ∥且l α∥B .αβ∥且l β⊥C .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l5.已知5(1)(1)ax x ++的展开式中的2x 的系数为5,则a = ( )A .4-B .3-C .2-D .1-6.执行如图的程序框图,如果输入的10N =,则输出的S = ( ) A .11112310++++B .11112!310++++！！C .11112311++++ D .11112311++++！！！7.一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到的正视图可以为( )8.设3log 6a =,5log 10b =,7log 14c =,则( )A .c b a >>B .b a c >>C .a c b >>D .a b c >>9.已知0a >,x ,y 满足约束条件1,3,(3).x x y y a x ⎧⎪+⎨⎪-⎩≥≤≥若2z x y =+的最小值为1,则a = ( )A .14B .12C .1D .210.已知函数32()f x x ax bx c =+++,下列结论中错误的是( )A .0x ∃∈R ,0()0f x =B .函数()y f x =的图象是中心对称图形C .若0x 是()f x 的极小值点,则()f x 在区间0(,)x -∞上单调递减D .若0x 是()f x 的极值点,则0()0f x '=11.设抛物线C :22(0)y px p =>的焦点为F ,点M 在C 上,||5MF =.若以MF 为直径的圆过点(0,2),则C 的方程为( )A .24y x =或28y x =B .22y x =或28y x =C .24y x =或216y x = D .22y x =或216y x =12.已知点(1,0)A -,(1,0)B ,(0,1)C ,直线(0)y ax b a =+>将ABC △分割为面积相等的两部分,则b 的取值范围是( )A .(0,1)B .21(1,)22-C .21(1,]23-D .11[,)32第Ⅱ卷本卷包括必考题和选考题两部分.第13题～第21题为必考题,每个试题考生都必须作答.第22题～第24题为选考题,考生根据要求作答.二、填空题：本大题共4小题,每小题5分.13.已知正方形ABCD 的边长为2,E 为CD 的中点,则AE BD =________. 14.从n 个正整数1,2,,n 中任意取出两个不同的数,若取出的两数之和等于5的概率为114,则n =________.15.设θ为第二象限角,若π1tan()42θ+=,则sin cos θθ+=________. 16.等差数列{}n a 的前n 项和为n S .已知100S =,1525S =,则n nS 的最小值为________.三、解答题：解答应写出文字说明,证明过程或演算步骤. 17.（本小题满分12分）ABC △在内角A ,B ,C 的对边分别为a ,b ,c ,已知cos sin a b C c B =+.（Ⅰ）求B ；（Ⅱ）若2b =,求ABC △面积的最大值. 18.（本小题满分12分） --------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________如图,直棱柱111ABC A B C -中,D ,E 分别是AB ,1BB 的中点,122AA AC CB AB ===. （Ⅰ）证明：1BC ∥平面1A CD ；（Ⅱ）求二面角1D AC E --的正弦值.19.（本小题满分12分）经销商经销某种农产品,在一个销售季度内,每售出1t 该产品获利润500元,未售出的产品,每1t 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t 该农产品.以X (单位：t ,100150X ≤≤)表示下一个销售季度内的市场需求量,T (单位：元)表示下一个销售季度内经销该农产品的利润. （Ⅰ）将T 表示为X 的函数；（Ⅱ）根据直方图估计利润T 不少于57 000元的概率；（Ⅲ）在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量[100,110)X ∈,则取105X =,且105X =的概率等于需求量落入[100,110)的频率),利润T 的数学期望.20.（本小题满分12分）平面直角坐标系xOy 中,过椭圆M :22221(0)x y a b a b+=>>右焦点的直线30x y +-=交M 于A ,B 两点,P 为AB 的中点,且OP 的斜率为12.（Ⅰ）求M 的方程；（Ⅱ）C ,D 为M 上的两点,若四边形ABCD 的对角线CD AD ⊥,求四边形ABCD 面积的最大值.21.（本小题满分12分）已知函数()e ln()xf x x m =-+.（Ⅰ）设0x =是()f x 的极值点,求m ,并讨论()f x 的单调性；（Ⅱ）当2m ≤时,证明:()0f x >.请考生在第22、23、24三题中任选一题作答,如果多做，则按做的第一题积分.作答时请写清题号.22.（本小题满分10分）选修4—1:几何证明选讲如图,CD 为ABC △外接圆的切线,AB 的延长线交直线CD 于点D ,E ,F 分别为弦AB 与弦AC 上的点,且BC AE DC AF =,B ,E ,F ,C 四点共圆.（Ⅰ）证明：CA 是ABC △外接圆的直径；（Ⅱ）若DB BE EA ==,求过B ,E ,F ,C 四点的圆的面积与ABC △外接圆面积的比值.23.（本小题满分10分）选修4—4:坐标系与参数方程已知动点P ,Q 都在曲线C ：2cos ,2sin x t y t =⎧⎨=⎩（t 为参数）上,对应参数分别为=t α与=2t α(02π)α<<,M 为PQ 的中点.（Ⅰ）求M 的轨迹的参数方程；（Ⅱ）将M 到坐标原点的距离d 表示为α的函数,并判断M 的轨迹是否过坐标原点.24.（本小题满分10分）选修4—5:不等式选讲设a ,b ,c 均为正数,且1a b c ++=.证明：（Ⅰ）13ab bc ca ++≤；（Ⅱ）2221a b c b c a++≥.2014年普通高等学校招生全国统一考试（全国新课标卷2）理科数学答案解析第Ⅰ卷一、选择题 1.【答案】A【解析】解不等式2(14)x -<，得13x <<-，即|13{}M x x =<<-，而1,0,1,,3{}2N =-，所以0,}2{1,M N =，故选A ．【提示】求出集合M 中不等式的解集，确定出M ，找出M 与N 的公共元素，即可确定出两集合的交集．【考点】集合的基本运算（交集），解一元二次不等式． 2.【答案】A【解析】2i 2i 1i 22i 1i 1i 1i 21+i z (+)-+====-(-)(+)-．【提示】根据所给的等式两边同时除以1i -，得到z 的表示式，进行复数的除法运算，分子和分母同乘以分母的共轭复数，整理成最简形式，得到结果．【考点】复数代数形式的四则运算． 3.【答案】C【解析】设数列{}n a 的公比为q ，若1q =，则由59a =，得19a =，此时327S =，而219+109a a =，不满足题意，因此1q ≠.∵1q ≠时，33111(1)1+10a S a a q q q --==，∴3+0111q qq =--，整理得29q =.（步骤1） ∵4519a a q ==，即1819a =，∴119a =．（步骤2）【提示】设等比数列{}n a 的公比为q ，利用已知和等比数列的通项公式即可求出．【考点】等比数列的通项和前n 项和． 4.【答案】D【解析】因为m α⊥，l m ⊥，l α⊄，所以l α∥．同理可得l β∥．又因为m ，n 为异面直线，所以α与β相交，且l 平行于它们的交线．故选D ．【提示】由题目给出的已知条件，结合线面平行，线面垂直的判定与性质，可以直接得到正确的结论．【考点】直线与平面的位置关系． 5.【答案】D【解析】因为5(1+)x 的二项展开式的通项为5C 0)5(r rr r x ≤≤∈Z ，，则含x 2的项为221552C +C )0+5(1x ax x a x =，所以10+55a =，1a =-.【提示由题意利用二项展开式的通项公式求得展开式中2x 的系数为221552C +C )0+5(1x ax x a x =，由此解得a 的值．【考点】二项式定理 6.【答案】B【解析】由程序框图知，当1k =，0S =，1T =时，1T =，1S =；当2k =时，12T =，11+2S =；当k =3时，123T =⨯，111+223S =+⨯；当k =4时，1234T =⨯⨯，1111+223234S =++⨯⨯⨯；；（步骤1）当k =10时，123410T =⨯⨯⨯⨯，1111+2!3!10!S =+++，k 增加1变为11，满足k N >，输出S ，所以B 正确．（步骤2）【提示】从赋值框给出的两个变量的值开始，逐渐分析写出程序运行的每一步，便可得到程序框图表示的算法的功能．【考点】循环结构的程序框图． 7.【答案】A【解析】如图所示，该四面体在空间直角坐标系O －xyz 的图象为下图：第7题图则它在平面zOx 上的投影即正视，故选A ．【提示】由题意画出几何体的直观图，然后判断以zOx 平面为投影面，则得到正视图即可．【考点】空间直角坐标系，三视图． 8.【答案】D【解析】根据公式变形，lg6lg 21lg3lg3a ==+，lg10lg 21lg5lg5b ==+，lg14lg 21lg 7lg 7c ==+，因为lg 7lg 5g 3l >>，所以lg2lg2lg2lg7lg5lg3<<，即c b A <<．故选D ．【提示】利用log ()log log (0)a a a xy x y x y =+>、，化简a ，b ，c 然后比较3log 2，5log 2，7log 2大小即可．【考点】对数函数的化简和大小的比较． 9.【答案】B【解析】由题意作出1,3x x y ≥⎧⎨+≤⎩所表示的区域如图阴影部分所示，作直线2+1x y =，因为直线2+1x y =与直线1x =的交点坐标为(1,)1-，结合题意知直线(3)y a x =-过点(1,)1-，代入得12a =，所以12a =．第9题图【提示】先根据约束条件画出可行域，设2z x y =+，再利用z 的几何意义求最值，只需求出直线2zx y=+过可行域内的点B 时，从而得到a 值即可．【考点】二元线性规划求目标函数的最值．10.【答案】C【解析】由于2()32f x x ax b '=++是二次函数，()f x 有极小值点0x ，必定有一个极大值点1x ，若10x x <，则()f x 在区间0(,)x -∞上不单调递减，C 不正确．【提示】利用导数的运算法则得出()00f x '∆>∆≤，分与讨论，即可得出．【考点】利用导数求函数的极值． 11.【答案】C【解析】设点M 的坐标为00(,)x y ，由抛物线的定义，得052|+MF x p ==|，则052x p =-．（步骤1）又点F 的坐标为,02p ⎛⎫ ⎪⎝⎭，所以以MF 为直径的圆的方程为00+0()()2p x y x x y y ⎛⎫⎪-- ⎝⎭-=.（步骤2）将0x =，2y =代入得00+840px y -=，即02+2480y y -=，所以04y =. 由0202y px =，得16252p p ⎛⎫=- ⎪⎝⎭，解之得2p =，或8p =.（步骤3）所以C 的方程为24y x =或216y x =．故选C ．【提示】已知抛物线焦点到抛物线上点的线段的距离和以这条线段为直径的圆上的一点，求出抛物线的方程．【考点】抛物线的定义和抛物线的标准方程． 12.【答案】B【解析】根据题意画出图形，如图（1），由图可知，直线BC 的方程为1x y +=．由1,,x y y ax b +=⎧⎨=+⎩解得1,11b a b M a a -+⎛⎫⎪++⎝⎭．可求()0,N b ，,0b D a ⎛⎫- ⎪⎝⎭．直线y ax b =+将△ABC 分割为面积相等的两部分，∴12S S =△△BDM ABC ．又12BOC ABC S S =△△，CMN ODN S S ∴=△△，即111(1)221b b b b a a -⎛⎫⨯-⨯=-⨯ ⎪+⎝⎭．整理得22(1)1b b a a -=+． 22(1)1b ab a-+∴=，11b ∴-=，11b =即b =，可以看出，当a 增大时，b 也增大．当a →+∞时，12b →，即12b <．当0a →时，直线+y ax b =接近于y b =．当y b =时，如图（2），2222(1)112CDM ABC S CN b S CO -===△△．1b ∴-1b =1b ∴>-．由上分析可知1122b -<<，故选B ．第12题图（1）第12题图（2）【提示】已知含有参数的直线将三角形分割为面积相等的两部分和点的坐标，求出参数的取值范围．【考点】函数单调性的综合应用．第Ⅱ卷二、填空题 13.【答案】2【解析】以AB 所在直线为x 轴，AD 所在直线为y 轴建立平面直角坐标系，如图所示，则点A 的坐标为(0,0)，点B 的坐标为(2,0)，点D 的坐标为(0,2)，点E 的坐标为(1,2)，则1(),2AE =，)2(2,BD =-，所以2AE BD =．第13题图【提示】结合几何的关系，求出向量的数量积．【考点】平面向量的数量积运算． 14.【答案】8【解析】从1，2，…，n 中任取两个不同的数共有2C n 种取法，两数之和为5的有(1,4)，(2,3)2种，所以221C 14n =，即24111142n n n n ==(-)(-)，解得8n =.【提示】列出从n 个正整数1，2，…，n 中任意取出两个不同的数的所有取法种数，求出和等于5的种数，根据取出的两数之和等于5的概率为114列式计算n 的值．【考点】古典概型，排列组合的应用．15.【答案】【解析】由π1tan 1tan 41tan 2θθθ+⎛⎫+== ⎪-⎝⎭，得tan 13θ=-，即1s 3in cos θθ-=．（步骤1）将其代入22sin +cos 1θθ=，得210cos 19θ=．因为θ为第二象限角，所以10cos θ-=0in 1s θ=，sin +cos 5θθ=-．（步骤2）【提示】已知等式利用两角和与差的正切函数公式及特殊角的三角函数值化简，求出tan θ的值，再根据θ为第二象限角，利用同角三角函数间的基本关系求出sin cos θθ与的值，即可求出sin cos θθ+的值．【考点】两角和与差的正切，同角三角函数的基本关系． 16.【答案】49-【解析】设数列{}n a 的首项为a 1，公差为d ，则110110910+210+450S a d d a =⨯==，① 1151151415215+10525a d a d S =⨯==+.②（步骤1）联立①②，得13a =-，23d =，所以2(1)211032333n n n n n n S -=-+⨯=-．（步骤2）令()n f n nS =，则32110()33f n n n =-，220()3f n n n '=-．令()0f n '=，得0n =或203n =．（步骤3）当203n >时，()0f n '>，200<<3n 时，()0f n '<，所以当203n =时，()f n 取最小值，而n ∈N ＋，则(6)48f =-，(7)49f =-，所以当7n =时，()f n 取最小值－49.（步骤4）【提示】已知等差数列前10项和与前15项和，求出n 与前n 项和乘积的最小值．【考点】等差数列的前n 项，利用导数求函数的最值．三、解答题 17.【答案】（1）π4（2【解析】（1）由已知及正弦定理得sin sin cos +sin sin A B C C B =．①又()+A B C π=-，故sin sin +sin cos +co )s i (s n A B C B C B C ==．②由①，②和π()0,C ∈得sin cos B B =，即tan 1B =，又π()0,B ∈，所以π4B =．（步骤1）（2）△ABC的面积1sin 2S ac B ==．由已知及余弦定理得22π2cos 44+ac a c =-．（步骤2）又22+2a c ac ≥，故ac ≤，当且仅当a c =时，等号成立．因此△ABC．（步骤3）【提示】（1）已知等式利用正弦定理化简，再利用两角和与差的正弦函数公式及诱导公式变形，求出tan B 的值，由B 为三角形的内角，利用特殊角的三角函数值即可求出B 的度数；（2）利用三角形的面积公式表示出三角形ABC 的面积，把sin B 的值代入，得到三角形面积最大即为ac 最大，利用余弦定理列出关系式，再利用基本不等式求出ac 的最大值，即可得到面积的最大值．【考点】正弦定理，余弦定理，三角形面积公式，两角和与差的正弦． 18.【答案】（1）连结AC 1交A 1C 于点F ，则F 为AC 1中点．又D 是AB 中点，连结DF ，则1BC DF ∥．因为DF ⊂平面A 1CD ，BC 1⊄平面A 1CD ，所以BC 1∥平面A 1CD ．（步骤1）（2）由AC CB AB ==，得AC BC ⊥ 以C 为坐标原点，CA 的方向为x 轴正方向，建立如图所示的空间直角坐标系C －xyz ．设2CA =，则()1,1,0D ，()0,2,1E ，12,()0,2A ，(1),1,0CD =，(0),2,1CE =，12,0,2()CA =．设111,(),n x y z =是平面A 1CD 的法向量，则10,0,n CD n CA ⎧=⎪⎨=⎪⎩即1111+0,2+20.x y x z =⎧⎨=⎩ 可取1),(,11n =--．（步骤2）同理，设m 是平面A 1CE 的法向量，则10,0,m CE m CA ⎧=⎪⎨=⎪⎩可取2,1(),2m =-．（步骤3）从而3cos ,3||||n m m n n m <>==，故6sin ,3m n <>= 即二面角D －A 1C －E ．（步骤4）第18题图（1）【提示】（1）通过证明1BC 平行平面1ACD 内的直线DF ，利用直线与平面平行的判定定理证明11BC ACD 平面∥ （2）．由AC CB AB ==，得AC BC ⊥以C 为坐标原点，CA 的方向为x 轴正方向，建立如图所示的空间直角坐标系C －xyz ．设2CA =，111,(),n x y z =是平面A 1CD 的法向量，同理，设m 是平面A 1CE 的法向量，由3cos ,3||||n m m n n m <>==，故6sin ,3m n <>=【考点】直线与平面的判定，空间直角坐标系，空间向量及其运算．19.【答案】（1）80039000,100130,65000,130150.X X T X -≤<⎧=⎨≤≤⎩ （2）0.7（3）59400【解析】（1）当100[),130X ∈时，50030013()080039000T X X X =--=-，当130[],150X ∈时，50013065000T =⨯=. 所以80039000,10013065000,130150X X T X -≤<⎧=⎨≤≤⎩（步骤1）（2）由（1）知利润T 不少于57000元当且仅当120150X ≤≤.由直方图知需求量120[],150X ∈的频率为0.7，所以下一个销售季度内的利润T 不少于57000元的概率的估计值为0.7（步骤2）（3所以450000.1+530000.2+610000.3+650000.459400ET =⨯⨯⨯⨯=.（步骤3）【提示】（1）由题意先分段写出，当100[),130X ∈时，当130[],150X ∈时，和利润值，最后利用分段函数的形式进行综合即可．（2）由（1）知，利润T 不少于57000元，当且仅当120150X ≤≤再由直方图知需求量120[],150X ∈的频率为0.7，利用样本估计总体的方法得出下一个销售季度的利润T 不少于57000元的概率的估计值．（3）利用利润T 的数学期望=各组的区间中点值x 该区间的频率之和即得．【考点】频率分布直方图，分段函数的模型，离散型随机变量的数学期望．20.【答案】（1）22163x y +=（2 【解析】（1）设11(),A x y ，22(),B x y ，00(),P x y ，则2211221x y a b +=，2222221x y a b+=，21211y y x x -=--，由此可得22121221211b x x y y a y y x x (+)-=-=(+)-．因为120+2x x x =，120+2y y y =，0012y x =，所以222a b =（步骤1）又由题意知，M的右焦点为，故223a b -=. 因此26a =，23b =.所以M 的方程为22163x y +=．（步骤2）（2）由220,1,63x y x y ⎧+=⎪⎨+=⎪⎩解得x y ⎧=⎪⎪⎨⎪=⎪⎩或0,x y =⎧⎪⎨=⎪⎩因此||AB =．（步骤3）由题意可设直线CD的方程为3y x n n ⎛=+-<< ⎝，设33(),C x y ，44(),D x y ．由22,163y x n x y =+⎧⎪⎨+=⎪⎩得223+4+260x nx n -=.于是3,4x （步骤4）因为直线CD 的斜率为1，所以43|||x x CD - 由已知，四边形ACBD 的面积186||||29S CD AB ==．当n ＝0时，S 取得最大值，最大值为．所以四边形ACBD ．（步骤5）【提示】（1）把右焦点(,0)c 代入直线可解得C ．设11(),A x y ，22(),B x y ，线段AB 的中点00(),P x y ，利用“点差法”即可得到a ，b 的关系式，再与222a bc =+联立即可得到a ，b ，c ．（2）把直线0x y +=与椭圆的方程联立得到根与系数的关系，即可得到弦长||AB ，由CD AB ⊥，可设直线CD 的方程为y x n =+，与椭圆的方程联立得到根与系数的关系，即可得到弦长||CD ．利用1||||2ACBD S AB CD =四边形即可得到关于n 的表达式，利用二次函数的单调性即可得到其最大值．【考点】椭圆的方程、椭圆的简单几何性质、点差法的应用和直线与椭圆的位置关系． 21.【答案】（1）1()e x f x x m=-+．由0x =是()f x 的极值点得(0)0f '=，所以1m =.于是ln +)1(()xf e x x =-，定义域为()1,+-∞，1()e 1xf x x =-+．（步骤1）函数1()e 1x f x x =-+在()1,+-∞单调递增，且(0)0f '=.因此当,0()1x ∈-时，()0f x '<；当+()0,x ∈∞时，()0f x '>.所以()f x 在()1,0-单调递减，在(0,+)∞单调递增．（步骤2）（2）当2m ≤，,()+x m ∈-∞时，l ()()n +ln +2x m x ≤，故只需证明当2m =时，()0f x >. 当2m =时，函数1()e 2x f x x =-+在()2,+-∞单调递增．又1()0f '-<，(0)0f '>，故()0f x '=在()2,+-∞有唯一实根x 0，且0)0(1,x ∈-．（步骤3）当2+(),x ∈-∞时，()0f x '<；当0(),+x x ∈∞时，()0f x '>，从而当0x x =时，()f x 取得最小值．由0()0f x '=得001e 2x x =+，00ln +2()x x =-，故200000()()+11022f x f x x x x x ≥)=+++=(>. 综上，当2m ≤时，()0f x >.（步骤4）【提示】（1）求出原函数的导函数，因为0x =是函数()f x 的极值点，由极值点处的导数等于0求出m 的值，代入函数解析式后再由导函数大于0和小于0求出原函数的单调区间；（2）证明当2m ≤时，()0f x >，转化为证明当2m =时()0f x >求出当2m =时函数的导函数，可知导函数在(2,)-+∞上为增函数，并进一步得到导函数在(1,0)-上有唯一零点0x ，则当0x x =时函数取得最小值，借助于0x 是导函数的零点证出0()0f x >，从而结论得证．【考点】利用导数求函数的单调区间和极值，利用导数解决不等式问题． 22.【答案】（1）因为CD 为△ABC 外接圆的切线，所以DCB A ∠=∠，由题设知BC DCFA EA=，故CDB AEF △∽△，所以DBC EFA ∠=∠．（步骤1）因为B ，E ，F ，C 四点共圆，所以CFE DBC ∠=∠，故90EFA CFE ∠=∠=︒．所以90CBA ∠=︒，因此CA 是△ABC 外接圆的直径．（步骤2）（2）连结CE ，因为90CBE ∠=︒，所以过B ，E ，F ，C 四点的圆的直径为CE ，由DB BE =，有CE DC =，又222BC DB BA DB ==，所以222 2.4+6CA DB BC DB ==而2223DC DB D CE DA B ===，故过B ，E ，F ，C 四点的圆的面积与△ABC 外接圆面积的比值为12．（步骤3）第22题图【提示】（1）已知CD 为ABC △外接圆的切线，利用弦切角定理可得DCB A ∠=∠，及BC DCFA EA=，可知CDB AEF △∽△，于是DBC EFA ∠=∠．利用B 、E 、F 、C 四点共圆，可得CFE DBC ∠=∠，进而得到90EFA CFE ∠=∠=︒即可证明CA 是ABC △外接圆的直径；（2）要求过B 、E 、F 、C 四点的圆的面积与ABC △外接圆面积的比值．只需求出其外接圆的直径的平方之比即可．由过B 、E 、F 、C 四点的圆的直径为CE ，及DB BE =，可得CE DC =，利用切割线定理可得222BC DB BA DB ==，222 2.4+6CA DB BC DB ==，都用DB 表示即可．【考点】弦切角，圆内接四边形的性质．23.【答案】（1）cos cos 2,sin sin 2x y αααα=+⎧⎨=+⎩0()2παα<<为参数，（2）d (02π)α<< M 的轨迹过坐标原点【解析】（1）依题意有2cos (n )2si P αα，，2cos2,2si 2()n Q αα，因此cos +cos2,sin +i ()s n2M αααα．M 的轨迹的参数方程为cos cos 2sin sin 2x y αααα=+⎧⎨=+⎩0()2παα<<为参数，．（步骤1）（2）M 点到坐标原点的距离d =(02π)α<<．当πα=时，0d =，故M 的轨迹过坐标原点．（步骤2）【提示】（1）根据题意写出P ，Q 两点的坐标：2cos (n )2si P αα，，2cos2,2si 2()n Q αα，再利用中点坐标公式得PQ 的中点M 的坐标，从而得出M 的轨迹的参数方程；（2）利用两点间的距离公式得到M 到坐标原点的距离d 证当πα=时，0d =，故M 的轨迹过坐标原点．【考点】参数方程，轨迹方程．24.【答案】（1）由22+2b a ab ≥，22+2b c bc ≥，22+2c a ca ≥，得222++++a b c ab bc ca ≥．（步骤1）由题设得21)++(a b c =，即222+++2+2+21a b c ab bc ca =.所以3+(+)1ab bc ca ≤，即1++3ab bc ca ≤．（步骤2）（2）因为22a b a b +≥，22b c b c +≥，22c a c a+≥，故222(++(2))a b c a b c a b c b c a +++++≥，（步骤3）即222++a b c a c a c b b ++≥．所以2221a b c b c a++≥（步骤4）【提示】（1）依题意，由21)++(a b c =，即222+++2+2+21a b c ab bc ca =，利用基本不等式可得3+(+)1ab bc ca ≤，从而得证；（2）利用基本不等式可证得：22a b a b +≥，22b c b c +≥，22c a c a +≥，三式累加即可证得结论．【考点】不等式证明，均值不等式．。

2014年高考真题——理科数学(全国大纲卷)解析版 Word版含解析

第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1.设103i z i=+，则z 的共轭复数为（）A ．13i -+B ．13i --C ．13i +D ．13i -2.设集合2{|340}M x x x =--<，{|05}N x x =≤≤，则M N =I （）A ．(0,4]B ．[0,4)C ．[1,0)-D ．(1,0]-3.设sin 33,cos55,tan 35,a b c =︒=︒=︒则（）A ．a b c >>B ．b c a >>C ．c b a >>D ．c a b >>4.若向量,a b r r 满足：()()1,,2,a a b a a b b =+⊥+⊥r r r r r r r 则b =r （）A ．2B ．2C ．1D ．225.有6名男医生、5名女医生，从中选出2名男医生、1名女医生组成一个医疗小组，则不同的选法共有（）A ．60种B ．70种C ．75种D ．150种6.已知椭圆C ：22221x y a b +=(0)a b >>的左、右焦点为1F 、2F 3，过2F 的直线l 交C 于A 、B 两点，若1AF B ∆的周长为43C 的方程为（）A ．22132x y +=B ．2213x y +=C ．221128x y +=D ．221124x y +=7.曲线1x y xe-=在点（1, 1）处切线的斜率等于（） A ．2e B ．e C ．2 D ．18．正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（）A ．814πB ．16πC ．9πD ．274π 【答案】A ．【解析】考点：1.球的内接正四棱锥问题；2. 球的表面积的计算．9.已知双曲线C 的离心率为2，焦点为1F 、2F ，点A 在C 上，若122F A F A =，则21cos AF F ∠=（）A ．14B ．13C ．24D ．23 10.等比数列{}n a 中，452,5a a ==，则数列{lg }n a 的前8项和等于（）图2A ．6B ．5C ．4D ．311.已知二面角l αβ--为60︒，AB α⊂，AB l ⊥，A 为垂足，CD β⊂，C l ∈，135ACD ∠=︒，则异面直线AB 与CD 所成角的余弦值为（）A ．14B 2C 3D ．12【答案】B.【解析】12.函数()y f x =的图象与函数()y g x =的图象关于直线0x y +=对称，则()y f x =的反函数是（）A ．()y g x =B ．()y g x =-C ．()y g x =-D ．()y g x =--第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 8y x 的展开式中22x y 的系数为 . 【答案】70.14.设,x y 满足约束条件02321x y x y x y -≥⎧⎪+≤⎨⎪-≤⎩，则4z x y =+的最大值为.15．直线1l 和2l 是圆222x y +=的两条切线，若1l 与2l 的交点为()1,3，则1l 与2l 的夹角的正切值等于 .2l的夹角的正切值：12124 tan13k kk kθ-==+．考点：1.直线与圆的位置关系（相切）；2.两直线的夹角公式．16.若函数()cos2sinf x x a x=+在区间(,)62ππ是减函数，则a的取值范围是.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.（本小题满分10分）ABC∆的内角A，B，C的对边分别为a，b，c，已知3cos2cosa C c A=，1tan3A=，求B.18. （本小题满分12分）等差数列{}na的前n项和为nS，已知110a=，2a为整数，且4nS S≤.（I ）求{}n a 的通项公式；（II ）设11n n n b a a +=，求数列{}n b 的前n 项和n T . 19. （本小题满分12分）如图，三棱柱111ABC A B C -中，点1A 在平面ABC 内的射影D 在AC 上，090ACB ∠=，11,2BC AC CC ===. （I ）证明：11AC A B ⊥；（II ）设直线1AA 与平面11BCC B 31A AB C --的大小.20. （本小题满分12分）设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6,0.5,0.5,0.4,各人是否需使用设备相互独立.（I）求同一工作日至少3人需使用设备的概率；（II）X表示同一工作日需使用设备的人数，求X的数学期望.21.（本小题满分12分）已知抛物线C ：22(0)y px p =>的焦点为F ，直线4y =与y 轴的交点为P ，与C 的交点为Q ，且5||||4QF PQ =. （I ）求C 的方程；（II ）过F 的直线l 与C 相交于A ，B 两点，若AB 的垂直平分线l '与C 相较于M ，N 两点，且A ，M ，B ，N 四点在同一圆上，求l 的方程.【答案】（I ）24y x =；（II ）直线l 的方程为10x y --=或10x y +-=．22. （本小题满分12分）函数()()()ln 11ax f x x a x a=+->+. （I ）讨论()f x 的单调性；（II ）设111,ln(1)n n a a a +==+，证明：23+22n a n n <≤+. 【答案】（I ）（i ）当12a <<时，()f x 在()21,2a a --上是增函数，在()22,0a a -上是减函数，在()0,+∞上是增函数；（ii ）当2a =时,()f x 在()1,-+?上是增函数；（iii ）当2a >时，()f x 在是()1,0-上是增函数，在()20,2a a -上是减函数，在()22,a a -+∞上是增函数；（II）详见试题分析．1n k=+时有2333kak k<?++，结论成立．根据（i）、（ii）知对任何n N*Î结论都成立．考点：1．利用导数研究函数的单调性；2．利用数学归纳法证明数列不等式．。

2014年普通高等学校招生全国统一考试(海南卷)

2014年普通高等学校招生全国统一考试（海南卷）物理注意事项：1．本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第I 卷时，选出每小题的答案后，用2B 铅笔在答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第II 卷时，将答案写在答题卡上，写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

第I 卷一、单项选择题：本题共6小题，每小题3分，共18分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．如图，在一水平、固定的闭合导体圆环上方。

有一条形磁铁(N 极朝上， S 极朝下)由静止开始下落，磁铁从圆环中穿过且不与圆环接触，关于圆环中感应电流的方向（从上向下看），下列说法正确的是A ．总是顺时针B ．总是逆时针C ．先顺时针后逆时针D ．先逆时针后顺时针【答案】C【解析】磁铁从圆环中穿过且不与圆环接触，则导体环中，先是向上的磁通量增加，磁铁过中间以后，向上的磁通量减少，根据楞次定律，产生的感应电流先顺时针后逆时针，选项C 正确。

2．理想变压器上接有三个完全相同的灯泡，其中一个与该变压器的原线圈串联后接入交流电源，另外两个并联后接在副线圈两端。

已知三个灯泡均正常发光。

该变压器原、副线圈的匝数之比为A ．1:2B ．2:lC ．2:3D ．3:2【答案】B 【解析】三灯都正常工作，则电流相等，由此可知变压器的原副线圈的电流比1212I I =,对于单匝输入单匝输出的变压器，由于功率相等，12p p =，得1221u I u I =,得：1221u u =，选项A 正确。

3．将一物体以某一初速度竖直上抛。

物体在运动过程中受到一大小不变的空气阻力作用，它从抛出点到最高点的运动时间为t 1，再从最高点回到抛出点的运动时间为t 2，如果没有空气阻力作用，它从抛出点到最高点所用的时间为t 0，则A ．t 1> t 0 t 2< t 1B ．t 1< t 0 t 2> t 1C ．t 2> t 0 t 2> t 1D ．t 1< t 0 t 2< t 1【答案】 B【解析】三种情况的下的匀变速加速度是：12a g a >>，其中，1100a t v gt ==，得01t t >，又上升与下降过程：2211221122a t a t =，得21t t >，选项B 正确。

海南省海口市2014届高三高考调研测试(二) 数学(理)Word版含答案

2014年海口市高考调研测试数学（理科）试题(二)注意事项：1．本次考试的试卷分为试题卷和答题卷，本卷为试题卷，请将答案和解答写在答题卷指定的位置，在试题卷和其它位置解答无效．2．本试卷满分150分，考试时间120分钟．第Ⅰ卷选择题一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的；每小题选出答案后，请用2B 铅笔把机读卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在本卷上作答无效)1．设集合12{|,[1,4]}M y y x x ==∈，2{|log (1)}N x y x ==-，则()R C N M =A ．{|12}x x ≤≤B ．{|14}x x ≤≤C ．{2}x x ≤≤D ．∅ 2，设i 为虚数单位，则满足条件2(2)(1)i z i +=+的复数z 的共轭复数是A ．2455i +B ．2455i --C ．2455i -+D ．2455i -3．设n S 是数列{}n a 的前n 项和，命题p ：{}n a 是等差数列，命题q ：2n S An Bn C =++（,,A B C R ∈），则命题p 是命题q 成立的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．以上都不正确 4．设随机变量(0,1)N ξ，若(1)P p ξ>=，则(10)P ξ-<<= A ．12p + B ．12p - C ．12p - D ．1p - 5．某校派出5名老师去海口市三所中学进行教学交流活动，每所中学至少派一名教师，则不同的分配方案有A ．80种B ．90种C ．120种D ． 150种6．如右图是一个根据△ABC 的三条边的边长,,a b c 判断三角形形状的程序框图，则框图中菱形内应该填写的是( )A ．?a c >B ．?a c <C ．?b c >D ．?b c < 7．等比数列{}n a 的前项和为n S ，8417S S =，352a a =，则68a a =A ．32B ．64C ．128D ．2568．抛物线2x py =与直线10x ay ++=交于A 、B 两点，其中点A 的坐标为(2,1)，设抛物线的焦点为F ，则||||FA FB +等于A ．13 B ．176 C ．289 D ．3199．空间直角坐标系中，△ABC 的三视图如右图所示，已知(0,0,0)A ，(0,2,2)B ，则点C 的坐标是 A ．(0,2,2)- B ．(2,2,2)--C ．(2,0,0)D ．(2,2,2)-10．在区域1{(,)|[1,],[0,]}2c D x y x c y +=∈-∈上随机取一个点(,)P x y ，落在1000x y x y c y -+≥⎧⎪+-≤⎨⎪≥⎩所表示的可行域内的概率值 A ．14 B ．13 C ．12D ．与c 的值有关 11．在△AB C 中，已知16AB AC ⋅=，sin cos sin C A B =，6ABC S ∆=，P 为线段AC 上的点，且BA BC BP xyBABC=+, 则xy 的最大值为A ．4B ．3C ．2D ．112．设球O 是正方体ABCD 1111A B C D -的内切球，若平面1ACD 截球O 所得的截面面积为6π，则球O 的半径为 A ．32B ．3CD 第Ⅱ卷非选择题二、填空题(本大题共4小题，每小题5分，共20分，请把答案填在答题卷中的横线上)．13．计算2|1|x dx -=⎰_________．14．过点(1,1)-的直线与圆2224110x yx y +---=截得的弦长为，则该直线的方程为．15．设角θ为第四象限角,并且角θ的终边与单位圆交于点00(,)P x y ,若0013x y +=-,则cos2θ=_________．16．定义在R 上的运算“⊕”：对实数x 和y ，x y ⊕=(),(),x x y y x y ≥⎧⎨<⎩ 设函数()f x =()222x x +-（第6题图）（第9题图）()22x ⊕-+，x R ∈。

2014海南高考数学线性代数题及答案解析

2014海南高考数学线性代数题及答案解析一、题目解析2014年海南高考数学试卷中，线性代数部分是其中的一个重要部分。

以下是针对该部分题目的解析和答案分析。

1.选择题题目一：已知方程组：\[ \begin{cases} x - y + 2z = 4 \\ 2x + y + kz = 7 \\ 3x + 4y + 5z = 15\end{cases} \]若方程组有唯一解，则实数$k$的取值范围是：解析：首先，我们需要判断方程组的解的情况。

通过计算可知，若行列式的值为零，则方程组无解；若值不为零，则方程组有唯一解。

计算行列式：\[ \begin{vmatrix} 1 & -1 & 2 \\ 2 & 1 & k \\ 3 & 4 & 5 \end{vmatrix} = 31k - 14 \]要使得行列式的值不为零，即解存在，使得\[ 31k - 14 \neq 0 \]所以，$k \neq \frac{14}{31}$。

因此，实数$k$的取值范围是$k \neq \frac{14}{31}$。

题目二：已知二次型\[ f(x,y,z) = 2x^2 + 2y^2 + 2z^2 - 2xy + 2xz - 4yz \]则对于任意的实数$a$，当且仅当$a \geqslant \frac{5}{3}$时，二次型$f(x,y,z)$正定。

解析：对于一个二次型，判断其正定还是负定，需要计算其特征值。

特征值公式为：\[ \begin{vmatrix} 2-\lambda & -1 & 1 \\ -1 & 2-\lambda & -2 \\ 1 & -2 & 2-\lambda \end{vmatrix} = 0 \]计算得到特征方程：\[ (\lambda-1)(\lambda-3)(\lambda-5) = 0 \]所以，该二次型的特征值为$1, 3, 5$。

2014海南省高考试卷含解析试题及答案

1、下列词语中没有错别字的一组是A．透彻频律攻坚战振聋发聩B．通谍竞聘节骨眼锋芒毕露C．精悍杂糅识时务礼尚往来D．坐标博取辨证法大相径庭2、填入下面空缺处的语句，最恰当的一项是我需要清静……最好去处是到个庙宇前小河旁边大石头上坐坐，。

雨季来时上面长了些绿绒似地苔类。

雨季一过，苔已干枯了，在一片未干枯苔上正开着小小蓝花白花，有细脚蜘蛛在旁边爬。

A．阳光和雨露把这石头漂白磨光了 B．这石头被阳光和雨露漂白磨光了C．阳光和雨露已把这石头漂白磨光了的 D．这石头是被阳光和雨露漂白磨光了的3、阅读下文，完成22—26题。

（12分）治学（东汉）徐幹①昔之君子成德立行，身没而名不朽，其故何□？学也。

②学也者，所以疏神达思，怡情理性，圣人之上务也。

民之初载，其矇未知。

譬如宝在于玄室①，有所求而不见，白日照焉，则群物斯辩矣。

学者，心之白日也。

③学犹饰也，器不饰则无以为美观，人不学则无以有懿德。

有懿德，故可以经人伦；为美观，故可以供神明。

④夫听黄钟之声，然后知击缶之细；视衮龙之文，然后知被褐之陋；涉庠序之教，然后知不学之困。

故学者如登山焉，动而益高；如寤寐焉，久而愈足。

顾所由来，则杳然其远，以其难而懈之，误且非矣。

⑤倚立而思远，不如速行之必至也；矫首而徇飞，不如修翼之必获也；孤居而愿智，不如务学之必达也。

故君子心不苟愿，必以求学；身不苟动，必以从师；言不苟出，必以博闻。

⑥君子之于学也，其不懈，犹上天之动，犹日月之行，终身亹亹②，没而后已。

故虽有其才而无其志，亦不能兴其功也。

志者，学之帅也；才者，学之徒也。

学者不患才之不赡，而患志之不立。

是以为之者亿兆，而成之者无几，故君子必立其志。

【注】①玄室：暗室。

②亹亹：勤勉不倦的样子。

22、可填入第①段方框处的虚词是（）（1分）A、兮B、哉C、夫D、矣23、第②段使用了比喻论证的手法，请结合该段内容加以分析。

（3分）24、对第④段画线句理解正确的一项是（）（2分）A、治学不能因为目标过远而松懈。

2014理科数学高考真题与答案(全word收藏版)

2014年普通高等学校招生全国统一考试（广东卷）数学（理科）一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{1,0,1}M =-，{0,1,2}N =，则M N = A.{1,0,1}- B.{1,0,1,2}- C.{1,0,2}- D.{0,1}2．已知复数Z 满足(34)25i z +=，则Z=A.34i -B.34i +C.34i --D.34i -+3．若变量,x y 满足约束条件121y x x y z x y y ≤⎧⎪+≤=+⎨⎪≥-⎩且的最大值和最小值分别为m 和n ，则m n -=A.8B.7C.6D.54．若实数k 满足09k <<，则曲线221259x y k-=-与曲线221259x y k -=-的 A.离心率相等B.虚半轴长相等C.实半轴长相等D.焦距相等5．已知向量()1,0,1a =-，则下列向量中与a 成60︒夹角的是A.（-1,1,0）B.（1,-1,0）C.（0,-1,1）D.（-1,0,1）6．已知某地区中小学生人数和近视情况分别如图1和图2所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2％的学生进行调查，则样本容量和抽取的高中生近视人数分别是A.200,20B.100,20C.200,10D.100，107．若空间中四条两两不同的直线1234,,,l l l l ，满足122334,,l l l l l l ⊥⊥⊥，则下面结论一定正确的是 A.14l l ⊥ B.14//l l C.14,l l 既不垂直也不平行 D.14,l l 的位置关系不确定 8．设集合(){}12345=,,,,{1,0,1},1,2,3,4,5iA x x x x x x i ∈-=，那么集合A中满足条件“1234513x x x x x ≤++++≤”的元素个数为A.60B.90C.120D.130小学初中高中年级 O二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．（一）必做题（9～13题）9．不等式521≥++-x x 的解集为。

2014年高考真题——理科数学(新课标卷Ⅰ)解析版 Word版含答案

2014年高招全国课标1（理科数学word 解析版）第Ⅰ卷一．选择题：共12小题，每小题5分，共60分。

在每个小题给出的四个选项中，只有一项是符合题目要求的一项。

1.已知集合A={x |2230x x --≥}，B={}22x x -≤<，则A B ⋂=A .[-2,-1]B .[-1,2）C .[-1,1]D .[1,2）【答案】：A【解析】：∵A={x |2230x x --≥}={}13x x x ≤-≥或，B={}22x x -≤<， ∴A B ⋂={}21x x -≤≤，选A..2.32(1)(1)i i +-= A .1i + B .1i - C .1i -+ D .1i --【答案】：D【解析】：∵32(1)(1)i i +-=2(1)12i i i i+=---，选D..3.设函数()f x ，()g x 的定义域都为R ，且()f x 是奇函数，()g x 是偶函数，则下列结论正确的是A .()f x ()g x 是偶函数B .|()f x |()g x 是奇函数C .()f x |()g x |是奇函数D .|()f x ()g x |是奇函数【答案】：C【解析】：设()()()F x f x g x =，则()()()F x f x g x -=--，∵()f x 是奇函数，()g x 是偶函数，∴()()()()F x f x g x F x -=-=-，()F x 为奇函数，选C.4.已知F 是双曲线C ：223(0)x my m m -=>的一个焦点，则点F 到C 的一条渐近线的距离为A B .3 C D .3m【答案】：A【解析】：由C ：223(0)x my m m -=>，得22133x y m -=，233,c m c =+=设)F，一条渐近线y x =，即0x =，则点F 到C 的一条渐近线的距离d = A. .5.4位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率A .18B .38C .58D .78【答案】：D【解析】：4位同学各自在周六、周日两天中任选一天参加公益活动共有4216=种，周六、周日都有同学参加公益活动有两种情况：①一天一人一天三人有11428C A =种；②每天2人有246C =种，则周六、周日都有同学参加公益活动的概率为867168+=；或间接解法：4位同学都在周六或周日参加公益活动有2种，则周六、周日都有同学参加公益活动的概率为1627168-=；选D.6.如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示为x 的函数()f x ，则y =()f x 在[0,π]上的图像大致为【答案】：B【解析】：如图：过M 作M D ⊥OP 于Ｄ，则 PM=sin x ，OM=cos x ,在Rt OMP ∆中，MD=cos sin 1x xOM PM OP =cos sin x x = 1sin 22x =，∴()f x 1sin 2(0)2x x π=≤≤，选B. .7.执行下图的程序框图，若输入的,,a b k 分别为1,2,3，则输出的M =A .203 B .165 C .72 D .158【答案】：D【解析】：输入1,2,3a b k ===；1n =时：1331,2,222M a b =+===； 2n =时：28382,,3323M a b =+===；3n =时：3315815,,28838M a b =+===；4n =时：输出158M = . 选D.8.设(0,)2πα∈，(0,)2πβ∈，且1sin tan cos βαβ+=，则 A .32παβ-=B .22παβ-=C .32παβ+=D .22παβ+=【答案】：Ｂ【解析】：∵sin 1sin tan cos cos αβααβ+==，∴sin cos cos cos sin αβααβ=+ ()sin cos sin 2παβαα⎛⎫-==- ⎪⎝⎭，,02222ππππαβα-<-<<-<∴2παβα-=-，即22παβ-=，选B9.不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .有下面四个命题：1p ：(,),22x y D x y ∀∈+≥-，2p ：(,),22x y D x y ∃∈+≥, 3P ：(,),23x y D x y ∀∈+≤，4p ：(,),21x y D x y ∃∈+≤-.其中真命题是A .2p ，3PB .1p ，4pC .1p ，2pD .1p ，3P【答案】：C【解析】：作出可行域如图：设2x y z +=，即122zy x =-+，当直线过()2,1A -时，min 220z =-+=，∴0z ≥，∴命题1p 、2p 真命题，选C.10.已知抛物线C ：28y x =的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个交点，若4FP FQ =，则||QF =A .72 B .52C .3D .2 【答案】：C【解析】：过Q 作Q M ⊥直线L 于M ，∵4FP FQ = ∴34PQ PF=，又344QM PQ PF ==，∴3QM =，由抛物线定义知3QF QM == 选C11.已知函数()f x =3231ax x -+，若()f x 存在唯一的零点0x ，且0x ＞0，则a 的取值范围为A .（2，+∞）B .（-∞，-2）C .（1，+∞）D .（-∞，-1）【答案】：B【解析1】：由已知0a ≠，2()36f x ax x '=-，令()0f x '=，得0x =或2x a=，当0a >时，()22,0,()0;0,,()0;,,()0x f x x f x x f x a a ⎛⎫⎛⎫'''∈-∞>∈<∈+∞> ⎪ ⎪⎝⎭⎝⎭；且(0)10f =>，()f x 有小于零的零点，不符合题意。

海南省2014年高考模拟检测题理科数学详解

海南省2014年高考模拟检测题理科数学（一）1、解析：230,x x -≥≤则M={x 同时对于N 集合根据指数函数3x y =的单调性有3333,31x x -≤≤-≤≤，因此阴影部分为(){|1M C M N x x ⋂=< 2、解析：考察相等复数及运算5(2)12,1, 3.2(2)(2)i ai b b i a b a b i i +-=+=++==-+=--+3、解析：简单的程序框图，tan()3π-=4、解析：考察向量的数量积运算由,0a b a b ⊥⋅=则2212121122(23)(4)2(38)12e e ke e ke k e e e +⋅-=+-⋅-，16k = 5、解析：数形结合，首先排除k 取负数的情况（带入特殊点(0,1)检验），当0k =时所围成的面积大于16、解析：由n k S S ≤，转化为求等差数列前n 项和的最大值，由已知14725899....(1),93. (2)a a a a a a ++=++=，(2)(1)36,2,d d -==-=-带入（1）解得412,0,20.5n n a n a n =-≥≤令即则前20项和最大7、解析：对于A ，由于原命题为真，因此逆否命题一定为真，对于B ，σ方差越大，表示总体分布越分散，对于C 命题的否定要将结论否定，即2,10x R x x ∀∈++≥，对于D ，应为充分不必要条件（注意充分必要判断时的条件与结论）8、解析：考察定积分与几何概型，21132131200211||333x S S x dx x x =-=-=-=⎰阴因此13S P S ==阴正 9、解析：考察两角和差公式，30,2444ππππαα<<<+<结合1cos()043πα+=>有sin()43πα+=，同时0,0,2422244ππβπβππβ-<<-<<-<-<-有sin()243βπ-=-cos()cos[()()]24249βπβπαα+=++-= 10、解析：如图建立坐标系，根据正六边形的性质，设抛物线方程为22y px =抛物线上两个点分别为(,1)(a a 带入方程有21,2(4pa p a ==相除解得32a p ==11、解析：考察了复合函数求导及数形结合，函数有四个极值点，根据极值点处导数为零'()sin x f x x e ωωω-=-+令'()0,sin 0sin 0x x f x x e x ωωωω--=-+=-=即，e 转化为两函数()x f x e ω-=与g(x)=sin x 在[0,2]π上正好有四个交点，结合图像看只需要满足33222,222T T Tππω≤≤≤=≤ 12、解析：已知1cos 3023,sin 3012AB AC AB AC S AB AC ⋅====，因此12x y +=，所以141442()()2(5)2(518y x x y x y x y x y +=++=++≥+= 13、解析：根据三视图（注意虚线部分），可判断原几何体为一个长方体内挖掉一个半球，因此体积为1422214233V V ππ-=⨯⨯-=-长半球 14、解析：考察二项式展开式（采用特殊值法），令00,1x a ==，令0120131,...1x a a a =+++=-，又由于所求0102020130012013()()...()2012(...)2011a a a a a a a a a a ++++++=++++= 15、解析：由于线性回直线过样本中心点(,)x y ，有已知得42353.54x +++==带入回归方程有42y =，因此49395442,264a a +++==16、解析：由于曲线关于y 轴对称，因此只考虑右半部分，由已知得22225161717x y x y +=+，分类讨论，当0,0x y >>时， 22225162,1717x y xy xy xy +=+≥存在最大值（舍去）同理当22225160,0,2,1717x y x y xy xy xy ><+=+≥-存在最小值（当且仅当x y =-）带入原方程有：2225350x == 17、解析：（1）由于11222222n n n n n n n a a -+-==⋅-=-且122n n a a ==因此，则n n b na =因此121231*********...(1)22.....(1)21222...(1)22 (2)(2)(1):22....22222n n n n n n n n n n n S n n S n n S n n -++++=⋅+⋅++-⋅+⋅=⋅+⋅++-⋅+⋅-=----+⋅=-+⋅（2）110,12n n n kn b k b c c n k ++--+-=><-若前8项递增，则只需要保证71bk<-即可，则由已知条件知126k b k --≤<-，则1,2k =，分类讨论当1k =，13,12....7b =---七个取值当2,14,13k b ==--两个取值，因此满足条件的数列{}n c 个数为90 18、解析：(1)根据题意面试调题分三类：两次B 类，一次A 一次B ，两次A 类，X 的分布列如下：(2)由（1）得分布列为则()(1)(2)1424E X n n n n =++++=+ 19、解析：采用空间直角坐标系法：（1）以B 为原点，1B B 所在直线为Z 轴，BC 所在直线为Y 轴建立直角坐标系则可得：10,0,40B O A E （）（）（）（，）因此有：12,42000BO OA OE -=（0,2）,=（-2，，）,=（，）则：11BO OA BO OE ⋅⋅=0,,=0且OA OE ⊂⊂平面AEO ,平面AEO 则1B ⊥O 平面AEO(2)设平面AEO 的法向量为(,,)n x y z =根据已知条件(sin cos ,0),(sin ,cos ,0)A OA θθθθ= 由sin cos 00200x y n OA z n OE θθ⎫+=⎧⋅=⎪⎪⇒⎬⎨+=⎪⋅=⎪⎩⎭令2z =则2(,tan n θ=由于直线与平面所成夹角11sinn B On B Oα⋅===由于3[,]64ππθ∈结合正切函数图像可知当minsin624ππθθααα==时，tan最小，同时有最小值sin=20、解析：（1）由已知得B所以22:C x=，又(8,8P设21:2C y px=带入点得：P=8，即21:16C y x=同时216a=椭圆方程为221162x y+=（2）由于直线OP方程为y=因此设动直线方程为y x b=+联立22222581601162y x bx bx y⎧=-+⎪⎪⇒-+-=⎨⎪+=⎪⎩要保证动直线与椭圆交于不同两点则22)45(816)0,b b∆=-⨯-><<设两个交点分别为1122(,)(,)M x y N x y则221212128168,,555b bx x x x y y--+===因此21212121)2(91614)5QM QN x x x x y y b b⋅=++++=+-所以当838,99b QM QN=-⋅-取得最小值21、解析：（I）复合函数求导：22'[(ln(1))]'2ln(1)[ln(1)]'ln(1)1y x x x xx=+=++=++因此'(0)0f=且切点为(0,0)则切线方程为0y=22、解析：（1）连结BE ，AE 为直径，则90ABE ∠=又ACB AEB ∠=∠且90ADC ∠=因此,AC ADRt AEBRt ACD AC AB AD AE AE AB=⋅=⋅即又AB=BC 因此AC BC AD AE ⋅=⋅（2）由于FC 为切线FB 为割线，因此22649FC FA FB FB FB =⋅=⋅=，，，AB=5 又弦切角ACF ABC ∠=∠，因此510,463AC BC AC ACF CBF AC AF CF ∆∆===，， 23、解析：（1）考察极坐标与直角坐标的转化及参数方程与一般方程的转化222cos 2cos sin 2sin sin y x θθρρθθθ=⇒=⇒= （2）结合参数方程的意义可知：对应的直线方程为1()2y k x =-（过抛物线的焦点）设直线与抛物线的交点为1122(,)(,)A x y B x y 根据抛物线性质有121AB x x =++因此联立直线与抛物线方程组：222222(2)014()2y xk k x k x y k x ⎧=⎪⇒-++=⎨=-⎪⎩则2122222112k AB x x k k+=++=+=+则最小值为2，此时直线与X 轴垂直 24、解析：（1）22220,224x a x x a x x ax a x +-≤+≤⇒++≤化简得：22320x ax a --≥()(3)0(3a x a x a x a x -+≥⇒≤≥-舍去）或又{2}2,63aM x x a ⊆≥⇒-≥≤- （2）当6a =-，()62f x x x =--去掉绝对值得：6(6)()63(6)x x f x x x --≥⎧=⎨-<⎩最大值为(1)3f =。

2014海南省高考试卷含解析(必备资料)

1、下列各句中，加点的词语运用不正确的一项是（）A．在席卷全球的金融危机中，连那些科班出身的经济学博士都被赶出华尔街，到地铁卖热狗去了，何况他这个半路出家的？B．在外打拼数十年后，他回到了家乡，用省吃俭用的结余捐建了一所希望小学，为发展当地的教育事业奉献了拳拳爱心。

C．长期以来，杀虫剂、除草剂、增效剂等各种农药所导致的污染，严重侵害着与农业、农村、农民息息相关的城市环境与市民生活。

D．在热心公益蔚然成风的今天，百名青年在某市首届成人礼活动中，以无偿献血作为自己成长的见证，体现了当代青年的责任感。

2、下列词语中加点的字，每对读音都不相同的一组是A．棱角/菱形窒息/对峙稽首/稽查B．侥幸/阻挠绚烂/驯服称职/职称C．塑料/朔风叫嚣/发酵本末倒置/倒行逆施D．延伸/筵席瓦砾/罹难挑三拣四/挑拨离间3、下列词语中，字形和加点字的读音全都正确的一组是A．亲和力声名鹊起闹别（biâ）扭称（chēng）心如意B．倒胃口皇天后土瞭（liǎo）望哨金蝉脱壳（qiào）C．哈蜜瓜明眸皓齿撑（chēng）场面姹（chà）紫嫣红D．敞篷车异彩纷呈差（chà）不多白雪皑皑（ái）4、依次填入下面语段横线处的词语，最恰当的一组是散文能够真正地见出一位作家的个性和__________。

阅读散文，我们能体味到鲁迅的________，冰心的________，梁实秋的幽默机智，丰子恺的清雅淡泊。

“情”是散文的命脉和灵魂，对于散文的“情”来说，真挚_________。

A．情趣冷峻深沉温和娴雅至关重要B．情趣冷峭深沉冲淡平和至关重要C．情调冷峭阴沉温和娴雅举足轻重D．情调冷峻深沉冲淡平和举足轻重5、依次填入下面一段文字横线处的语句，前后衔接最为恰当的一组是中国人民抗日战争的胜利，充分证明了中国共产党是救亡图存、实现民族复兴的核心力量。

今天，我们纪念抗日战争胜利70周年，就是要_________，_________，_________，_________，_________。

海南2014高考数学卷(带解析)

海南2014高考数学卷(带解析)海南2014高考数学卷(带解析)导言：海南2014年高考数学卷是历年来高考数学卷中的一份，本文将对该数学卷进行解析，帮助考生们更好地理解和应对高考数学题型和解题方法。

一、选择题部分：选择题部分是高考数学卷中的必答题部分，共有25个小题，每题4分，总分100分。

该部分主要考察考生对基础数学概念和运算符号的理解能力，以及对数学思维和逻辑推理的运用。

1. 若二项式(x+1)^3的展开结果为ax^3+bx^2+cx+d，则abcd的和为多少？解析：根据二项式展开的公式，展开后的二项式共有4个项，分别为x^3、3x^2、3x、1。

根据对应项之间的系数，将abcd的值代入进去，可得：a=1，b=3，c=3，d=1。

所以，abcd的和为1+3+3+1=8。

2. 设集合A={x | -1 ≤ x ≤ 4}，集合B={x | 1 ≤ x ≤ 6}，则集合A∪B的区间表示为（）。

解析：根据集合并运算的定义，集合A∪B表示的是同时属于集合A或属于集合B的元素的集合。

根据题目给出的区间表示，集合A中的元素为[-1, 4]，集合B中的元素为[1, 6]。

将两个区间合并，得到集合A∪B的区间表示为[-1, 6]。

3. 已知a，b是锐角三角形ABC的两个内角的正弦值，且a＞b，则下列结论错误的是（）。

A. sinA＞sinBB. cosA＞cosBC. tanA＞tanBD. cotA＞cotB解析：由题目可知，a，b是锐角三角形ABC两个内角的正弦值，且a＞b。

根据正弦函数的性质，可得sinA＞sinB。

所以，选项A是正确的。

根据余弦函数和正切函数的性质，cosA＞cosB，tanA＞tanB，cotA＞cotB。

所以，选项B、C、D均是正确的。

因此，下列结论错误的选项为A。

二、解答题部分：解答题部分是高考数学卷中的开放性问题部分，共有5个小题，每题12分，总分60分。

该部分主要考察考生的数学应用能力，解决实际问题的能力。

2014年海南省高考理科数学试卷及答案解析(word版)

第Ⅰ卷
一．选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合题目要求的。（1）设集合 M 0,1, 2 ， N = x x 2 3 x 2 0 ，则 M N (A) 1 (B)
2
(C)
0,1
(D) 1, 2
解析：∵ N = x x 2 3 x 2 0 x 1 x 2 ，∴ M N 1, 2 答案：D （2）设复数 z1 ， z2 在复平面内的对应点关于虚轴对称， z1 2 i ，则 z1 z2 (A) 5 (B) 5 (C) 4 i (D) 4 i
0.6 0.8 0.75
答案：A （6）如图，网格纸上正方形小格的边长为 1（表示 1cm），图中粗线画出的是某零件的三视图，该零件有一个底面半径为 3cm，高为 6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为 (A) (C)
17 27 10 27
(B) (D)
5 9 1 3
答案：C
第Ⅱ卷
本卷包括必考题和选考题两部分。第 13 题～第 21 题为必考题，每个试题考生都必须做答。第 22 题～第 24 题为选考题，考生根据要求做答。二．填空题：本大题共 4 小题，每小题 5 分。（13） ( x a )10 的展开式中， x 7 的系数为 15 ，则 a ．（用数字填写答案）
由弦长公式得 | AB | (1 k 2 )[( x1 x2 ) 2 4 x1 x2 ] 12
由点到直线的距离公式得： O 到直线 AB 的距离 d
|
3 3 00 | 3 4 3 8 3 ( ) 2 (1) 2 3
1 3 9 ∴ S OAB 12 2 8 4

海南省海口市2014届高三高考调研测试(二)数学(理)Word版含答案

15 12
[45, 55)
10 5
[55, 65)
5 2
[65, 75)
5 1
（Ⅰ）由以上统计数据填写下面 2 2 列联表并回答是否有 99%的把握认为月收入以 5500元为分界点对
“国五条”的态度有差异；
月收入不低于 5500元的人数月收入低于 5500元的人数合计
赞成
a
c
不赞成
b
d
合计
参考公式： K 2
B． { x |1 x 4}
C． { x | 2 x 2}
D．
2，设 i 为虚数单位，则满足条件 (2 i ) z (1 i )2 的复数 z 的共轭复数是
A． 2
4 i
55
B．
2
4 i
55
C． 2
4 i
55
D． 2
4 i
55
3．设 Sn 是数列 { an} 的前 n 项和，命题 p ：{ an } 是等差数列，命题 q ： Sn An 2 Bn C（ A, B, C R ），
1 ,则
3
16．定义在 R 上的运算“ ”：对实数 x 和 y ， x y
x ( x y), 设函数 f x
y ( x y),
x2 2x 2
x2 2 ， x R 。若函数 f x a 的图像与直线 y 1 恰有两个公共点，则实数 __________ ．
a 的取值范围是
三、解答题（本大题共 6 个小题，共 70 分，解答应写出文字说明、证明过程或演算步骤
2
13．计算 | x 1| dx _________ ．
0
14．过点 ( 1,1)的直线与圆 x2 y2 2 x 4 y 11 0 截得的弦长为 4 3 ，则该直线的方程为

2014年高考海南卷理数

2014年普通高等学校招生全国统一考试理科（新课标卷二Ⅱ 海南卷）第Ⅰ卷一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合M=｛0,1,2｝，N={}2|320x x x -+≤，则M N ⋂=( ) A. ｛1｝B. ｛2｝C. ｛0，1｝D. ｛1，2｝2.设复数1z ，2z 在复平面内的对应点关于虚轴对称， 12z i =+，则12z z =（） A. - 5B. 5C. - 4+ iD. - 4 - i3.设向量a,b 满足|a+b|a-b，则a ⋅b = ( ) A. 1B. 2C. 3D. 54.钝角三角形ABC 的面积是12，AB=1，，则AC=( )A. 5B.C. 2D. 15.某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（） A. 0.8 B. 0.75 C. 0.6 D. 0.456.如图，网格纸上正方形小格的边长为1（表示1cm ）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（）A. 1727B. 59C. 1027D. 137.执行右图程序框图，如果输入的x,t 均为2，则输出的S=（）A. 4B. 5C. 6D. 78.设曲线y=a x-ln(x+1)在点(0,0)处的切线方程为y=2x ，则a =（）A. 0B. 1C. 2D. 39.设x,y 满足约束条件70310350x y x y x y +-⎧⎪-+⎨⎪--⎩≤≤≥，则2z x y =-的最大值为（）A. 10B. 8C. 3D. 210.设F 为抛物线C:23y x =的焦点，过F 且倾斜角为30°的直线交C 于A,B 两点，O 为坐标原点，则△OAB 的面积为（）A.B.C. 6332D. 9411.直三棱柱ABC-A 1B 1C 1中，∠BCA=90°，M ，N 分别是A 1B 1，A 1C 1的中点，BC=CA=CC 1，则BM 与AN 所成的角的余弦值为（） A. 110 B. 25C.D.12.设函数()x f x m π=.若存在()f x 的极值点0x 满足()22200x f x m +<⎡⎤⎣⎦，则m 的取值范围是（）A. ()(),66,-∞-⋃∞B. ()(),44,-∞-⋃∞C. ()(),22,-∞-⋃∞D.()(),14,-∞-⋃∞第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题，每个试题考生必须做答.第22题~第24题为选考题，考生根据要求做答. 二.填空题13.()10x a +的展开式中，7x 的系数为15，则a =________.(用数字填写答案) 14.函数()()()sin 22sin cos f x x x ϕϕϕ=+-+的最大值为_________.15.已知偶函数()f x 在[)0,+∞单调递减，()20f =.若()10f x ->，则x 的取值范围是__________.16.设点M （0x ,1），若在圆O:221x y +=上存在点N ，使得 ∠OMN=45°，则0x 的取值范围是________.三.解答题：解答应写出文字说明，证明过程或演算步骤. 17.（本小题满分12分）已知数列{}n a 满足1a =1，131n n a a +=+.（Ⅰ）证明{}12n a +是等比数列，并求{}n a 的通项公式；（Ⅱ）证明：1231112na a a ++<…+.18. （本小题满分12分）如图，四棱锥P-ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点. （Ⅰ）证明：PB ∥平面AEC ；（Ⅱ）设二面角D-AE-C 为60°，AP=1，求三棱锥E-ACD 的体积.19. （本小题满分12分）某地区2007年至2013年农村居民家庭纯收入y （单位：千元）的数据如下表：（Ⅰ）求y 关于t 的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入. 附：回归直线的斜率和截距的最小二乘法估计公式分别为：()()()121nii i ni i tty y b t t ∧==--=-∑∑，ˆˆay bt =-20. （本小题满分12分）设1F ,2F 分别是椭圆()222210y x a b a b+=>>的左右焦点，M 是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N.（Ⅰ）若直线MN 的斜率为34，求C 的离心率；（Ⅱ）若直线MN 在y 轴上的截距为2，且15MN F N =，求a,b .21. （本小题满分12分）已知函数()f x =2x x e e x --- （Ⅰ）讨论()f x 的单调性；（Ⅱ）设()()()24g x f x bf x =-，当0x >时，()0g x >,求b 的最大值；（Ⅲ）已知1.4142 1.4143<<，估计ln2的近似值（精确到0.001）请考生在第22、23、24题中任选一题做答，如果多做，同按所做的第一题计分，做答时请写清题号.22.（本小题满分10）选修4—1：几何证明选讲如图，P 是O 外一点，PA 是切线，A 为切点，割线PBC与O 相交于点B ，C ，PC=2PA ，D 为PC 的中点，AD 的延长线交O 于点E.证明：（Ⅰ）BE=EC ；（Ⅱ）AD ⋅DE=22PB23. （本小题满分10）选修4-4：坐标系与参数方程在直角坐标系xoy 中，以坐标原点为极点，x 轴为极轴建立极坐标系，半圆C 的极坐标方程为2cos ρθ=，0,2πθ⎡⎤∈⎢⎥⎣⎦.（Ⅰ）求C 的参数方程；（Ⅱ）设点D 在C 上，C 在D 处的切线与直线:2l y =+垂直，根据（Ⅰ）中你得到的参数方程，确定D 的坐标.24. （本小题满分10）选修4-5：不等式选讲设函数()f x =1(0)x x a a a++->（Ⅰ）证明：()f x ≥2；（Ⅱ）若()35f <，求a 的取值范围.。