八年级数学下册 2_6_1《菱形的性质》导学案(无答案)(新版)湘教版
八年级数学下册 2.6.1《菱形的性质》导学案(新版)湘教版

八年级数学下册 2.6.1《菱形的性质》导学案(新版)湘教版2、6、1菱形的性质教学目标:1、掌握菱形概念,知道菱形与平行四边形的关系、2、理解并掌握菱形的定义及性质1、2;会用这些性质进行有关的论证和计算,会计算菱形的面积、3、通过运用菱形知识解决具体问题,提高分析能力和观察能力、4、根据平行四边形与矩形、菱形的从属关系,通过画图渗透集合思想、学习重点:菱形的性质1、2、学习难点:菱形的性质及菱形知识的综合应用、学习内容:一、忆一忆1、什么叫做平行四边形?2、什么叫矩形?3、平行四边形和矩形之间的关系是什么?二、探一探1、我们已经学习了一种特殊的平行四边形矩形,其实还有另外的特殊平行四边形,请看下面的演示:改变平行四边形的边,使之一组邻边相等,从而引出菱形概念、2、菱形定义:、【强调】菱形(1)是平行四边形;(2)一组邻边相等、3、阅读教材P65页探究:菱形是轴对称图形吗?如果是,那么它有几条对称轴?对称轴之间有什么位置关系?你能看出图中哪些线段或角相等?ACBD4、菱形的性质1:菱形的性质2:菱形性质1证明:菱形性质2证明:5、(阅读教材P67页上面一段内容)比较菱形的对角线和一般平行四边形的对角线你会发现什么?你能利用菱形的对角线求菱形的面积吗?如果菱形的两条对角线长分别是a和b,计算菱形的面积S。
三、练一练1、教材P67练习:2、已知:如图,四边形ABCD是菱形,F是AB上一点,DF 交AC于E、求证:∠AFD=∠CBE、三、反馈:1、若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为、2、已知菱形的两条对角线分别是6cm和8cm ,求菱形的周长和面积、3、已知菱形ABCD的周长为20cm,且相邻两内角之比是1∶2,求菱形的对角线的长和面积、4、已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF、求证:∠AEF=∠AFE、5、菱形ABCD中,∠D∶∠A=3∶1,菱形的周长为8cm,求菱形的高、6、如图,四边形ABCD是边长为13cm的菱形,其中对角线AC长10cm。
新湘教版八年级下册数学 《菱形的判定》导学案1

2.6.2 菱形的判定一:复习:菱形有哪些特殊性质?1.边:__________________________;______________________________2.角:__________________________;______________________________3.对角线:_____________________________;___________________________________ 二:学习新知目标一:会用菱形的定义判定一个四边形是否是菱形,并会用该种方法进行有关的证明.1. (菱形的判定方法一)菱形的定义:有 的 叫做菱形.2.用符号语言可以表示为:∵四边形ABCD 是 四边形 ∵ ___ =____, ∴□ ABCD 是菱形3.如图在△ABC 中,AD 平分∠BAC 交BC 于D 点,过D 作DE ∥AC 交AB 于E 点, 过D 作DF ∥AB 交AC 于F 点.求证:(1)四边形AEDF 是平行四边形(2)∠2﹦∠3(3)四边形AEDF 是菱形321FED C B A目标二:探究并掌握菱形的判定方法二1.自学68页动脑筋2.你能发现四边形是菱形吗?3.(猜想)四边相等的四边形ABCD 是一个_____形.4.(证明)利用上图证明:“四边相等的四边形是菱形”已知:如上图,在四边形_______中,____=____=____=____求证:四边形ABCD是_____.证明:5.(总结)由上写出菱形的判定方法二:_______ .利用上图用符号语言表示为:在四边形ABCD中,∵____=____=____=____ ∴四边形ABCD是形目标三:探究并掌握菱形的判定方法三自学69页“动脑筋”,利用自制的学具探究菱形的判定方法并完成下面各题1.由“在一长一短的木条中点处固定一个小钉”可知:= ,=∴四边形ABCD是四边形2.转动十字,当∠_____= °时即___ ⊥ ___时,四边形变成了菱形.3. (猜想)对角线互相____ 的平行四边形是菱形.4.请利用下图证明你的猜想:已知:如图,在□ABCD中,AC和BD是对角线,并且AC⊥BD于点O,求证:□ABCD 是菱形.O D CBA5.总结写出菱形判定方法三:利用上图用符号语言可以表示为:∵四边形ABCD是平行四边形,∵AC___BD,∴□ABCD是菱形目标四:利用菱形判定方法进行计算和证明1.自学68页例2、69页例3,完成下题“在□ABCD中,对角线AC和BD相交于点O,并且AB=9,OB=6,OA.求证:(1)AC⊥BDD(2)□ABCD 是菱形吗?说说你的理由.(3)求四边形ABCD 的面积.OD C BA2.判断题,对的画“√”错的画“×”(1).对角线互相垂直的四边形是菱形( )(2).一条对角线垂直另一条对角线的四边形是菱形( )(3)..对角线互相垂直且平分的四边形是菱形( )(4).对角线相等的四边形是菱形( )三:小结:菱形的常用判定方法四:拓展延伸1.如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD 是菱形吗? 求证:(1)四边形ABCD 是平行四边形(2) 过A 作AE ⊥BC 于E 点, 过A 作AF ⊥CD 于F .用等积法说明BC =CD .(3) 求证:四边形ABCD 是菱形.A B CDE F2.已知:如图,顺次连接矩形ABCD 各边中点,得到四边形EFGH ,求证:四边形EFGH 是菱形。
湘教版数学八年级下册2.6.1《菱形的性质》教学设计

湘教版数学八年级下册2.6.1《菱形的性质》教学设计一. 教材分析《菱形的性质》是湘教版数学八年级下册第2章第6节的内容,本节课主要让学生掌握菱形的性质,包括菱形的四条边相等,对角线互相垂直平分,以及菱形是轴对称图形和中心对称图形等。
这些性质是学生进一步学习几何图形的基础,对于提高学生的空间想象能力和逻辑思维能力具有重要意义。
二. 学情分析学生在学习本节课之前,已经掌握了矩形、平行四边形的性质,具备了一定的几何图形基础。
但是,对于菱形的性质,学生可能较为陌生,需要通过实例和动手操作来理解和掌握。
同时,学生对于轴对称和中心对称的概念可能还不太熟悉,需要在教学中进行强化。
三. 教学目标1.知识与技能目标:让学生掌握菱形的性质,能够运用菱形的性质解决一些简单问题。
2.过程与方法目标:通过观察、操作、推理等过程,培养学生的空间想象能力和逻辑思维能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养学生的团队合作意识和探究精神。
四. 教学重难点1.重点:菱形的性质及证明。
2.难点:菱形性质在实际问题中的应用。
五. 教学方法1.采用问题驱动的教学方法,引导学生主动探究菱形的性质。
2.运用多媒体辅助教学,展示菱形的动态变化,增强学生的空间想象能力。
3.采用分组合作、讨论交流的形式,培养学生的团队合作意识和沟通能力。
4.通过实例分析,让学生学会运用菱形的性质解决实际问题。
六. 教学准备1.准备多媒体课件,包括菱形的图片、动画等。
2.准备纸质菱形模型,供学生操作观察。
3.准备一些与菱形相关的实际问题,用于巩固练习。
七. 教学过程1.导入(5分钟)利用多媒体展示一些生活中的菱形图案,如蜂巢、骰子等,引导学生关注菱形的存在。
提问:你们对这些菱形有什么观察和认识?2.呈现(10分钟)通过PPT呈现菱形的性质,包括四条边相等、对角线互相垂直平分、轴对称和中心对称等。
同时,配合动画演示,让学生直观地感受菱形的性质。
3.操练(10分钟)学生分组合作,利用纸质菱形模型进行操作。
2020年春湘教版八年级数学下册教案 2.6.1 菱形的性质

2.6 菱 形2.6.1 菱形的性质1.掌握菱形的定义和性质;(重点) 2.掌握菱形面积的求法;(重点)3.灵活运用菱形的性质解决问题.(难点)一、情境导入将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?这就是另一类特殊的平行四边形,即菱形.二、合作探究探究点一:菱形的性质【类型一】 利用菱形的性质证明线段相等如图,四边形ABCD 是菱形,CE⊥AB 交AB 的延长线于E ,CF ⊥AD 交AD 的延长线于F .求证:CE =CF.解析:连接AC ,根据菱形的性质可得AC 平分∠DAE ,再根据角平分线的性质可得CE =FC .证明:连接AC ,∵四边形ABCD 是菱形,∴AC 平分∠DAE ,∵CE ⊥AB ,CF ⊥AD ,∴CE =FC .方法总结:关键是掌握菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;角平分线的性质:角的平分线上的点到角的两边的距离相等.【类型二】 利用菱形的性质进行有关的计算如图,O 是菱形ABCD 对角线AC与BD 的交点,CD =5cm ,OD =3cm ;过点C 作CE ∥DB ,过点B 作BE ∥AC ,CE 与BE 相交于点E .(1)求OC 的长;(2)求四边形OBEC 的面积.解析:(1)在直角△OCD 中,利用勾股定理即可求解;(2)先证明四边形OBEC 为矩形,再利用矩形的面积公式即可直接求解.解:(1)∵四边形ABCD 是菱形,∴AC ⊥BD .在直角△OCD 中,OC =CD 2-OD 2=52-32=4(cm);(2)∵CE ∥DB ,BE ∥AC ,∴四边形OBEC 为平行四边形,又∵AC ⊥BD ,即∠COB =90°,∴平行四边形OBEC 为矩形,∵OB =OD =4cm ,∴S 矩形OBEC =OB ·OC =4×3=12(cm 2).方法总结:菱形的对角线互相垂直,则菱形对角线将菱形分成四个直角三角形,所以可以利用勾股定理解决一些计算问题.【类型三】运用菱形的性质解决探究性问题已知:如图①,在菱形ABCD中,AB=BD,点E、F分别在边AB、AD上.若AE=DF,易知△ADE≌△DBF.探究:如图②,在菱形ABCD中,AB=BD,点E、F分别在BA、AD的延长线上.若AE=DF,△ADE与△DBF是否全等?如果全等,请证明;如果不全等,请说明理由.拓展:如图③,在▱ABCD中,AD=BD,点O是AD边的垂直平分线与BD的交点,点E、F分别在OA、AD的延长线上.若AE=DF,∠ADB=50°,∠AFB=32°,求∠ADE的度数.解析:探究:△ADE和△DBF全等,利用菱形的性质首先证明三角形ABD为等边三角形,再利用全等三角形的判定方法即可证明△ADE≌△DBF;拓展:因为点O在AD的垂直平分线上,所以OA=OD,再通过证明△ADE≌△DBF,利用全等三角形的性质即可求出∠ADE的度数.解:探究:△ADE和△DBF全等.∵四边形ABCD是菱形,∴AB=AD.∵AB=BD,∴AB=AD=BD.∴△ABD为等边三角形.∴∠DAB=∠ADB=60°.∵AE=DF,∴△ADE≌△DBF;拓展:∵点O在AD的垂直平分线上,∴OA=OD.∴∠DAO=∠ADB=50°.∴∠EAD=∠FDB.∵AE=DF,AD=DB,∴△ADE≌△DBF.∴∠DEA=∠AFB=32°.∴∠EDA=50°-32°=18°.方法总结:本题考查了菱形的性质、等边三角形的判定和性质以及全等三角形的判定和性质,比较综合,但难度不大,一定要熟悉相关的基础知识,才能更快地解决问题.探究点二:菱形的面积已知菱形ABCD中,对角线AC与BD相交于点O,∠BAD=120°,AC=4,则该菱形的面积是()A.16 3 B.8 3C.4 3 D.8解析:∵四边形ABCD是菱形,∴AB=BC,OA=12AC=2,OB=12BD,AC⊥BD,∠BAD+∠ABC=180°,∵∠BAD=120°,∴∠ABC=60°,∴△ABC是等边三角形,∴AB=AC=4,∴OB=AB2-OA2=42-22=23,∴BD=2OB=43,∴菱形ABCD的面积=12AC·BD=12×4×43=83;故选B.方法总结:菱形的面积为两对角线长的积的一半,菱形的对角线平分对角.三、板书设计1.菱形的性质菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.2.菱形的面积S菱形=边长×对应高=12ab(a,b分别是两条对角线的长)通过折纸活动让学生主动探索菱形的性质,大多数学生能全部得到结论,少数的我们加以引导.在整个新知生成过程中,这个活动起了重要的作用.学生始终处于观察、比较、概括、总结和积极思维的状态,切身感受到自己是学习的主人.为学生今后获取知识、探索发现和创造打下了良好的基础,更增强了敢于实践,勇于探索,不断创新和努力学习数学知识的信心和勇气.。
八年级数学下册 2.6.2《菱形的判定》导学案(新版)湘教版

八年级数学下册 2.6.2《菱形的判定》导学案(新版)湘教版2、6、2菱形的判定教学目标:1、理解并掌握菱形的定义及两个判定方法;会用这些判定方法进行有关的论证和计算;2、在菱形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力、教学重点:菱形的两个判定方法、教学难点:判定方法的证明方法及运用、教学过程:一、忆一忆(1)菱形的定义:一组邻边相等的平行四边形;(2)菱形的性质1 菱形的四条边都相等;性质2 菱形的对角线互相平分,并且每条对角线平分一组对角;(3)运用菱形的定义进行菱形的判定,应具备几个条件?(判定:2个条件)二、探一探:要判定一个四边形是菱形,除根据定义判定外,还有其它的判定方法吗?用一长一短两根木条,在它们的中点处固定一个小钉,做成一个可转动的字,四周围上一根橡皮筋,做成一个四边形、转动木条,这个四边形什么时候变成菱形?通过演示,容易得到:菱形判定方法1 对角线互相垂直的平行四边形是菱形、注意此方法包括两个条件:(1)是一个平行四边形;(2)两条对角线互相垂直、通过教材P109下面菱形的作图,可以得到从一般四边形直接判定菱形的方法:菱形判定方法2 四边都相等的四边形是菱形、例2(补充)已知:如图ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F、求证:四边形AFCE是菱形、证明:∵四边形ABCD是平行四边形,∴AE∥FC、∴∠1=∠2、又∠AOE=∠COF,AO=CO,∴△AOE≌△COF、∴EO=FO、∴四边形AFCE是平行四边形、又EF⊥AC,∴AFCE是菱形(对角线互相垂直的平行四边形是菱形)、三、练一练1、填空:(1)对角线互相平分的四边形是;(2)对角线互相垂直平分的四边形是________;(3)对角线相等且互相平分的四边形是________;(4)两组对边分别平行,且对角线的四边形是菱形、2、画一个菱形,使它的两条对角线长分别为6cm、8cm、3、如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E,求证:四边形OCED是菱形。
湘教版8下数学教案 菱形的性质
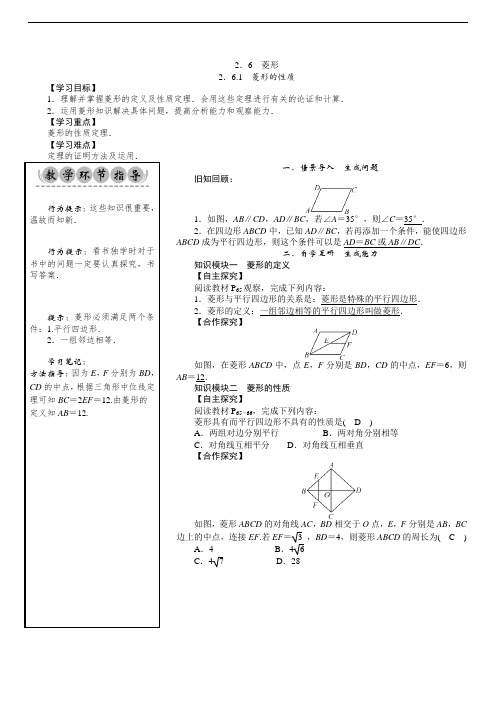
2.6 菱形2.6.1 菱形的性质【学习目标】1.理解并掌握菱形的定义及性质定理.会用这些定理进行有关的论证和计算.2.运用菱形知识解决具体问题,提高分析能力和观察能力.【学习重点】菱形的性质定理.【学习难点】行为提示:这些知识很重要,温故而知新.行为提示:看书独学时对于书中的问题一定要认真探究,书写答案.提示:菱形必须满足两个条件:1.平行四边形.2.一组邻边相等.学习笔记:方法指导:因为E ,F 分别为BD ,CD 的中点,根据三角形中位线定理可知BC =2EF =12.由菱形的定义知AB =12.一、情景导入 生成问题 旧知回顾: 1.如图,AB ∥CD ,AD ∥BC ,若∠A =35°,则∠C =35°. 2.在四边形ABCD 中,已知AD ∥BC ,若再添加一个条件,能使四边形ABCD 成为平行四边形,则这个条件可以是AD =BC 或AB ∥DC . 二、自学互研 生成能力 知识模块一 菱形的定义 【自主探究】 阅读教材P 65观察,完成下列内容: 1.菱形与平行四边形的关系是:菱形是特殊的平行四边形. 2.菱形的定义:一组邻边相等的平行四边形叫做菱形. 【合作探究】 如图,在菱形ABCD 中,点E ,F 分别是BD ,CD 的中点,EF =6,则AB =12. 知识模块二 菱形的性质 【自主探究】 阅读教材P 65-66,完成下列内容: 菱形具有而平行四边形不具有的性质是( D ) A .两组对边分别平行 B .两对角分别相等 C .对角线互相平分 D .对角线互相垂直 【合作探究】 如图,菱形ABCD 的对角线AC ,BD 相交于O 点,E ,F 分别是AB ,BC 边上的中点,连接EF .若EF =3 ,BD =4,则菱形ABCD 的周长为( C ) A .4 B .46 C .47 D .28知识模块三 菱形性质的应用 【自主探究】 阅读教材P 67例1,完成下列内容: 如图,在菱形ABCD 中,AB =6,∠ABD =30°,则菱形ABCD 的面积是( B ) A .18 B .183 C .36 D .363 【合作探究】 如图,四边形ABCD 是菱形,过AB 的中点E 作AC 的垂线EF 交AD 于点M ,交AC 于点N ,交CD 的延长线于点F . (1)试说明AM =DM ; (2)若DF =2,求菱形ABCD 的周长. 解:(1)∵四边形ABCD 是菱形,∴∠BAC =∠DAC .又∵EF ⊥AC ,∴AE =AM =12 AB =12 AD ,∴AM =DM ;(2)∵AE =AM ,∴∠AME =∠AEM .∵AB ∥CD ,∴∠AEM =∠F ,又∠FMD =∠AEM ,∴∠F =∠FMD ,∴DF=DM =12 AD ,∴AD =4,∴菱形ABCD 的周长是16. 三、交流展示 生成新知 1.将阅读教材时“生成的问题”和通过“自主探究、合作探究”得出的“结论”展示在各小组的小黑板上,并将疑难问题也板演到小黑板上,再一次通过小组间就上述疑难问题相互解疑. 2.各小组由小组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”. 知识模块一 菱形的定义 知识模块二 菱形的性质 知识模块三 菱形性质的应用 四、检测反馈 达成目标 见《名师测控》学生用书. 五、课后反思 查漏补缺 1.收获:_______________________________________ 2.存在困惑:________________________________________。
新湘教版八年级下册数学 《菱形的性质》导学案

2.6.1菱形的性质学习目标:1.探索菱形的定义,以及和平行四边形的联系与区别;2.会用菱形的性质进行有关的论证和计算;3.培养学生的观察能力、动手能力自学能力、计算能力、逻辑思维能力;4.在学习中渗透事物总是相互联系又相互区别的辨证唯物主义观点。
学习重点:菱形的性质学习难点: 菱形性质的灵活运用。
学习过程:一、复习1、矩形的性质(1) 角: _________________________________;(2)对角线: _________________________________.2、如图:矩形ABCD 的两条对角线相交于点O ,=∠OD A ︒60, BD = 8 ,则AD =______.二、预习1、菱形的定义:_________________________________叫做菱形2、菱形是平行四边吗?( )(1)因此菱形是_______对称图形,__________ ___是对称中心;(2)菱形的对边____ 且 ______ ;(3)菱形的对角______,邻角________.3、菱形的性质(1) 边: ___________________________________(2)对角线:_______________________________,每一条对角线______________________________.4、菱形的对称性菱形既是_______对称图形又是______对称图形,它的对称中心是____________、它的对称轴是_________________________5、菱形的面积等于_________________________________.三、达标练习1、已知:如图、在菱形ABCD中, AB = 5cm ,OB = 3cm ,则AC = _______、BD = ______,S菱形ABCD ___________ .2、已知,如图:在菱形ABCD中,∠ABC=120°,BD = 8cm,则菱形ABCD的周长为_________.3、菱形ABCD的面积为96㎝2,对角线AC的长为16㎝,则另一条对角线BD的长为__________.四、课堂小结1.通过本堂课的探索,你有何收获?最想说的一句话是什么?2.反思一下你所获成功的经验,课后写好数学日记,与同学交流!。
八年级数学下册 2_6_1 菱形的性质导学案 (新版)湘教版

2.6.1 菱形的性质1.掌握菱形的定义和性质;2.掌握菱形面积的求法;3.灵活运用菱形的性质解决问题.自学指导阅读课本P65~67,完成下列问题.1.有一组邻边相等的平行四边形叫做菱形.3.菱形具有平行四边形的一切性质.2.菱形是轴对称图形,它的对角线所在的直线就是它的对称轴.它有两条对称轴,两条对称轴互相垂直.4.菱形的四条边都相等.5.菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.知识探究1.请同学们用菱形纸片折一折,回答下列问题:(1)菱形是轴对称图形吗?如果是,它有几条对称轴?对称轴之间有什么位置关系?(2)菱形中有哪些相等的线段?解:(1)菱形是轴对称图形,有两条对称轴,是菱形领条对角线所在的直线。
两条对称轴互相垂直。
(1)菱形的邻边相等,对边相等,四条边都相等.自学反馈1.如图,在菱形ABCD中,对角线AC、BD相交于点O.(1)图中有哪些线段是相等的?哪些角是相等的?(2)有哪些特殊的三角形?解:(1)相等的线段:AB=CD=AD=BC,OA=O C,OB=OD.相等的角:∠DAB=∠BCD,∠ABC=∠CDA,∠AOB=∠DOC=∠AOD=∠BOC=90°,∠1=∠2=∠3=∠4,∠5=∠6=∠7=∠8. (2)等腰三角形:△ABC △DBC △ACD △ABD直角三角形:Rt△AOB Rt△BOC Rt△COD Rt△DOA活动1 小组讨论例如图,菱形ABCD的两条对角线AC,BD的长度分别为4cm,3cm,求菱形ABCD的面积和周长.解:菱形ABCD 的面积为 S=21×4×3=6(cm 2). 在直角三角形ABO 中, OA=21AC=21×4=2(cm). OB=21BD=21×3=1.5(cm), 所以 AB 2=OA 2+OB 2=22+1.52=6.25.从而 AB = 2.5(cm).因此,菱形ABCD 的周长为2.5×4=10.活动2 跟踪训练1.已知菱形ABCD 中,对角线AC 与BD 相交于点O ,∠BAD =120°,AC =4,则该菱形的面积是( B )A .16 3B .8 3C .4 3D .82.如图,四边形ABCD 是菱形,CE ⊥AB 交AB 的延长线于E ,CF ⊥AD 交AD 的延长线于F .求证:CE =CF .证明:连接AC ,∵四边形ABCD 是菱形,∴AC 平分∠DAE ,∵CE ⊥AB ,CF ⊥AD ,∴CE =FC .3.如图,O 是菱形ABCD 对角线AC 与BD 的交点,CD =5cm ,OD =3cm ;过点C 作CE ∥DB ,过点B 作BE ∥AC ,CE 与BE 相交于点E .(1)求OC 的长;(2)求四边形OBEC 的面积.解:(1)∵四边形ABCD 是菱形,∴AC ⊥BD .在直角△OCD 中,OC =CD 2-OD 2=52-32=4(cm);(2)∵CE ∥DB ,BE ∥AC ,∴四边形OBEC 为平行四边形,又∵AC ⊥BD ,即∠COB =90°,∴平行四边形OBEC 为矩形,∵OB =OD =4cm ,∴S 矩形OBEC =OB ·OC =4×3=12(cm 2).活动3 课堂小结有一组邻边相等的平行四边形叫做菱形.菱形的性质:(1)菱形是轴对称图形,两条对角线所在直线都是它的对称轴;(2)菱形的四条边都相等;(3)菱形的对角线互相垂直,并且每一条对角线平分一组对角;(4)菱形的面积等于两条对角线的乘积的一半.。
湘教版2019-2020年八年级数学下册学案:2.6.1 菱形的性质

2.6 菱形
2.6.1 菱形的性质
学习目标
1.记住菱形的概念及其与平行四边形的关系;
2.体会菱形的轴对称性,经历利用折纸等活动探索菱形性质的过程,得出菱形的特殊性质. 学习过程
一、准备开始呀!
观察课本第二页的图片后,你能从中发现你熟悉的图形吗?你认为它们有什么样的
共同特征呢?
定义:
二、想一想呀!
①菱形是特殊的平行四边形,它具有一般平行四边形的所有性质.你能列举一些
这样的性质吗?
②你认为菱形还具有哪些特殊的性质?请你与同伴交流.
三、做一做呀!
请同学们用菱形纸片折一折,回答下列问题:
(1)菱形是轴对称图形吗?如果是,它有几条对称轴?对称轴之间有什么位置关
系?
(2)菱形中有哪些相等的线段?
四、我们要共同完成呀!
已知:如图1,在菱形ABCD中,AB=AD, 对角线AC与BD相交于点O.
求证:(1)AB=BC=CD=AD;(2)AC⊥BD.
定理菱形的四条边相等
A
定理菱形的对角线互相垂直
五、看看自己能完成呀?
1、如图,在菱形ABCD中,对角线AC与BD相交于点
O, ∠BAD=60°,BD=6,求菱形的边长AB和对角线AC的长.
2、如图,在菱形ABCD中,对角线AC与BD 相交于点O.
已知AB=5cm,AO=4cm,求 BD的长.
六、我们一块总结呀!
1、菱形的定义:一组邻边相等的平行四边形是菱形.
C
2、菱形的性质:①菱形是轴对称图形,对称轴是两条对角线所在的直线;②菱形的四条边都相等;③菱形的对角线互相垂直平分.
3、菱形具有平行四边形的所有,应用菱形的性质可以进行计算和推理
.
A。
湘教版八下数学2.6.1菱形的性质教学设计

湘教版八下数学2.6.1菱形的性质教学设计一. 教材分析湘教版八下数学2.6.1菱形的性质是本节课的主要内容。
教材从学生的实际出发,以学生的已有知识为基础,通过观察、操作、猜想、验证等环节,引导学生发现并总结菱形的性质。
教材中既有对菱形性质的描述,也有对性质证明的引导,旨在培养学生推理、论证的能力。
二. 学情分析学生在学习本节课之前,已经掌握了平行四边形的性质,对图形的性质探究有一定的经验。
但学生对菱形的认识还不够深入,需要通过本节课的学习,进一步理解和掌握菱形的性质。
三. 教学目标1.理解菱形的性质,并会运用菱形的性质解决一些简单问题。
2.培养学生的观察能力、操作能力、推理能力和论证能力。
3.激发学生对数学的兴趣,培养学生的合作意识和探究精神。
四. 教学重难点1.重点:菱形的性质及证明。
2.难点:对菱形性质的理解和运用。
五. 教学方法1.引导发现法:通过引导学生观察、操作、猜想、验证等环节,发现并总结菱形的性质。
2.小组合作学习:学生在小组内进行讨论、探究,共同解决问题。
3.案例分析法:通过分析具体的菱形例子,帮助学生理解和掌握菱形的性质。
六. 教学准备1.教学课件:制作课件,展示菱形的性质及证明过程。
2.教学素材:准备一些菱形的图片或实物,供学生观察和操作。
3.练习题:设计一些有关菱形性质的练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)利用课件或实物,展示一些菱形的图片或实物,引导学生观察并说出菱形的特征。
2.呈现(10分钟)引导学生通过观察、操作、猜想、验证等环节,发现并总结菱形的性质。
教师在这个过程中给予适当的引导和提示。
3.操练(10分钟)学生分组进行讨论,共同探究菱形的性质。
教师在这个过程中给予适当的指导,帮助学生理解和掌握菱形的性质。
4.巩固(10分钟)学生独立完成一些有关菱形性质的练习题,检验自己是否真正理解和掌握了菱形的性质。
教师在这个过程中给予适当的辅导和指导。
5.拓展(10分钟)引导学生运用菱形的性质解决一些实际问题,如设计一些有关菱形的图案等。
湘教版八下数学2.6.1《菱形的性质》教学设计

湘教版八下数学2.6.1《菱形的性质》教学设计一. 教材分析湘教版八下数学2.6.1《菱形的性质》是本学期菱形相关知识的第一节课程。
本节课主要介绍了菱形的定义、性质及其在几何中的应用。
教材通过丰富的例题和练习题,帮助学生理解和掌握菱形的性质,培养学生的空间想象能力和逻辑思维能力。
本节课的内容为后续的菱形面积计算和应用打下基础。
二. 学情分析学生在学习本节课之前,已经掌握了平行四边形的性质,对平面几何图形有一定的认识。
但学生对菱形的定义和性质可能较为陌生,需要通过实例和操作来逐步理解和掌握。
此外,学生可能对菱形的实际应用场景了解不多,需要通过生活中的实例来增强其对菱形概念的理解。
三. 教学目标1.理解菱形的定义,掌握菱形的性质。
2.学会用菱形的性质解决实际问题,培养学生的应用能力。
3.培养学生的空间想象能力和逻辑思维能力。
四. 教学重难点1.菱形的定义及其性质。
2.菱形在实际问题中的应用。
五. 教学方法1.采用问题驱动的教学方法,引导学生主动探究菱形的性质。
2.利用几何画板等软件,直观展示菱形的性质,帮助学生理解。
3.通过生活中的实例,让学生感受菱形在实际中的应用。
4.采用小组合作、讨论交流的方式,培养学生的合作精神和沟通能力。
六. 教学准备1.准备PPT,包括菱形的定义、性质及其应用的实例。
2.准备几何画板软件,用于展示菱形的性质。
3.准备与菱形相关的实际问题,用于课堂讨论。
七. 教学过程1.导入(5分钟)利用PPT展示一些生活中的菱形图形,如蜂巢、骰子等,引导学生关注菱形的存在。
提问:“你们知道这些图形为什么是菱形吗?”让学生思考菱形的特征。
2.呈现(10分钟)通过PPT介绍菱形的定义和性质。
以几何画板软件为辅助,直观展示菱形的性质,如对角线互相垂直、四条边相等等。
引导学生观察、思考,并解释这些性质背后的几何原理。
3.操练(10分钟)分发练习题,让学生独立完成。
题目包括判断题、填空题和解答题,涵盖菱形的性质及应用。
湘教版八下数学2.6.1《菱形的性质》说课稿

湘教版八下数学2.6.1《菱形的性质》说课稿一. 教材分析湘教版八下数学2.6.1《菱形的性质》是初中数学的重要内容,也是学生对几何图形性质研究的深入。
本节内容通过介绍菱形的性质,让学生理解菱形的基本特征,掌握菱形的性质,并能够运用菱形的性质解决一些实际问题。
教材通过对菱形的定义、性质及其应用的阐述,让学生在掌握知识的同时,培养其空间想象能力和逻辑思维能力。
二. 学情分析学生在学习本节内容前,已经掌握了矩形、平行四边形的性质,他们对这些图形的性质有一定的了解。
但菱形作为一个新的图形,其性质与矩形、平行四边形有所不同,学生需要在新知识的基础上,进行对比学习,理解菱形的特殊性。
此外,学生需要通过实践活动,掌握菱形的性质,并能够运用性质解决实际问题。
三. 说教学目标1.知识与技能目标:让学生掌握菱形的性质,能够运用菱形的性质解决一些实际问题。
2.过程与方法目标:通过观察、操作、猜想、验证等活动,培养学生的空间想象能力和逻辑思维能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养学生的团队合作意识和探究精神。
四. 说教学重难点1.教学重点:菱形的性质及其应用。
2.教学难点:菱形性质的推导和证明,以及运用菱形性质解决实际问题。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法、小组合作法等。
2.教学手段:多媒体课件、几何画板、实物模型等。
六. 说教学过程1.导入新课:通过展示一些生活中的菱形物体,如钻石、蜂巢等,引导学生关注菱形,激发学生的学习兴趣。
2.探究菱形的性质:让学生通过观察、操作、猜想、验证等环节,探究菱形的性质。
首先,让学生用剪刀、彩纸等工具,自己制作菱形,并观察菱形的特点;然后,引导学生发现菱形的性质,如对角线互相垂直、四边相等等;最后,让学生通过数学语言,表达对菱形性质的理解。
3.性质的应用:让学生通过解决一些实际问题,运用菱形的性质。
例如,计算菱形对角线的长度,求菱形的面积等。
八年级数学下册2.6菱形的性质导学案(无答案)(新版)湘教版

菱形的性质一、学前反馈二、导入目标【学习目标】记忆菱形的定义;记忆菱形的性质; 能区别菱形与平行四边形;菱形的面积计算公式。
重点、难点:重点:1.菱形的作图;2.菱形的性质的应用。
难点:菱形的性质的应用。
三、自主学习阅读教材P65、66、67页的内容,回答下列问题:1、 的四边形叫做菱形。
2、菱形也是平行四边形,是特殊的平行四边形,特殊在于它是一组邻边 的平行四边形。
3、我也能在下方画几个菱形的图形:四、合作探究:说一说:菱形的性质:(1)菱形是 图形,对称中心是 ;(2)菱形的 相等, 相等,对角线 ;(3)菱形的四条边 。
我可以结合图1用几何语言将菱形的性质加以描述:(1)菱形ABCD 是中心对称图形,对称中心是点 ;(2)菱形ABCD 中,AB= ,AD= ;(3)菱形ABCD 的对角线AC 、BD 相交于点O ,则OA= =21 ;OD= =21 ; (4)菱形的四边 ,即:AB= = = 。
学一学:阅读教材P89“动脑筋”的内容,回答下列问题:菱形的性质:(1)菱形是 图形,它的对称轴是 ;(2)菱形的 互相垂直,并且每一条对角线 。
我可以结合图形2,将菱形的性质加以描述:(1)菱形ABCD 是轴对称图形,它的对称轴有 条,是直线 ;(2)菱形的对角线⊥AC ;(3)在菱形ABCD 中,=∠AOD = = =︒90;1∠= = = =DAB ∠21=21 ; 5∠= = = =ADC ∠21=21 ; 61∠+∠= = = =︒90(4)在图形2中,有 对全等的三角形,它们分别是1、在菱形ABCD 中,对角线AC 、BD 将菱形分成 对全等的三角形,它们分别是;2、菱形ABCD 面积计算公式是: 。
五、展示交流1. 如图4,菱形ABCD 的两条对角线AC 、BD 长度分别为8cm ,6cm.求菱形ABCD 的面积和周长。
六、达标提升已知菱形ABCD 的两条对角线的交点为O ,AB=13,OA=5。
八年级数学下册 2.6.1 菱形的性质导学案(无答案)湘教版(2021年整理)

广西北海市八年级数学下册2.6.1 菱形的性质导学案(无答案)(新版)湘教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(广西北海市八年级数学下册2.6.1 菱形的性质导学案(无答案)(新版)湘教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为广西北海市八年级数学下册2.6.1 菱形的性质导学案(无答案)(新版)湘教版的全部内容。
2.6。
1菱形的性质一、新课引入〈一〉、复习引入1、说说平行四边形、矩形的性质。
〈二〉、导读目标:学习目标:1、掌握菱形的概念与有关性质;2、会利用菱形的性质的进行简单的推理与计算.重点:菱形的概念与有关性质;菱形与平行四边形的区别.难点:运用菱形的性质的应用。
预习导学预习课本P65—66 ,解答下列的问题。
1、什么菱形?(一组邻边相等+平行四边形=菱形)由此可见,菱形是特殊的 ,它具有平行四边形的所有性质.2、如图,菱形ABCD有什么性质?①边的关系:②角的关系:③对角线的关系:④对称性:⑤面积:那些是菱形所特有的性质:ODB A三、合作探究例1:如图,菱形ABCD 的两条对角线AC ,BD 的长度分别为4cm,3 cm,求菱形ABCD 的面积和周长。
四、解法指导五、 堂上练习1、菱形ABCD 的两条对角线相并于点O ,已知AB=5 cm,OB=3 cm ,求菱形ABCD 的两条对角线的长度以及它的面积。
2、如图,点P 是菱形ABCD 的对角线AC 上一点,PE ⊥A D 于点E,PE=4 cm ,求点P 到AB 的距离。
六、 课堂小结谈谈你的收获和疑惑?七、 课后作业 1、如图,四边形ABCD 是菱形,边长为2 cm ,∠BCD=600,求菱形ABCD 的两条对角线的长度以及O DB AACBE P它的面积.2、如图,在菱形ABCD中,点E,F是边AD,CD的中点,AF=3 cm,求CE的长.A DF。
2020—2021年湘教版八年级数学下册2.6.1 菱形的性质教案(精品教学案).doc

2.6 菱形2.6.1 菱形的性质1.掌握菱形的定义和性质;(重点)2.掌握菱形面积的求法;(重点)3.灵活运用菱形的性质解决问题.(难点)一、情境导入将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?这就是另一类特殊的平行四边形,即菱形.二、合作探究探究点一:菱形的性质【类型一】利用菱形的性质证明线段相等如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于E,CF⊥AD交AD的延长线于F.求证:CE=CF.解析:连接AC,根据菱形的性质可得AC平分∠DAE,再根据角平分线的性质可得CE =FC.证明:连接AC,∵四边形ABCD是菱形,∴AC平分∠DAE,∵CE⊥AB,CF⊥AD,∴CE=FC.方法总结:关键是掌握菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;角平分线的性质:角的平分线上的点到角的两边的距离相等.【类型二】利用菱形的性质进行有关的计算如图,O是菱形ABCD对角线AC与BD 的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.(1)求OC的长;(2)求四边形OBEC的面积.解析:(1)在直角△OCD中,利用勾股定理即可求解;(2)先证明四边形OBEC为矩形,再利用矩形的面积公式即可直接求解.解:(1)∵四边形ABCD是菱形,∴AC ⊥BD.在直角△OCD中,OC=CD2-OD2=52-32=4(cm);(2)∵CE∥DB,BE∥AC,∴四边形OBEC 为平行四边形,又∵AC⊥BD,即∠COB=90°,∴平行四边形OBEC为矩形,∵OB=OD=4cm,∴S矩形OBEC=OB·OC=4×3=12(cm2).方法总结:菱形的对角线互相垂直,则菱形对角线将菱形分成四个直角三角形,所以可以利用勾股定理解决一些计算问题.【类型三】运用菱形的性质解决探究性问题已知:如图①,在菱形ABCD中,AB=BD,点E、F分别在边AB、AD上.若AE=DF,易知△ADE≌△DBF.探究:如图②,在菱形ABCD中,AB=BD,点E、F分别在BA、AD的延长线上.若AE=DF,△ADE与△DBF是否全等?如果全等,请证明;如果不全等,请说明理由.拓展:如图③,在▱ABCD中,AD=BD,点O是AD边的垂直平分线与BD的交点,点E、F分别在OA、AD的延长线上.若AE=DF,∠ADB=50°,∠AFB=32°,求∠ADE的度数.解析:探究:△ADE和△DBF全等,利用菱形的性质首先证明三角形ABD为等边三角形,再利用全等三角形的判定方法即可证明△ADE≌△DBF;拓展:因为点O在AD的垂直平分线上,所以OA=OD,再通过证明△ADE≌△DBF,利用全等三角形的性质即可求出∠ADE的度数.解:探究:△ADE和△DBF全等.∵四边形ABCD是菱形,∴AB=AD.∵AB=BD,∴AB=AD=BD.∴△ABD为等边三角形.∴∠DAB=∠ADB=60°.∵AE=DF,∴△ADE≌△DBF;拓展:∵点O在AD的垂直平分线上,∴OA=OD.∴∠DAO=∠ADB=50°.∴∠EAD =∠FDB.∵AE=DF,AD=DB,∴△ADE≌△DBF.∴∠DEA=∠AFB=32°.∴∠EDA=50°-32°=18°.方法总结:本题考查了菱形的性质、等边三角形的判定和性质以及全等三角形的判定和性质,比较综合,但难度不大,一定要熟悉相关的基础知识,才能更快地解决问题.探究点二:菱形的面积已知菱形ABCD中,对角线AC与BD相交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )A.16 3 B.8 3C.4 3 D.8解析:∵四边形ABCD是菱形,∴AB=BC,OA=12AC=2,OB=12BD,AC⊥BD,∠BAD+∠ABC=180°,∵∠BAD=120°,∴∠ABC=60°,∴△ABC是等边三角形,∴AB =AC=4,∴OB=AB2-OA2=42-22=23,∴BD=2OB=43,∴菱形ABCD 的面积=12AC·BD=12×4×43=83;故选B.方法总结:菱形的面积为两对角线长的积的一半,菱形的对角线平分对角.三、板书设计1.菱形的性质菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.2.菱形的面积S菱形=边长×对应高=12ab(a,b分别是两条对角线的长)通过折纸活动让学生主动探索菱形的性质,大多数学生能全部得到结论,少数的我们加以引导.在整个新知生成过程中,这个活动起了重要的作用.学生始终处于观察、比较、概括、总结和积极思维的状态,切身感受到自己是学习的主人.为学生今后获取知识、探索发现和创造打下了良好的基础,更增强了敢于实践,勇于探索,不断创新和努力学习数学知识的信心和勇气.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.6.1菱形的性质
教学目标:
1.掌握菱形概念,知道菱形与平行四边形的关系.
2.理解并掌握菱形的定义及性质1、2;会用这些性质进行有关的论证和计算,会计算菱形的面积.
3.通过运用菱形知识解决具体问题,提高分析能力和观察能力.
4.根据平行四边形与矩形、菱形的从属关系,通过画图渗透集合思想. 学习重点:菱形的性质1、2.
学习难点:菱形的性质及菱形知识的综合应用.
学习内容:
一、忆一忆
1.什么叫做平行四边形?2、什么叫矩形?3、平行四边形和矩形之间的关系是什么?
二、探一探
1.我们已经学习了一种特殊的平行四边形——矩形,其实还有另外的特殊平行四边形,请看下面的演示:改变平行四边形的边,使之一组邻边相等,从而引出菱形概念.
2. 菱形定义: .
【强调】 菱形(1)是平行四边形;(2)一组邻边相等.
3.阅读教材P65页探究:
菱形是轴对称图形吗?如果是,那么它有几条对称轴?对称轴之间有什么位置关系?你能看出图中哪些线段或角相等?
4.菱形的性质1:
菱形的性质
2:
菱形性质1证明:
菱形性质2证明:
5. (阅读教材P67页上面一段内容)比较菱形的对角线和一般平行四边形的对角线你会发现什么?你能利用菱形的对角线求菱形的面积吗?如果菱形的两条对角线长分别是a 和b ,计算菱形的面积S 。
三、练一练
1. 教材P67练习:
2. 已知:如图,四边形ABCD 是菱形,F 是AB 上一点,DF 交AC 于E .
求证:∠AFD=∠CBE .
三、反馈:
1.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为 .
2.已知菱形的两条对角线分别是6cm 和8cm ,求菱形的周长和面积.
3.已知菱形ABCD 的周长为20cm ,且相邻两内角之比是1∶2,求菱形的对角线的长和面积.
4.已知:如图,菱形ABCD 中,E 、F 分别是CB 、CD 上的点,
且BE=DF .求证:∠AEF=∠AFE .
5.菱形ABCD 中,∠D ∶∠A=3∶1,菱形的周长为 8cm ,求菱形的高.
6.如图,四边形ABCD 是边长为13cm 的菱形,其中对角线AC 长10cm 。
求(1)对角线BD 的长度;(2)菱形ABCD 的面积.
四、课后反思:。
