人教六年级上圆的面积与正方形的面积的关系
2022年秋季人教版六年级数学上册第十二周知识梳理

人教版小学数学六年级上册第 12 周学习清单本周知识梳理1.圆的面积:圆所占平面的大小叫做圆的面积,用字母 S 表示。
2.圆面积计算公式的推导过程:(1)把一个圆等分(偶数份)成的扇形份数越多,拼成的图像越接近长方形。
(2)拼出的图形与圆的周长和半径的关系:长方形的长近似于圆的周长的一半,长方形的宽近似于圆的半径。
(3)因为长方形面积=长×宽,所以圆的面积=圆周长的一半×圆的半径。
即S 圆=C÷2×r=πr×r=πr²。
3.圆环的面积计算:一个圆环,外圆的半径用字母 R 表示,内圆的半径用字母r 表示(R=r+圆环的宽度)S 环=πR²-πr²或S 环=π(R²-r²)4.一个圆,半径扩大或缩小多少倍,直径和周长也扩大或缩小相同的倍数。
而面积扩大或缩小的倍数是半径扩大或缩小倍数的平方倍。
例如:在同一个圆内,半径扩大 3 倍,那么直径和周长就都扩大 3 倍,而面积扩大9 倍(3 的平方倍)。
5.两个圆的半径比=直径比=周长比;而面积比等于半径比的平方。
例如:两个圆的半径比是 2:3,那么这两个圆的直径比和周长比都是 2:3,而面积比是 4:9。
6.外方内圆(内切圆):面积计算公式:S=0.86r²。
推导过程:S外方内圆=S正-S圆=d²-πr²=2r×2r-πr²=4r²-πr²=(4-π)r²=0.86r²。
7.任意一个正方形与它内切圆的面积之比都是一个固定值,即4:π。
8.当长方形、正方形、圆的周长相等时,圆面积最大,正方形居中,长方形面积最小。
反之,面积相同时,长方形的周长最长,正方形居中,圆的周长最短。
学习清单内容学号:评价:姓名:班级:一、填空。
1.将一个半径为r 的圆平均分成若干等份,然后拼成一个近似的平行四边形,这个平行四边形的底是(),高是(),面积 = ()×()。
人教版六年级数学上册第五单元《圆的面积公式的推导及应用》课件

四 等 分
八 等 分
十 六 等 分
三 十 二 等 分
以拼成的近似平行四边形为例: 圆面8等分时: 圆面16等分时: 圆面32等分时:
分的份数越多,拼成的图形越接近长方形。
从上图中可以看出圆的半径是r,长 方形的宽近似( 圆的半径 ),长近似于 ( 圆周长的一半 )。
因为长方形的面积=( 长 )×(宽 ), 所以圆面积=(πr)×( r )=(πr²)。 如果用S表示圆的面积,那么圆的面积计算公式就是 : S=πr²。
(2)一个圆的周长是12.56m,它的面积是多少平方米?
12.56÷3.14=4(m) 3.14×(4 ÷ 2)2 =3.14×4 =12.56(m2) 答:它的面积是12.56 m²。
(3)将一只羊拴在草地的木桩上,绳子的长度是4米。这只羊最 多可以吃到多少平方米的草?
3.14×42 =3.14×16 =50.24(m2) 答:这只羊最多可以吃到50.24 m²的草。
9.42÷3.14=3(dm) 34×3.14×32 =21.195(dm2) 答:阴影部分的面积是 21.195 dm2。
6.如图,从三块面积相等的正方形钢板上分别割 下大小不同的圆形钢片,请问三块钢板剩余部分 的面积相等吗?
解:设三块正方形钢板的边长为12a cm, 则第一块钢板剩余部分的面积为 12a×12a-3.14×(6a)2=30.96a2(cm2); 第二块钢板剩余部分的面积为 12a×12a-3.14×(3a)2×4=30.96a2(cm2); 第三块钢板剩余部分的面积为 12a×12a-3.14×(2a)2×9=30.96a2(cm2)。 答:三块钢板剩余部分的面积相等。
1.(1)把一张圆形纸片分成若干(偶数)等份,拼成一 个近似的长方形。如下图。
小学六年级圆_阴影部分面积含答案
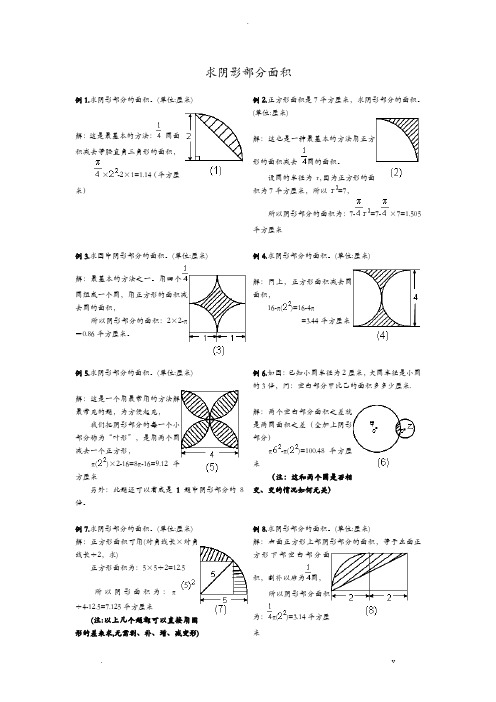
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米.解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
人教版六年级数学《圆的面积》教学设计【优秀6篇】

人教版六年级数学《圆的面积》教学设计【优秀6篇】(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如工作资料、求职资料、报告大全、方案大全、合同协议、条据文书、教学资料、教案设计、作文大全、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides you with various types of classic model essays, such as work materials, job search materials, report encyclopedia, scheme encyclopedia, contract agreements, documents, teaching materials, teaching plan design, composition encyclopedia, other model essays, etc. if you want to understand different model essay formats and writing methods, please pay attention!人教版六年级数学《圆的面积》教学设计【优秀6篇】作为一名人民教师,有必要进行细致的教案准备工作,教案是保证教学取得成功、提高教学质量的基本条件。
人教版六年级数学上册第五单元圆知识点总结

圆一、认识圆1、圆的定义:圆是由曲线围成的一种平面图形。
2、圆心:圆的中心位置叫做圆心。
一般用字母O表示。
它到圆上任意一点的距离都相等。
3、半径:连接圆心到圆上任意一点的线段叫做半径。
一般用字母r表示。
把圆规两脚分开,两脚之间的距离就是圆的半径。
4、直径:通过圆心并且两端都在圆上的线段叫做直径。
一般用字母d表示。
直径是一个圆内最长的线段。
5、圆心确定圆的位置,半径确定圆的大小。
6、在同圆或等圆内,有无数条半径,有无数条直径。
所有的半径都相等,所有的直径都相等。
1。
7、在同圆或等圆内,直径的长度是半径的2倍,半径的长度是直径的2d用字母表示为:d=2r或r =28、轴对称图形:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。
折痕所在的这条直线叫做对称轴。
(经过圆心的任意一条直线或直径所在的直线)9、长方形、正方形和圆都是对称图形,都有对称轴。
这些图形都是轴对称图形。
10、只有1一条对称轴的图形有:角、等腰三角形、等腰梯形、扇形、半圆。
只有2条对称轴的图形是:长方形只有3条对称轴的图形是:等边三角形只有4条对称轴的图形是:正方形;有无数条对称轴的图形是:圆、圆环。
二、圆的周长1、圆的周长:围成圆的曲线的长度叫做圆的周长。
用字母C表示。
2、圆周率:任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率。
用字母π(pai)表示。
(1)圆周率π是一个无限不循环的小数。
在计算时,一般取π ≈ 3.14。
(2)在判断时,圆周长与它直径的比值是π倍,而不是3.14倍。
(3)世界上第一个把圆周率算出来的人是我国的数学家祖冲之。
3、圆的周长公式:C= πd d = C ÷π或C=2π r r = C ÷2π5、在一个正方形里画一个最大的圆,圆的直径等于正方形的边长。
在一个长方形里画一个最大的圆,圆的直径等于长方形的宽。
如图:6、区分周长的一半和半圆的周长:(1)周长的一半:等于圆的周长÷2 计算方法:2π r÷ 2 即π r (2)半圆的周长:等于圆的周长的一半加直径。
小学六年级数学关于圆的知识点总结

一、圆的认识1、日常生活中的圆2、画图、感知圆的基本特征(1)实物画图(2)系绳画图3、对比,感知圆的特征:我们以前学过的长方形、正方形、平行四边形、梯形、三角形等,都是曲线段围成的平面图形,而圆是由曲线围成的一种平面图形.【归纳】:圆是由一条曲线围成的封闭图形二、圆的各部分名称1、圆心:用圆规画出圆以后,针尖固定的一点就是圆心,通常用字母O表示,圆心决定圆的位置2、半径:连接圆心到圆上任意一点的线段叫做半径.一般用字母r表示.把圆规两脚分开,两脚之间的距离就是圆的半径.3、直径:通过圆心并且两端都在圆上的线段叫做直径.一般用字母d表示.直径是一个圆内最长的线段三、圆的主要特征1、在同圆或等圆内,有无数条半径,有无数条直径.所有的半径都相等,所有的直径都相等.2、在同圆或等圆内,直径的长度是半径的2倍,半径的长度是直径的1/2.用字母表示为:d=2r或r=d/23、如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形.圆是轴对称图形且有无数条对称轴一、圆的周长的认识1、围成圆的曲线的长叫做圆的周长2、周长与圆的直径有关,圆的直径越长,圆的周长就越大二、圆周率的意义及圆的周长公式1、圆周率实验:在圆形纸片上做个记号,与直尺0刻度对齐,在直尺上滚动一周,求出圆的周长.发现一般规律,就是圆周长与它直径的比值是一个固定数(π).3、圆周率:任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率.用字母π(pai) 表示.4、一个圆的周长总是它直径的3倍多一些,这个比值是一个固定的数.圆周率π是一个无限不循环小数.在计算时,一般取π≈ 3.14.5、在判断时,圆周长与它直径的比值是π倍,而不是3.14倍.世界上第一个把圆周率算出来的人是我国的数学家祖冲之.6、圆的周长公式:C= πd —→d = C ÷π或C=2πr —→r = C ÷2π7、区分周长的一半和半圆的周长:(1)周长的一半:等于圆的周长÷2 计算方法:2πr ÷ 2 即πr(2)半圆的周长:等于圆的周长的一半加直径. 计算方法:πr+2r 即5.14 r8、正方形里最大的圆.两者联系:边长=直径;圆的面积=78.5%正方形的面积画法:(1)画出正方形的两条对角线;(2)以对角线交点为圆心,以边长为直径画圆.9、长方形里最大的圆.两者联系:宽=直径画法:(1)画出长方形的两条对角线;(2)以对角线交点为圆心,以宽为直径画圆.10、常用的3.14的倍数:3.14×2=6.28 3.14×3=9.42 3.14×4=12.56 3.14×5=15.7 3.14×6=18.843.14×7=21.98 3.14×8=25.12 3.14×9=28.26 3.14×12=37.68 3.14×14=43.963.14×16=50.24 3.14×18=56.52 3.14×24=75.36 3.14×25=78.5 3.14×36=113.04 3.14×49=153.86 3.14×64=200.96 3.14×81=254.34四、圆的面积与以它的半径为边长的正方形的面积的关系以正方形的边长为半径画的圆,正方形的面积实际就是这个圆半径的平方,因此得出“圆的面积是它半径平方的3倍多一些”圆的面积大约等于半径×半径×3五、圆的面积公式1、把圆拼成近似的长方形,知识形状改变了,图形的大小并没有发生变化,因此圆的面积=拼成的近似长方形的面积2、圆的面积推导:圆可以切拼成近似的长方形,长方形的面积与圆的面积相等(即S长方形=S圆);长方形的宽是圆的半径(即b=r);长方形的长是圆周长的一半(即a=C÷2=πr).即:S长方形= a × b↓ ↓S圆=πr × r=πr2所以,S圆=π r2注意:切拼后的长方形的周长比圆的周长多了两条半径.C长方形=2πr+2r=C 圆+d一、圆环的意义及面积的计算1、圆环的意义:以同一点为圆心,半径不相等的两个圆组成的图形,两元之间的部分就是圆环.2、圆环中半径较大的圆叫做外圆,半径较小的圆叫做内圆.外圆半径与内圆半径的差叫做环宽,两圆中间的部分大大小叫做圆环的面积3、外圆的半径=内圆半径+1个环宽;外圆的直径=内圆直径+2个环宽4、求圆环的面积一般是用外圆的面积减去内圆的面积,还可以利用乘法分配律进行简便计算.S圆环=S外圆—S内圆=πR2-πr2=π(R2-r2)5、几个直径和为n的圆的周长=直径为n的圆的周长(如图)几个直径和为n的圆的面积<直径为n的圆的周长6、常用的平方数:112=121 122=144 132=169 142=196 152=225162=256 172=289 182=324 192=361 202=4007、周长相等的平面图形中,圆的面积最大;面积相等的平面图形中,圆的周长最短.随堂练习1、一种钟表的分针长5厘米,3小时分针扫过的面积是多少?2、一个花坛,直径8米,在它的周围有一条宽1米的环形小路,小路的面积是多少平方米?3、一个圆桶的底面周长是62.8厘米,它的底面面积是多少平方厘米?4、杂技演员表演独轮车走钢丝,车轮的直径为40厘米,要骑过100米长的钢丝,车轮大约转动多少周?5、在长10厘米,宽8厘米的长方形纸上剪一个最大的半圆,这个半圆的面积是多少?周长是多少?6、用一根铁丝围成一个正方形,边长正好是6.28米.如果围成一个圆,这个圆的半径是多少?。
人教版六年级数学上册第五单元圆(知识梳理+课本例题+练习)

人教版六年级数学上册第五单元圆(知识梳理+课本例题+练习)一、知识梳理1、圆心:圆中心一点叫做圆心。
用字母“O ”来表示。
半径:连接圆心和圆上任意一点的线段叫做半径,用字母“r ”来表示。
直径:通过圆心并且两端都在圆上的线段叫做直径,用字母“d ”表示。
2、圆心确定圆的位置,半径确定圆的大小。
3、在同一个圆内,所有的半径都相等,所有的直径都相等。
在同一个圆内,有无数条半径,有无数条直径。
在同一个圆内,直径的长度是半径的2倍,半径的长度是直径的一半。
用字母表示为:r d 2= d r 21= 4、圆的周长:围成圆的曲线的长度叫做圆的周长。
5、圆的周长总是直径的3倍多一些,这个比值是一个固定的数。
我们把圆的周长和直径的比值叫做圆周率,用字母π表示。
圆周率是一个无限不循环小数。
在计算时,取14.3π≈。
世界上第一个把圆周率算出来的人是我国的数学家祖冲之。
6、圆的周长公式:πd C = 或πr 2C =7、圆的面积:圆所占平面的大小叫圆的面积。
8、把一个圆割成一个近似的长方形,割拼成的长方形的长相当于圆周长的一半,宽相当于圆的半径,因为长方形面积=长×宽,所以圆的面积2πr r ×r ×π==9、圆的面积公式:22)÷π(d S = 或者2πr S = 或者22)÷π÷π(C S =10、在一个正方形里画一个最大的圆,圆的直径等于正方形的边长。
圆的面积和正方形面积的比是π:4。
在一个圆里画一个最大正方形的,圆的直径的长度等于正方形的对角线的长度,正方形的面积=对角线×对角线÷2=直径×直径÷2 。
11、在一个长方形里画一个最大的圆,圆的直径等于长方形的短边。
12、一个环形,外圆的半径是R,内圆的半径是r,它的面积是22πr πR S -=或 )r π(R S 22-=(其中R =r +环的宽度.)13、环形的周长=外圆周长+内圆周长14、半圆的周长等于圆的周长的一半加直径。
人教版小学六年级上册数学课件 《圆的面积》圆PPT教学课件

拓展运用
1. 图中的大圆半径等于小圆的直径,求阴影部分的面积。
大圆面积:S=πr²=3.14×6²=113.04cm²
小圆半径:r=6÷2=3cm
6 cm
小圆面积:S=πr²=3.14×3²=28.26cm²
阴影面积:113.04–28.26=84.78cm²
拓展运用
2. 一个运动场(如图所示),两端是
半径是6cm,圆环的面积是多少?
2c
m
6c
m
S=πR²﹣πr²
S=π(R²﹣r²)
=3.14×6²-3.14×2²
=3.14×(6²-2²)
=113.04-12.56
=3.14×32
=100.48(cm²)
=100.48(cm²)
教学新知
中国建筑中经常能见到“外方内圆”和“外圆内方”的设
计(如图所示),图中的两个圆半径都是1米,你能求出正方形
和圆之间部分的面积吗?
教学新知
“外方内圆”面积的计算
“外圆内方”面积的计算
正方形边长:1×2=2(米)
圆的直径:1×2 = 2(米)
正方形面积:2×2=4(平方米)
内圆面积:3.14×1²=3.14(平方米)
正方形面积: 1 ×(2×1)×2 = 2(平方米)
2
内圆面积:3.14×1² = 3.14 (平方米)
A. 1
B. 2
C. 3
D
D. 3π
(3)若A.B两个圆的直径比是2:1,则它们的面积比是多少?(
A. 2 : 4
B. 4 : 1
C. 1 : 2
D. 1 : 4
)
)
B
课堂练习
4. 解决问题
(1)一个直径是4米的圆形花坛种上玫瑰花。一平方米只能种5株,这个
六年级上圆的面积与正方形的面积的关系

人教版六年级上圆的面积与正方形的面积的关系在小学数学六年级课本中,有关圆的面积与正方形的面积这两个知识点常常联系十分密切,那么圆的面积和正方形的面积有什么关系呢?圆内一个最大的正方形与圆的面积比是 2:π,正方形内的最大圆与正方形的面积之比是 π:4。
分析:(1)在圆中画的最大正方形的对角线就是圆的直径,从而可以分别利用圆和正方形的面积公式表示出它们的面积,即可求得正方形面积与圆面积的比;(2)在正方形中画的最大圆的直径就等于正方形的边长,分别利用圆和正方形的面积公式表示出它们的面积,即可求得圆面积与正方形面积的比.解答:解:如图所示,(1)在圆里面画一个最大的正方形,设圆的半径是R ,因为圆的面积=πR 2,正方形的面积=2R ×R ÷2×2=2R 2,所以正方形的面积:圆的面积=2R 2:πR 2 π2=2:π;(2)在正方形里面画一个最大的圆,设正方形的边长为a , ,因为正方形的面积=a ×a=a 2,圆的面积=π(2a )²=4π×a ²所以圆的面积:正方形的面积=4π×a ²:a 2=π:4;【典型例题】例题1、在下图中,已知正方形的面积是40平方厘米,这个圆的面积是多少平方厘米?例题2、在下图中,已知三角形的面积是10平方厘米,这个圆的面积是多少平方厘米?例题3、在下图中,已知外面的正方形的面积是80平方厘米,求圆的面积和小正方形的面积。
【经典练习】1、请你说出下面各图形中的空白部分、阴影部分的面积分别占整个图形的百分之几?o(1)(2)(3)(4)2、在三块面积相等的正方形铁板上,分别冲下1个、4个和9个圆片,(如图)。
这时,三块铁板剩余材料的面积相等吗?提高练习:1、下图中空白部分的面积有多大?5厘米2、下图中阴影部分的面积是43平方厘米,正方形的面积是多少平方厘米?3、下图中空白部分的面积是157平方厘米,正方形的面积是多少平方厘米?4、图中空白部分的面积是200平方厘米。
人教六年级数学上册全册教案之:第4课时 圆的面积(1)

人教六年级数学上册全册教案之:第4课时圆的面积(1)第4课时圆的面积(1)【教学内容】圆的面积【教学目标】知识与技能:通过操作,使学生理解圆的面积公式推导过程,掌握求圆的面积的方法并能正确计算。
过程与方法:激发学生参与整个课堂教学活动的学习兴趣,培养学生的分析、观察和概括能力,发展学生的空间观念。
情感、态度与价值观:培养学生的空间观念。
【教学重难点】重点:1、理解圆的面积公式的推导过程。
2、掌握圆的面积的计算公式,能够正确地计算圆的面积难点:理解圆的面积公式的推导过程。
【导学过程】【知识回顾】1、还记得这些平面图形的面积计算公式吗?2、平行四边形的面积公式推导过程还记得吗?我们是通过剪拼的方法把它转化成长方形的。
【新知探究】(一)、定义:1、请你摸一摸哪里是圆的面积?2、师:圆所占平面的大小就是圆的面积。
引导学生操作:师:(拿出一个圆片)我们怎么剪?圆的大小是由什么决定的?(直径、半径)生:(圆的大小由直径或半径决定。
)沿直径或半径剪。
师剪第一刀,再问:第二刀怎么剪?师:我们要把圆通过剪成多份并用拼的方法转化成学过的规则图形,为了计算上的方便,我们把圆平均分成多份。
将一个圆分别平均分成2份、4分、8分、16份,分别罗列排好。
请学生观察四组图。
师:随着等分份数的不断增加,你有什么发现吗?A:随着等分份数的不断增加,曲线越来越直。
B:随着等分份数的不断增加,每一小份越来越接近三角形。
(三)拼摆推导面积公式。
1、拼摆师:把圆转化成什么图形?我们来试一试。
学生操作,演示学生的作品。
师:转化后的图形面积与圆的面积有什么关系?面积不变。
课件出示:把圆等分成不同等份时的图形的趋势。
2、推导面积公式小组讨论:长方形各部分相当于圆的什么?请你推导圆的面积公式。
学生汇报:(2~3名学生说,老师说,全班说推导过程)(4)学生齐读圆面积公式(S=πr2)。
并说说圆面积的大小与什么有关?(半径)给直径怎办?(先求出半径,再求面积)【设计意图】在这个环节教师成为学生的学习伙伴,在教师的引导和启发中,让每个学生都动口,动手,动脑,培养学生学习的主动性和积极性。
人教版六年级数学上册第5单元圆第6课时 圆与正方形组合的面积问题的应用

图(1)
下图中正方形的边长是多少呢?
可以把图中的正方形看成两个三角 形,它的底和高分别是……
从图(2)可以看出:
图(2)
1 2
2
1
2
=
2
m2
3.14-2=1.14(m²)
那么我们解答得如对果不两对个呢圆?的半径都是 有什么方法验证r,吗结?果又是怎样的?
左图:(2r)²-3.14×r²=0.86r²
如果让你 算圆和方 之间的面 积,你会 算吗?请 看教材69
外面是一个圆形, 页例3. 里面是一个正方形。
第三步 精读教材
请仔细看课本69页例3,你该怎么解决问题呢?
从图中你知道正方形和 圆之间部分的面积是怎 样算的吗?
外方内圆:正方形面积 减去圆的面积 外圆内方:圆的面积减 去正方形的面积
正方形面积该怎样算呢?请 看教材第69页分析与解答。
RJ 六年级上册
第五单元 圆
第6课时 圆与正方形组合的 面积问题的应用
课前预习
第一步 旧知回顾
回顾一下,圆的面积是怎样计算的?
S=πr²
S=a²
正方形的面积又 是怎样计算的?
第二步 新知引入
你知道下面图形是由哪两个图形组成的吗?
外方内圆
外圆内方
外方内圆和外圆内方是什么意思呢?
外面是一个正方形, 里面是一个圆形。
3.14
r
2-
1 2
2r
r
2
=
1.14r
2
夯实基础 (选题源于《典中点》经典题库)
1. 右图是一面我国唐代外圆内方的铜镜。铜镜的 直径是24 cm。外面的圆与内部的正方形之间 的面积是多少? (选题源于教材P70做一做) 1.14×(24÷2)²=164.16(cm²)
六年级上册数学圆

六年级上册数学圆一、圆的认识1、日常生活中的圆2、画图、感知圆的基本特征(1)实物画图(2)系绳画图3、对比,感知圆的特征:我们以前学过的长方形、正方形、平行四边形、梯形、三角形等,都是曲线段围成的平面图形,而圆是由曲线围成的一种平面图形。
【归纳】:圆是由一条曲线围成的封闭图形二、圆的各部分名称1、圆心:用圆规画出圆以后,针尖固定的一点就是圆心,通常用字母O 表示,圆心决定圆的位置2、半径:连接圆心到圆上任意一点的线段叫做半径。
一般用字母r表示。
把圆规两脚分开,两脚之间的距离就是圆的半径。
3、直径:通过圆心并且两端都在圆上的线段叫做直径。
一般用字母d 表示。
直径是一个圆内最长的线段三、圆的主要特征1、在同圆或等圆内,有无数条半径,有无数条直径。
所有的半径都相等,所有的直径都相等。
2、在同圆或等圆内,直径的长度是半径的2倍,半径的长度是直径的1/2。
用字母表示为:d=2r或r=d/23、如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。
圆是轴对称图形且有无数条对称轴四、圆的周长的认识1、围成圆的曲线的长叫做圆的周长2、周长与圆的直径有关,圆的直径越长,圆的周长就越大五、圆周率的意义及圆的周长公式1、圆周率实验:在圆形纸片上做个记号,与直尺0刻度对齐,在直尺上滚动一周,求出圆的周长。
发现一般规律,就是圆周长与它直径的比值是一个固定数(π)。
3、圆周率:任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率。
用字母π(pai) 表示。
4、一个圆的周长总是它直径的3倍多一些,这个比值是一个固定的数。
圆周率π是一个无限不循环小数。
在计算时,一般取π≈3.14。
5、在判断时,圆周长与它直径的比值是π倍,而不是3.14倍。
世界上第一个把圆周率算出来的人是我国的数学家祖冲之。
6、圆的周长公式:C= πd —→d = C ÷π或C=2πr —→r = C ÷2π7、区分周长的一半和半圆的周长:(1)周长的一半:等于圆的周长÷2 计算方法:2πr ÷2 即πr (2)半圆的周长:等于圆的周长的一半加直径。
人教版数学六年级上册圆(三) 圆的面积课件

亲爱的读者: 1、盛生年活不重相来信,眼一泪日,难眼再泪晨并。不及代时表宜软自弱勉。,20岁.7.月14不7.待14人.2。02。020:2620:26:02Jul-2020:26 亲爱的读者: 20、.7世.1上47没.1有4.2绝0望20的20处:2境62,0:只26有:0对2J处ul-境20绝20望:2的6人。二〇二〇年七月十四日2020年7月14日 春去春又回,新桃换旧符。在那桃花 2星、期千二里之行,始于足下。2020年7月14日星期二
(2)用鸡舍的面积除以养一只鸡需要的面积,就是可以养的鸡 的只数。
4.一根铁丝恰好可以围成一个边长是4.71m的正方形,如果用 这根铁丝围成一个圆,这个圆的面积是多少平方米?
2020/7/26
【答案】 4.71×4=18.84(米) 18.84÷3.14÷2 =6÷2 =3(米) 3.14×32 =3.14×9 =28.26(平方米) 答:圆的面积是28.26平方米。
第五单元
圆(三) 圆的面积
温故而知新
25米
在长满青草的草地上一匹马被主人用一根绳子栓在 一棵树,这匹马最多能吃到多少青草?
圆所占平面的大小叫做圆的面积。
这是一个圆
分成四等份
分割上半圆
分割下半圆
拼在一起
这是一个圆
分成八等份
分割 上半圆
分割 下半圆
拼在一起
这是一个圆
分成十六等份
例2 光盘的银色部分是一个圆环,内圆半径是2cm,外圆半 径是6cm。它的面积是多少?
6cm
圆环面积= 外圆面积- - 内圆面积 3.14×62 - 3.14×22 3.14×(62 – 22 )
1.计算下列各圆的面积。 (1)半径是8厘米。 (2)周长9.42米。
人教版六年级上册数学 外圆内方 课件

3、如下图,已知正方形的面积是36c㎡,求圆的 面积。
分析:正方形的边长等于圆的半径。 因为:正方形的面积=边长×边长, 所以:正方形的面积(36c㎡)=圆的半径×圆的半径 圆的面积:3.14×36=113.04(c㎡) 答:圆的面积是113.04平方厘米。
人教版 六年级上册数学
第五单元《圆》圆的面积 正方形与圆的关系
引学
铜钱,古代铜质辅币, 指秦汉以后的各类方 孔圆钱,方孔圆钱的 铸期一直延伸到清末 民国初年。方孔铜钱 应天圆地方之说,古 代人们认为天是圆的, 地是方的,所以秦始 皇铸钱以此为型。
由此可见,方和圆在我国的历史由 来已久,人们对这两个特殊的图形 有着别样的喜爱。
4-3.14=0.86(m²)
右图中正方形的 边长是多少呢?
图(2)
可以把右图中的正方形 看成两个三角形,它的 底和高分别是……
底是圆的直径:2m 高是圆的半径:1m
正方形的面积:
圆的面积: 3.14×1²=3.14(m²) 正方形与圆之间的面积:3.14-2=1.14(m²)
如果两个圆的半径都 是r? 2.左图和右图各有什么特点?
(3分钟)
自学提示(一)
题目中告诉了我们哪些数学信息?
上图中两个圆的半径都是1m
自学提示(二)
左图和右图各有什么特点?
特点:左图是“外方内圆”,
。
方大圆小,正方形和圆之间部分的面积是:“方减圆”。
右图是“外圆内方”,
。
圆大方小,正方形和圆之间部分的面积是:“圆减方”。
答:剩下部分的面积是2.86cm²。
2、下图是一面我国唐代外圆内方的铜镜。铜镜的直 径是24 cm。外面的圆与内部的正方形之间的面积是 多少?
人教版小学数学六年级上册第五单元《圆》解决问题教学设计
学习活动设计教师二次设计
【环节一:情境激趣,导入新课。
】
同学们,图形世界是美丽的、奇妙的,世界因为有了五彩的图案
而更加美丽。
谁来说一说你知道哪些美丽的图案?它们是由哪些基本
图形组成的?
课件出示教材67页情境图,引导学生观察,然后提问:
你知道生活中还有哪些外方内圆和外圆内方的物体吗?外方内
圆的图形我们称它为圆外切正方形,外圆内方的图形我们称它为圆
内接正方形。
今天,我们一起来探究这两种组合图形中圆的面积和正
方形的面积之间的关系。
图:根据学生已有的知识经验和生活经验,让学生说一说生活
中与圆有关的组合图形,学生热情高涨,兴趣盎然,有主动学习的
欲望。
]
【环节二:实践探究,发现规律】
1.探究圆外切正方形与圆之间部分的面积。
(1)画一画,发现半径与边长的关系。
①用直尺画一个边长为10厘米的正方形,说说你是怎样画的。
②在正方形内画一个最大的圆。
你能说出你是怎样确定这个圆
的圆心和半径的吗?
(要收集学生不同的操作方法,让学生判断哪一种方法是正确
的,评选最优方法,并指出做错的同学错在哪里)
③学生到实物投影前展示自己的作品,并回答半径是多少及半
径与正方形边长的关系。
板书: d=a
(2)算一算,完成下表。
正方形的边长/米 1 2 3 4 5 r
正方形的面积/平方米。
人教版六年级数学上册第五单元《圆》第三节圆的面积教案

人教版六年级数学上册第五单元《圆》第三节圆的面积教案教材分析:《圆的面积》教材首先提出了圆的面积概念,接着让学生尝试运用以前曾多次采用过的“转化”的数学思想,把圆转化成已学过的图形来计算面积,引导学生推导圆面积的计算公式,再一次让学生熟悉运用“转化”这种数学思想方法来解决较复杂的问题的策略。
在引导学生推导圆面积的计算公式时,教材采用实验的办法,先把圆16等分,拼成一个近似的平行四边形,再把圆32等分,拼成一个近似长方形。
使学生看到分割的份数越多,拼成的图形就越接近于长方形。
当等分的份数达到无限,即把圆平均分成无数份时,拼成的图形就是长方形。
然后分析拼成的长方形的长、宽与圆的周长、半径之间的关系,由长方形的面积计算公式推导出圆的面积计算公式s=πr²。
然后引导学生观察公式,得出结论:要求圆的面积,必须知道半径,如果半径不知道,就要先求半径。
最后要求学生能够利用圆的面积计算公式来解决一些简单的实际问题。
圆面积公式的推导本节课的重点和难点。
在学生经过推导得出圆的面积计算公式后,就要求他们能利用面积计算公式来计算有关的题目,解决一些简单的实际问题。
学情分析:圆面积是在学生学过了圆各部分名称的认识、圆周长的计算和对平行四边形、三角形、梯形等平面图形面积公式的推导的基础上教学的,这部分内容是在学生学过了一些常见平面图形的认识,有关平面图形的周长和面积以及在低年级直观认识圆的基础上教学的,这部分内容不仅扩展了学生的知识面,而且从空间观念方面来说,进入了一个新的领域。
教学方法:1.创设生活化的学习氛围。
创设问题情境,引出要求进行面积,引导学生从身边的数学问题入手,激发学生学习积极性,并由学生通过自己的讨论提出问题,引出如何正确计算圆的面积这个学习内容。
2.组织学生自主探究。
通过观察、操作等实践活动,运用多种感官参与学习活动,接受转化的数学思想,理解和掌握圆的面积公式,并进行合作交流。
教学目标:【知识与技能目标】使学生经历圆的面积公式的推导过程,理解圆面积的计算公式,并能运用公式解决简单的实际问题。
六年级数学上册第五单元圆第7课时圆与正方形之间的关系课件新人教版

一、复习导入
1. 一个圆的周长是12.56cm,求它的半径?
12.56÷3.14÷2 =2(cm)
答:它的半径是2cm。
2. 一个圆形茶几面的半径是3dm ,它的面积是多 少平方分米?
3.14×3² =28.26(dm²)
答:它的面积是28.26dm²。
二、问题引入
3、古时候,由于人们的活动范围狭小,往往凭自 己的直觉认识世界,看到眼前的地面是平的,以为整 个大地是平的,并且把天空看作是倒扣着的一口巨大 的锅。我国古代有“天圆如张盖,地方如棋局”的说法 。(结合课件出示)虽然这种说法是错误的,却产生 了深远的影响,尤其体现在建筑设计上。 4、课件展示:鸟巢和水立方等建筑,精美的雕窗。
圆的面积: 3.14×1²=3.14(m²)
阴影部分面积: 3.14-2=1.14(m²)
二、新知探究
那么我如们果解两答个得圆对的不半对径呢都?是r, 有什么结方果法又验是证怎吗样?的?
左图: (2r)²-3.14×r²=0.86r ²
1 右图:3.14×r²-( 2 ×2r×r)×2=1.14r²
题目中都告诉了 我们什么? 上图中两个圆的半径都 是1m,怎样求正方形和圆之 间部分的面积呢?
左图求的是正方 形比圆多的面积,右 图求的是……
二、新知探究
形,它的底和高分别是……
图(2)
从图(2)可以看出:
正方形面积:(
1 2
×2×1)×2=2(m²)
当r=1 m时,和前面的结果 完全一致。
答:左图中正方形与圆之间的面积是0.86 m², 右图中圆与正方形之间的面积是1.14 m²。
三、学以致用 解决问题。
1、右图是一面我国唐代外圆内方的铜镜。 铜镜的直径是24 cm。外面的圆与内部的正方 形之间的面积是多少?
小学 六年级 圆与正方形关系

答:外面的圆与内部的正方形之间的面积约是452.16cm²。
提高练习 1、已知正方形的面积100平方厘米,圆的面积是____平方厘米.
把正方形平均分成两个三角形,每个三角 形的面积是100÷2=50(平方厘米),而 三角形的面积为2r×r÷2=r²,所以r²=50 ,所以因此圆的面积为3.14×50=157(平 方厘米) 。
题目中都告诉了我们什么?
上图中两个圆的半径都 是1 m,怎样求正方形 和圆之间部分的面积呢 ?左图求的是正方形比圆多的 面积,右图求的是……
图(1)
你能解决这个问题吗?
右图中正方形的边 长就是圆的直径。
从图(1)可以看出: 2×2=4(m²) 3.14×1²=3.14(m²) 4-3.14=0.86(m²)
我们把三个图合起来 旋转一下,通过观察 ,你发现了什么?
四、再次探究
你还能找到不同的方法,探究圆和正方形的面积关系吗?
1. 小正方形是涂色部分的2倍, 中等正方形是涂色部分的4倍; 2. 大正方形是小正方形的4倍。
圆的半径是r,最小正方 形的面积就是r²,其它两 个正方形和圆的面积分别 是小正方形的几倍呢?
我们把三个图合起来 旋转一下,通过观察 ,你发现了什么?
五、解决问题 图中两个圆半径都是1 m,求出正方形和圆之间部分的面积。
r=1 m
左图: 4r²-πr²
右图: πr²-2r²
=0.86r²
=1.14r²
=0.86(m²)
=1.14(m²)
做一做 右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24cm。 外面的圆与内部的正方形之间的面积是多少?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版六年级上圆的面积与正方形的面积的关系
————————————————————————————————作者:————————————————————————————————日期:
【知识点分析】
在小学数学六年级课本中,有关圆的面积与正方形的面积这两个知识点常常联系十分密切,那么圆的面积和正方形的面积有什么关系呢?
圆内一个最大的正方形与圆的面积比是 2:π,正方形内的最大圆与正方形的面积之比是 π:4。
分析:
(1)在圆中画的最大正方形的对角线就是圆的直径,从而可以分别利用圆和正
方形的面积公式表示出它们的面积,即可求得正方形面积与圆面积的比;
(2)在正方形中画的最大圆的直径就等于正方形的边长,分别利用圆和正方形
的面积公式表示出它们的面积,即可求得圆面积与正方形面积的比.
解答:
解:如图所示,
(1)在圆里面画一个最大的正方形,设圆的半径是R ,
因为圆的面积=πR 2
,
正方形的面积=2R ×R ÷2×2=2R 2,
所以正方形的面积:圆的面积=2R 2:πR 2 π
2=2:π;
(2)在正方形里面画一个最大的圆,设正方形的边长为a , ,
因为正方形的面积=a ×a=a 2,
圆的面积=π(2a )²=4
π×a ²
所以圆的面积:正方形的面积=4
π×a ²:a 2=π:4;
【典型例题】
例题1、在下图中,已知正方形的面积是40平方厘米,这个圆的面积是多少平
方厘米?
例题2、在下图中,已知三角形的面积是10平方厘米,这个圆的面积是多少平
方厘米?
例题3、在下图中,已知外面的正方形的面积是80平方厘米,求圆的面积和小正方形的面积。
【经典练习】
1、请你说出下面各图形中的空白部分、阴影部分的面积分别占整个图形的百分之几?
o
(1)(2)
(3)
(4)
2、在三块面积相等的正方形铁板上,分别冲下1个、4个和9个圆片,(如图)。
这时,三块铁板剩余材料的面积相等吗?
提高练习:1、下图中空白部分的面积有多大?
5厘米
2、下图中阴影部分的面积是43平方厘米,正方形的面积是多少平方厘米?
3、下图中空白部分的面积是157平方厘米,正方形的面积是多少平方厘米?
4、图中空白部分的面积是200平方厘米。
圆形的面积是多少平方厘米?
5、下图中阴影部分的面积是100平方厘米,空白部分的面积是多少平方厘米?
6、下图中空白部分的面积是114平方厘米,圆形的面积是多少平方厘米?
7、小正方形面积是200平方厘米,大圆的面积是多少平方厘米?
【挑战金牌】
(圆内一个最大的正方形与圆的面积比是2:π,正方形内的最大圆与正方形的面积之比是π:4。
)说一说圆的面积与正方形的面积有什么关系?。
