模式定理 积木块假设
遗传算法的数学基础

第3章遗传算法的数学基础遗传算法在机理方面具有搜索过程和优化机制等属性,数学方面的性质可通过模式定理和构造块假设等分析加以讨论,Markov链也是分析遗传算法的一个有效工具。
遗传算法的选择操作是在个体适应度基础上以概率方式进行的,在概率选择方式上与模拟退火法有些类似。
本章将较全局地介绍遗传算法的基础数学理论和分析工具,包括验证基础遗传算法(SGA)的有效性的模式定理,分析遗传算法过程的Walsh模式变换方法,遗传算法的欺骗问题以及遗传算法的动态分析工具—Markov链分析。
3.1 模式定理1. 模式我们将种群中的个体即基因串中的相似样板称为“模式”,模式表示基因串中某些特征位相同的结构,因此模式也可能解释为相同的构形,是一个串的子集。
在二进制编码中,模式是基于三个字符集{0,1,*}的字符串,符号* 代表0或1。
例1.*1*表示四个元的子集{010 011 110 111}对于二进制编码串,当串长为L时,共有3L个不同的模式。
例2.串长L=3,则其模式共有{*** *1* *0* **1 **0 1**0** *10 *00 *01 1*1 1*0 0*1 0*0 11* 10* 01* 00*111 110 101 011 001 010 100 000 }共27个1+2*3+22*3+23=33遗传算法中串的运算实际上是模式的运算。
如果各个串的每一位按等概率生成0或1,则模式为n 的种群模式种类总数的期望值为:12(1(1(1/2)))Lii i nl i C =--∑ 种群最多可以同时处理2l n 个模式,见下例例 一个个体(种群中只有一个),父个体011 要通过变异变为子个体001,其可能影响的模式为:被处理的模式总数为8个,8=1*23如果独立的考虑种群中的各个串,则仅能得到n 条信息,然而当把适应值与各个串结合考虑,发掘串群体的相似点,就可得到大量的信息来帮助指导搜索,相似点的大量信息包含在规模不大的种群中。
遗传算法原理与应用

一、遗传算法概述
1、智能优化算法 2、基本遗传算法 3、遗传算法的特点
1、智能优化算法
智能优化算法又称为现代启发式算法, 是一种具有全局优化性能、通用性强、 且适合于并行处理的算法。这种算法一 般具有严密的理论依据,而不是单纯凭 借专家经验,理论上可以在一定的时间 内找到最优解或近似最优解。
均点交叉运算 交叉前: 00000|01110|00000|00100|00 11100|00000|11111|10001|01 交叉后: 00000|00000|00000|10001|00 11100|01110|11111|00100|01 交叉点
均匀交叉又称“驻点交叉”,在交叉前先进行基因的变异 检测,通过后再行交叉。
(2) 利用比例选择算子的公式,计算每个个体被
选中遗传到下一代群体的概率;
(3) 采用模拟赌盘操作(即生成0到1之间的随机
数与每个个体遗传到下一代群体的概率进行匹配) 来确定各个个体是否遗传到下一代群体中。
以赌轮盘的方式來看,把一个轮盘分成若干扇形, 面积越大的编号,越容易中奖,因此奖金会比較低。 以适应性函数來看,其值越大者所占的面积就越大, 其选中的机率就越大。
轮盘赌选择又称比例选择算子,它的基本思想 是:各个个体被选中的概率与其适应度函数值大小 成正比。设群体大小为n ,个体i 的适应度为 Fi, 则个体i 被选中遗传到下一代群体的概率为:
P i F i / F i
i 1
n
轮盘赌选择方法的实现步骤
(1) 计算群体中所有个体的适应度函数值(需要 解码);
身的要求而定。
选择算子
遗传算法使用选择运算来实现对群体中的个 体进行优胜劣汰操作:适应度高的个体被遗传到
建模作业

智能优化算法之遗传算法一、智能优化算法智能优化算法又称为现代启发式算法,是一种具有全局优化性能、通用性强、且适合于并行处理的算法。
这种算法一般具有严密的理论依据,而不是单纯凭借专家经验,理论上可以在一定的时间内找到最优解或近似最优解。
定的概率在整个求解空间中探索最优解。
由于它们可以把搜索空间扩展到整个问题空间,因而具有全局优化性能。
二、遗传算法1.遗传算法产生与发展(1) 产生①早在50年代,一些生物学家开始研究运用数字计算机模拟生物的自然遗传与自然进化过程;② 1963年,德国柏林技术大学的I. Rechenberg和H. P. Schwefel,做风洞实验时,产生了进化策略的初步思想;③ 60年代,L. J. Fogel在设计有限态自动机时提出进化规划的思想。
1966年Fogel等出版了《基于模拟进化的人工智能》,系统阐述了进化规划的思想;④ 60年代中期,美国Michigan大学的J. H. Holland教授提出借鉴生物自然遗传的基本原理用于自然和人工系统的自适应行为研究和串编码技术;⑤ 1967年,他的学生J. D. Bagley在博士论文中首次提出“遗传算法(Genetic Algorithms)”一词;⑥1975年,Holland出版了著名的“Adaptation in Natural and Artificial Systems”,标志遗传算法的诞生。
(2) 发展①70年代初,Holland提出了“模式定理”(Schema Theorem),一般认为是“遗传算法的基本定理”,从而奠定了遗传算法研究的理论基础;②1985年,在美国召开了第一届遗传算法国际会议,并且成立了国际遗传算法学会(ISGA,International Society of Genetic Algorithms);③1989年,Holland的学生D. J. Goldherg出版了“Genetic Algorithms in Search, Optimization, and Machine Learning”,对遗传算法及其应用作了全面而系统的论述;④ 1991年,L. Davis编辑出版了《遗传算法手册》,其中包括了遗传算法在工程技术和社会生活中大量的应用实例。
遗传算法基本理论与方法

摘要:基本遗传算法的操作是以个体为对象,只使用选择、交叉和变异遗传算子,遗传进化操作过程的简单框架。
模式定理和积木块假设是解释遗传算法有效性的理论基础,理论分析与实际应用都表明基本的遗传算法不能处处收敛于全局最优解,因此基本遗传算法有待进一步改进。
关键词:遗传算法;遗传算法的改进1.标准遗传算法基本遗传算法包括选择、交叉和变异这些基本遗传算子。
其数学模型可表示为:sag=(c,e,p0,n,φ,г,ψ,t)其中c为个体的编码方法;e为个体适应度评价函数;p0为初始种群;n为种群大小;φ为选择算子;г为交叉算子;ψ为变异算子;t为遗传运算终止条件;2 遗传算法基本方法及其改进2.1编码方式编码方式决定了个体的染色体排列形式,其好坏直接影响遗传算法中的选择算子、交叉算子和变异算子的运算,也决定了解码方式。
二进制编码二进制编码使用的字符号{0,1}作为编码符号,即用一个{0,1}所组成的二进制符号串构成的个体基因型。
二进制编码方法应用于遗传算法中有如下优点:1)遗传算法中的遗传操作如交叉、变异很容易实现,且容易用生物遗传理论来解释;2)算法可处理的模式多,增强了全局搜索能力;3)便于编码、解码操作;4)符合最小字符集编码原则;5)并行处理能力较强。
二进制编码在存着连续函数离散化的映射误差,不能直接反应出所求问题的本身结构特征,不便于开发专门针对某类问题的遗传运算算子。
2.2初始种群的设定基本遗传算法是按随机方法在可能解空间内产生一个一定规模的初始群体,然后从这个初始群体开始遗传操作,搜索最优解。
初始种群的设定一般服从下列准则:1)根据优化问题,把握最优解所占空间在整个问题空间的分布范围,然后,在此分布范围内设定合适的初始群体。
2)先随机生成一定数目的个体,然后从中挑出最好的个体加入到初始群体中。
该过程不断迭代,直到初始群体中个体数目达到了预先确定的种群大小。
2.3选择算子的分析选择算子的作用是选择优良基因参与遗传运算,目的是防止有用的遗传信息丢失,从而提高全局收敛效率。
遗传算法的基本原理

第二章 遗传算法的基本原理2.1 遗传算法的基本描述2.1.1 全局优化问题全局优化问题的定义:给定非空集合S 作为搜索空间,f :S —>R 为目标函数,全局优化问题作为任务)(max x f Sx ∈给出,即在搜索空间中找到至少一个使目标函数最大化的点。
全局最大值(点)的定义:函数值+∞<=)(**x f f 称为一个全局最大值,当且仅当x ∀S x ∈,(ρi i b a <,i 12)定义适应度函数f(X);3)确定遗传策略,包括群体规模,选择、交叉、变异算子及其概率。
4)生成初始种群P ;5)计算群体中各个体的适应度值;6)按照遗传策略,将遗传算子作用于种群,产生下一代种群;7)迭代终止判定。
遗传算法涉及六大要素:参数编码,初始群体的设定,适应度函数的设计,遗传操作的设计,控制参数的设定,迭代终止条件。
2.1.3 遗传编码由于GA 计算过程的鲁棒性,它对编码的要求并不苛刻。
原则上任何形式的编码都可以,只要存在合适的对其进行操作的遗传算子,使得它满足模式定理和积木块假设。
由于编码形式决定了交叉算子的操作方式,编码问题往往称作编码-交叉问题。
对于给定的优化问题,由GA 个体的表现型集合做组成的空间称为问题(参数)空间,由GA 基因型个体所组成的空间称为GA 编码空间。
遗传算子在GA 编码空间中对位串个体进行操作。
定义:由问题空间向GA 编码空间的映射称为编码,而有编码空间向问题空间的映射成为译码。
1)2)3)它们对1)2)k =1,2,…,K; l =1,2,…,L; K=2L其中,个体的向量表示为),,,(21kL k k k a a a a =,其字符串形式为kL k k k a a a s 21=,s k 称为个体a k 对应的位串。
表示精度为)12/()(--=∆L u v x 。
将个体又位串空间转换到问题空间的译码函数],[}1,0{:v u L →Γ的公式定义为:对于n 维连续函数),,2,1](,[),,,,(),(21n i v u x x x x x x f i i i n =∈=,各维变量的二进制编码位串的长度为l i ,那么x 的编码从左到右依次构成总长度为∑==ni i l L 1的二进制编码位串。
近代工程优化简答题

1.简述传统优化算法与遗传算法的特点及其优缺点。
传统优化算法的特点:A.传统优化算法一般是确定性算法,有固定的结构和参数,计算复杂度和收敛性可做理论分析。
B.传统优化算法大多属于凸优化范畴,有唯一明确的全局最优解。
C.传统优化算法一般是针对结构化的问题,有较为明确的问题和条件描述,如线性规划、二次规划、整数规划、混合规划、带约束和不带约束等,即有清晰的结构信息。
遗传算法的特点:A.遗传算法是对参数的编码进行操作,而不是对参数本身,因而适应于求解复杂的优化问题,应用范围很广。
B.遗传算法属于种群搜索算法,易于并行处理,可以有效防止局部搜索过程收敛于局部最优解,而且有较大的可能求得全局最优解。
C.遗传算法通过目标函数来计算适应度值,而不需要其他信息,从而对问题的依赖性较小。
D.遗传算法使用概率的转变原则,而不是确定性的规则。
E.遗传算法在解空间内不是盲目地穷举或完全随机搜索,而是一种启发性搜索,其搜索效率往往优于其它方法。
F.遗传算法对于待寻优的函数基本无限制,因而应用范围很广。
遗传算法的优点:A. 与问题领域无关且具有快速随机的搜索能力。
B. 搜索从群体出发,具有潜在的并行性,可以进行多个个体的同时比较。
C. 搜索使用评价函数启发,过程简单D. 使用概率机制进行迭代,具有随机性。
E. 具有可扩展性,容易与其他算法结合。
遗传算法的缺点:A.收敛速度慢。
B.局部搜索能力较差。
C.控制变量较多。
D.无确定的终止准则。
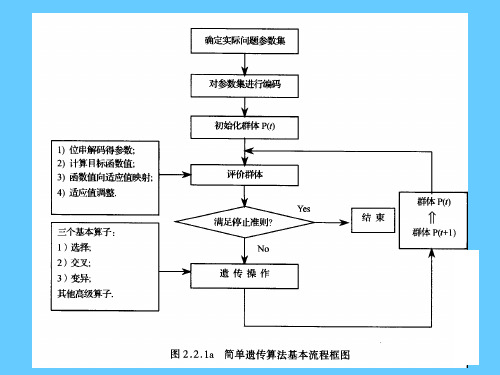
2. 简述遗传算法的基本原理,并给出基本遗传算法的求解步骤和流程图遗传算法的基本原理:遗传算法是模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象,在每次迭代中都保留一组候选解,并按某种指标(适应度函数)从解群中选择较优的个体,利用遗传算子(选择、交叉和变异)对这些个体进行重组,产生新一代的候选解群,重复此过程,直到满足某种收敛指标为止。
基本遗传算法的求解步骤:A.初始化。
设置进化代数计数器k=0,设置群体规模,最大进化代数M,交叉概率、变异概率。
遗传算法及其应用-毕业论文

摘要遗传算法是一种模拟自然界生物进化的搜索算法,由于它的简单易行、鲁棒性强,尤其是其不需要专门的领域知识而仅用适应度函数作评价来指导搜索过程,从而使它的应用范围极为广泛,并且己在众多领域得到了实际应用,取得了许多令人瞩目的成果,引起了广大学者和工程人员的关注。
在简要的介绍了遗传算法的发展历史和研究现状及其生物学、数学基础后,文中引出了遗传算法的基本概念和原理、分析了遗传算法的基本实现技术。
如:编码、适应度函数、遗传算法的三大遗传操作、参数规则等。
最后在介绍了遗传算法程序设计原则的基础上,编程实现了遗传算法在图像识别中的应用,在实践中检验了遗传算法的实际效果。
关键词:遗传算法,适应度函数,图像识别ABSTRACTThe genetic algorithmis akindof searching method which simulates the natural evolution. It is simple and easy to i mplement, especially it do not needthe special field knowledg e, so ithas been using in very broad fields. Now the genetic al gorithm has got a lotof fruits, andmore and more scholars beginto payattention on it.After brief introducted thegenetic algorithm and studyed the history of the development status andbiology, mathematicalbasis, we brought out the basic genetic algorithm concepts and principles, analysised the genetic algorithm to achieve t hebasic technology. Such as: coding, fitnessfunction, gen etic algorithm of the three major genetic manipulation, and othe r parameters of the rules. Finally, introduced a genetic algori thm procedures based on theprinciples of design, programming a genetic algorithm in the applicationof image recognition, in practice, wetest the practical effects of geneti c algorithm.Key word:geneticalgorithm,Fitness function,image recognition引言当前科学技术正进入多学科互相交叉、互相渗透、互相影响的时代,生命科学与工程科学的交叉、渗透和相互促进是其中的一个典型例子,也是近代科学技术发展的一个显著特点。
遗传算法与蚁群算法简介

实数编码的GA通常采用算术交叉: 双个体算术交叉:x1、x2为父代个体,α ∈(0, 1)为随机数 x1' = αx1 + (1 - α)x2 x2' = αx2 + (1 - α)x1 多个体算术交叉: x1, …, x2为父代个体; αi ∈(0, 1)且∑αi = 1 x' = α1x1 + α2x2 + … + αnxn 组合优化中的置换编码GA通常采用 部分映射交叉(partially mapping crossover, PMX):随机选择两个交叉点,交换交叉点之间的片段;对于其他基因,若它不与换过来的片段冲突则保留,若冲突则通过部分映射来确定最后的基因 p1 = [2 6 4 | 7 3 5 8 | 9 1] p1' = [2 3 4 | 1 8 7 6 | 9 5] p2 = [4 5 2 | 1 8 7 6 | 9 3] p2' = [4 1 2 | 7 3 5 8 | 9 6]
北京交通大学计算机与信息技术学院
*
智能优化算法简介
*பைடு நூலகம்
20世纪80年代以来,一些优化算法得到发展 GA、EP、ACO、PSO、SA、TS、ANN及混合的优化策略等 基本思想:模拟或揭示某些自然现象或过程 为用传统的优化方法难以解决的NP-完全问题提供了有效的解决途径 由于算法构造的直观性与自然机理,因而通常被称作智能优化算法(intelligent optimization algorithms),或现代启发式算法(meta-heuristic algorithms) [智能优化算法及其应用,王凌,清华大学出版社,2001]
线性次序交叉(LOX)
单位置次序交叉(C1)
类似于OX。选择一个交叉位置,保留父代个体p1交叉位置前的基因,并在另一父代个体p2中删除p1中保留的基因,将剩余基因填入p1的交叉位置后来产生后代个体p1'。如父代个体同前,交叉位置为4,则后代个体为p1' =[2 6 4 7 | 5 1 8 9 3],p2' =[4 5 2 1 | 6 7 3 8 9]
遗传算法的基本原理(1)
4.1 遗传算法的基本描述
4.1.3 遗传编码
根据模式定理,De Jong进一步提出了较为客观明确的 编码评估准则,称之为编码原理。具体可以概括为两 条规则:
1)有意义积木块编码规则:编码应易于生成与所求问题 相关的短距和低阶的积木块。
2)最小字符集编码规则:编码应采用最小字符集,以使 问题得到自然、简单的表示和描述。
akl 0,1
表示精度为x (v u) /(2L 1) 。
将个体又从位串空间转换到问题空间的译码函数 : {0,1}L [u, v]
的公式定义为:
xk
(ak1, ak2 ,, akL )
u
vu 2L 1
ቤተ መጻሕፍቲ ባይዱ
(
L j 1
akj
2L
j
)
4.1 遗传算法的基本描述
对于n维连续函数f (x), x (x1, x2 ,, xn ), xi [ui , vi ](i 1,2,, n) ,
操作后的期望数量为 n pn 。其它个体的期望数量按等差序
列计算
j
j1
n 1
,j
(
j
1)
( ) n 1
(
j
1,)
故现在排序选择概率为
ps (a
j
)
1 n
(
( )
n 1
(
j
1)),
j 1,2,, n
4.1.6 遗传算子
一、选择(selection)算子
4、联赛选择(tournament selection) • 基本思想:从当前群体中随机选择一定数量的个体(放回或者不
4.1.6 遗传算子
一、选择(selection)算子
2遗传算法介绍

对控制参数的改进
Srinvivas等人提出自适应遗传算法,即PC和Pm 能够随适应度自动改变,当种群的各个个体适应度 趋于一致或趋于局部最优时,使二者增加,而当种 群适应度比较分散时,使二者减小,同时对适应值 高于群体平均适应值的个体,采用较低的PC和Pm, 使性能优良的个体进入下一代,而低于平均适应值 的个体,采用较高的PC和Pm,使性能较差的个体被 淘汰。
对遗传算子的改进
排序选择 均匀交叉 逆序变异
(1) 随机产生一个与个体编码长度 相同的二进制屏蔽字P = W1W2„Wn ; (2) 按下列规则从A、B两个父代个 体中产生两个新个体X、Y:若Wi = 0, 则X的第i个基因继承A的对应基因,Y 的第i个基因继承B的对应基因;若Wi = 1,则A、B的第i个基因相互交换,从 而生成X、Y的第i个基因。
模式阶用来反映不同模式间确定性的 差异,模式阶数越高,模式的确定性就越高,
所匹配的样本数就越少。在遗传操作中,即
使阶数相同的模式,也会有不同的性质,而
模式的定义距就反映了这种性质的差异。
模式定理
模式定理:具有低阶、短定义距以及平 均适应度高于种群平均适应度的模式在子代
中呈指数增长。
模式定理保证了较优的模式(遗传算法
的质量越好。适应度函数是遗传算法进化过
程的驱动力,也是进行自然选择的唯一标准,
它的设计应结合求解问题本身的要求而定。
选择算子
遗传算法使用选择运算来实现对群体中的个体 进行优胜劣汰操作:适应度高的个体被遗传到下一
代群体中的概率大;适应度低的个体,被遗传到下
一代群体中的概率小。选择操作的任务就是按某种 方法从父代群体中选取一些个体,遗传到下一代群
遗传算法应用于组合优化
遗传算法编码及算子简介

遗传算法编码及算子简介遗传算法主要是通过遗传操作对群体中具有某种结构形式的个体施加结构重组处理,从而不断地搜索出群体中个体间的结构相似性,形成并优化积木块以逐渐逼近最优解。
由此可见,必须把群体中的个体转化成按一定基因结构组成的染色体或个体,即编码。
编码原则包括两条:1.有积极积木块编码规则,即所定编码应当易于生成所求问题相关的短距和低阶的积木块。
2.最小字符集编码规则,即所定编码应用最小字符集以使问题得到自然的表示或描述。
规则一是基于模式定理和积木块假设;规则二提供了一种更为实用的编码规则。
评估编码策略常采用的规范有:1.完备性:问题空间中的所有点都能作为GA空间的点表现。
2.健全性:GA空间中的染色体能对应所有问题空间中的候选解。
3.非冗余性:染色体和候选解一一对应。
这些评估规范是独立于问题领域的普遍准则。
对某个具体的应用领域而言,应该客观化地比较和评估该问题领域中所用的编码方法。
应用遗传算法进行优化,首先将问题描述成串的形式,以模拟染色体。
选择何种编码方式对算法的运行有很大的影响。
现在,流行的观点认为二进制编码能在相同的范围内表示最多的模式,能充分地体现所谓的隐含并行性。
但是,二进制编码方式的精度依赖于染色体的基因位数及设计变量的范围。
因而对于高精度、多变量问题,n值需很大,降低遗传算法的收敛速度。
另外,二进制编码不直接反映真实的设计空间。
其它的编码方式还有:格雷码编码、浮点编码、树结构编码、参数动态编码和多维编码等。
遗传算法主要有选择、交叉和突变算子选择算子遗传算法使用选择算子或称复制算子来对种群中的个体进行优胜劣汰操作:选择算子使适应性高的个体在后代中生存的概率较大,而适应度低的个体生存的概率很小甚至被淘汰。
遗传算法中的选择操作就是来确定如何从父代群体中按某种方法选取那些个体以传到下一代群体的一种遗传算法。
选择操作是建立在群体中个体的适应度评价基础上的。
选择操作的主要目的是为了避免基因缺失、提高全局收敛性和计算效率。
《遗传算法原理及应用》课程教学大纲

《遗传算法原理及应用》课程教学大纲课程名称:遗传算法原理及应用课程类别:任意选修课适用专业:电子信息工程考核方式:考查总学时、学分:24学时1.5学分一、课程性质、教学目标遗传算法原理及应用是电子信息工程专业的一门任意选修课。
通过本门课的学习,要求学生理解基本遗传算法的特点、思想及其实现过程,了解GA的发展及其应用,熟悉MATLAB遗传算法工具箱函数及其初步应用,并不断提高分析和解决具体问题的能力。
该课程主要包括基本遗传算法,遗传算法的基本、高级实现技术,并行遗传算法,遗传算法的数学理论及应用等。
本门课程与《数字图像处理》、《人工神经网络》、《机器学习与应用》等专业选修课程内容具有较强的相关性和融合性。
其具体的课程教学目标为:课程教学目标1:了解遗传算法的特点、发展及应用。
课程教学目标2:理解GA的基本实现方法以及一些高级实现技术。
理解模式和模式定理;了解评价遗传算法的一些常用测试函数。
课程教学目标3:了解遗传算法在数值函数优化、多目标优化、装箱、旅行商等问题中的应用。
课程教学目标与毕业要求对应的矩阵关系二、课程教学要求遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。
通过本课程的学习,使学生了解遗传算法的生物学基础、特点、发展及应用;理解SGA、GA的一些基本及高级实现技术;掌握模式的概念和模式定理的含义;了解进行遗传算法评价的常用测试函数,SGA的收敛性分析;了解遗传算法在多领域中的应用。
三、先修课程高等数学、算法与数据结构、计算机基础与应用、计算机仿真(Matlab和Multisim)等。
四、课程教学重、难点教学重点:遗传算法的各种基本编码方法、适应度函数、选择算子、交叉算子、变异算子;教学难点:GA倒位算子及二倍体显性操作算子的基本实现; GA 的运行参数和约束条件的处理方法;变长度染色体遗传算法、小生境遗传算法和混合遗传算法的基本思想。
五、课程教学方法与教学手段本课程以课堂讲授、讨论、交流为主,课下自学为辅。
遗传算法求复杂函数极值问题

遗传算法求复杂函数极值问题中文摘要:本文首先介绍遗传算法的历史背景,基本思想,对遗传算法的常见的编码解码方法进行了深入的阐述,并对算子选择方法进行深入分析和对比,在此基础上把遗传算法应用于求解复杂函数的极值计算。
最后在MATLAB语言环境下编写程序,对求解函数的最大值进行了仿真,并对调试的结果进行了分析,得出了部分结论。
关键词:遗传算法最优解算子选择复杂函数作者:xx xx指导老师:xxxx xxUsing Genetic Algorithm to Solve Extreme Problemof Complex FunctionAbstractFirstly,the historical background and basic idea of genetic algorithm are introduced in this paper. The common coding and decoding method of genetic algorithm are discussed too.Secondly, the selection method of genetic operator is analyzed and compared deeply, based on which genetic algorithm is used to solve extreme problem of complex function.Finally, with MATLAB software, the program is compiled and the maximum is sought out. At the end of the paper, the debugging result is analyzed and the conclusion is given.Keywords: Genetic Algorithm Optimal Solution Operator Selection Complex FunctionWritten by : xx xxSupervised by: xxxx xx目录第一章绪论 (5)1.1 遗传算法生物学背景 (5)1.1.1 遗传与变异 (5)1.1.2 进化 (5)1.2 本文主要内容 (5)第二章遗传算法简介 (6)2.1 遗传算法历史和发展 (6)2.2 遗传算法的基本原理 (6)2.3 遗传算法的特点 (7)2.4 遗传算法的目的 (7)2.5 遗传算法应用 (8)第三章遗传算法的参数和算子选择 (10)3.1 遗传算法的数学理论 (10)3.2 编码 (11)3.2.1 编码方法 (11)3.2.2 编码原则 (13)3.3 个体适应度函数 (13)3.3.1 评价个体适应 (13)3.2.2 适应度尺度变换 (14)3.3 算子选择 (14)3.3.1 选择运算 (14)3.3.2 交叉运算 (16)3.3.3 变异运算 (18)3.4 其他运行参数 (18)第四章遗传算法求解复杂函数极值问题 (20)4.1 遗传算法的求解步骤 (20)4.2 算例验证 (24)第五章结论 (28)参考文献 (28)附录(程序) (29)第一章绪论1.1遗传算法生物学背景生物的进化是一个奇妙的优化过程,它通过选择淘汰,突然变异,基因遗传等规律产生适应环境变化的优良物种。
《计算智能导论》教学大纲

《计算智能导论》教学大纲课程编号:课程名称:计算智能导论英文名称:Introduction of Computational Intelligence 学分:3 学时:48课程类型:必修课程性质:专业基础课适用专业:智能科学与技术专业先修课程:离散数学、高等数学、算法设计与分析开设学期:第6学期开课院系:电子工程学院一、课程的教学目标与任务计算智能是模拟自然以实现对复杂问题求解的科学,是生物学、神经科学、认知科学、计算机科学、免疫学、哲学、社会学、数学、信息科学、非线性科学、工程学、音乐、物理学等众多学科相互交叉融合的结果,是人们对自然智能认识和模拟的最新成果。
目前计算智能已经成为智能与信息科学中最活跃的研究领域之一,它的深入发展将极大地改变人们认识自然,求解现实问题的能力和水平。
计算智能导论这门课程主要介绍了计算智能的3个典型范例:人工神经网络、进化计算、模糊系统,它们分别建模了以下自然系统:生物神经网络、进化、和人类思维过程。
通过本课程的学习,要求学生了解并掌握人工神经网络、进化计算、和模糊系统等计算智能模型。
二、课程具体内容及基本要求(一)计算智能简介(4学时)内容:计算智能的基本概念,计算智能的典型方法和计算智能的发展历史。
1. 基本要求(1)了解人计算智能的发展历史、研究现状及发展过程中的几个研究途径;(2)掌握最计算智能的基本概念;2. 重点、难点重点:计算智能概念难点:计算智能的认知观3. 作业及课外学习要求(二)人工神经网络基础(6学时)内容:人工神经元与神经网络模型,人工神经网络结构及工作方式和人工神经网络的学习。
1. 基本要求(1)理解人工神经元与神经网络模型;(2)掌握人工神经网络结构及工作方式和人工神经网络的学习。
2. 重点、难点重点:工神经网络结构及工作方式难点:人工神经网络的学习3. 作业及课外学习要求(三)常用的学习神经网络(6学时)内容:监督学习神经网络(包括神经网络的类型,监督学习规则,隐层单元的功能和集成神经网络)和非监督学习神经网络(包括非监督学习,Hebb学习规则)1. 基本要求(1)掌握监督学习神经网络(2)理解相非监督学习神经网络的思想与算法。
第6章 智能计算及其应用(导论5)

满足
f f ,
avg
avg
f m ax Cmult f avg
a (Cmult 1) f avg f max f avg
满足最小适应度值非负
a
f avg
f avg f min
b ( f max Cmult f avg ) f avg f max f avg
b f min f avg f avg f min
7
6.1.2 进化算法的生物学背景
适者生存:最适合自然环境的群体往往产生了更大的后代群 体。
生物进化的基本过程:
染色体(chromosome):生物 的遗传物质的主要载体。
基因(gene):扩展生物性状 的遗传物质的功能单元和结 构单位。
基 因 座 ( locus ) : 染 色 体 中基因的位置。
6.3 遗传算法的改进算法
6.4 遗传算法的应用
6.5 群智能算法产生的背景
6.6 粒子群优化算法及其应用
6.7 蚁群算法及其应用
5
6.1 进化算法的产生与发展
6.1.1 进化算法的概念 6.1.2 进化算法的生物学背景 6.1.3 进化算法的设计原则
6
6.1.1 进化算法的概念
进化算法(evolutionary algorithms,EA)是基于自然 选择和自然遗传等生物进化机制的一种搜索算法。
③ 求解高维优化问题的二进制编码串长,算法的搜索效率低。
20
6.2.3 编码
1. 位串编码 (2) Gray 编码
Gray编码:将二进制编码通过一个变换进行转换得到的编码。
二进制串 12...n
Gray 1 2... n
二进制编码 Gray编码
k
药物设计常用方法QSAR方法介绍

药物设计常用方法QSAR方法介绍一QSAR方法定义和发展过程简介定量构效方法(quantitative structure-activity relationship, QSAR)是应用最为广泛的药物设计方法。
所谓定量构效方法就是通过一些数理统计方法建立其一系列化合物的生理活性或某种性质与其物理化学性质之间的定量关系,通过这些定量关系。
可以预测化合物的生理活性或某些性质,指导我们设计出具有更高活性的化合物。
早在1867年,Crum-Brow 和Fraser就提出了构效关系的概念,1900年前后,Overton 和Meyer等提出了麻醉作用的类脂学说,即化学结构各异的麻醉剂其活性随着脂-水分配系数增加而增加的现象,这可能是最早提出的化合物生理活性和物理化学性质之间的定量分配关系模型。
但只是到近几十年,尤其是Hansch法提出后,随着计算机技术的发展和多变量解析技术的引入,定量构效关系方法才逐渐发展和应用起来,现在它已经成为药物设计和药物开发中不可缺少的工具。
二:常用QSAR方法介绍1 二维定量构效关系方法(2D-QSAR)传统的二维定量构效关系方法很多,有Hansch法、模式识别Free-Wilson法和电子拓扑法。
其中最为著名应用最为广泛的就是Hansch和Fujita提出的Hansch法。
它假设同系列化合物某些生物活性的变化是和它们某些可测量物理化学性质的变化相联系的。
这些可测量的特性包括疏水性、电性质和空间立体性质等,都有可能影响化合物的生物活性。
Hansch法假定这些因子是彼此孤立的,故采用多重自由能相关法,借助多重线性回归等统计方法就可以得到定量构效关系模型。
Hansch法最初可以表达为下面的公式lg1/c=algp+bσ+cE+……+constant既活性和疏水性参数π或lgp、电负性参数σ以及立体参数E有关。
后来Hansch发现药物要交替穿过水相和类脂构成的体系,其移动难易程度和lgp呈现出函数关系。
GA算法

遗传算法的应用
5、节能设计方面对于汽车、机床等设备的电机类型、电 气控制参数、机械传动方案与参数等,以这些参数为参变 量编码,把能耗降低到最小目标,在满足功能要求的约 束下,利用遗传优化算法进行节能设计,使设备达到最佳效 果。 6、FMS(柔性制造系统)调度方面使待加工的零件在FMS 系统的制造时间最短,将该零件加工次序进行编码,用 遗传优化运算实现最短时间加工;针对一个需多工序加 工的零件,为确定每道工序所合理分配设备,对每道工序 分配设备号编码,在各台设备的负荷可能相等的前提下,用 遗传算法实现机床设备的最优分配。
模式示例:10**1
两个定义
– 定义1:模式 H 中确定位置的个数称为模式 H 的 阶,记作O(H)。 – 定义2:模式 H 中第一个确定位置和最后一个确 定位置之间的距离称为模式 H 的定义距,记作 δ(H)。
模式的描述:
模式的阶和定义距的含义
• 模式阶用来反映不同模式间确定性的差
异,模式阶数越高,模式的确定性就越
模拟生物在自然界环境变化,引起基因的突变.在染 色体二进制编码中,1变成0;或0变成1.突变产生染色 体的多样性,避免进化中早期成熟,陷入局部极值点, 突变的概率很低.
GA的流程
简单遗传算法(GA)的基本参数
①种群规模 P: 参与进化的染色体总数. ②代沟G: 二代之间不相同的染色体数目,无重叠G = 1;
变异概率对收敛性的影响
• 变异操作是对种群模式的扰动,有利于增 加种群的多样性 。但是,变异概率太小则 很难产生新模式,变异概率太大则会使遗 传算法成为随机搜索算法。
Schaffer建议的最优参数范围是: Population = 20-100, Generation = 100-500, Pc = 0.4-0.9, Pm = 0.001-0.01。
精品文档-MATLAB遗传算法工具箱及应用(第二版)雷英杰-第3章

第三章 遗传算法的理论基础 表3.1 二进制编码及函数值
编码 00 01 10 11
对应整数解 0 1 2 3
函数值 4 3 1 5
第三章 遗传算法的理论基础 表3.2 格雷编码及函数值
编码 00 01 11 10
对应整数解 0 1 2 3
函数值 4 3 1 5
第三章 遗传算法的理论基础 采用适当的适应度函数调整方法,设
第三章 遗传算法的理论基础
遗传算法中欺骗性的产生往往与适应度函数确定和调整、 基因编码方式选取相关。采用合适的编码方式或调整适应度函 数,就可能化解和避免欺骗问题。下面以合适的编码方式为例 来说明。
一个2位编码的适应度函数为
f (x) 4 11 x 4x2 7 x3
6
6
采用二进制编码,计算个体的函数值(见表3.1),则存在第二类 欺骗问题。采用格雷编码,计算个体的函数值(见表3.2),则第 二类欺骗问题化解为第一类欺骗问题。
第三章 遗传算法的理论基础 第三章 遗传算法的理论基础
第三章 遗传算法的理论基础
3.1 不失一般性,本节以二进制串作为编码方式来讨论模式定 理(PatternTheorem) 定义3.1 基于三值字符集{0,1,*}所产生的能描述具 有某些结构相似性的0、1 以长度为5的串为例,模式*0001描述了在位置2、3、4、 5具有形式“0001”的所有字符串,即(00001,10001)。由此 可以看出,模式的概念为我们提供了一种简洁的用于描述在某 些位置上具有结构相似性的0、1字符串集合的方法。
CC。个体S3含有
AA、CC,个体S7含有AA、BB。当种群进化到第二代后,第三代
种群如图3.3所示,在群体中,出现了含有积木块AA、BB、CC
模式定理 积木块假设

模式定理
模式是指种群个体基因串中的相似样板,它用来描述基因串中某些特征位相同的结构。
在二进制编码中,模式是基于三个字符集(0,1,*)的字符串,符号*代表任意字符,即 0 或者 1。
模式示例:10**1
定义1:模式 H 中确定位置的个数称为模式 H 的阶,记作O(H)。
例如O(10**1)=3 。
定义2:模式 H 中第一个确定位置和最后一个确定位置之间的距离称为模式 H 的定义距,记作δ(H)。
例如δ(10**1)=4 。
模式阶用来反映不同模式间确定性的差异,模式阶数越高,模式的确定性就越高,所匹配的样本数就越少。
在遗传操作中,即使阶数相同的模式,也会有不同的性质,而模式的定义距就反映了这种性质的差异。
模式定理:具有低阶、短定义距以及平均适应度高于种群平均适应度的模式在子代中呈指数增长。
模式定理保证了较优的模式(遗传算法的较优解)的数目呈指数增长,为解释遗传算法机理提供了数学基础。
积木块假设
遗传算法通过短定义距、低阶以极高平均适应度的模式(积木块),在遗传操作下相互结合,最终接近全局最优解。
模式定理保证了较优模式的样本数呈指数增长,从而使遗传算法找到了全局最优解的可能性存在;而积木块假设则指出了在遗传算子的作用下,能生成全局最优解。
多目标进化算法总结

MOGAi x 是第t 代种群中个体,其rank 值定义为:()(,)1t i i rank x t p =+()t i p 为第t 代种群中所有支配i x 的个体数目适应值(fitness value )分配算法:1、 将所有个体依照rank 值大小排序分类;2、 利用插值函数给所有个体分配适应值(从rank1到rank *n N ≤),一般采用线性函数3、 适应值共享:rank 值相同的个体拥有相同的适应值,保证后期选择时同一rank 值的个体概率相同最后采用共享适应值随机选取的方法选择个体进入下一代一种改进的排序机制(ranking scheme): 向量,1,(,,)a a a q y y y =⋅⋅⋅和,1,(,,)b b b q y y y =⋅⋅⋅比较 goal vector :()1,,q g g g =⋅⋅⋅ 分为以下三种情况:1、()(),,1,,1; 1,,;1,,; a i i a j j k q i k j k q y g y g ∃=⋅⋅⋅-∀=⋅⋅⋅∀=+⋅⋅⋅>∧≤2、(),1,,; a i i i q y g ∀=⋅⋅⋅>当a y 支配b y 时,选择a y 3、(),1,,; a j j j q y g ∀=⋅⋅⋅≤ 当b y 支配a y 时,选择b y优点:算法思想容易,效率优良 缺点:算法容易受到小生境的大小影响 理论上给出了参数share σ的计算方法NPGA基本思想: 1、初始化种群Pop2、锦标赛选择机制:随机选取两个个体1x 和2x 和一个Pop 的 子集CS (Comparison Set )做参照系。
若1x 被CS 中不少于一 个个体支配,而2x 没有被CS 中任一个体支配,则选择2x 。
3、其他情况一律称为死结(Tie ),采用适应度共享机制选择.个体适应度:i f小生境计数(Niche Count ):(),i j Popm Sh d i j ∈=⎡⎤⎣⎦∑共享函数:1-,()0,share shareshare d d Sh d d σσσ⎧≤⎪=⎨⎪>⎩共享适应度(the shared fitness ):iif m选择共享适应度较大的个体进入下一代优点:能够快速找到一些好的非支配最优解域 能够维持一个较长的种群更新期 缺点:需要设置共享参数需要选择一个适当的锦标赛机制限制了该算法的实际应用效果NPGA II基本思想: 1、初始化种群Pop2、Pareto 排序:非支配个体rank=0;其余个体 rank=支配该个体的个体数目3、锦标赛选择机制:种群中任选两个个体1x 和2x , 若()()12rank x rank x <,则选择1x ; 若是()()12rank x rank x =,称为死结(Tie ), 采用适应度共享机制选择。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模式定理
模式是指种群个体基因串中的相似样板,它用来描述基因串中某些特征位相同的结构。
在二进制编码中,模式是基于三个字符集(0,1,*)的字符串,符号*代表任意字符,即 0 或者 1。
模式示例:10**1
定义1:模式 H 中确定位置的个数称为模式 H 的阶,记作O(H)。
例如O(10**1)=3 。
定义2:模式 H 中第一个确定位置和最后一个确定位置之间的距离称为模式 H 的定义距,记作δ(H)。
例如δ(10**1)=4 。
模式阶用来反映不同模式间确定性的差异,模式阶数越高,模式的确定性就越高,所匹配的样本数就越少。
在遗传操作中,即使阶数相同的模式,也会有不同的性质,而模式的定义距就反映了这种性质的差异。
模式定理:具有低阶、短定义距以及平均适应度高于种群平均适应度的模式在子代中呈指数增长。
模式定理保证了较优的模式(遗传算法的较优解)的数目呈指数增长,为解释遗传算法机理提供了数学基础。
积木块假设
遗传算法通过短定义距、低阶以极高平均适应度的模式(积木块),在遗传操作下相互结合,最终接近全局最优解。
模式定理保证了较优模式的样本数呈指数增长,从而使遗传算法找到了全局最优解的可能性存在;而积木块假设则指出了在遗传算子的作用下,能生成全局最优解。
