中考圆知识点总结复习
中考圆的知识点总结(一)

中考圆的知识点总结(一)中考圆的知识点总结前言在中考数学中,圆是一个重要的知识点,掌握圆的性质和相关计算方法对于提高数学成绩至关重要。
本文将对中考圆相关的知识进行总结和归纳,以帮助同学们更好地掌握和应用。
正文1. 圆的定义和性质•圆的定义:圆是平面上到一个定点距离相等的所有点的集合。
•圆的性质:–圆心:圆上所有点到圆心的距离相等。
–半径:圆心到圆上任意一点的距离为半径。
–直径:通过圆心的两个点组成的线段,长度等于半径的两倍。
–弧:在圆上两个点之间的部分。
–相交:两个圆的交点即为相交的部分。
–切线:与圆只有一个交点的直线。
2. 圆的计算公式•圆的周长:C = 2πr,其中r为半径。
•圆的面积:S = πr²。
3. 圆的相关定理•弧长定理:弧长 = 弧度× 半径长度。
•弧度与度的关系:一周对应的弧度为2π弧度,180°对应π弧度,360°对应2π弧度。
•圆心角定理:圆心角的弧度等于对应的弧的弧度。
•切线定理:切线与半径垂直。
4. 圆的应用•判断点是否在圆的内部、外部或边界上。
•利用圆的性质解决几何问题,如求两个圆的位置关系、求切线等。
•应用圆的计算公式计算周长和面积。
结尾通过对中考圆的知识进行总结和归纳,我们可以更好地掌握和运用圆的相关性质和计算方法。
希望同学们在备考中能够深入理解这些知识,灵活运用,取得优异的成绩!5. 圆与三角形的关系•内切圆:三角形内部与三条边都相切的圆。
•外接圆:三角形三个顶点在圆上的圆。
•正切圆:三角形的一个顶点在圆上,另外两边分别与圆相切的圆。
6. 圆与直线的关系•弧的度数:弧所对圆心角的度数,通常表示为θ。
•弦:圆上两个点之间的线段。
•弦长定理:弦长等于过弧中点的直径的两倍乘以sin(θ/2)。
•弦切角定理:切线与弦的交点所对的圆心角等于弦上所对的弧的圆心角的一半。
7. 圆与平行线的关系•切割线定理:若两条平行线分别与一个圆相交,那么它们所切割出的弦、切线和割线都是相等的。
初中数学中考圆的知识点总结归纳(中考必备)

中考数学圆的知识点总结归纳一、圆的定义(1)平面上到定点的距离等于定长的所有点组成的图形叫做圆。
(2)平面上一条线段,绕它的一端旋转360°,留下的轨迹叫圆。
二、圆心(1)如定义(1)中,该定点为圆心(2)如定义(2)中,绕的那一端的端点为圆心。
(3)圆任意两条对称轴的交点为圆心。
(4)垂直于圆内任意一条弦且两个端点在圆上的线段的二分点为圆心。
注:圆心一般用字母O表示直径:通过圆心,并且两端都在圆上的线段叫做圆的直径。
直径一般用字母d表示。
半径:连接圆心和圆上任意一点的线段,叫做圆的半径。
半径一般用字母r表示。
圆的直径和半径都有无数条。
圆是轴对称图形,每条直径所在的直线是圆的对称轴。
在同圆或等圆中:直径是半径的2倍,半径是直径的二分之一.d=2r或r=二分之d。
圆的半径或直径决定圆的大小,圆心决定圆的位置。
圆的周长:围成圆的曲线的长度叫做圆的周长,用字母C表示。
圆的周长与直径的比值叫做圆周率。
圆的周长除以直径的商是一个固定的数,把它叫做圆周率,它是一个无限不循环小数(无理数),用字母π表示。
计算时,通常取它的近似值,π≈3.14。
直径所对的圆周角是直角。
90°的圆周角所对的弦是直径。
圆的面积公式:圆所占平面的大小叫做圆的面积。
πr^2,用字母S表示。
一条弧所对的圆周角是圆心角的二分之一。
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距也相等。
在同圆或等圆中,如果两条弧相等,那么他们所对的圆心角相等,所对的弦相等,所对的弦心距也相等。
在同圆或等圆中,如果两条弦相等,那么他们所对的圆心角相等,所对的弧相等,所对的弦心距也相等。
三、周长计算公式1.、已知直径:C=πd2、已知半径:C=2πr3、已知周长:D=c\π4、圆周长的一半:1\2周长(曲线)5、半圆的长:1\2周长+直径四、面积计算公式1、已知半径:S=πr平方2、已知直径:S=π(d\2)平方3、已知周长:S=π(c\2π)平方五、点、直线、圆和圆的位置关系1、点和圆的位置关系①点在圆内<=>点到圆心的距离小于半径②点在圆上<=>点到圆心的距离等于半径③点在圆外<=>点到圆心的距离大于半径2.过三点的圆不在同一直线上的三个点确定一个圆。
中考圆专题知识点总结

中考圆专题知识点总结一、圆的概念圆是平面上一个集合,该集合中任意两点的距离都相等,并且距离都等于圆的半径。
圆的周长叫做圆的周长,圆的面积叫做圆的面积。
圆的半径为r,圆的直径为d。
二、圆的性质1. 圆的周长和面积:圆的周长C = 2πr圆的面积S = πr²2. 弧和圆心角:- 弧:两点间的曲线部分,圆的一部分。
- 弧长:弧的长度,记作L。
- 圆心角:以圆心为顶点的角叫做圆心角,圆心角的度数等于它所对的弧的弧度数。
3. 弧长公式:L = rθ(θ用弧度表示)4. 圆周角:圆周角是一条弧所对的圆心角。
圆周角的度数等于它所对的圆心角的两倍。
5. 切线和切点:切线是与圆只有一个交点的直线。
切线与圆相切的点叫做切点。
6. 相交弧、对应弧和交角:- 相交弧:两个圆相交的弧。
- 对应弧:两个圆相交的弧的对应部分。
- 交角:两个相交弧的交角。
7. 圆内接四边形:如果一个四边形的四个顶点都在圆上,那么这个四边形叫做圆内接四边形。
8. 圆的切线和割线:切线是与圆只有一个交点的直线,割线是与圆相交而不相切的直线。
切线和割线的切点到圆心的连线和圆的半径相垂直。
三、圆周角、圆心角和弧对应的关系1. 圆周角的度数等于所对的圆心角的两倍。
2. 圆周角的度数等于所对的弧的度数。
3. 圆心角的度数等于所对的弧的度数。
四、圆的性质定理证明1. 同弧或同角:弧对应的圆心角和圆周角以及弧的长度都相等。
2. 切线定理:若直线与圆相交,且交点在圆外,则直线与圆的切点连线垂直于直线。
3. 切线与弦定理:如果一条切线和一条弦相交于圆上的同一点,则切线上这个点的两个切线段相等。
五、常见的圆相关问题1. 圆与圆之间的位置关系:相离、外切、相交、内切、相切。
2. 圆的面积和周长问题:求圆的面积和周长。
3. 圆心角、圆周角和弧的问题:根据给定的信息计算圆心角、圆周角和弧的长度。
4. 切线和切点的问题:计算切线和切点的位置以及相关长度。
5. 圆的切线和割线问题:计算切线和割线的位置以及相关长度。
中考圆的复习资料(经典+全)

圆的知识点复习知识点1垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
题型1.在直径为1000mm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=800mm,则油的最大深度为 mm.2. 如图,在△ABC中,∠C是直角,AC=12,BC=16,以C为圆心,AC为半径的圆交斜边AB于D,求AD的长。
3. 如图,弦AB垂直于⊙O的直径CD,OA=5,AB=6,求BC长。
CBDA4. 如图所示,在⊙O中,CD是直径,AB是弦,AB⊥CD于M,CD=15cm,OM:OC=3:5,求弦AB的长。
知识点2 圆心角:顶点在圆心的角叫做圆心角。
弦心距:过圆心作弦的垂线,圆心与垂足之间的距离叫弦心距。
定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角度数相等,所对的弦相等。
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角度数相等,所对的弧相等。
题型1. 如果两条弦相等,那么()A.这两条弦所对的弧相等 B.这两条弦所对的圆心角相等C.这两条弦的弦心距相等 D.以上答案都不对2.下列说法正确的是()A.相等的圆心角所对的弧相等 B.在同圆中,等弧所对的圆心角相等C.相等的弦所对的圆心到弦的距离相等 D.圆心到弦的距离相等,则弦相等3.线段AB是弧AB 所对的弦,AB的垂直平分线CD分别交弧AB、AC于C、D,AD的垂直平分线EF分别交弧AB、AB于E、F,DB的垂直平分线GH分别交弧AB、AB于G、H,则下面结论不正确的是()A.弧AC=弧CB B.弧EC=弧CG C.EF=FH D.弧AE=弧EC4. 弦心距是弦的一半时,弦与直径的比是________,弦所对的圆心角是_____.5. 如图,AB 为⊙O 直径,E 是BC 中点,OE 交BC 于点D ,BD=3,AB=10,则AC=_____.6. 如图,AB 和DE 是⊙O 的直径,弦AC ∥DE ,若弦BE=3,则弦CE=________.7. 如图,已知AB 、CD 为⊙O 的两条弦,弧AD =弧BC , 求证:AB =CD 。
中考圆形知识点总结归纳

中考圆形知识点总结归纳一、圆的定义及性质1. 定义:圆是平面上到一个定点的距离等于定长的点的全体构成的集合。
2. 圆心和半径:圆心是到圆上任一点的距离相等的点;半径是圆心到圆上任一点的距离。
3. 直径:通过圆心并且有圆上两点的线段叫做直径,直径的长度等于两倍的半径。
4. 切线和切点:在圆上的一点处与圆相切的直线叫做切线,切线与圆相切的点叫做切点。
二、圆的周长和面积1. 周长:圆的周长等于直径乘以π(π≈3.14)。
2. 面积:圆的面积等于半径的平方乘以π。
三、角与弧1. 圆心角与弧长的关系:圆心角的度数等于对应圆周的弧长所对应的圆心角的两倍。
2. 弧长的计算:弧长等于圆周长乘以所含圆心角的度数除以360度。
3. 弧度制:1弧度等于半径长所对应的圆心角的弧长。
4. 弧长与扇形面积的计算:扇形面积等于扇形对应的圆心角的弧度除以2π乘以圆的面积。
四、相交圆的位置关系1. 相交圆的位置关系:两个圆相交于两个不同的点,一个点,或者不相交。
2. 内切和外切圆:两个圆内切的位置关系就是一个圆在另一个圆内部,一个圆与另一个圆外切的位置关系就是一个圆的周长与另一个圆的圆心的距离相等。
五、圆的应用1. 圆的模型:圆在自然界中有丰富的应用,例如铁路辙、车轮、橱柜的拉手等都是圆形的。
2. 饼图:根据数据用圆形图示数据的比例和百分比,通过饼图可以直观的看出不同部分所占的比例。
综上所述,圆形是数学中重要的基本图形之一,在日常生活和工作中都有着广泛的应用,掌握圆形的基本概念和性质对于学习和生活都是非常有帮助的。
希望大家能够认真学习圆形知识,掌握相关的计算方法,提高自己的数学能力。
新人教版初中数学——圆的性质及与圆有关的位置关系-知识点归纳及中考典型题解析

人教版初中数学——圆的性质及与圆有关的位置关系知识点归纳及中考典型例题解析一、圆的有关概念1.与圆有关的概念和性质(1)圆:平面上到定点的距离等于定长的所有点组成的图形.(2)弦与直径:连接圆上任意两点的线段叫做弦,过圆心的弦叫做直径,直径是圆内最长的弦.(3)弧:圆上任意两点间的部分叫做弧,小于半圆的弧叫做劣弧,大于半圆的弧叫做优弧.(4)圆心角:顶点在圆心的角叫做圆心角.(5)圆周角:顶点在圆上,并且两边都与圆还有一个交点的角叫做圆周角.(6)弦心距:圆心到弦的距离.2.注意(1)经过圆心的直线是该圆的对称轴,故圆的对称轴有无数条;(2)3点确定一个圆,经过1点或2点的圆有无数个.(3)任意三角形的三个顶点确定一个圆,即该三角形的外接圆.二、垂径定理及其推论1.垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.关于垂径定理的计算常与勾股定理相结合,解题时往往需要添加辅助线,一般过圆心作弦的垂线,构造直角三角形.2.推论(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧.三、圆心角、弧、弦的关系1.定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.圆心角、弧和弦之间的等量关系必须在同圆等式中才成立.2.推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.四、圆周角定理及其推论1.定理一条弧所对的圆周角等于它所对的圆心角的一半.2.推论(1)在同圆或等圆中,同弧或等弧所对的圆周角相等.(2)直径所对的圆周角是直角.圆内接四边形的对角互补.在圆中求角度时,通常需要通过一些圆的性质进行转化.比如圆心角与圆周角间的转化;同弧或等弧的圆周角间的转化;连直径,得到直角三角形,通过两锐角互余进行转化等.五、与圆有关的位置关系1.点与圆的位置关系设点到圆心的距离为d.(1)d<r⇔点在⊙O内;(2)d=r⇔点在⊙O上;(3)d>r⇔点在⊙O外.判断点与圆之间的位置关系,将该点的圆心距与半径作比较即可.2.直线和圆的位置关系位置关系相离相切相交图形公共点个数0个1个2个数量关系d>r d=r d<r由于圆是轴对称和中心对称图形,所以关于圆的位置或计算题中常常出现分类讨论多解的情况.六、切线的性质与判定1.切线的性质(1)切线与圆只有一个公共点.(2)切线到圆心的距离等于圆的半径.(3)切线垂直于经过切点的半径.利用切线的性质解决问题时,通常连过切点的半径,利用直角三角形的性质来解决问题.2.切线的判定(1)与圆只有一个公共点的直线是圆的切线(定义法).(2)到圆心的距离等于半径的直线是圆的切线.(3)经过半径外端点并且垂直于这条半径的直线是圆的切线.切线判定常用的证明方法:①知道直线和圆有公共点时,连半径,证垂直;②不知道直线与圆有没有公共点时,作垂直,证垂线段等于半径.七、三角形与圆1.三角形的外接圆相关概念经过三角形各顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.外心是三角形三条垂直平分线的交点,它到三角形的三个顶点的距离相等.2.三角形的内切圆与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.内心是三角形三条角平分线的交点,它到三角形的三条边的距离相等.考向一圆的基本认识1.在一个圆中可以画出无数条弦和直径.2.直径是弦,但弦不一定是直径.3.在同一个圆中,直径是最长的弦.4.半圆是弧,但弧不一定是半圆.弧有长度和度数,规定半圆的度数为180°,劣弧的度数小于180°,优弧的度数大于180°.5.在同圆或等圆中能够互相重合的弧是等弧,度数或长度相等的弧不一定是等弧.典例1下列命题中正确的有①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.A.1个B.2个C.3个D.4个【答案】A【解析】①弦是圆上任意两点之间所连线段,所以①错误;②半径不是弦,所以②错误;③直径是最长的弦,正确;④只有180°的弧才是半圆,所以④错误,故选A.1.把圆的半径缩小到原来的14,那么圆的面积缩小到原来的A.12B.14C.18D.1162.半径为5的圆的一条弦长不可能是A.3 B.5 C.10 D.12考向二垂径定理1.垂径定理中的“弦”为直径时,结论仍然成立.2.垂径定理是证明线段相等、弧相等的重要依据,同时也为圆的计算和作图问题提供了理论依据.典例2如图,已知⊙O的半径为6 cm,两弦AB与CD垂直相交于点E,若CE=3 cm,DE=9 cm,则AB=A3cm B.3cm C.3D.3【答案】D【解析】如图,连接OA,∵⊙O的半径为6 cm,CE+DE=12 cm,∴CD是⊙O的直径,∵CD⊥AB,∴AE=BE,OE=3,OA=6,∴AE=2233OA OE-=,∴AB=2AE=63,故选D.典例3如图,将半径为2 cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为A.2 cm B.3cmC.23cm D.25cm【答案】C【解析】在图中构建直角三角形,先根据勾股定理得AD的长,再根据垂径定理得AB的长.作OD⊥AB于D,连接OA.根据题意得OD=12OA=1cm,再根据勾股定理得:AD3,根据垂径定理得AB3.故选C.3.如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为4,则弦AB的长是A.3 B.6 C.4 D.84.如图,某菜农在蔬菜基地搭建了一个横截面为圆弧形的蔬菜大棚,大棚的跨度弦AB的长为8515米,大棚顶点C离地面的高度为2.3米.(1)求该圆弧形所在圆的半径;(2)若该菜农的身高为1.70米,则他在不弯腰的情况下,横向活动的范围有几米?考向三弧、弦、圆心角、圆周角1.圆心角的度数等于它所对弧的度数,把顶点在圆心的周角等分成360份,每一份的圆心角是1°的角,1°的圆心角对着1°的弧.2.圆周角要具备两个特征:①顶点在圆上;②角的两边都和圆相交,二者缺一不可.典例4如图,在⊙O中∠O=50°,则∠A的度数为A.50°B.20°C.30°D.25°【答案】D【解析】∠A=12BOC=12×50°=25°.故选D.典例5如图,AB是⊙O的直径,△ACD内接于⊙O,延长AB,CD相交于点E,若∠CAD=35°,∠CDA=40°,则∠E的度数是A.20°B.25°C.30°D.35°【答案】B【解析】如图,连接BD,∵AB是⊙O的直径,∴∠ADB=90°,由三角形内角和定理得,∠ACD=180°﹣∠CAD﹣∠CDA=105°,∴∠ABD=180°﹣∠ACD=75°,∴∠BAD=90°﹣∠ABD=15°,∴∠E=∠CDA﹣∠DAB=25°,故选B.5.如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则BC的长为A.103πB.109πC.59πD.518π6.如图,AB是⊙O的直径,=BC CD DE,∠COD=38°,则∠AEO的度数是A.52°B.57°C.66°D.78°考向四点、直线与圆的位置关系1.点和圆的位置关系:①在圆上;②在圆内;③在圆外.2.直线和圆的位置关系:相交、相切、相离.典例6已知⊙O的半径是5,点A到圆心O的距离是7,则点A与⊙O的位置关系是A.点A在⊙O上B.点A在⊙O内C.点A在⊙O外D.点A与圆心O重合【答案】C【解析】∵O的半径是5,点A到圆心O的距离是7,即点A到圆心O的距离大于圆的半径,∴点A在⊙O外.故选C.【点睛】直接根据点与圆的位置关系的判定方法进行判断.典例7在△ABC中,AB=AC=2,∠A=150°,那么半径长为1的⊙B和直线AC的位置关系是A.相离B.相切C.相交D.无法确定【答案】B【解析】过B作BD⊥AC交CA的延长线于D,∵∠BAC=150,∴∠DAB=30°,∴BD=11222AB=⨯=1,即B到直线AC的距离等于⊙B的半径,∴半径长为1的⊙B和直线AC的位置关系是相切,故选B.【点睛】本题考查了直线与圆的位置关系的应用,过B作BD⊥AC交CA的延长线于D,求出BD和⊙B的半径比较即可,主要考查学生的推理能力.7.如图,⊙O的半径为5cm,直线l到点O的距离OM=3cm,点A在l上,AM=3.8cm,则点A与⊙O的位置关系是A.在⊙O内B.在⊙O上C.在⊙O外D.以上都有可能8.如图,⊙O的半径OC=5cm,直线l⊥OC,垂足为H,且l交⊙O于A、B两点,AB=8cm,则l沿OC 所在直线向下平移__________cm时与⊙O相切.考向五切线的性质与判定有圆的切线时,常常连接圆心和切点得切线垂直半径,这是圆中作辅助线的一种方法.典例8如图,⊙O以AB为直径,PB切⊙O于B,近接AP,交⊙O于C,若∠PBC=50°,∠ABC=A.30°B.40°C.50°D.60°【答案】B【解析】∵⊙O以AB为直径,PB切⊙O于B,∴∠PBA=90°,∵∠PBC=50°,∴∠ABC=40°.故选B.典例9如图,Rt△ABC中,∠C=90°,AB=5,AC=3,点E在中线AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径为A.78B.67C.56D.1【答案】B【解析】作EH⊥AC于H,EF⊥BC于F,EG⊥AB于G,连接EB,EC,设⊙E的半径为r,如图,∵∠C=90°,AB=5,AC=3,∴BC22AB AC-,而AD为中线,∴DC=2,∵以E为圆心的⊙E分别与AB、BC相切,∴EG=EF=r,∴HC=r,AH=3–r,∵EH∥BC,∴△AEH∽△ADC,∴EH∶CD=AH∶AC,即EH=233r-(),∵S △ABE +S △BCE +S △ACE =S △ABC , ∴()1112154333422232r r r ⨯⨯+⨯⨯+⨯⨯-=⨯⨯,∴67r =.故选B .9.已知四边形ABCD 是梯形,且AD ∥BC ,AD <BC ,又⊙O 与AB 、AD 、CD 分别相切于点E 、F 、G ,圆心O 在BC 上,则AB +CD 与BC 的大小关系是 A .大于 B .等于C .小于D .不能确定10.如图,以等腰△ABC 的腰AB 为⊙O 的直径交底边BC 于D ,DE AC ⊥于E .求证:(1)DB DC =; (2)DE 为⊙O 的切线.1.下列关于圆的叙述正确的有①圆内接四边形的对角互补; ②相等的圆周角所对的弧相等;③正多边形内切圆的半径与正多边形的半径相等; ④同圆中的平行弦所夹的弧相等.A .1个B .2个C .3个D .4个2.如图,AB 是⊙O 的直径,C 是⊙O 上一点(A 、B 除外),∠AOD =136°,则∠C 的度数是A .44°B .22°C .46°D .36°3.如图,半径为5的⊙A 中,弦BC ,ED 所对的圆心角分别是∠BAC ,∠EAD ,已知DE =6,∠BAC +∠EAD =180°,则弦BC 的长等于A .41B .34C .8D .64.如图,在平面直角坐标系中,过格点A ,B ,C 作一圆弧,则圆心坐标是A .点(1,0)B .点(2,1)C .点(2,0)D .点(2.5,1)5.如图,O 的直径8AB =,30CBD ∠=︒,则CD 的长为A .2B .3C .4D .36.如图,一圆内切四边形ABCD ,且BC =10,AD =7,则四边形的周长为A .32B .34C .36D .387.已知在⊙O 中,AB =BC ,且34AB AMC =∶∶,则∠AOC =__________.8.如图,A 、B 、C 、D 都在⊙O 上,∠B =130°,则∠AOC 的度数是__________.9.如图,PA 、PB 分别切⊙O 于A 、B ,并与圆O 的切线DC 分别相交于D 、C .已知△PCD 的周长等于14 cm ,则PA =__________cm .10.如图,在⊙O 的内接四边形ABCD 中,AB AD =,120C ∠=︒,点E 在弧AD 上.若AE 恰好为⊙O的内接正十边形的一边,DE 的度数为__________.11.如图,半圆O 的直径是AB ,弦AC 与弦BD 交于点E ,且OD ⊥AC ,若∠DEF =60°,则tan ∠ABD =__________.12.如图,AB为⊙O的直径,C、F为⊙O上两点,且点C为弧BF的中点,过点C作AF的垂线,交AF 的延长线于点E,交AB的延长线于点D.(1)求证:DE是⊙O的切线;(2)如果半径的长为3,tan D=34,求AE的长.13.如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.(1)判断直线DE与⊙O的位置关系,并说明理由;(2)若AC=6,BC=8,OA=2,求线段DE的长.14.如图1,⊙O是△ABC的外接圆,AB是直径,D是⊙O外一点且满足∠DCA=∠B,连接AD.(1)求证:CD是⊙O的切线;(2)若AD⊥CD,CD=2,AD=4,求直径AB的长;(3)如图2,当∠DAB=45°时,AD与⊙O交于E点,试写出AC、EC、BC之间的数量关系并证明.1.如图,在O 中,AB 所对的圆周角50ACB ∠=︒,若P 为AB 上一点,55AOP ∠=︒,则POB ∠的度数为A .30°B .45°C .55°D .60°2.如图,AD 是O 的直径,AB CD =,若40AOB ∠=︒,则圆周角BPC ∠的度数是A .40︒B .50︒C .60︒D .70︒3.如图,AB ,AC 分别是⊙O 的直径和弦,OD AC ⊥于点D ,连接BD ,BC ,且10AB =,8AC =,则BD 的长为A .25B .4C .213D .4.84.如图,PA 、PB 为圆O 的切线,切点分别为A 、B ,PO 交AB 于点C ,PO 的延长线交圆O 于点D ,下列结论不一定成立的是A .PA =PB B .∠BPD =∠APDC .AB ⊥PDD .AB 平分PD5.如图,PA 、PB 是⊙O 切线,A 、B 为切点,点C 在⊙O 上,且∠ACB =55°,则∠APB 等于A .55°B .70°C .110°D .125°6.如图,AB 是⊙O 的直径,AC 是⊙O 的切线,A 为切点,若∠C =40°,则∠B 的度数为A .60°B .50°C .40°D .30°7.如图,AB 是⊙O 的直径,点C 、D 是圆上两点,且∠AOC =126°,则∠CDB =A .54°B .64°C .27°D .37°8.如图,AB 为O 的直径,BC 为O 的切线,弦AD ∥OC ,直线CD 交的BA 延长线于点E ,连接BD .下列结论:①CD 是O 的切线;②CO DB ⊥;③EDA EBD △∽△;④ED BC BO BE ⋅=⋅.其中正确结论的个数有A .4个B .3个C .2个D .1个9.如图,C 、D 两点在以AB 为直径的圆上,2AB =,30ACD ∠=︒,则AD =__________.10.如图,△ABC 内接于⊙O ,∠CAB =30°,∠CBA =45°,CD ⊥AB 于点D ,若⊙O 的半径为2,则CD 的长为__________.11.如图,四边形ABCD内接于⊙O,AB=AC,AC⊥BD,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF.(1)求证:∠BAC=2∠CAD;(2)若AF=10,BC=45,求tan∠BAD的值.12.如图,在△ABC中,BA=BC,∠ABC=90°,以AB为直径的半圆O交AC于点D,点E是BD上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.(1)求证:△ADF≌△BDG;(2)填空:①若AB=4,且点E是BD的中点,则DF的长为__________;②取AE的中点H,当∠EAB的度数为__________时,四边形OBEH为菱形.1.【答案】D【解析】设原来的圆的半径为r ,则面积S 1=πr 2, ∴半径缩小到原来的14后所得新圆的面积22211π()π416S r r ==, ∴22211π116π16rS S r ==,故选D . 2.【答案】D【解析】∵圆的半径为5,∴圆的直径为10,又∵直径是圆中最长的弦,∴圆中任意一条弦的长度10l ≤,故选D . 3.【答案】B【解析】如图,连接OA ,∵O 的直径为10,5OA ∴=,∵圆心O 到弦AB 的距离OM 的长为4, 由垂径定理知,点M 是AB 的中点,12AM AB =, 由勾股定理可得,3AM =,所以6AB =.故选B .4.【解析】(1)如图所示:CO ⊥AB 于点D ,设圆弧形所在圆的半径为xm ,根据题意可得:DO 2+BD 2=BO 2, 则(x –2.3)2+851×12)2=x 2,解得x =3. 变式训练答:圆弧形所在圆的半径为3米;(2)如图所示:当MN =1.7米,则过点N 作NF ⊥CO 于点F ,可得:DF =1.7米,则FO =2.4米,NO =3米,故FN =223 2.4-=1.8(米), 故该菜农身高1.70米,则他在不弯腰的情况下,横向活动的范围有3.6米. 5.【答案】B【解析】根据题意可知:∠OAC =∠OCA =50°,则∠BOC =2∠OAC =100°,则弧BC 的长度为:100π210π1809⨯=,故选B .6.【答案】B【解析】∵=BC CD DE =,∴∠BOC =∠DOE =∠COD =38°, ∴∠BOE =∠BOC +∠DOE +∠COD =114°,∴∠AOE =180°–∠BOE =66°, ∵OA =OE ,∴∠AEO =(180°–∠AOE )÷2=57°,故选B . 7.【答案】A【解析】如图,连接OA ,则在直角△OMA 中,根据勾股定理得到OA =223 3.823.445+=<. ∴点A 与⊙O 的位置关系是:点A 在⊙O 内.故选A .8.【答案】2【解析】连接OA .∵直线和圆相切时,OH =5,又∵在直角三角形OHA 中,HA =AB ÷2=4,OA =5,∴OH =3. ∴需要平移5–3=2(cm ).故答案为:2.【点睛】本题考查垂径定理及直线和圆的位置关系.注意:直线和圆相切,应满足d =R . 9.【答案】B【解析】如图,连接OF ,OA ,OE ,作AH ⊥BC 于H .∵AD 是切线,∴OF ⊥AD ,易证四边形AHOF 是矩形,∴AH =OF =OE , ∵S △AOB =12•OB •AH =12•AB •OE ,∴OB =AB ,同理可证:CD =CO , ∴AB +CD =BC ,故选B .【点睛】本题考查了切线的性质,切线垂直于过切点的半径,正确作出辅助线是关键. 10.【解析】(1)如图,连AD ,∵AB 是直径,∴90ADB ∠=︒,AD BC ⊥, 又AB AC =,∴D 为BC 中点,DB DC =; (2)连OD ,∵D 为BC 中点,OA OB =, ∴OD 为ABC △中位线,OD AC ∥, 又DE AC ⊥于,E ∴90ODE DEC ∠=∠=︒, ∴DE 为⊙O 的切线.1.【答案】B【解析】①圆内接四边形的对角互补;正确;②相等的圆周角所对的弧相等;错误;③正多边形内切圆的半径与正多边形的半径相等;错误;④同圆中的平行弦所夹的弧相等;正确; 正确的有2个,故选B . 2.【答案】B【解析】∵∠AOD =136°,∴∠BOD =44°,∴∠C =22°,故选B . 3.【答案】C【解析】如图,延长CA ,交⊙A 于点F ,考点冲关∵∠BAC+∠BAF=180°,∠BAC+∠EAD=180°,∴∠BAF=∠DAE,∴BF=DE=6,∵CF是直径,∴∠ABF=90°,CF=2×5=10,∴BC=228CF BF-=.故选C.4.【答案】C【解析】根据勾股定理可知A、B、C点到(2,0)的距离均为5,然后可知圆心为(2,0)或者通过AB、BC的垂直平分线求解也可以.故选C.5.【答案】C【解析】如图,作直径DE,连接CE,则∠DCE=90°,∵∠DBC=30°,∴∠DEC=∠DBC=30°,∵DE=AB=8,∴12DC DE==4,故选C.6.【答案】B【解析】由题意可得圆外切四边形的两组对边和相等,所以四边形的周长=2×(7+10)=34.故选B.7.【答案】144°【解析】根据AB=BC可得:弧AB的度数和弧BC的度数相等,则弧AMC的度数为:(360°÷10)×4=144°,则∠AOC =144°. 8.【答案】100°【解析】∵∠B =130°,∴∠D =180°-130°=50°,∴∠AOC =2∠D =100°.故答案为100°. 9.【答案】7【解析】如图,设DC 与⊙O 的切点为E ;∵PA 、PB 分别是⊙O 的切线,且切点为A 、B ,∴PA =PB ; 同理,可得:DE =DA ,CE =CB ;则△PCD 的周长=PD +DE +CE +PC =PD +DA +PC +CB =PA +PB =14(cm ); ∴PA =PB =7cm ,故答案是:7. 10.【答案】84︒【解析】如图,连接BD ,OA ,OE ,OD ,∵四边形ABCD 是圆的内接四边形,∴180BAD C ∠+∠=︒, ∵120C ∠=︒,∴60BAD ∠=︒,∵AB AD =,∴ABD △是正三角形,∴60ABD ∠=︒,2120AOD ABD ∠=∠=︒, ∵AE 恰好是⊙的内接正十边形的一边,∴3603610AOE ︒∠==︒, ∴1203684DOE ∠=︒-︒=︒,∴DE 的度数为84°.故答案为:84°.113【解析】∵OD ⊥AC ,∠DEF =60°, ∴∠D =30°,∵OD=OB,∴∠ABD=∠D=30°,∴tan∠ABD=33,故答案为:33.12.【解析】(1)连接OC,如图.∵点C为弧BF的中点,∴弧BC=弧CF,∴∠BAC=∠FAC.∵OA=OC,∴∠OCA=∠OAC,∴∠OCA=∠FAC,∴OC∥AE.∵AE⊥DE,∴OC⊥DE,∴DE是⊙O的切线;(2)在Rt△OCD中,∵tan D=34OCCD=,OC=3,∴CD=4,∴OD=22OC CD+=5,∴AD=OD+AO=8.在Rt△ADE中,∵sin D=35OC AEOD AD==,∴AE=245.13.【解析】(1)直线DE与⊙O相切,理由如下:如图,连接OD,∵OD=OA,∴∠A=∠ODA,∵EF是BD的垂直平分线,∴EB=ED,∴∠B=∠EDB,∵∠C=90°,∴∠A+∠B=90°,∴∠ODA+∠EDB=90°,∴∠ODE=180°–90°=90°,∴直线DE与⊙O相切;(2)连接OE,设DE=x,则EB=ED=x,CE=8–x,∵∠C=∠ODE=90°,∴OC2+CE2=OE2=OD2+DE2,∴42+(8–x)2=22+x2,解得:x=4.75,则DE=4.75.14.【解析】(1)如图1,连接OC.∵OB=OC,∴∠OCB=∠B,∵∠DCA=∠B,∴∠DCA=∠OCB,∵AB是直径,∴∠ACB=90°,∴∠DCA+∠ACO=∠OCB+∠ACO=90°,即∠DCO=90°,∴CD是⊙O的切线.(2)∵AD⊥CD,CD=2,AD=4.∴222425AC=+=由(1)可知∠DCA=∠B,∠D=∠ACB=90°,∴△ADC∽△ACB,∴AD ACAC AB=2525=,∴AB=5.(3)2AC BC EC=+,如图2,连接BE,在AC上截取AF=BC,连接EF.∵AB 是直径,∠DAB =45°, ∴∠AEB =90°,∴△AEB 是等腰直角三角形, ∴AE =BE ,又∵∠EAC =∠EBC ,∴△ECB ≌△EFA ,∴EF =EC , ∵∠ACE =∠ABE =45°, ∴△FEC 是等腰直角三角形, ∴2FC EC =,∴2AC AF FC BC EC =+=.1.【答案】B【解析】∵∠ACB =50°,∴∠AOB =2∠ACB =100°,∵∠AOP =55°,∴∠POB =45°,故选B . 2.【答案】B【解析】∵AB CD =,40AOB ∠=︒,∴40COD AOB ∠=∠=︒, ∵180AOB BOC COD ∠+∠+∠=︒,∴100BOC ∠=︒, ∴1502BPC BOC ∠=∠=︒,故选B . 3.【答案】C【解析】∵AB 为直径,∴90ACB ∠=︒,∴22221086BC AB AC =--=,∵OD AC ⊥,∴142CD AD AC ===, 直通中考在Rt CBD △中,2246213BD =+=.故选C .4.【答案】D【解析】∵PA ,PB 是⊙O 的切线,∴PA =PB ,所以A 成立;∠BPD =∠APD ,所以B 成立; ∴AB ⊥PD ,所以C 成立;∵PA ,PB 是⊙O 的切线,∴AB ⊥PD ,且AC =BC ,只有当AD ∥PB ,BD ∥PA 时,AB 平分PD ,所以D 不一定成立,故选D . 5.【答案】B【解析】如图,连接OA ,OB ,∵PA ,PB 是⊙O 的切线,∴PA ⊥OA ,PB ⊥OB ,∵∠ACB =55°,∴∠AOB =110°, ∴∠APB =360°-90°-90°-110°=70°.故选B .6.【答案】B【解析】∵AC 是⊙O 的切线,∴AB ⊥AC ,且∠C =40°,∴∠ABC =50°,故选B . 7.【答案】C【解析】∵∠AOC =126°,∴∠BOC =180°-∠AOC =54°,∵∠CDB =12∠BOC =27°.故选C . 8.【答案】A【解析】如图,连接DO .∵AB 为O 的直径,BC 为O 的切线,∴90CBO ∠=︒,∵AD OC ∥,∴DAO COB ∠=∠,ADO COD ∠=∠. 又∵OA OD =,∴DAO ADO ∠=∠,∴COD COB ∠=∠.在COD △和COB △中,CO CO COD COB OD OB =⎧⎪∠=∠⎨⎪=⎩,∴COD COB △≌△,∴90CDO CBO ∠=∠=︒.又∵点D 在O 上,∴CD 是O 的切线,故①正确,∵COD COB △≌△,∴CD CB =,∵OD OB =,∴CO 垂直平分DB ,即CO DB ⊥,故②正确; ∵AB 为O 的直径,DC 为O 的切线,∴90EDO ADB ∠=∠=︒,∴90EDA ADO BDO ADO ∠+∠=∠+∠=︒,∴ADE BDO ∠=∠, ∵OD OB =,∴ODB OBD ∠=∠,∴EDA DBE ∠=∠, ∵E E ∠=∠,∴EDA EBD △∽△,故③正确;∵90EDO EBC ∠=∠=︒,E E ∠=∠,∴EOD ECB △∽△, ∴ED ODBE BC=,∵OD OB =, ∴ED BC BO BE ⋅=⋅,故④正确,故选A . 9.【答案】1【解析】∵AB 为直径,∴90ADB ∠=︒,∵30B ACD ∠=∠=︒,∴112122AD AB ==⨯=. 故答案为:1. 10.【答案】2【解析】如图,连接CO 并延长交⊙O 于E ,连接BE ,则∠E =∠A =30°,∠EBC =90°,∵⊙O 的半径为2,∴CE =4,∴BC =12CE =2, ∵CD ⊥AB ,∠CBA =45°,∴CD =22BC =2,故答案为:2. 11.【解析】(1)∵AB =AC ,∴AB AC =,∠ABC =∠ACB ,∴∠ABC =∠ADB ,∠ABC =(180°-∠BAC )=90°-∠BAC ,∵BD⊥AC,∴∠ADB=90°-∠CAD,∴12∠BAC=∠CAD,∴∠BAC=2∠CAD.(2)∵DF=DC,∴∠DFC=∠DCF,∴∠BDC=2∠DFC,∴∠BFC=12∠BDC=12∠BAC=∠FBC,∴CB=CF,又BD⊥AC,∴AC是线段BF的中垂线,AB=AF=10,AC=10.又BC=45,设AE=x,CE=10-x,由AB2-AE2=BC2-CE2,得100-x2=80-(10-x)2,解得x=6,∴AE=6,BE=8,CE=4,∴DE=648AE CEBE⋅⨯==3,∴BD=BE+DE=3+8=11,如图,作DH⊥AB,垂足为H,∵12AB·DH=12BD·AE,∴DH=11633105 BD AEAB⋅⨯==,∴BH2244 5BD DH-=,∴AH=AB-BH=10-446 55=,∴tan∠BAD=331162 DHAH==.12.【解析】(1)∵BA=BC,∠ABC=90°,∴∠BAC=45°,∵AB是⊙O的直径,∴∠ADB=∠AEB=90°,∴∠DAF+∠BGD=∠DBG+∠BGD=90°,∴∠DAF=∠DBG,∵∠ABD+∠BAC=90°,∴∠ABD=∠BAC=45°,∴AD=BD,∴△ADF≌△BDG.(2)①如图2,过F作FH⊥AB于H,∵点E是BD的中点,∴∠BAE=∠DAE,∵FD⊥AD,FH⊥AB,∴FH=FD,∵FHBF=sin∠ABD=sin45°2,∴22FDBF=BF2FD,∵AB=4,∴BD=4cos45°2,即BF+FD22+1)FD2,∴FD=2221=4-22,故答案为:4-22.②连接OH,EH,∵点H是AE的中点,∴OH⊥AE,∵∠AEB=90°,∴BE⊥AE,∴BE∥OH,∵四边形OBEH为菱形,∴BE=OH=OB=12 AB,∴sin∠EAB=BEAB=12,∴∠EAB=30°.故答案为:30°.31。
2023年中考数学复习---圆综合知识点总结与专项练习题(含答案解析)

2023年中考数学复习---圆综合知识点总结与专项练习题(含答案解析)知识点总结1.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
2.垂径定理的推论:推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
推论2:弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
推论3:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题。
3.圆心角、弦以及弧之间的关系:①定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
②推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧。
4.圆周角定理:5.圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
6.圆的内接四边形:①定义:四个顶点都在圆上的四边形叫做圆的内接四边形。
②性质:I:圆内接四边形的对角互补。
II:圆内接四边形的任意一个外角等于它的内对角。
7.三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆。
圆心是三角形三条边垂直平分线的交点,叫做三角形的外心。
8.切线的性质:①圆的切线垂直于经过切点的半径。
②经过圆心且垂直于切线的直线必经过切点。
③经过切点且垂直于切线的直线必经过圆心。
运用切线的性质进行计算或证明时,常常作的辅助线是连接圆心和切点,通过构造直角三角形或相似三角形解决问题。
9. 切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线。
在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径,可简单的说成“无交点,作垂线段,证半径”;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,可简单地说成“有交点,作半径,证垂直”。
数学中考复习 圆的相关知识点及习题

圆专题一、圆的相关概念1.圆的定义(1)描述性定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,其中固定端点O叫做圆心,OA叫做半径.(2)集合性定义:平面内到定点的距离等于定长的点的集合叫做圆,顶点叫做圆心,定长叫做半径.(3)圆的表示方法:通常用符号⊙表示圆,定义中以O为圆心,OA为半径的圆记作”O⊙“,读作”圆O“.(4)同圆、同心圆、等圆:圆心相同且半径相等的圆叫同圆;圆心相同,半径不相等的两个圆叫做同心圆;能够重合的两个圆叫做等圆.注意:注意:同圆或等圆的半径相等.2.弦和弧(1)弦:连结圆上任意两点的线段叫做弦.(2)直径:经过圆心的弦叫做圆的直径,直径等于半径的2倍.(3)弦心距:从圆心到弦的距离叫做弦心距.、为端点的圆弧记作AB,读作弧AB.(4)弧:圆上任意两点间的部分叫做圆弧,简称弧.以A B(5)等弧:在同圆或等圆中,能够互相重合的弧叫做等弧.(6)半圆:圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆.(7)优弧、劣弧:大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.(8)弓形:由弦及其所对的弧组成的图形叫做弓形.3.圆心角和圆周角(1)圆心角:顶点在圆心的角叫做圆心角.将整个圆分为360等份,每一份的弧对应1︒的圆心角,我们也称这样的弧为1︒的弧.圆心角的度数和它所对的弧的度数相等.(2)圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角.二、圆的对称性1.旋转对称性(1)圆是中心对称图形,对称中心是圆心;圆是旋转对称图形,无论绕圆心旋转多少度角,总能与自身重合.(2)圆的旋转对称性⇒圆心角、弧、弦、弦心距之间的关系.2.轴对称性(1)圆是轴对称图形,经过圆心的任一条直线是它的对称轴.(2)圆的轴对称性⇒垂径定理.三、圆的性质定理1.圆周角定理(1) 定理:一条弧所对的圆周角等于它所对的圆心角的一半. (2) 推论:推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧相等. 推论2:半圆(或直径)所对的圆周角是直角,90︒的圆周角所对的弦是直径.推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.2. 圆心角、弧、弦、弦心距之间的关系(1) 定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.(2) 推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量分别相等.注意:①前提条件是在同圆或等圆中;②在由等弦推出等弧时应注意:优弧与优弧相等;劣弧与劣弧相等.3. 垂径定理(1) 定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧. (2) 推论1:①平分弦(非直径)的直径,垂直于弦,并且平分弦所对的两条弧.②弦的垂直平分线经过圆心,并且平分弦所对的两条弧.③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧. (3) 推论2:圆的两条平行线所夹的弧相等.注意:若“过圆心的直线”、“垂直于弦”、“平分弦(非直径)”、“平分弦所对的优弧”、“平分弦所对的劣弧”中的任意两个成立,则另外三个都成立.注意:应用垂径定理与推论进行计算时,往往要构造如右图所示的直角三角形,根据垂径定理与勾股定理有:222()2ar d =+,根据此公式,在a ,r ,d 三个量中知道任何两个量就可以求出第三个量.F EBA CDOr a 2d O CBA所对的两圆心角相等所对的两条弦相等 所对的两条弧相等所对的两条弦的弦心距相等EO D B A【例1】 如图,点A D G M 、、、在半圆O 上,四边形ABOC DEOF HMNO 、、均为矩形,设BC a =,EF b =,NH c =则下列格式中正确的是( )A .a b c >>B .a b c ==C .c a b >>D .b c a >>【例2】 如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为216cm ,则该半圆的半径为______.二、圆的性质定理1. 圆周角定理【例3】 如图,量角器外沿上有A B 、两点,它们的度数分别是7040︒︒、,则1∠的度数为_________.【例4】 如图,量角器外缘边上有A P Q ,,三点,它们所表示的读数分别是180︒,70︒,30︒,则PAQ ∠的大小为( )A .10︒B .20︒C .30︒D .40︒【例5】 如图,O ⊙是ABC ∆的外接圆,已知60B ∠=︒,则CAO ∠的度数是( )A .15︒B .30︒C .45︒D .60︒【例6】 如图,已知O 的弦AB CD ,相交于点E ,AC 的度数为60︒,BD 的度数为100︒,则AEC ∠等于ON MHG FE DC BA( ) A .60°B .100°C .80°D .130°【例7】 如图所示的半圆中,AD 是直径,且32AD AC ==,,则sin B 的值是________.【例8】 如图,已知AB 为⊙O 的直径,20E ∠=︒,50DBC ∠=︒,则CBE ∠=______.【例9】 如图,在O ⊙中,AOB ∠的度数为m ,C 是ACB 上一点,D E 、是AB 上不同的两点(不与A B 、两点重合),则D E ∠+∠的度数为____________.【例10】 如图,AB 是O 的直径,点C ,D ,E 都在O 上,若C D E ==∠∠∠,求A B +∠∠.DCA BBA【例11】 如图,有一圆形展厅,在其圆形边缘上的点A 处安装了一台监视器,它的监控角度是65︒.为了监控整个展厅,最少需在圆形边缘上共安装...这样的监视器 台.【例12】 如图所示,在ABC ∆中,45C ∠=︒,4AB =,则O ⊙的半径为( )B.4D.5【例13】 如图AB 是半圆O 的直径,点C D 、在弧AB 上,且AD 平分CAB ∠,已知106AB AC ==,,求AD的长.【例14】 如图,半圆的直径10AB =,点C 在半圆上,6BC =.(1)求弦AC 的长;(2)若P 为AB 的中点,PE AB ⊥交AC 于点E ,求PE 的长.2. 圆内接四边形【例15】 如图,O ⊙外接于正方形ABCD ,P 为弧AD 上一点,且1AP =,PB =PC 的长.【例16】 如图,已知四边形ABCD 内接于直径为3的圆O ,对角线AC 是直径,对角线AC 和BD 的交点P ,BAPEC BAP DCBAAB BD =,且0.6PC =,求四边形ABCD 的周长.【例17】 如图,AB CD ,是O ⊙的两条弦,它们相交于点P ,连结AD BD 、,已知4AD BD ==,6PC =,求CD 的长.一、点与圆的位置关系4. 确定圆的条件(5) 圆心(定点),确定圆的位置; (6)半径(定长),确定圆的大小.注意:只有当圆心和半径都确定时,圆才能确定. 5. 点与圆的位置关系(7) 点与圆的位置关系有:点在圆上、点在圆内、点在圆外三种,这三种关系由这个点到圆心的距离与半径的大小关系决定. (8) 设O ⊙的半径为r ,点P 到圆心O 的距离为d ,则有:点在圆外⇔d r >;点在圆上⇔d r =;点在圆内⇔d r <.如下表所示:C二、过已知点的圆1. 过已知点的圆(1) 经过点A 的圆:以点A 以外的任意一点O 为圆心,以OA 的长为半径,即可作出过点A 的圆,这样的圆有无数个. (2) 经过两点A B 、的圆:以线段AB 中垂线上任意一点O 作为圆心,以OA 的长为半径,即可作出过点A B 、的圆,这样的圆也有无数个. (3) 过三点的圆:若这三点A B C 、、共线时,过三点的圆不存在;若A B C 、、三点不共线时,圆心是线段AB 与BC 的中垂线的交点,而这个交点O 是唯一存在的,这样的圆有唯一一个. (4) 过n ()4n ≥个点的圆:只可以作0个或1个,当只可作一个时,其圆心是其中不共线三点确定的圆的圆心.2. 定理:不在同一直线上的三点确定一个圆(1) “不在同一直线上”这个条件不可忽视,换句话说,在同一直线上的三点不能作圆; (2) “确定”一词的含义是”有且只有”,即”唯一存在”.三、三角形的外接圆及外心1. 三角形的外接圆(1) 经过三角形三个顶点的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心,这个三角形叫做这个圆的内接三角形. (2) 锐角三角形外接圆的圆心在它的内部;直角三角形外接圆的圆心在斜边中点处(即直角三角形外接圆半径等于斜边的一半);钝角三角形外接圆的圆心在它的外部. 2. 三角形外心的性质(1) 三角形的外心是指外接圆的圆心,它是三角形三边垂直平分线的交点,它到三角形各顶点的距离相等; (2) 三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合.一、点与圆的位置关系【例18】 已知圆内一点到圆周上的点的最大距离是7,最小距离是5,则该圆的半径是( )A .2B .6C .12D .7二、过三点的圆【例19】 如图,四边形ABCD 中,AB AC AD ==,若7613CAD BDC ∠=︒∠=︒,,则CBD ∠=_________,BAC ∠=__________.DCBA【例20】 如图,直角坐标系中一条圆弧经过网格点A B C ,,,其中B 点的坐标为()44,,则该圆弧所在圆的圆心的坐标为 .三、三角形的外接圆及外心【例21】 如图,ABC ∆内接于O ⊙,120BAC ∠=︒,AB AC =,BD 为O ⊙的直径,6AD =,则BC = .【例22】 等边三角形的外接圆的半径等于边长的( )倍. ABCD .12【例23】 ABC ∆中,10AB AC ==,12BC =,求其外接圆的半径.【例24】 已知如图,ACD ∆的外角平分线CB 交其外接圆于B ,连接BA 、BD ,求证:BA BD =.N【例25】 已知∆ABC 中,=AB AC ,D 是∆ABC 外接圆劣弧AC 上的点(不与点A C ,重合),延长BD 至E . ⑴ 求证:AD 的延长线平分∠CDE ;⑴ 若30∠=︒BAC ,∆ABC 中BC边上的高为2+∆ABC 外接圆的面积.直线与圆的位置关系设O ⊙的半径为r ,圆心O 到直线l 的距离为d ,则直线和圆的位置关系如下表:6. 切线的性质(9) 定理:圆的切线垂直于过切点的半径.推论1:经过圆心且垂直于切线的直线必经过切点. 推论2:经过切点且垂直于切线的直线必经过圆心.(10) 注意:这个定理共有三个条件,即一条直线满足:①垂直于切线②过切点③过圆心①过圆心,过切点⇒垂直于切线.AB 过圆心,AB 过切点M ,则AB l ⊥. ②过圆心,垂直于切线⇒过切点.AB 过圆心,AB l ⊥,则AB 过切点M . ③过切点,垂直于切线⇒过圆心.AB l ⊥,AB 过切点M ,则AB 过圆心.7. 切线的判定(1) 定义法:和圆只有一个公共点的直线是圆的切线; (2) 距离法:和圆心距离等于半径的直线是圆的切线; (3) 定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.注意:定理的题设是①“经过半径外端”,②“垂直于半径”,两个条件缺一不可;定理的结论是“直线是圆的切线”.因此,证明一条直线是圆的切线有两个思路:①连接半径,证直线与此半径垂直;②作垂直,证垂直在圆上.AB CD El8. 切线长和切线长定理(1) 切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长. (2) 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.三、三角形的内切圆1. 三角形的内切圆:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.2. 多边形的内切圆:和多边形的各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形.3. 直角三角形内切圆的半径与三边的关系设a 、b 、c 分别为ABC △中A ∠、B ∠、C ∠的对边,面积为S ,则内切圆半径为sr p=,其中()12p a b c =++.若90C ∠=︒,则()12r a b c =+-.二、切线的性质及判定【例1】 如图,ABC ∆为等腰三角形,AB AC =,O 是底边BC 的中点,O ⊙与腰AB 相切于点D ,求证AC 与O ⊙相切.lcb acbaO F ED CACBAB A【例2】 已知:如图,ABC ∆内接于O ,AD 是过A 的一条射线,且B CAD ∠=∠.求证:AD 是O 的切线.【例3】 已知:如图,AB 是O ⊙的直径,C 为O ⊙上一点,MN 过C 点,AD MN ⊥于D ,AC 平分DAB ∠.求证:MN 为O ⊙的切线.【例4】 如图,已知OA 是O ⊙的半径,B 是OA 中点,BC OA ⊥,P 是OA 延长线上一点,且PA AC =.求证:PC 是O ⊙的切线.【例5】 已知:如图,C 为O ⊙上一点,DA 交O ⊙于B ,连结AC BC 、,且DCB CAB ∠=∠DC 为O ⊙的切线;(2)2CD AD BD =⋅.【例6】 如图,以等腰ABC ∆中的腰AB 为直径作O ,交BC 于点D .过点D 作DE AC ⊥,垂足为E .(1)求证:DE 为O 的切线;(2)若O 的半径为5,60BAC ∠=︒,求DE 的长.C【例7】 如图,已知AB 为⑴O 的弦,C 为⑴O 上一点,⑴C =⑴BAD ,且BD ⑴AB 于B .(1)求证:AD 是⑴O 的切线.(2)若⑴O 的半径为3,AB =4,求AD 的长.【例8】 如图,Rt ABC ∆中,90ABC ∠=︒,以AB 为直径作O ⊙交AC 边于点D ,E 是边BC 的中点,连接DE .(1)求证:直线DE 是O ⊙的切线;(2)连接OC 交DE 于点F ,若OF CF =,求tan ACO ∠的值.【例9】 如图,AB 是O ⊙的的直径,BC AB ⊥于点B ,连接OC 交O ⊙于点E ,弦AD OC ∥,弦DF AB⊥于点G .(1)求证:点E 是BD 的中点; (2)求证:CD 是O ⊙的切线;(3)若4sin 5BAD ∠=,O ⊙的半径为5,求DF 的长.【例10】 如图,等腰三角形ABC 中,10AC BC ==,12AB =.以BC 为直径作O ⊙交AB 于点D ,交AC于点G ,DF AC ⊥,垂足为F ,交CB 的延长线于点E . (1)求证:直线EF 是O ⊙的切线; (2)求sin E ∠的值.一、切线长定理1.如图,PA PB ,分别是O 的切线,A B ,为切点,AC 是O 的直径,已知35BAC ∠=︒,P ∠的度数为( ) A .35︒ B .45︒ C .60︒ D .70︒2.如图,PA PB 、分别切O ⊙于A B ,两点,PC 满足AB PB AC PC AB PC AC PB ⋅-⋅=⋅-⋅,且AP PC ⊥,2PAB BPC ∠=∠,求ACB ∠的度数.3.如图,从圆O 外一点P 引圆O 的两条切线PA PB ,,切点分别为A B ,.如果60APB ∠=,8PA =,那么弦AB 的长是( )A .4B .8C.D.P则OP =( )A .50cm B.cm Ccm D.cm5.如图,已知以直角梯形ABCD 的腰CD 为直径的半圆O 与梯形上底AD 、下底BC 以及腰AB 均相切,切点分别是D C E ,,.若半圆O 的半径为2,梯形的腰AB 为5,则该梯形的周长是( )A .9B .10C .12D .146.等腰梯形ABCD 外切于圆,且中位线MN 的长为10,那么这个等腰梯形的周长是________.7.如图,PA PB DE 、、分别切O ⊙于A B C 、、,若10PO =,PDE ∆周长为16,求O ⊙的半径.8.如图,PA PB ,切O 于AB ,,MN 切O 于C ,交PA PB ,于M N ,两点,已知8PA =,求PMN ∆的周长.PB P于G,交AB AC、于MN,则BMN∆的周长为______________.10.如图,已知AB是O⊙的直径,BC是和O⊙相切于点B的切线,O⊙的弦AD平行于OC,若2OA=,且6AD OC+=,求CD的长.补充讲义两圆的公切线(选讲自己了解)9.两圆的外公切线(11)求两圆外公切线长:构造外公切线、圆心距、大圆与小圆半径的差为边的特征直角三角形.如图,设大圆的半径为R,小圆的半径为r,两圆的圆心距为d,两外公切线的夹角为α,则两圆的外公切线长为:l=,sin2R rdα-=(12)求两圆内公切线长:构造外公切线、圆心距、大圆与小圆半径的和为边的特征直角三角形.10.两圆的内公切线如图,设大圆的半径为R,小圆的半径为r,两圆的圆心距为d,两外公切线的夹角为α,则两圆的内公切线长l=,sin2R r dα+ =CB AP圆与相似三角形经典证明题1.如图,A、B、C、D依次为一直线上4个点,BC=2,△BCE为等边三角形,⊙O过A、D、E3 点,且∠AOD=120°.设AB=x,CD=y,则y与x的函数关系为.2.如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.(1)求证:AE为⊙O的切线.(2)当BC=8,AC=12时,求⊙O的半径.(3)在(2)的条件下,求线段BG的长.3.如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.(1)求证:直线DF与⊙O相切;(2)若AE=7,BC=6,求AC的长.4..Rt.ABC...ACB=90°.D.AB.......BD.....O.AC..E...DE.....BC.......F..BD=BF..1....AC..O....2..BC=6.AB=12...O....5....AB..O......A..O..........C...OC..O..D.BD.....AC.E...AD..1.....CDE..CAD..2..AB=2.AC=2..AE...6. 已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB 于点E..1....AC•AD=AB•AE..2...BD.⊙O....D....E.OB.....BC=2...AC...7.如图所示,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.8. 如图,已知在△ABC中,AD是BC边上的中线,以AB为直径的⊙O交BC于点D,过D作MN⊥AC于点M,交AB的延长线于点N,过点B作BG⊥MN于G.(1)求证:△BGD∽△DMA;(2)求证:直线MN是⊙O的切线.9. 如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.(1)求证:∠1=∠2.(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.10......O..AB....OC.AB..CD.OB...F..AB.......E..EF=ED..1....DE..O.....2..OF.OB=1.3..O...R=3.....11....AB .⊙O .....D ......∠BDE =∠CBE .BD .AE ...F .(1)求证:BC 是⊙O 的切线;(2)若BD 平分∠ABE ,求证:DE 2=DF •DB ;(3)在(2)的条件下,延长ED ,BA 交于点P ,若PA =AO ,DE =2,求PD 的长和⊙O 的半径.12.如图,AB 是⊙O 的直径,点C 为⊙O 上一点,AE 和过点C 的切线互相垂直,垂足为E ,AE 交⊙O 于点D ,直线EC 交AB 的延长线于点P ,连接AC ,BC ,PB :PC =1:2. (1)求证:AC 平分∠BAD ;(2)探究线段PB ,AB 之间的数量关系,并说明理由; (3)若AD =3,求△ABC 的面积.13.已知,如图,AB 是⊙O 的直径,点C 为⊙O 上一点,OF ⊥BC 于点F ,交⊙O 于点E ,AE 与BC 交于点H ,点D 为OE 的延长线上一点,且∠ODB =∠AEC . (1)求证:BD 是⊙O 的切线; (2)求证:2CE EH EA =⋅; (3)若⊙O 的半径为5,3sin 5A =,求BH 的长.第13题图FH EOC B A。
(完整版)中考初三圆知识点专题复习

、圆中重要的知识点 1、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:( 1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧 简称2推3定理:此定理中共 5个结论中,只要知道其中 2个即可推出其它3个结论,即:3、如图,已知在O O 中,弦AB CD ,且AB CD ,垂足为H , 0E(1) 求证:四边形OEHF 是正方形.(2) 若CH 3 , DH 9,求圆心0到弦AB 和CD 的距离.以上共4个定理,①AB 是直径 ②AB CD ③ CEDE ④弧BC 弧BD ⑤弧AC 弧AD中任意2个条件推出其他3个结论。
推论2:圆的两条平行弦所夹的弧相等。
即:在O O 中,••• AB // CD•••弧 AC 弧 BD例题1、基本概念1. F 面四个命题中正确的一个是( A. 平分一条直径的弦必垂直于这条直径 •平分一条弧的直线垂直于这条弧所对的弦C. 弦的垂线必过这条弦所在圆的圆心 .在一个圆内平分一条弧和它所对弦的直线必过这个圆的圆心2. F 列命题中,正确的是().A.过弦的中点的直线平分弦所对的弧B.过弦的中点的直线必过圆心C.弦所对的两条弧的中点连线垂直平分弦,且过圆心D.弦的垂线平分弦所对的弧例题2、垂径定理1、在直径为 52cm 的圆柱形油槽内装入一些油后,为 16cm, 那么油面宽度AB 是cm.2、在直径为52cm 的圆柱形油槽内装入一些油后,,如果油面宽度是 48cm,那么油的最大深度为 _______ cm.AB 于 E , OF CD 于 F .截面如图所示,如果油的最大深度4、已知:△ ABC内接于O O, AB=AC半径OB=5cm圆心O到BC的距离为3cm,求AB的长.5、如图,F是以O为圆心,BC为直径的半圆上任意一点,A是〒的中点,AD丄BC于D,求证:AD=1 BF.2F例题3、度数问题1、已知:在O O中,弦AB 12cm , 0点到AB的距离等于AB的一半,求:AOB的度数和圆的半径2、已知:O O的半径0A 1,弦AB AC的长分别是J2、J3.求BAC的度数。
中考数学知识点总结圆的位置

中考数学知识点总结圆的位置中考数学知识点总结圆的位置中学数学中的圆是一个基础的几何图形,其位置关系也是需要掌握的数学知识点之一。
在中考中,圆的位置关系常常与其他几何图形相结合,考查学生对几何形状的理解和应用能力。
下面将对中考中关于圆的位置关系进行总结。
1. 圆的内外关系对于两个不同的圆,它们之间有三种可能的位置关系:内含、外切和相离。
(1)内含:若一个圆完全位于另一个圆内部,则称这两个圆是内含关系。
内含关系中,小圆的半径小于大圆的半径。
(2)外切:若两个圆仅有一个切点,则称这两个圆是外切关系。
外切关系中,两个圆的半径相等。
(3)相离:若两个圆没有公共点,则称这两个圆是相离关系。
相离关系中,两个圆的半径大小没有固定关系。
2. 圆与直线的位置关系圆与直线的位置关系主要有内切、外切和相割三种情况。
(1)内切:若直线仅有一个切点与圆相切,则称该直线与圆是内切关系。
内切关系中,切点在圆的外部,直线通过圆心且垂直于半径。
(2)外切:若直线仅有一个切点与圆相切,则称该直线与圆是外切关系。
外切关系中,切点在圆的外部,直线通过圆心但不垂直于半径。
(3)相割:若直线与圆相交,并且不是内切或外切关系,则称该直线与圆是相割关系。
相割关系中,直线与圆有两个交点。
3. 圆与圆的位置关系圆与圆的位置关系主要有内切、外切和相交三种情况。
(1)内切:若两个圆仅有一个切点,则称这两个圆是内切关系。
内切关系中,切点在两个圆的外部,两个圆的半径之差等于切点到两个圆心的距离。
(2)外切:若两个圆仅有一个切点,则称这两个圆是外切关系。
外切关系中,切点在两个圆的外部,两个圆的半径之和等于切点到两个圆心的距离。
(3)相交:若两个圆有两个交点,则称这两个圆是相交关系。
相交关系中,两个圆的半径之和大于切点到两个圆心的距离,但小于两个圆的半径之和。
4. 圆心角与弦的位置关系圆心角与弦的位置关系是圆心角的一种特殊情况。
圆心角的度数与其所对应的弧度相等。
中考圆知识点总结复习

初中数学——《圆》【知识结构】⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧侧面积、全面积计算侧面展开图定义圆柱和圆锥形面积计算圆面积、扇形、组合图形周长计算圆周长、弧长、组合图画法应用边长、面积的计算计算半径、边心距、中心角计算概念正多边形正多边形与圆内含内切相交外切外离圆和圆的位置关系切割线定理及推论相交弦定理及推论相交性质判定相切相离直线和圆的位置关系反证法点的轨迹圆内接四边形圆周角定理距之间的关系圆心角、弧、弦、弦心垂径定理及推论基本性质三点定圆定理点与圆的位置关系定义圆的有关性质圆一、圆及与圆相关的概念二、圆的对称性(1)圆既是轴对称图形,又是中心对称图形。
(2)对称轴——直径所在的直线,对称中心——圆心。
三、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;知2推3定理:①AB是直径②AB CD=④弧BC=弧BD⑤弧AC=弧AD⊥③CE DE推论2:圆的两条平行弦所夹的弧相等。
四、圆心角定理圆心角定理:同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,弦心距相等。
知1推3定理:①AOB DOE=;④弧BA=弧BD∠=∠;②AB DE=;③OC OF五、圆周角定理1、圆周角定理:同弧所对的圆周角等于它所对的圆心的角的一半。
2、推论:1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧;2:半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径。
3:若三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
六、圆接四边形圆的接四边形定理:圆的接四边形的对角互补,外角等于它的对角。
中考数学圆知识点总结5篇

中考数学圆知识点总结5篇第1篇示例:数学是中考考试的必考科目,而关于圆的知识点在数学中占有非常重要的地位。
掌握了圆的相关知识,不仅能够在中考中取得更好的成绩,也有助于我们理解和运用数学知识。
下面我们来总结一下关于中考数学圆知识点的内容。
一、圆的基本概念圆是由平面上距离给定点(圆心)的所有点构成的集合,圆心到圆上任意一点的距离称为半径,圆内不经过圆心的线段称为弦,圆内的一段是弦分成的弧,半径的两端和圆上的一点共线,相交于该点的两条切线长度相等等。
二、圆的性质1. 同圆的弦长相等,异圆的弦长不等。
2. 相等圆的半径相等,而且圆周相等。
3. 圆内角、弦的角平分线和半径三者相交于一点。
4. 圆的外接角是对半的,即半径与切线相交于90度,弦与弦的夹角、切线与切线的夹角相等。
5. 内角落在圆弧内的叫做圆心角。
三、圆的相关定理1. 存在唯一的过三点的圆定理(就是圆的唯一性)。
2. 切、割定理(切线与切线、弦、割线各自乘积相等)。
3. 平行/相似判定定理(有什么情况判断两个圆是否平行或相似)。
4. 余弦定理(三角形当中,直角三角形含有的一种特殊情况)。
5. 弦切角定理(描述弦在圆内部与对应的两平行切线的关系)。
6. 余切定理(指两个切线、或一条切线和半径之间的倍率关系)。
7. 切线定理(圆外一点到圆的切线与切点连线的长度之积)。
四、圆的应用1. 圆的相关计算问题:包括求圆周长、面积等。
2. 圆与三角形、正方形/矩形的结合题:针对圆与其他几何形状的相互作用问题。
3. 圆与证明题:利用圆的性质,进行证明题目。
圆的知识点在中考数学中具有非常重要的地位,掌握了圆的相关知识,可以更好地完成相关题目。
在复习中,我们需要通过大量的练习,加深对圆的概念和性质的理解,提高解题的能力和速度。
希望同学们能够认真学习和练习,取得优异的成绩,顺利通过中考。
第2篇示例:中考数学圆知识点总结圆是我们日常生活中常见的几何图形之一,具有许多特殊性质和规律。
专题30 圆的基本性质-中考数学一轮复习精讲+热考题型(解析版)

专题30 圆的基本性质【知识要点】知识点一圆的基础概念圆的概念:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫圆.这个固定的端点O叫做圆心,线段OA叫做半径.以O点为圆心的圆记作⊙O,读作圆O.特点:圆是在一个平面内,所有到一个定点的距离等于定长的点组成的图形.确定圆的条件:⑴圆心;⑵半径,⑶其中圆心确定圆的位置,半径长确定圆的大小.补充知识:1)圆心相同且半径相等的圆叫做同圆;2)圆心相同,半径不相等的两个圆叫做同心圆;3)半径相等的圆叫做等圆.弦的概念:连结圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径,并且直径是同一圆中最长的弦.⏜,读作弧AB.在同圆或弧的概念:圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作AB等圆中,能够重合的弧叫做等弧.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.在一个圆中大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.弦心距概念:从圆心到弦的距离叫做弦心距.弦心距、半径、弦长的关系:(考点)知识点二垂径定理垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;常见辅助线做法(考点):1)过圆心,作垂线,连半径,造RT△,用勾股,求长度;2)有弧中点,连中点和圆心,得垂直平分.知识点一圆的基础概念圆的概念:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫圆.这个固定的端点O叫做圆心,线段OA叫做半径.以O点为圆心的圆记作⊙O,读作圆O.特点:圆是在一个平面内,所有到一个定点的距离等于定长的点组成的图形.确定圆的条件:⑷圆心;⑸半径,⑹其中圆心确定圆的位置,半径长确定圆的大小.补充知识:1)圆心相同且半径相等的圆叫做同圆;2)圆心相同,半径不相等的两个圆叫做同心圆;3)半径相等的圆叫做等圆.弦的概念:连结圆上任意两点的线段叫做弦。
中考圆的知识点总结

中考圆的知识点总结前言中考是每个初中毕业生都要面临的重要考试。
其中,圆的知识点在数学科目中占据着重要的地位。
圆是几何学中的基本形状之一,了解和掌握圆的相关知识是学生们在中考中取得优异成绩的关键之一。
本文将对中考圆的知识点进行总结,以帮助学生们更好地复习和备考。
正文圆的定义与特征•圆的定义:圆是平面上所有距离中心点相等的点的集合。
•圆的符号表示:圆的中心点用大写字母 O 表示,圆的半径用小写字母 r 表示,整个圆用符号 O(r) 表示。
圆的基本要素与术语•圆心:圆的中心点,用大写字母 O 表示。
•半径:从圆心到圆上任意一点的距离,用小写字母 r 表示。
•圆上的点:圆上的任意一点,与圆心的距离等于半径。
圆的性质与定理1.直径:通过圆心并且在圆上的一条线段,其长度等于圆的半径的两倍。
2.弦:在圆上连接两点的线段。
3.弧:在圆上连接两点的弧。
4.切线:与圆只有一个交点的直线,与圆的切点处于圆的外部。
5.弦切定理:如果一条弦经过圆心,那么它一定是直径。
6.切线切割定理:切线与圆的切点处的切割线段长度相等。
7.弦心定理:一条弦中点连线与该弦对应的圆心连线垂直且相等。
圆的计算公式与应用1.圆的周长公式:C = 2πr(其中,C 表示圆的周长,r 表示圆的半径)。
2.圆的面积公式:A = πr²(其中,A 表示圆的面积,r 表示圆的半径)。
结尾通过本文的总结,我们对中考圆的相关知识点进行了梳理和归纳。
掌握圆的定义、特征、基本要素与术语,以及圆的性质与定理,可以更好地理解和运用圆的知识。
此外,熟悉圆的计算公式与应用,可以帮助学生们在解题中更加准确地计算圆的周长和面积。
希望本文对学生们的中考备考有所帮助,祝愿大家取得优异成绩!。
2025年中考数学考点分类专题归纳之 圆
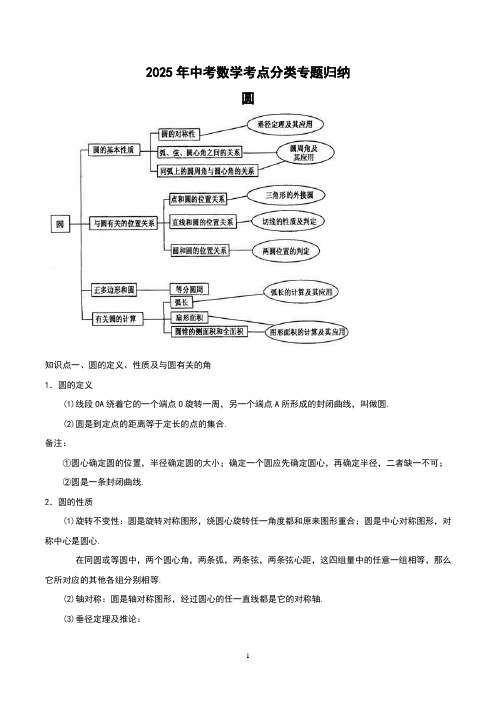
2025年中考数学考点分类专题归纳圆知识点一、圆的定义、性质及与圆有关的角1.圆的定义(1)线段OA绕着它的一个端点O旋转一周,另一个端点A所形成的封闭曲线,叫做圆.(2)圆是到定点的距离等于定长的点的集合.备注:①圆心确定圆的位置,半径确定圆的大小;确定一个圆应先确定圆心,再确定半径,二者缺一不可;②圆是一条封闭曲线.2.圆的性质(1)旋转不变性:圆是旋转对称图形,绕圆心旋转任一角度都和原来图形重合;圆是中心对称图形,对称中心是圆心.在同圆或等圆中,两个圆心角,两条弧,两条弦,两条弦心距,这四组量中的任意一组相等,那么它所对应的其他各组分别相等.(2)轴对称:圆是轴对称图形,经过圆心的任一直线都是它的对称轴.(3)垂径定理及推论:①垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.②平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.③弦的垂直平分线过圆心,且平分弦对的两条弧.④平分一条弦所对的两条弧的直线过圆心,且垂直平分此弦.⑤平行弦夹的弧相等.备注:在垂经定理及其推论中:过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧,在这五个条件中,知道任意两个,就能推出其他三个结论.(注意:“过圆心、平分弦”作为题设时,平分的弦不能是直径)3.与圆有关的角(1)圆心角:顶点在圆心的角叫圆心角.圆心角的性质:圆心角的度数等于它所对的弧的度数.(2)圆周角:顶点在圆上,两边都和圆相交的角叫做圆周角.4.圆周角的性质:①圆周角等于它所对的弧所对的圆心角的一半.②同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.③90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.④如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.⑤圆内接四边形的对角互补;外角等于它的内对角.备注:(1)圆周角必须满足两个条件:①顶点在圆上;②角的两边都和圆相交.(2)圆周角定理成立的前提条件是在同圆或等圆中.知识点二、与圆有关的位置关系1.判定一个点P是否在⊙O上设⊙O的半径为,OP=,则有点P在⊙O 外;点P在⊙O 上;点P在⊙O 内.备注:点和圆的位置关系和点到圆心的距离的数量关系是相对应的,即知道位置关系就可以确定数量关系;知道数量关系也可以确定位置关系.2.判定几个点A1,A2……A n在同一个圆上的方法当A1O=A2O=……=A n O=R时,A1,A2……A n在⊙O 上.3.直线和圆的位置关系设⊙O 半径为R,点O到直线的距离为.(1)直线和⊙O没有公共点直线和圆相离.(2)直线和⊙O有唯一公共点直线和⊙O相切.(3)直线和⊙O有两个公共点直线和⊙O相交.4.切线的判定、性质(1)切线的判定:①经过半径的外端并且垂直于这条半径的直线是圆的切线.②到圆心的距离等于圆的半径的直线是圆的切线.(2)切线的性质:①圆的切线垂直于过切点的半径.②经过圆心作圆的切线的垂线经过切点.③经过切点作切线的垂线经过圆心.(3)切线长:从圆外一点作圆的切线,这一点和切点之间的线段的长度叫做切线长.(4)切线长定理:从圆外一点作圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.5.圆和圆的位置关系设的半径为,圆心距.(1)和没有公共点,且每一个圆上的所有点在另一个圆的外部外离.(2)和没有公共点,且的每一个点都在内部内含(3)和有唯一公共点,除这个点外,每个圆上的点都在另一个圆外部外切.(4)和有唯一公共点,除这个点外,的每个点都在内部内切.(5)和有两个公共点相交.知识点三、三角形的外接圆与内切圆、圆内接四边形与外切四边形1.三角形的内心、外心、重心、垂心(1)三角形的内心:是三角形三条角平分线的交点,它是三角形内切圆的圆心,在三角形内部,它到三角形三边的距离相等.(2)三角形的外心:是三角形三边中垂线的交点,它是三角形外接圆的圆心,锐角三角形外心在三角形内部,直角三角形的外心是斜边中点,钝角三角形外心在三角形外部,三角形外心到三角形三个顶点的距离相等.(3)三角形重心:是三角形三边中线的交点,在三角形内部;它到顶点的距离是到对边中点距离的2倍,通常用G表示.(4)垂心:是三角形三边高线的交点.备注:(1) 任何一个三角形都有且只有一个内切圆,但任意一个圆都有无数个外切三角形;(2) 解决三角形内心的有关问题时,面积法是常用的,即三角形的面积等于周长与内切圆半径乘积的一半,即(S为三角形的面积,P为三角形的周长,r为内切圆的半径).(3) 三角形的外心与内心的区别:2.圆内接四边形和外切四边形(1)四个点都在圆上的四边形叫圆的内接四边形,圆内接四边形对角互补,外角等于内对角.(2)各边都和圆相切的四边形叫圆外切四边形,圆外切四边形对边之和相等.知识点四、圆中有关计算1.圆中有关计算圆的面积公式:,周长.圆心角为、半径为R的弧长.圆心角为,半径为R,弧长为的扇形的面积.弓形的面积要转化为扇形和三角形的面积和、差来计算.圆柱的侧面图是一个矩形,底面半径为R,母线长为的圆柱的体积为,侧面积为,全面积为.圆锥的侧面展开图为扇形,底面半径为R,母线长为,高为的圆锥的侧面积为,全面积为,母线长、圆锥高、底面圆的半径之间有.备注:(1)对于扇形面积公式,关键要理解圆心角是1°的扇形面积是圆面积的,即;(2)在扇形面积公式中,涉及三个量:扇形面积S、扇形半径R、扇形的圆心角,知道其中的两个量就可以求出第三个量.(3)扇形面积公式,可根据题目条件灵活选择使用,它与三角形面积公式有点类似,可类比记忆;(4)扇形两个面积公式之间的联系:.1.(2024•贺州)如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB,BD=5,则AH的长为()A.B.C.D.2.(2024•张家界)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=()A.8cm B.5cm C.3cm D.2cm3.(2024•襄阳)如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为()A.4 B.2C.D.24.(2024•衢州)如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是()A.3cm B.cm C.2.5cm D.cm5.(2024•枣庄)如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为()A.B.2C.2D.86.(2024•安顺)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为()A.2cm B.4cm C.2cm或4cm D.2cm或4cm7.(2024•临安区)如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=()A.B.C.D.8.(2024•乐山)《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆柱形木材的直径是多少?”如图所示,请根据所学知识计算:圆柱形木材的直径AC是()A.13寸B.20寸C.26寸D.28寸9.(2024•日照)如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED 的正切值等于()A.B.C.2 D.10.(2024•巴中)如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB 等于()A.B.2 C.2D.311.(2024•赤峰)如图,AB是⊙O的直径,C是⊙O上一点(A、B除外),∠AOD=130°,则∠C的度数是()A.50°B.60°C.25°D.30°12.(2024•盘锦)如图,⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为()A.15°B.25°C.30°D.50°13.(2024•陕西)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为()A.15°B.35°C.25°D.45°14.(2024•柳州)如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为()A.84°B.60°C.36°D.24°15.(2024•铜仁市)如图,已知圆心角∠AOB=110°,则圆周角∠ACB=()A.55°B.110°C.120°D.125°16.(2024•通辽)已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是()A.30°B.60°C.30°或150°D.60°或120°17.(2024•咸宁)如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为()A.6 B.8 C.5D.518.(2024•陇南)如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是()A.15°B.30°C.45°D.60°19.(2024•盐城)如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为()A.35°B.45°C.55°D.65°20.(2024•邵阳)如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是()A.80°B.120°C.100°D.90°21.(2024•泰安)如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为()A.3 B.4 C.6 D.822.(2024•牡丹江)如图,△ABC内接于⊙O,若sin∠BAC,BC=2,则⊙O的半径为()A.3B.6C.4D.223.(2024•自贡)如图,若△ABC内接于半径为R的⊙O,且∠A=60°,连接OB、OC,则边BC的长为()A.B.C.D.24.(2024•湘西州)已知⊙O的半径为5cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系为()A.相交B.相切C.相离D.无法确定25.(2024•湘西州)如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为5,CD=8,则弦AC的长为()A.10 B.8 C.4D.426.(2024•福建)如图,AB是⊙O的直径,BC与⊙O相切于点B,AC交⊙O于点D,若∠ACB=50°,则∠BOD等于()A.40°B.50°C.60°D.80°27.(2024•宜昌)如图,直线AB是⊙O的切线,C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为()A.30°B.35°C.40°D.45°28.(2024•重庆)如图,已知AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则PA的长为()A.4 B.2C.3 D.2.529.(2024•海南)如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D 在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为_______.30.(2024•烟台)如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为_________.31.(2024•孝感)已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是______cm.32.(2024•广元)如图是一块圆环形玉片的残片,作外圆的弦AB与内圆相切于点C,量得AB=8cm、点C 与的中点D的距离CD=2cm.则此圆环形玉片的外圆半径为___cm.33.(2024•舟山)如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为60°,则该直尺的宽度为________cm.34.(2024•毕节市)如图,AB是⊙O的直径,C、D为半圆的三等分点,CE⊥AB于点E,∠ACE的度数为_____.35.(2024•随州)如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则∠B=____度.36.(2024•黑龙江)如图,AC为⊙O的直径,点B在圆上,OD⊥AC交⊙O于点D,连接BD,∠BDO=15°,则∠ACB=_____.37.(2024•吉林)如图,A,B,C,D是⊙O上的四个点,,若∠AOB=58°,则∠BDC=____度.38.(2024•北京)如图,点A,B,C,D在⊙O上,,∠CAD=30°,∠ACD=50°,则∠ADB=_____.39.(2024•绥化)如图,△ABC是半径为2的圆内接正三角形,则图中阴影部分的面积是________(结果用含π的式子表示).40.(2024•常州)如图,△ABC是⊙O的内接三角形,∠BAC=60°,的长是,则⊙O的半径是___.41.(2024•新疆)如图,△ABC是⊙O的内接正三角形,⊙O的半径为2,则图中阴影部分的面积是__.42.(2024•临沂)如图.在△ABC中,∠A=60°,BC=5cm.能够将△ABC完全覆盖的最小圆形纸片的直径是______cm.43.(2024•内江)已知△ABC的三边a,b,c,满足a+b2+|c﹣6|+28=410b,则△ABC的外接圆半径=_.44.(2024•益阳)如图,在圆O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,AD=DC,则∠C=____度.45.(2024•枣庄)如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.(1)求线段AD的长度;(2)点E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.46.(2024•徐州)如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.(1)CD与⊙O有怎样的位置关系?请说明理由;(2)若∠CDB=60°,AB=6,求的长.。
中考数学圆知识点总结5篇

中考数学圆知识点总结5篇篇1一、圆的定义圆是由所有到定点距离等于定长的点组成的封闭曲线,这个定点称为圆心,定长称为半径。
圆有无数条对称轴,对称轴经过圆心。
圆具有旋转对称性,任意绕圆心旋转一定的角度都可能与原来的圆重合。
二、圆的性质1. 圆心距性质:任意两个圆的圆心距离等于两圆半径之和的,两圆外离;任意两个圆的圆心距离等于两圆半径之差的,两圆内含;任意两个圆的圆心距离小于两圆半径之和但大于两圆半径之差的,两圆相交。
2. 切线性质:圆的切线垂直于经过切点的半径。
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等。
3. 圆的幂性质:如果两条弦与同一条直径垂直,那么这两条弦所对的直径段相等。
4. 圆锥曲线性质:以圆锥的底面直径为长轴,以圆锥的高为短轴的椭圆,叫做圆锥椭圆。
圆锥椭圆的两焦点是圆锥的底面圆心和顶点。
双曲线类似。
三、圆的应用1. 在建筑设计中,可以利用圆的旋转对称性,设计出美观大方的建筑外观。
如圆形广场、圆形剧场等。
2. 在机械制造中,许多零部件都是圆形或环形的设计,如轴承、齿轮等。
这些零部件的精确制造和安装对于整个机械的性能和稳定性至关重要。
3. 在电子科技领域,许多电子元件和电路板都是基于圆形或环形的布局设计,如电容、电感等。
这些元件的形状和布局对于电子设备的功能和性能有着重要影响。
4. 在生物学和医学领域,许多生物体的结构和器官都是圆形或近似的圆形设计,如人体的大脑、心脏等。
对于这些结构和器官的研究和理解,有助于我们更好地认识生命的奥秘。
四、圆的解题技巧1. 圆的题目中,常常会出现一些隐含的条件,如切线的性质、圆的幂性质等。
我们需要认真分析题目中的条件,找出这些隐含的条件,并加以利用。
2. 对于一些复杂的题目,我们可以利用几何软件进行辅助分析,如使用CAD软件进行绘图分析,可以帮助我们更好地理解题意和解题思路。
3. 在解题过程中,我们需要注重几何语言的准确性和规范性,避免出现混淆概念、计算错误等问题。
中考圆形知识点总结归纳

中考圆形知识点总结归纳圆形是中考数学中的一个重要知识点,它涉及到多个概念和性质,以下是对中考圆形知识点的总结归纳:圆的基本定义圆是一个平面上所有与给定点(圆心)距离相等的点的集合。
这个距离称为半径。
圆的方程圆的标准方程是 \( (x - h)^2 + (y - k)^2 = r^2 \),其中 \( (h, k) \) 是圆心的坐标,\( r \) 是半径。
圆的性质1. 圆周上的任意一点到圆心的距离都等于半径。
2. 圆的直径是圆上两点之间的最长距离,直径的长度是半径的两倍。
3. 圆内任意两点之间的线段,最短的是直线段,即直径。
4. 圆的切线在切点处与半径垂直。
圆的面积和周长- 圆的面积公式是 \( A = \pi r^2 \)。
- 圆的周长(圆周)公式是 \( C = 2\pi r \)。
圆与直线的位置关系1. 直线与圆相离:直线与圆没有公共点。
2. 直线与圆相切:直线与圆有一个公共点,即切点。
3. 直线与圆相交:直线与圆有两个公共点。
圆与圆的位置关系1. 两圆外离:两圆没有公共点。
2. 两圆外切:两圆只有一个公共点。
3. 两圆相交:两圆有两个公共点。
4. 两圆内切:一个圆完全包含在另一个圆内,只有一个公共点。
5. 两圆内含:一个圆完全包含在另一个圆内,没有公共点。
圆的内接多边形1. 内接于圆的多边形,其所有顶点都在圆上。
2. 正多边形是内接于圆的多边形,且所有边长相等,所有内角相等。
圆的外切多边形1. 外切于圆的多边形,其所有边都与圆相切。
2. 正多边形的外接圆是所有顶点都与圆相切的圆。
圆的弧和扇形1. 弧是圆上两点之间的线段。
2. 扇形是圆心角和它所对的弧所围成的区域。
圆的切线和割线1. 切线是与圆相切的直线。
2. 割线是与圆相交的直线,但不经过圆心。
结束语通过以上对中考圆形知识点的总结归纳,我们可以看到圆的几何性质和计算在中考数学中占有重要地位。
掌握这些知识点对于解决相关的几何问题至关重要。
最全面初中圆的知识点总结-初中数学圆知识点总结(完整版)

最全面初中圆的知识点总结-初中数学圆知识点总结(完整版)名师总结:中考数学圆的知识点考点一:圆的相关概念1.圆的定义:在平面内,以一个固定点为圆心,以固定距离为半径,绕圆心旋转一周所形成的图形叫做圆。
2.圆的几何表示:以圆心为中心的圆记作“⊙O”,读作“圆O”。
考点二:弦、弧等与圆有关的定义1.弦:连接圆上任意两点的线段。
2.直径:经过圆心的弦,等于半径的2倍。
3.半圆:圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆。
4.弧、优弧、劣弧:圆上任意两点间的部分叫做圆弧,用符号“⌒”表示。
大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧。
考点三:垂径定理及其推论垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
推论2:圆的两条平行弦所夹的弧相等。
考点四:圆的对称性1.圆的轴对称性:圆是轴对称图形,经过圆心的每一条直线都是它的对称轴。
2.圆的中心对称性:圆是以圆心为对称中心的中心对称图形。
考点五:弧、弦、弦心距、圆心角之间的关系定理1.圆心角:顶点在圆心的角叫做圆心角。
2.弦心距:从圆心到弦的距离叫做弦心距。
3.定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距相等。
考点六:圆周角定理及其推论1.圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角。
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等。
中考数学圆知识点归纳

中考数学圆知识点归纳1.基本概念-圆:由平面上距离固定点的所有点构成的集合。
-圆心:圆的中心点,用O表示。
-半径:圆心到任意一个点的距离,用r表示。
-直径:通过圆心并且两端点在圆上的线段,其长度为2r。
-弦:连接圆上任意两点的线段。
-弧:圆上两点之间的一段弧。
-弧长:圆的周长。
-弦长:弦的长度。
-切线:只与圆相交于一个点的直线。
-弦切角:以一个弦为直角边的角。
-弦割角:以一个切线和弦为直角边的角。
2.圆的性质-圆上任意两点与圆心的距离相等。
-圆上任意一点到圆心的距离等于半径的长度。
-直径是圆的一条特殊的弦,其长度是任意弦长的两倍。
-圆切线与半径垂直。
-圆切线与切点之间的弦是弦切角的平分线。
-圆切线与半径的夹角等于弦割角。
3.弦长定理-弦长定理:在同一个圆或等圆的两条弦上,如果有一条弦分别与这两条弦垂直,则这两条弦的乘积等于弦的和与弦的差的乘积。
即a*b=c*d,其中a、b为弦的长度,c、d为弦的长度。
4.弧长与扇形面积-弧长:扇形所对的弧的长度,记为L。
-弧长公式:弧长L=rθ,其中r为半径,θ为弧所对的圆心角的度数。
-扇形面积:扇形所对的圆心角所包含的面积,记为S。
-扇形面积公式:扇形面积S=(1/2)r²θ,其中r为半径,θ为弧所对的圆心角的度数。
5.圆周角-圆周角:以圆心为顶点的角。
-弧度制:圆周角的度数换算为弧度的形式,1弧度=180°/π。
-弧度公式:弧长L=rθ,其中r为半径,θ为圆周角的弧度数。
6.相交弦与切线关系-相交弦的性质:-相交弦的线段积相等:如果两条相交弦AD与BC在圆上,且E为相交弦的交点,则AE*DE=BE*CE。
-斜弦的性质:如果两条斜弦在圆上且互不相交,且两条斜弦分别与同一条直径AB相交于两个点C和D,则角ACD+∠ABD=180°。
-弦割弦定理:若弦AB与弦CD相交,则AB/CD=(AD/BC)^2-切线的性质:-切线长度:切线长等于圆心到切点的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中圆复习、圆的概念集合形式的概念:1、圆可以看作是到定点的距离等于定长的点的集合;2、圆的外部:可以看作是到定点的距离大于定长的点的集合;3、圆的内部:可以看作是到定点的距离小于定长的点的集合轨迹形式的概念:1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;2 、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线);3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。
点与圆的位置关系1、点在圆内2、点在圆上3、点在圆外直线与圆的位置关系d r 点C在圆内;d r 点B 在圆上;d r 点A在圆外;1、直线与圆相离2、直线与圆相切d r 无交点;d r 有一个交点;3、直线与圆相交 d r 有两个交点;四、圆与圆的位置关系外离(图1)无交点 d R r ;外切(图2)有一个交点 d R r ;相交(图3)有两个交点内切(图4)有一个交点 d R r ;内含(图5)无交点 d R r ;J.R五、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:①AB是直径②AB CD ③CE DE ④弧BC 弧BD ⑤ 弧AC 弧AD中任意2个条件推出其他3个结论。
推论2 :圆的两条平行弦所夹的弧相等。
即:在O O 中,••• AB // CD•••弧AC 弧BD六、圆心角定理圆心角定理:同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,弦心距相等。
此定理也称1 推3 定理,即上述四个结论中,只要知道其中的1 个相等,则可以推出其它的3 个结论,即:① AOB DOE :② AB DE ;③OC OF ;④弧BA弧BD七、圆周角定理1 、圆周角定理:同弧所对的圆周角等于它所对的圆心的角的一半。
即:••• AOB和ACB是弧AB所对的圆心角和圆周角• AOB 2 ACB2、圆周角定理的推论:推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧;即:在。
O中C、D都是所对的圆周角CD推论2 :半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径。
即:在O O中,••• AB是直径或••• C 90••• C 90 二AB是直径推论3:若三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
即:在厶ABC中OC OA OB•••△ ABC是直角三角形或C 90注意:此推论实是初二年级几何中矩形的推论:在直角三角形中斜边上的中线等于斜边的一半的逆定理。
八、圆内接四边形圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角。
即:在。
O中,•••四边ABCD是内接四边形••• C BAD 180 B D 180DAE C九、切线的性质与判定定理1 、切线的判定定理:过半径外端且垂直于半径的直线是切线;两个条件:过半径外端且垂直半径,二者缺一不可即:••• MN OA且MN过半径OA外端••• MN是O O的切线2 、性质定理:切线垂直于过切点的半径(如上图)推论1:过圆心垂直于切线的直线必过切点。
推论2:过切点垂直于切线的直线必过圆心。
以上三个定理及推论也称二推一定理:即:①过圆心;②过切点;③垂直切线,三个条件中知道其中两个条件就能推出最后一个。
十、切线长定理切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角。
即::PA、PB是的两条切线••• PA PB; PO 平分BPA十一、圆幂定理1、相交弦定理:圆内两弦相交,交点分得的两条线段的乘积相等。
即:在。
O中,•••弦AB、CD相交于点P ,••• PA PB PC PD推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。
即:在O O中,•••直径AB CD ,••• CE AE BE2、切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
即:在。
O中,:PA是切线,PB是割线2••• PA PC PB3、割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等(如右图)。
即:在。
O中,:PB、PE是割线2••• PC PB PD PE十二、两圆公共弦定理圆公共弦定理:两圆圆心的连线垂直并且平分这两个圆的的公共弦。
如图:0Q2垂直平分AB。
即P:v© O i、O O2相交于A、B两点二0102垂直平分AB十三、圆的公切线两圆公切线长的计算公式:(1 )公切线长:Rt OQ2C 中,AB2 CO,2 OQ22 CO22;(2)外公切线长:CO2是半径之差;内公切线长:CO2是半径之和十四、圆内正多边形的计算(1 )正三角形在。
O中厶ABC是正三角形,有关计算在Rt BOD中进行:OD:BD:OB 1:、一3:2 ;(2 )正四边形同理,四边形的有关计算在Rt OAE中进行,OE:AE:OA 1:1: .2 :(3 )正六边形十五、扇形、圆柱和圆锥的相关计算公式1、扇形:(1)弧长公式:,n R180 ;(2 )扇形面积公式:。
n R21S IR360 2n:圆心角R:扇形多对应的圆的半径I :扇形弧长S:扇形面积2、圆柱:(1 )圆柱侧面展开图同理,六边形的有关计算在Rt OAB中进行, AB: OB : OA 1: 3:2.S表S侧2S底=2 rh 2 r(2)圆柱的体积:V r2h3、圆锥侧面展开图(1)S表S侧S底=Rr r1(2)圆锥的体积:V - r2h3十六、内切圆及有关计算(1)三角形内切圆的圆心是三个内角平分线的交点,它到三边的距离相等。
(2) △ ABC 中,/ C=90 ° , AC=b , BC=a , AB=c,则内切圆的半径1(3) S△ ABC= r (a b c),其中a, b , c是边长,r是内切圆的半径。
(4) 弦切角:角的顶点在圆周上,角的一边是圆的切线,另一边是圆的弦。
如图,BC切O O于点B , AB为弦,/ ABC叫弦切角,/ ABC= / D。
C练习题1 •若O O的半径为4cm,点A到圆心O的距离为3cm,那么点A与O O的位置关系是()A.点A在圆内B .点A在圆上c.点A在圆外D .不能确定2 .已知O O的半径为5,弦AB的弦心距为3,则AB的长是___________3 .如图,MN是半径为1的O O的直径,点A在O O上,/ AMN =30 ° , B为AN弧的中点,点P是直径MN 上一个动点,则求PA+PB的最小值4如图2,已知BD 是O O 的直径,O O 的弦AC 丄BD 于点E ,若/ AOD=60 °,则/ DBC 的度数为 _5 .与直线L 相切于已知点的圆的圆心的轨迹是 __________ .6 .已知直角三角形的两直角边长分别为 5和12,则它的外接圆半径 R= ________ ,内切圆半径r= ________ .7 . O O 的半径为6 , O O 的一条弦AB 为6 3,以3为半径的同心圆与直线 AB 的位置关系是 _________________8 .PA 、PB 是O O 的切线,切点是 A 、B ,/APB =50。
,过A 作O O 直径AC ,连接CB ,则/ PBC = ________9 .如图4, AB 是O O 的直径,弦 AC 、BD 相交于P ,贝U CD: AB 等于构成圆环面积为A . sin BPC C . tan BPC D . cot BPC10 .如图5,点则PC 的长是 A .,2 P 为弦AB 上一点,连结 OP ,过 PC 作 PC 丄OP , PC 交O O 于 C ,若 AP =4 , PB =2 ,C . 2.211 .圆的最大的弦长为 12 cm ,如果直线与圆相交,且直线与圆心的距离为d ,那么 A . d <6 cm6 cm< d <12 cm C . d > 6 cmd >12 cm 12 .如图6,在以O 为圆心的两个同心圆中,大圆的弦AB 是小圆的切线, P 为切点,设AB =12,则两圆B . cos BPC 图5图413 .如图 7, PE 是O O 的切线,E 为切点,PAB 、PCD 是割线,AB =35 , CD =50 , AC : DB =1 : 2,则 PA= _____ .14 .如图8 , AB 是O O 的直径,点 D 在AB 的延长线上,且 BD =OB ,点C 在O O 上,/ CAB =30 ° , 求证:DC 是O O 的切线.15.如图,AB 既是O C 的切线也是O D 的切线,O C 与O D 相外切, O C 的半径r=2 , O D 的半径R=6,求四边形 ABCD 的面积。
(1) AC 是O O 的切线.(2)若 AD : DB =3 : 2 , AC =15,求O O 的直径.(12 分)图1017 .如图11 , AB 是O O 的直径,点P 在BA 的延长线上,弦 CD 丄AB ,垂足为E ,且PC 2=PE • PO . (1) 求证:PC 是O O 的切线;(2)若0E : EA =1 : 2 , PA =6,求O O 的半径;(3)求sin PCA 的值.(12分)图1118 .如图,O O 的两条割线 AB 、AC 分别交圆 0于D 、B 、E 、C ,弦DF//AC 交BC 于C .(1)求证:AC FG BC CG ;(2 )若CF = AE .求证:△ ABC 为等腰三角形.19. 如图,AB 是O O 的直径,弦 CD 丄AB 与点E ,点P 在O O 上,/ 1= / C , (1 )求证:CB // PD; 16 .如图10 , BC 是O O 的直径, A 是弦BD 延长线上一点,切线 DE 平分AC 于E ,求证:图6 图73(2 )若BC=3 , sinP= ,求O O 的直径。
520 .如图,△ ABC内接于O O, AB是O O的直径,PA是过A点的直线,/ PAC =Z B .(1)求证:PA是O O的切线;(2)如果弦CD交AB于E, CD的延长线交PA 于F, AC = 8 , CE : ED = 6: 5 , AE : EB = 2 : 3 ,求AB的长和/ ECB的正切值.21 •如图,在Rt△ ABC中,/ B = 90 °,/ A的平分线交BC于点D , E为AB上的一点,DE = DC,以D为圆心,DB长为半径作O D ,求证:(I) AC是O D的切线;(2 ) AB + EB = AC.22 •如图,AB是O O的直径,以OA为直径的O O1;与O O的弦AC相交于D , DE丄OC,垂足为E .(l)求证:AD = DC ;(2 )求证:DE是O。
