2014年高考全国各地模拟卷型题整理(一)
百强重点名校高考备考_2014年高考名校语文模拟卷诗歌鉴赏题精汇(3)(完美整理版)

2014年高考名校语文模拟卷诗歌鉴赏题精汇(3)诗歌鉴赏指导0109 1627:2014年高考名校语文模拟卷诗歌鉴赏题精汇【27】、阅读下面这首宋词,然后回答问题。
南歌子贺铸疏雨池塘见,微风襟袖知。
阴阴夏木啭黄鹂。
何处飞来白鹭、立移时,易醉扶头酒,难逢敌手棋。
日长偏与睡相宜。
睡起芭蕉叶上、自题诗。
【注】贺铸,出身于没落贵族家庭,但他秉性刚直,不阿权贵,一生屈居下僚,郁郁不得志。
(1)词的上片描绘了一幅怎样的画面?结合内容作简要分析。
(4分)(2)词的下片一连写了士大夫消夏乐闲的哪四件生活琐事?在笔下,这些事似乎都有一种和韵事格格不入的苦涩味,与上片大异其趣,请简要分析(6分)【参考答案】(1)上片描绘出一幅闲适恬谈、生机勃勃的夏日风景图。
(2分)词人独立庭院,点点疏雨在池塘中留下了微微的涟漪,轻风拂面而来。
周围树木成阴,枝头上黄鹂婉转啼鸣,一只不知从何处飞来的白鹭,落在池畔,迟迟不愿离去。
词人观疏雨、沐轻风、听黄鹂、友白鹭,怡然自得,其乐陶陶。
(2分)[来源高考资源网](2)写了饮酒、下棋、睡觉、题诗四件生活琐事。
(2分,两个1分,四个2分)饮酒而“易醉”,下棋而敌手“难逢”,字里行间蕴含着的仍然是一种百无聊赖的心绪;夏日长长,无所事事,最适合于睡觉,自我解嘲;睡起题诗,则只能“自题”自赏,自取其乐。
(2分)透露着孤寂落寞、知音难求的情怀和无所事事、壮志难酬的痛苦。
(2分,大意对即可)【28】阅读下面这首宋词,然后回答问题。
(10分)阮郎归·初夏苏轼绿槐高柳咽新蝉,薰风初入弦。
碧纱窗下水沉烟,棋声惊昼眠。
微雨过,小荷翻,榴花开欲燃。
玉盆纤手弄清泉,琼珠碎却圆。
(1)诗人是从哪些角度描写初夏之景的?试简析。
(4分)(2)试析“燃”字的妙用(3分)(3)简析划线句表现了人物怎样的心情。
(3分)【参考答案】(1).诗人分别从视觉、听觉和触觉的角度描写初夏之景:写看到了枝叶繁茂的槐树,高大的柳树,水花散溅到荷叶上,像珍珠那样圆润晶亮的景象;听到了浓绿深处的新蝉鸣声乍歇;感受到了怡人的熏风(和风)。
2014年高考语文课标卷模拟试题参考答案

(2)从前汉高祖仅能统领十 万军队,李景隆有什么才能, 他的部众正好可以成为我的 军资了!。 (5分,“止”“何 才”“适”“资”各1分,句 意1分)
(二)(11分)8、(5分)
①前四句表现下层人民的饥寒和后 四句表现上层社会的糜烂的对比; (1分)②前四句中表现的下层人民 辛苦劳作的现实和本应过上温饱生 活的情理之间的推理对比;(2分) ③后四句中假设燕赵美女变成丑妇, 笑值千金变成笑不值钱之间的转化 对比。(2分)
(3)不好。(1分)用第二人称
“你”和第一人称对应起来,更 便于“我”讲述七个小板凳的故 事,也更便于表达“我”的真情 实感;(2分)用第二人称“你”拉
近了主人公和读者的距离,就好像一 位长者在你面前讲故事,让人感到亲 切。(2分)第三人称“他”一般用 于客观叙述,达不到这样的效果。 (1分)
(4)我认同“我”借七个小板凳对 “你”进行了深刻的思想教育。(2分) ①艰苦岁月中的相互扶持和关爱是一 笔宝贵的精神财富。(2分)②在物质 财富丰富的今天,也要学会珍惜并传 递这笔宝贵的精神财富,学会感恩。 (2分)③这样家庭才会和谐温馨,人 们才不会成为金钱和物质的奴隶。(2 分)
四、12、(25分)
(1)
BC(3分、2分)
(2) ①当许多学子留在法国巴黎“呼吸浓郁的 艺术气息”时,吴冠中选择了回国。②上 世纪八九十年代,吴冠中《笔墨等于零》 等几篇言辞激烈的艺术文笔引发强烈纷议。 ③吴冠中大量焚烧自己不中意的画作。④ 吴冠中的逆耳言论由美术创作延伸到教育、 文化等领域。
三、(25分) 11、(25分)
(1)CE(3分、2分)
(2)①“我”在艰苦岁月中,关爱 体贴家人,营造亲情氛围,关心孩 子成长,在过上新生活的当下,懂 得珍惜并希望儿子能够传递这份精 神财富。②“你”虽经历过艰苦岁 月,但那时还懵懂无知,在优裕的 生活状态下,追求物质享受,却忽 略了美好情感的继承和传递。 (每点3分,共6分)
2014北京高考真题生物(含解析)

2014年普通高等学校招生全国统一考试理科综合生物试题(北京卷)一、选择题1.蓝细菌(蓝藻)与酵母菌的相同之处是()A.都有拟核B. 均能进行有氧呼吸C. 都有线粒体D.均能进行光合作用2.在我国北方,游泳爱好者冬泳入水后,身体立即发生一系列生理反应,以维持体温恒定。
此时,机体不会发生的反应是()A.兴奋中枢神经系统,加强肌肉收缩B.通过反射活动引起皮肤毛细血管收缩C. 通过神经调节减少汗腺分泌D.抑制垂体活动导致甲状腺激素分泌减少3.比较生物膜和人工膜(双层磷脂)对多种物质的通透性.结果如右图,据此不能得出的推论是()A.生物膜上存在着协助H2O通过的物质B.生物膜对K+、Na+、Cl-的通透具有选择性C.离子以易化(协助)扩散方式通过人工膜D.分子的大小影响其通过人工膜的扩散速率4.为控制野兔种群数量,澳洲引入一种主要由蚊子传播的兔病毒。
引入初期强毒性病毒比例最高,兔被强毒性病毒感染后很快死亡,致兔种群数量大幅下降。
兔被中毒性病毒感染后可存活一段时间,几年后中毒性病毒比例最高,兔种群数量维持在低水平。
由此无法推断出()A.病毒感染对兔种群的抗性具有选择作用B.毒性过强不利于维持病毒与兔的寄生关系C.中毒性病毒比例升高是因为兔抗病毒能力下降所致D.蚁子在兔和病毒之间的协同(共同)进化中发挥了作用5. 在25℃的实验条件下可顺利完成的是()A.光合色素的提取与分离B. 用斐林(本尼迪特)试剂鉴定还原糖C.大鼠神经细胞的培养D.制备用于植物组织培养的固体培养基二、非选择题29. (18分)为研究赤霉素(GA5)和生长素(IAA)对植物生长的影响,切取菟丝子茎顶端2.5cm长的部分(茎芽)。
置于培养液中无菌培养(图分为三组,分别培养至第1、8、15天,每组再用适宜浓度的激素处理30天,测量茎芽长度。
结果见图2:(1)植物激素是植物细胞之间传递________的分子。
(2)本实验中,试管用滤膜封口是为了在不影响________通过的情况下起到________的作用。
2014年普通高等学校招生全国统一考试模拟试题

2014年普通高等学校招生全国统一考试模拟试题DC.甲和乙受到的合力都可能是恒力D.甲受到的合力可能是恒力,乙受到的合力不可能是恒力6.如图,在固定斜面上的一物块受到一外力F的作用,F平行于斜面向上.若要物块在斜面上保持静止,F的取值应有一定范围,已知其最大值和最小值分别为F1和F2(F2>0).由此可求出()A.物块的质量B.斜面的倾角C.物块与斜面间的最大静摩擦力D.物块对斜面的正压力7.导体A、B、C的伏安特性曲线分别是图线1、2、3,其中导体C为一非线性电阻.当它们串联后接在电压恒为6 V 的直流电源两端时,它们的电阻分别为R1、R2、R3,则下列说法正确的是()A.此时流过三导体的电流均为1 AB.R1∶R2∶R3=1∶3∶2C.若将三导体串联后接在3 V的直流电源上,则三导体的阻值之比不变D .若将三导体并联后接在3 V 的直流电源上,则通过它们的电流之比I 1∶I 2∶I 3=3∶2∶18.自耦变压器的输入端接在内阻为r 的交流电源上,输出端接阻值为R 的负载.如果要求负载R 上消耗的电功率最大,变压器原、副线圈的匝数比应为(变压器为理想变压器,输入端的电动势恒定)( )A .小于r R B .等于r R C .等于R r D .大于R r9.如图所示,两个质量均为m 的完全相同的小球A 和B 用轻杆连接,由静止从曲面上释放至滑到水平面的过程中,不计一切摩擦,则杆对A 球做的功为( ) A.12mgh B .-12mgh C .mgh D .-mgh10.如图所示,质量为M 的足够长金属导轨abcd 放在光滑的绝缘水平面上.一电阻为r,质量为m的导体棒PQ放置在导轨上,始终与导轨接触良好,PQbc构成矩形.棒与导轨间光滑、棒左侧有两个固定于水平面的光滑立柱.导轨bc段电阻为R,长为L,其他部分电阻不计.以ef为界,其左侧匀强磁场方向竖直向上,右侧匀强磁场水平向右,磁感应强度大小均为B.在t=0时,一水平向左的拉力F垂直作用在导轨的bc边上,使导轨由静止开始做匀加速直线运动,加速度为a.则() A.F与t成正比B.F与t2成正比C.当t达到一定值时,QP刚好对轨道无压力D.若F=0,PQbc静止,ef左侧磁场均匀减小,当ΔB Δt达到一定值时,QP刚好对轨道无压力答题栏第Ⅱ卷(非选择题共60分)二、非选择题:本题共5小题,共60分.按题目要求作答.解答题应写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题,答案中必须明确写出数值和单位.11.(5分)现用如图所示的装置探究“加速度与物体受力的关系”.小车所受拉力及其速度可分别由拉力传感器和速度传感器记录下来.速度传感器安装在距离L=48.0 cm的长木板的A、B 两点.(1)实验主要步骤如下:A.将拉力传感器固定在小车上;B.平衡摩擦力,让小车在没有拉力作用时能做匀速直线运动;C.把细线的一端固定在拉力传感器上,另一端通过定滑轮与轻质小盘(盘中放置砝码)相连;D.接通电源后自C点释放小车,小车在细线拉动下运动,记录细线拉力F的大小及小车分别到达A、B时的速率v A、v B;E.改变小盘中砝码的数量,重复D的操作.由以上实验可得出加速度的表达式a=________.(2)现已得出理论上的a-F图线,某同学又用描点法根据实验所得数据,在坐标纸上作出了由实验测得的a-F图线.对比实验结果与理论计算得到的两个关系图线,,偏差的主要原因是___________________________.12.(10分)某同学要测量一节干电池的电动势和内阻.他根据老师提供的以下器材画出了如图所示的原理图.A.电压表V(15 V,10 kΩ)B.电流表G(量程3.0 mA,内阻R g为10 Ω)C.电流表A(量程0.6 A,内阻约为0.5 Ω)D.滑动变阻器R1(0~20 Ω,10 A)E.滑动变阻器R2(0~100 Ω,1 A)F.定值电阻R3=990 ΩG.开关S和导线若干(1)该同学没有选用电压表是因为________;(2)该同学将电流表G与定值电阻R3串联,实际上是进行了电表的改装,则他改装的电压表对应的量程是________V;(3)为了能准确地进行测量,同时为了操作方便,实验中应选用的滑动变阻器是________(填写器材前的字母编号);(4)该同学利用上述实验原理图测得以下数据,并根据这些数据绘出了如图所示的图线,根据图线可求出干电池的电动势E=________V(保留3位有效数字),干电池的内阻r =________Ω(保留2位有效数字).序号12345 6电流表G (I1/m A)1.371.351.261.241.181.11电流0.10.10.20.20.30.426186 3表A(I2/A)13.(13分)如图所示,在光滑水平面上有一长为L1、宽为L2的单匝矩形闭合导体线框abcd,处于磁感应强度为B的有界匀强磁场中,其ab边与磁场的边界重合.线框由同种粗细均匀的导线制成,它的总电阻为R.现用垂直于线框ab 边的水平拉力,将线框以速度v向右沿水平方向匀速拉出磁场(此过程中保持线框平面与磁感线垂直,且ab边与磁场边界平行),线框中产生的焦耳热与导体线框abcd以ab为轴匀速顺时针(cd向上)转动90°过程中线框中产生的焦耳热相同.求线框匀速转动的角速度.14.(14分)如图所示,传送带A、B间距离L=5 m且在同一水平面内,两个轮子半径均为r=0.2 m,半径R=0.4 m的固定竖直光滑圆轨道与传送带相切于B点,C点是圆轨道的最高点.当传送带静止不动时,质量m=1kg的小煤块在A点以初速度v0=215 m/s开始运动,刚好能运动到C点.重力加速度g=10 m/s2.求:(1)当传送带的轮子以ω=10 rad/s的角速度匀速转动时,将小煤块无初速地放到传送带上的A点,求小煤块从A点运动到B点的过程中在传送带上划过痕迹的长度.(2)当传送带的轮子匀速转动的角速度在什么范围内时,将小煤块无初速地放到传送带上的A点,小煤块运动到C点时对圆轨道的压力最大,最大压力F C是多大.15.(18分)如图所示,电源电动势为E0(未知),内阻不计,滑动变阻器的滑片P处于R的中点.一质量为m,带电荷量为q的粒子(重力不计)从加速电场AK中的s1点由静止经加速电场加速后,沿s1s2方向从边长为L的正方形场区的中间进入有界均匀场区.当场区内只加竖直向上的匀强电场(电场强度为E)时,带电粒子恰从b点射出场区.(1)求加速电源的电动势E0.(2)若滑动变阻器的滑片位置不变,场区内只加垂直纸面向里大小为B的匀强磁场,带电粒子仍从b点射出,则带电粒子的比荷qm为多大?(3)若使带电粒子进入场区后不改变方向,需在场区内同时加匀强电场和匀强磁场,求所加复合场的电场强度E1与磁感应强度B1之比.附加题:本题共3小题,每小题15分.分别考查3-3、3-4、3-5模块.请考生根据本省考试情况选择相应题目作答,其分值不计入总分.1.[物理——选修3-3](15分)(1)(5分)下列说法中正确的是________.A.物体是由大量分子组成的,分子间的引力和斥力同时随分子间距离的增大而减小B.悬浮在水中的花粉颗粒运动不是水分子的运动,而是花粉分子的运动C.物体的机械能可以为零,而内能不可以为零D.第二类永动机违反能量守恒定律E.一定质量的理想气体压强不变,温度升高时吸收的热量一定大于内能的增加量(2)(5分)已知家用煤气的主要成分是一氧化碳,其密度小于空气的密度,且空气在常温下的密度为1.29 kg/m3,如果家庭出现了煤气泄漏,当煤气的质量达到空气总质量的6%时可发生爆炸.若某家庭密闭的厨房中煤气发生泄漏,且泄漏的速度是10 g/min,则煤气可发生爆炸时煤气已经泄漏了________h;若爆炸时厨房的温度迅速上升到1 500℃,则此时厨房内的气体压强为________Pa.(假设厨房的空间体积为30 m3,大气压强为105 Pa,厨房温度为27℃,忽略煤气泄漏及爆炸反应对厨房内空气分子数的影响)(3)(5分)如图所示,光滑水平地面上放有一质量为m的导热气缸,用活塞封闭了一部分气体.活塞质量为m2,截面积为S,可无摩擦滑动,气缸静止时与缸底距离为L0.现用水平恒力F向右推气缸,最后气缸与活塞达到相对静止状态.已知大气压强为p0.求:①稳定时封闭气体的压强;②稳定时活塞与气缸底部的距离.2.[物理——选修3-4](15分)(1)(5分)欧洲大型强子对撞机是现在世界上体积最大、能量最高的加速器,是一种将粒子加速对撞的高能物理设备.该设备能把数以万计的粒子加速到相当于光速的99.9%,粒子流每秒可在隧道内狂飙11 245圈,单束粒子能量可达7万亿电子伏.则下列说法中错误的是________.A.如果继续对粒子进行加速,粒子的速度不能达到光速B.如果继续对粒子进行加速,粒子的速度能够达到光速C.如果继续对粒子进行加速,粒子的速度能够超过光速D.粒子高速运动时的质量大于静止时的质量E.粒子高速运动时的质量小于静止时的质量(2)(5分)一简谐横波以2 m/s的波速沿x轴正方向传播.已知t=0时的波形如图所示,则该波的周期为________,t=0时刻x=0处的质点运动方向为________,x=0处的质点在最短时间t=________s时速度值最大.(3)(5分)为了研究光通过折射率n=1.6的球形玻璃的偏折现象,让一细束光线射入玻璃球,玻璃球的半径R=10 mm,球心O到入射光线的垂直距离d=8mm.(sin 53°=0.8)①在图上画出该束光线射入玻璃球后,第一次从玻璃球中射出的光路图.②求这束光线从射入玻璃球到第一次射出玻璃球,光线偏转的角度.3.[物理——选修3-5](15分)(1)(5分)关于近代物理内容的若干叙述正确的是________.A.自然界中含有少量的14C,14C具有放射性,能够自发地进行β衰变,因此在考古中可利用14C来测定年代B.重核的裂变过程质量增大,轻核的聚变过程有质量亏损C.比结合能越大,表示原子核中核子结合得越牢固,原子核越稳定D.根据玻尔理论,氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能增大,电势能减小E.紫外线照射到金属锌板表面时能够发生光电效应,则当增大紫外线的照射强度时,从锌板表面逸出的光电子的最大初动能也随之增大(2)(5分)核能发电已经成为人类开发和利用新能源的重要途径,某舰艇想依靠所携带的10.9 kg铀丸,利用其放射性衰变释放的能量发电.已知铀丸(238 92U)衰变后成为234 90Th,则衰变方程为________;若分别用m1、m2、m3表示衰变过程中238 92U核、234 90Th核和放出的粒子的质量,则衰变过程中释放出的核能可以表示为________.(3)(5分)如图所示,质量为m1=60 kg的滑块在光滑水平面上以速度v1=0.5 m/s向右运动,质量为m2=40 kg的滑块(包括小孩)在光滑水平面上以速度v2=3 m/s向左运动,为了避免两滑块再次相碰,在两滑块靠近的瞬间,m2上的小孩用力将m1推开.求小孩对m1做功的范围.(滑块m2与右边竖直墙壁碰撞时无机械能损失,小孩与滑块不发生相对滑动,光滑水平面无限长)高考模拟试题精编(一)参考答案1.D洛伦兹提出了磁场对运动电荷的作用力公式,A 错.奥斯特发现了电流的磁效应,B错.法拉第发现了电磁感应现象,C错.库仑利用扭秤发现了电荷之间的相互作用规律,D正确.2.A因为两个等量异种点电荷对称地放在大平面的两侧,电场线应该垂直平面,且该平面应该是一个等势面,所以C、D说法是正确的,根据电场线的分布情况,说法A错、B 正确,故选A.3.AD由v-t图象可知,两车的加速度分别为a a=1510m/s2=1.5 m/s2,a b=3015m/s2=2 m/s2,车的加速度是表示车的速度变化快慢的物理量,A对;相遇时,x a=12×10×15 m=75 m ,x b =12×15×30 m =225 m ,x a +Δx =x b ,所以a 车在b 车前Δx =x b -x a =150 m ,B 、C 错误;由图象可知,两车位移差随时间的增加而增大,且它们在15 s 时相遇,即意味着它们的距离从150 m 一直减小到0,所以D 正确.4.D 根据ω=v r 可知,做圆周运动的角速度不仅与r 有关,还与线速度v 有关,所以A 、B 均错;因为“蛟龙”属于天体自转问题,它转动的角速度与地球同步卫星相同,“神九”与同步卫星相比,根据G Mm r 2=mω2r 得“神九”的角速度较大,即“神九”的角速度大于“蛟龙”随地球自转的角速度,根据a =ω2r 得C 错、D 正确.5.BD 甲、乙两物体速度的方向在改变,不可能做直线运动,则A 错;从速度变化量的方向看,甲的方向一定,乙的发生了变化,甲的合力可能是恒力,也可能是变力,而乙的合力不可能是恒力,则C 错误;B 、D 正确.6.C 物块在斜面上处于静止状态,先对物块进行受力分析,确定其运动趋势,列平衡方程可得F f max .物块受与斜面平行的外力F 作用,而在斜面上静止,此时摩擦力的大小和方向将随F 的变化而变化.设斜面倾角为θ,由平衡条件F 1-mg sin θ-F f max =0,F 2-mg sin θ+F f max=0,解得F f max =F 1-F 22,故选项C 正确. 7.AB 由题给的伏安特性曲线可知,当三导体串联接在电压恒为6 V 的直流电源的两端时,作平行U 轴的直线使三导体两端的总电压为6 V ,R 1、R 2、R 3两端的电压分别为1 V 、3 V 、2V ,此直线恰好过I 轴的1 A 处,可知A 、B 正确;同样可判断C 错误;若将三导体并联后接在3 V 的直流电源上,过U 轴3 V 作平行I 轴的竖直线可知,通过三导体的电流分别约为3 A 、1 A 和2.2 A ,可知D 错.8.B 设变压器原、副线圈的匝数分别为n 1、n 2,输入端的电动势为E ,电流分别为I 1、I 2,电压分别为U 1、U 2,则:U 1=E -I 1r ,电阻R 消耗的电功率P =U 2I 2=U 1I 1,即P =(E -I 1r )I 1=-I 21r +EI 1,可见当I 1=E 2r时,P 有最大值P max =E 24r ,此时U 1=E -I 1r =E -E 2r r =E 2,则U 2=n 2n 1U 1=n 2n 1E 2,I 2=U 2R =n 2n 1E 2R ,又因I 1I 2=n 2n 1,联立以上各式得:n 1n 2=r R,故A 、C 、D 错,B 对.9.B 由初、末状态看出,A 、B 的机械能:E A 初-E B 初=mgh ①,E A 末-E B 末=0②,由①②得:(E A 初-E A 末)+(E B 末-E B 初)=mgh ,即ΔE A 减+ΔE B 增=mgh ③,由A 、B 系统机械能守恒可知ΔE A 减=ΔE B 增④,联立③④得:ΔE A 减=12mgh ,根据功能关系得,杆对A 球做的功为-12mgh ,则A 、C 、D 错,B 对.10.C bc 切割磁感线运动时产生的感应电动势为E =BL v ,感应电流I =E R +r,由于bc 做初速度为0的匀加速运动,所以v =at ,bc 受到的安培力F A =BIL ,对于金属导轨abcd ,根据牛顿第二定律得:F -F A =Ma ,联立上面各式得:F=Ma +B 2L 2a R +rt ,所以A 、B 均错;当bc 向左运动时,根据楞次定律,QP 的电流方向由Q →P ,根据左手定则可知,C 正确;若F =0,PQbc 静止,当ef 左侧磁场均匀减小时,QP 的电流方向由P →Q ,根据左手定则可知,D 错.11.解析:(1)小车从A 到B 做匀加速直线运动,由运动学公式2aL =v 2B -v 2A ,得加速度a =v 2B -v 2A 2L. (2)实验所得图线为直线,但不过原点,当F 有一定数值时,小车加速度仍为零,说明没有完全平衡摩擦力,也可能拉力传感器读数存在误差,即读数偏大.答案:(1)v 2B -v 2A 2L(3分) (2)没有完全平衡摩擦力或拉力传感器读数偏大(2分)12.解析:(1)因为电压表量程远大于干电池的电动势;(2)改装电压表的量程等于电流表G 的满偏电流与电流表G 所在支路总电阻的乘积,即U V =I g (R 3+R g )=3.0×10-3×(990+10)V =3.0 V ;(3)为了便于调节,滑动变阻器的阻值不能太大,选择R 1比较合适;(4)由于R 3支路电阻远大于滑动变阻器R 1所在支路电阻,所以干路电流近似等于I 2,闭合电路欧姆定律E =U +Ir 可变形为:E =I 1(R 3+R g )+I 2r ,即I 1=E R 3+R g -r R 3+R gI 2,由图象知直线与纵轴的截距为E R 3+R g =1.48 mA ,解得E =1.48 V ,直线斜率的绝对值为r R 3+R g=(1.48-1.06)×10-30.5,解得r =0.84 Ω. 答案:(1)电压表量程太大(2分) (2)3(2分)(3)D(2分) (4)1.48(2分) 0.84(2分)13.解:线框被拉出磁场的过程中:产生的感应电流I =BL 2v R (2分)需要的时间t =L 1v (1分)所以产生的焦耳热Q =I 2Rt =B 2L 1L 22v R ①(2分) 线框转动90°过程中:产生感应电流的最大值I max =BL 1L 2ωR (2分)有效值I ′=BL 1L 2ω2R (1分) 需要的时间t ′=π2ω(1分) 所以产生的焦耳热Q =I ′2Rt ′=πBL 21L 22ω4R②(2分) 联立①②得:ω=4v πL 1(2分)14.解:(1)当传送带静止不动时,小煤块刚好能运动到C点,则在C 点,根据牛顿第二定律得:mg =m v 2C R ①(1分)小煤块从A →C 过程中,由动能定理得:-μmgL -2mgR =12m v 2C -12m v 20 ②(1分) 联立①②得μ=0.4(1分)当传送带的轮子以ω=10 rad/s 的角速度匀速转动时,传送带的线速度v =ωr =2 m/s(1分)由v 22μg=0.5 m<L ,得小煤块在传送带上加速的时间t =v μg =0.5 s(1分)小煤块与传送带的相对位移为l =v t -v 2t =0.5 m ,即划过痕迹的长度为0.5 m(2分)(2)当小煤块在传送带上一直加速时,小煤块到达B 点的速度最大,在C 点对圆轨道的压力最大.设小煤块到达B 点的最大速度为v B ,则:μmgL =12m v 2B (1分) 解得v B =210 m/s(1分)传送带的线速度v ≥210 m/s ,即传送带的角速度ω≥1010 rad/s 时,小煤块在C 点对圆轨道的压力最大(1分)小煤块从B →C ,由机械能守恒定律得:2mgR =12m v 2B -12m v 2C max ③(1分) 小煤块此时在C 点,由牛顿第二定律得:F max +mg =m v 2C max R ④(1分)联立③④得F max =50 N(1分)根据牛顿第三定律得,对圆轨道最大压力F C =F max =50 N(1分)15.解:(1)设带电粒子加速后的速度大小为v 0,则在加速电场中,由动能定理得:Uq =12m v 20 ①(2分) 在偏转电场中做类平抛运动:L =v 0t ②(1分)L 2=12Eq mt 2 ③(1分) 联立解得:U =EL 2④(1分) 由闭合电路欧姆定律得:E 0=2U =EL (2分)(2)带电粒子在匀强磁场中做匀速圆周运动,设轨道半径为R ,如图,由几何关系得:R 2=L 2+⎝⎛⎭⎪⎪⎫R -L 22 ⑤(2分) 由向心力为洛伦兹力得:Bq v 0=m v 20R ⑥(2分)联立解得:q m =16E 25B 2L⑦(2分) (3)带电粒子在复合场中做直线运动,电场力与洛伦兹力平衡:q v 0B 1=qE 1 ⑧(3分)联立解得:E 1B 1=4E 5B(2分) 附加题1.(1)解析:根据分子动理论,A 对;布朗运动不是分子的运动,B 错;物体的内能是物体的所有分子动能与分子势能的总和,由于分子动能不可能为零,所以物体内能不可以为零,C 对;第二类永动机违反热力学第二定律,不违反能量守恒定律,D 错;由pV T =C 得,气体压强不变温度升高时体积V 变大,气体对外做功,W <0,根据热力学第一定律Q +W =ΔU 得E 正确.答案:ACE(5分)(2)解析:由题意可知煤气可发生爆炸时的质量m =6%ρV=2.322 kg ,则煤气泄漏的时间t =m 10 g/min232.2 min =3.87 h .把空气近似看做理想气体,则由题意可知在爆炸瞬间可看做是体积不变的过程,则由查理定律可得p 1T 1=p 2T 2,所以爆炸瞬间产生的气体压强为p 2=p 1T 2T 1=6×105Pa. 答案:3.87(2分) 6×105(3分)(3)解:①对整体:F =⎝⎛⎭⎪⎪⎫m +m 2a (1分) 对活塞:(p -p 0)S =m 2a (1分) 联立可得:p =p 0+F 3S(1分) ②根据玻意耳定律得:p 0L 0=pL (1分)所以L =p 0p 0+F 3S L 0(1分)2.(1)解析:根据公式u =u ′+v 1+u ′v c 2可知粒子的速度u 不可能等于或大于光速,所以A 正确,B 、C 错误;根据公式m =m 01-⎝ ⎛⎭⎪⎪⎫v c 2可知高速运动的粒子的质量m 大于静止时的质量m 0,故D 正确、E 错误.答案:BCE(5分)(2)解析:由图可知,该波的波长λ=4 m ,所以该波的周期T =λv =2 s ;根据波的传播方向与质点振动方向的关系得t =0时刻x =0处的质点运动方向为y 轴负方向;根据波的传播方向和t =0时刻的波的图象及y =A sin ⎝⎛⎭⎪⎪⎫2πT t +φ0可得,x =0处的质点的φ0=5π6,x =0处的质点运动到平衡位置时速度值最大,所以最短时间t =16s.答案:2 s(1分)y轴负方向(2分)16(2分)(3)解:①如图所示(1分)②由几何关系得sin θ1=dR=0.8(1分)即θ1=53°(1分)由折射定律得sin θ1=n sin θ2解得θ2=30°(1分)则φ=2(θ1-θ2)=46°(1分)3.(1)解析:根据原子核衰变的半衰期规律及其应用可知A 对;重核的裂变过程中有质量亏损,B错;原子核的比结合能越大越稳定,C对;核外电子由较高能级跃迁到较低能级时,电势能减小,线速度增大,动能增大,总能量减小,部分转化为光子的能量,D对;根据光电效应规律,从金属表面逸出的光电子的最大初动能只与入射光的频率有关,与入射光的强度无关,E错.答案:ACD(5分)(2)解析:根据衰变过程中质量数和电荷数守恒可知,放出的粒子应为α粒子,衰变方程为238 92U→234 92Th+42He.由爱因斯坦的质能方程可知,释放出的核能为(m1-m2-m3)c2.答案:238 92U→234 90Th+42He(2分)(m1-m2-m3)c2(3分)(3)解:小孩用力将m1推开的过程中,m1、m2组成的系统动量守恒,得:m2v2-m1v1=m1v1′+m2v2′(1分)其中v2′=±v1′是避免两滑块再次相碰的临界条件,即v2′=m2v2-m1v1m2±m1(1分)代入数据解得v11′=0.9 m/s,v12′=4.5 m/s(1分)所以小孩对m1做功的最小值是W min=12m1(v′211-v21)=16.8J(1分)小孩对m1做功的最大值是W max=12m1(v′212-v21)=600 J(1分)31。
超实用高考英语复习:2014年高考英语试题(新课标全国卷Ⅱ)完型填空(含答案解析)

2014年全国高考试题独家解析(新课标卷II)英语试题第三部分英语知识运用(共两节,满分45分)第一节完形填空(共20小题;每题1.5分,满分30分)阅读下面短文,从短文后各题所给的四个选项(A, B, C和D)中,选出可以填入空白处的最佳选项。
Joe Simpson and Simon Yates were the first people to climb the West Face of the Siula Grande in the Andes mountains.They reached the top 41,but on their way back conditions were very 42.Joe fell and broke his leg.They both knew that if Simon 43 alone,he would probably get back 44.But Simon decided to risk his 45and try to lower Joe down the mountain on a rope (绳).As they 46 down,the weather got worse.Then another 47occurred.They couldn't see or hear each other and,48 ,Simon lowered his friend over the edge of a precipice (峭壁).It was 49for Joe to climb back or for Simon to pull him up.Joe's 50 was pulling Simon slowly towards the precipice.51,after more than an hour in the dark and the icy cold,Simon had to 52 .In tears,he cut the rope.Joe 53into a huge crevasse (裂缝) in the ice below.He had no food or water and he was in terrible pain.He couldn't walk,but he 54 to get out of the crevasse and started to 55towards their camp,nearly ten kilometers 56.Simon had 57the camp at the foot of the mountain.He thought that Joe must be 58,but he didn't want to leave 59.Three days later,in the middle of the night,he heard Joe's voice.He couldn't 60it.Joe was there,a few meters from their tent,still alive.41.A.hurriedly B.carefully C.successfully D.early 42.A.difficult B.similar C.special D.normal 43.A.climbed B.worked C.rested D.continued 44.A.unwillingly B.safely C.slowly D.regretfully 45.A.fortune B.time C.health D.life46.A.lay B.settled C.went D.looked 47.A.damage B.storm C.change D.trouble48.A.by mistake B.by chance C.by chance D.by luck 49.A.unnecessary B.practical C.important D.impossible 50.A.height B.weight C.strength D.equipment 51.A.Finally B.Patiently C.Surely D.Quickly 52.A.stand back B.take a rest C.make a decision D.hold on 53.A.jumped B.fell C.escaped D.backed 54.A.managed B.planned C.waited D.hoped55.A.run B.skate C.move D.march 56.A.around B.away C.above D.along 57.A.headed for B.travelled C.left for D.returned to 58.A.dead B.hurt C.weak D.late 59.A.secretly B.tiredly C.immediately D.anxiously 60.A.find B.believe 41.C but 一词说明前后为转折关系,他们成功到达山顶。
2014年高考数学模拟试题及答案一

2014年高考数学模拟试题及答案一高三数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页,共150分.考试时间120分钟.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷(选择题 共40分)注意事项:1.考生务必将答案答在答题卡上,在试卷上作答无效.2.答题前考生务必用黑色字迹的签字笔在答题卡上填写姓名、准考证号,然后再用2B 铅笔将与准考证号对应的信息点涂黑.3.答题卡上第Ⅰ卷必须用2B 铅笔作答,将选中项涂满涂黑,黑度以遮住框内字母为准,修改时用橡皮擦除干净.第Ⅱ卷必须用黑色字迹的签字笔按照题号顺序在各题目的答题区域内作答,未在对应的答题区域内作答或超出答题区域作答的均不得分.一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. (1)1.已知全集U =R ,集合{}|12A x x =->,{}2|680B x x x =-+<,则集合()U A B = ð( ) A .{}|14x x -≤≤ B .{}|14x x -<< C .{}|23x x <≤ D . {}|23x x <≤ 【解析】 D ;容易解得{3A x x x =>或者}0x <,{}26B x x =<<. 于是()U A B = ð{}23x x <≤.(2)2.一个单位共有职工200人,其中不超过45岁的有120人,超过45岁的有80人. 为了调查职工的健康状况,用分层抽样的方法从全体职工中抽出一个容量为25的样本,应抽取不超过45岁的职工人数为 ( )A . 5B . 10C .15D .50 【解析】 C ;容易知道样本中不超过45岁的人与超过45岁的人数之比为1203802=.于是抽取不超过45岁的职工人数为325155⋅=人.(3)3.已知PA 是O 的切线,切点为A ,2PA =,AC 是O 的直径,PC 交O 于点B ,30PAB ∠= ,则O 的半径为 ( )PAA .1B .2CD .【解析】 C;30,tan30PAPCA PAB CA ∠=∠===(4)4.已知等比数列{}n a 为递增数列,且373a a +=,282a a ⋅=,则117a a = ( ) A .2 B . 43 C . 32 D .12【解析】 A ;不妨设等比数列的公比为q .由2375213a a a q q ⎛⎫+=+= ⎪⎝⎭知50a >.于是228552a a a a ⋅==⇒=代入上式知22q =2q =而数列单调增,于是2q =42q =.(5)5.已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的为 ( ) A .若,,αγβγ⊥⊥则αβ∥ B .若,,m n αα⊥⊥则m n ∥ C .若,m n αα∥∥,则m n ∥ D .若,,m m αβ∥∥则αβ∥【解析】 B ;A 中,αβ可以是任意关系;B 正确;C 中,m n 平行于同一平面,其位置关系可以为任意.D 中平行于同一直线的平面可以相交或者平行.(6)6.设33,,2x yx y M N P ++===(其中0x y <<), 则,,M N P 大小关系为 ( ) A .M N P << B .N P M << C .P M N << D .P N M << 【解析】 D ;由0x y <<,有2x y+.由指数函数的单调性,有23x y x y P N ++=<==;23332x yx y M N ++=>==.(7)7.2位男生和3位女生共5位同学站成一排.若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数为 ( )A .36B .42C . 48D .60【解析】 C ;不妨将5个位置从左到右编号为1,2,3,4,5.于是甲只能位于2,3,4号位. ①当甲位于2号位时,3位女生必须分别位于1,3,4位或者1,4,5位.于是相应的排法总数为33212A =;②当甲位于3号位时,3位女生必须分别位于1,2,4位或者1,2,5位或者1,4,5或者2,4,5位.于是相应的排法总数为33424A =.③当甲位于4号位时,情形与①相同.排法总数为33212A =. 综上,知本题所有的排法数为12+24+12=48.(8)8.设定义在R 上的函数1,(1),1()1,(1)x x f x x ⎧≠⎪-=⎨⎪=⎩. 若关于x 的方程2()()0f x bf x c ++=有3个不同的实数解1x ,2x ,3x ,则123x x x ++等于 ( ) A . 3 B .2 C .1b -- D .c【解析】 A ;易知()f x 的图像关于直线1x =对称.2()()0f x bf x c ++=的解必有一根使()1f x =.不妨设为1x .23,x x 关于直线1x =对称.于是1233x x x ++=.第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分. (9)9.如果复数()()2i 1i m m ++(其中i 是虚数单位)是实数,则实数m =___________. 【解析】 1-;()()()()223i 1i 1mm m m i m ++=-++.于是有3101m m +=⇒=-.(10)10.若12a x ⎫⎪⎭的展开式中的常数项为220-,则实数a =___________.【解析】 1-;由二项式定理4124311212CC rrr rr r r a T a x x --+⎛⎫== ⎪⎝⎭.令44033r r -=⇒=.于是有3312C 2201a a =-⇒=-.(11)11.将参数方程12cos ,2sin ,x y θθ=+⎧⎨=⎩(θ为参数)化成普通方程为 .【解析】 ()2214x y -+=;由12cos ,2sin x y θθ-==知()2214x y -+=.(12)12.某程序框图如图所示,该程序运行后输出,M N 的值分别为 .【解析】 13,21;依据程序框图画出运行n 次后,,M N i 的值..(13)13.若数列{}n a 的前n 项和为n S ,则11,(1),,(2)n nn S n a S S n -=⎧=⎨-⎩.≥若数列{}n b 的前n 项积为n T ,类比上述结果,则n b =_________;此时,若2()n T n n *=∈N ,则n b =___________.【解析】 11,2;, 1.nT n T T n ⎧⎪⎨⎪=⎩≥,()221,1;, 2.1n n n n =⎧⎪⎨⎪-⎩≥; 由12....n n T b b b =,知()1211...n n n n n T b b b b T b --==.(14)14.定义在R 上的函数满足1(0)0,()(1)1,()()52x f f x f x f f x =+-==,且当1201x x <≤≤时,12()()f x f x ≤,则12010f ⎛⎫= ⎪⎝⎭_________________.【解析】 132;容易知道()11,f =于是()1111522f f ⎛⎫== ⎪⎝⎭.而1111112222f f f ⎛⎫⎛⎫⎛⎫+-=⇒= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.又由()f x 单调增,知()1,2f x =当1152x ≤≤时.而441111155201052⋅⋅≤≤,4411111522232f f ⎛⎫⎛⎫⎛⎫⋅== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.于是11201032f ⎛⎫= ⎪⎝⎭.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)15.在ABC ∆中,角,,A B C 所对的边分别为,,a b c,满足sin2A ,且ABC ∆的面积为2.⑴求bc 的值;⑵若6b c +=,求a 的值. 【解析】 ⑴∵sin2A =0πA <<.∴cos 2A =. ∴4sin 2sin cos 225A A A ==.∵1sin 22ABC S bc A ∆==,∴5bc =. --------------------6分⑵∵sin 2A ∴23cos 12sin 25A A =-=.∵5bc =,6b c +=,∴2222cos a b c bc A =+-2()2(1cos )b c bc A =+-+20=∴a = -----------12分(16)16.为了调查某厂2000名工人生产某种产品的能力,随机抽查了m 位工人某天生产该产品的数量,产品数量的分组区间为[)10,15,错误!未找到引用源。
2014年普通高等学校招生全国统一考试(湖北卷)模拟卷 文综参考答案
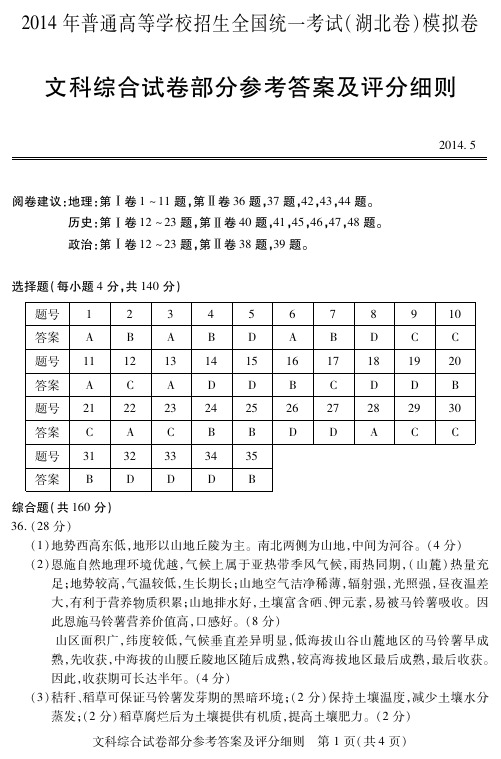
2014年普通高等学校招生全国统一考试(湖北卷)模拟卷文科综合试卷部分参考答案及评分细则 2014 5阅卷建议:地理:第Ⅰ卷1~11题,第Ⅱ卷36题,37题,42,43,44题。
历史:第Ⅰ卷12~23题,第Ⅱ卷40题,41,45,46,47,48题。
政治:第Ⅰ卷12~23题,第Ⅱ卷38题,39题。
选择题(每小题4分,共140分)题号12345678910答案ABABDABDCC题号11121314151617181920答案ACADDBCDDB题号21222324252627282930答案CACBBDDACC题号3132333435答案BDDDB综合题(共160分)36.(28分)(1)地势西高东低,地形以山地丘陵为主。
南北两侧为山地,中间为河谷。
(4分)(2)恩施自然地理环境优越,气候上属于亚热带季风气候,雨热同期,(山麓)热量充足;地势较高,气温较低,生长期长;山地空气洁净稀薄,辐射强,光照强,昼夜温差大,有利于营养物质积累;山地排水好,土壤富含硒、钾元素,易被马铃薯吸收。
因此恩施马铃薯营养价值高,口感好。
(8分)山区面积广,纬度较低,气候垂直差异明显,低海拔山谷山麓地区的马铃薯早成熟,先收获,中海拔的山腰丘陵地区随后成熟,较高海拔地区最后成熟,最后收获。
因此,收获期可长达半年。
(4分)(3)秸秆、稻草可保证马铃薯发芽期的黑暗环境;(2分)保持土壤温度,减少土壤水分蒸发;(2分)稻草腐烂后为土壤提供有机质,提高土壤肥力。
(2分)(4)省工省力,降低了劳动成本和强度;增产增收,促进农业发展,增加农民收入;秸秆还田,实现了资源循环利用。
(6分)37.(18分)(1)当时国际产业转移,韩国政策主导支持;西部和南部海岸线曲折,多天然良港,海运便利;劳动力丰富。
(6分)(2)城市分布不均,发展不平衡;城市化起步晚,发展快,平均水平高。
(4分)(3)首尔经济发达,世界级大企业集中,国际化程度高,服务市场需求量大;国家政策导向,顺应国际潮流,推进产业结构的调整与升级;海陆空交通便捷,信息网络发达,对外辐射能力强;科技文化水平高,高素质人才多;人口众多,劳动力丰富。
2014年高考适应性考试试题和答案

高三第三次诊断测试题文科综合·政治文科综合考试时间共150分钟。
满分300分。
政治、历史、地理各100分。
政治试题卷分第I卷(选择题)和第II卷(非选择题)。
第I卷1-3页,第II卷3-4页。
共4页。
考生作答时,须将答案答在答题卡上,在本试卷、草稿纸上答题无效。
考试结束后,将答题卡交回。
第I卷(选择题共48分)注意事项:必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑。
第Ⅰ卷共12题,每题4分,共48分。
在每题给出的四个选项中,只有一项是最符合题目要求的。
1.汽车和蔬菜产量大幅度增加,将会导致汽车价格(L)及其需求量(T)、蔬菜价格(P)及其需求量(Q)的变动。
其他条件不变,下图能较为准确反映这种变化趋势的是A.①③ B.①④ C.②③ D.②④2.2013年10月31日,著名企业家马云对淘宝网的爆炸式发展展现出美好前景,认为沃尔玛创造了B2C模式,希望在中国创建一个新的C2B模式,即按需定制,这是制造业转型提升的重要平台。
马云这一说法体现了A.生产决定消费方式、消费质量和水平B.消费对生产的调整和升级起着导向作用C.物质资料的生产是人类存在发展的基础D.消费是整个社会再生产过程的决定环节3.十八届三中全会提出:“必须加快形成企业自主经营、公平竞争,消费者自由选择、自主消费,商品和要素自由流动、平等交换的现代市场体系”。
下列措施中,有利于实现“商品和要素自由流动、平等交换”的是①国家出台价格调控政策,避免价格波动②完善市场信息服务,畅通商品流通渠道③加速城乡一体化建设,消除城乡差距④保障市场主体公平竞争,维护市场秩序A.①③ B.①④ C.②③ D.②④4.当前,我国要加快完善社会保障体系,实现新型农村社会养老保险和城镇居民社会养老保险制度全覆盖,扩大各项社会保险覆盖面,增加企业退休人员基本养老金,加强城乡低保和社会救助工作,加快发展社会福利事业和慈善事业等。
从市场经济的角度看,我国政府不断完善社保体系是因为①市场调节的弱点和缺陷会导致收入分配不公平②我国社会主义市场经济以共同富裕为根本目标③加强宏观调控是社会主义市场经济的内在要求④这是全面建成小康社会,促进和谐的中心任务A.①②③ B.①②④ C.①③④ D.②③④5.2013年3月26日,李克强主持召开新一届国务院第一次廉政工作会议,强调要打造廉洁政府,给权力涂上防腐剂,戴上“紧箍咒”。
2014高考真题+模拟新题 地理分类汇编:B单元 宇宙中的地球 纯word版解析可编辑

B单元宇宙中的地球地球的宇宙环境及太阳对地球的影响[2014·新课标全国卷Ⅰ] 太阳能光热电站(图1)通过数以十万计的反光板聚焦太阳能,给高塔顶端的锅炉加热,产生蒸汽,驱动发电机发电。
据此完成1~2题。
图11.我国下列地区中,资源条件最适宜建太阳能光热电站的是()A.柴达木盆地B.黄土高原C.山东半岛D.东南丘陵1.A[解析] 建设太阳能光热电站应选择太阳辐射量丰富的地区。
柴达木盆地位于青藏高原,海拔高,空气稀薄,大气对太阳辐射的削弱作用弱,太阳辐射强,故太阳能资源丰富,适宜建设太阳能电站。
2.太阳能光热电站可能会()A.提升地表温度B.干扰飞机电子导航C.误伤途经飞鸟D.提高作物产量2.C[解析] 反光板具有反射作用,使地面获得的太阳辐射减少,地表温度降低;太阳能光热电站不会产生电子辐射,故不会干扰飞机电子导航;图中显示太阳能反光板可以聚焦太阳能,给高塔顶端加热,强光、高热会使飞鸟飞过时被灼伤,故C项正确;太阳能电站的建设对农作物没有影响,不会导致作物产量提高。
地球自传及其地理意义2014·北京卷图3示意北半球夏季4个气旋的移动路径。
读图,回答4~5题。
图34.气旋()A.①给南亚地区带来大风暴雨天气B.②自东南向西北方向移动C.③移动方向与地球自转方向相反D.④生成于太平洋热带洋面4.D[解析] 依据海陆分布规律及经纬度信息可知,①位于大西洋中低纬度且向西北移动,影响区域为北美洲东海岸,不会影响南亚地区,A项错误;②位于太平洋中高纬度,自西南向东北方向移动,B项错误;③沿逆时针方向移动,与北半球俯视图上的地球自转方向一致,C项错误;④生成于太平洋的热带洋面,故选D项。
[2014·安徽卷] 图9为我国科考队在北极点放置中国结时拍摄的照片。
读图完成29~30题。
图929.该照片拍摄日期、拍摄者或中国结影子的方位是()A.3月21日、中国结影子指向正南B.6月22日、拍摄者位于中国结东南C.8月20日、拍摄者位于中国结正南D.9月16日、中国结影子指向东北29.C[解析] 本题主要考查地球上极点的方位以及物体的影子与所在季节的关系。
第2课 极化恒等式 谱写新篇+向量+命题探秘第二版一题一课

视角 1 从两个向量的模与它们和、差的模之间的关系切入
(1)由恒等式 a 十 b 十{a-bI 一艺叫。{ 十协尸)可知,}川, b}, 巨一州, }。十川任意给定三个,可求另外一个.
例如,如果给定同 = 1, IbI=2, Ia b}=2,则可由}。十川 2 十阵一川 2 =2(Ia12 十囚 2) ,解得}。十 bI= 派,据此. b = 李 [(a+b)2 (a b)21.
|
任一
一
第 2 课 极化恒等式 谱写新篇
⑤式就是著名的“极化恒等式”,它表明,向量的数量积可以由向量线性运算的模导
出,它是沟通向量的数量积运算和线性运算的重要公式.若“,占是实数,则恒等式⑤也叫
“广义平方差”公式.
极化恒等式是高等数学《泛函分析》中的知识内容,它表明数量积可以由它诱导出的
州
: B;M七 一言1(,; A吉 c 一;A;丑溉)・
“
图2
极化恒等式也可看成是这两个关系式的逆向使用.
极化恒等式可将平面向量的数量积运算转化为两个平面向量的长度运算,使不可度
量的数量积关系转化为可度量、可计算的数量关系,其意义非同凡响.
由定理 1,可得以下推论. 推论 若 AM 是△ABC 的中线,则 AB2 十 AC2 = 2(AM2 十 BM2).
x
(a 十吞)・(“一吞)一 a2 一 b2.
课本中利用平面向量数量积的运算律证明了这两个等式.
将(。十 b)2==矿十 2a ・ b 十扩中的向量 b 换成向量一 b,又有
(a 一吞)2 一。2 一 2a ・ 吞十 b2.
y
将①式与②式相加,可得
伍十 b)2 十(“一 b)2 = 2(矿十 b2).
范数来表示.把极化恒等式降维至二维平面,则可以非常巧妙地建立起向量与几何长度
2014年高考英语全国卷1(含详细答案)

英语试卷 第1页(共32页)英语试卷 第2页(共32页)绝密★启用前2014普通高等学校招生全国统一考试(全国新课标卷1)英语使用地区:河南、山西、河北本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
共150分,共12页。
考试时间结束后,将本试卷和答题卡一并交回。
注意事项:1. 答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2. 选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3. 请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4. 保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
注:山西卷赋分不同,满分180分。
听力30分不计入总分,考试成绩录取时提供给高校作参考。
第Ⅰ卷第一部分 听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节 (共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A 、B 、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例: How much is the shirt? A. £19.15.B. £9. 18.C. £9.15.答案是C 。
1. What does the woman want to do? A. Find a place.B. Buy a map.C. Get an address.2. What will the man do for the woman? A. Repair her car.B. Give her a ride.C. Pick up her aunt.3. Who might Mr. Peterson be? A. A new professor.B. A department head.C. A company director.4. What does the man think of the book? A. Quite difficult.B. Very interesting.C. Too simple.5. What are the speakers talking about? A. Weather.B. Clothes.C. News.第二节 (共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
高考真题2014年地理全国卷1(含答案)

绝密★启用前2014年普通高等学校招生全国统一考试文科综合·地理(全国Ⅰ卷)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共11小题,每小题4分,共44分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
太阳能光热电站(图1)通过数以十万计的反光板聚焦太阳能,给高塔顶端的锅炉加热,产生蒸汽,驱动发电机发电。
据此完成1~3题。
图11.我国下列地区中,资源条件最适宜建太阳能光热电站的是【A】A.柴达木盆地B.黄土高原C.山东半岛D.东南丘陵2.太阳能光热电站可能会【C】A.提升地表温度B.干扰飞机电子导航C.误伤途经飞鸟D.提高作物产量3.若在北回归线上建一太阳能光热电站,其高塔正午影长与塔高的比值为P,则【D】A.春、秋分日P=0 B.夏至日P=1 C.全年P<1 D.冬至日P>1 20世纪50年代,在外国专家的指导下,我国修建了兰新铁路。
兰新铁路在新疆吐鲁番附近的线路如图2所示。
读图2,完成4~6题。
图24.推测外国专家在图示区域铁路选线时考虑的主导因素是【D】A.河流B.聚落C.耕地D.地形5.后来,我国专家认为,兰新铁路在该区域的选线不合理,理由可能是【B】A.线路过长B.距城镇过远C.易受洪水威胁D.工程量过大6.50多年来,兰新铁路并没有改变该区域城镇的分布,是因为该区域的城镇分布受控于【B】A.地形分布B.绿洲分布C.河流分布D.沙漠分布人类活动导致大气中含氮化合物浓度增加,产生沉降,是新出现的令人担忧的全球变化问题。
一科研小组选择受人类干扰较小的某地,实验模拟大气氮沉降初期对植被的影响。
实验地植被以灌木植物为主,伴生多年生草本植物。
2014年高考全国卷1 语文真题及 答案详解(Word)

2014年普通高等学校招生全国统一考试语文试卷第Ⅰ卷阅读题甲必做题一、现代文阅读I 9分,每小题3分)阅读下面的文字,完成l~3题。
悲剧产生于社会的矛盾、两种社会力量的冲突。
冲突双方分别代表着真与假、善与恶、新与旧等对立的两极,却总是以代表真、善、新等美好的一方的失败、死亡、毁灭为结局,他们是悲剧的主人公。
因为他们的力量还比较弱小,还无法与强大的旧势力或邪恶力量抗衡,正义的要求不能实现,于是形成了悲剧。
古希腊学者亚里士多德指出,悲剧描写了比现实中更美好同时又是“与我们相似的”人物,通过他们的毁灭“引起怜悯和恐惧来使感情得到陶冶”,即产生净化的作用。
然而,悲剧不仅表现冲突与毁灭,而且表现抗争与拼搏,这是悲剧具有审美价值的最根本的原因。
鲁迅说过:“悲剧将人生的有价值的东西毁灭给人看”。
这种毁灭是抗争、拼搏以后的毁灭,抗争与拼搏体现了人的一种精神。
古希腊神话中普罗米修斯为了人类从天上盗取火种,触怒了主神宙斯,被锁在高加索山崖上,每日遭神鹰啄食肝脏,但普罗米修斯毫不屈服,最后坠入深渊。
罗丹的大理石雕塑《马身人首》中,人臂绝望地扑向一个它所抓不到的目标,而马足则陷于尘土不能自拔,表现出人性与兽性的冲突,象征着灵与肉的斗争,具有强烈的悲剧性。
可以说,没有抗争就没有悲剧,冲突、抗争与毁灭是构成悲剧的三个主要因素。
悲剧的审美价值的载体只能是文学艺术。
因为人生有价值的东西、美好事物的毁灭是令人伤悲的,因此现实中的悲剧不能作为直接的审美对象来欣赏,否则人就是泯灭了人性的人了。
现实中的悲剧只能激起人的同情、义愤,迫使人采取严肃的伦理态度和实践行动。
民主革命时期,在演出歌剧《白毛女》的过程中,曾多次出现扮演地主黄世仁的演员被打甚至险遭枪击的事件,这是人们以实际的道德评价代替了审美活动。
现实的悲剧只在客观上具有悲剧的审美性质,它们必须以文学艺术的形式表现出来,才能成为欣赏的对象,美学上所谓的“以悲为美”才能实现。
悲剧成为审美对象只能以文学艺术的形式出现,原因在于它需要建立悲剧事件与人的心理距离。
数学培优专题:解析几何(选填题、简答题)全国各地高考数学模拟题汇编(含解析)一

培优专题:解析几何(选填题、简答题)选填题:1.(5分)设m,θ∈R,则的最小值为()A.3 B.4 C.9 D.162.(5分)边长为8的等边△ABC所在平面内一点O,满足=,若M为△ABC边上的点,点P满足|,则|MP|的最大值为()A.B.C.D.3.(5分)已知点A,B的坐标分别为(﹣1,0),(1,0).直线AM,BM相交于点M,且它们的斜率之和是2,则点M的轨迹方程为.4.(5分)已知椭圆的左焦点为F1,y轴上的点P在椭圆外,且线段PF1与椭圆E交于点M,若,则E椭圆的离心率为()A.B. C.D.5.(5分)已知菱形ABCD的边长为2,∠DAB=60°,P是线段BD上一点,则的最小值是.6.(5分)已知SC是球O的直径,A,B是球O球面上的两点,且,若三棱锥S﹣ABC的体积为1,则球O的表面积为()A.4πB.13πC.16πD.52π7.(5分)在△ABC中,AB=AC=5,BC=6,I是△ABC的内心,若=m(m,n∈R),则=()A.B.C.2 D.8.(5分)设点P为椭圆C:+=1上一点,F1、F2分别是椭圆C的左、右焦点,且△PF1F2的重心为点G,若|PF1|:|PF2|=3:4,那么△GPF1的面积为()A.24 B.12 C.8 D.69.(5分)如图,O是坐标原点,过E(p,0)的直线分别交抛物线y2=2px(p >0)于A、B两点,直线BO与过点A平行于x轴的直线相交于点M,过点M 与此抛物线相切的直线与直线x=p相交于点N.则|ME|2﹣|NE|2=()A.2p2B.2p C.4p D.p10.(5分)已知F1,F2是双曲线(a>0,b>0)的左右焦点,以F1F2为直径的圆与双曲线的一条渐近线交于点M,与双曲线交于点N,且M,N均在第一象限,当直线MF1∥ON时,双曲线的离心率为e,若函数f(x)=x2+2x﹣,则f(e)=()A.1 B.C.2 D.11.(5分)已知F1,F2是双曲线﹣=1(a>0,b>0)的左右焦点,过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段F1F2为直径的圆外,则双曲线离心率的取值范围是()A.(2,+∞)B.(,2)C.(,) D.(1,)12.(5分)已知抛物线C:y2=4x的焦点为F,过点F分别作两条直线l1,l2,直线l1与抛物线C交于A、B两点,直线l2与抛物线C交于D、E两点,若l1与l2的斜率的平方和为1,则|AB|+|DE|的最小值为()A.16 B.20 C.24 D.3213.(5分)已知,是单位向量,,若向量满足,则的取值范围为()A. B. C.D.14.(5分)已知抛物线和圆,直线y=k(x﹣1)与C1,C2依次相交于A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4)四点(其中x1<x2<x3<x4),则|AB|•|CD|的值为()A.1 B.2 C.D.k215.(5分)抛物线M:y2=4x的准线与x轴交于点A,点F为焦点,若抛物线M 上一点P满足PA⊥PF,则以F为圆心且过点P的圆被y轴所截得的弦长约为(参考数据:≈2.24)()A.B.C.D.16.(5分)已知椭圆的左顶点和上顶点分别为A,B,左、右焦点分别是F1,F2,在线段AB上有且只有一个点P满足PF1⊥PF2,则椭圆的离心率的平方为()A. B.C.D.17.(5分)过点P(﹣1,1)作圆C:(x﹣t)2+(y﹣t+2)2=1(t∈R)的切线,切点分别为A,B,则•的最小值为()A.B.C.D.2﹣318.(5分)已知双曲线C:(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=60°,且,则双曲线C的离心率为()A. B. C.D.19.(5分)已知点F1,F2为椭圆C1:+=1(a>b>0)和双曲线C2:﹣=1(a′>0,b′>0)的公共焦点,点P为两曲线的一个交点,且满足∠F1PF2=90°,设椭圆与双曲线的离心率分别为e1,e2,则+= .20.(5分)已知△ABC是直角边为2的等腰直角三角形,且A为直角顶点,P 为平面ABC内一点,则的最小值是.21.(5分)已知双曲线的右焦点为F,过点F向双曲线的一条渐近线引垂线,垂足为M,交另一条渐近线于N,若,则双曲线的渐近线方程为.22.(5分)已知抛物线C:y2=4x,过其焦点F作一条斜率大于0的直线l,l与抛物线交于M,N两点,且|MF|=3|NF|,则直线l的斜率为.23.(5分)已知F是椭圆C:+=1的右焦点,P是C上一点,A(﹣2,1),当△APF周长最小时,其面积为.简答题:1.(12分)已知椭圆与直线l:bx﹣ay=0都经过点.直线m与l平行,且与椭圆C交于A,B两点,直线MA,MB 与x轴分别交于E,F两点.(1)求椭圆C的方程;(2)证明:△MEF为等腰三角形.2.(12分)已知椭圆(a>b>0),其焦距为2,离心率为(1)求椭圆C的方程;(2)设椭圆的右焦点为F,K为x轴上一点,满足,过点K作斜率不为0的直线l交椭圆于P,Q两点,求△FPQ面积s的最大值.3.(12分)已知圆C:x2+y2+2x﹣2y+1=0和抛物线E:y2=2px(p>0),圆心C到抛物线焦点F的距离为.(1)求抛物线E的方程;(2)不过原点的动直线l交抛物线于A,B两点,且满足OA⊥OB.设点M为圆C上任意一动点,求当动点M到直线l的距离最大时的直线l方程.4.(12分)给定椭圆C:+=1(a>b>0),称圆心在原点O,半径为的圆是椭圆C的“准圆”.已知椭圆C的离心率,其“准圆”的方程为x2+y2=4.(I)求椭圆C的方程;(II)点P是椭圆C的“准圆”上的动点,过点P作椭圆的切线l1,l2交“准圆”于点M,N.(1)当点P为“准圆”与y轴正半轴的交点时,求直线l1,l2的方程,并证明l1⊥l2;(2)求证:线段MN的长为定值.5.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.6.(12分)设O为坐标原点,动点M在椭圆上,过M作x轴的垂线,垂足为N,点P满足.(Ⅰ)求点P的轨迹方程E;(Ⅱ)过F(1,0)的直线l1与点P的轨迹交于A、B两点,过F(1,0)作与l1垂直的直线l2与点P的轨迹交于C、D两点,求证:为定值.7.(12分)已知椭圆C:的离心率为,且以两焦点为直径的圆的内接正方形面积为2.(1)求椭圆C的标准方程;(2)若直线l:y=kx+2与椭圆C相交于A,B两点,在y轴上是否存在点D,使直线AD与BD的斜率之和k AD+k BD为定值?若存在,求出点D坐标及该定值,若不存在,试说明理由.8.(12分)已知曲线C的方程为ax2+ay2﹣2a2x﹣4y=0(a≠0,a为常数).(1)判断曲线C的形状;(2)设曲线C分别与x轴,y轴交于点A,B(A,B不同于原点O),试判断△AOB的面积S是否为定值?并证明你的判断;(3)设直线l:y=﹣2x+4与曲线C交于不同的两点M,N,且•=﹣,求a的值.9.(12分)已知抛物线E:y2=2px(p>0)的准线与x轴交于点k,过点k做圆C:(x﹣5)2+y2=9的两条切线,切点为.(1)求抛物线E的方程;(2)若直线AB是讲过定点Q(2,0)的一条直线,且与抛物线E交于A,B两点,过定点Q作AB的垂线与抛物线交于G,D两点,求四边形AGBD面积的最小值.10.(16分)在平面直角坐标系中,已知椭圆C:+y2=1 (a>0,a≠1)的两个焦点分别是F1,F2,直线l:y=kx+m(k,m∈R)与椭圆交于A,B两点.(1)若M为椭圆短轴上的一个顶点,且△MF1F2是直角三角形,求a的值;(2)若k=1,且△OAB是以O为直角顶点的直角三角形,求a与m满足的关系;(3)若a=2,且k OA•k OB=﹣,求证:△OAB的面积为定值.11.(12分)已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足•=0,=2.(Ⅰ)当点P在圆上运动时,求点Q的轨迹方程;(Ⅱ)若斜率为k的直线l与圆x2+y2=1相切,直线l与(Ⅰ)中所求点Q的轨迹交于不同的两点F,H,O是坐标原点,且≤•≤时,求k的取值范围.12.(12分)已知椭圆的左焦点为F,左顶点为A.(1)若P是椭圆上的任意一点,求的取值范围;(2)已知直线l:y=kx+m与椭圆相交于不同的两点M,N(均不是长轴的端点),AH⊥MN,垂足为H且,求证:直线l恒过定点.13.(12分)设椭圆+=1(a>b>0)的离心率e=,左焦点为F,右顶点为A,过点F的直线交椭圆于E,H两点,若直线EH垂直于x轴时,有|EH|=(1)求椭圆的方程;(2)设直线l:x=﹣1上两点P,Q关于x轴对称,直线AP与椭圆相交于点B(B 异于点A),直线BQ与x轴相交于点D.若△APD的面积为,求直线AP的方程.14.(12分)已知椭圆C:的离心率,且过点.(1)求椭圆C的方程;(2)过P作两条直线l1,l2与圆相切且分别交椭圆于M,N两点.①求证:直线MN的斜率为定值;②求△MON面积的最大值(其中O为坐标原点).15.(12分)如图,A,B是椭圆长轴的两个端点,P,Q是椭圆C 上都不与A,B重合的两点,记直线BQ,AQ,AP的斜率分别是k BQ,k AQ,k AP.(1)求证:;(2)若k AP=4k BQ,求证:直线PQ恒过定点,并求出定点坐标.参考答案与解析1.(5分)设m,θ∈R,则的最小值为()A.3 B.4 C.9 D.16【解答】解:令点P(2﹣m,2+m),Q(cosθ,sinθ).点P在直线上,点Q的轨迹为单位圆:x2+y2=1.因此的最小值为:单位圆上的点到直线的距离的平方,故其最小值==(4﹣1)2=9.故选:C.2.(5分)边长为8的等边△ABC所在平面内一点O,满足=,若M为△ABC边上的点,点P满足|,则|MP|的最大值为()A.B.C.D.【解答】解:如图,由=,得,即,取AB中点G,AC中点H,连接GH,则,即,取GH中点K,延长KG到O,使KG=GO,则O为所求点,∵点P满足|,M为△ABC边上的点,∴当M与A重合时,|MP|有最大值为|OA|+|OP|,而|OA|=,∴|MP|的最大值为,故选:D.3.(5分)已知点A,B的坐标分别为(﹣1,0),(1,0).直线AM,BM相交于点M,且它们的斜率之和是2,则点M的轨迹方程为x2﹣xy﹣1=0(x≠±1).【解答】解:设M(x,y),∵AM,BM的斜率存在,∴x≠±1,又∵k AM=,k BM=,∴由k AM+k BM=2得:•=0,整理得:x2﹣xy﹣1=0,∴点M的轨迹方程为:x2﹣xy﹣1=0(x≠±1).故答案为:x2﹣xy﹣1=0(x≠±1)4.(5分)已知椭圆的左焦点为F1,y轴上的点P在椭圆外,且线段PF1与椭圆E交于点M,若,则E椭圆的离心率为()A.B. C.D.【解答】解:如图所示|OM|=|MF1|=|OP|,不妨设|OP|=,则|OM|=|MF1|=1,设∠MF1O=θ,在△MOF1中由余弦定理可得cosθ===,∴sinθ==,∴tanθ===,∵tanθ==,∴=,解得c=1,∴△MOF1为等边三角形,∴M(﹣,),∴+=1,①∵a2﹣b2=c2=1,②,由①②可得4a4﹣8a2+1=0,解得a2=<1(舍去),a2=,∴a2===()2,∴a==,∴e===﹣1,故选:C.5.(5分)已知菱形ABCD的边长为2,∠DAB=60°,P是线段BD上一点,则的最小值是.【解答】解:建立平面直角坐标系,如图所示,菱形ABCD的边长为2,∠DAB=60°,可设P(0,b),且﹣1≤b≤1;∴A(﹣,0),C(,0),D(0,1),∴=(﹣,﹣b),=(,﹣b),=(0,1﹣b),∴+=(,1﹣2b),∴=﹣3﹣b(1﹣2b)=﹣3﹣b+2b2=2﹣,当且仅当b=时,取得最小值﹣.故答案为:﹣.6.(5分)已知SC是球O的直径,A,B是球O球面上的两点,且,若三棱锥S﹣ABC的体积为1,则球O的表面积为()A.4πB.13πC.16πD.52π【解答】解:∵SC是球O的直径,A,B是球O球面上的两点,且,∴∠SAC=∠SBC=90°,cos∠ACB==﹣,∴∠ACB=120°,∴∠CAB=∠CBA=30°,∴∠ASB=60°,∴SA=SB=AB=,∴SC==2,∴球半径R=1,∴球O的表面积S=4πR2=4π.故选:A.7.(5分)在△ABC中,AB=AC=5,BC=6,I是△ABC的内心,若=m(m,n∈R),则=()A.B.C.2 D.【解答】解:设BC中点为D,以BC为x轴,DA为y轴建立平面直角坐标系如图所示:∵AB=5,BD=BC=3,∴AD=4.∵△ABC是等腰三角形,∴内心I在线段AD上,设内切圆的半径为r,则tan∠IBD=,∴tan∠ABC===,又tan∠ABC==,∴=,解得r=或r=﹣6(舍).∴I(0,),又B(﹣3,0),A(0,4),C(3,0),∴=(3,),=(3,4),=(6,0),∵=m,∴,解得,∴=.故选:B.8.(5分)设点P为椭圆C:+=1上一点,F1、F2分别是椭圆C的左、右焦点,且△PF1F2的重心为点G,若|PF1|:|PF2|=3:4,那么△GPF1的面积为()A.24 B.12 C.8 D.6【解答】解:∵点P为椭圆C:+=1上一点,|PF1|:|PF2|=3:4,|PF1|+|PF2|=2a=14∴|PF1|=6,|PF2|=8,又∵F1F2=2c=10,∴△PF 1F2是直角三角形,S=,∵△PF 1F2的重心为点G.∴S=,∴△GPF1的面积为8,故选:C9.(5分)如图,O是坐标原点,过E(p,0)的直线分别交抛物线y2=2px(p >0)于A、B两点,直线BO与过点A平行于x轴的直线相交于点M,过点M 与此抛物线相切的直线与直线x=p相交于点N.则|ME|2﹣|NE|2=()A.2p2B.2p C.4p D.p【解答】解:过E(p,0)的直线分别交抛物线y2=2px(p>0)于A、B两点为任意的,不妨设直线AB为x=p,由,解得y=±2p,则A(﹣p,﹣p),B(p,p),∵直线BM的方程为y=x,直线AM的方程为y=﹣p,解得M(﹣p,﹣p),∴|ME|2=(2p)2+2p2=6p2,设过点M与此抛物线相切的直线为y+p=k(x+p),由,消x整理可得ky2﹣2py﹣2p+2p2k=0,∴△=4p2﹣4k(﹣2p+2p2k)=0,解得k=,∴过点M与此抛物线相切的直线为y+p=(x+p),由,解得N(p,2p),∴|NE|2=4p2,∴|ME|2﹣|NE|2=6p2﹣4p2=2p2,故选:A10.(5分)已知F1,F2是双曲线(a>0,b>0)的左右焦点,以F1F2为直径的圆与双曲线的一条渐近线交于点M,与双曲线交于点N,且M,N均在第一象限,当直线MF1∥ON时,双曲线的离心率为e,若函数f(x)=x2+2x﹣,则f(e)=()A.1 B.C.2 D.【解答】解:双曲线的c2=a2+b2,e=,双曲线的渐近线方程为y=±x,与圆x2+y2=c2联立,解得M(a,b),与双曲线(a>0,b>0)联立,解得,∵直线MF1与直线ON平行时,即有,即(a+c)2(c2﹣a2)=a2(2c2﹣a2),即有c3+2ac2﹣2a2c﹣2a3=0,∴e3+2e2﹣2e﹣2=0,即e2+2e﹣=2,∴f(e)=e2+2e﹣=2,故选:C.11.(5分)已知F1,F2是双曲线﹣=1(a>0,b>0)的左右焦点,过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段F1F2为直径的圆外,则双曲线离心率的取值范围是()A.(2,+∞)B.(,2)C.(,) D.(1,)【解答】解:双曲线﹣=1的渐近线方程为y=x,不妨设过点F2与双曲线的一条渐过线平行的直线方程为y=(x﹣c),与y=﹣x联立,可得交点M(,﹣),∵点M在以线段F1F2为直径的圆外,∴|OM|>|OF2|,即有+>c2,∴>3,即b2>3a2,∴c2﹣a2>3a2,即c>2a.则e=>2.∴双曲线离心率的取值范围是(2,+∞).故选A.12.(5分)已知抛物线C:y2=4x的焦点为F,过点F分别作两条直线l1,l2,直线l1与抛物线C交于A、B两点,直线l2与抛物线C交于D、E两点,若l1与l2的斜率的平方和为1,则|AB|+|DE|的最小值为()A.16 B.20 C.24 D.32【解答】解:抛物线C:y2=4x的焦点F(1,0),设直线l1:y=k1(x﹣1),直线l2:y=k2(x﹣1),由题意可知,则,联立,整理得:k12x2﹣(2k12+4)x+k12=0,设A(x1,y1),B(x2,y2),则x1+x2=,设D(x3,y3),E(x4,y4),同理可得:x3+x4=2+,由抛物线的性质可得:丨AB丨=x1+x2+p=4+,丨DE丨=x3+x4+p=4+,∴|AB|+|DE|=8+==,当且仅当=时,上式“=”成立.∴|AB|+|DE|的最小值24,故选:C.13.(5分)已知,是单位向量,,若向量满足,则的取值范围为()A. B. C.D.【解答】解:令,,,如图所示:则,又,所以点C在以点D为圆心、半径为1的圆上,易知点C与O、D共线时达到最值,最大值为+1,最小值为﹣1,所以的取值范围为[﹣1,+1].故选A.14.(5分)已知抛物线和圆,直线y=k(x﹣1)与C1,C2依次相交于A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4)四点(其中x1<x2<x3<x4),则|AB|•|CD|的值为()A.1 B.2 C.D.k2【解答】解:∵y2=4x,焦点F(1,0),准线l0:x=﹣1.由定义得:|AF|=x A+1,又∵|AF|=|AB|+1,∴|AB|=x A,同理:|CD|=x D,由题意可知直线l的斜率存在且不等于0,则直线l的方程为:y=k(x﹣1)代入抛物线方程,得:k2x2﹣(2k2+4)x+k2=0,∴x A x D=1,则|AB|•|CD|=1.综上所述,|AB|•|CD|=1,故选:A.15.(5分)抛物线M:y2=4x的准线与x轴交于点A,点F为焦点,若抛物线M 上一点P满足PA⊥PF,则以F为圆心且过点P的圆被y轴所截得的弦长约为(参考数据:≈2.24)()A.B.C.D.【解答】解:由题意,A(﹣1,0),F(1,0),点P在以AF为直径的圆x2+y2=1上.设点P的横坐标为m,联立圆与抛物线的方程得x2+4x﹣1=0,∵m>0,∴m=﹣2+,∴点P的横坐标为﹣2+,∴|PF|=m+1=﹣1+,∴圆F的方程为(x﹣1)2+y2=(﹣1)2,令x=0,可得y=±,∴|EF|=2=2=,故选:D.16.(5分)已知椭圆的左顶点和上顶点分别为A,B,左、右焦点分别是F1,F2,在线段AB上有且只有一个点P满足PF1⊥PF2,则椭圆的离心率的平方为()A. B.C.D.【解答】解:方法一:依题意,作图如下:A(﹣a,0),B(0,b),F1(﹣c,0),F2(c,0),∴直线AB的方程为,整理得:bx﹣ay+ab=0,设直线AB上的点P(x,y),则bx=ay﹣ab,x=y﹣a,∵PF1⊥PF2,则•=(﹣c﹣x,﹣y)•(c﹣x,﹣y)=x2+y2﹣c2=()2+y2﹣c2,令f(y)=()2+y2﹣c2,则f′(y)=2(y﹣a)×+2y,∴由f′(y)=0得:y=,于是x=﹣,∴•=(﹣)2+()2﹣c2=0,整理得:=c2,又b2=a2﹣c2,整理得:c4+3c2c2﹣a4=0,两边同时除以a4,由e2=,∴e4﹣3e2+1=0,∴e2=,又椭圆的离心率e∈(0,1),∴e2=.椭圆的离心率的平方,故选B.方法二:由直线AB的方程为,整理得:bx﹣ay+ab=0,由题意可知:直线AB与圆O:x2+y2=c2相切,可得d==c,两边平方,整理得:c4+3c2c2﹣a4=0,两边同时除以a4,由e2=,e4﹣3e2+1=0,∴e2=,又椭圆的离心率e∈(0,1),∴e2=.椭圆的离心率的平方,故选B.17.(5分)过点P(﹣1,1)作圆C:(x﹣t)2+(y﹣t+2)2=1(t∈R)的切线,切点分别为A,B,则•的最小值为()A.B.C.D.2﹣3【解答】解:圆C:(x﹣t)2+(y﹣t+2)2=1的圆心坐标为(t,t﹣2),半径为1,∴|PC|2=(t+1)2+(t﹣3)2=2t2﹣4t+10,∴|PA|2=|PB|2=|PC|2﹣1=(t+1)2+(t﹣3)2﹣1=2t2﹣4t+9,cos∠APC==,∴cos∠PAB=2cos2∠APC﹣1=2×()﹣1==∴•=||•||cos∠PAB=(2t2﹣4t+9)•=[(t2﹣2t+5)+(t2﹣2t+4)]•,设t2﹣2t+4=x,则x≥3,则•=f(x)=(x+x+1)•=,∴f′(x)=>0恒成立,∴f(x)在[3,+∞)单调递增,∴f(x)min=f(3)=,∴•的最小值为故选:C18.(5分)已知双曲线C:(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=60°,且,则双曲线C的离心率为()A. B. C.D.【解答】解:设双曲线的一条渐近线方程为y=x,A(a,0),P(m,),(m>0),由=3,可得Q(3m,),圆的半径为r=|PQ|==2m•,PQ的中点为H(2m,),由AH⊥PQ,可得=﹣,解得m=,r=.A到渐近线的距离为d==,则|PQ|=2=r,即为d=r,即有=•.可得=,e====.故选C.19.(5分)已知点F1,F2为椭圆C1:+=1(a>b>0)和双曲线C2:﹣=1(a′>0,b′>0)的公共焦点,点P为两曲线的一个交点,且满足∠F1PF2=90°,设椭圆与双曲线的离心率分别为e1,e2,则+=2.【解答】解:可设P为第一象限的点,|PF1|=m,|PF2|=n,由椭圆的定义可得m+n=2a,由双曲线的定义可得m﹣n=2a'可得m=a+a',n=a﹣a',由∠F1PF2=90°,可得m2+n2=(2c)2,即为(a+a')2+(a﹣a')2=4c2,化为a2+a'2=2c2,则+=2,即有+=2.故答案为:2.20.(5分)已知△ABC是直角边为2的等腰直角三角形,且A为直角顶点,P 为平面ABC内一点,则的最小值是﹣1.【解答】解:以BC为x轴,以BC边上的高为y轴建立坐标系,△ABC是直角边为2的等腰直角三角形,且A为直角顶点,斜边BC=2,则A(0,),B(﹣,0),C(,0),设P(x,y),则+=2=(﹣2x,﹣2y),=(﹣x,﹣y),∴=2x2+2y2﹣2y=2x2+2(y﹣)2﹣1,∴当x=0,y=时,则取得最小值﹣1.故答案为:﹣1.21.(5分)已知双曲线的右焦点为F,过点F向双曲线的一条渐近线引垂线,垂足为M,交另一条渐近线于N,若,则双曲线的渐近线方程为y=±x .【解答】解:由题意得右焦点F(c,0),设一渐近线OM的方程为y=x,则另一渐近线ON的方程为y=﹣x,由FM的方程为y=﹣(x﹣c),联立方程y=x,可得M的横坐标为,由FM的方程为y=﹣(x﹣c),联立方程y=﹣x,可得N的横坐标为.由2=,可得2(﹣c)=﹣c,即为﹣c=,由e=,可得﹣1=,即有e4﹣5e2+4=0,解得e2=4或1(舍去),即为e=2,即c=2a,b=a,可得渐近线方程为y=±x,故答案为:y=±x.22.(5分)已知抛物线C:y2=4x,过其焦点F作一条斜率大于0的直线l,l与抛物线交于M,N两点,且|MF|=3|NF|,则直线l的斜率为.【解答】解:抛物线C:y2=4x,焦点F(1,0),准线为x=﹣1,分别过M和N作准线的垂线,垂足分别为C和D,过NH⊥CM,垂足为H,设|NF|=x,则|MF|=3x,由抛物线的定义可知:|NF|=|DH|=x,|MF|=|CM|=3x,∴|HM|=2x,由|MN|=4x,∴∠HMF=60°,则直线MN的倾斜角为60°,则直线l的斜率k=tan60°=,故答案为:.方法二:抛物线C:y2=4x,焦点F(1,0),准线为x=﹣1,设直线MN的斜率为k,则直线MN的方程y=k(x﹣1),设M(x1,y1),N(x2,y2),,整理得:k2x2﹣2(k2+2)x+k2=0,则x1+x2=,x1x2=1,由|MF|=3|NF|,=3,即(1﹣x1,﹣y1)=3(x2﹣1,y2),x1+3x2=4,整理得:3x2﹣4x2+1=0,解得:x2=,或x2=1(舍去),则x1=3,解得:k=±,由k>0,则k=故答案为:.方法三:抛物线C:y2=4x,焦点F(1,0),准线为x=﹣1,设直线MN的方程x=mx+1,设M(x1,y1),N(x2,y2),,整理得:y2﹣4my﹣4=0,则y1+y2=4m,y1y2=﹣4,由|MF|=3|NF|,=3,即(1﹣x1,﹣y1)=3(x2﹣1,y2),﹣y1=3y2,即y1=﹣3y2,解得:y2=﹣,y1=2,∴4m=,则m=,∴直线l的斜率为,故答案为:.23.(5分)已知F是椭圆C:+=1的右焦点,P是C上一点,A(﹣2,1),当△APF周长最小时,其面积为 4 .【解答】解:椭圆C:+=1的a=2,b=2,c=4,设左焦点为F'(﹣4,0),右焦点为F(4,0).△APF周长为|AF|+|AP|+|PF|=|AF|+|AP|+(2a﹣|PF'|)=|AF|+|AP|﹣|PF'|+2a≥|AF|﹣|AF'|+2a,当且仅当A,P,F'三点共线,即P位于x轴上方时,三角形周长最小.此时直线AF'的方程为y=(x+4),代入x2+5y2=20中,可求得P(0,2),=S△PF'F﹣S△AF'F=×2×8﹣×1×8=4.故S△APF故答案为:4.简答题1.(12分)已知椭圆与直线l:bx﹣ay=0都经过点.直线m与l平行,且与椭圆C交于A,B两点,直线MA,MB 与x轴分别交于E,F两点.(1)求椭圆C的方程;(2)证明:△MEF为等腰三角形.【解答】解:(1)由直线l:bx﹣ay=0都经过点,则a=2b,将代入椭圆方程:,解得:b2=4,a2=16,∴椭圆C的方程为;(2)证明:设直线m为:,A(x1,y1),B(x2,y2)联立:,整理得x2+2tx+2t2﹣8=0,∴x1+x2=﹣2t,x1x2=2t2﹣8,设直线MA,MB的斜率为k MA,k MB,要证△MEF为等腰三角形,只需k MA+k MB=0,由,k MA+k MB=,=0,所以△MEF为等腰三角形.2.(12分)已知椭圆(a>b>0),其焦距为2,离心率为(1)求椭圆C的方程;(2)设椭圆的右焦点为F,K为x轴上一点,满足,过点K作斜率不为0的直线l交椭圆于P,Q两点,求△FPQ面积s的最大值.【解答】解:(1)因为椭圆焦距为2,即2c=2,所以c=1,,所以a=,从而b2=a2﹣c2=1,所以,椭圆的方程为+y2=1.(2)椭圆右焦点F(1,0),由可知K(2,0),直线l过点K(2,0),设直线l的方程为y=k(x﹣2),k≠0,将直线方程与椭圆方程联立得(1+2k2)x2﹣8k2x+8k2﹣2=0.设P(x1,y1),Q(x2,y2),则,,由判别式△=(﹣8k2)2﹣4(2k2+1)(8k2﹣2)>0解得k2<.点F(1,0)到直线l的距离为h,则,,=••,=|k|•,=,令t=1+2k2,则1<t<2,则S=•=,当时,S取得最大值.此时,,S取得最大值.3.(12分)已知圆C:x2+y2+2x﹣2y+1=0和抛物线E:y2=2px(p>0),圆心C到抛物线焦点F的距离为.(1)求抛物线E的方程;(2)不过原点的动直线l交抛物线于A,B两点,且满足OA⊥OB.设点M为圆C上任意一动点,求当动点M到直线l的距离最大时的直线l方程.【解答】解:(1)圆C:x2+y2+2x﹣2y+1=0可化为(x+1)2+(y﹣1)2=1,则圆心为(﹣1,1).抛物线E:y2=2px(p>0),焦点坐标F(),由于:圆心C到抛物线焦点F的距离为.则:,解得:p=6.故抛物线的方程为:y2=12x(2)设直线的方程为x=my+t,A(x1,y1),B(x2,y2),则:,整理得:y2﹣12my﹣12t=0,所以:y1+y2=12m,y1y2=﹣12t.由于:OA⊥OB.则:x1x2+y1y2=0.即:(m2+1)y1y2+mt(y1+y2)+t2=0.整理得:t2﹣12t=0,由于t≠0,解得t=12.故直线的方程为x=my+12,直线经过定点(12,0).当CN⊥l时,即动点M经过圆心C(﹣1,1)时到直线的距离取最大值.当CP⊥l时,即动点M经过圆心C(﹣1,1)时到动直线L的距离取得最大值.k MP=k CP=﹣,则:m=.此时直线的方程为:x=,即:13x﹣y﹣156=0.4.(12分)给定椭圆C:+=1(a>b>0),称圆心在原点O,半径为的圆是椭圆C的“准圆”.已知椭圆C的离心率,其“准圆”的方程为x2+y2=4.(I)求椭圆C的方程;(II)点P是椭圆C的“准圆”上的动点,过点P作椭圆的切线l1,l2交“准圆”于点M,N.(1)当点P为“准圆”与y轴正半轴的交点时,求直线l1,l2的方程,并证明l1⊥l2;(2)求证:线段MN的长为定值.【解答】解:(I)由准圆方程为x2+y2=4,则a2+b2=4,椭圆的离心率e===,解得:a=,b=1,∴椭圆的标准方程:;(Ⅱ)证明:(1)∵准圆x2+y2=4与y轴正半轴的交点为P(0,2),设过点P(0,2)且与椭圆相切的直线为y=kx+2,联立,整理得(1+3k2)x2+12kx+9=0.∵直线y=kx+2与椭圆相切,∴△=144k2﹣4×9(1+3k2)=0,解得k=±1,∴l 1,l2方程为y=x+2,y=﹣x+2.∵=1,=﹣1,∴•=﹣1,则l 1⊥l2.(2)①当直线l1,l2中有一条斜率不存在时,不妨设直线l1斜率不存在,则l1:x=±,当l1:x=时,l1与准圆交于点(,1)(,﹣1),此时l2为y=1(或y=﹣1),显然直线l1,l2垂直;同理可证当l1:x=时,直线l1,l2垂直.②当l1,l2斜率存在时,设点P(x0,y0),其中x02+y02=4.设经过点P(x0,y0)与椭圆相切的直线为y=t(x﹣x0)+y0,∴由得(1+3t2)x2+6t(y0﹣tx0)x+3(y0﹣tx0)2﹣3=0.由△=0化简整理得(3﹣x02)t2+2x0y0t+1﹣y02=0,∵x02+y02=4.,∴有(3﹣x02)t2+2x0y0t+(x02﹣3)=0.设l1,l2的斜率分别为t1,t2,∵l1,l2与椭圆相切,∴t1,t2满足上述方程(3﹣x02)t2+2x0y0t+(x02﹣3)=0,∴t1•t2=﹣1,即l1,l2垂直.综合①②知:∵l1,l2经过点P(x0,y0),又分别交其准圆于点M,N,且l1,l2垂直.∴线段MN为准圆x2+y2=4的直径,|MN|=4,∴线段MN的长为定值.5.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.【解答】解:(1)由N(),点Q的坐标为(),得直线NQ的方程为y=x﹣,令x=0,得点B的坐标为(0,﹣).所以椭圆的方程为+=1.将点N的坐标(,)代入,得+=1,解得a2=4.所以椭圆C的标准方程为+=1.(2):设直线BM的斜率为k(k>0),则直线BM的方程为y=x﹣.在y=kx﹣中,令y=0,得x P=,而点Q是线段OP的中点,所以x Q=.所以直线BN的斜率k BN=k BQ==2k.联立,消去y,得(3+4k2)x2﹣8kx=0,解得x M=.用2k代k,得x N=.又=2,所以x N=2(x M﹣x N),得2x M=3x N,故2×==3×,又k>0,解得k=.所以直线BM的方程为y=x﹣6.(12分)设O为坐标原点,动点M在椭圆上,过M作x轴的垂线,垂足为N,点P满足.(Ⅰ)求点P的轨迹方程E;(Ⅱ)过F(1,0)的直线l1与点P的轨迹交于A、B两点,过F(1,0)作与l1垂直的直线l2与点P的轨迹交于C、D两点,求证:为定值.【解答】(Ⅰ)解:设P(x,y),则N(x,0),,又∵,∴,由M在椭圆上,得,即;(Ⅱ)证明:当l1与x轴重合时,|AB|=6,,∴.当l1与x轴垂直时,,|CD|=6,∴.当l1与x轴不垂直也不重合时,可设l1的方程为y=k(x﹣1)(k≠0),此时设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),把直线l1与曲线E联立,得(8+9k2)x2﹣18k2x+9k2﹣72=0,可得△=(﹣18k2)2﹣4(8+9k2)(9k2﹣72)>0.,.∴,把直线l2与曲线E联立,同理可得.∴为定值.7.(12分)已知椭圆C:的离心率为,且以两焦点为直径的圆的内接正方形面积为2.(1)求椭圆C的标准方程;(2)若直线l:y=kx+2与椭圆C相交于A,B两点,在y轴上是否存在点D,使直线AD与BD的斜率之和k AD+k BD为定值?若存在,求出点D坐标及该定值,若不存在,试说明理由.【解答】解:(1)由已知可得解得a2=2,b2=c2=1,所求椭圆方程为.(2)由得(1+2k2)x2+8kx+6=0,则△=64k2﹣24(1+2k2)=16k2﹣24>0,解得或.设A(x1,y1),B(x2,y2),则,,设存在点D(0,m),则,,所以==.要使k AD+k BD为定值,只需6k﹣4k(2﹣m)=6k﹣8k+4mk=2(2m﹣1),k与参数k无关,故2m﹣1=0,解得,当时,k AD+k BD=0.综上所述,存在点,使得k AD+k BD为定值,且定值为0.8.(12分)已知曲线C的方程为ax2+ay2﹣2a2x﹣4y=0(a≠0,a为常数).(1)判断曲线C的形状;(2)设曲线C分别与x轴,y轴交于点A,B(A,B不同于原点O),试判断△AOB的面积S是否为定值?并证明你的判断;(3)设直线l:y=﹣2x+4与曲线C交于不同的两点M,N,且•=﹣,求a的值.【解答】解:(1)将曲线C的方程化为x2+y2﹣2ax﹣y=0,∴(x﹣a)2+(y﹣)2=a2+,可知曲线C是以点(a,)为圆心,以为半径的圆.(2)△AOB的面积S为定值.证明如下:在曲线C的方程中令y=0,得ax(x﹣2a)=0,得点A(2a,0),在曲线C方程中令x=0,得y(ay﹣4)=0,得点B(0,),∴S=|OA||OB|=|2a|||=4(为定值),(3)直线l与曲线C方程联立可得5ax2﹣(2a2+16a﹣8)x+16a﹣16=0,设M(x1,y1),N(x2,y2),则x1+x2=,x1x2=,∴•=x1x2+y1y2=5x1x2+8(x1+x2)+16=﹣,即(80a﹣80﹣16a2﹣128a+64+80a)=﹣,即2a2﹣5a+2=0,解得a=2或a=,当a=2或时,都满足△>0,故a=2或9.(12分)已知抛物线E:y2=2px(p>0)的准线与x轴交于点k,过点k做圆C:(x﹣5)2+y2=9的两条切线,切点为.(1)求抛物线E的方程;(2)若直线AB是讲过定点Q(2,0)的一条直线,且与抛物线E交于A,B两点,过定点Q作AB的垂线与抛物线交于G,D两点,求四边形AGBD面积的最小值.【解答】解:(1)根据题意,抛物线的E的方程为y2=2px(p>0),则设MN与x轴交于点R,由圆的对称性可知,.于是,所以∠CMR=30°,∠MCR=60°,所以|CK|=6,所以p=2.故抛物线E的方程为y2=4x.(2)设直线AB的方程为x=my+2,设A=(x1,y1),B=(x2,y2),联立得y2﹣4my﹣8=0,则y1+y2=4m,y1y2=﹣8.∴设G=(x3,y3),D=(x4,y4),同理得,则四边形AGBD的面积=令,则是关于μ的增函数,故S min=48,当且仅当m=±1时取得最小值48.10.(16分)在平面直角坐标系中,已知椭圆C:+y2=1 (a>0,a≠1)的两个焦点分别是F1,F2,直线l:y=kx+m(k,m∈R)与椭圆交于A,B两点.(1)若M为椭圆短轴上的一个顶点,且△MF1F2是直角三角形,求a的值;(2)若k=1,且△OAB是以O为直角顶点的直角三角形,求a与m满足的关系;(3)若a=2,且k OA•k OB=﹣,求证:△OAB的面积为定值.【解答】解:(1)∵M为椭圆短轴上的一个顶点,且△MF1F2是直角三角形,∴△MF1F2为等腰直角三角形,∴OF1=OM,当a>1时,=1,解得a=,当0<a<1时,=a,解得a=,(2)当k=1时,y=x+m,设A(x1,y1),(x2,y2),由,即(1+a2)x2+2a2mx+a2m2﹣a2=0,∴x1+x2=﹣,x1x2=,∴y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2=,∵△OAB是以O为直角顶点的直角三角形,∴•=0,∴x1x2+y1y2=0,∴+=0,∴a2m2﹣a2+m2﹣a2=0∴m2(a2+1)=2a2,(3)证明:当a=2时,x2+4y2=4,设A(x1,y1),(x2,y2),∵k OA•k OB=﹣,∴•=﹣,∴x1x2=﹣4y1y2,由,整理得,(1+4k2)x2+8kmx+4m2﹣4=0.∴x1+x2=,x1x2=,∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=++m2=,∴=﹣4×,∴2m2﹣4k2=1,∴|AB|=•=•=2•=∵O到直线y=kx+m的距离d==,=|AB|d==•==1∴S△OAB11.(12分)已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足•=0,=2.(Ⅰ)当点P在圆上运动时,求点Q的轨迹方程;(Ⅱ)若斜率为k的直线l与圆x2+y2=1相切,直线l与(Ⅰ)中所求点Q的轨迹交于不同的两点F,H,O是坐标原点,且≤•≤时,求k的取值范围.【解答】解:(I)由题意知MQ中线段AP的垂直平分线,∴,∴点Q的轨迹是以点C,A为焦点,焦距为2,长轴为的椭圆,,故点Q的轨迹方程是.(II)设直线l:y=kx+b,F(x1,y1),H(x2,y2)直线l与圆x2+y2=1相切联立,(1+2k2)x2+4kbx+2b2﹣2=0,△=16k2b2﹣4(1+2k2)2(b2﹣1)=8(2k2﹣b2+1)=8k2>0,可得k≠0,∴,===,∴为所求.12.(12分)已知椭圆的左焦点为F,左顶点为A.(1)若P是椭圆上的任意一点,求的取值范围;(2)已知直线l:y=kx+m与椭圆相交于不同的两点M,N(均不是长轴的端点),AH⊥MN,垂足为H且,求证:直线l恒过定点.【解答】解:(1)设P(x0,y0),又A(﹣2,0),F(﹣1,0)所以=,因为P点在椭圆上,所以,即,且﹣2≤x0≤2,所以=,函数在[﹣2,2]单调递增,当x0=﹣2时,f(x0)取最小值为0;当x0=2时,f(x0)取最大值为12.所以的取值范围是[0,12].(2)由题意:联立得,(3+4k2)x2+8kmx+4m2﹣12=0由△=(8km)2﹣4×(3+4k2)(4m2﹣12)>0得4k2+3>m2①设M(x1,y1),N(x2,y2),则.==0,所以(x1+2)(x2+2)+y1y2=0即,4k2﹣16km+7m2=0,所以或均适合①.当时,直线l过点A,舍去,当时,直线过定点.13.(12分)设椭圆+=1(a>b>0)的离心率e=,左焦点为F,右顶点为A,过点F的直线交椭圆于E,H两点,若直线EH垂直于x轴时,有|EH|=(1)求椭圆的方程;(2)设直线l:x=﹣1上两点P,Q关于x轴对称,直线AP与椭圆相交于点B(B 异于点A),直线BQ与x轴相交于点D.若△APD的面积为,求直线AP的方程.【解答】解:(1)设F(﹣c,0)(c>0),∵e=,∴a=2c,又由|EH|=,得,且a2=b2+c2,解得,因此椭圆的方程为:;(2)设直线AP的方程为x=my+1(m≠0),与直线l的方程x=﹣1联立,可得点P(﹣1,﹣),故Q(﹣1,).将x=my+1与联立,消去x,整理得(3m2+4)y2+6my=0,解得y=0,或y=.由点B异于点A,可得点B().由Q(﹣1,),可得直线BQ的方程为,令y=0,解得,故D().∴|AD|=.又∵△APD的面积为,故,整理得,解得|m|=,∴m=.∴直线AP的方程为,或3x﹣﹣3=0.14.(12分)已知椭圆C:的离心率,且过点.(1)求椭圆C的方程;(2)过P作两条直线l1,l2与圆相切且分别交椭圆于M,N两点.①求证:直线MN的斜率为定值;②求△MON面积的最大值(其中O为坐标原点).【解答】(12分)解:(1)由,设椭圆的半焦距为c,所以a=2c,因为C过点,所以,又c2+b2=a2,解得,所以椭圆方程为.(4分)(2)①显然两直线l1,l2的斜率存在,设为k1,k2,M(x1,y1),N(x2,y2),由于直线l1,l2与圆相切,则有k1=﹣k2,直线l1的方程为,联立方程组消去y,得,因为P,M为直线与椭圆的交点,所以,同理,当l2与椭圆相交时,,所以,而,所以直线MN的斜率.②设直线MN的方程为,联立方程组,消去y得x2+mx+m2﹣3=0,所以,原点O到直线的距离,△OMN得面积为,当且仅当m2=2时取得等号.经检验,存在r(),使得过点的两条直线与圆(x﹣1)2+y2=r2相切,且与椭圆有两个交点M,N.所以△OMN面积的最大值为.(12分)15.(12分)如图,A,B是椭圆长轴的两个端点,P,Q是椭圆C 上都不与A,B重合的两点,记直线BQ,AQ,AP的斜率分别是k BQ,k AQ,k AP.(1)求证:;(2)若k AP=4k BQ,求证:直线PQ恒过定点,并求出定点坐标.【解答】证明:(1)设Q(x1,y1),由椭圆,得B(﹣2,0),A(2,0),∴;(2)由(1)知:.设P(x2,y2),直线PQ:x=ty+m,代入x2+4y2=4,得(t2+4)y2+2mty+m2﹣4=0,∴,,由k AP•k AQ=﹣1得:(x1﹣2)(x2﹣2)+y1y2=0,∴,∴(t2+1)(m2﹣4)+(m﹣2)t(﹣2mt)+(m﹣2)2(t2+4)=0,∴5m2﹣16m+12=0,解得m=2或m=.∵m≠2,∴,∴直线PQ:,恒过定点.。
2014年高考理综全国卷1(含详细答案)

8.化学与社会、生活密切相关。对下列现象或事实的解释正确的是()
选项
现象或事实
解释
A
用热的烧碱溶液洗去油污
可直接与油污反应
B
漂白粉在空气中久置变质
漂白粉中的 与空气中的 反应生成
C
施肥时,草木灰(有效成分为 )不能与 混合使用
与 反应生成氨气会降低肥效
D
溶液可用于铜质印刷线路板制作
A.点电荷 一定在MP的连线上
B.连接PF的线段一定在同一等势面上
C.将正试探电荷从 点搬运到N点,电场力做负功 NhomakorabeaD. 大于
第Ⅱ卷(非选择题 共174分)
三、非选择题(包括必考题和选考题两部分,第22~第32题为必考题,每个试题考生都必须做答。第33~第40题为选考题,考生根据要求做答)
(一)必考题(共129分)
A.原子最外层电子数:X>Y>Z
B.单质沸点:X>Y>Z
C.离子半径:
D.原子序数:X>Y>Z
11.溴酸银( )溶解度随温度变化曲线如图所示,下列说法错误的是()
A.溴酸银的溶解是放热过程
B.温度升高时溴酸银溶解速度加快
C. 60 时溴酸银的 约等于
D.若硝酸钾中含有少量溴酸银,可用重结晶方法提纯
12.下列有关仪器使用方法或实验操作正确的是()
R/Ω
1.0
2.0
3.0
4.0
5.0
6.0
7.0
I/A
0.143
0.125
①
0.100
0.091
0.084
0.077
6.99
8.00
②
10.0
11.0
2014年高考真题——文综(新课标II)精校版 Word版含答案
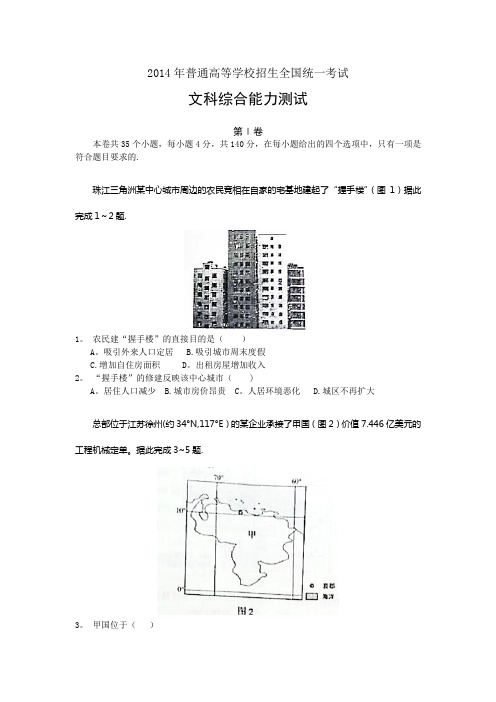
2014年普通高等学校招生全国统一考试文科综合能力测试第Ⅰ卷本卷共35个小题,每小题4分,共140分,在每小题给出的四个选项中,只有一项是符合题目要求的.珠江三角洲某中心城市周边的农民竞相在自家的宅基地建起了“握手楼”(图1)据此完成1~2题.1。
农民建“握手楼”的直接目的是()A。
吸引外来人口定居 B.吸引城市周末度假C.增加自住房面积 D。
出租房屋增加收入2。
“握手楼”的修建反映该中心城市( )A。
居住人口减少 B.城市房价昂贵 C。
人居环境恶化 D.城区不再扩大总部位于江苏徐州(约34°N,117°E)的某企业承接了甲国(图2)价值7.446亿美元的工程机械定单。
据此完成3~5题.3。
甲国位于()A。
欧洲 B.非洲 C.北美洲 D.南美洲4。
2011年6月21日,该定单的首批产品从徐州发货.这一日,徐州与甲国首都相比( )A.徐州的正午太阳高度较高 B。
徐州的白昼较短C.两地正午物影方向相同 D。
两地日出方位角相同5. 该批产品运往甲国,最近的海上航线需经()A。
好望角 B。
苏伊士运河 C。
巴拿马运河 D。
麦哲伦海峡降水在生态系统中被分为蓝水和绿水,蓝水是形成径流的部分(包括地表径流和地下径流);绿水是被蒸发(腾)的部分,其中被植物蒸腾的部分称为生产性绿水,被蒸发的部分称为非生产性绿水。
据此完成6~7题.6。
下列河流中,绿水比例最大的是()A.塔里木河流域B.长江流域 C。
雅鲁藏布江流域 D.黑龙江流域7。
在干旱和半干旱地区,下列措施中,使绿水中生产性绿水比重提高最多的是()A。
水田改旱地 B。
植树造林 C.覆膜种植农作物 D。
修建梯田图3示意科隆群岛(加拉帕戈斯群岛)的地理位置,读图3,完成8~9题。
图38. 科隆群岛特有动物种属比例较大,形成这一现象的地理条件是该群岛()A.地处赤道附近 B。
远离大陆 C.构造运动强烈 D。
地形复杂9。
科伦群岛是耐寒的企鹅和喜暖的鼠蜥的共同家园,主要因为该群岛()A.气温日较差大B.处在动物迁徙路线上C。
2024年高考全国各地模拟考作文汇编【原题+审题+立意+例文】第10辑

2024年高考全国各地模拟考作文汇编【原题+审题+立意+例文】第10辑01【原题呈现】阅读下面的材料,根据要求写作。
(60分)材料一:假舆马者,非利足也,而致千里;假舟楫者,非能水也,而绝江河。
(荀子《劝学》)材料二:《红楼梦》中薛宝钗咏柳时说:“韶华休笑本无根,好风凭借力,送我上青云。
”习近平总书记曾在东西部扶贫协作座谈会上说过:“用好外力、激发内力是必须把握好的一对重要关系。
”一个人完成一件事或成就一番事业也是这样的,既要依靠自身内力,往往也要借助外力。
以上材料引发了你怎样的联想和思考?请写一篇文章。
要求:选准角度,确定立意,明确文体,自拟标题;不要套作,不得抄袭;不得泄露个人信息;不少于800字。
【审题】本次作文的写作方向及写作内容,意在引导考生对学习、为人、成事、人生经历等的思考:完成一件事或成就一番事业,既要依靠自身因素,又要借助其他外物。
材料摘自《劝学》和《红楼梦》的相关内容,材料一“假舆马者,非立足也,而致千里;假舟楫者,非能水也,而绝江河”说明要到达远方或渡河需要外物相助;《红楼梦》中薛宝钗借咏柳寄寓了善借外力,成就自我。
在写作提示语中,引用习总书记的话,又在强调说明“用好外力与激发内力的关系”。
考生可根据自己的人生经历、人生理想等进行立意,在人生的道路上,需要借助外力、外物来帮助自己更好地发展。
可以是他人(老师、父母、朋友等人)的帮助,借助他人的智慧、经验、资源;也可以机遇、平台、时代国家的大背景、大环境等,更好地帮助解决问题,实现自我提升。
将借助外物、外力与自身努力构成二元思辨关系进行论证。
可以从以下角度进行辩证分析:①从借助外力并不意味着放弃自我努力,只依靠外力而没有自身的努力,最终也无法实现自我提升;②从需要自身努力外还要选择借助正确的外力。
比如应该选择那些能够帮助自己更好地发展的人和事物。
如,选择优秀的导师,可以指导我们的方向、给予我们经验;选择一份适合自己的工作,可以让我们更好地发挥自己的优势、实现自我价值;③从借助外力需要有一个度,在借助外力的同时,保持自我思考和独立性。
2014年全国高考英语试题分类汇编 语法填空(含解析)

2014全国高考汇编阅读之广告应用类一(2014福建卷)第一节短文填词(共10小题;每小题1分,满分10分)阅读下面短文,根据以下提示:1)汉语提示,2)首字母提示,3)语境提示,在每个空格内填人一个适当的英语单词,所填单词要求意义准确,拼写正确,并将该词完整地写在答题卡中相应的横线上。
Many of us were raised with the saying "Waste not, want not.” None of us, (76) _h , can completely avoid waste in our lives.Any kind of waste is thoughtless. Whether we waste our potential talents, our own time, our limited natural(77) (资源),our money, or other people's time, each of us can become more aware and careful. The smallest good habits can make a big (78) _d . It's a good feeling to know in our hearts we are doing our(79)h in a world that is in serious trouble. By focusing on( 80) (节省)oil, water, paper, food, and clothing, we are playing a part (81) cutting down on waste.We must keep reminding (82) (白己)that it is easier to get into something (83) it is to get out of it. Actually, severe damage( 84)d ____to our land is fairly recent in the history of our evolution. It's time for us to( 85)____no to waste so that our grandchildren’s children will be able to develop well. We can't solve all the problems of waste, but we can encourage mindfulness.Waste not!76. 【答案】however【试题解析】很多人都知道:勤俭节约,吃穿不愁。
2014年四川省高考数学(四川卷)试题及解答

2014年普通高等学校招生全国统一考试理科(四川卷)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的。
1.已知集合2{|20}A x x x =--≤,集合B 为整数集,则A B ⋂=( ) A .{1,0,1,2}- B .{2,1,0,1}-- C .{0,1} D .{1,0}- 【答案】A【解析】{|12}A x x =-≤≤,B Z =,故A B ⋂={1,0,1,2}- 2.在6(1)x x +的展开式中,含3x 项的系数为( ) A .30 B .20 C .15 D .10 【答案】C【解析】含3x 项为24236(1)15x C x x ⋅=3.为了得到函数sin(21)y x =+的图象,只需把函数sin 2y x =的图象上所有的点( )A .向左平行移动12个单位长度 B .向右平行移动12个单位长度 C .向左平行移动1个单位长度 D .向右平行移动1个单位长度【答案】A【解析】因为1sin(21)sin[2()]2y x x =+=+,故可由函数sin 2y x =的图象上所有的点向左平行移动12个单位长度得到4.若0a b >>,0c d <<,则一定有( ) A .a b c d > B .a b c d < C .a b d c > D .a b d c< 【答案】D【解析】由1100c d d c<<⇒->->,又0a b >>,由不等式性质知:0a b d c ->->,所以a b d c< 5.执行如图1所示的程序框图,如果输入的,x y R ∈,则输出的S 的最大值为( )A .0B .1C .2D .3 【答案】C【解析】当001x y x y ≥⎧⎪≥⎨⎪+≤⎩时,函数2S x y =+2()22x y y y ≤+-≤-≤ ∴ S 的最大值为2.6.六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有( )A .192种B .216种C .240种D .288种 【答案】B【解析】当最左端为甲时,不同的排法共有55A 种;当最左端为乙时,不同的排法共有14C 44A 种。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年高考全国各地模拟卷型题整理(一):吴锡畴《春日》韶光大半去匆匆,几许幽情递不通。
燕未成家寒食雨,人如中酒落花风。
一窗草忆濂溪老,五亩园思涑水翁。
无赋招魂成独啸,且排春句答春工。
1、颈联中“逆”、“私”二字极为精妙,请结合诗句简要赏析其妙处。
(炼字题,5分)答:逆”是迎接的意思,“私”是偏爱的意思。
(步骤一,2分)颈联使用拟人手法,赋予绿草田园以人性人情,写出它们对其主人的亲昵之状,(步骤二,2分)曲折而又深刻地表现了诗人对田园生活的喜爱之情。
(步骤三,1分)2、“幽情”在诗中指什么情感?请结合全诗(审题重点)加以分析。
(思想感情题,6分)答:幽情”在本诗中有两个层面的意思:一是伤春之情。
(步骤一,1分)面对“韶光”匆匆逝去,目睹“落花”满地堆积,一种“春去也”的感慨油然而生。
(步骤二,2分)一是忧国之情。
(步骤一,1分)身处南宋,国运衰微,盛景不再,大势已去,一种忧国伤时之情郁结心头。
(步骤二,2分)(这道题的答案,取AA’,BB’的组织形式)王海椿《雪画》兖州城外农庄有个书生叫柳应寒。
柳应寒家贫,仕途又颇不得意。
自恃画得一手好画,却无人赏识。
常自怨自叹,恨无知音。
一日,他歇息田垄,迎面走来个书生,长得白白净净,眉含英气。
书生见他满面忧郁,便坐下和他攀谈。
柳应寒向书生诉说功名不就的苦恼,书生好言相劝,句句都说在他心坎上。
知己难求,他遂邀书生到寒舍小坐。
柳应寒弄了两个小菜,欲去买酒,书生说不用了,从腰间摸出一个葫芦,斟起酒来,顿时香气扑鼻,令人生津。
应寒从没喝过如此佳酿,遂开怀畅饮。
席间得知书生姓白名如雪,生于富豪之家,因不忍家父严管,负气离家。
应寒说:“为兄若不嫌我家贫寒,就此住下如何?”白如雪说:“好。
”两人畅饮之时,门外飘起雪花。
白如雪赞:“好雪!”便磨墨展纸,画了几幅松、竹、梅图。
运笔之时,应寒已知书生功底非同小可,泼墨大胆,非常人所为。
可如雪搁笔之后,应寒看来看去总觉得几幅画少了一种气韵。
在他愣神之时,白如雪已跨出门外,从雪地抓了个雪团回来,放到白瓷碗中,用口一呵,顷刻,雪团融化成水。
白如雪净了笔,蘸上雪水,在画上圈圈点点、任意挥洒,几幅画上立时雪花片片,静中有动。
雪梅、雪松、雪竹,顿时有了神韵。
“真是神来之笔、神来之笔!为兄莫非神人也。
”柳应寒赞叹。
白如雪说:“这有何难,你也能画。
只不过你平时不知个中诀窍罢了。
”便叫应寒试试,应寒将信将疑,摸过纸笔,效仿起来,果真不假,清水落到纸上便成了飞雪。
翌日,白如雪嘱柳应寒将画皆以他的名义拿去卖。
柳应寒说:“这样不妥吧?”如雪道:“我只求活得逍遥自在,名利于我无用,而你需摆脱眼下处境。
”应寒也就不再推辞,他来到集市,将画悬于一店铺壁,顷时就围拢了许多人,赞不绝口,争相购买。
应寒得了好些银两,很是欣喜。
便又买了好酒好菜,回家和如雪畅饮起来。
之后,他乘着酒兴又作了好多雪景图,如雪也在一旁连连赞好。
他将画拿到集市,又被人抢购一空。
此后,两人常在一起交流画艺,柳应寒大有长进,很快就和白如雪齐肩了。
柳应寒的名气渐渐大了起来。
他的雪景画一时被商贾名流争相收藏。
钦差大臣李相亭巡视兖州,闻应寒画名,特意召见。
柳应寒当场表演画艺,所画《雪荷》,甚得李相亭赏识。
古人画荷,要么是夏日艳荷,要么是秋日残荷,他却画冬日之荷。
冬荷也是残荷,可他笔下之荷,泼墨淋漓酣畅,深浅层次皆以用墨浓淡分之。
荷叶虽萎,衬以雪景,并无丝毫萧条败落之气。
莲梗裹雪,更显荷之冰清玉洁。
整个画面只有黑白二色,一方朱印又使画面免去冷清压抑之感,生动异常。
得知他仍无功名,李相亭便封他一个小官,在县衙混口饭吃。
得知此讯,白如雪也甚是为他高兴。
后来,兖州县令擢升,得李相亭引荐,柳应寒被封为一县之主。
当上县令后,柳应寒就很少回去和白如雪叙谈了,只是时常托人捎些银子回去。
一天,一个衙役跑到大堂,对柳应寒说:“大人,有一人在街头卖画,全是仿你的画风,有损大人声誉,请查访。
”柳应寒从官轿下来,发现卖画者竟是白如雪。
他说:“哎呀,原是白兄,缺钱花向我说一声不就行了,何苦出来卖画呢?”白如雪道:“我卖画又不是为钱,只是找个乐儿。
”柳应寒叫他快收了画摊,跟他到县衙叙叙,白如雪怎么也不应。
柳应寒很是不悦,只好打道回府。
一连几日,白如雪都来县城卖画。
这天,来了几个衙役,二话不说将白如雪的画摊踢翻了,说他冒仿县太爷手笔,骗取钱财,不容白如雪分辩,就将白如雪绑了押回县衙,打进监狱。
不几日,兖州降了一场大雪。
柳应寒在府上独自畅饮,乘着酒兴,作了一幅瑞雪丰年图:座座村落,尽披银装,柴门红灯,玉树雪墙,一片祥和之气,隐喻皇恩浩荡,恩泽山河。
柳应寒摇头晃脑自我欣赏一番,甚是满意,当下差人冒雪送往京城,希望得到皇上赏识。
皇上听说兖州县令画界名流柳应寒雪天送来雪画,很是高兴。
可待他展开画轴,不禁气得胡须直抖。
原来,此画哪有什么雪景,却见幢幢茅舍,腐草凄凄,秃树枯枝,显得万般荒凉。
分明是讥讽当今皇上昏庸无能。
是日,柳应寒正在备案,忽觉脖子一阵冰凉,他觉得好生蹊跷。
一抬头,满堂飘着雪花。
再细看,雪花却是从他所作的几幅雪画上飘落,顷刻之间,几幅画上的雪已然落尽,萧索之气令他不寒而栗!蓦地,他想起自己献给皇上的那幅瑞雪图,不禁惊出一身冷汗……(选自《微型小说》)3、请试着拟写一副对联来概括小说情节发展。
(情节概括题,6分)(解析:既然是概括小说情节发展,就应该把情节理清,并一一写出来,这是答题的第一个步骤。
小说的情节发展大致如下:柳应寒仕途失意;偶遇白如雪;得到白如雪帮助,画艺大进;因雪画受钦差大臣李相亭赏识,当上县令;疏远白如雪;拘押白如雪;献画京城,却激怒皇上;柳应寒发现所画雪景图飞雪尽销,画面变得萧索荒凉。
第二步将以上情节在语言上做提炼浓缩。
第三步,依照对联的格式将提炼浓缩后的内容组织起来。
第四步,对组织后的对联进行润色修改,如果是在答题卡上直接修改,注意使用规范的修改符号。
)例:困窘时遇如雪作画当县令,得意日害旧交献画毁前程。
(格式2分,内容4分)4、人们常说“成也萧何,败也萧何”,由此来谈一谈你对小说标题作用的认识。
(探究题,探究的是标题的作用,8分)(解析:先要理解题意,萧何是汉高祖高邦的丞相,曾向刘邦推荐韩信,后又献计除了韩信。
这个成语的意思是比喻事情的成功和失败都是由这一个人或一个因素造成的。
联系这篇小说的故事情节,发现雪画正是柳应寒成功的直接原因,也是他失败的直接原因。
这道题设题妙,考查了考生的阅读积累,是个干扰也是个提示。
)答:“雪画”作为标题在小说中起到了线索(或推动故事情节发展)的作用,柳应寒的人生起伏变化皆源于雪画。
(2分)①柳应寒得到白如雪的帮助提高了自己的雪画画艺和名气,也因此得到钦差大臣的提携,走上了仕途。
(3分)②柳应寒想要借献画给皇上谋求仕途进阶,却因忘恩负义拘押白如雪令自己雪画的雪意全失气氛大变,从而自毁前程。
(3分,总说一句,然后分条作答,一条回答成也萧何,一条回答败也萧何)胡忠伟《陈忠实:乡居得静五谷养人》陈忠实话少,不会客套,他说话几乎不用形容词,偶尔一两句玩笑话,会逗乐在场所有人。
别人拿他开玩笑时,他那张沟壑纵横的脸上,会现出憨厚的一笑。
他生活简单、沉静,一门心思都扑在了创作上;他语言简朴,却总能一语中的。
对人生的感悟,他可以用最简单直观的语言来描述:“馍蒸到一半,最害怕啥?最害怕揭锅盖。
因为锅盖一揭,气就放了,所以,馍就生了。
”1942年,陈忠实出生在陕西西安灞桥西蒋村。
高中毕业之前,陈忠实也谨慎地为自己谋划着未来,他的打算是:上上策是上大学深造,其次是当兵,再次是回乡村。
遗憾的是当年大学招生名额锐减,他落榜了,军营也对他关了门。
于是他便只得归去,时在1962年。
陈忠实感到了命运对自己的捉弄。
完完全全当一个农民,陈忠实显然难以接受。
好在他对文学怀有强烈的兴趣。
缘于此,陈忠实变得沉静起来。
水深了才能沉静,而且沉静之中也许还潜藏着波澜大惊。
于是,在乡村当教师、当公社干部之余,他把自己埋进了文学创作之中。
1965年初《西安日报》发表了他的散文处女作。
1973年陈忠实发表第一部短篇小说,以后就每年一部。
陈忠实大水深藏,一旦地裂土开,才见其汪与洌。
1992年接到人民文学出版社高贤均的信,得知长篇小说《白鹿原》即将出版,并有高度之议,他流泪了。
后来,这部小说果然获得了茅盾文学奖,版本数种,行世百万册之余,为其它众多艺术形式所使用,计有广播、绘画、泥塑、秦腔、话剧、舞剧等,翻译为日本语、韩国语、越南语。
这正是他沉静写作的开花结果。
《白鹿原》获奖后,陈忠实及时回到了乡下,他避开了热闹和喧哗,在沉静中积蓄着创作的力量,“我现在又回到原下祖居的老屋了。
老屋是一种心理蕴藏——新房子在老房子原来的基础上盖成的,也是一种心理因素吧……获得的是宁静。
”在一篇散文中陈忠实这样自陈心迹。
这是他的生活,也是他的一种心理状态。
宁静,从容,甚至还有一些悠闲。
尽管现在陈忠实已达到“小康”,但他仍保持着先前粗茶淡饭的生活习惯和节俭美德,他常说:“粗茶淡饭、五谷杂粮最养人,衣着朴实最惬意。
”陈忠实习惯白天写作,晚上休息。
他尊重身体的生物钟,起居有常。
写作时,当顺畅地写到一定字数的时候,陈忠实便奖励自己去轻松娱乐一下,要么听秦腔,要么找知己聊天,要么找人“杀”一盘象棋。
2000年腊月,陈忠实及一批文艺家应邀去外县采风。
晚上休息时,主人问明日何时起来,陈忠实随口说:“睡觉睡到自然醒吧。
”第二天,主人求他写字,陈忠实写了这句话,但他没有给主人,也没有依主人的要求写得很大挂在宾馆大堂,而是写了小小一幅,并主张挂在房间里。
有一年“五四”青年节,陈忠实应邀给西安的一些青年谈创作,有读者问他近年为什么没有写小说,他说:“没有写是因为没有感觉,没有关于小说的感觉。
艺术上没有新的发现,干脆不要写。
”此次谈话不久,他写了《日子》等小说,引起很大反响。
《日子》写的是底层农民的“日子”,有底层农民生活的悲辛以及对社会的批判;《作家和他的弟弟》写一个作家的农民兄弟的狡猾与愚蠢,可笑与可哀,触及灵魂,滋味复杂。
这些小说都写得简洁、含蓄而精到,作家与他笔下的人物和生活是贴近的,而他的目光又是悠远的,有入乎其内的深刻,更有出乎其外的透视与开阔。
我想,这与陈忠实近年一直住在乡下而带来的宁静的心态大有关系吧。
宁静,才能产生从容和悠远。
4、“乡居得静,五谷养人”,这两方面与陈忠实创作成功有关,请任选一个方面结合文本并联系自己熟悉的文学作品简要分析。
(探究题,8分)(解析:与上一题同卷,说明命题人很用心。
也要先理解题意,实际上是理解这篇传记的标题。
什么是乡居得静?就是乡居可以远离城市的喧闹,更可以远离各种诱惑。
什么是五谷养人?五谷不仅代表乡村生活,更是指作家创作的现实生活源头,文学来源于现实生活,这个现实生活,就是五谷。
