大学物理 第5章习题解答
《大学物理》课后解答题 第五章静电场

第五章 真空中的静电场一、思考讨论题1、电场强度与电势有什么关系?试回答下列问题,并举例说明: (1)场强为零的地方,电势是否一定为零? (2)电势高的地方,场强是否一定大? (3)电势相等处,场强是否一定相等?(4)已知某一点的电势,可否求出该点的场强?反之如何? 解:(1)不一定。
比如两同种点电荷连线中点,场强为零,电势不为零。
(2)不一定。
匀强电场,场强处处相等,而电势不等。
(3)不一定。
点电荷产生的电场线中,电势相等的地方场强方向不一样。
(4)都不可以求。
2、已知某一高斯面所包围的空间内0=∑q ,能否说明穿过高斯面上每一部分的电通量都是0?能否说明高斯面上的场强处处为0?解:由高斯定理∑⎰=⋅=q S d E S1εψ ,0=∑q 仅指通过高斯面的电通量为零,并非场强一定在高斯面处处为零(高斯面外的电荷也在高斯面上各点产生场强)。
3、已知某高斯面上处处E =0,可否肯定高斯面内0=∑q ,可否肯定高斯面处处无电荷?解:可以肯定。
高斯面上处处E =0,0=⋅⎰S d E S,由高斯定理必有0=∑q 。
4、如图1.1所示,真空中有A 、B 两均匀带电平板相互平行并靠近放置,间距为d (d 很小),面积均为S ,带电分别为+Q 和-Q 。
关于两板间的相互作用力,有人说,根据库仑定律应有:2024dQ f πε=; 又有人说,根据f QE =,应有:SQ f 02ε=。
他们说得对吗?你认为f 应等于多少?解:(1)2024dQ f πε=是错误的,因为库仑定律只适用于点电荷,两个带电平板不能直接用库仑定律计算。
(2)SQ f 02ε=也错误。
因为用sqE 0ε=计算的场强是两带电平板产生的合场强,而Eq F =中的场强是一个带电板的电荷量乘以另一个所产生的场强,而不是合场强。
电荷与图1.1自身产生的场强作用力恒为零。
正确答案是:Sq q S qEdq F 02022εε=⋅==⎰ 5、在无限大带电平面和无限长带电直线的电场中,确定各点电荷时,可否选无穷远处为0势点?为什么?解:不能。
大学物理 第5章 练习答案

第五章 气体动理论练 习 一一. 选择题1. 一个容器内贮有1摩尔氢气和1摩尔氦气,若两种气体各自对器壁产生的压强分别为1p 和2p ,则两者的大小关系是( C )(A ) 21p p >; (B ) 21p p <; (C ) 21p p =; (D ) 不确定的。
2. 一定量的理想气体贮于某一容器中,温度为T ,气体分子的质量为m. 根据理想气体的分子模型和统计假设,分子速度在x 方向的分量平方的平均值为( D )(A ) 2x v =m kT 3; (B ) 2x v = (1/3)m kT 3 ; (C ) 2x v = 3kT /m ; (D ) 2x v = kT/m 。
3. 设M 为气体的质量,m 为气体分子质量,N 为气体分子总数目,n 为气体分子数密度,0N 为阿伏伽德罗常数,下列各式中哪一式表示气体分子的平均平动动能( A )(A )pV M m ⋅23; (B ) pV M Mmol⋅23; (C ) npV 23; (D ) 023N pV M M mol ⋅。
4. 关于温度的意义,有下列几种说法,错误的是( D ) (A ) 气体的温度是分子平动动能的量度;(B ) 气体的温度是大量气体分子热运动的集体表现,具有统计意义; (C ) 温度的高低反映物质内部分子运动剧烈程度的不同; (D ) 从微观上看,气体的温度表示每个气体分子的冷热程度。
二.填空题1. 在容积为10-2m 3的容器中,装有质量100g 的气体,若气体分子的方均根速率为200m/s ,则气体的压强为ap 51034⨯。
2. 如图1所示,两个容器容积相等,分别储有相同质量的N 2和O 2气体,它们用光滑细管相连通,管子中置一小滴水银,两边的温度差为30K ,当水银滴在正中不动时,N 2和O 2的温度为2N T = 210k ,2O T = 240k 。
( N 2的摩尔质量为28×10-3kg/mol,O 2的摩尔质量为32×10-3kg/mol)3.分子物理学是研究大量微观粒子的集体运动的统计表现 的学科, 它应用的方法是 统计学 方法。
大学物理课后习题答案第五章

大学物理课后习题答案第五章-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第五章 机械波5.1 已知一波的波动方程为y = 5×10-2sin(10πt – 0.6x ) (m). (1)求波长、频率、波速及传播方向;(2)说明x = 0时波动方程的意义,并作图表示.[解答](1)与标准波动方程2cos()xy A t πωλ=-比较得:2π/λ = 0.6,因此波长为:λ = 10.47(m);圆频率为:ω = 10π,频率为:v =ω/2π = 5(Hz);波速为:u = λ/T = λv = 52.36(m·s -1). 且传播方向为x 轴正方向.(2)当x = 0时波动方程就成为该处质点的振动方程: y = 5×10-2sin10πt = 5×10-2cos(10πt – π/2), 振动曲线如图.5.2 一平面简谐波在媒质中以速度为u = 0.2m·s -1沿x 轴正向传播,已知波线上A 点(x A = 0.05m )的振动方程为0.03cos(4)2A y t ππ=-(m).试求:(1)简谐波的波动方程;(2)x = -0.05m 处质点P 处的振动方程.[解答](1)简谐波的波动方程为:cos[()]Ax x y A t uωϕ-=-+;即 0.050.03cos[4()]0.22x y t ππ-=--= 0.03cos[4π(t – 5x ) + π/2].(2)在x = -0.05m 处质点P 点的振动方程为:y = 0.03cos[4πt + π + π/2] = 0.03cos(4πt - π/2).5.3 已知平面波波源的振动表达式为20 6.010sin 2y t π-=⨯(m).求距波源5m处质点的振动方程和该质点与波源的位相差.设波速为2m·s -1.[解答]振动方程为:26.010sin ()2xy t u π-=⨯- 50.06sin()24t ππ=-,位相差为 Δφ = 5π/4(rad).5.4 有一沿x 轴正向传播的平面波,其波速为u = 1m·s -1,波长λ = 0.04m ,振幅A = 0.03m .若以坐标原点恰在平衡位置而向负方向运动时作为开始时刻,试求:(1)此平面波的波动方程;(2)与波源相距x = 0.01m 处质点的振动方程,该点初相是多少?[解答](1)设原点的振动方程为:y 0 = A cos(ωt + φ),其中A = 0.03m . 由于u = λ/T ,所以质点振动的周期为:T = λ/u = 0.04(s),圆频率为:ω = 2π/T = 50π.当t = 0时,y 0 = 0,因此cos φ = 0;由于质点速度小于零,所以φ = π/2.原点的振动方程为:y 0 = 0.03cos(50πt + π/2), 平面波的波动方程为:0.03cos[50()]2x y t u ππ=-+= 0.03cos[50π(t – x ) + π/2).(2)与波源相距x = 0.01m 处质点的振动方程为:y = 0.03cos50πt . 该点初相φ = 0.5.5 一列简谐波沿x 轴正向传播,在t 1 = 0s ,t 2 = 0.25s 时刻的波形如图所示.试求:(1)P 点的振动表达式; (2)波动方程; (3)画出O 点的振动曲线. [解答](1)设P 点的振动方程为 y P = A cos(ωt + φ),其中A = 0.2m .在Δt = 0.25s 内,波向右传播了Δx = 0.45/3 = 0.15(m), 所以波速为u = Δx/Δt = 0.6(m·s -1).波长为:λ = 4Δx = 0.6(m), 周期为:T = λ/u = 1(s), 圆频率为:ω = 2π/T = 2π.当t = 0时,y P = 0,因此cos φ = 0;由于波沿x 轴正向传播,所以P 点在此时向上运动,速度大于零,所以φ = -π/2.P 点的振动表达式为:y P = 0.2cos(2πt - π/2). (2)P 点的位置是x P = 0.3m ,所以波动方程为0.2cos[2()]2P x x y t u ππ-=--100.2cos(2)32t x πππ=-+. (3)在x = 0处的振动方程为y 0 = 0.2cos(2πt + π/2),曲线如图所示.5.6 如图所示为一列沿x 负向传播的平面谐波在t = T /4时的波形图,振幅A 、波长λ以及周期T 均已知.(1)写出该波的波动方程; (2)画出x = λ/2处质点的振动曲线; (3)图中波线上a 和b 两点的位相差φa – φb 为多少?[解答](1)设此波的波动方程为:图5.5cos[2()]t xy A T πϕλ=++,当t = T /4时的波形方程为:cos(2)2x y A ππϕλ=++sin(2)xA πϕλ=-+.在x = 0处y = 0,因此得sin φ = 0, 解得φ = 0或π.而在x = λ/2处y = -A ,所以φ = 0.因此波动方程为:cos 2()t xy A T πλ=+.(2)在x = λ/2处质点的振动方程为:cos(2)cos 2t t y A A T Tπππ=+=-, 曲线如图所示.(3)x a = λ/4处的质点的振动方程为 cos(2)2a t y A T ππ=+; x b = λ处的质点的振动方程为 cos(22)b t y A Tππ=+. 波线上a 和b 两点的位相差φa – φb = -3π/2.5.7 已知波的波动方程为y = A cosπ(4t – 2x )(SI ).(1)写出t = 4.2s 时各波峰位置的坐标表示式,并计算此时离原点最近的波峰的位置,该波峰何时通过原点( 2)画出t = 4.2s 时的波形曲线. [解答]波的波动方程可化为:y = A cos2π(2t – x ), 与标准方程cos[2()]t xy A T πϕλ=-+比较, 可知:周期为T = 0.5s ,波长λ = 1m .波速为u = λ/T = 2m·s -1.(1)当t = 4.2s 时的波形方程为y = A cos(2πx – 16.8π)= A cos(2πx – 0.8π). 令y = A ,则cos(2πx – 0.8π) = 1,因此 2πx – 0.8π = 2k π,(k = 0, ±1, ±2,…),各波峰的位置为x = k + 0.4,(k = 0, ±1, ±2,…).当k = 0时的波峰离原点最近,最近为:x = 0.4(m).通过原点时经过的时间为:Δt = Δx/u = (0 – x )/u = -0.2(s), 即:该波峰0.2s 之前通过了原点.(2)t = 0时刻的波形曲线如实线所示.经过t = 4s 时,也就是经过8个周期,波形曲线是重合的;再经Δt = 0.2s ,波形向右移动Δx = u Δt = 0.4m ,因此t = 4.2s 时的波形曲线如虚线所示.[注意]各波峰的位置也可以由cos(2πx – 16.8π) = 1解得,结果为x = k + 8.4,(k = 0, ±1, ±2,…),取同一整数k 值,波峰的位置不同.当k = -8时的波峰离原点最近,最近为x = 0.4m .5.8 一简谐波沿x 轴正向传播,波长λ = 4m ,周期T = 4s ,已知x = 0处的质点的振动曲线如图所示.(1)写出时x = 0处质点的振动方程; (2)写出波的表达式;(3)画出t = 1s 时刻的波形曲线.[解答]波速为u = λ/T = 1(m·s -1). (1)设x = 0处的质点的振动方程为y = A cos(ωt + φ),其中A = 1m ,ω = 2π/T = π/2.当t = 0时,y = 0.5,因此cos φ = 0.5,φ = ±π/3.在0时刻的曲线上作一切线,可知该时刻的速度小于零,因此φ = π/3.振动方程为:y = cos(πt /2 + π/3). (2)波的表达式为:cos[2()]t xy A T πϕλ=-+ cos[()]23t x ππ=-+. (3)t = 1s 时刻的波形方程为 5cos()26y x ππ=-,波形曲线如图所示.5.9 在波的传播路程上有A 和B 两点,都做简谐振动,B 点的位相比A 点落后π/6,已知A 和B 之间的距离为2.0cm ,振动周期为2.0s .求波速u 和波长λ.[解答] 设波动方程为:cos[2()]t xy A T πϕλ=-+,那么A 和B 两点的振动方程分别为:cos[2()]A A xt y A T πϕλ=-+,cos[2()]B B xt y A T πϕλ=-+.两点之间的位相差为:2(2)6B A x x πππλλ---=-,由于x B – x A = 0.02m ,所以波长为:λ = 0.24(m).波速为:u = λ/T = 0.12(m·s -1).5.10 一平面波在介质中以速度u = 20m·s -1沿x 轴负方向传播.已知在传播路径上的某点A 的振动方程为y = 3cos4πt .(1)如以A 点为坐标原点,写出波动方程; (2)如以距A 点5m 处的B 点为坐标原点,写出波动方程;(3)写出传播方向上B ,C ,D 点的振动方程.[解答](1)以A 点为坐标原点,波动方程为3cos 4()3cos(4)5x xy t t u πππ=+=+.(2)以B 点为坐标原点,波动方程为3cos 4()Ax x y t u π-=+3cos(4)5x t πππ=+-.(3)以A 点为坐标原点,则x B = -5m 、x C = -13m 、x D = 9m ,各点的振动方程为3cos 4()3cos(4)B B xy t t u πππ=+=-,33cos 4()3cos(4)5C C x y t t u πππ=+=-,93cos 4()3cos(4)5D D x y t t u πππ=+=+.[注意]以B 点为坐标原点,求出各点坐标,也能求出各点的振动方程.5.11 一弹性波在媒质中传播的速度u = 1×103m·s -1,振幅A = 1.0×10-4m ,频率ν= 103Hz .若该媒质的密度为800kg·m -3,求:(1)该波的平均能流密度;(2)1分钟内垂直通过面积S = 4×10-4m 2的总能量. [解答](1)质点的圆频率为:ω = 2πv = 6.283×103(rad·s -1),波的平均能量密度为:2212w A ρω== 158(J·m -3),平均能流密度为:I wu == 1.58×105(W·m -2).(2)1分钟内垂直通过面积S = 4×10-4m 2的总能量为:E = ItS = 3.79×103(J).5.12 一平面简谐声波在空气中传播,波速u = 340m·s -1,频率为500Hz .到达人耳时,振幅A = 1×10-4cm ,试求人耳接收到声波的平均能量密度和声强此时声强相当于多少分贝已知空气密度ρ = 1.29kg·m -3.[解答]质点的圆频率为:ω = 2πv = 3.142×103(rad·s -1),声波的平均能量密度为:2212w A ρω== 6.37×10-6(J·m -3),平均能流密度为:I wu == 2.16×10-3(W·m -2), 标准声强为:I 0 = 1×10-12(W·m -2),图5.10此声强的分贝数为:010lgIL I == 93.4(dB).5.13 设空气中声速为330m·s -1.一列火车以30m·s -1的速度行驶,机车上汽笛的频率为600Hz .一静止的观察者在机车的正前方和机车驶过其身后所听到的频率分别是多少?如果观察者以速度10m·s -1与这列火车相向运动,在上述两个位置,他听到的声音频率分别是多少?[解答]取声速的方向为正,多谱勒频率公式可统一表示为BB S Su u u u νν-=-,其中v S 表示声源的频率,u 表示声速,u B 表示观察者的速度,u S 表示声源的速度,v B 表示观察者接收的频率.(1)当观察者静止时,u B = 0,火车驶来时其速度方向与声速方向相同,u S = 30m·s -1,观察者听到的频率为33060033030B S S u u u νν==--= 660(Hz).火车驶去时其速度方向与声速方向相反,u S = -30m·s -1,观察者听到的频率为33060033030B S S u u u νν==-+= 550(Hz).(2)当观察者与火车靠近时,观察者的速度方向与声速相反,u B = -10m·s -1;火车速度方向与声速方向相同,u S = 30m·s -1,观察者听到的频率为3301060033030B B S S u u u u νν-+==--= 680(Hz).当观察者与火车远离时,观察者的速度方向与声速相同,u B = 10m·s -1;火车速度方向与声速方向相反,u S = -30m·s -1,观察者听到的频率为3301060033030B B S S u u u u νν--==-+= 533(Hz).[注意]这类题目涉及声速、声源的速度和观察者的速度,规定方向之后将公式统一起来,很容易判别速度方向,给计算带来了方便.5.14.一声源的频率为1080Hz ,相对地面以30m·s -1速率向右运动.在其右方有一反射面相对地面以65m·s -1的速率向左运动.设空气中声速为331m·s -1.求:(1)声源在空气中发出的声音的波长; (2)反射回的声音的频率和波长.[解答](1)声音在声源垂直方向的波长为:λ0 = uT 0 = u /ν0 = 331/1080 = 0.306(m);在声源前方的波长为:λ1 = λ0 - u s T 0 = uT 0 - u s T 0 = (u - u s )/ν0 = (331-30)/1080 = 0.2787(m);在声源后方的波长为:λ2 = λ0 + u s T 0 = uT 0 + u s T 0 = (u + u s )/ν0= (331+30)/1080 = 0.3343(m).(2)反射面接收到的频率为1033165108033130B S u u u u νν++==⨯--= 1421(Hz). 将反射面作为波源,其频率为ν1,反射声音的频率为`11331142133165B u u u νν==⨯--= 1768(Hz).反射声音的波长为`1111331651421B B uu u u λννν--=-===0.1872(m).或者 `1`13311768u λν=== 0.1872(m).[注意]如果用下式计算波长`111650.27871768B u λλν=-=-=0.2330(m),结果就是错误的.当反射面不动时,作为波源发出的波长为u /ν1 = 0.2330m ,而不是入射的波长λ1.5.15 S 1与S 2为两相干波源,相距1/4个波长,S 1比S 2的位相超前π/2.问S 1、S 2连线上在S 1外侧各点的合成波的振幅如何?在S 2外侧各点的振幅如何?[解答]如图所示,设S 1在其左侧产生的波的波动方程为 1cos[2()]t xy A T πϕλ=++, 那么S 2在S 1左侧产生的波的波动方程为2/4cos[2()]2t x y A T λππϕλ-=++-cos[2()]t xA T πϕπλ=++-,由于两波源在任意点x 产生振动反相,所以合振幅为零.S 1在S 2右侧产生的波的波动方程为1cos[2()]t xy A T πϕλ=-+,那么S 2在其右侧产生的波的波动方程为2/4cos[2()]2t x y A T λππϕλ-=-+-cos[2()]t xA T πϕλ=-+,由于两波源在任意点x 产生振动同相,所以合振幅为单一振动的两倍.5.16 两相干波源S 1与S 2相距5m ,其振幅相等,频率都是100Hz ,位相差为π;波在媒质中的传播速度为400m·s -1,试以S 1S 2连线为坐标轴x ,以S 1S 2连线中点为原点,求S 1S 2间因干涉而静止的各点的坐标.[解答]如图所示,设S 1在其右侧产生的波的波动方程为1 2121/2cos[2()]x l y A t u πνϕ+=-+ 5cos(2)24A t x πππνϕ=-+-,那么S 2在其左侧产生的波的波动方程为2/2cos[2()]x l y A t u πνϕπ-=+++cos(2)24A t x πππνϕ=++-.两个振动的相差为Δφ = πx + π,当Δφ = (2k + 1)π时,质点由于两波干涉而静止,静止点为x = 2k , k 为整数,但必须使x 的值在-l /2到l /2之间,即-2.5到2.5之间.当k = -1、0和1时,可得静止点的坐标为:x = -2、0和2(m).5.17 设入射波的表达式为1cos 2()t xy A T πλ=+,在x = 0处发生反射,反射点为一自由端,求:(1)反射波的表达式; (2)合成驻波的表达式.[解答](1)由于反射点为自由端,所以没有半波损失,反射波的波动方程为2cos 2()t xy A T πλ=-.(2)合成波为y = y 1 + y 2,将三角函数展开得222cos cos y A x t Tππλ=,这是驻波的方程.5.18 两波在一很长的弦线上传播,设其表达式为:1 6.0cos (0.028.0)2y x t π=-,2 6.0cos(0.028.0)2y x t π=+,用厘米、克、秒(cm,g,s )制单位,求:(1)各波的频率,波长、波速;(2)节点的位置;(3)在哪些位置上,振幅最大?[解答](1)两波可表示为:1 6.0cos 2()0.5200t x y π=-,2 6.0cos 2()0.5200t xy π=+,可知它们的周期都为:T = 0.5(s),频率为:v = 1/T = 2(Hz);波长为:λ = 200(cm);波速为:u = λ/T = 400(cm·s -1).(2)位相差Δφ = πx /50,当Δφ = (2k + 1)π时,可得节点的位置x = 50(2k + 1)(cm),(k = 0,1,2,…).(3)当Δφ = 2k π时,可得波腹的位置x = 100k (cm),(k = 0,1,2,…).。
第5章 刚体的定轴转动 习题解答

由此可算出自施加制动闸开始到飞轮停止转动的时间为
0 900 2 3 7.06 s 60 40
这段时间内飞轮的角位移为
1 900 2 1 40 0t t 2 7.06 7.062 53.1 2 rad 2 60 2 3 可知在这段时间里,飞轮转了 53.1 转。 2 (2) 0 900 rad s 1 ,要求飞轮转速在 t 2 s 内减少一半,可知 60
M M f J 1
t1
。移去力矩 M 后,根据转动定律,有
M f J 2
2
联立解得此转轮的转动惯量
0 t2
J
M 20 17.36 kg m 2 1 1 1 100 2 1 60 10 100 t1 t2
由以上诸式求得角加速度
(2)
Rm1 rm2 g I m1 R 2 m2 r 2 0.2 2 0.1 2
1 1 10 0.202 4 0.102 2 0.202 2 0.102 2 2
9.8 6.13 rad s 2
T2 m2 r m2 g 2 0.10 6.13 2 9.8 20.8N T1 m1 g m1 R 2 9.8 2 0.2. 6.13 17.1N v 2a1h 2 Rh 2 6.13 0.2 2 2.21 m s 1
A
B
题 5-2 图 解: (1)先作闸杆和飞轮的受力分析图(如图).图中 N 、 N 是正压力,Fr 、Fr 是摩擦力,Fx 和 Fy 是杆在 A 点转轴处所受支承力, P 是轮的重力, R 是轮在 O 轴处所受支承力。 杆处于静止状态,所以对 A 点的合力矩应为零,设闸瓦厚度不计,则有
大学物理第五章机械振动习题解答和分析

5-1 有一弹簧振子,振幅m A 2100.2-⨯=,周期s T 0.1=,初相.4/3πϕ=试写出它的振动位移、速度和加速度方程。
分析 根据振动的标准形式得出振动方程,通过求导即可求解速度和加速度方程。
解:振动方程为:]2cos[]cos[ϕπϕω+=+=t TA t A x 代入有关数据得:30.02cos[2]()4x t SI ππ=+ 振子的速度和加速度分别是:3/0.04sin[2]()4v dx dt t SI πππ==-+ 2223/0.08cos[2]()4a d x dt t SI πππ==-+5-2若简谐振动方程为m t x ]4/20cos[1.0ππ+=,求: (1)振幅、频率、角频率、周期和初相; (2)t=2s 时的位移、速度和加速度.分析 通过与简谐振动标准方程对比,得出特征参量。
解:(1)可用比较法求解.根据]4/20cos[1.0]cos[ππϕω+=+=t t A x 得:振幅0.1A m =,角频率20/rad s ωπ=,频率1/210s νωπ-==, 周期1/0.1T s ν==,/4rad ϕπ=(2)2t s =时,振动相位为:20/4(40/4)t rad ϕππππ=+=+ 由cos x A ϕ=,sin A νωϕ=-,22cos a A x ωϕω=-=-得 20.0707, 4.44/,279/x m m s a m s ν==-=-5-3质量为kg 2的质点,按方程))](6/(5sin[2.0SI t x π-=沿着x 轴振动.求: (1)t=0时,作用于质点的力的大小;(2)作用于质点的力的最大值和此时质点的位置.分析 根据振动的动力学特征和已知的简谐振动方程求解,位移最大时受力最大。
解:(1)跟据x m ma f 2ω-==,)]6/(5sin[2.0π-=t x 将0=t 代入上式中,得: 5.0f N =(2)由x m f 2ω-=可知,当0.2x A m =-=-时,质点受力最大,为10.0f N =5-4为了测得一物体的质量m ,将其挂到一弹簧上并让其自由振动,测得振动频率Hz 0.11=ν;而当将另一已知质量为'm 的物体单独挂到该弹簧上时,测得频率为Hz 0.22=ν.设振动均在弹簧的弹性限度内进行,求被测物体的质量.分析 根据简谐振动频率公式比较即可。
大学物理课后答案第5章

第五章 热力学基础5-1 在水面下50.0 m 深的湖底处(温度为4.0℃),有一个体积为1.0×10-5 m 3的空气泡升到湖面上来,若湖面的温度为17.0℃,求气泡到达湖面的体积。
(大气压P 0 = 1.013×105 Pa ) 分析:将气泡看成是一定量的理想气体,它位于湖底和上升至湖面代表两个不同的平衡状态。
利用理想气体物态方程即可求解本题。
位于湖底时,气泡内的压强可用公式gh p p ρ+=0求出,其中ρ为水的密度(常取ρ = 1.0⨯103 kg·m -3)。
解:设气泡在湖底和湖面的状态参量分别为(p 1,V 1,T 1)和(p 2,V 2,T 2)。
由分析知湖底处压强为ghp gh p p ρρ+=+=021。
利用理想气体的物态方程可得空气泡到达湖面的体积为()3510120121212m 1011.6-⨯=+==T p V T gh p T p V T p V ρ5-2 氧气瓶的容积为3.2×10-2 m 3,其中氧气的压强为1.30×107 Pa ,氧气厂规定压强降到1.00×106 Pa 时,就应重新充气,以免经常洗瓶。
某小型吹玻璃车间,平均每天用去0.40 m 3 压强为1.01×105 Pa 的氧气,问一瓶氧气能用多少天?(设使用过程中温度不变) 分析:由于使用条件的限制,瓶中氧气不可能完全被使用。
从氧气质量的角度来分析。
利用理想气体物态方程pV = mRT /M 可以分别计算出每天使用氧气的质量m 3和可供使用的氧气总质量(即原瓶中氧气的总质量m 1和需充气时瓶中剩余氧气的质量m 2之差),从而可求得使用天数321/)(m m m n -=。
解:根据分析有RT V Mp m RT V Mp m RT V Mp m 333122111===;;则一瓶氧气可用天数()()5.933121321=-=-=V p V p p m m m n5-3 一抽气机转速ω=400r ּmin -1,抽气机每分钟能抽出气体20升。
第5章 刚体的定轴转动 习题解答

对飞轮,由转动定律,有 式中负号表示摩擦力的力矩方向与角速度 方向相反。
联立解得
以 F 100 N 等代入上式,得
Fr R 2 (l1 l2 ) F J mRl1
5-1
第 5 章 刚体的定轴转动
2 0.40 (0.50 0.75) 40 100 rad s 2 60 0.25 0.50 3 t
由以上诸式求得角加速度
(2)
Rm1 rm2 g I m1 R 2 m2 r 2 0.2 2 0.1 2
1 1 10 0.202 4 0.102 2 0.202 2 0.102 2 2
9.8 6.13 rad s 2
T2 m2 r m2 g 2 0.10 6.13 2 9.8 20.8N T1 m1 g m1 R 2 9.8 2 0.2. 6.13 17.1N v 2a1h 2 Rh 2 6.13 0.2 2 2.21 m s 1
M M f J 1
t1
。移去力矩 M 后,根据转动定律,有
M f J 2
2
联立解得此转轮的转动惯量
0 t2
J
M 20 17.36 kg m 2 1 1 1 100 2 1 60 10 100 t1 t2
v0
6(2 3 3m M l J l 1M (1 2 ) (1 ) 2 ml 2 3m 12 m
(2) 由①式求得相碰时小球受到的冲量为:
I Fdt mv mv mv0
负号说明所受冲量的方向与初速度方向相反。
大学物理基础教程答案第05章习题分析与解答

5-1 若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻尔兹曼常数,R 为摩尔气体常数,则该理想气体的分子数为( )。
(A )PV m (B )PV kT (C )PV RT (D ) PVmT解:由N p nkT kT V ==得,pVN kT=,故选B 5-2 两个体积相同的容器,分别储有氢气和氧气(视为刚性气体),以1E 和2E 分别表示氢气和氧气的内能,若它们的压强相同,则( )。
(A )12E E = (B )12E E > (C )12E E < (D ) 无法确定 解:pV RT ν=,式中ν为摩尔数,由于两种气体的压强和体积相同,则T ν相同。
又刚性双原子气体的内能52RT ν,所以氢气和氧气的内能相等,故选A 5-3 两瓶不同种类的气体,分子平均平动动能相同,但气体分子数密度不同,则下列说法正确的是( )。
(A )温度和压强都相同 (B )温度相同,压强不同 (C )温度和压强都不同(D )温度相同,内能也一定相等解:所有气体分子的平均平动动能均为32kT ,平均平动动能相同则温度相同,又由p nkT =可知,温度相同,分子数密度不同,则压强不同,故选B5-4 两个容器中分别装有氦气和水蒸气,它们的温度相同,则下列各量中相同的量是( )。
(A )分子平均动能 (B )分子平均速率 (C )分子平均平动动能 (D )最概然速率解:分子的平均速率和最概然速率均与温度的平方根成正比,与气体摩尔质量的平方根成反比,两种气体温度相同,摩尔质量不同的气体,所以B 和D 不正确。
分子的平均动能2i kT ε=,两种气体温度相同,自由度不同,平均动能则不同,故A 也不正确。
而所有分子的平均平动动能均为k 32kT ε=,只要温度相同,平均平动动能就相同,如选C 5-5 理想气体的压强公式 ,从气体动理论的观点看,气体对器壁所作用的压强是大量气体分子对器壁不断碰撞的结果。
大学物理第五章题解_-_复件

第五章 相对论基础5-1.设某事件在S 系中发生的地点为180km x =,10km y =,1km z =,发生时刻为42.010s t -=⨯.S '系以0.8v c =沿公共x 、x '轴正向运动,两惯性系的原点在0t t '==时重合.求该事件在S '系中的时空坐标x '、y '、z '、t '各为多少?解由题意知10.6γ===,所以 4180082010()220(km)06.c .x'x vt .γ--⨯⨯=-==10km y'y == ,1km z'z == 4242201008180()46710(s)06vx ..c c t't .c .γ--⨯-⨯=-==-⨯5-2.一个事件于0t =时刻发生在S 系原点,另一个事件于4s t =发生在S 系的51s x c =⨯、0y =、0z =处.若S '系沿公共x 、x '轴正向匀速运动,则以上两事件在S '系内同时发生,求S '系相对S 系的速率.解 设两事件在S 系和S '系中的时空坐标分别为11()x ,t ,11()x ,t '',22()x ,t ,22()x ,t ''.根据洛仑兹变换 2121212[()()]vt t t t x x c γ''-=--- 由于2151s x x c -=⨯,214t t -=,210t t ''-=,则 22121()()t t v c x x -=-245c c =08.c =5-3.火箭平行于惯性系S 的x 轴飞行,从S 系观测火箭长度为其固有长度的一半,求火箭相对于S 系的速率.解根据动尺收缩公式l l =012l l ==所以0866v .c ==.5-4.在海拔50km 处,由高能宇宙射线产生的π+介子,以0.995c 的速率垂直飞向地面,已知其固有平均寿命82.610s τ-=⨯.问:(1)在地面惯性系中π+介子的平均寿命是多少?它们平均在海拔多少米处衰变?(2)若不是由于相对论效应,它们平均只能飞越多少距离?解 (1)以地面惯性系为S 系,与π+介子相对静止的惯性系为S '系. 在S 系中π+介子的平均寿命为8702610(s)r .ττ--===⨯π+介子在其平均寿命时间内运动的距离为0995776(m)s .c .τ=⨯=,所以π+介子衰变的平均海拔为()500007761499224m h'h s ..=-=-=(2)若不是相对论效应,π+介子平均飞越的距离为()809952610776m s .c ..-=⨯⨯=5-5.惯性系S 和S '有公共的x 和x '轴,在S 系中有两个事件同时发生在x 轴上相距31.010m ⨯的两处,在S '系中两事件相距32.010m ⨯.试问由S '系测得两事件的时间间隔为多少?解 设两事件在S 系和S '系中的时空坐标分别为11()x ,t ,11()x ,t '',22()x ,t ,22()x ,t ''.根据洛仑兹变换212121[()()]x x x x v t t γ''-=---33320101010110..γ⨯=⨯⨯=⨯ 所以2γ=,2v c =.由洛仑兹变换,由S '系测得两事件的时间间隔为2121212[()()]vt t t t x x c γ''-=--- ()36212101025810(s)2v x x ..c c γ-=--=-⨯⨯=-⨯5-6.火箭以0.6c 的速率相对地球运动,火箭中的观察者测得火箭长度为60m ,从火箭尾部向火箭前端的靶发射一颗相对火箭以0.8c 的速率运动的高速子弹.求:(1)火箭中的观察者测得的子弹击中靶所用的时间;(2)地球上的观察者测得的子弹击中靶所用的时间.解法一 以地球为S 系,以火箭为S '系,x 和x '轴沿火箭运动方向,发射子弹为事件1,子弹击中靶为事件2.设两事件在S 系和S '系中的时空坐标分别为11()x ,t ,11()x ,t '',22()x ,t ,22()x ,t ''.根据洛仑兹变换 2121212[()()]vt t t t x x cγ''''-=-+- 由于2160x x ''-=,06v .c =, 1.25γ==;又可知火箭中的观察者测得的子弹击中靶所用的时间72160251008t t ..c-''-==⨯ 可知地球上的观察者测得的子弹击中靶所用的时间7721206(251060) 1.254610(s).c t t ..c---=⨯+⨯⨯=⨯ 解法二 22080614061481108x x xu v .c .c .u c v .c .u .c c c'++==='++⨯在S 系中观测到子弹相对于火箭的速率14060346148x .w u v c .c .c .=-=-= 在S 系中观测到火箭的长度6048(m)l l ===所以地球上的观察者测得的子弹击中靶所用的时间7484610(s)0346l t .w .c-∆===⨯5-7.从地球上观测一星系以速率0.3c 向某一方向退行,另一星系以同样速率向相反方向退行.求从某一星系观测另一星系的退行速率.解 以地球为S 系,星系A 为S '系,x 和x '轴沿星系A 运动方向,则在相对论速度变换公式21x x x u vu vu c-'=- 中03v .c =、03x u .c =-,所以从星系A (S '系)观测星系B 的运动速率20303055103(03)x.c .cu .c .c .c c --'==--⨯- 所以从某一星系观测另一星系的退行速率为055.c .5-8.设有两把互相平行的尺,在各自相对静止的惯性系中的长度均为0l .它们以相同的速率v 相对某一惯性系运动,两尺均与运动方向平行,但彼此运动方向相反.求在与其中一尺固连的惯性系内测量另一尺的长度.解 以某一惯性系为S 系,其中一尺为S '系,x 和x '轴沿S '系运动方向,则在相对论速度变换公式21x x x u vu vu c -'=-中x u v =-,所以在S '系内测量另一尺的运动速率为2222221x v v vc u v c c v---'==++ 根据动尺收缩公式,在S '系内测量另一尺的长度为22022c v l l l l c v-===+5-9.静止μ子的平均寿命为62.210s -⨯,实验室中测得运动μ子平均寿命为66.610s -⨯.求:(1)μ子在实验室中的速率;(2)μ子的质量;(3)μ子的动能和动量各为多少?(μ子静质量为e 207m ,31e 9.110kg m -=⨯为电子静质量.)解(1)根据动钟变慢公式t τγ∆=∆⨯,由62.210s τ-∆=⨯和66.610s t -∆=⨯可知3γ=所以μ子在实验室中的速率v =09428.c =.(2)根据质速关系,μ子的质量为e 621m m ===(3)μ子的动能和动量为220k E mc m c =-222e e e 621207414m c m c m c =-=3182114149110(3010)33910(J)...-=⨯⨯⨯⨯=⨯212MeV =e 6210943p mv m .c ==⨯318196219110094331016010(kg m s)...--=⨯⨯⨯⨯⨯=⨯⋅5-10.如果将100kg 铜的温度升高100K ,它的质量会增加多少?铜的比热容390J (kg K)c '=⋅.解 100k g铜的温度升高100K 的过程中吸收的热量为 Q c'm t =∆63901001003910(J).=⨯⨯=⨯质量的增加为 611228239104310(kg)(3010)E Q .m .c c .-∆⨯∆====⨯⨯5-11.氘(2H )和氚(3H )可发生聚变反应,生成氦(He )和中子(n ).若反应前氘和氚的静质量总和为503g ,反应后氦和中子的静质量总和为501g ,求该聚变反应中的质量亏损及释放出的能量.解 质量亏损为 5035012(g)M ∆=-=释放出的能量为 ()2E M c∆=∆38214210(310)1810(J ).-=⨯⨯⨯=⨯5-12.有一立方体,各棱的固有长度均为0l ,静质量为0m .现沿其一棱的方向以速率v 运动,求静止观察者测得立方体的体积和密度.解静止观察者测得立方体沿运动方向的棱长为l l =长仍为0l ,所以静止观察者测得立方体的体积为200V l l l =⋅=静止观察者测得立方体的质量为m =,所以立方体的密度为03220(1)m m V l v c ρ===-5-13.要求误差不超过5%,质量用0m 或m ,动能可以表示成20112m u 或2212mu 时的最大速率1u 或2u 大约是多少?解222k 001)E mc m c m c =-=-224101013()28u m u m c c ≈+表示成2k 0112E m u '=,误差401k k 2k01385%12m u E E c E m u '-=≤',即221115u c ≤,所以10258u .c ≤.222200(1)(1k E mc m c mc m m mc =-=-=2242211()28u mu mc c≈+表示成2k 212E mu '=,误差422k k 2k218512mu E E c %E mu '-=≤',即22215u c ≤,所以20447u .c ≤. (第五章题解结束)。
(完整版)大学物理学(课后答案)第5-6章
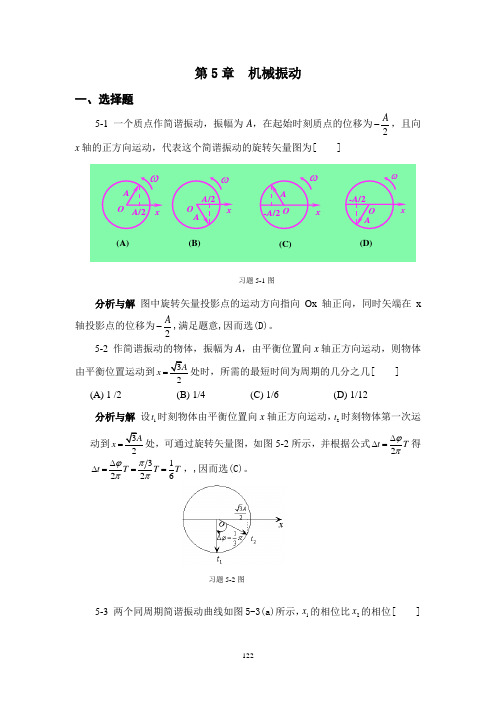
第5章 机械振动一、选择题5-1 一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为2A-,且向x 轴的正方向运动,代表这个简谐振动的旋转矢量图为[ ]分析与解 图中旋转矢量投影点的运动方向指向Ox 轴正向,同时矢端在x 轴投影点的位移为2A-,满足题意,因而选(D)。
5-2 作简谐振动的物体,振幅为A ,由平衡位置向x 轴正方向运动,则物体由平衡位置运动到32Ax =处时,所需的最短时间为周期的几分之几[ ] (A) 1 /2 (B) 1/4 (C) 1/6 (D) 1/12分析与解 设1t 时刻物体由平衡位置向x 轴正方向运动,2t 时刻物体第一次运动到32A x =处,可通过旋转矢量图,如图5-2所示,并根据公式2t T ϕπ∆∆=得31226t T T T ϕπππ∆∆===,,因而选(C)。
5-3 两个同周期简谐振动曲线如图5-3(a)所示,1x 的相位比2x 的相位[ ] O O OO A Axxx(A) (B)(D)(C)A /2-A /2 A /2 -A /2A Aωωωωx习题5-1图习题5-2图(A) 落后2π (B) 超前2π(C) 落后π (D) 超前π分析与解 可通过振动曲线作出相应的旋转矢量图(b ),正确答案为(B )。
5-4 一弹簧振子作简谐振动,总能量为E ,若振幅增加为原来的2倍,振子的质量增加为原来的4倍,则它的总能量为[ ](A) 2E (B) 4E (C) E (D) 16E 分析与解 因为简谐振动的总能量2p k 12E E E kA =+=,因而当振幅增加为原来的2倍时,能量变为原来的4倍,因而答案选(B)。
5-5 两个同振动方向、同频率、振幅均为A 的简谐振动合成后,振幅仍为A ,则这两个简谐振动的相位差为[ ](A) 60 (B) 90 (C) 120 (D) 180分析与解 答案(C )。
由旋转矢量图可知两个简谐振动的相位差为120时,合成后的简谐运动的振幅仍为A 。
大学物理第5章题库(含答案)

大学物理第5章题库(含答案)05章气体动理论一、填空题(一)易(基础题)1、一定质量的气体处于平衡态,则气体各部分的压强相等(填相等或不相等),各部分的温度相等(填相等或不相等)。
2、根据能量按自由度均分原理,设气体分子为刚性分子,分子自由度为i,则当温度为T1时,(1)一个分子的平均能量为(平均总动能)ikT2i2;(2)摩尔理想气体的内能为(3)一个双原子分子的平均转动动能为kTRT;3、对于单原子分子理想气体,①体的内能;②3RT代表的物理意义为:1mol单原子分子理想气23R代表的物理意义为:单原子分子理想气体的定体摩尔热容2iPV。
24、自由度数为i的一定量的刚性分子理想气体,其体积为V,压强为p时,其内能E=5.两瓶不同种类的理想气体,它们温度相同,压强也相同,但体积不同,则它们分子的平均平动动能相同,单位体积内分子的总平动动能相同。
(均填相同或不相同)6.一定量的某种理想气体,装在一个密闭的不变形的容器中,当气体的温度升高时,气体分子的平均动能增大,气体分子的密度不变,气体的压强增大,气体的内能增大(均填增大、不变或减少)7、理想气体的压强公式为PnkT,理想气体分子的平均平动动能与温度的关系为k3kT28、有两瓶气体,一瓶是氧气,另一瓶是氢气(均视为刚性分子理想气体),若它们的压强、体积、温度均相同,则氧气的内能是氢气的▁▁1▁▁倍。
9、一容器内贮有气体,其压强为1atm,温度为27oC,密度为1.3kgm,则气体的摩尔质量为__3210____kgmol,由此确定它是__氧____气.31310、Nf(u)du表示的物理意义是表示速率分布在~d内的分子数------------------------------------。
11、òu2u1f(u)du表示的物理意义是表示速率分布在1~2范围内的分子数3___倍.5占总分子数的比率.12、在相同条件下,氧原子的平均动能是氧分子的平均动能的___(二)中(一般综合题)1、如图1所示,两条曲线分别表示相同温度下,氢气和氧气分子的速率分布曲线,则a表示▁氧▁▁气分子的速率分布曲线;b表示▁▁氢▁气分子的速率分布曲线。
大学物理第5章习题解答

第五章 机械振动5-1一远洋货轮,质量为t M 4102⨯=,浮在水面对其水平截面积为23102m S ⨯=。
设在水面附近货轮的截面积与货轮高度无关,试证明此货轮在水中的铅直自由运动是简谐振动,并求其自由振动的周期。
解:取固定坐标xOy ,坐标原点O 在水面上(图题所示)设货轮静止不动时,货轮上的A 点恰在水面上,则浮力为S ρga .这时 ga s Mg ρ= 往下沉一点时,合力 )(y a g s Mg F +-=ρ gy s ρ-=. 又 22d d t yMMa F == 故0d d 22=+gy s t y M ρ022=+y M gs dt dy ρ 故作简谐振动 M gs ρω=2)(35.68.910102101022223334s g s M T =⨯⨯⨯⨯⨯===πρπωπ5-2 重物A 的质量M=1kg ,放在倾角030=θ的光滑斜面上,并用绳跨过定滑轮与劲度系数149-⋅=m N k 的轻弹簧连接,如习题5-2图所示,将物体由弹簧未形变的位置静止释放,并开始计时,试求:(1)不计滑轮质量,物体A 的运动方程;(2)滑轮为质量M ,半轻r 的均质圆盘,物体A 的运动方程。
解:取物体A 为研究对象,建立坐标Ox 轴沿斜面向下,原点取在平衡位置处,即在初始位置斜下方距离l 0处,此时:)(1.0sin 0m kmg l ==θ(1) 习题5-1图(1) A 物体共受三力;重mg, 支持力N, 张力T.不计滑轮质量时,有 T =kx列出A 在任一位置x 处的牛顿方程式220d d )(sin sin txm x l k mg T mg =+-=-θθ将(1)式代入上式,整理后得0d d 22=+x mkt x 故物体A 的运动是简谐振动,且)rad/s (7==mkω 由初始条件,000⎩⎨⎧=-=v l x 求得,1.00⎩⎨⎧===πϕml A 故物体A 的运动方程为x =(7t+π)m(2) 当考虑滑轮质量时,两段绳子中张力数值不等,如图所示,分别为T 1、T 2,则对A 列出任一位置x 处的牛顿方程式为:221d d sin txm T mg =-θ (2)对滑轮列出转动方程为:22221d d 2121t x Mr r a Mr J r T r T =⎪⎭⎫ ⎝⎛==-β (3)式中,T 2=k (l 0+x ) (4)由式(3)、(4)知2201d d 21)(t xM x l k T ++=代入(2)式知22021)(sin dtxd m M x l k mg ⎪⎭⎫ ⎝⎛+=+-θ又由(1)式知0sin kl mg =θ故0d d )21(22=++kx txm M即0)2(d d 22=++x m M ktx 习题5-2图m M k +=22ω可见,物体A 仍作简谐振动,此时圆频率为:rad/s)(7.52=+=m M k ω由于初始条件:0,000=-=v l x可知,A 、ϕ不变,故物体A 的运动方程为:m t x )7.5cos(1.0π+=由以上可知:弹簧在斜面上的运动,仍为简谐振动,但平衡位置发生了变化,滑轮的质量改变了系统的振动频率.5-3质点作简谐振动的振动曲线如习题5-3图所示,试根据图得出该质点的振动表达式。
大学物理第五章和第六章习题答案

大学物理习题集(上)专业班级 姓名_ 学号_第五章 刚体的定轴转动一.选择题1.关于刚体对轴的转动惯量,下列说法中正确的是[ C ](A )只取决于刚体的质量,与质量的空间分布和轴的位置无关。
(B )取决于刚体的质量和质量的空间分布,与轴的位置无关。
(C )取决于刚体的质量、质量的空间分布和轴的位置。
(D )只取决于转轴的位置,与刚体的质量和质量的空间分布无关。
2. 均匀细棒 OA 可绕通过某一端 O 而与棒垂直的水平固定光滑轴转动,今使棒从水平位置由静止开始自 由下降,在棒摆到竖直位置的过程中,下述说法哪一种是正确的?[ A ](A )角速度从小到大,角加速度从大到小。
A(B )角速度从小到大,角加速度从小到大。
(C )角速度从大到小,角加速度从大到小。
(D )角速度从大到小,角加速度从小到大。
3. 如图所示,一圆盘绕水平轴 0 做匀速转动,如果同时相向地射来两个质量相同、速度大小相同,且沿同一直线运动的子弹。
子弹射入圆盘均留在盘内,则 子弹射入后的瞬间,圆盘的角速度将 [ B ](A )增大; (B )减小; (C )不变; (D )无法确定。
解答 以圆盘和两子弹为系统,外力矩为零,系统的角动量守恒。
按题意, 两个子弹的初始角动量(对 0 轴之和为零。
两子弹留在圆盘内,增大了圆盘的 转动惯量。
设圆盘的转动惯为 J ,转动的角速度为 ω0 ,则有J ω0 = ( J + ∆J )ωω0 > ω有速度减小,所以应选(B )4. 一轻绳绕在具有水平转轴的定滑轮上,绳下端挂物体,物体的质量为 m ,此时滑轮的角加速度为 a 。
若将物体卸掉,而用大小等于 mg 、方向向下的力拉绳子,则滑轮的角加速度将[ A ](A)变大; (B )不变; (C )变小; (D )无法判断。
解答如图 5-4(a)所示,设滑轮半径为 R,转动惯量为 J。
当绳下滑挂一质量为m 的物体时,受绳的张力F T 和重力W=mg 作用,加速度a 铅直向下。
大学物理习题答案第五章

[习题解答]5-1 作定轴转动的刚体上各点的法向加速度,既可写为a n= v2 /R,这表示法向加速度的大小与刚体上各点到转轴的距离R成反比;也可以写为a n= 2 R,这表示法向加速度的大小与刚体上各点到转轴的距离R成正比。
这两者是否有矛盾为什么解没有矛盾。
根据公式,说法向加速度的大小与刚体上各点到转轴的距离R成反比,是有条件的,这个条件就是保持v不变;根据公式,说法向加速度的大小与刚体上各点到转轴的距离R成正比,也是有条件的,条件就是保持不变。
5-2一个圆盘绕通过其中心并与盘面相垂直的轴作定轴转动,当圆盘分别在恒定角速度和恒定角加速度两种情况下转动时,圆盘边缘上的点是否都具有法向加速度和切向加速度数值是恒定的还是变化的解(1)当角速度一定时,切向速度也是一定的,所以切向加速度,即不具有切向加速度。
而此时法向加速度,可见是恒定的。
(2)当角加速度一定时,即恒定,于是可以得到,这表示角速度是随时间变化的。
由此可得.切向加速度为,这表示切向加速度是恒定的。
法向加速度为,显然是时间的函数。
5-3 原来静止的电机皮带轮在接通电源后作匀变速转动,30s后转速达到152 rad s1 。
求:(1)在这30 s内电机皮带轮转过的转数;(2)接通电源后20 s时皮带轮的角速度;(3)接通电源后20 s时皮带轮边缘上一点的线速度、切向加速度和法向加速度,已知皮带轮的半径为5.0 cm。
解(1)根据题意,皮带轮是在作匀角加速转动,角加速度为.在30 s内转过的角位移为.在30 s内转过的转数为.(2)在t = 20 s时其角速度为.(3)在t = 20 s时,在皮带轮边缘上r = 5.0 cm处的线速度为,切向加速度为,法向加速度为.5-4 一飞轮的转速为250 rads1 ,开始制动后作匀变速转动,经过90 s停止。
求开始制动后转过103 rad时的角速度。
解飞轮作匀变速转动,,经过90 s,,所以角加速度为.从制动到转过,角速度由0变为,应满足.所以.5-5 分别求出质量为m = 0.50 kg、半径为r = 36 cm的金属细圆环和薄圆盘相对于通过其中心并垂直于环面和盘面的轴的转动惯量;如果它们的转速都是105 rad s1 ,它们的转动动能各为多大解(1)细圆环:相对于通过其中心并垂直于环面的轴的转动惯量为,转动动能为.(2)相对于通过其中心并垂直于盘面的轴的转动惯量为,转动动能为.5-6 转动惯量为20 kgm2 、直径为50 cm的飞轮以105 rad s1 的角速度旋转。
大学物理习题解答5第五章稳恒电流 (1)

第五章 稳恒电流本章提要1.电流强度· 当导体中存在电场时,导体中的电荷会发生定向运动形成电流。
如果在t ∆时间内通过导体某一截面的电量为q ∆,则通过该截面的电流I 为qI t∆=∆ · 如果电流随时间变化,电流I 的定义式为tqt q I t d d lim 0=∆∆=→∆2.电流密度· 导体中任意一点的电流密度j 的大小规定为单位时间内通过该点单位垂直截面的电量,j 的方向规定为通过该点的正电荷运动的方向。
根据电流密度的定义,导体中某一点面元d S 的电流密度为d d Ij S ⊥=· 对于宏观导体,当导体中各点的j 有不同的大小和方向,通过导体任意截面S 的电流可通过积分计算,即d j S S=⋅⎰⎰I3.欧姆定律· 对于一般的金属导体,在恒定条件下欧姆定律有如下表达形式RU U I 21-=其中R 为导体的电阻,21U U -为导体两端的电势差· 欧姆定律的微分形式为E j σ=其中ρσ1=为电导率4.电阻· 当导体中存在恒定电流时,导体对电流有一定的电阻。
导体的电阻与导体的材料、大小、形状以及所处状态(如温度)有关。
当导体的材料与温度一定时,对一段截面积均匀的导体,其电阻表达式为Sl R ρ= 其中l 为导体的长度,S 为导体的横截面积,ρ为导体的电阻率5.电动势· 非静电力反抗静电力移动电荷做功,把其它种形式的能量转换为电势能,产生电势升高。
qA 非=ε· 当非静电力不仅存在于内电路中,而且存在于外电路中时,整个回路的电动势为l E lk ⎰⋅=d ε6.电源电动势和路端电压· 若电源正负极板的电势分别为U +和U -,电源内阻为r ,电路中电流为I ,则电源电动势为()U U Ir +-ε=--· 路端电压为Ir U U -=--+ε7.接触电动势· 因电子的扩散而在导体接触面上形成的等效电动势。
大学物理第05章 静电场习题解答

第5章 静电场习题解答5.1一带电体可作为点电荷处理的条件是( C ) (A )电荷必须呈球形分布。
(B )带电体的线度很小。
(C )带电体的线度与其它有关长度相比可忽略不计。
(D )电量很小。
5.2图中所示为一沿 x 轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+λ(x >0)和 -λ(x < 0),则 oxy 坐标平面上点(0,a )处的场强 E 为:( B ) ( A ) 0 ( B )02aλπεi ( C )04a λπεi ( D ) ()02aλπε+i j 5.3 两个均匀带电的同心球面,半径分别为R 1、R 2(R 1<R 2),小球带电Q ,大球带电-Q ,下列各图中哪一个正确表示了电场的分布 ( d )(C) (D)5.4 如图所示,任一闭合曲面S 内有一点电荷q ,O 为S 面上任一点,若将q 由闭合曲面内的P 点移到T 点,且OP =OT ,那么 ( d )(A) 穿过S 面的电通量改变,O 点的场强大小不变; (B) 穿过S 面的电通量改变,O 点的场强大小改变; (C) 穿过S 面的电通量不变,O 点的场强大小改变;(D) 穿过S 面的电通量不变,O 点的场强大小不变。
5.5如图所示,a 、b 、c 是电场中某条电场线上的三个点,由此可知 ( c ) (A) E a >E b >E c ; (B) E a <E b <E c ; (C) U a >U b >U c ; (D) U a <U b <U c 。
5.6关于高斯定理的理解有下面几种说法,其中正确的是 ( c )(A) 如果高斯面内无电荷,则高斯面上E处处为零;(B) 如果高斯面上E处处不为零,则该面内必无电荷; (C) 如果高斯面内有净电荷,则通过该面的电通量必不为零;(D) 如果高斯面上E处处为零,则该面内必无电荷。
5.7 下面说法正确的是 [ D ](A)等势面上各点场强的大小一定相等; (B)在电势高处,电势能也一定高; (C)场强大处,电势一定高;(D)场强的方向总是从电势高处指向低处.5.8 已知一高斯面所包围的体积内电量代数和0i q =∑ ,则可肯定:[ C ] (A )高斯面上各点场强均为零。
大学物理05刚体的定轴转动习题解答

第五章 刚体的定轴转动一 选择题1. 一绕定轴转动的刚体,某时刻的角速度为ω,角加速度为α,则其转动加快的依据是:( )A. α > 0B. ω > 0,α > 0C. ω < 0,α > 0D. ω > 0,α < 0解:答案是B 。
2. 用铅和铁两种金属制成两个均质圆盘,质量相等且具有相同的厚度,则它们对过盘心且垂直盘面的轴的转动惯量。
( )A. 相等;B. 铅盘的大;C. 铁盘的大;D. 无法确定谁大谁小解:答案是C 。
简要提示:铅的密度大,所以其半径小,圆盘的转动惯量为:2/2Mr J =。
3. 一轻绳绕在半径为r 的重滑轮上,轮对轴的转动惯量为J ,一是以力F 向下拉绳使轮转动;二是以重量等于F 的重物挂在绳上使之转动,若两种情况使轮边缘获得的切向加速度分别为a 1和a 2,则有: ( )A. a 1 = a 2B. a 1 > a 2C. a 1< a 2D. 无法确定解:答案是B 。
简要提示:(1) 由定轴转动定律,1αJ Fr =和11αr a =,得:J Fr a /21=(2) 受力分析得:⎪⎩⎪⎨⎧===-2222ααr a J Tr ma T mg ,其中m 为重物的质量,T 为绳子的张力。
得:)/(222mr J Fr a +=,所以a 1 > a 2。
4. 一半径为R ,质量为m 的圆柱体,在切向力F 作用下由静止开始绕轴线作定轴转动,则在2秒内F 对柱体所作功为: ( )A. 4 F 2/ mB. 2 F 2 / mC. F 2 / mD. F 2 / 2 m解:答案是A 。
简要提示:由定轴转动定律: α221MR FR =,得:mRF t 4212==∆αθ 所以:m F M W /42=∆=θ5. 一电唱机的转盘正以ω 0的角速度转动,其转动惯量为J 1,现将一转动惯量为J 2的唱片置于转盘上,则共同转动的角速度应为: ( )A .0211ωJ J J +B .0121ωJ J J +C .021ωJ JD .012ωJ J 解:答案是A 。
大学物理课后习题答案第五章

第五章 机械波5.1 已知一波的波动方程为y = 5×10-2sin(10πt – 0.6x ) (m). (1)求波长、频率、波速及传播方向;(2)说明x = 0时波动方程的意义,并作图表示. [解答](1)与标准波动方程比较得:2π/λ = 0.6, 因此波长为:λ = 10.47(m);圆频率为:ω = 10π,频率为:v =ω/2π = 5(Hz);波速为:u = λ/T = λv = 52.36(m·s -1).且传播方向为x 轴正方向.(2)当x = 0时波动方程就成为该处质点的振动方程: y = 5×10-2sin10πt = 5×10-2cos(10πt – π/2), 振动曲线如图.5.2 一平面简谐波在媒质中以速度为u = 0.2m·s -1沿x 轴正向传播,已知波线上A 点(x A = 0.05m )的振动方程为(m).试求:(1)简谐波的波动方程;(2)x = -0.05m 处质点P 处的振动方程.[解答](1)简谐波的波动方程为:; 即 = 0.03cos[4π(t – 5x ) + π/2]. (2)在x = -0.05m 处质点P 点的振动方程为:y = 0.03cos[4πt + π + π/2] = 0.03cos(4πt -π/2).5.3 已知平面波波源的振动表达式为(m).求距波源5m 处质点的振动方程和该质点与波源的位相差.设波速为2m·s -1.[解答]振动方程为: , 位相差为 Δφ = 5π/4(rad).5.4 有一沿x 轴正向传播的平面波,其波速为u = 1m·s -1,波长λ = 0.04m ,振幅A = 0.03m .若以坐标原点恰在平衡位置而向负方向运动时作为开始时刻,试求:(1)此平面波的波动方程;(2)与波源相距x = 0.01m 处质点的振动方程,该点初相是多少? [解答](1)设原点的振动方程为:y 0 = A cos(ωt + φ),其中A = 0.03m .由于u = λ/T ,所以质点振动的周期为:T = λ/u = 0.04(s),圆频率为:ω = 2π/T = 50π. 当t = 0时,y 0 = 0,因此cos φ = 0;由于质点速度小于零,所以φ = π/2. 原点的振动方程为:y 0 = 0.03cos(50πt + π/2), 平面波的波动方程为:= 0.03cos[50π(t – x ) + π/2).(2)与波源相距x = 0.01m 处质点的振动方程为:y = 0.03cos50πt . 该点初相φ = 0.5.5 一列简谐波沿x 轴正向传播,在t 1 = 0s ,t 2 = 0.25s 时刻的波形如图所示.试求:2cos()xy A t πωλ=-0.03cos(4)2A y t ππ=-cos[()]Ax x y A t uωϕ-=-+0.050.03cos[4()]0.22x y t ππ-=--20 6.010sin 2y t π-=⨯26.010sin()2xy t u π-=⨯-50.06sin()24t ππ=-0.03cos[50()]2x y t u ππ=-+(1)P 点的振动表达式; (2)波动方程;(3)画出O 点的振动曲线.[解答](1)设P 点的振动方程为 y P = A cos(ωt + φ), 其中A = 0.2m .在Δt = 0.25s 内,波向右传播了Δx = 0.45/3 = 0.15(m),所以波速为u = Δx/Δt = 0.6(m·s -1).波长为:λ = 4Δx = 0.6(m), 周期为:T = λ/u = 1(s), 圆频率为:ω = 2π/T = 2π.当t = 0时,y P = 0,因此cos φ = 0;由于波沿x 轴正向传播,所以P 点在此时向上运动,速度大于零,所以φ = -π/2.P 点的振动表达式为:y P = 0.2cos(2πt - π/2). (2)P 点的位置是x P = 0.3m ,所以波动方程为. (3)在x = 0处的振动方程为y 0 = 0.2cos(2πt + π/2),曲线如图所示.5.6 如图所示为一列沿x 负向传播的平面谐波在t = T /4时的波形图,振幅A 、波长λ以及周期T 均已知.(1)写出该波的波动方程;(2)画出x = λ/2处质点的振动曲线;(3)图中波线上a 和b 两点的位相差φa – φb 为多少? [解答](1)设此波的波动方程为: ,当t = T /4时的波形方程为:. 在x = 0处y = 0,因此得sin φ = 0,解得φ = 0或π.而在x = λ/2处y = -A ,所以φ = 0. 因此波动方程为:. (2)在x = λ/2处质点的振动方程为:, 曲线如图所示.(3)x a = λ/4处的质点的振动方程为; x b = λ处的质点的振动方程为.波线上a 和b 两点的位相差0.2cos[2()]2P x x y t u ππ-=--100.2cos(2)32t x πππ=-+cos[2()]t xy A T πϕλ=++cos(2)2xy A ππϕλ=++sin(2)xA πϕλ=-+cos 2()t x y A T πλ=+cos(2)cos 2t t y A A T Tπππ=+=-cos(2)2a t y A T ππ=+cos(22)b ty A Tππ=+图5.5φa – φb = -3π/2.5.7 已知波的波动方程为y = A cosπ(4t – 2x )(SI ).(1)写出t = 4.2s 时各波峰位置的坐标表示式,并计算此时离原点最近的波峰的位置,该波峰何时通过原点?(2)画出t = 4.2s 时的波形曲线.[解答]波的波动方程可化为:y = A cos2π(2t – x ),与标准方程比较,可知:周期为T = 0.5s ,波长λ = 1m .波速为u = λ/T = 2m·s -1. (1)当t = 4.2s 时的波形方程为y = A cos(2πx – 16.8π)= A cos(2πx – 0.8π). 令y = A ,则cos(2πx – 0.8π) = 1,因此 2πx – 0.8π = 2k π,(k = 0, ±1, ±2,…), 各波峰的位置为x = k + 0.4,(k = 0, ±1, ±2,…).当k = 0时的波峰离原点最近,最近为:x = 0.4(m).通过原点时经过的时间为:Δt = Δx/u = (0 – x )/u = -0.2(s), 即:该波峰0.2s 之前通过了原点.(2)t = 0时刻的波形曲线如实线所示.经过t = 4s 时,也就是经过8个周期,波形曲线是重合的;再经Δt = 0.2s ,波形向右移动Δx = u Δt = 0.4m ,因此t = 4.2s 时的波形曲线如虚线所示.[注意]各波峰的位置也可以由cos(2πx – 16.8π) = 1解得,结果为x = k + 8.4,(k = 0, ±1, ±2,…),取同一整数k 值,波峰的位置不同.当k = -8时的波峰离原点最近,最近为x = 0.4m .5.8 一简谐波沿x 轴正向传播,波长λ = 4m ,周期T = 4s ,已知x = 0处的质点的振动曲线如图所示. (1)写出时x = 0处质点的振动方程;(2)写出波的表达式;(3)画出t = 1s 时刻的波形曲线.[解答]波速为u = λ/T = 1(m·s -1).(1)设x = 0处的质点的振动方程为y = A cos(ωt + φ), 其中A = 1m ,ω = 2π/T = π/2.当t = 0时,y = 0.5,因此cos φ = 0.5,φ = ±π/3.在0时刻的曲线上作一切线,可知该时刻的速度小于零,因此φ = π/3.振动方程为:y = cos(πt /2 + π/3).(2)波的表达式为:.(3)t = 1s 时刻的波形方程为,波形曲线如图所示.5.9 在波的传播路程上有A 和B 两点,都做简谐振动,B 点的位相比A 点落后π/6,cos[2()]t x y A T πϕλ=-+cos[2()]t xy A T πϕλ=-+cos[()]23t x ππ=-+5cos()26y x ππ=-图5.8已知A 和B 之间的距离为2.0cm ,振动周期为2.0s .求波速u 和波长λ.[解答] 设波动方程为:, 那么A 和B 两点的振动方程分别为:,.两点之间的位相差为:,由于x B – x A = 0.02m ,所以波长为:λ = 0.24(m).波速为:u = λ/T = 0.12(m·s -1).5.10 一平面波在介质中以速度u = 20m·s -1沿x 轴负方向传播.已知在传播路径上的某点A 的振动方程为y = 3cos4πt .(1)如以A 点为坐标原点,写出波动方程;(2)如以距A 点5m 处的B 点为坐标原点,写出波动方程; (3)写出传播方向上B ,C ,D 点的振动方程. [解答](1)以A 点为坐标原点,波动方程为 .(2)以B 点为坐标原点,波动方程为. (3)以A 点为坐标原点,则x B = -5m 、x C = -13m 、x D = 9m ,各点的振动方程为, ,.[注意]以B 点为坐标原点,求出各点坐标,也能求出各点的振动方程.5.11 一弹性波在媒质中传播的速度u = 1×103m·s -1,振幅A = 1.0×10-4m ,频率ν= 103Hz .若该媒质的密度为800kg·m -3,求:(1)该波的平均能流密度;(2)1分钟内垂直通过面积S = 4×10-4m 2的总能量. [解答](1)质点的圆频率为:ω = 2πv = 6.283×103(rad·s -1), 波的平均能量密度为:= 158(J·m -3), 平均能流密度为:= 1.58×105(W·m -2).(2)1分钟内垂直通过面积S = 4×10-4m 2的总能量为:E = ItS = 3.79×103(J).5.12 一平面简谐声波在空气中传播,波速u = 340m·s -1,频率为500Hz .到达人耳时,振幅A = 1×10-4cm ,试求人耳接收到声波的平均能量密度和声强?此时声强相当于多少分贝?已知空气密度ρ = 1.29kg·m -3.[解答]质点的圆频率为:ω = 2πv = 3.142×103(rad·s -1),cos[2()]t xy A T πϕλ=-+cos[2()]A A xt y A T πϕλ=-+cos[2()]B B xt y A T πϕλ=-+2(2)6B A x x πππλλ---=-3cos 4()3cos(4)5x x y t t u πππ=+=+3cos 4()Ax x y t u π-=+3cos(4)5x t πππ=+-3cos 4()3cos(4)BB x y t t u πππ=+=-33cos 4()3cos(4)5C C x y t t u πππ=+=-93cos 4()3cos(4)5D D x y t t u πππ=+=+2212w A ρω=I wu =图5.10声波的平均能量密度为:= 6.37×10-6(J·m -3), 平均能流密度为:= 2.16×10-3(W·m -2), 标准声强为:I 0 = 1×10-12(W·m -2), 此声强的分贝数为:= 93.4(dB).5.13 设空气中声速为330m·s -1.一列火车以30m·s -1的速度行驶,机车上汽笛的频率为600Hz .一静止的观察者在机车的正前方和机车驶过其身后所听到的频率分别是多少?如果观察者以速度10m·s -1与这列火车相向运动,在上述两个位置,他听到的声音频率分别是多少?[解答]取声速的方向为正,多谱勒频率公式可统一表示为, 其中v S 表示声源的频率,u 表示声速,u B 表示观察者的速度,u S 表示声源的速度,v B 表示观察者接收的频率.(1)当观察者静止时,u B = 0,火车驶来时其速度方向与声速方向相同,u S = 30m·s -1,观察者听到的频率为= 660(Hz). 火车驶去时其速度方向与声速方向相反,u S = -30m·s -1,观察者听到的频率为= 550(Hz). (2)当观察者与火车靠近时,观察者的速度方向与声速相反,u B = -10m·s -1;火车速度方向与声速方向相同,u S = 30m·s -1,观察者听到的频率为= 680(Hz). 当观察者与火车远离时,观察者的速度方向与声速相同,u B = 10m·s -1;火车速度方向与声速方向相反,u S = -30m·s -1,观察者听到的频率为= 533(Hz). [注意]这类题目涉及声速、声源的速度和观察者的速度,规定方向之后将公式统一起来,很容易判别速度方向,给计算带来了方便.5.14.一声源的频率为1080Hz ,相对地面以30m·s -1速率向右运动.在其右方有一反射面相对地面以65m·s -1的速率向左运动.设空气中声速为331m·s -1.求:(1)声源在空气中发出的声音的波长; (2)反射回的声音的频率和波长.[解答](1)声音在声源垂直方向的波长为:λ0 = uT 0 = u /ν0 = 331/1080 = 0.306(m); 在声源前方的波长为:λ1 = λ0 - u s T 0 = uT 0 - u s T 0 = (u - u s )/ν0 = (331-30)/1080 = 0.2787(m); 在声源后方的波长为:λ2 = λ0 + u s T 0 = uT 0 + u s T 0 = (u + u s )/ν0= (331+30)/1080 = 0.3343(m).(2)反射面接收到的频率为 = 1421(Hz).将反射面作为波源,其频率为ν1,反射声音的频率为2212w A ρω=I wu =010lgIL I =BB S Su u u u νν-=-33060033030B S S u u u νν==--33060033030B S S u u u νν==-+3301060033030B B S S u u u u νν-+==--3301060033030B B S S u u u u νν--==-+1033165108033130B Su u u u νν++==⨯--= 1768(Hz). 反射声音的波长为=0.1872(m).或者 = 0.1872(m). [注意]如果用下式计算波长=0.2330(m), 结果就是错误的.当反射面不动时,作为波源发出的波长为u /ν1 = 0.2330m ,而不是入射的波长λ1.5.15 S 1与S 2为两相干波源,相距1/4个波长,S 1比S 2的位相超前π/2.问S 1、S 2连线上在S 1外侧各点的合成波的振幅如何?在S 2外侧各点的振幅如何?[解答]如图所示,设S 1在其左侧产生的波的波动方程为,那么S 2在S 1左侧产生的波的波动方程为,由于两波源在任意点x 产生振动反相,所以合振幅为零.S 1在S 2右侧产生的波的波动方程为,那么S 2在其右侧产生的波的波动方程为,由于两波源在任意点x 产生振动同相,所以合振幅为单一振动的两倍.5.16 两相干波源S 1与S 2相距5m ,其振幅相等,频率都是质中的传播速度为400m·s -1,试以S 1S 2连线为坐标轴x ,以S 1S 2连线中点为原点,求S 1S 2间因干涉而静止的各点的坐标.[解答]如图所示,设S 1在其右侧产生的波的波动方程为 ,那么S 2在其左侧产生的波的波动方程为. 两个振动的相差为Δφ = πx + π,当Δφ = (2k + 1)π时,质点由于两波干涉而静止,静止点为x = 2k , k 为整数,但必须使x 的值在-l /2到l /2之间,即-2.5到2.5之间.当k = -1、0和1时,可得静止点的坐标为:x = -2、0和2(m).`11331142133165B u u u νν==⨯--`1111331651421BBu u u u λννν--=-==`1`13311768u λν==`111650.27871768Bu λλν=-=-1cos[2()]t xy A T πϕλ=++2/4cos[2()]2t x y A T λππϕλ-=++-cos[2()]t xA T πϕπλ=++-1cos[2()]t xy A T πϕλ=-+2/4cos[2()]2t x y A T λππϕλ-=-+-cos[2()]t xA T πϕλ=-+1/2cos[2()]x l y A t u πνϕ+=-+5cos(2)24A t x πππνϕ=-+-2/2cos[2()]x l y A t u πνϕπ-=+++cos(2)24A t x πππνϕ=++-S 1 S 2S 125.17 设入射波的表达式为,在x = 0处发生反射,反射点为一自由端,求:(1)反射波的表达式; (2)合成驻波的表达式.[解答](1)由于反射点为自由端,所以没有半波损失,反射波的波动方程为.(2)合成波为y = y 1 + y 2,将三角函数展开得,这是驻波的方程.5.18 两波在一很长的弦线上传播,设其表达式为:,,用厘米、克、秒(cm,g,s )制单位,求:(1)各波的频率,波长、波速;(2)节点的位置;(3)在哪些位置上,振幅最大?[解答](1)两波可表示为:,, 可知它们的周期都为:T = 0.5(s),频率为:v = 1/T = 2(Hz);波长为:λ = 200(cm);波速为:u = λ/T = 400(cm·s -1).(2)位相差Δφ = πx /50,当Δφ = (2k + 1)π时,可得节点的位置x = 50(2k + 1)(cm),(k = 0,1,2,…).(3)当Δφ = 2k π时,可得波腹的位置x = 100k (cm),(k = 0,1,2,…).1cos 2()t xy A T πλ=+2cos 2()t xy A T πλ=-222coscosy A x t Tππλ=1 6.0cos(0.028.0)2y x t π=-2 6.0cos(0.028.0)2y x t π=+1 6.0cos 2()0.5200t x y π=-2 6.0cos 2()0.5200t x y π=+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 机械振动5-1一远洋货轮,质量为t M 4102⨯=,浮在水面对其水平截面积为23102m S ⨯=。
设在水面附近货轮的截面积与货轮高度无关,试证明此货轮在水中的铅直自由运动是简谐振动,并求其自由振动的周期。
解:取固定坐标xOy ,坐标原点O 在水面上(图题所示)设货轮静止不动时,货轮上的A 点恰在水面上,则浮力为S ρga .这时 ga s Mg ρ= 往下沉一点时,合力 )(y a g s Mg F +-=ρ gy s ρ-=. 又 22d d ty MMa F ==故0d d 22=+gy s ty Mρ022=+y Mg s dtdy ρ故作简谐振动 M gs ρω=2)(35.68.910102101022223334s gs M T =⨯⨯⨯⨯⨯===πρπωπ5-2 重物A 的质量M=1kg ,放在倾角030=θ的光滑斜面上,并用绳跨过定滑轮与劲度系数149-⋅=mN k 的轻弹簧连接,如习题5-2图所示,将物体由弹簧未形变的位置静止释放,并开始计时,试求:(1)不计滑轮质量,物体A 的运动方程;(2)滑轮为质量M ,半轻r 的均质圆盘,物体A 的运动方程。
解:取物体A 为研究对象,建立坐标Ox 轴沿斜面向下,原点取在平衡位置处,即在初始位置斜下方距离l 0处,此时:)(1.0sin 0m kmg l ==θ(1)习题5-1图(1) A 物体共受三力;重mg, 支持力N, 张力T.不计滑轮质量时,有 T =kx列出A 在任一位置x 处的牛顿方程式220d d )(sin sin tx mx l k mg T mg =+-=-θθ将(1)式代入上式,整理后得0d d 22=+x mk tx故物体A 的运动是简谐振动,且)rad/s (7==mk ω由初始条件,000⎩⎨⎧=-=v l x 求得,1.00⎩⎨⎧===πϕml A 故物体A 的运动方程为 x =0.1cos(7t+π)m(2) 当考虑滑轮质量时,两段绳子中张力数值不等,如图所示,分别为T 1、T 2,则对A 列出任一位置x 处的牛顿方程式为:221d d sin tx mT mg =-θ (2) 对滑轮列出转动方程为:22221d d 2121t x Mr raMr J r T r T =⎪⎭⎫ ⎝⎛==-β (3) 式中,T 2=k (l 0+x ) (4) 由式(3)、(4)知2201d d 21)(tx M x l k T ++=代入(2)式知22021)(sin dtxd m M x l k mg ⎪⎭⎫ ⎝⎛+=+-θ 又由(1)式知0sin kl mg =θ故0d d )21(22=++kx tx m M即0)2(d d 22=++x m M ktx习题5-2图mM k +=22ω可见,物体A 仍作简谐振动,此时圆频率为:rad/s)(7.52=+=mM k ω由于初始条件:0,000=-=v l x可知,A 、ϕ不变,故物体A 的运动方程为:m t x )7.5cos(1.0π+=由以上可知:弹簧在斜面上的运动,仍为简谐振动,但平衡位置发生了变化,滑轮的质量改变了系统的振动频率.5-3质点作简谐振动的振动曲线如习题5-3图所示,试根据图得出该质点的振动表达式。
解:简谐振动的振动表达式:)cos(ϕω+=t A x由题图可知,m 1042-⨯=A ,当t=0时,将m 1022-⨯=x 代入简谐振动表达式,得:21cos =ϕ由)sin(ϕωωυ+-=t A ,当t=0时,ϕωυsin A -= 由图可知,υ>0,即0sin <ϕ,故由21cos =ϕ,取3πϕ-=又因:t=1s 时,,1022m x -⨯=将其入代简谐振动表达式,得213cos ,3cos 42=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=πωπω由t=1s 时,⎪⎭⎫⎝⎛--=3sin πωωυA <0知,03sin >⎪⎭⎫ ⎝⎛-πω,取33ππω=-, 即 s 32πω=质点作简谐振动的振动表达式为m t x ⎪⎭⎫ ⎝⎛-⨯=-332cos 1042ππ5-4在一个电量为Q ,半径为R 的均匀带电球中,沿某一直径挖一条隧道,另一质量为m,习题5-3图电量为-q 的微粒在这个隧道中运动,试求证该微粒的运动是简谐振动,并求出振动周期(设带电球体介电常数为0ε)。
解:以该球的球心为原点,假设微粒在某一任意时刻位于遂道中的位矢为r,由高斯定理可知304Rr Q E πε =,则微粒在此处受电场力为:r RQq F304πε-=式中,负号表明电场F 的方向与r的正方向相反,指向球心.由上式及牛顿定律,得:4d d 04d d 043022302230=+⇒=+=+r mRQq tr r RQq tr mr RQq F πεπεπε 令 mR Qq 3024πεω=则0d d 222=+r tr ω故微粒作简谐振动,平衡点在球心处.由ωπ2=T 知: QqmR T 3042πεπ=5-5如习题5-5图所示,有一轻质弹簧,其劲度系数k=5001-⋅mN ,上端固定,下端悬挂一质量M=4.0kg 的物体A ,在物体A 的正下方h=0.6m 处,以初速度1010.4-⋅=s m v 的速度向上抛出一质量m=1.0kg 的油灰团B ,击中A 并附着于A 上。
(1)证明A 与B 作简谐振动;(2)写出它们共同作简谐振动的振动表达式; (3)弹簧所受的最大拉力是多少?(取210-⋅=s m g ,弹簧未挂重物时,其下端端点位于/O 点)解:(1)取弹簧原长所在位置为O '点.当弹簧挂上物体A 时,处于静止位置P 点,有:P O k Mg '=将A 与B 粘合后,挂在弹簧下端,静止平衡所在位置O 点,取O 点为原坐标原点如图题5-5所示,则有:g m M O O k )(+='设当B 与A 粘在一起后,在其运动过程的任一位置,弹簧形变量x O O +',则A 、B 系统所受合力为:kx x O O k g m M F -=+'-+=)()(即 0d d )(22=++kx tx m M可见A 与B 作简谐和振动. (2) 由上式知,rad/s)(10=+=mM k ω以B 与A 相碰点为计时起点,此时A 与B 在P 点,由图题5-5可知kmg kMg g km M P O O O OP =-+='-'=则t=0时,m 02.00-=-=-=kmg OP x (负号表P 点在O 点上方)又B 与A 为非弹性碰撞,碰撞前B 的速度为:m/s 2220101=-='gh υυ碰撞后,A 、B 的共同速度为:m/s 4.0010=+'=mM m υυ (方向向上)则t=0时,⎩⎨⎧=-=s m mx /4.002.000υ可求得:)m (0447.02202=+=ωυx Aπωυϕ65.0arctan 00=⎪⎪⎭⎫⎝⎛-=x 可知A 与B 振动系统的振动表达式为:m t x )65.010cos(0447.0π+= (3) 弹簧所受的最大拉力,应是弹簧最大形变时的弹力,最大形变为:m A g km M A O O x 1447.0=++=+'=∆则最大拉力 N 4.72max ==x k F ∆5-6 一物体竖直悬挂在劲度系数k 的弹簧上简谐振动,设振幅A=0.24m ,周期T=4.0s ,开始时在平衡位置下方0.12m 处向上运动。
求: (1)物体作简谐振动的振动表达式;习题5.5图(2)物体由初始位置运动到平衡位置上方0.12处所需的最短时间;(3)物钵在平衡位置上方0.12m 处所受到的合外刀的大小及方向(设物体的质量为l.0kg)。
解:(1) 已知A=0.24m, 22ππω==T,如选x 轴向下为正方向.已知初始条件0m,12.000<=υx 即 3,21c o s ,c o s 24.012.0πϕϕϕ±===而 ,0sin ,0sin 0><-=ϕϕωυA 取3πϕ=,故:m t x ⎪⎭⎫⎝⎛+=32cos 24.0ππ(2) 如图题所示坐标中,在平衡位置上方0.12m, 即x=-0.12m 处,有32322132cos πππππ±=+-=⎪⎭⎫ ⎝⎛+t t因为所求时间为最短时间,故物体从初始位置向上运动,0<υ.故0)32sin(>+ππt则取3232πππ=+t可得:s t 32min =(3) 物体在平衡位置上方0.12m 处所受合外力0.3N x m =-=ωF ,指向平衡位置.5-7如习题5-7图所示,质量m=10g 的子弹,以11000-⋅=s m v 的速度射入一在光滑平面上与弹簧相连的木块,并嵌入其中,致使弹簧压缩而作简谐振动,若木块质量M=4.99kg ,弹簧的劲度系数13108-⋅⨯=mN k ,求简谐振动的振动表达式。
解:子弹射入木块为完全非弹性碰撞,设u 为子弹射入木块后二者共同速度,由动量定理可知:m/s)(0.2=+=υmM m u不计摩擦,弹簧压缩过程中系统机械能守恒,即:20221)(21kx um M =+ (x 0为弹簧最大形变量)m u km M x 20100.5-⨯=+=由此简谐振动的振幅 20100.5-⨯==x A习题5-6图系统圆频率rad/s)(40=+=mM k ω若取物体静止时的位置O (平衡位置)为坐标原点,Ox 轴水平向右为正,则初始条件为: t =0时,x =0,0m/s 0.20>==u υ由,sin ,cos 00ϕωυϕA A x -==得:2πϕ-=则木块与子弹二者作简谐振动,其振动表达式为:m t x )240cos(100.52π-⨯=-5-8 如习题5-8图所示,质量为m 1的光滑物块和弹簧构成振动系统,已知两弹簧的劲度系数分别为k 1=3.01-⋅m N ,k 2=1.01-⋅m N ,:此系统沿弹簧的长度方向振动,周朗T 1=1.0s ,振幅A 1=0.05m ,当物块经过平衡位置时有质量为m 2=0.10kg 的油泥块竖直落到物体上并立即粘住,求新的振动周期T 2和振幅A 。
解:当物体m 1向右移动x 时,左方弹簧伸长x ,右方弹簧缩短x ,但它们物体的作用方向是相同的,均与物体的位移方向相反,即)(21x k x k F +-=令F =-kx ,有:N/m 421=+=k k k由 km T π2=得)kg (1.0442212211≈==ππk T k T m则粘上油泥块后,新的振动系统质量为:kg 20.021=+m m新的周期 )s (4.12212=+=km m T π在平衡位置时,m 2与m 1发生完全非弹性碰撞. 碰撞前,m 1的速度m/s 10.0111πωυ==A 设碰撞后,m 1和m 2共同速度为υ. 根据动量守恒定律,υυ)(2111m m m +=则 m /s 05.0)(2111πυυ=+=m m m新的振幅 m)(035.0222===πυωυTA5-9质量为0.2kg 的质点作简谐振动,其振动方程为⎪⎭⎫⎝⎛-=25sin 60.0πt x ,式中x 的单位为m ,t 的单位为s ,求: (1)振动周期;(2)质点初始位置,初始速度; (3)质点在经过2A 且向正向运动时的速度和加速度以及此时质点所受的力;(4)质点在何位置时其动能、势能相等? 解:(1)由振动方程)25sin(60.0π-=t x 知,5(rad/s)m,6.0==ωA故振动周期: )s (26.1)s (256.1522≈===πωπT(2) t=0时,由振动方程得:)25cos(0.3|m60.0000=-==-==πυt dtdx x t(3) 由旋转矢量法知,此时的位相:3πϕ-=速度 m /s )(6.2m /s )23(560.0sin =-⨯⨯-=-=ϕωυA 加速度 )m/s (5.7m/s21560.0cos 2222-=⨯⨯-=-=ϕωA a所受力 N)(5.1N )5.7(2.0-=-⨯==ma F(4)设质点在x 处的动能与势能相等,由于简谐振动能量守恒,即:221kA E E E p k ==+ 故有: )21(21212kA E E E p k === 即22212121kA kx⨯=可得: m)(42.022±=±=A x5-10手持一块平板。
