2007年第18届“希望杯”全国数学邀请赛试卷(初一第1试)
[整理]年第十八届希望杯全国数学邀请赛初一第一试.
![[整理]年第十八届希望杯全国数学邀请赛初一第一试.](https://img.taocdn.com/s3/m/50c3e73952ea551811a68710.png)
2007年第十八届希望杯全国数学邀请赛初一第一试一、选择题(每小题4分,共40分)以下每题的四个选项中,仅有一个是正确的)1. 在2007(-1),3-1, -18(-1),18这四个有理数中,负数共有( )(A )1个 (B )2个 (C )3个 (D )4个2.小明在作业本上画了4个角,它们的度数如图1所示,这些角中钝角有( )(A )1个 (B )2个 (C )3个 (D )4个3.If the n-th prime number is 47, then n is ( )(A )12 (B )13 (C )14 (D )15(英汉词典:the n-th prime number 第n 个质数)4.有理数a,b,c 在数轴上对应的点的位置如图2所示,给出下面四个命题:(A )abc <0 (B )a b b c a c -+-=-(C )(a-b)(b-c)(c-a)>0 (D )1a bc 〈- 其中正确的命题有( )(A )4个 (B )3个 (C )2个 (D )1个5.如图3,“人文奥运”这4个艺术字中,轴对称图形有( )(A )1个 (B )2个 (C )3个 (D )4个6.已知p ,q ,r ,s 是互不相同的正整数,且满足p r q s=,则( ) (A )p r s q = (B )p s r q = (C ) p p r q q s +=+ (D )r r p s s q-≠- 7.韩老师特制了4个同样的立方块,并将它们如图4(a )放置,然后又如图4(b )放置,则图4(b )中四个底面正方形中的点数之和为( )(A )11 (B )13 (C )14 (D )168.如图5,若AB//CD ,则∠B 、∠C 、∠E 三者之间的关系是( )(A )∠B+∠C+∠E=180º (B )∠B+∠E-∠C=180º(C )∠B+∠C-∠E=180º (D )∠C+∠E-∠B=180º9.以x 为未知数的方程2007x+2007a+2008a=0(a,b 为有理数,且b>0)有正整数解,则ab 是( )(A )负数 (B )非负数 (C )正数 (D )零10.对任意四个有理数a ,b ,c ,d 定义新运算:a bc d =ad-bc ,若241x x -=18,则x=( )(A )-1 (B )2 (C )3 (D )4二、A 组填空题(每小题4分,共40分)11.小明已进行了20场比赛,其中赢的场数占95%,若以后小明一场都不输,则赢的场数恰好占96%,小明还需要进行 场比赛。
2007年第18届希望杯全国数学竞赛初一决赛试题与答案.doc

第十八届“希望杯”全国数学邀请赛初一第 2试2007年4月15日上午8:30至10:30一、选择题(本大题共10小题,每小题4分,共40分)以下每题的四个选项中,仅有一个是正确的,请将正确答案的英文字母写在每题后面的圆括号内。
1、 假定未拧紧的水龙头每秒钟渗出2滴水,每滴水约0.05毫升,现有一个水龙头未拧紧,4小时后,才被发现拧紧,在这段时间内,水龙头共滴水约( )(用科学记数法表示,结果保留两位有效数字) (A )1440毫升。
(B )31.410⨯毫升。
(C )40.1410⨯毫升。
(D )21410⨯毫升。
2、 如图1,直线L 与∠O 的两边分别交于点A 、B ,则图中以O 、A 、B 为端点的射线的条数总和是( )。
(A )5. (B )6. (C )7. (D)8. 3、 整数a,b 满足:a b ≠O 且a+b =O ,有以下判断:○1a,b 之间没有正分数; ○2a,b 之间没有负分数; ○3a,b 之间至多有一个整数; ○4a,b 之间至少有一个整数 。
其中,正确判断的个数为( )(A )1. (B )2. (C)3. (D)4.4、 方程13153520052007x x x x +++=⨯的解是 x =( ) (A )2006,2007 (B )2007,2006 (C)2007,1003 (D)100320075、 如图2,边长为1的正六边形纸片是轴对称图形,它的对称轴的条数是( )。
(A )1. (B)3. (C)6. (D)9.图1LOB A图26、 在9个数:-5,-4,-3,-2,-1,0,1,2,3中,能使不等式-32x <-14成立的数的个数是( )(A )2. (B)3. (C)4. (D)5.7、 韩老师特制了4个同样的立方块,并将它们如图3(a )放置,然后又如图3(b )放置,则图3(b )中四个底面正方形中的点数之和为( ) (A )11. (B)13. (C)14. (D)16.图38、 对于彼此互质的三个正整数,,a b c ,有以下判断:①,,a b c 均为奇数 ②,,a b c 中必有一个偶数 ③,,a b c 没有公因数 ④,,a b c 必有公因数 其中,不正确的判断的个数为( )(A )1 (B )2 (C )3 (D )49、 将棱长为1厘米的42个立方体积木拼在一起,构成一个实心的长方体。
“希望杯”国数学邀请赛试卷(初一第1试)

2007年第18届“希望杯”全国数学邀请赛试卷(初一第1试)一、选择题(共6小题,每小题5分,满分30分)1.(5分)如图,在数轴上有六个点,且AB=BC=CD=DE=EF,则这条数轴的原点在()A.在点A,B之间B.在点B,C之间C.在点C,D之间D.在点D,E之间2.(5分)(2006•济宁)(﹣8)2006+(﹣8)2005能被下列数整除的是()A.3B.5C.7D.93.(5分)图中的小方格式边长为1的正方形,则在图中一共可以数出正方形的个数是()A.66 B.50 C.60 D.2104.(5分)(2006•济南)如图,直线a与直线b互相平行,则|x﹣y|的值是()A.20 B.80 C.120 D.1805.(5分)将一个正方形的纸片分成四块,要求这四块大小相等,形状一样,则分的方法共有()A.2种B.4种C.6种D.无数种6.(5分)某商店同时售出两种服装,每套均卖198元,以成本价计算,其中一套盈利20%,另一套亏本20%,如果不考虑其因素,则这次出售过程中商店()A.不赚不赔B.赚16.5元C.赔25元D.非以上答案二、填空题(共6小题,每小题5分,满分30分)7.(5分)北京与纽约的时差为﹣13时(负号表示同一时刻纽约时间比北京时间晚),如果现在是北京时间18时,那么纽约时间是_________.8.(5分)(2009•枣庄)如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB=_________度.9.(5分)用定义新运算,对于任意有理数x,y都有x y=2x+y2+1,例如35=2×3+52+1=32,那么2[(﹣7)3]=_________.10.(5分)计算=_________.11.(5分)为估计某水库鲢鱼的数量,养鱼户李老板先捞上150条鲢鱼并在上做红色的记号,然后立即将这150条鲢鱼放回水库中,一周后,李老板又捞取200条鲢鱼,数一数带红色记号的鱼有三条,据此可估计出该水库中鲢鱼约有_________条.12.(5分)若P为质数,P3+9仍为质数,则P2﹣7=_________.三、解答题(共4小题,满分40分)13.(10分)为响应“建设节约型社会”的号召,某市制定如下规定:每户用煤气如果不超过m立方米,按每立方米0.8元收费,超过m立方米,超过的部分按每立方米1.2元收费.小颖家10,11月的交煤气费的情况如下表:月份用气量缴费金额10 50 4011 75 66(1)求m的值;(2)由于天气转冷,小颖家12月份的用气量预计将增大20%,为了节约煤气,小颖的爸爸换用了高科技煤气灶具,该灶具在提供相同热量的情况下的用气量是原灶具的60%,试问小颖家12月份比预计可少交煤气费多少元?14.(10分)某城市平面图如图所示,每条线段均表示街道:(1)图中共有多少条线段?(2)小饶需从A1到B6办事,怎样走最近,最近的走法共有几种?15.(10分)如图,在六边形的顶点处,分别标上数3,4,5,6,7,8,能否使任意三个相邻顶点处的三个数之和(1)大于15?(2)大于16?若能,请在图中标出来;若不能,请说明理由.16.(10分)如图,时钟在四点到五点之间,什么时刻时针与分针成一直角?2007年第18届“希望杯”全国数学邀请赛试卷(初一第1试)参考答案与试题解析一、选择题(共6小题,每小题5分,满分30分)1.(5分)如图,在数轴上有六个点,且AB=BC=CD=DE=EF,则这条数轴的原点在()A.在点A,B之间B.在点B,C之间C.在点C,D之间D.在点D,E之间考点:数轴.专题:计算题;数形结合.分析:根据图示,求得AF间的距离,然后由已知条件AB=BC=CD=DE=EF来确定条数轴的原点的大致位置.解答:解:∵|11﹣(﹣5)|=16,AB=BC=CD=DE=EF,∴AB=BC=CD=DE=EF==3.2,∴这条数轴的原点在B与C之间.故选B.点评:本题主要考查了数轴上对应点的几何意义.2.(5分)(2006•济宁)(﹣8)2006+(﹣8)2005能被下列数整除的是()A.3B.5C.7D.9考点:因式分解的应用.分析:根据乘方的性质,提取公因式(﹣8)2005,整理即可得到是7的倍数,所以能被7整除.解答:解:(﹣8)2006+(﹣8)2005,=(﹣8)(﹣8)2005+(﹣8)2005,=(﹣8+1)(﹣8)2005,=﹣7×(﹣8)2005=7×82005.所以能被7整除.故选C.点评:本题考查提公因式法分解因式,关键在于提取公因式,然后再对所剩的因数进行计算.3.(5分)图中的小方格式边长为1的正方形,则在图中一共可以数出正方形的个数是()A.66 B.50 C.60 D.210考点:规律型:图形的变化类.分析:题中的正方形共有4类,即边长为1,边长为2,边长为3,边长为4,分别找出其对应的正方形的个数再求和即可.解答:解:由图可知,边长为1的小正方形共有4×7=28个;边长为2的正方形共有18个;边长为3的正方形共有10个;边长为4的正方形的个数为4个.所以题中的正方形的个数为28+18+10+4=60个,故选C.点评:本题主要考查了正方形四条边相等的性质问题,应熟练掌握正方形的性质,并能求解一些简单的问题.4.(5分)(2006•济南)如图,直线a与直线b互相平行,则|x﹣y|的值是()A.20 B.80 C.120 D.180考点:平行线的性质;对顶角、邻补角.专题:计算题.分析:根据平行线的性质可得x的度数,然后根据邻补角概念,求出y,即可解答.解答:解:∵直线a与直线b互相平行,∴x=30,∴3y°=180°﹣30°=150°,得y=50,∴|x﹣y|=|30﹣50|=20.故选A.点评:本题主要考查平行线的性质与绝对值的概念.5.(5分)将一个正方形的纸片分成四块,要求这四块大小相等,形状一样,则分的方法共有()A.2种B.4种C.6种D.无数种考点:轴对称的性质;正方形的性质.专题:常规题型.分析:根据正方形的性质,一定被经过中心的直线平分即可解决.解答:解:因为只是要求分成形状、大小都相同的四个部分,没要求具体什么图形,所以只要这两条直线过正方形中心且相互垂直即可,因而不同的折法共有无数种.故选D.点评:本题考查了轴对称及正方形的性质,解决此类问题,要充分考虑题意的要求.6.(5分)某商店同时售出两种服装,每套均卖198元,以成本价计算,其中一套盈利20%,另一套亏本20%,如果不考虑其因素,则这次出售过程中商店()A.不赚不赔B.赚16.5元C.赔25元D.非以上答案考点:一元一次方程的应用.专题:应用题.分析:可分别设两种衣服的进价为未知数,根据盈利情况可列出方程,求解后再比较两种衣服的总进价和总售价的差,即可知盈亏损情况.解答:解:设盈利20%的衣服进价为x元,亏本20%的衣服进价为y,根据题意得:x(1+20%)=198,y(1﹣20%)=198,解得x=165(元),y=247.5(元),两套衣服的进价和为165+247.5=412.5(元),两套衣服的售价和为198×2=396(元),则这次出售过程中商店赔412.5﹣396=16.5(元).故选D.点评:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程.二、填空题(共6小题,每小题5分,满分30分)7.(5分)北京与纽约的时差为﹣13时(负号表示同一时刻纽约时间比北京时间晚),如果现在是北京时间18时,那么纽约时间是5时.考点:正数和负数.分析:首先审清题意,明确“正”和“负”所表示的意义;再根据题意作答.解答:解:由题意得,纽约时间为18﹣13=5,故纽约时间为5时.点评:解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.8.(5分)(2009•枣庄)如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB=180度.考点:角的计算.专题:计算题.分析:本题考查了角度的计算问题,因为本题中∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.解答:解:设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,所以∠AOC+∠BOD=90°+a+90°﹣a=180°.故答案为180°.点评:在本题中要注意∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.9.(5分)用定义新运算,对于任意有理数x,y都有x y=2x+y2+1,例如35=2×3+52+1=32,那么2[(﹣7)3]=21.考点:有理数的混合运算.专题:计算题;新定义.分析:由于对于任意有理数x,y都有x y=2x+y2+1,那么利用这个定义的新运算首先计算(﹣7)3,然后计算括号外面的即可求解.解答:解:∵对于任意有理数x,y都有x y=2x+y2+1,∴(﹣7)3=2×(﹣7)+32+1=﹣4,∴2[(﹣7)3]=2(﹣4)=2×2+(﹣4)2+1=21.故答案为:21.点评:此题主要考查有理数的混合运算,解题的关键是首先正确理解新定义的运算法则,然后把数据代入其中计算即可求解.10.(5分)计算=.考点:绝对值.专题:规律型.分析:根据绝对值的定义,去掉绝对值符合,化简求值.解答:解:== ==故答案为点评:解决本题的关键是去掉绝对值符号后,部分数值恰好是互为相反数,其和等于0.11.(5分)为估计某水库鲢鱼的数量,养鱼户李老板先捞上150条鲢鱼并在上做红色的记号,然后立即将这150条鲢鱼放回水库中,一周后,李老板又捞取200条鲢鱼,数一数带红色记号的鱼有三条,据此可估计出该水库中鲢鱼约有10000条.考点:用样本估计总体.专题:计算题;应用题.分析:设该水库中鲢鱼约有x条,由于李老板先捞上150条鲢鱼并在上做红色的记号,然后立即将这150条鲢鱼放回水库中,一周后,李老板又捞取200条鲢鱼,数一数带红色记号的鱼有三条,由此即可列出方程200:3=x:150,解此方程即可求出该水库中鲢鱼约有多少条.解答:解:设该水库中鲢鱼约有x条,依题意得200:3=x:150,∴x=10000,∴估计出该水库中鲢鱼约有10000条.故答案为:10000.点评:此题主要考查了利用样本估计总体的思想,解题时首先正确理解题意,然后根据题意和样本估计总体的思想列出方程即可解决问题.12.(5分)若P为质数,P3+9仍为质数,则P2﹣7=﹣3.考点:质数与合数.专题:计算题.分析:由于在所有的质数中,只有2是偶数,故P为质数,P3+9仍为质数,则P=2,代入P2﹣7即可求解.解答:解:∵P为质数,P3+9仍为质数,当P为奇质数时,P3+9为大于2的偶数,不符合题意;当P为2时,P3+9=17,仍为质数,符合题意.∴P=2.当P=2时,P2﹣7=4﹣7=﹣3.故答案为:﹣3.点评:本题考查了质数的基本性质,解题的关键是熟悉所有的质数中,只有2是偶数,从而确定p=2.三、解答题(共4小题,满分40分)13.(10分)为响应“建设节约型社会”的号召,某市制定如下规定:每户用煤气如果不超过m立方米,按每立方米0.8元收费,超过m立方米,超过的部分按每立方米1.2元收费.小颖家10,11月的交煤气费的情况如下表:月份用气量缴费金额10 50 4011 75 66(1)求m的值;(2)由于天气转冷,小颖家12月份的用气量预计将增大20%,为了节约煤气,小颖的爸爸换用了高科技煤气灶具,该灶具在提供相同热量的情况下的用气量是原灶具的60%,试问小颖家12月份比预计可少交煤气费多少元?考点:一元一次方程的应用.专题:应用题.分析:(1)根据小颖家10,11月的交煤气费的情况可知m的取值在50和75之间,再根据11月份的交费金额和“不超过m立方米,按每立方米0.8元收费,超过m立方米,超过的部分按每立方米1.2元收费”可列出方程,求解即可.(2)根据上题的关系式可先求出未用高科技时应付的煤气费,再求出使用高科技时应付的煤气费,二者之差即可得少交的煤气费.解答:解:(1)如果用户用煤气不超过m立方米,按每立方米0.8元收费;由图可知小颖家10月11月用气分别为50、75立方米,∵50×0.8=40,75×0.8=60,小颖家交费为40元,60元,∴可知m的范围为50≤m<75,根据题意得:0.8m+(75﹣m)×1.2=66,解得:m=60.(2)在11月基础上预交煤气费为:60×0.8+[75(1+20%)﹣60]×1.2=48+36=84(元);换用了高科技煤气灶具后:用气量为75×(1+20%)×60%=54(立方米),则应交煤气费为:54×0.8=43.2(元);可少交煤气费:84﹣43.2=40.8(元).答:(1)m的值为60;(2)小颖家12月份比预计可少交煤气费40.8元.点评:本题考查了一元一次方程的应用及列代数式,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.14.(10分)某城市平面图如图所示,每条线段均表示街道:(1)图中共有多少条线段?(2)小饶需从A1到B6办事,怎样走最近,最近的走法共有几种?考点:计数方法.分析:(1)根据两点可以确定一条线段,水平方向每行有15条线段,竖直方向除含点F列外,每列有10条线段,含F点这列有15条线段,D4B6方向有3条线段,还有线段A1C2这一条,于是可以计算出总条数;(2)从A1到B6的路线有很多条,若线路最近,观察可以找到6条线路,即最近的走法有6种.解答:解:(1)15×5+10×5+15×1+1+3=144(条);(2)最近路线为:①A1→C2→C3→C4→E4→D4→F→B6;②A1→C2→E2→D2→D3→D4→F→B6;③A1→C2→C3→E3→E4→D4→F→B6;④A1→C2→E2→E3→D3→D4→F→B6;⑤A1→C2→C3→E3→D3→D4→F→B6;⑥A1→C2→E2→E3→E4→D4→F→B6,共6种走法.点评:本题主要考查计数方法的知识点,熟练掌握计数原理,此题难度有点大,第二问很容易漏掉一种或几种.15.(10分)如图,在六边形的顶点处,分别标上数3,4,5,6,7,8,能否使任意三个相邻顶点处的三个数之和(1)大于15?(2)大于16?若能,请在图中标出来;若不能,请说明理由.考点:整数问题的综合运用.分析:(1)可以分别设这六个数为a,b,c,d,e,f然后将其三个数相加,根据题中给出的条件可知,这把各数的和判断即可得出结论.(2)根据上题的出的结论直接判断即可解答.解答:解:(1)能,如图.6个点的顺序分别为8﹣3﹣6﹣7﹣4﹣5.任意三个相邻顶点处的和分别为17﹣16﹣17﹣16﹣17﹣16.满足均大于15,(2)但不满足均大于16.如图,设按要求所填的六个数顺次为a、b、c、d、e、f.它们任意相邻三数和大于16,即大于或等于17.所以a+b+f≥17,b+c+d≥17,c+d+e≥17,d+e+f≥17,e+f+a≥17,f+a+b≥17.则每个不等式左边相加一定大于或等于102,即3(a+b+c+d+e+f)≥102故(a+b+c+d+e+f)≥34.而1+2+3+4+5+6=33,所以不能使每三个相邻的数之和都大于16.点评:此题主要考查了整数问题的综合应用,分别得出相邻数据之和规律是解题关键.16.(10分)如图,时钟在四点到五点之间,什么时刻时针与分针成一直角?考点:一元一次方程的应用;钟面角.专题:创新题型.分析:时针在四点与五点之间,时针与分针有2种可能会成直角,四点与五点成30度角,时针每分钟走0.5度,而分针每分钟走6度.并且时针与分针成直角分两种情况进行讨论.解答:解:时针每分钟走0.5度,而分针每分钟走6度,4点钟时针与分针角度为120度,设时针在四点x分钟时,时针与分针成直角,分两种情况讨论:(1)时针在分针前面时,120﹣6x+0.5x=90解得x=5;(2)时针在分针后面时,6x﹣120﹣0.5x=90解得x=38;所以在4点5分或者4点38分时,时针与分针成直角.点评:解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.注意四点到五点之间,时针与分针成直角有两种情况.如获取更多相关试题及答案,请联系京翰教育,服务电话4006767133。
历届(第1-23届)希望杯数学竞赛初一七年级真题及答案

8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( )
A.乘以同一个数.B.乘以同一个整式.C.加上同一个代数式.D.都加上1.
9.杯子中有大半杯水,第二天较第一天减少了10%,第三天又较第二天增加了10%,那么,第三天杯中的水量与第一天杯中的水量相比的结果是( )
7.注意到:
当a=-0.2,b=0.04时,a2-b=(-0.2)2-0.04=0,b+a+0.16=0.04-0.2+0.16=0.
8.食盐30%的盐水60千克中含盐60×30%(千克)设蒸发变成含盐为40%的水重x克,即0.001x千克,此时,60×30%=(0.001x)×40%
解得:x=45000(克).
9.设杯中原有水量为a,依题意可得,
第二天杯中水量为a×(1-10%)=0.9a;
第三天杯中水量为(0.9a)×(1+10%)=0.9×1.1×a;
第三天杯中水量与第一天杯中水量之比为
所以第三天杯中水量比第一天杯中水量少了,选C.
10.设两码头之间距离为s,船在静水中速度为a,水速为v0,则往返一次所用时间为
5.三个连续自然数的平方和(填“是”或“不是”或“可能是”)______某个自然数的平方.
三、解答题(写出推理、运算的过程及最后结果.每题5分,共15分)
1.两辆汽车从同一地点同时出发,沿同一方向同速直线行驶,每车最多只能带24桶汽油,途中不能用别的油,每桶油可使一辆车前进60公里,两车都必须返回出发地点,但是可以不同时返回,两车相互可借用对方的油.为了使其中一辆车尽可能地远离出发地点,另一辆车应当在离出发地点多少公里的地方返回?离出发地点最远的那辆车一共行驶了多少公里?
(整理)历届1 24希望杯数学竞赛初一七年级真题及答案

.................
17.希望杯第九届(1998 年)初中一年级第一试试题 ........................................... 113-129 18.希望杯第九届(1998 年)初中一年级第二试试题 ...........................................122-138 19.希望杯第十届(1999 年)初中一年级第二试试题 ...........................................129-147 20.希望杯第十届(1999 年)初中一年级第一试试题 ...........................................148-151 21.希望杯第十一届(2000 年)初中一年级第一试试题 .......................................142-161 22.希望杯第十一届(2000 年)初中一年级第二试试题 .......................................149-169 23.希望杯第十二届(2001 年)初中一年级第一试试题 .......................................153-174 24.希望杯第十二届(2001 年)初中一年级第二试试题 .......................................157-178 25.希望杯第十三届(2002 年)初中一年级第一试试题 .......................................163-184 26.希望杯第十三届(2001 年)初中一年级第二试试题 .......................................167-189 27.希望杯第十四届(2003 年)初中一年级第一试试题 .......................................174-196 28.希望杯第十四届(2003 年)初中一年级第二试试题 .......................................178-200 29.希望杯第十五届(2004 年)初中一年级第一试试题 .............................................. 182 30.希望杯第十五届(2004 年)初中一年级第二试试题 .............................................. 183 31.希望杯第十六届(2005 年)初中一年级第一试试题 .......................................213-218 32.希望杯第十六届(2005 年)初中一年级第二试试题 .............................................. 183 33.希望杯第十七届(2006 年)初中一年级第一试试题 .......................................228-233 34.希望杯第十七届(2006 年)初中一年级第二试试题 .......................................234-238 35.希望杯第十八届(2007 年)初中一年级第一试试题 .......................................242-246 26.希望杯第十八届(2007 年)初中一年级第二试试题 .......................................248-251 37.希望杯第十九届(2008 年)初中一年级第一试试题 .......................................252-256 38.希望杯第十九届(2008 年)初中一年级第二试试题 .......................................257-262 39.希望杯第二十届(2009 年)初中一年级第一试试题 .......................................263-266 20.希望杯第二十届(2009 年)初中一年级第二试试题 .......................................267-271 21.希望杯第二十一届(2010 年)初中一年级第一试试题 ...................................274-276 22.希望杯第二十二届(2011 年)初中一年级第二试试题 ...................................270-273 23.希望杯第二十三届(2012 年)初中一年级第二试试题 ...................................270-273 23.希望杯第二十四届(2013 年)初中一年级第二试试题 ...................................274-281 23.希望杯第二十四届(2013 年)初中一年级第二试试题 ...................................
最新历届(1-24)希望杯数学竞赛初一七年级真题及答案

“希望杯”全国数学竞赛(第1-24届)初一年级/七年级第一/二试题目录1.希望杯第一届(1990年)初中一年级第一试试题............................................. 003-0052.希望杯第一届(1990年)初中一年级第二试试题............................................. 010-0123.希望杯第二届(1991年)初中一年级第一试试题............................................. 015-0204.希望杯第二届(1991年)初中一年级第二试试题............................................. 021-0265.希望杯第三届(1992年)初中一年级第一试试题............................................. 028-0326.希望杯第三届(1992年)初中一年级第二试试题............................................. 033-0407.希望杯第四届(1993年)初中一年级第一试试题............................................. 042-0508.希望杯第四届(1993年)初中一年级第二试试题............................................. 049-0589.希望杯第五届(1994年)初中一年级第一试试题............................................. 056-06610.希望杯第五届(1994年)初中一年级第二试试题 .......................................... 062-07311.希望杯第六届(1995年)初中一年级第一试试题 ........................................... 069-08012希望杯第六届(1995年)初中一年级第二试试题........................................... 076-08713.希望杯第七届(1996年)初中一年级第一试试题........................................... 085-09814.希望杯第七届(1996年)初中一年级第二试试题............................................. 90-10515.希望杯第八届(1997年)初中一年级第一试试题............................................. 98-11316.希望杯第八届(1997年)初中一年级第二试试题........................................... 105-12017.希望杯第九届(1998年)初中一年级第一试试题........................................... 113-12918.希望杯第九届(1998年)初中一年级第二试试题........................................... 122-13819.希望杯第十届(1999年)初中一年级第二试试题........................................... 129-14720.希望杯第十届(1999年)初中一年级第一试试题........................................... 148-15121.希望杯第十一届(2000年)初中一年级第一试试题....................................... 142-16122.希望杯第十一届(2000年)初中一年级第二试试题....................................... 149-16923.希望杯第十二届(2001年)初中一年级第一试试题....................................... 153-17424.希望杯第十二届(2001年)初中一年级第二试试题....................................... 157-17825.希望杯第十三届(2002年)初中一年级第一试试题....................................... 163-18426.希望杯第十三届(2001年)初中一年级第二试试题....................................... 167-18927.希望杯第十四届(2003年)初中一年级第一试试题....................................... 174-19628.希望杯第十四届(2003年)初中一年级第二试试题....................................... 178-20029.希望杯第十五届(2004年)初中一年级第一试试题 (182)30.希望杯第十五届(2004年)初中一年级第二试试题 (183)31.希望杯第十六届(2005年)初中一年级第一试试题....................................... 213-21832.希望杯第十六届(2005年)初中一年级第二试试题 (183)33.希望杯第十七届(2006年)初中一年级第一试试题....................................... 228-23334.希望杯第十七届(2006年)初中一年级第二试试题....................................... 234-23835.希望杯第十八届(2007年)初中一年级第一试试题....................................... 242-246 26.希望杯第十八届(2007年)初中一年级第二试试题....................................... 248-25137.希望杯第十九届(2008年)初中一年级第一试试题....................................... 252-25638.希望杯第十九届(2008年)初中一年级第二试试题....................................... 257-26239.希望杯第二十届(2009年)初中一年级第一试试题....................................... 263-26620.希望杯第二十届(2009年)初中一年级第二试试题....................................... 267-27121.希望杯第二十一届(2010年)初中一年级第一试试题 ................................... 274-27622.希望杯第二十二届(2011年)初中一年级第二试试题 ................................... 270-27323.希望杯第二十三届(2012年)初中一年级第二试试题 ................................... 270-273 23.希望杯第二十四届(2013年)初中一年级第二试试题 ................................... 274-281 23.希望杯第二十四届(2013年)初中一年级第二试试题 ................................... 274-281希望杯第一届(1990年)初中一年级第1试试题一、选择题(每题1分,共10分)1.如果a ,b 都代表有理数,并且a +b=0,那么 ( )A .a ,b 都是0.B .a ,b 之一是0.C .a ,b 互为相反数.D .a ,b 互为倒数.2.下面的说法中正确的是 ( )A .单项式与单项式的和是单项式.B .单项式与单项式的和是多项式.C .多项式与多项式的和是多项式.D .整式与整式的和是整式.3.下面说法中不正确的是 ( )A. 有最小的自然数. B .没有最小的正有理数.C .没有最大的负整数.D .没有最大的非负数.4.如果a ,b 代表有理数,并且a +b 的值大于a -b 的值,那么( ) A .a ,b 同号. B .a ,b 异号.C .a >0. D .b >0.5.大于-π并且不是自然数的整数有( ) A .2个. B .3个.C .4个. D .无数个.6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身.这四种说法中,不正确的说法的个数是 ( )A .0个.B .1个.C .2个.D .3个.7.a 代表有理数,那么,a 和-a 的大小关系是 ( )A .a 大于-a .B .a 小于-a .C .a 大于-a 或a 小于-a .D .a 不一定大于-a .8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( )A .乘以同一个数.B .乘以同一个整式.C .加上同一个代数式.D .都加上1.9.杯子中有大半杯水,第二天较第一天减少了10%,第三天又较第二天增加了10%,那么,第三天杯中的水量与第一天杯中的水量相比的结果是( )A .一样多.B .多了.C .少了.D .多少都可能.10.轮船往返于一条河的两码头之间,如果船本身在静水中的速度是固定的,那么,当这条河的水流速度增大时,船往返一次所用的时间将( )A .增多.B .减少.C .不变.D .增多、减少都有可能.二、填空题(每题1分,共10分)1. 21115160.01253(87.5)(2)4571615⨯-⨯-÷⨯+--= ______. 2.198919902-198919892=______.3.2481632(21)(21)(21)(21)(21)21+++++-=________. 4. 关于x 的方程12148x x +--=的解是_________. 5.1-2+3-4+5-6+7-8+…+4999-5000=______.6.当x=-24125时,代数式(3x 3-5x 2+6x -1)-(x 3-2x 2+x -2)+(-2x 3+3x 2+1)的值是____. 7.当a=-0.2,b=0.04时,代数式272711()(0.16)()73724a b b a a b --++-+的值是______.8.含盐30%的盐水有60千克,放在秤上蒸发,当盐水变为含盐40%时,秤得盐水的重是______克.9.制造一批零件,按计划18天可以完成它的13.如果工作4天后,工作效率提高了15,那么完成这批零件的一半,一共需要______天.10.现在4点5分,再过______分钟,分针和时针第一次重合.答案与提示一、选择题1.C 2.D 3.C 4.D 5.C 6.B 7.D 8.D 9.C 10.A提示:1.令a=2,b=-2,满足2+(-2)=0,由此2.x2,2x2,x3都是单项式.两个单项式x3,x2之和为x3+x2是多项式,排除A.两个单项式x2,2x2之和为3x2是单项式,排除B.两个多项式x3+x2与x3-x2之和为2x3是个单项式,排除C,因此选D.3.1是最小的自然数,A正确.可以找到正所以C“没有最大的负整数”的说法不正确.写出扩大自然数列,0,1,2,3,…,n,…,易知无最大非负数,D正确.所以不正确的说法应选C.5.在数轴上容易看出:在-π右边0的左边(包括0在内)的整数只有-3,-2,-1,0共4个.选C.6.由12=1,13=1可知甲、乙两种说法是正确的.由(-1)3=-1,可知丁也是正确的说法.而负数的平方均为正数,即负数的平方一定大于它本身,所以“负数平方不一定大于它本身”的说法不正确.即丙不正确.在甲、乙、丙、丁四个说法中,只有丙1个说法不正确.所以选B.7.令a=0,马上可以排除A、B、C,应选D.8.对方程同解变形,要求方程两边同乘不等于0的数.所以排除A.我们考察方程x-2=0,易知其根为x=2.若该方程两边同乘以一个整式x-1,得(x-1)(x -2)=0,其根为x=1及x=2,不与原方程同解,排除B.若在方程x-2=0两边加上同一个代数式去了原方程x=2的根.所以应排除C.事实上方程两边同时加上一个常数,新方程与原方程同解,对D,这里所加常数为1,因此选D.9.设杯中原有水量为a,依题意可得,第二天杯中水量为a×(1-10%)=0.9a;第三天杯中水量为(0.9a)×(1+10%)=0.9×1.1×a;第三天杯中水量与第一天杯中水量之比为所以第三天杯中水量比第一天杯中水量少了,选C.10.设两码头之间距离为s,船在静水中速度为a,水速为v0,则往返一次所用时间为设河水速度增大后为v,(v>v0)则往返一次所用时间为由于v-v0>0,a+v0>a-v0,a+v>a-v所以(a+v0)(a+v)>(a-v0)(a-v)∴t0-t<0,即t0<t.因此河水速增大所用时间将增多,选A.二、填空题提示:2.198919902-198919892=(19891990+19891989)×(19891990-19891989)=(19891990+19891989)×1=39783979.3.由于(2+1)(22+1)(24+1)(28+1)(216+1)=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)=(22-1)(22+1)(24+1)(28+1)(216+1)=(24-1)(24+1)(28+1)(216+1)=(28-1)(28+1)(216+1)=(216-1)(216+1)=232-1.2(1+x)-(x-2)=8,2+2x-x+2=8解得;x=45.1-2+3-4+5-6+7-8+…+4999-5000=(1-2)+(3-4)+(5-6)+(7-8)+…+(4999-5000)=-2500.6.(3x3-5x2+6x-1)-(x3-2x2+x-2)+(-2x3+3x2+1)=5x+27.注意到:当a=-0.2,b=0.04时,a2-b=(-0.2)2-0.04=0,b+a+0.16=0.04-0.2+0.16=0.8.食盐30%的盐水60千克中含盐60×30%(千克)设蒸发变成含盐为40%的水重x克,即0.001x千克,此时,60×30%=(0.001x)×40%解得:x=45000(克).10.在4时整,时针与分针针夹角为120°即希望杯第一届(1990年)初中一年级第2试试题一、选择题(每题1分,共5分)以下每个题目里给出的A,B,C,D四个结论中有且仅有一个是正确的.请你在括号填上你认为是正确的那个结论的英文字母代号.1.某工厂去年的生产总值比前年增长a%,则前年比去年少的百分数是( )A.a%.B.(1+a)%. C.1100aa+D.100aa+2.甲杯中盛有2m毫升红墨水,乙杯中盛有m毫升蓝墨水,从甲杯倒出a毫升到乙杯里, 0<a<m,搅匀后,又从乙杯倒出a毫升到甲杯里,则这时( )A.甲杯中混入的蓝墨水比乙杯中混入的红墨水少.B.甲杯中混入的蓝墨水比乙杯中混入的红墨水多.C.甲杯中混入的蓝墨水和乙杯中混入的红墨水相同.D.甲杯中混入的蓝墨水与乙杯中混入的红墨水多少关系不定.3.已知数x=100,则( )A.x是完全平方数.B.(x-50)是完全平方数.C.(x-25)是完全平方数.D.(x+50)是完全平方数.4.观察图1中的数轴:用字母a,b,c依次表示点A,B,C对应的数,则111,,ab b a c-的大小关系是( )A.111ab b a c<<-; B.1b a-<1ab<1c; C.1c<1b a-<1ab; D.1c<1ab<1b a-.5.x=9,y=-4是二元二次方程2x2+5xy+3y2=30的一组整数解,这个方程的不同的整数解共有( )A.2组.B.6组.C.12组.D.16组.二、填空题(每题1分,共5分)1.方程|1990x-1990|=1990的根是______.2.对于任意有理数x,y,定义一种运算*,规定x*y=ax+by-cxy,其中的a,b,c表示已知数,等式右边是通常的加、减、乘运算.又知道1*2=3,2*3=4,x*m=x(m≠0),则m 的数值是______.3.新上任的宿舍管理员拿到20把钥匙去开20个房间的门,他知道每把钥匙只能开其中的一个门,但不知道每把钥匙是开哪一个门的钥匙,现在要打开所有关闭着的20个房间,他最多要试开______次.4.当m=______时,二元二次六项式6x2+mxy-4y2-x+17y-15可以分解为两个关于x,y 的二元一次三项式的乘积.5.三个连续自然数的平方和(填“是”或“不是”或“可能是”)______某个自然数的平方.三、解答题(写出推理、运算的过程及最后结果.每题5分,共15分)1.两辆汽车从同一地点同时出发,沿同一方向同速直线行驶,每车最多只能带24桶汽油,途中不能用别的油,每桶油可使一辆车前进60公里,两车都必须返回出发地点,但是可以不同时返回,两车相互可借用对方的油.为了使其中一辆车尽可能地远离出发地点,另一辆车应当在离出发地点多少公里的地方返回?离出发地点最远的那辆车一共行驶了多少公里?2.如图2,纸上画了四个大小一样的圆,圆心分别是A,B,C,D,直线m通过A,B,直线n通过C,D,用S表示一个圆的面积,如果四个圆在纸上盖住的总面积是5(S-1),直线m,n之间被圆盖住的面积是8,阴影部分的面积S1,S2,S3满足关系式S3=13S1=13S2,求S.3.求方程11156x y z++=的正整数解.答案与提示一、选择题1.D 2.C 3.C 4.C 5.D提示:1.设前年的生产总值是m,则去年的生产总值是前年比去年少这个产值差占去年的应选D.2.从甲杯倒出a毫升红墨水到乙杯中以后:再从乙杯倒出a毫升混合墨水到甲杯中以后:乙杯中含有的红墨水的数量是①乙杯中减少的蓝墨水的数量是②∵①=②∴选C.∴x-25=(10n+2+5)2可知应当选C.4.由所给出的数轴表示(如图3):可以看出∴①<②<③,∴选C.5.方程2x2+5xy+3y2=30可以变形为(2x+3y)(x+y)=1·2·3·5∵x,y是整数,∴2x+3y,x+y也是整数.由下面的表可以知道共有16个二元一次方程组,每组的解都是整数,所以有16组整数组,应选D.二、填空题提示:1.原方程可以变形为|x-1|=1,即x-1=1或-1,∴x=2或0.2.由题设的等式x*y=ax+by-cxy及x*m=x(m≠0)得a·0+bm-c·0·m=0,∴bm=0.∵m≠0,∴b=0.∴等式改为x*y=ax-cxy.∵1*2=3,2*3=4,解得a=5,c=1.∴题设的等式即x*y=5x-xy.在这个等式中,令x=1,y=m,得5-m=1,∴m=4.3.∵打开所有关闭着的20个房间,∴最多要试开4.利用“十字相乘法”分解二次三项式的知识,可以判定给出的二元二次六项式6x2+mxy-4y2-x+17y-15中划波浪线的三项应当这样分解:3x -52x +3现在要考虑y,只须先改写作然后根据-4y2,17y这两项式,即可断定是:由于(3x+4y-5)(2x-y+3)=6x2+5xy-4y2-x+17y-15就是原六项式,所以m=5.5.设三个连续自然数是a-1,a,a+1,则它们的平方和是(a-1)2+a2+(a+1)2=3a2+2,显然,这个和被3除时必得余数2.另一方面,自然数被3除时,余数只能是0或1或2,于是它们可以表示成3b,3b+1,3b+2(b是自然数)中的一个,但是它们的平方(3b)2=9b2(3b+1)2=9b2+6b+1,(3b+2)2=9b2+12b+4=(9b2+12b+3)+1被3除时,余数要么是0,要么是1,不能是2,所以三个连续自然数平方和不是某个自然数的平方.三、解答题1.设两辆汽车一为甲一为乙,并且甲用了x升汽油时即回返,留下返程需的x桶汽油,将多余的(24-2x)桶汽油给乙.让乙继续前行,这时,乙有(24-2x)+(24-x)=48-3x桶汽油,依题意,应当有48-3x≤24,∴x≥8.甲、乙分手后,乙继续前行的路程是这个结果中的代数式30(48-4x)表明,当x的值愈小时,代数式的值愈大,因为x≥8,所以当x=8时,得最大值30(48-4·8)=480(公里),因此,乙车行驶的路程一共是2(60·8+480)=1920(公里).2.由题设可得即2S-5S3=8……②∴x,y,z都>1,因此,当1<x≤y≤z时,解(x,y,z)共(2,4,12),(2,6,6),(3,3,6),(3,4,4)四组.由于x,y,z在方程中地位平等.所以可得如下表所列的15组解.希望杯第二届(1991年)初中一年级第1试试题一、选择题(每题1分,共15分)以下每个题目的A,B,C,D四个结论中,仅有一个是正确的,请在括号内填上正确的那个结论的英文字母代号.1.数1是( )A.最小整数.B.最小正数.C.最小自然数.D.最小有理数.2.若a>b,则( )A.11a b; B.-a<-b.C.|a|>|b|.D.a2>b2.3.a为有理数,则一定成立的关系式是( )A.7a>a.B.7+a>a.C.7+a>7.D.|a|≥7.4.图中表示阴影部分面积的代数式是( )A.ad+bc.B.c(b-d)+d(a-c).C.ad+c(b-d).D.ab-cd.5.以下的运算的结果中,最大的一个数是( )A.(-13579)+0.2468; B.(-13579)+1 2468;C.(-13579)×12468; D.(-13579)÷124686.3.1416×7.5944+3.1416×(-5.5944)的值是( ) A.6.1632. B.6.2832.C.6.5132.D.5.3692.7.如果四个数的和的14是8,其中三个数分别是-6,11,12,则笫四个数是( )A.16. B.15. C.14. D.13.8.下列分数中,大于-13且小于-14的是( )A.-1120; B.-413; C.-316; D.-617.9.方程甲:34(x-4)=3x与方程乙:x-4=4x同解,其根据是( )A.甲方程的两边都加上了同一个整式x.B.甲方程的两边都乘以43x;C. 甲方程的两边都乘以43; D. 甲方程的两边都乘以34.10.如图: ,数轴上标出了有理数a,b,c的位置,其中O是原点,则111,,a b c的大小关系是( ) A.111a b c>>; B.1b >1c >1a ; C. 1b >1a >1c ; D. 1c >1a >1b .11.方程522.2 3.7x =的根是( ) A .27. B .28. C .29. D .30. 12.当x=12,y=-2时,代数式42x y xy -的值是( )A .-6.B .-2.C .2.D .6.13.在-4,-1,-2.5,-0.01与-15这五个数中,最大的数与绝对值最大的那个数的乘积是( )A .225.B .0.15.C .0.0001.D .1.14.不等式124816x x x xx ++++>的解集是( ) A .x <16. B .x >16.C .x <1. D.x>-116. 15.浓度为p%的盐水m 公斤与浓度为q%的盐水n 公斤混合后的溶液浓度是 ( ) A.%2p q +; B.()%mp nq +; C.()%mp nq p q ++;D.()%mp nq m n++.二、填空题(每题1分,共15分)1. 计算:(-1)+(-1)-(-1)×(-1)÷(-1)=______. 2. 计算:-32÷6×16=_______. 3. 计算:(63)36162-⨯=__________.4. 求值:(-1991)-|3-|-31||=______. 5. 计算:1111112612203042-----=_________. 6.n 为正整数,1990n -1991的末四位数字由千位、百位、十位、个位、依次排列组成的四位数是8009.则n 的最小值等于______.7. 计算:19191919199191919191⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=_______.8. 计算:15[(-1989)+(-1990)+(-1991)+(-1992)+(-1993)]=________.9.在(-2)5,(-3)5,512⎛⎫-⎪⎝⎭,513⎛⎫-⎪⎝⎭中,最大的那个数是________.10.不超过(-1.7)2的最大整数是______.11.解方程21101211,_____. 3124x x xx-++-=-=12.求值:355355113113355113⎛⎫---⎪⎝⎭⎛⎫- ⎪⎝⎭=_________.13.一个质数是两位数,它的个位数字与十位数字的差是7,则这个质数是______.14.一个数的相反数的负倒数是119,则这个数是_______.15.如图11,a,b,c,d,e,f均为有理数.图中各行,各列、两条对角线上三个数之和都相等,则ab cd efa b c d e f+++++++=____.答案与提示一、选择题1.C 2.B 3.B 4.C 5.C 6.B 7.B 8.B 9.C 10.B 11.D 12.A 13.B 1 4.A 15.D提示:1.整数无最小数,排除A;正数无最小数,排除B;有理数无最小数,排除D.1是最小自然数.选C.有|2|<|-3|,排除C;若2>-3有22<(-3)2,排除D;事实上,a>b必有-a<-b.选B.3.若a=0,7×0=0排除A;7+0=7排除C|0|<7排除D,事实上因为7>0,必有7+a>0+a=a.选B.4.把图形补成一个大矩形,则阴影部分面积等于ab-(a-c)(b-d)=ab-[ab-ad-c(b-d)]=ab-ab+ad+c(b-d)=ad+c(b-d).选C.5.运算结果对负数来说绝对值越小其值越大。
第18届“希望杯”全国数学邀请赛试卷初第2试

2007 年第 18 届“希望杯”全国数学邀请赛试卷(初一第2 试)一、选择题(共 10 小题,每题 4 分,满分 40 分)1.(4 分)假定未拧紧的水龙头每秒钟溢出2 滴水, 每滴水约 0.05 毫升, 现有一个水龙头未拧紧, 4 小时后,才被发现拧紧,在这段时间内,水龙头共滴水约(用科学记数法表示,结果保存两位有效数字) ( )A .1440 毫升B . 1.4×10 3毫升4D . 14× 10 2毫升C . 0.14× 10 毫升2.( 4 分)如图,直线 l 与∠ O 的两边分别交于点A 、B ,则图中以 O 、 A 、B 为端点的射线的条数总和是( )A .5B .6C . 7D . 83.(4 分)整数 a ,b 知足: ab ≠ 0 且 a+b = 0,有以下判断: ① a ,b 之间没有正分数; ② a ,b 之间没有负分数; ③ a , b 之间至多有一个整数;④ a , b 之间起码有一个整数.此中,正确判断的个数为( ) A .1B .2C . 3D . 44.( 4 分)方程的解是 x =()A .B .C .D .5.( 4 分)如图,边长为 1 的正六边形纸片是轴对称图形,它的对称轴的条数是()A .1B .3C . 6D . 96.( 4 分)在 9 个数:﹣ 5,﹣ 4,﹣ 3,﹣ 2,﹣ 1, 0,1, 2,3 中,能使不等式﹣ 3x 2<﹣ 14建立的数的个数是( )A .2B .3C . 4D . 57.( 4 分)韩老师特制了 4 个相同的立方块,并将它们如图 A 搁置,而后又如图 B 搁置,则图 B 中四个底面正方形中的点数之和为()A .11B .13 C. 14 D. 168.( 4 分)对于相互互质的三个正整数a, b, c,有以下判断:① a, b, c 均为奇数;② a,b, c 中必有一个偶数;③ a, b,c 没有公因数;④ a, b,c 必有公因数.此中,不正确的判断的个数为()A .1B .2 C. 3 D. 49.( 4 分)将棱长为 1 厘米的 42 个立方体积木拼在一同,组成一个实心的长方体.假如长方体底面的周长为18 厘米,那么这个长方体的高是()A .2 厘米B .3 厘米C. 6 厘米D. 7 厘米10.( 4 分) If 0< c< b< a,then()A .B.C.D.二、填空题(共10 小题,每题 4 分,满分40 分)11.(4 分)如有理数 m, n, p 知足,则=.12.( 4 分)今日( 2007 年 4 月 15 日,礼拜日)是第 18 届“希望杯”全国数学邀请赛举行第 2 试的日子,那么今日此后的第4.2007 +15 天是礼拜13.(4 分)孔子出生在公元前 551 年 9 月 28 日,则 2007 年 9 月 28 日是孔子寿辰周年.(注:不存在公元 0 年)14.( 4 分) In Fig , ABCD is a rectangle .The area of the shaded rectangle is .15.( 4 分)下表是某中学初一(5)班 2007 年第一学期期末考试数学成绩统计表:这个班数学成绩的均匀分不低于分,不高于分.(精准到0.1)16.( 4 分)已知,此中 x, y, z 代表非2 2 2.0 数字,那么 x +y +z =17.( 4 分)某城市有一百万户居民,每户用水量定额为月均匀 5 吨,因为 6,7,8 月天热,每户每个月多用水 1 吨,为了不超出整年用水定额,则整年的其余月份每户的用水量应控制在每个月均匀吨以内.假如每户每日节俭用水 2 千克,则全市一年(按 365 天计)节俭的水量约占整年用水定额的%(保存三位有效数字)18.( 4 分) a, b, c 都是质数,且知足a+b+c+abc= 99,则=.19.( 4 分)一项机械加工作业,用 4 台 A 型车床, 5 天能够达成;用 4 台 A 型车床和 2 台 B 型车床, 3 天能够达成;用 3 台 B 型车床和 9 台 C 型车床, 2 天能够达成.若 A 型、 B 型和 C 型车床各一台一同工作 6 天后,只余下一台 A 型车床持续工作,则再用天就能够达成这项作业.20.( 4 分)设 0< a<1,﹣ 2< b<﹣ 1,则和四个式子中,值最大的是,值最小的是.三、解答题(共 3 小题,满分 40 分)21.( 10 分)小明在平面上标出了2007 个点并画了一条直线 L,他发现:这 2007 个点中的每一点对于直线 L 的对称点,仍在这2007 个点中,请你说明:这2007 个点中起码有 1 个点在直线 L 上.22.( 15 分)小明和哥哥在环形跑道上练习长跑.他们从同一同点沿相反方向同时出发,每隔 25 秒钟相遇一次.此刻,他们从同一同跑点沿相同方向同时出发,经过25 分钟哥哥追上了小明,而且比小明多跑了20 圈,求:(1)哥哥速度是小明速度的多少倍?(2)哥哥追上小明时,小明跑了多少圈?23.( 15 分)知足 1+3n≤ 2007,且使得1+5n 是完整平方数的正整数n 共有多少个?2007 年第 18 届“希望杯” 全国数学邀请赛试卷 (初一第2 试)参照答案与试题分析一、选择题(共 10 小题,每题4 分,满分 40 分)1.(4 分)假定未拧紧的水龙头每秒钟溢出2 滴水, 每滴水约 0.05 毫升, 现有一个水龙头未拧紧, 4 小时后,才被发现拧紧,在这段时间内,水龙头共滴水约(用科学记数法表示,结果保存两位有效数字) ( )A .1440 毫升B . 1.4×10 3毫升4毫升D . 14× 10 2毫升C . 0.14× 10 【剖析】 先列式表示 4 小时后水龙头滴水的毫升数,再把结果用科学记数法表示.有效数字是从左侧第一个不是0 的数字起,后边全部的数字都是有效数字.用科学记数法表示的数的有效数字只与前面的a 有关,与 10 的多少次方没关.【解答】 解:∵水龙头每秒钟滴水的体积为:0.05× 2=0.1(毫升),4 小时= 3600 秒× 4= 14400 秒,3∴水龙头 4 小时共滴水的体积为:0.1× 14400= 1440≈1.4× 10 (毫升).应选: B .【评论】 本题主要考察了有理数的乘法在实质生活中的应用,科学记数法的表示方法,以及用科学记数法表示的数的有效数字确实定方法.2.( 4 分)如图,直线 l 与∠ O 的两边分别交于点A 、B ,则图中以 O 、 A 、B 为端点的射线的条数总和是()A .5B .6C . 7D . 8【剖析】依据射线的定义,分别数出以O 、A 、B 为端点的射线的条数, 再相加即可解得.【解答】 解:以 O 为端点的射线有 2 条, 以 A 为端点的射线有 3 条,以B 为端点的射线有 3 条,共有 2+3+3= 8 条.应选: D .【评论】本题主要考察射线的定义,娴熟依据定义判断射线是解题的重点.3.(4 分)整数 a,b 知足: ab≠ 0 且 a+b= 0,有以下判断:① a,b 之间没有正分数;② a,b 之间没有负分数;③ a,b之间至多有一个整数;④ a,b之间起码有一个整数.此中,正确判断的个数为()A .1B .2C. 3D. 4【剖析】先知道整数包含正整数、0、负整数,而后再依据ab≠ O 且 a+b=O,判断出正确的个数即可.【解答】解:∵ ab≠ O 且 a+b= O,∴a 与 b 互为相反数.又∵ a, b 是整数,∴ a,b 之间起码有一个整数;a,b 之间没有正分数;a, b 之间没有负分数∴结论中只有一个正确.应选: A.【评论】认真掌握整数、分数的定义与特色,注意整数和正数的差别,注意0 是整数,但不是正数.4.( 4 分)方程的解是x=()A .B .C.D.【剖析】这是一个比较复杂的方程,解答本题的重点是将方程变形为x[(1﹣)+(﹣) +(﹣)++(﹣)]=1,而后提取公因式,移项,归并同类项,系数化为1,即可求解.【解答】解:,提取公因式,得x ( + + + + )= 1,将方程变形,得第 5 页(共 17 页)x[ ( 1﹣ ) + ( ﹣ )+ ( ﹣ )+ + ( ﹣) ] = 1,提取公因式,得(1﹣ + ﹣+ ﹣ + + ﹣ )= 1,移项,归并同类项,得(1﹣)= 1,系数化为 1,得x = .应选: C .【评论】 本题主要考察学生对解一元一次方程的理解和掌握,本题有必定的拔高难度,是道难题.5.( 4 分)如图,边长为 1 的正六边形纸片是轴对称图形,它的对称轴的条数是( )A .1B .3C . 6D . 9【剖析】 依据轴对称图形的定义及性质求解.假如一个图形沿一条直线折叠,直线两旁的部分能够相互重合,这个图形叫做轴对称图形,这条直线叫做对称轴.【解答】 解:正六边形是轴对称图形,有6 条对称轴,分别是 3 条对角线和三组对边的垂直均分线.应选: C .【评论】 本题主要考察了轴对称图形的定义及性质.轴对称图形拥有以下性质:( 1)轴对称图形被对称轴分红的两部分是全等的;( 2)对称轴是连结两个对称点的线段的垂直均分线.6.( 4 分)在 9 个数:﹣ 5,﹣ 4,﹣ 3,﹣ 2,﹣ 1, 0,1, 2,3 中,能使不等式﹣ 3x 2<﹣ 14建立的数的个数是( )A .2B .3C . 4D . 5【剖析】 本题只要依据解不等式的知识先计算出 x 2的范围,而后将各数代入即可得出答案.【解答】 解:由题意得: x 2>,∴知足条件的数有﹣ 5.﹣ 4,﹣ 3, 3 共 4 个.应选: C .【评论】 本题考察一元二次不等式的知识,解答本题的重点是依据不等式的形式表示出2x 的范围,而后辈入查验.7.( 4 分)韩老师特制了 4 个相同的立方块,并将它们如图A 搁置,而后又如图B 搁置,则图 B 中四个底面正方形中的点数之和为()A .11B .13C . 14D . 16【剖析】 从 a 中间 2 个图形看,和点4 相邻的有点 1,点 3,点 5,点 6,那么和点 4 相对的就是点 2,再由图形 1 和图形 4 可看出和点 5 相对的是点 1,即可求出点 6 的相对面是点 3.依此将点 5、点 6、两个点 3 的相对面相加即可.【解答】 解:依据四个图形的点数,可推测出来,点4 对面是点 2;点5 对面是点 1;点6 对面是点 3.则图 B 中四个底面正方形中的点数是1,3, 6, 6,1+3+6+6 = 16,则图 B 中四个底面正方形中的点数之和为16.应选: D .【评论】 本题主要考察学生的空间想象能力和推理能力,也可着手制作一个正方体,依据题意在各个面上标上点数,再确立对面上的点数,能够培育着手操作能力和空间想象能力,解题的重点是依据图形 1 和图形 4 的旋转得出点 5 相对的面是点 1.8.( 4 分)对于相互互质的三个正整数 a , b , c ,有以下判断: ① a , b , c 均为奇数; ② a ,b , c 中必有一个偶数; ③ a , b ,c 没有公因数; ④ a , b ,c 必有公因数.此中,不正确的判断的个数为()A .1B .2C . 3D . 4【剖析】 分别依据质数与和数的性质对每题进行剖析即可.【解答】 解: ① 、当 a = 2 时, 2 是偶数,故此小题不建立;③、因为 a, b, c 都能整除因数1,所以 a, b, c 有公因数1,故此小题不建立;④、由③可知 a, b,c 有公因数1,所以此小题建立.应选: C.【评论】本题考察的是质数与合数,解答本题的重点是熟知在全部质数中只有 2 是偶数这一重点知识点.9.( 4 分)将棱长为 1 厘米的 42 个立方体积木拼在一同,组成一个实心的长方体.假如长方体底面的周长为18 厘米,那么这个长方体的高是()A .2 厘米B .3 厘米C. 6 厘米D. 7 厘米【剖析】第一依据底面周长确立底面的长宽,从而依据长方体的体积公式,求得高.【解答】解:∵假如长方体底面的周长为18 厘米,且立方体积是有棱长为1 厘米的 42 个立方体积木拼在一同,∴长方体的长与宽的和是 9,长宽高均为整数,体积为42,故设长为 a,宽为 b,高为 c,则有且 a、b 均为整数,解得 a= 7、 b= 2、 c= 3;a= 2、 b=7、 c= 3(不合题意,舍去).应选: B.【评论】本题考察几何体的表面积.培育学生的察看能力和实质问题应用能力,注意a、b、 c 均为整数这一隐含条件.10.( 4 分) If 0< c< b< a,then()A .B.C.D.【剖析】可代入特别值一一考证.【解答】解:∵ 0< c< b<a,∴可设 a= 3,b= 2, c= 1.A、=,,,∵ << 2,∴,故本选项错误;B、=2,=,=,∵,∴≤≤,故本选项错误;C、=,=2,=,∵<<2,∴,故本选项错误;D 、=,=,= 2,∵,∴,故本选项正确.应选: D .【评论】本题考察了有理数的大小比较.解答本题时,采纳了“特别值”代入法.二、填空题(共10 小题,每题 4 分,满分40 分)11.(4 分)如有理数m, n, p 知足,则=.【剖析】有理数 m,n,p 知足,所以m、n、p≠ 0,依据绝对值的性质,本题可分三种状况:①当 m> 0, n>0, p< 0 时②当 m>0, n< 0,p> 0 时③当 m< 0, n> 0, p> 0 时,根据以上三种情况分类解答.【解答】解:有理数m, n, p 知足,所以m、n、p≠ 0;依据绝对值的性质:① 当m>0,n>0,p<0时,原式=1+1﹣1=1,则=;②当 m> 0, n< 0, p>0 时,原式= 1﹣ 1+1= 1,则=;③当 m< 0, n> 0, p>0 时,原式=﹣1+1+1= 1,则=;故答案为【评论】 本题综合考察了绝对值的性质,能够依据已知条件正确地判断出 m 、 n 、p 的值是解答本题的重点.12.( 4 分)今日( 2007 年 4 月 15 日,礼拜日)是第18 届“希望杯”全国数学邀请赛举行第 2 试的日子,那么今日此后的第4三 .2007 +15 天是礼拜【剖析】 第一算出 2002 能整除 7,2007 除以 7 的余数为5,转变等于 20074 就和 54= 625除以 7 的余数相同,再利用( 625+15)÷ 7= 914除以 7 的余数,从 余 3,得出 2007 +15 而得出是礼拜几.【解答】 解:因为 2002 能被 7 整除,所以 2007 除以 7 的余数为 5.这样, 2007 4 就和 54= 625 除以 7 的余数相同,4的余数相同;所以 2007 +15 与 625+15 除以 7而后( 625+15 )÷ 7= 91 余 3,4所以, 2007 +15 除以 7 的余 3,4∴第2007 +15 天是礼拜三;故答案为:三.【评论】 本题主要考察了带余数的除法运算性质,正确的分解数据是解决问题的重点.13.( 4 分)孔子出生在公元前 551 年 9 月 28 日,则 2007 年 9 月 28 日是孔子寿辰 2557 周年.(注:不存在公元 0 年)【剖析】 公元前有 550 周年,公元 2007 周年,即 550+2007 = 2557,或 2007﹣(﹣ 551)﹣ 1.【解答】 解:依据题意得, 2007﹣(﹣ 551)﹣ 1,= 2007+551 ﹣ 1,= 2557(年).故答案为: 2557.【评论】 本题考察了有理数的减法以及应用,是基础知识比较简单.14.( 4 分) In Fig , ABCD is a rectangle .The area of the shaded rectangle is 18 .第 10 页(共 17 页)【剖析】在直角三角形BCG 中,利用勾股定理的知识求出BG,再依据锐角三角函数值的定义求出∠GBE 的正弦和正切值,而后再直角三角形中求出EF 和 FG ,最后依据矩形面积公式求出头积.【解答】解:在直角三角形BCG 中,由勾股定理得,BG= 10,tan∠BGC =,又知∠ BGC =∠ GBE,∴ tan∠ GBE =,所以 EF = sin∠ GBE?BE=× 5=3,BF= cot∠ GBE× 3= 4,FG= BG﹣ BF = 6,故知暗影面积=3× 6= 18,故答案为18.【评论】本题主要考察面积及等积变换的知识,解答本题的重点是利用好勾股定理和三角函数的知识求出边长EF 和 GF 的值.15.( 4 分)下表是某中学初一(5)班 2007 年第一学期期末考试数学成绩统计表:这个班数学成绩的均匀分不低于67.9分,不高于80.9分.(精准到0.1)【剖析】分别计算每组中最低分的均匀数和最高分的均匀数即可确立本题的答案.【解答】解:最低分的均匀分不低于(40× 5+60× 19+71× 12+86×14)÷(5+19+12+14)=67.92≈ 67.9;最低分的均匀分不低于( 59× 5+70× 19+85× 12+100 × 14)÷( 5+19+12+14 )= 80.9;故答案为: 67.9, 80.9.16.( 4 分)已知,此中 x, y, z 代表非 0 数字,那么2 2 2= 98 .x +y +z【剖析】第一依据题意的方程:( 70+x)( 100y+10z+6)= 41388,将方程化简,依据 x,y, z 代表非 0 数,则 x,y,z 皆为大于等于 1 而小于等于 9 的正整数,挨次剖析 y 的取值, x 的取值, z 的取值,即可求得结果.【解答】解:依据题意得:( 70+x)( 100y+10z+6)= 41388,整理得: 3500y+50xy+350z+5xz+3z=20694,∵ x, y,z 代表非 0 数,则x, y, z 皆为大于等于 1 而小于等于9 的正整数,∴3500y< 20694,∴y= 5,∵50x×5+350z+5xz+3 x=3194,∵3194,个位是 4,∴x= 8,∴350z+5× 8× z= 1170,∴z= 3;2 2 2∴ x +y +z = 98.故答案为: 98.【评论】本题考察了数字的表示方法与性质.解本题的重点是理解各数字间的关系,注意解题时要仔细.17.( 4 分)某城市有一百万户居民,每户用水量定额为月均匀 5 吨,因为 6,7,8 月天热,每户每个月多用水1 吨,为了不超出整年用水定额,则整年的其余月份每户的用水量应控制在每个月均匀 4 吨以内.假如每户每日节俭用水 2 千克,则全市一年(按 365 天计)节俭的水量约占整年用水定额的 1.22 %(保存三位有效数字)【剖析】设整年的其余月份每户的用水量应控制在每个月均匀x 吨,则6,7, 8 月均匀每天用水( x+1)吨,依据每户用水量定额为月均匀 5 吨,列出不等式求出x 的最大值,然后算出每户一年节俭用水量,既而可求解.【解答】解:设整年的其余月份每户的用水量应控制在每个月均匀x 吨,则 6, 7,8 月平均每日用水(x+1)吨,由题意得, 9x+3(x+1 )≤ 12× 5,解得: x≤ 4 ,即整年的其余月份每户的用水量应控制在每个月均匀4吨以内,若每户每日节俭用水 2 千克,则每户每年节俭2× 365=730(千克)= 0.73 吨,≈ 1.22%.答:全市一年节俭的水量约占整年用水定额的 1.22%.故答案为: 4, 1.22%.【评论】本题考察了一元一次不等式的应用,解答本题的重点是读懂题意,设出未知数,找出适合的等量关系,列出不等式求解.18.( 4 分) a,b, c 都是质数,且知足a+b+c+abc=99,则=.【剖析】先依据假定a, b,c 都是奇数,判断出与已知相矛盾,可得出a, b, c 中必有两个偶数是2,再求出另一个数的值,代入所求代数式进行计算即可.【解答】解:若 a,b,c 都是奇数,那么 abc 也为奇数,则 a+b+c+abc 为偶数,与 a+b+c+abc = 99 矛盾,∴a, b, c 中必有一个偶数,又∵ a, b, c 都是质数,∴a, b, c 中必有一个偶数是 2,令 a=2,则 b+c+2bc= 97,同理,若b, c 都是奇数,则bc 为奇数,则b+c+2 bc 为偶数,与b+c+2bc= 97 矛盾,∴ b,c 中也必有一个偶数,则偶数必是2,令 b=2,可得 c= 19,∴=.故答案为:.【评论】本题考察的是质数与合数,熟知“在全部质数中只有 2 是偶数”是解答本题的重点.19.( 4 分)一项机械加工作业,用 4 台 A 型车床, 5 天能够达成;用 4 台 A 型车床和2 台 B第 13 页(共 17 页)型和 C 型车床各一台一同工作6 天后,只余下一台 A 型车床持续工作,则再用 2 天就能够达成这项作业.【剖析】 由 A 型车床达成工作的台数和时间可获得其工作效率,从而获得B 、C 型车床的工作效率,依据A 型机床 6 天的工作量 +B 型机床 6 天的工作量 +C 型机床 6 天的工作量 +A 型机床 x 天的工作量= 1,把有关数值代入计算即可.【解答】 解:∵用 4 台 A 型车床, 5 天能够达成;∴ A 型机床的工作效率为 1÷ 5÷ 4=,∵用 4 台 A 型车床和 2 台 B 型车床, 3 天能够达成;∴ B 型机床的工作效率为( 1﹣× 4× 3)÷ 3÷ 2= ,∵用 3 台 B 型车床和 9 台 C 型车床, 2 天能够达成.∴ C 型机床的工作效率为( 1﹣× 3×2)÷ 9÷2= ,设再用 x 天达成这项工作.+ + += 1,解得 x =2,故答案为 2.【评论】考察一元一次方程的应用; 获得 3 种种类机床的工作效率是解决本题的打破点;获得 3 种种类机床总工作量1 的等量关系是解决本题的重点.20.( 4 分)设 0< a <1,﹣ 2< b <﹣ 1,则和四个式子中,值最大的是,值最小的是.【剖析】 第一由 0< a < 1,﹣ 2< b <﹣ 1,即可求得: a 2﹣ b 2< a+b < 0< a <a ﹣ b ,则可求得和 四个式子的大小.【解答】 解:∵ 0< a < 1,﹣ 2< b <﹣ 1,∴ a ﹣ b > a > 0,a+b < 0,∴ a 2﹣ b 2=( a+b )( a ﹣ b )< 0, a 2﹣ b 2=( a+b )( a ﹣ b )< a+b , ∴ a 2﹣ b 2< a+b < 0< a < a ﹣b ,∴<<< ,∴值最大的是,值最小的是.故答案为:,.【评论】本题考察了分式的求值与实数大小的比较.题目难度不大,注意认真剖析求解.三、解答题(共 3 小题,满分 40 分)21.( 10 分)小明在平面上标出了2007 个点并画了一条直线 L,他发现:这 2007 个点中的每一点对于直线L 的对称点,仍在这 2007 个点中,请你说明:这2007 个点中起码有 1 个点在直线 L 上.【剖析】第一假定这 2007 个点都不在直线L 上,得出每个点 A i( i= 1,2,, 2007 )对于直线 L 的对称点 A′1仍在这 2007 个点中,不在直线 L 上点 A i( i = 1, 2, 2007)与 A i 对于直线 L 对称的点 A′i成对出现,即平面上标出的点的总数应是偶数个,与点的总数2007 相矛盾.【解答】证明:假定这 2007 个点都不在直线L 上,因为此中每个点A( i= 1,2,,2007 )对于直线 L 的对称点 A′1 仍在这 2007 个点中,i所以 A′i不在直线L 上.也就是说,不在直线L 上点 A i( i= 1,2, 2007)与 A i对于直线L 对称的点A′i成对出现,即平面上标出的点的总数应是偶数个,与点的总数2007 相矛盾,所以,“这 2007 个点都不在直线L 上”的假定不可以建立,即这2007 个点中起码有 1 个点在直线 L 上.【评论】本题主要考察了反证法的应用,从命题的反面出发,假定出2007 个点都不在直线 L 上,依据平面上点的坐标性质得出矛盾,从而必定数题正确是解决问题的重点.22.( 15 分)小明和哥哥在环形跑道上练习长跑.他们从同一同点沿相反方向同时出发,每隔 25 秒钟相遇一次.此刻,他们从同一同跑点沿相同方向同时出发,经过25 分钟哥哥追上了小明,而且比小明多跑了20 圈,求:( 1)哥哥速度是小明速度的多少倍?( 2)哥哥追上小明时,小明跑了多少圈?【剖析】( 1)由“他们从同一同点沿相反方向同时出发,每隔25 秒钟相遇一次”获得等量关系:哥哥所跑行程 +小明所跑行程=环形跑道的周长;由“经过25 分钟哥哥追上小明,而且比小明多跑了20 圈”,知经过 分钟哥哥追上小明,而且比小明多跑了 1 圈,获得等量关系:哥哥所跑行程﹣小明所跑行程=环形跑道的周长,据此列出方程组,求出问题的解.( 2)由( 1)中求出的哥哥的速度与小明的速度的比为2: 1,可知在时间相同时,他们所行的行程比也为2:1.假如设小明跑了 x 圈,那么哥哥跑了 2x 圈.依据哥哥比小明多跑了 20 圈列式解答即可.【解答】解:设哥哥的速度是 V 1 米 /秒,小明的速度是 V 2 米 /秒.环形跑道的周长为 s 米.( 1)由题意,有,整理得, 4v 2= 2v 1, 所以, V 1= 2V 2.答:哥哥速度是小明速度的2 倍.( 2)设小明跑了 x 圈,那么哥哥跑了 2x 圈.依据题意,得 2x ﹣ x = 20, 解得, x = 20.故经过了 25 分钟小明跑了20 圈.【评论】 本题考察分式方程、一元一次方程的应用.解题重点是要读懂题目的意思,根 据题目给出的条件,找出适合的等量关系,列出方程组,再求解.本题要注意追及问题 和相遇问题不一样的求解方法实时间相同,行程比等于速度比.23.( 15 分)知足 1+3n ≤ 2007,且使得 1+5n 是完整平方数的正整数 n 共有多少个?【剖析】 第一求出 n 的取值范围,而后设1+5n = m 2(m 是正整数),则,这是正整数,而后对 m ﹣ 1 和 m+1 进行议论确立n 的值.【解答】 解:由条件 1+3n ≤ 2007 得, n ≤ 668, n 是正整数.设 1+5n = m 2(m 是正整数),则,这是正整数.故可设 m+1= 5k ,或 m ﹣ 1= 5k ( k 是正整数)① 当 m+1 = 5k 时,2,由 5k ≤ 668,得, k ≤ 112所以,此时有11 个知足题意的正整数n 使 1+5n 是完整平方数;②当 m﹣ 1= 5k 时,,2 2 2又 5k ﹣ 2k< 5k +2k,且当 k= 11 时5k +2k= 627< 668,所以,此时有11 个知足题意的正整数n 使 1+5n 是完整平方数.所以,知足 1+3n≤ 2007 且使 1+5n 使完整平方数的正整数n 共有 22 个.【评论】本题主要考察完整平方数的知识点,解答本题的重点是对m﹣ 1 和 m+1 进行讨论确立 k 的取值范围,本题难度较大.。
(完整)1-27届希望杯数学竞赛初一试题及答案,推荐文档

所以
去了原方程第三天杯中水量与第一天杯中水量之比为
,a+v>a-v 0
8.食盐30%的盐水60千克中含盐60×30%(千克)设蒸发变成含盐为
,则去年的生产总值是前年比去年少
这个产值差占去年的应选
乙杯中含有的红墨水的数量是
乙杯中减少的蓝墨水的数量是
可以看出
∴①<②<③,∴选C.
解得
>b2..|a|≥7.
ab-cd.
: ,数轴上标出了有理数
有
新方程13.-4,-1,-2.5,-0.01与-15中最大的数是
.6.1990n的末四位数字应为1991+8009的末四位数字.即为
13.十位数比个位数大7的两位数有
.
6.设所求的四个连续整数分别为a
9.显然全班人数被9整除,也被4整除,所以被解得x=3.即该河水速每小时3公里.
故选D.
=2a+5b-2a+2b=7b
,所以a+b>b+c,成立,选B.
下,只能是b=1.于是a=-1.
即9≤a<
9.将2,3,4,5,6,7,8,9,10,11填入这
的最大值是_______..△ABC是等边三角形,表示其边长的代数式均已在
=
的是B.
7.当a=0,显然A,B,C,均不正确,应排除,所以选
11.由(a-b)3<0,得出a-b<0.即a<b.14.第1行只有1=20,第2行1+1=2=21,
15.设这个班共有学生x人.在操场踢足球的学生共根据题意列方程如下:
合并同类项,移项得
24中标出
; C.(1-a)(c-b); D.ac(1-bc).日,是星期日,从今天算起第19933天之后的那一天是
2.你能找到三个整数a,b,c,使得关系式。
2018年第十八届“希望杯”全国数学邀请赛初一培训题(含答案)

第十八届(2018年)“希望杯”全国数学邀请赛培训题“希望杯”命题委员会(未署名的题,均为命题委员会命题)初中一年级一、选择题(以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母填在每题后面的圆括号内)1.在2001,2003,2005,2007四个数中,质数有()个.(A)1 (B)2 (C)3 (D)42.边长为1的正方形是轴对称图形,它共有()条对称轴.(A)1 (B)2 (C)4 (D)83.已知a1,a2,…,a100均为整数,则│a1-a2│,│a2-a3│,│a3-a4│,…,│a99-a100│,│a100-a1│中必有()(A)奇数个奇数,奇数个偶数(B)偶数个奇数,奇数个偶数(C)奇数个奇数,偶数个偶数(D)偶数个奇数,偶数个偶数4.若A<b<D<C<-b,则│a-b│+│c+b│=()(A)a+b (B)-a-c (C)│a│+c (D)│a-c│5.在89°,126°,180°,216°这4个角中,共有()个钝角.(A)1 (B)2 (C)3 (D)46.In a hundred integers from 1 to 100,the number of those which •aredivisable by 2,3 and 5 simui taneously is()(A)2 (B)3 (C)4 (D)5(英汉词典:integer整数;•number•数,•个数;•divisable •by •可能…除尽的;7.In Fig.1,there are()rays.(A)2 (B)3 (C)4 (D)5.(英汉词典:ray线)8.有5个分数:25151012,,,,38231719,将它们按从小到大的顺序排列是()1512105210512152(),,,,(),,,,2319178317819233A B2510121525151012(),,,,(),,,,3817192338231719C D9.“射击名将在金牌争夺战中也会脱靶”是()(A)不可能的(B)必然的(C)可能性很小的(D)可能性很大的10.“美丽奥运”这4个艺术字中有()个不是轴对称图形.美丽奥运(A)1 (B)2 (C)3 (D)411.观察图中三角形个数的变化规律,当图中横线增加到一定数量时,可能有( •)个三角形.(A)2004 (B)2005 (C)2006 (D)2007(拟题:万黎明河北省承德市民族中学067000)12.2007有()个约数.(A)2 (B)4 (C)6 (D)813.一个体积为V的圆柱体锯掉一块后所成物体的三视图如图3所示,则锯掉部分的体积为()(A )()()()46812VVVV B C D 14.a ,b 均为有理数,则( )(A )(a+6)2一定是正数 (B )a 2+0.01b 2一定是非负数(C )a+(2b )2一定是正数 (D )ab+12一定是非负数 15.已知a ,b 均为有理数,且b<D ,关于x 的方程(2007a+2008b )x+2007=0无解,则a+b是( )(A )正数 (B )负数 (C )非正数 (D )非负数16.有如下4个判断性语句:①符号相反的数是互为相反数;②任何有理数的绝对值都是非负数;③一个数的相反数一定是负数;④如果一个数的绝对值等于它本身,那么这个数是正数,其中正确的有( )个.(A )1 (B )2 (C )3 (D )417.我国最新居民身份证的编号有18位,含义是:前两个数字表示所在省份,第三、四两个数字表示所在市,第五、六两个数字表示所在县、乡,•接下来的四个数字是出生的年份,后两个数是出生的月份,再后两个数是出生的日期,最后四位是编码.若韩光同学的身份证编号是:110106************,则韩光出生的时间是( •)(A )1995年8月15日 (B )1977年2月6日(C )1995年8月1日 (D )1981年5月7日18.汽车站A 到火车站F 有四条不同的路线,如图4所示,其中路程最短的是( )(A )AB →BME →EF (B )AB →BE →EF(C)ABC→CEF (D)ABCD→DE→EF19.李先生以一笔资金投资甲、乙两个企业,若从对甲、•乙企业的投资额中各抽回10%和5%,则总投资额减少8%;若从对甲、乙企业的投资额中各抽回15%和10%,•则总投资额减少130万元,李先生投资的这笔资金为()(A)600万元(B)800万元(C)900万元(D)1000万元20.若关于z的方程(a-4)x+b=-bx+a-2有无穷多个解,则(ab)4等于()(A)0 (B)1 (C)81 (D)25621.如果a,b,c是△ABC三边的长,且a2+b2-ab=c(a+b-c),那△ABC是()(A)等边三角形(B)直角三角形(C)钝角三角形(D)形状不确定22.At 3:30,the acute angle formed by hour tand and minute hand on •aclock is ()(A)70°(B)75°(C)85°(D)90°[英汉词典:acute angle锐角;to form作成、形成;•hour •hand•指针;•minutehand 分针)23.由两个角的和组成的角与由这两个角的差组成的角互补,则这两个角()(A)都是钝角(B)都是直角(C)必有一个是直角(D)一个角是锐角,另一个角是钝角24.已知a,b是质数,且3a+2b是小于20的质数.则满足条件的数组(a,b)共有()组(A)1 (B)2 (C)3 (D)425.关于x的不等式│x-3│≤│x+a│的解包含了不等式x≥a,则实数a的取值范围是()(A)a≥-3 (B)a≥-1且a=-3 (C)a≥1或a=-3 (D)a≥2或a=-3 (拟题:俞倾萱上海市浦江教育培训中心200434)26.已知代数式│x-3│+│x-7│=4,则下列三条线段一定能构成三角形的是( •)(A)1,x,5 (B)2,x,5 (C)3,x,5 (D)3,x,4(拟题:徐伟建浙江省龙游华茂外国语学校324400)27.两个有理数a,b在数轴上对应的点A、B如图5所示,数c表示的点C在A、B两点之间,则下列关系式中一定成立的是()ab(A)│a-c│<│b-c│(B)a+b<b(C)a+b+c>0 (D)│a-c│=b+c28.若a是有理数,给出下列判断:①2a是偶数;②-a2<0;③a2>a;④│a│是正数;⑤(-a)3=-a3其中,正确的个数是()(A)1 (B)2 (C)3 (D)429.在数轴上,点A对应的数是-2007,点B对应的数是+19,点C对应的数是-4032,•记A、B两点间的距离为d1,A、C两点间的距离为d2,B、C两点间的距离为d3,则有()(A)d1>d2(B)d2>d3(C)d1>d3(D)d3=2d1+130.命题甲:a,b是两个相邻的正整数,则a与b互质.命题乙:两个正整数a与b互质,则a,b是相邻的,则()(A)甲真,乙真(B)甲真,乙不真(C)甲不真,乙真(D)甲不真,乙不真二、填空题31.孔子出生于公元前551年,如果用-555表示,那么(1)司马迁出生于公元前145元,应表示为_________年;(2)李白出生于公元701年,应表示为________年.32.In Fig.6,if M is the •mid-•point •of •the •line •segment •AB •anddivides segment MB into two parts such that MC:CB=1:2,•then •the •lengthof AC is(英汉词典:mid-point 中点;line segment 线段;to divide …into 分为、•分成;length 长度)33.下图是一个数值转换机的示意图,若输入x 的值为3,y 的值为-2,则输出结果为___________.34.已知a=200520072006200820072009,,200620072008b c ⨯⨯⨯==,则a ,b ,c 的大小关系是____________.35.已知,在数轴上的位置如图所示.化简制的值是|1|||1a a +-的值是________. a (拟题:徐伟建浙江省龙游华茂外国语学校324400)36.若灯泡瓦数是a ,使用t 小时,则耗电量是1000at 度.如果平均每天使用3小时,用一个15瓦的灯泡比用一个40瓦的灯泡每月(按30天计)可节约________度电.37.若a b b +=-58,则b a=__________. 38.当b=-1时,多项式3a 2+4a 2b-3b 2与-3a 2-4a 2b+2b 2+1的和等于________.39.如图,在直角坐标系中,右边的不倒翁图是由左边的不倒翁图案经过平移得到的,左图案中两眼的坐标分别是(-4,2),(-2,2),右图案中一只眼睛的坐标是(3,4),则另一只眼睛的坐标是________.(拟题:王定海江苏省金湖县涂沟镇唐港初中211643)40.大小相同的小球不超过40个,将它们紧挨着可以摆成一个正方形,•还可以摆成一个等边三角形,则小球的个数是________.41.把两根毛线从中间打结系在一起,然后由4名同学分别抓住一端拉紧,若最多能形成a对对顶角,最少能形成b 对邻补角,则a+b 的值为_________.(拟题:王可民山东省梁山县梁山镇二中272600)42.224682008123420061234200512342007-⨯的值是________. 43.若a+b=3,a 2b+ab 2=-30,则a 2+b 2的值是________.44.已知211n n x x+=,x 5n +x n +2=________. (拟题:俞颂萱 上海市浦江教育培训中心200434)45.多项式4x 2+1加上一个单项式后,使它能成为一个整式的完全平方,•则可以加上的单项式共有_____个.(拟题:夏建平 江苏省江阴市要塞中学214432)46.工厂要用长方形的铁皮制作易拉罐.一张长方形铁皮根据图中的数据下料,假设焊接的部分忽略不计,则这个易拉罐的容积是________立方厘米.(π=3.14)(第46题) (第48题) (第50题)47.小林每天下午5点放学时,爸爸总是从家开车按时到达学校接他回家,有一天学校提前一个小时放学,小林自己步行回家,在途中遇到开车来接他的爸爸,•结果比平时早20分钟到家,则小林步行________分钟遇到来接他的爸爸.(拟题:陈武海南省海口市义龙中学570206)48.如图,两个正方形ABCD与CEFG并排放在一起,连结AG交CE于M,连结HF,则图中阴影部分的面积为_________平方厘米.49.在1,3,5,…,101这51•个奇数中的每个数的前面任意添加一个正号或一个负号,则其代数和的绝对值最小为_________.50.如图,一条东西走向的公路修到某自然保护区边缘时,要拐弯绕道而过,若第一次拐的角是∠是100°,第二次拐的角∠B是150°,第三次拐弯后的公路CD•仍是东西走向,则第三次拐的角∠C=________.(拟题:王可民山东省梁山县梁山镇二中272600)51.设P=a2b2+5,Q=2ab-a2-4a,若P=Q,则实数a=_______;b=_______.52.如图,在数轴上有若干个点,每相邻个点之间的距离是1个单位长,•有理数a,b,d,d所表示的点是这些点中的4个,且在数轴上的位置如图所示,如果3a=4b-3,那么∠c+2d=_______.dcba53.已知m+n=3,m2+n2=7,则m3+n3=______.54.若实数x,y满足│x-y+1│+│x+y-2007│=0,则[-xy]=_______.(其中[-xy]表示:不超过-xy的最大整数)55.若2│3a-2b│+(4b-12)2=0,则代数式14a2b-1-(a3+127b b+4)的值为_______.56.若以x为未知数的方程43x-a=25x+140有正整数解,则a的最小整数值是_____.57.设x-y=1,则y3+3xy-x3=________.58.已知x,y,z均不为0,并且x2+4y2+9z2=x3+2y3+3z3=x4+y4+z4,则(2x-1)2+(2y-2)2+(2z-3)2的值等于_________.59.计算: 33333333333333332468101214163691215182124-+-+-+--+-+-+-=__________. 60.远望巍巍塔七层,灯光点点倍加增,共灯六百三十五,请问顶层几盏灯?答:___________.61.国际上公认的男女出生时的性别比例为男:女=0.517:0.483,•我国某地区出生的性别比例为男:女=160:70,这个比值是公认的比值的_________倍.62.数码0,1,2,…,9中的四个:a ,b ,c ,d 使等式成立,则21377111313,b a a b c de d c -=⨯⨯⨯-成立则=•___________. 63.若1立方米的水重1000千克,而1吨97#汽油是1374升,那∠1升水与1升97#•汽油的重量之比为__________.64.2006年北京密云水库鱼王节上一条34斤的胖头鱼拍出23.6万元的价钱,若按180元可买1克黄金来折算,1两黄金可买胖头鱼_________两.65.计算220076200772008-⨯-=__________. 66.已知有理数a ,b 满足-1<a<0,0<b<1,那么,-ab ,a 2b 2,-a 3b 3中,最大的是________,最小的是_______.67.能使不等式│2m │>m+1成立的m 的取值范围是________.68.如图所示,有一只蜗牛从直角坐标系的原点O 向y 轴正方向出发,它前进1厘米后,右转90°,再前进1厘米后,左转90°,再前进1厘米后,右转90°,……当它走到点P (n ,n )时,左边碰到障碍物,就直行1厘米,再右转90°,前进1厘米,再左转90°,前进1厘米,……最后回到x 轴上,则蜗牛所走过的路程s 为________厘米.(拟题:蔡世英福建省晋江市南岳中学362272)(第68题) (第71题) (第73题)69.一个两位数ab是质数,而ba是合数,且ab+ba是完全平方数,这样的两位数ab是________;•若一个两位数ab是合数,且ba也是合数,ab+ba是完全平方数,这样的两位数ab是_____.70.满足方程│x-2007│-1│=2007的x的值是________.71.如图所示,在4×4的方格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=______.72.In △ABC,the degrees of∠A,∠B and ∠C are α,βand γ•respectively.•If the degree of∠B is two times of that of ∠A,and the •exterior •angleof ∠C is equal to 120°,thenα:β:γ=__________.(英语词典:degree度、度数;respectively分别地;time倍数;exterior •angle 外角)73.两条平行直线L1,L2被第三条直线L3所截,如图所示,图中的8个角中,•互为补角的共有______对,互为邻补角的共有_______对.74.某校初一气象小组在整个暑假期间不间断地观察天气变化,最后有如下一些资料:75.甲乙丙丁四人参加某商场的抽奖活动,现知道:(1)如果甲中奖,那么乙也中奖.(2)如果乙中奖,那么丙中奖或甲不中奖.(3)如果丁不中奖,那么甲中奖,丙不中奖.(4)如果丁中奖,那么甲也中奖.则这四个人中有_______人中奖.(拟题:陈武海南省海口市义龙中学570206)76.有位诗人这样赞美桂林的山:云中的神啊,雾中的仙,神姿仙态桂林的山.•翻译出版的诗集中这段话的英译文是:“Gods in the cloud and fairies in the •mist,•The •Hills •in •Guilinlook like.”请统计这段英文诗句中26个英文字母出现的次数,则26•个英文字母中出现次数最少的共有_____个字母;出现次数最多的字母的频率是________.77.已知p,q都是质数,且x-1满足关于x的一元一次方程p3x+q p=11,则p=______.(拟题:蔡世英福建省江市南岳中学362272)三、解答题78.奥地利数学家皮克发现了一个计算正方形网格纸中多边形面积的公式:S=a+12b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如:在图?中,方格纸中每个小正方形的边长为1cm,点A、B、C、D都正好在格点上,那么四边形ABCD的面积S=7+12×4-1=8(cm2).运用上述知识回答:(1)如图,方格纸中每个小正方形的边长为1cm,点A、B、C、D都正好在格点上,求四边A、B、C、D的面积;(2)如图,横向或纵向的两个相邻格点的距离都是1,若多边形(•可以是凸的或凹的)的面点都在格点上,且面积为6,请画出这样三个形状不同的多边形(•多边形的边数≥6).(拟题:蔡风山江苏省兴化市明升双语学校225700)79.如图,在一块周长为2007米的正六边形场地上,小明位于AB边(点A、B除外)上任意一点P,小明首先由P沿平行于BC的方向跑到CD边上的P1点,再由P1沿平行于DE的方向跑到EF边上的P2点,再由P2沿平行于FA的方向跑到AB边上的P3点……此后按上述规律一直跑下去,问小明能否返回到P点?如果能回到,他至少要跑多少米?(拟题:袁林春深圳市新世纪阶梯教室518101)80.小明向母校捐赠语文、数学、英语三种书共40册,总价值391元,这三种书的单价分别为:语文每册7元,数学每册8元,英语每册10元,那么语文、数学、英语课本分别有多少册?81.已知b≥0,且a+b=c+1,b+c=d+2,c+d=a+3,求a+b+c+d的最大值.(拟题:俞颂萱上海市浦江教育培训中心200434)82.如图?,已知∠1=∠2,EF⊥AD于P,它延长后交BC延长线于M,求证:∠M=12(∠ACB-∠ABC).83.右边5×5的表中的文字代表有理数,而表中的数字分别是各行、各列的文字所代表的有理数的和,试求出这些文字所代表的数值.84.甲、乙、丙完成某工程,甲单独完成所需时间是乙、•丙合作所需时间的4倍,乙单独完成工作所需时间是甲、丙合作所需时间的3倍,•问:丙单独完成所需时间是甲、乙合作所需时间的几倍?85.能否找到五个不同的正整数,它们中任意三个数的和是3的倍数;任意四个数的和是4的倍数,并且这五个正整数之和恰等于2007?若能找到,试举出一个例子;•若不能找到,请说明理由.第十八届(2007年)“希望杯”全国数学邀请赛初一培训题(1~85题)答案.解析一、选择题1.由于3│2001,5│2005,9│2007,所以2001,2005,2007都是合数.经检验知,2,3,5,7,11,13,15,17,19,23,29,31,37,41,43都不是2003的约数,所以,2003是质数,选(A).2.正方形有4条对称轴,其中2条是对角线,另两条是对边中点的连线,选(C).3.│a1-a2│,│a2-a3│,│a3-a4│,…,│a99-a100│,│a100-a1│中各数的奇偶性分别与a1-a2,a2-a3,a3-a4,…,a99-a100,a100-a1中各数的奇偶性相同.又(a1-a2)+(a2-a3)+(a3-a4)+…+(a99-a100)+(a100-a1)=0,故这组数中有偶数个奇数.又这组数共有100个,故其中也有偶数个偶数,故选(D).4.因为 a<b,所以 a-b<0,│a-b│=-(a-b)又因为 b<0<c<-b,│a-b│+│c+b│,因此 =-(a-b )-(c+b )=-a-c 选(B ).5.大于90°,且小于180°的角叫钝角,所以度数为89°,126°,180°,216•°的4个角中只有126°的角是钝角,选(A ).6.译文:在1~100这100个自然数中,能同时被2,3,5整除的数共有( )个. (A )2 (B )3 (C )4 (D )5 7.译文:图1中共有( )条射线.(A )2 (B )3 (C )4 (D )5以A 为端点的射线有2条,以B 为端点的射线有3条,共有5条,选(D ). 8.分子的最小公倍数是60,题给的5个分数依次是260560159010601260,,,,3908962392171021995===== 分子相同的分数,分母较大的分数值较小,所以题给的5•个分数按从小到大的顺序排列是10512152,,,,17819233,选(B ). 9.由上次奥运会中美国射击名将失利可知,•“可能性很小”的事件也是可以出现的,选(C ). 10.观察图形知,“丽”、“运”两字不是轴对称图形.选(B ).11.每增加一条横线,就增加6个三角形,则三角形个数是6的倍数,故选(A ). 12.2007=32×223,所以2007的约数是1,3,9,223,669,2007,共计6个,选(C ). 13.这个圆柱体最上面的三分之一的圆柱锯掉了四分之一,所以锯掉部分的体积为12V.选(D ). 14.当a=-b 时,a+b=0,排除(A );当a=-1,b=0时,a+(2b )2=-1<0,排除(C ); 当a=1,b=-1时,ab+12=-12<0,排除(D ),故选(B ).事实上,由于a 2≥0,0.01b 2≥0, 所以a 2+0.01b 2≥0.15.已知关于x 的方程(2007a+2008b )x+2007=0无解, 故可知 2007a+2008b=0,于是 a+b=2007b, 由b<0,知2007b->0,即a+b>0,选(A ).16.2与-1为符号相反的两个数,但2与-1不互为相反数,易知①错误; 0的相反数与绝对值都是0,但是0既不是正数也不是负数,故③和④错误. 只有②正确,故选(A ).17.由题意可知,出生时间应该是身份证编号中的第7到第14位,所以韩光出生的时间是1995年8月15日选(A ).18.根据两点之间线段最短,知选(B ).19.“从对甲、乙企业的投资额中各抽回15%和10%”与“从对甲、•乙企业的投资额中各抽回10%和5%”,相比,前者比后者各多抽回5%,即从对甲、乙企业的投资额中各抽回5%+8%-13%,总投资额减少130万元,所以李先生投资的这笔资金为130•÷13%=1000(万元),故选(D ). 20.原方程整理为 (a+b-q )x=a-b-2,由于此方程有无穷多个解,所以4020a b a b +-=⎧⎨--=⎩解得 a=3,b=1,所以(ab )4=81,选(C ).21.已知关系式可化为 a 2+b 2+c 2-ab-bc-ca=0,即112(2a 2+2b 2+2c 2-2ab-2bc-2ac )=0, 所以112[(a-b )2+(b-c )2+(a-c )2]=0,故 a=b ,b=c ,a=c . 即 a=b=c .选(A ).22.译文:在3点半时,钟表上的时针和分针所成的锐角是()(A)70°(B)75°(C)85°(D)90°钟表在3点时,时针与分针成90°角,再过半小时,分针转过180°指向“6”,•而时针转了36012×12=15°,所以在3点半时,钟表上的时针和分针所成的锐角是90°-15°=75°,选(B).23.设这两个角为α和β(α>β),则(α+β)+(α-β)=180°,所以a=90°,选(C).24.因为 a是质数,b是质数,3a+2b是质数,3a+2b<20.所以 a只能取3,5,b只能取2,5,经检验,只有(3,2),(3,5),(5,2)适合,故选(C).25.由已知得(x-3)2≤(x+a)2,(a+3)[2x+(a-3)]≥0.当a=-3时,解是一切实数,包含x≥a;当a>-3时,x≥32a -,要包含x≥a,则必有 a≥32a -,则 a≥1;当a<-3时,x≤32a-,不能包括x≥a.所以 a≥1或a=-3,选(C).26.如图所示,x当3≤x≤7时,│x-3│+│x-7│=4若三条线段能构成三角形,那么各选项中x的范围应能包含3≤x≤7,选(C).27.令c=0,则可排除(A),(C),(D),所以选(B).事实上,由图知a<0,b>0.若0<c<b,又a<0,相加得a+c<;右a<c≤0,得a+c<0<b.所以总有 a+c<b.28.若a不是整数,则2a不是偶数,①不成立;当a=0时,-a2=0,②不成立;当0≤a≤1时,a2≤a,③不成立;当a=0时,│a│=0,④不成立;(-a)3=(-1)3,(a)3=a3,⑤成立,选(A).29.计算得d1=│-2007-(+19)│=2026;d2=│-2007-(-4032)│=2025;d3=│(+19)-(-4032)│=4051,比较知,选(A).30.由“a、b是两个相邻的正整数”必能推得“a与b互质”,甲真;但反过来,•知3,7两个数互质,但3与7不是两个相邻正整数,乙不真,选(B).二、填空题31.-149;+697 32.8 33.-1 34.a<b<c 35.1 36.2.25 37.-81338.039.(5,4) 40.36 41.2 42.24682008 43.29 44.1 45.5 46.100.4847.50 48.32 49.1 50.130º 51.-2;-1252.-2 53.-18 54.-1 55.-556.14 57.-1 58.14 59.82760.5 61.2.135 62.3 63.1.374;1 64.1365.2000 66.-ab;-ab 67.m<-23或m>2 68. 69.29,47,83;56,6570.4015;-1 71.315º 72.2:4:3 73.16;8 74.39 75.4 76.9;105777.8解析:31.司马迁出生于公元-149元;李白出生于公元+697年.32.译文:如图6,长度为12的线段AB的中点为M,点C将AB分成MC:CB=1:2,•则线段AC的长度是________.AC=AM+MC=6+13MB=6+2=8.33.(2x+y3)÷2=[2×3+(-2)3]÷2=(6-8)÷2=-1.34.a=2(20061)(20061)2006120062006-+-==2006-12006.同理可得 b=2007-12007,c=2008-12008.显然 a=2006-12006<2006-12006<2007-12007<2007-12007=b<2007-12008即 a<b<c.35.由图知a<-1所以a+1<0原式11aa----=136.15瓦的灯泡每月耗电:153301000⨯⨯=135100(度)40瓦的灯泡每月耗电:40330100⨯⨯=360100(度)每月可节约用电:360100-135100=2.25(度)37.由a bb+=-58,得ab+1=-58即ab=-138所以ba=-81338.(3a2+4a2b-3b2)+(-3a2-4a2b+2b2+1)]=-b2+1=-(-1)2+1=039.(5,4)40.摆成等边三角形时第1排1个,第2排2个,第3排3个,……,第8排8个.而(81)82+⨯=36.又 6×6=36.所以,小球的个数是36.41.两根毛线从中间打结后拉紧,相当于有公共端点的四条线段.易知,最多能形成2对对顶角,最少能形成0对邻补角,即a=2,b=0. 所以a+b=242.以n 表示12342006,则原分数的分母=n 2-(n-1)(n+1)=n 2-n 2+1=1. 所以原式的值是24682008.43.因为 a+b=3,a 2b+ab 2-ab (a+b )=-30, 所以 ab=-10,则 a 2+b 2=(a+b )2-2ab=32-2×(-1)=29. 44.由211nnx x +=. 得x 3n -x 2n +1=0,从而原式 -(x 3n -x 2n +1)(x 2n +x n +1)+1=1.45.可以加上的单项式有-4x 2,-1,4x ,-4x ,4x 4,共5个.46.设易拉罐底面圆的半径为r 厘米,则EF•等于4r ,•所以船应等于27πr ,•故有2r+27πr=AB=16.56,解得 r=2. 所以易拉罐的容积是πr 2×EF=3.14×2×4×2=100.48(立方厘米). 47.如图,小林学校在A ,家在B ,下午4点他步行从A 出发,与按时从B 来接他的车相遇于C ,结果汽车由C 返回B 比往常提前了20分钟,表明汽车由C-A-C 共需20分钟,•因此汽车由C 到A 需10分钟,则汽车在4:50与小林相遇,即小林步行50分钟遇到来接他的爸爸.48.连结AC 、EG ,如图,则AC ∥EG .即ACGE是梯形,△AHE的面积等于△CHG的面积.△AHE的面积+△EHF的面积=△CHG的面积+△EHF的面积=正方形CEFG的面积-△HFG的面积=8×8-882=32(平方厘米).49.由于1+3+5+…+101=512为奇数,最小的正奇数为1,所以前3个奇数添加符号如下-1-3+5=1,而其余48个连续奇数按每连续四个添加符号如下,使其结果为0,即(2n+1)-(2n+3)-(2n+5)+(2n+7)=0.于是推知和的绝对值的最小值是1.50.由题意知AE∥CD.过点B在∠ABC内部作BF∥AE,则BF∥CD,所以∠ABF=∠A=100°,∠FBC=∠ABC-∠ABF=150°-100°=50°.所以∠C=180°-∠FBC=180°-50°=130°.51.由P-Q=a2b2+5-2ab+a2+4a=(ab-1)2+(a+2)2=0,所以ab=1,a=-2,b=-12.52.易知b=a+2,代入3a=4b-3中,得3a=4(a+2)-3,解得a=-5,于是b=-3,c=-2,d=0,所以C+2d=-2.53.(m+n)2=m2+2mn+n2=9,mn=1,(m+n)3=m3+3m2n+3mn2+n3=m3+n3+3mn(m+n)=-27,所以m3+n3=-27+9=-18.54.因为│x-y+1│≥0,│x+y-2007│≥0,所以│x-y+1│+│x+y-2007│≥0.又由题设知│x-y+1│+│x+y-2007│=0,所以│x-y+1│+│x+y-2007│=0.解方程组10,1003,200701004.x y x x y y -+==⎧⎧⎨⎨+-==⎩⎩得 于是[-x y ]=[-10031004]=-1 55.因为│3a-2b │≥0,(4b-12)2≥0,又2│3a-2b │+(4b-12)2=0,所以 3a-2b=4b-12=0,于是a=2,b=3.所以,原式=14×22×3-1-(23+127×33+4)=-5. 56.由原方程,得a=1415x-140,因为a 为正整数,所以1415x>140,所以x>150. 又因为1415x 为整数,所以x 是15的倍数,所以=x min =165,所以a min =1415×165-140=14. 即 a 的最小正整数值是14.57.Y 3+3xy-x 3=(y-x )(y 2+xy+x 2)+3xy=-(y 2+xy+x 2)+3xy=-y 2+2xy-x 2=-(y-x )2=-1.58.由已知等式,得x 4+y 4+z 4+x 2+4y 2+9z 2-2(x 3+2y 3+3z 3)=0,即x 2(x-1)2+y 2(y-2)2+z 2(z-3)2=0,由于x 2(x-1)2,y 2(y-2)2,z 2(z-3)2均为非负数,•所以x 2(x-1)2=y 2(y-2)2=z 2(z-3)2=0,因为x ,y ,z≠0,所以x=1,x=2,z=3.因此,原式=(4x 2-4x+1)+(4y 2-8y+4)+(4z 2+12z+9)=1+4+9=14.59.原式=333333333333333333332(12345678)283(12345678)327-+-+-+-==-+-+-+- 60.设顶层有灯x 盏,则有x+2x+4x+8x+16x+32x+64x=635,即127x=635,解得x=561.公认比值为0.5170.483=1.0704,而该地区出生的性别比例为16070=2.2857,•这个比值是公认比值的2.28571.0704≈2.135倍. 62.因为7×11×13=1001,一个六位数137a b c 等于1001乘以一个三位数13d ,这恰好是将此三位数13d 重写一遍,即1313d d ,所以c=3,d=7,b=1,a=7,因此3b a d c--=3. 63.1升水重1千克,1升97#汽油重(1000÷1374)千克,它们的比是1.374:1. 64.1两鱼价值236000÷(34×10)=694.1(元),1两黄金价值180×50=9000(元). 故9000÷694.1=13.65.令a=2007,则原式=22267(1)(66)(1)(1)6(1)111a a a a a a a a a a ----++--+==+++=a-7=2007-7=2000. 66.由已知得-1<ab<0,因此0<1+ab<1,因而-1<ab (1+ab )<0,a 2b 2-(-ab )=ab (•ab+1)<0,所以a 2b 2<-ab .又a 2b 2-(-a 3b 3)=a 2b 2(1+ab )>0,所以-a 3b 3<a 2b 2.因此,在-1<a<0,0<b<1•的条件下,-ab ,a 2b 2,-a 3b 3中最大的是-ab ,最小的是-a 3b 3. 此题也可以用特殊值法来检验判断.67.当m ≥0时,原不等式化为2m-1>m+1,解得m>2,当m<0时,原不等式化为-2m-•1>m+1,解得m<-23, 所以m 的取值范围是m<-23m>2. 68.显然,蜗牛所走过的路线是一个轴对称图形,所以S=2n ×2=4n (cm ).69.设ab =10a+b ,ba =10b+a ,其中1≤a ,b ≤9, 于是ab +ba =(10a+b )+(10b+a )=11(a+b ),且2•≤a+b ≤18.因为ab +ba 是完全平方数,只须a+b=11,其中29,47,83均为质数,而92,74,38是合数;另外56与65均为合数.70.原方程等价于│x-2007│-1=±2007,因为│x-2007│≥0,所以│x-2007│=2007,即│x-2007│=2008,那么x-2007=±2008,所以x=4015或x=1.71.由题图可知∠4=45°,∠1+∠7=90°,∠2+∠6=90°,∠3+∠5=90°.四式相加得∠1+∠2+∠3+∠4+∠5+∠6+∠7=3×90°+45°=315°.72.译文:在△ABC中,∠A,∠B,∠C的度数分别为α,β,γ,已知β是a的2倍,∠C•的外角等于120°,则α:β:γ=_______.由已知得β=2a,a+β=120°,所以α+β=120°,解得a=40°.因此β=80°,γ=60°,故有α:β:γ=2:4:3.73.互为补角的有∠1,∠2;∠2,∠3;∠3,∠4;∠4,∠1;∠5,∠6;∠6,∠7;∠7,∠8;∠8,∠5;∠1,∠6;∠1,∠8;∠2,∠5;∠2,∠7;∠3,∠6;∠3,∠8;∠4,∠5;∠4,∠7,共计16对.其中∠1,∠2;∠2,∠3;∠3,∠4;∠4,∠1;∠5,∠6;∠6,∠7;∠7,∠8;∠8,•∠5共8对互为邻补角.74.设有x天的上午下雨,则暑假有(30+x)天,则依题意列出方程:13+(35-x)=30+x,解得x=9,即这个暑假有39天.75.假设③成立,则与①、②矛盾,故④成立,由此可知甲、乙、丙、丁4•人均中奖.76.依统计26个英文字母出现的次数为:其中,一次都未出现的字母有9个(b,j,p,q,v,w,x,y,z);出现次数最多的字母为i,共出现10次,其频率为10 57.77.将x=1代入p3x+q=11得p3+q=11,则p3,q必为一奇一偶.若p=2,则p3-8,q=3,此时p,q都是质数,符合题意;若q=2,则p3=9,此时不存在符合条件的质数p.故p3=23=8.三、解答题78.(1)通过观察可知a=5,b=6,则S=a+12b-1=5+12×6-1=7(cm 2). (2)由题意知S=6,根据公式S=a+12b-1,可列出关于a ,b 的二元一次方程a+12b-1=6,其中b ≥6.不妨设b=6,则a=4,可画出如图25的四种图形.79.若P 与AB 中点重点,如左图,易知P 3就与P 重合,则小明的路程为六边形周长的34,即为34×2007=60214(米).? 若P 与A 中点不重合,如右图,由PP 1∥EF ∥P 3P 4,P 1P 2∥DE ∥P 4P 5,P 2P 3∥CD ∥P 4P 5, 所以P•与P 重合,小明的总路程为3(PP+PP )=3(BC+AD )=60212(米). 80.设语文、数学、英语分别有x 册、y 册、z 册. 则40,7810391.x y z x y z ++=⎧⎨++=⎩①×10-②得,3x+2y=9,所以x=923y -, 因为x ,y 是正整数,所以y 只能等于3,此时x=1,z=36.即语文、数学、英语课本分别有1,3,36册.81.由a-c=1-b ,①d-c=b-2,②d=a-c+3.③①代入③得d=4-b ,再代入②得c=6-2b ,从而由①得a=7-3b .所以 a+b+c+d=(7-3b )+b+(6-2b )+(4-b )=17-5b .因为b ≥0,所以a+b+c+d 的最大值为17.82.由EF ⊥AD 于P ,所以∠1+∠AEP=90°,∠2+∠AFP=90°,已知∠1=∠2,•所以∠AEP=∠AFP .由三角形外角的性质得∠ACB=∠CFM+∠M=∠AFP+∠M=∠AEP+∠M=∠ABC+∠M+∠M , 因此2∠M=∠ACB-∠ABC ,所以∠M=12(∠ACB-∠ABC ). 83.从第2列 京+京+奥+京=8, 第3行 京+奥+京+奥=16,即38,2216,⨯+=⎧⎨⨯+⨯=⎩京奥京奥,解得 京=0,奥=8. 再从第1行 北+0+8+运=36.8,即 北+运=28.8,从第4列 运+运+8+北=45.6,即 北+2×运=37.6,解得 北=20,运=8.8. 再从第1列 北+在+京+在=60,即 20+在+0+在=60,可得 在=20,从第2行 在+京+•开+运=36.8,即 20+0+开+8.8=36.8,可得 开=8,最后从第4行 在+京+之+北=48;即 20+0+之+20=48,可得 之=8. 即表中文字代表的数值如下:北=20,京=0,•奥=8,运=8.8,在=20,开=8,之=8.84.设甲、乙、丙单独完成工程所需时间分别为x ,y ,z ,丙单独完成工程所需时间是甲、乙合作所需时间的a 倍,依题意可得 411,311,11.x y z y x za z x y ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩①×②+③,得12a=222222 ()()()2x y y z z x xyz x y y z z x y x zx yz xyz xyz+++++++++==2+x(1y+1z)+y(1x+1z)+z(1x+1y)=2+4+3+a,所以a=911.85.假定存在这样的五个正整数,设它们分别是x,y,z,u,v.由于“它们中任意三个数的和是3的倍数”,可知x,y,z,u,v被3•除的余数相同.由于“它们中任意四个数的和是4的倍数”,可知x,y,z,u,v被4除的余数也相同.由于(3,4)=1,因此x,y,z,u,v被12除的余数相同,由x+y+z+u+v=2007.而上式右边的2007被12除余3.左边的x,y,z,u,v被12除的余数都相同,所以,满足题设要求的五个正整数x,y,z,u,v都应是被12除余3的数.如3,15,27,39,1923即是满足题设要求的一组数.。
历届(1-23)希望杯数学竞赛初一七年级真题及答案(最新整理WORD版)

“希望杯”全国数学竞赛(第1-23届)初一年级/七年级第一/二试题目录1.希望杯第一届(1990年)初中一年级第一试试题............................................. 003-0052.希望杯第一届(1990年)初中一年级第二试试题............................................. 010-0123.希望杯第二届(1991年)初中一年级第一试试题............................................. 016-0204.希望杯第二届(1991年)初中一年级第二试试题............................................. 022-0265.希望杯第三届(1992年)初中一年级第一试试题............................................. 029-0326.希望杯第三届(1992年)初中一年级第二试试题............................................. 034-0407.希望杯第四届(1993年)初中一年级第一试试题............................................. 043-0508.希望杯第四届(1993年)初中一年级第二试试题............................................. 050-0589.希望杯第五届(1994年)初中一年级第一试试题............................................. 057-06610.希望杯第五届(1994年)初中一年级第二试试题 .......................................... 063-07311.希望杯第六届(1995年)初中一年级第一试试题 ........................................... 070-080 12希望杯第六届(1995年)初中一年级第二试试题........................................... 077-08713.希望杯第七届(1996年)初中一年级第一试试题........................................... 086-09814.希望杯第七届(1996年)初中一年级第二试试题............................................. 91-10515.希望杯第八届(1997年)初中一年级第一试试题............................................. 99-11316.希望杯第八届(1997年)初中一年级第二试试题........................................... 106-12017.希望杯第九届(1998年)初中一年级第一试试题........................................... 114-12918.希望杯第九届(1998年)初中一年级第二试试题........................................... 123-13819.希望杯第十届(1999年)初中一年级第二试试题........................................... 130-14720.希望杯第十届(1999年)初中一年级第一试试题........................................... 148-15121.希望杯第十一届(2000年)初中一年级第一试试题....................................... 143-16122.希望杯第十一届(2000年)初中一年级第二试试题....................................... 150-16923.希望杯第十二届(2001年)初中一年级第一试试题....................................... 154-17424.希望杯第十二届(2001年)初中一年级第二试试题....................................... 158-17825.希望杯第十三届(2002年)初中一年级第一试试题....................................... 164-18426.希望杯第十三届(2001年)初中一年级第二试试题....................................... 168-18927.希望杯第十四届(2003年)初中一年级第一试试题....................................... 175-19628.希望杯第十四届(2003年)初中一年级第二试试题....................................... 179-20029.希望杯第十五届(2004年)初中一年级第一试试题 (183)30.希望杯第十五届(2004年)初中一年级第二试试题 (184)31.希望杯第十六届(2005年)初中一年级第一试试题....................................... 213-21832.希望杯第十六届(2005年)初中一年级第二试试题 (184)33.希望杯第十七届(2006年)初中一年级第一试试题....................................... 228-23334.希望杯第十七届(2006年)初中一年级第二试试题....................................... 234-23835.希望杯第十八届(2007年)初中一年级第一试试题....................................... 242-246 26.希望杯第十八届(2007年)初中一年级第二试试题....................................... 248-25137.希望杯第十九届(2008年)初中一年级第一试试题....................................... 252-25638.希望杯第十九届(2008年)初中一年级第二试试题....................................... 257-26239.希望杯第二十届(2009年)初中一年级第一试试题....................................... 263-26620.希望杯第二十届(2009年)初中一年级第二试试题....................................... 267-27121.希望杯第二十一届(2010年)初中一年级第一试试题 ................................... 274-27622.希望杯第二十二届(2011年)初中一年级第二试试题 ................................... 285-28823.希望杯第二十三届(2012年)初中一年级第二试试题 ................................... 288-301希望杯第一届(1990年)初中一年级第1试试题一、选择题(每题1分,共10分)1.如果a ,b 都代表有理数,并且a +b=0,那么 ( )A .a ,b 都是0.B .a ,b 之一是0.C .a ,b 互为相反数.D .a ,b 互为倒数.2.下面的说法中正确的是 ( )A .单项式与单项式的和是单项式.B .单项式与单项式的和是多项式.C .多项式与多项式的和是多项式.D .整式与整式的和是整式.3.下面说法中不正确的是 ( )A. 有最小的自然数. B .没有最小的正有理数.C .没有最大的负整数.D .没有最大的非负数.4.如果a ,b 代表有理数,并且a +b 的值大于a -b 的值,那么( ) A .a ,b 同号. B .a ,b 异号.C .a >0. D .b >0.5.大于-π并且不是自然数的整数有( ) A .2个. B .3个.C .4个. D .无数个.6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身.这四种说法中,不正确的说法的个数是 ( )A .0个.B .1个.C .2个.D .3个.7.a 代表有理数,那么,a 和-a 的大小关系是 ( )A .a 大于-a .B .a 小于-a .C .a 大于-a 或a 小于-a .D .a 不一定大于-a .8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( )A .乘以同一个数.B .乘以同一个整式.C .加上同一个代数式.D .都加上1.9.杯子中有大半杯水,第二天较第一天减少了10%,第三天又较第二天增加了10%,那么,第三天杯中的水量与第一天杯中的水量相比的结果是( )A .一样多.B .多了.C .少了.D .多少都可能.10.轮船往返于一条河的两码头之间,如果船本身在静水中的速度是固定的,那么,当这条河的水流速度增大时,船往返一次所用的时间将( )A .增多.B .减少.C .不变.D .增多、减少都有可能.二、填空题(每题1分,共10分)1. 21115160.01253(87.5)(2)4571615⨯-⨯-÷⨯+--= ______. 2.198919902-198919892=______.3.2481632(21)(21)(21)(21)(21)21+++++-=________. 4. 关于x 的方程12148x x +--=的解是_________. 5.1-2+3-4+5-6+7-8+…+4999-5000=______.6.当x=-24125时,代数式(3x 3-5x 2+6x -1)-(x 3-2x 2+x -2)+(-2x 3+3x 2+1)的值是____. 7.当a=-0.2,b=0.04时,代数式272711()(0.16)()73724a b b a a b --++-+的值是______. 8.含盐30%的盐水有60千克,放在秤上蒸发,当盐水变为含盐40%时,秤得盐水的重是______克.9.制造一批零件,按计划18天可以完成它的13.如果工作4天后,工作效率提高了15,那么完成这批零件的一半,一共需要______天.10.现在4点5分,再过______分钟,分针和时针第一次重合.答案与提示一、选择题1.C 2.D 3.C 4.D 5.C 6.B 7.D 8.D 9.C 10.A提示:1.令a=2,b=-2,满足2+(-2)=0,由此2.x2,2x2,x3都是单项式.两个单项式x3,x2之和为x3+x2是多项式,排除A.两个单项式x2,2x2之和为3x2是单项式,排除B.两个多项式x3+x2与x3-x2之和为2x3是个单项式,排除C,因此选D.3.1是最小的自然数,A正确.可以找到正所以C“没有最大的负整数”的说法不正确.写出扩大自然数列,0,1,2,3,…,n,…,易知无最大非负数,D正确.所以不正确的说法应选C.5.在数轴上容易看出:在-π右边0的左边(包括0在内)的整数只有-3,-2,-1,0共4个.选C.6.由12=1,13=1可知甲、乙两种说法是正确的.由(-1)3=-1,可知丁也是正确的说法.而负数的平方均为正数,即负数的平方一定大于它本身,所以“负数平方不一定大于它本身”的说法不正确.即丙不正确.在甲、乙、丙、丁四个说法中,只有丙1个说法不正确.所以选B.7.令a=0,马上可以排除A、B、C,应选D.8.对方程同解变形,要求方程两边同乘不等于0的数.所以排除A.我们考察方程x-2=0,易知其根为x=2.若该方程两边同乘以一个整式x-1,得(x-1)(x -2)=0,其根为x=1及x=2,不与原方程同解,排除B.若在方程x-2=0两边加上同一个代数式去了原方程x=2的根.所以应排除C.事实上方程两边同时加上一个常数,新方程与原方程同解,对D,这里所加常数为1,因此选D.9.设杯中原有水量为a,依题意可得,第二天杯中水量为a×(1-10%)=0.9a;第三天杯中水量为(0.9a)×(1+10%)=0.9×1.1×a;第三天杯中水量与第一天杯中水量之比为所以第三天杯中水量比第一天杯中水量少了,选C.10.设两码头之间距离为s,船在静水中速度为a,水速为v0,则往返一次所用时间为设河水速度增大后为v,(v>v0)则往返一次所用时间为由于v-v0>0,a+v0>a-v0,a+v>a-v所以(a+v0)(a+v)>(a-v0)(a-v)∴t0-t<0,即t0<t.因此河水速增大所用时间将增多,选A.二、填空题提示:2.198919902-198919892=(19891990+19891989)×(19891990-19891989)=(19891990+19891989)×1=39783979.3.由于(2+1)(22+1)(24+1)(28+1)(216+1)=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)=(22-1)(22+1)(24+1)(28+1)(216+1)=(24-1)(24+1)(28+1)(216+1)=(28-1)(28+1)(216+1)=(216-1)(216+1)=232-1.2(1+x)-(x-2)=8,2+2x-x+2=8解得;x=45.1-2+3-4+5-6+7-8+…+4999-5000=(1-2)+(3-4)+(5-6)+(7-8)+…+(4999-5000)=-2500.6.(3x3-5x2+6x-1)-(x3-2x2+x-2)+(-2x3+3x2+1)=5x+27.注意到:当a=-0.2,b=0.04时,a2-b=(-0.2)2-0.04=0,b+a+0.16=0.04-0.2+0.16=0.8.食盐30%的盐水60千克中含盐60×30%(千克)设蒸发变成含盐为40%的水重x克,即0.001x千克,此时,60×30%=(0.001x)×40%解得:x=45000(克).10.在4时整,时针与分针针夹角为120°即希望杯第一届(1990年)初中一年级第2试试题一、选择题(每题1分,共5分)以下每个题目里给出的A,B,C,D四个结论中有且仅有一个是正确的.请你在括号填上你认为是正确的那个结论的英文字母代号.1.某工厂去年的生产总值比前年增长a%,则前年比去年少的百分数是( )A.a%.B.(1+a)%. C.1100aa+D.100aa+2.甲杯中盛有2m毫升红墨水,乙杯中盛有m毫升蓝墨水,从甲杯倒出a毫升到乙杯里, 0<a<m,搅匀后,又从乙杯倒出a毫升到甲杯里,则这时( )A.甲杯中混入的蓝墨水比乙杯中混入的红墨水少.B.甲杯中混入的蓝墨水比乙杯中混入的红墨水多.C.甲杯中混入的蓝墨水和乙杯中混入的红墨水相同.D.甲杯中混入的蓝墨水与乙杯中混入的红墨水多少关系不定.3.已知数x=100,则( )A.x是完全平方数.B.(x-50)是完全平方数.C.(x-25)是完全平方数.D.(x+50)是完全平方数.4.观察图1中的数轴:用字母a,b,c依次表示点A,B,C对应的数,则111,,ab b a c-的大小关系是( )A.111ab b a c<<-; B.1b a-<1ab<1c; C.1c<1b a-<1ab; D.1c<1ab<1b a-.5.x=9,y=-4是二元二次方程2x2+5xy+3y2=30的一组整数解,这个方程的不同的整数解共有( )A.2组.B.6组.C.12组.D.16组.二、填空题(每题1分,共5分)1.方程|1990x-1990|=1990的根是______.2.对于任意有理数x,y,定义一种运算*,规定x*y=ax+by-cxy,其中的a,b,c表示已知数,等式右边是通常的加、减、乘运算.又知道1*2=3,2*3=4,x*m=x(m≠0),则m 的数值是______.3.新上任的宿舍管理员拿到20把钥匙去开20个房间的门,他知道每把钥匙只能开其中的一个门,但不知道每把钥匙是开哪一个门的钥匙,现在要打开所有关闭着的20个房间,他最多要试开______次.4.当m=______时,二元二次六项式6x2+mxy-4y2-x+17y-15可以分解为两个关于x,y 的二元一次三项式的乘积.5.三个连续自然数的平方和(填“是”或“不是”或“可能是”)______某个自然数的平方.三、解答题(写出推理、运算的过程及最后结果.每题5分,共15分)1.两辆汽车从同一地点同时出发,沿同一方向同速直线行驶,每车最多只能带24桶汽油,途中不能用别的油,每桶油可使一辆车前进60公里,两车都必须返回出发地点,但是可以不同时返回,两车相互可借用对方的油.为了使其中一辆车尽可能地远离出发地点,另一辆车应当在离出发地点多少公里的地方返回?离出发地点最远的那辆车一共行驶了多少公里?2.如图2,纸上画了四个大小一样的圆,圆心分别是A,B,C,D,直线m通过A,B,直线n通过C,D,用S表示一个圆的面积,如果四个圆在纸上盖住的总面积是5(S-1),直线m,n之间被圆盖住的面积是8,阴影部分的面积S1,S2,S3满足关系式S3=13S1=13S2,求S.3.求方程11156x y z++=的正整数解.答案与提示一、选择题1.D 2.C 3.C 4.C 5.D提示:1.设前年的生产总值是m,则去年的生产总值是前年比去年少这个产值差占去年的应选D.2.从甲杯倒出a毫升红墨水到乙杯中以后:再从乙杯倒出a毫升混合墨水到甲杯中以后:乙杯中含有的红墨水的数量是①乙杯中减少的蓝墨水的数量是②∵①=②∴选C.∴x-25=(10n+2+5)2可知应当选C.4.由所给出的数轴表示(如图3):可以看出∴①<②<③,∴选C.5.方程2x2+5xy+3y2=30可以变形为(2x+3y)(x+y)=1·2·3·5∵x,y是整数,∴2x+3y,x+y也是整数.由下面的表可以知道共有16个二元一次方程组,每组的解都是整数,所以有16组整数组,应选D.二、填空题提示:1.原方程可以变形为|x-1|=1,即x-1=1或-1,∴x=2或0.2.由题设的等式x*y=ax+by-cxy及x*m=x(m≠0)得a·0+bm-c·0·m=0,∴bm=0.∵m≠0,∴b=0.∴等式改为x*y=ax-cxy.∵1*2=3,2*3=4,解得a=5,c=1.∴题设的等式即x*y=5x-xy.在这个等式中,令x=1,y=m,得5-m=1,∴m=4.3.∵打开所有关闭着的20个房间,∴最多要试开4.利用“十字相乘法”分解二次三项式的知识,可以判定给出的二元二次六项式6x2+mxy-4y2-x+17y-15中划波浪线的三项应当这样分解:3x -52x +3现在要考虑y,只须先改写作然后根据-4y2,17y这两项式,即可断定是:由于(3x+4y-5)(2x-y+3)=6x2+5xy-4y2-x+17y-15就是原六项式,所以m=5.5.设三个连续自然数是a-1,a,a+1,则它们的平方和是(a-1)2+a2+(a+1)2=3a2+2,显然,这个和被3除时必得余数2.另一方面,自然数被3除时,余数只能是0或1或2,于是它们可以表示成3b,3b+1,3b+2(b是自然数)中的一个,但是它们的平方(3b)2=9b2(3b+1)2=9b2+6b+1,(3b+2)2=9b2+12b+4=(9b2+12b+3)+1被3除时,余数要么是0,要么是1,不能是2,所以三个连续自然数平方和不是某个自然数的平方.三、解答题1.设两辆汽车一为甲一为乙,并且甲用了x升汽油时即回返,留下返程需的x桶汽油,将多余的(24-2x)桶汽油给乙.让乙继续前行,这时,乙有(24-2x)+(24-x)=48-3x桶汽油,依题意,应当有48-3x≤24,∴x≥8.甲、乙分手后,乙继续前行的路程是这个结果中的代数式30(48-4x)表明,当x的值愈小时,代数式的值愈大,因为x≥8,所以当x=8时,得最大值30(48-4·8)=480(公里),因此,乙车行驶的路程一共是2(60·8+480)=1920(公里).2.由题设可得即2S-5S3=8……②∴x,y,z都>1,因此,当1<x≤y≤z时,解(x,y,z)共(2,4,12),(2,6,6),(3,3,6),(3,4,4)四组.由于x,y,z在方程中地位平等.所以可得如下表所列的15组解.希望杯第二届(1991年)初中一年级第1试试题一、选择题(每题1分,共15分)以下每个题目的A,B,C,D四个结论中,仅有一个是正确的,请在括号内填上正确的那个结论的英文字母代号.1.数1是( )A.最小整数.B.最小正数.C.最小自然数.D.最小有理数.2.若a>b,则( )A.11a b; B.-a<-b.C.|a|>|b|.D.a2>b2.3.a为有理数,则一定成立的关系式是( )A.7a>a.B.7+a>a.C.7+a>7.D.|a|≥7.4.图中表示阴影部分面积的代数式是( )A.ad+bc.B.c(b-d)+d(a-c).C.ad+c(b-d).D.ab-cd.5.以下的运算的结果中,最大的一个数是( )A.(-13579)+0.2468; B.(-13579)+1 2468;C.(-13579)×12468; D.(-13579)÷124686.3.1416×7.5944+3.1416×(-5.5944)的值是( ) A.6.1632. B.6.2832.C.6.5132.D.5.3692.7.如果四个数的和的14是8,其中三个数分别是-6,11,12,则笫四个数是( )A.16. B.15. C.14. D.13.8.下列分数中,大于-13且小于-14的是( )A.-1120; B.-413; C.-316; D.-617.9.方程甲:34(x-4)=3x与方程乙:x-4=4x同解,其根据是( )A.甲方程的两边都加上了同一个整式x.B.甲方程的两边都乘以43x;C. 甲方程的两边都乘以43; D. 甲方程的两边都乘以34.10.如图: ,数轴上标出了有理数a,b,c的位置,其中O是原点,则111,,a b c的大小关系是( ) A.111a b c>>; B.1b >1c >1a ; C. 1b >1a >1c ; D. 1c >1a >1b .11.方程522.2 3.7x =的根是( ) A .27. B .28. C .29. D .30. 12.当x=12,y=-2时,代数式42x y xy -的值是( )A .-6.B .-2.C .2.D .6.13.在-4,-1,-2.5,-0.01与-15这五个数中,最大的数与绝对值最大的那个数的乘积是( )A .225.B .0.15.C .0.0001.D .1.14.不等式124816x x x xx ++++>的解集是( ) A .x <16. B .x >16.C .x <1. D.x>-116. 15.浓度为p%的盐水m 公斤与浓度为q%的盐水n 公斤混合后的溶液浓度是 ( ) A.%2p q +; B.()%mp nq +; C.()%mp nq p q ++;D.()%mp nq m n++.二、填空题(每题1分,共15分)1. 计算:(-1)+(-1)-(-1)×(-1)÷(-1)=______. 2. 计算:-32÷6×16=_______. 3. 计算:(63)36162-⨯=__________.4. 求值:(-1991)-|3-|-31||=______. 5. 计算:1111112612203042-----=_________. 6.n 为正整数,1990n -1991的末四位数字由千位、百位、十位、个位、依次排列组成的四位数是8009.则n 的最小值等于______.7. 计算:19191919199191919191⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=_______.8. 计算:15[(-1989)+(-1990)+(-1991)+(-1992)+(-1993)]=________.9.在(-2)5,(-3)5,512⎛⎫-⎪⎝⎭,513⎛⎫-⎪⎝⎭中,最大的那个数是________.10.不超过(-1.7)2的最大整数是______.11.解方程21101211,_____. 3124x x xx-++-=-=12.求值:355355113113355113⎛⎫---⎪⎝⎭⎛⎫- ⎪⎝⎭=_________.13.一个质数是两位数,它的个位数字与十位数字的差是7,则这个质数是______.14.一个数的相反数的负倒数是119,则这个数是_______.15.如图11,a,b,c,d,e,f均为有理数.图中各行,各列、两条对角线上三个数之和都相等,则ab cd efa b c d e f+++++++=____.答案与提示一、选择题1.C 2.B 3.B 4.C 5.C 6.B 7.B 8.B 9.C 10.B 11.D 12.A 13.B 1 4.A 15.D提示:1.整数无最小数,排除A;正数无最小数,排除B;有理数无最小数,排除D.1是最小自然数.选C.有|2|<|-3|,排除C;若2>-3有22<(-3)2,排除D;事实上,a>b必有-a<-b.选B.3.若a=0,7×0=0排除A;7+0=7排除C|0|<7排除D,事实上因为7>0,必有7+a>0+a=a.选B.4.把图形补成一个大矩形,则阴影部分面积等于ab-(a-c)(b-d)=ab-[ab-ad-c(b-d)]=ab-ab+ad+c(b-d)=ad+c(b-d).选C.5.运算结果对负数来说绝对值越小其值越大。
2007年第18届“希望杯”全国数学邀请赛第一试试题及详解【圣才出品】
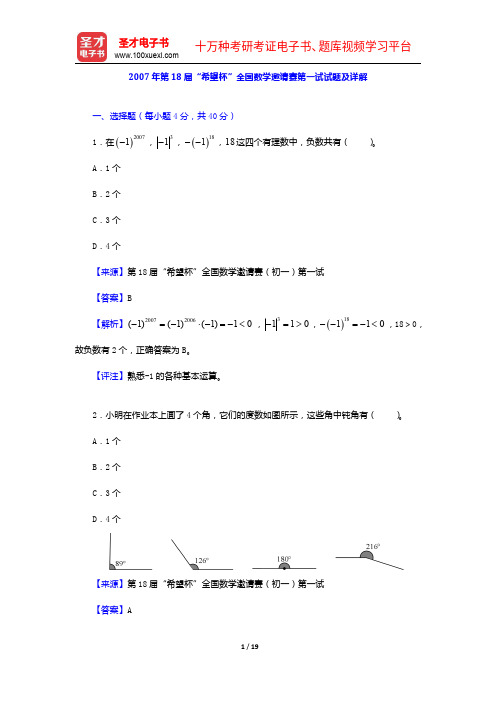
故负数有 2 个,正确答案为 B。 【评注】熟悉-1 的各种基本运算。
2.小明在作业本上画了 4 个角,它们的度数如图所示,这些角中钝角有( )。 A.1 个 B.2 个 C.3 个 D.4 个
观察可发现 47 排在第 15 位,故 n 15 。
【评注】对于数目太大的数可直接利用列举法。
4.有理数 a , b , c 在数轴上对应的点的位置如图所示,给出下面四个命题:
① abc 0
② ab bc ac
③ (a b)(b c)(c a) 0 ④ a 1 bc
其中正确的命题有( )。
任取 p 1, q 2 , r 3 , s 6 。
对于 A 项: p 1 , r 3 ,显然 p r ,故 A 项不正确,排除 A 项;
s 6 q2
sq
对于 B 项: p 1 , s 6 3 ,显然 p s ,故 B 项不正确,排除 B 项;
r 3 q2
rq
对于 D 项: r 3 1 , r p 3 1 2 1 ,显然 r r p ,故 D 项不正确,排
s 6 2 sq 62 4 2
s sq
除 D 项。
所以正确答案为 C 项。
4 / 19
圣才电子书 十万种考研考证电子书、题库视频学习平台
解法二:由 p r 可得: s r ;两边同时加 1, s 1 r 1 ,即 s q r p即 p r p ,故 C 项正确。 q sq
【来源】第 18 届“希望杯”全国数学邀请赛(初一)第一试 【答案】A
1 / 19
圣才电子书 十万种考研考证电子书、题库视频学习平台
历届(1-23)希望杯数学竞赛初一七年级真题及答案(最新整理WORD版)

“希望杯”全国数学竞赛(第1-23届)初一年级/七年级第一/二试题目录1.希望杯第一届(1990年)初中一年级第一试试题............................................. 003-0052.希望杯第一届(1990年)初中一年级第二试试题............................................. 010-0123.希望杯第二届(1991年)初中一年级第一试试题............................................. 016-0204.希望杯第二届(1991年)初中一年级第二试试题............................................. 022-0265.希望杯第三届(1992年)初中一年级第一试试题............................................. 029-0326.希望杯第三届(1992年)初中一年级第二试试题............................................. 034-0407.希望杯第四届(1993年)初中一年级第一试试题............................................. 043-0508.希望杯第四届(1993年)初中一年级第二试试题............................................. 050-0589.希望杯第五届(1994年)初中一年级第一试试题............................................. 057-06610.希望杯第五届(1994年)初中一年级第二试试题 .......................................... 063-07311.希望杯第六届(1995年)初中一年级第一试试题 ........................................... 070-080 12希望杯第六届(1995年)初中一年级第二试试题........................................... 077-08713.希望杯第七届(1996年)初中一年级第一试试题........................................... 086-09814.希望杯第七届(1996年)初中一年级第二试试题............................................. 91-10515.希望杯第八届(1997年)初中一年级第一试试题............................................. 99-11316.希望杯第八届(1997年)初中一年级第二试试题........................................... 106-12017.希望杯第九届(1998年)初中一年级第一试试题........................................... 114-12918.希望杯第九届(1998年)初中一年级第二试试题........................................... 123-13819.希望杯第十届(1999年)初中一年级第二试试题........................................... 130-14720.希望杯第十届(1999年)初中一年级第一试试题........................................... 148-15121.希望杯第十一届(2000年)初中一年级第一试试题....................................... 143-16122.希望杯第十一届(2000年)初中一年级第二试试题....................................... 150-16923.希望杯第十二届(2001年)初中一年级第一试试题....................................... 154-17424.希望杯第十二届(2001年)初中一年级第二试试题....................................... 158-17825.希望杯第十三届(2002年)初中一年级第一试试题....................................... 164-18426.希望杯第十三届(2001年)初中一年级第二试试题....................................... 168-18927.希望杯第十四届(2003年)初中一年级第一试试题....................................... 175-19628.希望杯第十四届(2003年)初中一年级第二试试题....................................... 179-20029.希望杯第十五届(2004年)初中一年级第一试试题 (183)30.希望杯第十五届(2004年)初中一年级第二试试题 (184)31.希望杯第十六届(2005年)初中一年级第一试试题....................................... 213-21832.希望杯第十六届(2005年)初中一年级第二试试题 (184)33.希望杯第十七届(2006年)初中一年级第一试试题....................................... 228-23334.希望杯第十七届(2006年)初中一年级第二试试题....................................... 234-23835.希望杯第十八届(2007年)初中一年级第一试试题....................................... 242-246 26.希望杯第十八届(2007年)初中一年级第二试试题....................................... 248-25137.希望杯第十九届(2008年)初中一年级第一试试题....................................... 252-25638.希望杯第十九届(2008年)初中一年级第二试试题....................................... 257-26239.希望杯第二十届(2009年)初中一年级第一试试题....................................... 263-26620.希望杯第二十届(2009年)初中一年级第二试试题....................................... 267-27121.希望杯第二十一届(2010年)初中一年级第一试试题 ................................... 274-27622.希望杯第二十二届(2011年)初中一年级第二试试题 ................................... 285-28823.希望杯第二十三届(2012年)初中一年级第二试试题 ................................... 288-301希望杯第一届(1990年)初中一年级第1试试题一、选择题(每题1分,共10分)1.如果a ,b 都代表有理数,并且a +b=0,那么 ( )A .a ,b 都是0.B .a ,b 之一是0.C .a ,b 互为相反数.D .a ,b 互为倒数.2.下面的说法中正确的是 ( )A .单项式与单项式的和是单项式.B .单项式与单项式的和是多项式.C .多项式与多项式的和是多项式.D .整式与整式的和是整式.3.下面说法中不正确的是 ( )A. 有最小的自然数. B .没有最小的正有理数.C .没有最大的负整数.D .没有最大的非负数.4.如果a ,b 代表有理数,并且a +b 的值大于a -b 的值,那么( ) A .a ,b 同号. B .a ,b 异号.C .a >0. D .b >0.5.大于-π并且不是自然数的整数有( ) A .2个. B .3个.C .4个. D .无数个.6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身.这四种说法中,不正确的说法的个数是 ( )A .0个.B .1个.C .2个.D .3个.7.a 代表有理数,那么,a 和-a 的大小关系是 ( )A .a 大于-a .B .a 小于-a .C .a 大于-a 或a 小于-a .D .a 不一定大于-a .8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( )A .乘以同一个数.B .乘以同一个整式.C .加上同一个代数式.D .都加上1.9.杯子中有大半杯水,第二天较第一天减少了10%,第三天又较第二天增加了10%,那么,第三天杯中的水量与第一天杯中的水量相比的结果是( )A .一样多.B .多了.C .少了.D .多少都可能.10.轮船往返于一条河的两码头之间,如果船本身在静水中的速度是固定的,那么,当这条河的水流速度增大时,船往返一次所用的时间将( )A .增多.B .减少.C .不变.D .增多、减少都有可能.二、填空题(每题1分,共10分)1. 21115160.01253(87.5)(2)4571615⨯-⨯-÷⨯+--= ______. 2.198919902-198919892=______.3.2481632(21)(21)(21)(21)(21)21+++++-=________. 4. 关于x 的方程12148x x +--=的解是_________. 5.1-2+3-4+5-6+7-8+…+4999-5000=______.6.当x=-24125时,代数式(3x 3-5x 2+6x -1)-(x 3-2x 2+x -2)+(-2x 3+3x 2+1)的值是____. 7.当a=-0.2,b=0.04时,代数式272711()(0.16)()73724a b b a a b --++-+的值是______. 8.含盐30%的盐水有60千克,放在秤上蒸发,当盐水变为含盐40%时,秤得盐水的重是______克.9.制造一批零件,按计划18天可以完成它的13.如果工作4天后,工作效率提高了15,那么完成这批零件的一半,一共需要______天.10.现在4点5分,再过______分钟,分针和时针第一次重合.答案与提示一、选择题1.C 2.D 3.C 4.D 5.C 6.B 7.D 8.D 9.C 10.A提示:1.令a=2,b=-2,满足2+(-2)=0,由此2.x2,2x2,x3都是单项式.两个单项式x3,x2之和为x3+x2是多项式,排除A.两个单项式x2,2x2之和为3x2是单项式,排除B.两个多项式x3+x2与x3-x2之和为2x3是个单项式,排除C,因此选D.3.1是最小的自然数,A正确.可以找到正所以C“没有最大的负整数”的说法不正确.写出扩大自然数列,0,1,2,3,…,n,…,易知无最大非负数,D正确.所以不正确的说法应选C.5.在数轴上容易看出:在-π右边0的左边(包括0在内)的整数只有-3,-2,-1,0共4个.选C.6.由12=1,13=1可知甲、乙两种说法是正确的.由(-1)3=-1,可知丁也是正确的说法.而负数的平方均为正数,即负数的平方一定大于它本身,所以“负数平方不一定大于它本身”的说法不正确.即丙不正确.在甲、乙、丙、丁四个说法中,只有丙1个说法不正确.所以选B.7.令a=0,马上可以排除A、B、C,应选D.8.对方程同解变形,要求方程两边同乘不等于0的数.所以排除A.我们考察方程x-2=0,易知其根为x=2.若该方程两边同乘以一个整式x-1,得(x-1)(x -2)=0,其根为x=1及x=2,不与原方程同解,排除B.若在方程x-2=0两边加上同一个代数式去了原方程x=2的根.所以应排除C.事实上方程两边同时加上一个常数,新方程与原方程同解,对D,这里所加常数为1,因此选D.9.设杯中原有水量为a,依题意可得,第二天杯中水量为a×(1-10%)=0.9a;第三天杯中水量为(0.9a)×(1+10%)=0.9×1.1×a;第三天杯中水量与第一天杯中水量之比为所以第三天杯中水量比第一天杯中水量少了,选C.10.设两码头之间距离为s,船在静水中速度为a,水速为v0,则往返一次所用时间为设河水速度增大后为v,(v>v0)则往返一次所用时间为由于v-v0>0,a+v0>a-v0,a+v>a-v所以(a+v0)(a+v)>(a-v0)(a-v)∴t0-t<0,即t0<t.因此河水速增大所用时间将增多,选A.二、填空题提示:2.198919902-198919892=(19891990+19891989)×(19891990-19891989)=(19891990+19891989)×1=39783979.3.由于(2+1)(22+1)(24+1)(28+1)(216+1)=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)=(22-1)(22+1)(24+1)(28+1)(216+1)=(24-1)(24+1)(28+1)(216+1)=(28-1)(28+1)(216+1)=(216-1)(216+1)=232-1.2(1+x)-(x-2)=8,2+2x-x+2=8解得;x=45.1-2+3-4+5-6+7-8+…+4999-5000=(1-2)+(3-4)+(5-6)+(7-8)+…+(4999-5000)=-2500.6.(3x3-5x2+6x-1)-(x3-2x2+x-2)+(-2x3+3x2+1)=5x+27.注意到:当a=-0.2,b=0.04时,a2-b=(-0.2)2-0.04=0,b+a+0.16=0.04-0.2+0.16=0.8.食盐30%的盐水60千克中含盐60×30%(千克)设蒸发变成含盐为40%的水重x克,即0.001x千克,此时,60×30%=(0.001x)×40%解得:x=45000(克).10.在4时整,时针与分针针夹角为120°即希望杯第一届(1990年)初中一年级第2试试题一、选择题(每题1分,共5分)以下每个题目里给出的A,B,C,D四个结论中有且仅有一个是正确的.请你在括号填上你认为是正确的那个结论的英文字母代号.1.某工厂去年的生产总值比前年增长a%,则前年比去年少的百分数是( )A.a%.B.(1+a)%. C.1100aa+D.100aa+2.甲杯中盛有2m毫升红墨水,乙杯中盛有m毫升蓝墨水,从甲杯倒出a毫升到乙杯里, 0<a<m,搅匀后,又从乙杯倒出a毫升到甲杯里,则这时( )A.甲杯中混入的蓝墨水比乙杯中混入的红墨水少.B.甲杯中混入的蓝墨水比乙杯中混入的红墨水多.C.甲杯中混入的蓝墨水和乙杯中混入的红墨水相同.D.甲杯中混入的蓝墨水与乙杯中混入的红墨水多少关系不定.3.已知数x=100,则( )A.x是完全平方数.B.(x-50)是完全平方数.C.(x-25)是完全平方数.D.(x+50)是完全平方数.4.观察图1中的数轴:用字母a,b,c依次表示点A,B,C对应的数,则111,,ab b a c-的大小关系是( )A.111ab b a c<<-; B.1b a-<1ab<1c; C.1c<1b a-<1ab; D.1c<1ab<1b a-.5.x=9,y=-4是二元二次方程2x2+5xy+3y2=30的一组整数解,这个方程的不同的整数解共有( )A.2组.B.6组.C.12组.D.16组.二、填空题(每题1分,共5分)1.方程|1990x-1990|=1990的根是______.2.对于任意有理数x,y,定义一种运算*,规定x*y=ax+by-cxy,其中的a,b,c表示已知数,等式右边是通常的加、减、乘运算.又知道1*2=3,2*3=4,x*m=x(m≠0),则m 的数值是______.3.新上任的宿舍管理员拿到20把钥匙去开20个房间的门,他知道每把钥匙只能开其中的一个门,但不知道每把钥匙是开哪一个门的钥匙,现在要打开所有关闭着的20个房间,他最多要试开______次.4.当m=______时,二元二次六项式6x2+mxy-4y2-x+17y-15可以分解为两个关于x,y 的二元一次三项式的乘积.5.三个连续自然数的平方和(填“是”或“不是”或“可能是”)______某个自然数的平方.三、解答题(写出推理、运算的过程及最后结果.每题5分,共15分)1.两辆汽车从同一地点同时出发,沿同一方向同速直线行驶,每车最多只能带24桶汽油,途中不能用别的油,每桶油可使一辆车前进60公里,两车都必须返回出发地点,但是可以不同时返回,两车相互可借用对方的油.为了使其中一辆车尽可能地远离出发地点,另一辆车应当在离出发地点多少公里的地方返回?离出发地点最远的那辆车一共行驶了多少公里?2.如图2,纸上画了四个大小一样的圆,圆心分别是A,B,C,D,直线m通过A,B,直线n通过C,D,用S表示一个圆的面积,如果四个圆在纸上盖住的总面积是5(S-1),直线m,n之间被圆盖住的面积是8,阴影部分的面积S1,S2,S3满足关系式S3=13S1=13S2,求S.3.求方程11156x y z++=的正整数解.答案与提示一、选择题1.D 2.C 3.C 4.C 5.D提示:1.设前年的生产总值是m,则去年的生产总值是前年比去年少这个产值差占去年的应选D.2.从甲杯倒出a毫升红墨水到乙杯中以后:再从乙杯倒出a毫升混合墨水到甲杯中以后:乙杯中含有的红墨水的数量是①乙杯中减少的蓝墨水的数量是②∵①=②∴选C.∴x-25=(10n+2+5)2可知应当选C.4.由所给出的数轴表示(如图3):可以看出∴①<②<③,∴选C.5.方程2x2+5xy+3y2=30可以变形为(2x+3y)(x+y)=1·2·3·5∵x,y是整数,∴2x+3y,x+y也是整数.由下面的表可以知道共有16个二元一次方程组,每组的解都是整数,所以有16组整数组,应选D.二、填空题提示:1.原方程可以变形为|x-1|=1,即x-1=1或-1,∴x=2或0.2.由题设的等式x*y=ax+by-cxy及x*m=x(m≠0)得a·0+bm-c·0·m=0,∴bm=0.∵m≠0,∴b=0.∴等式改为x*y=ax-cxy.∵1*2=3,2*3=4,解得a=5,c=1.∴题设的等式即x*y=5x-xy.在这个等式中,令x=1,y=m,得5-m=1,∴m=4.3.∵打开所有关闭着的20个房间,∴最多要试开4.利用“十字相乘法”分解二次三项式的知识,可以判定给出的二元二次六项式6x2+mxy-4y2-x+17y-15中划波浪线的三项应当这样分解:3x -52x +3现在要考虑y,只须先改写作然后根据-4y2,17y这两项式,即可断定是:由于(3x+4y-5)(2x-y+3)=6x2+5xy-4y2-x+17y-15就是原六项式,所以m=5.5.设三个连续自然数是a-1,a,a+1,则它们的平方和是(a-1)2+a2+(a+1)2=3a2+2,显然,这个和被3除时必得余数2.另一方面,自然数被3除时,余数只能是0或1或2,于是它们可以表示成3b,3b+1,3b+2(b是自然数)中的一个,但是它们的平方(3b)2=9b2(3b+1)2=9b2+6b+1,(3b+2)2=9b2+12b+4=(9b2+12b+3)+1被3除时,余数要么是0,要么是1,不能是2,所以三个连续自然数平方和不是某个自然数的平方.三、解答题1.设两辆汽车一为甲一为乙,并且甲用了x升汽油时即回返,留下返程需的x桶汽油,将多余的(24-2x)桶汽油给乙.让乙继续前行,这时,乙有(24-2x)+(24-x)=48-3x桶汽油,依题意,应当有48-3x≤24,∴x≥8.甲、乙分手后,乙继续前行的路程是这个结果中的代数式30(48-4x)表明,当x的值愈小时,代数式的值愈大,因为x≥8,所以当x=8时,得最大值30(48-4·8)=480(公里),因此,乙车行驶的路程一共是2(60·8+480)=1920(公里).2.由题设可得即2S-5S3=8……②∴x,y,z都>1,因此,当1<x≤y≤z时,解(x,y,z)共(2,4,12),(2,6,6),(3,3,6),(3,4,4)四组.由于x,y,z在方程中地位平等.所以可得如下表所列的15组解.希望杯第二届(1991年)初中一年级第1试试题一、选择题(每题1分,共15分)以下每个题目的A,B,C,D四个结论中,仅有一个是正确的,请在括号内填上正确的那个结论的英文字母代号.1.数1是( )A.最小整数.B.最小正数.C.最小自然数.D.最小有理数.2.若a>b,则( )A.11a b; B.-a<-b.C.|a|>|b|.D.a2>b2.3.a为有理数,则一定成立的关系式是( )A.7a>a.B.7+a>a.C.7+a>7.D.|a|≥7.4.图中表示阴影部分面积的代数式是( )A.ad+bc.B.c(b-d)+d(a-c).C.ad+c(b-d).D.ab-cd.5.以下的运算的结果中,最大的一个数是( )A.(-13579)+0.2468; B.(-13579)+12468;C.(-13579)×12468; D.(-13579)÷124686.3.1416×7.5944+3.1416×(-5.5944)的值是( ) A.6.1632. B.6.2832.C.6.5132.D.5.3692.7.如果四个数的和的14是8,其中三个数分别是-6,11,12,则笫四个数是( )A.16. B.15. C.14. D.13.8.下列分数中,大于-13且小于-14的是( )A.-1120; B.-413; C.-316; D.-617.9.方程甲:34(x-4)=3x与方程乙:x-4=4x同解,其根据是( )A.甲方程的两边都加上了同一个整式x.B.甲方程的两边都乘以43x;C. 甲方程的两边都乘以43; D. 甲方程的两边都乘以34.10.如图: ,数轴上标出了有理数a,b,c的位置,其中O是原点,则111,,a b c的大小关系是( ) A.111a b c>>; B.1b >1c >1a ; C. 1b >1a >1c ; D. 1c >1a >1b .11.方程522.2 3.7x =的根是( ) A .27. B .28. C .29. D .30. 12.当x=12,y=-2时,代数式42x y xy -的值是( )A .-6.B .-2.C .2.D .6.13.在-4,-1,-2.5,-0.01与-15这五个数中,最大的数与绝对值最大的那个数的乘积是( )A .225.B .0.15.C .0.0001.D .1.14.不等式124816x x x xx ++++>的解集是( ) A .x <16. B .x >16.C .x <1. D.x>-116. 15.浓度为p%的盐水m 公斤与浓度为q%的盐水n 公斤混合后的溶液浓度是 ( ) A.%2p q +; B.()%mp nq +; C.()%mp nq p q ++;D.()%mp nq m n++.二、填空题(每题1分,共15分)1. 计算:(-1)+(-1)-(-1)×(-1)÷(-1)=______. 2. 计算:-32÷6×16=_______. 3. 计算:(63)36162-⨯=__________.4. 求值:(-1991)-|3-|-31||=______. 5. 计算:1111112612203042-----=_________. 6.n 为正整数,1990n -1991的末四位数字由千位、百位、十位、个位、依次排列组成的四位数是8009.则n 的最小值等于______.7. 计算:19191919199191919191⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=_______.8. 计算:15[(-1989)+(-1990)+(-1991)+(-1992)+(-1993)]=________.9.在(-2)5,(-3)5,512⎛⎫-⎪⎝⎭,513⎛⎫-⎪⎝⎭中,最大的那个数是________.10.不超过(-1.7)2的最大整数是______.11.解方程21101211,_____. 3124x x xx-++-=-=12.求值:355355113113355113⎛⎫---⎪⎝⎭⎛⎫- ⎪⎝⎭=_________.13.一个质数是两位数,它的个位数字与十位数字的差是7,则这个质数是______.14.一个数的相反数的负倒数是119,则这个数是_______.15.如图11,a,b,c,d,e,f均为有理数.图中各行,各列、两条对角线上三个数之和都相等,则ab cd efa b c d e f+++++++=____.答案与提示一、选择题1.C 2.B 3.B 4.C 5.C 6.B 7.B 8.B 9.C 10.B 11.D 12.A 13.B 1 4.A 15.D提示:1.整数无最小数,排除A;正数无最小数,排除B;有理数无最小数,排除D.1是最小自然数.选C.有|2|<|-3|,排除C;若2>-3有22<(-3)2,排除D;事实上,a>b必有-a<-b.选B.3.若a=0,7×0=0排除A;7+0=7排除C|0|<7排除D,事实上因为7>0,必有7+a>0+a=a.选B.4.把图形补成一个大矩形,则阴影部分面积等于ab-(a-c)(b-d)=ab-[ab-ad-c(b-d)]=ab-ab+ad+c(b-d)=ad+c(b-d).选C.5.运算结果对负数来说绝对值越小其值越大。
历年初中希望杯数学竞赛试题大全

历年初中希望杯数学竞赛试题大全][ 真诚为您服务试试题希望杯”全国数学邀请赛初二第 2 ·2009 年第20 届“次·161 ·[4-30]★ 详细简介请参考下载页]·[ 竞赛 2 试试题届“希望杯”全国数学邀请赛初一第年第·200920 次·153 ·[4-28]详细简介请参考下载页★]·[ 竞赛数学大赛初赛试卷(扫描版)届5“希望杯”年湖北省黄冈市第·2009 ·76 次·[4-17]★ 详细简介请参考下载页]·[ 竞赛试试题”全国数学邀请赛初二第1·2009 年第20 届“希望杯次·133 ·[4-7]对不起,尚无简介☆]竞赛·[ 试试题全国数学邀请赛初一第 1 届“希望杯”20 ·2009年第·122 次·[4-7]详细简介请参考下载页★]·[ 竞赛全国数学邀请赛初二训练题”第十四届“希望杯·次·44 ·[9-9]详细简介请参考下载页★]竞赛·[ 2 试试题“希望杯”全国数学邀请赛初一第19 ·2008年第届次·203 ·[9-4]详细简介请参考下载页★]·[ 竞赛 1 ”“19 ·2008 年第届希望杯全国数学邀请赛初一第试试题次·169 ·[9-4]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第219 年第届“希望杯”·2008 次·156 ·[9-2]详细简介请参考下载页★]·[ 竞赛 1 试试题希望杯”全国数学邀请赛初二第“·2008 年第19 届·146 次·[9-2]详细简介请参考下载页★]竞赛·[ 2 试试题”届“希望杯全国数学邀请赛初二第18 ·2007年第·101 次·[9-2]详细简介请参考下载页★]竞赛·[ 1 全国数学邀请赛初二第试试题” “18 ·2007 年第届希望杯次·95 ·[9-2]详细简介请参考下载页★]竞赛·[ 试试题”全国数学邀请赛初二第2·2006 年第17 届“希望杯次·76 ·[9-2]详细简介请参考下载页★]竞赛·[ 1 试试题“希望杯”全国数学邀请赛初二第届·2006年第17 ·76 次·[9-2]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第 2 希望杯·2005 年第16 届“”次·65 ·[9-1]详细简介请参考下载页★]·[ 竞赛 1 试试题全国数学邀请赛初二第届·2005 年第16“希望杯”次·52 ·[9-1]详细简介请参考下载页★]·[ 竞赛试试题全国数学邀请赛初二第希望杯”2·2004 年第15 届“次·47 ·[9-1]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第115 届“希望杯”年第·2004 次·38 ·[9-1]详细简介请参考下载页★]·[ 竞赛 2 试试题希望杯”全国数学邀请赛初二第届·2003 年第14 “次·30 ·[9-1]详细简介请参考下载页★]竞赛·[ 1 试试题希望杯届“”全国数学邀请赛初二第年第·200314 ·26 次·[9-1]详细简介请参考下载页★]竞赛·[ 2 试试题全国数学邀请赛初二第希望杯届年第·200213 “”·31 次·[9-1]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第 1 ”年第13 届“希望杯·2002 次·23 ·[9-1]详细简介请参考下载页★]竞赛·[ 2 试试题“希望杯”全国数学邀请赛初二第·2001 年第12 届·17 次·[9-1]详细简介请参考下载页★]]·[ 竞赛试试题”全国数学邀请赛初二第1“·2000 年第11 届希望杯次·15 ·[9-1]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第210 届“希望杯”·1999年第次·13 ·[9-1]详细简介请参考下载页★]·[ 竞赛试试题 1 希望杯”全国数学邀请赛初二第·1999 年第10 届“次·15 ·[9-1]详细简介请参考下载页★]竞赛·[ 2 试试题“希望杯”全国数学邀请赛初二第9 ·1998年第届次·11 ·[8-29]详细简介请参考下载页★]·试题[ 竞赛 1 ”“9·1998 年第届希望杯全国数学邀请赛初二第试竞赛·[ 试试题全国数学邀请赛初二第112 年第届“希望杯”·2001 ·17 次·[9-1]详细简介请参考下载页★]竞赛·[ 试试题2“届希望杯”全国数学邀请赛初二第11 ·2000 年第次·15 ·[9-1]★详细简介请参考下载页次·10 ·[8-29]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第28 年第届“希望杯”·1997 次·13 ·[8-29]详细简介请参考下载页★]·[ 竞赛 1 试试题希望杯”全国数学邀请赛初二第“·1997 年第8 届·10 次·[8-29]详细简介请参考下载页★]竞赛·[ 2 试试题”届“希望杯全国数学邀请赛初二第7·1996年第·11 次·[8-29]详细简介请参考下载页★]竞赛·[ 1 全国数学邀请赛初二第试试题” “7·1996 年第届希望杯次·10 ·[8-29]详细简介请参考下载页★]·[ 竞赛试试题”希望杯全国数学邀请赛初二第2·1995 年第6 届“次·14 ·[8-29]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第16 届“希望杯”·1995年第次·14 ·[8-29]★详细简介请参考下载页]·[ 竞赛 2 试试题希望杯”全国数学邀请赛初二第5·1994 年第届“次·12 ·[8-29]详细简介请参考下载页★]竞赛·[ 1 试试题“届希望杯”全国数学邀请赛初二第·1994年第5 ·12 次·[8-29](每一、选择题: 年第五届希望杯全国数学邀请赛1994 初中二年级第一试试题[] Ax 1.303 小题分,共分)使等式成立的的值是.是]·[ 竞赛试试题初二第 2 ”年第4 届“希望杯全国数学邀请赛·1993 次·9 ·[8-29]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第14 届“希望杯”·1993年第次·10 ·[8-29]详细简介请参考下载页★]·[ 竞赛试试题2 希望杯”全国数学邀请赛初二第·1992 年第3 届“次·11 ·[8-29]详细简介请参考下载页★]竞赛·[ 1 试试题“希望杯”全国数学邀请赛初二第 3 ·1992年第届次·9 ·[8-29]详细简介请参考下载页★]·[ 竞赛 2 ”“2·1991 年第届希望杯全国数学邀请赛初二第试试题·14 次·[8-28]详细简介请参考下载页★]·[ 竞赛试试题”全国数学邀请赛初二第 1 年第·19912 届“希望杯次·12 ·[8-28]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第21 届“希望杯”·1990年第·13 次·[8-28]详细简介请参考下载页★]·[ 竞赛试试题”全国数学邀请赛初二第 1 希望杯·1990 年第1 届“次·11 ·[8-28]分,(每题1 ”全国数学邀请赛初二第一试一、选择题: “1990 年第一届希望杯() 倍,那么这个角是 1 .一个角等于它的余角的 5 分)共10]竞赛·[ 2 试试题全国数学邀请赛初一第希望杯届年第·200718 “”·94 次·[8-28]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初一第118 届“希望杯”·2007年第次·42 ·[8-28]详细简介请参考下载页★]·[ 竞赛试试题”希望杯全国数学邀请赛初一第2·2006 年第17 届“次·41 ·[8-28]详细简介请参考下载页★]竞赛·[ 试试题 1 希望杯”全国数学邀请赛初一第“·2006 年第17 届次·43 ·[8-28]试第1 全国数学邀请赛初一希望杯年第十七届2006 “”中考资源网,竞赛试题任你选!更多数学竞赛试题请点击。
2007年第18届希望杯初一1试题

(26个)出现的次数,出现次数最少的英文字母有
字母的频率是 。
个;出现次数最多的英文
Hale Waihona Puke 3.If then-th
prime
number is 47, then n is( (D)15 number第n个质数)
)
(A)12 (B)13
(C)14
(英汉词典:the n-th prime
4.有理数a,b,c在数轴上对应的点的位置如图2所示,给出下面四个命题: (1)abc<0 (3)(a-b)(b-c)(c-a)>0 其中正确的命题有( (A)4个 (B)3个 a -1 0 ) (C)2个 bc 1 (D)1个 (2) a b b c a c (4)
(A)11
(B)13
(C)14
(D)16
8.如图5,若AB//CD,则∠B、∠C、∠E 三者之间的关系是(
)
(A)∠B+∠C+∠E=180º (C)∠B+∠C-∠E=180º
(B)∠B+∠E-∠C=180º (D)∠C+∠E-∠B=180º
9.以x 为未知数的方程2007x+2007a+2008b=0(a,b为有理数,
且b>0)有正整数解,则ab是( )
(A)负数 (B)非负数 (C)正数 (D)零
10.对任意四个有理数 a,b,c,d 定义新运算: ( ) (A)-1 (B)2 (C)3
a c
b d
=ad-bc,已知
2 x 4 x 1
=18,则 x=
(D)4
11.小明已进行了20场比赛,其中赢的场数占95%, 若以后小明一场都不输,则赢的场数恰好占96%, 小明还需要进行 场比赛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007年第18届“希望杯”全国数学邀请赛试卷(初一第1试)© 2011 菁优网一、选择题(共6小题,每小题5分,满分30分)1、如图,在数轴上有六个点,且AB=BC=CD=DE=EF,则这条数轴的原点在()A、在点A,B之间B、在点B,C之间C、在点C,D之间D、在点D,E之间2、(2006•济宁)(﹣8)2006+(﹣8)2005能被下列数整除的是()A、3B、5C、7D、93、图中的小方格式边长为1的正方形,则在图中一共可以数出正方形的个数是()A、66B、50C、60D、2104、(2006•济南)如图,直线a与直线b互相平行,则|x﹣y|的值是()A、20B、80C、120D、1805、将一个正方形的纸片分成四块,要求这四块大小相等,形状一样,则分的方法共有()A、2种B、4种C、6种D、无数种6、某商店同时售出两种服装,每套均卖198元,以成本价计算,其中一套盈利20%,另一套亏本20%,如果不考虑其因素,则这次出售过程中商店()A、不赚不赔B、赚16.5元C、赔25元D、非以上答案二、填空题(共6小题,每小题5分,满分30分)7、北京与纽约的时差为﹣13时(负号表示同一时刻纽约时间比北京时间晚),如果现在是北京时间18时,那么纽约时间是_________.8、(2009•枣庄)如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB=_________度.9、用定义新运算,对于任意有理数x,y都有x y=2x+y2+1,例如35=2×3+52+1=32,那么2[(﹣7)3]=_________.10、计算=_________.11、为估计某水库鲢鱼的数量,养鱼户李老板先捞上150条鲢鱼并在上做红色的记号,然后立即将这150条鲢鱼放回水库中,一周后,李老板又捞取200条鲢鱼,数一数带红色记号的鱼有三条,据此可估计出该水库中鲢鱼约有_________条.12、若P为质数,P3+9仍为质数,则P2﹣7=_________.三、解答题(共4小题,满分40分)13、为响应“建设节约型社会”的号召,某市制定如下规定:每户用煤气如果不超过m立方米,按每立方米0.8元收费,超过m立方米,超过的部分按每立方米1.2元收费.小颖家10,11月的交煤气费的情况如下表:(1)求m的值;(2)由于天气转冷,小颖家12月份的用气量预计将增大20%,为了节约煤气,小颖的爸爸换用了高科技煤气灶具,该灶具在提供相同热量的情况下的用气量是原灶具的60%,试问小颖家12月份比预计可少交煤气费多少元?14、某城市平面图如图所示,每条线段均表示街道:(1)图中共有多少条线段?(2)小饶需从A1到B6办事,怎样走最近,最近的走法共有几种?15、如图,在六边形的顶点处,分别标上数3,4,5,6,7,8,能否使任意三个相邻顶点处的三个数之和(1)大于15?(2)大于16?若能,请在图中标出来,若不能,请说明理由.16、如图,时钟在四点到五点之间,什么时刻时针与分针成一直角?答案与评分标准一、选择题(共6小题,每小题5分,满分30分)1、如图,在数轴上有六个点,且AB=BC=CD=DE=EF,则这条数轴的原点在()A、在点A,B之间B、在点B,C之间C、在点C,D之间D、在点D,E之间考点:数轴。
专题:计算题;数形结合。
分析:根据图示,求得AF间的距离,然后由已知条件AB=BC=CD=DE=EF来确定条数轴的原点的大致位置.解答:解:∵|11﹣(﹣5)|=16,AB=BC=CD=DE=EF,∴AB=BC=CD=DE=EF==3.2,∴这条数轴的原点在B与C之间.故选B.点评:本题主要考查了数轴上对应点的几何意义.2、(2006•济宁)(﹣8)2006+(﹣8)2005能被下列数整除的是()A、3B、5C、7D、9考点:因式分解的应用。
分析:根据乘方的性质,提取公因式(﹣8)2005,整理即可得到是7的倍数,所以能被7整除.解答:解:(﹣8)2006+(﹣8)2005,=(﹣8)(﹣8)2005+(﹣8)2005,=(﹣8+1)(﹣8)2005,=7×82005.所以能被7整除.故选C.点评:本题考查提公因式法分解因式,关键在于提取公因式,然后再对所剩的因数进行计算.3、图中的小方格式边长为1的正方形,则在图中一共可以数出正方形的个数是()A、66B、50C、60D、210考点:规律型:图形的变化类。
分析:题中的正方形共有4类,即边长为1,边长为2,边长为3,边长为4,分别找出其对应的正方形的个数再求和即可.解答:解:由图可知,边长为1的小正方形共有4×7=28个;边长为2的正方形共有18个;边长为3的正方形共有10个;边长为4的正方形的个数为4个.所以题中的正方形的个数为28+18+10+4=60个,故选C.点评:本题主要考查了正方形四条边相等的性质问题,应熟练掌握正方形的性质,并能求解一些简单的问题.4、(2006•济南)如图,直线a与直线b互相平行,则|x﹣y|的值是()A、20B、80C、120D、180考点:平行线的性质;对顶角、邻补角。
专题:计算题。
分析:根据平行线的性质可得x的度数,然后根据邻补角概念,求出y,即可解答.解答:解:∵直线a与直线b互相平行,∴x=30,∴3y°=180°﹣30°=150°,得y=50,∴|x﹣y|=|30﹣50|=20.故选A.点评:本题主要考查平行线的性质与绝对值的概念.5、将一个正方形的纸片分成四块,要求这四块大小相等,形状一样,则分的方法共有()A、2种B、4种C、6种D、无数种考点:轴对称的性质;正方形的性质。
专题:常规题型。
分析:根据正方形的性质,一定被经过中心的直线平分即可解决.解答:解:因为只是要求分成形状、大小都相同的四个部分,没要求具体什么图形,所以只要这两条直线过正方形中心且相互垂直即可,因而不同的折法共有无数种.故选D.点评:本题考查了轴对称及正方形的性质,解决此类问题,要充分考虑题意的要求.6、某商店同时售出两种服装,每套均卖198元,以成本价计算,其中一套盈利20%,另一套亏本20%,如果不考虑其因素,则这次出售过程中商店()A、不赚不赔B、赚16.5元C、赔25元D、非以上答案考点:一元一次方程的应用。
专题:应用题。
分析:可分别设两种衣服的进价为未知数,根据盈利情况可列出方程,求解后再比较两种衣服的总进价和总售价的差,即可知盈亏损情况.解答:解:设盈利20%的衣服进价为x元,亏本20%的衣服进价为y,根据题意得:x(1+20%)=198,y(1﹣20%)=198,解得x=165(元),y=247.5(元),两套衣服的进价和为165+247.5=412.5(元),两套衣服的售价和为198×2=396(元),则这次出售过程中商店赔412.5﹣396=16.5(元).故选D.点评:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程.二、填空题(共6小题,每小题5分,满分30分)7、北京与纽约的时差为﹣13时(负号表示同一时刻纽约时间比北京时间晚),如果现在是北京时间18时,那么纽约时间是5时.考点:正数和负数。
分析:首先审清题意,明确“正”和“负”所表示的意义;再根据题意作答.解答:解:由题意得,纽约时间为18﹣13=5,故纽约时间为5时.点评:解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.8、(2009•枣庄)如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB=180度.考点:角的计算。
专题:计算题。
分析:本题考查了角度的计算问题,因为本题中∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.解答:解:设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,所以∠AOC+∠BOD=90°+a+90°﹣a=180°.故答案为180°.点评:在本题中要注意∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.9、用定义新运算,对于任意有理数x,y都有x y=2x+y2+1,例如35=2×3+52+1=32,那么2[(﹣7)3]=21.考点:有理数的混合运算。
专题:计算题;新定义。
分析:由于对于任意有理数x,y都有x y=2x+y2+1,那么利用这个定义的新运算首先计算(﹣7)3,然后计算括号外面的即可求解.解答:解:∵对于任意有理数x,y都有x y=2x+y2+1,∴(﹣7)3=2×(﹣7)+32+1=﹣4,∴2[(﹣7)3]=2(﹣4)=2×2+(﹣4)2+1=21.故答案为:21.点评:此题主要考查有理数的混合运算,解题的关键是首先正确理解新定义的运算法则,然后把数据代入其中计算即可求解.10、计算=.考点:绝对值。
专题:规律型。
分析:根据绝对值的定义,去掉绝对值符合,化简求值.解答:解:====故答案为点评:解决本题的关键是去掉绝对值符号后,部分数值恰好是互为相反数,其和等于0.11、为估计某水库鲢鱼的数量,养鱼户李老板先捞上150条鲢鱼并在上做红色的记号,然后立即将这150条鲢鱼放回水库中,一周后,李老板又捞取200条鲢鱼,数一数带红色记号的鱼有三条,据此可估计出该水库中鲢鱼约有10000条.考点:用样本估计总体。
专题:计算题;应用题。
分析:设该水库中鲢鱼约有x条,由于李老板先捞上150条鲢鱼并在上做红色的记号,然后立即将这150条鲢鱼放回水库中,一周后,李老板又捞取200条鲢鱼,数一数带红色记号的鱼有三条,由此即可列出方程200:3=x:150,解此方程即可求出该水库中鲢鱼约有多少条.解答:解:设该水库中鲢鱼约有x条,依题意得200:3=x:150,∴x=10000,∴估计出该水库中鲢鱼约有10000条.故答案为:10000.点评:此题主要考查了利用样本估计总体的思想,解题时首先正确理解题意,然后根据题意和样本估计总体的思想列出方程即可解决问题.12、若P为质数,P3+9仍为质数,则P2﹣7=﹣3.考点:质数与合数。
专题:计算题。
分析:由于在所有的质数中,只有2是偶数,故P为质数,P3+9仍为质数,则P=2,代入P2﹣7即可求解.解答:解:∵P为质数,P3+9仍为质数,当P为奇质数时,P3+9为大于2的偶数,不符合题意;当P为2时,P3+9=17,仍为质数,符合题意.∴P=2.当P=2时,P2﹣7=4﹣7=﹣3.故答案为:﹣3.点评:本题考查了质数的基本性质,解题的关键是熟悉所有的质数中,只有2是偶数,从而确定p=2.三、解答题(共4小题,满分40分)13、为响应“建设节约型社会”的号召,某市制定如下规定:每户用煤气如果不超过m立方米,按每立方米0.8元收费,超过m立方米,超过的部分按每立方米1.2元收费.小颖家10,11月的交煤气费的情况如下表:(1)求m的值;(2)由于天气转冷,小颖家12月份的用气量预计将增大20%,为了节约煤气,小颖的爸爸换用了高科技煤气灶具,该灶具在提供相同热量的情况下的用气量是原灶具的60%,试问小颖家12月份比预计可少交煤气费多少元?考点:一元一次方程的应用。
