正弦型函数的图像ppt课件
合集下载
正弦函数的图像PPT课件

伸长为原来的2倍 图象上各点纵坐标 缩短为原来的一半
缩短为原来的一半
图象上各点横坐标 伸长为原来的2倍
y
1
2 O
3
4 x
1
例3 作函数
及
的图象。
x
0
1 O 1 y
1
0
-1
0
2
x
三、函数y=sin(x+φ)图象
y
1 O 1 2 x
三、函数y=sin(x+φ)图象
1
2
伸长为原来的多少倍?
例5 作函数
1 O 1
及
的图象。
2
x
函数y=sin(x +φ) ( >0且≠1)的图象可以看作
是把 y=sin(x +φ) 的图象上所有点的横坐标缩短(当 >1时)或伸长(当0<<1时) 到原来的 变) 而得到的。 倍(纵坐标不
y=sinx 的图象上所有点的横坐标缩短(当>1时)或伸 长(当0<<1时) 到原来的 倍(纵坐标不变) 而得到 的。
练习:作下列函数在长度为一个周期的闭区间上的简图:
法一:
图象上各点纵坐标
图象上各点横坐标
伸长为原来的2倍
缩短为原来的一半
1
2
O
3
4 x
法一: 法二:
图象上各点纵坐标
图象上各点横坐标
y
2 1 2 O 1 2 y=2sinx的图象可以看作是把 y=sinx的图象上所有点 的纵坐标伸长到原来的2倍。 y= sinx的图象可以看作是把 y=sinx的图象上所有点的 纵坐标缩短到原来的 倍。 x
一、函数y=Asinx(A>0)的图象
缩短为原来的一半
图象上各点横坐标 伸长为原来的2倍
y
1
2 O
3
4 x
1
例3 作函数
及
的图象。
x
0
1 O 1 y
1
0
-1
0
2
x
三、函数y=sin(x+φ)图象
y
1 O 1 2 x
三、函数y=sin(x+φ)图象
1
2
伸长为原来的多少倍?
例5 作函数
1 O 1
及
的图象。
2
x
函数y=sin(x +φ) ( >0且≠1)的图象可以看作
是把 y=sin(x +φ) 的图象上所有点的横坐标缩短(当 >1时)或伸长(当0<<1时) 到原来的 变) 而得到的。 倍(纵坐标不
y=sinx 的图象上所有点的横坐标缩短(当>1时)或伸 长(当0<<1时) 到原来的 倍(纵坐标不变) 而得到 的。
练习:作下列函数在长度为一个周期的闭区间上的简图:
法一:
图象上各点纵坐标
图象上各点横坐标
伸长为原来的2倍
缩短为原来的一半
1
2
O
3
4 x
法一: 法二:
图象上各点纵坐标
图象上各点横坐标
y
2 1 2 O 1 2 y=2sinx的图象可以看作是把 y=sinx的图象上所有点 的纵坐标伸长到原来的2倍。 y= sinx的图象可以看作是把 y=sinx的图象上所有点的 纵坐标缩短到原来的 倍。 x
一、函数y=Asinx(A>0)的图象
正弦函数图像课件
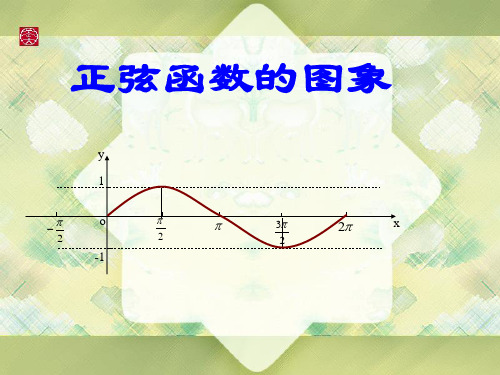
y=sinx
终边相同角的同一三角函数值相等
即: sin(x+2k)=sinx, kZ
x[0,2]
y=sinx
f (x 2k ) f (x) 利用图象平移
xR
y=sinx x[0,2]
y
y=sinx xR
1
-4 -3
-2
- o
-1
函数y=sinx, xR的图象
2
3
4
正弦曲线
5 6 x
3)作正弦函数的简图(在精确度要求不太高时)
y 1
(0,0)o
2
-1
( 2 ,1)
2
五点画图法
( ,0)
3 2
3
( 2 ,-1)
( 2 ,0)
2
x
五点法
x
3
0
2
2
2
0
1
0
-1
0
y=sinx
4)函数的图象变换
y x2
向右平移 一个单位
y
(x
1)2
向下平移 一个单位
y (x 1)2 1
y
o1
x
-1
四. 解题示范
例1:用五点法作函数y=1+sinx, [0,2]的图象
x
0
2
y=sinx 0
1
3
2
2
0
-1
0
1
2
1
y=1+sin
0
1
x
. 2
y=1+sinx, x[0,2]
1.
.
.
.
o
/2
3/2
作函数 y sin x , x [0,2 ] 的图象
正弦函数、余弦函数的图象_优质课件

3) y 3sin(1 x ), x R 一般
35
结论:
函数y Asin(x )及y Acos(x ), x R
( A,,为常数, A 0, 0)的周期T 2
新课讲解. 正弦函数、余弦函数的性质 (三)关于奇偶性(复习)
一般地, •如果对于函数f( x )的定义域内任意一个x, 都有f(- x )= f( x ),那么就说f( x )是偶函数 •如果对于函数f( x )的定义域内任意一个x, 都有f(- x )= -f( x ),那么就说f( x )是奇函数
小结回顾
正切函数的基本性质
4 5
应用提升
练习1:试着画出y | tan x | 和y tan | x |
并讨论它们的单调性,周期性和奇偶性.
练习2.如果、
(
,
)且
tan
cot
,
2
那么必有( )
A.
B.
C. 3 D. 3
2
2
应用提升
例3.求函数y tan x 1 的定义域 3 tan x
例4.试讨论函数y loga tan x的单调性
2
2
y=cosx
y cos x : 定义域为R,值域[1,1]
1
最-6大 值1,此-5时 x
2-k4; 最小值-3-1,
此时x
-2
2k
-;
-1
2 3 2 3
4 5 4 5
6 x 6 x
五.定义域 、值域及取到最值时相应的x的集合:
-6 -5
-4 -3
复习回顾
-2 -
y y=sinx
1 o
-1
2 3
(2) y sin x, y cosx与y Asin(x ), y Acos(x )间的换元思想
正弦函数完整ppt课件
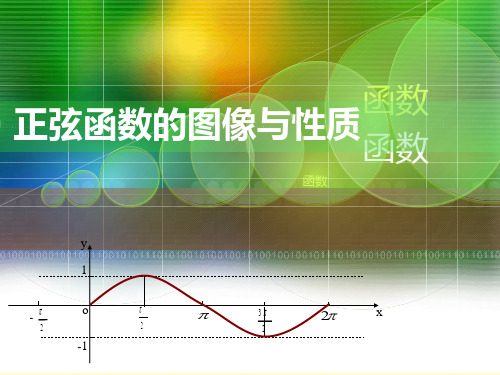
-2
1
-
o
-1
正弦曲线
2
3
4
精选编辑ppt
5 6x
3
五y点作图法
1-
-
o
6
3
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2
-1 -
简图作法
(五点作图法)
(1) 列表(列出对图象形状起关键作用的五点坐标)
( ,1) 图象的最高点 2
x 与x轴的交点
(0,0) ( ,0) (2,0)
图象的最低点
7 6
4
3 3 2
y
3
y=sinx ( x[0, 2] )
1
●
●
●
●
●
6
7 4 3 5 11 6 3 2 3 6 2
2
●
0
11
6
32
2 5 ●
36
●
●
x
●
5
6
-1
●
●
●
3
精选编辑ppt
2
正弦函数的图象
y 1
o
2
2
-1
3
2
2
x
y=sinx x[0,2] y
y=sinx xR
-4 -3
一般地,对于函数 f (x),如果存在一个非零常数 T ,
使得当 x 取定义域内的每一个值时,都有
f ( x+T )= f (x)
,那么函数 f (x) 就叫做周期函数,非零常数 T 叫做这个
函数的周期.
对于一个周期函数,如果在它的所有周期中存在一个
最小的正数,那么这个最小正数就叫做它的最小正周期.
正弦型函数的图像与性质(课堂PPT)

当函数y=Asin(ωx+φ)(A>0,ω>0,x∈[0,+∞))表示一个
简谐振动时,则A叫做振幅,T=
2π ω
叫做周期,f=
1 T
叫做频率,
ωx+φ叫做相位,x=0时的相位φ叫做初相.
第三章 第4讲
第12页
金版教程 ·高三一轮总复习 ·新课标 ·数学(文)
[填一填]
抓住2个必备考点 突破3个热点考向 破译5类高考密码 迎战2年高考模拟
抓住2个必备考点 突破3个热点考向 破译5类高考密码
迎战2年高考模拟
限时规范特训
1个特别提醒——图象平移时必须注意的一个问题 由y=Asinωx的图象得到y=Asin(ωx+φ)的图象时,需平移的单 位数应为|ωφ |,而不是|φ|.原因在于相位变换和周期变换都是针对x 而言,即x本身加减多少值,而不是依赖于ωx加减多少值.
第4讲 正弦型函数y=Asin(ωx+φ)的图象及应用
第三章 第4讲
第2页
金版教程 ·高三一轮总复习 ·新课标 ·数学(文)
抓住2个必备考点 突破3个热点考向 破译5类高考密码
迎战2年高考模拟
限时规范特训
1.了解函数y=Asin(ωx+φ)的物理意义,能画出函数y=Asin(ωx +φ)的图象,了解参数A、ω、φ对函数图象变化的影响.
第三章 第4讲
第3页
金版教程 ·高三一轮总复习 ·新课标 ·数学(文)
抓住2个必备考点 突破3个热点考向 破译5类高考密码
迎战2年高考模拟
限时规范特训
2.了解三角函数是描述周期变化现象的重要函数模型,会用三 角函数解决一些简单的实际问题.
第三章 第4讲
第4页
金版教程 ·高三一轮总复习 ·新课标 ·数学(文)
正弦函数的图像课件(用)

正弦函数的图像 课件
PPT,a click to unlimited possibilities
汇报人:PPT
添加目录标题 课件概述
正弦函数基础 知识
正弦函数的图 像绘制
正弦函数图像 的变换与性质
正弦函数的应 用实例
总结与回顾
添加章节标题
课件概述
适用对象:高中生
课件简介
教学目标:掌握正弦函数的图 像特点,理解其性质和应用
信号的滤波:正弦函数可以 作为滤波器的一种基础波形
信号的表示:正弦函数可以 用来表示周期信号
信号的调制:正弦函数可以用 于调制信号,例如在无线通信
中
总结与回顾
知识点总结
正弦函数的定义 与性质
正弦函数的图像 与特点
正弦函数的应用 与实例
回顾与总结:加 深对正弦函数的 理解和掌握
回顾与思考题
正弦函数的定义和性质 正弦函数的图像特点和绘制方法 正弦函数的应用和实际意义 回顾与思考:如何更好地理解和掌握正弦函数的图像?
感谢观看
汇报人:PPT
设置x的范围:例 如x = np.linspace(-2 * pi, 2 * pi, 1000)
绘制图像:例如 plt.plot(x, y)
正弦函数图像的变换与 性质
振幅变换与周期变换
振幅变换:改变正 弦函数的幅度大小, 图像形状不变
周期变换:改变正 弦函数的周期,图 像形状不变
振幅与周期的关系 :振幅越大,周期 越短;振幅越小, 周期越长
振幅与周期变换的 应用:在信号处理 、电子工程等领域 有广泛的应用
相位变换的方法
相位变换
相位变换对函数图像的影响
相位的概念
相位变换在实际问题中的应 用
PPT,a click to unlimited possibilities
汇报人:PPT
添加目录标题 课件概述
正弦函数基础 知识
正弦函数的图 像绘制
正弦函数图像 的变换与性质
正弦函数的应 用实例
总结与回顾
添加章节标题
课件概述
适用对象:高中生
课件简介
教学目标:掌握正弦函数的图 像特点,理解其性质和应用
信号的滤波:正弦函数可以 作为滤波器的一种基础波形
信号的表示:正弦函数可以 用来表示周期信号
信号的调制:正弦函数可以用 于调制信号,例如在无线通信
中
总结与回顾
知识点总结
正弦函数的定义 与性质
正弦函数的图像 与特点
正弦函数的应用 与实例
回顾与总结:加 深对正弦函数的 理解和掌握
回顾与思考题
正弦函数的定义和性质 正弦函数的图像特点和绘制方法 正弦函数的应用和实际意义 回顾与思考:如何更好地理解和掌握正弦函数的图像?
感谢观看
汇报人:PPT
设置x的范围:例 如x = np.linspace(-2 * pi, 2 * pi, 1000)
绘制图像:例如 plt.plot(x, y)
正弦函数图像的变换与 性质
振幅变换与周期变换
振幅变换:改变正 弦函数的幅度大小, 图像形状不变
周期变换:改变正 弦函数的周期,图 像形状不变
振幅与周期的关系 :振幅越大,周期 越短;振幅越小, 周期越长
振幅与周期变换的 应用:在信号处理 、电子工程等领域 有广泛的应用
相位变换的方法
相位变换
相位变换对函数图像的影响
相位的概念
相位变换在实际问题中的应 用
正弦型函数的图象PPT优秀课件

函数 y=sinx (1)向左平移 3
y=sin(x+ ) 的图象 3
(2)横坐标缩短到原来的
1 2
倍
纵坐标不变
y=sin(2x+ ) 的图象 3
(3)横坐标不变 纵坐标伸长到原来的3倍
y=3sin(2x+ 3 )的图象
方法1:先平移后伸缩一般规律
(1)向左( >0)或向右( <0)
y=Sin( x+ ) 的图象
(3)横坐标不变,纵坐标伸长(A>1) y=ASin(x+ )的图象 或缩短(0<A<1)到原来的A倍
做一做
y=sinx经过怎样的变换可以得到
y 3sin(2x) 图象?
3
注意
我们的每一步变换对于函数上任意 一点(x,y)而言的,它的每一步 变换只能有一个变量。要么横变纵 不变,要么纵变横不变。伸缩变换 是定型的,平移变换是定位的。
函数y=Asin( x+ )的图象
例 用五点法作函数 y 3sin(2x) ,
3
x R 的图象 y
3
y=3sin(2x+ 3 )
o
6 12
3
7
5
x
12
6
-3
如何得到
yAsin(x)
演示启发
的图像呢?
二、
?
⒈ y sin x
y=Asinx
⒉ y sin x ? y sinx
⒊ y sin x
?
ysin(x)
通过变换是否可以得到
yAsinx 的图象呢?
方法1: 先平移后伸缩
y
y=sin(x+ ) 的图象 3
(2)横坐标缩短到原来的
1 2
倍
纵坐标不变
y=sin(2x+ ) 的图象 3
(3)横坐标不变 纵坐标伸长到原来的3倍
y=3sin(2x+ 3 )的图象
方法1:先平移后伸缩一般规律
(1)向左( >0)或向右( <0)
y=Sin( x+ ) 的图象
(3)横坐标不变,纵坐标伸长(A>1) y=ASin(x+ )的图象 或缩短(0<A<1)到原来的A倍
做一做
y=sinx经过怎样的变换可以得到
y 3sin(2x) 图象?
3
注意
我们的每一步变换对于函数上任意 一点(x,y)而言的,它的每一步 变换只能有一个变量。要么横变纵 不变,要么纵变横不变。伸缩变换 是定型的,平移变换是定位的。
函数y=Asin( x+ )的图象
例 用五点法作函数 y 3sin(2x) ,
3
x R 的图象 y
3
y=3sin(2x+ 3 )
o
6 12
3
7
5
x
12
6
-3
如何得到
yAsin(x)
演示启发
的图像呢?
二、
?
⒈ y sin x
y=Asinx
⒉ y sin x ? y sinx
⒊ y sin x
?
ysin(x)
通过变换是否可以得到
yAsinx 的图象呢?
方法1: 先平移后伸缩
y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
y=sin 1 x
2
1
O
2
3
4
x
1
y=sin2x
y=sinx
y=sin
1 2
x的图象可以看作是把
y=sinx的图象上所
有点的横坐标伸长到原来的2倍(纵坐标不变)。
y=sin 2x的图象可以看作是把 y=sinx的图象上所
有点的横坐标缩短到原来的1 2 Nhomakorabea倍(纵坐标不变)。
10
函数y=sinx ( >0且≠1)的图象可以看作是 把 y=sinx 的图象上所有点的横坐标缩短(当>1
4 1
3
8
8
2
1
0
2
y=sin2x
5
7
8
8
3 2
2
-1
0
x
15
四、函数y=sinωx与 y=sin(ωx+φ)图象的关系
y
1
8
2
y sin(2x )
3
x
O
y sin( 2x )
6
4 1
y=sin2x
函数y=sin ( x +)( >0且≠1)的图象可以看
作(当是把﹤y0=时sin)平移x 的图| 象个|向单左位(而当得到>0的时。)或向右
7
例2 1.
作函数 列表:
y
sin
2x
及
y
sin
1 2
x
的图象。
x
0
4
2
3
4
2x
0
2
3
2
2
sin 2x
0
1
0
1
0
x 0
1x 2
0
2
sin 2x 0 1
2 3 4
3 2
2
0
-1 0
8
2. 描点 作图:
y 1
y=sin1 x
2
2
3
4
O
x
1
y=sinx
y=sin2x
9
二、函数y=sinx(>0)的图象
纵坐标不变,横坐标
变为原来的 1 倍
y sin(x )
y sinx
纵坐标不变,横坐标
变为原来的 1 倍
y sin(x )
向左或向右平
移| |个单位
横坐标不变,纵坐标 变为原来的A倍
y Asin(x )
20
课后作业:
课本 P49 练习A,T1(4)
T2(4),T3,T4; P50 练习B.
纵坐标不变
36
(3)纵坐标伸长到原来的2倍 y 2sin(1 x )的图象
横坐标不变
36
18
y
3
2
y=sin(x-
)①
6
1
o
6
-1
2
-2
y=sinx
-3
y 2sin(1 x ) ③
36
y sin(1 x ) ②
36
13
2
2
7
x
2
19
总结:
y sin x
向左或向右平
移 ||个单位
提示:由于我们研究的函数仅限于 >0的情况, 16
所以只需要判断 的正负即可判断平移方向
17
思考 :怎样由y sin x的图象得到y 2sin(1 x )
36
的图象?
(1)向右平移
函数y sin x
6
y sin( x )的图象
6
(2)横坐标伸长到原来的3倍 y sin(1 x )的图象
y
y=2sinx
2
1
2
O
x
1
y=
1 2
sinx
A
周期不变,振幅变化 6
函数y=Asinx (A >0且A≠1)的图象可以看作是把 y=sinx 的图象上所有点的纵坐标伸长 (当A>1时) 或缩短(当0<A<1时) 到原来的A倍(横坐标不变) 而得到的。 y=Asinx ,x∈R的值域为[-A,A],最 大值 为A,最小值为-A.
时)或伸长(当0<<1时) 到原来的 1 倍(纵坐标
不变) 而得到的。
11
例3 作函数y sin(x ) 及y sin(x )的图象。
3
4
5 4 11 7
x
36
3
6
3
x 0
3
2
3 2
2
sin(x ) 0
1
0
3
-1
0
1y
y sin(x )
3
2
4
O
x
1y
3
sin(
x
)
12
4
三、函数y=sin(x+φ)图象
1y
y sin(x )
3
2
4
O
x
1
y
3
sin(
x
)
4
函数y=sin(x+φ) 的图象可以看作是把 y=sinx 的 图象上所有的点向左(当φ>0时)或向右(当φ<0时) 平移|φ|个单位而得到的。
13
例4 作函数y sin(2x ) 及y sin(2x )的图象。
3
4
x
6
2x 0
3
sin(2x ) 0
3
y
1
O
6 1
5 2 11
12 3
12
2
3 2
1
0
-1
2
y sin(2x )
3
y=sin2x
7
6
2
0
x
14
例4 作函数y sin(2x ) 及y sin(2x )的图象。
3
4
x
8
2x
4
0
sin(2x )
4
0
y 1
O
y sin( 2x )
6
21
❖ 世上没有什么天才
❖天才是勤奋的结果
22
2
3
新课讲解:
例1 作函数 y 2sin x 及 y 1 sin x 的图象。
2
解:1.列表
x
0
2
3 2
2
sin x
0
1
0
1
0
2sin x 0
2
0
2
0
1 2
sin
x
0
1 2
0
1 2
0
4
2. 描点、作图:
y
y=2sinx
2
1
y=sinx
2
O
x
1 y= 1sinx
2
2
周期相同 5
一、函数y=Asinx(A>0)的图象
函数
y=Asin(x+)的图象
高一数学组 三部
1
知识y回顾:
1-
y sin x x[0,2]
-
-1
o
6
3
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2
x
-1 -
在函数 y sin x, x [0, 2 ] 的图象上,起关键作用的点有:
最高点: ( ,1)
2
最低点:
(
3 2
,1)
与x轴的交点: (0,0) ( ,0) (2 ,0)
