西北工大版机械原理第4章平面机构的力分析
西工大教材-机械原理各章习题及答案
电动机所需的功率为
p = ρ • v /η = 5500 ×1.2 ×10−3 / 0.822 = 8.029(KW )
5-8 在图示斜面机构中,设已知摩擦面间的摩擦系数 f=0.2。求在 G 力作用下(反行程),此斜面 机构的临界自锁条件和在此条件下正行程(在 F 力作用下)的效率。 解 1)反行程的自锁条件 在外行程(图 a),根据滑块的平衡条件:
解 1 ) 取 比 例 尺 μ 1 = 1mm/mm 绘 制 机 构 运 动 简 图 ( 图 b )
(a)
2 )计算该机构的自由度
n=7
pι=9
ph=2(算齿轮副,因为凸轮与齿轮为一体) p’=
F’= F=3n-2pe-ph
=3x7-2x8-2 =1
G7
D 64 C
EF
3
9
B
2
8
A
ω1
b)
2-6 试计算如图所示各机构的自由度。图 a、d 为齿轮一连杆组合机构;图 b 为凸轮一连杆组合 机构(图中在 D 处为铰连在一起的两个滑块);图 c 为一精压机机构。并问在图 d 所示机构中, 齿轮 3 与 5 和齿条 7 与齿轮 5 的啮合高副所提供的约束数目是否相同?为什么?
C3 重合点继续求解。
解 1)速度分析(图 b)取重合点 B2 与 B3,有
方向 大小 ?
v vv vB3 = vB2 + vB3B2 ⊥ BD ⊥ AB // CD ω1lAB ?
D
C
3 d3
ω3
4
ω3 90°
2
B(B1、B2、B3)
ω1
A1 ϕ = 90°
西北工业大学机械原理课后答案第4章

第四章 平面机构的力分析题4-7机械效益Δ是衡量机构力放大程度的一个重要指标,其定义为在不考虑摩擦的条件下机构的输出力(力矩)与输入力(力矩)之比值,即Δ=d r d r F F M M //=。
试求图示各机构在图示位置时的机械效益。
图a 所示为一铆钉机,图b 为一小型压力机,图c 为一剪刀。
计算所需各尺寸从图中量取。
(a ) (b) (c)解:(a)作铆钉机的机构运动简图及受力 见下图(a )由构件3的力平衡条件有:02343=++R R rF F F由构件1的力平衡条件有:04121=++d R R按上面两式作力的多边形见图(b )得θcot ==∆d r F F(b )作压力机的机构运动简图及受力图见(c )由滑块5的力平衡条件有:04565=++R R F F G由构件2的力平衡条件有:0123242=++R R R 其中 5442R R =按上面两式作力的多边形见图(d ),得tF G =∆(c) 对A 点取矩时有 b F a F d r ⋅=⋅ab =∆其中a 、b 为F r 、F d 两力距离A 点的力臂。
tF G =∆(d)(a)(b)drR41F R43F dG题4-8在图示的曲柄滑块机构中,设已知l AB=0.1m,l BC=0.33m,n1=1500r/min(为常数),活塞及其附件的重量G3=21N,连杆质量G2=25N,J S2=0.0425kg·m2,连杆质心S2至曲柄销B的距离l BS2=l BC/3。
试确定在图示位置时活塞的惯性力以及连杆的总惯性力。
解:1) 选定比例尺, mmml005.0=μ绘制机构运动简图。
(图(a) )2)运动分析:以比例尺vμ作速度多边形,如图(b)以比例尺aμ作加速度多边形如图4-1 (c)244.23smcpaaC=''=μ2222100smspaaS=''=μ22215150sBCcnlalaBCtBC=''==μμα3) 确定惯性力活塞3:)(37673333NagGamFCSI=-=-=方向与cp''相反。
机械原理平面机构的力分析

机械原理平面机构的力分析机械原理平面机构的力分析是对平面机构进行力学分析和力学设计的过程。
平面机构是平面运动副的组合,由多个刚体构成,通过运动副连接起来的,因此需要进行力学分析来了解各个部件之间的力的传递和影响。
平面机构力分析的目的是确定各个部件之间的相对运动和受力情况,从而确定设计参数和优化设计。
首先,进行平面机构的力分析需要了解机构的运动副类型和特点。
平面机构包括直线副、转动副和滑动副等,而不同类型的运动副对应不同的受力情况。
例如,直线副的受力主要是拉力和压力,转动副的受力主要是转轴上的扭矩和轴承力,滑动副的受力主要是摩擦力和压力等。
其次,需要确定机构的约束和自由度,以及受力分析的基准点和坐标系。
约束是机构中连接各部件的运动约束,包括固定约束和运动约束;自由度是机构允许的运动自由度,通过自由度的分析可以了解机构的运动特性。
基准点和坐标系的选择是为了方便受力分析和结果的表示。
接下来,通过自由度分析和约束条件,可以得到机构中各个部件之间的受力关系。
根据受力分析的原理,可以采用静平衡条件、动力学方程或功率分析等方法来计算各个部件的受力情况。
静平衡条件可以用来计算处于平衡状态时的受力情况,动力学方程可以用来计算部件在运动过程中的受力情况,功率分析可以用来计算部件之间的能量传递和能量转换情况。
最后,通过力分析的结果可以进行力学设计和性能评估。
根据受力情况,可以确定各个部件的尺寸、材料和结构形式,以满足所要求的工作条件。
同时,还可以通过分析得到的各个部件的受力情况,来评估机构的运动稳定性和工作性能,从而进行优化设计和改进。
总的来说,机械原理平面机构的力分析是对平面机构进行力学分析和力学设计的过程。
通过力分析可以了解机构中各个部件之间的力的传递和影响,为机构的设计和优化提供基础。
力分析需要了解机构的运动副类型和特点,确定约束和自由度,选择基准点和坐标系,采用适当的方法进行受力分析,最后进行力学设计和性能评估。
机械原理第2、3、4、6章课后答案西北工业大学(第七版)

第二章 机构的结构分析题2-11 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
解:1)取比例尺,绘制机构运动简图。
(图2-11a)2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件,但齿轮1和凸轮2是固装在轴A 上,只能作为一个活动件,故 3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数,此简易冲床不能运动,即不能实现设计意图。
分析:因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案:可以在机构的适当位置增加一个活动构件和一个低副,或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-11b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-11c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-11d)。
11(c)题2-11(d)5364(a)5325215436426(b)321讨论:增加机构自由度的方法一般是在适当位置上添加一个构件(相当于增加3个自由度)和1个低副(相当于引入2个约束),如图2-1(b )(c )所示,这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度,如图2-1(d )所示。
题2-12 图a 所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
机械原理,孙恒,西北工业大学版第4章平面机构的力分析

§4-1 作用在机械上的力和力分析的方法
1、作用在机械上的力: 驱动力----驱动机械运动的力 阻抗力----阻止机械运动的力 有效阻力(工作阻力)----有效功,(输出功) 有害阻力(摩擦力、介质阻力),----损失功 2、分析的目的和方法 目的:①确定运动副中的反力(大小和性质) ②确定机械上的平衡力(或平衡力偶),(即确定驱动力) 步骤:①求出各构件的惯性力和力偶,视为外加的力 ②根据静定条件将机构分解为若干构件组和平衡力系 (从最远的构件组,即外力全部已知的构件组开始) ③逐步推算到平衡力作用的构件
M f = f v ⋅ G ⋅ r = FR21.ρ
其中:
ρ = f v .r
称为摩擦圆半径
摩擦圆的概念: 1)以轴颈中心O 为圆心,以ρ为半径的圆。 2)在转动副中,只要发生相对转动,总反力 就总是切于摩擦圆,即轴承对轴颈的总反力 FR21始终相切于摩擦圆。 3)FR21对铰联中心所形成的摩擦力矩的方向 总是与相对角速度的方向相反。的确切方向 须从该构件的其它力平衡条件中得到。
3、什么是静力分析和动态静力分析: 静力分析----不计惯性力对机械进行力分析 动态静力分析----计入惯性力,利用达朗伯 原理(动静法)作力分析 方法: 图解法 解析法:矢量方程式法 直角坐标法(矩阵法) 复数法
§4-2 构件惯性力的确定
FIi-----i构件质心上的惯心力 FIi’--- i构件偏离质心某一点上的惯心力 mi -----各构件的质量 Jsi-----绕过质心轴的转动惯量 asi-----质心Si的加速度 αi-----角加速度
需水平驱动力F,:F,=G tan (α - φ)
图4-5----矩形螺纹:
等速拧紧螺母所需力矩: M = Fd2 / 2 = Gd2 tan(α + ϕ) / 2 等速放松螺母所需力矩: M ′ = Gd tan(α −ϕ) / 2 2
机械原理ppt西北工业

§4-2 构件惯性力的确定
1、一般力学方法 (续)
B
1 A
2 3
C
(1)作平面运动的构件 (如连杆2)
F —— 水平力 Ff21 —— 摩擦力
§4-3 运动副中摩擦力的确定
(1)摩擦力的确定 (续)
1)平面接触 FN21
2)槽面接触
θ
θ
3)半圆柱面接触
G FN21 = GF来自21 = f FN21 =fG
FN21 2
FN21 G2
FN21= G / sinθ
Ff21 = f FN21 = f G / sinθ
普通高等教育“十五”国家级规划教材
机械原理
Theory of Machines and Mechanisms
第七版 西北工业大学机械原理及
机械零件教研室
编
主编 孙桓 陈作模 葛文杰
第4章 平面机构的力分析
学习要求 §4-1 机构力分析的任务、目的和方法 §4-2 构件惯性力的确定 §4-3 运动副中摩擦力的确定 §4-4 不考虑摩擦时机构的力分析 §4-5 考虑摩擦时机构的力分析
作业解析
学习要求
基本要求
了解机构中作用的各种力及机构力分析的目的和方法。 掌握构件惯性力的确定方法。 能对几种常见运动副中的摩擦力及总反力进行分析和计算。 能用图解法对平面Ⅱ级机构进行动态静力分析。
本章重点
运动副中摩擦力及总反力的确定。 不考虑摩擦时机构的动态静力分析。
§4-1 机构力分析的任务、目的和方法
4 《机械原理》平面机构的力分析

C ε
FI′
FI
ε
可以用总惯性力FI’来代替FI和MI ,FI’ = FI,作用线由质心
S 偏移 lh
MI lh = F I
在确定构件惯性力时,如用一般的力学方法, 在确定构件惯性力时 , 如用一般的力学方法 , 就需先求出 构件质心的加速度和角加速度,如对一系列位置分析非常繁琐, 构件质心的加速度和角加速度,如对一系列位置分析非常繁琐, 为简化,可采用质量代换法。 为简化,可采用质量代换法。
ƒv ------当量擦系数 当量擦系数
5)槽面接触效应 所以在其它条件相同的情况下 槽面、 其它条件相同的情况下,槽面 因为 f v > f ,所以在其它条件相同的情况下 槽面、圆柱 面的摩擦力大于平面摩擦力。 面的摩擦力大于平面摩擦力
2. 移动副中总反力方向的确定
1)总反力和摩擦角 总反力FR21 :法向反力 N21和摩擦力 f21的合力。 法向反力F 和摩擦力F 的合力。 总反力 总反力和法向反力之间的夹角。 摩擦角ϕ :总反力和法向反力之间的夹角。
绕质心的转动惯量 用一个力简化之
v FI
v FIlhS源自εv MIv aS v v FI = − ma S v J Sε MI v lh = F = ma I S
2. 作平面移动的构件
v v 等速运动: 等速运动: FI = 0; M I = 0 v v v 变速运动: 变速运动: FI = − m a S ; M I = 0
mB + mK = m mBb = mkk mBb2 + mKk2 = Js
优点:代换精确。 优点:代换精确。
S B
b c
C
S B
m
B
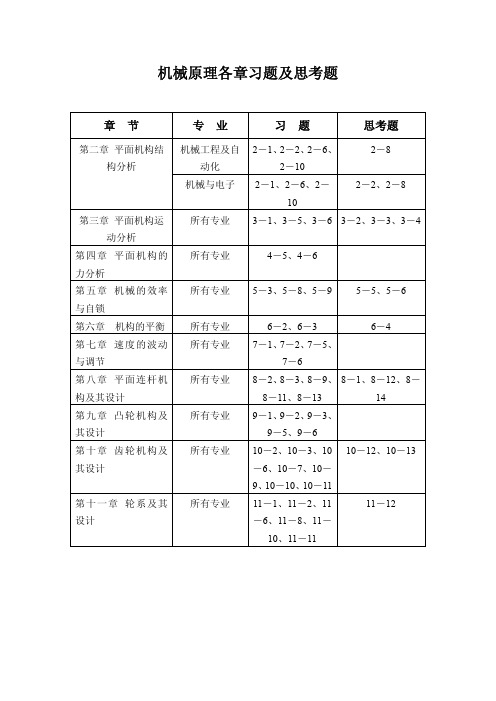
☆西北工业大学国家精品课程]-机械原理PPT课件完整版
![☆西北工业大学国家精品课程]-机械原理PPT课件完整版](https://img.taocdn.com/s3/m/acb827fe960590c69ec376dc.png)
西北工业大学【国家精品教程】机械原理(课件完整版)目录• 第一章 绪论 • 第二章 机构的结构分析 • 第三章 平面机构的运动分析 • 第四章 平面机构的力分析 • 第五章 机械的效率及自锁 • 第六章 机械的平衡目录• 第七章 机械的运转及其速度 波动的调节• 第八章 平面连杆机构及其设计 • 第九章 凸轮机构及其设计 • 第十章 齿轮机构及其设计目录• 第十一章 齿轮系及其设计 • 第十二章 其他常用机构 • 第十三章 工业机器人机构及其设计第一章 绪 论§1-1 本课程研究的对象及内容 §1-2 学习本课程的目的 §1-3 如何进行本课程的学习返回§1-1 本课程研究的对象及内容1.研究对象机械 是机构和机器的总称。
机构是指一种用来传递与变换运动和力的可动装置。
机器是指一种执行机械运动装置,操 作 机可用来变换和传递能量、物料和信息。
实例:示 教内燃机板工件自动装卸装置六自由度工业机器人2.研究内容 有关机械的基本理论控制系统§1-2 学习本课程的目的课程性质、任务及作用 机械未来发展§1-3 如何进行本课程的学习掌握本课程的特点 注重理论联系实际 逐步建立工程观点 认真对待每个教学环节机器和机构的概念(1)机构机构 是指一种用来传递与变换运动和力的可动装置。
如常 见的机构有带传动机构、链传动机构、齿轮机构、凸轮机构、螺 旋机构等等。
这些机构一般被认为是由刚性件组成的。
而现代机构中除了 刚性件以外,还可能有弹性件和电、磁、液、气、声、光…等元 件。
故这类机构称为广义机构;而由刚性件组成的机构就称为狭 义机构。
(2)机器机器 是指一种执行机械运动装置,可用来变换和传递能量、 物料和信息。
例如: 电动机、内燃机用来变换能量;机器和机构的概念(2/3)机床用来变换物料的状态; 汽车、起重机用来传递物料; 计算机用来变换信息。
由于各种机器的主要组成部分都是各种机构。
第4章 平面机构的力分析

第四章 平面机构的力分析
二、质量代换法(课程设计中讲)
3. 质量代换时必须满足的三个条件: 1)代换前后构件的质量不变; 2)代换前后构件的质心位置不变; 以原构件的质心为坐标原点时,应满足:
m i x i 0 i 1 n m i y i 0 i 1
当机构中各个构件的惯性力确定后,即可根据机构所受的 外力(包括惯性力)来确定各个运动副中的反力和需要加在该 机构上的平衡力。因为运动副中的反力对整个机构是内力,因 此必须把机构拆成若干杆组进行逐个分析,最终获得机构力分 析的结果。但为了使得所有的未知因素都可以求出,必须使得 所拆得的杆组必须是静定的。
5.运动副反力(约束反力):当机构受到外力作用时,在运 动副中产生的反作用力。
其特征是对于整个机构表现为内力,而对于单个构ห้องสมุดไป่ตู้则表现为 它起着阻止运动副两元素作 外力。 相对运动作用。 Northwest A&F University 整个运动副反力可分解为沿着运动副两元素接触处的法向反力 第四章 平面机构的力分析 (正压力)和切向反力(摩擦力)。
第4章
平面机构的力分析
第一节 机构力分析的任务、目的和方法
第二节 构件惯性力的确定 第三节 运动副中摩擦力的确定
第四节 不考虑摩擦时机构的力分析
第五节 考虑摩擦力时机构的力分析
Northwest A&F University
《机械原理》
第一节 机构力分析的任务、目的和方法
一、作用在机构上的力: 1. 驱动力:驱使机械运动的力。
第四章 平面机构的力分析
二、机构的动态静力分析:
例题1:在如图所示的曲柄滑块机构中,设已知各构件的尺寸,曲 柄1绕其转动中心A的转动惯量为JA(质心S1与A点重合), 连杆2的重量G2,转动惯量JS2(质心S2在杆BC的1/2处), 滑块3的重量G3(质心S3在C处)。原动件1以角速度ω1和 角加速度α1顺时针方向回转,作用于滑块3上C点的生产阻 力为F,各运动副的摩擦忽略不计。求机构在图示位置时各 运动副中的反力以及需要加在构件1上的平衡力矩Mb。
机械原理第4章 平面机构的力分析

Fig.4-7 Friction in a journal bearing(径向轴承中的摩擦)
2) 推力轴承的摩擦。 图4-8a为推力轴承示意图,G为轴向载荷。未经跑合时,接 触面压强p为常数,p=c。经过跑合时,压强与半径的乘积为 常数,pρ=c。
Fig.4-8 Friction in a thrust bearing(推力轴承的摩擦)
例4-4 图4-12a所示的摆动从动件盘形凸轮机构中,已知凸轮机构的尺 寸、轴径尺寸、运动副处的摩擦因数f以及作用在从动件F点的阻力Fr, 在不计构件质量和惯性力时,求各运动副处的反作用力及作用在凸轮上 的平衡力矩Mb。
2.计入摩擦力的力分析
例4-3 图4-11所示的曲柄滑块机构中,已知各构件尺寸和曲柄的位置和 作用在滑块4上的阻力Fr以及各运动副中的摩擦因数f,忽略各构件质量和 惯性力。在图4-11上标注出各运动副的反力以及加在曲柄上的平衡力矩Mb。
Fig.4-11 Force analysis considering the friction in a slider-crank linkage (考虑摩擦的曲柄滑块机构力分析)
Байду номын сангаас
(3)螺旋副中的摩擦 根据螺纹牙型可将螺纹分为矩形螺纹 和三角形螺纹。 图4-9a所示为一矩形螺纹,将螺母2简化为图4-9b所示的滑 块,承受轴向载荷[WTBX]G,由于螺纹可以看成是斜面缠 绕在圆柱体上形成的,故将矩形螺纹沿螺纹中径[WTBX]d展 开,该螺纹成为图4-9b所示的斜面,斜面底长为螺纹中径 处圆周长,高度为螺纹的导程l。驱动力F等于拧紧力矩M除 以螺纹半径d/2,方向一般垂直于螺纹轴线。
3) 槽面摩擦。如果将图4-6a所示滑块作成图4-6b所示夹角为 2θ的楔形滑块,并置于相应的槽面中,楔形滑块1在外力F 的作用下沿槽面等速运动。设两侧法向反力分别为N21 , 铅直载荷为G,总摩擦力为Ff。
机械原理04机构的力分析

三、螺旋副中的摩擦
1. 矩形螺纹螺旋副中的摩擦 1)矩形螺纹螺旋副的简化
将螺纹沿中径d2 圆柱面展开,其螺纹将展成为一个斜 面,该斜面的升角a等于螺旋在其中径d2上的螺纹升角。 tg l zp
d2 d2 l--导程, z--螺纹头数, p--螺距
螺旋副可以化为斜面机构进行力分析。
由 Fx 0
2
由 MC 0
2
得:R12 (F2x F23x ) / sin1
得:T12 ( yC ys2 )F2x ( xS 2 xC )F2 y T2
就可以将所有解求出。
关于可变杆长二杆组的副反力的求解
由 MA 0 和 M3 0 得:
1、2
3
yC yA
yB
yC
2
进行整理得到
yC yB
yD
yC
xB xC
xC xD
R23x
R23
y
( (
yB yD
yS 2 )F2 x yS 3 )F3 x
( xS 2 ( xS 3
xB )F2 y xD )F3 y
T2 T3
求出内副C的反力后,可分别取BC、CD杆作力平衡方程 式,求得B、D两点的反力。
力开始,逐副进行,最后对含平衡力得杆件进行力分析。
一般是力矩平衡方程和导路方向的力平衡方程两种交替使用。
4.2 机构的传动角
衡量一个机构传力效果的指标: (1)输出功相同时,输入功最少。 (摩擦损失最小) (2)构件受力最小。(构件截面积小,重量轻) (3)运动副摩擦少。(运动精度高,动载荷和噪声小)
0
1、2
3
移动副的反力R12D可以由构件2对E取矩和构件1 对E 取矩求得。
第四章平面机构的力分析

图4-2 a)
平台2对滑块1产生的反力有:法向反力N21、摩擦力F21。 它们的合力称为总反力,以R21表示。 即: R21= N21+F21 其中: 大小 :F21=f N21 f——摩擦系数;(N21=G) F21 方向:与1相对于2的相对速度V12的方向相反。
两接触面间摩擦系数f 相同时,摩擦力F21的大小取决 于接触面的几何形状: 1)两构件沿单一平面接触(图a)
所需的水平力F′。
图4-3
图4-4
解: 1)滑块等速上升:如图4-3a) 斜面2对滑块1的总反力为R21。 根据力的平衡条件:
G + F + R21=0 方向:√ √ √v12 大小: √ ? ?
作力多边形,如图4-3 b)。 ∴ F = G· tan(α+ψ)
图4-3 a)
图4-3 b)
2)滑块等速下滑:如图4-4a) 斜面2对滑块1的总反力为R21′。 根据力的平衡条件: G + F′ + R21′=0 方向:√ √ √v12 大小:√ ? ? 作力多边形,如图4-4 b)。 ∴ F′= G·tan(α-ψ)
图4-4 a)
由以上分析可知,当已经列出 了正行程的力关系式后,反行程的 力关系式可以直接用 -ψ 代替ψ即 可,而不必再作力多边形来求解。
图4-4 b)
F′= G·tan(α-ψ) 注意: 在反行程中G为驱动力,当α>ψ时, F′为正值,是阻 止滑块沿斜面加速下滑的阻抗力;当α<ψ时, F′为负值, 其方向与图示方向相反, F′为驱动力,其作用是促使滑块 沿斜面等速下滑。
F + R23 + R43= 0 √ √R32 √v34 方向: √ 大小: ? ?
机械原理(平面机构的力分析新).

质量来代替。 B
FI ε
1
2
MI
A aS
S2 m2
C3
质量代换法的方法
把构件的质量用集中作用在构件的几个选定点的假想集中 质量来代替,这些假想的集中质量被称作代换质量。 B、K为所选定的代换点 mB 、 mk为代换质量
mB B
1
2
A
mk
S2
k
C3
应用质量代换法应满足的条件
1) 代换前后构件的质量不变; 2) 代换前后构件的质心位置不变;
aS
FI ,M 合成I 为距质心S为距离h的总
h MI
FI
FI
ε
MI S
aS
, FI ε S
例 1 在图示的凸轮机构中,已知凸轮的半径R=200mm,LOA=100mm
从动件的质量为m2=20kg,凸轮的角速度ω1=20rad/s。当OA线 在水平的位置时,求从动件2的惯性力。
解:1. 高副低代
2.运动分析(过程略)
aB2
o (b )
C
3
b
C
3
2
B R
FI2 2
aB2
B
p
p
o
o
A
1
1
O
A
aB2 pba
1
3.受力分析 F I 2 m2aB2 m2pba2023.4468N
例2 在图示的摆动导杆机构中,已知LAC=200mm, LAB=100mm,
φ=90°,导杆的重心在C点,导杆对重心C的转动惯量J3=0.2kg·m2 曲柄的等角速度ω1=20rad/s。求导杆3的惯性力矩。
件的外形、位置或状态时所受到的阻力,克服这些阻力 就完成了工作。如机床中作用在刀具上的切削阻力,起 重机提升重物的重力等都是有效阻力。
机械原理(平面机构的力分析新)

§4—1机构力分析的任务、目的和方法 §4—2 构件惯性力的确定 § 4 —3 机构力分析的任务、目的和方法
§4—4 不考虑摩擦时机构的力分析
§4—1机构力分析的任务、目的和方法
机构力分析的任务 1)确定运动副中的反力 运动副反力指运动副处作用的正压力和摩擦力的合力 2)确定机械中的平衡力 平衡力是指机械在已知外力的作用下,为了使该机械能按 给定运动规律运动,还须加于机械上的未知外力
例3 在图示发动机曲柄滑块机构中,已知曲柄长度 l AB 0.35m ,
连杆长度 l BC 2.35m , 连杆重心 S 2 至曲柄销轴B的距离 l BS 2 0.83m , 连杆的质量 m2 19kg , 活塞及其附件的质量 2 连杆对其重心的转动惯量 ,曲柄转 J 16 . 9 kgm m3 6kg , S2 速 n1 300r / min , 45 , 求图示位置时活塞3的的惯性力和 连杆2的总惯性力。 B 1 φ S2
上式中有四个未知量:
m B b mk k 2 2 mB b mK k J S 2
B
mB mk m2
、 b 、k 选定b后求出其余的三个量:
mB 、 mK
1
mB
2
m2 S2
k J S 2 /( m2 b ) mB m2 k /( b k ) mK m2 b /( b k )
mB m2 c /(b c) mC m2 b /(b c)
小结:1 动质量代换须同时满足三个条件。
1) 代换前后构件的质量不变; 2) 代换前后构件的质心位置不变;
3) 代换前后构件对质心轴的转动惯量不变;
即
mBb mk k mBb 2 mK k 2 J S 2
西北工大版机械原理课件第4章平面机构的力分析

G ωM12d
1 2
FR21 Mf
N21 F21
ρ
ω1M2 d
r G
FR21 Mf
2 1N21
F21
ρ
当G的方向改变时,FR21的方向也跟着改变,但ρ不变。 以ρ作圆称为摩擦圆,ρ-摩擦圆半径。且FR21恒切
于摩擦圆。
分析:由ρ= fv r 知,r↑→ρ↑→Mf↑ 对减小摩擦不利。
运动副总反力判定准则
∑△N=G 三角形螺纹 ――∑△Ncosβ=G, β-牙形半角
可得: ∑△N=G /cosβ
摩擦力: Ff = ∑△N . f = f . G /cosβ
引入当量摩擦系数: fv = f / cosβ
当量摩擦角: φv= arctan fv
可直接引用矩形螺纹的结论:
拧紧:Md22Gtan(v)
轴
拧松:M'd22Gtan(v)
= fv G
fv-称为当量摩擦系数
柱面接触:
矢量和:N21=Σ△N21 =-G 代数和:N’21= Σ|△N21|
=kG >|N21|
1
2
N21
△N21 G
理论分析和实验结果有: k =1~π/2
F21 = f N’21 = f k G = fv G
同理,称 fv为当量摩擦系数。 结论:不论何种运动副元素,有计算通式:
1. 由力平衡条件,初步确定总反力方向(不考虑摩擦时)
2. 对于转动副有: FR21恒切于摩擦圆。 于移动副有: FR21恒切于摩擦锥
3. 对于转动副有:Mf 的方向与ω12相反
对于移动副有:∠FR21 V12=(90°+φ)
例1 :图示机构中,已知驱动力F和阻力Mr和摩擦圆
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
决于运动副元素的几何形状。
N”21
θ
平面接触: N21=-G
G N’21
F21=f N21= f G
槽面接触: N’21 +N”21= -G N’21 = N”21 = G / (2sinθ)
N21
F21
F1 v21
G2
θ
θ
N’21 1
N”21
2 G
F21 = f N’21 + f N”21 = ( f / sinθ)• G
G d1
d2 d3
v Fv
αG
l
πd2
FGtan ()
从端面看
F-螺纹拧紧时必须施加在中径处的圆周力,所产生的
拧紧所需力矩M为:
MFd2d2Gtan()
22
拧松时直接引用斜面摩擦的结论有:
d2 Mf
F'Gtan ()
F
F’-螺纹拧松时必须施加在中径处的圆周力,所产生 的拧松所需力矩M’为:
M 'F'd2d2Gtan()
= fv G
fv-称为当量摩擦系数
柱面接触:
矢量和:N21=Σ△N21 =-G 代数和:N’21= Σ|△N21|
=kG >|N21|
1
2
N21
△N21 G
理论分析和实验结果有: k =1~π/2
F21 = f N’21 = f k G = fv G
同理,称 fv为当量摩擦系数。 结论:不论何种运动副元素,有计算通式:
F21= f N21 = fv G 非平面接触时 ,摩擦力增大了,为什么? 是 f 增大了? 原因:是由于N21 分布不同而导致的。
应用:当需要增大滑动摩擦力时,可将接触面设计
成槽面或柱面。如圆形皮带(缝纫机)、三角形皮
带、螺栓联接中采用的三角形螺纹。
θ 对于三角带:
=18° fv=3.24 f
不论P的方向如何改变,P与R两 者始终在同一平面内
F21 = f N21 = f kG = fv G
根据平衡条件有: FR21=-G,
产生的摩擦力矩为:
ω1M2 d
r G
FR21 Mf
2 1 N21
F21
Md =-Mf
Mf= F21 r =f N21 r = fv r G= Gρ 方向:与ω12相反。
G ωM12d
1 2
FR21 Mf
N21 F21
有害(工作)阻力----机械运转过程受到的非生产阻 力,克服了这类阻力所作的功纯粹是浪费能量。如 摩擦力、介质阻力等。
2.机构力分析的任务和目的
▲确定运动副中的反力----为进一步研究构件强度、 运动副中的摩擦、磨损、机械效率、机械动力性能 等作准备。
反力----运动副元素接触处的正压力与摩擦力的合力
力分析实例:
a)求使滑块沿斜面等速上行所需水平力F
根据平衡条件:F + FR21+G = 大小:? ? √
0n
FR21
φNα1
v
方向:√ √ √ 作图 得: F=Gtan(α+φ)
Fα21 G
F 2
n
b)求使滑块沿斜面等速下滑所需水平力F’
F
FαR2+1φ
G
根据平衡条件: F’ + F’R21+G = 0
22
若α>φ,则M’为正值,其方向与螺母运动方向相反, 是阻力;
若α<φ,则M’为负值,方向相反,其方向与预先假 定
的方向相反,而与螺母运动方向相同,成为
2.三角形螺纹螺旋中的摩擦
β
作者:潘存云教授
β
G △N
△N β
β △N G
△N
矩形螺纹――忽略升角影响时,△N近似垂直向上,
∑△N=G 三角形螺纹 ――∑△Ncosβ=G, β-牙形半角
制动器(刹车)。
研究目的: 减少不利影响,发挥其优点。
运 动 副 中 摩 低副-产生滑动摩擦力 擦的类型: 高副-滑动兼滚动摩擦力。
一、移动副的摩擦
1. 移动副中摩擦力的确定 G-铅垂载荷; N21-法向反力; F-水平力, F21-摩擦力。
得: F21=f N21
N21 1 v21
F21 F 2
若质心位于回转中心: MI1 =- Js1α1
2.质量代换法
一般力学方法的缺陷:
▲质心位置难以精确测定;
▲求解各构件质心加速度较繁琐。 B mB
质量代换法的思路:
S2 B
将各构件的质量,按一定
条件用集中于某些特定点 1 的假想质量来替代, A
S1
2
S2
只需求集中质量的惯性力,
as1 as2
而无需求惯性力偶矩。从
ρ
ω1M2 d
r G
FR21 Mf
2 1N21
F21
ρ
当G的方向改变时,FR21的方向也跟着改变,但ρ不变。 以ρ作圆称为摩擦圆,ρ-摩擦圆半径。且FR21恒切
于摩擦圆。
分析:由ρ= fv r 知,r↑→ρ↑→Mf↑ 对减小摩擦不利。
运动副总反力判定准则
1. 由力平衡条件,初步确定总反力方向(不考虑摩擦时)
可得: ∑△N=G /cosβ
摩擦力: Ff = ∑△N . f = f . G /cosβ
引入当量摩擦系数: fv = f / cosβ
当量摩擦角: φv= arctan fv
可直接引用矩形螺纹的结论:
拧紧:Md22Gtan(v)
轴
拧松:M'd22Gtan(v)
轴径
轴承
三、转动副中的摩擦 1.轴径摩擦 直接引用前面的结论有:
力的类型
原动力 生产阻力 重力 摩擦力 介质阻力 惯性力
运动副反力
按作用分为
驱动力 阻抗力 有效阻力
有害阻力
驱动力----驱使机械运动,其方向与力的作用点速 度之间的夹角为锐角,所作功为正功。
阻抗力----阻碍机械运动,其方向与力的作用点速 度之间的夹角为钝角,所作功为负功。
有效(工作)阻力----机械在生产过程中为了改变工 作物的外形、位置或状态所受到的阻力,克服了阻 力就完成了有效的工作。如车削阻力、起重力等。
而将问题简化。
质量代换的条件:
1)代换前后各构件质量不变; 2)质心位置不变; 3)对质心轴的转动惯量不变。
C 3 mC
C as3
S3
代换质量的计算:
mB B
若替换质量集中在B、K两点, 则 由三个条件分别得:
b
mB + mk =m2 mB b = mk k
mB b2+ mk k2 =JS2
1
四个未知量,只有三个方程,A
mB + mk =m2 mB b = mk k
mB b2+ mk k2 =JS2
为了计算方便,工程上常采用 静代换,只满足前两个条件。
此时可同时选定B、C
1
两点作为质量代换点。 A
则有:
mB B B
2 S1
B
k
b
S2 mk K
C
S2
c
C
S2
3
m2
C
S3
mB = m2 c /(b+c) mC = m2 b /(b+c)
第四章 平面机构的力分析
§4-1机构力分析的任务、目的与方法 §4-2构件惯性力的确定 §4-3运动副中摩擦力的确定 §4-4机构力分析实例
§4-1机构力分析的任务、目的与方法
力分析的必要性:
▲作用在机械上的力是影响机械运动和动力性能 的主要因素;
▲是决定构件尺寸和结构形状的重要依据。
1.作用在机械上的力
螺纹的旋向: 右旋
左旋
螺纹的用途:传递动力或联接 从摩擦的性质可分为:矩形螺纹和三角形螺纹
1.矩形螺纹螺旋中的摩擦
假定载荷集中在中径d2 圆柱面内,展开
作者:潘存云教授
斜面其升角为:α
tanα=l /πd2 =zp /πd2
式中l-导程,z-螺纹头数,p-螺距
螺旋副的摩擦转化为=>斜面摩擦。
螺纹的拧紧-螺母在F和G的联合作 用下,逆着G等速向上运动。 螺纹的拧松-螺母在F和G的联合作 用下,顺着G等速向下运动。 拧紧时直接引用斜面摩擦的结论有:
ω221 ω23 R12
v34
C3 F 4
R32 90°+φ
FRF4R323 F
2. 轴端摩擦 在G的作用下产生摩擦力矩Mf
取环形面积: ds=2πρdρ
设ds上的压强为p,正压力为:
dN=p ds
摩擦力为:dF= f dN = f p ds
摩擦力矩:dMf =ρdF =ρf dN =ρf p ds
0.05 ~ 0.1 0.05 ~ 0.15
0.07
0.15 0.15 ~ 0.21 0.15 ~ 0.20 0.3 ~ 0.5
0.8
0.07 ~ 0.12 0.07 ~ 0.15 0.04 ~ 0.1 0.12 ~ 0.15
0.5
F21=f N21
当材料确定之后,F21大小取决于
法向反力N21
而G一定时,N21 的大小又取
▲确定机械平衡力(或力偶)---目的是已知生产负 荷确定原动机的最小功率;或由原动机的功率来确 定所能克服的最大生产阻力。
平衡力----机械在已知外力作用下,为了使机械按 给定的运动规律运动所必需添加的未知外力。
3.机械力分析的方法
图解法 解析法
机械力分析的理论依据 : 静力分析----适用于低速机械,惯性力可忽略不计; 动态静力分析----适用于高速重型机械,惯性力往往比 外力要大,不能忽略。
因为不满足第三个条件,故构件的惯性力偶会
