凸轮机构图解法
第6章 凸轮机构

(3)该机构的最大压力角αmax与最小压力角 αmin;
(4)从动件的推程运动角和回程运动 角;
(5)从动件的最大速度vmax。
解
第二十八页,共36页。
解 (1) rbRO A8 03 050mm
(2) A 1 B 1 (1 1 10 2 5 )2 1 5 1.5 46 0 A 0B 0 (5 0 15 2 )2 1 5 5.7 51
例1 图示偏置直动滚子从动件盘形 凸轮机构中,凸轮以角速度ω 逆时 针方向转动。
试在图上画出: (1)画出理论轮廓曲线、基圆与偏距圆;
(2)标出凸轮图示位置压力角α1和位 移s1以及转过150°时的压力角α2 和位 移 s2 。
解
第十九页,共36页。
思路与技
本题目主要考察对凸轮廓线、基圆、偏距 圆、压力角及位移等基本概念的理解和对反转
0
ω
n
第八页,共36页。
从动件运动规律的选择与设计原则
从动件的最大速度vmax应尽量小
从动件的最大加速度amin应尽量小,且无突变 从动件的最大跃度jmax应尽量小
第九页,共36页。
凸轮机构的反转法原理
-ω
1
B0
ωO
B1 B 1
2
3
()s()
结论
B 3 B 2 B 2 B3
从动件尖顶相对凸轮的运 动轨迹形成了凸轮的轮廓曲 线。
hA 1B 1A 0B 08.8 4m 5 m
(3) max mi n 45
(4) ==180°
(5)当凸轮从从动件最低位置转过90°时, 从动件与凸轮的相对瞬心P至A点的距 离达到最大
A P O2 A3 02
vma x A P 13 024.4 22 m6m
第四章 凸轮机构

直动从动件凸轮机构
摆动从动件凸轮机构
7
4.1 凸轮机构的应用和类型
凸轮机构分类 按从动件的形式分:
尖顶从动件凸轮机构
平底从动件凸轮机构
滚子从动件凸轮机构
8
4.1 凸轮机构的应用和类型
凸轮机构分类
按凸轮与从动件保持接触的方式分类(锁合方式):
重力锁合
,t
h cos 2 2
2 2
,t
加速度曲线不连续,存在 柔性冲击。余弦加速度运动 规律适用于中低速中载场 合。
a
amax4.93h2Φ 2
,t
4.2 从动件的运动规律
3. 余弦加速度运动规律
v 5 h /20 4 3 6 2
速度线图
7 1
8 0
第四章 凸轮机构
4.1 凸轮机构的应用和类型
4.2 从动件的常用运动规律 4.3 凸轮机构的压力角
4.4 图解法设计凸轮轮廓
1
4.1 凸轮机构的应用和类型
凸轮机构实例
内燃机配气机构
2
4.1 凸轮机构的应用和类型
凸轮机构实例
自动机床进刀机构
3
4.1 凸轮机构的应用和类型
凸轮机构实例
绕线机构
4
4.1 凸轮机构的应用和类型
弹簧力锁合
槽道凸轮机构
等宽凸轮机构
力封闭凸轮机构
等径凸轮机构
共轭凸轮机构
几何结构封闭凸轮机构
4.1 凸轮机构的应用和类型 凸轮机构的特点:
优点:只需设计适当的凸轮轮廓,便可使从动件得到 所需的运动规律,并且结构简单、紧凑,设计方便。
缺点:凸轮廓线与推杆之间为点接触或线接触,易 磨损,所以凸轮机构多用在传力不大的场合。
凸轮机构

一、滚子半径的选择
滚子半径 rT 过大,导致实际轮 廓线变尖或交叉,如b、c所示。 ' rT , '实际轮廓曲率半径;
理论轮廓曲率半径; rT 滚子半径;
当 rT, ' 0,实际轮廓线为 光滑连续的曲线,没问 题; 当 rT, ' 0,实际轮廓线交叉, ,加工时被切除,导致 从动件运动
§第一节 凸轮机构的基本类型
二、凸轮机构的分类
移动凸轮
1.按凸轮的形状
当盘形构件的回 转中心趋于无穷 大时,绕轴转动 的盘形凸轮就变 成相对于机架作 往复直线移动的 凸轮。
§第一节 凸轮机构的基本类型
二、凸轮机构的分类
圆柱凸轮
1.按凸轮的形状
凸轮的轮廓曲线位于圆柱面上,它可以看作是把移动凸轮 卷成圆柱体而得。
(1)力封闭:利用从动件的重力、弹簧力或其他外力使从动件与 凸轮保持接触,如图6-1所示。 (2)形封闭:依靠凸轮与从动件的特殊结构来保持从动件与凸轮 接触,如图6-2所示。
§第一节 凸轮机构的基本类型
二、凸轮机构的分类 3.按凸轮与从动件保持接触的方式分
(2)形封闭:依靠凸轮与从动件的特殊结构来保持从 动件与凸轮接触,下图是常用的形封闭凸轮机构。
2.对心滚子直动从动件盘形凸轮
已知凸轮的基圆半径rb 、滚子半径rT 、角速度 ω和从动件的运动规律,设计该凸轮轮廓曲线。
8’
-ω
ω
7’ 5’ 3’ 1’
9’ 11’ 12’
13’ 14’ 9 11 13 15
理论轮廓η
1 3 5 78
设计步骤小结: 实际轮廓η’ ①选比例尺μ l作基圆rb。 ②反向等分各运动角。原则是:陡密缓疏。 ③确定反转后,从动件尖顶在各等份点的位置。 ④将各尖顶点连接成一条光滑曲线。 ⑤作各位置滚子圆的内(外)包络线。
机械原理凸轮机构-201810

2. 对心滚子移动从动件盘形凸轮廓线的设计
已知凸轮的基圆半径rb,滚子
半径rr、凸轮角速度和从动件的运
动规律,设计该凸轮轮廓曲线。
s
8
7
5
3
1
9 10 11 12
13 14
实际轮廓曲线 A
O
1 3 5 7 8 9 11 13 15
120º 60º 90º 90º
设计步骤 ①③按作尖各顶滚直子动圆从的动内件(外盘)形包凸络轮 11 作线出—廓实线际—廓理线论。廓线。 ②以理论廓线上的各点为圆心
ρa=ρ-rr
轮廓失真
ρa=ρ-rr<0
ρ
ρ
rr
ρ =rr
rr
ρa=ρρ<-rr rr<0
外凸凸轮中:ρ实=ρ理-rr
1)若ρ实=0则出现尖点,磨损严重; 2)若ρ实<0则运动失真;
经验公式: rr=(0.1-0.5)r0 ;
rr≤0.8ρ理min ;
出现尖点,运动失真时所采取的办法:
1)r0↑→ρa↑; 2)rr ↓ ;
二、基圆半径r0:
rb
d
s d tan[ ]
e
s
2
e2
α、r0成反比关系: α↑→r0↓; α↓→r0↑;
三、滚子半径rr:
外凸凸轮:
内凹凸轮:
rr ρ
rr
ρa
ρ
ρ > rr
ρa=ρ-rr
ρa
ρa=ρ+rr
外凸凸轮中:
轮廓正常
rr
轮廓变尖:
ρ
ρa
ρ > rr
ρa=ρ-rr=0
机械原理-凸轮轮廓曲线设计图解法

-ω
3’ 2’ 1’ ω O 1 2
1
2
3
3
直动从动件盘形凸轮轮廓的绘制
1.对心直动尖顶从动件盘形凸轮 已知凸轮的基圆半径r0,角速度ω 和从 动件的运动规律,设计该凸轮轮廓曲线。
4’ 5’ 6’
-ω ω
3’ 2’ 1’
7’
8’ 5 6 7 8
1 2 3 4
设计步骤: ①作基圆r0。
②反向等分各运动角,得到一系列与基圆的交点。
7’ 5’ 3’ 1’ 1 3 5 78 8’ 9’ 11’ 12’ 13’ 14’ 9 11 13 15
e
-ω
ω 15’ 15 14’14
k12 k11 k10 k9 k15 k14 k13
A
13’
12’
k1 13 k 12 k32 k8 k7k6 k5k4 11 10 9
O
注意:与前不同的是——过 各等分点作偏距圆的一系列 切线,即是从动件导路在反 转过程中的一系列位置线。
11’
10’ 9’
直动平底从动件盘形凸轮轮廓的绘制
直动平底从动件盘形凸轮轮廓的绘制
-
实际廓线
直动平底从动件盘形凸轮轮廓的绘制
-
实际廓线
③过各交点作从动件导路线,确定反转后从动件尖顶在各等分点的位置。 ④将各尖顶点连接成一条光滑曲线。
直动从动件盘形凸轮轮廓的绘制
2.对心直动滚子从动件盘形凸轮 已知凸轮的基圆半径r0,滚子半径 rT ,角速度ω 和从动件的运动规 律,设计该凸轮轮廓曲线。
3’ 2’ 1’ 7’ 8’ 1 2 3 4 5 6 7 8 4’
-ω
理论轮廓
ω
5’ 6’
机械原理第10章 凸轮设计

①等分位移曲线;
②选定r0,画基圆;
③应用反转法逐点作图确 定 各 接 触 点 位 置 B0 , B1 , B2,……;
④光滑连接B0,B1,B2 , …… 点 , 就 得 所 要 设 计 的 凸轮廓线。
10.2 凸轮机构的廓线设计
2)滚子从动件
第10章 凸轮机构设计
Design of Cam Mechanisms
第10章 凸轮机构及其设计
1
凸轮机构的运动与传力特性
2
凸轮机构的廓线设计
10.1 凸轮机构的运动与传力特性
10.1.1 凸轮机构的工作循环
基圆——以凸轮轮廓的最小向径rb (或r0)为半径的圆。
图10-1 尖端移动从动件盘形凸轮机构的工作循环
从动件一方面随机架和导路以角速度-ω 绕O点转动,另一方面又在导 路中往复移动。由于尖端始终与凸轮轮廓相接触,所以反转后尖端的运动 轨迹就是凸轮轮廓。
10.2 凸轮机构的廓线设计
10.2.2 图解法设计过程
添加!
凸轮轮廓曲线的绘制 (图解法凸轮廓线的设计)
(26分钟)
10.2 凸轮机构的廓线设计
10.2 凸轮机构的廓线设计
10.2.3 凸轮廓线设计的解析方法
移动滚子从动件盘形凸轮机构
如图所示为一偏置移动滚子从动件盘形凸轮机构。建立直角坐标系oxy。若已
知凸轮以等角速度逆时针方向转动,凸轮基圆半径rb、滚子半径rr,偏距e,从动 件的运动规律s=s()。
1、理论廓线方程 B点坐标(凸轮的理论廓线方程)
s
v
a
j
h (1 cos)
机械原理第9章凸轮机构及其设计

第二十一页,编辑于星期日:十四点 分。
②等减速推程段:
当δ =δ0/2 时,s = h /2,h/2 = C0+C1δ0/2+C2δ02/4 当δ = δ0 时,s = h ,v = 0,h = C0+C1δ0+C2δ02
0 = ωC1+2ωC2δ ,C1=-2 C2δ0 C0=-h,C1= 4h/δ0, C2=-2h/δ02
如图所示,选取Oxy坐标系,B0 点为凸轮廓线起始点。当凸轮转过δ 角度时,推杆位移为s。此时滚子中 心B点的坐标为
x (s0 s) sin e cos
y
(s0
s) cos
A7
C8 A6 C7
w
A8
-w
A9
C9 B8 B9 B7 r0
C10
B12100 ° B0
O
B1 a B2
C1 L C2φ1φ0
A10 A0
φ
Φ
o
2
1
2 3 456
180º
7 8 9 10
60º 120º
δ
(1)作出角位移线图;
(2)作初始位置;
A5
C6
B6 B1580°B4
C4
C5
φ3
φC23
A1
↓对心直动平底推杆盘形凸 轮机构
↑偏置直动尖端推杆盘形凸轮机 构
第十一页,编辑于星期日:十四点 分。
↑尖端摆动凸轮机构
↓平底摆动凸轮机构
↑滚子摆动凸轮机构
第十二页,编辑于星期日:十四点 分。
(4)按凸轮与从动件保持接触的方式分
力封闭型凸轮机构
利用推杆的重力、弹簧力或其他外力使推杆与凸轮保持接
触的
此外,还要考虑机构的冲击性能。
机械原理 第3章 凸轮机构
2
26
§3.3 凸轮轮廓曲线的设计 一、凸轮轮廓曲线设计是根据凸轮参数如 基圆半径、推程和推程运动角、回程及回程 运动角、远、近休止角、偏距等参数,用反 转法设计凸轮轮廓曲线。
27
二、1-对心反转图解法设计凸轮廓线,见下图:
28
29
2-偏心反转 图解法设计凸轮轮廓
主要介绍已知从动件运动规律线图设计凸轮轮廓。 一、直动从动件盘形凸轮轮廓的绘制 分别介绍以下两种类型。 1、偏置尖顶直动从动件盘形凸轮 已知从动件位移线图如图3-8 (b)所示,基圆半径 r0,凸轮行程h,推程运动角Φ=1800,休止角 Φs=300,回程角Φ'=900,按图示画出凸轮轮廓线。 作图步骤按反转法如下: 1)将Φ、Φ'各平为4等份,如图(b)中1-1';...8-8'。 并以偏距e和r0画圆,如图(a)所示。基圆与导 路的交点B0(C0)即为从动件的起始点。 2)以OC0为起点,在基圆上平分Φ=180和Φ'=90 分别得C1、C2、C3、和C6、C7、C8各点,并过 C0、C1 . . . 各点向偏距圆作切线,这些切线就是 反转法导路在此点的位置。 3)在各对应的切线上,取C1B1=11' ;C2B2=22' ....得从动件尖顶位置B1、B2、B3... 4)将B0、B1、B2…连接成光滑的曲线就是凸轮 轮廓线(注意:B4、B5是圆弧,B9、B0之间是基 圆) 最后画出图纸进行加工。 30 当e=0时,各切线变成通过O点的射线。
10
一、从动件的运动规律的描述与术语
从动杆位移线图的作图方法及基本名词术语
首先应确认,从动件的运 动规律是由主动件凸轮的轮 廓形状决定的。在图 3-5 中, 回转中心 O 到半径最小点 A 的 K' 圆叫基圆。图 3-5 中凸轮的轮 ϕk 廓规律是,弧 AB 间的半径逐 渐变大,对应的圆心角为 ϕ; 弧 BC 间半径保持不变,对应 K ϕk 的圆心角为 ϕ s ;弧 CD 间半径 逐步变小到基圆半径,对应 的圆心角为 ϕ ' ;弧 DA 间半径 保持基圆半径不变,对应的 圆心角为ϕs'。现凸轮以ω速度 顺时针转动,以 φ=ωt 为横坐 标,从动杆的移动 S为纵坐标, 则从动杆的移动曲线展开图 图3-12:凸轮轮廓与从动件位移线图 如(b)所示。其中: h--升程;ϕ--推程运动角;ϕs--远休止角; ϕ‘--回程运动角;ϕ's--近休止角。这 些角度总和为360˚。从图中可知,当凸轮从A点转过ϕk角到K点时,从动杆升高 到K’点;当凸轮从A点转过ϕ角度,从动杆升高了h到B点。其他各点作图方法 11 一样,然后将各点连成光滑的曲线,就是从杆的位移线图(b).
第三章 凸轮机构

第三章凸轮机构§3-1 凸轮机构的组成和类型一、凸轮机构的组成1、凸轮:具有曲线轮廓或沟槽的构件,当它运动时,通过其上的曲线轮廓与从动件的高副接触,使从动件获得预期的运动。
2、凸轮机构的组成:由凸轮、从动件、机架这三个基本构件所组成的一种高副机构。
二、凸轮机构的类型1.按照凸轮的形状分:空间凸轮机构:盘形凸轮:凸轮呈盘状,并且具有变化的向径。
它是凸轮最基本的形式,应用最广。
移动(楔形)凸轮:凸轮呈板状,它相对于机架作直线移动。
盘形凸轮转轴位于无穷远处。
空间凸轮机构:圆柱凸轮:凸轮的轮廓曲线做在圆柱体上。
2.按照从动件的形状分:(1)尖端从动件从动件尖端能与任意形状凸轮接触,使从动件实现任意运动规律。
结构简单,但尖端易磨损,适于低速、传力不大场合。
(2)曲面从动件:从动件端部做成曲面,不易磨损,使用广泛。
(3)滚子从动件:滑动摩擦变为滚动摩擦,传递较大动力。
(4)平底从动件优点:平底与凸轮之间易形成油膜,润滑状态稳定。
不计摩擦时,凸轮给从动件的力始终垂直于从动件的平底,受力平稳,传动效率高,常用于高速。
缺点:凸轮轮廓必须全部是外凸的。
3.按照从动件的运动形式分:4.按照凸轮与从动件维持高副接触的方法分:(1)力封闭型凸轮机构:利用重力、弹簧力或其它外力使从动件与凸轮轮廓始终保持接触。
封闭方式简单,对从动件运动规律没有限制。
5、其它反凸轮机构:摆杆为主动件,凸轮为从动件。
应用实例:自动铣槽机应用反凸轮实现料斗翻转§3-2 凸轮机构的特点和功能一.凸轮机构的特点1、优点: (1)结构简单、紧凑,具有很少的活动构件,占据空间小。
(2)最大优点是对于任意要求的从动件运动规律都可以毫无困难地设计出凸轮廓线来实现。
2、缺点:由于是高副接触,易磨损,因此多用于传力不大的场合。
二.功能1、实现无特定运动规律要求的工作行程应用实例:车床床头箱中利用凸轮机构实现变速操纵2、实现有特定运动规律要求的工作行程应用实例:自动机床中利用凸轮机构实现进刀、退刀3、实现对运动和动力特性有特殊要求的工作行程应用实例:船用柴油机中利用凸轮机构控制阀门的启闭4、实现复杂的运动轨迹应用实例:印刷机中利用凸轮机构适当组合实现吸纸吸头的复杂运动轨迹§3-3 从动件运动规律设计一.基础知识1、从动件运动规律:从动件的位移、速度、加速度及加速度变化率随时间或凸轮转角变化的规律。
图解法设计凸轮轮廓

已知凸轮的基圆半径rmin,角速度ω、
e
从动件的运动规律和偏心距e,设计该
凸轮轮廓曲线。
8’ 7’ 5’ 3’ 1’
1 3 5 78
9’ 11’ 12’
13’ 14’
9 11 13 15
ωA
15’15 14’14
13’ 12’
13 12
11
10
kk9k1k0k1181kk21k73k14k6O1k55k4kk3k21
的距离d,摆杆角位移方程,设计该凸轮轮廓曲线。
4’ 3’ 2’ 1’
12 3 4
5’ 6’
7’
8’ 5 67 8
d A8
A7
A
l B’1 B B1
rminω1
A1-ω1
φ1
B’2 B’3φ2
A2
B2 B3
B’φ4 3
120°B4A3来自φ790 °B8 B7
60 B6
B’7
设计:潘存云
°B5
B’6
B’5
1 3 5 78
9’ 11’ 12’
13’ 14’
9 11 13 15
理论轮廓
ω
设计:潘存云
设计步骤:
实际轮廓
①选比例尺μl作基圆rmin。 ②反向等分各运动角。原则是:陡密缓疏。
③确定反转后从动件尖顶在各等份点的位置。
④将各尖顶点连接成一条光滑曲线。
⑤作各位置滚子圆的内(外)包络线。
ρa-工作轮廓的曲率半径,ρ-理论轮廓的曲率半径,
8’ 7’ 5’ 3’ 1’
1 3 5 78
9’10’ 11’ 12’
13’ 14’
9 11 13 15
-ω ω
设计:潘存云
第3章 凸轮机构

2 0
02
a
4h12
/
2 0
推程时等减速段
s
h 2h(0 4h1 (0
)2 /
)
/
2 0
2 0
a
4h12
/
2 0
速度连续,加速度不
连续,称为柔性冲击。
用于中、低速场合。
§3 – 2 从动件的常用运动规律
V0=0,
等加速等减速
s
1 2
at 2
当时间为→ 位移为 →
1 1
: :
2 4
: :
对心直动尖顶从动件盘形凸轮机构 摆动滚子从动件盘形凸轮机构
§3 – 2 从动件的常用运动规律
凸轮机构的运动循环及基本名词术语
凸轮机构的一个运动循环大 致包括:推程、远休程、回 程、近休程四个部分
§3 – 2 从动件的常用运动规律
基圆:以轮廓的最小向径所作的圆 r0-基圆半径 推程:从动件从离回转中心最近→最远的这一过程。 升程h:推程所移动的距离。
机械设计基础
机械设计基础
绪论
机械零件设计概论
平面机构的自由度和速度分析
连接
平面连杆机构
齿轮传动
凸轮机构
蜗杆传动
齿轮机构
带传动和链传动
轮系
轴间歇运动机构 机构运转速 Nhomakorabea波动的调节
滑动轴承
滚动轴承
联轴器、离合器和制动器
回转件的平衡
弹簧
第3章 凸轮机构
§3 – 1 凸轮机构的应用和类型 §3 – 2 从动件的常用运动规律 §3 – 3 凸轮机构的压力角 §3 – 4 图解法设计凸轮轮廓 §3 – 5 解析法设计凸轮轮廓*
什么是凸轮机构
凸轮机构图解法

滚子从动件凸轮机构设计当根据使用场合和工作要求选定了凸轮机构的类型和从动件的运动规律后,即可根据选定的基圆半径着手进行凸轮轮廓曲线的设计。
凸轮廓线的设计方法有图解法和解析法,其依据的基本原理相同。
凸轮机构工作时,凸轮和从动件都在运动,为了在图纸上绘制出凸轮的轮廓曲线,可采用反转法。
下面以图示的对心尖端移动从动件盘形凸轮机构为例来说明其原理。
从图中可以看出:凸轮转动时,凸轮机构的真实运动情况:凸轮以等角速度ω绕轴O 逆时针转动,推动从动件在导路中上、下往复移动。
当从动件处于最低位置时,凸轮轮廓曲线与从动件在A点接触,当凸轮转过φ1角时,凸轮的向径OA 将转到OA´的位置上,而凸轮轮廓将转到图中兰色虚线所示的位置。
这时从动件尖端从最低位置A 上升到B´,上升的距离s1=AB´。
采用反转法,凸轮机构的运动情况:现在设想凸轮固定不动,而让从动件连同导路一起绕O点以角速度(-ω)转过φ1角,此时从动件将一方面随导路一起以角速度(-ω)转动,同时又在导路中作相对移动,运动到图中粉红色虚线所示的位置。
此时从动件向上移动的距离与前相同。
此时从动件尖端所占据的位置B 一定是凸轮轮廓曲线上的一点。
若继续反转从动件,可得凸轮轮廓曲线上的其它点。
由于这种方法是假定凸轮固定不动而使从动件连同导路一起反转,故称反转法(或运动倒置法)。
凸轮机构的形式多种多样,反转法原理适用于各种凸轮轮廓曲线的设计。
一、直动从动件盘形凸轮廓线的设计(1)尖端从动件以一偏置移动尖端从动件盘形凸轮机构为例。
设已知凸轮的基圆半径为rb,从动件轴线偏于凸轮轴心的左侧,偏距为e,凸轮以等角速度ω顺时针方向转动,从动件的位移曲线如图(b)所示,试设计凸轮的轮廓曲线。
依据反转法原理,具体设计步骤如下:1)选取适当的比例尺,作出从动件的位移线图。
将位移曲线的横坐标分成若干等份,得分点1,2, (12)2)选取同样的比例尺,以O 为圆心,rb为半径作基圆,并根据从动件的偏置方向画出从动件的起始位置线,该位置线与基圆的交点B0,便是从动件尖端的初始位置。
第三章 凸轮机构

凸轮机构的应用和类型 从动件的常用运动规律 图解法设计凸轮轮廓 设计凸轮机构应注意的问题
§3-1 凸轮机构的应用和类型
凸轮机构是一种常用机构,常用于自动化和 凸轮机构是一种常用机构, 半自动化机械中。 半自动化机械中。 一、凸轮机构的组成
凸轮机构由机架、 凸轮机构由机架、 凸轮和从动件组成。 凸轮和从动件组成。 通常,凸轮为主动件, 通常,凸轮为主动件, 作匀速运动, 作匀速运动,从动件 随主动件按一定规律 运动。改变凸轮形状, 运动。改变凸轮形状, 从动件运动规律改变。 从动件运动规律改变。
常用加大凸轮基圆半 受力分析: F”=F’tgα 受力分析: 有害力 F”=F’tgα 径的方法减小α 径的方法减小αmax F’一定时 一定时, F”↑ 当F’一定时,α↑, F”↑;当α增 大到一定程度时, F’’引起的摩 大到一定程度时,由F’’引起的摩 擦力将大于F’ 擦力将大于F’ ,此时机构发生 自锁”现象。因此,需控制α “自锁”现象。因此,需控制α。 直动从动件 [α]max=30° =30° 摆动从动件 [α]max=45° =45°
§3-2 从动件的常用运动规律
设计凸轮机构时,首先应根据工作要求确定从动件 设计凸轮机构时, 的运动规律.然后按照这一运动规律设计凸轮轮廓线。 的运动规律.然后按照这一运动规律设计凸轮轮廓线。
一、凸轮机构运动 中的基本概念
从动件位移线图: 从动件位移线图: 在以凸轮转角 凸轮转角为 在以凸轮转角为 横坐标, 横坐标, 从动件位移 为纵坐标的直角坐 纵坐标的直角坐 标系中画出从动件 位移和凸轮转角间 的关系曲线。 的关系曲线。
习题讲解
P51: P51:题3-1、3-2
作 业
P51: P51:题3-3、3-4、3-6
第三章 凸轮机构

3-1 凸轮机构的应用和类型
在机械装置中,尤其是在自动控制机械中,为实现某些特殊 或复杂的运动规律,广泛地应用着各种凸轮机构
二、凸轮机构应用
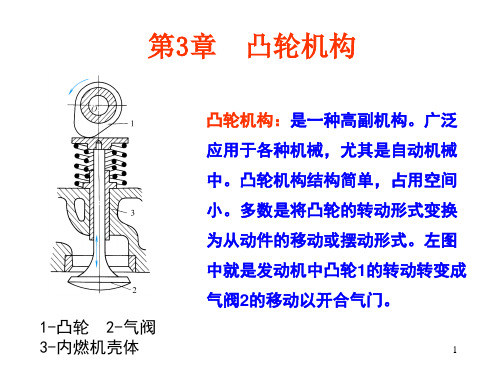
内燃机凸轮机构 凸轮以等角速度回 转,它的轮廓驱使从 动件(阀杆)按预期 的运动规律打开或关 闭阀门。
3-1 凸轮机构的应用和类型
二、凸轮机构应用
所示为绕线机中用 于排线的凸轮机构, 当绕线轴3快速转 动时,经齿轮带动 凸轮1缓慢地转动, 通过凸轮轮廓与尖 顶A之间的作用, 驱使从动件2往复 摆动,从而使线均 匀地缠绕地绕线轴 上
凸轮1随放音键 上下移动。放音 时,凸轮1处于 图示最低位置, 在弹簧的作用下, 安装于带轮轴上 2 的摩擦轮4紧靠 1 1 卷带轮5,从而 放音键 将磁带卷紧。 放音键
卷带轮 5
3 3 4 4
皮带轮 皮带轮
摩擦 轮
录音机卷带机构
二、凸轮机构应用
当带有凹槽的 凸轮1转动时, 通过槽中的滚 子,驱使从动 件2作往复移动。 凸轮1每回转一 周,从动件即 从储料器中推 出一个毛坯, 送到加工位置。
v o a
δ +∞ δ -∞
o
§3—3
凸轮机构压力角
一、压力角与作用力的关系
二、压力角与凸轮机构尺寸的关系
一、压力角与作用力的关系
压力角: 从动件上的驱动力与 该力作用点绝对速度之间 所夹的锐角。 凸轮机构的压力角:
1
n
F
3
α
v
2 B
S2 n
e
O C
P
接触点法线与从 动件上作用点速度方 向所夹的锐角。
两滚子中心间的距 离始终保持不变。
缺点:
从动件运动规律的选择受到一定的限制
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
滚子从动件凸轮机构设计
当根据使用场合和工作要求选定了凸轮机构的类型和从动件的运动规律后,即可根据选定的基圆半径着手进行凸轮轮廓曲线的设计。
凸轮廓线的设计方法有图解法和解析法,其依据的基本原理相同。
凸轮机构工作时,凸轮和从动件都在运动,为了在图纸上绘制出凸轮的轮廓曲线,可采用反转法。
下面以图示的对心尖端移动从动件盘形凸轮机构为例来说明其原理。
从图中可以看出:
凸轮转动时,凸轮机构的真实运动情况:
凸轮以等角速度ω绕轴O 逆时针转动,推动从动件在导路中上、下往复移动。
当从动件处于最低位置时,凸轮轮廓曲线与从动件在A点接触,当凸轮转过φ1角时,凸轮的向径OA 将转到OA´的位置上,而凸轮轮廓将转到图中兰色虚线所示的位置。
这时从动件尖端从最低位置A 上升到B´,上升的距离s1=AB´。
采用反转法,凸轮机构的运动情况:
现在设想凸轮固定不动,而让从动件连同导路一起绕O点以角速度(-ω)转过φ1角,此时从动件将一方面随导路一起以角速度(-ω)转动,同时又在导路中作相对移动,运动到图中粉红色虚线所示的位置。
此时从动件向上移动的距离与前相同。
此时从动件尖端所占据的位置B 一定是凸轮轮廓曲线上的一点。
若继续反转从动件,可得凸轮轮廓曲线上的其它点。
由于这种方法是假定凸轮固定不动而使从动件连同导路一起反转,故称反转法(或运动倒置法)。
凸轮机构的形式多种多样,反转法原理适用于各种凸轮轮廓曲线的设计。
一、直动从动件盘形凸轮廓线的设计
(1)尖端从动件
以一偏置移动尖端从动件盘形凸轮机构为例。
设已知凸轮的基圆半径为rb,从动件轴线偏于凸轮轴心的左侧,偏距为e,凸轮以等角速度ω顺时针方向转动,从动件的位移曲线如图(b)所示,试设计凸轮的轮廓曲线。
依据反转法原理,具体设计步骤如下:
1)选取适当的比例尺,作出从动件的位移线图。
将位移曲线的横坐标分成若干等份,得分点1,2, (12)
2)选取同样的比例尺,以O 为圆心,rb为半径作基圆,并根据从动件的偏置方向画出从动件的起始位置线,该位置线与基圆的交点B0,便是从动件尖端的初始位置。
3)以O 为圆心、OK=e 为半径作偏距圆,该圆与从动件的起始位置线切于K点。
4)自K点开始,沿(-ω)方向将偏距圆分成与图(b)横坐标对应的区间和等份,得若干个分点。
过各分点作偏距圆的切射线,这些线代表从动件在反转过程中从动件占据的位置线。
它们与基圆的交点分别为C1,C2,…,C11。
5)在上述切射线上,从基圆起向外截取线段,使其分别等于图(b)中相应的坐标,即C1B1=11',C2B2=22', …,得点B1,B2,…,B11,这些点即代表反转过程中从动件尖端依次占据的位置。
6)将点B0,B1,B2,…连成光滑的曲线,即得所求的凸轮轮廓曲线。
(2)滚子从动件
对于下图示偏置移动滚子从动件盘形凸轮机构,当用反转法使凸轮固定不动后,从动件的滚子在反转过程中,将始终与凸轮轮廓曲线保持接触,而滚子中心将描绘出一条与凸轮廓线法向等距的曲线η。
由于滚子中心B 是从动件上的一个铰接点,所以它的运动规律就是从动件的运动规律,即曲线η可根据从动件的位移曲线作出。
一旦作出了这条曲线,就可顺利地绘制出凸轮的轮廓曲线了。
(1)将滚子中心B假想为尖端从动件的尖端,按照上述尖端从动件凸轮轮廓曲线的设计方法作出曲线η,这条曲线是反转过程中滚子中心的运动轨迹,称之为凸轮的理论廓线。
(2)以理论廓线上各点为圆心,以滚子半径r r为半径,作一系列滚子圆,然后作这族滚子圆的内包络线η', 它就是凸轮的实际廓线。
很显然,该实际廓线是上述理论廓线的等距曲线(法向等距,其距离为滚子半径)。
若同时作出这族滚子圆的内、外包络线η'和η" 则形成槽凸轮的轮廓曲线。
由上述作图过程可知,在滚子从动件盘形凸轮机构的设计中,r b指的是理论廓线的基圆半径。
需要指出的是,在滚子从动件的情况下,从动件的滚子与凸轮实际廓线的接触点是变化的。
