高一数学函数单调性

合集下载

高一数学函数的单调性知识点

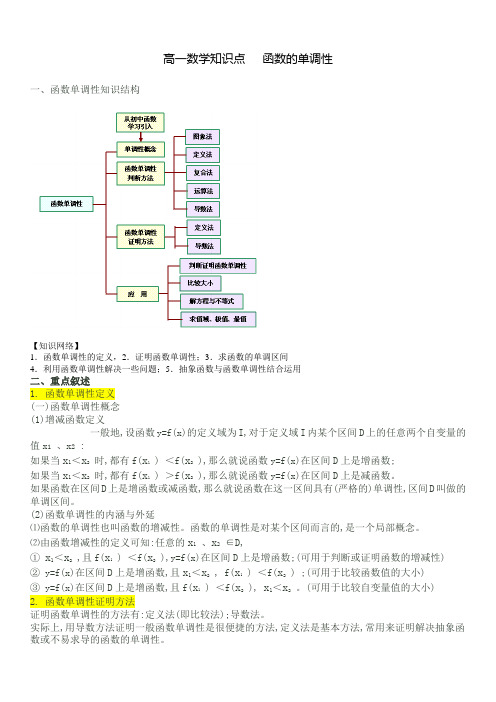
高一数学知识点函数的单调性

一、函数单调性知识结构

【知识网络】

1．函数单调性的定义，2．证明函数单调性；3．求函数的单调区间

4．利用函数单调性解决一些问题；5．抽象函数与函数单调性结合运用

二、重点叙述

1. 函数单调性定义

(一)函数单调性概念

(1)增减函数定义

一般地,设函数y=f(x)的定义域为I,对于定义域I内某个区间D上的任意两个自变量的值x1、x2 :

如果当x1＜x2时,都有f(x1 ) ＜f(x2 ),那么就说函数y=f(x)在区间D上是增函数;

如果当x1＜x2时,都有f(x1 ) ＞f(x2 ),那么就说函数y=f(x)在区间D上是减函数。

如果函数在区间D上是增函数或减函数,那么就说函数在这一区间具有(严格的)单调性,区间D叫做的单调区间。

(2)函数单调性的内涵与外延

⑴函数的单调性也叫函数的增减性。函数的单调性是对某个区间而言的,是一个局部概念。

⑵由函数增减性的定义可知:任意的x1、x2∈D,

① x1＜x2 ,且f(x1 ) ＜f(x2 ),y=f(x)在区间D上是增函数;(可用于判断或证明函数的增减性)

② y=f(x)在区间D上是增函数,且x1＜x2 , f(x1 ) ＜f(x2 ) ;(可用于比较函数值的大小)

③ y=f(x)在区间D上是增函数,且f(x1 ) ＜f(x2 ), x1＜x2。(可用于比较自变量值的大小)

2. 函数单调性证明方法

证明函数单调性的方法有:定义法(即比较法);导数法。

实际上,用导数方法证明一般函数单调性是很便捷的方法,定义法是基本方法,常用来证明解决抽象函数或不易求导的函数的单调性。

高一数学函数单调性讲解

高中数学必修一函数——单调性

考纲解读：了解单调函数及单调区间的意义，掌握判断函数单调性的方法；掌握增，减函数的意义，理解函数单调函数的性质。

能力解读：函数单调性的判断和函数单调性的应用。利用函数单调性判断方法来判断函数的单调性，利用函数的单调性求解函数的最值问题。掌握并熟悉抽象函数以及符合函数的单调性判断方法。

知识要点：

1．函数单调性的定义， 2．证明函数单调性； 3．求函数的单调区间

4．利用函数单调性解决一些问题； 5．抽象函数与函数单调性结合运用

一、单调性的定义

（1）设函数)(x f y =的定义域为A ，区间A I ⊆

如果对于区间I 内的任意两个值1x ，2x ，当21x x

)(x f y =在区间I 上是单调增函数，I 称为)(x f y =的单调增区间

如果对于区间I 内的任意两个值1x ，2x ，当21x x ，那么就说

)(x f y =在区间I 上是单调减函数，I 称为)(x f y =的单调减区间

（2）设函数)(x f y =的定义域为A

如果存在定值A x ∈0，使得对于任意A x ∈，有)()(0x f x f ≤恒成立，那么称)(0x f 为

)(x f y =的最大值；

如果存在定值A x ∈0，使得对于任意A x ∈，有)()(0x f x f ≥恒成立，那么称)(0x f 为

)(x f y =的最小值。

二、函数单调性的证明

重点：函数的单调性只能在函数的定义域内来讨论,所以求函数的单调区间,必须先求函数的定义域；（1）定义法求单调性

函数单调性定义中的1x ，2x 有三个特征：一是任意性；二是大小，即

高一数学单调性知识点总结

在高中数学学习中，单调性是一个非常重要的概念。单调性可以帮

助我们理解函数的增减趋势以及函数图像的形状。在本文中，我们将

总结高一数学中与单调性相关的知识点，并探讨其应用。

一、函数的单调性

函数的单调性是指函数在定义域内的增减趋势。具体来说，我们可

以分为递增和递减两种情况进行讨论。

1. 函数的递增性

如果对于定义域内的任意两个实数a和b，当a<b时有f(a)<f(b)，

那么我们称函数为递增函数。简单来说，递增函数的函数值随着自变

量的增大而增大。

通过求导可以帮助我们判断函数的递增性。如果函数的导数大于零，则函数递增；如果导数小于零，则函数递减；如果导数等于零，则函

数在该区间内的单调性不确定，需要进行进一步的分析。

2. 函数的递减性

如果对于定义域内的任意两个实数a和b，当a<b时有f(a)>f(b)，

那么我们称函数为递减函数。递减函数的函数值随着自变量的增大而

减小。

二、函数图像的单调性分析

在图像上观察函数的单调性，可以通过以下几个方面来判断。

1. 函数图像在某个区间内递增或递减

通过观察函数图像，在某个区间内如果图像整体上升，则该区间内

函数递增；如果图像整体下降，则该区间内函数递减。

2. 函数图像在特定点的切线斜率

通过求导函数，可以得到函数的导函数。根据导函数的正负性，可

以判断函数图像在特定点的切线斜率的正负。如果导函数大于零，则

函数图像在该点的切线斜率大于零，即函数递增；如果导函数小于零，则函数图像在该点的切线斜率小于零，即函数递减。

3. 函数图像的拐点与极值点

高一数学讲义函数的单调性

函数的单调性、

知能点全解：

知能点一：函数单调性的定义 1、图形描述：

从函数2x y =的图象（图1）看到：图象在 y 轴的右侧部分是从左向右连续上升的，也就是说，当x 在区间[0，+∞)上取值时，随着x 的

增大,相应的y 值也随着增大，即如果任取21,x x [)0,∈+∞，得到1y =)(1x f ,2y =)(2x f ,那么当

1x <2x 时，有1y <2y 。这时我们就说函数)(x f =2x 在[0,+ ∞)上是增函数。

图象在y 轴的左侧部分是从左向右连续下降的，也就是说，当x 在区间(],0-∞上取值时，随着x 的增大，相应的y 值反而随着减小，即如果任取21,x x (],0∈-∞，得到1y =)(1x f ,2y =)(2x f ,那么当1x <2x 时，有1y >2y 。这时我们就说函数)(x f =2x 在(-∞,0)上是减函数. 2、定量描述

对于函数)(x f 的定义域I 内某个区间D 上的任意两个自变量的值21,x x ，（1）若当1x <2x 时，都有)(1x f <)(2x f ,则说)(x f 在区间D 上是增函数；（2）若当1x <2x 时，都有)(1x f >)(2x f ,则说)(x f 在区间D 上是减函数。 3、单调性与单调区间

若函数y =)(x f 在某个区间是增函数或减函数，则就说函数)(x f 在这一区间具有（严格的）单调性，这一区间叫做函数)(x f 的单调区间。此时也说函数是这一区间上的单调函数。在单调区间上，增函数的图象是上升的，减函数的图象是下降的。特别提醒：

高一数学人必修件时函数的单调性

当$k<0$时，函数在整个定义域内单调递减。
当$k>0$时，函数在整个定义域内单调递增。
二次函数单调性变化规律
二次函数$f(x)=ax^2+bx+c$ （$a neq 0$）的单调性由系数$a$决定。
当$a>0$时，函数在区间$(infty, -frac{b}{2a}]$上单调递减，在区间$[-frac{b}{2a}, +infty)$上单调递增。
解答
解不等式得$- frac{5pi}{12} + kpi leqslant x leqslant frac{pi}{12} + kpi$，所以函数$y = sin(2x + frac{pi}{3})$的单调递增区间为$[ - frac{5pi}{12} + kpi, frac{pi}{12} + kpi]$ ，其中$k in mathbf{Z}$。
证明
设x1,x2∈R且x1<x2，则f(x1)-f(x2)=2^x12^x2=2^x1(1-2^(x2-x1))。由于2^x1>0且1-2^(x2x1)<0（因为x2-x1>0且2^(x2-x1)>1），所以f(x1)f(x2)<0，即f(x1)<f(x2)。因此，y=2^x在R上是增函数
例题2
判断函数y=log2(x)在(0,+∞)上的单调性，并证明。

高一函数的单调性知识点

函数的单调性是数学中的一个重要概念，它描述了函数在定义域上

的增减情况。了解函数的单调性有助于我们更好地理解和运用函数，

下面就是关于高一函数的单调性知识点的详细介绍。

一、函数的递增和递减区间

在讨论函数的单调性时，首先需要了解函数的递增和递减区间。我

们将函数在定义域上递增（或递减）的部分称为函数的递增（或递减）区间。

1. 函数的递增区间

对于函数 f(x)，如果对于任意两个 x1 和 x2（x1 < x2），都有 f(x1)

< f(x2)，那么 f(x) 在 [x1, x2] 上递增。我们可以通过求函数的导数来确

定函数的递增区间。

2. 函数的递减区间

对于函数 f(x)，如果对于任意两个 x1 和 x2（x1 < x2），都有 f(x1) > f(x2)，那么 f(x) 在 [x1, x2] 上递减。同样地，我们可以通过求函数的导

数来确定函数的递减区间。

二、函数单调性的判定

在大部分情况下，我们可以通过函数的导数来判定函数的单调性。

具体而言，可以根据函数导数的正负性来确定函数的单调性。

1. 函数导数的正负性

如果函数 f(x) 的导数在某个区间内恒大于 0，则 f(x) 在该区间上递增；如果导数恒小于 0，则 f(x) 在该区间上递减。通过求导数，我们可以得到函数的递增区间和递减区间。

2. 临界点和极值点

函数的单调性与其临界点和极值点也有密切关系。在函数的临界点和极值点处，其单调性会发生改变。

- 临界点：函数 f(x) 在定义域上的某个点 x=c 处，如果 f'(c)=0 或者f'(c) 不存在，那么点 c 称为函数的临界点。在临界点之间，函数的单调性可能会改变。

高一数学函数的单调性

观察演示并思考问题：
想看看函数的图象吗？
函数单调性的概念：
一般地，设函数f(x)定义域为I：
1. 如果对于属于定义域I内某个区间的任意任意两个自变量值x x 当x x 时都有f(x ) f(x ),
, , 1 2
1
2
,
1
2
称函数 f(x)在这个区间上是增函数。 2. 如果对于属于定义域I内某个区间的任意自变量
1 2
1 2
¸ Ø Ï µ À ´ Å Ð ¶ ¨¹ ¯ Ê ý µ ¥ µ ôÐ Ô
例
题
ห้องสมุดไป่ตู้
证明函数f(x)=3x+2在R上是增函数证明： É è x£ ¬ xÊ Ç RÉ Ï È Î Ò â Á ½ · ö Ê µ Ê ý £ ¬ Ç Ò x <x
1 2 1
2
Ô ò f ( x1 ) - f ( x2 ) =(3 x1 +2)-(3 x2 +2) =3 x1 +2-3 x2 -2 =3( x1 - x2 ) ¡ ß x1 < x2 ¡ à x1 - x2 <0 ¡ à f ( x1 ) - f ( x2 ) =3( x1 - x2 )<0 ¡ à ¹ ¯ Ê ý f(x)=3x+2 Ô Ú RÉ Ï Ê Ç Ô ö ¹ ¯ Ê ý
两个值x x2 , 当x1 x 2时, 都有f(x 1, 1 ) f(x2 ),

高一函数单调性的求法和步骤

书籍好比一架梯子，它能引导我们登上知识的殿堂。书籍如同一把钥匙，它能帮助我们开启心灵的智慧之窗。下面给大家分享一些关于高一函数单调性的求法和步骤，希望对大家有所帮助。

一.高一函数单调性的求法和步骤

1、导数法

首先对函数进行求导，令导函数等于零，得X值，判断X与导函数的关系，当导函数大于零时是增函数，小于零是减函数。

2、定义法

设x1，x2是函数f(x)定义域上任意的两个数，且x1f(x2)，则此函数为减函数.

3、性质法

若函数f(x)、g(x)在区间B上具有单调性，则在区间B上有：

① f(x)与f(x)+C(C为常数)具有相同的单调性;

②f(x)与c?f(x)当c>0具有相同的单调性，当c<0具有相反的单调性;

③当f(x)、g(x)都是增(减)函数，则f(x)+g(x)都是增(减)函数;

④当f(x)、g(x)都是增(减)函数，则f(x)?g(x)当两者都恒大于0时也是增(减)函数，当两者都恒小于0时也是减(增)函数;

4、复合函数同增异减法

对于复合函数y=f [g(x)]满足“同增异减”法(应注意内层函数的值域)，令 t=g(x)，则三个函数 y=f(t)、t=g(x)、y=f [g(x)]中，若有两个函数单调性相同，则第三个函数为增函数;若有两个函数单调性相反，则第三个函数为减函数。

拓展资料：

函数的定义：

给定一个数集A，假设其中的元素为x。现对A中的元素x施加对应法则f，记作f(x)，得到另一数集B。假设B中的元素为y。则y与x 之间的等量关系可以用y=f(x)表示。我们把这个关系式就叫函数关系

高一数学函数知识点总结(3篇)

高一数学函数知识点总结

函数的单调性

1、单调函数

对于函数f（x）定义在某区间[a，b]上任意两点x1，x2，当

x1>x2时，都有不等式f（x1）>（或<）f（x2）成立，称f（x）在[a，b]上单调递增（或递减）;增函数或减函数统称为单调函数.

对于函数单调性的定义的理解，要注意以下三点：

（1）单调性是与“区间”紧密相关的概念.一个函数在不同的区

间上可以有不同的单调性.

（2）单调性是函数在某一区间上的“整体”性质，因此定义中的x1，x2具有任意性，不能用特殊值代替.

（3）单调区间是定义域的子集，讨论单调性必须在定义域范围内.

（4）注意定义的两种等价形式：

设x1、x2∈[a，b]，那么：

①在[a、b]上是增函数;

在[a、b]上是减函数.

②在[a、b]上是增函数.

在[a、b]上是减函数.

需要指出的是：①的几何意义是：增（减）函数图象上任意两点（x1，f（x1））、（x2，f（x2））连线的斜率都大于（或小于）零.

（5）由于定义都是充要性命题，因此由f（x）是增（减）函

数，且（或x1>x2），这说明单调性使得自变量间的不等关系和函数值之间的不等关系可以“正逆互推”.

5、复合函数y=f[g（x）]的单调性

若u=g（x）在区间[a，b]上的单调性，与y=f（u）在[g（a），g （b）]（或g（b），g（a））上的单调性相同，则复合函数y=f[g （x）]在[a，b]上单调递增;否则，单调递减.简称“同增、异减”.

在研究函数的单调性时，常需要先将函数化简，转化为讨论一些熟知函数的单调性。因此，掌握并熟记一次函数、二次函数、指数函数、对数函数的单调性，将大大缩短我们的判断过程.

高一数学函数单调性与最值(含解析)

函数单调性

引入

对于二次函数，我们可以这样描述“在区间（0，）上，随着的增大，相应的也随

着增大”；在区间（0，）上，任取两个，，得到，

，当时，有 .这时，我们就说函数在区间（0，）上是增函数.

一、函数单调性的判断与证明 1、函数增减性的定义

一般地，设函数的定义域为：

如果对于定义域内某个区间D 上的任意两个自变量的值，，当时，都有，那么就说函数在区间D 上是增函数（increasing function ）

如果对于定义域内某个区间D 上的任意两个自变量的值，，当时，都有，那么就说函数在区间D 上是减函数（decreasing function ）.

【例1】下列四个函数中，在(0，＋∞)上为增函数的是( )

A ．f (x )＝3－x

B ．f (x )＝x 2－3x

C ．f (x )＝－

x ＋1

D ．f (x )＝－|x | 【解析】选C 当x >0时，f (x )＝3－x 为减函数；当x ∈⎝⎛⎭⎫0，32时，f (x )＝x 2－3x 为减函数，当x ∈⎝⎛⎭⎫32，＋∞时，f (x )＝x 2－3x 为增函数；当x ∈(0，＋∞)时，f (x )＝－1

x ＋1为增函数；当x ∈(0，＋∞)时，f (x )＝－|x |为

减函数．故选C.

【例2】判断函数g (x )＝－2x

x －1在(1，＋∞)上的单调性．

【解】任取x 1，x 2∈(1，＋∞)，且x 1<x 2，则g (x 1)－g (x 2)＝

－2x 1x 1－1－－2x 2x 2－1＝2(x 1－x 2)

（推荐）高一数学中函数的单调性4种求法

高一数学中函数的单调性非常重要，分析函数的单调性方法有：定义法，图像法，性质法,复合法.下边结合例题加以说明：

1.定义法

例题已知函数y=x^3-x在（0，a]上是减函数，在[a,+)上是增函数，求a的值。

解分析函数在R+上的单调性

任取x1>x2>0

Y1-Y2=(X1^3-X2^3)-(X1-X2)=(X1-X2)(X1^2+X1X2+X2^2)-(X1-X2)

=(X1-X2)(X1^2+X1X2+X2^2-1)

令y1-y2>0 所以X1^2+X1X2+X2^2-1>0

因为X1^2+X1X2+X2^2-1>X2^2+X2X2+X2^2-1=3X2^2-1 当3X2^2-1>=0时即X2^2>=1/3 X2>=根号3/3时y1-y2>0 函数是递增的

同理当3X1^2-1<=0时即X1<=根号3/3时y1-y2<0 函数是递减的

故函数在R+上的增区间为[根号3/3,+）减区间为（0，根号3/3) 因此 a=根号3/3

一般情况下，用定义求函数的单调区间就是求出使y1-y2>0(<0)的x1,x2的取值范围，要变换不等式，求出x1和x2的范围，就可求出函数的单调区间。

2.图像法

例题求y=x+3/x-1的单调区间

解函数定义域为（-，1）并（1，+)

Y=X+3/X-1=X-1+4/X-1=1+4/X-1

由图像可知函数在（-，1）和（1，+0）上递减。

函数的图像是解决这类问题的关键。

高一数学函数单调性知识点

随着高中数学课程的深入，函数的概念成为重中之重。而在函数中，单调性的概念也是非常重要的一个知识点。掌握函数的单调性不仅可

以帮助我们更好地理解和应用函数，还可以在解题过程中起到一定的

指导作用。下面，我们就来了解一下高一数学中关于函数单调性的知

识点。

一、函数单调性的定义

在介绍函数单调性之前，我们先来回顾一下函数的定义。函数是两

个集合之间的一种对应关系，通常用字母表示，比如f(x)。数学上，我们把自变量的每个值称为定义域中的一个元素，而函数值称为值域中

的一个元素。

函数的单调性指的是函数值的增减趋势。如果一个函数在定义域上

是递增的，那么我们称其为递增函数；如果一个函数在定义域上是递

减的，那么我们称其为递减函数。如果一个函数既不递增也不递减，

我们称其为非单调函数。

二、函数单调性的判断方法

1. 利用导数的符号判断函数的单调性

高中数学中，我们常常通过求函数的导数来判断函数的单调性。函

数的导数是函数在某一点的变化率，可以帮助我们推断函数在该点的

单调性。

具体的判断方法如下：

- 若导数大于零，则函数递增；

- 若导数小于零，则函数递减；

- 若导数等于零，则函数在该点不增不减，可能是极值点。

通过这种方法，我们可以将函数图像分成若干个区间，在每个区间内判断函数的单调性。

2. 利用函数的一阶导数和二阶导数判断函数的单调性

有些函数的导数难以求解，此时我们可以通过一阶导数和二阶导数的符号来判断函数的单调性。

具体的判断方法如下：

- 若一阶导数大于零，而二阶导数小于零，则函数递减；

- 若一阶导数大于零，而二阶导数大于零，则函数递增；

高一数学中函数的单调性4种求法

高一数学中函数的单调性非常重要，分析函数的单调性方法有：定义法，图像法，性质法,复合法.下边结合例题加以说明：

1.定义法

例题已知函数y=x^3-x在（0，a]上是减函数，在[a,+)上是增函数，求a的值。

解分析函数在R+上的单调性

任取x1>x2>0

Y1-Y2=(X1^3-X2^3)-(X1-X2)=(X1-X2)(X1^2+X1X2+X2^2)-(X1-X2)

=(X1-X2)(X1^2+X1X2+X2^2-1)

令y1-y2>0 所以X1^2+X1X2+X2^2-1>0

因为X1^2+X1X2+X2^2-1>X2^2+X2X2+X2^2-1=3X2^2-1

当3X2^2-1>=0时即X2^2>=1/3 X2>=根号3/3时 y1-y2>0 函数是递增的

同理当3X1^2-1<=0时即X1<=根号3/3时 y1-y2<0 函数是递减的

故函数在R+上的增区间为[根号3/3,+）减区间为（0，根号3/3)

因此 a=根号3/3

一般情况下，用定义求函数的单调区间就是求出使y1-y2>0(<0)的x1,x2的取值范围，要变换不等式，求出x1和x2的范围，就可求出函数的单调区间。

2.图像法

例题求y=x+3/x-1的单调区间

解函数定义域为（-，1）并（1，+)

Y=X+3/X-1=X-1+4/X-1=1+4/X-1

由图像可知函数在（-，1）和（1，+0）上递减。

函数的图像是解决这类问题的关键。

3.性质法

性质：增+增=增减+减=减

高中数学单调性

高中数学———有关函数单调性

永德二中王冬梅

单调性是高中数学的重要内容，又是学习高等数学的基础。在高考和各种数学竞赛中都占有重要的地位。

下面，简单介绍下有关函数单调性解题的基本方法和技巧。

一、函数的单调性的概念

首先，我们要弄清楚什么是函数的单调性

a 、函数的单调性也叫函数的增减性。（函数的单调性是对某个区间而言的，它是一个局部概念。）

b 、增函数与减函数的概念：

一般地，设函数)(x f 的定义域为I ：如果对于I 内某个子区间D 上的任意两个自变量的值1x 、2x ，当21x x <时都有)()(21x f x f <。那么就说)(x f 在这个区间D 上是增函数。相反地，如果对于属于I 内某个区间D 上的任意两个自变量的值1x 、2x ，当21x x <时都有)()(21x f x f >。那么就说)(x f 在这个区间D 上是减函数。

c 、单调性与单调区间

若函数)(x f y =在某个子区间D 是增函数或减函数，那么就说函数)(x f y =在这一区间D 具有（严格的）单调性，这一区间D 叫做函数的单调区间。此时也说函数)(x f y =是这一区间D 上的单调函数。

二、如何求函数的单调性

a 、利用函数图像判断

如果可以画出函数的图像，或者已知函数的图像。我们就可以直接通过图像观察写出函数的单调区间。

在单调区间上，增函数的图像是上升的，减函数的图像是下降的。

简单地说：就是走上坡路的区间是增区间，走下坡路的区间是减区间。

b 、利用函数定义证明

（同号为增）)()()(212121x f x f x f x x D x x ⇒⎪⎩

高一函数单调性的求法和步骤

一.高一函数单调性的求法和步骤

1、导数法

首先对函数进行求导，令导函数等于零，得X值，判断X与导函数的关系，当导函数大于零时是增函数，小于零是减函数。

2、定义法

设x1，x2是函数f(x)定义域上任意的两个数，且x1f(x2)，则此函数为减函数.

3、性质法

若函数f(x)、g(x)在区间B上具有单调性，则在区间B上有：

① f(x)与f(x)+C(C为常数)具有相同的单调性;

②f(x)与c?f(x)当c>0具有相同的单调性，当c<0具有相反的单调性;

③当f(x)、g(x)都是增(减)函数，则f(x)+g(x)都是增(减)函数;

④当f(x)、g(x)都是增(减)函数，则f(x)?g(x)当两者都恒大于0时也是增(减)函数，当两者都恒小于0时也是减(增)函数;

4、复合函数同增异减法

拓展资料：

函数的定义：

高一数学上函数的单调性知识点

高一数学上函数的单调性知识点函数的单调性是高一数学中重要的知识点之一。对于一个给定的函数，我们可以通过研究它的单调性来了解函数的增减变化规律。在本

篇文章中，将介绍函数的单调性的基本概念、判断方法和应用。

一、函数的单调性的概念

函数的单调性是指函数在定义域内的增减变化规律。基本上，函数

的单调性可以分为三种情况：递增、递减和不变。当函数的值随着自

变量的增加而增加时，我们称该函数为递增函数。相反地，当函数的

值随着自变量的增加而减少时，我们称该函数为递减函数。若函数在

自变量取值范围内既递增又递减，或者在某些区间内递增，在其他区

间内递减，我们则称该函数是不变函数。

二、函数单调性的判断方法

判断函数的单调性，一般可以通过函数的导数、变化率和二阶导数

等方法进行推导。

1. 函数的导数法

对于给定的函数f(x)，我们通过求函数的导数f'(x)来判断函数的单

调性。

若函数在定义域内的导数恒大于0，则函数递增；若导数恒小于0，则函数递减。

例如，对于函数f(x) = x^2，求导得到f'(x) = 2x。由于函数的导数

f'(x)在定义域内恒大于0，所以该函数是递增的。

2. 函数的变化率法

利用函数的变化率来判断函数的单调性是另一种常用的方法。

对于给定的函数f(x)，通过计算任意两个点(x1, f(x1))和(x2, f(x2))之间的斜率来判断函数的单调性。

若对于任意两个不同的点(x1, f(x1))和(x2, f(x2))，斜率k = (f(x2) - f(x1)) / (x2 - x1) 恒大于0，则函数递增；若斜率k恒小于0，则函数递减。若存在某些点斜率为0，则表示函数的区间不变。

高一数学函数单调性

高一数学函数的单调性知识点

高一数学 函数单调性讲解

高一数学单调性知识点总结

高一数学讲义函数的单调性

高一数学人必修件时函数的单调性

高一函数的单调性知识点

高一数学 函数的单调性

高一函数单调性的求法和步骤

高一数学函数知识点总结(3篇)

高一数学 函数单调性与最值(含解析)

（推荐）高一数学中函数的单调性4种求法

高一数学函数单调性知识点

高一数学中函数的单调性4种求法

高中数学单调性

高一函数单调性的求法和步骤

高一数学上函数的单调性知识点

高一数学函数单调性讲解

高一数学函数的单调性

高一数学函数单调性与最值(含解析)