2012年数学建模竞赛答案之一 葡萄酒
2012年全国大学生数学建模竞赛A题 附件1-葡萄酒品尝评分表

2 葡萄酒样品2
外观分析 澄清度 色调
香
6
7
7
7
6
7
7
19
16
16
16
10
9
9
8
3
4
4
4
8
8
8
8
5
4
5
4
7
6
7
7
14
12
12
12
4
5
5
5
6
6
7
7
7
6
6
7
16
16
16
22
9
9
9
10
4
4
3
4
8
8
6
8
5
5
4
5
7
7
6
6
14
12
12
12
5
5
4
5
7
6
7
7
6
6
7
7
19
16
16
7
14
12
12
14
5
4
5
5
6
6
6
6
6
6
6
6
16
16
16
19
9
9
9
10
4
4
4
4
8
8
6
8
4
4
5
4
6
7
6
6
12
12
12
12
4
5
5
4
6
6
7
2012年全国大学生数学建模竞赛a题 葡萄酒的评价 答案.

葡萄酒的评价摘要本文主要研究的是如何对葡萄酒进行评价的问题。
通过对评酒员的评分与酿酒葡萄的理化指标和葡萄酒的理化指标等原始数据进行统计、分析和处理,我们得出了一个较为合理地评价葡萄酒质量优劣的模型。
在问题一中,我们采用T检验法,首先进行正态分布拟合检验,判断出它们服从正态分布。
之后,我们通过T检验法判断出了两组评酒员的评价结果具有显著性差异。
而对于如何判断哪一组评酒员的评价结果更可信,由于评酒员评分的客观性,我们通过计算评酒员评分均值的置信区间,利用置信区间的长短来判断评分的可信程度。
置信区间越窄,说明其越可信。
利用Matlab软件求出了第二组评酒员的评分均值的置信区间更窄,所以第二组评酒员的评价结果更可信。
在问题二中,我们采用主成分分析法,把给定的一组相关变量通过线性变换转成另一组不相关的变量,这些新的变量再按照方差依次递减的顺序排列。
在数学变换中保持变量的总方差不变,使第一变量具有最大的方差。
第二变量的方差次大,并且和第一变量不相关。
由于变量较多,虽然每个变量都提供了一定的信息,但其重要性有所不同。
依次类推,最后我们将酿酒葡萄分为了四个等级:优质、次优、中等、下等。
在问题三中,我们通过多项式曲线拟合的方法,构造一个以葡萄酒的理化指标为自变量,酿酒葡萄的理化指标为因变量的函数,并利用Matlab软件进行曲线拟合,最后得出酿酒葡萄与葡萄酒的理化指标之间的关系为呈线性正相关。
在问题四中,我们用无交互作用的双因素试验的方差分析方法,通过对观测、比较、分析实验数据的结果,鉴别出了两个因素在水平发生变化时对实验结果产生显著性影响的大小程度。
最后,我们认为能用酿酒葡萄和葡萄酒的理化指标来评价葡萄酒的质量,且酿酒葡萄的理化指标对葡萄酒质量影响相对葡萄酒的理化指标更显著。
关键词:T检验法,Matlab,正态分布,主成分分析法,多项式曲线拟合,方差分析一.问题的重述确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
2012年全国大学生数学建模竞赛A题国一

摘要
在问题一中,首先根据 T 检验、方差显著性检验和 Wilcoxon 秩和检验对两组评酒 员给葡萄酒的评价结果的差异的显著性检验。在大多数评酒员评分可靠的假设下,分别 利用评分方差比较模型,说明第二组结果可靠。在此基础上引入了评酒员“失误度”概 念来衡量每位评酒员与所有评酒员总体评价的差异, 对各组失误度求和得到第二组结果 更可靠。为了进一步优化评酒员评分,利用根据失误度对评酒员排序,跨组选取失误度 最小的 10 位评酒员组成新的评分组,其平均值认为比第二组更可靠,作为整个文章中 评价葡萄酒质量的标准指标。 在问题二中,由于红、白葡萄的理化指标有较大差异,分开考虑红白两种葡萄酒: 对于红葡萄酒,对应问题一得出的葡萄酒质量指标,从三个角度,即外观分析(又分为 由大分子因子决定的澄清度和基于 LAB 色彩模型的色调考虑到指标间存在的竞争关系 采用非线性回归分析和逐步回归分析) 、香气分析(Fisher 线性判别分析)和口感分析 (主成分分析和因子分析) ,后进行异常点检验,逐一剔除异常点来求解酿酒葡萄的量 化指标。对于白葡萄酒的三个指标采用 Fisher 判别分析求解。最后将三个方面得分加权 平均得到酿酒葡萄量化的总分,进行聚类分析,根据聚类分析结果将红葡萄和白葡萄各 分为四级。 在问题三中,为研究酿酒葡萄与葡萄酒的理化指标之间的联系,将葡萄酒的理化指 标用酿酒葡萄的理化指标来表示。根据指标间的相关性,剔除部分相关性不强的指标, 选择部分相关性较好的酿酒葡萄的指标作为自变量, 对不同的葡萄酒指标分别进行多元 线性回归、逐步回归和回归检验。根据指标本身的特点及 AIC 信息统计量,剔除不显著 的自变量,而达到用尽量少的葡萄的理化指标来表示葡萄酒的理化指标的目的。在求解 过程中,建立典型相关分析模型来分析红葡萄酒色泽指标间的关系,利用主成分分析将 白葡萄的多个指标综合为少数几个主成分,再进行回归分析。模型求解结果显示,葡萄 酒的每个指标都能用部分葡萄的指标来线性表示,且具有较好的拟合效果。 在问题四中,为了分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,结合问 题一、二、三的结果以及理化指标和芳香物质的化学意义,综合评估各个广义上的理化 指标(附件二和附件三) ,针对红葡萄酒和白葡萄酒的区别分别在酿酒葡萄和葡萄酒的 理化指标中选取对葡萄酒质量影响较大的指标, 通过线性回归分析将理化指标和葡萄酒 质量进行拟合,从而得出酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响。为进一步 论证结果,首先,对模型进行残差分析以及拟合情况分析;其次,用分组样本检验方法, 将白葡萄酒的 28 个样本数据分成两组,采用用一组进行拟合,另一组进行结果回带分 析的方式,进一步论证用葡萄和葡萄酒的理化指标来评价葡萄酒的质量的可靠性。通过 论证分析得出结论:葡萄和葡萄酒的理化指标可以用来评价葡萄酒的质量,但也有其不 足之处,如当从葡萄酒食用性方便角度考虑,用评酒员评价方法就更直接。 关键词:葡萄酒质量 识别聚类 失误度 非线性回归 逐步回归 Fisher 判别分析 主成 分分析 因子分析 显著性检验 残差分析 异常点检测
2012年数学建模A题资料

(一)葡萄酒观察方法1 酒液总体观察1.1 澄清度观察衡量葡萄酒澄清程度的指标有透明度、浑浊度等,与之相关的指标还有是否光亮、有无沉淀等。
优良的葡萄酒必须澄清、透明(色深的红葡萄酒例外)、光亮。
a.澄清:是衡量葡萄酒外观质量的重要指标。
澄清表示的是葡萄酒明净清澈、不含悬浮物。
通常情况下,澄清的葡萄酒也具有光泽。
b.透明度:表示的是葡萄酒允许可见光透过的程度。
红葡萄酒如果颜色很深,则澄清的葡萄酒也不一定透明。
c.浑浊度:表示的是葡萄酒的浑浊程度,浑浊的葡萄酒含有悬浮物。
葡萄酒的浑浊往往是由微生物病害、酶破败或金属破败引起的。
浑浊的葡萄酒其口感质量也差。
d.沉淀:指的是从葡萄酒中析出的固体物质。
沉淀是由于在陈酿过程中,葡萄酒构成成份的溶解度变小引起的,一般不会影响葡萄酒的质量。
1.2 颜色观察葡萄酒的颜色受酒龄影响,新红葡萄酒由于源于果皮花色素苷的作用,通常颜色鲜艳,为紫红色和宝石红色,带紫色色调;在葡萄酒的成熟过程中,丹宁逐渐与游离花色素苷等结合而使成年葡萄酒带有黄色色调。
瓦红或砖红色为成年红葡萄酒的常有的颜色,而棕红色则为在瓶内陈酿10年以上的红葡萄酒的颜色。
因此,可根据颜色,判断葡萄酒的成熟状况。
葡萄酒的颜色和口感的变化存在着平行性,颜色和口感之间必须相互协调平衡。
颜色的深浅反应葡萄酒的结构、丰满度以及尾味和余味。
如在红葡萄酒中,颜色的深浅与丹宁的含量往往正相关。
如果红葡萄酒颜色深而浓,几乎处于半透明状态,多数情况下它必然醇厚、丰满、丹宁感强。
相反,色浅的葡萄酒,则味淡、味短。
当然,如果较柔和,具醇香,仍不失为好酒。
例如瓦红色的红葡萄酒,必须与浓郁的醇香和柔顺的口感同时存在,否则表明该酒是人工催熟条件下陈酿而未能表现出最佳感官质量。
带紫色的新葡萄酒往往口味平淡、瘦弱、尖酸、粗糙;褐色过重的成年葡萄酒,氧化过重、老化。
1.3 浑浊度观察观察葡萄酒有无下列情况:略失光,失光,欠透明,微混浊,极浑浊,雾状混浊,乳状混浊;1.4 沉淀观察观察葡萄酒有无下列情况:有无沉淀,沉淀类型:纤维状沉淀,颗粒状沉淀,絮状沉淀,酒石结晶,片状沉淀,块状沉淀。
2012数学建模葡萄酒原题

2012数学建模葡萄酒原题【正文】2012数学建模葡萄酒原题葡萄酒是一种历史悠久且备受喜爱的饮品,它也是经济学家和数学建模者们研究的对象之一。
在2012年的数学建模竞赛中,与葡萄酒相关的题目引发了广泛的讨论和研究。
本文将围绕这个题目展开阐述,并探讨葡萄酒在经济学和数学建模中的应用。
1. 葡萄酒行业概述葡萄酒作为一种高级饮品,具有独特的制作工艺和品质要求。
葡萄种植、酿造和销售是葡萄酒行业的三大环节。
葡萄种植需要考虑气候、土壤和品种等因素,而酿造则需要精确的工艺控制和时间管理。
销售方面,葡萄酒的价格受到供需关系、品牌价值以及市场营销因素的影响。
2. 葡萄酒供需模型葡萄酒供需模型是研究葡萄酒市场供求平衡关系的重要工具。
它基于市场上的供求曲线,考虑了价格、消费者偏好和生产成本等因素。
通过分析供需模型,我们可以预测葡萄酒市场的供给量和价格波动情况,为决策者提供参考。
3. 葡萄酒评分模型葡萄酒评分模型是对葡萄酒品质进行客观评价和分类的工具。
通常,葡萄酒的品质评分基于口感、香气和口感等方面进行评估。
评分模型可以帮助葡萄酒酿造商根据评估结果进行改良和调整,以提高产品质量和市场竞争力。
4. 葡萄酒预测模型葡萄酒预测模型是基于历史数据和市场趋势进行葡萄酒销售和需求预测的工具。
借助数学建模方法和统计学分析,我们可以预测不同品种和产地的葡萄酒在未来的销售趋势,并作出相应的调整和安排。
5. 葡萄酒市场策略在竞争激烈的葡萄酒市场中,制定有效的市场策略至关重要。
数学建模可以帮助分析市场份额、品牌竞争力、产品定价和市场推广等因素,为企业制定合适的市场策略提供指导。
6. 葡萄酒运输和配送优化葡萄酒的运输和配送环节也是影响葡萄酒行业效益的重要因素之一。
通过数学建模和优化方法,我们可以对葡萄酒运输网络和配送路径进行优化,以减少成本和时间,并提高运输效率。
7. 葡萄酒消费者行为分析葡萄酒消费者行为分析可以帮助了解消费者对葡萄酒的选择、购买和消费习惯。
2012年数学建模竞赛A题答案参考

22012高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):A题:葡萄酒的评价一、摘要确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
附件1给出了某一年份一些葡萄酒的评价结果,附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。
请尝试建立数学模型讨论下列问题:1. 分析附件1中两组评酒员的评价结果有无显著性差异,哪一组结果更可信?2. 根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。
3. 分析酿酒葡萄与葡萄酒的理化指标之间的联系。
4.分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量?附件1:葡萄酒品尝评分表(含4个表格)附件2:葡萄和葡萄酒的理化指标(含2个表格)附件3:葡萄和葡萄酒的芳香物质(含4个表格)本文针对灾情巡视路线问题,通过分块的方法,建立了动态规划模型,成功的解决了分组数,最短时间和最佳巡视路线问题。
对于问题一:我们先通过Prime 算法求出了最小生成树,通过初步观察将其分为三块,在每块中寻找最优回路,并计算出每条回路的长度。
同时我们建立了巡视路线均衡度评估体系和动态规划模型,通过均衡度的大小来对每个回路及回路之间的顶点进行调整,最终求解出最佳的三条巡视路线,并求出了巡视路线的均衡度0.0785a =。
分组巡视路线如下:123:1343532313329302827242326:2521171622181151413192025:34891012117652L O B A A R Q Q N P O L O M K K J L M O L O C D E F F H G E O--------------------------------------------------------------对于问题二:在考虑了巡视人员在各乡镇及村停留的时间,还有汽车行驶速度的基础上,我们确定了组数和最短巡视路程的约束关系min173524T t m V++≤,采用了逐步讨论法,先对3m =的情况进行了检验,得知不满足条件,再对4m =的情况进行了讨论,最终我们确定了最小组数为4,并求出了最佳的四条巡视路线及每条巡视路线所需要的时间,其中巡视时间的均衡度为:0.088b =。
2012年全国大学生数学建模竞赛A题(葡萄酒理化指标与质量的评鉴分析,获全国二等奖)

葡萄酒理化指标与质量的评鉴分析摘要用好的葡萄也许酿不出好酒,但没人能用劣质葡萄酿出好酒。
巧妇难为无米之炊,再优秀的酿酒师,如果没有优质的葡萄,也很难酿出好酒。
不同葡萄品种酿制出的葡萄酒是不同的,但是,除了品种间的差异,葡萄自身的质量是酿制高品质葡萄酒的关键。
本文通过建立meansK-聚类模型、典型相关分析等模型,逐步探求用葡萄和葡萄酒的理化指标来评鉴葡萄酒质量的方法。
问题一要求我们分析附件1中两组评酒员的评价结果是否存在显著性差异,为此我们依据小概率原理建立模型Ⅰ-显著性检验模型。
首先我们利用F检验求解两组评酒员之间是否存在显著性差异,再利用配对t检验对检验样本做再次检验,以提高研究效率,确保评价结果的准确性。
利用Excel软件处理数据后,进行t、F的联合检验,当联合检验均被接受,得到两组评酒员的评价结果有显著性差异的结论。
同时通过对两组品酒员对55种葡萄酒样品评分的稳定性、统一性分析,确定第二组品酒员的评价结果更可信。
针对问题二本文根据附件2提供的数据,利用模糊数学原理[3],建立模型ⅢK-聚类模型,对酿酒葡萄进行分类,再以葡萄酒品尝评分作为质量评价依据,means对酿酒葡萄进行分级。
首先,考虑到酿酒葡萄的理化指标过多,不便分类,我们利用多元统计分析原理对红、白酿酒葡萄进行主成分分析,得出红、白酿酒葡萄分别有8个和11个主成分,从而大大减少了分类指标。
再利用meansK-算法求出最佳聚类数k,建立meansK-聚类模型对各种葡萄样品在各个主成分上的得分进行聚类,将红、白葡萄样品分别划分为3类和4类。
最后,根据每个类别中葡萄样品对应的葡萄酒的品尝评分,对各类酿酒葡萄进行分级。
针对问题三建立模型Ⅳ-典型相关分析模型,定量分析酿酒葡萄与葡萄酒的理化指标之间的联系。
我们首先选取酿酒葡萄与葡萄酒皆含有的花色苷、单宁等成分作为理化指标,然后构建典型相关分析模型,研究酿酒葡萄与葡萄酒两组样品的理化指标之间的相关性。
2012数学建模A题葡萄酒答案
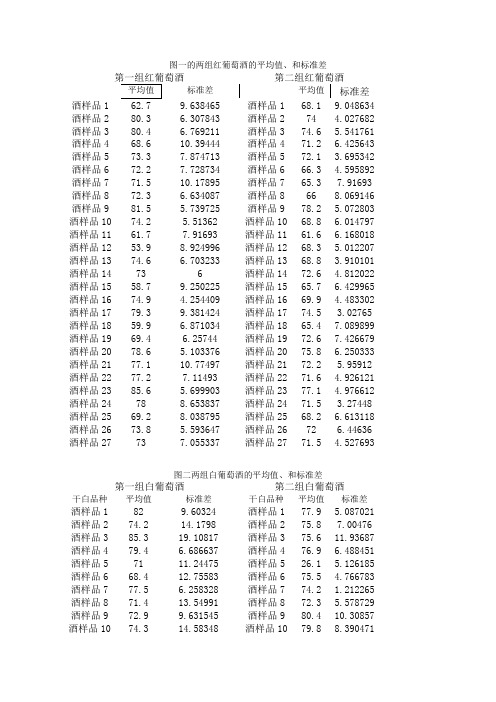
图一的两组红葡萄酒的平均值、和标准差第二组红葡萄酒标准差平均值标准差酒样品1 9.638465 酒样品1 68.1 9.048634 酒样品2 80.3 6.307843 酒样品2 74 4.027682 酒样品3 80.4 6.769211 酒样品3 74.6 5.541761 酒样品4 68.6 10.39444 酒样品4 71.2 6.425643 酒样品5 73.3 7.874713 酒样品5 72.1 3.695342 酒样品6 72.2 7.728734 酒样品6 66.3 4.595892 酒样品7 71.5 10.17895 酒样品7 65.3 7.91693 酒样品8 72.3 6.634087 酒样品8 66 8.069146 酒样品9 81.5 5.739725 酒样品9 78.2 5.072803 酒样品10 74.2 5.51362 酒样品10 68.8 6.014797 酒样品11 61.7 7.91693 酒样品11 61.6 6.168018 酒样品12 53.9 8.924996 酒样品12 68.3 5.012207 酒样品13 74.6 6.703233 酒样品13 68.8 3.910101 酒样品14 73 6 酒样品14 72.6 4.812022 酒样品15 58.7 9.250225 酒样品15 65.7 6.429965 酒样品16 74.9 4.254409 酒样品16 69.9 4.483302 酒样品17 79.3 9.381424 酒样品17 74.5 3.02765 酒样品18 59.9 6.871034 酒样品18 65.4 7.089899 酒样品19 69.4 6.25744 酒样品19 72.6 7.426679 酒样品20 78.6 5.103376 酒样品20 75.8 6.250333 酒样品21 77.1 10.77497 酒样品21 72.2 5.95912 酒样品22 77.2 7.11493 酒样品22 71.6 4.926121 酒样品23 85.6 5.699903 酒样品23 77.1 4.976612 酒样品24 78 8.653837 酒样品24 71.5 3.27448 酒样品25 69.2 8.038795 酒样品25 68.2 6.613118 酒样品26 73.8 5.593647 酒样品26 72 6.44636 酒样品27 73 7.055337 酒样品27 71.5 4.527693图二两组白葡萄酒的平均值、和标准差第一组白葡萄酒第二组白葡萄酒干白品种平均值标准差干白品种平均值标准差酒样品1 82 9.60324 酒样品1 77.9 5.087021 酒样品2 74.2 14.1798 酒样品2 75.8 7.00476 酒样品3 85.3 19.10817 酒样品3 75.6 11.93687 酒样品4 79.4 6.686637 酒样品4 76.9 6.488451 酒样品5 71 11.24475 酒样品5 26.1 5.126185 酒样品6 68.4 12.75583 酒样品6 75.5 4.766783 酒样品7 77.5 6.258328 酒样品7 74.2 1.212265 酒样品8 71.4 13.54991 酒样品8 72.3 5.578729 酒样品9 72.9 9.631545 酒样品9 80.4 10.30857 酒样品10 74.3 14.58348 酒样品10 79.8 8.390471酒样品11 72.3 13.30873 酒样品11 71.4 9.371351 酒样品12 63.3 10.76052 酒样品12 72.4 11.83404 酒样品13 65.9 13.06777 酒样品13 73.9 6.838616 酒样品14 72 10.68748 酒样品14 77.1 3.984693 酒样品15 72.4 11.4717 酒样品15 78.4 7.351493 酒样品16 74 13.34166 酒样品16 53.1 9.06826 酒样品17 78.8 12.00741 酒样品17 80.3 6.201254 酒样品18 73.1 12.51177 酒样品18 76.7 5.498485 酒样品19 72.2 6.811755 酒样品19 76.4 5.103376 酒样品20 77.8 8.024961 酒样品20 43.2 7.07421 酒样品21 76.4 13.14196 酒样品21 79.2 8.024961 酒样品22 71 11.77568 酒样品22 79.4 7.321202 酒样品23 75.9 6.607235 酒样品23 77.4 3.405877 酒样品24 73.3 10.54145 酒样品24 76.1 6.208417 酒样品25 77.1 5.820462 酒样品25 79.5 10.31988 酒样品26 81.3 8.53815 酒样品26 74.3 7.532168 酒样品27 64.8 12.01666 酒样品27 77 5.962848 酒样品28 81.3 8.969702 酒样品28 79.6 5.037636描述统计量N 均值标准差方差统计量统计量标准误统计量统计量VAR00003 27 68.5185 1.50722 7.83174 61.336 VAR00004 27 74.4444 2.24201 11.64980 135.718 VAR00005 27 72.7037 2.70265 14.04338 197.217 VAR00006 27 65.2963 1.44393 7.50290 56.293 VAR00007 27 74.1852 2.64469 13.74223 188.849 VAR00008 27 72.7037 2.13091 11.07254 122.601 VAR00009 27 71.2222 1.51002 7.84628 61.564 VAR00010 27 72.0741 1.95456 10.15619 103.148 VAR00011 27 78.4444 1.23035 6.39311 40.872 VAR00012 0Zscore(VAR00003) 0Zscore(VAR00004) 0Zscore(VAR00005) 0Zscore(VAR00006) 0Zscore(VAR00007) 0Zscore(VAR00008) 0Zscore(VAR00009) 0Zscore(VAR00010) 0Zscore(VAR00011) 0Zscore(VAR00012) 0描述统计量N 均值标准差方差统计量统计量标准误统计量统计量VAR00003 27 68.5185 1.50722 7.83174 61.336 VAR00004 27 74.4444 2.24201 11.64980 135.718 VAR00005 27 72.7037 2.70265 14.04338 197.217 VAR00006 27 65.2963 1.44393 7.50290 56.293 VAR00007 27 74.1852 2.64469 13.74223 188.849 VAR00008 27 72.7037 2.13091 11.07254 122.601 VAR00009 27 71.2222 1.51002 7.84628 61.564 VAR00010 27 72.0741 1.95456 10.15619 103.148 VAR00011 27 78.4444 1.23035 6.39311 40.872 VAR00012 0Zscore(VAR00003) 0Zscore(VAR00004) 0Zscore(VAR00005) 0Zscore(VAR00006) 0Zscore(VAR00007) 0Zscore(VAR00008) 0Zscore(VAR00009) 0Zscore(VAR00010) 0Zscore(VAR00011) 0Zscore(VAR00012) 0有效的 N (列表状态)0模型描述模型名称MOD_2因变量 1 VAR000032 VAR000073 VAR000054 VAR000115 VAR00008方程 1 二次自变量VAR00004常数包含其值在图中标记为观测值的变量未指定用于在方程中输入项的容差.0001个案处理摘要N变量处理摘要变量因变量自变量VAR00003 VAR00007 VAR00005 VAR00011 VAR00008 VAR00004 正值数27 27 27 27 27 27 零的个数0 0 0 0 0 0 负值数0 0 0 0 0 0 缺失值数用户自定义缺失0 0 0 0 0 0 系统缺失0 0 0 0 0 0模型描述模型名称MOD_2因变量 1 VAR000032 VAR000073 VAR000054 VAR000115 VAR00008方程 1 二次自变量VAR00004常数包含其值在图中标记为观测值的变量未指定用于在方程中输入项的容差.0001个案处理摘要N个案总数27已排除的个案a0模型描述模型名称MOD_2因变量 1 VAR000032 VAR000073 VAR000054 VAR000115 VAR00008方程 1 二次自变量VAR00004常数包含其值在图中标记为观测值的变量未指定用于在方程中输入项的容差.0001模型描述模型名称MOD_2因变量 1 VAR000032 VAR000073 VAR000054 VAR000115 VAR00008方程 1 二次自变量VAR00004常数包含其值在图中标记为观测值的变量未指定用于在方程中输入项的容差.0001。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):54所属学校(请填写完整的全名):齐鲁师范学院参赛队员(打印并签名) :1. 官震2. 董军卫3. 耿敏敏指导教师或指导教师组负责人(打印并签名):马燕日期: 2012 年 9 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):葡萄酒的评价摘要本文对于葡萄酒的评价问题进行了研究,主要用到了层次分析法、模糊综合评价法、数据的拟合等方法,利用SPSS、MATLAB和EXCEL等软件对题目所给的数据进行了一系列的处理,进行了分析。
对于问题一:我们综合考虑了影响评酒员评判的因素,以及附录一的资料,采用综合分析法,和参数假设检验中的t检验,建立计算模型,比较了两组评酒员对红葡萄酒和白葡萄酒的评价结果,分析出了第二组的结果更加可靠。
对于问题二:对于附录二中的大量数据我们采用主成分分析法分析出了酿酒葡萄理化指标的重要指标,求出各理化指标的平均值,比较了酿酒葡萄的理化指标和葡萄酒的质量(我们认为葡萄酒的质量即为评酒师对葡萄酒的所有评分的平均值)的大量数据,使用波士顿矩阵,对比及分析得出对酿酒葡萄的分级,即将酿酒葡萄分成了四级。
对于问题三:我们将酿酒葡萄与葡萄酒的理化指标中选取主要指标,并且分别以酿酒葡萄的理化指标和葡萄酒的理化指标为自变量和因变量,使用数据拟合的方法,首先画出数据的散点图,然后观察、分析散点图的形状,在此基础上选择几种合适的曲线分别拟合,通过比较,看哪条曲线的最小二乘指标J最小,最小者即为最好的拟合曲线,使用MATLAB软件,通过拟合曲线假设出通过自变量与因变量的一组观察值来确定拟合函数中待定系数的方法,使得最小二乘指标J最小,从而判断出酿酒葡萄和葡萄酒的理化指标之间的联系为)4(2 分布对于问题四:我们将红(白)酿酒葡萄的理化指标和芳香物质的数据分别与葡萄酒的质量进行比较,并且同理比较红(白)葡萄酒的理化指标和芳香物质的数据分别与葡萄酒的质量进行比较,使用SPSS软件将这些数据进行相关性检验,通过判断相关性的数据来考虑酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,取出相关性数据大的因素,并将它判断为能评价葡萄酒的质量,如若各个因素的相关性数据相同或者相差不大,则判断这些因素均能评价葡萄酒的质量。
关键词:模糊综合评价数据拟合主成分分析模糊数学波士顿矩阵一、问题重述随着葡萄酒在生活中的需求越来越多质量越来越高,酒厂在确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
因此,我们就需要解决一个很重要的问题:判断评酒员对评酒的可信度。
而酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
现在我们就建立数学模型讨论下列问题:问题一:分析附件1中两组评酒员的评价结果有无显著性差异,哪一组结果更可信?问题二:根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。
问题三:分析酿酒葡萄与葡萄酒的理化指标之间的联系。
问题四:分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量?二、模型假设1.评酒员在外观分析时候,不考虑不同评酒员在评酒时的位置、光线2.评酒员在香气分析的时候,不考虑不同评酒员离玻璃酒杯的偏差距离3.评酒员在口感分析的时候,不考虑个人对品酒的不同标准4.附录中与正常数据之间相差很大的数据或存在缺失变量现象,我们在计算中适当舍弃5.选取可信度高的一组作为依据,续做后题6.不考虑总体的主要成分与各个酒样的主要成分之间的差别7.经过主成分分析得出十个主要成分,选取主要成分中的前六个进行分析8.在处理数据时我们采用的是四舍五入的方法,保存到小数点后四位三、符号说明μ——所有的评酒师对抽样的红葡萄酒样品评分的均值红μ——所有的评酒师对抽样的白葡萄酒样品评分的均值白μ——评酒师对一组中红葡萄酒评分的均值红1μ——评酒师对二组中红葡萄酒评分的均值2红μ——评酒师对一组中白葡萄酒评分的均值白1μ——评酒师对二组中白葡萄酒评分的均值2白2σ——评酒师对抽样的红葡萄酒样品和白葡萄酒样品评分的方差,评酒师对一组和二组中红葡萄酒和白葡萄酒评分的方差1n ——28个第一组白样品酒所有评酒师的评分 2n ——28个第二组白样品酒所有评酒师的评分21*1n S ——第一组白葡萄酒的方差的无偏估计22*2n S ——第二组白葡萄酒的方差的无偏估计t ——统计量M ——白酿酒葡萄主要的理化指标比例的均值 N ——红酿酒葡萄主要的理化指标比例的均值i δ——第i 个点的拟合值与实际值得绝对误差)(i x f ——第i 个点的拟合值 i y ——第i 个点的实际值四、模型建立4.1问题一的模型及结果模型一:我们通过对数据的分析,利用正态分布等方法来找到两组评酒员评价结果中的差异。
在判断哪组结果更可信的过程中,我们首先求出所有的评酒师对抽样的红葡萄酒样品和白葡萄酒样品评分的均值红μ,白μ和方差2σ。
然后,我们再分别求出评酒师对一组和二组中红葡萄酒和白葡萄酒评分的均值,红1μ和方差2σ。
现在我们假定评酒师对抽样的红葡萄酒样品和白葡萄酒样品评分和评酒师对一组和二组中红葡萄酒和白葡萄酒评分的方差相等设1ξ,2ξ,....,1n ξ是取自正态母体N (1μ,2σ)的子样,1η,32,,ηη 是取自正态母体N (2μ,2σ)的子样。
并且这两个子样相互独立,2σ是未知常数。
现在要检验假设0H :1μ=2μ,1H :1μ≠2μ.令这两个子样的均值与方差的无偏估计分别为:in i i n i n n ηηξξ2112111,1==∑=∑=211*1)(11121ξξ-∑-==i n i n n S212*2)(11222ηη-∑-==i n i n n S如果原假设0H :1μ-2μ=0为真,那么ηξ-应该在零的周围随机的摆动,则可选取这样的统计量2111n n S t w+-=ηξ,其中2)()1(21*212*1122221-+-+-=n n S n n S n S n n w,统计量t 在0H 为真时服从自由度为221-+n n 的t 分布。
给出显著性水平α(0.0005) ,在0H 为真下αα=-+≥-))2((21210n n t t P H这里)2(2121-+-n n tα由自由度为221-+n n 的t 分布表查得.若由子样观察值),,,(21n x x x 算出的)2(2121-+≥-n n tt α,则拒绝原假设0H :1μ=2μ,即认为两个母体的均值有显著的差别.否则,没有显著差别。
[1]现在有上述公式计算出所需要的量,将第一二组白葡萄酒的评分的均值与方差和第一二组红葡萄酒的评分的均值与方表1一组白葡萄酒评分的均值 二组白葡萄酒评分的均值两者之差外观分析澄清度 3.2714 3.42 -0.1486 外观分析色调 6.7036 6.79 -0.0864 香气分析纯正度 4.5179 4.52 -0.0021 香气分析浓度 6.3643 6.32 0.0443 香气分析质量 12.6536 12.6 0.0536 口感分析纯正度 4.0214 4.51 -0.4886 口感分析浓度 5.9107 6.17 -0.2593 口感分析持久性 6.2929 6.33 -0.0371 口感分析质量 15.5607 16.76 -1.1993 平衡/整体评价 8.9643 9.26 -0.2957 平均值 7.42608 7.668 -0.24192表2一组白葡萄酒评分的方差二组白葡萄酒评分的方差一组白葡萄酒评分方差的无二组白葡萄酒评分方差的无偏估计2w St偏估计外观分析澄清度 1.245 0.459 1.2495 0.4606外观分析色调 4.281 1.993 4.2963 2.0001香气分析纯正度 1.068 0.573 1.0718 0.5751香气分析浓度 1.487 1.329 1.4923 1.3338香气分析质量 3.589 2.356 3.6019 2.3644口感分析纯正度 1.247 0.509 1.2515 0.5108口感分析浓度 2.017 1.223 2.0242 1.2274口感分析持久性19.197 0.551 19.266 0.553口感分析质量9.581 5.129 9.6153 5.1474平衡/整体评价 1.081 0.579 1.0849 0.5811平均值 4.3712 1.4701 4.49535 1.4754 10.1043 10.6548 表3一组红葡萄酒评分的均值二组葡萄酒评分的均值两者的差外观分析澄清度 3.41 3.4926 -0.0826 外观分析色调7.13 6.3185 0.8115 香气分析纯正度 4.31 4.1519 0.1581 香气分析浓度 5.88 5.6704 0.2096 香气分析质量12.26 11.7704 0.4896 口感分析纯正度 4.03 3.9667 0.0633 口感分析浓度 5.72 5.5185 0.2015 口感分析持久性 5.92 5.8185 0.1015 口感分析质量15.39 15.0444 0.3456 整体评价8.79 8.763 0.027 平均值7.284 7.05149 0.23251 表4一组红葡萄酒评分的方差二组红葡萄酒评分的方差一组的方差无偏估计二组的方差无偏估计Sw T外观分析澄清度 1.085 0.392 1.0892 0.3935 外观分析色调 3.52 3.155 3.5336 3.1667 香气分析纯正度 1.266 0.642 1.2709 0.6444 香气分析浓度 1.951 1.404 1.9585 1.4092 香气分析质量 4.256 2.311 4.2724 2.3196口感分析纯正度1.076 0.434 1.0802 0.4356 口感分析浓度2.011 1.358 2.0188 1.363 口感分析持久性0.805 0.58 0.8081 0.5822 口感分析质量 7.66 4.169 7.6896 4.1845 整体评价 0.94 0.464 0.9436 0.4657平均值 2.4571.49092.46651.49641.73971.5382由表1和表2221-+n n ,由t 检验的临界值表可以查得当100050021≤+≤n n 时,581.2))2((586.221210≤-+≥≤-n n tt P H α,也就是说,)2(6548.102121-+≥=-n n tt α,即拒绝原假设,认为两个母体的均值有显著的差别,即第一组和第二组白葡萄酒评酒员的评价结果有显著性差异;并且,由方差4701.13712.4>可得第二组的评酒员的评价结果更可信。
