2016年全国大学生数学建模竞赛试题D
2016数学建模国赛赛题

2016数学建模国赛赛题
2016年数学建模国赛赛题一般是指《数学建模入门教程》中的赛题,主要
有以下三类:
1. 问题一:水深测量与海洋动力现象模拟。
要求:使用集中质量法将系统中的各个物体视为一个质点,对各个物体建立静力平衡方程,在水深18m时给定浮标在海水中所受浮力,从而根据建
立的平衡方程求出各物体的倾斜角度,再根据几何关系求出海域的模拟深度。
通过不断修正浮标的浮力,使得海域的模拟深度等于18m,最终求得风速
分别为12m/s和24m/s时浮标的吃水深度和各节钢管的倾斜角度。
2. 问题二:交通流模型与小区开放对周边道路通行的影响。
要求:利用元胞自动机的方法,分别分析不同道路车量位置与车流量变化、负荷系数以及基于交通流的车速。
先对不同小区进行划分,再利用问题一的方法和结论,分别模拟不同小区、不同路段开放小区对车辆通行情况的分析。
最后根据第一问选取出的六个指标,依据其计算公式,分别得出所有样本的所有指标值。
再根据这些指标值,利用投影寻踪法,得到不同小区、不同路段下,开放小区对周围道路通行的影响。
3. 问题三: Braess 悖论。
要求:对于这个问题没有给出具体的要求,因为这是一个理论问题,主要探讨的是网络流理论中的一个著名悖论。
请注意,由于题目较为复杂,建议在数学建模课程或相关论坛中寻找更详细的解答。
2016年全国大学生数学建模竞赛题
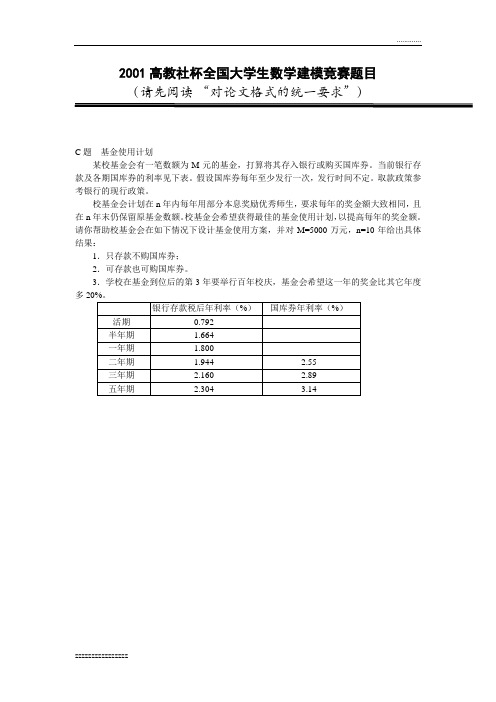
2001高教社杯全国大学生数学建模竞赛题目(请先阅读“对论文格式的统一要求”)C题基金使用计划某校基金会有一笔数额为M元的基金,打算将其存入银行或购买国库券。
当前银行存款及各期国库券的利率见下表。
假设国库券每年至少发行一次,发行时间不定。
取款政策参考银行的现行政策。
校基金会计划在n年内每年用部分本息奖励优秀师生,要求每年的奖金额大致相同,且在n年末仍保留原基金数额。
校基金会希望获得最佳的基金使用计划,以提高每年的奖金额。
请你帮助校基金会在如下情况下设计基金使用方案,并对M=5000万元,n=10年给出具体结果:1.只存款不购国库券;2.可存款也可购国库券。
3.学校在基金到位后的第3年要举行百年校庆,基金会希望这一年的奖金比其它年度多摘要:运用基金M分成n份(M1,M2,…,Mn),M1存一年,M2存2年,…,Mn存n 年.这样,对前面的(n-1)年,第i年终时M1到期,将Mi及其利息均取出来作为当年的奖金发放;而第n年,则用除去M元所剩下的钱作为第n年的奖金发放的基本思想,解决了基金的最佳使用方案问题.关键词:超限归纳法;排除定理;仓恩定理1问题重述某校基金会有一笔数额为M元的基金,欲将其存入银行或购买国库券.当前银行存款及各期国库券的利率见表1.假设国库券每年至少发行一次,发行时间不定.取款政策参考银行的现行政策.表1 存款年利率表校基金会计在n年内每年用部分本息奖励优秀师生,要求每年的奖金额大致相同,且在n年末仍保留原基金数额.校基金会希望获得最佳的基金使用计划,以提高每年的奖金额.需帮助校基金会在如下情况下设计基金使用方案,并对M=5 000万元,n=10年给出具体结果:①只存款不购国库券;②可存款也可购国库券.③学校在基金到位后的第3年要举行百年校庆,基金会希望这一年的奖金比其它年度多20%.2模型的分析、假设与建立2.1模型假设①每年发放的奖金额相同;②取款按现行银行政策;③不考虑通货膨胀及国家政策对利息结算的影响;④基金在年初到位,学校当年奖金在下一年年初发放;⑤国库券若提前支取,则按满年限的同期银行利率结算,且需交纳一定数额的手续费;⑥到期国库券回收资金不能用于购买当年发行的国库券.2.2符号约定K——发放的奖金数;ri——存i年的年利率,(i=1/2,1,2,3,5);Mi——支付第i年奖金,第1年开始所存的数额(i=1,2,…,10);U——半年活期的年利率;2.3模型的建立和求解2.3.1情况一:只存款不购国库券(1)分析令:支付各年奖金和本金存款方案———Mij (i =1,…,10,i ;j 属于N ). 将各方案ij M 看成元素,构成集合A则ij M 属于A1,210;I =所以A 按I 取值分10行根据仓恩定理:分行集中,任何一单行有上界,则必包含一个极大元素。
2016数学建模d题

2016数学建模d题摘要:一、数学建模简介1.数学建模的定义2.数学建模的重要性3.数学建模的应用领域二、2016 数学建模D 题背景及内容1.题目背景2.题目内容3.题目难度及挑战三、解题思路及方法1.问题分析2.解题思路3.常用数学建模方法四、2016 数学建模D 题案例分析1.案例一2.案例二3.案例三五、总结与反思1.2016 数学建模D 题的启示2.数学建模能力的培养3.对未来数学建模比赛的展望正文:数学建模是一种运用数学方法解决实际问题的过程,它涉及到多个学科领域,如统计学、计算机科学、经济学等。
数学建模在现代社会具有很高的实用价值,可以帮助我们更好地理解世界、预测未来和优化决策。
在我国,数学建模竞赛是一项重要的赛事,吸引了大量的高校学生参与。
2016 年的数学建模D 题以“飞行器航迹优化问题”为背景,要求参赛者针对给定的飞行器、目标和航路约束条件,设计出一种飞行器航迹优化算法。
该题目具有一定的难度和挑战性,需要参赛者具备较强的数学功底和实际问题解决能力。
在解题过程中,首先要对题目进行深入分析,明确问题的关键信息和隐含条件。
然后根据问题特点,选择合适的解题思路和方法。
常用的数学建模方法有:线性规划、动态规划、遗传算法、模拟退火算法等。
为了更好地理解2016 数学建模D 题,我们可以通过以下三个案例进行分析:案例一:采用线性规划方法求解飞行器航迹优化问题。
通过建立线性目标函数和约束条件,求解最优航迹。
该方法简单易行,但对于复杂问题可能无法得到全局最优解。
案例二:利用动态规划方法解决飞行器航迹优化问题。
通过将问题拆分为子问题,并采用动态规划的思想,逐步求解子问题,最终得到全局最优解。
该方法在时间复杂度上具有优势,但在空间复杂度上可能较高。
案例三:采用遗传算法求解飞行器航迹优化问题。
通过模拟自然界的生物进化过程,对飞行器航迹进行迭代优化。
遗传算法具有全局搜索能力,能够较快地找到最优解,但可能受初始种群和参数设置的影响。
2016高教社杯全国大学生数学建模竞赛题目

电池剩余放电时间预测摘要铅酸电池的剩余放电时间是电池性能指标中的一个重要参数,对电池的输出性能和使用寿命有着至关重要的影响。
但是在生活中不免遇到电池用完了却没有备用电池的情况,而且电池的使用时间在我们生活中与我们息息相关,有时候这会给我们的生活造成很大的困扰。
本文就是对电池剩余电量和放电时间的矛盾进行讨论得出一个相对准确的电池剩余放电时间预测的一个模型的建立。
针对问题一:电池的剩余放电量这一问题。
首先,根据题目我们得知铅酸电池在放电过程中电流时恒定的,并且铅酸电池的额定保护电压是9V ,我们根据{附件一}给出的数据进行分析,然后利用MATLAB 软件进行图像拟合,得到一个电压与时间的放电曲线图,并且,根据MATLAB 软件拟合得出的图像,经过figure 对图像的精确处理,最终得出初等函数来表示各放电曲线。
又根据平均相对误差定义得出:平均相对误差(MRE 是预测误差相对值的平均值,其计算公式为:)'|i i |1j j j j MRE n i -=∑根据公式和附件一中给出的数据按照比例筛选出231组数据【附件二】,并对数据进行处理,我们分别求出各放电曲线的平均相对误差。
并且根据测得电压都为9.8V 时,根据模型得出电池剩余放电时间分别是多少。
针对问题二:根据数据拟合的曲线图像得出三种情况进行讨论。
用初等函数表示A20-A100的放电曲线,并根据放电曲线的平均相对误差。
然后分别求出它们剩余放电时间。
然后我们利用求平均数的方法大概绘制出55A 的曲线图。
针对问题三:根据附件2中的数据,利用Excel 表格数据整理得出图形【附件三】,分析并计算得出模型1、模型2,通过优化得出模型3。
由于同一电池在不同衰减状态下,在同一电流强度情况下从充满电开始放电,时间随电压不断变化,所以我们从电压方面进行具体分析。
一.问题重述铅酸电池作为电源被广泛用于工业、军事、日常生活中。
在铅酸电池以恒定电流强度放电过程中,电压随放电时间单调下降,直到额定的最低保护电压(Um )。
全国大学生数学建模竞赛D题解析

汇报人:
CONTENTS
PRT ONE
PRT TWO
竞赛名称:全国大学生数学建模竞 赛
竞赛目的:培养大学生数学建模能 力提高解决实际问题的能力
添加标题
添加标题
竞赛级别:国家级
添加标题
添加标题
竞赛影响:促进大学生数学建模技 术的发展选拔优秀人才
竞赛起始于XXXX年 每年举办一次 参赛对象为全国大学生 竞赛目的是提高大学生数学建模能力和科技创新能力
组建合适的团队分工明确
制定详细的计划合理安排时间
充分准备所需的知识和技能
准备阶段:研究 题目收集资料建 立模型
实施阶段:编程 实现模拟实验优 化模型
总结阶段:撰写 论文整理思路提 炼经验
反思阶段:总结 得失分析原因改 进策略
赛题分析:对竞赛题目进行深入剖析明确解题思路和要点 经验教训:总结竞赛过程中遇到的问题和不足提出改进措施 团队协作:评估团队成员在竞赛中的表现和贡献提出优化建议 未来规划:根据竞赛经验和教训制定个人和团队未来的学习和发展计划
模型验证:通过对比实际数据和模型预测结果对模型的准确性和可靠性进行评估和改进
数据清洗:去除异常值、缺失值和重复值 数据筛选:根据需求筛选有效数据 数据转换:对数据进行必要的转换以适应分析需求 数据可视化:通过图表、图像等形式直观展示数据
确定问题类型和目 标函数
确定算法的输入和 输出
设计算法的流程图 和伪代码
培养团队协作精神 提升大学生数学应用能力
促进学科交叉融合
为国家和社会培养创新型人 才
PRT THREE
题目背景:全国大学生数学建模竞赛D题 题目要求:分析D题所涉及的数学建模方法和技巧 题目内容:对D题进行解析包括问题分析、模型建立、求解过程等 题目难度:对D题的难度进行评估并给出解题建议
2016数学建模d题

2016数学建模d题(最新版)目录1.2016 年数学建模竞赛 D 题概述2.题目背景及要求3.题目分析4.解题思路与方法5.结论正文【2016 年数学建模竞赛 D 题概述】2016 年数学建模竞赛 D 题是一道涉及运筹学、图论和最短路径问题的题目,要求参赛选手具备一定的数学基础和编程能力。
题目要求参赛选手分析一个快递公司的运营情况,通过构建数学模型来优化快递员的派送路线,从而提高派送效率。
【题目背景及要求】随着电子商务的快速发展,快递行业也呈现出高速增长的态势。
为了降低运营成本、提高服务质量,快递公司需要对快递员的派送路线进行合理规划。
题目要求参赛选手根据给定的城市地图、快递员的位置、派送任务以及时间限制等因素,构建一个最优的派送路线。
【题目分析】题目的核心是要求建立一个最优的派送路线,可以通过图论中的最短路径问题来解决。
首先,将城市地图抽象为一个加权图,其中节点表示快递员的位置,边表示相邻位置之间的距离。
然后,通过最短路径算法(如Dijkstra 算法或 A*算法)求解从快递员位置到所有派送任务的最短路径,从而得到最优派送路线。
【解题思路与方法】1.根据题目给出的数据,构建城市地图的加权图模型。
2.选择合适的最短路径算法(如 Dijkstra 算法或 A*算法)。
3.编写程序实现最短路径算法,求解从快递员位置到所有派送任务的最短路径。
4.根据求解结果,得到最优派送路线。
【结论】通过以上步骤,可以得到 2016 年数学建模竞赛 D 题的解答。
构建合理的数学模型,结合图论中的最短路径问题,可以有效地解决快递员的派送路线优化问题。
2016数学建模d题

2016数学建模d题【原创实用版】目录A.2016 年数学建模竞赛 D 题概述1.竞赛背景2.题目内容B.题目解析1.题目要求2.解题思路C.竞赛对学生的意义1.提升数学应用能力2.增强团队协作能力3.锻炼问题分析与解决能力D.结论正文【提纲】2016 年数学建模竞赛 D 题概述1.竞赛背景2.题目内容2016 年数学建模竞赛 D 题是一道具有挑战性的题目,它要求参赛选手在规定时间内运用所学的数学知识来解决实际问题。
此次竞赛吸引了众多高校的优秀学生参加,竞争非常激烈。
题目内容涉及多个领域,包括数学、物理、计算机等,要求参赛选手具备较强的综合素质和创新能力。
B.题目解析1.题目要求题目要求参赛选手在规定时间内完成对某一问题的数学建模,并将建立的数学模型应用于实际问题的解决。
参赛选手需要撰写论文,详细阐述问题分析、模型建立、求解过程以及结果验证等环节。
2.解题思路解题思路主要包括以下几个步骤:(1)认真阅读题目,理解题意,明确题目所要求的内容。
(2)根据题目内容,搜集相关资料,对问题进行深入分析,找出问题的关键所在。
(3)建立数学模型,将实际问题转化为数学问题,以便于运用数学方法进行求解。
(4)运用相应的数学方法,对建立的数学模型进行求解,得到问题的解。
(5)对求解结果进行分析,验证模型的正确性和有效性,撰写论文,详细阐述解题过程。
C.竞赛对学生的意义1.提升数学应用能力通过参加数学建模竞赛,学生可以加深对数学知识的理解,提高运用数学知识解决实际问题的能力。
在竞赛过程中,学生需要将所学的数学知识运用到实际问题的解决中,从而提高自己的数学应用能力。
2.增强团队协作能力数学建模竞赛是一个团队赛,参赛选手需要在规定时间内完成对某一问题的数学建模。
在这个过程中,团队成员之间需要保持良好的沟通,发挥各自的专长,共同完成竞赛任务。
因此,参加数学建模竞赛可以增强学生的团队协作能力。
3.锻炼问题分析与解决能力数学建模竞赛要求参赛选手在规定时间内对某一问题进行深入分析,并建立相应的数学模型。
数学建模2016年D题

数学建模2016年D题风电场运行状况分析及优化模型摘要在充分理解题意及合理假设的基础上,通过对问题的深入分析,利用Excel 对数据处理分析,建立了风能资源利用情况模型并对其进行评估;对实测风速和功率的拟合,建立了最优风机选择模型;最后从经济效益最大化为主要目标,通过多目标规划,建立人员分配模型,进行人员排班优化。
·问题一:为了研究该风电场的风能资源和风能资源的利用情况,对附件1的数据处理及分析,然后对原始数据的完整性和合理性进行判断,选择合理数据,计算出年、月、日的平均风速和各时期的平均功率。
根据平均风功率密度公式311()()2nwp i i D v n ρ==∑计算出平均风功率密度为290.39/wp D W m =。
然后对其进行评估,根据wp D 和风的功率wp =n P D S ??风计算出风能利用率为40.92%。
根据贝茨极限得出大型风力发电机对风能的最高利用率为59.3%,从而得出该风电场的风能利用率相对合理,进而可以判断该风电场的风能资源利用情况较好。
·问题二:从风能资源与风机匹配角度出发,根据附件2风速信息,对数据进行聚类分析,并绘制频率分布直方图,并得出一期和二期工程风机的年平均风速均为6/m s 。
根据附件3的数据,通过最小二乘法对各期风速和功率进行数据拟合,得出系数k 越大,发电效果越好。
对附件4中新型电机的参数分析,计算出系数k 值。
最终,得出新型风机功效略好于二期工程,相较一期工程功效略差,因此新型风机比二期风机更适合此风力发电厂,应使一期工程与新型风机作为发电厂设备。
·问题三:以风电场经济效益最大化为主要目标,通过分析风电场的效能为出发点,先确立风机停机维护时段的基础上,再运用“0-1”规划建立人员分配模型,用枚举法得到人员排班方案,从而得到每组两天轮班工作并由在3月4日至5日、8月20日至21日值班人员进行停机维护的工作排班方案。
本文还进一步建立了多目标规划的人员分配模型,并进一步检验,得到值班与提及维护分立进行的模式以每组一天轮流值班并分别于每年的三月上旬和八月下旬进行停机维护,每年两组轮换进行维护。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
D题风电场运行状况分析及优化
风能是一种最具活力的可再生能源,风力发电是风能最主要的应用形式。
我国某风电场已先后进行了一、二期建设,现有风机124台,总装机容量约20万千瓦。
请建立数学模型,解决以下问题:
1. 附件1给出了该风电场一年内每隔15分钟的各风机安装处的平均风速和风电场日实际输出功率。
试利用这些数据对该风电场的风能资源及其利用情况进行评估。
2. 附件2给出了该风电场几个典型风机所在处的风速信息,其中4#、16#、24#风机属于一期工程,33#、49#、57#风机属于二期工程,它们的主要参数见附件3。
风机生产企业还提供了部分新型号风机,它们的主要参数见附件4。
试从风能资源与风机匹配角度判断新型号风机是否比现有风机更为适合。
3. 为安全生产需要,风机每年需进行两次停机维护,两次维护之间的连续工作时间不超过270天,每次维护需一组维修人员连续工作2天。
同时风电场每天需有一组维修人员值班以应对突发情况。
风电场现有4组维修人员可从事值班或维护工作,每组维修人员连续工作时间(值班或维护)不超过6天。
请制定维修人员的排班方案与风机维护计划,使各组维修人员的工作任务相对均衡,且风电场具有较好的经济效益,试给出你的方法和结果。
附件1 平均风速和风电场日实际输出功率表。
附件2 风电场典型风机报表。
附件3 风电场风机型号及其参数。
附件4 风机生产企业提供的新型号风机主要参数。
