方位角及坐标数据处理题目
方位角问题2

方位角问题21、如图,在小岛上有一观察站A .据测,灯塔B 在观察站A 北偏西45°方向,灯塔 C 在灯塔B 正东方向,且灯塔 B 与观察站 A 相距102海里,灯塔 C 与观察站A 相距20 海里,请你测算灯塔C 在观察站A 的什么方向?2、在沿东西走向的河岸南岸,某人自西向东行走,在A 处测得河北岸建筑物P 在北偏东60°的方向上,继续向东走400 米到达 B 处时,在B 处测得河北岸建筑物P在北偏东45°的方向上,如果建筑物P 距河北岸100 米,求河宽(人与河南岸距离忽略不计,3= 1 . 7)3、游艇在湖面上以12 千米/小时的速度向正东方向航行,在O处看到灯塔A 在游艇北偏东60 °方向上,航行 1 小时到达 B 处,此时看到灯塔 A 在游艇北偏西30°方向上.求灯塔 A 到航线OB的最短距离(答案可以含根号).4、我市准备在相距 2 千米的 A 、B 两工厂间修一条笔直的公路,但在 B 地北偏东 60 °方向、 A 地北偏西 45°方向的 C 处,有一个半径为 0 . 6 千米的住宅小区(见下图),问修筑公路时,这个小区是否有居民需要搬迁? ( 参考数据:2= 1 . 41 。
3= 1 . 73 )5、如图,小明同学在东西方向的海岸线上的 A 处,测得海中灯塔P 在北偏东 60 °方向上,在 A 处东如图,甲船在港口 P 的北偏西 600方向,距港口 80 海里的 A 处,沿 AP 方向以 12 海里/时的速度驶向港口 P .乙船从港口 P 出发,沿北偏东 450方向匀速驶离港口 P ,现两船同时出发, 2 小时后甲船到 B 处,乙船在甲船的正东方向的C 处.求乙船的航行速度.(结果保留根号)6、如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A 处测得灯塔C 在北偏西30°方向,轮船航行2小时后到达B 处,在B 处测得灯塔C 在北偏西60°方向.当轮船到达灯塔C 的正东方向的D 处时,求此时轮船与灯塔C 的距离.(结果保留根号)C D B 北 60° 30°7、为打击索马里海盗,保护各国商船的顺利通行,我海军某部奉命前往该海域执行护航任务.某天我护航舰正在某小岛A北偏西45︒并距该岛20海里的B处待命.位于该岛正西方向C处的某外国商船遭到海盗袭击,船长发现在其北偏东60︒的方向有我军护航舰(如图9所示),便发出紧急求救信号.我护航舰接警后,立即沿BC航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置C处?(结果1.4 1.7)8、如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2km,点B位于点A北偏东60°方向且与A相距10km处.现有一艘轮船从位于点B南偏西76°方向的C 处,正沿该航线自西向东航行,5min后该轮船行至点A的正北方向的D处.(1)求观测点B到航线l的距离;(2)求该轮船航行的速度(结果精确到0.1km/h).1.73,sin760.97°≈,cos760.24°≈,tan76 4.01°≈)C AB60°45°北北图99、载着“点燃激情,传递梦想”的信念,奥运圣火于6月2日在古城荆州传递,途经A,B、C、D四地.如图,其中A,B、C三地在同一直线上,D地在A地北偏东45 方向,在B地正北方向,在C地北偏西60 方向.C地在A地北偏东75 方向.B,D两地相距2km.问奥运圣火从A地传到D地的路程大约是多少?(最后结果保留整数,参考数据:2≈1.4,3≈1.7)10、如图,AC是某市环城路的一段,AE、F B、CD都是南北方向的街道,其与环城路AC 的交叉路口分别是A、B、C,经测量花卉世界D位于点A的北偏东45 方向、点B的北偏东30 方向上,AB=2km,∠DAC=15 .(1)求B,D之间的距离;(2)求C,D之间的距离.(结果保留根号)。
115、已知图中AB的坐标方位角...

《工程测量员/地籍测量员-四级》(中级)考试复习题第一部分测量基础知识一、填空题(把答案填在各空横线上,每空0.5分)1、地面某点到大地水准面的垂直距离,称为该点的高程。
2.象限角的取值范围是[0°, 90°]。
3、用钢尺丈量某段距离,往测为48.214m,返测为48.216m,则相对误差为1/24107 。
4、在同一幅地形图上,等高线愈密,则地面坡度愈陡,等高线愈疏,则地面坡度愈缓。
5、高程系统有1956黄海高程系和1985国家高程基准两套。
6、在同一幅地形图上,等高线平距越大,则地面坡度越小(越缓)。
7、水准测量测站检核可以采用变动仪高法或双面尺法测量两次高差。
8、在1∶2000地形图上,量得某直线的图上距离为18.17cm,则实地长度为363.40 m。
9、已知某点的大地经度为115°29',则该点在6°带第20 带内,其中央子午线的经度为117°;该点在3°带第38 带内,其中央子午线的经度为114 。
10、测绘行业高新技术中的“3S”技术分别是: RS , GPS 和GIS ;“4D”产品分别是DEM , DLG , DRG 和DOM 。
11、水准测量前后视距相等可消除:仪器i角误差,地球曲率差,大气折光差。
12、在水准测量过程中临时选定的立尺点,其上既有前视读数,又有后视读数,这些点称为转点,通常用TP表示。
它在水准测量中起转移仪器、传递高程的重要作用。
13、确定地面点的基本要素:高程、角度、距离。
14、闭合n边形内角和计算公式:Σβ=(n-2)×180°。
15、已知AB两点间的距离D,AB与X轴的夹角为α,则A到B的坐标增量:Δx ab=Dcosα、Δy ab=Dsinα。
16、起始子午面与赤道面交点的大地经度、大地纬度分别是L= 00、B= 00;或L=1800 、B= 00。
17、地面点的经度为该点的子午面与本初子午面所夹的二面角。
课本73方位角例题一题多解

一题多解练习姓名题目: 如图,C 岛在A 岛的北偏东50 方向,B 岛在A 岛的北偏东80 方向,C 岛在B 岛的北偏西40 方向。
从C 岛看A ,B 两岛的视角∠ACB 是多少度?方法1: C 岛在A 岛的北偏东50 方向∴∠ =50B 岛在A 岛的北偏东80 方向 ∴∠ =80∴CAB ∠=∠ - ∠ =80 -50 =C 岛在B 岛的北偏西40 方向 ∴∠ =40//AD BE∴∠ + ∠ =180 ∴ABE ∠=180 -∠ =180 - = ∴ABC ∠=∠ -∠= -=在ABC 中,CAB ∠= ,ABC ∠= , 则180ACB ∠=-∠ -∠ =180 - -=B 岛的北偏西40 方向。
从C 岛看A ,B 两岛的视角∠ACB 是多少度?方法2:延长 交BE 于点F ; C 岛在A 岛的北偏东50 方向 ∴∠ =50//AD BE∴AFB ∠ =∠ = C 岛在B 岛的北偏西40 方向 ∴∠ =40在BCF 中,已知∠ = ,∠ = ,则180FCB ∠=-∠ -∠ =180 -=则180ACB ∠=-∠=180 -=B 岛的北偏西40 方向。
从C 岛看A ,B 两岛的视角∠ACB 是多少度?方法3:过点C 做GH AD ⊥,交AD 于点G ,因为//AD BE ,则GH BE ⊥于HGH AD ⊥,GH BE ⊥∴∠ =∠ =90 C 岛在A 岛的北偏东50 方向 ∴∠ =50C 岛在B 岛的北偏西40 方向 ∴∠ =40在ACG 中,GAC ∠= ,AGC ∠= ,∠ACG 180=-∠ -∠ =180 -=在BCH 中,HBC ∠= ,BHC ∠= ,∠BCH 180=-∠ -∠ =180 -=GH 是一条直线∴∠ +∠ +∠ =180 ( ) ∴ACB ∠ 180=-∠ -∠ =180 -=B 岛的北偏西40 方向。
从C 岛看A ,B 两岛的视角∠ACB 是多少度?方法4:(初一(5)班孙慧然提供)过点 作//CM AD 交AB 于点 //AD BE ,//CM AD∴CM //C 岛在A 岛的北偏东50 方向 ∴∠ =50C 岛在B 岛的北偏西40 方向 ∴∠ =40//CM AD ,CM // ∴ACM ∠=∠ = ( ) BCM ∠=∠ = ( ) ∴ACB ∠ =∠ +∠= + =。
坐标,方位角计算公式

坐标,方位角计算公式坐标方位角=磁方位角+(±磁坐偏角)。
方位角是卫星接收天线,在水平面上转0°-360°。
设定方位角时,抛物面在水平面上左右移动。
方位角(方位角,缩写为Az)是用于测量平面中物体之间的角度差的方法之一。
它是从点的北方向顺时针方向和目标方向之间的水平角度。
一、计算方法1、按给定的坐标数据计算方位角αBA、αBPΔxBA=xA-xB=+123.461m;ΔyBA=yA-yB=+91.508m;由于ΔxBA>0,ΔyBA>0;可知αBA位于第Ⅰ象限,即αBA=arctg=36°32'43.64";ΔxBP=xP-xB=-37.819m;ΔyBP=yP-yB=+9.048m;由于ΔxBP<0,ΔyBP>0;公式计算出来的方位角,可知αBP位于第Ⅱ象限。
αBP=180o-α=180o-arctg=180o-13o27'17.33"=166°32'42.67";此外,当Δx<0,Δy<0;位于第Ⅲ象限,方位角=180°+arctg;当Δx>0,Δy<0;位于第Ⅳ象限,方位角=360°-arctg。
2、计算放样数据∠PBA、DBP∠PBA=αBP-αBA=129°59'59.03"。
3、测设时,把经纬仪安置在B点,瞄准A点,按顺时针方向测设∠PBA,得到BP方向,沿此方向测设水平距离DBP,就得到P点的平面位置。
当受地形限制不便于量距时,可采用角度交会法测设放样点平面位置上例中,当BP间量距受限时,通过计算测设∠PAB、∠PBA来定P点。
根据给定坐标计算∠PAB;ΔxAP=xP-xA=-161.28m;ΔyAP=yP-yA=-82.46m;αAP=180°+arctg=207°4'47.88";又αAB=180°+αBA=180°+36°32'43.64"=216°32'43.64";∠PAB=αAB-αAP=9°27'55.76"。
方位坐标练习题

方位坐标练习题1. 对于以下给定的方位坐标,请写出相应的坐标点。
a) 西北b) 东南c) 东北d) 西南e) 正北f) 正南g) 西h) 东2. 在一个笛卡尔坐标系中,有两个坐标点A(-3, 2)和B(5, -4)。
求解下列问题:a) 求点A和点B的横坐标之和。
b) 求点A和点B的纵坐标之差。
c) 求点A和点B的距离。
3. 在一个方位坐标系中,有一个城市的中心点位于坐标原点O(0,0)。
有两个城市A和B位于坐标点A(-5, 3)和B(7, -2)。
请计算以下问题:a) 城市A相对于中心点O的方位。
b) 城市B相对于中心点O的方位。
c) 城市A相对于城市B的方位。
4. 锚点P(2, -1)和Q(-4, 3)分别固定在地图上,一个船只从锚点P出发,朝锚点Q航行。
船只按照每分钟航行3个坐标单位的速度,求以下问题:a) 船只从锚点P到锚点Q需要多长时间(以分钟计)?b) 船只经过哪些坐标点?5. 请根据下列方位坐标,将这些点依次用折线连接起来,并写出它所表示的方位。
A(-3, 1), B(0, -2), C(2, -4), D(-1, -1)思考题:利用方位坐标系,设计一个小游戏。
游戏规则如下:- 游戏地图为一个10x10的方格。
- 玩家从出发点(0, 0)开始,通过输入方位指令进行移动。
- 玩家只能上下左右移动一个坐标单位。
- 游戏目标为到达某个特定终点坐标。
- 游戏要求玩家给出达到终点所需的方位指令序列。
题目结束请根据上述题目,按照题目所要求的格式,完成文章的写作。
1. 对于以下给定的方位坐标,请写出相应的坐标点。
a) 西北b) 东南c) 东北d) 西南e) 正北f) 正南g) 西h) 东2. 在一个笛卡尔坐标系中,有两个坐标点A(-3, 2)和B(5, -4)。
求解下列问题:a) 求点A和点B的横坐标之和。
b) 求点A和点B的纵坐标之差。
c) 求点A和点B的距离。
3. 在一个方位坐标系中,有一个城市的中心点位于坐标原点O(0,0)。
南西北练习题

南西北练习题南、西、北练习题是一种常见的地理知识测试工具,用来考察人们对南、西、北方位的理解和应用。
这种练习题广泛运用于学校教育,特别是小学的地理课程中。
通过解答这些练习题,学生可以加深对南、西、北方位的认识,提升空间方位感,从而更好地理解地理知识和进行实际应用。
一、基础练习题1. 东方位与南方位之间的夹角是多少度?2. 西方位与东方位之间的夹角是多少度?3. 北方位与西方位之间的夹角是多少度?4. 南方位与北方位之间的夹角是多少度?二、方位判断题根据下列语境,判断正确的方位:1. 早上起床后,你能看到太阳升起的方向是哪个方位?2. 当你背对太阳时,太阳位于哪个方位?3. 在西方的地方,太阳的位置是在哪个方位?4. 当地图上的箭头指向上方时,箭头表示的方位是哪个?5. 在夏至的时候,太阳直射地球的位置在哪个方位?三、方位应用题根据下列情境,选择恰当的方位回答问题:1. 如果你从北京出发,向南行驶,你的目的地最可能是哪个城市?2. 如果你从南京出发,向西北方向行驶,你最终可能到达哪个城市?3. 如果你要去位于北京西南方向的一个地方,你应该选择哪个交通工具?4. 如果你的家在纽约市,你应该向什么方向出发,才能到达加拿大?5. 如果一个风筝从西边的山上放飞,向北飘去,风筝最终可能会飞到哪个地方?四、应用拓展题根据下列情境,进行进一步的思考和探索:1. 在中国,哪个城市是最东边的?2. 在中国,哪个城市是最南边的?3. 在中国,哪个城市是最西边的?4. 在中国,哪个城市是最北边的?5. 如果你要从中国最东边的城市一直向西行驶,你最终会到达哪个地方?通过解答以上练习题,你可以加深对南、西、北方位的理解。
希望这些练习题能够帮助你提升对地理方位的认识,并在实际生活中灵活运用。
三角函数方位角问题
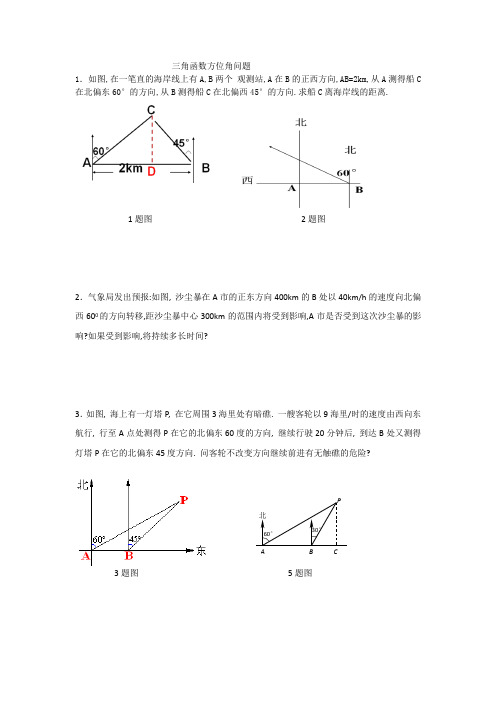
三角函数方位角问题1.如图,在一笔直的海岸线上有A,B 两个 观测站,A 在B 的正西方向,AB=2km,从A 测得船C 在北偏东60°的方向,从B 测得船C 在北偏西45°的方向.求船C 离海岸线的距离.1题图 2题图2.气象局发出预报:如图, 沙尘暴在A 市的正东方向400km 的B 处以40km/h 的速度向北偏西600的方向转移,距沙尘暴中心300km 的范围内将受到影响,A 市是否受到这次沙尘暴的影响?如果受到影响,将持续多长时间?3.如图, 海上有一灯塔P , 在它周围3海里处有暗礁. 一艘客轮以9海里/时的速度由西向东航行, 行至A 点处测得P 在它的北偏东60度的方向, 继续行驶20分钟后, 到达B 处又测得灯塔P 在它的北偏东45度方向. 问客轮不改变方向继续前进有无触礁的危险?3题图5题图PC30°60°北4.大海中某小岛A 的周围22km 范围内有暗礁. 一海轮在该岛的南偏西55°方向的B 处,由西向东行驶了20km 后到达该岛的南偏西25°方向的C 处.如果该海轮继续向东行驶,会有触礁的危险吗? (精确到0.1km).5.如图,小明同学在东西方向的环海路A 处,测得海中灯塔P 在北偏东60°方向上,在A 处向东500米的B 处,测得海中灯塔P 在北偏东30°方向上,则灯塔P 到环海路的距离PC = 米(结果保留根号).6.如图所示,A 、B 两城市相距100km. 现计划在这两座城市间修筑一条高速公路(即线段AB ),经测量,森林保护中心P 在A 城市的北偏东30°和B 城市的北偏西45°的方向上. 已知森林保护区的范围在以P 点为圆心,50km 为半径的圆形区域内. 请问:计划修筑的这条高速公路会不会穿越保护区. 为什么?(参考数据:732.13≈,414.12≈)6题图 7题图7.海上有一小岛A ,它周围8.7海里内有暗礁,某海船跟踪鱼群由西向东航行,在B 点测得小岛在北偏东60°,航行10海里后到达C 点,这时测得小岛A 在北偏东30°,如果渔船不改变航向,继续向东追踪捕捞,有没有触礁的危险?tan 250.47tan 55 1.43°≈°≈A B。
方位角配套练习题

北
●
D
45°40° O 60° C
●
●
B
西
●
东
10°
南
●
A
射线 OD 的方向就是南偏西 45°即海岛D所在的方向。
画一画,做一做
北 北
B
1 2 A
东
东
4、 小明从点A出发向北偏西50° 方向走了3米,到达点B,小林从点A 出发向南偏西40°方向走了4米,试 画图确定出A、B、C三点的位置(用 1厘米表示3米),并从图上求出B点 到C点的实际距离。 北
B 500
西
400 A 东
C
南
你知道方位角吗?
西北 北 东北
西
东
西南
南
东南
如图,下列说法中错误的是(
A.OD的方向是北偏东30°
D
)
北
A
60° 45° O
D
60° 30°
B.OC的方向是南偏东60°
C.OB的方向是西南方向
C B
D.OA的方向是北偏西60°
3:如图,OA表示北偏东32°方向线, OB表示 南偏东43°方向线,则∠AOB等于多少度?
解: ∠AOB
=(90°- 32°)+(90°- 43°) =58°+47 °
=105°
例2:如图.货轮O在航行过程中 ,发现灯塔A在它南偏东 60°的方向上,同时,在它北偏东40°,南偏西10°,西 北 ( 即北偏西 45 ° ) 方向上又分别发现了客轮 B, 货轮 C 和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货 轮C和海岛D方向的射线.
7.2 坐标方法的简单应用 人教版数学七年级下册重难点专项练习(含答案)

7.2《坐标方法的简单应用》重难点题型专项练习考查题型一方位角典例1.观察下图.书店在小玲家北偏西方向距离800米处,书店应该在()A.点A处B.点B处C.点C处D.以上均可【答案】B【分析】A、B、C三个点的方向不同,根据书店的方向即可判断书店在三个点中的哪一个点.【详解】解答:解:书店在小玲家北偏西方向上,即书店与小玲家的连线在小玲家正北方与正西方之间,与正北方组成的角;由图可得书店应该在点B处.故选:B.【点睛】解答此题关键在于掌握了在图中辨别用方向词和角度表示的方向.变式1-1.如图,货船A与港口B相距35海里,我们用有序数对(南偏西,35海里)来描述港口B相对货船A的位置,那么货船A相对港口B的位置可描述为()A.(南偏西,35海里)B.(北偏西,35海里)C.(北偏东,35海里)D.(北偏东,35海里)【答案】C【分析】以点B为中心点,来描述点A的方向及距离即可.【详解】解:由题意知货船A相对港口B的位置可描述为(北偏东,35海里),故选:C.【点睛】本题考查坐标确定位置,用方向角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方向角时,一般先叙述北或南,再叙述偏东或偏西.变式1-2.(2022春·福建厦门·七年级校联考期中)如图,李老师家与学校相距,相对于李老师家,能够准确描述出学校位置的是()A.学校在李老师家的南偏东30°方向B.李老师家在学校的南偏东30°方向C.学校在李老师家的南偏东30°方向,相距处D.李老师家在学校的南偏东30°方向,相距处【答案】C【分析】平面直角坐标系是常见的确定位置的方法,同时通过确定一个参照物,用目标与参照物的距离,及目标相对参照物的方位角或其他规定的角度,也可以唯一确定目标的位置.【详解】解:∵如图,李老师家与学校相距,所以相对于李老师家,学校在李老师家的南偏东30°方向,相距处,故选C.【点睛】本题考查了坐标确定位置,解题时由已知条件正确确定坐标轴的位置是解决本题的关键.变式1-3.(2022春·河南许昌·七年级统考期中)如图,用方向和距离描述图书馆相对于小青家的位置是()A.北偏东,3km B.北偏东,3km C.东偏北D.东偏北,3km【答案】B【分析】根据方向角的定义解答即可.【详解】图书馆在小青家北偏东方向的3km处,或者图书馆在小青家东偏北方向的3km处,故选:B.【点睛】本题考查了坐标确定位置,主要是方向角的定义,熟练掌握概念是本题的关键.考查题型二求点平移后的坐标典例2.(2022秋·山东东营·七年级东营市东营区实验中学校考期末)点向右平移1个单位长度,再向上平移1个单位长度后点的坐标是( )A.B.C.D.【答案】C【分析】根据向右平移横坐标加,向上平移纵坐标加求解即可.【详解】解:∵点先向右平移1个单位长度,再向上平移1个单位长度得到点,∴点的横坐标为,纵坐标为,∴点的坐标是.故选:C.【点睛】本题考查了坐标与图形变化-平移,主要利用了平移中点的变化规律:横坐标右移加,左移减;纵坐标上移加,下移减.变式2-1.将点向左平移个单位,再向上平移个单位后得到的点,则点的坐标为( )A.B.C.D.【答案】D【分析】根据向左平移横坐标减,向上平移纵坐标加求解即可.【详解】解:∵点向左平移个单位,再向上平移个单位后得到的点,∴点的横坐标为,纵坐标为,∴点的坐标为,故选:D.【点睛】本题考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.变式2-2.(2021·四川成都·三模)将点P(2,1)沿x轴方向向左平移3个单位,再沿y轴方向向上平移2个单位( )A.(﹣1,﹣1)B.(﹣1,3)C.(5,﹣1)D.(5,3)【答案】B【分析】根据平移的方法:横坐标,右移加,左移减;纵坐标,上移加,下移减,即可得结论.【详解】解:将点P(2,1)沿x轴方向向左平移3个单位,再沿y轴方向向上平移2个单位,则横坐标减3,纵坐标加2,∴所得的点的坐标是.故选:B.【点睛】本题考查了点的平移,掌握点的平移规律是解题的关键.变式2-3.(2021春·湖南湘西·七年级校考期中)将点(1,2)向左平移3个单位,再向上平移1个单位,所得的点的坐标是()A.(-2,3)B.(4,3)C.(-2,1)D.(4,1)【答案】A【分析】根据左减右加,上加下减的规律即可得.【详解】解:将点(1,2)向左平移3个单位,再向上平移1个单位,所得的点的坐标是(1-3,2+1),即(-2,3),故选:A.【点睛】本题考查了坐标与图形变化-平移,熟记左减右加,上加下减的规律是解题的关键.考查题型三求平移方式典例3.(2022春·海南省直辖县级单位·七年级统考期中)在平面直角坐标系中,若将原图形上的每个点的纵坐标都加2,横坐标保持不变,则所得图形的位置与原图相比()A.向左平移2个单位B.向右平移2个单位C.向上平移2个单位D.向下平移2个单位【答案】C【分析】根据点坐标平移特点:向左平移,横坐标减,向右平移,横坐标加,向上平移纵坐标加,向下平移,纵坐标减进行求解即可.【详解】解:∵将原图形上的每个点的纵坐标都加2,横坐标保持不变,∴所得图形的位置与原图相比向上平移了2个单位长度,故选C【点睛】本题主要考查了坐标与图形,图形的平移,熟知点坐标平移的特点是解题的关键.变式3-1.(2022春·江苏南通·七年级统考期中)在平面直角坐标系中,将三角形顶点的横坐标都减去6,纵坐标不变,所得图形与原图形相比()A.向左平移了6个单位B.向下平移了6个单位C.向上平移了6个单位D.向右平移了6个单位【答案】A【分析】根据把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度可直接得到答案.【详解】将三角形各顶点的横坐标都减去6,纵坐标不变,所得图形的位置与原图形相比向左平移6个单位;故选:A.【点睛】此题主要考查了坐标与图形变化-平移,关键是掌握点的坐标的变化规律:横坐标,右移加,左移减;纵坐标,上移加,下移减.变式3-2.(2022春·甘肃定西·七年级统考阶段练习)如果将三角形的三个顶点的横坐标都加上,纵坐标都减去后,得到新的三角形,那么三角形在三角形的基础上()A.先向左平移个单位长度,再向下平移个单位长度B.先向右平移个单位长度,再向上平移个单位长度C.先向左平移个单位长度,再向上平移个单位长度D.先向右平移个单位长度,再向下平移个单位长度【答案】D【分析】利用平移的性质,解决问题即可.【详解】解:的三个顶点的横坐标都加上,纵坐标都减去后,得到新的三角形A'B'C',A'B'C'是由向右平移个单位,再向下平移个单位得到的,故选:D.【点睛】本题考查了坐标与图形的变化,以及平移的性质,在直角坐标系中准确找出各点的位置是解题的关键.变式3-3.(2022春·山东德州·七年级统考期中)将点通过以下哪种方式的平移得到点()A.沿x轴向右平移3个单位长度,再沿y轴向下平移4个单位长度B.沿x轴向左平移3个单位长度,再沿y轴向下平移4个单位长度C.沿x轴向左平移4个单位长度,再沿y轴向上平移3个单位长度D.沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度【答案】D【分析】根据点平移的规律解答.【详解】解:∵-2-3=-5,3+4=7,∴点沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度得到点,故选:D.【点睛】此题考查了点平移的规律:沿着x轴平移:左减右加;沿着y轴平移:上加下减,熟记平移的规律是解题的关键.考查题型四根据图形的平移求点的坐标典例4.在直角坐标系中,点A,B的坐标分别是、,将线段平移,平移后点A的对应点的坐标是,那么点B的对应点的坐标是( )A.B.C.D.【答案】A【分析】利用平移变换的性质,画出图形可得结论.【详解】解:如图,观察图像可知,,故选:A.【点睛】本题考查坐标与图形变化﹣平移,解题的关键是理解题意,正确画出图形解决问题.变式4-1.在平面直角坐标系中,已知线段的两个端点分别是,,将线段平移后得到线段,如点的坐标为,则点坐标为( )A.B.C.D.【答案】B【分析】各对应点之间的关系是横坐标加2,纵坐标加3,那么让点的横坐标加2,纵坐标加3即为点的坐标.【详解】解:由的对应点的坐标为,得坐标的变化规律为:各对应点之间的关系是横坐标加2,纵坐标加3,所以点的横坐标为,纵坐标为,即所求点的坐标为,故选:.【点睛】本题主要考查了坐标与图形的变化-平移,解题的关键是能根据已知对应点找到各对应点之间的变化规律.变式4-2.已知线段的端点,,将线段平移后,点坐标是,则点的坐标是()A.B.C.D.【答案】A【分析】比较平移前A(-1,2),平移后(1,2)的横坐标、纵坐标,可知平移后横坐标加2,纵坐标加4,由于点A、B的平移规律相同,坐标变化也相同,即可得的坐标.【详解】解:∵平移前A(-1,2),平移后(1,2)∴平移方式为向右平移2个单位长度,向上平移4个单位长度,∵平移前点B的坐标为(1,2),∴平移后点B的坐标为(1+2,2+4)即(3,6),故选A.【点睛】本题主要考查了图形的平移,根据A点平移前后的坐标判断出平移方式是解题的关键.变式4-3.(2022春·江苏南通·七年级统考期中)把坐标平面内的圆(点为圆心)平移到圆(点为圆心)的位置(如图①②),如果圆上一点的坐标为,那么平移后在圆上的对应点的坐标为()A.B.C.D.【答案】D【分析】直接利用平移中点的变化规律求解即可.【详解】解:由点A的平移规律可知,此点的移动规律是横坐标加2,纵坐标减1,照此规律计算可知P'的坐标为(m+2,n-1).故选D.【点睛】本题考查了坐标与图形的变化,解决本题的关键是分别根据已知对应点找到各对应点的横纵坐标之间的变化规律.考查题型五根据平移后坐标求原坐标典例5.若将点A先向左平移1个单位,再向上平移4个单位,得到的,则点A的坐标为()A.B.C.D.【答案】D【分析】设A(x,y),将点A先向左平移1个单位,再向上平移4个单位可得(x-1,y+4),再根据B (-3,2)可得x-1=-3,y+4=2,然后再解方程即可.【详解】解:设A(x,y),将点A先向左平移1个单位,再向上平移4个单位可得(x-1,y+4),∵得到的B(-3,2),∴x-1=-3,y+4=2,解得:x=-2,y=-2,∴A(-2,-2),故选D.【点睛】此题主要考查了平移变换与坐标变化,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.变式5-1.将点A先向下平移3个单位,再向右平移2个单位后得B(﹣1,5),则A点坐标为()A.(﹣4,11)B.(﹣2,6)C.(﹣4,8)D.(﹣3,8)【答案】D【分析】让点B先向上平移3个单位,再向左平移2个单位即可得到点A的坐标,让点B的横坐标减2,纵坐标加3即可得到点A的坐标.【详解】解:∵将点A先向下平移3个单位,再向右平移2个单位后得B(﹣1,5),∴点A的横坐标为﹣1﹣2=﹣3,纵坐标为5+3=8,∴A点坐标为(﹣3,8).故选D.【点睛】在平面直角坐标系中,图形的平移与图形上某点的平移相同,本题需注意的是已知新点的坐标,求原来点的坐标,注意平移的顺序的反过来的运用.解决本题的关键是得到由点B到点A的平移过程.变式5-2.(2020春·河北邯郸·七年级校考阶段练习)在平面直角坐标系中,线段A'B'是由线段AB经过平移得到的,已知点A(-2,1)的对应点为A'(3,-1),点B的对应点为B'(4,0),则点B的坐标为( ) A.(9,-2)B.(-1,-2)C.(-1,3)D.(−1,2)【答案】D【分析】直接利用平移中点的变化规律求解即可.【详解】横坐标从-2到3,说明是向右移动了3-(-2)=5,纵坐标从1到-1,说明是向下移动了1-(-1)=2,求原来点的坐标,则为让新坐标的横坐标都减5,纵坐标都加2.则点B的坐标为(-1,2).故答案为:D.【点睛】本题考查了图形的平移变换,注意左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.求原来点的坐标正好相反.变式5-3.已知△ABC内任意一点P(a,b)经过平移后对应点P1(a+2,b-6),如果点A在经过此次平移后对应点A1(4,-3),则A点坐标为()A.(6,-9)B.(2,-6)C.(-9,6)D.(2,3)【答案】D【分析】点A向右平移2个单位,向下平移6个单位得到A1(4,3),由此可得结论.【详解】解:由题意,点A向右平移2个单位,向下平移6个单位得到A1(4,3),∴点A坐标(4−2,−3+6),即(2,3),故选:D.【点睛】本题考查的是坐标与图形变化——平移,牢记平面直角坐标系内点的平移规律:上加下减、右加左减是解题的关键.考查题型六用坐标表示位置典例6.某体育馆的平面示意图如图所示,已知游泳馆的坐标是,足球场的坐标是.(1)根据上述条件建立平面直角坐标系;(2)若篮球场的坐标为,请在图中标出篮球场的位置.【答案】(1)见解析(2)见解析【分析】(1)根据数对表示的位置,即可建立出平面直角坐标系.(2)根据数对表示的位置,第一个数字表示列,第二个数字表示行,即可标出篮球场的位置.【详解】(1)建立平面直角坐标系如图所示.(2)篮球场的位置如图所示.【点睛】本题考查了坐标方法的简单应用以及数对表示位置的方法,正确建立平面直角坐标系是解题的关键.变式6-1.如图是某学校平面图的一部分,若宿舍楼的坐标为,致远楼的坐标为,请解答下列问题:(1)根据题目信息,建立平面直角坐标系;(2)根据你建立的平面直角坐标系,写出教务处的坐标;(3)若图书馆的坐标为,请在图中标出图书馆的位置.【答案】(1)见解析(2)(3)见解析【分析】(1)根据宿舍楼和致远楼的坐标,确定出原点以及坐标轴,即可求解;(2)根据直角坐标系以及教务处的位置,即可求解;(3)根据图书馆的坐标,在坐标系中标记即可.【详解】(1)建立平面直角坐标系如图所示.(2)教务处的坐标为.(3)图书馆的位置如图所示.【点睛】此题考查了直角坐标系的应用,坐标确定位置,根据题意正确得到原点的位置以及坐标轴是解题的关键.变式6-2.如图是游乐园的一角,如果用表示摩天轮的位置,用表示碰碰车的位置,请解答下列问题:(1)请建立符合题意的平面直角坐标系;(2)若跳跳床的位置用坐标表示,请在图中标出跳跳床的位置.【答案】(1)建立平面直角坐标系见解析(2)标出跳跳床位置见解析【分析】(1)根据题中用表示摩天轮的位置,用表示碰碰车的位置,建立平面直角坐标系,详情见解析;(2)在(1)建立的平面直角坐标系中,结合跳跳床的位置用坐标表示,即可标出其对应点.【详解】(1)解:建立平面直角坐标系如图所示:(2)解:跳跳床的位置如图所示:【点睛】本题考查平面直角坐标系及在坐标系中根据坐标找到点的位置,熟记平面直角坐标系相关知识是解决问题的关键.变式6-3.(2022春·陕西渭南·七年级统考期中)多多和爸爸.妈妈周末到动物园游玩,回到家后,她利用平面直角坐标系画出了动物园的景区地图,如图所示.可是她忘记了在图中标出原点,轴和轴,只知道东北虎的坐标为,两栖动物的坐标为.请你帮她画出平面直角坐标系,并写出其他各点的坐标.【答案】坐标系见解析,非洲狮的坐标为;南门的坐标为;飞禽的坐标为【分析】根据东北虎和两栖动物的坐标先建立坐标系,然后写出其他点的坐标即可.【详解】解:如图所示坐标系即为所求;由坐标系可知非洲狮的坐标为;南门的坐标为;飞禽的坐标为.【点睛】本题主要考查了实际问题中用坐标表示位置,正确理解题意建立正确的坐标系是解题的关键.考查题型七图形的平移典例7.(2022春·江西上饶·七年级统考期中)如图在平面直角坐标系中,已知点,.(1)画出向上平移个单位,向左平移个单位后所得的图形;(2)求平移、、后的对应点的坐标;(3)求平移过程中扫过的面积.【答案】(1)画图见解析(2)、、(3)22【分析】根据网格结构找出平移后A、B、O的对应点、、的位置,然后顺次连接即可;根据网格结构写出点、、的坐标即可;分向上平移和向左平移两个部分,利用平行四边形的面积公式列式计算即可得解.(1)解:如图所示∶(2)由(1)可得:、、;(3)向上平移个单位扫过的面积为,接着向左平移个单位扫过的面积为,所以平移过程中扫过的面积一共为.【点睛】本题考查了利用平移变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键.变式7-1.如图,平面直角坐标系中,三角形ABC的顶点都在网格点上,其中B点坐标为(-1,-1).(1)将△ABC先向上平移2个单位长度,再向右平移3个单位长度,得到,画出;(2)求的面积.【答案】(1)画图见解析;(2).【分析】(1)先找出A点和B点坐标,利用点的坐标平移规律写出点A′、B′、C′的坐标,然后描点连线得到;(2)用一个矩形的面积分别减去三个三角形的面积可得到的面积.(1)解:由图可得:,;经过平移后,,;如图,为所作;(2)解:如图∶的面积.【点睛】本题考查了坐标与图形变化—平移:在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.变式7-2.(2022春·黑龙江齐齐哈尔·七年级校考期中)如图,已知A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ ABC经过平移得到的,△ ABC中任意一点平移后的对应点为.(1)画出平移后的;(2)写出点的坐标;(3)求△ ABC的面积.【答案】(1)见解析(2)(3)5.5【分析】(1)由题意分析出点的平移规律,把A、B、C的对应点在坐标系画出,连接得(2)从图形直接写出(3)用割补法求出即可(1)解:由点平移后的对应点为知:点的横坐标右移6个单位,纵坐标上移4个单位平移后的图形如下所示:图中即为所求(2)解:由(1)的图形直接得:(3)解:【点睛】本题主要考查了运用平移变换作图,确定平移后图形的基本要素有:平移方向、平移距离,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.变式7-3.(2022春·海南省直辖县级单位·七年级统考期末)△ABC与在平面直角坐标系中的位置如图.(1)分别写出下列各点的坐标:;;;(2)说明由△ABC经过怎样的平移得到?(3)求△ABC的面积.【答案】(1)(﹣3,1),(﹣2,﹣2),(﹣1,﹣1)(2)先向左平移4个单位,再向下平移2个单位(3)2【分析】(1)根据图示即可得出、、三点的坐标;(2)利用对应点位置变化得出答案;(3)直接利用△ABC所在直角梯形面积减去周围三角形面积进而得出答案.(1)根据图示,得A′(﹣3,1),B′(﹣2,﹣2),C′(﹣1,﹣1);故答案为:(﹣3,1),(﹣2,﹣2),(﹣1,﹣1).(2)△ABC先向左平移4个单位,再向下平移2个单位;(或先向下平移2个单位,再向左平移4个单位)得到△A′B′C′;(3)如图,=×(1+3)×2﹣×1×3﹣×1×1=2.【点睛】本题考查了利用平移变换作图,图形与坐标,根据网络图中对应点的位置确定出平移的方法是解题的关键.。
陀螺仪应用案例之:数据处理.
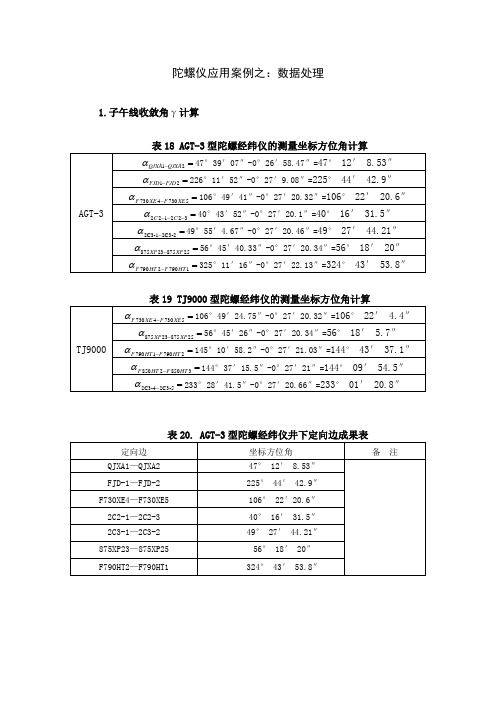
106°49′41″-0°27′20.32″=106°22′20.6″
40°43′52″-0°27′20.1″=40°16′31.5″
49°55′4.67″-0°27′20.46″=49°27′44.21″
56°45′40.33″-0°27′20.34″=56°18′20″
144°37′15.5″-0°27′21″=144°09′54.5″
233°28′41.5″-0°27′20.66″=233°01′20.8″
表20. AGT-3型陀螺经纬仪井下定向边成果表
定向边
坐标方位角
备注
QJXA1—QJXA2
47°12′8.53″
FJD-1—FJD-2
225°44′42.9″
顾和和地点已知边bq3bq2陀螺方位角vv仪器常数一次测定中误差铜矿875中段观测值平均值t测定顺序14353521435354253205261435356202708仪器常数平均值中误差
陀螺仪应用案例之:数处理
1.子午线收敛角γ计算
表18 AGT-3型陀螺经纬仪的测量坐标方位角计算
AGT-3
47°39′07″-0°26′58.47″=47°12′8.53″
°′″
°′″
α
°′″
1
00 02 29
00 02 39
-10
100
53 20 52.6
2
00 02 40
+1
1
γ
3
00 02 42
+3
9
0°27′08″
4
00 02 45
+6
36
仪器常数平均值中误差:
课时练习:解直角三角形的应用(方位角问题)

方位角问题知识点一 与方位角有关的问题1.如图,B 点在A 点的南偏西 或 ;A 点在B 点的北偏东 或 . 2.如图,小明从A 地沿北偏东030方向走1003m 到B 地,再从B 地向正南方向走200m 到C 地,此时小明离A 地 m .3.两座灯塔A 和B 与海洋观测站的距离相等,灯塔A 在观测站的北偏东40°,灯塔B 在观测站的南偏东60°,那么灯塔A 在灯塔B 的( ). A.北偏东10° B.南偏东10° C.北偏西10° D.南偏西20°4.小明同学在东西方向的沿江大道A 处,测得江中灯塔P 在北偏东60°方向上,在A 处正东400米的B 处,测得江中灯塔P 在北偏东30°方向上,则灯塔P 到沿江大道的距离为___________米.5.如图,小明同学在东西方向的环海路A 处,测得海中灯塔P 在北偏东60°方向上,在A 处东500m 的B 处,测得海中灯塔P 在北偏东30°方向上,则灯塔P 到环海路的距离PC = m .(用根号表示) 技能点一 利用方位角解决与航海、航空有关的实际问题6.如图,客轮在海上以30km/h 的速度由B 向C 航行,在B 处测得灯塔A 的方位角为北偏东80,测得C 处的方位角为南偏东25,航行1小时后到达C 处,在C 处测得A 的方位角为北偏东20,则C 到A 的距离是( ). A .156kmB .152kmC .15(62)+kmD .5(632)+km7.如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A 处测得灯塔C 在北偏西30°方向,轮船航行2小时后到达B 处,PA B C30°60°北第5题图030第2题图40第1题图 北东ABC第6题图在B 处测得灯塔C 在北偏西60°方向.当轮船到达灯塔C 的正东方向的D 处时,求此时轮船与灯塔C 的距离.(结果保留根号)技能点二 解决底部不能到达的测量问题8.燕尾槽的横断面是等腰梯形.如图是一燕尾槽的横断面,其中燕尾角B 是55,外口宽AD 是16cm ,燕尾槽的深度是6cm ,求它的里口宽BC (精确到0.1cm ).9.某电视发射塔BC ,为稳固塔身,周围拉有钢丝地锚线(如图线段AB ),若AB =60m ,并且AB 与地面成45°角,欲升高发射塔的高度到CB /,同时原地锚线仍使用,若塔升高后使地锚线与地面成60°角,求电视发射塔升高了多少米?(即BB /的高度)(精确到0.01m ).参考答案1.040 西偏南050 040 东偏北050第8题图A /ACBB / 第9题图2.100 3.C4.5.6.D7.轮船与灯塔C 的距离为8.作AE BC DF BC ⊥⊥,,垂足分别为E ,F ,在Rt ABE △中,tan AEB BE=,∴ tan AE BE B ==6tan55.∴6221624.4tan55BC BE AD =+=⨯+≈(cm ).答:燕尾槽的里口宽BC 约为24.4cm .9.解:在Rt △ACB 中,因为∠BAC=450,AB=60m ,所以BC=AB·sin ∠BAC=60×sin450=302(m ).在Rt △A /B /C 中,A /B /=60m ,∠B /A /C=600,所以B /C=A /B /·sin600=60×33023=(m ).所以电视塔升高的高度:BB /=B /C-BC = 9.54(m)≈。
坐标方位角计算实验报告

一、实验目的1. 理解坐标方位角的概念和计算方法。
2. 掌握坐标方位角的计算步骤和注意事项。
3. 通过实际操作,提高测量精度和计算能力。
二、实验原理坐标方位角是指在平面直角坐标系中,从起点出发,沿着直线的方向所形成与正北方向之间的夹角。
坐标方位角的计算公式为:方位角 = arctan((y2 - y1) / (x2 - x1))其中,(x1, y1)和(x2, y2)分别为直线上两点的坐标。
三、实验仪器与材料1. 测量仪器:经纬仪、水准仪、钢尺等。
2. 实验材料:坐标纸、记录本、计算器等。
四、实验步骤1. 选择实验场地,搭建测量控制网。
2. 在控制网上选取两个已知坐标点A和B。
3. 利用经纬仪和水准仪,测量点A和B的坐标和高程。
4. 根据测得的坐标和高程,计算A、B两点的坐标方位角。
5. 利用坐标方位角,绘制直线的方向。
6. 对比理论计算结果和实际测量结果,分析误差来源。
五、实验数据1. 点A坐标:x1 = 100.0m,y1 = 200.0m2. 点B坐标:x2 = 150.0m,y2 = 250.0m六、实验结果与分析1. 计算A、B两点的坐标方位角:方位角 = arctan((y2 - y1) / (x2 - x1))= arctan((250.0 - 200.0) / (150.0 - 100.0))≈ arctan(1.0)≈ 45°2. 绘制直线的方向,实际测量结果与理论计算结果基本一致。
3. 误差分析:(1)测量误差:在实验过程中,由于仪器精度、人为操作等因素,导致测量结果存在一定的误差。
(2)计算误差:在计算过程中,由于计算方法、计算器精度等因素,导致计算结果存在一定的误差。
(3)绘图误差:在绘制直线方向时,由于绘图工具和人为操作等因素,导致绘图结果存在一定的误差。
七、实验总结1. 通过本次实验,我们掌握了坐标方位角的计算方法和步骤,提高了测量精度和计算能力。
2. 在实际操作过程中,要注意仪器的使用、数据的记录和计算过程的准确性,以减小误差。
工程测量坐标方位角计算例题

工程测量坐标方位角计算例题
工程测量中,坐标方位角是指某一点相对于参考方向的角度,通常以正北方向作为参考方向。
计算坐标方位角的方法可以根据具体情况采用不同的方式,下面我将给出一个计算坐标方位角的例题并进行详细解答。
假设有一点A的坐标为(100, 200),现在需要计算点A相对于正北方向的方位角。
首先,我们需要确定参考方向,通常正北方向被定义为0度或360度,顺时针方向为角度递增的方向。
接下来,我们需要确定点A相对于参考方向的角度。
我们可以使用反正切函数来计算这个角度。
假设点A相对于参考方向的角度为α,则有:
α = arctan(Δy/Δx)。
其中,Δx为点A的x坐标,Δy为点A的y坐标。
代入点A的坐标(100, 200),我们可以得到:
α = arctan(200/100) = arctan(2) ≈ 63.43度。
因此,点A相对于正北方向的方位角为约63.43度。
需要注意的是,这里的角度是以顺时针方向为正,如果需要转换为以逆时针方向为正的角度,可以使用360度减去上述计算得到的角度。
除了使用反正切函数计算方位角外,还可以使用其他方法,比如利用三角函数或者坐标变换等方式来计算坐标方位角。
不同的方法适用于不同的情况,需要根据具体的测量问题来选择合适的计算方法。
综上所述,计算坐标方位角的方法可以根据具体情况采用不同的方式,而在工程测量中,通常可以使用反正切函数来计算点相对于参考方向的角度。
希望这个例题的解答能够帮助你更好地理解工程测量中坐标方位角的计算方法。
坐标反算方位角例题

坐标反算方位角例题
当涉及到坐标反算和方位角的例题时,通常是指根据给定的两个坐标点,计算出一个点相对于另一个点的方位角。
下面是一个坐标反算方位角的例题及其解答:
例题:已知点A的坐标为(2, 3),点B的坐标为(5, 7),求点B相对于点A的方位角。
解答:
1.首先,计算出点B相对于点A的水平和垂直距离。
水平距离
= 点B的x坐标 - 点A的x坐标,即 5 - 2 = 3。
垂直距离 = 点B的y坐标 - 点A的y坐标,即 7 - 3 = 4。
2.接下来,利用反正切函数(atan2)计算出方位角。
方位角=
arctan(垂直距离 / 水平距离)。
方位角 = arctan(4 / 3) ≈ 51.34°
3.最后,根据计算结果得出点B相对于点A的方位角为约
51.34°。
注意:方位角一般以角度表示,可以用度数(°)或弧度(rad)表示,具体要根据题目要求或上下文来确定使用哪种表示方式。
九年级数学上册4.4解直角三角形的应用第3课时与方位角有关的应用问题练习湘教版

第3课时与方位角有关的应用问题基础题知识点与方位角有关的应用问题1.如图,某海监船和一渔船同时从点A动身,海监船沿正北方向MN航行,渔船往北偏东60°方向以40海里/时的速度航行,渔船半小时后抵达B处,现在渔船恰好在海监船的正东方向,则现在渔船与海监船的距离为( )A.20海里B.103海里C.202海里D.30海里2.如图,某人从O点沿北偏东30°的方向走了20米抵达A点,B在O点的正东方,且在A 的正南方,则现在AB间的距离是________米.(结果保留根号)3.如图,C、D是两个村落,别离位于一个湖的南、北两头A和B的正东方向上,且D位于C的北偏东30°方向上,且CD=6 km,则AB=________km.4.(长春中考)如图,海面上B、C两岛别离位于A岛的正东和正北方向,一艘船从A岛动身,以18海里/时的速度向正北方向航行2小时抵达C岛,现在测得B岛在C岛的南偏东43°.求A、B两岛之间的距离.(结果精准到海里,参考数据:sin43°≈,cos43°≈,tan43°≈5.(湘西中考)钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队受命在钓鱼岛周围海域进行维权活动,如图,一艘海监船以30海里/时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船抵达点B处,发觉现在钓鱼岛C与该船距离最短.(1)请在图中作出该船在点B处的位置;(2)求钓鱼岛C到B处的距离.(结果保留根号)6.(宜宾中考)如图,某市对位于笔直公路AC上两个小区A、B的供水线路进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为300(3+1)米,求供水站M别离到小区A、B的距离.(结果可保留根号)中档题7.(滨湖区校级二模)某人从A处动身沿北偏东30°方向走了100米抵达B处,再沿北偏西60°方向走了100米抵达C处,则他从C处回到A处至少要________米.8.(昭通中考)小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处动身,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时刻到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精准到1米)?(参考数据:sin37°≈,cos37°≈,tan37°≈,2≈,3≈9.(邵阳中考)一艘参观游船从口岸A以北偏东60°的方向出港参观,航行80海里至C处时发生了侧翻沉船事故,当即发出了求救信号,一艘在口岸正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前去救援,求海警船抵达事故船C处所需的大约时刻.(温馨提示:sin53°≈,cos53°≈10.如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里.(参考数据:sin32°≈,cos32°≈,sin55°≈,cos55°≈(1)求船P到海岸线MN的距离(精准到海里);(2)若船A、船B别离以20海里/时、15海里/时的速度同时动身,匀速直线前去救援,试通过计算判断哪艘船先抵达船P处.综合题11.(苏州中考改编)如图,口岸A在观测站O的正东方向,OA=4 km,某船从口岸A动身,沿北偏东15°方向航行一段距离后抵达B处,现在从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).参考答案基础题1.B4.由题意得,AC=18×2=36(海里),∠ACB=43°.在Rt△ABC中,∵∠A=90°,∴AB=AC·tan∠ACB=36×≈(海里),故A、B两岛之间的距离约为海里.5.(1)如图所示.(2)AB=30×=15(海里),由题意知CB⊥AB,在Rt△ABC中,∠BAC=30°,tan∠BAC=BC AB,∴BC=AB·tan∠BAC=AB·tan30°=15×33=53(海里).答:钓鱼岛C到B处的距离为53海里.6.过点M作MN⊥AB于N,设MN=x米.在Rt△AMN中,∵∠ANM=90°,∠MAN=30°,∴MA=2MN=2x,AN=3MN=3x.在Rt△BMN中,∵∠BNM=90°,∠MBN=45°,∴BN=MN=x,MB=2MN=2x.∵AN+BN=AB,∴3x+x=300(3+1).∴x=300.∴MA=2x=600,MB=2x=300 2.故供水站M到小区A的距离是600米,到小区B的距离是3002米.中档题7.100 28.过P作PC⊥AB于C.在Rt△APC中,AP=200 m,∠ACP=90°,∠PAC=60°,∴PC =200×sin60°=200×32=100 3.∵在Rt △PBC 中,sin37°=PC PB, ∴PB =PCsin37°=错误!≈288(m).答:小亮与妈妈相距约288米. 9.过点C 作CD ⊥AB 交AB 延长线于D.在Rt △ACD 中,∵∠ADC =90°,∠CAD =30°,AC =80海里,∴CD =12AC =40海里.在Rt △CBD 中,∵∠CDB =90°,∠CBD =90°-37°=53°,∴BC =CDsin ∠CBD≈错误!=50(海里).∴海警船抵达事故船C 处所需的时刻大约为:50÷40=54(小时).答:海警船抵达事故船C 处所需时刻约为54小时.10.(1)过点P 作PD ⊥A B 于点D.由题意,得∠PAB =90°-58°=32°,∠PBD =90°-35°=55°,AP =30,在Rt △ADP 中,sin ∠PAD =PDAP ,得PD =AP·sin∠PAD =30×sin32°≈.答:船P 到海岸线MN 的距离约为海里. (2)在Rt △BDP 中,sin ∠PBD =PDBP,∴BP =PDsin ∠PBD =错误!≈,A 船需要时刻为错误!=(小时),B 船需要时刻为错误!≈(小时). ∵>,∴B 船先抵达P 处.答:B 船先抵达P 处. 综合题11.过点A 作AD ⊥OB 于D.在Rt △AOD 中,∵∠ADO =90°,∠AOD =30°,OA =4, ∴AD =OA·sin∠AOD =2.在Rt △ABD 中,∵∠ADB =90°,∠B =∠CAB -∠AOB =75°-30°=45°, ∴BD =AD =2.∴AB =2AD =22,即该船航行的距离(即AB 的长)为2 2 km.。
