3篇5章习题解答

合集下载

第5章习题解答

第5章汇编语言程序设计习题参考答案1．(1) BUFF DB 240 DUP(?)(2) xx DB “BYTE”，”WORD”2．：0000H，则内存分配如下：V AR1V AR2V AR3V AR4V AR53．(1) 段的类型：段的类型有4种，分别是代码段、数据段、堆栈段和附加段。

(2) 段的定义：定义段使用伪指令SEGMENT/ENDS来定义的。

即：段名SEGMENT [定位类型] [组合类型] […类别‟]……段名ENDS(3) 选项的作用和含义：定位类型：告诉汇编程序如何确定逻辑段的边界在存储器的位置，共有4种。

①BYTE：表示逻辑段从字节的边界开始，即本段的起始地址紧接前一段。

②WORD：表示逻辑段从字的边界开始，即本段的起始地址必须是偶数。

③PARA：表示逻辑段从节的边界开始，即本段的起始地址后4位为0。

④PAGE：表示逻辑段从节的边界开始，即本段的起始地址后8位为0。

组合类型：告诉汇编程序当装入存储器时各个逻辑段如何进行组合，共有6种。

①不组合：如果缺省，则不组合。

② PUBLIC：对于不同逻辑段只要有相同段名就把他们集中成一段装入内存。

③ STACK：同PUBLIC相同，但仅限于堆栈段。

④ COMMON：对于不同逻辑段若有相同的段名，则都从同一地址装入。

⑤ MENORY：表示在几个逻辑段连接时，本段定位在地址最高的地方。

⑥ AT 表达式：表示以表达式的值来定位段地址。

‘类别’：在连接时决定各逻辑段的装入顺序。

4. 假设程序中有4个不同类型的段，则名为initprogram宏指令的宏定义如下：initprogram MACRO csname，dsname，esname，ssnameASSUME CS:csname，DS:dsname，ES:esname，SS:ssnameSTART: MOV AX，dsnameMOV DS，AXMOV AX，esnameMOV ES，AXMOV AX，ssnameMOV SS，AXENDM5．假设需传送的数据块为字节数据块，则名为Datastranaction宏指令的宏定义如下：Datastranaction MACRO buffer1，buffer2，lengthLEA SI，buffer1LEA DI，buffer2MOV CX，lengthCLDREP MOVSBENDM6．有效地指令为：(2)、(5)、(9)无效的指令为：(1) 数据类型不一致(3) 两个操作数不能同时为存储器操作数(4) CS不能作为目的操作数(6) 不能用两个变址寄存器作有效地址分量(7) 一个操作数不能是两个变量名的表达式(8) 基址和变址只能相加不能相减(10) 目的操作数不能是立即数(11) 在有效地址中不能减基址或变址严格地说：(9)也不对，因为没有指出存储器的数据类型，即操作数类型不明确。

复变函数第3篇习题课

y
C2
解设C1 : z x, x : 1 1
C1 1 O
|z|z dz C1
0 1
1
x
|x|x dx
1
C2 : z ei t , t : 0 d z eit i d t
|z|z dz
C2
ei
t
e i
t
i d t
idt i
0
0
i 原式= | z | z d z | z | z d z
解(C解3i1C)Cg自C22C：1CC：1z原C11zz2z：：C22点d1dzzCz3沿xz2虚3ix•iy3iy轴,,0,1,03yx(至(i3yx::x::0i0,00i再yi))1水223dd13平((x3C至1 zCi3i21y)zd)2izd6z3019(ii原y032原)3式x62 式d2i=(d=i6yx)6232962363ii i
故被积函数在 | z | 1 上处处解析
积分结果为0. 6
49页8 直接得到下列积分的结果，并说明理由
Ñ (3) ez (z2 1) d z |z|1
解结果为 0 , 因为被积函数 ez (z2 1) 在 | z | 1上处处解析，所以积分结果为0.
Ñ (4)
|z| 1 2
1 (z2 1) (z3 1)
dz
解结果为 0 , 由 (z2 1) (z3 1) 0 得到
z 1, z 1 3 i
2 这2些点都在圆 | z | 1 的外部。
故
被积函数
在
|
z
|
1
上
2
处处解析
2
积分结果为0. 7
49页9 沿指定曲线的正向计算下列积分

第5章感应电机习题与解答

A ；B ；
C ；D 。
答A
6.★三相异步电动机气隙增大，其他条件不变，则空载电流（）。
A 增大； B 减小；
C 不变； D 不能确定。
答A
7.三相感应电动机等效电路中的附加电阻上所消耗的电功率应等于（）：
A输出功率；B输入功率；
C电磁功率；D总机械功率。
答D
8.与普通三相感应电动机相比，深槽、双笼型三相感应电动机正常工作时，性能差一些，主要是（）。
答A
12.★设计在电源上运行的三相感应电动机现改为在电压相同频率为的电网上，其电动机的（）。
A 减小，减小，增大；B 减小，增大，减小；
C 减小，减小，减小；D 增大，增大，增大。
答C
13.一台绕线式感应电动机，在恒定负载下，以转差率运行，当转子边串入电阻 ,测得转差率将为（）（已折算到定子边）。
。
答1，
4.★感应电动机起动时，转差率，此时转子电流的值， ,主磁通比，正常运行时要，因此起动转矩。
答 1，很大，很小，小一些，不大
5.★一台三相八极感应电动机的电网频率，空载运行时转速为735转/分，此时转差率为，转子电势的频率为。当转差率为0.04时，转子的转速为，转子的电势频率为。
答0.02，，，
6.三相感应电动机空载时运行时，电机内损耗包括，，，和，电动机空载输入功率与这些损耗相平衡。
答定子铜耗，定子铁耗，机械损耗，附加损耗
7.三相感应电机转速为，定子旋转磁场的转速为，当时为运行状态；当时为运行状态；当与反向时为运行状态。
答电动机，发电机，电磁制动
8.增加绕线式异步电动机起动转矩方法有，。
Ａ４极，；Ｂ６极，；

《模拟电子技术基础》第三版习题解答第5章放大电路的频率响应

仅供个人使用，请勿用于商业目的第五章放大电路的频率响应自测题一、选择正确答案填入空内。

（1）测试放大电路输出电压幅值与相位的变化，可以得到它的频率响应，条件是。

A.输入电压幅值不变，改变频率B.输入电压频率不变，改变幅值C.输入电压的幅值与频率同时变化（2）放大电路在高频信号作用时放大倍数数值下降的原因是而低频信号作用时放大倍数数值下降的原因是。

A.耦合电容和旁路电容的存在B.半导体管极间电容和分布电容的存在。

C.半导体管的非线性特性D.放大电路的静态工作点不合适（3）当信号频率等于放大电路的fL 或fH时，放大倍数的值约下降到中频时的。

A.0.5倍B.0.7倍C.0.9倍即增益下降A.3dBB.4dBC.5dB相位关系是。

与U （4）对于单管共射放大电路，当f ＝ fL时，U ioA.＋45˚B.－90˚C.－135˚的相位关系是。

与U 当f ＝ fH时，UioA.－45˚B.－135˚C.－225˚解：（1）A （2）B，A （3）B A （4）C C本文档仅供参考第五章题解－1仅供个人使用，请勿用于商业目的二、电路如图T5.2所示。

已知：VCC＝12V；晶体管的Cμ＝4pF，fT = 50MHz，rbb'＝＝80。

试求解：（1）中频电压放大倍数；（2）C'；（3）fH和fL；（4）画出波特图。

图T5.2解：（1）静态及动态的分析估算：br26mVEQ∥RgIEQT本文档仅供参考第五章题解－2 仅供个人使用，请勿用于商业目的' （2）估算：（3）求解上限、下限截止频率：∥∥∥（4）在中频段的增益为频率特性曲线如解图T5.2所示。

解图T5.2本文档仅供参考第五章题解－3 仅供个人使用，请勿用于商业目的三、已知某放大电路的波特图如图T5.3所示，填空：＝ dB，＝。

（1）电路的中频电压增益20lg|Au mu m（2）电路的下限频率fL≈ Hz，上限频率fH≈ kHz.＝。

第5章思考题和习题解答

第五章电气设备的选择5-1 电气设备选择的一般原则是什么?答：电气设备的选择应遵循以下3项原则：(1) 按工作环境及正常工作条件选择电气设备a 根据电气装置所处的位置,使用环境和工作条件,选择电气设备型号；b 按工作电压选择电气设备的额定电压；c 按最大负荷电流选择电气设备和额定电流。

(2) 按短路条件校验电气设备的动稳定和热稳定 (3) 开关电器断流能力校验5-2 高压断路器如何选择？答：（1）根据使用环境和安装条件来选择设备的型号。

（2）在正常条件下，按电气设备的额定电压应不低于其所在线路的额定电压选择额定电压，电气设备的额定电流应不小于实际通过它的最大负荷电流选择额定电流。

（3）动稳定校验(3)max shi i ≥ 式中，(3)sh i 为冲击电流有效值，max i 为电气设备的额定峰值电流。

（4）热稳定校验2(3)2th th ima I t I t ∞≥式中，th I 为电气设备在th t 内允许通过的短时耐热电流有效值；th t 为电气设备的短时耐热时间。

（5）开关电器流能力校验对具有分断能力的高压开关设备需校验其分断能力。

设备的额定短路分断电流不小于安装地点最大三相短路电流，即(3).max cs K I I ≥5-3跌落式熔断器如何校验其断流能力?答：跌落式熔断器需校验分断能力上下限值,应使被保护线路的三相短路的冲击电流小于其上限值,而两相短路电流大于其下限值。

5-4电压互感器为什么不校验动稳定，而电流互感器却要校验？答：电压互感器的一、二次侧均有熔断器保护，所以不需要校验短路动稳定和热稳定。

而电流互感器没有。

5-5 电流互感器按哪些条件选择？变比又如何选择？二次绕组的负荷怎样计算？答：(1）电流互感器按型号、额定电压、变比、准确度选择。

( 2）电流互感器一次侧额定电流有20，30，40，50，75，100，150，200，400，600，800，1000，1200，1500，2000（A ）等多种规格，二次侧额定电流均为5A ，一般情况下，计量用的电流互感器变比的选择应使其一次额定电流不小于线路中的计算电流。

概率论第五章习题解答

概率论第五章习题解答第一篇：概率论第五章习题解答第五章习题解答1.设随机变量X的方差为2，则根据车比雪夫不等式有估计P{X-E(X)≥2}≤ 1/2.P{X-E(X)≥2}≤D(X)22=122.随机变量X和Y的数学期望分别为-2和2，方差分别为1和4，相关系数为-0.5，则根据车比雪夫不等式有估计P{X+Y≥6}≤1/12.P{X+Y≥6}=P{(X+Y)-[E(X)+E(Y)]≥6}≤D(X)62=1123.电站供应一万户用电．设用电高峰时，每户用电的概率为0.9，利用中心极限定理，（1）计算同时用电的户数在9030户以上的概率；（2）若每户用电200 w，电站至少应具有多大发电量才能以0.95的概率保证供电？解：⑴ 设X表示用电户数，则X~B(10000,0.9),n=10000,p=0.9,np=9000,npq=900由中心定理得X~N(9000,900)近似P{X>9030}=1-P{X≤9030}⎧X-90009030-9000⎫=1-P⎨≤⎬900900⎩⎭=1-Φ(1)=1-0.8413=0.1587⑵ 设发电量为Y，依题意P{200X≤Y}=0.95⎧X-9000Y-9000⎫⎪⎪200即 P⎨≤⎬=0.95900900⎪⎪⎩⎭-9000200Φ()=0.95900Y-9000200≈1.65900Y=1809900 4.某车间有150台同类型的机器，每台机器出现故障的概率都是0.02，设各台机器的工作是相互独立的，求机器出现故障的台数不少于2的概率．解：设X表示机器出故障的台数，则X:B(150,0.02)Ynp=3,npq=2.94 由中心定理得X~N(3,2.94)近似P{X≥2}=1-P{X<2}2-3⎫⎧X-3=1-P⎨<⎬2.942.94⎩⎭=1-P{X<-0.58 32}=Φ(0.5832)=0.7201 5.用一种对某种疾病的治愈率为80%的新药给100个患该病的病人同时服用，求治愈人数不少于90的概率．解：设X表示治愈人数，则X:B(100,0.8)其中n=100,p=0.8,np=80,npq=16P{X≥90}=1-P{X<90}⎧X-8090-80⎫=1-P⎨<⎬1616⎩⎭=1-Φ(2.5)=0.0062 6.设某集成电路出厂时一级品率为0.7，装配一台仪器需要100只一级品集成电路，问购置多少只才能以99.9%的概率保证装该仪器是够用(不能因一级品不够而影响工作)．解：设购置n台，其中一级品数为X，X:B(n,0.7)p=0.7,np=0.7n,npq=0.21nP{X≥100}=1-P{X<100}⎧X-0.7n100-0.7n⎫=1-P⎨<⎬0.21n0.21n⎩⎭10 0-0.7n=1-Φ()0.21n=0.999故Φ(-100-0.7n0.21n)=0.999有-100-0.7n0.21n=3.1⇒n=121(舍)或n=1707.分别用切比雪夫不等式与隶莫弗—拉普拉斯中心极限定理确定：当掷一枚硬币时，需要掷多少次才能保证出现正面的频率在0.4～0.6之间的概率不小于90%．解：设掷n次，其中正面出现的次数为X，X:B(n,p),p=⑴由切贝雪夫不等式，要使得P⎨0.4<12⎧⎩X⎫<0.6⎬≥0.9成立n⎭D(X)X⎧X⎫⎧XX⎫25⎧⎫n由于P⎨0.4< <0.6⎬=P⎨-p<0.1⎬=P⎨-E()<0.1⎬≥1-=1-2nnnn0.1n⎩⎭⎩⎭⎩⎭只要1-25X⎧⎫<0.6⎬≥0.9成立≥0.9，就有P⎨0.4<nn⎩⎭从而⇒n≥250⑵中心极限定理，要使得P⎨0.4<⎧⎩X⎫<0.6⎬≥0.9成立n⎭由于X:N(0.5n,0.25n)近似X⎧0.4n-0.5nX-0.5n0.6n-0.5n⎫⎧⎫P⎨0.4<<0.6⎬=P{0.4n<X<0.6n} =P⎨<<⎬n0.25n0.25n0.25n⎩⎭⎩⎭X-0.5n⎧-0.1n=P⎨<<0.25n⎩0.25n所以Φ(0.1n⎫0.1n-0.1n0.1n=Φ()-Φ()=2Φ()-1>0.9⎬0.25n⎭0.25n0.25n0.25 n0.1n0.25n)>0.95查表0.1n0.25n>1.65⇒n≥688.某螺丝钉厂的废品率为0.01，今取500个装成一盒．问废品不超过5个的概率是多少？解：设X表示废品数，则X:B(500,0.01) p=0.01,np=5,npq=4.955-5⎫⎧X-5P{X≤5}=P⎨≤⎬=Φ(0)=0.54.95⎭⎩4.95第二篇：概率论第一章习题解答1.写出下列随机试验的样本空间：1)记录一个小班一次数学考试的平均分数（以百分制记分）；2)一个口袋中有5个外形相同的球，编号分别为1、2、3、4、5，从中同时取出3个球；3)某人射击一个目标，若击中目标，射击就停止，记录射击的次数；4)在单位圆内任意取一点，记录它的坐标.解：1）设小班共有n 个学生，每个学生的成绩为0到100的整数，分别记为x1,x２，Λxn，则全班平均分为x=∑xi=1nin，于是样本空间为12100niS={0，,Λ,}={|i=0,1,2,3,Λ100n}nnnn32）所有的组合数共有C5=10种，S={123,124,125,134,135,145,234,235,245,345} 3）至少射击一次，S={1,2,3,Λ}4）单位圆中的坐标(x,y)满足x2+y2<1，S={(x,y)|x2+y2<1}2.已知A⊂B，P(A)=0.3，P(B)=0.5，求P(A)，P(AB)，P(AB)和P(AB).解 P(A)=1-P(A)=1-0.3=0.7 P(AB)=P(A)=0.3（因为A⊂B）P(AB)=P(B-A)=P(B)-P(A)=0.2P(AB)=P(B)=0.5（因为A⊂B，则B⊂A）3.设有10件产品，其中6件正品，4件次品，从中任取3件，求下列事件的概率：1）只有一件次品； 2）最多1件次品； 3）至少1件次品.12C4C 解 1）设A表示只有一件次品，P(A)=36.C102)设B为最多1件次品，则表示所取到的产品中或者没有次品，或者只有一件次312C6C4C品，P(B)=3+36.C10C103）设C表示至少1件次品，它的对立事件为没有一件次品，3C6P(C)=1-P(C)=1-3C104.盒子里有10个球，分别标有从1到10的标号，任选3球，记录其号码.（1）求最小号码为5的概率.（2）求最大号码为5的概率.解1）若最小号码为5，则其余的2个球必从6，7，8，9，10号这5个球中取得。

无机化学习题解答第五章

第五章氧化-还原反应无机化学习题解答（5）思考题1．什么是氧化数如何计算分子或离子中元素的氧化数氧化数是某一原子真实或模拟的带电数。

若某一原子并非真实得到若失去电子而带电荷，可以认为得到与之键合的电负性小于它的原子的电子或给予与之键合的电负性大于它的原子电子，然后计算出来的带电情况叫氧化数。

已知其他原子的氧化数，求某一原子的氧化数时可用代数和的方法，中性分子总带电数为零；离子总带电数为离子的电荷。

2．指出下列分子、化学式或离子中划线元素的氧化数：As2O3 KO2 NH4+ Cr2O72- Na2S2O3 Na2O2 CrO5 Na2PtCl6 N2H2 Na2S52．As2O3 +3，KO2 +1，NH4+ -3，Cr2O72-+3，Na2S2O3 +2，Na2O2 -1，CrO5 +10，Na2PtCl6 +4，N2H2 -1，Na2S5 -2/5，3．举例说明下列概念的区别和联系：⑴氧化和氧化产物⑵还原和还原产物⑶电极反应和原电池反应⑷电极电势和电动势3．⑴氧化是失去电子氧化数升高，所得氧化态较高产物即为氧化产物。

⑵还原是得到电子氧化数降低，所得氧化态较较产物即为还原产物。

⑶在某个电极上发生的反应为电极反应，分为正极的还原反应和负极的氧化反应，总反应为原电池反应。

⑷固体电极材料与所接触的溶液间的电势差即为该原电池的电极电势。

两电极构成原电池时两电极间的电势差为该原电池的电动势。

4．指出下列反应中何者为氧化剂，它的还原产物是什么何者为还原剂，它的氧化产物是什么⑴2FeCl3+Cu→FeCl2+CuCl2⑵Cu+CuCl2+4HCl→2H2[CuCl3]⑶Cu2O+H2SO4→Cu+CuSO4+H2O4．⑴氧化剂：FeCl3，还原产物：FeCl2，还原剂：Cu，氧化产物：CuCl2。

⑵氧化剂：CuCl2，还原产物：2H2[CuCl3]，还原剂：Cu，氧化产物：2H2[CuCl3]。

⑶氧化剂：Cu2O，还原产物：Cu，还原剂：Cu2O，氧化产物：CuSO4。

习题答案：第5章拉深

第5章拉深一、填空1．拉深系数m是筒形直径和坯料直径的比值，m越小，则变形程度越大。

(5-1)2．拉深过程中，变形区是坯料的凸缘部分，其它部分是传力区。

(5-1)3．拉深中，产生起皱现象是因为该区域内受较大压应力的作用，导致材料失稳而引起的。

(5-1)4．影响拉深坯料起皱的主要因素有：材料相对厚度，拉深系数和拉深模工作部分的几何形状和尺寸。

(5-1)5．防止圆筒形件拉深起皱的方法通常是采用压料装置，并采用适当的压边力。

(5-1) 6．利用拉深模将一定形状的平面坯料或空心件制成开口件的冲压工序叫做拉深。

(5-1)7．拉深件的壁厚是不均匀的，下部壁厚略有变薄，上部分却有所增厚。

(5-1)8．板料的相对厚度t/D越小，则抗失稳能力越小，越容易起皱。

(5-1)9．一般情况下，拉深件的尺寸精度应在 IT13级以下，不宜高出 IT11 级。

(5-2)10．实践证明，拉深件的平均厚度与坯料厚度相差不大，由于塑性变形前后体积不变，因此，可以按坯料面积等于拉深件表面积原则确定坯料尺寸。

(5-3)11．拉深件的毛坯尺寸确定依据是等面积法。

(5-3)12．确定拉深件坯料形状和尺寸的原则是久里金法则。

(5-3)13．影响极限拉深系数的因素有：材料的组织与力学性能、板料的相对厚度、拉深工作条件等。

(5-4)14．有凸缘拉深件多次拉深必须遵循一个原则，即第一次拉深成有凸缘的工序件时，其凸缘的外径应等于成品零件的尺寸，在以后的拉深工序中仅仅使已拉深成形的工序件的直筒部分参与变形，逐步减少其直径并增加其高度，而第一次拉深时已成形的凸缘外径必须保持不变。

即在以后的拉深工序中不再收缩。

(5-4)15．为了提高工艺稳定性，提高零件质量，必须采用稍大于极限值的拉深系数。

(5-4)16．窄凸缘圆筒形状零件的拉深，为了使凸缘容易成形，在拉深窄凸缘圆筒零件的最后两道工序可采用锥形凹模和锥形压料圈进行拉深。

(5-4)17．压料力的作用为：防止拉深过程中坯料起皱(5-5)18．目前采用的压料装置有弹性压料和刚性压料装置。

软件项目管理第3版第5章习题答案参考答案范围管理

软件项⽬管理第3版第5章习题答案参考答案范围管理[填空][⼦项⽬]1.任务分解是将⼀个项⽬分解为更多的⼯作细⽬或者()，是项⽬变得更⼩、更易管理、更易操作。

[填空][清单，图表]2. ⼀般来说，进⾏项⽬分解时，可以采⽤()或()两种形式来表达任务分解的结果。

[填空][任务分解结构，Work Breakdown Structure]3.WBS的全称是()。

[填空][⼯作包，work package]4.WBS最底层次课交付成果是()。

[是⾮][A]1.WBS提供了项⽬范围基线。

（）[A]正确[B]错误[是⾮][A]2.⼀个⼯作包可以分配给另⼀个项⽬经理去完成。

（）原⽂：⼯作包应当由唯⼀主体负责，可以分配给另外⼀位项⽬经理通过⼦项⽬的⽅式完成。

[A]正确[B]错误[是⾮][B]3.如果开发⼈员对项⽬⽐较熟悉或者对项⽬⼤局有把握，开发WBS时最好采⽤⾃底向上⽅法。

（）[A]正确[B]错误[是⾮][A]4.对于⼀个没有做过的项⽬，开发WBS时可以采⽤⾃底向上⽅法。

（）[A]正确[B]错误[是⾮][A]5.在任务分解结果中，最底层的要素必须是实现项⽬⽬标的充分必要条件。

（）[A]正确[B]错误[是⾮][A]6.任务分解是将⼀个项⽬分解为更多的⼯作细⽬或者⼦项⽬，是项⽬变得更⼩、更易管理和操作。

（）[A]正确[B]错误[是⾮][A]7.⼀个⼯作包应当由唯⼀主题负责。

（）[A]正确[B]错误[是⾮][B]8.WBS的最⾼层次的可交付成果是⼯作包。

（）[A]正确[B]错误[是⾮][B]9.对任务的分解只能是⾃上⽽下的。

（）[A]正确[B]错误[是⾮][A]10.WBS的最底层任务是能分配到⼀个⼈完成的任务。

（）[A]正确[B]错误原⽂：⼯作包应当由唯⼀主体负责，可以分配给另外⼀位项⽬经理通过⼦项⽬的⽅式完成。

[单选][D]1.WBS⾮常重要，因为下列原因，除了（）[A]帮助组织⼯作[B]防⽌遗漏⼯作[C]为项⽬估算提供依据[D]确定团队成员责任[单选][A]2.WBS中的每⼀个具体细⽬通常都指定唯⼀的（）[A]编码[B]地点[C]功能模块[D]提交截⾄期限[单选][C]3.下列不是创建WBS的⽅法的是（）[A]⾃顶向下[B]⾃底向上[C]控制⽅法[D]模板参照[单选][D]4.任务分解时，（）⽅法从特殊到⼀般的⽅向进⾏，⾸先定义⼀些特殊的任务，然后将这些任务组织起来，形成更⾼级别的WBS层。

5章化学平衡原理习题及全解答

第5章化学平衡原理习题及全解答1. 写出下列反应的标准平衡常数表达式。

(1) CH 4(g) + 2O 2(g) == CO 2(g) + 2H 2O(l) (2) PbI 2(s) == Pb 2+(aq) + 2I -(aq)(3) BaSO 4(s) + 2C(s) == BaS(s) + 2CO(g) (4) Cl 2(g) + H 2O(l) == HCl(aq) + HClO(aq) (5) ZnS(s) + 2H +(aq) == Zn 2+(aq) + H 2S(g) (6) CN -(aq) + H 2O(l) == HCN(aq) + OH -(aq)答： (1) 224242θCO CO θθθ22CH O CH O /(/)(/)pp p p K p p p p p p==(相对压力)(2) 2+-2+-θθθ22Pb I Pb I (/)(/)c K c c c c c c == (相对浓度)(3) θθ2CO (/)p K p p = (4) 2θθHCl HClO Cl /(/)K c c p p =(5) 2++2θθ2H S Zn H (/)/K c p p c = (6) --θHCN OH CN /K c c c =2. 填空题(1) 对于反应：C(s)+CO(g)==2CO(g)，=172.5 kJ ⋅mol -1，填写下表：532定量的惰性气体，反应将移动。

(3) 对化学反应而言，r m G ∆是的判据，r m G ∆是的标志，若r m G ∆ =r mG ∆，则反应物和生成物都处于状态。

动。

(3) 反应方向；反应进行倾向性；平衡。

3. 氧化亚银遇热分解：2Ag 2O(s) == 4Ag(s) + O 2(g)。

已知Ag 2O 的f m H ∆ =-31.1kJ ⋅mol -1，f m G ∆=-11.2 kJ·mol -1。

求：（1）在298K 时Ag 2O —Ag 体系的2O p =？（2） Ag 2O 的热分解温度是多少(在分解温度，2O p ＝100kPa)？解： (1) -1r m Bf m 62.2 kJ mol H H ν∆=∆=⋅∑ ，-1r m B f m 22.4 kJ mol G G ν∆=∆=⋅∑2θθO /p K p p=，根据r m ln ()/K G T RT =-∆ ，当T =298 K 时， 3ln 22.410/(8.314298)9.04K =-⨯⨯=- 41.210K -=⨯P (o 2) =Pa 12k 100102.14=⨯⨯=⨯- p K p(2) 在分解温度，2O p ＝100 kPa ， 1.0K = ，r m ()G T ∆=0根据Gibbs 方程：r m r m r m ()G T H T S ∆=∆-∆ ，r m r m/T H S =∆∆ 根据r m H ∆ 、r m S ∆ 随温度变化不大，故：-1r m r m ()(298)62.2 kJ mol H T H ∆≈∆=⋅ -1-1r m r m r m r m(298)(298)()(298)0.134 kJ mol K 298H G S T S ∆-∆∆≈∆==⋅⋅r mr m/465 K T H S =∆∆分解＝或者：根据van ’t Hoff 方程：22r m 211112()ln ()K T H T T K T RT T ∆-=，412(298) 1.210, ()1K K T -=⨯=分解，解得：465 K T =分解。

第五章课后练习题三及答案

第五章课后练习题三资料：某公司12月发生的经济业务要求：根据12月发生的经济业务编制会计分录（1）12月1日，公司开出现金支票从开户银行提取现金5000元，以备零星开支用。

（2）12月2日，公司用银行存款100000元预付给友谊工厂订购丙材料。

（3）12月3日，公司接受A投资人的投资1000,000元，存入银行，已办完各种手续。

接受B投资者投入设备1台，该设备的账面原值为500万，已提折旧400万；公司接受投资时，经双方同意，该设备按150万的价值入账。

（4）12月3日，签发并承兑商业汇票购入丁材料，发票注明价款350000元，增值税进项税额59500元。

另外，公司用银行存款5500元支付丁材料的运杂费。

丁材料验收入库。

（5）12月3日，公司发行股票1000，000股，发行价1.5元，所得款项1500，000元，存入银行。

（6）12月4日，公司购入下列材料：甲材料6000千克单价30元价款计180000元乙材料3500千克单价20元价款计70000元用银行存款支付材料价款及增值税款（增值税税率17%）。

材料尚在运输途中。

（7）12月5日，公司用银行存款7200元预付明年的报章杂志订阅费。

（8）12月6日，公司的业务部张良出差归来报销差旅费1680元，余款补足现金（原借款1500元）。

（9）12月8日，公司从某商店购入一台需要安装的Q非生产用设备，其买价260000元，增值税税额44200元，包装运杂费等4800元，款项通过银行支付；设备投入安装。

（10）12月9日，公司用银行存款7600元支付本月购入的甲、乙材料的外地运杂费，按材料的重量比例分配。

材料验收入库。

（11）12月10日，公司开出现金支票从银行提取现金568000元，直接发放工资。

（12）12月12日，公司向某客户销售S产品一批，价款850000元，增值税销税率17%。

另外，公司用银行存款代客户垫付运杂费6500元。

全部款项收到一张已承兑商业汇票。

第5章习题解答

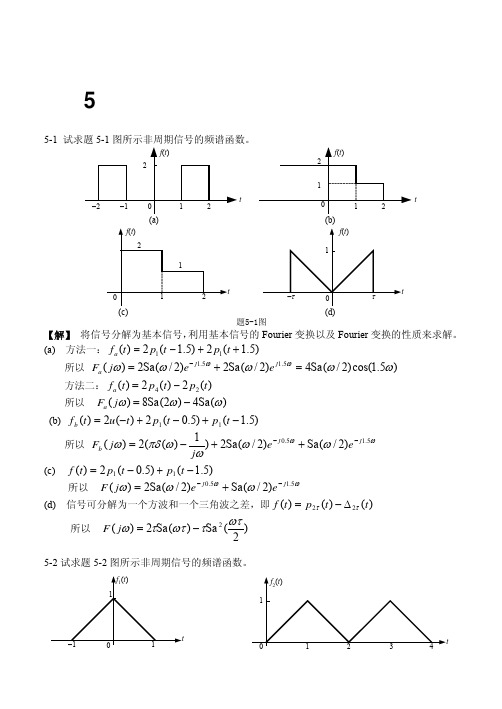
− e− j3ω )
(d) f4 (t) = − f1(t −1) − f1(t − 3) = − f2 (t)
所以
F4 ( jω)
=
−Sa 2 (ω )(e− jω 2
+ e − j3ω )
5-3 试写出下列信号的频谱函数, ω 0 为常数。 (1) f (t) = sin ω0t + cosω0 (t − t0 ) (2) f (t) = e−2t cosω0t ⋅ u(t)
∫0
(6) F{e−αtu(−t)} = e−αte− jωtdt = −
1
, α <0
−∞
α + jω
(7) f (−5t) ↔ 1 F (− j ω ) , f (5 − 5t) = f (−5(t −1)) ↔ 1 F (− j ω )e− jω
5
5
5
5
(8)
F{(t − 2) f (t)} =
(b) fb (t) = 2u(−t) + 2 p1 (t − 0.5) + p1 (t −1.5)
所以
Fb ( jω) = 2(πδ (ω) −
1 ) + 2Sa(ω / 2)e− j0.5ω + Sa(ω / 2)e− j1.5ω jω
(c) f (t) = 2 p1 (t − 0.5) + p1 (t −1.5) 所以 F ( jω) = 2Sa(ω / 2)e− j0.5ω + Sa(ω / 2)e− j1.5ω
所以
F3 (
jω)
=
F(
jω)e− jω
+
F1(
jω)e jω
=
F(
jω)e− jω

第五章习题解答

习题五1. 设V 是数域F 上向量空间，假如V 至少含有一个非零向量α，问V 中的向量是有限多还是无限多？有没有n (n ≥ 2)个向量构成的向量空间？解无限多；不存在n (n ≥ 2)个向量构成的向量空间(因为如果F 上一个向量空间V 含有至少两个向量, 那么V 至少含有一个非零向量α , 因此V 中含有α , 2α , 3α , 4α , …,这无穷多个向量互不相等,因此V 中必然含有无穷多个向量).2. 设V 是数域F 上的向量空间，V 中的元素称为向量，这里的向量和平面解析几何中的向量α，空间解析几何中的向量β有什么区别？解这里的向量比平面中的向量意义广泛得多,它可以是多项式,矩阵等,不单纯指平面中的向量.3. 检验以下集合对所指定的运算是否构成数域F 上的向量空间.（1）集合：全体n 阶实对称矩阵；F ：实数域；运算：矩阵的加法和数量乘法；（2）集合：实数域F 上全体二维行向量；运算： (a 1, b 1)+ (a 2, b 2)＝(a 1＋a 2, 0) k • (a 1, b 1)＝(ka 1, 0)（3）集合：实数域上全体二维行向量；运算： (a 1, b 1)+ (a 2, b 2)＝(a 1＋a 2, b 1＋b 2)k •( a 1, b 1)＝(0, 0)解 (1) 是; (2) 不是(因为零向量不唯一);(3) 不是(不满足向量空间定义中的(8)).4. 在向量空间中，证明，(1) a (－α)=－a α=(－a ) α ,(2) (a -b )α＝a α－b α ,a ,b 是数，α是向量.证明 (1) a a a a =+-=+-))(()(αααα 0= 0ααa a -=-∴)(又 ==+-=+-a a a a a 0))(()(ααα 0ααa a -=-∴)(综上, .)()(αααa a a -=-=-(2) ααααααb a b a b a b a -=-+=-+=-)())(()(.5. 如果当k 1＝k 2＝…＝k r ＝0时，k 1α1＋k 2α2＋…＋k r αr ＝0, 那么α1, α2, …, αr 线性无关. 这种说法对吗？为什么?解这种说法不对. 例如设α1=(2,0, -1), α2=(-1,2,3), α3=(0,4,5), 则0α1+0α2+0α3=0. 但α1, α2, α3线性相关, 因为α1+2α2－α3=0.6. 如果α1, α2, …, αr 线性无关，而αr ＋1不能由α1, α2, …, αr 线性表示，那么α1, α2,…, αr , αr ＋1线性无关. 这个命题成立吗？为什么？解成立. 反设α1, α2,…, αr , αr ＋1线性相关,由条件α1, α2, …, αr 线性无关知αr ＋1一定能由α1, α2, …, αr 线性表示,矛盾.7. 如果α1, α2, …, αr 线性无关，那么其中每一个向量都不是其余向量的线性组合. 这种说法对吗？为什么？解对. 反设 αi = k 1α1+k 2α2+…k i -1αi-1+k i+1αi ＋1 +…+k r αr ,则 k 1α1+k 2α2+…k i -1αi-1+(－1) αi +k i+1αi ＋1 +…+k r αr =0. 由于－1≠0, 故α1, α2, …, αr 线性相关.8. 如果向量α1, α2, …, αr 线性相关，那么其中每一个向量都可由其余向量线性表示. 这种说法对吗？为什么？解不对. 设α1=(1,0) , α2=(2,0) , α3=(0,1) , 则α1, α2, α3线性相关, 但α3不能由α1, α2线性表示.9. 设α1＝ (1, 0, 0), α2＝ (1, 2, 0), α3＝(1, 2, 3)是F 3中的向量，写出α1, α2, α3的一切线性组合. 并证明F 3中的每个向量都可由{α1, α2, α3}线性表示.解 k 1α1+k 2α2+k 3α3 k 1, k 2 , k 3∈F .设k 1α1+k 2α2+k 3α3=0,则有⎪⎩⎪⎨⎧==+=++030220332321k k k k k k , 解得 k 1= k 2 =k 3=0.故α1, α2, α3线性无关.对任意(a,b,c)∈F 3, (a,b,c)=3213)32())322((αααc c b c ba +-+--,所以F 3中的每个向量都可由{α1, α2, α3}线性表示.10. 下列向量组是否线性相关(1) α1＝ (1, 0, 0), α2＝ (1, 1, 0), α3＝(1, 1, 1)；(2) α1＝(3, 1, 4), α2＝(2, 5, -1), α3＝(4, -3, 7).解 (1) 线性无关; (2) 线性无关.11. 证明，设向量α1, α2, α3线性相关，向量α2, α3, α4线性无关，问：(1) α1能否由α2, α3线性表示？说明理由；(2) α4能否由α1, α2, α3线性表示？说明理由.解 (1)因为α2, α3线性无关而α1, α2, α3线性相关,所以α1能由α2, α3线性表示;(2)反设α4能由α1, α2, α3线性表示,但α1能由α2, α3线性表示,故α4能由α2, α3线性表示,这与α2, α3, α4线性无关矛盾,所以α4不能由α1, α2, α3线性表示.12. 设α1＝ (0, 1, 2), α2＝ (3, －1, 0), α3＝(2, 1, 0)，β1＝ (1, 0, 0), β2＝ (1, 2, 0), β3＝(1, 2, 3)是F 3中的向量. 证明，向量组{α1, α2, α3}与{β1, β2, β3}等价.证明 (β1, β2, β3)=(321,,εεε)A(α1, α2, α3)= (321,,εεε)B其中A=⎪⎪⎪⎭⎫ ⎝⎛300220111, B=⎪⎪⎪⎭⎫ ⎝⎛-002111230.易验证A , B 均可逆, 这样 (β1, β2, β3) = (α1, α2, α3 )(B -1A )(α1, α2, α3) = (β1, β2, β3)(A -1B ) ,故向量组{α1, α2, α3}与{β1, β2, β3}等价.13. 设数域F 上的向量空间V 的向量组{α1, α2, …, αs }线性相关，并且在这个向量组中任意去掉一个向量后就线性无关. 证明，如果∑=s i i ik 1α＝0 (k i ∈F )，那么或者k 1＝k 2＝…＝k s ＝0, 或k 1，k 2，…，k s 全不为零.证明由条件∑=s i i ik 1α＝0 (k i ∈F )知k i αi = - (k 1α1+k 2α2+…k i -1αi-1+k i+1αi ＋1 +…+k s αs ) （*）(1) 当k i =0时,（*)式左边等于零,故k 1α1+k 2α2+…k i -1αi-1+k i+1αi ＋1 +…+k s αs =0. 由于这s -1个向量线性无关,所以k 1＝k 2＝…＝k s ＝0.(2) 当k i ≠0时, αi = -ik 1(k 1α1+k 2α2+…k i -1αi-1+k i+1αi ＋1 +…+k s αs ),下证对于任意i j s j ≠∈},,2,1{ 时k j ≠0. 反设k j =0, 则αi 可由s -2个向量线性表示.这与任意s -1个向量线性无关矛盾,所以此时k 1,k 2，…，k s 全不为零.14. 设α1＝(1, 1), α2＝(2, 2), α3＝(0, 1) , α4＝(1, 0)都是F 2中的向量. 写出{α1, α2, α3, α4}的所有极大无关组.解 α1, α3 ; α1, α4 ; α2 ,α3 ; α2 ,α4 ; α3 ,α4 .15. 设A 1＝⎪⎪⎭⎫ ⎝⎛-2001,A 2＝⎪⎪⎭⎫ ⎝⎛-0021, A 3＝⎪⎪⎭⎫ ⎝⎛0120,A 4＝⎪⎪⎭⎫ ⎝⎛-2142∈M 2×2(F ). 求向量空间M 2×2(F )中向量组{A 1, A 2,A 3, A 4}的秩及其极大无关组. 解秩{A 1, A 2,A 3, A 4}=3, {A 1, A 2,A 3}是向量组{A 1, A 2, A 3, A 4}的一个极大无关组.16．设由F 4中向量组｛α1=(3，1，2，5)，α2＝(1，1，1，2)，α3＝(2，0，1，3)，α4 =(1，－1，0，1)，α5 =(4，2，3，7)｝. 求此向量组的一个极大无关组.解 (α1,α2,α3,α4,α5)= (4321,,,εεεε)A , 其中A=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-71325301122101141213, 则秩A =2. 又(α1,α2 )= (4321,,,εεεε)B , 其中B =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛25121113. 秩B =2, 故{α1,α2}线性无关, 它是向量组{α1,α2,α3,α4,α5}的一个极大无关组.17. 证明，如果向量空间V 的每一个向量都可以唯一表成V 中向量α1, α2, …, αn 的线性组合，那么dim V ＝n .证明由条件零向量可唯一的表示成α1, α2, …, αn 的线性组合, 这说明α1, α2, …, αn 线性无关, 故可作为V 的基, 从而dim V ＝n .18. 设β1, β2，…，βn 是F 上n (>0)维向量空间V 的向量，并且V 中每个向量都可以由β1, β2，…，βn 线性表示. 证明, {β1, β2，…，βn }是V 的基.证明由条件标准正交基{ e 1, e 2, …,e n }可由β1, β2，…，βn 线性表示, 反过来β1, β2，…，βn 又可由{ e 1, e 2, …,e n }线性表示,所以{ e 1, e 2, …,e n }和{β1, β2，…，βn }等价. 由{ e 1, e 2, …,e n }线性无关知{β1, β2，…，βn }线性无关,又因V 中每个向量都可以由β1, β2，…，βn 线性表示, 由基的定义知{β1, β2，…，βn }是V 的基.19. 复数集C 看作实数域R 上的向量空间（运算: 复数的加法，实数与复数的乘法）时，求C 的一个基和维数.解基为{1, i }； dim C ＝2.20. 设V 是实数域R 上全体n 阶对角形矩阵构成的向量空间（运算是矩阵的加法和数与矩阵的乘法）. 求V 的一个基和维数.解基为E ii (i =1,2, …,n )； dim V ＝n .21. 求§5.1中例9给出的向量空间的维数和一个基.解任意一个不等于1的正实数都可作为V 的基； dim V ＝1.22. 在R 3中，求向量α＝(1, 2, 3)在基ε1＝(1, 0, 0)，ε2＝(1, 1, 0)，ε3＝(1, 1, 1)下的坐标.解 (-1,-1,3)T .23. 求R 3中由基{α1, α2, αs }到基{β1, β2, β3 }的过渡矩阵，其中α1＝(1, 0, -1), α2＝(-1, 1, 0), α3＝(1, 2, 3)，β1＝(0, 1, 1), β2＝(1, 0, 1), β3＝(1, 1, 1).解所求过渡矩阵为⎪⎪⎪⎭⎫ ⎝⎛-32204230061. 24. 设{α1, α2,…, αn }是向量空间V 的一个基，求由这个基到基{α3, α4, …, αn ，α1, α2}的过渡矩阵.解所求过渡矩阵为⎪⎪⎭⎫ ⎝⎛-0022n I I . 25. 已知F 3中向量α关于标准基ε1＝(1, 0, 0)，ε2＝(0, 1, 0) ，ε3＝(0, 0, 1)的坐标是(1, 2, 3)，求α关于基β1＝(1, 0, 1), β2＝(0, 1, 1), β3＝(1, 1, 3)的坐标.解 (1,2,0)T .26. 判断R n 的下列子集哪些是子空间(其中R 是实数域，Z 是整数集).(1) {(a 1, 0, …, 0, a n )| a 1, a n ∈R };(2) {(a 1, a 2, …, a n )|∑==ni i a 10，a 1, a 2, …, a n ∈R };(3) {(a 1, a 2, …, a n )|a i ∈Z , i ＝1, 2, …, n };解 (1) 是; (2) 是; (3) 不是(数乘不封闭).27. 设V 是一个向量空间，且V ≠{0}. 证明，V 不能表成它的两个真子空间的并集.证明设W 1与W 2是V 的两个真子空间(1) 若21W W ⊆，则W 1⋃W 2= W 2≠V ;(2) 若21W W ⊇,则W 1⋃W 2= W 1≠V ;(3) 若21W W ⊄且12W W ⊄, 取1W ∈α但2W ∉α,2W ∈β但1W ∉β, 那么1W ∉+βα,否则将有1)(W ∈=-+βαβα,这与1W ∉β矛盾, 同理2W ∉+βα, 所以V 中有向量21W W ∉+βα,即V ≠21W W .28. 设V 是n 维向量空间，证明V 可以表示成n 个一维子空间的直和.证明设{α1, α2,…, αn }是向量空间V 的一个基, (α1), (α2) ,…, (αn )分别是由α1, α2,…, αn 生成的向量空间, 要证(α1+α2+…+αn )= (α1)⊕ (α2)⊕…⊕ (αn )(1) 因为{α1, α2,…, αn }是V 的一个基, 所以V 中任一向量α都可由α1, α2,…, αn 线性表示, 此即(α1+α2+…+αn )= (α1)+ (α2)+…+ (αn ).(2) 对任意i ≠j ∈{1,2,…, n },下证 (αi )∩ (αj )={0}. 反设存在0 ≠∈x (αi )∩ (αj ),由∈x (αi )知存在k F ∈使得x =k αi ；由 x ∈ (αj )知存在F l ∈使得x =l αj , 从而αi =kl αj , 即α1与α2线性相关, 矛盾, 所以 (αi )∩ (αj )={0}. 综上, (α1+α2+…+αn )= (α1)⊕ (α2)⊕…⊕ (αn ).29. 在R 3中给定两个向量组α1＝(2, -1, 1, -1), α2＝(1, 0, -1, 1),β1＝(-1, 2, -1, 0), β2＝(2, 1, -1, 1).求 (α1, α2)＋ (β1, β2) 的维数和一个基.解取R 4的标准正交基{4321,,,εεεε},于是(α1, α2, β1, β2)= (4321,,,εεεε)A ,其中 A =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------1011111112012112 , 秩A = 4. 故α1, α2, β1, β2线性无关, 又因为 (α1, α2)∩ (β1, β2)={0},所以dim (α1, α2) + dim (β1, β2)= 4,{ α1, α2, β1, β2}是它的基.30. 设W 1, W 2都是向量空间V 的子空间，证明下列条件是等价的：(1) W 1⊆W 2;(2) W 1∩W 2＝W 1;(3) W 1＋W 2＝W 2.证明 (i) (1)⇒(2) 因为W 1⊆W 2 , 所以W 1∩W 2＝W 1. (ii) (2)⇒(3) W 1＋W 2 ={α1+α2 | α1∈W 1, α2∈W 2} 由(2)知对任意α∈W 1, 都有α∈W 2 , 所以W 1＋W 2 ={α1+α2 | α1, α2∈W 2}=W 2 .(iii) (3)⇒(1) W 1＋W 2 ={α1,+α2 | α1∈W 1, α2∈W 2}=W 2 , 说明对任意α∈W 1, 都有α∈W 2 , 此即W 1⊆W 2 .31. 设V 是实数域R 上n 阶对称矩阵所成的α2向量空间；W 是数域R 上n 阶上三角矩阵所成的向量空间，给出V 到W 的一个同构映射.解对∈∀A V (A =(a ij )且a ij = a ji )和B ∈W (B =(a ij ),当i>j 时, a ij =0) 定义f : V → WA B 易验证f 是V 到W 的一个同构映射.32. 设V 与W 都是数域F 上的向量空间，f 是V 到W 的一个同构映射，证明{α1, α2, …, αn }是V 的基当且仅当{f (α1), f (α2), …, f (αn )}是W 的基.证明设{α1, α2, …, αn }是V 的基.(1) 由α1, α2, …, αn 线性无关知f (α1), f (α2), …, f (αn ) 线性无关.(2) 任取∈ηW , 由f 是同构映射知存在∈ξV 使得f (ξ)=η.但ξ=∑=n i i ia 1α, a i ∈F , f (ξ)=f (∑=n i i i a 1α)=)(1∑=n i i i f a α=η. 由η的任意性知{f (α1), f (α2), …, f (αn )}是W 的基.反过来, {f (α1), f (α2), …, f (αn )}是W 的基(1) 由f (α1), f (α2), …, f (αn )线性无关知α1, α2, …, αn 线性无关.(2) 任取∈ξV , 由f 是同构映射知存在∈ηW 使得f (ξ)=η.但η=∑=n i i i f k 1)(α= f (∑=n i i i k 1α), k i ∈F , 从而ξ=∑=ni i i k 1α, k i ∈F .由ξ的任意性知{ α1, α2, …, αn }是V 的基.补充题1. 设W 1, W 2是数域F 上向量空间V 的两个子空间. α,β是V 的两个向量，其中α∈W 2，但α∉ W 1，β∉W2. 证明：（1）对于任意k ∈F ，αβk +∉W 2；（2）至多有一个k ∈F ，使得αβk +∈W 1.证明 (1)反设存在k 1∈F 使得αβ1k +∈W 2 , 又α∈W 2 , 因此β=β+ k 1α-k 1α∈W 2 , 这与β∉W 2矛盾. 所以对于∀k ∈F ，αβk +∉W 2 .(2)若有k 1, k 2∈F , k 1≠k 2使得αβ1k +, αβ2k +∈W 1, 那么。

第5章-习题详解

z B w 0
α
Φ = ∫ B ⋅ dS = e y Bm sin(ωt ) ⋅ en hw
S
h y en
= Bm hw sin(ωt ) cos α dΦ = −ωBm hw cos(ωt ) cos α in = − dt
x 穿过线圈的磁通变化既 (2) 线圈以角速度 ω 旋转时，习题 5-1 题图有因磁场随时间变化引起的，又有因线圈转动引起的。此时线圈面的法线 e n 是时间的函数，表示为 en (t ) ， α = ωt 。因此
Φ = B (t ) ⋅ en (t ) S = e y Bm sin(ωt ) ⋅ e y hw cos α = Bm hw sin(ωt ) cos(ωt )
故
in
=−
dΦ = −ωBm hw cos 2ωt dt
5-2
长直导线载有电流 i = I m cos ωt ，其附近有一 a × b 的矩形线框，如图所示。在下列两种情况下求线圈中的感应电动势：(1)线圈静止不动；(2)线圈以速度 v 向右方运动。
导体表面外侧的坡印廷矢量s由高斯定理可知面电荷在导体外产生的电场为当轴向通以均匀分布的恒定电流i设以电流流向为z坐标方向时导体内的电场为根据边界条件导体表面上电场的切向分量应连续即oz恒定电流i在导体外产生的磁场为521在球坐标系下已知真空中时变电磁场的电场强度为cossin
第 5 章时变电磁场
5-1
C/ m 2
10 4 cos(ωt − kz ) ，电缆的内外导体之间填充了理想 r 介质，介质参数为 ε r = 2, µ r = 1 。求：理想介质中的电场强度 E 和磁场强度 H 。
在无源区域，已知电磁场的电场强度 E = e x 0.1sin(6.28 ×109 t − 20.9 z ) V/m，求空间任一点的磁场强度 H 和磁感应强度 B。

移动通信原理习题答案5章

Chapter 11、为什么寻呼系统需要提供较低的数据传输速率？较低的数据速率如何实现更好的覆盖？答：寻呼系统用来提供高度可靠地覆盖，甚至包括建筑物内部。

而建筑物能削弱无线信号20-30dB 。

因此我们希望在信号传输过程中提高信噪比。

发射功率是一定的，因此提高信噪比要求降低接收端的噪声电平，因为噪声电平和射频带宽成正比，因此提高信噪比必然要求我们减小射频带宽，射频带宽的减小导致较低的数据传输速率。

寻呼机的接收信噪比随着寻呼机与基站距离的增加而减小。

若将寻呼系统的覆盖范围用寻呼机正确接收所需的最低信噪比门限来表示，那么为了得到更好的覆盖，可以通过降低噪声功率来使得信噪比满足门限限制，即降低频带宽度（使得速率降低）。

2、假设蜂窝电话使用容量为1安培小时的电池。

假设蜂窝电话在空闲时耗电35mA ，通话时耗电250mA 。

如果用户一直开机，并且每天通话3分钟，那么这个电池能用多久？每天通话6小时呢？该电池最多能通话多久。

答：每天通话三分钟，则每天耗电：35*（24-3/60）+250*3/60=850.75mAh ，故可用1000/850.75=1.175天=28.21小时每天通话6小时，则每天耗电：35*18+250*6=2130mAh>1000mAh ，故一天不能通话6小时，最长通话时间为：1000/250=4小时。

移动通信原理习题Chapter 31、证明对六边形系统，同频复用因子为Q =3N ,其中22N i j ij =++. 答：如图，由余弦定理：RD2、一个FDD 蜂窝电话系统分配有24MHz 总带宽，并使用两个30kHz 信道来提供全双工语音和控制信道。

设每个小区电话用户的业务量为0.1 Erlang 。

假设使用Erlang B 公式。

()2222222233222232cos12023333D i R j R i j R i j ij R NR ⎛⎫⎛⎫=⨯⨯+⨯⨯ ⎪ ⎪⎝⎭⎝⎭⎛⎫-⨯⨯⨯ ⎪⎝⎭=++=233D NRQ N R R⇒===（a ）计算在4小区复用系统中每个小区的信道数。

PLC-3、4、5章习题参考答案

3章习题答案1．填空1）输出指令（对应于梯形图中的线圈）不能用于过程映像输入寄存器。

2）SM 0.1 在首次扫描时为ON，SM0.0一直为ON。

3）每一位BCD码用_4_位二进制数来表示，其取值范围为二进制数2#0000_～2#_1001_。

4）二进制数2#0100 0001 1000 0101对应的十六进制数是_16#4185_，对应的十进制数是_16773_，绝对值与它相同的负数的补码是2#_1011 1110 0111 1011_。

5）BCD码2#0100 0001 1000 0101对应的十进制数是_4185_。

6）接通延时定时器TON的使能（IN）输入电路接通时开始定时，当前值大于等于预设值时其定时器位变为ON，梯形图中其常开触点接通，常闭触点断开。

7）接通延时定时器TON的使能输入电路断开时被复位，复位后梯形图中其常开触点断开，常闭触点接通，当前值等于0。

8）有记忆接通延时定时器TONR的使能输入电路接通时开始定时，使能输入电路断开时，当前值保持不变。

使能输入电路再次接通时继续定时。

必须用复位指令来复位TONR。

9）断开延时定时器TOF的使能输入电路接通时，定时器位立即变为ON，当前值被清零。

使能输入电路断开时，当前值从0开始增大。

当前值等于预设值时，输出位变为OFF，梯形图中其常开触点断开，常闭触点接通，当前值保持不变。

10）若加计数器的计数输入电路CU 由断开变为接通、复位输入电路R断开，计数器的当前值加1。

当前值大于等于预设值PV时，梯形图中其常开触点接通，常闭触点断开。

复位输入电路接通时，计数器被复位，复位后其常开触点断开，常闭触点接通，当前值为0。

2．不是，因为1010的10进制数为10超过9，BCD码最大是9即1001。

3．-914．16#5．无符号数。

6．VB20和VB21，VB207．VW20和VW22，VB20~VB23，VW22，VB208．十进制小数9．字符的个数10．3212．4个，8、16、32位13．程序组织单元，主程序、子程序、中断程序14．AIW215．VB100的地址，地址指针VD120所指的存储单元中的数16．在程序中修改操作数的地址，用于间接寻址题3-17~3-19的语句表程序I0.0Q0.0题3-20的答案21．图3-38中的错误：I2.1的常开触点不能放在线圈的右边，I0.8中的位地址不能大于7，立即输入触点只能用于输入位I，梯形图中不能出现过程映像输入I的线圈，正向转换触点不能接在左侧电源线上。

第五章习题解答与问题

9．设
f (x)
=
1 1+ x2
，在-5≤x≤5 上取
n = 10，按等距结点求分段线性插值函数Ih(x)，
计算各结点间中点处的Ih(x)和f(x) 的值，并估计误差。解：因为 f(xk) = 1/(1+ k2)，(k = -5，…，-1，0，1，…，5)分段线性插值函数为
∑ I h
( x)
=
5
lk
y2 y2
− −
y) y1 )
u1
+
(x (x2
− −
x1 )( y2 x1 )( y2
− −
y) y1 )
u2
+
(x (x2
− −
x1 )( y − y1 ) x1 )( y2 − y1 )
u3
+
( x2 − x)( ( x2 − x1 )(
y2 y2
− −
y) y1 )
u4
二、例题
1．在代数插值问题中，x0，x1，……，xn是(n+1)个互异的插值结点，由这(n+1)个结点构
F (t) = f (t) − H (t) − C ( x)(t − xk )2 (t − xk+1 )2
显然，F(t)有三个零点xk, x, xk+1,由Roll定理知,存在F’(t)的两个零点t0,t1 满足xk<t0<t1<xk+1,
而xk和xk+1 也是F’(x)的零点,故F’(x)至少有四个相异零点. 反复应用Roll定理,得F(4)(t)至少
∑ P( x) = n Aj
ω(x) j=0 x − x j
5．设x0，x1，……，xn是(n+1)个互异的插值结点，ω(x) = (x – x0) (x – x1)……(x – xn)，试证明n阶差商的函数值表达式

运筹学习题答案第五章

第五章习题解答
5.11 某城市可划分为11个防火区，已设有4个消防站，见下图所示。
page 16 2 January 2024
School of Management
运筹学教程
第五章习题解答
上图中，虚线表示该消防站可以在消防允许时间
内到达该地区进行有效的消防灭火。问能否关闭若干消防站，但仍不影响任何一个防火区的消防救灾工作。 (提示：对每—个消防站建立一个表示是否将关闭的01变量。)
x1, x2 0,且为整数
解：x1 1, x2 3, Z 4
min Z 5x1 x2
3x1 x2 9
(2)
st
x1 x1
x2 5 8x2 8
.
x1, x2 0,且为整数
解：x1 4, x2 1, Z 5
page 8 2 January 2024
School of Management
School of Management
运筹学教程
第五章习题解答
5.12 现有P个约束条件
n
aij xij bi
j 1
i 1,2,, p
需要从中选择q个约束条件，试借助0-1变量列出表达式。
解：设yi是0 1变量,i 1,2,, p
n
yi ( aij xij bi ) 0 j 1
i 1,2,, p
运筹学教程
第五章习题解答
5.1 某地准备投资D元建民用住宅。可以建住宅
的造分地价别点为建有d几j；n幢处，，：最才A多能1，可使A造建2，a造j幢…的。，住问A宅n应。总当在数在A最i哪处多几每，处幢试建住建住宅立宅的问，题的数学模型。
解：设xi表示在Ai处所建住宅的数量, i 1,2,, n。

第五章习题解答

第五章化学反应系统热力学习题解答1.在298.15K 、p θ时，环丙烷、石墨及氢的θm c H Δ分别为-2092，-393.5及-285.84KJ ·mol -1，若已知丙稀（g ）的，θm f H Δ=20.5 KJ ·mol -1，试求（1）环丙烷的θm f H Δ；（2）环丙烷异构化变为丙稀的θm r H Δ。

解：（1）环丙烷的生成反应为：3C(石墨)+3H 2(g)====C 3H 6(g)环丙烷）（氢气）（石墨）环丙烷）(33(θθθθθm c mc m c m f m r H H H H H ∆-∆+∆=∆=∆ =3×(-393.5)+3×(-285.84)-(-2092)=53.98kJ ·mol -1(2)环丙烷的异构化反应为：环丙烷（g ）=====丙烯（g ）环丙烷）丙烯）((θθθ∆∆∆m f m f m r H H H -==20.5-53.98=-33.48 kJ ·mol -1 2.试判断298K ，标准态下，下列反应能否正向自发？（1）SiO 2（s ）+2Cl 2（g ）＝SiCl 4（g ）+O 2（g ）（2）SiO 2（s ）+2Cl 2（g ）+2C （s ）＝SiCl 4（g ）+2CO （g ）根据以上结果说明制备SiCl 4时，加碳为何对反应有利？已知298K 时，SiO 2（s ），SiCl 4（g ），CO （g ）的θm f G Δ分别为-857，-617，-137 kJ ·mol -1 。

解：（1）SiO 2（s ）+2Cl 2（g ）＝SiCl 4（g ）+O 2（g ）反应)()()1(24SiO G SiCl G G m f m f m r θθθ∆∆∆-==-617-（-857）=240kJ ·mol -1所以反应正向非自发。

（2）SiO 2（s ）+2Cl 2（g ）+2C （s ）＝SiCl 4（g ）+2CO （g ）反应)()(2)()2(24SiO G CO G SiCl G G m f m f m f m r θθθθ∆∆∆∆-+==-617+2×（-137）-（-857）=-34 kJ ·mol -1则反应正向自发进行。

现代写作教程-第5章3节-习题答案

练习题参考答案：一、选择题1A(罗曼·罗兰是法国现实主义作家)2C（贝克特是荒诞派戏剧作家）3B4D《劫掠者》（福克纳）5C二、名词解释意识流：它是从西方意识流小说中引入的一种创作手法。

用于表现人物意识深处的流变状态。

它包括内心独白、自由联想、时空交错等。

它兴起于20世纪20年代的英国，以后波及欧美各国。

意识流小说是西方现代社会意识的产物，它的理论基础是柏格森的直觉主义哲学，弗洛伊德的精神分析学说和威廉·詹姆斯的心理学。

“意识流”概念是由威廉?詹姆斯提出的。

他认为人的意识活动像一条河流一样，是不间断的主观思想意识的流动。

意识流小说的主要特征是描写人的意识活动，特别注重表现人的潜意识，它打破传统时序和情节的因果关系，形成时空倒置、交叉，让人物的意识活动去结构作品，采用内心独白、自由联想的写作手法，并进行语言形式的各种试验。

法国普鲁斯特的《追忆逝水年华》是意识流小说的奠基作品，代表作是爱尔兰乔伊斯的《尤利西斯》、美国福克纳的《喧哗与骚动》。

黑色幽默：是美国20世纪60年代出现的一种重要的文学流派。

名称来源于弗里德曼的同名短篇小说集。

这派作家信奉存在主义哲学，强调世界的荒谬、混乱与神秘，他们以夸张和超现实的手法揭露讽刺现实中的丑恶，用喜剧的方式处理悲剧性的内容，使读者哭笑不得，从而对生活有更深一层的认识。

代表作是约瑟夫·海勒的《第22条军规》。

写法上，黑色幽默小说往往将滑稽、丑恶、畸形的人物和故事放大、扭曲，显出其荒诞，以达到对社会、历史的某种隐喻。

反讽：是一种以超然的态度、戏谑的口吻表达言外之意的表达方式。

它一般通过两项对立内容的悖逆冲突，拓展作品的艺术空间，丰富作品的内在意蕴。

在叙述情节事件、塑造人物形象、显示作者的情感态度上，具有意婉旨微、深刻有力、耐人寻味。

三、查相关资料，介绍下列作家的基本情况，文学主张和代表作品。

弗吉尼亚·伍尔夫（1882-1941）是二十世纪英国文坛最重要的女作家和文学评论家之一。

3篇5章习题解答

第5章习题解答

复变函数第3篇习题课

第5章感应电机习题与解答

《模拟电子技术基础》第三版习题解答第5章 放大电路的频率响应

第5章思考题和习题解答

概率论第五章习题解答

无机化学习题解答第五章

习题答案：第5章拉深

软件项目管理第3版第5章习题答案参考答案范围管理

5章 化学平衡原理习题及全解答

第五章课后练习题三及答案

第5章 习题解答

第五章习题解答

第5章-习题详解

移动通信原理习题答案5章

PLC-3、4、5章习题参考答案

第五章习题解答与问题

运筹学习题答案第五章

第五章习题解答

现代写作教程-第5章3节-习题答案

《模拟电子技术基础》第三版习题解答第5章放大电路的频率响应

5章化学平衡原理习题及全解答

第5章习题解答