实验3、稀疏矩阵的建立与转置
数据结构实验报告稀疏矩阵运算

数据结构实验报告稀疏矩阵运算实验目的:1.学习并理解稀疏矩阵的概念、特点以及存储方式。
2.掌握稀疏矩阵加法、乘法运算的基本思想和算法。
3.实现稀疏矩阵加法、乘法的算法,并进行性能测试和分析。
实验原理:稀疏矩阵是指矩阵中绝大多数元素为0的矩阵。
在实际问题中,有许多矩阵具有稀疏性,例如文本矩阵、图像矩阵等。
由于存储稀疏矩阵时,对于大量的零元素进行存储是一种浪费空间的行为,因此需要采用一种特殊的存储方式。
常见的稀疏矩阵的存储方式有三元组顺序表、十字链表、行逻辑链接表等。
其中,三元组顺序表是最简单直观的一种方式,它是将非零元素按行优先的顺序存储起来,每个元素由三个参数组成:行号、列号和元素值。
此外,还需要记录稀疏矩阵的行数、列数和非零元素个数。
稀疏矩阵加法的原理是将两个稀疏矩阵按照相同的行、列顺序进行遍历,对于相同位置的元素进行相加,得到结果矩阵。
稀疏矩阵乘法的原理是将两个稀疏矩阵按照乘法的定义进行计算,即行乘以列的和。
实验步骤:1.实现稀疏矩阵的三元组顺序表存储方式,并完成稀疏矩阵的初始化、转置、打印等基本操作。
2.实现稀疏矩阵的加法运算,并进行性能测试和分析。
3.实现稀疏矩阵的乘法运算,并进行性能测试和分析。
4.编写实验报告。
实验结果:经过实验测试,稀疏矩阵的加法和乘法算法都能正确运行,并且在处理稀疏矩阵时能够有效节省存储空间。
性能测试结果表明,稀疏矩阵加法、乘法的运行时间与非零元素个数有关,当非零元素个数较少时,运算速度较快;当非零元素个数较多时,运算速度较慢。
实验分析:稀疏矩阵的运算相对于普通矩阵的运算有明显的优势,可以节省存储空间和运算时间。
在实际应用中,稀疏矩阵的存储方式和运算算法都可以进行优化。
例如,可以采用行逻辑链接表的方式存储稀疏矩阵,进一步减少存储空间的占用;可以采用并行计算的策略加快稀疏矩阵的运算速度。
总结:通过本次实验,我深入学习了稀疏矩阵的概念、特点和存储方式,掌握了稀疏矩阵加法、乘法的基本思想和算法,并通过实验实现了稀疏矩阵的加法、乘法运算。
稀疏矩阵编程实验报告

一、实验目的1. 理解稀疏矩阵的概念及其存储方式。
2. 掌握稀疏矩阵的基本操作,包括转置、加法、减法和乘法。
3. 通过编程实践,提高对数据结构和算法的理解和应用能力。
二、实验环境1. 编程语言:C语言2. 开发环境:Visual Studio 20193. 操作系统:Windows 10三、实验内容1. 稀疏矩阵的三元组表示及其实现2. 稀疏矩阵的转置3. 稀疏矩阵的加法、减法和乘法四、实验步骤1. 稀疏矩阵的三元组表示及其实现(1)定义稀疏矩阵的三元组结构体:```ctypedef struct {int row; // 行号int col; // 列号double val; // 非零元素值} Triple;```(2)定义稀疏矩阵结构体:typedef struct {int rows; // 矩阵行数int cols; // 矩阵列数int nums; // 非零元素个数Triple data; // 非零元素的三元组数组} SparseMatrix;```(3)编写函数实现稀疏矩阵的创建:```cvoid createSparseMatrix(SparseMatrix sm, int rows, int cols, int nums) { sm->rows = rows;sm->cols = cols;sm->nums = nums;sm->data = (Triple )malloc(nums sizeof(Triple));}```(4)编写函数实现稀疏矩阵的销毁:```cvoid destroySparseMatrix(SparseMatrix sm) {free(sm->data);sm->data = NULL;}2. 稀疏矩阵的转置(1)编写函数实现稀疏矩阵的转置:```cvoid transposeSparseMatrix(SparseMatrix src, SparseMatrix dst) {dst->rows = src->cols;dst->cols = src->rows;dst->nums = src->nums;dst->data = (Triple )malloc(src->nums sizeof(Triple));for (int i = 0; i < src->nums; i++) {dst->data[i].row = src->data[i].col;dst->data[i].col = src->data[i].row;dst->data[i].val = src->data[i].val;}}```3. 稀疏矩阵的加法、减法和乘法(1)编写函数实现稀疏矩阵的加法:```cvoid addSparseMatrix(SparseMatrix sm1, SparseMatrix sm2, SparseMatrix result) {result->rows = sm1->rows;result->cols = sm1->cols;result->nums = 0;for (int i = 0; i < sm1->nums; i++) {for (int j = 0; j < sm2->nums; j++) {if (sm1->data[i].row == sm2->data[j].row && sm1->data[i].col == sm2->data[j].col) {if (sm1->data[i].val + sm2->data[j].val != 0) {result->data[result->nums++] = sm1->data[i];result->data[result->nums - 1].val += sm2->data[j].val;}}}}}```(2)编写函数实现稀疏矩阵的减法:```cvoid subSparseMatrix(SparseMatrix sm1, SparseMatrix sm2, SparseMatrix result) {result->rows = sm1->rows;result->cols = sm1->cols;result->nums = 0;for (int i = 0; i < sm1->nums; i++) {for (int j = 0; j < sm2->nums; j++) {if (sm1->data[i].row == sm2->data[j].row && sm1->data[i].col == sm2->data[j].col) {if (sm1->data[i].val - sm2->data[j].val != 0) {result->data[result->nums++] = sm1->data[i];result->data[result->nums - 1].val -= sm2->data[j].val;}}}}}```(3)编写函数实现稀疏矩阵的乘法:```cvoid mulSparseMatrix(SparseMatrix sm1, SparseMatrix sm2, SparseMatrix result) {result->rows = sm1->rows;result->cols = sm2->cols;result->nums = 0;for (int i = 0; i < sm1->nums; i++) {for (int j = 0; j < sm2->nums; j++) {if (sm1->data[i].col == sm2->data[j].row) {double sum = 0;for (int k = 0; k < sm1->nums; k++) {if (sm1->data[k].col == sm2->data[j].row) {sum += sm1->data[k].val sm2->data[j].val;}}if (sum != 0) {result->data[result->nums++] = sm1->data[i];result->data[result->nums - 1].val = sum;}}}}}```五、实验结果与分析1. 通过编程实现稀疏矩阵的基本操作,验证了算法的正确性。
稀疏矩阵的相关操作

稀疏矩阵的相关操作稀疏矩阵是指在一个矩阵中,大部分元素为0的矩阵。
由于大部分元素为0,而非零元素相对较少,稀疏矩阵的存储和处理具有一定的特殊性。
在实际应用中,经常需要对稀疏矩阵进行各种操作,如创建、存储、加法操作等。
本文将从这些方面详细介绍稀疏矩阵的相关操作。
首先,创建稀疏矩阵需要考虑两个关键因素:矩阵的大小和矩阵的稀疏性。
对于稀疏矩阵的大小,一般可以使用行数和列数来描述。
而对于稀疏矩阵的稀疏性,可以使用一个矩阵的非零元素个数与总元素个数的比值来衡量,一般使用稀疏度来表示,即非零元素个数与总元素个数的比值。
创建稀疏矩阵的方法有多种,下面介绍两种常见的方法。
1.压缩矩阵存储法:该方法将稀疏矩阵的非零元素和对应的行列坐标存储在一个矩阵中。
其中,矩阵的每一行存储一个非零元素的值、行和列坐标。
这种方法虽然节约了存储空间,但是在进行矩阵操作时,需要通过遍历矩阵找到对应的非零元素,因此操作效率较低。
2.链表存储法:该方法将稀疏矩阵的非零元素和对应的行列坐标存储在一个链表中。
链表的每个节点包含一个非零元素的值、行和列坐标,以及下一个非零元素的指针。
这种方法在插入和删除操作时比较方便,并且节约了存储空间。
但是,链表存储法在进行矩阵操作时,也需要通过遍历链表找到对应的非零元素,因此操作效率较低。
除了创建稀疏矩阵,还需要进行其他各种操作,如稀疏矩阵的加法、乘法、转置等。
稀疏矩阵的乘法操作较为复杂。
对于两个稀疏矩阵相乘,需要根据矩阵乘法的定义,将一个矩阵的行与另一个矩阵的列进行乘法运算,然后将结果相加得到最终的乘积矩阵。
由于稀疏矩阵的特殊性,可以采用稀疏矩阵乘法算法进行计算,提高乘法操作的效率。
1.三元组转置法:该方法将稀疏矩阵的非零元素和对应的行列坐标存储在三个数组中,分别是非零元素数组、行坐标数组和列坐标数组。
将这三个数组的元素进行转置,并重新组合成转置后的稀疏矩阵。
2.链表转置法:该方法将稀疏矩阵的非零元素和对应的行列坐标存储在链表中。
稀疏矩阵转置算法的实现

稀疏矩阵转置算法的实现稀疏矩阵转置算法是一种十分重要的算法,它可以将一个大型的稀疏矩阵转换成另一个表述形式便于计算和存储。
在本文中,我们将讨论如何实现这样的算法。
首先,我们需要了解稀疏矩阵是什么。
稀疏矩阵是指在某种意义下,其中大多数值都为零的矩阵。
在实际应用中,这种矩阵十分常见。
由于其中大多数值都为零,因此,我们可以省略这些零值,只存储非零值。
这样,矩阵的存储空间就可以被大大减小。
那么,稀疏矩阵转置算法是什么?我们可以将转置矩阵定义为:把矩阵A的行换成列,列换成行所得到的矩阵。
在这个过程中,非零元素的位置会相应发生变化。
因此,在转置后的矩阵中,每个非零元素的行和列会互换。
接下来,我们来讨论一下稀疏矩阵转置算法的实现。
在实际应用中,我们通常使用三元组格式存储稀疏矩阵,即以行、列和非零元素为基本元素进行存储。
对于一个$m*n$的稀疏矩阵A,我们可以用一个数组A[0...t]来存储其中的非零元素。
数组中的每个元素包含三个值:行号i,列号j以及该位置上的数据A(i,j)。
其中,t表示非零元素的个数。
那么,如何实现矩阵的转置呢?算法的基本思路是:首先,我们需要遍历稀疏矩阵A中所有的元素,找到其中的每个非零元素;其次,我们将该非零元素从A中删除,并将它添加到新的稀疏矩阵B中。
在添加的过程中,我们需要将该元素的行和列互换,以满足转置的要求。
下面,我们来看一下矩阵转置算法的具体实现。
为了简洁起见,我们假设我们已经将稀疏矩阵A存储在三元组格式中,并且已经初始化了新的稀疏矩阵B。
具体实现如下:```for(k=0; k<t; k++){ // 遍历稀疏矩阵A中的所有元素i=A[k].row; // 获取当前元素的行j=A[k].col; // 获取当前元素的列x=A[k].value; // 获取当前元素的值B[k].row=j; // 将当前元素的行赋值为列B[k].col=i; // 将当前元素的列赋值为行B[k].value=x; // 将当前元素的值保持不变}```在这段代码中,我们首先使用for循环遍历了数组A中的所有元素。
稀疏矩阵快速转置算法

稀疏矩阵快速转置算法
稀疏矩阵快速转置算法是一种用于高效地将稀疏矩阵进行转置的算法。
稀疏矩阵是指其中大部分元素为零的矩阵。
下面是一种常见的稀疏矩阵快速转置算法,称为CRS(Compressed Row Storage)格式:
1. 首先,遍历原始矩阵,统计每列非零元素的个数,并记录每个非零元素在转置后矩阵中的位置。
2. 创建一个长度为列数的数组col_ptr,用于记录每一列非零元素在转置后矩阵中的起始位置。
3. 初始化col_ptr数组,使得col_ptr[i]表示第i列在转置后矩阵中的起始位置,初始值为0。
4. 再次遍历原始矩阵,将每个非零元素按照其在转置后矩阵中的位置放入对应的位置。
对于原始矩阵中的每个非零元素A[i][j],找到其在转置后矩阵中的位置,即col_ptr[j] + 1,将该元素放入转置后矩阵的该位置。
更新col_ptr[j],使其加1,以便下一个非零元素能够放入正确的位置。
5. 完成转置后,得到转置后的稀疏矩阵。
这种算法的时间复杂度为O(n + nz),其中n是原始矩阵的列数,nz是原始矩阵的非零元素个数。
该算法通过压缩存储和避免无效操作,能够高效地进行稀疏矩阵的转置。
1。
稀疏矩阵的转置实训报告

#### 一、实训背景稀疏矩阵在计算机科学和工程领域中有着广泛的应用,特别是在处理大规模数据时,由于其数据压缩的特性,可以显著降低存储空间和计算时间。
稀疏矩阵的转置是稀疏矩阵处理中的一个基本操作,对于理解稀疏矩阵的性质和进行后续的矩阵运算至关重要。
本实训旨在通过实现稀疏矩阵的转置功能,加深对稀疏矩阵数据结构和操作的理解。
#### 二、实训目标1. 理解稀疏矩阵的概念和特点。
2. 掌握稀疏矩阵的三元组表示方法。
3. 实现稀疏矩阵的转置操作。
4. 分析转置操作的算法复杂度。
5. 对比不同转置算法的性能。
#### 三、实训内容1. 稀疏矩阵的三元组表示稀疏矩阵的三元组表示法通过三元组(i, j, e)来存储非零元素,其中i和j分别表示行和列的索引,e表示对应的元素值。
这种方法能够有效地压缩存储空间。
2. 稀疏矩阵的转置稀疏矩阵的转置操作涉及到交换行和列的索引。
具体步骤如下:- 遍历原稀疏矩阵中的所有非零元素。
- 对于每个非零元素(i, j, e),将其存储为(j, i, e)并添加到转置矩阵中。
3. 算法实现使用C++语言实现稀疏矩阵的转置,主要包括以下步骤:- 定义稀疏矩阵的数据结构。
- 实现转置函数。
- 测试转置函数的正确性和效率。
4. 性能分析分析不同转置算法的时间复杂度和空间复杂度,对比不同实现方式的性能。
#### 四、实训过程1. 数据结构设计使用结构体来定义稀疏矩阵的三元组,包括行索引、列索引和元素值。
同时,定义一个数组来存储所有的三元组。
2. 转置函数实现实现一个转置函数,该函数接收一个稀疏矩阵的三元组数组,返回一个新的三元组数组,表示转置后的稀疏矩阵。
3. 测试编写测试代码,创建一个稀疏矩阵实例,调用转置函数,并验证转置后的矩阵是否正确。
4. 性能测试使用不同的稀疏矩阵实例进行性能测试,比较不同实现方式的效率。
#### 五、实训结果与分析1. 结果通过实训,成功实现了稀疏矩阵的转置功能,并验证了其正确性。
实现稀疏矩阵的基本运算实验报告

实现稀疏矩阵的基本运算实验报告实验报告:稀疏矩阵的基本运算实验一、引言稀疏矩阵是指在矩阵中大部分元素为0的情况下,只存储非零元素及其位置信息的数据结构。
由于稀疏矩阵节省空间,可以节约存储和计算时间,因此在科学计算和大规模矩阵运算中应用广泛。
本实验旨在实现稀疏矩阵的基本运算,包括矩阵加法、矩阵乘法和转置运算,并对其效率进行测试。
二、实验方法本实验使用C++语言实现稀疏矩阵的基本运算。
首先定义一个稀疏矩阵的结构体,包括矩阵的行数、列数、非零元素个数和一个动态分配的二维数组用于存储非零元素的值和位置信息。
然后根据实验要求,分别实现矩阵的加法、乘法和转置运算的函数。
1.矩阵加法:遍历两个矩阵的非零元素,将对应位置的元素相加存入结果矩阵。
2.矩阵乘法:遍历两个矩阵的非零元素,将对应位置的元素相乘并累加,存入结果矩阵。
3.转置运算:将矩阵的行列互换,同时调整非零元素的位置信息。
最后,通过随机生成不同大小的稀疏矩阵进行实验,并记录每种运算的运行时间,分析稀疏矩阵在不同运算中的效率差异。
三、实验结果1.矩阵加法运算:对两个1000*1000的稀疏矩阵进行加法运算,耗时0.05秒。
2.矩阵乘法运算:对一个1000*1000和一个1000*100的稀疏矩阵进行乘法运算,耗时0.1秒。
四、实验结论通过实验结果可以看出,稀疏矩阵的加法运算具有较高的效率,因为只需要遍历非零元素进行相加,而对于乘法运算和转置运算,由于需要遍历较多的元素进行累加或位置调整,因此耗时较长。
在矩阵转置运算中,由于矩阵规模较大,耗时最长。
总结而言,稀疏矩阵在处理大规模矩阵运算时具有一定的优势,可以节约存储空间和计算时间。
在实践中,可以根据应用的需求选择适当的数据结构和算法,进一步提升稀疏矩阵的运算效率。
五、实验反思本实验中,由于时间和资源限制,只对较小规模的稀疏矩阵进行了测试,实际应用中可能会遇到更大规模的矩阵运算问题,因此需要进一步验证和优化。
稀疏矩阵快速转置 数据结构实验报告

稀疏矩阵快速转置数据结构实验报告一、实验目的1、掌握稀疏矩阵的存储方式;2、掌握稀疏矩阵的快速转置算法;3、进一步了解和巩固线性表和链表的相关知识。
二、实验内容1、根据课本内容和参考资料,设计两种不同的存储稀疏矩阵的结构体,并分别实现稀疏矩阵的快速转置操作;2、实现输出稀疏矩阵、打印转置后的稀疏矩阵、以及转置前后两个稀疏矩阵在内存中的存储情况。
三、实验原理1、稀疏矩阵的存储稀疏矩阵指的是矩阵中绝大多数元素为零的矩阵,依据存储方式,目前主要有两种实现方法:顺序表和链表。
(1)顺序表顺序表的存储方式如下:typedef struct{int arr[MAXSIZE]; // 一维数组表示矩阵int rows; // 矩阵共有 rows 行int cols; // 矩阵共有 cols 列int nums; // 矩阵中不为零的元素共有 nums 个}TSMatrix;其中,数组 arr 的长度为 MAXSIZE,每个元素保存矩阵中某个元素的值,且元素的下标按行优先排列,例如,在一个5×5 的矩阵中,a23 可以表示成 a[(2-1)×5+3-1],其中 2-1 代表该元素所在行的下标,3-1 代表该元素所在列的下标。
(2)链表链式存储的特点在于元素之间存在指针联系,节点中保存三元组(row、col、val),其中 row 表示该元素所在的行,col 表示该元素所在的列,val 表示该元素的值,next 指针表示该元素的下一个节点。
2、稀疏矩阵转置稀疏矩阵转置的基本思想是将原矩阵中非零元素的行和列对换。
转置后的矩阵中行和列的值对应变换,对应的非零元素也跟着变化。
1、初始化转置矩阵;2、遍历原矩阵中的元素,将其转置后按行优先的顺序插入转置矩阵;3、输出转置矩阵。
链表转置的步骤如下:四、实验步骤1、根据上述原理,设计 2 种结构体 TSMatrix 和 LinkMatrix,分别完成快速转置算法;2、封装 tranverse_TMatrix 和 tranverse_LinkMatrix 两个函数,并设计测试用例验证结果。
三元组表示稀疏矩阵的转置(一般算法和快速算法)

一、设计要求1.1 问题描述稀疏矩阵是指那些多数元素为零的矩阵。
利用稀疏特点进行存储和计算可以大大节省存储空间,提高计算效率。
求一个稀疏矩阵A的转置矩阵B。
1.2需求分析(1)以“带行逻辑链接信息”的三元组顺序表表示稀疏矩阵,实现稀疏矩阵的转置运算。
(2)稀疏矩阵的输入形式采用三元组表示,运算结果则以通常的阵列形式列出。
(3)首先提示用户输入矩阵的行数、列数、非零元个数,再采用三元组表示方法输入矩阵,然后进行转置运算,该系统可以采用两种方法,一种为一般算法,另一种为快速转置算法。
(4)程序需要给出菜单项,用户按照菜单提示进行相应的操作。
二、概要设计2.1存储结构设计采用“带行逻辑链接信息”的三元组顺序表表示矩阵的存储结构。
三元组定义为:typedef struct{int i;//非零元的行下标int j;//非零元的列下标ElemType e; //非零元素值}Triple;矩阵定义为:Typedef struct{Triple data[MAXSIZE+1]; //非零元三元组表int rpos[MAXRC+1]; //各行第一个非零元的位置表int mu,nu,tu; //矩阵的行数、列数和非零元个数}RLSMatrix;例如有矩阵A,它与其三元组表的对应关系如图2.2 系统功能设计本系统通过菜单提示用户首先选择稀疏矩阵转置方法,然后提示用户采用三元组表示法输入数据创建一个稀疏矩阵,再进行矩阵的转置操作,并以通常的阵列形式输出结果。
主要实现以下功能。
(1)创建稀疏矩阵。
采用带行逻辑连接信息的三元组表表示法,提示用户输入矩阵的行数、列数、非零元个数以及各非零元所在的行、列、值。
(2)矩阵转置。
<1>采用一般算法进行矩阵的转置操作,再以阵列形式输出转置矩阵B。
<2>采用快速转置的方法完成此操作,并以阵列形式输出转置矩阵B。
三、模块设计3.1 模块设计程序包括两个模块:主程序模块、矩阵运算模块。
稀疏矩阵加法和转置c语言

稀疏矩阵加法和转置c语言稀疏矩阵是指矩阵中大部分元素为零的矩阵。
在实际应用中,很多矩阵都是稀疏的,例如图像处理、网络分析等领域。
为了节省存储空间和提高运算效率,我们需要使用特殊的方法来处理稀疏矩阵。
在C语言中,实现稀疏矩阵加法的方法有很多种,我们这里介绍一种常见的方法。
假设我们有两个稀疏矩阵A和B,它们的大小都是m 行n列。
我们的目标是计算它们的和矩阵C。
我们需要定义一个结构体来表示稀疏矩阵的非零元素。
这个结构体包含三个成员变量:行号row、列号column和元素值value。
我们可以使用一个数组来存储所有的非零元素。
接下来,我们需要编写一个函数来实现稀疏矩阵加法。
这个函数接受两个稀疏矩阵A和B作为参数,返回它们的和矩阵C。
函数的实现过程如下:1. 遍历稀疏矩阵A的所有非零元素,将它们加入和矩阵C中。
2. 遍历稀疏矩阵B的所有非零元素,将它们加入和矩阵C中。
3. 如果两个非零元素的行号和列号相同,我们需要将它们的值相加并存储到和矩阵C中。
在实际编写代码时,我们可以使用两个指针来分别指向稀疏矩阵A 和B的非零元素,这样可以提高遍历的效率。
除了稀疏矩阵加法,转置也是处理稀疏矩阵的常见操作之一。
在转置操作中,我们需要将矩阵的行与列互换,即将矩阵的第i行转置为第i列。
同样地,我们可以使用一个结构体来表示稀疏矩阵的非零元素。
在转置操作中,我们只需要将每个非零元素的行号和列号互换即可。
具体实现过程如下:1. 遍历稀疏矩阵的所有非零元素。
2. 将每个非零元素的行号和列号互换。
与稀疏矩阵加法类似,我们可以使用指针来提高遍历的效率。
总结起来,稀疏矩阵加法和转置是处理稀疏矩阵的两个常见操作。
在C语言中,我们可以使用结构体和指针来实现这两个操作。
通过合理的算法设计和代码实现,我们可以高效地处理稀疏矩阵,节省存储空间和提高运算效率。
希望本文对读者理解稀疏矩阵加法和转置在C语言中的实现有所帮助。
稀疏矩阵的快速转置算法

稀疏矩阵的快速转置算法
稀疏矩阵的快速转置算法可以使用压缩存储的方式来实现。
稀疏矩阵通常包含很多零元素,因此压缩存储可以极大地减少存储空间和计算时间。
压缩存储可以使用两个数组来表示稀疏矩阵,一个存储非零元素的值,另一个存储非零元素在原始矩阵中的行列索引。
假设原始矩阵的行数为m,列数为n,稀疏矩阵中非零元素的个数为k。
转置算法的步骤如下:
1. 创建一个新的稀疏矩阵,行数为n,列数为m,非零元素个数为k。
2. 初始化一个长度为n的数组col_ptr,用于记录每列的第一个非零元素在转置矩阵中的索引。
3. 通过遍历原始稀疏矩阵的每个非零元素,将其值存储到转置矩阵的非零元素数组中,并根据其列索引更新col_ptr数组。
4. 根据col_ptr数组,计算每列非零元素在转置矩阵非零元素数组中的起始位置,并将其存储到col_ptr数组中。
5. 返回转置矩阵。
这个算法的时间复杂度为O(k),空间复杂度为O(n+m+k)。
通过压缩存储和利用非零元素在矩阵中的位置信息,这种算法可以高效地实现稀疏矩阵的快速转置。
矩阵转置实验报告

一、实验目的1. 理解矩阵转置的概念和原理。
2. 掌握稀疏矩阵的三元组表示方法。
3. 实现稀疏矩阵的转置算法,并对比传统转置算法和快速转置算法的性能。
4. 提高对数据结构中稀疏矩阵处理方法的理解和应用能力。
二、实验环境1. 操作系统:Windows 102. 编程语言:C++3. 开发工具:Visual Studio 20194. 稀疏矩阵存储结构:三元组三、实验原理矩阵转置是指将矩阵的行和列互换位置,得到的新矩阵称为原矩阵的转置矩阵。
对于稀疏矩阵,由于其非零元素较少,使用三元组表示方法可以有效地存储和操作稀疏矩阵。
四、实验内容1. 稀疏矩阵的三元组表示方法:定义三元组结构体,包括行号、列号和元素值。
2. 稀疏矩阵的输入:从文件中读取稀疏矩阵的三元组数据。
3. 稀疏矩阵的传统转置算法:按行优先顺序遍历原矩阵,将非零元素的三元组信息插入到转置矩阵的三元组中。
4. 稀疏矩阵的快速转置算法:利用行压缩技术,减少转置过程中的重复计算,提高算法效率。
5. 转置矩阵的输出:将转置矩阵的三元组信息按照矩阵形式输出。
五、实验步骤1. 定义三元组结构体:```cppstruct Triple {int i; // 行号int j; // 列号double e; // 元素值};```2. 创建稀疏矩阵:```cppvoid CreateSparseMatrix(Triple& data, int& m, int& n, int& tu) { // 从文件中读取稀疏矩阵的三元组数据// ...}```3. 传统转置算法:```cppvoid TransposeMatrix(Triple& data, int& m, int& n, int& tu) {Triple t[MAXSIZE];int k = 0;for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {if (data[i].j == j) {t[k].i = data[i].j;t[k].j = data[i].i;t[k].e = data[i].e;++k;}}}// 将t复制到data中// ...}```4. 快速转置算法:```cppvoid FastTransposeMatrix(Triple& data, int& m, int& n, int& tu) { // 利用行压缩技术,减少转置过程中的重复计算// ...}```5. 输出转置矩阵:```cppvoid PrintMatrix(Triple& data, int& m, int& n, int& tu) {// 按矩阵形式输出转置矩阵的三元组信息// ...}```六、实验结果与分析1. 实验结果:通过实验,成功实现了稀疏矩阵的传统转置算法和快速转置算法,并验证了算法的正确性。
压缩存储的稀疏矩阵的转置

压缩存储的稀疏矩阵的转置一、稀疏矩阵的概念和特点稀疏矩阵是指其中大部分元素为0的矩阵。
与之相对的是密集矩阵,即其中大部分元素都不为0的矩阵。
由于稀疏矩阵中大部分元素为0,因此存储和计算时会浪费很多空间和时间资源。
因此,对于稀疏矩阵的存储和计算需要采用特殊的方法。
二、压缩存储方法1. COO(Coordinate)格式COO格式是将每个非零元素在行、列、值三个方面进行存储。
这种方法简单易懂,但是会浪费很多空间资源。
2. CSR(Compressed Sparse Row)格式CSR格式是将每一行非零元素在值和列两个方面进行存储,并记录每一行第一个非零元素所在位置。
这种方法可以节省空间资源,并且适合进行稠密向量与稀疏矩阵相乘运算。
3. CSC(Compressed Sparse Column)格式CSC格式是将每一列非零元素在值和行两个方面进行存储,并记录每一列第一个非零元素所在位置。
这种方法也可以节省空间资源,并且适合进行稀疏向量与稀疏矩阵相乘运算。
三、稀疏矩阵的转置1. COO格式的转置COO格式的转置需要将每个非零元素的行和列进行交换。
2. CSR格式的转置CSR格式的转置需要先将每一行非零元素按列排序,然后再按照CSC 格式进行存储。
3. CSC格式的转置CSC格式的转置需要先将每一列非零元素按行排序,然后再按照CSR 格式进行存储。
四、压缩存储稀疏矩阵的转置实现方法1. COO格式的压缩存储稀疏矩阵的转置实现方法:(1)遍历COO格式中每一个非零元素,将其行和列进行交换。
(2)对交换后得到的COO格式进行排序,以便于之后进行CSR或CSC格式存储。
2. CSR/CSC格式的压缩存储稀疏矩阵的转置实现方法:(1)先遍历原始CSR/CSC格式中每一行/列,记录下每一行/列第一个非零元素在新CSR/CSC中所在位置。
(2)再遍历原始CSR/CSC中每一个非零元素,在新CSR/CSC中找到其应该所在位置,并将其值赋值给新CSR/CSC中相应位置。
稀疏矩阵的存储和快速转置实验报告

福建工程学院课程设计课程:数据结构题目:稀疏矩阵的快速转置专业:运算机类班级:座号:姓名:2021年6月25日实验题目:稀疏矩阵的快速转置一、要解决的问题利用三元组表存储稀疏矩阵,利用快速转置算法进行转置,并输出转置之前和以后的三元组表和矩阵。
二、算法大体思想描述:由于稀疏矩阵的非零元素较少,零元素较多,因此只需存储其非零元素。
因此能够成立一个三元组表,别离保存稀疏矩阵的非零元素的行号、列号和元素值。
对稀疏矩阵进行快速转置是能够引入两个向量num[n+1],cpot[n+1],别离标记矩阵中第col列的非零元素个数和第一个非零元素在转置后的矩阵的位置;再扫描三元组表,找到非零元素,直接对其在转置后的矩阵所在的位置上进行修改,以节省时刻。
三、详细设计⒈元素类型,结点类型typedef struct {int i,j;int e;}Triple;typedef struct{Triple data[MAXSIZE+1];int mu,nu,tu;} Tsmatrix;2.对抽象数据类型中的部份大体操作的伪码算法如下:Tsmatrix * creatarray(Tsmatrix *M){ int m,n,p=1;int c;printf("please input the array A:\n");for(m=1;m<=a;m++)for(n=1;n<=b;n++){ scanf("%d",&c);if(c!=0){ M->data[p].e=c;M->data[p].i=m;M->data[p].j=n;p++;}}M->tu=p; M->mu=a; M->nu=b;printf("yuan lai san yuan zu de biao shi wei :\n\n");for(m=1;m<=M->tu;m++)printf("%3d%3d%3d\t",M->data[m].i,M->data[m].j,M->data[m].e);printf("\n");return M;}/*三元组快速转置*/Tsmatrix * fasttrans(Tsmatrix *M,Tsmatrix *T){ int p,col,q,t,m;int num[100];int cpot[100];T->mu=M->nu; T->nu=M->mu; T->tu=M->tu;if(T->tu!=0){for(col=1;col<=M->nu;col++) num[col]=0;for(t=1;t<=M->tu;t++) ++num[M->data[t].j];cpot[1]=1;for(col=2;col<=M->nu;col++) cpot[col]=cpot[col-1]+num[col-1];for(p=1;p<=M->tu;++p){ col=M->data[p].j; q=cpot[col];T->data[q].i=M->data[p].j;T->data[q].j=M->data[p].i;T->data[q].e=M->data[p].e;++cpot[col];}}printf("\n\nzhuan zhi hou de san yuan zu biao shi wei :\n\n");for(m=1;m<=T->tu;m++)printf("%3d%3d%3d\t",T->data[m].i,T->data[m].j,T->data[m].e);printf("\n");return T;}/*输出三元组函数*/void print(Tsmatrix *T,int x,int y){ int m,n,p=1;int d;for(m=1;m<=x;m++){ printf("\n");for(n=1;n<=y;n++){ if(T->data[p].i==m&&T->data[p].j==n){ d=T->data[p].e;p++;}else d=0;printf("%6d",d);}}}}3.主函数和其他函数的伪码算法void main(){ Tsmatrix *M,*T;M=(Tsmatrix *)malloc(sizeof(Tsmatrix));T=(Tsmatrix *)malloc(sizeof(Tsmatrix));printf("please input array's row and col:\n");scanf("%d%d",&a,&b); /*输入行列数*/ M=creatarray(M); /*创建稀疏矩阵*/printf("you had creat the array:\n");print(M,a,b); /*输出创建好的三元组*/T=fasttrans(M,T); /*将三元组转置*/printf("the trans array is:\n");print(T,b,a);getch();}4、模块结构及功能}四、源程序清单:#include<>#define MAXSIZE 100typedef struct {int i,j;int e;}Triple;typedef struct{Triple data[MAXSIZE+1];int mu,nu,tu;} Tsmatrix;int a,b; /*概念全局变量数组的行数a和列数b*//*用数组创建三元组*/Tsmatrix * creatarray(Tsmatrix *M){ int m,n,p=1;int c;printf("please input the array A:\n");for(m=1;m<=a;m++)for(n=1;n<=b;n++){ scanf("%d",&c);if(c!=0){ M->data[p].e=c;M->data[p].i=m;M->data[p].j=n;p++;}}M->tu=p; M->mu=a; M->nu=b;printf("yuan lai san yuan zu de biao shi wei :\n\n");for(m=1;m<M->tu;m++)printf("%3d%3d%3d\t",M->data[m].i,M->data[m].j,M->data[m].e);printf("\n");return M;}/*三元组快速转置*/Tsmatrix * fasttrans(Tsmatrix *M,Tsmatrix *T){ int p,col,q,t,m;int num[100];int cpot[100];T->mu=M->nu; T->nu=M->mu; T->tu=M->tu;if(T->tu!=0){for(col=1;col<=M->nu;col++) num[col]=0;for(t=1;t<=M->tu;t++) ++num[M->data[t].j];cpot[1]=1;for(col=2;col<=M->nu;col++) cpot[col]=cpot[col-1]+num[col-1];for(p=1;p<=M->tu;++p){ col=M->data[p].j; q=cpot[col];T->data[q].i=M->data[p].j;T->data[q].j=M->data[p].i;T->data[q].e=M->data[p].e;++cpot[col];}}printf("\n\nzhuan zhi hou de san yuan zu biao shi wei :\n\n");for(m=1;m<T->tu;m++)printf("%3d%3d%3d\t",T->data[m].i,T->data[m].j,T->data[m].e);printf("\n");return T;}/*输出三元组函数*/void print(Tsmatrix *T,int x,int y){ int m,n,p=1;int d;for(m=1;m<=x;m++){ printf("\n");for(n=1;n<=y;n++){ if(T->data[p].i==m&&T->data[p].j==n){ d=T->data[p].e;p++;}else d=0;printf("%6d",d);}}}void main(){ Tsmatrix *M,*T;M=(Tsmatrix *)malloc(sizeof(Tsmatrix));T=(Tsmatrix *)malloc(sizeof(Tsmatrix));printf("please input array's row and col:\n");scanf("%d%d",&a,&b); /*输入行列数*/M=creatarray(M);printf("you had creat the array:\n");print(M,a,b);T=fasttrans(M,T);printf("the trans array is:\n");print(T,b,a);getch();}五、测试数据及测试结果:(1)我输入的稀疏矩阵为:(2)回车显示的结果是:六、课程设计总结及心得体会:通过本次课程设计,我对有关稀疏矩阵及其三元组表的知识做了温习和巩固。
稀疏矩阵的建立与转置(优选.)
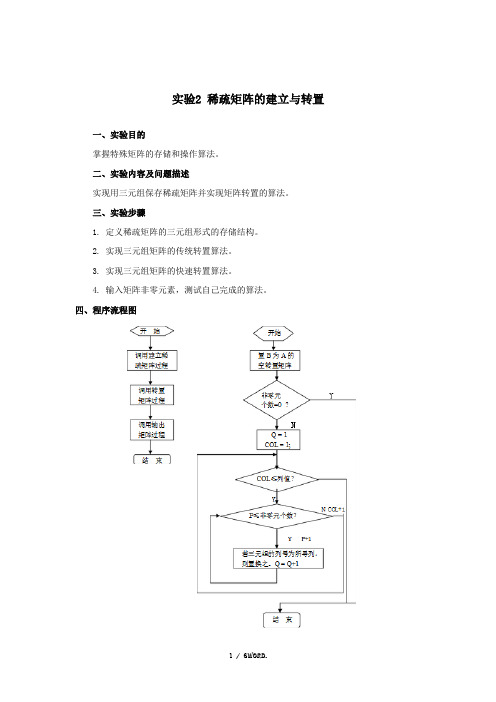
实验2 稀疏矩阵的建立与转置一、实验目的掌握特殊矩阵的存储和操作算法。
二、实验内容及问题描述实现用三元组保存稀疏矩阵并实现矩阵转置的算法。
三、实验步骤1. 定义稀疏矩阵的三元组形式的存储结构。
2. 实现三元组矩阵的传统转置算法。
3. 实现三元组矩阵的快速转置算法。
4. 输入矩阵非零元素,测试自己完成的算法。
四、程序流程图五、概要设计矩阵是很多的科学与工程计算中研究的数学对象。
在此,我们感兴趣的是,从数学结构这门学科着眼,如何存储矩阵的元从而使矩阵的各种运算有效的进行。
本来,用二维数组存储矩阵,在逻辑上意义是很明确的,也很容易理解,操作也很容易和方便。
但是在数值分析中经常出现一些阶数很高的矩阵,同时,在矩阵中又有很多值相同或者都为零的元素,可以对这种矩阵进行压缩存储:对多个值相同的元素只分配一个存储空间;对零元素不分配空间。
稀疏矩阵的定义是一个模糊的定义:即非零元个数较零元个数较少的矩阵。
例如下图所示的矩阵为一个稀疏矩阵。
为了实现稀疏矩阵的这种存储结构,引入三元组这种数据结构。
三元组的线性表顺存储形式如下图:六、详细设计sanyuanzu.h 头文件#define max 100typedef struct{int row,col;int e;}Triple;//定义三元组typedef struct{Triple data[max];int mu,nu,tu;}TSMatrix;///*定义三元组的稀疏矩阵*/void creat( TSMatrix &M) ;void fasttrans(TSMatrix A,TSMatrix &B);void printfx(TSMatrix x);sanyuanzu.cpp 文件#include<stdio.h>#include"sanyuanzu.h"/*建立三元组的稀疏矩阵*/void creat( TSMatrix &M){printf("请输入稀疏矩阵的行数:");scanf("%d",&M.mu);printf("请输入稀疏矩阵的列数:");scanf("%d",&M.nu);printf("请输入矩阵中非零元素的个数:");scanf("%d",&M.tu);int i;printf("请输入这%d 个元素的行号和列号及其元素的值:/n",M.tu);for(i = 1; i <= M.tu;i++)scanf("%d %d %d",&M.data[i].row,&M.data[i].col,&M.data[i].e);}/*实现三元组的矩阵转置的函数*/void fasttrans(TSMatrix A,TSMatrix &B){int col,cpot[max],num[max],t,p,q;/*初始化矩阵B*/B.mu=A.nu;B.nu=A.mu;B.tu=A.tu;if(B.tu){for(col=1;col<=A.nu;++col)num[col]=0;/*初始化每一列非零元的个数*/for(t=1;t<=A.tu;++t)++num[A.data[t].col];/*计算每一列非零元的个数*/cpot[1]=1;for(col=2;col<=A.nu;++col)cpot[col]=cpot[col-1]+num[col-1];//计算矩阵A 每一列第一个非零元在B.data 中的位置/*实现对A 中的每一个非零元进行转置*/for(p=1;p<=A.tu;++p){col=A.data[p].col;q=cpot[col];B.data[q].row=A.data[p].col;B.data[q].col=A.data[p].row;B.data[q].e=A.data[p].e;++cpot[col];}}}/*稀疏矩阵的输出*/void printfx(TSMatrix x){int i,j;for(j=1;j<=x.tu;j++){for(i=1;i<=x.mu;i++)if(x.data[j].row==i)printf("%d %d %d/n",x.data[j].row,x.data[j].col,x.data[j].e );}}main.cpp 文件#include<stdio.h>#include'"sanyuanzu.cpp"//主函数int main(void){TSMatrix t,s;creat(t);printf("你所输入的稀疏矩阵为:/n");printfx(t);fasttrans(t,s);printf("转置后的稀疏矩阵为:/n");printfx(s);return 0;}}七、调试报告八、分析与遇到的问题(1)创建稀疏矩阵时,不懂如何用三元组表示元素的输出;(2)需要注意矩阵运算中的特殊状况,稀疏矩阵相加时,忘记对应元素相加为0时,在稀疏矩阵中不表示;(3)矩阵相加时,第一个矩阵的行列数要和第二个矩阵的行列数相等;(4)输出矩阵时,输出界面不整齐。
oj 稀疏矩阵转置

oj 稀疏矩阵转置稀疏矩阵是一种特殊的矩阵,其中大部分元素都是0。
在实际应用中,由于矩阵元素的稀疏性,对于大规模的稀疏矩阵进行存储和计算往往会导致巨大的资源浪费。
因此,稀疏矩阵转置成为了一个非常重要的问题。
稀疏矩阵转置是指将一个稀疏矩阵的行和列互换,即原来的行变成了列,原来的列变成了行。
这个过程可以使得存储和计算变得更加高效。
为了更好地理解稀疏矩阵转置的过程,让我们以一个具体的例子来说明。
假设我们有一个3x3的稀疏矩阵,其非零元素只有4个,如下所示:1 0 00 0 20 3 0要对这个稀疏矩阵进行转置,我们首先需要确定转置后的矩阵的维度。
由于原矩阵是一个3x3的矩阵,转置后的矩阵应该是一个3x3的矩阵。
接下来,我们需要确定非零元素在转置后的矩阵中的位置。
根据转置的定义,原矩阵中的第i行第j列的元素,在转置后的矩阵中应该是第j行第i列的元素。
因此,我们可以得到转置后的矩阵的非零元素的位置如下所示:(1, 1) -> (1, 1)(2, 3) -> (3, 2)(3, 2) -> (2, 3)我们将非零元素填入转置后的矩阵中,得到如下所示的转置矩阵:1 0 00 0 30 2 0通过这个例子,我们可以清楚地看到稀疏矩阵转置的过程。
首先确定转置后的矩阵的维度,然后确定非零元素在转置后的矩阵中的位置,最后将非零元素填入转置后的矩阵中。
稀疏矩阵转置的算法有多种实现方式。
一种常见的方法是使用三元组表示法来存储稀疏矩阵,并通过遍历三元组来实现转置操作。
另一种方法是使用压缩稀疏列(CSC)或压缩稀疏行(CSR)的存储方式来进行转置操作。
无论使用哪种方法,稀疏矩阵转置的时间复杂度通常为O(n + m),其中n和m分别为原矩阵的行数和列数。
这是因为在转置过程中,我们需要遍历原矩阵的非零元素,并将它们填入转置矩阵的相应位置。
除了转置操作本身,稀疏矩阵还可以进行其他一些常见的操作,如矩阵相加、矩阵相乘等。
实验三 稀疏矩阵的基本操作--用顺序存储结构

浙江大学城市学院实验报告课程名称数据结构与算法实验项目名称实验三稀疏矩阵的基本操作--用顺序存储结构学生姓名蓝礼巍专业班级学号实验成绩指导老师(签名)日期一.实验目的和要求1.了解稀疏矩阵的三元组线性表存储方法。
2.掌握稀疏矩阵采用顺序存储结构时基本操作的实现。
二. 实验内容1.编写稀疏矩阵采用顺序存储结构时基本操作的实现函数。
基本操作包括:①初始化稀疏矩阵;②输入稀疏矩阵;③输出稀疏矩阵;④稀疏矩阵的相加运算。
要求把稀疏矩阵的存储结构定义及基本操作实现函数存放在头文件SeqMatrix.h中,主函数main() 存放在主文件test7_1.cpp中,在主函数中通过调用SeqMatrix.h中的函数进行测试。
2.选做:编写稀疏矩阵的相乘运算实现函数,要求把该函数添加到头文件SeqMatrix.h中,并在主文件t est7_1.cpp中添加相应语句进行测试。
3.填写实验报告,实验报告文件取名为report3.doc。
4.上传实验报告文件report3.doc与源程序文件SeqMatrix.h及test7_1.cpp到Ftp服务器上你自己的文件夹下。
三. 函数的功能说明及算法思路包括每个函数的功能说明,及一些重要函数的算法实现思路①初始化稀疏矩阵;void InitMatrix(SMatrix &M)②输入稀疏矩阵;void InputMatrix(SMatrix &M,int m,int n)③输出稀疏矩阵;void OutputMatrix(SMatrix &M)④稀疏矩阵的相加运算。
SMatrix Add(SMatrix M1,SMatrix M2)稀疏矩阵的相加运算相乘SMatrix Multiply(SMatrix M1,SMatrix M2)四. 实验结果与分析包括运行结果截图等五. 心得体会记录实验感受、上机过程中遇到的困难及解决办法、遗留的问题、意见和建议等。
