华师大13章整式的乘除单元练习题(精品)
华师大版八年级(上) 中考题单元试卷:第13章 整式的乘除(05)

华师大版八年级(上)中考题单元试卷:第13章整式的乘除(05)一、选择题(共26小题)1.下列运算中,正确的是()A.a2+a3=a5B.a3•a4=a12C.a6÷a3=a2D.4a﹣a=3a2.下面是一位同学做的四道题:①2a+3b=5ab;②(3a3)2=6a6;③a6÷a2=a3;④a2•a3=a5,其中做对的一道题的序号是()A.①B.②C.③D.④3.下列计算正确的是()A.x+x2=x3B.x2•x3=x6C.(x3)2=x6D.x9÷x3=x34.下列运算正确的是()A.a6÷a3=a2B.5a2﹣3a2=2aC.(a3)3=a9D.(a﹣b)2=a2﹣b25.下列运算正确的是()A.x2•x3=x6B.(x3)2=x5C.(xy2)3=x3y6D.x6÷x3=x26.下列运算正确的是()A.a6÷a2=a3B.(a+b)2=a2+b2C.2﹣3=﹣6D.=﹣37.下列计算正确的是()A.(a5)2=a10B.x16÷x4=x4C.2a2+3a2=6a4D.b3•b3=2b38.下列运算正确的是()A.(﹣a2)•a3=﹣a6B.a6÷a3=a2C.a2+a3=a5D.(a3)2=a69.下列运算结果为a6的是()A.a2+a3B.a2•a3C.(﹣a2)3D.a8÷a210.下列计算正确的是()A.a2+a2=2a4B.(﹣a2b)3=﹣a6b3C.a2•a3=a6D.a8÷a2=a411.下列运算中正确的是()A.a3﹣a2=a B.a3•a4=a12C.a6÷a2=a3D.(﹣a2)3=﹣a6 12.下列计算正确的是()A.23+26=29B.23﹣24=2﹣1C.23×23=29D.24÷22=22 13.下列计算正确的是()A.(a3)3=a6B.a6÷a3=a2C.2a+3b=5ab D.a2•a3=a5 14.下列计算正确的是()A.x+y=xy B.﹣y2﹣y2=0C.a2÷a2=1D.7x﹣5x=2 15.下列计算正确的是()A.a3﹣a2=a B.a3•a2=a6C.a3÷a2=a D.(a3)2=a5 16.下列计算正确的是()A.a2+a3=a5B.a2•a3=a6C.(a2)3=a5D.a5÷a2=a3 17.下列运算正确的是()A.a+2a=3a2B.3a3•2a2=6a6C.a8÷a2=a4D.(2a)3=8a318.下列各运算中,计算正确的是()A.a2+a3=a5B.a6÷a2=a3C.(﹣2)﹣1=2D.(a2)3=a6 19.下列运算正确的是()A.a3•b3=(ab)3B.a2•a3=a6C.a6÷a3=a2D.(a2)3=a520.下列运算中,正确的是()A.a2+a4=a6B.a6÷a3=a2C.(﹣a4)2=a6D.a2•a4=a6 21.下列运算正确的是()A.(a2)3=a5B.a2•a3=a6C.a8÷a2=a4D.a6÷a2=a4 22.下列计算正确的是()A.x3+x=x4B.x2•x3=x5C.(x2)3=x5D.x9÷x3=x3 23.下列计算正确的是()A.a6÷a3=a3B.(a2)3=a8C.a2•a3=a6D.a2+a2=a4 24.下列计算正确的是()A.2a•3b=5ab B.a3•a4=a12C.(﹣3a2b)2=6a4b2D.a5÷a3+a2=2a225.下列计算正确的是()A.(﹣8)﹣8=0B.3+=3C.(﹣3b)2=9b2D.a6÷a2=a3 26.计算()3×()4×()5之值与下列何者相同?()A.B.C.D.二、填空题(共4小题)27.a6÷a2=.28.计算:(a2b)3=.29.地震中里氏震级增加1级,释放的能量增大到原来的32倍,那么里氏级地震释放的能量是3级地震释放能量的324倍.30.已知实数a,b满足a+b=2,a﹣b=5,则(a+b)3•(a﹣b)3的值是.华师大版八年级(上)中考题单元试卷:第13章整式的乘除(05)参考答案一、选择题(共26小题)1.D;2.D;3.C;4.C;5.C;6.D;7.A;8.D;9.D;10.B;11.D;12.D;13.D;14.C;15.C;16.D;17.D;18.D;19.A;20.D;21.D;22.B;23.A;24.D;25.C;26.B;二、填空题(共4小题)27.a4;28.a6b3;29.7;30.1000;。
华师大版八年级(上) 中考题单元试卷:第13章 整式的乘除(13)

华师大版八年级(上)中考题单元试卷:第13章整式的乘除(13)一、选择题(共18小题)1.下列运算正确的是()A.2a3÷a=6B.(ab2)2=ab4C.(a+b)(a﹣b)=a2﹣b2D.(a+b)2=a2+b22.下列计算正确的是()A.m3+m2=m5B.m3•m2=m6C.(1﹣m)(1+m)=m2﹣1D.3.图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是()A.ab B.(a+b)2C.(a﹣b)2D.a2﹣b24.下列运算正确的是()A.a2•a3=a6B.(﹣a+b)(a+b)=b2﹣a2C.(a3)4=a7D.a3+a5=a85.下列各式的变形中,正确的是()A.(﹣x﹣y)(﹣x+y)=x2﹣y2B.﹣x=C.x2﹣4x+3=(x﹣2)2+1D.x÷(x2+x)=+16.下列运算正确的是()A.a2•a3=a6B.(a2)3=a5C.2a2+3a2=5a6D.(a+2b)(a﹣2b)=a2﹣4b27.下列计算正确的是()A.a4+a4=a8B.(a3)4=a7C.12a6b4÷3a2b﹣2=4a4b2D.(﹣a3b)2=a6b28.下列运算正确的是()A.3x﹣2x=x B.2x•3x=6x C.(2x)2=4x D.6x÷2x=3x9.下列运算正确的是()A.(﹣3mn)2=﹣6m2n2B.4x4+2x4+x4=6x4C.(xy)2÷(﹣xy)=﹣xy D.(a﹣b)(﹣a﹣b)=a2﹣b210.下列运算正确的是()A.4ab÷2a=2ab B.(3x2)3=9x6C.a3•a4=a7D.11.下列计算正确的是()A.2a2﹣4a2=﹣2B.3a+a=3a2C.3a•a=3a2D.4a6÷2a3=2a212.下列计算正确的是()A.a2•a3=a6B.(﹣2ab)2=4a2b2C.(a2)3=a5D.3a3b2÷a2b2=3ab13.下列运算正确的是()A.a4•a2=a8B.(a2)4=a6C.(ab)2=ab2D.2a3÷a=2a2 14.计算多项式﹣2x(3x﹣2)2+3除以3x﹣2后,所得商式与余式两者之和为何?()A.﹣2x+3B.﹣6x2+4x C.﹣6x2+4x+3D.﹣6x2﹣4x+3 15.下列运算正确的是()A.a3+a3=2a6B.(x2)3=x5C.2a6÷a3=2a2D.x3•x2=x516.如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为()A.a2+4B.2a2+4a C.3a2﹣4a﹣4D.4a2﹣a﹣2 17.请你计算:(1﹣x)(1+x),(1﹣x)(1+x+x2),…,猜想(1﹣x)(1+x+x2+…+x n)的结果是()A.1﹣x n+1B.1+x n+1C.1﹣x n D.1+x n18.有3张边长为a的正方形纸片,4张边长分别为a、b(b>a)的矩形纸片,5张边长为b的正方形纸片,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长可以为()A.a+b B.2a+b C.3a+b D.a+2b二、填空题(共9小题)19.填空:x2+10x+=(x+)2.20.已知a+b=3,a﹣b=﹣1,则a2﹣b2的值为.21.已知a+b=3,a﹣b=5,则代数式a2﹣b2的值是.22.已知m+n=3,m﹣n=2,则m2﹣n2=.23.若a2﹣b2=,a﹣b=,则a+b的值为.24.已知a+b=4,a﹣b=3,则a2﹣b2=.25.化简:(x+1)(x﹣1)+1=.26.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是(用a、b的代数式表示).27.若,则=.三、解答题(共3小题)28.(1)填空:(a﹣b)(a+b)=;(a﹣b)(a2+ab+b2)=;(a﹣b)(a3+a2b+ab2+b3)=.(2)猜想:(a﹣b)(a n﹣1+a n﹣2b+…+ab n﹣2+b n﹣1)=(其中n为正整数,且n≥2).(3)利用(2)猜想的结论计算:29﹣28+27﹣…+23﹣22+2.29.化简:(a+b)(a﹣b)+2b2.30.如图1所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形(其面积=(上底+下底)×高).(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a、b的式子表示S1和S2;(2)请写出上述过程所揭示的乘法公式.华师大版八年级(上)中考题单元试卷:第13章整式的乘除(13)参考答案一、选择题(共18小题)1.C;2.D;3.C;4.B;5.A;6.D;7.D;8.A;9.C;10.C;11.C;12.B;13.D;14.C;15.D;16.C;17.A;18.D;二、填空题(共9小题)19.25;5;20.﹣3;21.15;22.6;23.;24.12;25.x2;26.ab;27.6;三、解答题(共3小题)28.a2﹣b2;a3﹣b3;a4﹣b4;a n﹣b n;29.;30.;。
(完整版)华师大版八年级上数学-整式的乘除单元测试(附答案)(可编辑修改word版)

华师大版八年级上学期“整式的乘除”单元测试一、填空题:(每空3 分,共36 分)1.计算:a3⋅a5=. 2.计算:(-2a3)2=.3.计算:-14a 2b ÷ 2a =. 4.计算:(2x -1)2=. 5.计算:(x - 2)(x + 3) =.6.因式分解:x 2- 25x =.7.因式分解:4 -x 2=.8.因式分解:x 2- 4x + 4 =.9.计算:(1.9 ⨯1027 ) ÷ (5.98 ⨯1024 ) ≈.(保留三个有效数字)10.有三个连续的自然数,中间一个是x,则它们的积是。
11.若多项式x 2+ 4kx + 4 恰好是另一个多项式的平方,则k= 。
12.一块边长为a 米的正方形广场,扩建后的正方形边长比原来长2 米,问扩建后的广场面积增大了平方米。
二、选择题:(每小题4 分,共24 分)13.下列运算中正确的是()A.x +x3=x 4B.x ⋅x3=x 4C.(x 2 )3=x5D.x6÷x3=x 214.计算:(3x 2y) ⋅ (-4 x 4y) 的结果是()3A.x6y 2B.- 4x6yC.- 4x6y 2D.5x8y 315.下列从左边到右边的变形,属于因式分解的是()A.(x +1)(x -1) =x 2-1B.x 2- 2x +1 =x(x - 2) +1C.x 2- 4 y2= (x + 4 y)(x - 4 y) D.x 2-x - 6 = (x + 2)(x - 3)16.下列多项式,能用公式法分解因式的有()① x 2+y 2② -x 2+y 2③ -x 2-y 2④ x 2+xy +y 2⑤ x 2+ 2xy -y 2⑥ -x 2+ 4xy - 4 y 2A.2 个B.3 个C.4 个D.5 个17.若(x+t)(x+6)的积中不含有x 的一次项,则t 的值是()A.6 B.-6 C.0 D.6 或-6 18.长方形的长增加50%,宽减少50%,那么长方形的面积()A.不变B.增加75% C.减少25% D.不能确定三、解答题:(共90 分)19.计算题:(每小题6 分,共24 分)(1)1 x 4y 2.(-2xy 3).(-1x)3(2)a 2 (a - 1) + (a - 5)(a + 7)2 10(3)(x - 5 y)2- (x + 5 y)2(4)[(ab +1)(ab -1) - 2a 2b 2+1] ÷ (-ab)20.(8 分)化简求值:[(x - 2 y)2+ (x - 2 y)(x + 2 y) - 2x(2x -y)] ÷ 2x 。
华师大八年级数学上 第13章 整式的乘除单元复习(含答案)
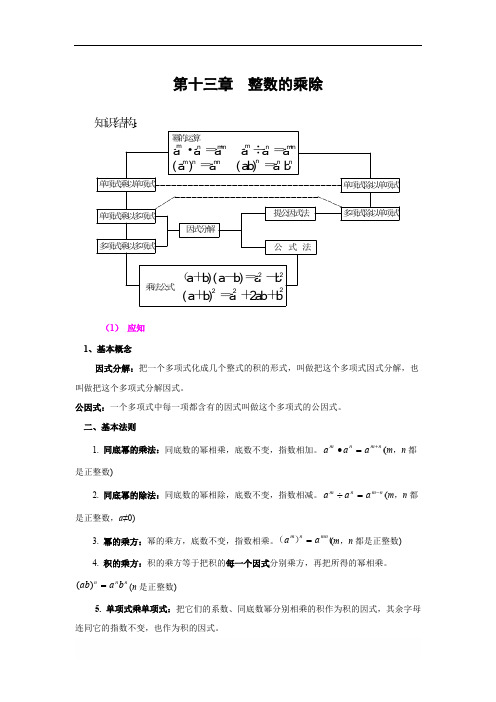
第十三章 整数的乘除知识结构:单项式乘以单项式单项式乘以多项式多项式乘以多项式因式分解冪的运算a ·a =a a ÷a =amn m +n m n m +n (a )=a (a b )=a b m m n n n n n 多项式除以单项式提公因式法公式法(a +b )(a -b )=a -b 22(a +b )=a +2a b +b222乘法公式单项式除以单项式(1)应知1、基本概念因式分解:把一个多项式化成几个整式的积的形式,叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
公因式:一个多项式中每一项都含有的因式叫做这个多项式的公因式。
二、基本法则1. 同底冪的乘法:同底数的幂相乘,底数不变,指数相加。
m ,n 都,(都是正整数n m a a a n m n m +=∙是正整数)2. 同底冪的除法:同底数的幂相除,底数不变,指数相减。
m ,n 都0,,(≠=÷-a n m a a a n m n m 都是正整数是正整数,a ≠0)3. 冪的乘方:幂的乘方,底数不变,指数相乘。
(m ,n 都是正整数),(都是正整数)(n m a a mn n m =4. 积的乘方:积的乘方等于把积的每一个因式分别乘方,再把所得的幂相乘。
(n 是正整数)()(都是正整数n b a ab n n n =5. 单项式乘单项式:把它们的系数、同底数幂分别相乘的积作为积的因式,其余字母连同它的指数不变,也作为积的因式。
6. 单项式乘多项式:用单项式乘以多项式的每一项,再把所得的积相加。
7. 多项式乘多项式:先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
8. 单项式除以单项式:把系数、同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式。
9. 多项式除以单项式:先把多项式的每一项除以单项式,再把所得的商相加。
【注意】(1)单项式乘单项式的结果仍然是单项式。
华师大版八年级(上) 中考题单元试卷:第13章 整式的乘除(25)

华师大版八年级(上)中考题单元试卷:第13章整式的乘除(25)一、选择题(共5小题)1.下列何者是22x7﹣83x6+21x5的因式?()A.2x+3B.x2(11x﹣7)C.x5(11x﹣3)D.x6(2x+7)2.如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为()A.140B.70C.35D.243.下面的多项式在实数范围内能因式分解的是()A.x2+y2B.x2﹣y C.x2+x+1D.x2﹣2x+14.若A=101×9996×10005,B=10004×9997×101,则A﹣B之值为何?()A.101B.﹣101C.808D.﹣8085.多项式ax2﹣4ax﹣12a因式分解正确的是()A.a(x﹣6)(x+2)B.a(x﹣3)(x+4)C.a(x2﹣4x﹣12)D.a(x+6)(x﹣2)二、填空题(共18小题)6.因式分解:ax2﹣7ax+6a=.7.若x2+x+m=(x﹣3)(x+n)对x恒成立,则n=.8.分解因式:(a+2)(a﹣2)+3a=.9.在实数范围内因式分解:x2y﹣3y=.10.已知a2﹣a﹣1=0,则a3﹣a2﹣a+2015=.11.已知a+b=2,ab=1,则a2b+ab2的值为.12.分解因式:2x(x﹣3)﹣8=.13.分解因式:ax2+2ax﹣3a=.14.在实数范围内分解因式:x3﹣6x=.15.因式分解:x3﹣5x2+6x=.16.分解因式:a3b﹣9ab=.17.分解因式:x2+3x(x﹣3)﹣9=.18.如图,边长为a、b的矩形,它的周长为14,面积为10,则a2b+ab2的值为.19.设a=192×918,b=8882﹣302,c=10532﹣7472,则数a,b,c按从小到大的顺序排列,结果是<<.20.已知实数a,b满足:a2+1=,b2+1=,则2015|a﹣b|=.21.分解因式:x2y﹣4y=.22.分解因式:x2﹣3x+2=.23.已知a,b是方程x2﹣x﹣3=0的两个根,则代数式2a3+b2+3a2﹣11a﹣b+5的值为.三、解答题(共4小题)24.如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数叫做“和谐数”.例如:自然数64746从最高位到个位排出的一串数字是6,4,7,4,6,从个位到最高位排出的一串数字也是:6,4,7,4,6,所以64746是“和谐数”.再如:33,181,212,4664,…,都是“和谐数”.(1)请你直接写出3个四位“和谐数”,猜想任意一个四位数“和谐数”能否被11整除,并说明理由;(2)已知一个能被11整除的三位“和谐数”,设个位上的数字为x(1≤x≤4,x为自然数),十位上的数字为y,求y与x的函数关系式.25.如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数称为“和谐数”.例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,因此12321是一个“和谐数”,再如22,545,3883,345543,…,都是“和谐数”.(1)请你直接写出3个四位“和谐数”;请你猜想任意一个四位“和谐数”能否被11整除?并说明理由;(2)已知一个能被11整除的三位“和谐数”,设其个位上的数字x(1≤x≤4,x为自然数),十位上的数字为y,求y与x的函数关系式.26.已知ab=﹣3,a+b=2.求代数式a3b+ab3的值.27.设y=kx,是否存在实数k,使得代数式(x2﹣y2)(4x2﹣y2)+3x2(4x2﹣y2)能化简为x4?若能,请求出所有满足条件的k的值;若不能,请说明理由.华师大版八年级(上)中考题单元试卷:第13章整式的乘除(25)参考答案一、选择题(共5小题)1.C;2.B;3.D;4.D;5.A;二、填空题(共18小题)6.a(x﹣1)(x﹣6);7.4;8.(a﹣1)(a+4);9.y(x﹣)(x+);10.2015;11.2;12.2(x﹣4)(x+1);13.a(x+3)(x﹣1);14.x(x+)(x﹣);15.x (x﹣3)(x﹣2);16.ab(a+3)(a﹣3);17.(x﹣3)(4x+3);18.70;19.a;c;b;20.1;21.y(x+2)(x﹣2);22.(x﹣1)(x﹣2);23.23;三、解答题(共4小题)24.;25.;26.;27.;。
华师大版八年级(上) 中考题单元试卷:第13章 整式的乘除(12)

一、选择题(共 19 小题) 1.下列运算正确的是( )
A.(a+b)2=a2+b2 C.﹣2(a﹣1)=﹣2a﹣1 2.下列运算正确的是( ) A.a﹣2a=a C.a6+a3=a2 3.下列运算正确的是( ) A.(a+b)2=a2+b2 C.(a3)2=a5 4.下列计算正确的是( ) A.a3+a2=a5 C.(﹣ab3)2=a2b6 5.下列计算正确的是( ) A.(a+b)2=a2+b2 C.(a3)2=a5 6.下列运算中,计算正确的是( ) A.(x3)2=x5 C.(﹣2)﹣1=﹣
30.(1)计算:sin60°﹣|1﹣ |+
﹣1
(2)化简:(a+3)2﹣(a﹣3)2.
第3页(共4页)
华师大版八年级(上)中考题单元试卷:第 13 章 整式 的乘除(12)
参考答案
一、选择题(共 19 小题) 1.B; 2.B; 3.D; 4.C; 5.D; 6.C; 7.C; 8.D; 9.C; 10.D; 11.D; 12.D; 13.A; 14.D; 15.B; 16.C; 17.D; 18.D; 19.D; 二、填空题(共 9 小题)
.
26.已知 a>b,如果 + = ,ab=2,那么 a﹣b 的值为
.
27.已知 a、b 满足 a+b=328.若 a+b=5,ab=6,则 a﹣b=
.
三、解答题(共 2 小题)
29.计算:
(1) ﹣(﹣2)2+(﹣0.1)0;
(2)(x+1)2﹣(x+2)(x﹣2).
八年级数学上册 第13章 整式的乘除练习 华东师大版 试题

轧东卡州北占业市传业学校整式的乘除趋势一考查整式的有关知识,题型以选择题、填空题为主1.〔2007,〕以下各式中,与〔a-1〕2相等的是〔〕A.a2-1 B.a2-2a+1 C.a2-2a-1 D.a2+12.〔2007,〕计算x3÷x的结果是〔〕A.x4 B.x3 C.x2 D.33.〔2007,〕以下计算正确的选项是〔〕A.a3+a2=2a5 B.〔-2a3〕2=4a6 C.〔a+b〕2=a2+b2 D.a6÷a2=a34.〔2007,〕计算6m3÷〔-3m2〕的结果是〔〕A.-3m B.-2m C.2m D.3m5.〔2007,〕假设a+b=4,那么a2+2ab+b2的值是〔〕A.8 B.16 C.2 D.46.〔2007,〕〔m2〕3·m4等于〔〕A.m9 B.m10 C.m12 D.m147.〔2007,〕因式分解〔x-1〕2-9的结果是〔〕A.〔x+8〕〔x+1〕 B.〔x+2〕〔x-4〕C.〔x-2〕〔x+4〕 D.〔x-10〕〔x+8〕8.〔2007,〕假设x为任意实数时,二次三项式x2-6x+c的值都不小于0,那么常数c满足的条件是〔〕 A.c≥0 B.c≥9 C.c>0 D.c>99.〔2007,〕如图1,阴影局部的面积是〔〕A.112xy B.132xy C.6xy D.3xy 图1 图210.〔2007,〕将x3-xy2分解因式的结果为_______.11.〔2007,〕分解因式:x3-6x2+9x=_______.12.〔2007,宁夏〕〔9a2b-6ab2〕÷3ab=_______.13.〔2007,〕假设a2+a=0,那么2a2+2a+2007的值为_______.14.〔2007,〕一个长方形的面积是〔x2-9〕平方米,其长为〔x+3〕米,用含x•的整式表示宽为_________.15.〔2005,〕在日常生活中如取款,上网等都需要密码,有一种用“因式分解〞法产生的密码,方便记忆.原理是:如对于多项式x4-y4,因式分解的结果是〔x-y〕〔x+y〕〔x2+y2〕,假设取x=9,y=9时,那么各个因式的值是:〔x-y〕=0,〔x+y〕=18,〔x2+y2〕=162,•于是就可以把“018162〞作为一个六位数的密码,对于多项式4x3-xy2,取x=10,y=10时,•用上述方法产生的密码是_________〔写出一个即可〕.16.〔2006,〕三种不同类型的矩形地砖长宽如图2所示,假设现有A类4块,•B类4块,C类2块,要拼成一个正方形,那么应多余出1块______型地砖;这样的地砖拼法表示了一个两数和的平方的几何意义,这个两数和的平方是_________.趋势二运用乘法公式和整式乘法法那么化简求值17.〔2007,〕先化简,再求值:2a〔a+b〕-〔a+b〕2,其中a=4,b=3.18.〔2007,〕先化简,再求值:〔2x-1〕2+〔x+2〕〔x-2〕-4x〔x-1〕,其中x=2.19.〔2007,荆口〕先化简,再求值:[〔xy+2〕〔xy-2〕-2〔x2y2-2〕]÷xy,其中x=10,y=-1 25.20.〔2007,〕给出三个多项式.12x2+x-1,12x2+3x+1,12x2-x,请你选择其中两个进行加法运算,并把结果因式分解.趋势三探求图形或事物开展的规律,并用代数式表示发现的规律21.〔2007,〕根据以下10个乘积,答复以下问题:11×29; 12×28; 13×27; 14×26; 15×25;16×24; 17×23; 18×22; 19×21; 20×20.〔1〕试将以上乘积分别写成一个“□2-○2〞〔两数平方差〕的形式,并写出其中一个的思考过程.〔2〕将以上10个乘积按照从小到大的顺序排列起来.〔3〕试由〔1〕,〔2〕猜测一个一般性的结论〔不要求证明〕.趋势四运用几何图形探究整式乘法法那么,题目新颖,能力要求较高22.〔2005,〕阅读材料并解答问题:我们已经知道,完全平方公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如,〔2a+b〕〔a+b〕=2a2+3ab+b2•就可以用图1或图2等图形的面积表示.图1 图2 图3〔1〕请写出图3所表示的代数恒等式:_________.〔2〕试画出一个几何图形,使它的面积能表示:〔a+b〕〔a+3b〕=a2+4ab+3b2.〔3〕请仿照上述方法另写一个含有a,b的代数恒等式,•并画出与之对应的几何图形.答案:1.B 2.C 3.B 4.B 5.B 6.B 7.B 8.B 9.A10.x〔x+y〕〔x-y〕 11.x〔x-3〕2 12.3a-2b 13.200714.x-3 15.101030或103010或301010 16.c 〔2m+n〕2=4m2+4mn+n217.解:原式=2a2+2ab-〔a2+2ab+b2〕=2a2+2ab-a2-2ab-b2=a2-b2,当a=4,b=3时,原式=42-32=7.18.解:原式=4x2-4x+1+x2-4-4x2+4x=x2-3.当x=2时,原式=22-3=1.19.解:原式=〔x2y2-4-2x2y2+4〕÷xy=-x2y2÷xy=-xy.当x=10,y=-125时,原式=-10×〔-125〕=25.20.答案不唯一.21.解:〔1〕11×29=202-92;12×28=202-82; 13×27=202-72;14×26=202-62;15×25=202-52;16×24=202-42;17×23=202-32;18×22=202-22; 19×21=202-12;20×20=202-02; 例如,11×29,假设11×29=□2-○2, 因为□2-○2=〔□+○〕〔□-○〕, 所以,可以令□-○=11,□+○=29,解得,□=20,○=9,故11×29=202-92. 或11×29=〔20-9〕〔20+9〕=202-92. 〔2〕这10个数乘积按照从小到大的顺序依次是:11×29<12×28<13×27<14×26<15×25<16×24<17×23<18×22<19×21<20×20. 〔3〕①假设a+b=40,那么ab ≤202=400, ②假设a+b=m ,a 、b 是自然数,故ab ≤〔2m 〕2. 22.〔1〕〔2a+b 〕〔a+2b 〕=2a 2+5ab+2b 2 〔2〕画出几何图形,如图4〔答案不唯一〕.图4 图5〔3〕〔a+3b 〕〔2a+b 〕=2a 2+7ab+3b 2,如图5所示.〔不唯一〕。
最新-八年级数学上册 第13章 整式的乘除 135 因式分解

13.5因式分解因式分解应用宝典因式分解是中学数学的重要内容之一,不但在我们平时的考试中经常考到它,就是在各级各类数学竞赛题中都能看到用因式分解求解的题目.下面举例说明因式分解在以下几个方面的应用.一. 计算例1.【“希望杯”】:计算: 9421715(981)2(33)8+⨯+⨯. 解:原式=181621621715152(33)23(31)4(33)83(31)8+⨯+⨯=+⨯+⨯=32练习1:【“希望杯”】:计算:123369510157142113539155152572135⨯⨯+⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯. 二. 求值例2.【“希望杯”】:若1x y +=-,则4325x x y x y ++228x y + 2345xy xy y +++的值等于( )A .0B .-1C .1D .3解:原式=432234(464)x x y x y xy y +++++322322(2)()x y x y xy x y xy ++++ =42()()()x y xy x y xy x y +++++把1x y +=-代入上式,得:原式=4(1)1xy xy -+-= 因此,选C .练习2:【北京市】:若正数,,a b c 满足ab a b bc b c ++=++=ca c a ++=3,则(1)(1)(1)a b c +++=_____.三. 确定方程的整数解例3【“希望杯”】:如果,x y 是整数,且22200420051x xy y +-=,那么x =_____, y =______.解:由已知方程得:()(2005)1x y x y -+=由于x 和y 都是整数,所以有: 1,20051x y x y -=+= 或1,20051x y x y -=-+=-解得1,0x y == 或1,0x y =-=练习3:【“希望杯”】:若,x y 是非负整数,那么满足方程225y +=2x 的解有( )A .1组B .2组C .3组D .4组四. 判断整除性问题例4.【天津市】:已知9621-可以被在60至70之间的两个数整除,则它们是 ( )A .63,61B .61,65C .63,65D .63,67解:因为 96484848242421(21)(21)(21)(21)(21)-=+-=++-48241212(21)(21)(21)(21)=+++-48241266(21)(21)(21)(21)(21)=++++- 482412(21)(21)(21)6563=+++⋅⨯因此,9621-能被63,65两个数整除.因此,选C .练习4.【江苏省】:已知2471-可被40至50之间的两个数整除,则这两个整数是 ( )A .41,48B .45,47C .43,48D .41,47五.比较代数式的大小例5【 “希望杯”】:已知:a b c >>,222M a b b c c a =++,N =222ab bc ca ++,则M 与N 的大小关系是( )A .M N <B .M N >C .M N =D 不能确定解:222222M N a b b c c a ab bc ca -=++--- 222222()()()a b ab b c ca c a bc =-+-+-222()()()ab a b c b a c a b =-+-+-2()()a b ab bc ac c =---+=()()()a b a c b c ---因为 a b c >>, 所以 0,0,0a b a c b c ->->->,所以 ()()()0a b a c b c ---> 故M N > 选B练习5:【北京市】已知:219961995199619951996m =+⨯+⨯ 1994...19951996++⨯+1995⨯199519961996,1996n =,则m 与n 的大小关系是______.六.判断几何图形的形状例6.【“希望杯”】:已知一个凸四边形ABCD 的四条边的长依次为,,,a b c d ,且20,a ab ac bc b bc bd cd +--=+--,那么四边形ABCD 是( )A .平行四边形B .矩形C 菱形D .梯形解:由20a ab ac bc +--=得()()0a b a c +-=因为0a b +>,所以0a c -=,所以a c =,同理可得 b d =.所以,四边形ABCD 是平行四边形(两组对边分别相等的四边形是平行四边形)练习6.【“希望杯”】:若三角形的三边,,a b c 满足关系式422224a b c a c b +--=0,则此三角形的形状是______.因式分解有着广泛的应用,考虑篇幅及同学们所学知识范围,在此不再赘述.【练习题参考答案】1.25; 2.8; 3.B 4.C 5.m n = 6.等腰三角形或直角三角形.。
华师大13章整式的乘除单元练习题(精品)

蓬溪中学初2014级数学练习题幂的运算班 姓名 得分一、选择题(每小题3分,共24分)1.下列运算正确的是 ( ) A .a 5·a 2=a 10B .(a 2) 4=a 8C .a 6÷a 2=a 3D .a 3+a 5=a 82.下列等式正确的是 ( ) A .(-x 2) 3=-x 5B .x 8÷x 4=x 2C .x 3+x 3=2x3D .(xy)3=xy 33.化简[-(-a) 2] 3的结果为 ( ) A .-a 6B .a 6C .61a -D .61a4.计算25m÷5m的结果为 ( )A .5B .20C .5mD .20m5.若x 2n=2,则x 6n的值为 ( ) A .6 B .8 C .9 D .126.若一个正方体的棱长为102cm ,则这个正方体的体积为 ( ) A .102cm 3B .103cm 3C .104cm 3D .106cm 37.下列各式计算结果为a 7的是 ( ) A .(-a) 2·(-a) 5B .(-a) 2·(-a 5) C .(-a 2)·(-a)5D .(-a)·(-a) 68.若223a -⎛⎫=- ⎪⎝⎭,01b π⎛⎫=- ⎪⎝⎭,c=0.8-1,则a 、b 、c 的大小关系是 ( )A .a <b <cB .a >b >cC .a >c >bD .c >a >b 二、填空题(每小题3分,共15分) 1.计算:(-x 2) 4=_________.2.填上适当的代数式:x 3·x 4·__________=x 8. 3.计算:20092010122⎛⎫⨯- ⎪⎝⎭=__________.4.一个三角形的面积为4a 3b 4.底边的长为2ab 2,则这个三角形的高为_______. 5.若32x+1=1,则x=__________.三、计算(每小题4分,共16分)(1)、(-3pq) 2; (2)、(-3a 3) 2÷a 2(3)、3x 2·xn -2+3(-x) 2·xn -3·(-x)(4)、[]233234)()()()(x x x x-÷-∙-÷-.四、解答题(每小题5分,共45分) 1、已知3×9m×27m=321,求m 的值.2、若2×8x ×16x =222,求x 的值.3、若(27x ) 2=38,求x 的值. 4、已知3x+4y -5=0,求8x ×16y的值.5、已知2m=3,2n=22,求22m+n的值。
华师大第13章整式的乘除单元试题(精品)

蓬溪中学初2014级数学练习题整式的乘除单元测试题班 姓名 得分一、选择题(每小题2分,共16分)1、 下列各题的计算,正确的是( )A 。
523)(a a = B. ()63293a a -=- C 。
()()54a a a -=-•- D. 6332a a a =+2、如果(a -b )2加上一个单项式便等于(a +b )2,则这个单项式是( )A 、ab 2B 、ab 2-C 、ab 4D 、ab 4-3、下列从左边到右边的变形,属于因式分解的是 ( )A. 1)1)(1(2-=-+x x x B. 1)2(122+-=+-x x x x C. )4)(4(422y x y x y x -+=- D. )3)(2(62-+=--x x x x4.÷c b a 468( )=224b a ,则括号内应填的代数式是 ( ) A 、c b a 232 B 、232b a C 、c b a 242 D 、c b a 2421 5、下列各式计算正确的是( )。
A 。
5)5)(5(2-=-+x x x B.222)(b a b a -=- C.65)3)(2(2--=-+x x x x D 。
2294)32)(23(m n m n n m -=--- 6、下列各式中,运算结果是22169b a -的是 ( )A 。
)83)(23(b a b a -+B. )34)(34(a b a b --+- C 。
)43)(43(b a b a --+- D. )34)(34(a b a b -+7、下列多项式相乘,不能用平方差公式计算的是( )A 、(x -2y )(2y+x )B 、(-2y -x)(x+2y)C 、(x -2y )(-x -2y)D 、(2y -x )(-x -2y )8、若多项式4x 2+2kx +25是另外一个多项式的平方,则k 的值是( )。
A 、 10B 、 20C 、 ±10D 、 ±20二、填空题(9题每空1分,其余每空2分,共14分)9、 =÷623)(x x 。
华师版八年级数学单元试题 全套第13章整式的乘除

第13章 整式的乘除学校 班别 姓名 座号一、选择题(每小题4分,共20分)1. 下列各题的计算,正确的是( )A. 927)(a a = B. 1427a a a =⋅ C. 522632a a a =+ D. 22)5.0(101100=⨯- 2. 如果单项式243y x b a --与b a y x +331是同类项,那么这两个单项式的积是( ). A.46y x B.23y x - C.2338y x - D.46y x - 3. 计算223)3(a a ÷-的结果是( ).A.49aB. 49a -C.46aD. 39a4. 若,12,7==+mn n m 则22n mn m +-的值是( )A. 11B. 13C. 37D. 615.下列各式计算正确的是( ).A.3)3)(3(2-=-+x x xB.92)32)(32(2-=-+x x xC.92)3)(32(2-=-+x x xD.125)15)(15(22-=-+b a ab ab二、填空题(每小题5分,共25分)6. 532)(y y ÷=_______.7. 若194a a a y =⋅,则=y .8. 分解因式:=+22xy y x .9. ++=+222)(b a b a .10. 若多项式92++mx x 恰好是另一个多项式的平方,则=m ______. 三、解答题(每小题9分,共27分)11. 计算: a a a ⋅+-)1(62312. 计算:2004200220032⨯-13. 计算:)3()324(23x x x x -÷--四、解答题(每小题9分,共18分)14. 先化简,再求值:)32(3)143(222--+-x x x x x ,其中3-=x .15. 公园里两片草地的尺寸及面积分别如图所示,由题意试列出方程组并且求出m和n的值.五、解答题(共10分)16. 观察下列单项式:,16,8,4,2,5432x x x x x --(1) 计算一下这里任一个单项式与前面的单项式的商,你有什么发现?(2) 根据你发现的规律写出第10个单项式.第13章 整式的整除一、选择题(每小题4分,共20分)1.D2.D3.A4.B5.D二、填空题(每小题5分,共25分)6. y7.158. )(y x xy +9.(-2ab) 10.±6 三、解答题(每小题9分,共27分)11. a a -35 12.1 13. 132342++-x x四、解答题(每小题9分,共18分)14. 原式=x x 22+;315. m =2、1=n五、解答题(共10分)16.(1)通项n n x 1)2(-- (2)10=n 时,。
八年级数学上册 第13章 整式的乘除 13.3 乘法公式拓展练习 华东师大版

乘法公式运用“八字诀”在八年级数学13.3《乘法公式》中,有两个重要的公式——平方差公式和完全平方公式,这两个公式的应用十分广泛.解题时,若能根据题目特点灵活运用,则能达到迅速解题的目的.如何运用上述公式呢?1.套:分清题中哪些数或式可以看作公式中的a 、b ,对号入座,直接套用公式. 例1.计算:)421)(214(22x x +-.分析:此题是两个二项式相乘,且这两个二项式中各有一完全相同的项24x ,另外一项-21与21互为相反数,符合平方差公式的结构特点,因此,可直接套用平方差公式. 解:)421)(214(22x x +-=4116)21()4(4222-=-x x . 2.连:连续应用乘法公式.例2.计算:))()()()((884422b a b a b a b a b a ++++-分析:本题可以连续应用平方差公式来计算.解:原式=))()(())()()((88444488442222b a b a b a b a b a b a b a ++-=+++- =16168888))((b a b a b a -=+-.3.逆:有些题目正向思考解题较为麻烦,若抓住题目的特征,逆用公式解题,往往显得简单. 例4.计算:22)43()32(a b b a --+ 分析:若直接运用完全平方公式展开再相减,运算量大,若把式中的“32b a +”与 “a b 43-”分别视为平方差公式中的a 、b ,逆用平方差公式,则运算简便. 4.选:有的题目能用几个公式计算,应选用哪个公式计算,这就要仔细观察全盘考虑,合理选用公式,才能使运算简便.例4.计算:222222)1()1()1()1(+++-+-a a a a a a分析:此题若将四个因式都按完全平方公式展开再相乘,则运算相当繁琐,若先应用乘法的交换律和结合律再逆用积的乘方法则,然后利用立方和(差)公式来解,便可化繁为简. 解:原式=23232222)1()1()]1)(1[()]1)(1[(+-=+-+++-a a a a a a a a = 12)1()]1)(1[(61226233+-=-=+-a a a a a .5.凑:有些题目乍一看不符合公式的结构特征,但经过适当地拼凑,可以变成公式的形式.例5.计算:)52)(52(++-+-+z y x z y x分析:利用加法交换律和结合律,将上面的式子拼凑成符合公式的形式.解:原式=22)()52()]()52)][(()52[(z y x z y x z y x --+=--+-++= 222225204z xy y x x -+-++.6.拆:将题目中的某些项有目的地进行分拆,使其符合公式的形式.例6.计算:)532)(132(+----y x y x分析:本题中的两个因式不符合乘法公式的特点,因而不能应用平方差公式来解.但若将本题两个因式中的项分别进行拆项完形:将前一因式的“-1”拆成“-3+2”,将后一因式的“5”拆成“3+2”,便可用平方差公式来计算.解:原式=)532)(132(+----y x y x =)]32()32)][(32()32[(----+-x y x y = 22)32()32(---x y =512412922-+--x x y y .7.添:就是在不改变原式的值的前提下,将原式添上一个因式,使得它能运用乘法公式计算.例7.计算;1)12)(12)(12)(12(842+++++.分析:本题若添上一个因式“2-1”后,则可以连续四次运用平方差公式计算. 解:原式==+++++-1)12)(12)(12)(12)(12(842 1)12)(12)(12)(12(8422++++-=1)12)(12)(12(844+++-=16168821121)12)(12(=+-=++-.8.活:将公式巧妙变形,活用公式解题.乘法公式的变形有:ab b a b a 2)(222-+=+;ab b a b a 2)(222+-=+ ; 2)()(2222b a b a b a -++=+;22)(41)(41b a b a ab --+=,同学们在运用公式时,不应拘泥于公式的形式而要深刻理解、灵活运用.例3.已知a ,b 为自然数且a+b=40,①求22b a +的最小值;②求ab 的最大值.解:①∵2)()(2222b a b a b a -++=+=])(40[2122b a -+,∵2)(b a -≥0,∴当a=b 时,22b a +的有最小值,最小值为80040212=⨯;∵22)(41)(41b a b a ab --+== 22)(41)2(b a b a ab --+==222)(41400)(414041b a b a --=--⨯,∵2)(b a -≥0,∴当a=b 时,ab 有最大值,最大值为400.。
八年级数学上册 第13章 整式的乘除 13.2 整式的乘法特色训练2 华东师大版

【知能点分类训练】知能点1 单项式与单项式相乘法则1.计算:(-2xy2)(3x2y)=_______,(-0.25x2)·(-4x)=________.2.(-5a2b3)·(3a3b2)等于().A.-15a6b6 B.15a6b6 C.-15a5b5 D.15a5b53.下列计算正确的是().A.2a2·4ab2=6a3b2 B.3a3·4a4=7a12 C.3x2·2x5=6x10 D.0.1x·10x2=x3 4.计算(-5x2y)2·x n·y的结果是().A.-5x n+2y2 B.-5x x+n·y3 C.25x n+4y3 D.25x n+2y25.用科学记数法表示(2×102)×(15×106)的结果应为().A.30×108 B.3.0×107 C.3.0×109 D.3.0×10106.计算:(1)(2x2)3·(-4xy2)(2)(-2a2b2c)2·(-14abc2)(3)-6a2b·(x-y)3·13ab(y-x)2; (4)(-12a2b2c)(-14abc2)2知能点2 应用与创新7.长方形的长是宽的a倍,宽为b,则其面积为(). A.ab B.a2b C.ab2 D.a2b28.如果单项式-3x2a-b y2与13x3a+b y5a+8b是同类项,那么这两个单项式的积为().A.-x10y4 B.-x6y4 C.-x25y4 D.-x5y29.有一长为am,宽为bm的长方形空地,因基建用去了其中的一部分,•已知用去的长方形空地的长为am,宽为13bm,求:用去的这块地的面积是多少?剩下的面积又是多少?10.如图所示,计算变压器铁心片的面积.(单位:cm)【综合应用提高】11.若(4×10n)×(20×103)×(5×102)=4×109,那么n的值等于().A.2 B.3 C.4 D.512.下列四个算式中正确的是().A.2a3-a3=1 B.(-xy2)(-3x3y)=3x4y3 C.(x3)3·x=x9 D.2a2b3·2ab4=2a3b713.若a=-3,b=-13,则a2n·(ab n+1)2=________.(n是正整数)14.已知x,y满足│x-2│+│y+1│2=0,试求代数式-2xy·5xy2+(12x2y2-3x)·2y+6xy•的值.15.解不等式2x(7-3x)+5x(2x+1)≤x(4x-3)+32.16.解方程x2-1=-2x(x+1)+(3x-2)x.17.先化简再求值:(-12a3b)·(2abc2)3·(12a)2·(-18bc)3,其中a=-1,b=1,c=-1.18.已知-2x3m+1y2n与7x n-6y-3-m的积与x4y是同类项,求m和n的值.【开放探索创新】19.请尽可能多地写出两个整式,使每个整式中至少含有一个字母,并使它们的乘积为12a2b3(a-b).【中考真题实战】20.(烟台)下列计算正确的是()A.4a3·3a2=12a6 B.(-3y8)(-5x2)=15x10C.(-6a n+2)·3a n b=-18a2n+2b D.4x2·2x2=8x221.(云南)计算(-4x n y)2·3x n-1y的计算结果是()A.48x3n-1y3 B.-48x3n-1y3 C.48x2n-1y3 D.48x3n y3参考答案1.-6x3y3 x32.C 提示:原式=(-5×3)a2·a3·b3·b2=-15a5b5.3.D 提示:0.1x·10x2=(0.1×10)·(x·x2)=1·x1+2=x3.4.C 提示:原式=(-5)2·(x2)2·y2·x n y=25·x4·y2·x n y=25(x4·x n)·(y2·y)=25x n+4y3.5.C 提示:原式=(2×15)×(102×106)=30×108=3.0×109.6.(1)原式=23·(x2)3·(-4xy2)=8x6·(-4xy2)=-32x7y2.(2)原式=(-2)2·(a2)2·(b2)2c2(-14abc2)=4a4b4c2·(-14)abc2=4×(-14)·a4·a·b4·b·c2·c2.=-1·a5b5c4=-a5b5c4.(3)原式=-6a2b(x-y)3·13ab(x-y)2=-6×13a2·a·b·b·(x-y)3·(x-y)2=-2a3b2(x-y)5.(4)原式=(-12a2b2c)(-14)2·a2·b2·(c2)2=-12a2b2c·116·a2b2c4=-12×116·a2·a2·b2·b2·c·c4=-34a4b4c5.7.C 提示:长为ab,宽为b,故面积为ab2.8.A 提示:2a-b=3a+b且2=5a+8b,∴a=2,b=-1,∴原单项式分别为-3x5y2与13x5y2.∴-3x5y2·13x5y2=-x10y4.9.用去的面积为a·13b=13ab;剩余的面积a·b-13ab=23ab.10.两种方法:方法1:用整个长方形面积减去空白部分面积.(1.5a+2.5a)(a+2a+2a+2a+a)-2a·2.5a-2a·2.5a=4a·8a-5a2-5a2=32a2-10a2=22a2.方法2:分割求和,即分割成4块的和.1.5a·(a+2a+2a+2a+a)+2.5a·a+2.5a·2a+2.5a·a=1.5a·8a+2.5a2+5a2+2.5a2=12a2+2.5a2+5a2+2.5a2=22a2.11.A 提示:原式=(4×20×5)×(10n×103×102)=400×105+n=4×102×105+n=4×107+n=4×109,∴7+n=9,n=2.12.B13.1 提示:原式=a2n·a2·(b n+1)2=a2n+2·(b n+1)2=(a2n+2)·(b2n+2)=(ab)2n+2=[-3×(-13)2n+2]=12n+2=1.14.由题意得x-2=0,y+1=0,即x=2,y=-1.∴原式=-10x2y3+x2y3-6xy+6xy=-9x2y3=-9×22×(-1)3=36.15.原不等式变为2x·7+2x·(-3x)+5x·2x+5x·1≤x·4x+x·(-3)+32, 14x-6x2+10x2+5x≤4x2-3x+32.14x-6x2+10x2+5x-4x2+3x≤32,22x≤32,x≤16 11.16.原方程变为x2-1=-2x2-2x+3x2-2x, x2+2x2-3x2+2x+2x=1,4x=1,x=14.17.原式=-12a3b·23b3·(c2)3·(12)2·a2·(-18)3·b3c3=-12a3b·8b3c6·14a2·(-1512)b3c3=[-12×8×14×(-1512)] ·(a3·a2)(b·b3·b3)(c6·c3)=1512·a5·b7·c9.当a=-1,b=1,c=-1时,原式=1512a5b7c9=1512×(-1)5×17×(-1)9=1512×(-1)(-1)=1512.18.依题意有(-2x3m+1y2n)·(7x n-6y-3-m)=-14x3m+n-5·y2n-m-3,∴354,2, 231, 3. m n mn m n+-==⎧⎧∴⎨⎨--==⎩⎩19.答案不唯一,如3a2b3,4(a-b)或2ab3,6a(a-b)等.20.C21.A。
八年级数学上册 第13章 整式的乘除 13.5 因式分解拓展练习 华东师大版

因式分解应用宝典因式分解是中学数学的重要内容之一,不但在我们平时的考试中经常考到它,就是在各级各类数学竞赛题中都能看到用因式分解求解的题目.下面举例说明因式分解在以下几个方面的应用.一. 计算例1.【“希望杯”】:计算: 9421715(981)2(33)8+⨯+⨯.解:原式=181621621715152(33)23(31)4(33)83(31)8+⨯+⨯=+⨯+⨯=32练习1:【“希望杯”】:计算:123369510157142113539155152572135⨯⨯+⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯.二. 求值例2.【“希望杯”】:若1x y +=-,则4325x x y x y ++228x y +2345xy xy y +++的值等于( )A .0B .-1C .1D .3解:原式=432234(464)x x y x y xy y +++++322322(2)()x y x y xy x y xy ++++ =42()()()x y xy x y xy x y +++++把1x y +=-代入上式,得:原式=4(1)1xy xy -+-= 因此,选C .练习2:【北京市】:若正数,,a b c 满足ab a b bc b c ++=++=ca c a ++=3,则(1)(1)(1)a b c +++=_____.三. 确定方程的整数解例3【“希望杯”】:如果,x y 是整数,且22200420051x xy y +-=,那么x =_____, y =______.解:由已知方程得:()(2005)1x y x y -+=由于x 和y 都是整数,所以有:1,20051x y x y -=+= 或1,20051x y x y -=-+=-解得1,0x y == 或1,0x y =-=练习3:【“希望杯”】:若,x y 是非负整数,那么满足方程225y +=2x 的解有( )A .1组B .2组C .3组D .4组四. 判断整除性问题例4.【天津市】:已知9621-可以被在60至70之间的两个数整除,则它们是 ( )A .63,61B .61,65C .63,65D .63,67解:因为 96484848242421(21)(21)(21)(21)(21)-=+-=++-48241212(21)(21)(21)(21)=+++-48241266(21)(21)(21)(21)(21)=++++- 482412(21)(21)(21)6563=+++⋅⨯因此,9621-能被63,65两个数整除.因此,选C .练习4.【江苏省】:已知2471-可被40至50之间的两个数整除,则这两个整数是 ( )A .41,48B .45,47C .43,48D .41,47五.比较代数式的大小例5【 “希望杯”】:已知:a b c >>,222M a b b c c a =++,N =222ab bc ca ++,则M 与N 的大小关系是( )A .M N <B .M N >C .M N =D 不能确定解:222222M N a b b c c a ab bc ca -=++--- 222222()()()a b ab b c ca c a bc =-+-+-222()()()ab a b c b a c a b =-+-+-2()()a b ab bc ac c =---+=()()()a b a c b c ---因为 a b c >>, 所以 0,0,0a b a c b c ->->->,所以 ()()()0a b a c b c ---> 故M N > 选B练习5:【北京市】已知:219961995199619951996m =+⨯+⨯ 1994...19951996++⨯+1995⨯199519961996,1996n =,则m 与n 的大小关系是______.六.判断几何图形的形状例6.【“希望杯”】:已知一个凸四边形ABCD 的四条边的长依次为,,,a b c d ,且20,a ab ac bc b bc bd cd +--=+--,那么四边形ABCD 是( )A .平行四边形B .矩形C 菱形D .梯形解:由20a ab ac bc +--=得()()0a b a c +-=因为0a b +>,所以0a c -=,所以a c =,同理可得 b d =.所以,四边形ABCD 是平行四边形(两组对边分别相等的四边形是平行四边形)练习6.【“希望杯”】:若三角形的三边,,a b c 满足关系式422224a b c a c b +--=0,则此三角形的形状是______.因式分解有着广泛的应用,考虑篇幅及同学们所学知识范围,在此不再赘述.【练习题参考答案】1.25; 2.8; 3.B 4.C 5.m n = 6.等腰三角形或直角三角形.。
华师大版八年级上数学-整式的乘除单元测试(附答案)

华师大版八年级上学期之羊若含玉创作“整式的乘除”单元测试一、填空题:(每空3分,共36分)1.盘算:._______53=⋅a a 2.盘算:._____)2(23=-a3.盘算:._______2142=÷-a b a 4.盘算:._________________)12(2=-x5.盘算:.___________________)3)(2(=+-x x6.因式分化:.______________252=-x x7.因式分化:.__________42=-x8.因式分化:.___________________442=+-x x9.盘算:._______)1098.5()109.1(2427≈⨯÷⨯(保存三个有效数字)10.有三个持续的自然数,中间一个是x ,则它们的积是____________.11.若多项式442++kx x 恰好是另一个多项式的平方,则k=___________.12.一块边长为a 米的正方形广场,扩建后的正方形边长比原来长2米,问扩建后的广局势积增大了______________平方米.二、选择题:(每小题4分,共24分)13.下列运算中正确的是( )A .43x x x =+B .43x x x =⋅C .532)(x x =D .236x x x =÷14.盘算:)34()3(42y x y x -⋅的成果是( )A .26y xB .y x 64-C .264y x -D .y x 835 15.下列从左边到右边的变形,属于因式分化的是( )A .1)1)(1(2-=-+x x xB .1)2(122+-=+-x x x xC .)4)(4(422y x y x y x -+=-D .)3)(2(62-+=--x x x x16.下列多项式,能用公式法分化因式的有()①22y x +②22y x +-③22y x --④22y xy x ++⑤222y xy x -+⑥2244y xy x -+-A .2个B .3个C .4个D .5个17.若(x+t )(x+6)的积中不含有x 的一次项,则t 的值是( )A .6B .-6C .0D .6或-618.长方形的长增加50%,宽削减50%,那么长方形的面积( )A .不变B .增加75%C .削减25%D .不克不及确定三、解答题:(共90分)19.盘算题:(每小题6分,共24分)(1)3324)101).(2.(21x xy y x --(2))7)(5()1(2+-+-a a a a (3)22)5()5(y x y x +-- (4))(]12)1)(1[(22ab b a ab ab -÷+--+20.(8分)化简求值:x y x x y x y x y x 2)]2(2)2)(2()2[(2÷--+-+-.其中 6,5-==y x .21.(8分)已知1,5==+xy y x ,求:①22y x +;②2)(y x -.22.分化因式(各小题6分,共24分)(1)223242ab b a a +-(2)44y x -(3)22125)(5m y x -+(4))34(3422y xy x ++23.(8分)有一块直径为2a + b 的圆形木板,挖去直径分离为2a 和 b 的两个圆,问剩下的木板的面积是若干?24.(8分)说明对于任意正整数n ,式子n (n+5)-(n -3)(n+2)的值都能被6整除.25.应用题:(10分)如图1,在边长为a 的正方形中挖失落一个边长为b 的小正方形(a>b ),把余下的部分剪成一个矩形(如图2),通过盘算两个图形(阴影部分)的面积,验证了一个等式,你通过剖析能找出来吗?依据以上所提供的办法,你能设计出一个图形说明下面等式:(a+2b )(2a -b )=2a2+3ab -2b2吗?并配文字加以说明.参考答案一、填空题1.8a 2.64a 3.ab 7- 4.1442+-x x 5.62-+x x 6.)25(-x x7.)2)(2(x x -+ 8.2)2(-x 9.318 10.x x -3 11.1± 12.)44(+a二、选择题13.B 14.C 15.D 16.A 17.B 18.C三、 解答题19.(1)5810001y x (2)3523-+a a (3)xy 20- (4)ab20.化简成果为 y x --,当6,5-==y x 时,原式=121.① 23 ②2122.(1))2(222b ab a a +- (2)))()((22y x y x y x -++(3))5)(5(5m y x m y x -+++ (4)2)32(y x + 23.ab π24.n (n+5)-(n -3)(n+2)=n2 +5n -n2 +n +6=6n +6=6(n +1)∵n 为任意正整数∴6(n +1) ÷6=n +1∴n (n+7)-(n+3)(n -2)总能被6整除 25.略.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蓬溪中学初2014级数学练习题幂的运算班 姓名 得分一、选择题(每小题3分,共24分)1.下列运算正确的是 ( ) A .a 5·a 2=a 10B .(a 2) 4=a 8C .a 6÷a 2=a 3D .a 3+a 5=a 82.下列等式正确的是 ( ) A .(-x 2) 3=-x 5B .x 8÷x 4=x 2C .x 3+x 3=2x3D .(xy)3=xy 33.化简[-(-a) 2] 3的结果为 ( ) A .-a 6B .a 6C .61a -D .61a4.计算25m÷5m 的结果为 ( )A .5B .20C .5mD .20m5.若x 2n=2,则x 6n的值为 ( ) A .6 B .8 C .9 D .126.若一个正方体的棱长为102cm ,则这个正方体的体积为 ( ) A .102cm 3B .103cm 3C .104cm 3D .106cm 37.下列各式计算结果为a 7的是 ( ) A .(-a) 2·(-a) 5B .(-a) 2·(-a 5) C .(-a 2)·(-a)5D .(-a)·(-a) 68.若223a -⎛⎫=- ⎪⎝⎭,01b π⎛⎫=- ⎪⎝⎭,c=0.8-1,则a 、b 、c 的大小关系是 ( )A .a <b <cB .a >b >cC .a >c >bD .c >a >b 二、填空题(每小题3分,共15分) 1.计算:(-x 2) 4=_________.2.填上适当的代数式:x 3·x 4·__________=x 8. 3.计算:20092010122⎛⎫⨯- ⎪⎝⎭=__________.4.一个三角形的面积为4a 3b 4.底边的长为2ab 2,则这个三角形的高为_______. 5.若32x+1=1,则x=__________.三、计算(每小题4分,共16分)(1)、(-3pq) 2; (2)、(-3a 3) 2÷a 2(3)、3x 2·xn -2+3(-x) 2·xn -3·(-x)(4)、[]233234)()()()(x x x x-÷-∙-÷-.四、解答题(每小题5分,共45分) 1、已知3×9m×27m=321,求m 的值. 2、若2×8x ×16x =222,求x 的值.3、若(27x ) 2=38,求x 的值. 4、已知3x+4y -5=0,求8x ×16y的值.5、已知2m=3,2n=22,求22m+n的值。
6、已知3,9m n a a ==,求32m na-的值7、比较下列一组数的大小.61413192781,,8.若n 为自然数,试确定34n-1的末位数字.8、 已知2a =3,2b =6,2c=12,试找出a 、b 、c 之间的等量关系.9、已知,710,510,310===cba试把105写成底数是10的幂的形式.蓬溪中学初2014级数学练习题整式的乘法班 姓名 得分一、选择题(每小题3分,共24分) 1.计算2322)(xy y x -⋅的结果是( ) A. 105y xB. 84y xC. 85y x -D.126y x2.22343)()2(yc x y x -⋅-等于( ) A. 214138c y x -B. 214138c y xC. 224368c y x -D. 224368c y x3.992213y x y x yx n n m m =⋅⋅++-,则=-n m 34( )A. 8B. 9C. 10D.无法确定4.下列计算错误的是( )A.122332)()(a a a =-⋅ B.743222)()(b a b a ab =-⋅- C.212218)3()2(++=-⋅n n n n y xy x xyD.333222))()((z y x zx yz xy -=---5.化简2(21)(2)x x x x ---的结果是( ) A .3x x --B .3x x -C .21x --D .31x -6、计算(2a -3b )(2a +3b )的正确结果是( ) A .4a 2+9b 2B .4a 2-9b 2C .4a 2+12ab +9b 2D .4a 2-12ab +9b 27、(x 2-px +3)(x -q )的乘积中不含x 2项,则( ) A .p =qB .p =±qC .p =-qD .无法确定8、如图14-2是L 形钢条截面,它的面积为( )A .ac+bcB .ac+(b-c)cC .(a-c)c+(b-c)cD .a+b+2c+(a-c)+(b-c)二、填空题:(每小题3分,共24分)1、._____________)(4)3(523232=-⋅-b a b a 2、._______________)104)(105.2)(102.1(9113=⨯⨯⨯ 3、22(3)(21)x x x --+-= 。
4、228(34)(3)m m m m m -+--= 。
5、若20x y +=,则代数式3342()x xy x y y +++的值为 。
6、(x 3+3x 2+4x -1)(x 2-2x +3)的展开式中,x 4的系数是__________.7、若(x +a )(x +2)=x 2-5x +b ,则a =__________,b =__________.8、若(x 2+ax +8)(x 2-3x +b )的乘积中不含x 2和x 3项,则a =____,b =_____. 三、计算题(每小题5分,共30分)1、)83(4322yz x xy -⋅2、(-3xy n ) ·(-x 2·z) ·(-2xy 2)23、)47(123)5(232y x y x xy -⋅-⋅- 4、32325431()(2)4(75)2a ab ab a b ab -⋅--⋅--5、(3x 2+2x +1)(2x 2+3x -1)6、(3x +2y )(3x -2y )四、解答题1、已知26ab =,求253()ab a b ab b --的值。
(7分)2、已知:20a b +=,求证:332()40a ab a b b +++=。
(7分)3、2(2x -1)(2x +1)-5x (-x +3y )+4x (-4x 2-52 y ),x =-1,y =2.(8分)蓬溪中学初2014级数学练习题 乘法公式班 姓名 得分一、选择题(每小题3分,共24分) 1、下列可以用平方差公式计算的是( )A 、(x -y) (x + y)B 、(x -y) (y -x)C 、(x -y)(-y + x)D 、(x -y)(-x + y) 2、下列各式中,运算结果是22169b a -的是( ) A 、)43)(43(b a b a --+-B 、)34)(34(a b a b --+-C 、)34)(34(a b a b -+D 、)83)(23(b a b a -+3、若2422549))(________57(y x y x -=--,括号内应填代数式( ) A 、y x 572+B 、y x 572--C 、y x 572+-D 、y x 572-4、2)2(n m +-的运算结果是 ( )A 、2244n mn m ++B 、2244n mn m +--C 、2244n mn m +-D 、2242n mn m +- 5、运算结果为42421x x +-的是 ( )A 、22)1(x +- B 、22)1(x + C 、22)1(x -- D 、2)1(x - 6、已知2264b Nab a +-是一个完全平方式,则N 等于 ( ) A 、8B 、±8C 、±16D 、±327、如果22)()(y x M y x +=+-,那么M 等于 ( ) A 、 2xyB 、-2xyC 、4xyD 、-4xy8、已知)(==-=+ab b a b a ,4,822 A.-2 B.-4 C.-0.5 D.4二、填空题(每小题4分,共24分)1、 (3a + b) (3a -b) =______________, (2x 2-3) (-2x 2-3) = ____________________;2、 (x + y) (-x + y) = ____________, (-7m -11n) (11n -7m) = _________________;3、 _____________________)2)(4)(2(___,__________)2)(2(2=++-=---a a a y x x y4、______________________)2(_________,__________)3(22=+-=-b a b a5、_________________________)2(__,__________)()(222=--+-=+y x b a b a 6、计算:5002-502×498= 三、计算题1、)1)(1(---xy xy2、)23)(23(2222b a ab b a ab ++- 3、2)2332(y x -4、22)()(y x y x +- 5、22)23()32(+-+x x 6、(a + b -c) (a -b + c)四、解答题1、用简便方法计算 ⑴ 92×88(2) 9992 (3)2220012003-2、已知(a + b) 2 =3,(a -b) 2 =2 ,分别求a 2 + b 2, ab 的值3、已知a +a 1=4,求a 2+21a 和a 4+41a的值.4、计算:(2+1)(22+1)(24+1) (22)+1)+1 .5、计算:22222110099989721-+-++-蓬溪中学初2014级数学练习题整式的除法班 姓名 得分一、填空1.4x 4y 2÷(-2xy)2=______. 2.2(-a 2)3÷a 3=______. 3.______÷5x 2y=5xy 2.4.ym+2n+6=y m+2·______.5.______÷(-5my 2z)=-m 2y 3z 4.6.(16a 3-24a 2)÷(-8a 2)=______. 7.(m+n)2(m-n)÷(m+n)2=______.8.(-8x 4y+12x 3y 2-4x 2y 3)÷(4x 2y)=______.9.如果4x 3+9x 2+mx+n 能被x 2+2x-3整除,则m=______,n=______. 10.已知x 2-3x-2=0,则-x 3+11x+6=______. 二、选择题1.21a 8÷7a 2= [ ] A .7a 4;B .3a 6;C.3a 10;D .3a 16.2.下列计算,结果正确的是( )A.8x 6÷2x 2=4x 3B.10x 6÷5x 3=21x 3 C.(-2x 2y 2)3÷(-xy )3=-2x 3y 3 D.(-xy 2)2÷(-x 2y )=-y 3 3.(a 2-b 2)÷(a -b )的结果是( ) A.a -bB.a +bC.-a +bD.-a -b4.下列计算中正确的是( ) A.(-a 2)3=a 6B.a 6÷a 3=a 2C.(a +b )÷(-a -b )=-1D.a 1+aa 3121 5.如果计算(x 2-1)÷(x +1)的结果为0,则x 的值是( ) A.1B.-1C.0D.±16.(-43a 2bc )÷(-3ab )等于( ) A. 41a 2c B. 41acC.49a 2c D.49ac 7.下列计算中,正确的是( )A.a 2+2a 2=3a 4B.2x 3·(-x 2)=-2x 5C.(-2a 2)3=-8a 5D.6x 2m ÷2x m =3x 2三、计算1、 -12a 5b 3c ÷(-3a 2b )2. (28x 3-14x 2+7x )÷7x3. 242215()(5)a bc ab -÷4、(102)3×104÷(-103)3.5、(2a)3·(b 3)2÷4a 3b 4.6、82443215(3)(4)x y z x yz x y ÷-÷-四、解答题1.已知8a 3b m ÷28a n b 2=72b 2,求m ,n 的值.2.已知9m·27m-1÷32m的值为27,求m 的值.3.一颗人造地球卫星的速度是2.6×107 m/h ,一架飞机的速度是1.3×106 m/h ,试求人造地球卫星的速度是飞机的几倍?蓬溪中学初2014级数学练习题因式分解班 姓名 得分一、选择题(每小题3分,共24分)1.下列各式恒等变形属于因式分解的是( ) A .(x+3)(x -3)=x 2-9 B .x 2-9+x=(x+3)(x -3)+x C .3x 2-5x=2x(x -2)+x 2-xD .a 2+2ab+b 2=(a+b)22.下列从左到右的变形中,错误的是( ) A .(y -x)2=(x -y)2B .-m+n=-(m+n)C .-a -b=-(a+b)D .(m -n)3=-(n -m)33.下列式子中,哪个式子包含(a -b )的因式( ) A .m(a -b)-ma -nb B .m(a -b)-a -b C .m(a -b)-ma -mbD .m(a -b)-a+b4.-13ab 2x 6-39a 3b 2x 5分解因式等于( )A .-abx 3(13+39a 2x 2) B .-13ab 2x 6(1+3a 2) C .-13ab 2x 5(x+3a 2) D .-13ab 2x 5(x -3a 2) 5.把多项式-x 2+y 2分解因式,正确的结果是( ) A .(x+y)(x -y) B .(x+y)(y -x)C .-(x+y)(y -x)D .(-x+y)(-x -y)6.下列各式能用完全平方公式分解因式的是( ) A .1+4a2B .x 2-4x+4C.4a 2-4a -1D .x 2+xy+y 27.在完全平方式x 2-5x+k 中,k 的值是( ) A .25B .45C .225D .425 8.下列各式中,能用公式分解因式的有( )①x 2-3xy+9y 2;②x 2-y 2-2xy ;③-a 2-b 2-2ab ;④-x 2-16y 2;⑤-a 2+9b 2;⑥4x 2-2xy+41y 2A .5个B .4个C .3个D .2个二、填空题(每小题3分,共21分)1.多项式27m 2n 2+18m 2n -36mn 的公因式是________. 2.3a 2b -3ab+6b=(___________)(a 2-a+2).3.x -y+k(y -x)=(___________)(k -1).4.计算:22×3.14+54×3.14+24×3.14=__________. 5.9m 2-6mn+n 2=(_________________)2. 6.-x 2+4xy -4y 2=-(___________________)2.7.如果x+y=0,xy=-4,则x 3y -xy 3=_______________.三、解答题1、把下列各式分解因式:(每小题4分,共12分)⑴、4m 3-7m 2n+m ; ⑵、3a 2b 2+2a 2b -ab ;⑶、(x+1)2(2x -3)+(x+1)(2x -3)2-(x+1)(3-2x) .2、把下列各式分解因式:(每小题4分,共12分) ⑴、12x 2y 3-27x 2y ; ⑵、-2x 2+21y 2; ⑶、25+(a+2b)2-10(a+2b) .3、已知:21=-b a ,81=ab ,求32232ab b a b a +-的值.(本题7分)4、已知:4x 2+1+4kx 是关于x 的完全平方式,求k 2-2k+2的值.(本题7分)5、不解方程组⎩⎨⎧=-=+1362y x y x ,求7y(x -3y)2-(3y -x)3的值.(本题7分)蓬溪中学初2014级数学练习题整式的乘除单元测试题 班 姓名 得分一、选择题(每小题2分,共16分)1、 下列各题的计算,正确的是( )A. 523)(a a =B. ()63293a a-=- C. ()()54a a a -=-∙- D. 6332a a a =+2、如果(a -b )2加上一个单项式便等于(a +b )2,则这个单项式是( )A 、ab 2B 、ab 2-C 、ab 4D 、ab 4-3、下列从左边到右边的变形,属于因式分解的是 ( )A. 1)1)(1(2-=-+x x xB.1)2(122+-=+-x x x x C. )4)(4(422y x y x y x -+=- D. )3)(2(62-+=--x x x x4.÷c b a 468( )=224b a ,则括号内应填的代数式是 ( )A 、c b a 232B 、232b aC 、c b a 242D 、c b a 2421 5、下列各式计算正确的是( ).A.5)5)(5(2-=-+x x xB.222)(b a b a -=-C.65)3)(2(2--=-+x x x xD.2294)32)(23(m n m n n m -=---6、下列各式中,运算结果是22169b a -的是 ( )A. )83)(23(b a b a -+B. )34)(34(a b a b --+-C. )43)(43(b a b a --+-D. )34)(34(a b a b -+ 7、下列多项式相乘,不能用平方差公式计算的是( )A 、(x -2y)(2y+x)B 、(-2y -x)(x+2y)C 、(x -2y)(-x -2y)D 、(2y -x)(-x -2y)8、若多项式4x 2+2kx +25是另外一个多项式的平方,则k 的值是( ).A 、 10B 、 20C 、 ±10D 、 ±20二、填空题(9题每空1分,其余每空2分,共14分)9、 =÷623)(x x 。
