Dynamical directions in numeration
高三英语学术研究方法创新不断探索单选题30题

高三英语学术研究方法创新不断探索单选题30题1. In academic research, a hypothesis is a ______ that is tested through experiments and observations.A. predictionB. conclusionC. theoryD. assumption答案:D。
本题考查学术研究中“假说”相关的基本概念。
选项A“prediction”意为“预测”,通常是基于现有信息对未来的估计;选项B“conclusion”指“结论”,是在研究后得出的最终判断;选项C“theory”是“理论”,是经过大量研究和验证形成的体系;选项D“assumption”表示“假定、设想”,更符合“假说”的含义,即在研究初期未经充分验证的设想。
2. The main purpose of conducting academic research is to ______ new knowledge and understanding.A. discoverB. createC. inventD. produce答案:A。
此题考查学术研究目的相关的词汇。
选项A“discover”意思是“发现”,强调找到原本存在但未被知晓的事物;选项B“create”意为“创造”,侧重于从无到有地造出新的东西;选项C“invent”指“发明”,通常指创造出新的工具、设备等;选项D“produce”有“生产、产生”的意思,比较宽泛。
在学术研究中,主要是“发现”新知识和理解,所以选A。
3. A reliable academic research should be based on ______ data and methods.A. accurateB. preciseC. correctD. valid答案:D。
本题关于可靠学术研究的基础。
选项A“accurate”侧重于“准确无误”,强调与事实完全相符;选项B“precise”意为“精确的、明确的”,更强调细节的清晰和明确;选项C“correct”指“正确的”;选项D“valid”表示“有效的、有根据的”,强调数据和方法具有合理性和可靠性。
基于双语词典的远距离语对无监督神经机器翻译方法

现代电子技术Modern Electronics Technique2024年4月1日第47卷第7期Apr. 2024Vol. 47 No. 70 引 言2013年,Nal Kalchbrenner 和Phil Blunsom 提出了端到端编码器⁃解码器结构[1],这一创新将神经机器翻译引入了主流研究领域。
近年来,基于深度学习的方法逐渐在机器翻译领域占据主导地位。
这些方法在许多语言对之间的翻译任务上表现出色,有些情况下甚至超越了人类翻译的质量。
然而,基于神经网络的翻译模型高度依赖于可用平行数据的数量和语言之间的相关性。
在一些拥有丰富平行语料的语言对,尤其是同一语系的语言对上,神经机器翻译已经展现出了卓越性能[2]。
但在实际应用中,存在很多语言对之间缺乏足够平行语料的情况,有些语言甚至没有可用的平行数据,导致神经机器翻译的性能下降。
为了减少神经机器翻译模型对平行数据的依赖,文献[3]提出了无监督神经机器翻译(Unsupervised Neural Machine Translation, UNMT )方法。
这种方法仅利用两种语言的单语语料库进行翻译,而不使用平行语料,从而摆脱了对大量平行数据的需求。
在某些语言对上,无监督神经机器翻译已经取得了出色的效果,甚至能够媲美基于双语词典的远距离语对无监督神经机器翻译方法黄孟钦(昆明理工大学 信息工程与自动化学院, 云南 昆明 650500)摘 要: 为了缓解大型平行语料库稀缺性对机器翻译质量的影响,无监督方法在神经机器翻译领域备受关注,但其在远距离语言对上的翻译表现仍有待提高。
因此,文中引入了翻译语言模型(TLM )并提出了Dict⁃TLM 方法。
该方法的核心思想是结合单语语料和无监督双语词典训练语言模型。
具体而言,模型首先接受源语言句子作为输入,然后,不同于传统TLM 只接受平行语料,Dict⁃TLM 模型还接受源语言句子通过无监督双语词典处理后的数据作为输入,在这种输入中,模型将源语言句子中在双语词典中出现的单词替换为相应的目标语言翻译词,重要的是,该方法中的双语词典是无监督获得的。
llm大语言模型量化方法

llm大语言模型量化方法LLM大语言模型量化方法是一种新的语言模型量化方法,它使用深度学习技术,在处理自然语言时能够大幅提高计算效率和准确率。
目前,LLM大语言模型量化方法已经被广泛应用于机器翻译、语音识别、自然语言处理等领域,并且取得了显著的成果。
量化是指将一个连续的数值空间转化为一个离散的数值空间。
在深度学习中,由于参数的数量极多,如果使用传统的精确计算方法,计算复杂度将会极高,从而导致计算时间过长,无法满足实时计算的需求。
因此,如何有效地降低计算复杂度成为一项关键技术。
LLM大语言模型量化方法就是一种高效降低计算复杂度的方法。
其基本思路是通过对神经网络中权重和激活输出的数值空间进行硬件友好的离散化处理,从而将实数域上的计算转化为整数域上的计算,从而降低计算复杂度,提高了计算效率。
具体来说,LLM大语言模型量化方法可分为三个步骤:第一步是量化网络的参数。
在此步骤中,通过对网络的参数进行离散化处理,将实数值离散化为整数值。
这样做可以有效地降低网络的存储空间,并且加速运算速度。
第二步是量化网络的输出。
在此步骤中,对网络的输出进行离散化处理,将实数域的输出转化为整数域的输出。
这样做可以大幅降低计算复杂度,提高运算速度,并且保持了原始网络的输出准确度。
第三步是训练量化网络。
在此步骤中,通过对离散化嵌入层的训练,可以提高网络的分辨率和准确性,使其更好地适应任务的要求。
同时,网络中的量化参数也可以被训练,以提高网络的分类精度。
总之,LLM大语言模型量化方法是一种高效的深度学习方法,其优点在于可以大幅降低计算复杂度,提高计算速度,并且保持了原始网络的输出准确度。
所以,LLM大语言模型量化方法在深度学习领域中有着广泛的应用前景,将为我们的生活带来更多的便利和创新。
拉马努金恒等式的证明

∞ k=−∞
(q/a, q/b, q/c, q/d, q/e)k (aq, bq, cq, dq, eq)k
(abcdeq−1)k
=
(q, ab, bc, ac)∞ (aq, bq, cq, abc/q)∞
∞ k=0
(q/a, (q, q2
q/b, q/c, /abc, dq,
de)k eq)k
qk
jouhet@math.univ-lyon1.fr, http://math.univ-lyon1.fr/~jouhet
3Universit´e de Lyon, Universit´e Lyon 1, UMR 5208 du CNRS, Institut Camille Jordan, F-69622, Villeurbanne Cedex, France
∞ k=−∞
(q/a)k (a)k
ak
qk2
−k
=
(q)∞ (a)∞
,
while the right-hand side of (1.7) is equal to 0 (since ab/q = 1). Similarly, if bc = 1, the left-hand side of (1.8) becomes
=
(q, ab/q, bc/q, ac/q)∞ (a, b, c, abc/q2)∞
∞ k=0
(q/a, q/b, q/c)k (q, q3/abc)k
qk
,
∞ k=−∞
(q/a, q/b, q/c)k (aq, bq, cq)k
(abc)k
q
k2
=
(q, ab, bc, ac)∞ (aq, bq, cq, abc/q)∞
毕业设计93基于连续隐马尔科夫模型的语音识别 (2)

SHANGHAI UNIVERSITY 毕业设计(论文)UNDERGRADUATE PROJECT (THESIS)论文题目基于连续隐马尔科夫模型的语音识别学院机自专业自动化学号03122669学生姓名金微指导教师李昕起讫日期2007 3.20—6.6目录摘要---------------------------------------------------------------------------2 ABSTRACT ------------------------------------------------------------------------2绪论---------------------------------------------------------------------------3第一章语音知识基础---------------------------------------------------------------6 第一节语音识别的基本内容-------------------------------------------6第二节语音识别的实现难点-------------------------------------------9第二章HMM的理论基础--------------------------------------------------------10 第一节HMM的定义----------------------------------------------------10第二节隐马尔科夫模型的数学描述---------------------------------10第三节HMM的类型----------------------------------------------------12第四节HMM的三个基本问题和解决的方-----------------------15第三章HMM算法实现的问题----------------------------------------------21 第一节HMM状态类型及参数B的选择---------------------------21第二节HMM训练时需要解决的问题-----------------------------23第四章语音识别系统的设计---------------------------------------------------32 第一节语音识别系统的开发环境-----------------------------------32第二节基于HMM的语音识别系统的设计------------------------32第三节实验结果---------------------------------------------------------49第五章结束语-------------------------------------------------------------------67致谢------------------------------------------------------------------------------68参考文献------------------------------------------------------------------------69摘要语音识别系统中最重要的部分就是声学模型的建立,隐马尔可夫模型作为语音信号的一种统计模型,由于它能够很好地描述语音信号的非平稳性和时变性,因此在语音识别领域有着广泛的应用。
【计算机应用】_全局优化_期刊发文热词逐年推荐_20140723
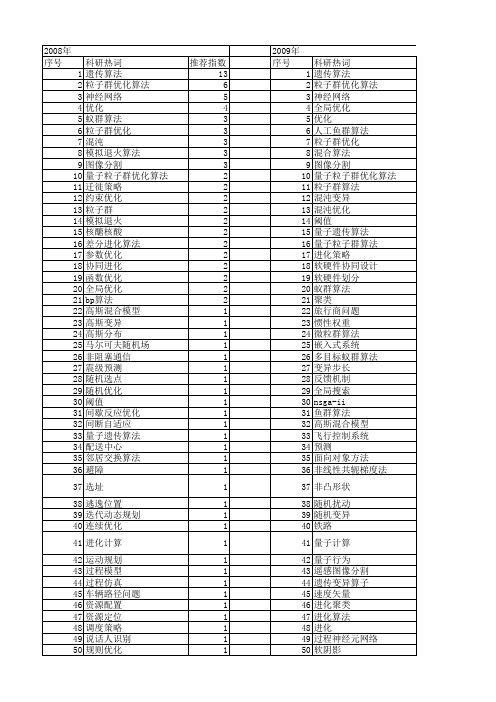
差分演化 局部搜索 小生境 密度泛函理论 学习算法 存储布局 多维函数优化 多样性规则 外点法 基于量子行为的微粒群优化算法 图像配准 图像增强 名老中医病例 可扩展标记语言编辑距离 可扩展标记语言描述文档 变异算子 变异概率 原子分解法 化学化工应用 动态调度 动力学模型 分类算法 分类器 分形理论 分子动力学 具体算法 全局最优解 全局最优 入侵率 免疫微粒群优化算法 免疫 充要强度 供应链管理 作业车间调度 伙伴选择 优化控制 优化参数 任务映射 人工鱼群算法 产生式规则 交通流预测 交叉概率 交互式进化计算 互信息 二次蚁群算法 事件 下降单纯形法 γ -氨基丁酸培养基 web服务语法业务流程树 web服务 tsk模糊神经网络 powell算法 mpi_allgather markov
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1ห้องสมุดไป่ตู้1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
科研热词 遗传算法 粒子群优化算法 神经网络 全局优化 优化 人工鱼群算法 粒子群优化 混合算法 图像分割 量子粒子群优化算法 粒子群算法 混沌变异 混沌优化 阈值 量子遗传算法 量子粒子群算法 进化策略 软硬件协同设计 软硬件划分 蚁群算法 聚类 旅行商问题 惯性权重 微粒群算法 嵌入式系统 多目标蚁群算法 变异步长 反馈机制 全局搜索 nsga-ii 鱼群算法 高斯混合模型 飞行控制系统 预测 面向对象方法 非线性共轭梯度法 非凸形状 随机扰动 随机变异 铁路 量子计算 量子行为 遥感图像分割 遗传变异算子 速度矢量 进化聚类 进化算法 进化 过程神经元网络 软阴影 转向架 路由优化
人工智能专业英语Unit3

Exercises I. Read the following statements carefully, and decide whether they are true (T) or false (F) according to the text.
Section A: Reasoning with Uncertainty
II. Choose the best answer to each of the following questions according to the text.
1. When was Thomas Bayes born? A. In 1936 B. In 1702 C. In 1761 D. In 1985
Contents
• Part 1 Reading and Translating
空间句法各数值英文

空间句法各数值英文When it comes to syntax, the concept of spatial relationships plays a crucial role in understanding the structure of a sentence. There are several numerical values associated with spatial syntax that are important to know.First, there's the concept of "distance" between words. This refers to the number of intervening words between two specific words in a sentence. For example, in the sentence "The cat sat on the mat," the distance between "cat" and "mat" is two.Another important spatial value in syntax is "depth." Depth refers to how deeply embedded a phrase or clause is within a sentence. The deeper a phrase or clause, the more complex the sentence structure becomes."Constituent order" is another crucial factor in understanding spatial syntax. This refers to the order in which sentence elements appear in relation to one another. For example, the constituent order in a sentence like "She ate the apple" is subject-verb-object.In addition to these values, there are also specific rules for spatial syntax in different languages. For example, in some languages, the verb must always come at the end of the sentence or certain words must be placed in a certain order. Understanding these rules is essential for mastering the nuances of different languages.Overall, understanding spatial syntax is a key element in understanding language structure and can help content creators craft effective and clear communication. Keep thesenumerical values in mind as you create content in different languages and strive for clear and effective language use.。
2022年考研考博-考博英语-厦门大学考试全真模拟易错、难点剖析AB卷(带答案)试题号:88

2022年考研考博-考博英语-厦门大学考试全真模拟易错、难点剖析AB卷(带答案)一.综合题(共15题)1.单选题Scientific evidence from different_______demonstrates that in most humans the left hemisphere of the brain controls language.问题1选项A.scopesB.rangesC.disciplinesD.arrays【答案】C【解析】scopes范围, 领域; ranges范围, 区间; disciplines学科; arrays阵列, 数组。
句意:来自不同学科的科学证据表明, 大多数人的大脑左半球控制着语言功能。
选项C符合句意。
2.单选题To survive in the intense trade competition between countries, we must_______the qualities and varieties of products we make to the world market demand.问题1选项A.improveB.enhanceC.guaranteeD.gear【答案】D【解析】improve改善, 增进; enhance增加, 提高; guarantee保证, 担保; gear适合。
句意:为了在国家间激烈的贸易竞争中生存, 我们必须使我们生产的产品的质量和品种适应世界市场的需求。
gear to 使适应, 所以选项D正确。
3.单选题London's Heathrow airport,alongside many other major airports,is hoping that_______passenger numbers will be swallowed up by a new generation of huge aircraft.问题1选项A.probateB.obsoleteC.swellingD.recapitulating【答案】C【解析】probate遗嘱认证的; obsolete荒废的, 淘汰的; swell增大; 磁胀; recapitulate 重述要点, 概述。
基于低秩约束的熵加权多视角模糊聚类算法

基于低秩约束的熵加权多视角模糊聚类算法张嘉旭 1王 骏 1, 2张春香 1林得富 1周 塔 3王士同1摘 要 如何有效挖掘多视角数据内部的一致性以及差异性是构建多视角模糊聚类算法的两个重要问题. 本文在Co-FKM 算法框架上, 提出了基于低秩约束的熵加权多视角模糊聚类算法(Entropy-weighting multi-view fuzzy C-means with low rank constraint, LR-MVEWFCM). 一方面, 从视角之间的一致性出发, 引入核范数对多个视角之间的模糊隶属度矩阵进行低秩约束; 另一方面, 基于香农熵理论引入视角权重自适应调整策略, 使算法根据各视角的重要程度来处理视角间的差异性. 本文使用交替方向乘子法(Alternating direction method of multipliers, ADMM)进行目标函数的优化. 最后, 人工模拟数据集和UCI (University of California Irvine)数据集上进行的实验结果验证了该方法的有效性.关键词 多视角模糊聚类, 香农熵, 低秩约束, 核范数, 交替方向乘子法引用格式 张嘉旭, 王骏, 张春香, 林得富, 周塔, 王士同. 基于低秩约束的熵加权多视角模糊聚类算法. 自动化学报, 2022,48(7): 1760−1770DOI 10.16383/j.aas.c190350Entropy-weighting Multi-view Fuzzy C-means With Low Rank ConstraintZHANG Jia-Xu 1 WANG Jun 1, 2 ZHANG Chun-Xiang 1 LIN De-Fu 1 ZHOU Ta 3 WANG Shi-Tong 1Abstract Effective mining both internal consistency and diversity of multi-view data is important to develop multi-view fuzzy clustering algorithms. In this paper, we propose a novel multi-view fuzzy clustering algorithm called en-tropy-weighting multi-view fuzzy c-means with low-rank constraint (LR-MVEWFCM). On the one hand, we intro-duce the nuclear norm as the low-rank constraint of the fuzzy membership matrix. On the other hand, the adaptive adjustment strategy of view weight is introduced to control the differences among views according to the import-ance of each view. The learning criterion can be optimized by the alternating direction method of multipliers (ADMM). Experimental results on both artificial and UCI (University of California Irvine) datasets show the effect-iveness of the proposed method.Key words Multi-view fuzzy clustering, Shannon entropy, low-rank constraint, nuclear norm, alternating direction method of multipliers (ADMM)Citation Zhang Jia-Xu, Wang Jun, Zhang Chun-Xiang, Lin De-Fu, Zhou Ta, Wang Shi-Tong. Entropy-weighting multi-view fuzzy C-means with low rank constraint. Acta Automatica Sinica , 2022, 48(7): 1760−1770随着多样化信息获取技术的发展, 人们可以从不同途径或不同角度来获取对象的特征数据, 即多视角数据. 多视角数据包含了同一对象不同角度的信息. 例如: 网页数据中既包含网页内容又包含网页链接信息; 视频内容中既包含视频信息又包含音频信息; 图像数据中既涉及颜色直方图特征、纹理特征等图像特征, 又涉及描述该图像内容的文本.多视角学习能有效地对多视角数据进行融合, 避免了单视角数据数据信息单一的问题[1−4].多视角模糊聚类是一种有效的无监督多视角学习方法[5−7]. 它通过在多视角聚类过程中引入各样本对不同类别的模糊隶属度来描述各视角下样本属于该类别的不确定性程度. 经典的工作有: 文献[8]以经典的单视角模糊C 均值(Fuzzy C-means, FCM)算法作为基础模型, 利用不同视角间的互补信息确定协同聚类的准则, 提出了Co-FC (Collaborative fuzzy clustering)算法; 文献[9]参考文献[8]的协同思想提出Co-FKM (Multiview fuzzy clustering algorithm collaborative fuzzy K-means)算法, 引入双视角隶属度惩罚项, 构造了一种新型的无监督多视角协同学习方法; 文献[10]借鉴了Co-FKM 和Co-FC 所使用的双视角约束思想, 通过引入视角权重, 并采用集成策略来融合多视角的模糊隶属收稿日期 2019-05-09 录用日期 2019-07-17Manuscript received May 9, 2019; accepted July 17, 2019国家自然科学基金(61772239), 江苏省自然科学基金(BK20181339)资助Supported by National Natural Science Foundation of China (61772239) and Natural Science Foundation of Jiangsu Province (BK20181339)本文责任编委 刘艳军Recommended by Associate Editor LIU Yan-Jun1. 江南大学数字媒体学院 无锡 2141222. 上海大学通信与信息工程学院 上海 2004443. 江苏科技大学电子信息学院 镇江2121001. School of Digital Media, Jiangnan University, Wuxi 2141222. School of Communication and Information Engineering,Shanghai University, Shanghai 2004443. School of Electronic Information, Jiangsu University of Science and Technology,Zhenjiang 212100第 48 卷 第 7 期自 动 化 学 报Vol. 48, No. 72022 年 7 月ACTA AUTOMATICA SINICAJuly, 2022度矩阵, 提出了WV-Co-FCM (Weighted view colla-borative fuzzy C-means) 算法; 文献[11]通过最小化双视角下样本与聚类中心的欧氏距离来减小不同视角间的差异性, 基于K-means 聚类框架提出了Co-K-means (Collaborative multi-view K-means clustering)算法; 在此基础上, 文献[12]提出了基于模糊划分的TW-Co-K-means (Two-level wei-ghted collaborative K-means for multi-view clus-tering)算法, 对Co-K-means 算法中的双视角欧氏距离加入一致性权重, 获得了比Co-K-means 更好的多视角聚类结果. 以上多视角聚类方法都基于成对视角来构造不同的正则化项来挖掘视角之间的一致性和差异性信息, 缺乏对多个视角的整体考虑.一致性和差异性是设计多视角聚类算法需要考虑的两个重要原则[10−14]. 一致性是指在多视角聚类过程中, 各视角的聚类结果应该尽可能保持一致.在设计多视角聚类算法时, 往往通过协同、集成等手段来构建全局划分矩阵, 从而得到最终的聚类结果[14−16]. 差异性是指多视角数据中的每个视角均反映了对象在不同方面的信息, 这些信息互为补充[10],在设计多视角聚类算法时需要对这些信息进行充分融合. 综合考虑这两方面的因素, 本文拟提出新型的低秩约束熵加权多视角模糊聚类算法(Entropy-weigh-ting multi-view fuzzy C-means with low rank con-straint, LR-MVEWFCM), 其主要创新点可以概括为以下3个方面:1)在模糊聚类框架下提出了面向视角一致性的低秩约束准则. 已有的多视角模糊聚类算法大多基于成对视角之间的两两关系来构造正则化项, 忽视了多个视角的整体一致性信息. 本文在模糊聚类框架下从视角全局一致性出发引入低秩约束正则化项, 从而得到新型的低秩约束多视角模糊聚类算法.2) 在模糊聚类框架下同时考虑多视角聚类的一致性和差异性, 在引入低秩约束的同时进一步使用面向视角差异性的多视角香农熵加权策略; 在迭代优化的过程中, 通过动态调节视角权重系数来突出具有更好分离性的视角的权重, 从而提高聚类性能.3)在模糊聚类框架下首次使用交替方向乘子法(Alternating direction method of multipliers,ADMM)[15]对LR-MVEWFCM 算法进行优化求解.N D K C m x j,k j k j =1,···,N k =1,···,K v i,k k i i =1,···,C U k =[µij,k ]k µij,k k j i 在本文中, 令 为样本总量, 为样本维度, 为视角数目, 为聚类数目, 为模糊指数. 设 表示多视角场景中第 个样本第 个视角的特征向量, , ; 表示第 个视角下, 第 个聚类中心, ; 表示第 个视角下的模糊隶属度矩阵, 其中 是第 个视角下第 个样本属于第 个聚类中心的模i =1,···,C j =1,···,N.糊隶属度, , 本文第1节在相关工作中回顾已有的经典模糊C 均值聚类算法FCM 模型[17]和多视角模糊聚类Co-FKM 模型[9]; 第2节将低秩理论与多视角香农熵理论相结合, 提出本文的新方法; 第3节基于模拟数据集和UCI (University of California Irvine)数据集验证本文算法的有效性, 并给出实验分析;第4节给出实验结论.1 相关工作1.1 模糊C 均值聚类算法FCMx 1,···,x N ∈R D U =[µi,j ]V =[v 1,v 2,···,v C ]设单视角环境下样本 , 是模糊划分矩阵, 是样本的聚类中心. FCM 算法的目标函数可表示为J FCM 可得到 取得局部极小值的必要条件为U 根据式(2)和式(3)进行迭代优化, 使目标函数收敛于局部极小点, 从而得到样本属于各聚类中心的模糊划分矩阵 .1.2 多视角模糊聚类Co-FKM 模型在经典FCM算法的基础上, 文献[9]通过引入视角协同约束正则项, 对视角间的一致性信息加以约束, 提出了多视角模糊聚类Co-FKM 模型.多视角模糊聚类Co-FKM 模型需要满足如下条件:J Co-FKM 多视角模糊聚类Co-FKM 模型的目标函数 定义为7 期张嘉旭等: 基于低秩约束的熵加权多视角模糊聚类算法1761η∆∆式(5)中, 表示协同划分参数; 表示视角一致项,由式(6)可知, 当各视角趋于一致时, 将趋于0.µij,k 迭代得到各视角的模糊隶属度 后, 为了最终得到一个具有全局性的模糊隶属度划分矩阵, Co-FKM 算法对各视角下的模糊隶属度采用几何平均的方法, 得到数据集的整体划分, 具体形式为ˆµij 其中, 为全局模糊划分结果.2 基于低秩约束的熵加权多视角模糊聚类算法针对当前多视角模糊聚类算法研究中存在的不足, 本文提出一种基于低秩约束的熵加权多视角模糊聚类新方法LR-MVEWFCM. 一方面通过向多视角模糊聚类算法的目标学习准则中引入低秩约束项, 在整体上控制聚类过程中各视角的一致性; 另一方面基于香农熵理论, 通过熵加权机制来控制各视角之间的差异性.同时使用交替方向乘子法对模型进行优化求解.U 1,···,U K U U U 设多视角隶属度 融合为一个整体的隶属度矩阵 , 将矩阵 的秩函数凸松弛为核范数, 通过对矩阵 进行低秩约束, 可以将多视角数据之间的一致性问题转化为核范数最小化问题进行求解, 具体定义为U =[U 1···U K ]T ∥·∥∗其中, 表示全局划分矩阵, 表示核范数. 式(8)的优化过程保证了全局划分矩阵的低秩约束. 低秩约束的引入, 可以弥补当前大多数多视角聚类算法仅能基于成对视角构建约束的缺陷, 从而更好地挖掘多视角数据中包含的全局一致性信息.目前已有的多视角的聚类算法在处理多视角数据时, 通常默认每个视角平等共享聚类结果[11], 但实际上某些视角的数据往往因空间分布重叠而导致可分性较差. 为避免此类视角的数据过多影响聚类效果,本文拟对各视角进行加权处理, 并构建香农熵正则项从而在聚类过程中有效地调节各视角之间的权重, 使得具有较好可分离性的视角的权重系数尽可能大, 以达到更好的聚类效果.∑Kk =1w k =1w k ≥0令视角权重系数 且 , 则香农熵正则项表示为U w k U =[U 1···U K ]T w =[w 1,···,w k ,···,w K ]K 综上所述, 本文作如下改进: 首先, 用本文提出的低秩约束全局模糊隶属度矩阵 ; 其次, 计算损失函数时考虑视角权重 , 并加入视角权重系数的香农熵正则项. 设 ; 表示 个视角下的视角权重. 本文所构建LR-MVEWFCM 的目标函数为其中, 约束条件为m =2本文取模糊指数 .2.1 基于ADMM 的求解算法(11)在本节中, 我们将使用ADMM 方法, 通过交替方向迭代的策略来实现目标函数 的最小化.g (Z )=θ∥Z ∥∗(13)(10)最小化式 可改写为如下约束优化问题:其求解过程可分解为如下几个子问题:V w U V 1) -子问题. 固定 和 , 更新 为1762自 动 化 学 报48 卷(15)v i,k 通过最小化式 , 可得到 的闭合解为U w Q Z U 2) -子问题. 固定 , 和 , 更新 为(17)U (t +1)通过最小化式 , 可得到 的封闭解为w V U w 3) -子问题. 固定 和 , 更新 为Z Q U Z(20)通过引入软阈值算子, 可得式 的解为U (t+1)+Q (t )=A ΣB T U (t +1)+Q (t )S θ/ρ(Σ)=diag ({max (0,σi −θ/ρ)})(i =1,2,···,N )其中, 为矩阵 的奇异值分解, 核范数的近邻算子可由软阈值算子给出.Q Z U Q 5) -子问题. 固定 和 , 更新 为w =[w 1,···,w k ,···,w K ]U ˜U经过上述迭代过程, 目标函数收敛于局部极值,同时得到不同视角下的模糊隶属度矩阵. 本文借鉴文献[10]的集成策略, 使用视角权重系数 和模糊隶属度矩阵 来构建具有全局特性的模糊空间划分矩阵 :w k U k k 其中, , 分别表示第 个视角的视角权重系数和相应的模糊隶属度矩阵.LR-MVEWFCM 算法描述如下:K (1≤k ≤K )X k ={x 1,k ,···,x N,k }C ϵT 输入. 包含 个视角的多视角样本集, 其中任意一个视角对应样本集 , 聚类中心 , 迭代阈值 , 最大迭代次数 ;v (t )i,k ˜Uw k 输出. 各视角聚类中心 , 模糊空间划分矩阵和各视角权重 ;V (t )U (t )w (t )t =0步骤1. 随机初始化 , 归一化 及 ,;(21)v (t +1)i,k 步骤2. 根据式 更新 ;(23)U (t +1)步骤3. 根据式 更新 ;(24)w (t +1)k 步骤4. 根据式 更新 ;(26)Z (t +1)步骤5. 根据式 更新 ;(27)Q (t +1)步骤6. 根据式 更新 ;L (t +1)−L (t )<ϵt >T 步骤7. 如果 或者 , 则算法结束并跳出循环, 否则, 返回步骤2;w k U k (23)˜U步骤8. 根据步骤7所获取的各视角权重 及各视角下的模糊隶属度 , 使用式 计算 .2.2 讨论2.2.1 与低秩约束算法比较近年来, 基于低秩约束的机器学习模型得到了广泛的研究. 经典工作包括文献[16]中提出LRR (Low rank representation)模型, 将矩阵的秩函数凸松弛为核范数, 通过求解核范数最小化问题, 求得基于低秩表示的亲和矩阵; 文献[14]提出低秩张量多视角子空间聚类算法(Low-rank tensor con-strained multiview subspace clustering, LT-MSC),7 期张嘉旭等: 基于低秩约束的熵加权多视角模糊聚类算法1763在各视角间求出带有低秩约束的子空间表示矩阵;文献 [18] 则进一步将低秩约束引入多模型子空间聚类算法中, 使算法模型取得了较好的性能. 本文将低秩约束与多视角模糊聚类框架相结合, 提出了LR-MVEWFCM 算法, 用低秩约束来实现多视角数据间的一致性. 本文方法可作为低秩模型在多视角模糊聚类领域的重要拓展.2.2.2 与多视角Co-FKM 算法比较图1和图2分别给出了多视角Co-FKM 算法和本文LR-MVEWFCM 算法的工作流程.多视角数据Co-FKM视角 1 数据视角 2 数据视角 K 数据各视角间两两约束各视角模糊隶属度集成决策函数划分矩阵ÛU 1U 2U K图 1 Co-FKM 算法处理多视角聚类任务工作流程Fig. 1 Co-FKM algorithm for multi-view clustering task本文算法与经典的多视角Co-FKM 算法在多视角信息的一致性约束和多视角聚类结果的集成策略上均有所不同. 在多视角信息的一致性约束方面, 本文将Co-FKM 算法中的视角间两两约束进一步扩展到多视角全局一致性约束; 在多视角聚类结果的集成策略上, 本文不同于Co-FKM 算法对隶属度矩阵简单地求几何平均值的方式, 而是将各视角隶属度与视角权重相结合, 构建具有视角差异性的集成决策函数.3 实验与分析3.1 实验设置本文采用模拟数据集和UCI 中的真实数据集进行实验验证, 选取FCM [17]、CombKM [19]、Co-FKM [9]和Co-Clustering [20]这4个聚类算法作为对比算法, 参数设置如表1所示. 实验环境为: Intel Core i5-7400 CPU, 其主频为2.3 GHz, 内存为8 GB.编程环境为MATLAB 2015b.本文采用如下两个性能指标对各算法所得结果进行评估.1) 归一化互信息(Normalized mutual inform-ation, NMI)[10]N i,j i j N i i N j j N 其中, 表示第 类与第 类的契合程度, 表示第 类中所属样本量, 表示第 类中所属样本量, 而 表示数据的样本总量;2) 芮氏指标(Rand index, RI)[10]表 1 参数定义和设置Table 1 Parameter setting in the experiments算法算法说明参数设置FCM 经典的单视角模糊聚类算法m =min (N,D −1)min (N,D −1)−2N D 模糊指数 ,其中, 表示样本数, 表示样本维数CombKM K-means 组合 算法—Co-FKM 多视角协同划分的模糊聚类算法m =min (N,D −1)min (N,D −1)−2η∈K −1K K ρ=0.01模糊指数 , 协同学习系数 ,其中, 为视角数, 步长 Co-Clustering 基于样本与特征空间的协同聚类算法λ∈{10−3,10−2, (103)µ∈{10−3,10−2,···,103}正则化系数 ,正则化系数 LR-MVEWFCM 基于低秩约束的熵加权多视角模糊聚类算法λ∈{10−5,10−4, (105)θ∈{10−3,10−2, (103)m =2视角权重平衡因子 , 低秩约束正则项系数, 模糊指数 MVEWFCMθ=0LR-MVEWFCM 算法中低秩约束正则项系数 λ∈{10−5,10−4, (105)m =2视角权重平衡因子 , 模糊指数 多视角数据差异性集成决策函数各视角模糊隶属度U 1U 2U K各视角权重W 1W 2W kLR-MVEWFCM 视角 1 数据视角 2 数据视角 K 数据整体约束具有视角差异性的划分矩阵Û图 2 LR-MVEWFCM 算法处理多视角聚类任务工作流程Fig. 2 LR-MVEWFCM algorithm for multi-viewclustering task1764自 动 化 学 报48 卷f 00f 11N [0,1]其中, 表示具有不同类标签且属于不同类的数据配对点数目, 则表示具有相同类标签且属于同一类的数据配对点数目, 表示数据的样本总量. 以上两个指标的取值范围介于 之间, 数值越接近1, 说明算法的聚类性能越好. 为了验证算法的鲁棒性, 各表中统计的性能指标值均为算法10次运行结果的平均值.3.2 模拟数据集实验x,y,z A 1x,y,z A 2x,y,z A 3x,y,z 为了评估本文算法在多视角数据集上的聚类效果, 使用文献[10]的方法来构造具有三维特性的模拟数据集A ( ), 其具体生成过程为: 首先在MATLAB 环境下采用正态分布随机函数normrnd 构建数据子集 ( ), ( )和 ( ), 每组对应一个类簇, 数据均包含200个样本.x,y,z 其中第1组与第2组数据集在特征z 上数值较为接近, 第2组与第3组数据集在特征x 上较为接近;然后将3组数据合并得到集合A ( ), 共计600个样本; 最后对数据集内的样本进行归一化处理. 我们进一步将特征x , y , z 按表2的方式两两组合, 从而得到多视角数据.表 2 模拟数据集特征组成Table 2 Characteristic composition of simulated dataset视角包含特征视角 1x,y 视角 2y,z 视角 3x,z将各视角下的样本可视化, 如图3所示.通过观察图3可以发现, 视角1中的数据集在空间分布上具有良好的可分性, 而视角2和视角3的数据在空间分布上均存在着一定的重叠, 从而影Z YZZXYX(a) 模拟数据集 A (a) Dataset A(b) 视角 1 数据集(b) View 1(c) 视角 2 数据集(c) View 2(d) 视角 3 数据集(d) View 3图 3 模拟数据集及各视角数据集Fig. 3 Simulated data under multiple views7 期张嘉旭等: 基于低秩约束的熵加权多视角模糊聚类算法1765响了所在视角下的聚类性能. 通过组合不同视角生成若干新的数据集, 如表3所示, 并给出了LR-MVEWFCM重复运行10次后的平均结果和方差.表 3 模拟数据实验算法性能对比Table 3 Performance comparison of the proposedalgorithms on simulated dataset编号包含特征NMI RI1视角1 1.0000 ± 0.0000 1.0000 ± 0.0000 2视角20.7453 ± 0.00750.8796 ± 0.0081 3视角30.8750 ± 0.00810.9555 ± 0.0006 4视角1, 视角2 1.0000 ± 0.0000 1.0000 ± 0.0000 5视角1, 视角3 1.0000 ± 0.0000 1.0000 ± 0.0000 6视角2, 视角30.9104 ± 0.03960.9634 ± 0.0192 7视角2, 视角3 1.0000 ± 0.0000 1.0000 ± 0.0000对比LR-MVEWFCM在数据集1~3上的性能, 我们发现本文算法在视角1上取得了最为理想的效果, 在视角3上的性能要优于视角2, 这与图3中各视角数据的空间可分性是一致的. 此外, 将各视角数据两两组合构成新数据集4~6后, LR-MVEWFCM算法都得到了比单一视角更好的聚类效果, 这都说明了本文采用低秩约束来挖掘多视角数据中一致性的方法, 能够有效提高聚类性能.基于多视角数据集7, 我们进一步给出本文算法与其他经典聚类算法的比较结果.从表4中可以发现, 由于模拟数据集在某些特征空间下具有良好的空间可分性, 所以无论是本文的算法还是Co-Clustering算法、FCM算法等算法均取得了很好的聚类效果, 而CombKM算法的性能较之以上算法则略有不足, 分析其原因在于CombKM算法侧重于挖掘样本之间的信息, 却忽视了多视角之间的协作, 而本文算法通过使用低秩约束进一步挖掘了多视角之间的全局一致性, 因而得到了比CombKM算法更好的聚类效果.3.3 真实数据集实验本节采用5个UCI数据集: 1) Iris数据集; 2) Image Segmentation (IS) 数据集; 3) Balance数据集; 4) Ionosphere数据集; 5) Wine数据集来进行实验. 由于这几个数据集均包含了不同类型的特征,所以可以将这些特征进行重新分组从而构造相应的多视角数据集. 表5给出了分组后的相关信息.我们在多视角数据集上运行各多视角聚类算法; 同时在原数据集上运行FCM算法. 相关结果统计见表6和表7.NMI RI通过观察表6和表7中的和指标值可知, Co-FKM算法的聚类性能明显优于其他几种经典聚类算法, 而相比于Co-FKM算法, 由于LR-MVEWFCM采用了低秩正则项来挖掘多视角数据之间的一致性关系, 并引入多视角自适应熵加权策略, 从而有效控制各视角之间的差异性. 很明显, 这种聚类性能更为优异和稳定, 且收敛性的效果更好.表6和表7中的结果也展示了在IS、Balance、Iris、Ionosphere和Wine数据集上, 其NMI和RI指标均提升3 ~ 5个百分点, 这也说明了本文算法在多视角聚类过程中的有效性.为进一步说明本文低秩约束发挥的积极作用,将LR-MVEWFCM算法和MVEWFCM算法共同进行实验, 算法的性能对比如图4所示.从图4中不难发现, 无论在模拟数据集上还是UCI真实数据集上, 相比较MVEWFCM算法, LR-MVEWFCM算法均可以取得更好的聚类效果. 因此可见, LR-MVEWFCM目标学习准则中的低秩约束能够有效利用多视角数据的一致性来提高算法的聚类性能.为研究本文算法的收敛性, 同样选取8个数据集进行收敛性实验, 其目标函数变化如图5所示.从图5中可以看出, 本文算法在真实数据集上仅需迭代15次左右就可以趋于稳定, 这说明本文算法在速度要求较高的场景下具有较好的实用性.综合以上实验结果, 我们不难发现, 在具有多视角特性的数据集上进行模糊聚类分析时, 多视角模糊聚类算法通常比传统单视角模糊聚类算法能够得到更优的聚类效果; 在本文中, 通过在多视角模糊聚类学习中引入低秩约束来增强不同视角之间的一致性关系, 并引入香农熵调节视角权重关系, 控制不同视角之间的差异性, 从而得到了比其他多视角聚类算法更好的聚类效果.表 4 模拟数据集7上各算法的性能比较Table 4 Performance comparison of the proposed algorithms on simulated dataset 7数据集指标Co-Clustering CombKM FCM Co-FKM LR-MVEWFCMA NMI-mean 1.00000.9305 1.0000 1.0000 1.0000 NMI-std0.00000.14640.00000.00000.0000 RI-mean 1.00000.9445 1.0000 1.0000 1.0000 RI-std0.00000.11710.00000.00000.00001766自 动 化 学 报48 卷3.4 参数敏感性实验LR-MVEWFCM算法包含两个正则项系数,λθθθθλλ即视角权重平衡因子和低秩约束正则项系数, 图6以LR-MVEWFCM算法在模拟数据集7上的实验为例, 给出了系数从0到1000过程中, 算法性能的变化情况, 当低秩正则项系数= 0时, 即不添加此正则项, 算法的性能最差, 验证了本文加入的低秩正则项的有效性, 当值变化过程中, 算法的性能相对变化较小, 说明本文算法在此数据集上对于值变化不敏感, 具有一定的鲁棒性; 而当香农熵正则项系数= 0时, 同样算法性能较差, 也说明引入此正则项的合理性. 当值变大时, 发现算法的性能也呈现变好趋势, 说明在此数据集上, 此正则项相对效果比较明显.4 结束语本文从多视角聚类学习过程中的一致性和差异性两方面出发, 提出了基于低秩约束的熵加权多视角模糊聚类算法. 该算法采用低秩正则项来挖掘多视角数据之间的一致性关系, 并引入多视角自适应熵加权策略从而有效控制各视角之间的差异性,从而提高了算法的性能. 在模拟数据集和真实数据集上的实验均表明, 本文算法的聚类性能优于其他多视角聚类算法. 同时本文算法还具有迭代次数少、收敛速度快的优点, 具有良好的实用性. 由于本文采用经典的FCM框架, 使用欧氏距离来衡量数据对象之间的差异,这使得本文算法不适用于某些高维数据场景. 如何针对高维数据设计多视角聚类算法, 这也将是我们今后的研究重点.表 5 基于UCI数据集构造的多视角数据Table 5 Multi-view data constructdedbased on UCI dataset编号原数据集说明视角特征样本视角类别8IS Shape92 31027 RGB99Iris Sepal长度215023 Sepal宽度Petal长度2Petal宽度10Balance 天平左臂重量262523天平左臂长度天平右臂重量2天平右臂长度11Iris Sepal长度115043 Sepal宽度1Petal长度1Petal宽度112Balance 天平左臂重量162543天平左臂长度1天平右臂重量1天平右臂长度113Ionosphere 每个特征单独作为一个视角135134214Wine 每个特征单独作为一个视角1178133表 6 5种聚类方法的NMI值比较结果Table 6 Comparison of NMI performance of five clustering methods编号Co-Clustering CombKM FCM Co-FKM LR-MVEWFCM 均值P-value均值P-value均值P-value均值P-value均值80.5771 ±0.00230.00190.5259 ±0.05510.20560.5567 ±0.01840.00440.5881 ±0.01093.76×10−40.5828 ±0.004490.7582 ±7.4015 ×10−172.03×10−240.7251 ±0.06982.32×10−70.7578 ±0.06981.93×10−240.8317 ±0.00648.88×10−160.9029 ±0.0057100.2455 ±0.05590.01650.1562 ±0.07493.47×10−50.1813 ±0.11720.00610.2756 ±0.03090.10370.3030 ±0.0402110.7582 ±1.1703×10−162.28×10−160.7468 ±0.00795.12×10−160.7578 ±1.1703×10−165.04×10−160.8244 ±1.1102×10−162.16×10−160.8768 ±0.0097120.2603 ±0.06850.38250.1543 ±0.07634.61×10−40.2264 ±0.11270.15730.2283 ±0.02940.01460.2863 ±0.0611130.1385 ±0.00852.51×10−90.1349 ±2.9257×10−172.35×10−130.1299 ±0.09842.60×10−100.2097 ±0.03290.04830.2608 ±0.0251140.4288 ±1.1703×10−161.26×10−080.4215 ±0.00957.97×10−090.4334 ±5.8514×10−172.39×10−080.5295 ±0.03010.43760.5413 ±0.03647 期张嘉旭等: 基于低秩约束的熵加权多视角模糊聚类算法1767表 7 5种聚类方法的RI 值比较结果Table 7 Comparison of RI performance of five clustering methods编号Co-ClusteringCombKM FCMCo-FKM LR-MVEWFCM均值P-value 均值P-value 均值P-value 均值P-value 均值80.8392 ±0.0010 1.3475 ×10−140.8112 ±0.0369 1.95×10−70.8390 ±0.01150.00320.8571 ±0.00190.00480.8508 ±0.001390.8797 ±0.0014 1.72×10−260.8481 ±0.0667 2.56×10−50.8859 ±1.1703×10−16 6.49×10−260.9358 ±0.0037 3.29×10−140.9665 ±0.0026100.6515 ±0.0231 3.13×10−40.6059 ±0.0340 1.37×10−60.6186 ±0.06240.00160.6772 ±0.02270.07610.6958 ±0.0215110.8797 ±0.0014 1.25×10−180.8755 ±0.0029 5.99×10−120.8859 ±0.0243 2.33×10−180.9267 ±2.3406×10−16 5.19×10−180.9527 ±0.0041120.6511 ±0.02790.01560.6024 ±0.0322 2.24×10−50.6509 ±0.06520.11390.6511 ±0.01890.0080.6902 ±0.0370130.5877 ±0.0030 1.35×10−120.5888 ±0.0292 2.10×10−140.5818 ±1.1703×10−164.6351 ×10−130.6508 ±0.01470.03580.6855 ±0.0115140.7187 ±1.1703×10−163.82×10−60.7056 ±0.01681.69×10−60.7099 ±1.1703×10−168.45×10−70.7850 ±0.01620.59050.7917 ±0.0353R I数据集N M I数据集(a) RI 指标(a) RI(b) NMI 指标(b) NMI图 4 低秩约束对算法性能的影响(横坐标为数据集编号, 纵坐标为聚类性能指标)Fig. 4 The influence of low rank constraints on the performance of the algorithm (the X -coordinate isthe data set number and the Y -coordinate is the clustering performance index)目标函数值1 096.91 096.81 096.61 096.71 096.51 096.41 096.31 096.21 096.1目标函数值66.266.065.665.865.465.2迭代次数05101520目标函数值7.05.06.55.54.04.53.03.5迭代次数05101520迭代次数05101520目标函数值52.652.251.451.851.050.6迭代次数05101520×106(a) 数据集 7(a) Dataset 7(b) 数据集 8(b) Dataset 8(c) 数据集 9(c) Dataset 9(d) 数据集 10(d) Dataset 101768自 动 化 学 报48 卷ReferencesXu C, Tao D C, Xu C. Multi-view learning with incompleteviews. IEEE Transactions on Image Processing , 2015, 24(12):5812−58251Brefeld U. Multi-view learning with dependent views. In: Pro-ceedings of the 30th Annual ACM Symposium on Applied Com-puting, Salamanca, Spain: ACM, 2015. 865−8702Muslea I, Minton S, Knoblock C A. Active learning with mul-tiple views. Journal of Artificial Intelligence Research , 2006,27(1): 203−2333Zhang C Q, Adeli E, Wu Z W, Li G, Lin W L, Shen D G. In-fant brain development prediction with latent partial multi-view representation learning. IEEE Transactions on Medical Imaging ,2018, 38(4): 909−9184Bickel S, Scheffer T. Multi-view clustering. In: Proceedings of the 4th IEEE International Conference on Data Mining (ICDM '04), Brighton, UK: IEEE, 2004. 19−265Wang Y T, Chen L H. Multi-view fuzzy clustering with minim-ax optimization for effective clustering of data from multiple sources. Expert Systems with Applications , 2017, 72: 457−4666Wang Jun, Wang Shi-Tong, Deng Zhao-Hong. Survey on chal-lenges in clustering analysis research. Control and Decision ,2012, 27(3): 321−328(王骏, 王士同, 邓赵红. 聚类分析研究中的若干问题. 控制与决策,2012, 27(3): 321−328)7Pedrycz W. Collaborative fuzzy clustering. Pattern Recognition Letters , 2002, 23(14): 1675−16868Cleuziou G, Exbrayat M, Martin L, Sublemontier J H. CoFKM:A centralized method for multiple-view clustering. In: Proceed-ings of the 9th IEEE International Conference on Data Mining,Miami, FL, USA: IEEE, 2009. 752−7579Jiang Y Z, Chung F L, Wang S T, Deng Z H, Wang J, Qian P J. Collaborative fuzzy clustering from multiple weighted views.IEEE Transactions on Cybernetics , 2015, 45(4): 688−70110Bettoumi S, Jlassi C, Arous N. Collaborative multi-view K-means clustering. Soft Computing , 2019, 23(3): 937−94511Zhang G Y, Wang C D, Huang D, Zheng W S, Zhou Y R. TW-Co-K-means: Two-level weighted collaborative K-means for multi-view clustering. Knowledge-Based Systems , 2018, 150:127−13812Cao X C, Zhang C Q, Fu H Z, Liu S, Zhang H. Diversity-in-duced multi-view subspace clustering. In: Proceedings of the2015 IEEE Conference on Computer Vision and Pattern Recog-nition, Boston, MA, USA: IEEE, 2015. 586−59413Zhang C Q, Fu H Z, Liu S, Liu G C, Cao X C. Low-rank tensor constrained multiview subspace clustering. In: Proceedings of the 2015 IEEE International Conference on Computer Visio,Santiago, Chile: IEEE, 2015. 1582−159014Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direc-tion method of multipliers. Foundations and Trends in Machine Learning , 2011, 3(1): 1−12215Liu G C, Lin Z C, Yan S C, Sun J, Yu Y, Ma Y. Robust recov-ery of subspace structures by low-rank representation. IEEE1616.216.015.815.615.415.215.0目标函数值目标函数值目标函数值51015迭代次数迭代次数迭代次数 711.2011.1511.1011.0511.0010.9510.90800700600500400300200目标函数值38.638.238.438.037.837.637.437.251015205101520迭代次数 705101520(e) 数据集 11(e) Dataset 11(f) 数据集 12(f) Dataset 12(g) 数据集 13(g) Dataset 13(h) 数据集 14(h) Dataset 14图 5 LR-MVEWFCM 算法的收敛曲线Fig. 5 Convergence curve of LR-MVEWFCM algorithm图 6 模拟数据集7上参数敏感性分析Fig. 6 Sensitivity analysis of parameters on simulated dataset 77 期张嘉旭等: 基于低秩约束的熵加权多视角模糊聚类算法1769。
多元算力 英语

多元算力英语Computational power, the cornerstone of modern digital infrastructure, has evolved significantly over the years. It is no longer confined to a single, monolithic entity but rather encompasses a diverse array of resources, techniques, and technologies that collectively form what we term as "multifaceted computational power." This concept represents a paradigm shift in how we harness, allocate, and utilize computing capabilities, enabling unprecedented advancements across various domains. This essay delves into the essence of multifaceted computational power, examining its key components, implications, and the transformative role it plays in today's data-driven world.Firstly, at the core of multifaceted computational power lies the notion of heterogeneity. It transcends the traditional boundaries of centralized, uniform hardware architectures and embraces a diverse ecosystem of devices, from high-performance supercomputers and cloud servers to edge devices like smartphones and Internet of Things (IoT) sensors. This diversity extends not only to the types ofdevices but also to their computational capabilities, energy efficiency, and specialized functions. For instance, Graphics Processing Units (GPUs) excel at parallel processing tasks such as deep learning, while Field-Programmable Gate Arrays (FPGAs) offer reconfigurability for customized, low-latency applications. The heterogeneous nature of multifaceted computational power allows for the most suitable resource to be allocated to each task, enhancing overall efficiency and performance.Secondly, this paradigm is inherently dynamic and distributed. Cloud computing, with its on-demand access to virtually unlimited computational resources, enables scalability and flexibility unattainable in conventional setups. Resources can be provisioned or decommissioned rapidly in response to fluctuating workloads, ensuring optimal utilization and cost-effectiveness. Moreover, distributed computing frameworks like Apache Hadoop and Spark facilitate the parallel processing of massive datasets across a network of interconnected devices, breaking down complex problems into smaller, more manageable chunks. This distributed nature not onlyaccelerates computation but also enhances fault tolerance and resilience, as the failure of a single node does not compromise the entire system.The advent of multifaceted computational power has profound implications for numerous sectors. In scientific research, it accelerates discoveries by expediting simulations, data analysis, and model training. For instance, Folding@Home utilizes idle computational power from millions of devices worldwide to simulate protein folding, advancing our understanding of diseases like Alzheimer's and cancer. In finance, high-frequency trading relies on ultra-low latency computing to execute trades within microseconds, exploiting fleeting market opportunities. In healthcare, wearable devices and IoT sensors generate vast amounts of patient data, which, when processed using distributed algorithms, can facilitate real-time monitoring, early diagnosis, and personalized treatment plans.Furthermore, multifaceted computational power fuels innovation in emerging technologies such as artificial intelligence, blockchain, and quantum computing. AI models, particularly deep neural networks, demand immensecomputational resources for training and inference. The ability to harness diverse, scalable resources accelerates AI development and deployment, driving advancements in fields like autonomous vehicles, natural language processing, and image recognition. Similarly, blockchain networks rely on distributed computing to maintain consensus and ensure transactional integrity, while quantum computing, still in its nascent stage, promises exponential speedups for specific computational problems through the exploitation of quantum entanglement and superposition.In conclusion, multifaceted computational power represents a fundamental shift in how we approach problem-solving in the digital realm. By embracing heterogeneity, dynamism, and distribution, it unlocks unprecedented efficiency, scalability, and innovation across a multitude of sectors. As technology continues to evolve, it is crucial that we harness the full potential of this multifaceted landscape, fostering a future where computational power is seamlessly integrated, accessible, and tailored to meet the ever-growing demands of our data-driven society.。
工业摩擦润滑技术国家地方联合工程研究中心技术委员会成立

108润滑与密封第45卷轮轨空间动态行为的影响,结果表明,轮轨系统动态响应随着非圆化磨耗幅值的增大而增大,但随非圆化磨耗阶次和车辆运行速度则呈非线性变化趋势。
参考文献[1]JOHANSSON A,NIELSEN J0.Out-of-round railway wheels:wheel-rail contact forces and track response derived from field tests and numerical simulations[J].Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,2003,217(2):135-146.[2]TAOG Q,WANG L F,WEN Z F,et al.Measurement and assessment of out-of-round electric locomotive wheels[J].Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,2018,232(1):275-287.[3]MORYS B.Enlargement of out-of-round wheel profiles on highspeed trains[J].Journal of Sound and Vibration,1999,227(5): 965-978.[4]ZHONG S Q,XIONG J Y,XIA0X B,et al.Effect of the first twowheelset bending modes on wheel-rail contact behavior[J].Journal of Zhejiang University Science A,2014,15(12):984-1001.[5]TAO G Q,WANG L F,WEN Z F,et al.Experimental investigation into the mechanism of the polygonal wear of electric locomotive wheels[J]. Vehicle System Dynamics,2018,56(6):883-899.[6]JIN X S,WU L,FANG J Y,et al.An investigation into the mechanism of the polygonal wear of metro train wheels and its effect on the dynamic behaviour of a wheel/rail system[J].Vehicle System Dynamics,2012,50(12):1817-1834.[7]王科,崔晓璐,陈光雄,等.高速铁路车轮多边形磨耗影响因素仿真研究[J].润滑与密封,2017,42(10):31-34.WANG K,CUI X L,CHEN G X,et al.Numerical study on the influence factors of wheel polygonalization of high-speed trains [J].Lubrication Engineering,2017,42(10):31-34.[8]陈光雄,金学松,鄒平波,等•车轮多边形磨耗机理的有限元研究[J].铁道学报,2011,33(1):14-1&CHEN G X,JIN X S,WU P B,et al.Finite element study on the generation mechanism of polygonal wear of railway wheels[J].Journal of the China Railway Society,2011,33(1):14-18.[9]肖乾,郑继峰,昌超,等.高速列车谐波磨耗车轮滚动接触疲劳特性分析[J].润滑与密封,2017,42(1):1-7.XIAO Q,ZHENG J F,CHANG C,et al.Analysis of harmonic wear wheels/rail rolling contact fatigue of high speed train[J].Lubrication Engineering,2017,42(1):1—7.[10]LIU X Y,ZHAI W M.Analysis of vertical dynamic wheel/railinteraction caused by polygonal wheels on high-speed trains [J].Wear,2014,314(1/2):282-290.[11]韩光旭,张捷,肖新标,等•高速动车组车内异常振动噪声特性与车轮非圆化关系研究[J].机械工程学报,2014,50(22):113-121,HAN G X,ZHANG J,XIAO X B,et al.Study on high-speed train abnormal interior vibration and noise related to wheel roughness[J].Journal of Mechanical Engineering,2014,50(22):113-121.[12]王兴宇,范军.高速列车车内噪声与车轮不圆顺关系的研究[J].铁道学报,2013,35(9)=14-18.WANG X Y,FAN J.Research on relation between interior noises and out-of-round wheels of high-speed EMU[J].Journal of the China Railway Society,2013,35(9):14-18.【13】刘佳,韩健,肖新标,等.高速车轮非圆化磨耗对轴箱端盖异常振动影响初探[J].机械工程学报,2017,53(20):98-105.LIU J,HAN J,XIAO X B,et al.Influence of wheel non-circular wear on axle box cover abnormal vibration in high-speed train [J].Journal of Mechanical Engineering,2017,53(20):98-105.【14】Railway applications:Noise emission:Rail roughness measurement related to rolling noise generation:BS EN15610:2009 [S].BSI British Standards,2009.[15]翟婉明•车辆-轨道耦合动力学[M].3版.北京:科学出版社,2007:12-84.[16]SHEN Z Y,HEDRICK J K,ELKINS J A.A comparison of alternative creep force models for rail vehicle dynamic analysis [J].Vehicle System Dynamics,1983,12(1/2/3):79-83. [17]LIU P F,ZHAI W M,WANG K Y.Establishment and verification of three-dimensional dynamic model for heavy-haul traintrack coupled system[J].Vehicle System Dynamics,2016,54(11):1511-1537.工业摩擦润滑技术国家地方联合工程研究中心技术委员会成立2020年11月25日,工业摩擦润滑技术国家地方联合工程研究中心技术委员会成立大会暨第一次全体会议在依托单位——广州机械科学研究院有限公司召开。
llm 模型指令微调 语料

llm 模型指令微调语料【最新版】目录1.LLM 模型概述2.指令微调的意义和方法3.语料的作用和选择4.总结正文1.LLM 模型概述LLM(Language Model)模型是一种被广泛应用于自然语言处理领域的模型,它的主要作用是预测一段文本的下一个词语。
LLM 模型通过学习大量的文本数据,掌握了语言的统计特征和语法规则,能够在一定程度上理解自然语言的表达方式。
在深度学习领域,LLM 模型已经成为了自然语言处理的基本工具之一。
2.指令微调的意义和方法指令微调(Instruction Tuning)是自然语言处理中的一种重要技术,其主要目的是通过修改模型的指令,来提高模型的性能和效果。
指令微调的意义主要体现在以下几个方面:(1)提高模型的泛化能力:通过指令微调,可以让模型更好地适应不同的任务和领域,提高模型的泛化能力。
(2)提高模型的效率:通过指令微调,可以让模型更快地学习和适应新的任务,提高模型的效率。
(3)提高模型的效果:通过指令微调,可以让模型更好地理解自然语言,提高模型的效果。
指令微调的方法主要包括以下几种:(1)基于规则的方法:通过设计一系列的规则,来修改模型的指令。
(2)基于模板的方法:通过设计一系列的模板,来修改模型的指令。
(3)基于学习的方法:通过训练模型,来学习如何修改模型的指令。
3.语料的作用和选择语料(Corpus)是自然语言处理中的一种重要资源,它主要包括了大量的文本数据。
语料对于 LLM 模型的训练和指令微调具有重要的作用,主要体现在以下几个方面:(1)提供训练数据:语料可以为 LLM 模型的训练提供大量的数据,帮助模型更好地学习语言的统计特征和语法规则。
(2)提供验证数据:语料可以为 LLM 模型的验证提供数据,帮助模型更好地理解自然语言。
(3)提供微调数据:语料可以为指令微调提供数据,帮助模型更好地适应不同的任务和领域。
因此,选择合适的语料对于 LLM 模型的训练和指令微调至关重要。
自然语言处理算法 k-m

自然语言处理算法 k-mk-means算法是一种常用的聚类算法,它可以将数据集划分为k个不同的簇。
本文将介绍k-means算法的基本原理、步骤和应用。
一、算法原理k-means算法的原理很简单,它通过迭代的方式将数据集划分为k 个簇,使得簇内的样本点相似度最高,而簇间的样本点相似度最低。
具体步骤如下:1. 初始化k个中心点,可以是随机选择或者根据经验选择。
2. 根据中心点,将数据集中的每个样本点分配给最近的中心点所在的簇。
3. 根据簇内的样本点,更新中心点的位置。
4. 重复步骤2和步骤3,直到中心点的位置不再发生变化或者达到最大迭代次数。
二、算法步骤k-means算法的步骤可以按照以下几个阶段进行描述:1. 初始化阶段:随机选择k个中心点作为初始值。
2. 分配阶段:将数据集中的每个样本点分配给离它最近的中心点所在的簇。
3. 更新阶段:根据簇内的样本点,更新中心点的位置。
4. 终止条件:当中心点的位置不再发生变化或者达到最大迭代次数时,停止算法。
三、算法应用k-means算法在实际应用中有很多场景,下面介绍几个常见的应用:1. 图像分割:将一幅图像分成若干个具有相似特征的区域,可以利用k-means算法将图像的像素点聚类成不同的颜色簇。
2. 文本聚类:将大量的文本数据划分为若干个簇,可以帮助用户更好地理解和分析文本数据。
3. 推荐系统:根据用户的历史行为和偏好,将用户划分到不同的簇,从而为用户推荐更加个性化的内容。
4. 无监督学习:k-means算法是一种无监督学习算法,可以在没有标记数据的情况下对数据进行聚类分析。
四、总结k-means算法是一种简单而有效的聚类算法,它通过迭代的方式将数据集划分为k个簇,使得簇内的样本点相似度最高,簇间的样本点相似度最低。
该算法在图像分割、文本聚类、推荐系统和无监督学习等领域都有广泛的应用。
通过理解k-means算法的原理和步骤,我们可以更好地应用它来解决实际问题。
memorybank训练技巧

关于MemoryBank训练技巧,存在一些策略和方法,以提升其性能和准确性。
以下是一些建议:
1. 确定合适的模型架构:选择适合任务的模型架构,例如卷积神经网络(CNN)、循环神经网络(RNN)或Transformer等。
2. 优化数据预处理:对数据进行适当的预处理,例如归一化、数据增强和随机裁剪等,以提高模型的泛化能力。
3. 使用标签平滑:在训练过程中,将标签进行平滑处理,以减少模型对硬标签的依赖,从而提高模型的鲁棒性。
4. 采用正则化技巧:使用一些正则化技巧,如Dropout、权重衰减等,以减少模型过拟合。
5. 学习率调整:选择合适的学习率,并使用学习率衰减等方法,以保证模型训练的稳定性和有效性。
6. 使用适当的训练技巧:例如使用梯度累积、学习率预热等技巧,以加速模型收敛并提高模型的性能。
7. 使用适当的损失函数:选择适合任务的损失函数,例如交叉熵损失函数、均方误差损失函数等。
8. 合理的数据集划分:将数据集划分为训练集、验证集和测试集,以保证模型的泛化能力。
9. 使用合适的评估指标:选择适合任务的评估指标,例如准确率、精确率、召回率、F1分数等,以全面评估模型的性能。
10. 调试和优化:在训练过程中,不断地调试和优化模型,通过调整
超参数、改进模型结构等方法,以提高模型的性能。
总之,MemoryBank训练技巧需要综合考虑多个方面,包括模型架构、数据预处理、正则化技巧、损失函数、评估指标等。
在实践中,可以通过反复试验和比较来找到最适合自己任务的训练技巧。
华中科技大学数学与统计学院硕、博研究生课表【模板】
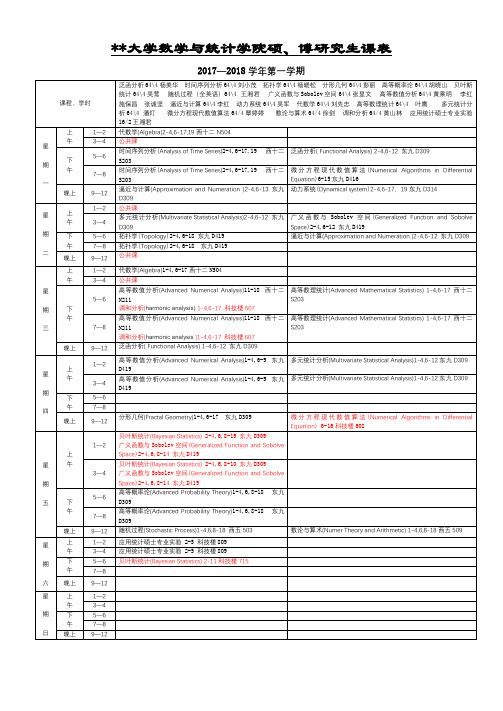
3—4
高等数值分析(Advanced NumericalAnalysis)1-4,6-9东九D419
多元统计分析(MultivariateStatisticalAnalysis)1-4,6-12东九D309
星
期
一
上
午
1—2
代数学(Algebra)2-4,6-17,19西十二N504
3—4
公共课
下
午
5—6
时间序列分析(Analysis ofTimeSeries)2-4,6-17,19西十二S203
泛函分析(FunctionalAnalysis)2-4,6-12东九D309
7—8
时间序列分析(Analysis ofTimeSeries)2-4,6-17,19西十二S203
数论与算术(Numer Theory and Arithmetic)1-4,6,8-18西五509
星
期
六
上
午
1—2
应用统计硕士专业实验2-5科技楼809
3—4
应用统计硕士专业实验2-5科技楼809
下
午
5—6
贝叶斯统计(Bayesian Statistics)2-11科技楼715
7—8
晚上
9—12
星
期
广义函数与Sobolev空间(GeneralizedFunctionand Sobolve Space)2-4,6,8-14东九D419
3—4
贝叶斯统计(Bayesian Statistics)2-4,6,8-10东九D309
广义函数与Sobolev空间(GeneralizedFunctionand Sobolve Space)2-4,6,8-14东九D419
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
2.5. Questions 3. Canonical numeration systems, β -expansions and shift radix systems 3.1. Canonical numeration systems in number fields 3.2. Generalisations 3.3. On the finiteness property of β -expansions 3.4. Shift radix systems 3.5. Numeration systems defined over finite fields 3.6. Lattice tilings 4. Some sofic fibred numeration systems 4.1. Substitutions and Dumont-Thomas numeration 4.2. Abstract numeration systems 4.3. Rauzy fractals 4.4. The Pisot conjecture 5. G-scales and odometers 5.1. G-scales. Building the odometer 5.2. Carries tree 5.3. Metric properties. Da capo al fine subshifts 5.4. Markov compacta 5.5. Spectral properties 6. Applications 6.1. Additive and multiplicative functions, sum-of-digits functions 6.2. Diophantine approximation 6.3. Computer arithmetics and cryptography 6.4. Mathematical crystallography: Rauzy fractals and quasicrystals acknowledgements References
22 25 26 30 31 33 38 39 43 43 48 50 53 55 56 58 61 64 65 66 66 70 71 72 74 74
1. Introduction 1.1. Origins. Numeration is the art of representation of numbers; primarily natural numbers, then extensions of them - fractions, negative, real, complex numbers, vectors, a.s.o. Numeration systems are algorithmic ways of coding numbers, i.e., essentially a process permitting to code elements of an infinite set with finitely many symbols. For ancient civilisations, numeration was necessary for practical use, commerce, astronomy, etc. Hence numeration systems have been created not only for writing down numbers, but also in order to perform arithmetical operations. Numeration is inherently dynamical, since it is collated with infinity as potentiality, as already asserted by Aristotle1: if I can represent some natural number,
1“The infinite exhibits itself in different ways - in time, in the generations of man, and in the division of magnitudes. For generally the infinite has this mode of existence: one thing is always being taken after another, and each thing that is taken is always finite, but always different. Again, ‘being’ has more than one sense, so that we must not regard the infinite as a ‘this’, such as a man or a horse, but must suppose it to exist in the sense in which we speak of the day or the games as existing things whose being has not come to them like that of a substance, but consists in a process of coming
2000 Mathematics Subject Classification. Primary 37B10; Secondary 11A63, 11J70, 11K55, 11R06, 37A45, 68Q45, 68R15. Key words and phrases. Numeration, fibred systems, symbolic dynamics, odometers, numeration scales, subshifts, f -expansions, β -numeration, sum-of-digits function, abstract number systems, canonical numeration systems, shift radix systems, additive functions, tilings, Rauzy fractals, substitutive dynamical systems. The first author was supported by the Austrian Science Foundation FWF, project S9605, that is part of the Austrian National Research Network “Analytic Combinatorics and Probabilistic Number Theory”. The first threee authors were partially supported by ACINIM “Num´ eration” 2004–154. The fourth author was supported by the FWF grant S9610-Nhe next one? On that score, it is significant that motion (greek δυ ´ναµις ) and infinity are treated together in Aristotle’s work (Physics, third book). Furthermore, the will to deal with arbitrary large numbers requires some kind of invariance of the representation and a recursive algorithm which will be iterated, hence something of a dynamical kind again. In the sequel, we briefly mention the most important historical steps of numeration. We refer to the book of Ifrah [Ifr94] for an amazing amount of information on the subject and additional references. Numeration systems are the ultimate elaboration concerning representation of numbers. Most early representations are only concerned with finitely many numbers, indeed those which are of a practical use. Some primitive civilisations ignored the numeration concept and only had names for cardinals that were immediately perceptible without performing any action of counting, i.e., as anybody can experiment alone, from one to four. For example, the Australian tribe Aranda say “ninta” for one, “tara” for two, “tara-ma-ninta” for three, and “tara-ma-tara” for four. Larger numbers are indeterminate (many, a lot). Many people have developed a representation of natural numbers with fingers, hands or other parts of the human body. Using phalanxes and articulations, it is then possible to represent (or show) numbers up to ten thousand or more. A way of showing numbers up to 1010 just with both hands was implemented in the XVIth century in China (Sua fa tong zong, 1593). Clearly, the choice of base 10 was at the origin of these methods. Other bases were attested as well, like five, twelve, twenty or sixty by Babylonians. However, all representations of common use work with a base. Bases have been developed in Egypt and Mesopotamia, about 5000 years ago. The Egyptians had a special sign for any small power of ten: a vertical stroke for 1, a kind of horseshoe for 10, a spiral for 100, a loto flower for 1000, a finger for 10000, a tadpole for 105 , and a praying man for a million. For 45200, they drew four fingers, five loto flowers and two spirals (hieroglyphic writing). A similar principle was used by Sumerians with base 60. To avoid an over complicated representation, digits (from 1 to 59) were written in base 10. This kind of representation follows an additional logic. A more concise coding has been used by inventing a symbol for each digit from 1 to 9 in base 10. In this modified system, 431 is understood as 4 × 100 + 3 × 10 + 1 × 1 instead of 100 + 100 + 100 + 100 + 10 + 10 + 10 + 1. Etruscans used such a system, as did Hieratic and Demotic handwritings in Egypt. The next crucial step was the invention of positional numeration. It has been discovered independently four times, by Babylonians, in China, by the pre-Columbian Mayas, and in India. However, only Indians had a distinct sign for every digit. Babylonians only had two, for 1 and 10. Therefore, since they used base 60, they represented 157, say, in three blocks: from the left to the
