特殊三角函数值表
(完整版)三角函数特殊角值表

角度 函数 0 30 45 60 90 120 135 150 180 270 360 角a 的弧度0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 3π/2 2π sin 0 1/2 √2/2 √3/2 1 √3/2 √2/2 1/2 0 -1 0 cos 1 √3/2 √2/2 1/2 0 -1/2 -√2/2 -√3/2 -1 0 1 tan√3/31√3-√3-1-√3/31、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出: sin30°=cos60°=21,sin45°=cos45°=22, tan30°=cot60°=33, tan 45°=cot45°=1正弦函数 sinθ=y/r 余弦函数 cosθ=x/r 正切函数 tanθ=y/x 余切函数 cotθ=x/y 正割函数 secθ=r/x 余割函数 cscθ=r/y2、列表法:说明:正弦值随角度变化,即0˚ 30˚ 45˚ 60˚ 90˚变化;值从02122 23 1变化,其余类似记忆.3、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:① 有界性:(锐角三角函数值都是正值)即当0°<α<90°时,则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A <B <90°时,则sin A <sin B ;tan A <tan B ; cos A >cos B ;cot A >cot B ;特别地:若0°<α<45°,则sin A <cos A ;tan A <cot A 若45°<A <90°,则sin A >cos A ;tan A >cot A . 4、口决记忆法:观察表中的数值特征 正弦、余弦值可表示为2m 形式,正切、余切值可表示为3m 形式,有关m 的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.30˚ 123145˚ 1212 60˚ 3函数名正弦余弦正切余切正割余割符号sin cos tan cot sec csc正弦函数sin(A)=a/c余弦函数cos(A)=b/c正切函数tan(A)=a/b余切函数cot(A)=b/a其中a为对边,b为邻边,c为斜边三角函数对照表三角函数SIN COS TAN 三角函数SIN COS TAN 0°0 1 0 90° 1 0 无1°0.0174 0.9998 0.0174 89°0.9998 0.0174 57.2899 2°0.0348 0.9993 0.0349 88°0.9993 0.0348 28.6362 3°0.0523 0.9986 0.0524 87°0.9986 0.0523 19.0811 4°0.0697 0.9975 0.0699 86°0.9975 0.0697 14.3006 5°0.0871 0.9961 0.0874 85°0.9961 0.0871 11.4300 6°0.1045 0.9945 0.1051 84°0.9945 0.1045 9.5143 7°0.1218 0.9925 0.1227 83°0.9925 0.1218 8.1443 8°0.1391 0.9902 0.1405 82°0.9902 0.1391 7.1153 9°0.1564 0.9876 0.1583 81°0.9876 0.1564 6.3137 10°0.1736 0.9848 0.1763 80°0.9848 0.1736 5.6712 11°0.1908 0.9816 0.1943 79°0.9816 0.1908 5.1445 12°0.2079 0.9781 0.2125 78°0.9781 0.2079 4.7046 13°0.2249 0.9743 0.2308 77°0.9743 0.2249 4.3314 14°0.2419 0.9702 0.2493 76°0.9702 0.2419 4.0107 15°0.2588 0.9659 0.2679 75°0.9659 0.2588 3.7320二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin 22sin cos cos 2cos 2sin 22cos 2112sin 2αααααααα==-=-=-2tan tan 21tan 2ααα=--sin 33sin 4sin 3cos34cos33cos .3tan tan 3tan 313tan 2αααααααααα=-=--=--三角函数的和差化积公式 三角函数的积化和差公式sin sin 2sincos 22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅[][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+--化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)22sin cos sin()a x b x a b x φ±=+±其中φ角所在的象限由a 、b 的符号确定,φ角的值由tan ba φ=确定六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
特殊角三角函数值表Word版
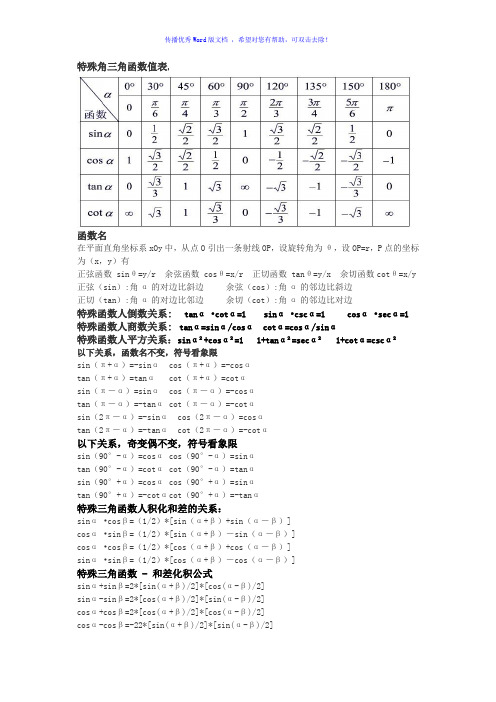
特殊角三角函数值表:函数名在平面直角坐标系xOy中,从点O引出一条射线OP,设旋转角为θ,设OP=r,P点的坐标为(x,y)有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y 正弦(sin):角α的对边比斜边余弦(cos):角α的邻边比斜边正切(tan):角α的对边比邻边余切(cot):角α的邻边比对边特殊函数人倒数关系: tanα •cotα=1sinα •cscα=1cosα •secα=1特殊函数人商数关系:tanα=sinα/cosαcotα=cosα/sinα特殊函数人平方关系:sinα²+cosα²=11+tanα²=secα²1+cotα=cscα²以下关系,函数名不变,符号看象限sin(π+α)=-sinα cos(π+α)=-cosαtan(π+α)=tanα cot(π+α)=cotαsin(π-α)=sinα cos(π-α)=-cosαtan(π-α)=-tanα cot(π-α)=-cotαsin(2π-α)=-sinα cos(2π-α)=cosαtan(2π-α)=-tanα cot(2π-α)=-cotα以下关系,奇变偶不变,符号看象限sin(90°-α)=cosα cos(90°-α)=sinαtan(90°-α)=cotα cot(90°-α)=tanαsin(90°+α)=cosα cos(90°+α)=sinαtan(90°+α)=-cotαcot(90°+α)=-tanα特殊三角函数人积化和差的关系:sinα •cosβ=(1/2)*[sin(α+β)+sin(α-β)]cosα •sinβ=(1/2)*[sin(α+β)-sin(α-β)]cosα •cosβ=(1/2)*[cos(α+β)+cos(α-β)]sinα •sinβ=(1/2)*[cos(α+β)-cos(α-β)]特殊三角函数 - 和差化积公式sinα+sinβ=2*[sin(α+β)/2]*[cos(α-β)/2]sinα-sinβ=2*[cos(α+β)/2]*[sin(α-β)/2]cosα+cosβ=2*[cos(α+β)/2]*[cos(α-β)/2]cosα-cosβ=-22*[sin(α+β)/2]*[sin(α-β)/2]特殊三角函数 - 两角和与差的三角函数公式sin(α+β)=sinαcosβ+cosαsinβcos(α+β)=cosαcosβ-sinαsinβtan(α+β)==(tanα+tanβ )/(1-tanα •tanβ) sin(α-β)=sinαcosβ-cosαsinβcos(α-β)=cosαcosβ+sinαsinβtan(α-β)=(tanα-tanβ )/(1+tanα •tanβ)。
三角函数特殊角值表

三角函数特殊角值表75587(总3页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--三角函数特殊值1、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出:sin30°=cos60°=21 sin45°=cos45°=22 tan30°=cot60°=33tan 45°=cot45°=1230˚ 1 23 1 45˚ 12 1 2 60˚3说明:正弦值随角度变化,即0˚ 30˚ 45˚ 60˚ 90˚变化;值从022 变化,其余类似记忆.3、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:① 有界性:(锐角三角函数值都是正值)即当0°<α<90°时,则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A <B <90°时,则sin A <sin B ;tan A <tan B ; cos A >cos B ;cot A >cot B ;特别地:若0°<α<45°,则sin A <cos A ;tan A <cot A若45°<A <90°,则sin A >cos A ;tan A >cot A .4、口决记忆法:观察表中的数值特征 正弦、余弦值可表示为2m 形式,正切、余切值可表示为3m 形式,有关m 的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.巧记特殊角的三角函数值初学三角函数,记忆特殊角三角函数值易错易混。
若在理解掌握的基础上,经过变形,使其呈现某种规律,再配以歌诀,则可浅显易记,触目成诵。
仔细观察表1,你会发现重要的规律。
表1中,三角函数值的前三行,分子被开方数排列特征依次为“1,2,3,3,2,1,3,9,27”。
三角函数特殊角值表

只想上传这一个表 下面的都是无用的话 不用看了。
1、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出: sin30°=cos60°=
2
1
sin45°=cos45°=22
tan30°=cot60°=3
3
tan 45°=cot45°=1
2说明:正弦值随角度变化,即0˚ 30˚ 45˚ 60˚ 90˚变化;值从0 23 1变化,其余类似记忆.
3、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:
① 有界性:(锐角三角函数值都是正值)即当0°<α<90°时,
30˚ 1
2
3 1
45˚ 1
2 1
2 60˚ 3
则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A <B <90°时,则sin A <sin B ;tan A <tan B ; cos A >cos B ;cot A >cot B ;特别地:若0°<α<45°,则sin A <cos A ;tan A <cot A 若45°<A <90°,则sin A >cos A ;tan A >cot A . 4、口决记忆法:观察表中的数值特征 正弦、余弦值可表示为
2m 形式,正切、余切值可表示为3
m 形式,有关m 的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.。
特殊三角函数值初中

特殊三角函数值初中特殊三角函数值
一、余弦函数值:
1. 余弦90°:cos 90° = 0
2. 余弦60°:cos 60° = 0.5
3. 余弦45°:cos 45° = 0.707
4. 余弦30°:cos 30° = 0.866
二、正弦函数值:
1. 正弦90°:sin 90° = 1
2. 正弦60°:sin 60° = 0.866
3. 正弦45°:sin 45° = 0.707
4. 正弦30°:sin 30° = 0.5
三、正切函数值:
1. 正切90°:tan 90° = 无穷大
2. 正切60°:tan 60° = 1.732
3. 正切45°:tan 45° = 1
4. 正切30°:tan 30° = 0.577
特殊三角函数的值有很大的作用,它能够让我们清楚地了解三角有关的概念,同时又能在编程中更加方便快捷地对三角形处理。
余弦函数值0.866主要用来计算其他角度的余弦值;正弦函数值1就是为了计算90°之后的角度的正弦值;而正切函数值0.577主要是为了计算夹角的角度的正切值。
此外,特殊三角函数值还可以用在圆周率道具的计算中,比如面积、速度等等。
特殊角三角函数值表
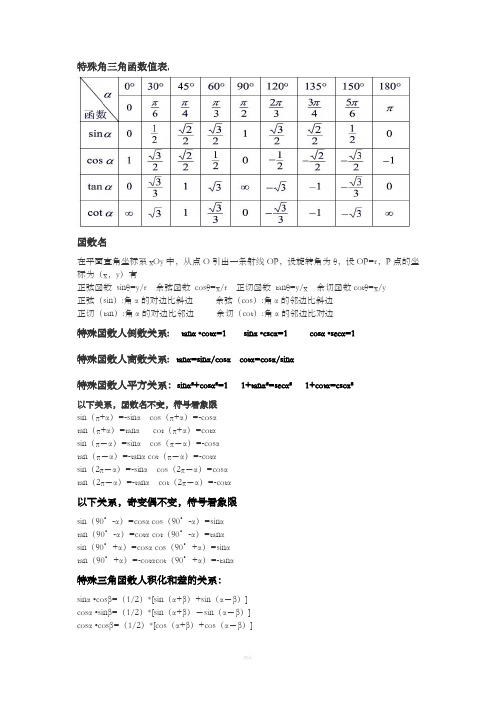
特殊角三角函数值表:函数名在平面直角坐标系xOy中,从点O引出一条射线OP,设旋转角为θ,设OP=r,P点的坐标为(x,y)有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正弦(sin):角α的对边比斜边余弦(cos):角α的邻边比斜边正切(tan):角α的对边比邻边余切(cot):角α的邻边比对边特殊函数人倒数关系: tanα •cotα=1sinα •cscα=1cosα •secα=1特殊函数人商数关系:tanα=sinα/cosαcotα=cosα/sinα特殊函数人平方关系:sinα²+cosα²=11+tanα²=secα²1+cotα=cscα²以下关系,函数名不变,符号看象限sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanα cot(π-α)=-cotαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα以下关系,奇变偶不变,符号看象限sin(90°-α)=cosα cos(90°-α)=sinαtan(90°-α)=cotα cot(90°-α)=tanαsin(90°+α)=cosα cos(90°+α)=sinαtan(90°+α)=-cotαcot(90°+α)=-tanα特殊三角函数人积化和差的关系:sinα •cosβ=(1/2)*[sin(α+β)+sin(α-β)]cosα •sinβ=(1/2)*[sin(α+β)-sin(α-β)]cosα •cosβ=(1/2)*[cos(α+β)+cos(α-β)]sinα •sinβ=(1/2)*[cos(α+β)-cos(α-β)]特殊三角函数- 和差化积公式sinα+sinβ=2*[sin(α+β)/2]*[cos(α-β)/2]sinα-sinβ=2*[cos(α+β)/2]*[sin(α-β)/2] cosα+cosβ=2*[cos(α+β)/2]*[cos(α-β)/2]cosα-cosβ=-22*[sin(α+β)/2]*[sin(α-β)/2]特殊三角函数- 两角和与差的三角函数公式sin(α+β)=sinαcosβ+cosαsinβcos(α+β)=cosαcosβ-sinαsinβtan(α+β)==(tanα+tanβ )/(1-tanα •tanβ)sin(α-β)=sinαcosβ-cosαsinβcos(α-β)=cosαcosβ+sinαsinβtan(α-β)=(tanα-tanβ )/(1+tanα •tanβ)。
三角函数特殊角值表

三角函数特殊值1、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出: sin30°=cos60°=21sin45°=cos45°=22tan30°=cot60°=33tan 45°=cot45°=1230˚ 1 23145˚ 12 12 60˚ 3说明:正弦值随角度变化,即0˚ 30˚ 45˚ 60˚ 90˚变化;值从023 1变化,其余类似记忆.3、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:① 有界性:(锐角三角函数值都是正值)即当0°<α<90°时,则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A <B <90°时,则sin A <sin B ;tan A <tan B ; cos A >cos B ;cot A >cot B ;特别地:若0°<α<45°,则sin A <cos A ;tan A <cot A 若45°<A <90°,则sin A >cos A ;tan A >cot A .4、口决记忆法:观察表中的数值特征 正弦、余弦值可表示为2m 形式,正切、余切值可表示为3m 形式,有关m 的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.巧记特殊角的三角函数值初学三角函数,记忆特殊角三角函数值易错易混。
若在理解掌握的基础上,经过变形,使其呈现某种规律,再配以歌诀,则可浅显易记,触目成诵。
仔细观察表1,你会发现重要的规律。
表1中,三角函数值的前三行,分子被开方数排列特征依次为“1,2,3,3,2,1,3,9,27”。
“一二三,三二一,三九二十七”。
记此歌诀即可。
观察表2也可发现重要的规律。
特殊三角函数值表格

特殊三角函数值表图及sin cos tan相关方程式sin cos tan特殊角的三角函数值表图sin cos tan相关方程式1.数关系tanα·cotα=1sinα·cscα=1cosα·secα=12.商的关系tanα=sinα/cosαcotα=cosα/sinα3.平方关系sin2α+cos2α=11+tan2α=sec2α1+cot2α=csc2α4.积化和差公式sinα·cosβ=(1/2)*[sin(α+β)+sin(α-β)] cosα·sinβ=(1/2)*[sin(α+β)-sin(α-β)] cosα·cosβ=(1/2)*[cos(α+β)+cos(α-β)] sinα·sinβ=-(1/2)*[cos(α+β)-cos(α-β)] 5.和差化积公式sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2]6.三倍角公式sin3α=3sinα-4sin^3α;cos3α=4cos^3α-3cosα特殊角三角函数值记忆口诀三十,四五,六十度,三角函数记牢固;分母弦二切是三,分子要把根号添;一二三来三二一,切值三九二十七;递增正切和正弦,余弦函数要递减。
口诀说明:30°,45°,60°这三个角的正弦值和余弦值的共同点是:分母都是2,若把分子都加上根号,则被开方数就相应地变成了1,2,3.正切的特点是将分子全部都带上根号,令分母值为3,则相应的被开方数就是3,9,27.另外,正弦值和正切值随着角度的增大而增大,余弦值随着角度的增大而减小。
特殊三角函数数值表

特殊三角函数数值表 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB) tan(A-B) = (tanA-tanB)/(1+tanAtanB) cot(A+B) = (cotAcotB-1)/(cotB+cotA) cot(A-B) = (cotAcotB+1)/(cotB-cotA)sin3A = 3sinA-4(sinA)^3;cos3A = 4(cosA)^3 -3cosAtan3a = tan a · tan(π/3+a)· tan(π/3-a)公式sin(A/2) = √{(1--cosA)/2}cos(A/2) = √{(1+cosA)/2}tan(A/2) = √{(1--cosA)/(1+cosA)}cot(A/2) = √{(1+cosA)/(1-cosA)}tan(A/2) = (1--cosA)/sinA=sinA/(1+cosA) sin(a)+sin(b) = 2sin[(a+b)/2]cos[(a-b)/2] sin(a)-sin(b) = 2cos[(a+b)/2]sin[(a-b)/2] cos(a)+cos(b) = 2cos[(a+b)/2]cos[(a-b)/2] cos(a)-cos(b) = -2sin[(a+b)/2]sin[(a-b)/2] tanA+tanB=sin(A+B)/cosAcosBsin(a)sin(b) = -1/2*[cos(a+b)-cos(a-b)] cos(a)cos(b) = 1/2*[cos(a+b)+cos(a-b)] sin(a)cos(b) = 1/2*[sin(a+b)+sin(a-b)] cos(a)sin(b) = 1/2*[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sin(a)cos(-a) = cos(a)sin(π/2-a) = cos(a)cos(π/2-a) = sin(a)sin(π/2+a) = cos(a)cos(π/2+a) = -sin(a)sin(π-a) = sin(a)cos(π-a) = -cos(a)sin(π+a) = -sin(a)cos(π+a) = -cos(a)tgA=tanA = sinA/cosA万能公式sin(a) = [2tan(a/2)] / {1+[tan(a/2)]^2}cos(a) = {1-[tan(a/2)]^2} / {1+[tan(a/2)]^2}tan(a) = [2tan(a/2)]/{1-[tan(a/2)]^2}a·sin(a)+b·cos(a) = [√(a^2+b^2)]*sin(a+c) [其中,tan(c)=b/a]a·sin(a)-b·cos(a) = [√(a^2+b^2)]*co s(a-c) [其中,tan(c)=a/b]1+sin(a) = [sin(a/2)+cos(a/2)]^2;1-sin(a) = [sin(a/2)-cos(a/2)]^2;;这是高考用的正割函数与余割函数正割函数在y=secx中,以x的任一使secx有意义的值与它对应的y值作为(x,y).在直角坐标系中作出的图形叫正割函数的图像,也叫正割曲线.y=secx的性质:(1)定义域,{x|x≠π/2+kπ,k∈Z}(2)值域,|secx|≥1.即secx≥1或secx≤-1;(3)y=secx是偶函数,即sec(-x)=secx.图像对称于y轴;(4)y=secx是周期函数.周期为2kπ(k∈Z,且k≠0),最小正周期T=2π.并附上很难找到的正割图像.(正割函数图像中值域在-1到1之间的图像不包括。
特殊三角函数数值表

特殊三角函数数值表Revised on November 25, 2020两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB) tan(A-B) = (tanA-tanB)/(1+tanAtanB) cot(A+B) = (cotAcotB-1)/(cotB+cotA) cot(A-B) = (cotAcotB+1)/(cotB-cotA)sin3A = 3sinA-4(sinA)^3;cos3A = 4(cosA)^3 -3cosAtan3a = tan a · tan(π/3+a)· tan(π/3-a)公式sin(A/2) = √{(1--cosA)/2}cos(A/2) = √{(1+cosA)/2}tan(A/2) = √{(1--cosA)/(1+cosA)}cot(A/2) = √{(1+cosA)/(1-cosA)}tan(A/2) = (1--cosA)/sinA=sinA/(1+cosA) sin(a)+sin(b) = 2sin[(a+b)/2]cos[(a-b)/2] sin(a)-sin(b) = 2cos[(a+b)/2]sin[(a-b)/2] cos(a)+cos(b) = 2cos[(a+b)/2]cos[(a-b)/2] cos(a)-cos(b) = -2sin[(a+b)/2]sin[(a-b)/2] tanA+tanB=sin(A+B)/cosAcosBsin(a)sin(b) = -1/2*[cos(a+b)-cos(a-b)] cos(a)cos(b) = 1/2*[cos(a+b)+cos(a-b)] sin(a)cos(b) = 1/2*[sin(a+b)+sin(a-b)] cos(a)sin(b) = 1/2*[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sin(a)cos(-a) = cos(a)sin(π/2-a) = cos(a)cos(π/2-a) = sin(a)sin(π/2+a) = cos(a)cos(π/2+a) = -sin(a)sin(π-a) = sin(a)cos(π-a) = -cos(a)sin(π+a) = -sin(a)cos(π+a) = -cos(a)tgA=tanA = sinA/cosA万能公式sin(a) = [2tan(a/2)] / {1+[tan(a/2)]^2}cos(a) = {1-[tan(a/2)]^2} / {1+[tan(a/2)]^2}tan(a) = [2tan(a/2)]/{1-[tan(a/2)]^2}a·sin(a)+b·cos(a) = [√(a^2+b^2)]*sin(a+c) [其中,tan(c)=b/a]a·sin(a)-b·cos(a) = [√(a^2+b^2)]*cos(a-c) [其中,tan(c)=a/b]1+sin(a) = [sin(a/2)+cos(a/2)]^2;1-sin(a) = [sin(a/2)-cos(a/2)]^2;;这是高考用的正割函数与余割函数正割函数在y=secx中,以x的任一使secx有意义的值与它对应的y值作为(x,y).在直角坐标系中作出的图形叫正割函数的图像,也叫正割曲线.y=secx的性质:(1)定义域,{x|x≠π/2+kπ,k∈Z}(2)值域,|secx|≥1.即secx≥1或secx≤-1;(3)y=secx是偶函数,即sec(-x)=secx.图像对称于y轴;(4)y=secx是周期函数.周期为2kπ(k∈Z,且k≠0),最小正周期T=2π.并附上很难找到的正割图像.(正割函数图像中值域在-1到1之间的图像不包括。
特殊角三角函数值表
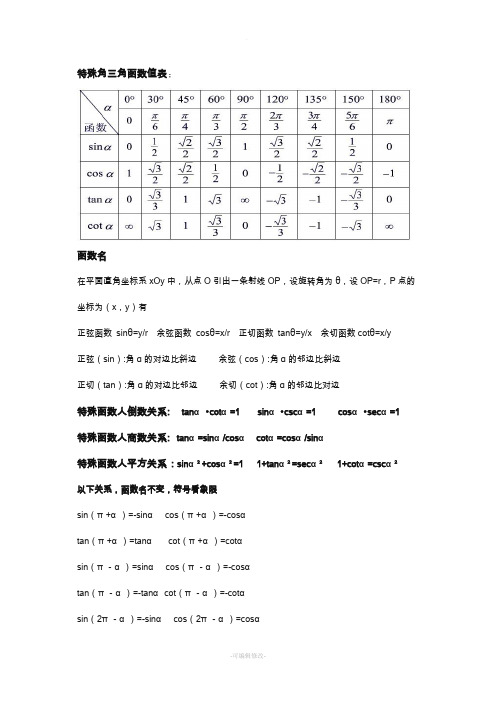
特殊角三角函数值表:函数名在平面直角坐标系xOy中,从点O引出一条射线OP,设旋转角为θ,设OP=r,P点的坐标为(x,y)有正弦函数sinθ=y/r 余弦函数cosθ=x/r 正切函数tanθ=y/x 余切函数cotθ=x/y正弦(sin):角α的对边比斜边余弦(cos):角α的邻边比斜边正切(tan):角α的对边比邻边余切(cot):角α的邻边比对边特殊函数人倒数关系: tanα•cotα=1 sinα•cscα=1 cosα•secα=1特殊函数人商数关系:tanα=sinα/cosαcotα=cosα/sinα特殊函数人平方关系:sinα²+cosα²=1 1+tanα²=secα²1+cotα=cscα²以下关系,函数名不变,符号看象限sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanα cot(π-α)=-cotαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα以下关系,奇变偶不变,符号看象限sin(90°-α)=cosα cos(90°-α)=sinαtan(90°-α)=cotα cot(90°-α)=tanαsin(90°+α)=cosα cos(90°+α)=sinαtan(90°+α)=-cotαcot(90°+α)=-tanα特殊三角函数人积化和差的关系:sinα•cosβ=(1/2)*[sin(α+β)+sin(α-β)] cosα•sinβ=(1/2)*[sin(α+β)-sin(α-β)] cosα•cosβ=(1/2)*[cos(α+β)+cos(α-β)] sinα•sinβ=(1/2)*[cos(α+β)-cos(α-β)] 特殊三角函数- 和差化积公式sinα+sinβ=2*[sin(α+β)/2]*[cos(α-β)/2]sinα-sinβ=2*[cos(α+β)/2]*[sin(α-β)/2]cosα+cosβ=2*[cos(α+β)/2]*[cos(α-β)/2]cosα-cosβ=-22*[sin(α+β)/2]*[sin(α-β)/2]特殊三角函数- 两角和与差的三角函数公式sin(α+β)=sinαcosβ+cosαsinβcos(α+β)=cosαcosβ-sinαsinβtan(α+β)==(tanα+tanβ )/(1-tanα•tanβ)sin(α-β)=sinαcosβ-cosαsinβcos(α-β)=cosαcosβ+sinαsinβtan(α-β)=(tanα-tanβ )/(1+tanα•tanβ)THANKS !!!致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求欢迎您的下载,资料仅供参考。
特殊角的三角函数值 表格

特殊角的三角函数值表格
在三角学中,特殊角的三角函数值是非常重要的知识点。
特殊角是指常见的角度值,如0度、30度、45度、60度和90度,它们的三角函数值是固定的,具有特殊性。
下表列出了这些特殊角的正弦、余弦和正切函数值:
角度正弦(sin)余弦(cos)正切(tan)
0度010
30度1/2√3/21/√3
45度√2/2√2/21
60度√3/21/2√3
90度10无穷大
这些特殊角的三角函数值是在解决三角函数问题时经常会用到的基本数值,对于计算各种三角函数式子和题目的解答都具有很大的帮助。
熟练掌握这些数值可以提高解题效率,并对理解三角函数的概念和性质有很大帮助。
特殊三角函数数值表

两角和公式sinA+B = sinAcosB+cosAsinBsinA-B = sinAcosB-cosAsinBcosA+B = cosAcosB-sinAsinBcosA-B = cosAcosB+sinAsinBtanA+B = tanA+tanB/1-tanAtanBtanA-B = tanA-tanB/1+tanAtanBcotA+B = cotAcotB-1/cotB+cotAcotA-B = cotAcotB+1/cotB-cotAsin3A = 3sinA-4sinA^3;cos3A = 4cosA^3 -3cosAtan3a = tan a · tanπ/3+a· tanπ/3-a 公式sinA/2 = √{1--cosA/2}cosA/2 = √{1+cosA/2}tanA/2 = √{1--cosA/1+cosA}cotA/2 = √{1+cosA/1-cosA}tanA/2 = 1--cosA/sinA=sinA/1+cosAsina+sinb = 2sina+b/2cosa-b/2sina-sinb = 2cosa+b/2sina-b/2 cosa+cosb = 2cosa+b/2cosa-b/2 cosa-cosb = -2sina+b/2sina-b/2 tanA+tanB=sinA+B/cosAcosBsinasinb = -1/2cosa+b-cosa-b cosacosb = 1/2cosa+b+cosa-b sinacosb = 1/2sina+b+sina-b cosasinb = 1/2sina+b-sina-b诱导公式sin-a = -sinacos-a = cosasinπ/2-a = cosacosπ/2-a = sinasinπ/2+a = cosacosπ/2+a = -sinasinπ-a = sinacosπ-a = -cosasinπ+a = -sinacosπ+a = -cosatgA=tanA = sinA/cosA万能公式sina = 2tana/2 / {1+tana/2^2}cosa = {1-tana/2^2} / {1+tana/2^2}tana = 2tana/2/{1-tana/2^2}a·sina+b·cosa = √a^2+b^2sina+c 其中;tanc=b/aa·sina-b·cosa = √a^2+b^2cosa-c 其中;tanc=a/b1+sina = sina/2+cosa/2^2;1-sina = sina/2-cosa/2^2;;这是高考用的正割函数与余割函数正割函数在y=secx中;以x的任一使secx有意义的值与它对应的y值作为x;y.在直角坐标系中作出的图形叫正割函数的图像;也叫正割曲线. y=secx的性质:1定义域;{x|x≠π/2+kπ;k∈Z}2值域;|secx|≥1.即secx≥1或secx≤-1;3y=secx是偶函数;即sec-x=secx.图像对称于y轴;4y=secx是周期函数.周期为2kπk∈Z;且k≠0;最小正周期T=2π.并附上很难找到的正割图像.正割函数图像中值域在-1到1之间的图像不包括..更好的图像请参考正割与余弦互为倒数;余割与正弦互为倒数..正割函数无限趋向于直线x=π/2+kπ ..正割函数是无界函数正割函数的导数:secx'=secxtanx正割函数的不定积分:∫secxdx=㏑|secx+tanx|+C余割函数对于任意一个实数x;都对应着唯一的角弧度制中等于这个实数;而这个角又对应着唯一确定的余割值cscx与它对应;按照这个对应法则建立的函数称为余割函数..记作fx=cscx 余割函数的性质1、定义域:{x|x≠kπ;k∈Z}2、值域:{y|y<-1或y>1}3、奇偶性:奇函数4、周期性:最小正周期为2π5、图像:图像渐近线为:x=kπ ;k∈Z余割函数与正弦函数互为倒数HM2761EAENT0018DD7844。
