七上数学《整式的加减》知识点整理

合集下载

七年级数学整式的加减知识点

整式的加减
1.都是数或字母的积的式子叫做单项式，单独的一个数或一个字母也是单项式。

2.单项式中的数字因数叫做这个单项式的系数。

3.一个单项式中，所有字母的指数的和叫做这个单项式的次数。

4.几个单项的和叫做多项式，其中，每个单项式叫做多项式的项，不含字母的项叫做常数项。

5.多项式里次数最高项的次数，叫做这个多项式的次数。

6.把多项式中的同类项合并成一项，叫做合并同类项。

合并同类项后，所得项的系数是合并前各同类项的系数的和，且字母部分不变。

7.如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同。

8.如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反。

9.一般地，几个整式相加减，如果有括号就先去括号，然后再合并同类项。

七年级上册数学整式的加减整式加减知识点整理

整式加减一．知识框架二、知识要点1、单项式〔1〕、都是数或字母的积的式子叫做单项式。

〔单独的一个数或一个字母也是单项式。

〕如：2,2bc,3m,a,都是单项式。

〔2〕、单项式中的数字因数叫做这个单项式的系数。

如：2ab 中2是这个单项式的系数。

〔3〕、单项式系数应注意的问题：① 单项式表示数字及字母相乘时，通常把数字写在前面；② 当单项式的系数是带分数时，要把带分数化成假分数；③ 当单项式的系数是1或-1时，“1〞通常省略不写；④ 圆周率π是常数；⑤ 单项式的系数应包括它前面的“正〞、“负〞符号。

〔4〕、一个单项式中，所有字母的指数的与叫做这个单项式的次数。

如：xy2,这个单项式的次数是3 次，而不是2次。

〔单独的一个数的次数是0.〕2、多项式〔1〕、几个单项的与叫做多项式。

其中，每个单项式叫做多项式的项，不含字母的项叫做常数项。

多项式的每一项都包含它前面的符号。

如：2a2+3b-5 是一个多项式，2a2,3b,-5是这个多项式项，-5是常数项。

〔2〕、多项式里次数最高项的次数，叫做这个多项式的次数。

如：2a2+3b-5的次数是2.〔3〕、单项式及多项式统称整式。

3、合并同类项〔1〕、所含字母一样，并且一样字母的指数也一样的项叫做同类项。

几个常数项也是同类项。

如：2a+3a-a+3a2中2a,3a,a是同类项，而2a,3a2那么不是同类项。

〔2〕、把多项式里的同类项合并成一项，叫做合并同类项。

〔3〕、合并同类项法那么：合并同类项后，所得项的系数是合并前各同类项的系数的与，且字母局部不变。

如：2a+3a-a 合并同类项得：4a,数字相加或相减，字母不变。

4、去括号〔1〕、去括号法那么：① 如果括号外的因数是正数，去括号后括号内每一项的符号都不变。

〔“+〞不变〕如：〔2a+5〕去括号后不变：2a+5② 如果括号外的因数是负数，去括号后括号内每一项的符号都变。

〔“-〞全变〕如：-〔2a+5〕去括号后变成：-2a-5〔2〕、去括号应注意：① 去括号应考虑括号内的每一项的符号，做的要变都变，要不变都不变；② 括号内原来有几项，去掉括号后仍有几项，同时括号前的符号也要去掉。

七上数学第二章整式的加减

七上数学第二章整式的加减摘要：1.整式的概念及其分类2.整式的加减运算法则3.整式的加减运算实例分析4.整式的加减运算技巧和方法5.整式的加减在实际问题中的应用正文：七上数学第二章整式的加减一、整式的概念及其分类整式是指由常数、变量和它们的乘积以及它们的和差所组成的代数式。

整式可以分为单项式和多项式两大类。

单项式是只包含一个变量或常数的代数式，例如：3x、-2y等；多项式是由多个单项式通过加减运算组合而成的代数式，例如：x+3xy-2y等。

二、整式的加减运算法则整式的加减运算主要遵循以下法则：1.同类项相加减：同类项是指具有相同变量和相同次数的项，例如：3x 和4x 是同类项，而2x 和3y 不是同类项。

2.合并同类项：将同类项的系数相加减，字母和字母的指数不变。

3.遵循交换律和结合律：整式的加减运算可以交换顺序，也可以先计算部分项的和差，再进行总的加减运算。

三、整式的加减运算实例分析例如：计算以下整式的和差。

(1) 5x + 3xy - 2y + 2x - xy首先合并同类项，得到：7x + 2xy - 2y。

(2) 4a - 2b + 3c - (2a - b + c)去括号后，合并同类项，得到：2a - b + c。

四、整式的加减运算技巧和方法1.观察运算符号，根据符号进行相应的加减运算。

2.利用分配律，将加减运算分解为多个简单的加减运算。

3.注意合并同类项，避免遗漏或重复计算。

4.可以使用括号改变运算顺序，简化计算过程。

五、整式的加减在实际问题中的应用整式的加减在解决实际问题中具有重要作用，例如：在几何中求解面积、周长等问题时，需要用到整式的加减运算；在代数方程中，整式的加减是求解方程的重要手段。

七年级整式的加减知识点

七年级整式的加减知识点整式是由常数、变量及它们的积或幂次积，以及它们的和或差组成的代数式。

整式的加减是初中阶段数学中基础且重要的知识点，本文将从整式的定义、基本概念、加减法规则等方面，为大家详细介绍七年级整式的加减知识点。

一、整式的定义及基本概念1. 整式的定义：由常数和变量的积、幂以及它们的和或差组成的关于变量的代数式。

例如：2xy+3y-5a²b+4ab²+a²b+2a²b²2. 同类项：整式中，含有相同的字母和相同的次数的代数式称为同类项。

例如：2xy, 5xy, -9xy都是同类项；4a²b², -3a²b², 2a²b²也都是同类项。

3. 非同类项：整式中，不是同类项的代数式称为非同类项。

例如：2xy, 5xz, -9y都是非同类项；4a²b, -3h²j, 2cd也都是非同类项。

二、整式的加法原则两个整式相加，将它们的同类项合并在一起，非同类项则保留原样。

具体来说，可按如下方法进行：1. 去括号：如果有括号，先把括号去掉。

例如：(3x + 4y) + (2x - 5y) = 3x + 4y + 2x - 5y2. 合并同类项：把其中相同的项相加或相减，并保留非同类项。

例如：3x + 4y + 2x - 5y = 5x - y三、整式的减法原则整式相减时，也是先合并同类项，再保留非同类项。

具体来说，可按如下方法进行：1. 按一般加法步骤准备整式，要注意被减式的所有项都要取相反数。

例如：(5x² - 3x + 2) - (2x² - 4x + 1) = 5x² - 3x + 2 + (-2x² + 4x - 1)2. 合并同类项。

例如：5x² - 3x + 2 + (-2x² + 4x - 1) = 3x² + x + 1四、整式加减混合运算整式加减混合运算是指在同一道题目中，既有整式的加法运算，又有整式的减法运算。

人教版七年级数学上第2章整式的加减知识点总结及题型汇总

整式的加减知识点总结及题型汇总整式知识点1．单项式：在代数式中，若只含有乘法（包括乘方）运算。

或虽含有除法运算，但除式中不含字母的一类代数式叫单项式.2．单项式的系数与次数：单项式中不为零的数字因数，叫单项式的数字系数，简称单项式的系数；系数不为零时，单项式中所有字母指数的和，叫单项式的次数.3．多项式：几个单项式的和叫多项式.4．多项式的项数与次数：多项式中所含单项式的个数就是多项式的项数，每个单项式叫多项式的项；多项式里，次数最高项的次数叫多项式的次数；注意：（若a 、b 、c 、p 、q 是常数）ax 2+bx+c 和x 2+px+q 是常见的两个二次三项式.5．整式：凡不含有除法运算，或虽含有除法运算但除式中不含字母的代数式叫整式.整式分类为：⎩⎨⎧多项式单项式整式 .6．同类项：所含字母相同，并且相同字母的指数也相同的单项式是同类项.7．合并同类项法则：系数相加，字母与字母的指数不变.8．去（添）括号法则：去（添）括号时，若括号前边是“+”号，括号里的各项都不变号；若括号前边是“-”号，括号里的各项都要变号.9．整式的加减：整式的加减，实际上是在去括号的基础上，把多项式的同类项合并.10.多项式的升幂和降幂排列：把一个多项式的各项按某个字母的指数从小到大（或从大到小）排列起来，叫做按这个字母的升幂排列（或降幂排列）.注意：多项式计算的最后结果一般应该进行升幂（或降幂）排列.11. 列代数式列代数式首先要确定数量与数量的运算关系，其次应抓住题中的一些关键词语，如和、差、积、商、平方、倒数以及几分之几、几成、倍等等.抓住这些关键词语，反复咀嚼，认真推敲，列好一般的代数式就不太难了.12.代数式的值根据问题的需要，用具体数值代替代数式中的字母，按照代数式中的运算关系计算，所得的结果是代数式的值.13. 列代数式要注意①数字与字母、字母与字母相乘，要把乘号省略；②数字与字母、字母与字母相除，要把它写成分数的形式；③如果字母前面的数字是带分数，要把它写成假分数。

七年级整式加减知识点归纳

七年级整式加减知识点归纳整式加减是初中数学中非常基础而重要的知识点，也是后续学习代数方程组、二次函数以及三角函数等内容的基础。

七年级学生需要通过大量的练习和实践，熟练掌握整式加减的方法和运算规律。

一、整式整式指用字母和常数表示的代数式，其中字母表示数或量。

整式分为单项式和多项式两类。

单项式是只有一个项的一种代数式，如3a、7x²等。

多项式是由若干个单项式经过加、减运算组成的代数式，如3x+2、4a-7b-5c²等。

二、加减法则整式加减的法则和常数加减的法则类似，主要是对同类项进行合并和简化。

1. 合并同类项只有同类项才可以进行合并，即其中字母部分相同，次数相同的项。

如：2. 简化多项式当一组多项式中存在相反数时，可以通过相减的方法进行简化，如：3. 去括号整式加减时，需要先去掉括号。

一般情况下，括号内的内容需要乘以括号前的系数，如：4. 绝对值绝对值可以表示一个数的距离，常用于计算误差和误差范围。

整式中的绝对值运算需要根据括号内的值是否小于0进行分类讨论。

当括号内的值大于等于0时，绝对值内的值不变，如：当括号内的值小于0时，需要将括号内的值加上一个负号，再去掉绝对值符号，如：三、练习题1. 将以下两组多项式相加，并将结果化简：2. 将以下两组多项式相减，并将结果化简：3. 将以下两组多项式相加，并将结果化简：4. 将以下两组多项式相减，并将结果化简：五、总结整式加减是整个代数学习过程的基础，初中阶段学生需要通过大量练习，熟练掌握整式加减的方法和规律。

在实际计算中，要注意合并同类项、简化多项式、去括号以及绝对值等常用的加减法则，以提高计算效率和准确性。

七年级整式加减知识点

七年级整式加减知识点在七年级数学课程中，整式加减是重要的基础知识点。

掌握了整式加减，对学习其他数学知识也会产生积极的影响。

下面，本文将介绍七年级整式加减的一些基本知识点。

一、整式的基本概念整式是指由常数和各种字母乘方及它们的积的和构成的代数式。

比如，x + 3、2x² - 5x + 1、y³ + 2y² - y 等都是整式。

二、同类项的概念同类项是指只有字母的指数不同的代数式。

例如，3x²和-2x²是同类项，因为它们都只有x的平方，并且它们的系数不同。

三、整式的加减整式的加减实际上就是把同类项合并起来，得到简化的整式。

比如，对于3x² + 2xy - 5x² + 3xy + 7，我们可以先把同类项3x²和-5x²合并，把同类项2xy和3xy合并，得到-2x² + 5xy + 7。

四、加减的练习方法对于初学者来说，整式的加减并不是一件容易的事情。

因此，我们需要进行一些练习，以提高我们的能力。

1.练习识别同类项。

在练习中，我们需要将不同的整式拆分成同类项，然后再进行合并。

2.练习合并同类项。

在练习中，我们需要手动计算每个同类项的系数，然后再把它们相加或相减。

3.练习整理整式。

在练习中，我们需要把整式溯源到它最简单的形式，也就是没有括号和乘积的形式。

五、常见的错误在学习整式加减过程中，有一些常见的错误需要注意：1.错误识别同类项。

如果我们没有正确地识别同类项，我们就无法正确地计算整式。

2.错误加减系数。

如果我们没有正确地计算系数，我们就会得到错误的结果。

3.错误理解复杂的整式。

在处理复杂的整式时，我们需要仔细分析它们，并考虑清楚每个步骤的细节。

总之，七年级的整式加减是数学的基本知识，它对学习其他数学知识也是至关重要的。

我们需要了解整式的基本概念和概念，练习合并同类项，并避免常见的错误。

只有通过反复练习，我们才能提高自己的技能。

七年级上整式的加减知识点

七年级上整式的加减知识点整式是代数学中的一个重要概念，是由若干个含有同一变量的项按照加减法规则组成的式子。

在七年级上学期，我们学习了整式的加减法运算。

本文将介绍七年级上整式的加减知识点，包括整式的概念、同类项的概念和加减法运算规则。

一、整式的概念整式是由常数和含有同一变量的项按照加减法规则组成的式子。

其中，常数是不含变量的项，如5、-3；变量是表示数值未知的字母，如x、y。

例子如下：3x²-5y+2xy+7上述式子中，3x²、-5y、2xy、7都是项，其中3x²、2xy是含有同一变量x的项，-5y是只含有y的项，7是常数。

整式是由这些项按照加减法规则组成的。

二、同类项的概念同类项是指具有相同变量因子的项，变量因子指项中各变量的积。

如3x²和7x²就是同类项，因为它们的变量因子都是x²；而3x²和5xy就不是同类项，因为它们的变量因子不同。

同类项可以合并，即加减时将同类项相加减后组成一个整式。

例如：3x²+7x²-4x²=6x²在这个例子中，3x²、7x²、-4x²都是同类项，它们相加减后得出一个整数6x²。

三、加减法运算规则1. 同类项相加减同类项可以相加减，合并后得到一个整式。

其中，同类项相加时，系数直接相加；同类项相减时，系数相减。

例如：2x+3x=5x2xy-3xy=-xy2x²+3x²+5x²=10x²2y-5y=-3y2. 对于多项式的加减法运算，可以采用如下规则：先将各同类项进行合并，得到一个新的整式，然后对其进行简化。

例如：(3x²+2xy-5y)+(7y-2xy+4)=3x²+7y-1在此例中，先将同类项2xy和-2xy进行相加减得到0，再将同类项3x²和-5y、7y和4进行相加减得到3x²+7y-1。

人教版七年级数学第二章整式的加减知识点归纳

第二章整式的加减知识点1.单项式：数字与字母的积或者字母与字母的积。

一个单独的数字或者具体的数字也是单项式。

注意：数字与字母或者字母与字母相乘时乘号省略不写，且把数字写在字母的前面。

2.单项式的系数：单项式中的数字因数。

如果在一个单项式中没有出现具体的数字，则它的系数是1.例如：xy 它的系数是1，-n 它的系数是-1.常数项（具体的数字）的系数就是它本身，例如：3的系数就是3，π的系数就是π。

π是一个常数（具体的数字），不是字母。

3.单项式的次数：单项式中所以字母指数的和。

例如：xy 6的次数是2次，323n m 的次数是5次，y x 233的次数是3次。

常数（具体的数字）的次数是0次，例如：3的次数就是0，π的次数是0。

4.多项式：几个单项式的和叫做多项式，其中每个单项式叫做多项式的项，不含字母的项叫常数项。

例如：多项式4y 32xy 22-+-m 是由单项式22xy 、m 2-、y 3、7-相加组成，所以22xy 、m 2-、y 3、7-就是多项式4y 32xy 22-+-m 的项，7-就是常数项。

5.多项式的次数：多项式中次数最高项的次数。

要求一个多项式的次数，应该先求出它的每一个项的次数，然后再看哪个项的次数最高，那么次数最高项的次数就是这个多项式的次数。

其中次数最高的项叫最高次项，例如：多项式4y 32xy 22-+-m ，22xy 的次数是3次，m 2-的次数是1次，y 3的次数是1次，7-的次数是0次，所以22xy 的次数最高，那么22xy 就是最高次项，则这个多项式的次数就是3次。

6.整式：多项式和单项式统称为整式。

如果一个式子的分母中出现了字母（π除外），那么它就不是整式（即它不是单项式，也不是多项式）。

7.同类项：含有相同的字母且相同字母的指数也相同的项叫做同类项，例如233-n m 与325m n 是同类项，因为这两个项中都含有字母m 、n ，并且字母m 的指数都是3，字母n 的指数都是2，所以他们是同类项。

七年级数学上册整式的加减知识点梳理

七年级数学上册整式的加减知识点梳理
七年级数学上册整式的加减知识点梳理
在平凡的学习生活中，大家都背过不少知识点，肯定对知识点非常熟悉吧！知识点就是学习的重点。

哪些知识点能够真正帮助到我们呢？下面是店铺帮大家整理的七年级数学上册整式的加减知识点梳理，欢迎大家借鉴与参考，希望对大家有所帮助。

1、单项式：在代数式中，若只含有乘法（包括乘方）运算。

或虽含有除法运算，但除式中不含字母的一类代数式叫单项式.
2、单项式的系数与次数：单项式中不为零的数字因数，叫单项式的数字系数，简称单项式的系数；系数不为零时，单项式中所有字母指数的和，叫单项式的次数.
3、多项式：几个单项式的和叫多项式.
4、多项式的项数与次数：多项式中所含单项式的个数就是多项式的项数，每个单项式叫多项式的'项；多项式里，次数最高项的次数叫多项式的次数。

通过本章学习，应使学生达到以下学习目标：
1、理解并掌握单项式、多项式、整式等概念，弄清它们之间的区别与联系。

2、理解同类项概念，掌握合并同类项的方法，掌握去括号时符号的变化规律，能正确地进行同类项的合并和去括号。

在准确判断、正确合并同类项的基础上，进行整式的加减运算。

3、理解整式中的字母表示数，整式的加减运算建立在数的运算基础上；理解合并同类项、去括号的依据是分配律；理解数的运算律和运算性质在整式的加减运算中仍然成立。

4、能够分析实际问题中的数量关系，并用还有字母的式子表示出来。

【七年级数学上册整式的加减知识点梳理】。

七年级上册数学整式的加减法知识点归纳

整式的加减法是初中数学中的重要知识点，掌握好整式的加减法对于学生来说非常关键。

在七年级上册数学教学中，学生们将接触整式的加减法，并且在以后的学习中会不断用到这些知识。

我们有必要对七年级上册数学整式的加减法知识点进行归纳和总结。

一、整式的概念整式是指由常数、变量及其指数和次数有限次加、减、乘、除运算得到的代数和。

一般表示为a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0，其中a_n、a_{n-1}、...、a_1、a_0为常数，x为变量，n为自然数。

二、整式的加法1. 同类项的加法同类项是指它们具有相同的字母和字母的指数相同的项。

在进行整式的加法时，首先要将同类项合并，然后将它们的系数相加。

例如：3x^2y+2xy^2-5x^2y-3xy^2= 3x^2y-5x^2y+2xy^2-3xy^2= -2x^2y-xy^22. 不同类项的加法对于不同类项的加法，直接将它们按照位置进行相加即可。

例如：2x^2y+3xy^2+4xy-5y+ 3x^2y+6xy^2-2xy+8y= 5x^2y+9xy^2+2xy+3y三、整式的减法整式的减法与加法相似，只是减法需要将被减数取相反数，然后按照加法的规则进行计算。

例如：2x^2y-3xy+4y-5- (x^2y+2xy-3y+6)= 2x^2y-3xy+4y-5-x^2y-2xy+3y-6= x^2y-5xy+7y-11四、综合运用在实际运用整式的加减法时，需要综合运用多种运算法则。

例如：(3x^2y+5xy^2-2xy+7y) - (2x^2y-3xy+4y-5)= 3x^2y+5xy^2-2xy+7y-2x^2y+3xy-4y+5= x^2y+5xy^2-5xy+3y+2五、练习题1. 计算：(2x^2y-3xy+4y-5) + (x^2y+2xy-3y+6)2. 计算：(3x^2y+5xy^2-2xy+7y) - (2x^2y-3xy+4y-5)3. 计算：2x^2y+3xy^2+4xy-5y - (3x^2y+6xy^2-2xy+8y)4. 计算：(3x^2y+2xy^2-5x^2y-3xy^2) + (4x^2y-xy^2+2x^2y+3xy^2)六、总结与思考整式的加减法是基础中的基础，对学生来说需要理解清楚，并且在反复练习中掌握。

初一数学上册整式的加减知识点_知识点总结

初一数学上册整式的加减知识点_知识点总结在初一数学上册中，整式的加减是一个重要的知识板块，它为后续的数学学习打下了坚实的基础。

下面让我们一起来详细了解一下整式的加减的相关知识点。

一、整式的概念整式是代数式的一部分，代数式是由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子。

整式包括单项式和多项式。

单项式是只有一个项的整式，它由数字因数和字母因数的积组成，其中数字因数称为系数，所有字母的指数和称为次数。

例如，＼（5x\），系数是\（5\），次数是\（1\）；＼（－2xy^2\），系数是\（－2\），次数是\（3\）。

多项式是几个单项式的和，每个单项式叫做多项式的项，不含字母的项叫做常数项。

多项式里，次数最高项的次数，就是这个多项式的次数。

例如，多项式\（3x^2 2x ＋ 1\），有三项，分别是\（3x^2\）、＼（－2x\）、＼（1\），其中\（1\）是常数项，最高次项是\（3x^2\），次数是\（2\），所以这个多项式是二次三项式。

二、同类项同类项是指所含字母相同，并且相同字母的指数也相同的项。

几个常数项也是同类项。

例如，＼（3x^2y\）和\（－5x^2y\）是同类项，＼（7\）和\（－2\）是同类项。

判断同类项需要注意两个“相同”：一是所含字母相同；二是相同字母的指数也相同。

两个“无关”：一是与系数无关；二是与字母的排列顺序无关。

三、合并同类项把多项式中的同类项合并成一项，叫做合并同类项。

合并同类项的法则是：同类项的系数相加，所得的结果作为系数，字母和字母的指数不变。

例如，计算\（3x^2 ＋ 2x^2\），因为这两项是同类项，所以将系数相加，得到\（（3 ＋ 2)x^2 ＝ 5x^2\）。

四、去括号法则括号前是“＋”号，把括号和它前面的“＋”号去掉后，原括号里各项的符号都不改变；括号前是“”号，把括号和它前面的“”号去掉后，原括号里各项的符号都要改变。

例如，＼（a ＋（b c) ＝ a ＋ b c\），＼（a （b c) ＝ a b ＋ c\）。

数学七年级上册整式的加减知识点

数学七年级上册整式的加减知识点数学七年级上册整式的加减知识点主要包括以下内容：1. 整式的加法和减法：整式是由常数和字母按照乘法运算符号连接起来的表达式。

整式的加法和减法是指将同类项相加或相减，并保留结果中的同类项。

例如，对于整式3x^2 + 2xy + 5和2x^2 - 3xy + 6，进行加法运算时，将同类项相加得到：(3x^2 + 2xy + 5) + (2x^2 - 3xy + 6) = 5x^2 - xy + 11。

2. 合并同类项：在整式中，有时会出现相同的字母的幂次相同的项，这些项叫做同类项。

进行整式的加减运算时，需要将同类项合并，即将同类项的系数相加或相减，并保留相同的字母和幂次。

例如，对于整式2x^2 + 3x^2 + 4x^2，将同类项合并得到：2x^2 + 3x^2 + 4x^2 = 9x^2。

3. 去括号：在整式的加减运算中，如果遇到括号，需要先去括号。

可以使用分配律进行括号的去除。

例如，对于整式2(x + y) - 3x(x - y)，可以先去括号得到：2(x + y) = 2x + 2y，-3x(x - y) = -3x^2 + 3xy，然后再进行合并同类项或简化运算。

4. 提取公因式：在整式的加减运算中，如果遇到相同的公因式，可以将公因式提取出来。

公因式是指能够整除所有同类项的因式。

例如，对于整式4x^2 + 6xy，可以提取公因式2得到：4x^2 + 6xy = 2(2x^2 + 3xy)。

5. 消去同类项：在整式的加减运算中，如果遇到相反数的同类项，可以互相消去。

相反数是指具有相同绝对值但符号相反的数。

例如，对于整式5x + 2y - 3x - 2y，可以将同类项5x和-3x互相消去，将2y和-2y互相消去，最终得到：5x + 2y - 3x - 2y = 2x。

七年级上册数学整式的加减全章知识点总结

七年级上册数学整式的加减全章知识点总结第二章整式的加减知识点1：单项式的概念单项式是由数或字母的积组成的式子。

它只包含一种运算，即乘法，不能有加、减、除等运算符号。

单项式可以分为三种类型：数字与字母相乘组成的式子，如2ab；字母与字母组成的式子，如xy；单独的一个数或字母，如2，-a，m。

知识点2：单项式的系数单项式中的数字因数叫做这个单项式的系数。

系数可以是整数、分数或小数，并且可以是正数或负数。

对于只含有字母因素的单项式，其系数是1或-1，不能认为是0.表示圆周率的π，在单项式中应将其作为系数的一部分，而不能当成字母。

知识点3：单项式的次数一个单项式中，所有字母的指数和叫做这个单项式的次数。

计算单项式的次数时，应注意是所有字母的指数和，不要漏掉字母指数是1的情况。

单项式是一个单独字母时，它的指数是1，单项式是单独的一个常数时，一般不讨论它的次数。

单项式的指数只和字母的指数有关，与系数的指数无关。

知识点4：多项式的有关概念多项式是由几个单项式相加组成的式子。

多项式中的每个单项式叫做多项式的项。

不含字母的项叫做常数项。

多项式里次数最高项的次数叫做多项式的次数。

单项式与多项式统称整式。

B、一个多项式中的每一项都包含符号，例如多项式-2xy+6a-9共有三项，分别是-2xy，6a，-9.一个多项式中包含几个单项式，就称这个多项式为几项式，例如-332xy3+6a-9就是一个三项式。

C、多项式的次数不是所有项的次数之和，也不是各项字母的指数和，而是组成这个多项式的单项式中次数最高的那个单项式的次数。

例如多项式-2xy+6a-9由三个单项式-2xy，6a，-9组成，其中-2xy的次数最高，为4次，因此这个多项式的次数就是4.它是一个四次三项式。

对于一个多项式而言，没有系数这一说法。

1）书写含乘法运算的式子时，要注意省略乘号，数字与字母相乘时，数字必须写在字母的前面。

带分数要化成假分数。

2）书写含除法运算的式子时，结果一般用分数线表示。

人教版七年级上册数学《整式的加减》和《一元一次方程》知识点详细梳理

人教版七年级上册数学《整式的加减》和《一元一次方程》知识点详细梳理人教版七年级上册数学《整式的加减》知识点详细梳理一．用字母表示数(代数初步知识)1. 代数式：用运算符号“＋－ × ÷ …… ”连接数及表示数的字母的式子称为代数式.注意：用字母表示数有一定的限制，首先字母所取得数应保证它所在的式子有意义，其次字母所取得数还应使实际生活或生产有意义；单独一个数或一个字母也是代数式；用基本运算符号把数和字母连接而成的式子叫做代数式，如n,-1,2n+500,abc 。

2. 代数式书写规范：（1）数与字母相乘，或字母与字母相乘中通常使用“· ” 乘，或省略不写；（2）数与数相乘，仍应使用“×”乘，不用“· ”乘，也不能省略乘号；（3）数与字母相乘时，一般在结果中把数写在字母前面，如a ×5应写成5a ；（4）带分数与字母相乘时，要把带分数改成假分数形式，如a ×211应写成23a ；（5）在代数式中出现除法运算时，一般用分数线将被除式和除式联系，如3÷a 写成a3的形式；（6）a 与b 的差写作a-b ，要注意字母顺序；若只说两数的差，当分别设两数为a 、b 时，则应分类，写做a-b 和b-a .出现除式时，用分数表示；(7)若运算结果为加减的式子，当后面有单位时，要用括号把整个式子括起来。

3.几个重要的代数式：（m 、n 表示整数）（1）a 与b 的平方差是： a 2-b 2 ； a 与b 差的平方是：（a-b ）2；（2）若a 、b 、c 是正整数，则两位整数是： 10a+b ,则三位整数是：100a+10b+c ；（3）若m 、n 是整数，则被5除商m 余n 的数是： 5m+n ；偶数是：2n ，奇数是：2n+1；三个连续整数是： n-1、n 、n+1 ；（4）若b ＞0，则正数是:a 2+b ，负数是： -a 2-b ，非负数是： a 2 ，非正数是：-a 2 . 二．整式1.单项式：表示数与字母的乘积的代数式叫单项式。

初中数学《整式的加减》知识全解

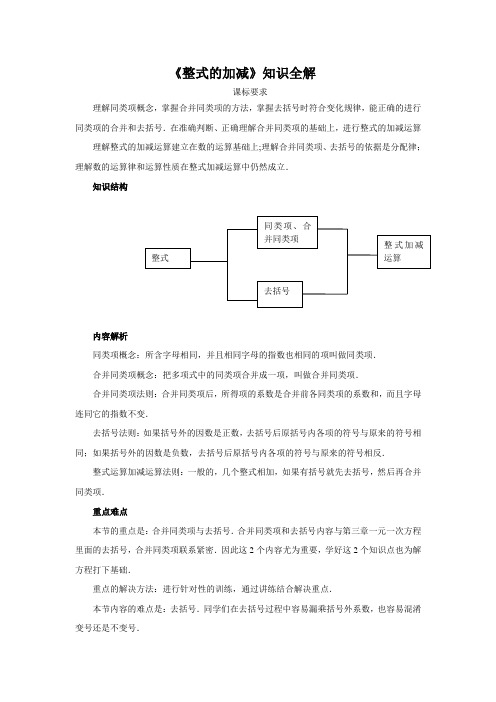
《整式的加减》知识全解课标要求理解同类项概念，掌握合并同类项的方法，掌握去括号时符合变化规律，能正确的进行同类项的合并和去括号．在准确判断、正确理解合并同类项的基础上，进行整式的加减运算理解整式的加减运算建立在数的运算基础上;理解合并同类项、去括号的依据是分配律；理解数的运算律和运算性质在整式加减运算中仍然成立．知识结构内容解析同类项概念：所含字母相同，并且相同字母的指数也相同的项叫做同类项．合并同类项概念：把多项式中的同类项合并成一项，叫做合并同类项．合并同类项法则：合并同类项后，所得项的系数是合并前各同类项的系数和，而且字母连同它的指数不变．去括号法则：如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同；如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反．整式运算加减运算法则：一般的，几个整式相加，如果有括号就先去括号，然后再合并同类项．重点难点本节的重点是：合并同类项与去括号．合并同类项和去括号内容与第三章一元一次方程里面的去括号，合并同类项联系紧密．因此这2个内容尤为重要，学好这2个知识点也为解方程打下基础．重点的解决方法：进行针对性的训练，通过讲练结合解决重点．本节内容的难点是：去括号．同学们在去括号过程中容易漏乘括号外系数，也容易混淆变号还是不变号．难点的解决方法是：不能简单的叫同学背去括号法则，要求同学们在理解的基础上背法则，也就是在教学过程中让学生体会去括号法则就是乘法分配律．理解透彻后再通过针对练习，开始时候设计简单点的题目，让学生练习时间久点．以达到边练边掌握法则．学法建议本节教学过程中教学中多用类比的思想方法学习式的运算，体现数式通性，利用学生数学的有关数的运算来学校整式的运算．使学生理解认识事物的过程是由特殊到一般，又由一般到特殊，不断重复中得到提高，培养学生初步的辩证唯物主义观点．本节在教学过程中必须抓好三个关键的环节．首先要使学生掌握同类项的概念，会辨别同类项，准确的掌握判断同类项的两条标准；其次要明确合并同类项的含义是把多项式中同类项合并成一项，经过合并同类项，多项式的项数会减少，这样多项式就得到了简化；最后，要明确合并是指同类项的系数相加，把得到的结果作为新的系数，要保持同类项的字母和字母的指数不变．去括号是对多项式变形，学习去括号时，括号的处理关键是让学生理解去括号．在教学过程中应该对教学重点加强练习．。

2022年数学七年级上册整式的加减知识点

数学七年级上册整式的加减知识点整式为单项式和多项式的统称，是有理式的一部分，在有理式中可以包含加，减，乘，除、乘方五种运算，但在整式中除数不能含有字母。

下面是我整理的数学七班级上册整式的加减学问点，仅供参考盼望能够关心到大家。

数学七班级上册整式的加减学问点整式①单项式：表示数或字母积的式子②单项式的系数：单项式中的数字因数③单项式的次数：一个单项式中，全部字母的指数和④几个单项式的和叫做多项式。

每个单项式叫做多项式的项，不含字母的项叫做常数项。

⑤多项式里次数最高项的次数，叫做这个多项式的次数。

⑥单项式与多项式统称整式。

整式的加减①同类项：所含字母相同，而且相同字母的次数相同的单项式。

②把多项式中的同类项合并成一项，叫做合并同类项。

③合并同类项后，所得项的系数是合并前各同类项的系数的和，且字母部分不变。

④假如括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同。

⑤假如括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反。

⑥一般地，几个整式相加减，假如有括号就先去括号，然后再合并同类项。

学校数学垂直平分线定理学问点性质定理：在垂直平分线上的点到该线段两端点的距离相等;判定定理：到线段2端点距离相等的点在这线段的垂直平分线上角平分线：把一个角平分的射线叫该角的角平分线。

定义中有几个要点要留意一下的，就是角的角平分线是一条射线，不是线段也不是直线，许多时，在题目中会消失直线，这是角平分线的对称轴才会用直线的，这也涉及到轨迹的问题，一个角个角平分线就是到角两边距离相等的点性质定理：角平分线上的点到该角两边的距离相等判定定理：到角的两边距离相等的点在该角的角平分线上数学的学习思维方法公式法运用定律、公式、规章、法则来解决问题的方法。

它体现的是由一般到特别的演绎思维。

公式法简便、有效，也是孩子学习数学必需学会和把握的一种方法。

但肯定要让孩子对公式、定律、规章、法则有一个正确而深刻的理解，并能精确运用。