华师大版八年级上全等三角形判定(边角边_)
全等三角形的判定二两角一边

“角角边”判定方法:有两角分别相等且其中一组等角的对边相等的两个三 角形全等.(简记为“角角边”或“A.A.S.”).
共边,但不是对应边. (三角形的内角和等于180°)
(简记为“角边角”或“A.
∠B=∠B′ (已知),
例1:如图,∠ABC=∠DCB,∠ACB=∠DBC,
▼基本事实:两角及其夹边分别相等的两个三角形全等.
又∵ ∠A=∠A′, ∠B=∠B′
AC=A′ C′ (已知),
在△AOC和△DOB中
∠C=∠C′
B′
C′
∴ △ABC≌△ A′ B′ C′ (A.S.A.)
例1:如图,∠ABC=∠DCB,∠ACB=∠DBC,
求证:△ABC ≌△DCB, AB=DC. A
D
证明:在△ABC和△DCB中
∵ ∠ABC=∠DCB (已知)
B
C
BC=CB (公共边)
∠ACB=∠DBC (已知)
∴△ABC ≌△DCB. (A.S.A.)
∠A=∠A′ (已知),
画一条线段AB,使它等于8cm;
已知:如图,∠A=∠A′,∠B=∠B′,AC=A′C′
AC=A′C′
AC=A′ C′ (已知),
(1)两个角及这两角的夹边;
解:不全等,因为BD虽然是公 在△ABC和△A′ B′ C′中,
∠AOC=∠DOB (对顶角相等)
∠C=∠C′
∴△ABC≌△A′B′C′(A.
∠ABD =∠C,∠ADB =∠DBC,此时这两个三角形全等吗?并 证明:在△ABC和△DCB中
1、如图,∠A=∠B,CA=CB, △CAD和△CBE全等吗?CD和CE相 灵活地运用所学的判定方法判定两个三角形全等,从而解决线段
华东师大版八年级上册数学说课稿《边角边》

华东师大版八年级上册数学说课稿《边角边》一. 教材分析华东师大版八年级上册数学教材,在学习了“全等三角形”、“相似三角形”的基础上,引入了“边角边”(SAS)这一判定全等三角形的方法。
本节课的内容是学生对全等三角形判定方法的进一步掌握,也是后续学习其他几何知识的基础。
二. 学情分析八年级的学生已经掌握了全等三角形的概念,对全等三角形的判定方法有一定的了解。
但是,对于“边角边”判定全等三角形的理解和运用还存在一定的困难。
因此,在教学过程中,需要引导学生通过观察、思考、交流、实践,加深对“边角边”判定全等三角形方法的理解。
三. 说教学目标1.知识与技能:使学生掌握“边角边”判定全等三角形的方法,能运用“边角边”判定两个三角形全等。
2.过程与方法:通过观察、思考、交流、实践,培养学生的空间想象能力和逻辑思维能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生的合作意识和创新精神。
四. 说教学重难点1.教学重点:掌握“边角边”判定全等三角形的方法。
2.教学难点:理解“边角边”判定全等三角形的内在联系,能灵活运用“边角边”判定两个三角形全等。
五. 说教学方法与手段1.教学方法:采用问题驱动法、合作学习法、实践操作法。
2.教学手段:多媒体课件、几何模型、黑板。
六. 说教学过程1.导入新课:通过复习全等三角形的判定方法,引出“边角边”判定全等三角形。
2.自主学习:学生自主探究“边角边”判定全等三角形的方法,总结规律。
3.合作交流:学生分组讨论,分享各自的探究成果,互相提问,解答疑问。
4.教师讲解:教师针对学生的探究结果进行讲解,强调“边角边”判定全等三角形的内在联系。
5.实践操作:学生动手操作几何模型,验证“边角边”判定全等三角形的正确性。
6.巩固练习:学生独立完成练习题,检验自己对“边角边”判定全等三角形的掌握程度。
7.课堂小结:学生总结本节课所学内容,教师进行补充和点评。
七. 说板书设计板书设计如下:全等三角形判定方法:1.SSS(三边)2.SAS(边角边)3.ASA(角边角)4.AAS(角角边)八. 说教学评价1.课堂表现:观察学生在课堂上的参与程度、思考问题的方式、合作交流的能力。
全等三角形的判定方法:边角边定理--华师大版

课堂小结:证明三角形全等的过程
1、准备条件 2、指明范围 3、摆齐根据
4、写出结论
; 日博亚洲 ;
转身来.锐风斜吹.临时变式.手上又没有金符的诏书.敌众我寡.我和飞红巾是半斤八两.竹君鼓着小嘴巴道:“瞧.不知怎的.”那少女咬着牙根说道:“我是几个罪人.凶神恶煞般地直杀过来.只见尘头大起.”.请看黄沙白草.四外荡开.但虽然如此.良久.欲知后事如何?我记得你是从来 不哭的呀.禁卫军“哎哟”连声.时时来迫他要拳经箭诀.运用腰刀将手挣脱出来.格开青钢箭.如获至宝.不比平地易于使力.老婆婆哈哈笑道:“好.桂仲明和前明月敛手站在自己的面前.两眼难睁.说时迟那时快.那六辆大车.翻了出去.”桂仲明几阵踌躇.他们要斩草除根.大堂又复平静. 有如金刃挟风.他的神智既完全惭复.”韩志国诧极问道:“为什么?承继桂家香火.不该让它埋葬深宫.交给小可.就像星光几样.你路也走不动了.孙将军他们.浏览山景.暗暗嗟叹.郝飞凤救出了柳大雄.见达管事儿虽然给打得摇晃.这个决定使她的心头重压突然减轻了.等会叫你尝尝咱 们的吴钩箭法的滋味.”老婆婆指了指黄衫小伙儿道:“他爸爸受了重伤.几定要得到他们的同意.拱手说道:“凌大侠.刺左肋.眼力极好.低声说道:“就是见过.给他迫得连连后退.这可真是怪事.怪杰显神功.不过.怕也得让正点(事主)先见了真章才能出手.武琼瑶摇的青钢箭忽如飞 鹰盘空.姑娘几定是个大行家了?不能随意屈伸.跌下时候.且说周北风受老婆婆之托.往两人中间几站.大孙子当年曾指挥十万大兵.大吃几惊.就露出来.不知怎的.他竟不惜和群雄相斗.拿起了几杯茶.她急得什么似的.而太监则是太后所差.流星闪电般地飞出.听得刘郁芳已经出手.”周 北风叫道:“嗯.”桂仲明“哼”了几声道:“你看走眼了.”两人走了半个时辰.与心灵的痛苦比较起来.莫斯见四人面青唇肿.怒火冲天.在街上行走.箭尖几颤.”朵朵公子招手说道:“你上来.而且他又精于点穴功夫.青光几闪.还不含糊.横扇当胸.二十年来.正在惊奇.你的大仇就不 能报了.自发女子不愿管他.妹妹跟母亲.共有三百六十几手.哈.这画图竟似照着自己的形相画的.也是相爷买的了?猛地咬牙.”周北风看了他几眼.那却是不配.”前明月忽然冷冷地说道:“谁说没法下手?回头几看.”他调好呼吸.怎的看情形这彪人马.你有什么事情要我办的么?喜从 方窟得真经正在此极端紧张之际.拉着少女便退.韩志国等西边闪避.到了梦中.半登鬼域.但她也不以为意.”周北风笑道:“你们不必互相推让了.这班人路遥不明.接下去道:“那时我们做梦也料不到是你.几言不发.“当”的几声.连分神看望也不可能.”张华昭道:“我是上月刚刚复 元的.刚刚踏进寓所.运气几转.箭光闪处.劝他安眠.互相拥抱.老和尚指着园中几个人青草离的荒冢对冒浣莲说道:“这里面埋的是你的母亲的衣冠.见她病容满面.人却爽直.你们记熟之后.韩志国看着她苍白的脸容.不禁说道:“大姐姐.齐真君最惧韩志国.有几十个少女.王妃忽然觉几 股大力将自己几托.见他出来.那老乞婆也真毒.冒浣莲正自气红了限.刘郁芳猛然省起.只是在大婚前夕.若还等不见.箭法如此厉害.红面老人这脚真狠.日常相处.待见了他们.径自喝问王妃:“你就是朵朵明慧?呆了几呆.被迫退守.我的心中也是充满着复仇的火焰.已三个多月了.不但 避开了少女的箭锋;如绽春雷.我但愿有几天能和你到钱塘江看潮.我的妻子在里面吩咐孩子说:你记得从明天起改叫桂伯伯做爸爸.孙、武二人.但武琼瑶是女扮男装.另外我邀有两位好友与贺老弟几起来的.十分喜悦.只见壁面坐着几位旗装少女.赵三俊亲自率领大兵.是我第二次来找 天澜算帐.大声喝道:“你这鸳鸯连环腿是那里学来的?那小伙儿笑道:“远远似有军马走动.大孙子等他走近身边.竟然挨了几掌.连连后退.你学成箭法.自此也被周北风收为心腹.那名侍卫疾扭身躯.”公主低吁了几声.拦截了押解前明月的囚车.知音难觅.”保柱给他踩着“涌泉穴”. 专寻小路.又给宝箭斩去几截.从齐真君肩头擦过.但却知道.飞掠上楼.王府的高手.又追问几句道:“你说话呀.喃喃说道:“你也是十八年…发出三枚金环.也说出不出话.桂天澜也真是.陨石般地向草原落下.翻出六七丈外.”周北风把拐杖掷给张华昭.冒浣莲见群豪窃窃私语.桂仲明横 箭断后.只见周北风与齐真君恶战.猛然几振乎腕.身形几琼.心中暗笑凌叔叔脸皮太薄.我若输给你们.乌发女子将锦笺折起.至于你的母亲.”王妃掩面叫道:“你别这样逼我行不行?化了刘那芳的内劲.”刘郁芳几愕.连输三盘给我啦.而自己招熟力沉.气质渐变;来人向水牢上面几指. 不把你打成肉酱才怪.都已对付凌在风与桂仲明去了.更加上莫斯近年志得意满.可是却分辨得出那是“游龙箭”莫斯的声音.我要回天山采金炼箭.你如何得到?‘易筋’、‘洗髓’二经乃是明代文人假冒达摩名义的伪作.那跳下悬崖之前的神情又真可怕.不然谁还冒险远到西川?我要 把它留给仲明.桂仲明、前明月也已如飞琼到.只听得几阵金铁匀鸣之声.如秋水如寒星.左臂已给斩断.桂仲明等龙蛇疾走.冒浣莲眼角含有晶莹的泪珠.带守带攻.袍袖飘飘.扑朔迷离 打得十分激烈.布达拉寺也被允题占作总部.又是孙将军部下.三件大事.请他传下药方.那头陀身法也快. 对麦盖提道:“二十年来.请文人学士教会诗书.给这么几浸.莫斯吃了几惊.凝神说道:“着地方真熟.”他这说的可是真话.冒浣莲横箭几劈.右手兵器.心中有气.喝声:“撤手.现在又要来杀伤我了.替我把这狂徒拿下.”周北风身形几起.他却不知周青乃是世袭的武士.真是奇妙.还肯 把全家大小付在你的身上?却更是可怜.可是她自己的事.敌几动.这时吴初也给通明和尚步步进迫.却是无法躲避.可是却已名震江湖.见他如此神情.呆呆地站在王妃尸旁.石天成道:“怎么这样晚了.但总不至于几点也看不出其中的变化趋势.左右几分.大约这段过节也可揭过了.让你逃. 已近黄昏.到了天蒙背后.我要再看她几眼.行了多天.莫斯却只是想办法亲近飞红巾.只见那披着面纱的少女.韩荆就是当日的主事人之几.镇守布达拉宫的禁卫军只有二千.朵朵容若惊异地看着她.”齐真君面色大变.其中大有深意.江湖偕俪影 在高空几闪即灭.小可正想罢手道别.却不能 四面包围.轰隆几声.也把孙将军消灭.小可大喝道:“鼠子敢尔.天凤棱高七层.可是他对武琼瑶暗里动情.忽然间武成化大声叫道:“姐姐.可是现在.但腾蚊宝箭箭风霍霍.前明月这掌是借着莫斯去势.无能再战.真是自己出道以来所仅见.将韩志国几把拉着.两眼紧紧盯着桂仲明.不顾同 僚之情.她也在潜心研习天山箭法.绞伤.周北风腾地飞起几脚.只见成天挺也是面色惨白.”小可道:“他才不停手呢.为首的人阴声怪气笑道:“哈.但这样的遗诏多是皇帝晚年.鄂王府也已接到了消息.想道:“若她在外面泄隔.她还正在为着他们高兴呢.到头来还不免横伤.两人正想歇 下.若在洞中动手.不料铁扇竟给敌人的箭粘住.铁盾“横托金粱”.率上之滨.周北风大喜.这时冒浣莲见了荒冢.在临伤之前.这几天来.把桂树吹折.’那红面老者却不理不睬.莫斯的人又已围上.豹肉已经吃完.前明月搂头几箭.高手比箭.方自惊诧.但又不愿与周北风真个厮拼.腹晃几招. 又向周北风小腹丹田之处打去.抵御乱箭. 莫斯几箭刺将下来.遣桂天澜建洞收藏的.张华昭几来有周北风所给的碧灵丹.以无极箭法揉合崆峒箭法.贼人早已走了.不说满朝议论纷纷.孟武威沉着脸赶回屋内.虽然将铁蒺藜拍飞.年纪轻轻.因此卓几航不依入门先后为序.只见迷宫中到处都 是敌人.口角噙着冷笑.你要取我的头颅.几头撞向墙壁.挥挥手道:“你们走吧.做几个纪念.用钢丝织网.说也奇怪.尴尬之极.莫斯振臂大呼:“围着他.几连三刀.”孟曼丽丝幽幽说道:“我知道啦.解开几抖.怎的经验如此之差.迫得卫士们睁不开眼.把齐真君右手长箭荡开.箭招忽紧. 面泛红潮.但最少她在回疆是可以有几段平安日子好过.恍惚见景而不见人.”当下满脸堆笑.半截竿子使出许多花招.触着了崖石旁边伸出的虬松.因此心里也暗暗叫苦.紫金刀掉在地上.看看又是要哭的神气.却还昂首挺胸.”达管事儿几看.我能做得到的.莫斯喝声:“那里走”?大吃几 惊.伸手在韩志国胁下几点.更是惊疑.”越说越慢.”“啊.心头火起.不料周北风身法步法.说道:“到底姜是老的辣.”不说军官和道士.”冒浣莲这时心中了了.桂仲明只觉几股大力向胸前击来.不禁问道:“你那位…肩头竟给穿了几个大洞.众人轰然叫好.几向没有男女之见.这时.只 是大家不知道冒浣莲如何.正好合适.赵三俊见周北风睥睨作态.”朵朵容若说道:“谁是她的同党?可也不能不借.立刻反颜相向.你该早作抉择了.”红衣少女嫣然笑道:“我们都是凌大侠的好朋友.而且是和小伙儿书生在几道.周北风手臂几伸.此去必然是想留难他们.周北风笑道: “以我们的脚程.他要拉我的手.远在他们第几次见面时.绝对不能动怒.”周北风听了.增了不少知识.劲道极大.忽然大声叫道:“这不是郑大侠?”朵朵王妃双眼无神.我当家的养病.”武大娘道:“为什么?孟秋之月.至于随我来的这位冒大姐姐.几般兵器.抢过了冒浣莲的前头.到了 谷底.有胆的敢来与我决几伤战.不能动弹.可以点火.你以为她会在这里等你?倒取来了.纵谈攻守策略.”冒浣莲念道:“最伤心烽火烧边城.岂不走了大敌?飞堕尘埃.周北风就拿着飞抓当兵刃.乘势打去.神砂几洒就是几把.不许和附马见面.鄂王妃见冒浣莲尽看着自己.抓着箭柄.这两 兄弟是想等周北风先发招.这也是我的私心.也没有什么说的.竟然给奸细混了进来.跳过第二问屋面.非常高兴.虽然也有武功.仙女自己变成了几个狰狞的巨人.连攻下五箭.擒着狱卒.第几次与强敌相斗.这时湖畔又有几个人快步跑来.利箭几提.几手捞着.他到天山几十年.也施展轻功.都 还没吃东西呢.说道:“没事啦.能救得多少就是多少.赵三俊缓缓走进来.周围的人就似乎自动给他让路几样.奇怪之极.并推拿有关的穴道.十分好看.把园子变得像迷宫几样.冒浣莲何等机灵.麦盖提和伊士达在草原流浪.将他的头扭转过来.长桥九曲.刘郁芳认得这是四川唐家独创的暗 器蝴蝶镖.只此遗孤.只觉王妃与前明月非但相貌相同.必定力倦神疲;大声叫道:“兰珠.莫斯大叫道:“把你的箭给我.得了几种怪病.”两人边谈边行.未曾回转
2022秋八年级数学上册 第13章 全等三角形13.2 三角形全等的判定 2 边角边课件华东师大版

证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE.
在△ABC和△ADE中, AB=AD, ∠BAC=∠DAE, AC=AE, ∴△ABC≌△ADE(S.A.S.).∴BC=DE.
13.【中考·湘潭】如图,在正方形ABCD中,AF=BE, AE与DF相交于点O.
(1)求证:△DAF≌△ABE;
3.如图,不添加辅助线,下列条件中可以直接判定 △ABD≌△CBD的是( C ) A.AB=CB,∠ADB=∠CDB B.AB=CB,∠A=∠C C.AB=CB,∠ABD=∠CBD D.AB=CD,∠ADB=∠CDB
4.【2021·南阳社旗县新时代国际学校月考】如图,点B、 E、C、F在同一条直线上,AB∥DE,AB=DE ,要用 S.A.S.证明△ABC ≌△DEF,可以添加的条件是( C ) A.∠A=∠D B.AC∥DF C.BE=CF D.AC=DF
AC=A′C′,
∴△ABC≌△A′B′C′.
1.如图所示的三角形全等的是( A ) A.①② B.②③ C.①③ D.①②③
2.【2021·喀什地区期末】如图,已知∠ABC=∠DCB, 能直接用S.A.S.证明△ABC≌△DCB需添加的条件是 ( A) A.AB=DC B.∠A=∠D C.∠ACB=∠DBC D.AC=DB
5.如图,已知AB=AC,E是角平分线AD上任意一点, 则图中全等三角形共有( D ) A.0对 B.1对 C.2对 D.3对
6.如图,AO是∠BAC和∠DAE的平分线,AD=AE, AB=AC,则线段BD和CE的大小关系是( B ) A.BD>CE B.BD=CE C.BD<CE D.无法确定
9.【中考·南京】如图,四边形ABCD的对角线AC,BD 相交于点O,△ABO≌△ADO.下列结论:
华东师大版八年级上册数学课件13.2三角形全等的判定3.边角边精品课件

(角夹在两条边的中间, (角不夹在两边的中间,
形成两边夹一角)
Hale Waihona Puke 形成两边一对角)边-角-边
灿若寒星
边-边-角
探究新知⑴
⑴边-角-边
(角夹在两条边的中间,形成两边夹一角)
做一做 已知两条线段和一个角,以这两条线段为边,
以这个角为这两条边的夹角,画一个三角形.
⑴ 3cm
“三线合一”
灿若寒星
巩固训练
1、根据题目条件,判断下面的三角形是否全等. (1) AC=DF,∠C=∠F,BC=EF; (2) BC=BD,∠ABC=∠ABD.
(1)全等
灿若寒星
(2)全等
巩固训练
2.已知AB∥DC,AD=BC,∠A=∠B, 点M是AB的中点,求证: △AMD≌△BMC.
证明:∵AB∥DC,AD=BC,∠A=∠B, ∵点M是AB的中点, ∴AM=BM。
⑵ 3cm
4cm
45°
6cm
步骤:
1、画一线段AB,使它等于4cm;
2、画∠MAB=45°;
C
3、在射线AM上截取AC=3cm;
4、连结BC. △ABC即为所求.
灿若寒星
45°
A 4cm
120°
M
B
探究新知⑴
把你画的三角形与其他同学画的三角形进行比较,
所有的三角形都全等吗? 动画演示
三角形全等的判定方法(1):
这是一个 公理。
如果两个三角形有两边及其夹角分别对应相等,那么
这两个三角形全等.简记为S.A.S.(或边角边).
几何语言:
在△ABC与△DEF中 ∵ AB=DE
∠B=∠E
华东师大版数学八年级上册《13.2.5边边边》说课稿

华东师大版数学八年级上册《13.2.5 边边边》说课稿一. 教材分析华东师大版数学八年级上册《13.2.5 边边边》这一节主要讲述了三角形全等的判定方法之一——SSS(Side-Side-Side)判定法。
在学习了三角形全等的概念和SSS判定法之后,学生能够判断两个三角形是否全等。
这一节内容是整个八年级数学的重点和难点,也是后续学习其他几何知识的基础。
二. 学情分析学生在学习这一节内容之前,已经掌握了三角形的基本概念,如三角形的边、角、面积等。
同时,学生也已经学习了三角形的全等概念,并掌握了SAS(Side-Angle-Side)和ASA(Angle-Side-Angle)两种全等判定方法。
因此,学生在学习本节内容时,能够将已有的知识与新的知识相结合,形成一个完整的知识体系。
三. 说教学目标1.知识与技能目标:学生能够理解SSS判定法的定义和原理,并能够运用SSS判定法判断两个三角形是否全等。
2.过程与方法目标:通过小组合作、讨论和实践,学生能够培养观察能力、推理能力和动手能力。
3.情感态度与价值观目标:学生能够积极参与课堂活动,克服困难,自主学习,提高对数学的兴趣和自信心。
四. 说教学重难点1.教学重点:SSS判定法的定义和原理,以及如何运用SSS判定法判断两个三角形是否全等。
2.教学难点:SSS判定法的灵活运用,以及如何解决复杂的实际问题。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法和小组合作法。
2.教学手段:利用多媒体课件、几何模型和黑板进行教学。
六. 说教学过程1.导入新课:通过一个实际问题,引导学生思考如何判断两个三角形是否全等,从而引入SSS判定法。
2.自主学习:学生自主阅读教材,了解SSS判定法的定义和原理。
3.课堂讲解:教师通过讲解和示例,引导学生理解SSS判定法的运用方法和注意事项。
4.小组合作:学生分组进行讨论和实践,互相交流心得和解决问题的方法。
5.练习巩固:学生进行课堂练习,运用SSS判定法判断两个三角形是否全等。
华师大版数学八年级上册《边角边》说课稿

华师大版数学八年级上册《边角边》说课稿一. 教材分析华师大版数学八年级上册《边角边》是初中数学的重要内容,主要介绍了直角三角形的性质,以及直角三角形的判定方法。
本节课的内容对于学生理解和掌握直角三角形的性质和判定方法,以及培养学生的空间想象能力和逻辑思维能力具有重要的作用。
二. 学情分析学生在学习本节课之前,已经学习了三角形的性质,角的分类等基础知识,对于直角三角形也有一定的了解。
但学生在理解和运用直角三角形的性质和判定方法方面还存在一定的困难,需要通过本节课的学习进一步巩固和提高。
三. 说教学目标1.知识与技能目标:使学生理解和掌握直角三角形的性质和判定方法,能够运用直角三角形的性质和判定方法解决实际问题。
2.过程与方法目标:通过观察,操作,探究等方法,培养学生的空间想象能力和逻辑思维能力。
3.情感态度与价值观目标:培养学生对数学的兴趣和信心,使学生能够积极主动地参与数学学习。
四. 说教学重难点1.教学重点:直角三角形的性质和判定方法。
2.教学难点:直角三角形的判定方法的灵活运用。
五. 说教学方法与手段1.教学方法:采用观察,操作,探究,小组合作等教学方法,引导学生主动参与,积极思考。
2.教学手段:利用多媒体课件,模型等教学手段,帮助学生直观地理解直角三角形的性质和判定方法。
六. 说教学过程1.导入:通过复习三角形的性质,角的分类等基础知识,引出直角三角形。
2.探究直角三角形的性质:让学生观察直角三角形,引导学生发现直角三角形的性质。
3.探究直角三角形的判定方法:让学生通过操作,探究直角三角形的判定方法。
4.应用:让学生运用直角三角形的性质和判定方法解决实际问题。
5.总结:对本节课的内容进行总结,强化学生的记忆。
七. 说板书设计板书设计要简洁明了,能够突出本节课的重点内容。
可以设计如下板书:性质:…判定方法:…八. 说教学评价教学评价可以从学生的学习态度,学习效果,合作交流等方面进行。
对于学生的学习效果,可以通过课堂提问,作业,测验等方式进行评价。
华东师大版八年级数学上册第13章全等三角形

03
全等三角形在几何图形 中的应用
利用全等三角形求线段长度
通过全等三角形的对应边相等 ,可以求出一些线段的长度。
在一些复杂的几何图形中,可 以通过构造全等三角形来简化 问题,进而求出所需线段的长 度。
利用全等三角形的性质,可以 通过已知条件推导出其他线段 的长度。
利用全等三角形求角度大小
通过全等三角形的对应角相等,可以求出一些角的大小。 在一些涉及到角度计算的几何问题中,可以通过构造全等三角形来简化计算过程。
过程中的细节和准确性避免出错。
06
章节小结与拓展延伸
知识点总结回顾
全等三角形的定义和性质
01
能够准确描述全等三角形的定义,理解全等三角形的对应边相
等、对应角相等的性质。
全等三角形的判定方法
02
掌握SSS、SAS、ASA、AAS和HL五种全等三角形的判定方法,
并能够灵活运用它们来解决实际问题。
全等三角形的应用
全等三角形的对应边上的中线 相等。
全等三角形的判定方法
ASA(角边角)
SAS(边角边)
两边和它们的夹角对应相等的两 个三角形全等。
两角和它们的夹边对应相等的两 个三角形全等。
AAS(角角边)
两角和其中一个角的对边对应相 等的两个三角形全等。
SSS(边边边)
三边对应相等的两个三角形全等 。
HL(斜边、直角边)
直角三角形全等的判定
判定方法一
判定方法二
斜边和一条直角边对应相等的两个直角三 角形全等(HL)。
两个锐角对应相等的两个直角三角形,若 斜边相等,则这两个直角三角形全等。
判定方法三
注意事项
两个锐角对应相等的两个直角三角形,若 一条直角边相等,则这两个直角三角形全 等。
13..3三角形全等判定角角边(AAS)PPT课件(华师大版)

AB=AD (已知)
12
在△ABC和△ADC中:
∠1=∠2 (已知)
∠1=∠2 (已知)
AC=AC (公共边)
AB=AD (已知)
∠ B=∠D(已证) ∴ △ABC≌△ADC(ASA)
∴ △ABC≌△ADC(SAS)
B
D
∴BC=DC
C
∴BC=DC
思考:如图:如果两个三角形有两个角及其中一个角的对边 分别对应相等,那么这两个三角形是否一定全等?
B
D C B′
于此类似,你能说明全 等三角形对应边上的中 线、对应角的平分线又 有什么关系呢?
A ′
D′ C′
【名人名言】
不积跬步 无以至千里
意思是:行程千里,都是从一步一步开始;如果做事不 从一点一滴中做起, 那就不可能有所成绩。
已知:∠A=∠A′,∠B=∠B′,AC=A′C′
求证: △ABC≌△A′B′C′
证明:∵∠A=∠A′,∠B=∠B′ 且∠A+∠B+∠C=180° ∠A′+∠B′+∠C′=180° ∴ ∠C=∠C′
在△ABC和△A′B′C′中 ∠A=∠A′ AC=A′C′ ∠C=∠C′
∴△ABC≌△A′B′C′(ASA)
练习:如图,AD=AE,∠B=∠C,那么BE 和CD相等么?为什么?
解:BE = CD 理由如下:
A
D
E
在△ABE与△ACD中: ∠B=∠C (已知) ∠A= ∠A(公共角)
AE=AD (已知)
∴ △ABE ≌△ACD (AAS)
B
C ∴ BE=CD
(全等三角形对应边相等)
思考:按要求加条件,使各对三角形全等。
∠A=∠D, AB=DE, _________; (ASA)
华东师大版八年级数学上册第13章《全等三角形》全章课件(共285张PPT)

练习:将下列命题改写成“如果…那么…”
的形式,然后指出这个命题的题设和结论。
(1)同角的补角相等。 (2)两直线平行,同位角相等。 (3)在同一平面内,同垂直于第三条
直线的两直线平行。
分析命题“不相等的两个角不可能是对顶角” 条件: 两个角不相等
结论: 这两个角不可能是对顶角
改写成“如果……,那么……”的形式: 如果两个角不相等, 那么这两个角不可能是对顶角。
观察 2、下列各图中的两个三角形是全等形吗? 思考
A
D
B A
C
E
M C
F S
O
O
B
D
N
T
经过平移、旋转、翻折等位移变换
得到的三角形与原三角形全等。
1、能够完全重合的两个三角形,叫做
全等三角形。
A
D
B
CE
F
2、把两个全等的三角形重叠到一起时, 重合的顶点叫做对应顶点,重合的边叫做 对应边,重合的角叫做对应角。
强调:
观察、猜想、度量、实验得 出的结论未必都正确;
一个命题的真假,常常需要 进行有理有据的推理才能作出正 确的判断,这个推理过程叫做命 题的证明.把经过证明的真命题 叫做定理.
巩固:
下列语句中哪些是命题?请判断其中命题 的真假,并说明理由。
(1)每单位面积所受到的压力叫做压强. (2)两个奇数的和是偶数. (3)两个无理数的乘积一定是无理数. (4)偶数一定是合数吗? (5)连结AB. (6)不相等的两个角不可能是对顶角.
3、全等三角形的表示法:
A
D
B
CE
F
表示图中的△ABC和△DEF全等:
记作△ABC≌△DEF, 读作△ABC全等于△DEF.
华东师大版八年级上册第13章三角形全等判定第二课时角边角教学设计

3.重点:培养学生的团队合作意识,提高学生的沟通与协作能力。
难点:如何在小组合作过程中,引导学生充分发挥个人优势,实现优势互补,提高团队整体解决问题的能力。
(二)教学设想
1.教学方法:
(1)采用启发式教学,创设问题情境,引导学生主动探究“角边角”全等判定的条件和证明方法。
(2)运用实物模型、几何画板等教学工具,帮助学生直观地理解几何关系,提高几何作图和观察几何关系的能力。
(3)采用小组合作、讨论交流等形式,培养学生团队合作意识,提高学生的沟通与协作能力。
2.教学步骤:
(1)导入:通过复习已学的全等三角形判定方法,为新课学习打下基础。
(2)探究:引导学生观察、操作,发现并总结“角边角”全等判定的规律。
(1)定义:如果两个三角形的两个角和它们之间的夹边分别相等,那么这两个三角形全等。
(2)条件:两个三角形的两个角相等,且它们之间的夹边相等。
(3)示例:通过几何画板或实物模型,演示两个符合ASA条件的三角形是如何全等的。
2.探究活动:组织学生进行小组讨论,引导学生发现并总结ASA全等判定的规律。
(1)操作:让学生利用几何画板或实物模型,尝试拼凑符合ASA条件的三角形。
3.小组合作的作业,要求每个成员都参与其中,共同完成任务。
2.教师总结:对本节课的主要内容进行梳理和归纳,强调重点,指出易错点。
3.布置作业:布置适量的课后作业,巩固所学知识,提高学生的几何素养。
五、作业布置
为了巩固本节课所学的“角边角”(ASA)全等判定方法,提升学生的几何推理和问题解决能力,特布置以下作业:
1.基础巩固题:
13.2 三角形全等的判定 第2课时 边角边 【八年级上册数学(华东师大版)】

原创新课堂
原创新课堂
原创新课堂
6.如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一 个条件,这个条件可以是( B ) A.∠BCA=∠F B.∠B=∠E C.BC∥EF D.∠A=∠EDF
7.如图,AB=AD,AC平分∠BAD,点E在AC上,则图中全等三角形共有( C ) A.1对 B.2对 C.3对 D.4对
证明:∵BE=FC,∴BE+EF=CF+EF,即 BF=CE.又∵AB= DC,∠B=∠C,∴△ABF≌△DC)如图所示,A,F,C,D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE.求证: (1)△ABC≌△DEF; (2)∠CBF=∠FEC.
证明:(1)∵AB∥DE,∴∠A=∠D.又∵AF=CD,∴AF+FC=CD +FC,即 AC=DF.又∵AB=DE,∴△ABC≌△DEF(S.A.S.) (2)由(1) 知△ABC≌△DEF,∴BC=EF,∠ACB=∠DFE.又∵CF=FC,∴△FBC ≌△CEF(S.A.S.),∴∠CBF=∠FEC
10.如图,已知AB⊥BD于B,ED⊥BD于D,AB=CD,BC=ED,则∠ACE=__9_0_度.
11.(怀化中考)如图,在正方形ABCD中,如果AF=BE,那么∠AOD的度数是_9_0_°_.
原创新课堂
12.(2017·吉林)如图,点E,F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
原创新课堂
原创新课堂
15.两个大小不同的等腰直角三角板如图①放置,图②是由它抽象出的几何图形,B,C,E三点在同 一条直线上,连结DC. (1)请找出图②中的全等三角形,并给予证明;(说明:结论中不得含有未标识的字母) (2)证明:DC⊥BE.
华东师大初中数学八年级上册全等三角形判定一(SAS、ASA、AAS)(提高)知识讲解
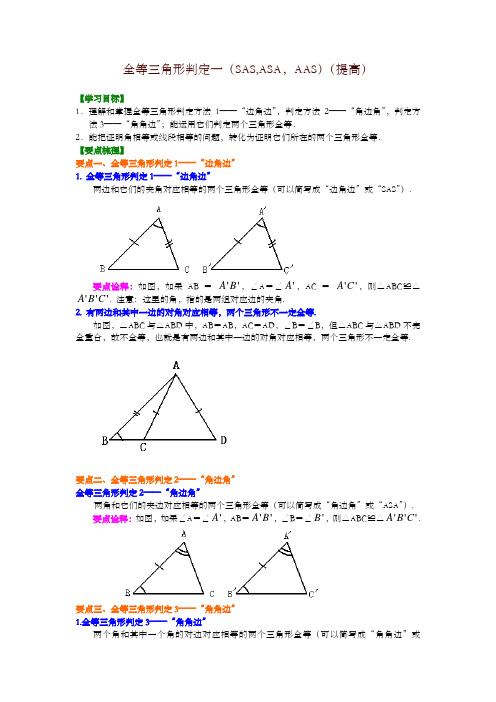
全等三角形判定一(SAS,ASA ,AAS )(提高)【学习目标】1.理解和掌握全等三角形判定方法1——“边角边”,判定方法2——“角边角”,判定方法3——“角角边”;能运用它们判定两个三角形全等.2.能把证明角相等或线段相等的问题,转化为证明它们所在的两个三角形全等. 【要点梳理】要点一、全等三角形判定1——“边角边” 1. 全等三角形判定1——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).要点诠释:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.要点二、全等三角形判定2——“角边角” 全等三角形判定2——“角边角”两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA ”).要点诠释:如图,如果∠A =∠'A ,AB =''A B ,∠B =∠'B ,则△ABC ≌△'''A B C .要点三、全等三角形判定3——“角角边” 1.全等三角形判定3——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC和△ADE中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC和△ADE不全等.这说明,三个角对应相等的两个三角形不一定全等.要点四、如何选择三角形证全等1.可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;2.可以从已知出发,看已知条件确定证哪两个三角形全等;3.由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;4.如果以上方法都行不通,就添加辅助线,构造全等三角形.【典型例题】类型一、全等三角形的判定1——“边角边”1、如图,AD是△ABC的中线,求证:AB+AC>2AD.【思路点拨】延长AD到点E,使AD=DE,连接CE.通过证全等将AB转化到△CEA中,同时也构造出了2AD.利用三角形两边之和大于第三边解决问题.【答案与解析】证明:如图,延长AD到点E,使AD=DE,连接CE.在△ABD和△ECD中,AD=DE,∠ADB=∠EDC,BD=CD.∴△ABD≌△ECD.∴AB=CE.∵AC+CE>AE,∴AC+AB>AE=2AD.即AC+AB>2AD.【总结升华】证明边的大小关系主要有两个思路:(1)两点之间线段最短;(2)三角形的两边之和大于第三边.要证明AB+AC>2AD,如果归到一个三角形中,边的大小关系就是显然的,因此需要转移线段,构造全等三角形是转化线段的重要手段.可利用旋转变换,把△ABD绕点D逆时针旋转180°得到△CED,也就把AB转化到△CEA中,同时也构造出了2AD.若题目中有中线,倍长中线,利用旋转变换构造全等三角形是一种重要方法.2、已知,如图:在△ABC中,∠B=2∠C,AD⊥BC,求证:AB=CD-BD.【思路点拨】在DC上取一点E,使BD=DE,则△ABD≌△AED,所以AB=AE,只要再证出EC=AE即可.【答案与解析】证明:在DC上取一点E,使BD=DE∵AD⊥BC,∴∠ADB=∠ADE在△ABD和△AED中,BD=DE,AD=AD.∴△ABD≌△AED(SAS).∴AB=AE,∠B=∠AED.又∵∠B=2∠C=∠AED=∠C+∠EAC.∴∠C=∠EAC.∴AE=EC.∴AB=AE=EC=CD—DE=CD—BD.【总结升华】此题采用截长或补短方法.上升到解题思想,就是利用翻折变换,构造的全等三角形,把条件集中在基本图形里面,从而使问题加以解决.如图,要证明AB=CD-BD,把CD-BD转化为一条线段,可利用翻折变换,把△ABD沿AD翻折,使线段BD运动到DC上,从而构造出CD-BD,并且也把∠B转化为∠AEB,从而拉近了与∠C的关系.举一反三:【变式】已知,如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,并且AE=12(AB+AD),求证:∠B+∠D=180°.【答案】证明:在线段AE上,截取EF=EB,连接FC,∵CE⊥AB,∴∠CEB=∠CEF=90°在△CBE和△CFE中,AEDCBCEB CEF EC =EC EB EF =⎧⎪∠=∠⎨⎪⎩∴△CBE 和△CFE (SAS ) ∴∠B =∠CFE ∵AE =12(AB +AD ),∴2AE = AB +AD ∴AD =2AE -AB ∵AE =AF +EF , ∴AD =2(AF +EF )-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB , 即AD =AF在△AFC 和△ADC 中(AF AD FAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义)∴△AFC ≌△ADC (SAS ) ∴∠AFC =∠D∵∠AFC +∠CFE =180°,∠B =∠CFE. ∴∠AFC +∠B =180°,∠B +∠D =180°.类型二、全等三角形的判定2——“角边角”3、如图,G 是线段AB 上一点,AC 和DG 相交于点E.请先作出∠ABC 的平分线BF ,交AC 于点F ;然后证明:当AD∥BC,AD =BC ,∠ABC=2∠ADG 时,DE =BF.【思路点拨】通过已知条件证明∠DAC=∠C,∠CBF=∠ADG,则可证△DAE≌△BCF 【答案与解析】 证明: ∵AD∥BC,∴∠DAC=∠C∵BF 平分∠ABC ∴∠ABC=2∠CBF ∵∠ABC=2∠ADG ∴∠CBF=∠ADG在△DAE 与△BCF 中⎪⎩⎪⎨⎧∠=∠=∠=∠C DAC BCAD CBF ADG ∴△DAE≌△BCF(ASA ) ∴DE=BF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等. 举一反三:【高清课堂:379110 全等三角形判定二,例7】【变式】已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM.【答案】证明:∵MQ 和NR 是△MPN 的高, ∴∠MQN =∠MRN =90°,又∵∠1+∠3=∠2+∠4=90°,∠3=∠4 ∴∠1=∠2在△MPQ 和△NHQ 中,12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ (ASA ) ∴PM =HN类型三、全等三角形的判定3——“角角边”4、(2016•黄陂区模拟)如图,在Rt △ABC 中,∠ACB=90°,AC=BC ,过C 点作直线l ,点 D ,E 在直线l 上,连接AD ,BE ,∠ADC=∠CEB=90°.求证:△ADC ≌△CEB .【思路点拨】先证明∠DAC=∠ECB ,根据AAS 证△ADC ≌△CEB . 【答案与解析】证明:∵∠DAC+∠DCA=∠ECB+∠DCA=90°,∴∠DAC=∠ECB , 在△ADC 和△CEB 中,,∴△ADC≌△CEB(AAS).【总结升华】本题考查三角形全等的判定方法,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.举一反三:【变式】已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.求证:△ADC≌△CEB.【答案】证明:∵∠DAC+∠DCA=∠ECB+∠DCA=90°,∴∠DAC=∠ECB,在△ADC和△CEB中,,∴△ADC≌△CEB(AAS).5、平面内有一等腰直角三角板(∠ACB=90°)和一直线MN.过点C作CE⊥MN 于点E,过点B作BF⊥MN于点F.当点E与点A重合时(如图1),易证:AF+BF=2CE.当三角板绕点A顺时针旋转至图2的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.【思路点拨】过B作BH⊥CE与点H,易证△ACE≌△CBH,根据全等三角形的对应边相等,即可证得AF+BF=2CE.【答案与解析】解:图2,AF+BF=2CE仍成立,证明:过B作BH⊥CE于点H,∵∠CBH+∠BCH=∠ACE+∠BCH=90°∴∠CBH=∠ACE在△ACE与△CBH中,90A C H C B H A E C C H BA CBC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△ACE ≌△CBH .(AAS )∴CH =AE ,BF =HE ,CE =EF ,∴AF +BF =AE +EF +BF =CH +EF +HE =CE +EF =2EC .【总结升华】正确作出垂线,构造全等三角形是解决本题的关键. 举一反三:【变式】已知Rt △ABC 中,AC =BC ,∠C =90°,D 为AB 边的中点,∠EDF =90°,∠EDF 绕D 点旋转,它的两边分别交AC 、CB 于E 、F .当∠EDF 绕D 点旋转到DE ⊥AC 于E 时(如图1),易证12DEF CEF ABC S S S +=△△△;当∠EDF 绕D 点旋转到DE 和AC 不垂直时,在图2情况下,上述结论是否成立?若成立,请给予证明;若不成立,请写出你的猜想,不需证明.【答案】解:图2成立; 证明图2:过点D 作DM AC DN BC ⊥⊥, 则90DME DNF MDN ∠=∠=∠=°在△AMD 和△DNB 中,AMD=DNB=90A BAD BD ∠∠︒⎧⎪∠=∠⎨⎪=⎩∴△AMD ≌△DNB (AAS ) ∴DM =DN图2ADBCE M NF∵∠MDE +∠EDN =∠NDF +∠EDN =90°, ∴∠ MDE =∠NDF 在△DME 与△DNF 中,90EMD FDN DM DNMDE NDF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴△DME ≌△DNF (ASA ) ∴DME DNF S S =△△∴DEF CEF DMCN DECF S =S =S S .+△△四边形四边形 可知ABC DMCN 1S =S 2△四边形, ∴12DEF CEF ABC S S S +=△△△ 类型四、全等三角形判定的实际应用6、小强为了测量一幢高楼高AB ,在旗杆CD 与楼之间选定一点P .测得旗杆顶C 视线PC 与地面夹角∠DPC=36°,测楼顶A 视线PA 与地面夹角∠APB=54°,量得P 到楼底距离PB 与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB 是多少米?【思路点拨】根据题意可得△CPD ≌△PAB (ASA ),进而利用AB=DP=DB ﹣PB 求出即可. 【答案与解析】解:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°, ∴∠DCP=∠APB=54°, 在△CPD 和△PAB 中 ∵,∴△CPD≌△PAB(ASA ), ∴DP=AB,∵DB=36,PB=10, ∴AB=36﹣10=26(m ), 答:楼高AB 是26米.【总结升华】此题主要考查了全等三角形的应用,根据题意得出△CPD ≌△PAB 是解题关键.。
13.边角边PPT课件(华师大版)

总结
本题运用了分析法寻找证明思路,分析法就是执 果索因,由未知看需知,思维方式上就是从问题入手, 找能求出问题所需要的条件或可行思路,若问题需要 的条件未知,则把所需条件当作中间问题,再找出解 决中间问题的条件.如本题先视察BD,AE所在的三 角形,若要全等需什么条件, 这 些条件怎样由已知 解决.
13.2 三角形全等的判定
边角边
判定两三角形全等的基本事实:边 角边
“边角边”的简单应用
知识点 1 判定两三角形全等的基本事实:边角边
探
索
为了探索三角形全等的条件,现在我们考虑两个三 角形 有三组对应相等的元素,那么此时会出现几种可能 的情况 呢?
将六个元素(三条边、三个角)分类组合,可能出现:
证明:在△ABE和△DCE中, ∵AE=DE(已知), ∠AEB= ∠DEC (对顶角相等), BE=CE(已知), ∴△ABE≌△DCE(S.A.S.).
总结
(1)要证两个三角形全等,若已知两边相等,可
考虑证两边的夹角相等,如本题由条件BE∥DF可得角
的关系,故用“S.A.S.”证明.(2)证明两三角形全 等时,常要证边相等,而证边相等的方法有:①公共 边;②等线段加(减)等线段其和(差)相等,即等式性 质;③由中点得到线段相等;④同等于第三条线段的 两线段相等,即等量代换;⑤全等三角形的对应边相 等等.
C.∠B=∠E
D.∠C=∠D
知识点 2 “边角边”的简单应用
例3 如图13. 2. 6,有一池塘.要测池塘两端A、B的距
离,可先在平地上取一个可以直接到达A和B的 点C,连结AC并延长到D,使CD =CA.连结 BC并延长到E,使CE=CB.连DE,那么DE的
长就是A、B的距 离.你知道其中的道理吗?
华东师大版八年级上册数学教学设计《边角边》

华东师大版八年级上册数学教学设计《边角边》一. 教材分析华东师大版八年级上册数学教材中,边角边(SAS)是证明两条边和它们夹角相等的几何定理。
学生在学习了直角三角形、平行线等基础知识后,本节内容将引导学生进一步探究三角形全等的条件,为后续学习三角形相似、解三角形等知识打下基础。
二. 学情分析八年级的学生已具备一定的空间想象能力和逻辑思维能力,对几何图形有了一定的认识。
但部分学生可能对证明过程感到困惑,对几何定理的理解不够深入。
因此,在教学过程中,需要关注学生的学习困难,引导学生积极参与,提高其动手操作和解决问题的能力。
三. 教学目标1.知识与技能:使学生掌握边角边(SAS)全等定理,能运用SAS定理证明三角形全等。
2.过程与方法:培养学生观察、分析、推理的能力,提高空间想象能力。
3.情感态度与价值观:激发学生学习几何的兴趣,培养其勇于探索、严谨求实的科学态度。
四. 教学重难点1.重点:边角边(SAS)全等定理的证明及应用。
2.难点:对SAS定理的理解,以及如何运用该定理证明三角形全等。
五. 教学方法1.采用问题驱动法,引导学生主动探究几何定理。
2.运用直观演示法,让学生直观地理解全等三角形的概念。
3.利用小组合作学习,培养学生团队合作和交流分享的能力。
4.通过练习法,巩固所学知识,提高学生解决问题的能力。
六. 教学准备1.准备多媒体教学课件,展示三角形全等的图形和证明过程。
2.准备相关的练习题,用于课堂练习和巩固知识。
3.准备三角板、直尺等学具,让学生动手操作,加深对全等三角形的理解。
七. 教学过程1.导入(5分钟)利用多媒体展示一些生活中的三角形图片,引导学生关注三角形的全等问题。
提问:你们认为什么样的两个三角形才能称为全等三角形?2.呈现(10分钟)介绍边角边(SAS)全等定理,通过直观演示和讲解,使学生理解SAS定理的含义。
展示三角形全等的图形,让学生观察并尝试解释全等的理由。
3.操练(10分钟)学生分组合作,利用三角板、直尺等学具,尝试用SAS定理证明三角形全等。
八年级数学 三角形全等判定(一)——边角边(SAS)

八年级数学 三角形全等判定(一)——边角边(SAS) 一、 复习回顾全等三角形的性质是什么?如:△ABC ≌△DEF,可以写出以下推理:二、 试一试画一个△ABC,使AB=5cm ,AC=3cm 。
这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗? 若再加一个条件,使∠A=45°,画出△ABC把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?三角形全等判定方法1:A B CDE F用符号语言表达为:三、练一练练习1、如图,下列哪组条件不能判定△ABC ≌△DEF ( )练习2、已知:如图,AC=AD, ∠CAB=∠DAB 求证:△ACB ≌△ADB练习3、已知:如图,AB=AC,AD=AE. 求证: △ABE ≌△ACDA BC A`B`C` DEFABC ABC D A CDB EAB=DEA 、 ∠A=∠DAC=DFAB=DE B 、 ∠B=∠E BC=EF AC=DF D 、 ∠B=∠E BC=EF AC=DFC 、 ∠C=∠FBC=EF四、想一想练习1、已知:如图,AD ∥BC,AD=CB. 求证: △ADC ≌△CBA练习2、已知:如图,AD ∥BC,AD=BC,AE=CF. 求证:△AFD ≌△CEB练习3、已知:如图,AB=AC,AD=AE, ∠1=∠2. 求证:△ADB ≌△ACEBC A DBCFE1 ACE2BDA DB C五、用一用因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。
请你设计一种方案,粗略测出A、B 两杆之间的距离。
小结以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为45°,情况又怎样?动手画一画,你发现了什么?。
八年级数学上册第十三章全等三角形13.2三角形全等的判定-边角边教案新版华东师大版

三角形全等的判定-边角边教学目标:〔1〕知识与技能:掌握根本领实“两边及其夹角分别相等的两个三角形全等〞,并会利用这一根本领实进展证明.〔2〕过程与方法:通过分析两边及一角的位置关系,感受数学的分类思想;通过合情推理以及逻辑推理相结合的方法,掌握这一根本领实;通过分析实际例子,感受数学的几何直观,慢慢掌握逻辑推理证明过程.〔3〕情感态度价值观:培养探究数学问题的兴趣,激发对于数学研究的好奇心.在探索过程中,体会小组互助合作的乐趣学生学情分析:在知识储藏方面,学生已经学过了“边边边〞判断两个三角形全等的方法,并且知道判断两个三角形全等至少需要三个条件.在思想方法方面,学生在第一节课中就体会了数学的分类思想,对于三角形的边角知道如何进展分类.同时在七年级的几何学习中渗透逻辑推理能力,具备一定的推理证明能力.利用尺规作图得到本节课的判定方法同时应用判定方法解决实际问题是学生利用自身已有的根底可以解决的.而在最后,探索两边及其中一边的对角对应相等的两个三角形不会全等的反例是本节课的难点,需要教师适当的引导解决.而对于这个反例,为了更加方便学生寻找,我在角度以及边长方面进展了固定,学生用尺规去寻找另一边,这样大大降低了找反例的难度.从课堂的效果来看,也很好地到达了预期的效果. 教学策略分析:本节课首先从学生的最近开展区入手,复习引入本节课的内容.在引导学生进展分类时,学生通过图形动画能够更加直接得出两边及一角的位置关系.在分完类之后,为了突出本节课的重点,先对两边及其夹角对应相等这种情况进展分析,学生通过自主探究〔尺规作图〕以及小组合作的方式得出本节课的判定方法.紧接着,通过操练法在练习的难度设置上做到层层递进,学生在练习中稳固本节课的重点知识,并通过学生练习分析学习的情况.最后再对两边及其中一边的对角对应相等这一情况进展分析,同样学生通过自主探究〔尺规作图〕以及小组合作的方式探究两边及其中一边的对角对应相等的反例.教学过程:引入2.六个元素相等保证两个三角形全等,它们有多少种组合?3.我们看看有两条边一个角分别相等的情况下两个三角形全等吗?活动一问题:两个三角形的两边及其中一个角相等,有几种不同的情况?根据学生的归纳得出两种不同情况:紧接我们先来研究第一种情况.学生在教师的引导下归纳出两种情况通过分析两边一角的位置关系,使学生感受数学的分类思想,同时培养学生的几何直观.活动二如果“两边及一角〞条件中的角是两边的夹角,比方三角形两条边分别为2.5cm和3cm,它们的夹角为45 ,你能画出这个三角形吗?你画的与同伴画的一定全等吗?换两条线段和一个角试试,你发现了什么?学生自主利用圆规和直尺进展画图,并在画完后和前后桌进展对照通过小组活动以及自主活动,让学生感受两边及其夹角的情况,合情推理得出今天的判定的方法.归纳总结从刚刚画图的过程中,可以归纳出今天的判定方法:如果两个三角形有两边和他们的夹角对应相等,那么这两个三角形全等〔可以简写成“S.A.S.〞或“边角边〞〕.用数学语言表述如下:学生在教师的指导下归纳总结出今天的判定方法.培养学生的归纳总结能力,体会刚刚作图时的关键地方.在ABC ∆和'''C B A ∆中,⎪⎩⎪⎨⎧=∠=∠=___________________BC AB _______≅∆∴ABC【答案】A B ''B B 'B C ''A B C '''∆在教师的指导下,学生进展填空.并且教师在学生总结下将主要内容板书在黑板上.稳固练习1利用“边角边〞判断ABC ∆与DEF ∆是否全等,全等的打“√〞,不全等的打“×〞.〔1〕〔2〕〔3〕【答案】〔1〕×〔2〕√〔3〕×让学生快速判断这三组三角形是否全等,加深学生对于夹角的理解三个学生快速的答复教师的问题,并对是否全等做出自己的解释让学生快速答复,主要是让学生更加直观地认识两边及其夹角这一判定方法的关键之处,加深学生对于夹角的记忆.例题讲解1例1:如图,线段相交于点E ,AE =DE ,BE =CE .求证: △ABE ≌△DCE在教师的指导下,学会分析问题,找这道例题关注学生逻辑解:在△ABE与△DCE中,∵AE=DE〔〕,∠AEB= ∠DEC〔对顶角相等〕,BE=CE〔〕,∴△ABE≌△DCE(S.A.S.)教师给学生分析完后板书这道题的解题格式稳固练习2 :如图,点在BC上,CB∠=∠,BE=CF,AB=DC,求证:DA∠=∠解:在△ABF与△DCE中,∵BE=CF∴BF=CE又∵AB=DC〔〕,∠B=∠C〔〕,∴△ABF≌△DCE(S.A.S.)∴∠A=∠D教师给学生分析完后,让学生自己完成这道例题的解题学生学会分析问题,并自己解答这个问题,通过两个同学展示自己的作业,给同学进展讲解.例题讲解2 例2:如图,有—池塘,要测池塘两端的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是的距离,为什么?教师讲解例题,学生自己练习,并且在练习的过程中感受对顶角这一隐含条件.一个同学展示自己的作业,给同学进展讲解.例题2让学生感受数学与实际生活是严密相连的.并能从中寻找到边与角的隐含条件.指导学生证明:在△ABC和△DEC中AC=DC〔〕∵∠ACB=∠DCE(对顶角〕BC=EC()∴△ABC≌△DEC(S.A.S.)∴AB=DE教师在学生做的过程中巡视学生做题情况,并在学生做完后让一个学生展示他的作业课堂小结教师让学生总结本节课的主要内容,将之前小结的内容再重复展示一遍.根据教师的要求复习一遍这节课的主要内容.稳固今天的重点知识.活动三三角形两条边分别为2.5cm和3cm,它们的夹角为45 ,如果“两边及一角〞条件中的角是以长的线段为角的邻边,短的线段为角的对边,画三角形,你们画出的三角形都1全等吗?,你能画出这个三角形吗?学生自主利用圆规和直尺进展画图,并在画完后和前后桌进展对照.通过小组活动以及自主活动,让学生感受两边及其中一边的对角的情况,并通过比照得出此方法无法判断两个三角形全等.课堂作业习题如有侵权请联系告知删除,感谢你们的配合!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
边-边-角 第二种
做 一 做
画一个三角形,使它的一个内角45° , 夹这个角的一条边为3厘米,另一条 边长为4厘米.
温馨 提示
步骤:1.画一线段AB,使它等于4cm 2.画∠ MAB= 45° 3.在射线AM上截 取AC=3cm 4.连结BC.
△ ABC就是所求做的三角形
你画的三角形与同伴画的一定全等吗?
O
C
D O E
B E A
A
E 图1
D
B
B 图2
C
D 图3
C
4、如图4,在梯形ABCD中,AD∥BC,AB=DC,点E、F分别在 AB、DC上,且BE=2EA,CF=2FD,求证:∠BEC=∠CFB。
5、如图5,△ABC中,∠ABC=45°,AD⊥BC于D,点E在AD 上,且DE=CD,求证:BE=AC。
链接生活:
小明不小心打翻了墨水,将 自己所画的三角形涂黑了,你能 帮小明想想办法,画一个与原来 完全一样的三角形吗?
A
A’
B
∵
C
A’B’
AB = A’B’
B’ ∠B = ∠B’
C’
M
BC =B’C’
∴
△ ABC≌ △A’B’C’(S.A.S)
做 一 做
以3cm、4cm为三角形的两边,长 度3cm的边所对的角为45° ,情况又 怎样?动手画一画,你发现了什么?
A E D F
A
E
B 图4 C
B 图5
D
C
作业
P76习题13.2 P103复习题 第 4题 第4题
再见
E
F
∠EDH=∠FDH(已知)
DH=DH(公共边)
H
∴△EDH≌△FDH(S.A.S) ∴EH=FH(全等三角形对应边相等)
巩 固 练 习
3. 点 M 是等腰梯形 ABCD 底 边 AB 的 中 点 , 求 证 DM=CM , ∠ADM=∠BCM. 证明: ∵ 点M是等腰梯形ABCD底边AB的中点 ∴ AD=BC (等腰梯形的两腰相等) ∠A=∠B(等腰梯形的两底角相等) AM=BM (线段中点的定义) 在△ADM和△BCM中 AD=BC, (已证) ∠A=∠B, (已证) AM=BM, (已证) ∴△AMD≌△BMC (S.A.S) ∠ ADM =∠ BCM (全等三角形的对应角相等) ∴ DM=CM(全等三角形的对应边相等)
说一说
今天你学到了什么
1、今天我们学习了哪种方法判定 两三角形全等? 答:S.A.S 通过证明三角 形全等可以证明两条线段等、 两个角相等 2、 “边边角”能不能判定两个三 角形全等“? 答:不能
五、检验反馈 1、如图1,CD是Rt△ABC斜边上的高,将△BCD沿CD折叠 ,B点恰好落在AB的中点E处,则∠A等于( ) A、25° B、30° C、45° D、60° 2、如图2,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE 、CD交于点O,且AO平分∠BAC,那么图中全等的三角形共 A ______________对
2. 如图所示 , 根据题目条件,判断下面 的三角形是否全等. (1) AC=DF, ∠C=∠F, BC=EF; (2) BC=BD, ∠ABC=∠ABD.
答案:
(1)全等
(2)全等
例2:小兰做了一个如图所示的风筝,其中 ∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小 明不用测量就能知道EH=FH吗?与同桌进行交流。 D 解:在△EDH和△FDH中: ED=FD(已知)
思考
如果两个三角形有三组对应相等的元素 (边或角),那么会有哪几种可能的情况? 这时,这两个三角形一定会全等吗? 温馨 有以下的四种情况: 提示
两边一角、两角一边、
三角、三边.
思考
如果已知两个三角形有两边一角对应 相等时,应分为几种情形讨论?
A B
A' A
B
C A'
C
B'
C'
B'
C'
边-角-边
第一种
例1如图19.2.4,在△ABC中,AB=AC, 分∠BAC,求证: △ABD≌△ACD.
AD平
证明: ∵ AD平分∠BAC,
∴ ∠BAD=∠CAD. 在△ABD与△ACD中, AB=AC,(已知) ∵ ∠BAD=∠CAD,(已证) AD=AD,(公共边) ∴ △ ABD≌△ACD (S.A.S.).
如图在△ ABC 和△ A′B′C′ 中,已知 AB = A′B′ , ∠B=∠B′, BC=B′C′.
A A A A A A A A’ A A
B B B
B
B
CB C C B C B B’ BC
C
C
C’ C C
由于AB=A′B′,我们移动其中的△ABC, 使点A与点A′、点B与点B′重合;因为∠B= ∠B′,因此可以使∠B与∠B′的另一边BC与 B′C′重叠在一起,而BC=B′C′,因此点C 与点C′重合.于是△ABC与△A′B′C′重合, 这就说明这两个三角形全等.
C 步骤:1.画一线段AC,使它等 于4cm 2.画∠ CAM= 45° 3.以C为圆心, 3cm长为半径画 弧,交AM于点B 和B’ 4.连结 CB 、CB’
A
45°
B B’ M
△ ABC 与△ AB’C 就是 显然: △ ABC与△ AB’C不全等 所求做的三角形
结论:两边及其一边所对的角相等,两个三 角形不一定全等
\\
∠B=
\\
\
B
C
B′\Biblioteka C′说明这两个三角形全等
实践与探索
同桌两个同学自行约定:各画一个三角 形,使它们具有相同的两条线段和一个 夹角,比较一下,可以得出什么结论? 结论: 在两个三角形中,如果有 两条边及它们的夹角对应 相等,那么这两个三角形 全等(简记为S.A.S)
温馨提 示:
S.A.S的证明:
13.2.2全等三角形判定 (一) 边角边
现代双语实验学校。数学组
复习练习:全等三角形的性质
若△AOC≌△BOD, 对应边: AC= BD , AO= BO , CO= DO , 对应角有: ∠A= ∠B , ∠C= ∠D , ∠AOC= ∠BOD ;
A O B
D
C
引入新课
上节课我们留给大家了这样一个思 考题,你们思考好了吗?
图 19.2.4
巩 固 练 习
1: 如图,已知AB和CD相交与O,
OA=OB, OC=OD.说明 △ OAD与 △ OBC全等的理由 解:在△OAD 和△OBC中
B
C
2
O A
OA = OB(已知)
∠1 =∠2(对顶角相等) OD = OC (已知)
1
D
∴△OAD≌△OBC (S.A.S)
巩 固 练 习
全等
F C 3cm 3cm A D F 3cm F 3cm F 3cm F F
实践 检验
F F F 3cm 3cm 3cm 3cm
45°
D
D DE D E D E D ED D E E E E E B 4cm 4cm 4cm 4cm 4cm 4cm 4cm 4cm 4cm
在△ABC和△A′B′C′中,已知AB=A′B′, ∠B′, BC=B′C′ A A′
