2.2.1直线与平面平行的判定课件免费下载
合集下载
2.2.1 直线与平面平行的判定-课件ppt
B B1
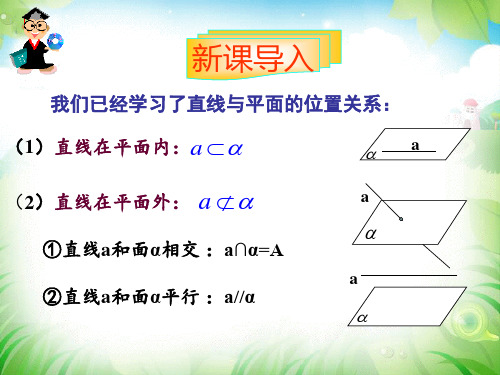
书页无论怎样翻动,书页边缘AB总与另一边 A1B1平行,AB与桌面不可能相交,所以AB所在直 线平行于桌面所在平面。
探 究
平面α外有直线 a平行于平面α内的直线 b。
(1)这两条直线共面吗?
共面
(2)直线a 与平面α相交吗? 不可能相交
a
b
直线和平面平行的判定定理:
平面外一条直线与此平面内的一条直 线平行,则该直线与此平面平行。
教学目标
知识与能力
➢理解并掌握直线与平面平行的判定定理。 ➢进一步培养学生观察、发现的能力和空间想象能力。
过程与方法 ➢学生通过观察图形,借助已有知识,掌握直线 与平面平行的判定定理。
情感态度与价值观 ➢让学生在发现中学习,增强学习的积极性。 ➢让学生了解空间与平面互相转换的数学思想。
教学重难点
ab
缺少条件2,定理也不成立。
(3)若直线a不平行于直线b,a// 吗?
a
b
缺少条件3,定理也不成立。
例一 如图,四面体ABCD中,E,F,G,
H分别是AB,BC,CD,AD的中点。
(1)E、F、G、H四点是否共面?
A
(2)判断AC与平面EFGH的位置关系。E H
(3)你能说出图中满足线面平行
位置关系的所有情况吗?
再见
符号表示:a//b a α a//α b α
简述为: 线线平行,则线面平行
已知:a α, b α, a//b, 求证: a//α
证明:假设a与α不平行,相交于P 过P在平面 内作直线c ∥b ∵ a ∥b
a
c
p
αb
∴ a ∥c
pa, pc a c p
这与a//c矛盾。∴假设错误,原命题正确 ∴a//α
书页无论怎样翻动,书页边缘AB总与另一边 A1B1平行,AB与桌面不可能相交,所以AB所在直 线平行于桌面所在平面。
探 究
平面α外有直线 a平行于平面α内的直线 b。
(1)这两条直线共面吗?
共面
(2)直线a 与平面α相交吗? 不可能相交
a
b
直线和平面平行的判定定理:
平面外一条直线与此平面内的一条直 线平行,则该直线与此平面平行。
教学目标
知识与能力
➢理解并掌握直线与平面平行的判定定理。 ➢进一步培养学生观察、发现的能力和空间想象能力。
过程与方法 ➢学生通过观察图形,借助已有知识,掌握直线 与平面平行的判定定理。
情感态度与价值观 ➢让学生在发现中学习,增强学习的积极性。 ➢让学生了解空间与平面互相转换的数学思想。
教学重难点
ab
缺少条件2,定理也不成立。
(3)若直线a不平行于直线b,a// 吗?
a
b
缺少条件3,定理也不成立。
例一 如图,四面体ABCD中,E,F,G,
H分别是AB,BC,CD,AD的中点。
(1)E、F、G、H四点是否共面?
A
(2)判断AC与平面EFGH的位置关系。E H
(3)你能说出图中满足线面平行
位置关系的所有情况吗?
再见
符号表示:a//b a α a//α b α
简述为: 线线平行,则线面平行
已知:a α, b α, a//b, 求证: a//α
证明:假设a与α不平行,相交于P 过P在平面 内作直线c ∥b ∵ a ∥b
a
c
p
αb
∴ a ∥c
pa, pc a c p
这与a//c矛盾。∴假设错误,原命题正确 ∴a//α
2.2.1《直线与平面平行的判定》课件

∵ AF∥ BE,∴ BN GN . NF NA ∵正方形ABCD与正方形ABEF全等,
连接CG。 【证明】连结 AN 并延长交 BE 于 G 点.
∴ AC=BF.
∵ CM=BN,∴ MA=NF.
∵ CM GN ,∴ MN∥ CG. MA NA MN 平面 BCE,∴ MN∥ 平面 BCE. ∵ CG 平面 BCE,
a
b
8
直线与平面平行的判定定理
若平面外一条直线与此平面内的一条直线平行,
则该直线与此平面平行.
a
b
a b a // a // b
线线平行
线面平行
9
典例展示
例1.空间四边形ABCD 中,E,F分别为AB,AD 的中点, 求证:直线EF与平面BCD平行.
A
5
将一本书平放在桌面上,翻动书的硬皮封面, 封面边缘AB所在直线与桌面所在平面具有什么样的 位置关系?
A
A
B
B
6
如果平面 内有直线 b 与直线 a 平行,那么直线 a 与平面 的位置关系如何?
是否可以保证直线 a 与平面 平行?
a
b
7
平面 外有直线 a 平行于平面 内的直线 b . (1)这两条直线共面吗? 共面 (2)直线 a 与平面 相交吗? 不可能相交
线线平行
线面平行
如果平面外一条直线和这个平面内的一条直线平行,那么这 条直线和这个平面平行。
a b a b a∥ b a∥
15
3
怎样判定直线与平面平行呢?
根据定义,判定直线与平面是否平行,只需判 定直线与平面有没有公共点.但是,直线无限延长, 平面无限延展,如何保证直线与平面没有公共点呢? a
连接CG。 【证明】连结 AN 并延长交 BE 于 G 点.
∴ AC=BF.
∵ CM=BN,∴ MA=NF.
∵ CM GN ,∴ MN∥ CG. MA NA MN 平面 BCE,∴ MN∥ 平面 BCE. ∵ CG 平面 BCE,
a
b
8
直线与平面平行的判定定理
若平面外一条直线与此平面内的一条直线平行,
则该直线与此平面平行.
a
b
a b a // a // b
线线平行
线面平行
9
典例展示
例1.空间四边形ABCD 中,E,F分别为AB,AD 的中点, 求证:直线EF与平面BCD平行.
A
5
将一本书平放在桌面上,翻动书的硬皮封面, 封面边缘AB所在直线与桌面所在平面具有什么样的 位置关系?
A
A
B
B
6
如果平面 内有直线 b 与直线 a 平行,那么直线 a 与平面 的位置关系如何?
是否可以保证直线 a 与平面 平行?
a
b
7
平面 外有直线 a 平行于平面 内的直线 b . (1)这两条直线共面吗? 共面 (2)直线 a 与平面 相交吗? 不可能相交
线线平行
线面平行
如果平面外一条直线和这个平面内的一条直线平行,那么这 条直线和这个平面平行。
a b a b a∥ b a∥
15
3
怎样判定直线与平面平行呢?
根据定义,判定直线与平面是否平行,只需判 定直线与平面有没有公共点.但是,直线无限延长, 平面无限延展,如何保证直线与平面没有公共点呢? a
(完整)2.2.1直线与平面平行的判定ppt

A
A
怎样判定直线与平面平行呢? 根据定义,判定直线与平面是否平行,只需判定
直线与平面有没有公共点. 但是,直线无限延长,平面无限延展,如何保
证直线与平面没有公共点呢?
a
2.2.1直线与平面平行的判定
1.理解直线与平面平行的判定定理.(重点) 2.会用判定定理证明简单的线面平行的问题.
(难点) 3.进一步培养空间想象能力和转化化归的数学思想.
知的条件怎样找这条直线?
定理的应用
A
例1. 如图,空间四边形ABCD中, F
E、F分别是 AB,AD的中点. E
D
求证:EF∥平面BCD.
B
证明:连结BD.
∵AE=EB,AF=FD
∴EF∥BD(三角形中位线性质)
又因为 EF 平面BCD BD 平面BCD EF//平面BCD
FE//BD
【提升总结】
点,F为AE的中点. 求证:AB//平面
DCF.
证明:连结OF,
B
∵ O为正方形DBCE 对角线的交点,
∴BO=OE,
又AF=FE,
∴AB//OF,
AB 平面DCF
OF 平面DCF AB//平面DCF
AB//OF
A
D
O
F E
C
反思~领悟:
1.线面平行,通常可以转化为线线平行来处理.
2.寻找平行直线可以通过三角形的中位线、 梯形的中位线、平行线的判定等来完成。
1.证明直线与平面平行的方法:
(1)利用定义;直线与平面没有公共点
(2)利用判定定理.
线线平行
线面平行
2.数学思想方法:转化的思想
空间问题
平面问题
【思考】
2.2.1直线与平面平行的判定)课件

或相交 3、判断下列命题是否正确?若不正确,请在原题上改正: (1)如果一条直线不在平面内,则这条直线就与平面平行. ( ) (2)过直线外一点可以作无数个平面与这条直线平行. ( ) (3)一条直线上有二个点到平面的距离相等,则这条直线与平 面平行. ( )
√
×
×
或相交
4、课本P62第3题. 5、课本P62第4题.
1、若直线 a 不平行于平面 ,则下列结论成立的是( A、 内的所有直线都与直线 a 异面 B、 内不存在与直线 a 平行的直线 C、 内的直线都与 a 相交 D、直线 a 与平面 有公共点
D
)
A、 a //
C、 a // 或 a
D、 a
B、 a
C)
1、空间中直线与平面的位置关系有:
直线a在平面内 直线a与平面相交 直线a与平面平行
a
a A
a
b
a//
a
有无数个公共点
a∩=A
有且只有一个 公共点
没有公共点
【新知探究】 ①转动门扇,当门扇绕着一边转动时另一边所在直 平行 ; 线与门框所在的平面的位置关系是__________
②将一本书平放在桌面上,翻动书的封面,封面边 平行 ; 缘所在的直线与桌面所在平面的位置关系是_______
是什么原因使该直线和此平面看上去是平行的?
该直线在平面外, 且与平面内的一条直线平行。
3、探究: 3、探究: 【新知探究】 (1)这两条直线共面吗? (1)这两条直线共面吗? 共面
外的直线 内的直线 外的直线 内的直线 图,平面 a 平行于平面 b。 b。 如图,平面 a 平行于平面
D1 B1
C1 C B
人教新课标A版必修2《2.2.1直线与平面平行的判定》课件

AE EB
FAD F ,则EF
与平面BCD的位置关系是_________.
A
E
F
B
D
C
变式2 如图,四棱锥 S ABCD 中,底面 ABCD
是正方形, E 为 SC 的中点. 求证: SA //平面 BDE .
O
思考题
如图,四棱锥 P ABCD 中, 底面 ABCD 为矩形,
M , N 分别为 AB, PC 的中点.
a
b
活动3、归纳理解定理
请同学们根据以上直观感知,归纳总结出 直线与平面平行的判定定理:
平面外的一条直线与此平面内的一条直线平行, 则该直线与此平面平行
_____________________________________________________________________________________________________________
(2)请同学们将一本书平放在桌面上, 翻动书的封面,视察:
①封面边缘所在直线a与桌面所在的平面
具有怎样的位置关系?
②桌面内有与a平行的直线吗?
a
b
活动2、“操作确认”直线与平面平行的条件
探究:如果平面 外的直线 a 与平面 内的直线 b 平行,
思考:(1)两直线是否共面?
(2)直线 a 与平面 是否有公共点?
面,并说明理由. (2)设E,F分别是A1B和 B1C的中点,求证
: 直线EF//平面ABCD.
2.2.1直线与平面平行的判定
一、复习回顾,引出定理
思考1:
在空间中,直线与平面有哪几种位置关系?
思考2: 是否有更方便、更易于操作的判定线面平 行的方法?
二、直观感知,归纳定理
课件12:2.2.1 直线与平面平行的判定

(1)求证:DE∥平面 BCP; (2)求证:四边形 DEFG 为矩形.
解:(1)因为D、E分别为AP、AC的中点,所以DE∥PC. 又因为DE⊄平面BCP,PC⊂平面BCP,所以DE∥平面BCP. (2)因为D、E、F、G分别为AP、AC、BC、PB的中点, 所以DE∥PC∥FG,DG∥AB∥EF.所以四边形DEFG为 平行四边形.又因为PC⊥AB,所以DE⊥DG.所以四边形 DEFG为矩形.
命题方向2 ⇨线面平行判定定理的实际应用
例 2 一木块如图所示,点 P 在平面 VAC 内,过点 P 将木 块锯开,使截面平行于直线 VB 和 AC,应该怎样画线?
解:在平面VAC内经过P作EF∥AC,且与VC的交点 为F,与VA的交点为E, 在平面VAB内,经过点E作EH∥VB,与AB交于点H, 如下图所示.
D.以上三种情形都有可能
预习自测
【解析】 如图,∵M、N 分别为 A1A 和 A1B1 中点, ∴MN∥AB1, 又∵P 是正方形 ABCD 的中心,∴P、A、C 三点共线, ∴AB1⊂平面 PB1C, ∵MN⊄平面 PB1C, ∴MN∥平面 PB1C.
预习自测
3.如下图,长方体 ABCD-A′B′C′D′中,
学科核心素养 转化思想的应用
线面平行的判定定理,将判断线面平行的位置关系转 化为判断这条直线与平面内一条直线的平行关系,为 了实现这一目标,“找”或“作”出平面内的这条直 线就成了应用判定定理的关键.
学科核心素养 转化思想的应用
实际解题时,要充分利用题目中给出的几何体的特征 性质或题设条件,借助于三角形的中位线,梯形的中 位线,平行四边形,平行线分线段成比例定理,公理4, 内错角(同位角)相等时两直线平行等等已学过的平面几 何与立体几何知识,作出必要的辅助线来解决.
解:(1)因为D、E分别为AP、AC的中点,所以DE∥PC. 又因为DE⊄平面BCP,PC⊂平面BCP,所以DE∥平面BCP. (2)因为D、E、F、G分别为AP、AC、BC、PB的中点, 所以DE∥PC∥FG,DG∥AB∥EF.所以四边形DEFG为 平行四边形.又因为PC⊥AB,所以DE⊥DG.所以四边形 DEFG为矩形.
命题方向2 ⇨线面平行判定定理的实际应用
例 2 一木块如图所示,点 P 在平面 VAC 内,过点 P 将木 块锯开,使截面平行于直线 VB 和 AC,应该怎样画线?
解:在平面VAC内经过P作EF∥AC,且与VC的交点 为F,与VA的交点为E, 在平面VAB内,经过点E作EH∥VB,与AB交于点H, 如下图所示.
D.以上三种情形都有可能
预习自测
【解析】 如图,∵M、N 分别为 A1A 和 A1B1 中点, ∴MN∥AB1, 又∵P 是正方形 ABCD 的中心,∴P、A、C 三点共线, ∴AB1⊂平面 PB1C, ∵MN⊄平面 PB1C, ∴MN∥平面 PB1C.
预习自测
3.如下图,长方体 ABCD-A′B′C′D′中,
学科核心素养 转化思想的应用
线面平行的判定定理,将判断线面平行的位置关系转 化为判断这条直线与平面内一条直线的平行关系,为 了实现这一目标,“找”或“作”出平面内的这条直 线就成了应用判定定理的关键.
学科核心素养 转化思想的应用
实际解题时,要充分利用题目中给出的几何体的特征 性质或题设条件,借助于三角形的中位线,梯形的中 位线,平行四边形,平行线分线段成比例定理,公理4, 内错角(同位角)相等时两直线平行等等已学过的平面几 何与立体几何知识,作出必要的辅助线来解决.
2.2.1_2.2.2直线与平面平行的判定平面与平面平行的判定课件人教新课标

直线与此平面平行
图形语言
符号语言
作 用
a⊄α,b⊂α,且 a∥b⇒a∥α
证明直线与平面平行
3.做一做:能保证直线a与平面α平行的条件是(
A.b⊂α,a∥b
B.b⊂α,c∥α,a∥b,a∥c
C.b⊂α,A,B∈a,C,D∈b,且AC∥BD
D.a⊄α,b⊂α,a∥b
答案:D
)
一
二
二、平面与平面平行的判定定理
1.三角板的一条边所在直线与平面α平行,这个三角板所在平面
与α平行吗?
提示:不一定平行.
2.三角板的两条边所在直线分别与平面α平行,这个三角板所在
平面与α平行吗?
提示:平行.
3.如图,平面BCC1B1内有多少条直线与平面ABCD平行?这两个平
面平行吗?
提示:无数条,不平行.
一
二
4.填表:平面与平面平行的判定定理
CC1,C1D1,D1D,CD的中点,N是BC的中点,点M在四边形EFGH的边
及其内部运动,当点M在
时,有MN∥平面B1BDD1.
探究一
探究二
探究三
思维辨析
解析:点M在F,H的连线上时,有MN∥平面B1BDD1.如图,平面
BDD1B1是正方体ABCD-A1B1C1D1的对角面,探究过点N且与平面
BDD1B1平行的直线,可取B1C1的中点N1,连接N1N,则NN1∥平面
探究三
思维辨析
延伸探究本例中,设P是棱AA1的中点,其他条件不变,求证:平面
PMN∥平面C1BD.
证明:连接AB1.
∵P,M分别是AA1,A1B1的中点,∴PM∥AB1.
又AB1∥C1D,∴PM∥C1D.
又PM⊄平面C1BD,C1D⊂平面C1BD,∴PM∥平面C1BD.
图形语言
符号语言
作 用
a⊄α,b⊂α,且 a∥b⇒a∥α
证明直线与平面平行
3.做一做:能保证直线a与平面α平行的条件是(
A.b⊂α,a∥b
B.b⊂α,c∥α,a∥b,a∥c
C.b⊂α,A,B∈a,C,D∈b,且AC∥BD
D.a⊄α,b⊂α,a∥b
答案:D
)
一
二
二、平面与平面平行的判定定理
1.三角板的一条边所在直线与平面α平行,这个三角板所在平面
与α平行吗?
提示:不一定平行.
2.三角板的两条边所在直线分别与平面α平行,这个三角板所在
平面与α平行吗?
提示:平行.
3.如图,平面BCC1B1内有多少条直线与平面ABCD平行?这两个平
面平行吗?
提示:无数条,不平行.
一
二
4.填表:平面与平面平行的判定定理
CC1,C1D1,D1D,CD的中点,N是BC的中点,点M在四边形EFGH的边
及其内部运动,当点M在
时,有MN∥平面B1BDD1.
探究一
探究二
探究三
思维辨析
解析:点M在F,H的连线上时,有MN∥平面B1BDD1.如图,平面
BDD1B1是正方体ABCD-A1B1C1D1的对角面,探究过点N且与平面
BDD1B1平行的直线,可取B1C1的中点N1,连接N1N,则NN1∥平面
探究三
思维辨析
延伸探究本例中,设P是棱AA1的中点,其他条件不变,求证:平面
PMN∥平面C1BD.
证明:连接AB1.
∵P,M分别是AA1,A1B1的中点,∴PM∥AB1.
又AB1∥C1D,∴PM∥C1D.
又PM⊄平面C1BD,C1D⊂平面C1BD,∴PM∥平面C1BD.
《2.2.1直线与平面平行的判定》课件07(共14张PPT)

A A1
D1
C1
B1 P M D N C
B
AC // MN
MN 面ABCD AC 面ABCD
MN // 面ABCD
证法2 (略写) 利用相似三角形对应边成比例 及平行线分线段成比例的性质
PM PB PBM∽ AA1 M MA AA1 PN PB PBN ∽CC 1 N NC CC 1
直线与平面的位置关系:
关系 内容 特征
直线在平面内 有无数个 公共点
直线与平面 相交
直线与平面 平行
有且只有一个 没有公共点 公共点
a
图形表示
a
A
a
符号表示
a
a∩=A a∥ a
理论迁移
例1 给出下列四个命题: (1)若直线l上有无数个点不在平面α 内,则 l∥α . (2)若直线l与平面α 平行,则l与平面α 内的 任意一条直线都平行. (3)若直线l与平面α 平行,则l与平面α 内的 任意一条直线都没有公共点. (4)若直线l在平面α 内,且l与平面β 平行, 则平面α 与平面β 平行. 1 个. 其中正确命题的个数共有 __
D1
F
B1
C1
A1
D
O
A
B
C E
∴EF∥D1O 又∵ EF
平面BB1DD1,
D O 平面BB DD
1 1
1
∴ EF ∥平面BB1DD1
巩固练习:
长方体ABCD -A1 B1C1 D1中,点P BB (异于 B、B1) 1 PA BA1 M , PC BC 1 N , 求证:MN // 平面ABCD
∴ l∥ α
例题1:
D1
C1
B1 P M D N C
B
AC // MN
MN 面ABCD AC 面ABCD
MN // 面ABCD
证法2 (略写) 利用相似三角形对应边成比例 及平行线分线段成比例的性质
PM PB PBM∽ AA1 M MA AA1 PN PB PBN ∽CC 1 N NC CC 1
直线与平面的位置关系:
关系 内容 特征
直线在平面内 有无数个 公共点
直线与平面 相交
直线与平面 平行
有且只有一个 没有公共点 公共点
a
图形表示
a
A
a
符号表示
a
a∩=A a∥ a
理论迁移
例1 给出下列四个命题: (1)若直线l上有无数个点不在平面α 内,则 l∥α . (2)若直线l与平面α 平行,则l与平面α 内的 任意一条直线都平行. (3)若直线l与平面α 平行,则l与平面α 内的 任意一条直线都没有公共点. (4)若直线l在平面α 内,且l与平面β 平行, 则平面α 与平面β 平行. 1 个. 其中正确命题的个数共有 __
D1
F
B1
C1
A1
D
O
A
B
C E
∴EF∥D1O 又∵ EF
平面BB1DD1,
D O 平面BB DD
1 1
1
∴ EF ∥平面BB1DD1
巩固练习:
长方体ABCD -A1 B1C1 D1中,点P BB (异于 B、B1) 1 PA BA1 M , PC BC 1 N , 求证:MN // 平面ABCD
∴ l∥ α
例题1:
2.2.1直线与平面平行、平面与平面平行的判定.pptx
生:由两个平面的位置关 系知①正确;由两个平面平行
一方面复 习巩固 已 学知 识, 另 一方面
行于另一个平面
的定义知②③正确;两个平面 通 过 开
④一个平面内有一条直线平 相交,其中一个平面内有无数 放 性 题
行于另一个平面
条直线与另一个平面平行,故 目 培 养
⑤一个平面内有两条直线平 行于另一个平面
体 ABCD –A1B1C1D1 证:平面 AB1D1∥平 面 C1BD.
证明:因为ABCD – 为正方体,
A1B1C1D1
所以 D1C1∥A1B1,D1C1 = A1B1 又 AB∥A1B1,AB = A1B1 所以 D1C1BA 为平行四边形. 所以 D1A∥C1B. 又 D1A 平面 C1BD,C1B 平 面 C1BD
D. 内的任何直线都与 平 行.
1. 直线与平面平行的判定 2. 平面与平面平行的判定 3. 面面平行 线面平行 线线 平行 4. 借助模型理解与解题
2.2 第一课时 习案
学生归纳、总结、教师点 评完善
学生独立完成
反思、归 纳所学 知 识, 提高 自 我整合 知识的 能 力. 固化知识
学海无 涯
么区别?
验,加深 理解.通过 讨论,培 养学生
探索新知
在平面具有什 么样的位置关系? 2. 问题 3:如图,如果在平 面 内有直线 b 与直线 a 平行,那 么直线 a 与平面
生:问题 2 增加了条件: 分 析 问
平面外. 直线平行于平面内直 题 的 能
线.
力.
师投影问题 3,学生讨论、
交流教师引导,要讨论直线 a
备选例题
提升能力
例 1 在正方体 ABCD – A1B1C1D1 中,E、F 分别为棱 BC、C1D1 的中点.求证:EF∥
一方面复 习巩固 已 学知 识, 另 一方面
行于另一个平面
的定义知②③正确;两个平面 通 过 开
④一个平面内有一条直线平 相交,其中一个平面内有无数 放 性 题
行于另一个平面
条直线与另一个平面平行,故 目 培 养
⑤一个平面内有两条直线平 行于另一个平面
体 ABCD –A1B1C1D1 证:平面 AB1D1∥平 面 C1BD.
证明:因为ABCD – 为正方体,
A1B1C1D1
所以 D1C1∥A1B1,D1C1 = A1B1 又 AB∥A1B1,AB = A1B1 所以 D1C1BA 为平行四边形. 所以 D1A∥C1B. 又 D1A 平面 C1BD,C1B 平 面 C1BD
D. 内的任何直线都与 平 行.
1. 直线与平面平行的判定 2. 平面与平面平行的判定 3. 面面平行 线面平行 线线 平行 4. 借助模型理解与解题
2.2 第一课时 习案
学生归纳、总结、教师点 评完善
学生独立完成
反思、归 纳所学 知 识, 提高 自 我整合 知识的 能 力. 固化知识
学海无 涯
么区别?
验,加深 理解.通过 讨论,培 养学生
探索新知
在平面具有什 么样的位置关系? 2. 问题 3:如图,如果在平 面 内有直线 b 与直线 a 平行,那 么直线 a 与平面
生:问题 2 增加了条件: 分 析 问
平面外. 直线平行于平面内直 题 的 能
线.
力.
师投影问题 3,学生讨论、
交流教师引导,要讨论直线 a
备选例题
提升能力
例 1 在正方体 ABCD – A1B1C1D1 中,E、F 分别为棱 BC、C1D1 的中点.求证:EF∥
2.2.1 直线与平面平行的判定(共25张PPT)

栏目 导引
第二章
点、直线、平面之间的位置关系
【名师点评】
利用判定定理证明线面平行,关键是在
平面内找一条直线与已知直线平行,由于两条直线首先
要保证共面,因此常常设法过已知直线作一平面与已知 平面相交,如果能证明已知直线和交线平行,就可用线
面平行的判定定理推出结论,这个证明线面平行的步骤
可概括为过直线,作平面,得交线,若线线平行,则线 面平行.
栏目 导引
第二章
点、直线、平面之间的位置关系
【方法感悟】
1.判定直线与平面平行的常用方法 (1)定义:证明直线与平面没有公共点,通常要借助反证 法来完成证明.
(2)判定定理:在平面内找到一条直线与它平行.
2.寻找线∥线时,仍然要用平面几何的知识,如中位 线、平行四边形等.
栏目 导引
第二章
点、直线、平面之间的位置关系
典题例证技法归纳
【题型探究】 题型一
例1
线面平行的判定定理的理解
下列说法中正确的是( )
A.若直线l平行于平面α内的无数条直线,则l∥α
B.若直线a在平面α外,则a∥α C.若直线a∥b,b⊂α,则a∥α D.若直线a∥b,b⊂α,那么直线a平行于平面α内的无 数条直线
栏目 导引
第二章
点、直线、平面之间的位置关系
【名师点评】
解答此题的关键点是会从特殊点入手.
栏目 导引
第二章
点、直线、平面之间的位置关系
跟踪训练
3.一木块如图所示,点P在平面VAC内,过点P将木块
锯开,使截面平行于直线VB和AC,应该怎样画线?并 证明你的结论.
栏目 导引
第二章
点、直线、平面之间的位置关系
解:在平面VAC内经过P作EF∥AC,且与VC的交点为 F,与VA的交点为E,在平面VAB内,经过点E作
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)试判断AC与平面EFGH的位置关系;
(3)你能说出图中满足线面平行位置 A
关系的所有情况吗?
H E
D
B
G
F C
解:(1)E、F、G、H四点共面。
∵在△ABD中,E、H分别是AB、 AD的中点.
A
∴EH∥BD且 EH= 1 BD
EH
2
同理GF ∥BD且 GF= 1 BD
B
2
EH ∥GF且EH=GF
D1
C1
A1
P B1
D A
C B
如何证明线面平行?
线线平行
线面平行
关键:找平行线
条件
面内 面外 平行
课堂练习
1、如图,在长方体ABCD——A1B1C1D1六个表面中,
(Ⅰ)与AB平行的直线有: (Ⅱ)与AB平行的平面有:A1B1、CD、C1D1
平面A1C1、平面D1C
D1 C1
A1 B1
D A
C B
问题3:把门打开,门上靠近把手的边与墙面所 在的平面有何关系?
抽象概括:
直线与平面平行的判定定理:
平面外一条直线与此平面内的一条直线平行,
则该直线与此平面平行.
a
a b
a // b
a // b
a//
简述为:线线平行线面平行
应用巩固:
例1.空间四边形ABCD中,E,F分别为AB,AD的
中点,试判断EF与平面BCD的位置关系,并予
D
G
F
C
∴E、F、G、H四点共面。
(2) AC ∥平面EFGH
(3)由EF ∥HG ∥AC,得 EF ∥平面ACD AC ∥平面EFGH HG ∥平面ABC
由BD ∥EH ∥FG,得 BD∥平面EFGH EH ∥平面BCD FG ∥平面ABD
A
EH
D
B
G
F
C
思考交流:
如图,正方体 ABCD A1B1C1D中1 ,P 是棱A1B1 的中点,过点 P 画一条直线使之与截面A1BCD1 平行.
线线平行
线面平行
反思2:能够运用定理的条 件是要满足六个字,
a
“面外、面内、平行”。 b
a // b
a //
反思3:运用定理的关键是找平行线。找平行线又经 常会用到三角形中位线定理。
例2. 如图,四面体ABCD中,E,F,G,H分别 是AB,BC,CD,AD的中点.
(1)E、F、G、H四点是否共面?
(1)面外,(2)面内,(3)平行。 3.应用判定定理判定线面平行的关键是找平行线
方法一:三角形的中位线定理;
方法二:平行四边形的平行关系。
课外探讨:
1、如何证明面面平行呢?
2、如图,已知有公共边AB的
E
两个全等矩形ABCD和ABEF
不在同一个平面内,P、Q对 F
角线AE、BD上的动点。
P
B
C
当P、Q满足什么条件时,
2.2.1直线与平面平行的判定
复习引入: 1.空间直线与平面的位置关系有哪几种?
直线a在平面内
a
直线a与平面相交
a A
直线a与平面平行
a
a
a∩=A
a//
2.如何判定一条直线和一个平面平行呢?
实例探究:
问题1:在黑板的上方装一盏日光灯,怎样才能使 日光灯与天花板平行呢?
问题2:将课本的一边紧贴桌面,沿着这条边转动 课本,课本的上边缘与桌面的关系如何呢?
Q
A
D
PQ∥平面CBE?
2、如图,在正方体ABCD——A1B1C1D1中, E为DD1的中点。试判断BD1与平面AEC的位 置关系,并说明理由。
D1
C1
A1 E D
A
ห้องสมุดไป่ตู้
B1
F
C
B
3、如图,在正方体ABCD——A1B1C1D1 中,E、F分别是棱BC与C1D1的中点。 求证:EF//平面BDD1B1.
D1
F
C1
D1
F
C1
M
以证明.
A
解:EF∥平面BCD。
证明:如图,连接BD。在△ABD中, E,
F分别为AB,AD的中点,
EF
∴EF ∥BD, 又EF 平面BCD,
D
C
BD 平面BCD,
B
∴EF ∥平面BCD。
解后反思:通过本题的解答,你可以总结出什么解题 思想和方法?
反思1:要证明直线与平面平行可以运用判定定理;
A1
A1
B1
B1
ND M
A
C E B
D A
C E B
4、如图,已知1-37,在三棱柱ABC—— A1B1C1中,D是AC的中点。
求证:AB1//平面DBC1 A1
C1
B1
P
D
A
C
B
小结: 1.直线与平面平行的判定: (1)运用定义; (2)运用判定定理:线线平行线面平行 2.应用判定定理判定线面平行时应注意六个字:
