作业5 电介质与电容、静电场能量
静电场的能量

【解】带电球形电容器的电场分布是对称的,由有介质中 的高斯定理可求其电场强度的大小为
E
Q
40 rr 2
则电场能量密度为
we
1 2
0
r
E
2
Q2
322 0 r r 4
现取半径为r、厚为dr的球壳为一体积元,则该体积元的体积为
dV 4r2dr
因此,球壳中储存的电场能量为
于是总能量为
dWe
wedV
Q2
8 0 r r 2
U Ed
将平行板电容器的电容公式(7-38)带入式(7-43),可得
We
=
1 2
CU
21 20r Sd(Ed )21 2
0r E2Sd
1 2
E 2V
上式说明了电场能量的携带者是电场本身。
由上式可得单位体积电场内所具有的电场能量为
we
We V
=
1 E2
2
上式表明,电场的强度越大,电场的能量密度也越大。上 式虽然是从平行板电容器中求得的,但可以证明,对于任意电 场,这个结论也成立。
对于非均匀电场,我们可以任取一体积元dV,可以认为dV 内是均匀电场,则在dV内电场所储存的能量为
dWe
wedV
1 E2dV
2
因此,整个电场的能量为
We
V dWe =
V wedV
1 E2dV
V2
【例7-11】一球形电容器,内、外半径分别为R1和R2,所 带电量分别为+Q和-Q,两球间充满相对电容率为εr的电介 质,如下图所示。求此电容器储存的电场能量是多少?
物理学
静电场的能量
1.1 电容器的静电能
电容器充电时,电源必须做功,才能克服电容器极板上
-静电场的能量和能量密度

l
-+ - + R1 - + R2 -+
_
_ _ _
++ + _ + + _ + ++ _
_
R2 Eb R2 U max Eb R1 ln 9.10103 V R1 2 e
9 – 5 静电场的能量 能量密度
C, U, q, E 的变化。 ( 1 ) 充电后切断电源 (2)充电后不切断电源
9 – 静电场的能量 5 静电场的能量 能量密度 第九章静电场中的导体和电介质 例9-9 求半径为R 带电量为Q 的均匀带电球的静电能。 解一:计算定域在电场中的能量 球内 r 处电场
Qr E , 3 4 0 R (r R)
1 2 0 R Qr 2 4r dr W 0 E dV 0 3 2 2 4 0 R
第九章静电场中的导体和电介质
例 1.平行板电容器,其间充满介质 r , 求下列情况充入介质前后的
A
K 300V
E0
d
B
r
U Ed U0
(1)q不变 解 : 提示: (1)q不变
(2)U不变
C r C0 E
r
U (2)U不变 C r C0 E 不变 q CU r CU d S U 基本公式: C E d d q C C r C0 U
Q2 We 8π R1
(孤立导体球贮存的能量)
9 – 5 静电场的能量 能量密度
第九章静电场中的导体和电介质
例2 如图圆柱形电容器,中间是空气,空气的击 2 6 -1 穿场强是 Eb 310 V m,电容器外半径 R2 10 m. 在空气不被击穿的情况下,内半径 R1 ? 可使电容器 存储能量最多. ( 空气 r 1 )43; ++ _
电容与能量 (先讲电容后讲电介质)讲解

1. 导体的静电感应
静电感应 静电平衡
静电屏蔽
导体是等势体 E内=0
导体表面是等势面
电荷分布在导体的外表面:
E外
0
1 R
E表 表面
2. 电介质的极化
介质的极化
极化规律——出现束缚电荷
E E 0
r
二、三个概念
①电位移矢量 D E 0rE
②电容
③电场的能量
§3 电容和电容器
一、孤立导体的电容
1.孤立导体: 指导体周围没有其它带电体和导体
2.孤立带电导体球: 已知:半径R、电量Q
导体球面的电势
ε Q
o++ + +
+
+ +
+
R
+
U
E dl
R
Q
R 4 0r 2 dr
Q
4 0R
当电势一定:半径越大,所带电荷越多
+ 当半径一定:所带电荷增加,电势相应增加
1 2
D
EdV
②电容器储能
W 1 Q2 1 C U2
2C 2
[例]空气平板电容器。已知S,d,ε0,εr,U(1)在 充电后,注入介质(电源不断开);(2)在充 电后,电源断开,注入介质. 比较U,C,E,D,We,σ如何变化。
解:设空气电容器充电后,电场为
E
0
,
电压为U, 为电荷面密度,
q
4 0
(2) R
q U AB
4
0
(
R 2
)
C
3.两个任意形状导体组成的系统的电容
静电场中的电介质和电场能量
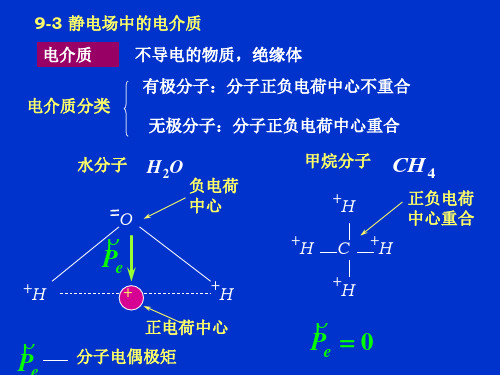
a
E0
E E0
E E0
E0
无限大均匀电介质中,令 E 介质中 真空中
E E0 r 1
E E0 r 1
r
相对电容率
9 – 3 静电场中的电介质
三 电介质对电容的影响
第九章静电场中的导体与电介质
U0
Q
+++++++
U
C0
-------
电介质中的电场强度 极化电荷与自由电荷的关系
E E0 E ' r r 1 E' E0 r E0 0 / 0 E ' ' / 0
r 1 ' 0 r
E0
d
r
-+ + + +-+-+-+ + + + + - -
E0
E' E
1 ' E dS (Q0 Q )
S
0
0 + + + + + + + + + + + ' - - - - - S
Q0 E dS
S
r
定义电容率
S
0 r E dS Q0
0 r
0 r
+ + + + + + 0 - - - - - - - - - - '
9-3 静电场中的电介质 电介质 不导电的物质,绝缘体 有极分子:分子正负电荷中心不重合
《静电场能量》课件

D1 1
r1
h
2
D2
r
2
在分界面上无自由电荷时,电位移 的法向分量是连续的。界面两侧电 场强度的法向分量是不连续的。
二、切向分量
E dl 0
ABCDA
E dl E dl E dl E dl 0
AB
R1
R2
解:若电容器两极板上电荷的分布是均匀的, 则球壳间的电场是对称的。由高斯定理可求得 球壳间的电场强度的大小为
E=
Q
4
r
2
电场总能量为
电场的能量密度为
e
1 2
E
2=
Q2
32 2
r4
取半径为r、厚为dr的球壳,其体
积为dV=4πr2dr。所以此体积元内
Q R2
2
We R1 8 r 2 dr
E1t=E2t
D1t = D2t
1 2
9-8 压电效应 铁电体 驻极体
一、压电效应
•压电效应(正压电效应):某些固体电介质,当它们发生机械形 变时,会产生极化,在它们相对的两个面上将产生异号的极化 电荷。这种因机械形变而产生的电极化现象称为压电效应。 •电致伸缩(逆压电效应):在电场的作用下,晶体发生机械形变。 •应用:
热驻极法 电驻极法 •应用:电容传声器、拾音器、拾振器等。
小结
•静电场的能量 •能量密度
W Q2 1 CU 2 1 QU
2C 2
2
we
1 2
0
r
E
2
1 2
DE
作业:
思考题:
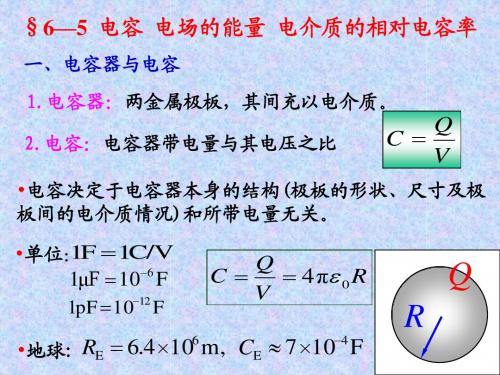
6—5 电容 电场的能量 电介质的相对电容率
6
Q C 4 π 0 R V
Q
6 4 R 6 . 4 10 m, C 7 10 F •地球: E E
R
二、电容的计算
步骤:
例1
1)设两极板分别带电 Q ; 2)求 E ; 3)求 U ;4)求C
平板电容器
+ + + + + +
d
(1)设两导体板分别带电 Q (2)两带电平板间的电场强度 Q E 0 0S
R
1 1 ( )dx x dx
o
d R d ln ln π 0 R π 0 R
x x dx
E E
P
d 单位长度的电容 C π 0 ln R U
d
三、电容器的串并联
C1
+
1
电容器的并联
C C1 C2
2 电容器的串联
+
C2
C1
C2
2 b 2 1
l
-+ -+ -+ -+
_
_
R1
R2
_ _
++ + _ + + _ ++ + _
_
R2 Eb R2 U max Eb R1 ln 9.10103 V R1 2 e
五、电介质 电介质—绝缘介质
1.电介质内没有可以自由移动的电荷 在电场作用下,电介质中的电荷只能在分子范围内移动。
•物理意义:电场 是一种物质,它具 有能量.
We we dV
V
V
1 2 0 E dV 2
例5 如图所示,球形电容器的内、外半径分别为R1 和R2,所带电荷为Q.问此电容器贮存的电场能量为多少?
静电场的能量

E
A
d
B
⑵球形电容器的电容
场强分布E q 4 0 r 2
q
q
r
B A
RA
电势差
1 1 u A uB dr ( ) 2 4 0 r 4 0 RA RB RA
RB
RB
q
q
4 0 RA RB q 电容C uA u B RB RA
当RB 时,C 40 RA
B
X
P
E 2 0 x 2 0 ( d x )
导线间电势差
B
a
d a d a d ln ln u A uB E dl E dx 0 a 0 a A a
电容
C
u A uB
板电容器。 已知d1、r1、d2、 r2、S
一、电容与电容器 定电位差下的电荷储藏量 ;电容(或称电容量) 是表征电容器容纳电荷本领的物理量。 1、孤立导体的电容 孤立导体: 周围没有其它导体和带电物体的导体 实验发现: 孤立导体上的 q U q CU q 其中 C 称为孤立导体的电容 U 它反映了导体容纳电荷的能力,其意义是: 导体的电势每升高一个伏特所需的电量。 例:求孤立导体球的电容 q q U E dl r dl R R 4 r 3 40 R 0
A
q1 C q2
U AC
B
UCB
q q q U AB C1 C 2 C 1 1 1 C C1 C 2
q
A B
C
二、电容器的储能 电容器的充放电过程
a
K b
q
q
Q
终 了 时 刻
电磁学-电容 静电场能量(执行)

a
U
C
b
b
特点: Uc Uc1 Uc2 Uc3 Uc4
qab qc1 qc2 qc3 qc4
qc1 : qc2 : qc3 : qc4 C1U : C2U : C3U : C4U
a
C1 C2 C3 C4
C
U
b
特点: Uc Uc1 Uc2 Uc3 Uc4 qab qc1 qc2 qc3 qc4 同除Uc qc1 : qc2 : qc3 : qc4 C1U : C2U : C3U : C4U
U c1
:Uc2
:Uc3
:Uc4
qc1 C1
:
qc 2 C2
:
qc3 C3
:
qc 4 C4
1:1:1:1 C1 C2 C3 C4
1 1 1 1 1 C C1 C2 C3 C4
若只有两个电容串联
C1 C2
11 1
C C1 C2
C C1C2 C1 C2
2、电容器的并联 a
C1 C2 C3 C4
中间充满电介质.
假定电容器带电+Q,-Q;
极板间电场是球对称的:
RB
E
Q
4 r
2
极板间电位差:
方向:沿半径向外
U AB
RRAB Edr
Q
4
RRAB
1 r2
dr
Q( RB RA )
4RA RB
C
Q U AB
4RA RB
RB RA
归纳:求电容器电容的方法
设极板带电荷Q 求极板间E 求极板间U C QU
则如:何Uq消AA除 C其它E、导F体上的的影感响应?电荷静影电响屏UA蔽
F E
UB=0 UA–UB=UA
静电场中的导体电介质电场能量s

∫∫ E ⋅
φ侧 +
dS =
φ上底
∑q
ε+0φ下底
∴E = λ 2πε 0 r
φ上底
φ=
= φ下底 =
φ侧 = ∫∫侧
0, ∵ EdS
E ⊥ dS
cos θ
=
E
2πrl
=
λl ε0
10
∴E = λ
高
2πε 0 r
斯 面
柱面间的电势差为:
∫ U AB
= =
B
E ⋅ dl
A
=
∫RB
RA
Edr
=
q ln RB
∫ ∫ w
=
1 2
ε
0
E
2
W
=
dW
V
=
V
1ε
2
0
E
2dV
积分范围是电场 存在的所有空间
∫ 根据高斯定理可知:
E
=
⎧ ⎨ ⎩
= =
0 Q
4πε 0r 2
r<R r>R
场是非均匀的,但是有什么特点呢?
dW = W=
1 2
ε0
E
2dV
1 2
ε0
(
Q
4πε0r2
)2
dV
取什么为积分微元dV 呢?
V = 4π r3 dV = 4πr2dr
电容 电容器 电场能量
作业:练习15 教材6-26
1
静电场
电荷 库仑定律 静电场 电场强度 电通量 高斯定理 静电场的环路定理 电势能 电势 电势差
等势面 电势与电场强度的关系 静电场中的导体 静电场中的电介质
电位移 有电介质时的高斯定理
电容器和电介质

可以证明,上式虽然从特例导出,但这是一个普遍适用公式,对任意电场都是正确的,因此,计算任一带电系统整个电场的能量为:
电场空间所存储的能量
解:
例1 如图所示,球形电容器的内、外半径分别为R1和R2,所带电荷为±Q.若在两球壳间充以电容率为 的电介质,问此电容器贮存的电场能量为多少?
+
+
+
Q
-Q
-
讨论:改变电容器的电容的方法 S d
2) 同轴柱形电容器的电容
RA
RB
L
设长为L, 带电量为q , 内半径为 , 外半径为
3) 同心球形电容器的电容
孤立导体球电容
+
+q
+
单击此处输入你的正文
+
设内球面半径RA,外球面半径RB,带电量为q + + + +
(2)介质外任一点P电势
球为等势体,电势为,
介质内任一点Q电势
R
PART 01
例4 常用的圆柱形电容器,是由半径为R1的长直圆柱导体和同轴的半径为R2的薄导体圆筒组成,并在直导体与导体圆筒之间充以相对电容率为 的电介质.设直导体和圆筒单位长度上的电荷分别为 和 .求(1)电介质中的电场强度、电位移和极化强度;(2)电介质内、外表面的极化电荷面密度; (3)此圆柱形电容器的电容.
+ + + + + + + + +
- - - - - - - - -
+
当电容器极板带电 ,两板电势差为 时,把电荷元 从B板移到A板,外力克服电场力作功为:
第十七讲§5.6静电场的能量—习题课

第十七讲 §5.6静电场的能量—习题课 一、电容和电容器1、电容:UqC =是描述孤立导体带电而引起自身电势变化的物理量。
即孤立导体的电容。
2、电容器:BA U U qC -=是描述两个导体组成电容器的电容,二者是相互关联的,即将一个导体放在无限远处就为孤立导体的电容。
二、电容器的储能(电容器的能量):静电场是一个物理场。
此物是否是物质的?其中的一个重要特性就是是否具有能量的特性,即在静电场中移动电荷是需要静电场力做功,这说明静电场是具有能量的。
下面通过对静电场形成能量的过程来说明静电场是具有能量的。
1、带电体的能量:外力做功就等于带电体的能量(电势能)P E W = ①把dq 从∞转移到带电体上,需外力做的微功:()Udq dqU dW U U dq dW A U B B A B ==−−−→−-==∞→0, q Q②把Q 从∞源源不断的转移到带电体上,需外力做的总功:⎰⎰==QUdq dW W 02、电容器的能量:通过电容器储能的过程来推导电容器能量的公式。
①把dq 从A B →上,需外力做的微功:Udq dW = −−→−=UqC dq CqdW =②把Q 从A B →上,需外力做的总功:QU CU C Q dq C q dW W Q21212220=====⎰⎰③电容器的能量:外力所做的总功就等于电容器的能量。
QU CU C Q dq C q dW W Qe 21212220=====⎰⎰可见,外力克服静电力所做的功,就是电容器的带电过程,即非静电能转化为静电能的过程,满足能量守恒定律。
上述三个表达式都非常有用,希望能熟记。
3、静电场的能量 能量密度①电场的能量密度(能量的体密度):单位体积内电场的能量。
()2020221V 2121E Ed d SV CU V W w e e εε==== Sd V = 可见,电能存在于电场之中,电场是电能的携带者,电场的能量是电场物质性的一个重要标志!静电场是物质的,是不以人们的意志为转移,是非精神的。
第二课堂 电介质、电容器及能量

均匀电介质棒,其半径为r,高度为h,相对介电常量
为r,其轴线与板面垂直,如图所示.试求圆柱电介质
中点的电场强度 和电位移矢量 .并求当h>>r时,介质
中点E 、D 的近似值. 解:假设极板上的电荷仍均匀分布 根据场的分布及边界条件得
E1t E2t 0 D2t D1t 0 D2 n S 0( D1n 0) S
4a
U BA U B
场具有球对称性
a
3a
解: a r 3a
Q
D dS DdS D4r 2 QA
S S
4a
a
3a
D QA QA E D 2 0 r 4 0 r r 2 4r r 4a D dS D4r 2 Q QA
P
1 1 2 2 A 外 A 静 mv mv 0 2 2 1 静电场的能量 We 2 D EdV V 1 Q2 W = CU 2 = 电容器的能量 2 2C
1 n W qiU i 点电荷系相互作用能(互能) 2 i 1
电势能
WP qUP
带电体的静电能 (自能):
3
1
R1
2
3
自测练习 p27 3
1)通电后维持电压不变插入 2)通电后断开再插入 A
C C1 C 2 S S ε0 ε 0ε r 2 2 d d ε 0S 1 ε r 2d Q CU C0 U 0 2 C0 U0 U U0 1 ε r C 2 EA : E A0 1 ε r
E'
E0
E' (r ) = E+ (r - l ) + E- (r + l ) 2 2 e l e l (r ) (r ) 2 3 2 3 0 0
大连理工大学大学物理作业5(静电场五)及答案详解
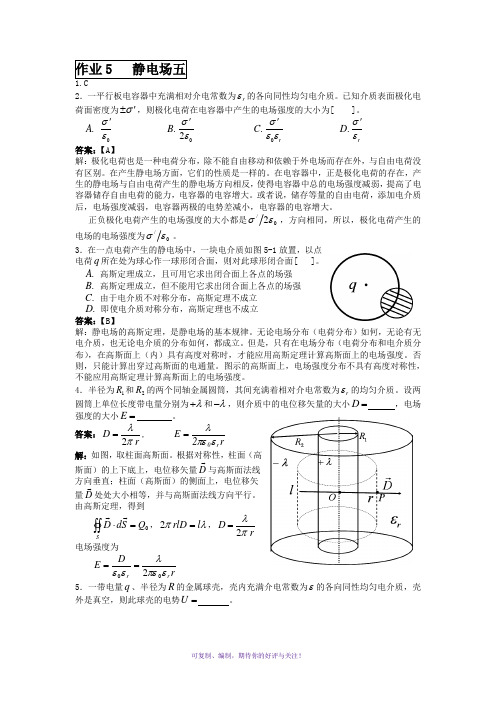
作业5 静电场五2.一平行板电容器中充满相对介电常数为r ε的各向同性均匀电介质。
已知介质表面极化电荷面密度为σ'±,则极化电荷在电容器中产生的电场强度的大小为[ ]。
.A0σε' .B 02σε' .C 0r σεε' .D rσε' 答案:【A 】解:极化电荷也是一种电荷分布,除不能自由移动和依赖于外电场而存在外,与自由电荷没有区别。
在产生静电场方面,它们的性质是一样的。
在电容器中,正是极化电荷的存在,产生的静电场与自由电荷产生的静电场方向相反,使得电容器中总的电场强度减弱,提高了电容器储存自由电荷的能力,电容器的电容增大。
或者说,储存等量的自由电荷,添加电介质后,电场强度减弱,电容器两极的电势差减小,电容器的电容增大。
正负极化电荷产生的电场强度的大小都是0/εσ,方向相同,所以,极化电荷产生的电场的电场强度为0/εσ。
3.在一点电荷产生的静电场中,一块电介质如图5-1放置,以点电荷q 所在处为球心作一球形闭合面,则对此球形闭合面[ ]。
.A 高斯定理成立,且可用它求出闭合面上各点的场强 .B 高斯定理成立,但不能用它求出闭合面上各点的场强 .C 由于电介质不对称分布,高斯定理不成立 .D 即使电介质对称分布,高斯定理也不成立答案:【B 】解:静电场的高斯定理,是静电场的基本规律。
无论电场分布(电荷分布)如何,无论有无电介质,也无论电介质的分布如何,都成立。
但是,只有在电场分布(电荷分布和电介质分布),在高斯面上(内)具有高度对称时,才能应用高斯定理计算高斯面上的电场强度。
否则,只能计算出穿过高斯面的电通量。
图示的高斯面上,电场强度分布不具有高度对称性,不能应用高斯定理计算高斯面上的电场强度。
4.半径为1R 和2R 的两个同轴金属圆筒,其间充满着相对介电常数为r ε的均匀介质。
设两圆筒上单位长度带电量分别为λ+和λ-,则介质中的电位移矢量的大小D = ,电场强度的大小E = 。
