初三数学月考卷
上海市静安区市西初中九年级数学月考卷(含答案)
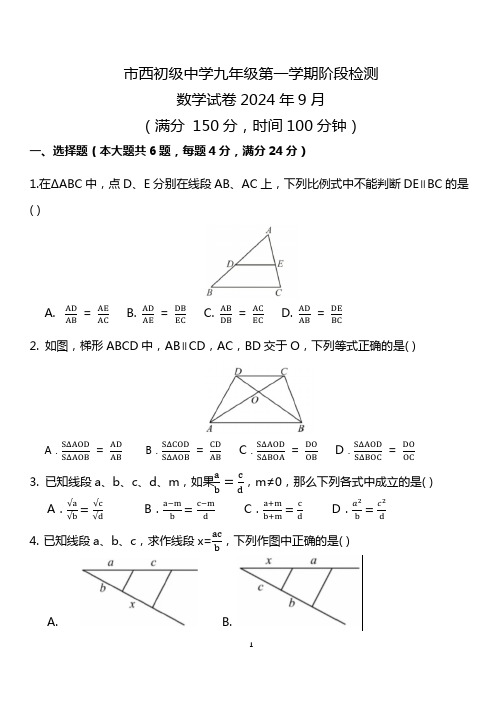
市西初级中学九年级第一学期阶段检测数学试卷2024年9月(满分 150分,时间100分钟)一、选择题(本大题共6题,每题4分,满分24分)1.在ΔABC中,点D、E分别在线段AB、AC上,下列比例式中不能判断DE∥BC的是( )A.ADAB = AEACB. ADAE= DBECC. ABDB= ACECD. ADAB= DEBC2. 如图,梯形ABCD中,AB∥CD,AC,BD交于O,下列等式正确的是( )A.SΔAODSΔAOB = ADABB.SΔCODSΔAOB= CDABC.SΔAODSΔBOA= DOOBD.SΔAODSΔBOC= DOOC3. 已知线段a、b、c、d、m,如果ab =cd,m≠0,那么下列各式中成立的是( )A.√a√b =√c√dB.a−mb=c−mdC.a+mb+m=cdD.a2b=c2d4.已知线段a、b、c,求作线段x=acb,下列作图中正确的是( )B.A.C. D.5.下列语句叙述正确的是( )A.有一个角是30°的等腰三角形都相似B.有一个角是30°的直角三角形都相似C.有一个角是30°的锐角三角形都相似D.有一个角是30°的钝角三角形都相似6.如图,DE∥BC,EF∥AB,则下列式子中成立的是( )A. ADDB = BFECB. ABBC= DEACC. EFAB= ACCED. ADDB= BFFC二、填空题(本大题共12题,每题4分,满分48分)7.已知线段a=5cm,b=20mm,则a:b= 。
8.线段AB是线段MN、CD的比例中项,且AB=3cm,MN=4cm,则CD长为 。
9.某班同学要测量学校升国旗的旗杆高度,在同一时刻,量得某同学的身高是1.5米,影长是1米,且旗杆的影长为8米,则旗杆的高度是 米。
10.如图,AE=5,4C=8,AB=10,当BD= 时,DE∥BC。
11.如图,AD∥EF∥BC,AEEB =23,DF=4,则DC= cm。
九年级数学第三次月考卷(12月份)

九年级数学第二次月考测试卷(九年级上册 总分120分)班级 姓名 座号 得分一、填空题(每小题3分,共30分)1.____________ __。
2. 方程x 2=x 的根是 ; 配方:x 2-10x +______=(x -______)23. 已知方程x 2−7x +12=0的两根恰好是Rt △ABC 的两条边的长,则Rt △ABC•的第三边长为_____ ___。
4. 如图,ΔABC 按顺时针方向旋转一个角后成为ΔADE 。
已知∠B =93°,∠AED =48°,则旋转角等于 (度)。
5. 如图,已知圆心角∠AOB 的度数为100°,则圆周角∠ACB 等于________(度)。
6. 如图,MN 是⊙O 的直径,PN 是⊙O 的弦,OD ⊥PN 于D ,OD=2cm ,∠DON 的度数是60°,则PN= cm 。
7. 如图,在△ABC 中,∠ABC =60°,∠ACB =80°,点O 是内心,则∠BOC 的度数为 。
8. 已知圆锥底面半径为2cm ,母线长为6cm ,则该圆锥的侧面积是 cm 2。
9. 掷一枚普通的正方体骰子,出现点数为偶数的概率为 。
10. 从装有5个红球和3个白球的袋中任意取4个,那么取到的“至少有1个是红球”与“没有红球”的概率分别为 和 。
二、选择题(每小题3分,共18分)11. 如果代数式x 2+4x +4的值是16,则x 的值一定是( )A 、−2B 、2√3,−2√3C 、2,−6D 、30,−34 12. 下列计算正确的是( )①694)9)(4(=-⋅-=--;②694)9)(4(=⋅=--;EDCB AOBCA第7 题第5题第4题 第6题M③145454522=-⋅+=-;④145452222=-=-;A 、1个B 、2个C 、3个D 、4个 13. 下列图中不是中心对称图形的是( )A 、①③B 、②④C 、②③D 、①④14. 半径为4的⊙O 中有弦AB ,以AB 为折痕对折,劣弧恰好经过圆心O ,则弦AB 的长度等于( )A 、2√3B 、4C 、4√3D 、8√3 15. 在RtΔABC 中,∠C=90°,AC=3cm ,BC=4cm ,以C 为圆心,r 的长为半径的圆与RtΔABC的斜边有一个交点,则r 的值为( )A 、2.4cmB 、3 cmC 、4 cmD 、2.4 cm 或4 cm 16. 下列事件是随机事件的是( )A 、两个奇数之和为偶数B 、某学生的体重超过200千克C 、宁波市在六月份下了雪D 、三条线段围成一个三角形 三、(第17、18题每小题5分,第19题7分,共27分) 17. 计算:(1) 12(√3+√2)−34(√2−√27) (2) 486)2718. 解方程:(1) x 2−3x −2=0 (2) (x +8)2−5(x +8)+6=019. 已知关于x 的方程210x mx --=(1)试判断此方程根的存在情况;(2)对m 取一个你喜欢的值代入,求出该方程的实数根。
初三数学月考测试卷及答案

一、选择题(每题3分,共30分)1. 下列各数中,正数是()A. -2.5B. 0.001C. -√9D. 3.142. 若a < b,则下列不等式中正确的是()A. a + 2 < b + 2B. a - 2 > b - 2C. 2a < 2bD. 2a > 2b3. 在等腰三角形ABC中,若AB = AC,且∠BAC = 60°,则∠ABC =()A. 30°B. 45°C. 60°D. 90°4. 下列函数中,是反比例函数的是()A. y = x + 2B. y = 2xC. y = 2/xD. y = 3x^25. 已知一次函数y = kx + b(k≠0)的图象与x轴、y轴分别交于A、B两点,若OA = 3,OB = 4,则k的值为()A. 1/3B. 1/4C. 3/4D. 4/36. 在直角坐标系中,点P(2,3)关于原点O的对称点是()A.(2,3)B.(-2,-3)C.(3,2)D.(-3,-2)7. 若等差数列{an}中,a1 = 2,公差d = 3,则a5 =()A. 10B. 13C. 16D. 198. 在△ABC中,若∠A = 45°,∠B = 30°,则sinC =()A. 1/2B. √3/2C. 1/√2D. √3/29. 若a,b,c是等比数列的连续三项,且a + b + c = 18,b = 3,则a =()A. 3B. 6C. 9D. 1210. 下列各式中,正确的是()A. (a + b)^2 = a^2 + b^2B. (a - b)^2 = a^2 + b^2C. (a + b)^2 = a^2 + 2ab + b^2D. (a - b)^2 = a^2 - 2ab + b^2二、填空题(每题3分,共30分)11. 若m^2 - 5m + 6 = 0,则m的值为______。
九年级数学上册第一次月考卷(1)

九年级数学上册第一次月考卷(1)一、选择题(每题4分,共40分)1. 下列选项中,有理数的是()A. √3B. πC. 3.14D. √12. 已知a、b是实数,且a+b=5,ab=3,则a²+b²的值为()A. 7B. 16C. 23D. 253. 下列各数中,最小的数是()A. |3|B. (3)²C. 3D. (3)³4. 下列各式中,是二次根式的是()A. √(x+1)B. √(x²1)C. √(x³1)D. √(x²+1)5. 已知一组数据的方差是5,那么这组数据每个数都加上3后,方差是()A. 2B. 5C. 8D. 166. 下列函数中,正比例函数的是()A. y=x²B. y=2x+1C. y=3xD. y=x²+17. 已知一组数据为2,3,5,7,x,平均数为5,则x的值为()A. 4B. 6C. 8D. 108. 下列图形中,一定是轴对称图形的是()A. 矩形B. 梯形C. 平行四边形D. 正五边形9. 下列各式中,能用平方差公式分解的是()A. x²2x+1B. x²3x+2C. x²4x+4D. x⁴110. 已知一组数据为4,6,8,10,12,则这组数据的众数为()A. 4B. 6C. 8D. 10二、填空题(每题4分,共40分)11. 已知|x|=3,则x的值为______。
12. 若|a|=5,|b|=3,则a+b的取值范围是______。
13. 已知一组数据为1,2,3,4,x,平均数为3,则x的值为______。
14. 下列函数中,______是反比例函数。
15. 已知等腰三角形的底边长为10,腰长为8,则该三角形的周长为______。
16. 一次函数y=kx+b的图象经过一、二、四象限,则k的取值范围是______。
17. 下列图形中,______是中心对称图形。
初三数学月考试卷带答案

考试时间:120分钟满分:100分一、选择题(每题3分,共30分)1. 下列数中,不是有理数的是()A. 3/5B. -2/3C. √4D. √-12. 下列图形中,是轴对称图形的是()A. 等腰三角形B. 等边三角形C. 平行四边形D. 长方形3. 已知一次函数y=kx+b的图象经过点(2,3),且k<0,则该函数的图象位于()A. 第一、二象限B. 第一、三象限C. 第二、四象限D. 第三、四象限4. 若x²-2x=0,则x的值为()A. 0B. 1C. 2D. 0或25. 在△ABC中,若∠A=60°,∠B=45°,则∠C的度数是()A. 75°B. 60°C. 45°D. 30°6. 下列命题中,正确的是()A. 平行四边形一定是矩形B. 矩形一定是正方形C. 对角线相等的四边形一定是矩形D. 对角线相等的四边形一定是菱形7. 已知a、b、c是等差数列的前三项,且a+b+c=12,a+c=8,则b的值为()A. 2B. 4C. 6D. 88. 若sinα=1/2,且α在第二象限,则cosα的值为()A. √3/2B. -√3/2C. 1/2D. -1/29. 下列函数中,是反比例函数的是()A. y=2x+3B. y=x²C. y=3/xD. y=x³10. 若方程ax²+bx+c=0(a≠0)的两根是x₁和x₂,则x₁+x₂的值为()A. b/aB. c/aC. -b/aD. c/b二、填空题(每题5分,共30分)11. 若a、b、c成等差数列,且a+b+c=12,a+c=8,则b=______。
12. 在直角坐标系中,点P(-2,3)关于x轴的对称点坐标是______。
13. 一次函数y=kx+b的图象与y轴的交点坐标是______。
14. 若sinα=√2/2,则cosα=______。
2022学年荆州市九年级数学上学期第一次月考卷附答案解析

2022学年荆州市九年级数学上学期第一次月考卷2022.09一、选择题(本大题共10小题,每小题只有唯一正确答案,每小题3分,共30分) 1.下列函数中,属于二次函数的是( )A .y=(x +l )2-x 2B .y=21x C .y=-5x 2D .y=2x -l2.把一元二次方程(x +2)(x -2)=x 化成一般形式,正确的是( )A .x 2-x +4=0B .x 2-x -4=0C .x 2+x +4=0D .x 2+x -4=0 3.已知x =m 是一元二次方程x 2-3x -1=0的一个根,则代数式m 2-3m -2022的值为( ) A .-2021B .-2023C .2021D .20234.一元二次方程2x 2-4x +2=0的根的情况是( ) A .有两个不相等的实数根 B .有两个负实数根 C .没有实数根D .有两个相等的实数根5.受国际油价影响,今年我国汽油价格总体呈上升趋势.某地92号汽油价格六月底是7.5元/升,八月底是8.4元/升.设该地92号汽油价格这两个月平均每月的增长率为x ,根据题意列出方程,正确的是( )A .7.5(1+x 2)=8.4B .7.5(1+x )2=8.4C .8.4(1-x )2=7.5D .7.5(1+x )+7.5(1+x )2=8.46.抛物线y =-3x 2与y =2x 2相同的性质是( ) A .有最高点 B .对称轴是x 轴 C .开口向上 D .顶点坐标 7.设a ,b 是方程x 2+x -2022=0的两个实数根,则a +b -ab 的值为( ) A .2023 B .-2021 C .2021 D .-2023 8.用配方法解方程x 2-4x -1=0时,原方程应变形为( )A .(x -2)2=3B .(x -2)2=5C .(x -4)2=5D .(x -4)2=39.若等腰三角形一条边的边长为4,另两条边的边长是关于x 的一元二次方程x 2-10x +c =0的两个根,则c 的值是( ) A .25B .24C .25或24D .36或1610.如图,平行于x 轴的直线AC 分别交抛物线21x y =与322x y =于B ,C 两点,过点C 作y 轴的平行线交1y 于点D ,直线DE∥AC 交2y 于点E ,则DCDE 2的值是( )A .336-B .13-C .3D .33-二、填空题(本大题共6小题,每小题3分,共18分)11.已知关于x 的方程x 2+kx -10=0的一个根是-2,则k =______. 12.若关于x 的方程x 2-8x +m =0有两个相等的实数根,则实数m =______.13.为增强学生身体素质,某校开展篮球比赛,赛制为单循环形式(每两队之间赛一场).现计划安排21场比赛,应安排______个球队参赛.14.若菱形的两条对角线的长是方程x 2-8x +6=0的两根,则菱形的面积是______. 15.如图是一座抛物线形拱桥侧面示意图,水面宽AB 与桥长CD 均为36 m ,桥拱顶部O 离水面的距离为6 m ,以桥拱顶点O 为原点,桥面为x 轴建立平面直角坐标系.OD 的中点E 到桥拱的距离EF 为______ m. 16.我们知道,一元二次方程x 2=-1没有实数根,即不存在一个实数的平方等于-1.若我们规定一个新数i ,使其满足i 2=-1(即方程x 2=-1有一个根为i ),并且进一步规定:一切实数可以与新数进行四则运算,且原有的运算法则仍然成立,于是有i 1=i ,i 2=-1,i 3=i 2•i =(-1)•i =-i ,i 4=(i 2)2=(-1)2=1,从而对任意正整数n ,我们可以得到i 4n +1=i 4n •i =(i 4)n •i =i ,同理可得i 4n +2=-1,i 4n +3=-i ,i 4n =1,那么i +i 2+i 3+i 4+…+i 2021+i 2022的值为______. 三、解答题(本大题共8小题,共72分) 17.(本题满分8分)解方程: (1)x 2-6x +4=0 (2)(x +3)(x -2)=2x18.(本题满分8分)已知函数y=232)2(-++k k x k 是关于x 的二次函数. (1)求k 的值;(2)当k 为何值时,抛物线有最低点? (3)当k 为何值时,函数有最大值?19.(本题满分8分)已知关于x 的一元二次方程x 2-(2m -1)x +m 2+2=0. (1)若该方程有两个实数根,求m 的取值范围;(2)若方程的两个实数根为x 1,x 2,且132221=+x x ,求m 的值.20.(本题满分8分)阅读材料,解答问题:材料1:为了解方程(x 2)2-13x 2+36=0,如果我们把x 2看作一个整体,然后设y =x 2,则原方程可化为y 2-13y +36=0,经过运算,原方程的解为x 1=2,x 2=-2,x 3=3,x 4=-3.我们把以上这种解决问题的方法通常叫做换元法.材料2:已知实数m ,n 满足m 2-m -1=0,n 2-n -1=0,且m≠n ,显然m ,n 是方程x 2-x -1=0的两个不相等的实数根,由根与系数的关系可知m +n =1,mn =-1. 根据上述材料,解决以下问题: (1)解方程(x 2-1)2+(x 2-1)-12=0;(2)已知实数a ,b 满足2a 2-6a +3=0,2b 2-6b +3=0且a≠b ,求ba 11 的值.21.(本题满分8分)某商店以30元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x (元/千克)之间的函数关系如图所示. (1)根据图象求y 与x 的函数关系式;(2)商店想在销售成本不超过2500元的情况下,使销售利润达到4000元,销售单价应定为多少?22.(本题满分10分)已知平行四边形ABCD 的两边AB ,AD 的长是关于x 的方程x 2-mx +2m =0的两个实数根.(1)m 为何值时,平行四边形ABCD 是菱形?求出这时菱形的边长; (2)若AB 的长为3,求平行四边形ABCD 的周长.23.(本题满分10分)如图,Rt∥ABC 中,∥C =90°,AC =12cm ,BC =15cm ,点P 从B 点出发以每秒3cm 的速度向C 点运动,同时点Q 从C 点出发以每秒2cm 的速度向A 点运动,当其中一个点到达终点时,另一点自动停止运动,设运动时间为t (s ). (1)用含t 的代数式表示CP ,CQ 的长,并直接写出t 的取值范围; (2)当∥CPQ 的面积为18cm 2时,求t 的值; (3)设y =PQ 2,求y 与t 的关系式.24.(本题满分12分)某“5A ”景区决定在“10.1”国庆节期间推出优惠套餐,预售“亲子两人游”套票和“家庭三人行”套票,预售中的“家庭三人行”套票的价格是“亲子两人游”套票的2倍. (1)若“亲子两人游”套票的预售额为27000元,“家庭三人行”套票的预售额为18000元,且“亲子两人游”套票的销售量比“家庭三人行”套票的销售量多400套,求“亲子两人游”套票和“家庭三人行”套票的价格;(2)套票在出售当天计划推出“亲子两人游”套票1600张,“家庭三人行”套票600张,由于预售的火爆,景区决定将“亲子两人游”套票的价格在(1)中价格的基础上增加a 元,而“家庭三人行”套票在(1)中价格的基础上增加32a 元,结果“亲子两人游”套票的销量比计划少20a 套,“家庭三人行”套票的销售量与计划保持一致,最终实际销售额比计划销售额多12000元,求a 的值.(票价均为整数)参考答案 一、选择题1.C2.B3.A4.D5.B6.D7.C8.B9.C 10.A 二、填空题11.﹣3 12.16 13.7 14.3 15.1.5 16.i ﹣1 三、解答题17.解:(1)∵a =1,b =﹣6,c =4, ∴△=36﹣16=20>0,∴x =2206±=53±, 解得:x 1=53+,x 2=53-; ………(4分)(2)方程整理得:x 2﹣x ﹣6=0, 分解因式得:(x ﹣3)(x+2)=0,解得:x 1=3,x 2=﹣2. ………(8分)18.解:(1)∵函数y=232)2(-++k k x k 是关于x 的二次函数, ∴k 满足k 2+3k-2=2,且k+2≠0,∴解得:k 1=1,k 2=-4; ………(4分)(2)∵抛物线有最低点, ∴图象开口向上,即k+2>0, ∴k =1; ………(6分)(3)∵函数有最大值,∴图象开口向下,即k+2<0, ∴k =-4. ………(8分)19.解:(1))∵该方程有两个实数根,∴△=[﹣(2m ﹣1)]2-4(m 2+2)≥0,∴m ≤﹣47; ………(4分)(2)∵x 1+x 2=2m ﹣1,x 1x 2=m 2+2,∴13)2(2)12(2)(22212212221=+--=-+=+m m x x x x x x , 解得m=4或-2, ………(7分)∵m ≤﹣47,∴m=-2. ………(8分)20.解:(1)设y =x 2﹣1,则原方程可化为y 2+y ﹣12=0, 解得y 1=3,y 2=-4,当y=3时,x 2﹣1=3,x=±2,当y=-4时,x 2﹣1=-4,方程无解,所以原方程的解为x 1=2,x 2=-2; ………(4分)(2)根据题意可知,a ,b 是方程2x 2﹣6x+3=0的两个不相等的实数根,由根与系数的关系可知a+b =3,ab =23,所以b a 11+=ab b a +=2. ………(8分)21.解:(1)设y=kx+b ,根据题意可得⎩⎨⎧=+=+012016040b k b k ,解得⎩⎨⎧=-=2402b k ,所以y 与x 的函数关系式为y=-2x+240; ………(3分)(2)设销售单价定为x 元/千克时,销售利润达到4000元,根据题意可列方程 (x-30)(-2x+240)=4000,解得x 1=70,x 2=80, ………(6分)当x=70时,y=100,成本为100×30=3000>2500, 当x=80时,y=80,成本为80×30=2400<2500, 所以销售单价应定为80元/千克. ………(8分)22.解:(1)∵平行四边形ABCD 是菱形, ∴AB=AD ,∴方程x 2﹣mx+2m =0有两个相等的实数根,∴△=(﹣m )2﹣8m =0,∴m 1=0(舍),m 2=8, ………(3分)当m =8时,方程为x 2﹣8x+16=0, 解得x 1=x 2=4,即菱形的边长为4; ………(5分)(2)∵AB ,AD 的长是方程x 2﹣mx+2m =0的两个实数根,AB 的长为3, ∴AB+AD=m ,3是方程的一个根, ∴32﹣3m+2m =0,∴m =9, ………(7分) ∴AB+AD=9,∴2(AB+AD )=18,即平行四边形ABCD 的周长为18. ………(10分)23.解:(1)由题意可得,CP=15-3t ,CQ=2t ,0≤t ≤5; ………(3分)(2)由题意可得,S △CPQ =21CP ·CQ=21(15-3t )×2t=18,解得t 1=2,t 2=3,即t 的值为2或3; ………(7分)(3)∵∠C =90°,∴PQ 2=CP 2+CQ 2,∴y=(15-3t )2+(2t )2=13t 2-90t+225. ………(10分)24.解:(1)设“亲子两人游”套票价格为x 元,则“家庭三人行”套票的价格是2x 元,根据题意得40021800027000+=xx , 解得x=45, ………(4分)经检验,x=45是原方程的解,且符合题意, 所以2x=90,即“亲子两人游”套票和“家庭三人行”套票的价格各是45元和90元;…(6分)(2)根据题意可得(1600-20a)(45+a)+600(90+32a)=1600×45+600×90+12000, ………(8分)化简得a 2﹣55a+600=0 解得a 1=15,a 2=40(舍),所以,a 的值为15. ………(12分)。
九年级数学上学期【第一次月考卷】(原卷版)

九年级数学上学期【第一次月考卷】(人教版)(满分120分,完卷时间100分钟)考生注意:1.本试卷含三个大题,共26题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出解题的主要步骤.一.选择题(共10小题)1.若关于x的一元二次方程(m﹣3)x2+5x+m2﹣3m+2=0的常数项为0,则m的值等于()A.1B.2C.1或2D.02.方程(x﹣1)(x+3)=12化为ax2+bx+c=0的形式后,a、b、c的值为()A.1、2、﹣15B.1、﹣2、﹣15C.﹣1、﹣2、﹣15D.﹣1、2、﹣153.某果园2012年水果产量为100吨,2014年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x,则根据题意可列方程为()A.144(1﹣x)2=100B.100(1﹣x)2=144C.144(1+x)2=100D.100(1+x)2=1444.下列一元二次方程中,两实数根之和为3的是()A.x2﹣3x+3=0B.x2+3x﹣3=0C.x2﹣3x﹣3=0D.x2+3x+3=05.二次函数y=2x2﹣x﹣1的顶点坐标是()A.(0,﹣1)B.(2,﹣1)C.(,﹣)D.(﹣,)6.方程x(x−2)=x−1化成一元二次方程的一般形式是()A.x2﹣2x+2=0B.x2﹣2x=0C.x2﹣3x﹣1=0D.x2﹣3x+1=07.如图,△ABC的边BC=y,BC边上的高AD=x,△ABC的面积为3,则y与x的函数图象大致是()A.B.C.D.8.已知三角形的一边长是3,三角形的另两条边长分别是关于x的方程x2﹣4x+2=0的两个根,则此三角形的周长为()A.10B.8C.7D.59.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是()A.(32﹣2x)(20﹣x)=570B.32x+2×20x=32×20﹣570C.(32﹣x)(20﹣x)=32×20﹣570D.32x+2×20x﹣2x2=57010.已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是()A.a1>a2>a3>a4B.a2>a1>a4>a3C.a2>a1>a3>a4D.a1>a2>a4>a3二.填空题(共8小题)11.当方程(m﹣1)x﹣(m+1)x﹣2=0是一元二次方程时,m的值为.12.如果关于x的方程x2﹣2x+m=0(m为常数)有两个相等实数根,那么m=.13.已知二次函数y=2x2﹣3x+m(m为常数)的图象与x轴的一个交点为(1,0),则m =.14.如图是一张长9cm、宽5cm的矩形纸板,将纸板四个角各剪去一个同样的正方形,可制成底面积是12cm2的一个无盖长方体纸盒,设剪去的正方形边长为xcm,则可列出关于x的方程为.15.参加一次聚会的每两人都握了一次手,所有人共握手66次,则有人参加聚会.16.若抛物线y=ax2+bx+c过点A(﹣1,2),B(3,2),则此抛物线的对称轴是直线.17.对于实数a,b,定义运算“⊗”:,例如:5⊗3,因为5>3,所以5⊗3=5×3﹣32=6.若x1,x2是一元二次方程x2﹣6x+8=0的两个根,则x1⊗x2=.18.已知抛物线y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②b2>4ac;③4a+2b+c>0;④(a+b)2<b2,其中正确的有.三.解答题(共8小题)19.解下列方程:5x2﹣3x=x+1.20.求二次函数y=x2﹣2x﹣1的顶点坐标及它与x轴的交点坐标.21.已知等腰三角形底边长为8,腰长是方程x2﹣9x+20=0的一个根,求这个三角形的面积.22.某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均每年增长的百分率为x.(1)用含x的代数式表示第3年的可变成本为万元;(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率x.23.已知关于x的方程x2﹣(k+1)x+k2+1=0.(1)当k取何值方程有两个实数根.(2)是否存在k值使方程的两根为一个矩形的两邻边长,且矩形的对角线长为.24.如图,抛物线y=ax2+4ax+2的顶点A在x轴上,经过点A的直线交该抛物线于点C,交y轴于点B,且点B是线段AC的中点,(1)求该抛物线的解析式;(2)求直线AC的解析式.25.在Rt△ABC中,∠C=90°,点O是AB的中点,M、N分别在边AC、BC上,OM⊥ON,连MN,AC=4,BC=8.设AM=a,BN=b,MN=c.(1)求证:a2+b2=c2;(2)①若a=1,求b;②探究a与b之间的函数关系式;(3)△CMN的面积等于△ABC的面积的时,求b.26.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:y=kx+n与y轴交于点C,与抛物线y=﹣x2+bx+c的另一个交点为D,已知A(﹣1,0),D(5,﹣6),P点为抛物线y=﹣x2+bx+c上一动点(不与A、D重合).(1)求抛物线和直线l的解析式;(2)当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作PF∥y轴交直线l于点F,求PE+PF的最大值;(3)设M为直线l上的点,探究是否存在点M,使得以点N、C,M、P为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.。
华师大初三数学第一次月考卷

嘉博教育阶段性测试试题华师大版九年级(上)数学第一次月考测试卷总分:120分 时间:90分钟姓名:______________ 得分:______________※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※【卷一】※※※ 此部分含两大题,共计17小题,共34分,每题2分。
答题完成后,请将答案转填至答题卡上。
※※※一.选择题。
本题共20分,共计10小题,每题2分。
1. 【2011•江苏徐州】若式子1x -实数范围内有意义,则x 的取值范围是( ) A 1≥x B x >1 C x <1 D x ≤12. 【2011·甘肃兰州】用配方法解方程x 2-2x -5=0时,原方程应变形为( )A (x +1)2=6 B (x +2)2=9 C (x -1)2=6 D (x -2)2=93. 【2011·山东日照】已知x 、y 为实数,且满足1+x -(y -1)1-y =0,则20112011y x -的值是( )A 0B -2C 2D 1 4. 【2011·福建福州】一元二次方程x (x -2)=0根的情况是( )A 有两个不相等的实数根B 有两个相等的实数根C 只有一个实数根D 没有实数根5. 【2011·贵州贵阳】如图,矩形OABC 的边OA 长为2 ,边AB 长为1,OA 在数轴上,以原点O 为圆心,对角线OB 的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )A 2.5B 2 2C 3D 56. 【2011·台湾】若一元二次方程式()()()()22211=++++++x bx x x x ax 的两根为0和2,则b a 43+之值是( )A 2B 5C 7D 87. 【2011·山东威海】关于x 的一元二次方程()0122=++-+m x m x 有两个相等的实数根,则m 的值是( )A 0B 8C 4±2 2D 0或88. 【第22届“希望杯”全国数学邀请赛初二第一试】当1≥x 时,不等式211--≥-++x m x x 恒成立,那么实数m 的最大值是( )A 1B 2C 3D 49. 【2011·山东济宁】已知关于x 的方程02=++a bx x 的一个根是a -(0≠a ),则b a -值为( )A -1B 0C 1D 2 10. 【2011·四川内江】若=m 20112012-1,则34520112m m m --的值是( )A 1B -1C 0D -2二.填空题。
2024-2025学年初中九年级上学期数学第一次月考卷及答案(北师大版)

2024-2025学年九年级数学上学期第一次月考模拟卷(考试时间:120分钟试卷满分:120分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.测试范围:第1章~第3章(北师版)。
5.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一.单项选择题(本题共12小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.下列方程中,是一元二次方程的是()A.xx2−3xx−5=−5B.2xx2−yy−1=0C.xx2−xx(xx+2.5)=0D.aaxx2+bbxx+cc=02.下列命题为真命题的是()A.有两边相等的平行四边形是菱形B.有一个角是直角的平行四边形是菱形C.对角线互相垂直的平行四边形是矩形D.有三个角是直角的四边形是矩形3.若关于xx的方程xx2+mmxx−6=2.则mm为()A.−2B.1 C.4 D.−34.a是方程xx2+2xx−1=0的一个根,则代数式aa2+2aa+2020的值是()A.2018 B.2019 C.2020 D.20215.如图,在正方形AAAAAAAA中,EE为AAAA上一点,连接AAEE,AAEE交对角线AAAA于点FF,连接AAFF,若∠AAAAEE=35°,则∠AAFFAA的度数为()A.80°B.70°C.75°D.45°6.有一块长40m,宽32m的矩形种植地,修如图等宽的小路,使种植面积为1140m2,求小路的宽.设小路的宽为x,则可列方程为()A.(40﹣2x)(32﹣x)=1140 B.(40﹣x)(32﹣x)=1140C.(40﹣x)(32﹣2x)=1140 D.(40﹣2x)(32﹣2x)=11407.在一个不透明的袋子中放有若干个球,其中有6个白球,其余是红球,这些球除颜色外完全相同.每次把球充分搅匀后,任意摸出一个球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0.25左右,则红球的个数约是()A.2 B.12 C.18 D.248.如图,在菱形AAAAAAAA中,对角线AAAA,AAAA相交于点OO,EE是AAAA的中点,若菱形的周长为20,则OOEE的长为()A.10 B.5 C.2.5D.19.在一次新年聚会中,小朋友们互相赠送礼物,全部小朋友共互赠了110件礼物,若假设参加聚会小朋友的人数为xx人,则根据题意可列方程为()A.xx(xx−1)=110B.xx(xx+1)=110C.(xx+1)2=110D.(xx−1)2=11010.关于xx的一元二次方程kkxx2−2xx−1=0有两个不相等的实数根,则kk的取值范围是()A.kk>−1B.kk>−1且kk≠0C.kk<1D.kk<1且kk≠011.如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则EF的长为()A.74B.95C.1910D.76�312.如图,在正方形AAAAAAAA中,AAAA=4,E为对角线AAAA上与点A,C不重合的一个动点,过点E作EEFF⊥AAAA于点F,EEEE⊥AAAA与点G,连接AAEE,FFEE,有下列结论:①AAEE=FFEE.②AAEE⊥FFEE.③∠AAFFEE=∠AAAAEE.④FFEE的最小值为3,其中正确结论的序号为()A.①②B.②③C.①②③D.①③④第Ⅱ卷二.填空题(本题共6小题,每小题3分,共18分.)13.一元二次方程5xx2+2xx−1=0的一次项系数二次项系数常数项.14.xx1,xx2为一元二次方程xx2−2xx−10=0的两根,则1xx1+1xx2=.15.如图,矩形ABCD中,对角线AC、BD相交于点O,若OB=2,∠ACB=30°,则AB的长度为.16.如图所示,菱形AAAAAAAA的对角线AAAA、AAAA相交于点OO.若AAAA=6,AAAA=8,AAEE⊥AAAA,垂足为EE,则AAEE的长为.17.如图,将一张长方形纸片AAAAAAAA沿AAAA折起,重叠部分为ΔΔAAAAEE,若AAAA=6,AAAA=4,则重叠部分ΔΔAAAAEE的面积为.18.如图,在正方形AAAAAAAA中,AAAA=6,点E,F分别在边AAAA,AAAA上,AAEE=AAFF=2,点M在对角线AAAA上运动,连接EEEE和EEFF,则EEEE+EEFF的最小值等于.三、解答题(本题共8小题,共66分.解答应写出文字说明、证明过程或演算步骤.)19.(6分)解下列方程:(1)3xx2−4xx−1=0;(2)2�xx−3�2=xx2−920.(8分)已知方程xx2+�kk+1−6=0是关于xx的一元二次方程.(1)求证:对于任意实数kk方程中有两个不相等的实数根.(2)若xx1,xx2是方程的两根,kk=6,求1xx1+1xx2的值.21.(8分)如图,在菱形AAAAAAAA中,对角线AAAA,AAAA交于点OO,AAEE⊥AAAA交AAAA延长线于EE,AAFF∥AAEE交AAAA延长线于点FF.(1)求证:四边形AAEEAAFF是矩形;(2)若AAEE=4,AAAA=5,求AAAA的长.22.(10分)“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,某食品公司为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如图两幅统计图.请根据以上信息回答:(1)参加本次调查的有______人,若该居民区有8000人,估计整个居民区爱吃D粽的有______人.(2)请将条形统计图补充完整;(3)食品公司推出一种端午礼盒,内有外形完全相同的A、B、C、D粽各一个,小王购买了一个礼盒,并从中任意取出两个食用,请用列表或画树状图的方法,求他恰好能吃到C粽的概率.23.(8分)阅读材料,回答问题.材料1:为了解方程�xx2�2−13xx2+36=0,如果我们把xx2看作一个整体,然后设yy=xx2,则原方程可化为yy2−13yy+36=0,经过运算,原方程的解为xx1,2=±2,xx3,4=±3,我们把以上这种解决问题的方法通常叫做换元法.材料2:已知实数mm,nn满足mm2−mm−1=0,nn2−nn−1=0,且mm≠nn,显然mm,nn是方程xx2−xx−1=0的两个不相等的实数根,由韦达定理可知mm+nn=1,mmnn=−1.根据上述材料,解决以下问题:(1)为解方程xx4−xx2−6=0,可设yy=____,原方程可化为____.经过运算,原方程的解是____.(2)应用:若实数aa,bb满足:2aa4−7aa2+1=0,2bb4−7bb2+1=0且aa≠bb,求aa4+bb4的值;24.(10分)中秋期间,某商场以每盒140元的价格购进一批月饼,当每盒月饼售价为180元时,每天可售出60盒.为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每盒月饼降价2元,那么商场每天就可以多售出5盒.(1)设售价每盒下降xx元,则每天能售出______盒(用含xx的代数式表示);(2)当月饼每盒售价为多少元时,每天的销售利润恰好能达到2550元;(3)该商场每天所获得的利润是否能达到2700元?请说明理由.25.(12分)在数学实验课上,老师让学生以“折叠筝形”为主题开展数学实践探究活动.定义:两组邻边分别相等的四边形叫做“筝形”.(1)概念理解:如图1,将一张纸对折压平,以折痕为边折出一个三角形,然后把纸展平,折痕为四边形AAAAAAAA.判断四边形AAAAAAAA的形状:筝形(填“是”或“不是”);(2)性质探究:如图2,已知四边形AAAAAAAA纸片是筝形,请用测量、折叠等方法猜想筝形的角、对角线有什么几何特征,然后写出一条性质并进行证明;(3)拓展应用:如图3,AAAA是锐角△AAAAAA的高,将△AAAAAA沿边AAAA翻折后得到△AAAAEE,将△AAAAAA沿边AAAA翻折后得到△AAAAFF,延长EEAA,FFAA交于点G.①若∠AAAAAA=50°,当△AAAAEE是等腰三角形时,请直接写出∠AAAAAA的度数;②若∠AAAAAA=45°,AAAA=2,AAAA=5,AAEE=EEEE=FFEE,求AAAA的长.26.(12分)探究式学习是新课程倡导的重要学习方式,某兴趣小组学习正方形以后做了以下探究:在正方形AAAAAAAA中,E,F为平面内两点.【初步感知】(1)如图1,当点E在边AAAA上时,AAEE⊥AAFF,且B,C,F三点共线.请写出AAEE与FFAA的数量关系______;【深入探究】(2)如图2,当点E在正方形AAAAAAAA外部时,AAEE⊥AAFF,AAEE⊥EEFF,E,C,F三点共线.若AAEE=2,AAEE=4,求AAEE的长;【拓展运用】(3)如图3,当点E在正方形AAAAAAAA外部时,AAEE⊥EEAA,AAEE⊥AAFF,AAEE⊥AAEE,且D,F,E三点共线,猜想并证明AAEE,AAEE,AAFF之间的数量关系.2024-2025学年九年级数学上学期第一次月考模拟卷(考试时间:120分钟试卷满分:120分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
九年级数学第二次月考卷及答案

九年级数学第二次月考卷一、选择题(每题4分,共40分)1. 下列选项中,( )是实数。
A. √1B. 3+4iC. 0D. 1+i2. 若|a|=5,|b|=3,则|a+b|的取值范围是( )。
A. 2≤|a+b|≤8B. 8≤|a+b|≤10C. 2≤|a+b|≤10D.8≤|a+b|≤183. 已知等差数列{an},a1=1,a3=3,则公差d为( )。
A. 1B. 2C. 3D. 44. 不等式2x3>0的解集是( )。
A. x>1.5B. x<1.5C. x>3D. x<35. 下列函数中,( )是奇函数。
A. y=x^2B. y=|x|C. y=x^3D. y=2x6. 一次函数y=kx+b的图象经过一、二、四象限,则k和b的取值范围是( )。
A. k>0,b>0B. k<0,b>0C. k<0,b<0D. k>0,b<07. 在△ABC中,a=8,b=10,cosA=3/5,则sinB的值为( )。
A. 3/5B. 4/5C. 3/4D. 4/38. 下列图形中,( )的面积可以通过底乘以高的一半来计算。
A. 正方形B. 矩形C. 三角形D. 梯形9. 已知函数f(x)=2x+1,那么f(f(x))的值为( )。
A. 2x+1B. 4x+3C. 2x+3D. 4x+110. 下列方程中,( )是一元二次方程。
A. x^2+y^2=1B. x^2+2x+1=0C. 2x3y=5D. x^33x=0二、填空题(每题4分,共40分)11. 已知数列{an}的通项公式为an=n^2n+1,则a5=______。
12. 若|a|=3,|b|=4,且a与b同向,则a•b=______。
13. 在平面直角坐标系中,点A(2,3)关于原点的对称点坐标为______。
14. 已知等差数列{an},a1=3,a5=11,则公差d=______。
24-25九年级数学上学期第一次月考卷(安徽专用,范围:二次函数与反比例函数)(考试版A4)

2024-2025学年九年级数学上学期第一次月考卷(安徽专用)(考试时间:120分钟试卷满分:150分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:沪科版九上第21章二次函数与反比例函数。
5.难度系数:0.6。
第Ⅰ卷一、选择题(本大题共10个小题,每小题4分,满分40分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)1.下列y关于x的函数中,属于二次函数的是( )A.y=(x+1)2﹣x2B.y=ax2+bx+cC.y=x(2x﹣3)D.y=2x+52.抛物线y=(x﹣3)2+4的顶点坐标是( )A.(﹣3,4)B.(﹣3,﹣4)C.(3,4)D.(3,﹣4)3.若反比例函数的图象经过点(﹣3,4),则该反比例函数图象一定经过点( )A.(3,﹣4)B.(﹣3,﹣4)C.(3,4)D.(﹣2,﹣6)4.点(2,﹣3)在函数图象上,下列说法中错误的是( )A.它的图象分布在二、四象限B.当x>0时,y的值随x的增大而增大C.当x<0时,y的值随x的增大而减小D.它的图象过点(﹣1,6)5.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则反比例函数cyx=-与一次函数y=ax﹣b的大致图象是( )A.B.C.D.6.若关于x的一元二次方程ax2+k=0的一个根为2,则二次函数y=a(x+1)2+k与x轴的交点坐标为( )A.(﹣3,0)、(1,0)B.(﹣2,0)、(2,0)C.(﹣1,0)、(1,0)D.(﹣1,0)、(3,0)7.如图,在反比例函数的图象上有点A,B,C,图中所构成的阴影部分面积从左到右依次为S1,S2,S3,已知点A,B,C的横坐标分别为2,3,4,S1+S2+S3=8,则k的值为( )A.10B.12C.14D.168.已知(x1,y1)、(x2,y2)、(x3,y3)为双曲线1yx=-上的三个点,且x1<x2<x3,则以下判断正确的是( )A.若x1x2>0,则y1y3<0B.若x1x3<0,则y1y2>0C.若x2x3>0,则y1y3>0D.若x2x3<0,则y1y3<09.如图,在平面直角坐标系中,由3个边长均为1的小正方形拼成矩形OABC,其中矩形的顶点O在坐标原点,顶点B在y轴正半轴上,顶点C在函数y=(k>0,x>0)的图象上,则k的值为( )A.B.C.3D.10.已知二次函数y=ax2+bx+c(a≠0)满足:(1)当x=﹣1时,y=0,(2)对一切x的值有成立.则该二次函数的解析式为( )A.B.C.D.第Ⅱ卷二、填空题(本大题共4小题,每小题5分,满分20分)11.抛物线y=x2﹣8x+c的顶点在x轴上,则c的值为 .12.若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是 .13.如图,在平面直角坐标系xOy中,点A(0,3),B(4,0),将△AOB向右平移到△CDE位置,点A,O分别与点C,D对应,函数的图象经过点C和CE的中点F,则k的值为 .14.图1是一个瓷碗,图2是其截面图,碗体DEC呈抛物线状(碗体厚度不计),碗口宽CD=12cm,此时面汤最大深度EG=8cm.(1)当面汤的深度ET为4cm时,汤面的直径PQ长为 ;(2)如图3,把瓷碗绕点B缓缓倾斜倒出部分面汤,当∠ABM=45°时停止,此时碗中液面宽度CH= .三、解答题(本大题共9个小题,共90分,其中15~18题每题8分,19~20题每题10分,21~22题每题12分,第23题14分.解答应写出文字说明,证明过程或演算步骤)15.(8分)根据下列条件,分别求二次函数的表达式(1)已知图象的顶点坐标为(﹣1,﹣8),且过点(0,﹣6);(2)已知图象经过点(3,0),(2,﹣3),并以直线x=0为的对称轴.16.(8分)如图,在左边托盘A(固定)中放置一个重物,在右边托盘B(可左右移动)中放置一定质量的砝码,可使得仪器左右平衡.托盘B中的砝码质量m随着托盘B与点O的距离d变化而变化,已知m 与d是反比例函数关系,下面是它们的部分对应值:托盘B与点O的距离d/厘米510152025托盘B中的砝码质量m/克3015107.56(1)根据表格数据求出m关于d的函数解析式.(2)当砝码质量为12克时,求托盘B与点O的距离.17.(8分)已知:y=y1+y2,并且y1与(x﹣1)成正比例,y2与x成反比例.当x=2时,y=5;当x=﹣2时,y=﹣9.(1)求y关于x的函数解析式;(2)求当x=8时的函数值.18.(8分)如图,一次函数y1=kx+b的图象与反比例函数的图象交于点A(﹣2,﹣5),C(5,n),交y轴于点B,交x轴于点D.(1)求反比例函数和一次函数y1=kx+b的表达式;(2)连接OA,OC,求△AOC的面积;(3)根据图象,直接写出时x的取值范围.19.(10分)某机械厂每月固定生产甲、乙两种零件共80万件,并能全部售出.甲零件每件成本10元,售价16元;乙零件每件成本8元,售价12元.设生产甲零件x万件.所获总利润y万元.(1)写出y与x的函数关系式;(2)如果每月投入的总成本不超过740万元,应该怎样安排甲、乙零件的产量,可使所获的总利润最大?最大总利润是多少万元?(3)该厂在销售中发现:某月甲零件售价每提高1元,甲零件销量会减少5万件,乙零件售价不变,不管生产多少都能卖出,在(2)获得最大利润的情况下,为了获得更大的利润,该厂决定提高甲零件的售价,并重新调整甲、乙零件的生产数量,求甲零件售价提高多少元时,可获总利润最大?最大总利润是多少万元?20.(10分)在跳绳时,绳甩到最高处的形状可近似看作抛物线,如图,已知甲、乙两名学生拿绳的手间距为6米,距地面均为1米,绳的最高点距离地面的高度为4米,以水平地面为x轴,垂直于地面且过绳子最高点的直线为y轴,建立平面直角坐标系,如图.(1)求抛物线的函数表达式;(2)身高为1.57米的小明此时进入跳绳,他站直时绳子刚好通过他的头顶,小明与甲的水平距离小于小明与乙的水平距离,求小明离甲的水平距离.21.(12分)掷实心球是南京市高中阶段学校招生体育考试的选考项目.如图1,一名女生投郑实心球,实心球行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示,已知掷出时起点处高度为,当水平距离为3m时,实心球行进至最高点3m处.(1)求y关于x的函数表达式;(2)根据南京市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.9m,此项考试得分为满分.该女生在此项考试中是否得满分,请说明理由.22.(12分)如图,抛物线与x轴交于A(﹣2,0),B两点,与y轴交于点C(0,﹣4).(1)求抛物线的表达式;(2)如图①,点P AP,BP,当S△ABP=9时,求点P的坐标;(3)如图②,连接AC,M,N是线段AC上的两个动点,且AM=CN,连接OM,ON,求OM+ON的最小值.23.(14分)二次函数y=x2+bx+c的图象与x轴交于点A(x1,0),B(x2,0)且x1≠x2.(1)当x1=2,且b+c=﹣6时,①求b,c的值;②当﹣2≤x≤t时,二次函数y=x2+bx+c的最大值与最小值的差为4,求t的值;(2)若x1=3x2,求证:.。
湖北省部分学校2024-2025学年九年级数学第一次月考卷(word版含答案)

2024-2025学年九年级数学上学期第一次月考卷(考试时间:120分钟 满分:120分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:人教版九上第21~22章(一元二次方程+二次函数)。
5.难度系数:0.65。
第一部分(选择题 共30分)一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.一元二次方程中一次项系数、常数项分别是( )A .2,B .0,C .1,D .1,02.解方程(x+1)2=3(1+x )的最佳方法是( )A .直接开平方法B .配方法C .公式法D .因式分解法3.抛物线与轴的交点坐标为( )A .B .C .D .4.若关于的一元二次方程有实数根,则的取值范围是( )A .B .C .且D .且5.若关于的方程的一个根是,则的值是( )A .B .2C .D .6.关于x 的方程|x 2﹣2x ﹣3|=a 有且仅有两个实数根,则实数a 的取值范围是( )A .a =0B .a =0 或a =4C .a >4D .a =0 或a >42430x x +-=3-3-3-2321y x x =-+-y ()0,1()0,1-()1,0-()1,0()2110k x x -++=54k ≥54k >54k >1k ≠54k ≤1k ≠230x kx --=3x =2-12-127.在手拉手学校联谊活动中,参加活动的每个同学都要给其他同学发一条励志短信,总共发了110条,设参加活动的同学有x 个,根据题意,下面列出的方程正确的是( )A.B .C .D .8.已知函数图象如图所示,则关于x 的方程根的情况是( )A .无实数根B .有两个相等实数根C .有两个异号实数根D .有两个同号不等实数根9.二次函数,若,,点,在该二次函数的图象上,其中,,则( )A .B .C .D .、的大小无法确定10.已知二次函数y=ax 2+bx+c (a≠0)的图象如图所示,有下列4个结论:①abc <0;②b >a+c ;③2a-b=0;④b 2-4ac <0.其中正确的结论个数是( )A .1个B .2个C .3个D .4个第二部分(非选择题 共90分)二、填空题:本题共5小题,每小题3分,共15分。
九年级数学月考卷

九年级数学月考卷一、选择题(每题1分,共5分)1. 下列函数中,不是正比例函数的是()A. y=2xB. y=3/xC. y=4x+0D. y=5x12. 在直角坐标系中,点P(2,3)位于()A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 下列图形中,既是轴对称图形又是中心对称图形的是()A. 等边三角形B. 正方形C. 长方形D. 梯形4. 若a+b=5,ab=3,则a²+b²的值为()A. 7B. 16C. 23D. 345. 下列等式中,正确的是()A. (a+b)²=a²+b²B. (ab)²=a²b²C. (a+b)²=a²+2ab+b²D. (ab)²=a²2ab+b²二、判断题(每题1分,共5分)1. 任何两个等腰三角形都可以通过平移、旋转、翻折相互重合。
()2. 两条平行线的斜率相等。
()3. 一元二次方程的解一定是实数。
()4. 对角线互相垂直的四边形一定是矩形。
()5. 相似三角形的面积比等于边长比的平方。
()三、填空题(每题1分,共5分)1. 若|x|=3,则x的值为______。
2. 在直角三角形中,若一个锐角为30°,则另一个锐角为______°。
3. 一次函数y=3x1的图象经过______、______两个象限。
4. 两个等圆的半径分别为3cm和6cm,它们的面积比为______。
5. 若a:b=3:4,则a与b的比值为______。
四、简答题(每题2分,共10分)1. 请写出平行线的性质。
2. 简述三角形的中位线定理。
3. 什么是反比例函数?请举例说明。
4. 请列举两种解一元二次方程的方法。
5. 如何判断两个三角形是否相似?五、应用题(每题2分,共10分)1. 某商品的原价为200元,现打8折销售,求现价。
初三数学考卷含答案)

初三数学考卷(含答案)一、选择题(每题4分,共40分)1. 下列选项中,既是奇数又是合数的是()A. 21B. 39C. 51D. 632. 已知a、b为实数,下列选项中,正确的是()A. 若a²=b²,则a=bB. 若a²+b²=0,则a=0且b=0C. 若a>b,则a²>b²D. 若a<b,则a²<b²3. 下列各数是无理数的是()A. √9B. √16C. √3D. √14. 已知平行线l1:3x4y+6=0,l2:3x4y8=0,点A(2,3)到l1的距离是()A. 1B. 2C. 3D. 45. 已知等腰三角形ABC,AB=AC,若∠B=70°,则∠C的度数是()A. 40°B. 50°C. 70°D. 110°6. 下列函数中,既是奇函数又是偶函数的是()A. y=x²B. y=x³C. y=|x|D. y=x²+x7. 下列各式中,正确的是()A. (a³)²=a⁶B. (a³)²=a⁹C. (a³)³=a⁶D. (a³)³=a⁹8. 已知a+b=5,ab=3,则a²+b²的值为()A. 7B. 16C. 23D. 349. 下列各式中,是分式方程的是()A. 2x+3=5B. 1/x+2=3C. x²+2x+1=0D. 3x4/x=710. 已知函数f(x)=2x²4x+3,则f(x)的最小值为()A. 1B. 2C. 3D. 4二、填空题(每题4分,共40分)11. 已知|a|=3,|b|=4,则a+b的值为______。
12. 已知一组数据的方差是9,那么这组数据的标准差是______。
初三数学月考卷.docx

初三数学月考卷班姓名学号一、(每小 3 分)1、在ABC中,C90, AB=15, sinA=1, BC等于()3A、 45B、 5C、1D、1 5452、李同学遇到了一道: 3 tan(α+=1,你猜想角α的度数是()A.40 °B.30°C.D.10°3、如果a3, 那么a等于⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯() b2a b(A)2(B)2(C)3(D)5 35534.如果两个相似三角形的相似比1:4 ,那么它的周比⋯⋯⋯⋯()(A) 1:16( B) 1:8( C) 1:4(D) 1:25.如所示 , 在 8cm,6cm 的矩形中 , 截去一个矩形( 中阴影部分 ), 如果剩下矩形与原矩形相似 , 那么剩下矩形的面是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( )A.28cm2B.27cm2C.21cm2D.2(第5 )(第6 )6.如,身高 1.6m 的某学生想量一棵大的高度,他沿着影BA 由 B 点向 A 点走去,当走到 C 点,他的影子端正好与的影子端重合,得BC=3.2m, CA=0.8m,的高度⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯()(A) 4.8m(B)6.4m(C)8m(D)10m7.在平面直角坐系中,以点( 2 , l)心、 1 半径的必与()A. x 相交B.y 相交C. x 相切D. y 相切8.已知⊙ O1与⊙ O2内切,它的半径分 2 和 3,两的心距 d 足()( A ) d=5(B)d=1(C)1<d<5(D)d>59.如, AB是⊙ O的直径, P 是 AB 延上的一点,PC切⊙ O于点C,PC=3、PB:AB=1:3,⊙ O的半径等于()A.5B.3C.9D.9(第9 ) 24210.如 ,在矩形 ABCD 中, E 是 AD 上的点,且∠ BEC=Rt ∠,A AE=5 , ED=4 , CE 的 是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯()(A )5 (B ) 6 (C ) 7 ( D ) 7.5B二、填空 (每小 3 分)1.如 , PA 、 PB 是⊙ O 的切 , A 、 B 切点,若∠ APB=60°, ∠ ABO= .EDC2.如 ,在△ABC 中,∠ A= 90°, AB=AC=2cm ,⊙A 与 BC 相切于点D , ⊙ A 的半径cm .3.数 3 和 12 的比例中 是。
初三数学月考卷

初三数学月考卷一、选择题(每题4分,共40分)1. 下列选项中,( )是实数。
A. √1B. 0C. √2D. π2. 若a、b为有理数,且a+b=5,ab=3,则a²+b²的值为( )。
A. 7B. 23C. 34D. 163. 下列各数中,( )是无理数。
A. 1.414B. 0.333…C. √3D. 1.1010010001…4. 已知等腰三角形的底边长为8,腰长为10,则该三角形的周长为( )。
A. 16B. 26C. 28D. 365. 下列函数中,( )是正比例函数。
A. y=2x+1B. y=x²C. y=3xD. y=x16. 下列各式中,( )是分式。
A. 2x+3B. x²y²C. 1/xD. √(x+y)7. 已知平行四边形的对角线互相平分,若一条对角线长为10,另一条对角线长为12,则平行四边形的面积是( )。
A. 60B. 100C. 120D. 1448. 下列方程中,( )是一元一次方程。
A. x²+y=5B. 2x3y=6C. 3x²5=0D. 1/x=29. 若|a|=3,|b|=5,则a+b的值为( )。
A. 8B. 8C. ±8D. 无法确定10. 下列图形中,( )是中心对称图形。
A. 等腰三角形B. 正方形C. 等边三角形D. 长方形二、填空题(每题4分,共40分)1. 已知数轴上A点表示3,B点表示5,则AB的长度为______。
2. 若a=3,b=2,则a²+b²的值为______。
3. 已知一组数据为2,3,5,7,10,12,则这组数据的平均数是______。
4. 在直角坐标系中,点P(2,3)关于x轴的对称点坐标为______。
5. 一次函数y=kx+b的图象经过一、二、四象限,则k的取值范围是______。
6. 已知平行线l₁:3x4y+7=0,l₂:4x+3y+c=0,则c的值为______。
