代数综合试卷(1)
考研数学一(线性代数)模拟试卷1(题后含答案及解析)

考研数学一(线性代数)模拟试卷1(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.设A是三阶矩阵,B是四阶矩阵,且|A|=2,|B|=6,则为( ).A.24B.一24C.48D.一48正确答案:D解析:知识模块:线性代数部分2.设A为二阶矩阵,且A的每行元素之和为4,且|E+A|=0,则|2E+A2|为( ).A.0B.54C.-2D.-24正确答案:B解析:因为A的每行元素之和为4,所以A有特征值4,又|E+A|=0,所以A有特征值一1,于是2E+A2的特征值为18,3,于是|2E+A2|=54,选(B).知识模块:线性代数部分3.设n维行向量,A=E—αTα,B=E+2αTα,则AB为( ).A.0B.一EC.ED.E+αTα正确答案:C解析:知识模块:线性代数部分4.设A,B为n阶矩阵,则下列结论正确的是( ).A.若A,B可逆,则A+B可逆B.若A,B可逆,则AB可逆C.若A+B可逆,则A—B可逆D.若A+B可逆,则A,B都可逆正确答案:B解析:若A,B可逆,则|A|≠0,|B|≠0,又|AB|=|A||B|,所以|AB|≠0,于是AB可逆,选(B).知识模块:线性代数部分5.设A,B为n阶对称矩阵,下列结论不正确的是( ).A.AB为对称矩阵B.设A,B可逆,则A-1+B-1为对称矩阵C.A+B为对称矩阵D.kA为对称矩阵正确答案:A解析:由(A+B)T=AT+BT=A+B,得A+B为对称矩阵;由(A-1+B-1)T=(A-1)T+(B-1)T=A-1+B-1,得A-1+B-1为对称矩阵;由(ka)T=kAT=kA,得kA为对称矩阵,选(A).知识模块:线性代数部分6.设A,B皆为n阶矩阵,则下列结论正确的是( ).A.AB=0的充分必要条件是A=0或B=0B.AB≠0的充分必要条件是A≠0且B≠0C.AB=0且r(A)=n,则B=0D.若AB≠0,则|A|≠0或|B|≠0正确答案:C解析:知识模块:线性代数部分7.n阶矩阵A经过若干次初等变换化为矩阵B,则( ).A.|A|=|B|B.|A|≠|B|C.若|A|=0则|B|=0D.若|A|>0则|B|>0正确答案:C解析:因为A经过若干次初等变换化为B,所以存在初等矩阵P1,Ps,Q1,…,Qt,使得B=Ps…P1AQ1…Qt,而P1,…,Ps,Q1,…,Q都是可逆矩阵,所以r(A)=r(B),若|A|=0,即r(A)<n,则r(B)<n,即|B|=0,选(C).知识模块:线性代数部分8.设A为m×n阶矩阵,C为n阶矩阵,B=AC,且r(A)=r,r(B)=r1,则( ).A.r>r1B.r<r1C.r≥r1D.r与r1的关系依矩阵C的情况而定正确答案:C解析:因为r1=r(B)=r(AC)≤r(A)=r,所以选(C).知识模块:线性代数部分9.设A为m×n阶矩阵,B为n×m阶矩阵,且m>n,令r(AB)=r,则( ).A.r>mB.r=mC.r<mD.r≥m正确答案:C解析:显然AB为m阶矩阵,r(A)≤n,r(B)≤n,而r(AB)≤min{r(A),r(B))≤n<m,所以选(C).知识模块:线性代数部分10.设A为四阶非零矩阵,且r(A*)=1,则( ).A.r(A)=1B.r(A)=2C.r(A)=3D.r(A)=4正确答案:C解析:因为r(A*)=1,所以r(A)=4—1=3,选(C).知识模块:线性代数部分11.设A,B都是n阶矩阵,其中B是非零矩阵,且AB=0,则( ).A.r(B)=nB.r(B)<nC.A2一B2=(A+B)(A—B)D.|A|=0正确答案:C解析:因为AB=0,所以r(A)+r(B)≤n,又因为B是非零矩阵,所以r(B)≥1,从而r(A)<n,于是|A|=0,选(D).知识模块:线性代数部分12.设A,B分别为m阶和n阶可逆矩阵,则的逆矩阵为( ).A.B.C.D.正确答案:D解析:知识模块:线性代数部分13.A.B=P1P2AB.B=P2P1AC.B=P2AP1D.B=AP2P1正确答案:D解析:P1=E12,P2=E23(2),显然A首先将第2列的两倍加到第3列,再将第1及第2列对调,所以B=AE23(2)E12=AP2P1,选(D).知识模块:线性代数部分14.A.B=P1AP2B.B=P2AP1C.B=P2-1AP1D.B=P1-1AP2-1正确答案:D解析:知识模块:线性代数部分填空题15.正确答案:23解析:按行列式的定义,f(x)的3次项和2次项都产生于(x+2)(2x+3)(3x+1),且该项带正号,所以x2项的系数为23.知识模块:线性代数部分16.设A为三阶矩阵,A的第一行元素为1,2,3,|A|的第二行元素的代数余子式分别为a+1,a一2,a一1,则a=_________.正确答案:1解析:由(a+1)+2(a一2)+3(a一1)=0得a=1.知识模块:线性代数部分17.设A是m阶矩阵,B是n阶矩阵,且=_________.正确答案:(-1)mnab解析:将B的第一行元素分别与A的行对调m次,然后将B的第二行分别与A的行对调m次,如此下去直到B的最后一行与A的行对调m次,则知识模块:线性代数部分18.设A=(α1,α2,α3)为三阶矩阵,且|A|=3,则|α1+2α2,α2—3α3,α3+2α1|=________.正确答案:-33解析:|α1+2α2,α2—3α3,α3+2α1|=|α1,α2—3α3,α3+2α1|+|2α2,α2—3α3,α3+2α1|=|α1,α2-3α3,α3|+2|α2,-3α3,α3+2α1|=|α1,α2,α3|一6|α2,α3,α3+2α1|=|α1,α2,α3|一6|α2,α3,2α1|=|α1,α2,α3|一12|α2,α3,α1|=|α1,α2,α3|一12|α1,α2,α3|=一33 知识模块:线性代数部分19.设三阶矩阵A=(α,γ1,γ2),B=(β,γ1,γ2),其中α,β,γ1,γ2是三维列向量,且|A|=3,|B|=4,则|5A一2B|=________.正确答案:63解析:由5A一2B=(5α,5γ1,5γ2)一(2β,2γ1,2γ2)=(5α一2β,3γ1,3γ2),得|5A一2B|=|5α一2β,3γ1,3γ2|=9|5α一2β,γ1,γ2|=9(5|α,γ1,γ2|一2|β,γ1,γ2|)=63 知识模块:线性代数部分20.设α=(1,一1,2)T,β=(2,1,1)T,A=αβT,则An=_________.正确答案:解析:知识模块:线性代数部分21.正确答案:0解析:由A2=2A得An=2n-1A,An-1=2n-2A,所以An一2An-1=0.知识模块:线性代数部分22.正确答案:解析:知识模块:线性代数部分23.A2一B2=(A+B)(A—B)的充分必要条件是_________.正确答案:AB=BA解析:A2一B2=(A+B)(A一B)=A2+BA—AB一B2的充分必要条件是AB=BA.知识模块:线性代数部分24.设A是三阶矩阵,且|A|=4,则=__________正确答案:2解析:知识模块:线性代数部分25.正确答案:解析:知识模块:线性代数部分26.正确答案:8解析:因为A为四阶矩阵,且|A*|=8,所以|A*|=|A|3=8,于是|A|=2.又AA*=|A|E=2E,所以A*=2A-1,故知识模块:线性代数部分27.设A为三阶矩阵,且|A|=3,则|(一2A)*|=_________.正确答案:576解析:因为(一2A)*=(一2)2A*=4A*,所以|(一2A)*|=|4A*|=43|A|2=64×9=576.知识模块:线性代数部分28.正确答案:解析:知识模块:线性代数部分29.正确答案:解析:知识模块:线性代数部分30.正确答案:解析:知识模块:线性代数部分31.正确答案:解析:知识模块:线性代数部分32.设A为n阶可逆矩阵(n≥2),则[(A*)*]-1=_________(用A*表示).正确答案:解析:知识模块:线性代数部分33.正确答案:解析:知识模块:线性代数部分34.设n维列向量α=(a,0,…,0,a)T,其中a<0,又A=E-ααT,,且B为A的逆矩阵,则a=________.正确答案:-1解析:知识模块:线性代数部分35.设三阶矩阵A,B满足关系A-1BA=6A+BA,且,则B=__________.正确答案:解析:由A-1BA=6A+BA,得A-1B=6E+B,于是(A-1-E)B=6E,知识模块:线性代数部分36.设A是4×3阶矩阵且r(A)=2,B=,则r(AB)=__________.正确答案:2解析:因为|B|=10≠0,所以r(AB)=r(A)=2.知识模块:线性代数部分37.正确答案:2解析:因为AB=0,所以r(A)+r(B)≤3,又因为B≠0,所以r(B)≥1,从而有r(A)≤2,显然A有两行不成比例,故r(A)≥2,于是r(A)=2.知识模块:线性代数部分38.正确答案:解析:知识模块:线性代数部分解答题解答应写出文字说明、证明过程或演算步骤。
高等代数试卷及答案1

高等代数一、填空题 (共10题,每题2分,共20 分)1.只于自身合同的矩阵是 矩阵。
2.二次型()()11212237,116x f x x x x x ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭的矩阵为__________________。
3.设A 是实对称矩阵,则当实数t _________________,tE A +是正定矩阵。
4.正交变换在标准正交基下的矩阵为_______________________________。
5.标准正交基下的度量矩阵为_________________________。
6.线性变换可对角化的充要条件为__________________________________。
7.在22P ⨯中定义线性变换σ为:()a b X X c d σ⎛⎫= ⎪⎝⎭,写出σ在基11122122,,,E E E E 下的矩阵_______________________________。
8.设1V 、2V 都是线性空间V 的子空间,且12V V ⊆,若12dim dim V V =,则_____________________。
9.叙述维数公式_________________________________________________________________________。
10.向量α在基12,,,n ααα⋅⋅⋅(1)与基12,,,n βββ⋅⋅⋅(2)下的坐标分别为x 、y ,且从基(1)到基(2)的过渡矩阵为A ,则x 与y 的关系为_____________________________。
二、判断题 (共10 题,每题1分,共10分)1.线性变换在不同基下的矩阵是合同的。
( ) 2.设σ为n 维线性空间V 上的线性变换,则()10V V σσ-+=。
( ) 3.平面上不平行于某一向量的全部向量所成的集合,对于向量的加法和数量乘法,构成实数域上的线性空间。
考研数学二(线性代数)历年真题试卷汇编1(题后含答案及解析)

考研数学二(线性代数)历年真题试卷汇编1(题后含答案及解析) 题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.记行列式为f(x),则方程f(x)=0的根的个数为A.1B.2C.3D.4正确答案:B解析:计算该行列式可以有多种方法.例如,为了便于降阶,先把第1列的(一1)倍分别加到第2、3、4列,得故方程f(x)=0的根为x=0和x=1,于是知(B)正确.2.行列式A.(ad一bc)2B.一(ad 一bc)2C.a2d2一b2c2D.b2c2一a2d2正确答案:B解析:按第1列展开,得所求行列式D等于=一ad (ad 一bc)+bc(ad 一bc)=一(ad 一bc)2.3.设A是任一n(n≥3)阶方阵,A*是A的伴随矩阵,又k为常数,且k≠0,±1,则必有(kA)*=A.kA*B.kn一1A*C.k一1A*D.k一1A*正确答案:B解析:由于n阶行列式的每个元素的余子式都是一个n一1阶行列式,故|kA|的每个元素的代数余子式等于|A|的对应元素的代数余子式的kn一1倍,于是由伴随矩阵的定义知(kA)*的每个元素等于A*的对应元素的kn一1倍,即(kA)*=kn 一1A*.4.设A是3阶方阵,将A的第1列与第2列交换得B,再把B的第2列加到第3列得C,则满足AQ=C的可逆矩阵Q为A.B.C.D.正确答案:D解析:记交换单位矩阵的第1列与第2列所得初等矩阵为E(1,2),记将单位矩阵第2列的k倍加到第3列所得初等矩阵为E(3,2(k)),则由题设条件,有AE(1,2)=B,BE(3,2(1))=C,故有AE(1,2)E(3,2(1))=C于是得所求逆矩阵为Q=E(1,2)E(3,2(1))=所以只有选项(D)正确.5.设A为n(n≥2)阶可逆矩阵,交换A的第1行与第2行得矩阵B,A*,B*分别为A,B的伴随矩阵,则A.交换A*的第1列与第2列得B*.B.交换A*的第1行与第2行得B*.C.交换A*的第1列与第2列得一B*.D.交换A*的第1行与第2行得一B*.正确答案:C解析:用排除法,以2阶方阵为例,设由此可见,交换A*的第1列与第2列得一B*,而其它选项均不对,故只有(C)正确.记P为交换n阶单位矩阵的第1行与第2行所得初等方阵,则由题设条件有B=PA,且|B|=一|A|,P一1=P.由A可逆知B可逆,利用B一1=|B|一1B*,得B*=|B|一1=一|A|(PA)一1=一(|A|A 一1)一1=一A*P或A*P=一B*因为用P右乘矩阵A*,等价于交换A*的第1列与第2列,故知选项(C)正确.也可利用B*=(PA)*=A*P*,及P*=|P|P一1=一P,得B*=一A*P.6.设A为3阶矩阵,将A的第2行加到第1行得B,再将B的第1列的一1倍加到第2列得C,记P=则A.C=P一1AP,B.C=PAP一1C.C=PTAP.D.C=PAPT.正确答案:B解析:将单位矩阵E的第2行加到第1行即得初等矩阵P,由初等变换与初等矩阵的关系,有B=PA.令矩阵则将E的第1列的一1倍加到第2列即得矩阵Q,于是有C=BQ,从而有C=PAQ.由于P一1=所以,C=PAQ=PAP一1,只有选项(B)正确.7.设A为n阶非零矩阵,E为n阶单位矩阵,若A3=0,则A.E一A不可逆,E+A不可逆.B.E一A不可逆,E+A可逆.C.E一A可逆,E+A可逆.D.E一A可逆,E+A不可逆.正确答案:C解析:由于(E一A)(E+A+A2)=E一A3=E,(E+A)(E—A+A2)=E+A3=E,故由可逆矩阵的定义知:E一A和E+A均是可逆的.8.设A,B均为2阶矩阵,A*,B*分别为A,B的伴随矩阵,若|A|=2,|B|=3,则分块矩阵的伴随矩阵为A.B.C.D.正确答案:B解析:记矩阵并记|C|的(i,j)元素的代数余子式为Aij(i,j=1,2,3,4),则计算可得:A11=0,A21=0,A31=|A|h,A41=一A|f,A12=0,A22=0,A32=一|A| g,A42=|A|e,A13=|B|d,A23=一|B|b,A33=0,A43=0,A14=一|B|c,A24=|B|a,A34=0,A44=0.于是由伴随矩阵的定义(C*的(i,j)元为Aji),得因此选(B).9.设A,P均为3阶矩阵,PT为P的转置矩阵,且PTAP=A.B.C.D.正确答案:A解析:由于Q=[α1+α2,α2,α3]=[α1,α2,α3]所以故只有选项(A)正确.10.设A为3阶矩阵,将A的第2列加到第1列得矩阵B,再交换B的第2行与第3行得单位矩阵.记P1=,则A=A.P1P2.B.P1一1P2.C.P2P1.D.P2P1一1.正确答案:D解析:由题设条件有P2AP1=I,两端左乘P2一1,两端右乘P1一1,得A=P2一1P2一1,因P2一1= P2,而P1一1≠P1,故只有(D)正确.11.设区域D由曲线y=sinx,x=±,y=1围成,则(xy5一1)dxdy=A.π.B.2.C.一2.D.一π.正确答案:B解析:已知A(α1+α2,α2,α3)=(α1+α2,α2,α3)(Aα1+Aα2,A α2,α3)=(α1+α2,α2,2α3)Aα1=α1,Aα2=α2,Aα3=2α3A(α1+α2)=A α1+Aα2=α1+α2AQ=A(α1+α2,α2,α3)=(A(α1+α2),Aα2,Aα3)=(α1+α2,α2 ,2α3)=(α1+α2,α2,α3)两端左乘Q一1,得Q一1AQ=.由已知A相似于对角矩阵diag(1,1,2),知α1+α2,α2,α3是A的3个线性无关特征向量,且依次属于特征值1,1,2.α1+α2≠0(否则α1,α2线性相关,与α1+α2,α2,α3线性无关矛盾),且A(α1+α2)=Aα1+Aα2=α1+α2,因此α1+α2是A的属于特征值1的一个特征向量.从而知α1+α2,α2,α3是A的3个线性无关特征向量,且依次属于特征值1,1,2,因此利用矩阵相似对角化可写出(α1+α2,α2,α3)一1A(α1+α2,α2,α3)=diag(1,1,2),即Q一1AQ=diag(1,1,2).因此选(B).填空题12.设E为4阶单位矩阵,且B=(E+A)一1(E—A),则(E+B)一1=________.正确答案:解析:由题设等式得E+B=E+(E+A)一1(E 一A)用(E+A)左乘上式两端,得(E+A)(E+B)=E+A+E一A=2E13.设α为3维列向量,αT是α的转置,若ααT=,则αTα=________.正确答案:3.解析:于是有a2=1,b2=1,c2=1,从而得αTα= [a b c]=a2+b2+c2=1+1+1=3.14.设三阶方阵A、B满足A2B一A一B=E,其中E为三阶单位矩阵,A=,则|B|=________.正确答案:解析:由题设方程移项得A2B一B=A+E,(A2一E)B=A+E,(A+E)(A—E)B=A+E,注意A+E=可逆,用(A+E)一1左乘上式两端,得(A 一E)B=E两端取行列式,得|A一E||B|=115.设矩阵A=,矩阵B满足ABA*=2BA*+E,其中A*是A的伴随矩阵,E是单位矩阵,则|B|=________.正确答案:解析:由于A*A=|A| E,而|A|=3,所以A*A=3E.用矩阵A右乘题设方程两端,可得3AB=6B+A,或3(A 一2E)B=A,两端取行列式,得33|A一2E||B|=|A|,由于|A一2E|=故有27|B|=3,所以|B|=16.设α1,α2,α3均为3维列向量,记矩阵A =(α1,α2,α3),B=(α1+α2+α3,α1+2α2+4α3,α1+3α2+9α3).如果|A|=1,那么|B|=________.正确答案:2.解析:对行列式|B|依次作等值变形(用c1+ kcj表示第i列加上第j列的k倍)c2 一c1,c3 一c1,得|B|=|α1|+α2+α3,α2+3α3,2α2+8α3|再作等值变形c3一2c2,得|B| =| α1+α2+α3,α2+3α3,2α3|=2|α1+α2+α3,α2+3α3,α3|=2 |α1+α2,α2,α3|=2 |α1,α2,α3|=2 |A|=2.17.设矩阵A=E为2阶单位矩阵,矩阵B满足BA=B+2E,则|B|=________.正确答案:2.解析:由给定矩阵方程得BA 一B=2E B(A 一E)=2E两端取行列式,得|B ||A一E|=|2E因|A一E|==2,|2E|= 22|E|=4所以有 2 |B|=4,从而得|B|=2.18.设矩阵A=则A3的秩为________.正确答案:1.解析:利用矩阵乘法,容易计算得A3=由于A3中非零子式的最高阶数为1,故由矩阵的秩的定义,即知r(A3)=1.19.设A,B为3阶矩阵,且|A|=3,|B|=2,|A一1+B|=2,则|A+B一1|=________.正确答案:3.解析:由于A+B一1=(AB+E)B一1=A(B+A一1)B一1=A(A一1+B)B一1,两端取行列式,并利用|ABC|=|A||B||C|及|B一1|=|B|一1,得|A+B一1|=|A|.|A一1+B|.|B一1}=3×2×=3.20.设A为3阶矩阵,|A|=3,A*为A的伴随矩阵.若交换A的第1行与第2行得矩阵B,则|BA*|=________.正确答案:一27.解析:由于互换行列式的两行,则行列式仅变号,于是知|B|=一3.再利用|A*|=|A|n一1|A|2=9,得|BA*|=|B||A*|=一27.记交换3阶单位矩阵的第1行与第2行所得初等矩阵为E12,则B=E12A,由于AA*=|A|E=3E,得BA*=E12AA*=E12(3E)=3E12,注意|E12|=一1,所以|BA*|=|3E12|= 33|E|12=一27.21.设A=(aij)是3阶非零矩阵,|A|为A的行列式,Aij为aij的代数余子式,若aij+Aij=0(i,j=1,2,3),则|A|=________.正确答案:一1.解析:由A≠0,不妨设a11≠0,由已知的Aij=一aij(i,j=1,2,3),得及A=一(A*)T,其中A*为A的伴随矩阵,以下有两种方法:方法1:用AT右乘A=一(A*)T的两端,得AA*=一(A*)AT=一(AA*)T=一(|A|I)T,其中I为3阶单位矩阵,上式两端取行列式,得|A|2=(一1)3|A|3,或|A|2(1+|A|)=0,因|A|≠0,所以|A|=一1.方法2:从A=一(A*)T两端取行列式,并利用|A*|= |A|2,得|A|= (一1)3 |A*|=一|A|2,或|A| (1+|A|)=0,因|A|≠0,所以|A|=一1.22.设矩阵等价,则a=________.正确答案:2.解析:由知矩阵B的秩为2,由于矩阵与矩阵B相似,所以A的秩也为2,因此A的行列式为零,由得a=一1,或a=2.若a=一1,则A=的秩为1,不合题意;若a=2,则的秩为2,符合题意,因此a=2.23.已知向量组α1=(1,2,一1,1),α2=(2,0,t,0),α3=(0,一4,5,一2)的秩为2,则t=________.正确答案:3.解析:以α1,α2,α3为行作成矩阵A,并对A作初等变换:由此可知当且仅当f=3时,矩阵A的秩、也即向量组α1,α2,α3的秩等于2.由于α1,α3线性无关,故向量组α1,α2,α3的秩为2当且仅当α2可由α1,α3线性表出,即存在常数x1,x2,使得x1α1+x2α3=α2,亦即由此解得t=3.解答题解答应写出文字说明、证明过程或演算步骤。
考研数学二(线性代数)模拟试卷1(题后含答案及解析)

考研数学二(线性代数)模拟试卷1(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.设n维行向量α=,A=E-αTα,B=E+2αTα,则AB为( ).A.OB.-EC.ED.E+αTα正确答案:C解析:由ααT=,得AB=(E-αTα)(E+2αTα)=E,选(C) 知识模块:线性代数部分2.设A,B都是n阶矩阵,其中B是非零矩阵,且AB=O,则( ).A.r(B)=nB.r(B)<nC.A2-B2=(A+B)(A-B)D.|A|=0正确答案:D解析:因为AB=O,所以r(A)+r(B)≤n,又因为B是非零矩阵,所以r(B)≥1,从而r(A)<n,于是|A|=0,选(D) 知识模块:线性代数部分3.设n阶矩阵A=(α1,α2,…,αn),B=(β1,β2,…,βn),AB=(γ1,γ2,…,γn),记向量组(Ⅰ):α1,α2,…,αn;(Ⅱ):β1,β2,…,βm;(Ⅲ):γ1,γ2,…,γm,若向量组(Ⅲ)线性相关,则( ).A.(Ⅰ),(Ⅱ)都线性相关B.(Ⅰ)线性相关C.(Ⅱ)线性相关D.(Ⅰ),(Ⅱ)至少有一个线性相关正确答案:D解析:若α1,α2,…,αn线性无关,β1,β2,…,βn线性无关,则r(A)=n,r(B)=n,于是r(AB)=n.因为γ1,γ2,…,γm线性相关,所以r(AB)=r(γ1,γ2,…,γn)只有零解,而无解,故(A)不对;方程组有非零解,而无解,故(B)不对;方程组无解,但只有零解,故(C)不对;若Ax=b有无穷多个解,则r(A)=r()B.C.λ|A|D.λ|A|n-1正确答案:B解析:因为A可逆,所以λ≠0,令AX=λX,则A*AX=λA*X,从而有A*X=选(B) 知识模块:线性代数部分6.设n阶矩阵A与对角矩阵合同,则A是( ).A.可逆矩阵B.实对称矩阵C.正定矩阵D.正交矩阵正确答案:B解析:因为A与对角阵合同,所以存在可逆矩阵P,使得pTAP=A,从而A=(pT)-1P-1=(p-1)TP-1,AT=[(P-1)TP-1]T=(P-1)TP-1=A,选(B) 知识模块:线性代数部分填空题7.设f(x)=,则x2项的系数为_______.正确答案:x解析:按行列式的定义,f(x)的3次项和2次项都产生于(x+2)(2x+3)(3x+1),且该项带正号,所以x2项的系数为23.知识模块:线性代数部分8.设A是三阶矩阵,且|A|=4,则=_______正确答案:2解析:=|2A-1|=23|A-1|=2 知识模块:线性代数部分9.设A=,则(A-2E)-1=_______.正确答案:解析:A-2E= 知识模块:线性代数部分10.设,且α,β,γ两两正交,则a=_______,b=_______.正确答案:-4,-13解析:因为α,β,γ正交,所以,解得a=-4,b=-13.知识模块:线性代数部分11.设A=(a(C1,C2为任意常数)解析:因为AX=0有非零解,所以|A|=0,而|A|==-(a+4)(a-6)且a(C1,C2为任意常数).知识模块:线性代数部分12.设A为三阶矩阵,A的各行元素之和为4,则A有特征值_______,对应的特征向量为_______正确答案:4,解析:因为A的各行元素之和为4,所以,于是A有特征值4,对应的特征向量为知识模块:线性代数部分13.设5x12+x22+tx3x2+4x1x2-2x1x3-2x2x3为正定二次型,则t的取值范围是_______.正确答案:t>2解析:二次型的矩阵为A=,因为二次型为正定二次型,所以有5>0,=1>0,|A|>0,解得t>2.知识模块:线性代数部分解答题解答应写出文字说明、证明过程或演算步骤。
线性代数期终考试卷

线性代数期终考试卷一、 试卷一1)填空题(每小题4分,共20分)(1)设A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡300220111,则A T A= (2)在分块矩阵A=⎥⎦⎤⎢⎣⎡O C B O 中,已知1-B 、1-C 存在,则=-1A(3)设A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡963042321,B 为三阶非零矩阵,满足AB=O ,则r(B)= (4)若⎥⎦⎤⎢⎣⎡3152X=⎥⎦⎤⎢⎣⎡-1264,则X= (5)三次代数方程321842184211111x x x--=0的根是2)选择题(每小题3分,共15分)(1)设A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡333231332221131211a a a a a a a a a ,B=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++133312321131131211232221a a a a a a a a a a a a P 1=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100001010,P 2=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101010001,则必有( ) (A)AP 1P 2=B (B)AP 2P 1=B(C)P 1P 2A=B (D)P 2P 1A=B(2)设A 是三阶矩阵,A*是其转置伴随矩阵,又k 为常数k ≠0,1±,则(kA)*=( ) (A)kA* (B)k 2A* (C)k 3A* (D)31A* (3)若r(A)=r<n,则n 元线性代数方程Ax=b ( ) (A ) 又无穷多个解 (B)有唯一解 (C)无解 (D)不一定有解(4)下列说法中正确的是( )(A )对向量组kαα,,1Λ,若有全不为零的数k c c ,,1Λ使011=++k k c c ααΛ,则k αα,,1Λ线性无关(B) 若有全不为零的数k c c ,,1Λ使011≠++k k c c ααΛ,则kαα,,1Λ线性无关(C)若向量组kαα,,1Λ线性相关,則其中每个向量皆可由其余向量线性表示 (D)任何n+2个n 维向量必线性相关(5)矩阵A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001010100的特征值是( ) (A)1,1,0 (B)-1,1,1 (C)1,1,1 (D) 1,-1,-13)(每小题6分,共12分)(1)计算行列式D= ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+-+y y x x1111111111111111 (2)已知q 1=T⎥⎦⎤⎢⎣⎡313131,q 2=T⎥⎦⎤⎢⎣⎡-21021,求q 3,使Q=[]321q q q为正交阵。
线性代数试题及答案

线性代数试题及答案线性代数(试卷⼀)1、填空题(本题总计20分,每⼩题2分)1. 排列7623451的逆序数是。
2. 若,则3. 已知阶矩阵、和满⾜,其中为阶单位矩阵,则。
4. 若为矩阵,则⾮齐次线性⽅程组有唯⼀解的充分要条件是_________5. 设为的矩阵,已知它的秩为4,则以为系数矩阵的齐次线性⽅程组的解空间维数为__2___________。
6. 设A为三阶可逆阵,,则7.若A为矩阵,则齐次线性⽅程组有⾮零解的充分必要条件是8.已知五阶⾏列式,则9. 向量的模(范数)。
10.若与正交,则⼆、选择题(本题总计10分,每⼩题2分)1. 向量组线性相关且秩为s,则(D)A.B.C.D.2. 若A为三阶⽅阵,且,则(A)A.B.C.D.3.设向量组A能由向量组B线性表⽰,则( d )A.B.C.D.4. 设阶矩阵的⾏列式等于,则等于。
c5. 设阶矩阵,和,则下列说法正确的是。
则 ,则或三、计算题(本题总计60分。
1-3每⼩题8分,4-7每⼩题9分)1. 计算阶⾏列式。
2.设A为三阶矩阵,为A的伴随矩阵,且,求.3.求矩阵的逆4. 讨论为何值时,⾮齐次线性⽅程组①有唯⼀解;②有⽆穷多解;③⽆解。
5. 求下⾮齐次线性⽅程组所对应的齐次线性⽅程组的基础解系和此⽅程6.已知向量组、、、、,求此向量组的⼀个最⼤⽆关组,并把其余向量⽤该最⼤⽆关组线性表⽰.7. 求矩阵的特征值和特征向量.四、证明题(本题总计10分)设为的⼀个解,为对应齐次线性⽅程组的基础解系,证明线性⽆关。
(答案⼀)、填空题(本题总计20分,每⼩题 2 分)15;2、3;3、;4、;5、2;6、;7、;8、0;9、3;10、1。
.⼆、选择题(本总计 10 分,每⼩题 2分 1、D;2、A;3、D;4、C;5、B、计算题(本题总计60分,1-3每⼩题8分,4-7他每⼩题9分)1、解: ------3分-------6分----------8分此题的⽅法不唯⼀,可以酌情给分。
西安电子科技大学线性代数试卷及参考答案1

{
x1 + x2 + x3 = 0, 2 x1 + 2 x2 + x3 = 0, xi ∈ R} ,则 dim V =
3.已知向量组 α1 , α 2 , α 3 , α 4 线性无关,而向量组 β 1 = 4α 1 + α 2 , β 2 = α 2 + α 3 ,
β 3 = α 3 + α 4 , β 4 = α 4 + 2λα 1 线性相关,则 λ =
经正交变换化为标准形
2
2
2
f ( y1 , y 2 , y3 ) = 2 y1 + 5 y 2 + 5 y3
2
2
2
, 求参数 a ,b 及用的正交变换。
⎛2 ⎜ ⎜1 六、 (6 分) 已知四阶方阵 A ,X 满足关系式 AXA − 2 A = XA , 且A=⎜ 0 ⎜ ⎜0 ⎝
2
5 3 0 0
0 0 4 7
(1) a ≠ −2 且 a ≠ 1 时,有唯一解 (2) a = −2 时,因为: R ( A) ≠ R( B) ,所以方程组无解。 (3) a = 1 时,因为: R ( A) = R( B) =1<3,所以方程组有无穷多解。
⎛ − 1⎞ ⎛ − 1⎞ ⎛ x1 ⎞ ⎛ 2 ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ 其通解为 ⎜ x 2 ⎟ = ⎜ 0 ⎟ + k1 ⎜ 1 ⎟ + k 2 ⎜ 0 ⎟ ⎜1⎟ ⎜0⎟ ⎜ x ⎟ ⎜ 0⎟ ⎝ ⎠ ⎝ ⎠ ⎝ 3⎠ ⎝ ⎠
3n + 1 3 L 3 3 3n + 1 3 L 3 3 c1 + c 2 3n + 1 4 L 3 3 r2 − r1 0 1 L 0 0 c1 + c3 L L L L L r3 − r1 L L L L L = 3n + 1 二 解: Dn 3n + 1 3 L 4 3 0 0 L 1 0 M M 0 L 0 1 c1 + c n 3n + 1 3 L 3 4 rn − r1 0
线性代数试题

.线性代数试卷(1)一. 填空题(每小题3分,满分30分) 1. 设21321,,,,ββααα 都是4维列向量,且4阶行列式,,3221121n m ==αβαααβαα 则4阶行列式()=+21123ββααα_-_m+n_____________2. 已知321,,ααα线性相关,3α不能由21,αα线性表示则21,αα线性__相关________3. 设A 是n m ⨯阶矩阵 ,,B 是s n ⨯阶矩阵,,()r A R =,且0=AB ,则()B R 的取值 范围是________________4.设A 是4⨯3矩阵,且A 的秩()2=A R 且⎪⎪⎪⎭⎫⎝⎛-=301020201B 则()=AB R __________-25.设0是矩阵⎪⎪⎪⎭⎫ ⎝⎛=a A 01020101的特征值,则=a _____________-6.设2123222213212),,(x x x k kx x x x x f +++=是正定二次型, 则t 的取值区间为 >17.矩阵⎪⎪⎪⎭⎫ ⎝⎛--=314120401A 对应的二次型是_______________ 8. 设⎪⎪⎪⎭⎫⎝⎛---=44644325x A 相似于对角阵⎪⎪⎪⎭⎫ ⎝⎛321,则=x9.设A 为3阶方阵,*A 为伴随矩阵,81=A ,则*1831A A -⎪⎭⎫ ⎝⎛-=____64______10.设⎪⎪⎪⎭⎫ ⎝⎛---=14523121x A 是不可逆矩阵,则=x ____________二. (8分)计算行列式yy x x -+-+1111111111111111……………..三.(8分) 三阶方阵B A ,满足关系式:BAE AB +=+2,且⎪⎪⎪⎭⎫ ⎝⎛=101020101A ,求B四.(10分)设()()()()()6,5,1,2,0,2,1,1,14,7,0,3,2,1,3,0,4,2,1,154321=-===-=ααααα求向量组的秩及其一个极大无关组.五. (12分)问常数k 取何值时, 方程组⎪⎩⎪⎨⎧-=+-=++-=++4243212321321x x x k x kx x kx x x无解,有唯一解,或有无穷多解,并在有无穷多解时写出其一般解.六. (16分)求正交变换PY X =,将二次型 ()32312123222132184444,,x x x x x x x x x x x x f -+-++=化为 标准形,并写出其标准形.七. (8分)设B A ,都是n 阶矩阵,且A 可逆,证明AB 与BA 有相同的特征值八. (8分)设向量组:A mααα,,,21线性无关,向量1β可由向量组A 线性表示,而向量2β不能由向量组A 线性表示.证明:1+m 个向量2121,,,,ββααα+l m 必线性无关.线性代数试卷(2)填空题 (每小题3分,满分30分) 1..________,___,04334221321111==-x xx x 的根方程2.().________)(,,2010,2101===⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=A R A 则矩阵设αββα3. 设A 、B 为4阶方阵,且2-=A ,3=B ,则_________1))((=-T AB4..______,=A A 则相似于单位矩阵设5. A 是34⨯矩阵,其秩rank ()A =1,⎪⎪⎪⎪⎪⎭⎫⎝⎛--=0030000108532001B , 则rank ()BA = _____6.._________ ,0,11223112321==⎪⎪⎪⎪⎪⎭⎫⎝⎛---=t Ax t A 则有非零解且方程组设7.设方阵A 有一特征值为λ,则()rr A a A a E a A f +++= 10的特征值为 。
线性代数试卷1(完整版带答案,可直接作为考试卷)

(3)当 时,增广矩阵为
~
,此方程组有无穷多解。。。。。。。。。。12分
4、解: )= ~ …….6分
所以 是最大无关组(8分),且 , ……..12分
5.解因 ,故对应的齐次方程组Ax=0的基础解系由
1个非零解构成,且 都是Ax=0的解, 即是Ax=0的基础解系,
所以Ax=b的通解为 (共12分,酌情给分)
1、 ,
2、
3、1,—34、 5、-32,0
二、选择题:(每小题4分,共20分)
1、 2、 3、A4、A5、B
三.计算题(每题12分,共60分)
1解
以上步骤每步3分,共12分。
2.
以上步骤每步4分,共12分。
3、解:因,方程组有唯一解;。。。。。。。。。4分
(2)当 时,方程组的增广矩阵为
1.齐次线性方程组 只有零解,则 应满足条件______。
(A) (B) (C) (D)
2.设A是4阶矩阵,且 ,则 。
(A)16 (B)32 (C)8 (D) 0
3.已知非齐次线性方程组 无解,则a=______。
(A)-1 (B)0 (C)2 (D) 3
4.已知方阵A的列向量组 线性无关,下列结论中正确的是_______。
(A)向量组 的任一部分向量组都线性无关;
(B)向量组 中存在两个向量分量对应成比例;
(C)齐次方程组 有非零解;
(D)向量组 中有一个是零向量
5.设 是可逆矩阵A的一个特征值,则矩阵 有一个特征值为_______。
(A)1 (B) (C)2 (D) 3
三.计算题(每题12分,共60分)
1.计算n阶行列式。
2.解矩阵方程
【新教材】人教版(2024)七年级上册数学第三章 代数式 综合素质评价试卷(Word版,含答案)

【新教材】人教版(2024)七年级上册数学第三章代数式 综合素质评价试卷时间:90分钟 满分:120分一、选择题(每题3分,共30分)1.下列数与式子:①2x -y +1;②1a +1b ;③2x +1=3;④ 3>2;⑤ a ;⑥ 0,其中是代数式的有( ) A .2个B .3个C .4个D .6个2.如果a ÷b =c ,那么当a 一定时,b 与c ( ) A .成正比例 B .成反比例 C .不成比例 D .无法确定比例关系 3.代数式x -y 2的意义是( )A . x 与y 的一半的差B . x 的一半与y 的差C . x 与y 的差的一半D .以上答案均不对4.如果某种药降价40%后的价格是a 元,那么此药的原价是( ) A .(1+40%)a 元B .(1-40%)a 元C .a1+40%元 D .a1-40%元5.下列表示图中阴影部分面积的代数式是( )(第5题)A . ad +bcB . c (b -d )+d (a -c )C . ad +c (b -d )D . ab -cd6.[情境题 生活应用]某文具店三月份销售铅笔100支,四、五两个月销售量连续增长.若月平均增长率为x ,则该文具店五月份销售铅笔的支数是( ) A .100(1+x )B .100(1+x )2C .100(1+x 2)D .100(1+2x )7.[2024烟台莱州市期末]有长为l 的篱笆,利用它和房屋的一面墙围成如图所示的长方形园子,园子的宽为t ,则所围成的园子面积为( )(第7题)A .(l -2t )tB .(l -t )tC . (l2-t)tD . (l -t2)t8.[新考法 整体代入法]若代数式2x 2+3x 的值是5,则代数式4x 2+6x -9的值是( )A .10B .1C .-4D .-89.如果|5-a |+(b +3)2=0,那么代数式1a(1-2b )的值为( ) A .57B .58C .75D .8510.[新视角 规律探究题 2024 北京西城区月考]如图为手的示意图,在各个手指间标记字母A ,B ,C ,D ,请你按图中箭头所指方向(即A ⇒B ⇒C ⇒D ⇒C ⇒B ⇒A ⇒B ⇒C ⇒…)从A 开始数连续的正整数1,2,3,4,…,当字母C 第2 024次出现时,恰好数到的数是( )(第10题)A .6 072B .6 071C .6 065D .6 066二、填空题(每题4分,共24分) 11.[2024锦州凌海市期中]下列书写:①1y ;②123x 2y ;③7m 2n 3;④n 23;⑤2 024×a ×b ;⑥m+3千克,其中正确的是 (填序号). 12.写出7(a -3)的意义: .13.一台电脑原价为a 元,降价20%后,又降低m 元,现售价为 元.14.[2024佛山顺德区期中]某地海拔高度h (km)与温度T (℃)的关系可用T =20-6h 来表示,则该地某海拔高度为2 000 m 的山顶上的温度为 .15.[教材P7习题T10变式 2024泰州兴化市期中]一个两位数x ,还有一个两位数y ,若把x 放在y 前面,组成一个四位数,则这个四位数为 (用含x ,y 的代数式表示). 16.[新视角 程序计算题]按如图所示的程序流程计算,若开始输入的值为x =3,则最后输出的结果是 .三、解答题(共66分)17.(6分)表中的两个量是否成比例关系,成什么比例关系? (1)每支圆珠笔的价钱/元 3 2 1.5 1.2 购买圆珠笔的支数10152025(2)每天的运货量/吨 100 120 150 200 需要的天数60504030(3)。
人教版六年级数学下册期末数与代数综合素质达标试卷附答案 (1)

人教版六年级数学下册数与代数综合素质达标一、填空。
(第1小题3分,其余每空1分,共28分) 1.( )∶( )=0.6=9( )=( )÷40=( )%=( )折2.地球绕太阳运行的轨道是微扁的椭圆形,太阳位于椭圆形的一个焦点上,这样地球离太阳有时会近些,有时会远些。
离太阳最远的一点叫“远日点”,距太阳约一亿五千二百零九万七千七百零一千米,横线上的数写作( ),省略“万”后面的尾数约是( )万。
3.1.5时=( )分 4 kg 50 g =( )kg 3.42 dm 2=( )cm 23公顷400平方米=( )平方米4.比7.5 kg 多15是( )kg ;1516 m 比( )多25%;17比25少( )%。
5.30的因数中,既是奇数又是合数的数是( ),既是偶数又是质数的数是( );从它的因数中选出4个组成的比例是( )。
6.在58、0.606、66%、0.6·这四个数中,最大的是( ),最小的是( )。
7.六年级买了5箱酸奶,每箱12瓶。
老师把这些酸奶平均分给4个班,每个班分得这些酸奶的(),每个班分到了()箱,有( )瓶。
8.观察数轴,点A 表示的数是( ),点B 表示的数用小数表示是( ),点C 表示的数写成分数是( )。
9.A =2×2×3×m ,B =2×3×5×m ,A 和B 的最大公因数是( ),最小公倍数是( )。
10.做一批3D 模型,A 机器单独做需要4天完成,B 机器单独做需要5天完成,A 机器、B 机器工作效率的比是( );A 、B 两台机器同时做( )天后还剩下这批3D 模型的110。
11.【杭州市期末】六一儿童节那天,某商店所有商品打九折,明明买了一副羽毛球拍便宜了15元,这副羽毛球拍的原价为( )元。
二、判断。
(对的画“√”,错的画“×”。
每小题1分,共5分) 1.自然数包括正整数、0和负整数。
大一线性代数试卷1含答案
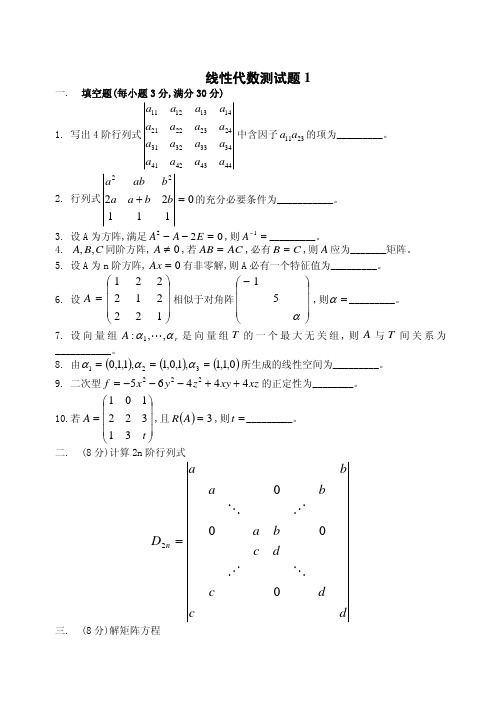
111
3. 设 A 为方阵,满足 A2 A 2E 0 ,则 A1 _________。 4. A, B,C 同阶方阵, A 0 ,若 AB AC ,必有 B C ,则 A 应为_______矩阵。
5. 设 A 为 n 阶方阵, Ax 0 有非零解,则 A 必有一个特征值为_________。
2 2 4
3 1 3
X
2 5
13
1 2 3
3 0 1
求X ?
四. (10 分)设向量组 A:
1 1,4,1,0,2 2,1,1,3,3 1,0,3,1,4 0,2,6,3
求向量组 A 的秩及一个最大无关组.
五. 12 分)讨论方程组的解的情况
x1 x1
x2 x2
x3 x3
9. 二次型 f 5x2 6 y2 4z2 4xy 4xz 的正定性为________。
1 10.若 A 2
0 2
1 3 ,且
RA
3
,则 t
_________。
1 3 t
二. (8 分)计算 2n 阶行列式
a
b
a
0
b
0
ab
0
D2n
cd
c
0
d
c
d
三. (8 分)解矩阵方程
1 2 3
1 (1, 1, 0)T 2
3
3
3, 2 2,2
2
(0,
1, 1)T
,标准化3
1 (0, 1, 1)T 2
因而 P (1 ,2 ,3 ) ,且 f 3 y22 3 y32
九. 令
1
2
3
n
1 1 1 1
2 2
2
北京市各区2019-2020学年上学期八年级期末数学试卷精选汇编:代数综合专题(含答案)

北京市各区2019-2020学年上学期八年级期末数学试卷精选汇编:代数综合专题(含答案)海淀区25.对于代数式,不同的表达形式能表现出它的不同性质.例如代数式245A x x =-+,若将其写成()221A x =-+的形式,就能看出不论字母x 取何值,它都表示正数;若将它写成()2=12(1)2A x x ---+的形式,就能与代数式B=222x x -+建立联系.下面我们改变x 的值,研究一下A ,B 两个代数式取值的规律:(1)完成上表; (2)观察表格可以发现:若x =m 时,222=B x x n =-+,则x =m +1时,245A x x n =-+=.我们把这种现象称为代数式A 参照代数式B 取值延后,此时延后值为1.①若代数式D 参照代数式B 取值延后,相应的延后值为2,求代数式D ;②已知代数式210ax x b -+参照代数式234x x c -+取值延后,请直接写出b -c 的值:_____________.25.解(1)2;2,1,2. ………………………2分(2)①∵代数式D 参照代数式B 取值延后,相应的延后值为2,∴22(2)2(2)2610D x x x x =---+=-+. …………………4分 ② 7 ………………………6分东城区26. 列方程,解应用题:第二届中国国际进口博览会于2019年11月5日至10日在上海国家会展中心举行.与首届相比,第二届进博会的展览面积更大,企业展设置科技生活、汽车、装备等七个展区,展览面积由的270 000平方米增加到330 000平方米.参展企业比首届多了约300家,参展企业平均展览面积增加了12.8%,求首届进博会企业平均展览面积.(1) 在解应用题时,我们常借助表格、线段图等分析题目中的数量关系. 设首届进博会企业平均展览面积为x 平方米,把下表补充完整:(2)270 000330000+300=(1+12.8%)x x.……………………6分 丰台区24.已知a ,b ,m 都是实数,若a +b =2,则称a 与b 是关于1的“平衡数”.(1)4与 是关于1的“平衡数”,3与 是关于1的“平衡数”;(2)若=2(-m +,判断m +与2-是否是关于1的“平衡数”,并说明理由.24. 解:(1);. 2分(2)不是.∵, ∴.∴. ∴.∴==3. 4分∴与不是关于 1的“平衡数”. 6分密云区26.数学课堂上,老师提出问题:可以通过通分将两个分式的和表示成一个分式的形式,是否也可以将一个分式31(1)(1)x x x ++-表示成两个分式和的形式?其中这两个分式的分母分别为x+1和x -1.小明通过观察、思考,发现可以用待定系数法解决上面问题.具体过程如下: 设31(1)(1)x x x ++-11A Bx x =++- 则有31(1)(1)x x x ++-(1)(1)()(1)(1)(1)(1)(1)(1)A xB x A B x B Ax x x x x x -+++-=+=+-+-+-故此31A B B A +=⎧⎨-=⎩ 解得12A B =⎧⎨=⎩所以31(1)(1)x x x ++-=1211x x ++- 问题解决: (1)设1(1)1x A Bx x x x -=+++,求A 、B.(2)直接写出方程111(1)(1)(2)2x x x x x x x --+=++++ 的解.26. (1)∵(1)=1(1)(1)A B A x Bx x x x x x x ++++++ ………………1分()1(1)(1)A B x A xx x x x ++-==++………………2分 ∴1,1A B A +=-= ………………3分 ∴2B =-………………4分(2)23x =………………6分门头沟区26.信息1:我们已经学完了解分式方程,它的一般步骤为:确定最简公分母、化为整式方程、求出整式方程的解、进行检验(第一,代入最简公分母验证是否为零,第二代入分式方程的左右两边检验是否相等)、确定分式方程的解。
考研数学三线性代数向量-试卷1_真题(含答案与解析)-交互

考研数学三线性代数(向量)-试卷1(总分56, 做题时间90分钟)1. 选择题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.设α1,α2,…,αs均为n维向量,下列结论中不正确的是( ) SSS_SINGLE_SELA若对于任意一组不全为零的数k1,k2,…,ks,都有k1α1+k2α2+…+ks αs≠0,则α1,α2,…,αs线性无关.B若α1,α2,…,αs线性相关,则对于任意一组不全为零的数k1,k2,…,ks,都有k1α1+k2α2+…+ksαs=0.Cα1,α2,…,αs线性无关的充分必要条件是此向量组的秩为sDα1,α2,…,αs线性无关的必要条件是其中任意两个向量线性无关该题您未回答:х该问题分值: 2答案:B解析:选项A的条件即齐次线性方程组 x1 a1+x2a2+…+xsas=0 只有零解,故α1,α2,…,αs线性无关,A选项正确.对于选项B,由α1,α2,…,αs线性相关知,齐次线性方程组 x1α1+x2α2+…+xsαs=0 存在非零解,但该方程组存在非零解,并不意味着任意一组不全为零的数均是它的解,因此选项B是错误的.选项C是教材中的定理.由“无关组减向量仍无关”(线性无关的向量组其任意部分组均线性无关)可知选项D也是正确的.综上可知,应选B.2.设A是m×n矩阵,则齐次线性方程组Ax=0仅有零解的充分条件是( ) SSS_SINGLE_SELA A的列向量线性无关.B A的列向量线性相关.C A的行向量线性无关.D A的行向量线性相关.该题您未回答:х该问题分值: 2答案:A解析:齐次线性方程组Ax=0的向量形式为 x1α1+x2α2+…+xnαn=0,其中α1,α2,…,αn为A的x个m维的列向量.由Ax=0只有零解α1,α2,…,αn线性无关.可知选项A正确.对于选项C、D,只要m<n,不管A的行向量线性相关性如何,该齐次线性方程组都必有非零解,故C、D均不正确.所以应选A.3.设则三条直线a1 x+b1y+c1=0,a2x+b2y+c1=0,a3x+b3y+c3=0(其中,i=1,2,3)交于一点的充分必要条件是( )SSS_SINGLE_SELAα1,α2,α3线性相关Bα1,α2,α3线性无关Cr(α1,α2,α3)=r(α1,α2).Dα1,α2,α3线性相关,α1,α2线性无关.该题您未回答:х该问题分值: 2答案:D解析:三直线交于一点的充分必要条件是以下线性方程组或xα1+yα2+α3, (2) 有唯一解.由(2)式可得α3=-xα1-yα2而方程组(2)(或(1))有唯一解α3可由α1,α2线性表示,且表示式唯一.α1,α2,α3线性相关,α1,α2线性无关.所以应选D.4.设向量组α1,α2,α3线性无关,则下列向量组线性相关的是( ) SSS_SINGLE_SELAα1 -α2,α2-α3,α3-α1Bα1+α2,α2+α3,α3+α1Cα1 -2α2,α2-2α3,α3-2α1Dα1+2α2,α2+2α3,α3+2α1该题您未回答:х该问题分值: 2答案:A解析:利用向量组线性相关的定义,令 x1(α1-α2)+x2(α2-α3)+x3(α3-α1)=0,(x1,x2,x3为不全为零的实数) 可得(x1-x3)α1+(-x1 +x2)α2+(-x2+x3)α3=0 又已知α1,α2,α3线性无关,则则齐次线性方程组(母)有非零解,故α1 -α2,α2-α3,α3 -α1线性相关.故应选A.5.若α1,α2线性无关,β是另外一个向量,则α1+β与α2+β( )SSS_SINGLE_SELA 线性无关.B 线性相关.C 即线性相关又线性无关.D 不确定.该题您未回答:х该问题分值: 2答案:D解析:例如,令α1 =(1,1),α2=(0,2),β=(-1,-1),则α1,α2线性无关,而α1+β=(0,0) 与α2+β=(-1,1)线性相关.如果设β=(0,0),那么α1+β与α2+β却是线性无关的.故选D6.已知向量组则向量组α1,α2,α3,α4,α5的一个极大无关组为( )SSS_SINGLE_SEL Aα1,α3Bα1,α2Cα1,α2,α5Dα1,α3,α5该题您未回答:х该问题分值: 2答案:D解析:对以α1,α2,α3,α4,α5为列向量的矩阵作初等行变换,有所以α1,α3,α5是一个极大无关组,且α2=α1+3α5,α4=α1+α3+α57.设α1 =(1,2,3,1) T,α2=(3,4,7,-1) T,α3=(2,6,0,6)T,α4 =(0,1,3,a) T,那么a=8是α1,α2,α3,α4线性相关的( )SSS_SINGLE_SELA 充分必要条件.B 充分而非必要条件.C 必要而非充分条件.D 既不充分也非必要条件该题您未回答:х该问题分值: 2答案:B解析:n个n维向量线性相关性一般用行列式|α1,α1,…αn|是否为零去判断.因为|α1,α1,…,α4|= 因此,当a=8时,行列式|α1,α2,…,α4|=0,向量组α1,α2,α3,α4线性相关,但a=2时仍有行列式|α1,α2,…,α4|=0,所以a=8是向量组α1,α2,α3,α4线性相关的充分而非必要条件.8.设向量β可由向量组α1,α2,…,αm线性表示,但不能由向量组(Ⅰ):α1,α2,…,αm-1线性表示,记向量组(Ⅱ):α1,α2,…,αm-1,β,则( )SSS_SINGLE_SEL Aαm不能由(Ⅰ)线性表示,也不能由(Ⅱ)线性表示.Bαm不能由(Ⅰ)线性表示,但可以由(Ⅱ)线性表示.Cαm可以由(Ⅰ)线性表示,也可以由(Ⅱ)线性表示.Dαm可以由(Ⅰ)线性表示,但不能由(Ⅱ)线性表示.该题您未回答:х该问题分值: 2答案:B解析:按题意,存在组实数k1,k2,…,km使得 k1α1+k2α2+…+km αm=β (*) 且必有km≠0.否则与β不能由α1,α2,…,αm-1线性表示相矛盾,从而即αm可由向量组(Ⅱ)线性表示,排除选项A、D.若αm 可以由(Ⅰ)线性表示,即存在实数l1,l2,…,lm-1,使得αm =l1α1+l2α2+…+lm-1αm-1,将其代入(*)中,整理得β=(k1 +kml1)α1+(k2+kml2)α2+…+(km-1+kmlm-1)αm-1,这与题设条件矛盾.因而αm不能由向量组(Ⅰ)线性表示,排除选项C.9.已知四维向量组α1,α2,α3,α4线性无关,且向量β1=α1+α3+α4,β2=α2-α4,β3=α3+α4,β4=α2+α3,β5=2α1+α2+α3.则r(β1,β2,β3,β4,β5)=( ) SSS_SINGLE_SELA 1.B 2.C 3.D 4.该题您未回答:х该问题分值: 2答案:C解析:将表示关系合并成矩阵形式有(β1,β2,β3,β4,β5)=(α1,α2,α3,α4) 因4个四维向量α1,α2,α3,α4线性无关,故|α1,α2,α3,α4|≠0.A=(α1,α2,α3,α4)是可逆矩阵,A左乘C,即对C作若干次初等行变换,故有r(C)=r(AC)=r(AC)=r(β1,β2,β3,β4,β5) 故知r(β1,β2,β3,β4,β5)=r(C)=3,因此应选C.10.设A是n阶方阵,且|A|=0,则A中( )SSS_SINGLE_SELA 必有一列元素全为0.B 必有两列元素对应成比例.C 必有一列向量是其余列向量的线性组合.D 任一列向量是其余列向量的线性组合.该题您未回答:х该问题分值: 2答案:C解析:对于方阵A,因为的行(列)向量组的秩小于n,所以A的列向量组必然线性相关,再由向量组线性相关的充分必要条件可知,其中至少有一个向量可由其余向量线性表示,故选C.选项A、B仅是|A|=0的充分条件,故均不正确.由向量组线性相关的充分必要条件之“至少存在一个向量可用其余向量线性表示”可知,D也不正确.2. 填空题1.如果β=(1,2,t) T可以由α1 =(2,1,1) T,α2=(-1,2,7) T,α3=(1,-1,-4) T线性表示,则t的值是_______SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案:5解析:β可以由向量组α1,α2,α3线性表示的充分必要条件是非齐次线性方程组x1α1+x2α2+x3α3=β有解,对该方程组的增广矩阵作初等行变换得而方程组有解的充分必要条件是系数矩阵与增广矩阵有相同的秩,因此t-5=0,即t=5.2.设x为3维单位列向量,E为3阶单位矩阵,则矩阵E—xx T的秩为_____ SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案:2解析:由题设知,矩阵xx T的特征值为0,0,1,故E-xx T的特征值为1,1,0.又由于实对称矩阵是可相似对角化的,故它的秩等于它非零特征值的个数,即r(E-xx T )=2.3.向量组α1 =(1,0,0),α2=(1,1,0),α3=(-5,2,0)的秩是________ SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案:2解析:对向量组构成的矩阵进行初等变换,变为阶梯形矩阵,其不全为0的行向量的个数就是向量组的秩,即,因此秩是2.4.已知r(α1,α2,…,αs)=r(α1,α2,…,αs,β)=r,r(α1,α2,…,αs,γ)=r+1,则r(α1,α2,…,αs,β,γ)=______SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案:r+1解析:已知r(α1,α2,…,αs)=r(α1,α2,…,αs,β)=r,表明向量β可以由向量组α1,α2,…,αs线性表示,但是r(α1,α2,…,αs,γ)=r+1,则表明向量γ不能由向量组α1,α2,…,αs 线性表示,因此通过对向量组α1,α2,…,αs,β,γ作初等列变换,可得(α1,α2,…,αs,β,γ)=(α1,α2,…,αs,0,γ),因此可得r(α1,α2,…,αs,β,γ)=r+1.5.设α1 =(1,2,1) T,α2=(2,3,a) T,α3=(1,a+2,-2) T,若β1=(1,3,4) T可以由α1,α2,α3线性表示,但是β2=(0,1,2) T不可以由α1,α2,α3线性表示,则a=________ SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案:-1解析:根据题意,β1 =(1,3,4) T可以由α1,α2,α3线性表示,则方程组x1α1+x2α2+x3α3=β1有解,β2=(0,1,2) T不可以由α1,α2,α3线性表示,则方程组x1α1+x2α2+x3α3=β无解,由于两个方程组的系数矩阵相同,因此可以合并一起做矩阵的初等变换,即因此可知,当a=-1时,满足方程组x1α1+x2α2+x3α3=β有解,方程组x1α1+x2α2+x3α3=β2无解的条件,故a=-1.6.已知α1 =(1,4,2) T,α2=(2,7,3) T,α3=(0,1,a) T可以表示任意一个三维向量,则a的取值是______SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案:a≠1解析:α1,α2,α3可以表示任一个3维向量,因此向量α1,α2,α3与ε1=(1,0,0) T,ε2=(0,1,0) T,ε=(0,0,1) T是等价向量,因此α1,α2,α3的秩为3,即|α1,α2,α3|≠0,于是因此a≠1.7.与α1 =(1,2,3,-1) T,α2=(0,1,1,2) T,α3=(2,1,3,0) T都正交的单位向量是_______SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案:解析:已知,若向量α,β正交,则内积α Tβ=0,设β=(x1,x2,x3,x4) T与α1,α2,α3均正交,那么对以上齐次方程组的系数矩阵作初等行变换,有得到基础解系是(-1,-1,1,0) T,将这个向量单位化得,即为所求向量.3. 解答题解答题解答应写出文字说明、证明过程或演算步骤。
近世代数期末考试试卷及答案1

抽代试题 2一、单项选择题(本大题共5小题,每小题3分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1、设G 有6个元素的循环群,a 是生成元,则G 的子集(c )是子群。
A 、{}aB 、{}e a ,C 、{}3,a eD 、{}3,,a a e 2、下面的代数系统(G ,*)中,( D )不是群A 、G 为整数集合,*为加法B 、G 为偶数集合,*为加法C 、G 为有理数集合,*为加法D 、G 为有理数集合,*为乘法3、在自然数集N 上,下列哪种运算是可结合的?( B )A 、a*b=a-bB 、a*b=max{a,b}C 、 a*b=a+2bD 、a*b=|a-b|4、设1σ、2σ、3σ是三个置换,其中1σ=(12)(23)(13),2σ=(24)(14),3σ=(1324),则3σ=( B ) A 、12σ B 、1σ2σ C 、22σ D 、2σ1σ5、任意一个具有2个或以上元的半群,它( A )。
A 、不可能是群B 、不一定是群C 、一定是群D 、 是交换群二、填空题(本大题共10小题,每空3分,共30分)请在每小题的空格中填上正确答案。
错填、不填均无分。
1、凯莱定理说:任一个子群都同一个----变换群------同构。
2、一个有单位元的无零因子-交换环----称为整环。
3、已知群G 中的元素a 的阶等于50,则4a 的阶等于----25--。
4、a 的阶若是一个有限整数n ,那么G 与---模n 剩余类加群----同构。
5、A={1.2.3} B={2.5.6} 那么A ∩B=---{2}--。
6、若映射ϕ既是单射又是满射,则称ϕ为----双射-------------。
7、α叫做域F 的一个代数元,如果存在F 的-----n a a a ,,,10 使得010=+++n n a a a αα 。
8、a 是代数系统)0,(A 的元素,对任何A x ∈均成立x a x = ,则称a 为---右单位元------。
高等代数试卷及答案__(一)[1]
![高等代数试卷及答案__(一)[1]](https://img.taocdn.com/s3/m/62321d0ff78a6529647d53c8.png)
一、填空题(共10 题,每题2分,共20分)。
1. 多项式可整除任意多项式。
2.艾森施坦因判别法是判断多项式在有理数域上不可约的一个 条件。
3.在n 阶行列式D 中,0的个数多于 个是0D =。
4.若A 是n 阶方阵,且秩1A n =-,则秩A *= 。
5.实数域上不可约多项式的类型有 种。
6.若不可约多项式()p x 是()f x 的k 重因式,则()p x 是(1)()k f x -的 重因式。
7.写出行列式展开定理及推论公式 。
8.当排列12n i i i 是奇排列时,则12n i i i 可经过 数次对换变成12n 。
9.方程组12312322232121x x x ax bx cx d a x b x c x d ++=⎧⎪++=⎨⎪++=⎩,当满足 条件时,有唯一解,唯一解为 。
10.若242(1)1x ax bx -∣++,则a = ,b = 。
二、判断题(共10 题,每题1分, 共 10分)。
1.任何两个多项式的最大公因式不因数域的扩大而改变。
( )2.两个多项式互素当且仅当它们无公共根。
( ) 3.设12n ααα 是nP 中n 个向量,若nP β∀∈,有12,n αααβ 线性相关,则12n ααα 线性相关。
( )4.设α是某一方程组的解向量,k 为某一常数,则k α也为该方程组的解向量。
( ) 5.若一整系数多项式()f x 有有理根,则()f x 在有理数域上可约。
( ) 6 秩()A B +=秩A ,当 且仅当秩0B =。
( ) 7.向量α线性相关⇔它是任一向量组的线性组合。
( )8. 若(),()[]f x g x P x ∈,且((),())1f x g x =,则(()(),()())1f x g x f x g x +=。
( ) 9.(),()[]f x g x Z x ∈,且()g x 为本原多项式,若()()()f x g x h x =则()[]h x Z x ∈。
