河北省唐山市开滦一中09-10学年高一下学期期中考试(数学)
2016-2017学年河北省唐山市开滦第一中学高一下学期期中考试数学(理)试题

开滦一中2016—2017年度第二学期高一年级期中考试数学试卷(理科) 命题人:说明:1.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
2.本试卷共 150 分,考试时间120 分钟。
注意事项:1.答第Ⅰ卷前,考生务必将自己的考试号、科目填涂在答题卡上。
2.每小题选出答案后,用2B 铅笔把答题卡上对应的题目标号涂黑。
答在试卷上无效。
3.考试结束,监考人员将试卷和机读卡一并收回。
第Ⅰ卷(选择题,共60分)一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知{}n a 是等比数列,21,441==a a ,则公比q =( ) A 、21- B 、2- C 、21 D 、2 2、在ABC ∆中,已知ab c b a 2222-=+,则C ∠=( ) A 、030 B 、045 C 、0135 D 、01503、1212+-与的等比中项是( )A 、1B 、1-C 、1±D 、以上选项都不对4、若集合}0107|{2<+-=x x x A ,集合}8221|{<<=x x B ,则=⋂B A ( ) A 、)3,1(- B 、)3,2( C 、)5,2( D 、)5,1(-5、n S 为等差数列{}n a 的前n 项和,已知18543=++a a a ,求7S =( )A 、35B 、42C 、30D 、1056、在ABC ∆中,角A,B,C 的对边分别是a,b,c,若A:B:C=1: 2:3,则a:b:c=( )A 、2:3:1B 、2:3:4C 、3:4:5D 、1:2:37、已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为( )A 、2B 、5C 、4D 、38、等差数列{}n a 的前m 项和为30,前2m 项和为120,则它的前3m 项和为( )A 、130B 、170C 、210D 、2709、在△ABC 中,如果sin :sin :sin 2:3:4A B C =,那么cosC 等于( )2A.3 41.-B 31.-C 32.-D 10.ABC ∆中,若︒===60,2,1B c a ,则ABC ∆的面积为( )A .21 B .3 C.1 D. 23 11设△ABC 的内角A , B , C 所对的边分别为a , b , c , 若cos cos sin b C c B a A +=, 则△ABC 的形状为( ) A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 不确定 12、已知两个等差数列{}n a ,{}n b 的前n 项和之比为)(27417*N n n n ∈++,则1111b a 值 A 、47 B 、23 C 、34 D 、7178 第Ⅱ卷(非选择题,共 100 分) 二、填空题:(本大题共4小题,每小题5分,共20分.把各题答案填写在答题纸相应位置.) 13、在ABC ∆中,已知3,60,1===a A c o ,则B= . 14、已知数列}{n a 的前n 项和为n S ,且22n S n n =++1,则=n a15、在两数1和16之间插入3个数,使它们成等比数列,则中间数等于_________16、140,0,1x y x y>>+=若且,则x y +的最小值是 . 三、解答题(本大题共7小题,共80分,解答应写出文字说明、证明过程或演算步骤)17、(本题满分10分)求函数y=)0(1<+x xx 的最值;班级____________ 姓名____________ 考号____________ 年级名次____________18、(本题满分12分)在等差数列{}n a 中,138a a +=,且4a =12,求数列{}n a 的通项公式及前n 项和.19、(本题满分12分)在ABC ∆中,三个内角A 、B 、C 的对边分别是c b a ,,,已知B c C b a sin cos +=,(1)求B ;(2)若b=22,求ABC ∆面积的最大值。
河北唐山市开滦第一中学高一下学期期中考试数学理试题word含答案

开滦一中2015—2016学年度第二学期高一年级 期中考试(数学理)试卷 命题人:张明刚第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项正确)1.在等比数列{a n }中,a 2=8,a 5=64,,则公比q 为( ) A .2 B .3 C .4 D .82.在⊿ABC 中,已知ba c b a 2222+=+,则∠C=( ) A 300B 1500C 450D 13503.一元二次不等式220ax bx ++>的解集是11(,)23-,则a b +的值 A. 10 B. 10- C. 14 D. 14-4.数列{},{}n n a b 满足1,(1)(2)n n n a b a n n ==++,则{}n b 的前10项之和 A .14 B .712 C .34 D . 5125.已知等比数列}{n a 的各项均为正数,公比1≠q ,设293a a P +=,75a a Q •=,则P 与Q 的大6.已知点(3,1)和(- 4,6)在在直线3x-2y+a=0的两侧,则a 的取值范围是 A.a<-7或 a>24 B. a=7 或 a=24 C. -7<a<24 D. -24<a<77. 不等式1213≥--xx 的解集是( ) A .⎭⎬⎫⎩⎨⎧≤≤243|x x B .⎭⎬⎫⎩⎨⎧<≤243|x x C .⎭⎬⎫⎩⎨⎧≤>432|x x x 或 D .{}2|<x x8.等差数列{a n }的前n 项和为S n ,若2462,10,S S S ==则等于A .12B .18C .24D .429.设ABC ∆的三内角A 、B 、C 成等差数列,sinA 、sinB 、 sinC 成等比数列,则这个三角形的形状是( )A.直角三角形 B.钝角三角形 C.等腰直角三角形 D.等边三角形10若x ,y ∈R +,且2x +8y -xy =0,则x +y 的最小值为( )A .12B .14C .16D .1811.△ABC 的三个内角A 、B 、C 所对的边分别为2a,b,c,a sin A sin B b cos A +=,则ba= ( )(A) 12. 设}{n a 为等差数列,若11101a a <-,且它的前n 项和S n 有最小值,那么当S n 取得最小正值时,n = A . 18 B .19 C .20 D .21 二、填空题(每题5分,共20分)13.在ABC ∆中, 若13,cos 2a A ==-,则ABC ∆的外接圆的半径为 .14.在横线上填上正确的不等号:.15不等式0)3)(2(2>--x x 的解集是 ----------16.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若(a-b)sinB =asinA -csin C.,且a 2+b 2-6(a+b)+18=0,则AB BC BC CA CA AB ++u u u r u u u r u u u r u u u r u u u r u u u rg gg =_开滦一中2015—2016学年度第二学期高一年级期中考试(数学理)试卷 命题人:张明刚二.填空题:.每小题5分,共20分.将答案直接填在题中横线上。
河北省唐山市唐山一中2019-2020学年高一数学下学期期中试题含解析

【详解】数列
an
为正数项的等比数列,
若 a1a7 4 ,则根据等比数列的性质得到
a1a7 =a42
4
a4
2 ,且 a4
2a7
5 2
,可得到 a7
1 4
,根据等比数列的公式得到
a7
a4q3
1q 4
1 2 ,a1
16 , S4
a1 1 q4 1 q
30.
故答案为 C.
【点睛】本题考查等比数列的通项公式,是基础的计算题,对于等比等差数列的 小题,常
1 半径 r 2 OM
2 ,又 Q 1, 1
∴|AQ| 2 2> 2 ,则点 Q 在圆外, ∴ PQ 的取值范围为 2,3 2
故选:A. 【点睛】本题考查了恒过定点的直线方程,圆的轨迹方程,线段中点坐标公式,以及两点 间的距离公式,确定点 P 的轨迹是关键,属于中档题
卷 II(非选择题共 90 分) 二、填空题(共 4 小题,每题 5 分,共 20 分) 13.两个男生一个女生并列站成一排,其中两男生相邻的概率为_____
个选项正确,有选错或不答的得 0 分)
1. 在 等差数列an中,若 a2 8, 公差 d 2 ,则 a12 (
)
A. 10
B. 12
C. 14
D. 16
【答案】B
【解析】
【分析】
根据等差数列的通项公式求解即可得到结果.
【详解】∵等差数列
an
中,
a2
8
,公差 d
2,
∴ a12 a2 10d 8 20 12 .
2a b
c
cos C cos B
,b
4,
则
ABC
的
河北省唐山一中高一数学下学期期中试卷理(含解析)

2014-2015学年河北省唐山一中高一(下)期中数学试卷(理科)一、选择题(共12小题,每小题5分,满分60分)1.(2015春•唐山校级期中)直线x+y+1=0的倾斜角和在y轴上的截距分别为()A.135°,﹣1 B.135°,1 C.45°,﹣1 D.45°,1考点:直线的斜截式方程.专题:直线与圆.分析:化直线的方程为截距式,可得斜率和截距,进而可得倾斜角和截距.解答:解:化直线x+y+1=0的方程为斜截式可得y=﹣x﹣1,∴直线的斜率为﹣1,截距为﹣1,∴倾斜角为135°,截距为﹣1故选:A.点评:本题考查直线的截距式方程,属基础题.2.已知非零实数a,b满足a>b,则下列不等式成立的是()A.a2>b2B.C.a2b>ab2D.考点:不等关系与不等式.专题:计算题.分析:举特列,令a=1,b=﹣2,经检验 A、B、C 都不成立,只有D正确,从而得到结论.解答:解:令a=1,b=﹣2,经检验 A、B、C 都不成立,只有D正确,故选D.点评:本题考查不等式与不等关系,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法.3.在△ABC中,角A,B,C所对边长分别为a,b,c,若a2+b2=2c2,则cosC的最小值为()A.B.C.D.考点:余弦定理.专题:计算题;压轴题.分析:通过余弦定理求出cosC的表达式,利用基本不等式求出cosC的最小值.解答:解:因为a2+b2=2c2,所以由余弦定理可知,c2=2abcosC,cosC==.故选C.点评:本题考查三角形中余弦定理的应用,考查基本不等式的应用,考查计算能力.4.若变量x,y满足约束条件,则x+2y的最大值是()A.B.0 C.D.考点:简单线性规划.专题:计算题;不等式的解法及应用.分析:作出题中不等式组表示的平面区域,得如图的△ABC及其内部,再将目标函数z=x+2y对应的直线进行平移,可得当x=,y=时,x+2y取得最大值为.解答:解:作出不等式组表示的平面区域,得到如图的△ABC及其内部,其中A(﹣,﹣1),B(,),C(2,﹣1)设z=F(x,y)=x+2y,将直线l:z=x+2y进行平移,当l经过点B时,目标函数z达到最大值∴z最大值=F(,)=故选:C点评:本题给出二元一次不等式组,求目标函数z的最大值,着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识,属于基础题.5.(2015春•银川校级期中)已知圆O1:(x﹣1)2+(y+3)2=4,圆O2:(x﹣2)2+(y+1)2=1,则两圆的位置关系是()A.相交B.内切C.内含 D.外切考点:圆与圆的位置关系及其判定.专题:计算题;直线与圆.分析:先求出两个圆的圆心和半径,再根据它们的圆心距与半径之和、差的关系,可得两圆的位置关系.解答:解:圆O1的圆心为O(1,﹣3),半径等于2,圆O2的圆心为(2,﹣1),半径等于1,它们的圆心距等于=,因为2﹣1<<2+1,故两个圆相交,故选:A.点评:本题主要考查圆的标准方程,圆和圆的位置关系的判定方法,属于中档题.6.(2015•滕州市校级模拟)设等差数列{a n}的前n项和为S n,若S m﹣1=﹣2,S m=0,S m+1=3,则m=()A. 3 B. 4 C. 5 D. 6考点:等差数列的性质;等差数列的前n项和.专题:计算题;等差数列与等比数列.分析:由a n与S n的关系可求得a m+1与a m,进而得到公差d,由前n项和公式及S m=0可求得a1,再由通项公式及a m=2可得m值.解答:解:a m=S m﹣S m﹣1=2,a m+1=S m+1﹣S m=3,所以公差d=a m+1﹣a m=1,S m==0,得a1=﹣2,所以a m=﹣2+(m﹣1)•1=2,解得m=5,故选C.点评:本题考查等差数列的通项公式、前n项和公式及通项a n与S n的关系,考查学生的计算能力.7.(2013•陕西)设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为()A.锐角三角形B.直角三角形C.钝角三角形D.不确定考点:正弦定理.专题:解三角形.分析:由条件利用正弦定理可得 sinBcosC+sinCcosB=sinAsinA,再由两角和的正弦公式、诱导公式求得sinA=1,可得A=,由此可得△ABC的形状.解答:解:△ABC的内角A,B,C所对的边分别为a,b,c,∵bcosC+cc osB=asinA,则由正弦定理可得 sinBcosC+sinCcosB=sinAsinA,即 sin(B+C)=sinAsinA,可得sinA=1,故A=,故三角形为直角三角形,故选B.点评:本题主要考查正弦定理以及两角和的正弦公式、诱导公式的应用,根据三角函数的值求角,属于中档题.8.(2013•安徽)已知一元二次不等式f(x)<0的解集为{x|x<﹣1或x>},则f(10x)>0的解集为()A.{x|x<﹣1或x>﹣lg2} B. {x|﹣1<x<﹣lg2}C.{x|x>﹣lg2} D. {x|x<﹣lg2}考点:其他不等式的解法;一元二次不等式的解法.专题:不等式的解法及应用.分析:由题意可得f(10x)>0等价于﹣1<10x<,由指数函数的单调性可得解集.解答:解:由题意可知f(x)>0的解集为{x|﹣1<x<},故可得f(10x)>0等价于﹣1<10x<,由指数函数的值域为(0,+∞)一定有10x>﹣1,而10x<可化为10x<,即10x<10﹣lg2,由指数函数的单调性可知:x<﹣lg2故选:D点评:本题考查一元二次不等式的解集,涉及对数函数的单调性及对数的运算,属中档题.9.(2015春•唐山校级期中)如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=BD,BC=2BD,则sinC的值为()A.B.C.D.考点:余弦定理.专题:解三角形.分析:设BD=a,则由题意可得:BC=2a,AB=AD=a,利用余弦定理表示出cosA,把三边长代入求出cosA的值,进而确定出sinA的值,由AB,BC,以及sinA的值,利用正弦定理求出sinC的值即可.解答:解:设BD=a,则由题意可得:BC=2a,AB=AD=a,在△ABD中,由余弦定理得:cosA===,∴sinA==,在△ABC中,由正弦定理得,=,即=,解得:sinC=,故选:D.点评:此题考查了正弦、余弦定理,以及同角三角函数间的基本关系,熟练掌握定理是解本题的关键.10.(2013•山东)设正实数x,y,z满足x2﹣3xy+4y2﹣z=0.则当取得最大值时,的最大值为()A.0 B. 1 C.D. 3考点:基本不等式.专题:不等式的解法及应用.分析:依题意,当取得最大值时x=2y,代入所求关系式f(y)=+﹣,利用配方法即可求得其最大值.解答:解:∵x2﹣3xy+4y2﹣z=0,∴z=x2﹣3xy+4y2,又x,y,z均为正实数,∴==≤=1(当且仅当x=2y时取“=”),∴=1,此时,x=2y.∴z=x2﹣3xy+4y2=(2y)2﹣3×2y×y+4y2=2y2,∴+﹣=+﹣=﹣+1≤1,当且仅当y=1时取得“=”,满足题意.∴的最大值为1.故选B.点评:本题考查基本不等式,由取得最大值时得到x=2y是关键,考查配方法求最值,属于中档题.11.(2013•北京)设关于x,y的不等式组表示的平面区域内存在点P (x0,y0),满足x0﹣2y0=2,求得m的取值范围是()A.B. C.D.考点:简单线性规划.专题:不等式的解法及应用.分析:先根据约束条件画出可行域.要使可行域存在,必有m<﹣2m+1,要求可行域包含直线y=x﹣1上的点,只要边界点(﹣m,1﹣2m)在直线y=x﹣1的上方,且(﹣m,m)在直线y=x﹣1的下方,从而建立关于m的不等式组,解之可得答案.解答:解:先根据约束条件画出可行域,要使可行域存在,必有m<﹣2m+1,要求可行域包含直线y=x﹣1上的点,只要边界点(﹣m,1﹣2m)在直线y=x﹣1的上方,且(﹣m,m)在直线y=x﹣1的下方,故得不等式组,解之得:m<﹣.故选C.点评:平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.12.(2015春•唐山校级期中)已知x>0,y>0,且+=1,若x+2y>m2+2m恒成立,则实数m的取值范围是()A.(﹣4,2)B.(﹣2,0)C.(﹣4,0)D.(0,2)考点:基本不等式在最值问题中的应用.专题:计算题.分析:先把x+2y转化为(x+2y)(+)展开后利用基本不等式求得其最小值,然后根据x+2y>m2+2m求得m2+2m<8,进而求得m的范围.解答:解:∵+=1,∴x+2y=(x+2y)(+)=4++≥4+2=8,∵x+2y>m2+2m恒成立,∴m2+2m<8,求得﹣4<m<2,故选:A.点评:本题主要考查了基本不等式在最值问题中的应用.考查了学生分析问题和解决问题的能力.二、填空题:本大题共4小题,每小题5分.13.(2015春•唐山校级期中)数列{a n},a n=n2﹣λn,若{a n}为递增数列,则λ的取值范围是(﹣∞,3).考点:数列的函数特性.专题:点列、递归数列与数学归纳法.分析:利用数列的通项公式,结合数列的单调性进行求解即可.解答:解:∵数列{a n}的通项公式为a n=n2﹣λn,对于任意自然数n(n≥1)都是递增数列,∴根据二次函数的性质可得:解得λ<3,故答案为:(﹣∞,3).点评:本题主要考查数列的函数性质的应用,利用数列的单调性是解决本题的关键.14.(2015春•唐山校级期中)已知数列{a n},a n=2a n+1,a1=1,则log2a100= ﹣99 .考点:等比关系的确定.专题:等差数列与等比数列.分析:由a n=2a n+1,得数列{a n}是等比数列,根据等比数列的通项公式进行求解即可.解答:解:∵a n=2a n+1,a1=1,∴=,即数列{a n}是公比q=的等比数列,∴a100=()99=2﹣99,则log2a100=log22﹣99=﹣99,故答案为:﹣99.点评:本题主要考查等比数列的判定以及等比数列的通项公式的求解,比较基础.15.(2012•冀州市校级模拟)在△ABC中,D为BC边上一点,BC=3BD,AD=,∠ADB=135°.若AC=AB,则BD= 2+.考点:余弦定理.专题:计算题;压轴题.分析:先利用余弦定理可分别表示出AB,AC,把已知条件代入整理,根据BC=3BD推断出CD=2BD,进而整理 AC2=CD2+2﹣2CD 得AC2=4BD2+2﹣4BD把AC=AB,代入整理,最后联立方程消去AB求得BD的方程求得BD.解答:用余弦定理求得AB2=BD2+AD2﹣2AD•BDcos135°AC2=CD2+AD2﹣2AD•CDcos45°即 AB2=BD2+2+2BD ①AC2=CD2+2﹣2CD ②又BC=3BD所以 CD=2BD所以由(2)得AC2=4BD2+2﹣4BD(3)因为 AC=AB所以由(3)得 2AB2=4BD2+2﹣4BD (4)(4)﹣2(1)BD2﹣4BD﹣1=0求得 BD=2+故答案为:2+点评:本题主要考查了余弦定理的应用.考查了学生创造性思维能力和基本的推理能力.16.(2013•天津)设a+b=2,b>0,则当a= ﹣2 时,取得最小值.考点:基本不等式.专题:不等式的解法及应用.分析:由于a+b=2,b>0,从而=,(a<2),设f(a)=,(a<2),画出此函数的图象,结合导数研究其单调性,即可得出答案.解答:解:∵a+b=2,b>0,∴=,(a<2)设f(a)=,(a<2),画出此函数的图象,如图所示.利用导数研究其单调性得,当a<0时,f(a)=﹣+,f′(a)==,当a<﹣2时,f′(a)<0,当﹣2<a<0时,f′(a)>0,故函数在(﹣∞,﹣2)上是减函数,在(﹣2,0)上是增函数,∴当a=﹣2时,取得最小值.同样地,当0<a<2时,得到当a=时,取得最小值.综合,则当a=﹣2时,取得最小值.故答案为:﹣2.点评:本题考查导数在最值问题的应用,考查数形结合思想,属于中档题.三、解答题:解答应写文字说明,证明过程或演算步骤.17.(2012•江西)在△ABC中,角A,B,C的对边分别为a,b,c.已知A=,bsin(+C)﹣csin(+B)=a,(1)求证:B﹣C=(2)若a=,求△ABC的面积.考点:解三角形.专题:计算题;证明题.分析:(1)通过正弦定理以及两角和与差的三角函数化简已知表达式,推出B﹣C的正弦函数值,然后说明B﹣C=.(2)利用a=,通过正弦定理求出b,c,然后利用三角形的面积公式求△ABC的面积.解答:解:(1)证明:由bsin(+C)﹣csin()=a,由正弦定理可得sinBsin(+C)﹣sinCsin()=sinA.sinB()﹣sinC()=.整理得sinBcosC﹣cosBsinC=1,即sin(B﹣C)=1,由于0<B,C,从而B﹣C=.(2)解:B+C=π﹣A=,因此B=,C=,由a=,A=,得b==2sin,c==2sin,所以三角形的面积S==cos sin=.点评:本题考查三角形的解法,正弦定理的应用,两角和与差的三角函数的应用,考查计算能力.18.(2012•江阴市模拟)已知A、B、C是△ABC的三个内角,且满足2sinB=sinA+sinC,设B的最大值为B0.(Ⅰ)求B0的大小;(Ⅱ)当时,求cosA﹣cosC的值.考点:余弦定理;余弦函数的单调性;正弦定理.专题:计算题.分析:(Ⅰ)利用正弦定理化简已知的等式得到2b=a+c,表示出b,再利用余弦定理表示出cosB,将表示出的b代入,整理后,利用基本不等式可得出cosB的最小值,根据余弦函数在(0,π)上单调递减,利用特殊角的三角函数值即可求出B的最大值;(Ⅱ)设所求的式子为x,记作①,由B与B0的关系及B0的度数,求出B的度数,代入已知的等式sinA+sinC=2sinB中,得到sinA+sinC的关系式,记作②,由①2+②2化简后,根据B 的度数,求出A+C的度数,代入化简后的式子中,得到关于x的方程,求出方程的解得到x 的值,即为所求式子的值.解答:解:(Ⅰ)由2sinB=sinA+sinC,利用正弦定理化简得:2b=a+c,即,由余弦定理知cosB==(2分)=≥=,(4分)∵y=cosx在(0,π)上单调递减,则B的最大值为B0=;(6分)(Ⅱ)设cosA﹣cosC=x,①(8分)∵B==,∴sinA+sinC=2sinB=,②由①2+②2得,2﹣2cos(A+C)=x2+2.又A+C=π﹣B=,∴x=±,即cosA﹣cosC=±.点评:此题考查了正弦、余弦定理,基本不等式,余弦函数的单调性,诱导公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.19.(2015春•唐山校级期中)解关于x的不等式ax2﹣2x+a<0.考点:一元二次不等式的解法.专题:分类讨论.分析:分a=0、a>0、a<0讨论不等式解集情况,结合不等式对应的方程求出不等式的解集.解答:解:(1)a=0时,有﹣2x<0,∴x>0.(2)a>0时,∵△=4﹣4a2.①当△>0,即0<a<1.方程ax2﹣2x+a=0的两根为,∴不等式的解集为{x|<x<}.②当△=0,即a=1时,有x2﹣2x+1<0,∴x∈∅;③当△<0,即a>1时,方程ax2﹣2x+a=0无实数根,不等式ax2﹣2x+a<0无解,∴x∈∅.(3)当a<0时.①当△>0,即﹣1<a<0时,不等式ax2﹣2x+a<0的解集为{x|x<或x>};②当△=0,即a=﹣1不等式化为(x+1)2>0,∴x≠﹣1;③当△<0时,即a<﹣1时,不等式ax2﹣2x+a<0的解集是R,∴x∈R.综上所述,原不等式的解集为当a≥1时,x∈∅;当a=0时,解集为{x|x>0};当0<a<1时,解集为{x|<x<};当﹣1<a<0时,解集为{x|x<或x>};当a=﹣1时,解集为{x|x≠﹣1};当a<﹣1时,解集为R.点评:本题考查了含有字母系数的一元二次不等式的解法问题,解题时需要分类讨论,是易错题.20.(2014•濮阳二模)设{a n}是等差数列,{b n}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13(Ⅰ)求{a n}、{b n}的通项公式;(Ⅱ)求数列的前n项和S n.考点:等差数列的通项公式;等比数列的通项公式;数列的求和.专题:等差数列与等比数列.分析:(Ⅰ)设{a n}的公差为d,{b n}的公比为q,根据等比数列和等差数列的通项公式,联立方程求得d和q,进而可得{a n}、{b n}的通项公式.(Ⅱ)数列的通项公式由等差和等比数列构成,进而可用错位相减法求得前n项和S n.解答:解:(Ⅰ)设{a n}的公差为d,{b n}的公比为q,则依题意有q>0且解得d=2,q=2.所以a n=1+(n﹣1)d=2n﹣1,b n=q n﹣1=2n﹣1.(Ⅱ),,①S n=,②①﹣②得S n=1+2(++…+)﹣,则===.点评:本题主要考查等差数列的通项公式和用错位相减法求和.21.(2013•沈河区校级模拟)设数列满足:a1=1,.(1)求a2,a3;(2)令,求数列的通项公式.考点:数列递推式.专题:综合题;等差数列与等比数列.分析:(1)利用数列{a n}满足:a1=1,,代入计算,可得a2,a3;(2)证明{b n﹣3}是以2为首项,以为公比的等比数列,即可求数列的通项公式.解答:解:(1)∵数列{a n}满足:a1=1,,∴=,==.(2)∵,∴,代入得化简可得,即2b n+1=b n+3.∴2(b n+1﹣3)=b n﹣3,∴{b n﹣3}是以2为首项,以为公比的等比数列,∴b n﹣3=,∴b n=+3.点评:本题主要考查等比数列的定义和性质,根据递推关系求通项公式,考查学生的计算能力,属于中档题.22.(2015春•唐山校级期中)已知各项均为正数的两个数列{a n}和{b n}满足:a n+1=,b n+1=1+,n∈N*,(1)求证:数列{()2}是等差数列;(2)若a1=b1=1,令()2=,求证:+++…+<2.考点:数列与不等式的综合.专题:等差数列与等比数列.分析:(1)通过对分子分母同除以a n,利用b n+1=,即得=,两边取平方整理即得结论;(2)通过(1)及a1=b1=1,可得c n=,通过放缩、裂项可得当n≥2时<﹣,并项相加即可.解答:证明:(1)∵b n+1=1+=,∴a n+1===,∴=,∴()2﹣()2=()2﹣()2=1,∴数列{()2}是以1为公差的等差数列;(2)∵a1=b1=1,∴=()2=n,∴c n=,∴当n≥2时,=<=﹣,∴+++…+<1+(1﹣)+(﹣)+…+(﹣)=2﹣<2.点评:本题考查等差数列的判断、数列和的取值范围,考查运算求解能力,注意解题方法的积累,属于中档题.。
河北省唐山市数学高一下学期理数期中考试试卷

B .
C .
D .
5. (2分) (2018高三上·大连期末) 平面向量 与 的夹角为 , , ,则 ( ).
A .
B .
C .
D .
6. (2分) 已知函数 其中( ) 则“f(0)=0”是“y=f(x)是奇函数”的( )
A . 充分但不必要条件
B . 必要但不充分条件
C . 充要条件
D . 既非充分也非必要条件
A . 等腰三角形
B . 锐角三角形
C . 直角三角形
D . 钝角三角形
10. (2分) (2017高三上·四川月考) 已知 , ,则 =( )
A .
B .
C .
D .
11. (2分) 在长方体ABCD﹣A1B1C1D1中,下列关于 的表达中错误的一个是( )
A . + +
B . + +
C . + +
参考答案
一、 单选题 (共12题;共24分)
1-1、
2-1、
3-1、ห้องสมุดไป่ตู้
4-1、
5-1、
6-1、
7-1、
8-1、
9-1、
10-1、
11-1、
12-1、
二、 填空题 (共4题;共5分)
13-1、
14-1、
15-1、
16-1、
三、 解答题 (共6题;共60分)
17-1、
17-2、
18-1、
18-2、
19-1、
三、 解答题 (共6题;共60分)
17. (10分) (2016高二上·包头期中) 在四边形ABCD中,已知 ∥ , =(6,1), =(x,y), =(﹣2,﹣3).
最新版河北省唐山一中高一下学期期中考试数学(理)试题Word版含答

最新版河北省唐山一中高一下学期期中考试数学(理)试题Word版含答唐山一中2022~2022学年度第二学期高一年级期中考试理科数学试卷命题人:王筱颖张同江本试卷分第Ⅰ卷(1~2页,选择题)和第Ⅱ卷(3~8页,非选择题)两部分.共150分,考试用时120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本题共12个小题,每题只有一个正确答案,每题5分,共60分。
请把答案涂在答题卡上)1.()BCD2.()A.18B.24C.32D.343()A.锐角三角形B.直角三角形C.钝角三角形D.不确定4.()AB.5CD.以上都不对5.()AB.21C.42D.846.,()ABC7.()A.11B.-11C.13D.-13 8.)ABCD9.()AB.1CD10.在△ABC中,围()ABD11.该不等式恒成立,的范围是()ABCD12.值为()A.2B.3C.4D.5试卷Ⅱ(共90分)二、填空题(本题共4个小题,每题5分,共计20分.请把答案写在答题纸上)13.________.14.________.15.设等比数列a1+a3=10,a2+a4=5,则a1a2…an的最大值为________.16.如图,在中,,分别是上一点,满足________.三、解答题(本题共6个小题,其中第17题10分,其余各题12分共计70分。
请把解答过程写在答题纸上)17.(本题满分10分)(I(II.18.(本题满分12分)A,B,C的对边分别为a,b,c,(I)求角C;(II19.(本题满分12分)某渔船在航行中不幸遇险,发出呼救信号,我海军舰艇在A处获悉后,立即测出该渔船在方位角为45°,距离A为10海里的C处,并测得渔船正沿方位角为105°的方向,以10海里/时的速度向小岛B靠拢,我海军舰艇立即以10海里/时的速度前去营救,求舰艇的航向为北偏东多少度?20.(本题满分12分)(I(II21.(本题满分12分)(I(II22.(A普班、实验班做)(本题满分12分)(III22.(B英才班做)(本题满分12分)(III.唐山一中2022~2022学年度第二学期高一年级期中考试理科数学答案一、DDCBBCACAACB二、131415、64;16三、解答题17、8时取等.9.18、(Ⅰ)由已知及正弦定理得,,即(Ⅱ)由已知,.又,所以.由已知及余弦定理得19、如图所示,设所需时间为t小时,则AB=10t,CB=10t,在△ABC中,根据余弦定理,则有AB2=AC2+BC2-2AC·BC·co120°,可得(10t)2=102+(10t)2-2某10某10tco120°.整理得2t2-t-1=0,解得t=1或t=-2(舍去),所以舰艇需1小时靠近渔船,此时AB=10,BC=10.在△ABC中,由正弦定理得in∠CABBC=in120°AB,∴in∠CAB=ABBC·in120°=2=21.∴∠CAB=30°.所以舰艇航向为北偏东75°.20、(Ⅰ)(Ⅱ)由(1)得原不等式可化为21、(Ⅰ)点在的图象上,,当时,;22、(A普班、实验班),,(Ⅱ)由(Ⅰ)得,所以,则,则(III)由恒成立,即恒成立,又22、(B英才班),,(Ⅱ)由(Ⅰ)得,所以,则,则(III的最小值是。
河北省唐山一中~学年高一数学第二学期期中考试【名校特供】
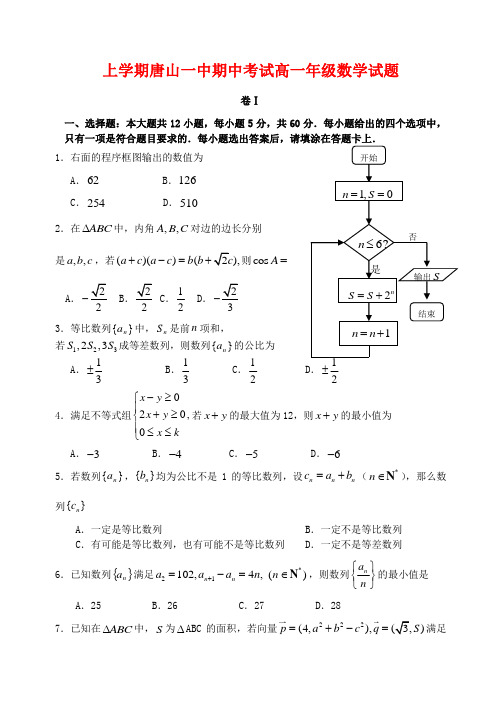
上学期唐山一中期中考试高一年级数学试题卷Ⅰ一、选择题:本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.每小题选出答案后,请填涂在答题卡上. 1.右面的程序框图输出的数值为 A .62 B .126C .254D .5102.在ABC ∆中,内角,,A B C对边的边长分别是,,a b c ,若()()(),a c a c b b +-=+则cos A =A .2-B .2C .12D .3- 3.等比数列}{n a 中,n S 是前n 项和,若123,2,3S S S 成等差数列,则数列}{n a 的公比为 A .13± B .13 C .12 D .2± 4.满足不等式组020,0x y x y x k -≥⎧⎪+≥⎨⎪≤≤⎩若x y +的最大值为12,则x y +的最小值为A .3-B .4-C .5-D .6-5.若数列}{n a ,{}n b 均为公比不是1的等比数列,设n n n c a b =+(*n ∈N ),那么数列{}n cA .一定是等比数列B .一定不是等比数列C .有可能是等比数列,也有可能不是等比数列D .一定不是等差数列6.已知数列{}n a 满足21102,4,n n a a a n +=-=*()n ∈N ,则数列n a n ⎧⎫⎨⎬⎩⎭的最小值是 A .25 B .26 C .27 D .287.已知在ABC ∆中,S 为∆ABC 的面积,若向量222(4,),(3,)p a b c q S =+-=满足//p q ,则C =A .30︒B .45︒C .60︒D .120︒8.设212121,1,1000,x x x x >>=则1213lg lg x x +的最小值为 A .763+.4 C .463 D . 7263- 9.若关于x 的不等式250x a -≤的正整数解有且只有1,2,3,则实数a 的取值范围是A .4580a ≤<B .4580a <<C .80a <D .45a > 10.某流程如图所示, 现输入如下四个函数, 则可以输出的函数是 A .2()f x x = B .1()f x x =C .()ln 26f x x x =+-D .()sin f x x =11.已知数列{}n a 满足*111,(,)()n n a P a a n +=∈N 在直线10x y -+=上,如果函数12111()nf n n a n a n a =++++++ *(,2)n n ∈≥N ,则函数()f n 的最小值为 A .13 B .14 C .712 D .51212.已知M 是ABC ∆内的一点,且23,30,AB AC BAC ⋅=∠=︒若,,MBC MCA MAB ∆∆∆的面积分别为1,,,2x y 则14x y +的最小值为A .20B .19C .16D .18卷Ⅱ二、填空题:本大题共4小题,每小题5分,共20分.答案填在答题纸相 应的空内. 13.等比数列{}n a 中,n S 是前n 项和,且1223+=S a ,1234+=S a ,则 公比=q * * .14.若实数y x ,满足00220y x y x y ≥⎧⎪-≥⎨⎪--≥⎩,则11y u x -=+ 的取值范围是 * *15.若框图所给的程序运行的结果为90S =,那么判断框中应填入的关于k 的判断条件是 * * . 16.给出下列结论:①当2x ≥时,11x x +-的最小值是3;②当02x <≤时,22xx-+存在最大值;③若]1,0(∈m ,则函数mm y 3+=的最小值为 ④当1x >时,1lg 2lg x x+≥. 其中一定成立的结论序号是 * * (把成立的序号都填上).三.解答题:本大题共6小题,共70分.请将解答过程书写在答题纸上,并写出文字说明、证明过程或演算步骤. 17.(本小题满分10分)解关于x 的不等式:2260x ax a +-<.18.(本小题满分12分)如下图,互相垂直的两条公路AP 、AQ 旁有一矩形花园ABCD ,现欲将其扩建成一个更大的三角形花园AMN ,要求点M 在射线AP 上,点N 在射线AQ 上,且直线MN 过点C ,其中36AB =米,20=AD 米. 记三角形花园AMN 的面积为S .(Ⅰ)问:DN 取何值时,S 取得最小值,并求出最小值; (Ⅱ)若S 不超过1764平方米,求DN 长的取值范围. 19.(本小题满分12分)在ABC ∆中,内角,,A B C 对边分别是,,a b c ,若4cos , 2.5B b == (1)当5,3a =求角A 的度数;(2)求ABC ∆面积的最大值。
河北省唐山市开滦第一中学2016-2017学年高一下学期期

开滦一中2016—2017年度第二学期高一年级期中考试 数学试卷(理科) 命题人:说明:1.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
2.本试卷共 150 分,考试时间120 分钟。
注意事项:1.答第Ⅰ卷前,考生务必将自己的考试号、科目填涂在答题卡上。
2.每小题选出答案后,用2B 铅笔把答题卡上对应的题目标号涂黑。
答在试卷上无效。
3.考试结束,监考人员将试卷和机读卡一并收回。
第Ⅰ卷(选择题,共60分)一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知{}n a 是等比数列,21,441==a a ,则公比q =( ) A 、21- B 、2- C 、21 D 、22、在ABC ∆中,已知ab c b a 2222-=+,则C ∠=( )A 、030B 、045C 、0135D 、0150 3、1212+-与的等比中项是( )A 、1B 、1-C 、1±D 、以上选项都不对4、若集合}0107|{2<+-=x x x A ,集合}8221|{<<=x x B ,则=⋂B A ( ) A 、)3,1(- B 、)3,2( C 、)5,2( D 、)5,1(- 5、n S 为等差数列{}n a 的前n 项和,已知18543=++a a a ,求7S =( )A 、35B 、42C 、30D 、1056、在ABC ∆中,角A,B,C 的对边分别是a,b,c,若A:B:C=1: 2:3,则a:b:c=( )A 、2:3:1B 、2:3:4C 、3:4:5D 、1:2:37、已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为( )A 、2B 、5C 、4D 、38、等差数列{}n a 的前m 项和为30,前2m 项和为120,则它的前3m 项和为( )三、解答题(本大题共7小题,共80分,解答应写出文字说明、证明过程或演算步骤) 17、(本题满分10分)求函数y=)0(1<+x xx 的最值;18、(本题满分12分)在等差数列{}n a 中,138a a +=,且4a =12,求数列{}n a 的通项公式及前n 项和.19、(本题满分12分)在ABC ∆中,三个内角A 、B 、C 的对边分别是c b a ,,,已知B cC b a sin cos +=,(1)求B ;(2)若b=22,求ABC ∆面积的最大值。
河北省唐山市开滦一中09-10学年高二下学期期中考试(数学理)

开滦一中2009—2010年度第二学期高二年级期中考试数学(理)试卷第Ⅰ卷说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至6页,满分150分另加附加题15分,考试时间120分钟。
注意事项:1.答题前,考生务必将自己的学校.姓名.考号.班级填写在试卷指定位置。
2.每小题选出答案后,用2B 铅笔把答题卡上对应的题目标号涂黑。
答在试卷上无效。
3.考试结束,监考人员将试卷和机读卡一并收回。
第Ⅰ卷(选择题,共60分)一.选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案填在答题卷的指定的答题栏内)1.若直线a 和直线b 都与直线c 垂直,则a 和b 的位置关系是( )A.平行B.相交C.异面D.以上都有可能2. 某人射击5枪,命中3枪,3枪中恰有2枪连中的概率为 ( )(A )0.6 (B )0.3 (C )0.1 (D )0.053.设a 、b 是两条异面直线,在下列命题中正确的是 ( )A.有且仅有一条直线与a 、b 都垂直,B.有一平面与a 、b 都垂直C.过直线a 有且仅有一个平面与b 平行D.过空间中任一点必可作一条直线与a 、b 都相交4.已知三棱锥P —ABC ,下列条件中:①PA=PB=PC ; ②PA 、PB 、PC 两两垂直; ③PA 、PB 、PC 与底面ABC 所成的角均相等。
④PA ⊥BC ,PB ⊥AC ;能推出点P 在底面ABC 上的射影为△ABC 垂心的是( )A.①②B.②③C.②④D.①④5.在120°的二面角内,放置一个半径为3的球,该球切二面角的两个半平面于A 、B 两点,那么这两个切点在球面上的最短距离为( ) A.3π B.π C. 2π D. 3π 6.棱柱成为直棱柱的一个必要但不充分条件是( )A.棱柱有一条侧棱与底面垂直B.棱柱有一条侧棱与底面的两条边垂直C.棱柱有两个相邻的侧面互相垂直D.棱柱有一个侧面与底面的一条边垂直7.12)1(--n x 展开式中,二项式系数最大的项是( )A .第n -1项B .第n 项C .第n -1项与第n +1项D .第n 项与第n +1项8.七个人坐成一排,现要调换其中3个人中每一个人的位置,其余4个人的位置不变,则不同的调换方式有( )A.37CB.337CC. 37AD. 237C9.已知m ,l 是直线,α、β、γ是平面,给出下列命题①l l ,=γβ ∥α,α⊂m 和m ⊥γ,则α⊥γ且m ∥β②若β⊂l 且l ⊥α,则α⊥β ③若α⊂m ,β⊂l 且α∥β,则m ∥l④若α∥β,α⊂m ,则m ∥β 其中正确命题的序号( )A.②③B.①②C.②④D.①④10.如图,正方形ABCD 边长为4,E 是AB 的中点,F 是BC边上的一个动点,将△ADE 和△DCF 分别沿DE 、DF 折起,使A 、C 重合于A ′,则A ′点到平面DEF 的距离的最大值为( ) A.455 B.554 C. 22 D. 32 11.正三棱锥P-ABC 的侧棱长为a ,各侧面三角形的顶角为30°,M 、N 为棱PB 、PC 上的动点,则△AMN 周长的最小值为( )A.a )213(+B.a )212(+C.a 223D.a 212.将一个四棱锥的每个顶点染上一种颜色,并使一条棱的两端异色,若只有4种颜色可供使用,则不同的染色方法种数为( )种A.24B.48C. 60D. 72二.填空题(本大题共4小题,每小题5分,共20分)13. 若41313--+=n n n C C C , 则n 的值为 .14. 5)21(x +的展开式中2x 项的系数..是 .(用数字作答) 15.三棱锥A -BCD 三个侧面两两垂直,底面BCD 上一点P 到三个侧面的距离分别为2,3,6,则P 点到三棱锥顶点A 的距离为 。
河北省唐山一中高一数学下学期期中试题理

唐山一中2015—2016学年度第二学期期中考试高一年级(理科) 数学试卷说明:1.考试时间120分钟,满分150分。
2.将卷Ⅰ答案用2B 铅笔涂在答题卡上,将卷Ⅱ答案答在答题纸上。
3.Ⅱ卷答题纸卷头和答题卡均填涂本次考试的考号,不要误填学号,答题卡占后5位。
卷Ⅰ(选择题 共60分)一.选择题(共12小题,每小题5分,计60分。
在每小题给出的四个选项中,只有一个选项符合题意)1.已知c b a 、、满足0<<<ac a b c 且,则下列选项中不一定能成立的是( )A. a b a c <B. 0>-c a bC.c a c b 22<D. 0<-acca2.集合{},02,0322⎭⎬⎫⎩⎨⎧≥-=>++-=x x xB x x x A 则=B A ( )A.{}31<<-x xB.{}2x 0≥<或x x C.{}01<<-x x D. {}3201<≤<<-x x x 或3.在△ABC 中,a=2,b=2,∠A=4π,则∠B=( ) A .30° B .30°或150° C .60° D .60°或120°4. 在△ABC 中,a 、b 、c 分别是角A 、B 、C 所对的边,若B A b A B a cos sin cos sin 22=,则△ABC 的形状为( )A .等腰直角三角形B .直角三角形C .等边三角形D .等腰三角形或直角三角形 5. 若实数x ,y 满足⎩⎪⎨⎪⎧x ≤2,y ≤2,x +y ≥1,则S =2x +y -1的最大值为( ).A .5B .4C .3D .26.等差数列{}n a 中,3485,+=22a a a =,则{}n a 的前8项和为( ) A.32 B.64 C.108 D. 1287. 在1和16之间插入3个数,使它们与这两个数依次构成等比数列,则这3个数的积等于( )A .128B .± 128C . 64D .±648.一个等比数列}{n a 的前n 项和为48,前2n 项和为60,则前3n 项和为( )A 、63B 、108C 、75D 、83 9. 执行如边的程序框图,则输出的n =( )A.6B.5C.8D.710.已知等比数列{}n a 满足0,1,2,n a n >=,且25252(3)n n a a n -⋅=≥,则当1n ≥时,2123lo g lo g l ogn a a a -+++=( ) A. (21)n n - B. 2(1)n + C. 2n D. 2(1)n - 11. 若数列{a n }是等差数列,首项a 1>0,020162015<⋅a a , 020162015>+a a ,使前n 项和S n >0成立最大自然数n 是( ) A .4 029 B .4 030C .4 031D .4 03212.设),,1(,+∞∈∈b a R n m 、、 若1424,2016=+==b a b a n m ,则nm 11+的最大值是( )A .21 B .23C .1D .2卷Ⅱ(非选择题 共90分)二.填空题(共4小题,每小题5分,计20分。
河北省唐山市开滦二中高一数学下学期期中试题新人教A版

说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1页至第2页,第Ⅱ卷第3页至第6页。
考试时间为120分钟,满分为150分。
第Ⅰ卷(选择题,共60分)一、选择题:(在每小题给出的四个选项中,只有一项是符合题目要求的. 本大题共12小题,每小题5分,共60分.)1.在△ABC 中,若030,6,90===B a C ,则b c -等于( ) A .1 B .1- C .32 D .32- 2. 若A 为△ABC 的内角,则下列函数中一定取正值的是( ) A. A sin B. A cos C. A tan D.Atan 13. 若a 、b 、c 成等差数列,b 、c 、d 成等比数列,111,,c d e成等差数列,则a 、c 、e 成( )A .等差数列B .等比数列C .既成等差数列又成等比数列D .以上答案都不是 4.已知1>x ,则函数11)(-+=x x x f 的最小值为 ( ) A .1 B .2 C .3 D .4 5.在△ABC 中,若)())((c b b c a c a +=-+,则∠A =( ) A .090 B .060 C .0120 D .01506.若a 、b 、c 为实数,则下列命题正确的是 ( )A .若a >b ,则ac 2>bc 2B .若a <b <0,则a 2>ab >b2C .若a <b <0,则1a <1bD .若a <b <0,则b a >ab7.设集合y x y x y x A --=1,,|),{(是三角形的三边长},则A 所表示的平面区域(不含边界的阴影部分)是()A .B .C .D .8.目标函数y x z +=2,变量y x ,满足43035251x y x y x -+<⎧⎪+≤⎨⎪≥⎩,则有( )A .3,12min max ==z zB .,12max =z z 无最小值C .z z ,3min =无最大值D .z 既无最大值,也无最小值9.在△ABC 中,角A 、B 、C 所对的边分别是a 、b 、c ,并且a =7,b =14,A =30°,则△ABC 有 ( ) A .一解 B .二解 C .无解 D .一解或二解 10. 数列 ,1614,813,412,211前n 项的和为 ( ) A .2212n n n ++ B .12212+++-nn n C .2212n n n ++- D . 22121nn n -+-+11. 在等差数列{}n a 中,若4,184==S S ,则20191817a a a a +++的值为( ) A .9 B .12C .16D .1712.等差数列{}n a ,{}n b 的前n 项和分别为n S ,n T ,若231n n S nT n =+,则n n a b =( )A .23 B .2131n n -- C .2131n n ++ D .2134n n -+开滦二中2010-2011学年第二学期高一年级期中考试第Ⅱ卷(非选择题共90分)二、填空题:(本题共4小题,每小题5分,共20分。
高一数学下学期期中试题答案 河北省滦南一中高一数学下学期期中试题PDF

卜人入州八九几市潮王学校参考答案1.B解析:6d=a7-a1=3,d=,a11=a1+10d=4,应选B.2.B解析:∵a∥b,∴(-1,2)=λ(,y),-1=λ,2=λy,∴y=3,(a•b)(a+2b)=-(2,-4)=(-15,30),应选B.3.C解析:sin B=,由正弦定理=解得b=5,应选C.4.B解析:由a2-2a•b+b2=7,|a|2+|a|-6=0,|a|=2,应选B.5.A解析:设公差为d,∴a n=23+(n-1)d,有a7<0,a6≥0解得-≤d<,∴d=-4,应选A.6.C解析:由a2-b2=c2-bc,bc=b2+c2-a2,cos A==,∠A=60°.选C.7.C解析:•=||•||cos(π-B)=-||cos B•||=-||2=-8,||=4,选C.8.D解析:设公差为d,∴(3+3d)2=8+28d,9d2-10d+1=0,d=1或者,应选D.9.D解析:由b2=2ac,2b2=a2+3c2,∴a2-4ac+3c2=0,a=3c或者a=c(舍),那么b=c,cos B==,应选D.10.C解析:设||=x,•=(+)(+)=(+)(-)=x2-()2=(x-1)2,解得x=5或者1,应选C.11.A解析:当q=1时,S n=na1,S-S n S n+2=(n+1)2a-n(n+2)a>0;当q≠1时,S-S n S n+2=()2[(1-q n+1)2-(1-q n)(1-q n+2)]=()2[q n+q n+2-2q n+1]=q n()2(1-q)2=aq n>0,应选A.12.A由余弦定理的正弦形式值sin2A=sin2B+sin2C-2sin B sin C cos A,令B=20°,C=40°,那么A=120°,sin2B+sin2C -2sin B sin C cos A=sin220°+sin240°+sin20°sin40°=sin2120°=,应选A.13.3解析:2a-3b=(2k,6)-(3,12)=(2k-3,-6),c•(2a-3b)=4k-6-6=0,k=3.14.-1或者3解析:两式相减2a5+2a4=a6-a4,∴q2-2q-3=0,q=-1或者3.15.30°解析:由b cos C+c cos B=b×+c×=a=c,由正弦定理sin A=sin C.sin C=<sin A,C<A,C=30°.16.-2解析:∵∠ABC=30°,BD=2AD=2DC,∴=+,=-,x-y=-2.17.解:(1)设公差为d,S4=4a1+6d=2+6d=8,d=1,∴a n=a1+(n-1)d=(2n-1),S n==n2.……5分(2)b n=4=22n-1,∴{b n}为等比数列,q=4,b1=2,∴T n==(4n-1).…10分18.解:(1)由a•b=0,∴x(x-2)+y=0,y=-x2+2x=-(x-1)2+1≤1,∴y≤,y的最大值为.……6分(2)由|a|=2|b|得:x2+y2=2(x-2)2+4,∴y2=x2-8x+12=(x-2)(x-6)≥0,解得x≤2或者x≥6.……12分19.解:(1)由正弦定理知(1+)sin C=2sin B,………………3分即(1+)sin C=2sin(-C),展开整理得sin C=cos C,C=…………6分(2)·=ab cos C=ab=1+,ab=+,由(1)知B=π,sin B=,由正弦定理得=,解得a=,b=1+.由正弦定理得c=2.…………12分20.解:(1)|3a-b|2=9a2-6a•b+b2=9-6|a|•|b|cos60°+4=7,|3a-b|=.|2a-b|2=4a2-4a•b+b2=4-4|a|•|b|cos60°+4=4,|2a-b|=2.……6分(2)∵(3a-b)(2a-b)=6a2-5a•b+b2=5,cosθ===.…12分21.解:(1)由正弦定理得sin A sin B+sin A cos C cos A=sin C sin2A,即sin B=-cos C cos A+sin C sin A=-cos(A+C)=cos B,tan B=,∴sin B=,cos B=.(2)由面积公式得S△ABC=ac sin B=×c2×=,那么c=2,a=2,由余弦定理得b2=a2+c2-2ac cos B=60+4-2×2×2×=34,b=.22.解:(1)由=即=+1,那么{}是等差数列,=+(n-1)=n.a n=n.…………5分(2)S n=2+22+23+…+2n=2n+1-2,nS n=n·2n+1-2n.T n=(1·22+2·23+…+n·2n+1)-2(1+2+…+n),设M=1·22+2·23+…+n·2n+1,2M=1·23+2·24+…+n·2n+2,-M=22+23+…+2n+1-n·2n+2=2n+2-4-n·2n+2,M=(n-1)·2n+2+4.T n =(n-1)·2n+2+4-n(n+1)………12分。
【推荐】河北省唐山一中 高一下册第二学期期中考试数学(理)试题word版有答案

唐山一中2017~2018学年度第二学期高一年级期中考试理科数学试卷本试卷分第Ⅰ卷(1~2页,选择题)和第Ⅱ卷(3~8页,非选择题)两部分.共150分,考试用时120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本题共12个小题,每题只有一个正确答案,每题5分,共60分。
请把答案涂在答题卡上)1. 如果,那么下列不等式成立的是 ( )A. B. C. D.2.在等比数列中,,则 ( )A.18 B.24 C.32 D.343.若的三个内角满足,则的形状是 ( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定4.在数列中,,则的值为 ( )A. B.5 C. D.以上都不对5.数列为等差数列,满足,则数列的前项的和等于( )A. B.21 C.42 D.846.已知数列为递增等比数列,其前项和为.若,,则( )A. B. C. D.7.若满足不等式,则的最大值为 ( )A.11 B.-11 C.13 D.-138.在等比数列中,若,则( )A. B. C. D.9.若实数满足约束条件,则的最大值为 ( )A. B.1 C. D.10.在△ABC中,两直角边和斜边分别为且满足条件,试确定实数的取值范围( )A. B. C. D.11.已知不等式,若对任意及,该不等式恒成立,则实数的范围是( )A. B. C. D.12.设是数列的前项和,且,则使取得最大值时的值为( )A.2 B.3 C.4 D.5试卷Ⅱ(共 90 分)二、填空题(本题共4个小题,每题5分,共计20分.请把答案写在答题纸上)13.不等式的解集为________.14.若集合,则实数的取值范围是________.15.设等比数列满足a1+a3=10,a2+a4=5,则a1a2 …an的最大值为________.16.如图,在中,,分别是上一点,满足,.若,则的面积为________.三、解答题(本题共6个小题,其中第17题10分,其余各题12分共计70分。
河北省唐山一中高一数学下学期期中试题卷 理

唐山一中2013-2014学年度第二学期期中考试高一年级数学试卷 (理科)说明:1.考试时间120分钟,满分150分。
2.将卷Ⅰ答案用2B 铅笔涂在答题卡上,卷Ⅱ用蓝黑钢笔或圆珠笔答在答题纸上。
卷Ⅰ(选择题 共60分) 一.选择题: (本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.ABC ∆的内角A 、B 、C 所对的边分别为a ,b ,c .若B =2A ,a =1, b =2,则这样的三角形有 ( ) A .只有一个 B .有两个 C .不存在 D .无数个2. 不等式(5)(6)6x x x -->-的解集是( )A .(5,)+∞B .(6,)+∞C .φD .(,5)(6,)-∞+∞3.若某程序框图如图所示,则输出的p 的值是 ( )A .30B .28C . 21D .554. .设等比数列{}n a 的前n 项和为n S ,且510S =,1030S =,则15S =( )A .60B .70C .90D .405.设=(1,1),=(3,1),O 为坐标原点,动点P(x,y)满足0≤·≤1,0≤·≤1,则2z x y =--的最大值是 ( )A . 0B .1C .12 D .12- 6.在正项等比数列{}n a 中,已知3512a a ⋅=,则71a a +的最小值为 ( )A.B. C. D.7. ABC ∆的内角A 、B 、C 所对的边分别为a ,b ,c ,若三边的长为连续的三个正整数,且A >B >C ,9b =10a cos C ,则sin A ∶sin B ∶sin C 为 ( )A .4∶3∶2B .5∶6∶7C .5∶4∶3D .6∶5∶48. 等差数列{}n a ,{}n b 的前n 项和分别为n S ,n T ,若n n S T =2431n n ++,则n a =n b 时n =( ) A .无解 B .6 C .2 D .无数多个9. 已知0a >,,x y 满足约束条件13(3)x x y y a x ≥⎧⎪+≤⎨⎪≥-⎩,若2z x y =+的最小值为0,则a =( )A .14B .1C .12D .2 10. 若数列{n a }的前n 项和2390n S n n =+-,则456123a a a a a a ++++ 的值为 ( )A .18B .2-C .2D .12-11.已知ABC ∆的三条边的边长分别为4米、5米、6米,将三边都截掉x 米后,剩余的部分组成一个钝角三角形,则x 的取值范围是 ( ) A .0<x <5 B . 1<x <5 C . 1<x <3 D .1<x <412. 下列各函数中,最小值为2的是( ).A .y =x +1xB .y =sin x +1sin x ,x ∈⎝⎛⎭⎪⎫0,π2C .y =x 2+3x 2+2D .y卷Ⅱ(非选择题 共90分)二.填空: 本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
河北省唐山市2022高一数学下学期期中试题

河北省唐山市2022-2022学年高一数学下学期期中试题一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.在△ABC 中,若a = 2 ,23b =,030A = , 则B 等于 ( ) A .60 B .60或 120 C .30 D .30或1502已知a b c d ,,,成等比数列,且曲线223y x x =-+的顶点是()b c ,,则ad 等于( )A.3 B.2 C.1 D.2-3△ABC 中,根据下列条件,确定△ABC 有两解的是=18,b=20,A=120° =60,c=48,B=60°=3,b=6,A=30° =14,b=16,A=45°4、若实数a 、b 满足2a b +=,则33a b +的最小值是 ( )A .18B .6C . 23D . 243 5 等差数列{a n }中,a 1=-5,它的前11项的平均值是5,若从中抽取1项,余下10项的平均值是4,则抽取的是 ( )A .a 8B .a 9C .a 10D .a 116在△ABC 中,ainB-inCbinC-inAcinA-inB 的值是A21.0 C D π 7已知 ( ) A B C 222≥+b a D 322≤+b a 8.已知两个等差数列{a n }和{b n }的前n 项和分别为A n 和B n ,且3457++=n n B A n n ,则使得n n b a 为整数的正整数n 的个数是( ).3 C9、点,x y 24,1,22,x y x y x y +≥⎧⎪-≥⎨⎪-≤⎩z x y =+1230a a a >>>2(1)1i a x -<(1,2,3)i =x 11a 12a 31a 32a c b a ,,21-=⋅b a ),(R y x y x ∈+=b a c 2221x y a b-=22214x a x ax ->++∈x ,13221=+a a 433a a ==+n n a S 2∈=+,n p p a a nn 为正常数(221223a b bc -=sin 23sin C B =b x a a x x f +-+-=)6(3)(20)(>x f a b {}{}2|60,|04,A x x x B x x a =-->=<+<A B =∅a ie ,并以20 nmie/h 的速度沿南偏西15°方向行驶,若甲舰以28 nmie/h 的速度行驶,应沿什么方向,用多少时间,能尽快追上乙舰21≥ab 21≤ab 则且,2,0,0=+≥≥b a b a20 (12分.已知数列的前项和为,点(,)()n n S n N *∈在函数()1322+-=x x x f 的图象上,(1)求数列的通项公式;⑵ 求数列{}n a 的前多少项和最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
开滦一中2009—2010年度第二学期高一年级期中考试
(数学)试卷
说明:
1.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
2.本试卷共150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
1.下列命题中,命题正确的是………………………………………………( )
A .终边相同的角一定相等
B .第一象限的角是锐角
C .若α-β=2k π(k ∈Z),则角α的三角函数值等于角β的同名三角函数值
D .半径为R ,α°的圆心角所对的弧长为R α°. 2.(2sin 30,2cos30),sin αα︒-︒如果角的终边过点则的值等于………( )
3.已知函数()sin ,()tan()2
x f x g x x π
π+==-,则 ( )
A .()f x 与()g x 都是奇函数
B .()f x 与()g x 都是偶函数
C .()f x 是奇函数,()g x 是偶函数
D .()f x 是偶函数,()g x 是奇函数
4.如图所示,D 是△ABC 的边AB 上的中点,则向量=CD ( ).
A .
BA BC 21+
- B .BA BC 21--
C .
BA BC 21-
D .BA BC 21+
5. 将函数sin()3
y x π
=-的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)
,再将所得图像向左平移
3π
个单位,则所得函数图像对应的解析式为( ) A .1sin()26y x π=- B .1sin()23y x π
=-
C .1sin 2y x =
D .sin(2)6
y x π
=-
6. 已知
αα
αα
αtan ,5cos 5sin 3cos 2sin 那么-=+-的值为 ( )
A .-2
B .2
C .16
23
D .-16
23
11. .- .-22A B C
D
7. 函数)2
5
2sin(π+
=x y 的图象的一条对称轴方程为( ) A . 4
π
-
=x B . 2
π
-
=x C .8
π
=
x D .π4
5
=
x 8.函数)sin(ϕω+=x A y 在一个周期内的图象如下,此函数的解析式为 ( ) A .)322sin(2π+=x y B .)3
2sin(2π+=x y C .)3
2sin(
2π-=x y
D .)3
2sin(2π
-
=x y
9.函数sin()4
y x π
=-
的一个单调增区间是 ( )
A .ππ⎛⎫
- ⎪44⎝⎭
, B .3ππ⎛⎫ ⎪44⎝⎭
, C .3π⎛⎫π ⎪2⎝
⎭
,
D .32π⎛⎫
π
⎪2⎝⎭
, 10.函数()f x 是周期为π的偶函数,且当0,2x π⎡⎫∈⎪
⎢⎣⎭
时,1tan 3)(-=x x f ,则8()3f π的值是( ).
A .4-
B .2-
C .0
D .2 11.已知4
π
βα=
+,则)tan 1)(tan 1(βα++的值是( )
A .-1
B .1
C .2
D .4
12.△ABC 中,090C ∠=,则函数2
sin 2sin y A B =+的值的情况( )
A .有最大值,无最小值
B .无最大值,有最小
C .有最大值且有最小值
D .无最大值且无最小值
第Ⅱ卷(非选择题,共90分)
13. 已知cos α=
35,且α∈3,22ππ⎛⎫
⎪⎝⎭
,则cos(3πα- )=____. 14. 在平行四边形ABCD 中,,,3A B a A D b A N N C ===,M 为BC 的中点,则
MN =_______.(用a b 、表示)
15、设
)c os ()s in()(21απαπ+++=x n x m x f ,其中
m 、n 、1α、2α都是非零
实数,若,
1)2004(=f =)2005(f ____.
16.关于函数))(3
2(4)(R x x Sin x f ∈+
=π
有下列命题:
①由0)()(21==x f x f 可得21x x -必是π的整数倍 ②由)(x f y =的表达式可改写为)6
2cos(4π
-=x y
③)(x f y =的图像关于点)0, 6
(π-
对称
④)(x f y =的图象关于直线6
π
-
=x 对称
其中正确命题的序号是____________________。
17:(10分)化简求值:(1)化简:23cos()sin (3)
tan()cos ()
θπθππθπθ+++--
(2)求值:
O
O
O O 170
cos 110cos 10cos 10sin 212
---
18:(12分)已知cos α=17,cos (α-β)=1314,且0<β<<π
2. (1)求tan2α的值; (2)求角β的值.
19.(12分) (本小题12分)已知函数3)sin(3)(++=π
x x f
20. (12分)已知函数2
()5sin cos f x x x x =-(其中x ∈R )
,求: (1)函数()f x 的最小正周期; (2)函数()f x 的单调区间;
21.(12分) 已知函数()sin(sin()cos 66f x x x x a π
π=++-++) ,02x π⎡⎤
∈-⎢⎥⎣⎦
的最大值为0
(1)求常数a 的值
(2)求使()2f x ≥-成立的x 的取值集合
22:(12分)在ABC ∆中,tan 2sin 2
A B
C += (1) 求∠C 的大小
(2) 求sin sin sin y A B C =++的取值范围
附加题:(5分)
[]
cos 0,0,x x a x π+-=∈有两个解,则a 的范围____________
数学答案
选择题:CCDAA DBABD CD
填空: 13 . 310- 14. 1
()2
b a - 15.1- 16. ②③ 解答题: 17:
18: 解:(1)由cos α=17,0<α<π
2,得sin α=437.所以tan α=
sin α
cos α
=4 3 tan2α=2tan α1-tan 2α
=-83
47. (2)由0<β<α<π2得0<α-β<π
2,又cos (α-β)=1314,所以sin (α-β)=3314.cos β=cos [α-(α-β)]=cos αcos (α-β)+sin αsin (α-β)=17×1314+437×3314=12,所以β=π
3.
②由)6
s in (
π
+=x y 的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得
)6
2sin(π
+=x y 的图象;
③由)6
2sin(
π
+=x y 的图象上各点的纵坐标伸长为原来的3倍(横坐标不变)
,得。
